Chemical Kinetics

The branch of physical chemistry which deals with rate of reaction, mechanism of reaction and the influence of concentration, temperature, pressure, catalyst etc., on the reaction rate is called the chemical kinetics.  On the basis of rates, the chemical reactions are broadly divided into three categories.
i) Very fast reactions,

ii) Very slow reactions and

iii) Moderately slow reactions

Rate of chemical reaction:
Rate of chemical reaction is defined as the change in concentration of any of the reactants or products per unit time.  In other words, rate may also be defined as the rate of decrease in concentration of any one of the reactant or increase in concentration of any one of the product or the rate of a reaction is generally defined as the change in molar concentration of a species (reactant or product) per unit time.

Rate of reactions having same stoichiometric coefficient of all the reactants and products:
For a hypothetical reaction
            A + B → C + D

$$\begin{gathered} \mathrm{Average} \mathrm{rate} =-\frac{-\mathrm{\Delta }\left[\mathrm{A}\right]}{\mathrm{\Delta t}}=-\frac{\mathrm{\Delta }\left[\mathrm{B}\right]}{\mathrm{\Delta t}}=+\frac{\mathrm{\Delta }\left[\mathrm{C}\right]}{\mathrm{\Delta t}}=\frac{+\mathrm{\Delta }\left[\mathrm{D}\right]}{\mathrm{\Delta t}} \\ \mathrm{Rate} \mathrm{of} \mathrm{disappearance} \mathrm{of} \mathrm{A}=-\frac{[\mathrm{A}{]}_{\text{final}}-[\mathrm{A}{]}_{\text{linitial}}}{\text{time}}=-\frac{\mathrm{\Delta }\left[\mathrm{A}\right]}{\mathrm{\Delta t}} \\ \mathrm{Rate} \mathrm{of} \mathrm{appearance} \mathrm{of} \mathrm{C}=+\frac{\mathrm{\Delta C}}{\mathrm{\Delta t}} \end{gathered}$$

The negative sign along with the change in concentration of the reactants indicates that the concentration of the reactant decreases with time, while positive sign along with concentration of product indicates that concentration of product increases with time.

Rate of reactions having different stoichiometric coefficients of the reactant and products:
For the decomposition of N₂O_{5
$2{\mathrm{N}}_2{\mathrm{O}}_5\left(\mathrm{g}\right)\to {4\mathrm{NO}}_2\left(\mathrm{g}\right)+{\mathrm{O}}_2\left(\mathrm{g}\right)$}

$\begin{array}{rl}& \text{The rate of disappearance of }{\mathrm{N}}_2{\mathrm{O}}_5=-\frac{\mathrm{\Delta }\left[{\mathrm{N}}_2{\mathrm{O}}_5\right]}{\mathrm{\Delta t}}\\ & \text{Rate of appearance of }{\mathrm{NO}}_2=+\frac{\mathrm{\Delta }\left[{\mathrm{NO}}_2\right]}{\mathrm{\Delta t}}\\ & \text{Rate of appearance of }{\mathrm{O}}_2=+\frac{\mathrm{\Delta }\left[{\mathrm{O}}_2\right]}{\mathrm{\Delta t}}\end{array}$

During the period in which one mole of O₂ is formed, four moles of NO₂ are formed and two moles of N₂O₅ disappear.  Hence the rate of appearance of NO₂ is four times the rate of appearance of O₂.  Thus to get a unique value of reaction rate, irrespective of the species selected, the rate of change of concentration is divided by stoichiometric coefficient of reactant or product involved in the reaction.  Thus,

$$\begin{gathered} \mathrm{Rate} \mathrm{of} \mathrm{reaction} =-\frac{1}{2}\frac{\mathrm{\Delta }\left[{\mathrm{N}}_2{\mathrm{O}}_5\right]}{\mathrm{\Delta t}}=+\frac{1}{4}\frac{\mathrm{\Delta }\left[{\mathrm{NO}}_2\right]}{\mathrm{\Delta t}}=+\frac{\mathrm{\Delta }\left[{\mathrm{O}}_2\right]}{\mathrm{\Delta t}} \\ \mathrm{Similarly} \mathrm{for} \mathrm{a} \mathrm{hypothetical} \mathrm{reaction} \\ \begin{array}{rl}\mathrm{aA}+\mathrm{bB}& ⟶\mathrm{CC}+\mathrm{dD}\\ & \\ \text{Rate of reaction }& =-\frac{1}{\mathrm{a}}\frac{\mathrm{\Delta }\left[\mathrm{A}\right]}{\mathrm{\Delta t}}=-\frac{1}{\mathrm{b}}\frac{\mathrm{\Delta }\left[\mathrm{B}\right]}{\mathrm{\Delta t}}=+\frac{1}{\mathrm{c}}\frac{\mathrm{\Delta }\left[\mathrm{C}\right]}{\mathrm{\Delta t}}=+\frac{1}{\mathrm{d}}\frac{\mathrm{\Delta }\left[\mathrm{D}\right]}{\mathrm{\Delta t}}\\ & \end{array} \\ \mathrm{Similarly} \mathrm{for} \mathrm{the} \mathrm{reaction} \\ 4{\mathrm{NH}}_3\left(\mathrm{g}\right)+5{\mathrm{O}}_2\left(\mathrm{g}\right)⟶4\mathrm{NO}\left(\mathrm{g}\right)+6{\mathrm{H}}_2\mathrm{O}\left(\mathrm{g}\right) \\ \mathrm{Rate} \mathrm{of} \mathrm{reaction} = -\frac{1}{4}\frac{\mathrm{\Delta }\left[{\mathrm{NH}}_3\right]}{\mathrm{\Delta t}}=-\frac{1}{5}\frac{\mathrm{\Delta }\left[{\mathrm{O}}_2\right]}{\mathrm{\Delta t}}=+\frac{1}{4}\frac{\mathrm{\Delta }\left[\mathrm{NO}\right]}{\mathrm{\Delta t}}=+\frac{1}{6}\frac{\mathrm{\Delta }\left[{\mathrm{H}}_2\mathrm{O}\right]}{\mathrm{\Delta t}} \end{gathered}$$

Units of rate of reaction:
As concentration of substance is expressed in mol L^–1 and time is measured in seconds or minutes or hours.  The
units for rate of reaction are moles litre^–1 sec^–1 or moles litre^–1 min^–1.
For gaseous reactants, concentrations are expressed in terms of partial pressure; therefore, the units of rate of reaction will be atm min^–1 or atm sec^–1 or atm hr^–1.

Illustration 1: Express the relation between the rates measured with respect to the disappearance of N₂, H₂ and the formation of NH₃ for  ${\mathrm{N}}_{2\left(g\right)}+3{\mathrm{H}}_{2\left(g\right)}⟶2{\mathrm{NH}}_{3\left(g\right)}$

Solution: $-\frac{\mathrm{d}\left[{\mathrm{N}}_2\right]}{\mathrm{dt}}=-\frac{1}{3}\frac{\mathrm{d}\left[{\mathrm{H}}_2\right]}{\mathrm{dt}}=+\frac{1}{2}\frac{\mathrm{d}\left[{\mathrm{NH}}_3\right]}{\mathrm{dt}}$  

Illustration 2: For the reaction 2NH₃ → N₂ + 3H₂ being carried out in a closed vessel if $-\frac{1}{2}\frac{\mathrm{\Delta }\left[{\mathrm{NH}}_3\right]}{\mathrm{\Delta t}}$ is 0.05 mol L^–1 S^–1.  Calculate the rate of appearance of N₂ and H₂.

Solution:$\begin{array}{rl}\text{Rate of reaction = }& -\frac{1}{2}\frac{\mathrm{\Delta }\left[N{H}_3\right]}{\mathrm{\Delta }t}=\frac{\mathrm{\Delta }\left[N_2\right]}{\mathrm{\Delta }t}=\frac{\mathrm{\Delta }\left[H_2\right]}{3\mathrm{\Delta }t}\\ & \text{Rate of appearance of nitrogen }\frac{\mathrm{\Delta }\left[{\mathrm{N}}_2\right]}{\mathrm{\Delta t}}=-\frac{1}{2}\frac{\mathrm{\Delta }\left[{\mathrm{NH}}_3\right]}{\mathrm{\Delta t}}=-.050{\mathrm{molL}}^{-1}{\mathrm{S}}^{-1}\\ & \text{Rate of appearance of hydrogen }\frac{\mathrm{\Delta }\left[{\mathrm{H}}_2\right]}{\mathrm{\Delta t}}=\frac{3}{2}\frac{\mathrm{\Delta }\left[{\mathrm{NH}}_3\right]}{\mathrm{\Delta t}}=3\times 0.050{\mathrm{mol}}^{-1}{\mathrm{S}}^{-1}=0.150 {\text{molL}}^{–}{\text{S}}^{-1}\\ & \text{moll}-{15}^{-1}\end{array}$

Illustration 3: A gaseous reaction X₂(g) → Y(g) + $\frac{1}{2}$Z(g) shows increase in pressure from 100 mm to 120 mm in 5 minutes.  Calculate the rate of disappearance of X₂.
Solution: In this reaction, 1 mol of X₂ gives 1 mol of Y and ½ moles of Z.  Thus, the increase of pressure refers to the increase in concentration of Z.
Thus, rate of appearance of Z =$\frac{\text{Rate of disappearance of }{X}_2}{2}$

$\therefore$ Rate of disappearance of X₂ = 2 × rate of appearance of Z.
= 2 × 4 = 8 mm min^–1.

Illustration 4: For the reaction 2A + B + C → A₂B + C; the rate law has been determined to be rate = k[A][B]² with k = 2.0 × 10^–6 mol^–2L²s^–1.
For this reaction determine the initial rate of the reaction with [A] = 0.2 mol L^–1;
[B] = 0.1 mol L^–1; C = 0.5 mol L^–1.  Determine the rate after 0.04 mol L^–1 of A has reacted.

Solution: Initial rate of reaction = k[A] [B]² = 2 × 10^–6 [0.2] [0.1]² = 4 × 10^–9 mol L^–1 sec^–1.
Concentration of A after 0.04 mol L^–1 of A has reacted = (0.2 – 0.04) = 0.16 mol L^–1.
According to rate law expression 1 mol of A combines with 2 moles of B,
0.04 moles of A will combine with 0.08 moles of B. 
Hence, remaining concentration of B = [0.1 – 0.08] = 0.02 mol L^–1.
$\therefore$ Rate of reaction = k[A] [B]² = 2×10^–6 × [0.16] [0.02]² = 1.28 × 10^–10 mol L^–1 s^–1.

Average rate and instantaneous rate:
Average rate:  It is the rate of change of concentration of a reactant or a product over measurable long time interval.
For a hypothetical reaction A → B
Average rate of reaction =$\frac{\text{change in concentration of one of the reactant or product}}{\text{time taken}}=\frac{-\mathrm{\Delta }\left[\mathrm{A}\right]}{\mathrm{\Delta t}}=+\frac{\mathrm{\Delta }\left[\mathrm{B}\right]}{\mathrm{\Delta t}}$

Instantaneous rate: 
The rate of change of concentration of any one of the reactants or products over a very small interval of time.
Mathematically, instantaneous rate may be expressed by the expression $\frac{\mathrm{dx}}{\mathrm{dt}}$ instead of $\frac{∆\mathrm{x}}{\mathrm{\Delta t}}$ .  Here dx is the change in concentration of any of the species in time interval dt.  In other words when Δt becomes very small and approaches zero, the ratio $\frac{\mathrm{\Delta }\left[\mathrm{x}\right]}{\mathrm{\Delta t}}$ may be replaced by the derivative $\frac{\mathrm{dx}}{\mathrm{dt}}$. 
That is instantaneous rate = ${\left(\frac{\mathrm{\Delta }x}{\mathrm{\Delta }t}\right)}_{\mathrm{\Delta }\to 0}=\frac{dx}{dt}$

For a hypothetical reaction, ${\mathrm{n}}_1\mathrm{A}+{\mathrm{n}}_2\mathrm{B}⟶{\mathrm{m}}_1\mathrm{C}+{\mathrm{m}}_2\mathrm{D}$

The instantaneous rate may be expressed as 
$\text{Rate}=-\frac{1}{n_1}\frac{d\left[A\right]}{dt}=-\frac{1}{n_2}\frac{d\left[B\right]}{dt}=+\frac{1}{m_1}\frac{d\left[C\right]}{dt}=+\frac{1}{m_2}\frac{d\left[D\right]}{dt}$

For example, the instantaneous rate for the gaseous reaction,

$2{\mathrm{N}}_2{\mathrm{O}}_5⟶4{\mathrm{NO}}_2+{\mathrm{O}}_2$

Instantaneous rate $=-\frac{1}{2}\frac{\mathrm{d}\left[{\mathrm{N}}_2{\mathrm{O}}_5\right]}{\mathrm{dt}}=\frac{1}{4}\frac{\mathrm{d}\left[{\mathrm{NO}}_2\right]}{\mathrm{dt}}=\frac{\mathrm{d}\left[{\mathrm{O}}_2\right]}{\mathrm{dt}}$

The concept of average rate cannot be used to measure the true rate of a chemical reaction.  This is because the calculated average rate would be constant for the whole span of time for which it is calculated.  But the rate of reaction depends on molar concentration of reactants.  Since concentration of reactants decreases with time, therefore the rate of a reaction also decreases with time.  Since rate of reaction varies with time, it is more appropriate to express the rate of a reaction at a particular moment of time.  This rate of reaction at a particular moment of time is called instantaneous rate.  Thus instantaneous rate gives a true rate of reaction.

Experimental determination of reaction rate:

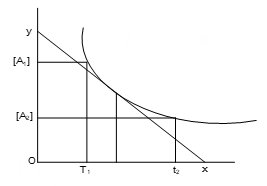
Rate of reaction is determined by measuring any property such as change in volume, pressure, pH, electrical conductivity, optical rotation etc. which is related to the concentration of reactants or products.  By measuring any of these properties, change in concentration of any species can be determined.  The change in this property is measured as a function of time.  Then a graph is plotted between concentration and time.

Average rate at time t $=\frac{\left[{\mathrm{A}}_1\right]-\left[{\mathrm{A}}_2\right]}{{\mathrm{t}}_2-{\mathrm{t}}_1}=\frac{-\{\left[{\mathrm{A}}_2\right]-\left[{\mathrm{A}}_1\right]\}}{\mathrm{\Delta t}}=-\frac{\mathrm{\Delta }\left[\mathrm{A}\right]}{\mathrm{\Delta t}}$

Instantaneous rate at any time is given by the slope of the tangent at the points corresponding to that time.

$\therefore$ Instantaneous rate at time t  $=\frac{\mathrm{OY}}{\mathrm{OX}}$

Factors affecting rate of reaction:
(i) Chemical nature of the reactants
(ii) Concentration of reactants
(iii) Temperature of the reactants (or reaction)
(iv) Exposure to radiations
(v) Presence or absence of catalyst

(i) Chemical nature of the reactants:

• Among solids rate increases with decrease in particle size. In powdered state rate of reaction is maximum, because in powdered state, surface area of reactant is maximum.

• Reactions which involve ionic substances such as double decomposition, neutralization occurs at very high rate.

• Reactions which involve rearrangement of bonds, transfer of electrons occurs at slow rate.

• Oxidation – reduction reactions are also slower than ionic reactions.

• Reactions in liquid state are faster than the reactions that occur in a heterogeneous system, when same concentrations of reactants are taken.

(ii) Concentration of reactants:

• If other factors remain constant, then the rate of a chemical reaction decreases with decrease in concentration of the reactants.
Guldberg and wage proposed a law that is known as “Law of mass action”.  This law relates rate of reaction with molar concentration of reactants.  It states that “At a given temperature, the rate of a chemical reaction is directly proportional to the product of the active masses of the reactants, with each concentration term raised to the power, equal to the stoichiometric coefficient of that species in the chemical reaction”.

• For a hypothetical reaction
aA + bB → cC + dD

• Rate of reaction according to law of mass action may be given as
Rate = k[A]^a [B]^b.  Here [A] and [B] are molar concentrations of the reactants and k is known as rate constant or specific reaction rate or velocity constant.

• When the concentration of each reactant is equal to unity then rate of a reaction is equal to rate constant.

• Higher the value of k faster is the reaction.

• The value of rate constant is independent of concentration of reactants.

• At a particular temperature, the rate constant has a definite value for a reaction,

• The value of rate constant changes with change in temperature.

(iii) Effect of temperature:
The rate of a reaction generally increases with increase in the temperature of the reaction.  The specific rate (k) of a reaction is approximately doubled for every 10⁰C rise of temperature for many reactions.
$\frac{{\mathrm{k}}_{{\mathrm{t}}^0\mathrm{C}+{10}^{\circ }\mathrm{C}}}{{\mathrm{K}}_{{\mathrm{t}}^0\mathrm{C}}}=2 \text{or }3$
The ratio of the two specific rates measured at temperatures that differ by 10⁰C is called the temperature coefficient of the reaction.
Normally ${\mathrm{t}}^0\mathrm{C}={25}^{\circ }\mathrm{C};(\mathrm{t}+10{)}^{\circ }\mathrm{C}={35}^{\circ }\mathrm{C}$.

Collision theory of reaction rates:
This theory was first proposed by Arrhenius.  This theory is based on the kinetic theory of gases.  According to this theory, chemical reactions occur only when the reactant molecules collide with each other.
Postulates of collision theory:

1. Reaching molecules shall have to collide for any reaction to occur.

2. All collisions do not lead to the formation of the products.

3. The colliding molecules shall have to possess a minimum energy to give products. This minimum energy is called Threshold energy.  This is higher than that of the molecules in the normal state.

4. The energy of the molecules at STP is very much less than this threshold energy.

5. The difference between the Threshold energy and the energy of molecules in the normal state is activation energy.
Activation energy = [Threshold energy – Energy of the normal molecules]

6. The molecules possessing the threshold energy are called activated molecules. These are formed in small numbers during collisions occurring between normal molecules.

7. Collisions occurring between activated molecules are called activated collisions. Activated collisions alone lead to the formation of the products of the reaction.

8. The fraction of the activated collisions amongst the total collisions is very much small.
The above facts are represented schematically as follows
$\begin{array}{l}\mathrm{A}+\mathrm{A}⟶{\mathrm{A}}^{\ast }+\mathrm{A}\\ {\mathrm{A}}^{\ast }+{\mathrm{A}}^{\star }⟶\text{products}\\ \end{array}$
A = normal molecule : A* = activated molecule.

9. No. of binary collision per unit time is given by
$\mathrm{Z}={\mathrm{\pi \sigma }}_{\mathrm{AB}}^2\sqrt{\frac{8\mathrm{kT}}{\mathrm{\pi \mu }}}{\mathrm{n}}_{\mathrm{A}}\cdot {\mathrm{n}}_{\mathrm{B}}$
where σAB is collision diameter, μ = reduced mass.

10. Specific rate ${\mathrm{Ae}}^{-\mathrm{Ea}/\mathrm{RT}}$.

11. The collisions that do not form a product are called ineffective elastic collisions. For a collision to be effective, the following two barriers are to be cleared.
a) Energy barrier b)  Orientation barrier

a) Energy barrier:
Out of the total number of collisions only those collisions result in the formation of products which possess energy equal to or greater than certain minimum energy called threshold energy.  The kinetic energy of the reactants in many reactions is less than their threshold energy and hence these reactants are not capable to form products.  It means there is an energy barrier between reactants and products which must be crossed for the reaction to occur.  Thus some extra energy has to be supplied to the reactants to make their kinetic energy equal to their threshold energy.  This extra energy is called activation energy of the reactants.
Activation energy = Threshold energy – average kinetic energy of reacting molecules.
E_a = E_T – E_R
Thus, the minimum amount of energy which must be supplied to the reactants to enable them to cross over the energy barrier is called activation energy.’
Activation energy depends upon the nature of chemical bonds undergoing rupture and is independent of the initial and final energy contents of reactants.  (i.e. independent of the fact that the reaction is exothermic or endothermic).  The energy changes during exothermic and endothermic reactions may be plotted against the progress of reaction as in figure.

• Rate of a reaction depends on activation energy. A reaction which has a lower value of its activation energy will proceed at a faster rate at a given temperature, while a reaction which has higher value of its activation energy proceed at low rate.

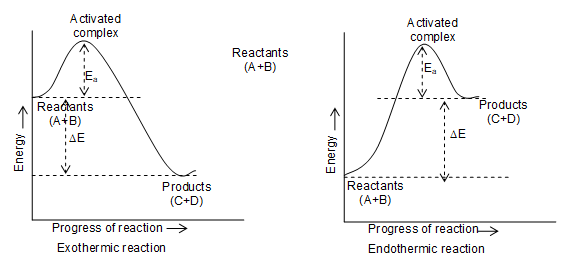
Activated complex: 
The reactants do not change directly into the desired products.  In the beginning of a reaction breaking of bonds predominates, therefore energy of system starts increasing till it reaches a energy maxima.  In this state reactants form activated complex.  The energy of activated complex is equal to threshold energy of the reactants.  After this, process of bond formation predominates, due to which energy starts decreasing and it results in the formation of products.
Thus, an activated complex is an unstable arrangement of atoms which is a very short lived high energy species.  In an effective collision, the activated complex separates into products.

b) Orientation barrier:
All the collisions among reactant molecules will not lead to the formation of products even if the energy of reactants is greater than the threshold energy.  It is because; the reacting molecules should have proper orientation for the collision, only than the collision will be effective.  All colliding molecules having sufficient energy but no proper orientation will bounce back without any reaction.
For example, the reaction between NO₂ and CO results in the formation of products CO₂ and NO the collision between CO and NO₂ will be effective only if the orientation of collision is proper.

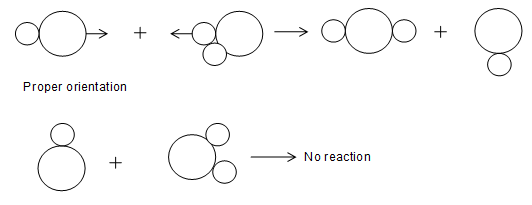
Here CO and NO₂ are not properly oriented and hence do not make the required product.

Molecularity of reaction: 
Molecularity of an elementary reaction is the total number of molecules or atoms which collide simultaneously to form the product molecules or the number of atoms or ions or molecules participating in an elementary step which must collide simultaneously to bring about a chemical reaction is called the molecularity of the elementary step or the number of atoms or ions or molecules participating in the elementary step is known as the molecularity of that reaction step.  Molecularity of the reaction can be 1, 2, or 3.  for example
(i) Hydrolysis of methyl acetate is a bimolecular reaction 
      CH₃COOCH₃ + H₂O → CH₃COOH + CH₃OH
(ii) Dissociation of PCl₅ is a unimolecular reaction
       PCl₅ → PCl₃ + Cl₂
(iii) Reaction between NO and O₂ is a trimolecular reaction.
        2NO + O₂ → 2NO₂.

Mechanism of elementary and complex reactions:

• In chemical kinetics, reactions which occur in single step are called elementary reaction, and the reactions which occur in two or more steps are termed as complex reactions.

• In case of complex reaction, molecularity is the minimum number of reacting particles that collide in a rate determining step to form products.

• Complex reactions proceed through a sequence of steps. Each step is an elementary step and involves the simultaneous collision of two or three species only.

The detailed description of various steps of the complex reactions is called mechanism of reaction. For example the molecularity of reaction
4HBr + O₂ → 2H₂ + 2Br₂
Seems to be 5, but the moleculairty does not exceed three.  Hence this reaction occurs in the following steps.
(i)     HBr       + O_{2       $\stackrel{\mathrm{slow}}{\to }$}    HOOBr
(ii)    HOOBr + HBr  $\stackrel{\mathrm{fast}}{\to }$  2HOBr
(iii)   2HOBr + 2HBr  $\stackrel{\mathrm{fast}}{\to }$ 2H₂O + 2Br₂
           —————————-
            4HBr + O₂    →     2H₂O + 2Br₂
           —————————–

• The slowest step of the reaction is called the rate determining step, hence the molecularity of this reaction for the slowest step is 2. Molecularity cannot be zero, negative, fractional, infinite.

Rate law or Rate equation:
The equation that describes mathematically the dependence of the rate of a reaction on the concentration terms of the reactants is known as the rate equation or rate law.  For example
a) A → P,                 rate = k[A]¹
b) 2A → 2P,            rate = k[A]²
c) A + B → P,          rate = k [A] [B]
d) A + B + C → P,  rate =k [A] [B] [C]

Order of reaction:
Order of a simple reaction is the number of molecules or atoms whose concentrations change as a result of chemical reaction.
Mathematically “The sum of powers to which the concentration terms are raised in the rate law expression is called order of reaction.
E.g.  For a hypothetical reaction;
aA + bB → cC + dD
Rate of reaction = k[A]^m [B]ⁿ
The exponents m and n are known as the order of the reaction with respect to A and B respectively.  m + n gives the overall order of the reaction.
m and n may and may not be equal to stoichiometric coefficients a and b respectively in the net reaction.
a) If the sum of the power is equal to one, the reaction is called first order reaction. e.g.,
i)  ${\mathrm{N}}_2{\mathrm{O}}_{5\left(\mathrm{g}\right)}\stackrel{}{\stackrel{\text{heat}}{\to }}{\mathrm{N}}_2{\mathrm{O}}_{4\left(g\right)}+\frac{1}{2}{\mathrm{O}}_{2\left(\mathrm{g}\right)}, \text{rate}=\mathrm{k}{\left[{\mathrm{N}}_2{\mathrm{O}}_5\right]}^1$ 
ii)  ${\mathrm{SO}}_2{\mathrm{Cl}}_{2\left(\mathrm{g}\right)}\stackrel{\mathrm{heat}}{\to }{\mathrm{SO}}_{2\left(\mathrm{g}\right)}+{\mathrm{Cl}}_{2\left(\mathrm{g}\right)}, \text{rate}=\mathrm{k}{\left[{\mathrm{SO}}_2{\mathrm{Cl}}_2\right]}^1$
iii)  ${\mathrm{H}}_2{\mathrm{O}}_{2\left(\mathrm{aq}\right)}⟶{\mathrm{H}}_2{\mathrm{O}}_{\left(\mathrm{I}\right)}+\frac{1}{2}{\mathrm{O}}_{2\left(\mathrm{g}\right)}, \text{rate}=\mathrm{k}{\left[{\mathrm{H}}_2{\mathrm{O}}_2\right]}^1$
iv) C₂H₅Cl → CH₂ = CH₂ + HCl,  rate = k[C₂H₅Cl]¹
v) 2N₂O → 2N₂ + O₂;    rate = k[N₂O]¹   

b) If the sum of the powers is two or three, the reaction is 2^nd order or 3^rd order respectively. e.g.,

i) $2{\mathrm{N}}_2{\mathrm{O}}_{2\left(\mathrm{g}\right)}\stackrel{}{\stackrel{\mathrm{heat}}{\to }}2{\mathrm{N}}_{2\left(\mathrm{g}\right)}+{\mathrm{O}}_{2\left(\mathrm{g}\right)}$ , rate = k[N2O]2	2nd order reaction
ii) $2{\mathrm{Cl}}_2{\mathrm{O}}_{2\left(\mathrm{g}\right)}\stackrel{\mathrm{heat}}{\to }2{\mathrm{Cl}}_{2\left(\mathrm{g}\right)}+{\mathrm{O}}_{2\left(\mathrm{g}\right)}$ , rate = k[Cl2O]3	2nd order reaction
iii) ${\mathrm{CH}}_3{\mathrm{COOC}}_2{\mathrm{H}}_{5\left(\mathrm{aq}\right)}+{\mathrm{NaOH}}_{\left(\mathrm{aq}\right)}⟶{\mathrm{CH}}_3{\mathrm{COONa}}_{\left(\mathrm{aq}\right)}+{\mathrm{C}}_2{\mathrm{H}}_5{\mathrm{OH}}_{\left(\mathrm{aq}\right)}$	2nd order reaction
iv) H2 + I2 → 2HI; rate = k[H2][I2]	2nd order reaction
v) 2NO2 → 2NO + O2; rate = k[NO2]2	2nd order reaction
vi) 2NO + O2 → 2NO2,  Rate = k[NO]2 [O2]	3rd order reaction
vii) 2NO + Br2 → 2NOBr,  rate = k[NO]2[Br2]	3rd order reaction
viii) $2{\mathrm{NH}}_3\stackrel{\mathrm{Pt}}{\to }{\mathrm{N}}_2+{\mathrm{H}}_2$ ix) ${\mathrm{N}}_2\mathrm{O}\stackrel{\mathrm{Pt}}{\to }{\mathrm{N}}_2+\frac{1}{2}{\mathrm{O}}_2$	zero order reaction

Specific rate or Rate constant:
The rate of a reaction corresponding to the unit concentrations of all the reactants of the reaction is called specific rate or rate constant (k).
Units of rate constant for reactions of different orders:

(i) For zero order reactions

$\text{Rate}=\frac{\mathrm{dx}}{\mathrm{dt}}=\mathrm{k}[\mathrm{A}{]}^{\circ }; \mathrm{k}={\mathrm{molL}}^{-1}{\sec }^{-1}$
(ii) For first order reactions

$\begin{array}{l}\text{Rate}=\mathrm{k}\left[\mathrm{A}\right]=\frac{\mathrm{dx}}{\mathrm{dt}}; \text{hence }\mathrm{k}\cdot \left[{\mathrm{molL}}^{-1}\right]=\left(\frac{\mathrm{mol}}{\mathrm{L}-\sec }\right)\\ \therefore \mathrm{k}=\left({\sec }^{-1}\right)\end{array}$

(iii) For second order reactions

$\begin{array}{l}\text{Rate}=\mathrm{k}[\mathrm{A}{]}^2=\frac{\mathrm{dx}}{\mathrm{dt}};\mathrm{k}{\left(\frac{\mathrm{mol}}{\mathrm{L}}\right)}^2=\left(\frac{\mathrm{mol}}{\mathrm{L}-\sec }\right)\\ \\ \text{Hence }\mathrm{k}=\mathrm{L}{\mathrm{mol}}^{-1}{\sec }^{-1}\end{array}$

(iv)  For third order reactions

$\begin{array}{l}\text{Rate}=\mathrm{k}[\mathrm{A}{]}^3=\frac{\mathrm{dx}}{\mathrm{dt}}\\ \mathrm{k}{\left(\frac{\mathrm{mol}}{\mathrm{L}}\right)}^3=\left(\frac{\mathrm{mol}}{\mathrm{L}-\sec }\right)\therefore \mathrm{k}={\mathrm{L}}^2{\mathrm{mol}}^{-2}{\sec }^{-1}.\end{array}$

Rate constant has different units for reactions of different order.  General rule for rate of reaction may be given as

$\begin{array}{l}\text{Rate}=\frac{\mathrm{dx}}{\mathrm{dt}}=\mathrm{k}[\text{conc.}{]}^{\mathrm{n}}\\ \therefore \mathrm{k}=\frac{1}{{\left[\text{conc.}\right]}^{\mathrm{n}}}\frac{\mathrm{dx}}{\mathrm{dt}}=\frac{1}{[\text{conc.}{]}^{\mathrm{n}}}\times \frac{\left[\text{conc.}\right]}{\text{time}}=[\text{conc.}{]}^{1-\mathrm{n}}\times {\text{time}}^{-1}\\ \\ \mathrm{or} \mathrm{k}={\left({\mathrm{molL}}^{-1}\right)}^{1-\mathrm{n}}{\sec }^{-1}\end{array}$

For gaseous reactants, concentration is expressed in atmosphere, hence units of k for gaseous reactants = (atm)^1–n × sec^–1 where n is the order of reaction.

Pseudo first order reactions:
Reactions whose order is different from that expected using rate law expression are called pseudo order reactions.  For example, acidic hydrolysis of ethyl acetate is pseudo first order reaction.
CH₃COOC₂H₅ + H₂O → CH₃COOH + C₂H₅OH
When water is taken in excess, then its concentration does not change appreciably during the reaction.  It means rate of reaction will depend on the single concentration term and it will follow the kinetics of the first order.
Expected rate law:
Rate = k[CH₃COOC₂H₅][H₂O]       order = 2
Actual rate law
Rate = k[CH₃COOC₂H₅]              order = 1

Method of determination of order of reaction:
1. Integrated rate law method:
Instantaneous rate of the reaction is given by the differential equations, but differential rate law equations involve infinitesimally small quantities like d[x], d[A], dt etc. which cannot be practically measured.  Hence differential rate law equations are transformed to integrated form of a rate law by the method of calculus.  Integrated rate law equations involve measurable quantities, thus these equations can be used for determining the rate constant, k, of the reaction.
(i) Zero order reaction:
A reaction is said to be of zero order if its rate is independent of the concentration of the reactants, for the reaction
A → Products
If initial concentration of reactant is [A]_$°$ and concentration after time t is [A] then rate of reaction = $-\frac{\mathrm{d}\left[\mathrm{A}\right]}{\mathrm{dt}}=\mathrm{k}[\mathrm{A}{]}^{°}=\mathrm{k}$
or         d[A] = -kdt.
Integrating both sides, [A] = -kt + C          ….. (i)
Where C is the constant of integration at t = 0, concentration = [A]₀ or [A] = [A]_o

$\therefore$   C = [A]_o
hence from equation (i)
[A] = -kt + [A]_o
or      kt = [A]_o – [A]  or
Photochemical reaction between hydrogen and chlorine is also a zero order reaction.
(ii)  First order reaction:
A reaction is said to be of first order if its rate is determined by the change of one concentration term only.
For the reaction A → products.
If initial concentration of reactant is [A]_o and, at time ‘t’ the concentration is [A], then the rate of reaction after time ‘t’ is given b
$\frac{-\mathrm{d}\left[\mathrm{A}\right]}{\mathrm{dt}}=\mathrm{k}\left[\mathrm{A}\right] \text{or }\frac{-\mathrm{d}\left[\mathrm{A}\right]}{\left[\mathrm{A}\right]}=\mathrm{kdt}$                        . . . . . (i)
on integrating both sides,
-log_e[A] = kt + C                                               . . . . . (ii)
where ‘c’ is the constant of integration
at t = 0, concentration of reactants = [A]₀.
$\therefore$ -log_e[A]₀ = 0 + C or C = -log_e [A]₀
substituting the value of ‘C’ in equation ‘2’
-log[A] = kt – log_e[A]_o

$\begin{array}{l}\mathrm{or} \mathrm{kt}={\log }_e[\mathrm{A}{]}_0-{\log }_e[\mathrm{A}]\\ \mathrm{or} \mathrm{kt}={\log }_e\frac{[\mathrm{A}{]}_0}{\left[\mathrm{A}\right]}=2.303\log \frac{[\mathrm{A}{]}_0}{\left[\mathrm{A}\right]}\\ \mathrm{or} \mathrm{k}=\frac{2.303}{\mathrm{t}}\log \frac{[\mathrm{A}{]}_0}{\left[\mathrm{A}\right]}\end{array}$

This equation is called integrated rate equation for the first order reaction.
This equation can also be represented as

$\frac{\mathrm{kt}}{2.303}=\log \frac{[\mathrm{A}{]}_{0 }}{\left[\mathrm{A}\right]} \text{or }\frac{\mathrm{kt}}{2.303}=\log [\mathrm{A}{]}_0-\log [\mathrm{A}] \mathrm{or}\log [\mathrm{A}]=\frac{-\mathrm{kt}}{2.303}+\log [\mathrm{A}{]}_{\mathrm{o}}$          
The graph between log[A] and time ‘t’ is a straight line, and the slope of this line is given by

$\text{Slope}=-\frac{\mathrm{k}}{2.303}$
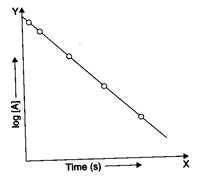
The intercept on y-axis would be equal to log [A]_o.
For first order reactions, any quantity which is proportional to concentration can be used in place of concentration for evaluation of k.
All natural and artificial radioactive decay of nuclei follow the first order kinetics.

Illustration 5: A first order reaction is 20% complete in 10 minutes.  Calculate (i) Specific rate constant of the reaction, and (ii) the time taken for the reaction to go to 75% completion.

Solution: $\mathrm{k}=\frac{2.303}{\mathrm{t}}\log \frac{[\mathrm{A}{]}_{\mathrm{a}}}{\left[\mathrm{A}\right]}$

Where [A]_o   → Initial amount of reactants.
[A] → Remaining amount of reactants.

$\therefore \mathrm{k}=\frac{2.303}{10}\log \frac{100}{100-20}$       

$\therefore$     k = 0.0223 min^–1.
The time taken for 75% of the reaction to complete

$\begin{array}{l}\mathrm{t}=\frac{2.303}{\mathrm{k}}\log \frac{100}{100-75}=\frac{2.303}{0.0223}\log 4\\ \\ \mathrm{t}=62.2 \min \end{array}$ 

Illustration 6: In a certain first order reaction, half of the reaction was completed in 500 seconds. How long will it be until one tenth is left.

Solution: $\mathrm{k}=\frac{0.6931}{{\mathrm{t}}_{1/2}}=\frac{0.6931}{500}$
Time required for the reaction to be completed until one tenth is left

$\mathrm{t}=\frac{2.303}{\mathrm{t}}\log \frac{100}{10}=\frac{2.303\times 500}{0.6931}=1661.37 \text{seconds.}$

Illustration 7: Rate constant of first order reaction is 0.0693 min^–1, initial conc. of reactants  10 mol L^-1.  What will be the rate of reaction after 10 minutes.

Solution:  $\mathrm{k}=\frac{2.303}{\mathrm{t}}\log \frac{[\mathrm{A}{]}_0}{\left[\mathrm{A}\right]}$  where [A]_o ⇒ remaining concentration of reactants.

$\begin{array}{rl}& \therefore 0.0693=\frac{2.303}{10}\log \frac{10}{\left[\mathrm{A}\right]}\\ & \text{or }\log \frac{10}{\mathrm{A}}=\frac{0.693}{2.303}=0.301\\ & \text{or }\frac{10}{4}=2\text{or }\mathrm{A}=\frac{10}{2}=5\mathrm{mol}/\mathrm{L}\end{array}$
Thus rate of reaction after 10 minutes
r = 0.0693 × 5 = 0.3465 mol/L-min

Illustration 8: For a chemical reaction A ® B, it is found that the rate of reaction doubles when the concentration of A is increased 4 times, what is the order of reaction with respect to A?

Solution: Rate of reaction = k[A]ⁿ  
r₁ = k[a]ⁿ            ….. (i)
r₂ = k[4a]ⁿ          ….. (ii)

$\begin{array}{rl}& \text{Since}=\frac{r_2}{r_1}=2\\ & \therefore \text{Dividing (ii) by (i)}\frac{r_2}{r_1}=(4{)}^n\\ & \text{or }2=(4{)}^n\therefore \mathrm{n}=\frac{1}{2}\\ & \text{Thus order of reaction}=\frac{1}{2}\text{.}\end{array}$

Illustration 9: A first order reaction is 90% complete in t minutes.  Calculate the time taken for the reaction to go to 99% completion.

Solution: For 90% completion of reaction

$\begin{array}{rl}& \begin{array}{rl}{\mathrm{t}}_1& =\frac{2.303}{\mathrm{k}}\log \frac{100}{100-90} ......\left(\mathrm{i}\right)\\ {\mathrm{t}}_2& =\frac{2.303}{\mathrm{k}}\log \frac{100}{100-99} ......\left(\mathrm{ii}\right)\end{array}\\ & \text{Dividing (ii) by (i)}\frac{{\mathrm{t}}_2}{{\mathrm{t}}_1}=\frac{\log 100}{\log 10}=\frac{2}{1}\\ & {\mathrm{t}}_2=2{\mathrm{t}}_1=2\mathrm{t}\end{array}$    

• For a first order reaction the time required to complete 99.9% of the reaction is 10 times that required for completion of half of the reaction. Similarly for a first order reaction, the time required for a 50% reaction is half that for 75% reaction.

 Half life of a reaction: 

The time in which the initial concentration of reactants becomes half is termed as half life period.
Half life of a zero order reaction is directly proportional to initial concentration.
${\mathrm{t}}_{1/2}=\frac{[\mathrm{A}{]}_0}{2\mathrm{k}}$

• Half life of first order reaction does not depend upon initial concentration of the reactants.

For 1^st order reaction $\mathrm{k}=\frac{2.303}{\mathrm{tk}}\log \frac{[\mathrm{A}{]}_0}{\left[\mathrm{A}\right]}$   

$\begin{array}{rl}\begin{array}{rl}t& =\frac{2.303}{k}\log \frac{[\mathrm{A}{]}_0}{\left[\mathrm{A}\right]}\end{array} \text{when }\mathrm{t}=\mathrm{t}1/2 \text{then }\left[\mathrm{A}\right]=\frac{1}{2}[\mathrm{A}{]}_{\circ }& \\ & \\ \text{therefore }{\mathrm{t}}_{1/2}=\frac{2.303}{\mathrm{k}}\log \frac{[\mathrm{A}{]}_{\mathrm{o}}}{\frac{1}{2}[\mathrm{A}{]}_0}=\frac{2.303}{\mathrm{k}}\log 2& \\ \text{or}{\mathrm{t}}_{1/2}=\frac{0.693}{\mathrm{k}}& \end{array}$

• For the first order reaction, the time required to reduce the concentration of the reactant to any fraction of the initial concentration is also independent of the initial concentration.

In general for nth order
${\mathrm{t}}_{1/2}\propto \frac{1}{[\mathrm{A}{]}_0^{\mathrm{n}-1}}$  where n is the order of reaction.
For zero order reaction t_1/2 ∝ [A]_o
For first order reaction T_1/2 ∝ $\frac{1}{[\mathrm{A}{]}_0^0}$ i.e., does not depend.
For second order reaction t_1/2 ∝  $\frac{1}{[\mathrm{A}{]}_0^{}}$
For third order reaction t_1/2 ∝ $\frac{1}{[\mathrm{A}{]}_0^2}$

2. Graphical method:
The various steps of this method are
(i) The concentration of reactant are determined at different time intervals.
(ii) A graph is plotted between time ‘t’ and the concentration of reactant or product from which a tangent is drawn.
(iii) The rate of reaction corresponding to different concentrations is determined by calculating slope of the tangent.
(iv) Different graphs are now plotted between reaction rate and concentration with different powers.
If a straight line is obtained between rate of reaction and concentration, then rate = k[conc.]; order = 1
For second order reaction,  rate = [conc]²
For third ordered rate = k[conc]³.

Initial rate method:
This method involves the determination of the order of different reactants separately.  In this method, the initial rate of a reaction is determined by varying the concentration of one of the reactant while others are kept constant.  For example, if a reaction involves reactants [A], [B], and [C], then initial rate of reaction is given by $\mathrm{r}=\mathrm{k} \left[\mathrm{A}{]}_0^{\mathrm{a}} \right[\mathrm{B}{]}_0^{\mathrm{b}} [\mathrm{C}{]}_0^{\mathrm{c}}$
If [B] and [C] are kept constant, then the value of ‘a’ can be determined by calculating the rate at different values of [A].
If r₁ and r₂ are initial rates at two different concentrations of A, then $\frac{{\mathrm{r}}_1}{{\mathrm{r}}_2}=\frac{{\left([\mathrm{A}{]}_0\right)}_1^{\mathrm{a}}}{{\left([\mathrm{A}{]}_0\right)}_2^{\mathrm{a}}}$
Taking log on both sides, $\log \left(\frac{{\mathrm{r}}_1}{{\mathrm{r}}_2}\right)=\mathrm{a} \log \frac{{\left(\right[\mathrm{A}{]}_{\mathrm{a}})}_1}{{\left(\right[\mathrm{A}{]}_0)}_2}$

$\therefore a= \frac{\log \left(\frac{r_1}{r_2}\right)}{\log \{{\left(\right[A{]}_0)}_1/{\left(\right[A{]}_0)}_2\}}$

Thus the order of reaction with respect to A can be determined.  In the same way, the order of reaction with respect to other reactants can also be determined and the overall order of the reaction is the sum of all the exponents in the rate law expression, i.e. order of reaction
n = a+b+c

4. Ostwald isolation method:
In this method, the concentration of all the reactants are taken in large excess except that of one, the concentration change only for this reactant is significant as other are so much in excess that practically there is no change in their concentrations.  The reactant which is not taken in excess, is said to be isolated from other reactants which are not taken in excess.  The total order of reaction will be the sum of the order of all isolated reactions. 
For a reaction,
aA + bB + cC → Products.
Rate = k[A]^a[B]^b[C]^c
If a is the order when A is isolated, b when [B] is isolated and c when [C] is isolated.
$\therefore$ Order of reaction = a + b + c.

Illustration 10: The following rate data were obtained at 295 K for the following reaction.
2NO + Cl₂ → 2NOCl                                                                  

Experiment	NO (mol/L)	Cl2 (mol/L)	Initial rate (mol/L-sec)
1.	0.05	0.05	1.0×10–3
2.	0.05	0.15	3.0×10–3
3.	0.15	0.05	9.0×10–3

(i) What is the rate law expression?

(ii) What is the order with respect to NO and Cl₂ in the reaction.

(iii) Determine the reaction rate when concentrations of Cl₂ and NO are 0.2 M and 0.4 M respectively.

Solution: (i) The expression for the initial rate of this reaction will be

Rate = k[NO]^x[Cl₂]^y
For experiment 1           1.0×10^–3 = k[0.05]^x [0.05]^y
For experiment 2           3.0×10^–3 = k[0.05]^x [0.15]^y
For experiment 3           9.0×10^–3 = k[0.15]^x[0.05]^y
Dividing equation (i) by (ii)

$\frac{1.0\times {10}^{-3}}{9.0\times {10}^{-3}}=\frac{\mathrm{k}[0.05{]}^{\mathrm{x}}[0.05{]}^{\mathrm{y}}}{\mathrm{k}[0.15{]}^{\mathrm{x}}[0.05{]}^{\mathrm{y}}}\text{or }\frac{1}{9}={\left(\frac{1}{3}\right)}^{\mathrm{x}}\text{or}{ \left(\frac{1}{3}\right)}^2={\left(\frac{1}{3}\right)}^{\mathrm{x}}$    

$\therefore$ x = 2 thus order with respect to NO = 2.
Dividing equation (i) by (ii)
$\begin{array}{l}\frac{1.0\times {10}^{-3}}{3\times {10}^{-3}}=\frac{\mathrm{k}[0.05{]}^{\mathrm{x}}[0.05{]}^{\mathrm{\gamma }}}{\mathrm{k}[0.05{]}^{\mathrm{x}}[0.15{]}^{\mathrm{\gamma }}}\\ \text{or}\left(\frac{1}{3}\right)={\left(\frac{1}{3}\right)}^{\mathrm{\gamma }}\text{or }\mathrm{y}=1\end{array}$
Thus order with respect to Cl₂ = 1
(ii) Rate law expression r = k[NO]²[Cl₂]
(iii) The value of rate constant $\mathrm{k}=\frac{\text{Rate}}{[\mathrm{NO}{]}^2\left[{\mathrm{Cl}}_2\right]}=\frac{1.0\times {10}^{-3}}{[0.05{]}^2[0.05]}=8{\mathrm{L}}^2{\mathrm{mol}}^{-2}{\mathrm{s}}^{-1}$.
Thus when [NO] = 0.2 M and [Cl₂] = 0.4 M
The rate of reaction = $8\times [0.4{]}^2\times [0.2]=0.256\mathrm{mol} {\mathrm{L}}^{-1}{\sec }^{-1}$.

Illustration 11:  The reaction between A and B is first order with respect to A and zero order with respect to B.  fill in the blanks in the following table.
Experiment        [A] (mol L^–1)      [B] (mol L^–1)      Initial rate (mol/L-sec)
(i)                                 0.1                    0.1                        2×10^–2  
(ii)                                  –                     0.2                        4×10^–2
(iii)                               0.4                   0.4                            –
(iv)                                 –                     0.2                          2×10^–2
Solution: The rate of this reaction depends only on the concentration of [A].
$\therefore$ The rate law for this reaction is
rate = k[A]¹[B]^o
For experiment (i)
2×10^–2 = k[0.1]¹
$\therefore \mathrm{k}=\frac{2\times {10}^{-2}}{01}=2\times {10}^{-1}{\min }^{-1}$.
For experiment (ii) $4\times {10}^{-2}=\mathrm{k}\left[\mathrm{A}\right][\mathrm{B}{]}^{\circ }$
or  4 × 10^–2 = 2 × 10^–1 [A]
$\therefore \left[\mathrm{A}\right]=\frac{4\times {10}^{-2}}{2\times {10}^{-1}}=2\times {10}^{-1}{\mathrm{molL}}^{-1 }\text{or }0.2\mathrm{mol} {\mathrm{L}}^{-1}$.
For experiment (iii) Rate = k[A] = 2×10^–1 × [0.4]  = 8 × 10^–2 mol L^–1 min^–1.
For experiment (iv) $\left[\mathrm{A}\right]=\frac{\text{Rate}}{\mathrm{k}}=\frac{2\times {10}^{-2}}{2\times {10}^{-1}}=0.1\mathrm{mol} {\mathrm{L}}^{-1}$.

Activation energy:
The difference between this barrier energy (i.e., threshold energy)  E_T and the energy of normal molecules E_B called activation energy, E_a.
$\therefore {\mathrm{E}}_{\mathrm{a}}={\mathrm{E}}_{\mathrm{T}}-{\mathrm{E}}_{\mathrm{R}}$ 

Illustration 12:  The threshold energy of a reacting molecule in a first order reaction is E_T.  The activation energy is E_A.  What is the energy of the normal molecules?

Solution:  Activation energy (E_A) = Threshold energy (E_T) – Energy of normal molecules.
$\therefore$ Energy of normal reacting molecule = (E_T – E_A)

Arrhenius equation (Temperature dependence of rate constant):
Arrhenius suggested an equation which describes rate constant as a function of temperature i.e.
$\mathrm{K}={\mathrm{Ae}}^{-\mathrm{Ea}/\mathrm{RT}}$
where A → frequency factor
E_a → Energy of activation; R® the gas constant.
T → Temperature in Kelvin.
At two temperatures T₁ and T₂ their rate constant are given by k₁ and k₂.
Taking log of Arrheniums equation
$\begin{array}{l}{\log }_{\mathrm{e}}{\mathrm{k}}_1=\mathrm{logA}-\frac{{\mathrm{E}}_{\mathrm{a}}}{{\mathrm{RT}}_1} \dots \dots \left(\mathrm{i}\right)\\ {\log }_{\mathrm{e}}{\mathrm{k}}_2=\mathrm{logA}-\frac{{\mathrm{E}}_{\mathrm{a}}}{{\mathrm{RT}}_2} \dots \dots \left(\mathrm{ii}\right)\end{array}$                                                   

Subtracting equation (i) from equation (ii)
${\mathrm{logk}}_2-{\log }_{\mathrm{e}}{\mathrm{k}}_1=\frac{{\mathrm{E}}_{\mathrm{a}}}{\mathrm{R}}\left[\frac{1}{{\mathrm{T}}_1}-\frac{1}{{\mathrm{T}}_2}\right]\text{or}\log \frac{{\mathrm{k}}_2}{{\mathrm{k}}_1}=\frac{{\mathrm{E}}_{\mathrm{a}}}{2.303\mathrm{R}}\left[\frac{{\mathrm{T}}_2-{\mathrm{T}}_1}{{\mathrm{T}}_1{\mathrm{T}}_2}\right]$
Another form of Arrhenius equation which is more useful for calculation of activation energy is

$\mathrm{logk}=\mathrm{logA}-\frac{{\mathrm{E}}_{\mathrm{a}}}{2.303\mathrm{R}}\frac{1}{\mathrm{T}}$

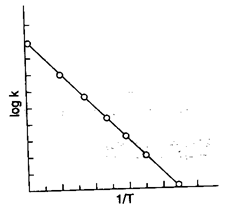
when a graph is plotted between look and 1/T then the slope of this curve is equal to $-\frac{{\mathrm{E}}_{\mathrm{a}}}{2.303\mathrm{R}}$

$\begin{array}{l}\therefore \text{Slope}=\frac{-{\mathrm{E}}_{\mathrm{a}}}{2.303\mathrm{R}}\\ \therefore {\mathrm{E}}_{\mathrm{a}}=-2.303\mathrm{R}\times \text{slope}\end{array}$

• As the value of E_a increases, the value of k decreases and, therefore reaction rate decreases.

Illustration 13:  For a reaction, the energy of activation is zero.  What is the value of rate constant at 300 K, if k = 1.6×10⁶ s^–1 at 280 K (R = 8.314 J mol^–1 k^–1)

Solution: Since E_a = 0

$\begin{array}{rl}& \therefore \log \frac{{\mathrm{k}}_2}{{\mathrm{k}}_1}=\frac{{\mathrm{E}}_{\mathrm{a}}}{2.303\mathrm{R}}\left[\frac{{\mathrm{T}}_2-{\mathrm{T}}_1}{{\mathrm{T}}_1{\mathrm{T}}_2}\right]=0\\ & \text{or }\log \frac{{\mathrm{k}}_2}{{\mathrm{k}}_1}=0\\ & \text{or}\\ & {\mathrm{k}}_1={\mathrm{k}}_2=1.6\times {10}^6{\mathrm{s}}^{-1}\end{array}$

Illustration 14:  The activation energy of a reaction is 140kJ mol^–1.  If its rate constant at 400K is 2.0×10^–6 s^–1, what is the value of rate constant at 500 K.
Solution: According to Arrhenius equation

=  $\begin{array}{l}\log \frac{{\mathrm{k}}_2}{{\mathrm{k}}_1}=\frac{{\mathrm{E}}_{\mathrm{a}}}{2.303\mathrm{R}}\left[\frac{{\mathrm{T}}_2-{\mathrm{T}}_1}{{\mathrm{T}}_1{\mathrm{T}}_2}\right]=\frac{140\times {10}^3}{2.303\times 8.314}\left[\frac{500-400}{500\times 400}\right]=3.655\\ \text{or }\frac{{\mathrm{k}}_2}{{\mathrm{k}}_1}=\text{antilog}3.655=4.515\times {10}^3\\ \text{or }{\mathrm{k}}_2={\mathrm{k}}_1\times 4.515\times {10}^3=2.0\times {10}^{-6}\times 4.515\times {10}^3=9.030\times {10}^{-3}{\mathrm{s}}^{-1}\end{array}$

Illustration 15:  Temperature coefficient $\mu =\frac{k_{{35}^{\circ }\mathrm{C}}}{{\mathrm{k}}_{{25}^{\circ }\mathrm{C}}}$  of a reaction is 1.82.  Calculate the energy of activation in calories. (R = 1.987 cal degree^–1 mol^–1).
Solution:         

$\begin{array}{l}\log \frac{k_2}{k_1}=\frac{E_a}{2.303R}\left[\frac{T_2-T_1}{T_1{T}_2}\right]\\ \\ \log 1.82=\frac{E_a}{2.303\times 1.987}\left(\frac{308-298}{308\times 298}\right)\\ \\ \text{or }0.2601=\frac{E_a}{2.303\times 1.987}\left(\frac{10}{308\times 298}\right)\\ \\ \\ \text{or }{E}_a=\frac{0.2601\times 2.303\times 1.987\times 308\times 298}{10}=10924.40 \text{calorie }mo{l}^{-1}\end{array}$

Illustration 16:  The rate of particular reaction doubles when temperature changes from 27^oC to 37^oC.  Calculate the energy of activation for such reaction?  (R = 8.314 JK^–1 mol^–1)

Solution: If k₁ and k₂ are the rate constants of same reaction at two different temperatures 27^oC (T₁) and 37^oC (T₂), then $\frac{{\mathrm{k}}_2}{{\mathrm{k}}_1}=2$
Activation energy E_a is related to rate constants by Arrhenius equation

$$\begin{gathered} \begin{array}{rl}\log \frac{{\mathrm{k}}_2}{{\mathrm{k}}_1}& =\frac{{\mathrm{E}}_{\mathrm{a}}}{2.303\mathrm{R}}\left[\frac{1}{{\mathrm{T}}_1}-\frac{1}{{\mathrm{T}}_2}\right]=\frac{{\mathrm{E}}_{\mathrm{a}}}{2.303\mathrm{R}}\left[\frac{{\mathrm{T}}_2-{\mathrm{T}}_1}{{\mathrm{T}}_1{\mathrm{T}}_2}\right]\\ \text{or }& \log 2=\frac{{\mathrm{E}}_{\mathrm{a}}}{2.303\mathrm{R}}\left[\frac{{\mathrm{T}}_2-{\mathrm{T}}_1}{{\mathrm{T}}_1{\mathrm{T}}_2}\right]\end{array} \\ 0.301=\frac{{\mathrm{E}}_{\mathrm{a}}}{2.303\times 8.314}\left[\frac{310-300}{300\times 310}\right] \\ {\mathrm{E}}_{\mathrm{a}}=\frac{0.301\times 2.303\times 8.314\times 300\times 310}{10} \\ =53.59\times {10}^3\mathrm{J}{\mathrm{mol}}^{-1}=53.59\mathrm{kJ}{\mathrm{mol}}^{-1} \end{gathered}$$

Effect of catalyst on reaction rate:
In the presence of a catalyst, the reaction follows a path of lower activation energy.  Under this condition a large number of reacting molecules are able to cross over the energy barrier and thus the rate of reaction increases.
A negative catalyst increases the activation energy of reaction by forming a new intermediate of high energy i.e. by changing the reaction mechanism i.e. by changing the reaction mechanism.
Photochemical reactions:
Rates of some reactions are influenced by radiations particularly visible and ultraviolet radiations.  Such reactions are called photochemical reactions.  In these reactions photons of radiant energy are absorbed by reactant molecules.  Activation energy required for reaction is supplied by radiant energy.  Temperature has no marked effect on the rate of photo chemical reactions.  The value of ΔG may be +ve or -ve for photochemical reactions.
Examples of photochemical reactions:
(i) Reaction between H₂ and Cl₂ to form HCl.
(ii) Photosynthesis, photography etc.

Quantum Yield:
It gives the relation between number of quanta absorbed and number of reacting molecules

$\mathrm{\varphi }=\frac{\text{Number of molecules reacting in a given time}}{\text{number of quanta of light absorbed in the same time}}$

Photosensitizer: 
These substances absorbs the light energy and passes it on to one of the reactants.  These substances help to start the photochemical reaction but not undergo any chemical change themselves.  The example of reaction in which photosensitizer acts as a carrier of energy is photosynthesis in which chlorophyll molecules absorb the visible light; after absorption chlorophyll molecules pass the energy to CO₂ and H₂O molecules which then combine to form carbohydrate and oxygen.

FORMULAE AND CONCEPTS AT A GLANCE

1. Order of a reaction is the no of those reactant molecules whose concentration change is measurable after the reaction. Order of a reaction is purely experimental

2. For a zero order reaction

differential rate = k₀(rate constant)

Integrated rate law x = k₀ t (where x = amount of reactant converted into products at time ‘t’.)

Unit of zero order rate constant (k₀) is mol lit^–1 sec^-1

Half life time (t_1/2) = $\frac{\mathrm{a}}{2{\mathrm{k}}_0}$, where ‘a’ is the initial concentration of reactant

3. For a first order reaction

Differential rate law r = k₁(a – x), where (a – x ) is the concentration of reactant left at time ‘t’

Integrated rate law  t = $\frac{2.303}{{\mathrm{k}}_1}\log \frac{\mathrm{a}}{(\mathrm{a}-\mathrm{x})}$. Unit of k₁ is time^–1 (e.g. sec^–1).t_{1/2 = $\frac{0.693}{{\mathrm{k}}_1}$.}

4. For n^th order reaction

Differential rate law r = k (a – x)ⁿ

Integrated rate law ${\mathrm{k}}_{\mathrm{n}}=\frac{1}{(\mathrm{n}-1)\mathrm{t}}\left[\frac{1}{(\mathrm{a}-\mathrm{x}{)}^{\mathrm{n}-1}}-\frac{1}{(\mathrm{a}{)}^{\mathrm{n}-1}}\right]$

Where n ≠ 1

Units of k_n = ${\text{ conc. }}^{(1-\mathrm{n})}{\mathrm{time}}^{-1},{\mathrm{t}}_{1/2}\propto \frac{1}{{\mathrm{a}}^{\mathrm{n}-1}}$

5. The ratio of rate constants of a reaction at two different temperatures separated by 10°C is called temperature coefficient. Temperature coefficient (μ) = $\frac{{\mathrm{k}}_{\mathrm{t}+10}}{{\mathrm{k}}_{\mathrm{t}}}$

Temperature coefficient always lies between 2 and 3 i.e. 2 £ m < 3

6. Variation of rate constant with temperature is given by Arrhenius equation

k = where,

A = pre–exponential or frequency factor

Ea = energy of activation

R = gas constant

T = Temperature in Kelvin

7. Integrated form of Arrhenius equation is log $\mathrm{k}=\left(\frac{-\mathrm{Ea}}{2.303\mathrm{R}}\right)\frac{1}{\mathrm{T}}+\log A$, which shows that a graph of log k vs $\frac{1}{\mathrm{T}}$ is a straight line with slope = $\frac{-\mathrm{Ea}}{2.303\mathrm{R}}$ and intercept = log A

8. Arrhenius equation takes the form log $\frac{{\mathrm{k}}_2}{{\mathrm{k}}_1}=\frac{\mathrm{Ea}}{2.303}\left[\frac{1}{{\mathrm{T}}_1}-\frac{1}{{\mathrm{T}}_2}\right]$ where ${\mathrm{T}}_1<{\mathrm{T}}_2$

9. For an endothermic reaction

(Ea)_f – (Ea)_b = $∆$H, where (Ea)_f and (Ea)_b are the energy of activation for forward and backward reaction, and $∆$H is the heat of reaction for an exothermic reaction

(Ea)_f – (Ea)_b = $∆$H

10. Nuclear disintegration or decay follows first order kinetic. Activity of decay $\left(–\frac{\mathrm{dN}}{\mathrm{dt}}\right)=\mathrm{\lambda N}$

Where $\lambda$ = decay constant and N = no of atoms of radioactive substance present at time ‘t’

$\mathrm{t}=\frac{2.303}{\mathrm{\lambda }}\log \frac{{\mathrm{N}}_0}{\mathrm{N}},\mathrm{\lambda }=\frac{0.693}{{\mathrm{t}}_{1/2}}$

Average life (T) of a radioactive substances = 1.44⨯t_1/2 = 1/$\lambda$

11. Number of atoms of radioactive substance left after ‘n’ half lives N = N₀(1/2)ⁿ

Where n = $\frac{\mathrm{t}}{{\mathrm{t}}_{1/2}}$.

SOLVED PROBLEMS-1

Prob 1. A chemical reaction $2\mathrm{A}\rightleftharpoons 4\mathrm{B}+\mathrm{C}$ in gas phase occurs in a closed vessel.  The concentration of B is found to increase by 5⨯10^-3 mol L^-1 in 10 seconds.  Calculate (i) Rate of disappearance of B (ii) Rate of appearance of A.

Sol: Rate of disappearance of B = $\frac{\mathrm{\Delta }\left[\mathrm{B}\right]}{\mathrm{\Delta t}}=\frac{5\times {10}^{-3}}{10}=5\times {10}^{-4}{\mathrm{molL}}^{-1}{\mathrm{S}}^{-1}$

Rate of reaction = $-\frac{\mathrm{\Delta }\left[\mathrm{A}\right]}{2\mathrm{\Delta t}}=\frac{\mathrm{\Delta }\left[\mathrm{B}\right]}{4\mathrm{\Delta t}}$

Rate of appearance of $\mathrm{A}=\frac{\mathrm{\Delta }\left[\mathrm{A}\right]}{\mathrm{\Delta t}}=\frac{2}{4}\frac{\mathrm{\Delta }\left[\mathrm{B}\right]}{\mathrm{\Delta t}}=\frac{2\times 5\times {10}^{-4}}{4}=2.5\times {10}^{-4}{\mathrm{molL}}^{-1}{\mathrm{S}}^{-1}$.

Prob 2. For the reaction 2A+B $\to$ C the rate of formation of C is 0.25 mol L^-1 hr^-1.  What is the rate of disappearance of A and B?

Sol: Rate of reaction = $\frac{\mathrm{\Delta }\left[\mathrm{A}\right]}{2\mathrm{\Delta t}}=\frac{-\mathrm{\Delta }\left[\mathrm{B}\right]}{\mathrm{\Delta t}}=\frac{\mathrm{\Delta }\left[\mathrm{C}\right]}{\mathrm{\Delta t}}=0.25 {\mathrm{molL}}^{-1}{\mathrm{hr}}^{-1}.$

Rate of disappearance of A = $\frac{\mathrm{\Delta }\left[\mathrm{A}\right]}{\mathrm{\Delta t}}=\frac{2\mathrm{\Delta }\left[\mathrm{C}\right]}{\mathrm{\Delta t}}=2\times 0.25=0.50{\mathrm{molL}}^{-1}{\mathrm{hr}}^{-1}.$

Rate of disappearance of B = $\frac{\mathrm{\Delta }\left[\mathrm{B}\right]}{\mathrm{\Delta t}}=\frac{\mathrm{\Delta }\left[\mathrm{C}\right]}{\mathrm{\Delta t}}=0.25{\mathrm{molL}}^{-1}{\mathrm{hr}}^{-1}$

Prob 3. When ammonia is treated with O₂ at elevated temperature, the rate of disappearance of NH₃ is found to be 3.5⨯10^–2 mol dm^–3 s^–1 during a measured time interval. Calculate the rate of appearance of nitric oxide and water?

Sol: For the reaction, 4NH₃ + 5O₂ $\to$ 4NO + 6H₂O

Rate of reaction, $r=\frac{-\mathrm{\Delta }\left[{\mathrm{NH}}_3\right]}{4\mathrm{\Delta }t}=\frac{-\mathrm{\Delta }\left[{\mathrm{O}}_2\right]}{5\mathrm{\Delta }t}=\frac{\mathrm{\Delta }\left[\mathrm{NO}\right]}{4\mathrm{\Delta }t}=\frac{\mathrm{\Delta }\left[{\mathrm{H}}_2\mathrm{O}\right]}{6\mathrm{\Delta }t}$

Rate of appearance of nitric oxide = $\frac{\mathrm{\Delta }\left[\mathrm{NO}\right]}{\mathrm{\Delta t}}=\frac{\mathrm{\Delta }\left[{\mathrm{NH}}_3\right]}{\mathrm{\Delta t}}=3.5\times {10}^{-2}\mathrm{mol}{\mathrm{dm}}^{-3}{\mathrm{s}}^{-1}.$

Rate of appearance of H₂O = $\frac{\mathrm{\Delta }\left[{\mathrm{H}}_2\mathrm{O}\right]}{\mathrm{\Delta t}}=\frac{6}{4}\frac{\mathrm{\Delta }\left[{\mathrm{NH}}_3\right]}{\mathrm{\Delta t}}=\frac{6}{4}\times 3.5\times {10}^{-2}$

$=5.25\times {10}^{-2}\mathrm{mol}{\mathrm{dm}}^{-3}{\mathrm{s}}^{-1}$.

Prob 4. The reaction 2NO + O₂ $\to$ 2NO₂ follows by the law, r = k[NO]² [O₂].  What is the order of reaction?  What is the rate of reaction when [NO] = 0.04 mol L^–1 and [O₂] = 0.3 mol L^–1, and k = 2.0 ⨯ 10^–6 mol^–2 L² s^–1.

Sol: From the rate law expression r = k[NO]²[O₂]

Order of reaction = 3.

Rate = k[NO]²[O₂] = k[0.04]² [0.3]

= 2⨯10^–6 ⨯ [0.04]²[0.3] = 9.6⨯10^–10 mol L^–1 sec^–1.

Prob 5. The gas phase reaction 2NO₂ + O₃ $\to$ N₂O₅ + O₂ has the rate constant k=2.0⨯10⁴ dm³ mol^–1 s^–1 at 300 K.  What is the order of this reaction.

Sol: From the units of rate constant order of reaction = 2.

Prob 6. For a reaction aA + bB ® products, following rate data were obtained. 

[A] (mol/L)      [B] (mol/L)         rate (mol/L-sec)

0.10                         0.10                  1⨯10^–2

0.20                         0.20                  8⨯10^–2

0.10                          0.20                  2⨯10^–2

Find the overall order of the reaction

Sol: The rate law expression for their reaction will be r = k[A]^x[B]^y

r₁= [0.10]^x.[0.10]^y       …. (1)

r₂ = [0.20]^x [0.20]^y       …..(2)

r₃ = [0.10]^x.[0.20]^y          …..(3)

$\therefore \frac{{\mathrm{r}}_3}{{\mathrm{r}}_1}=\frac{2\times {10}^{-2}}{1\times {10}^{-2}}=\frac{[0.10{]}^{\mathrm{x}}[0.20{]}^{\mathrm{y}}}{[0.10{]}^{\mathrm{x}}[0.10{]}^{\mathrm{y}}}$

or 2 = (2)^y        ∴  y = 1.

Thus order of reaction with respect to B = 1.

Similalry   $\frac{{\mathrm{r}}_2}{{\mathrm{r}}_3}=\frac{8\times {10}^{-2}}{2\times {10}^{-2}}=\frac{[0.20{]}^{\mathrm{x}}[0.20{]}^{\mathrm{y}}}{[0.10{]}^{\mathrm{x}}[0.20{]}^{\mathrm{y}}}$

or   4 = (2)^x

Thus order of reaction with respect to A = 2

overall order = 2+1 = 3.

Prob 7. The half life of a certain first order reaction is 60 minutes. How will it take for 80% reaction to occur?

Sol: Half life of a reaction t_1/2 = $\frac{0.6931}{\mathrm{k}}\text{ or }\mathrm{k}=\frac{0.6931}{{\mathrm{t}}_{1/2}}$

$\therefore \mathrm{k}=\frac{0.6931}{60}=0.01155{\min }^{-1}$

Time required for 80% reaction to occur

$\mathrm{t}=\frac{2.303}{\mathrm{k}}=\log \frac{100}{(100-80)}=\frac{2.303}{0.01155}\log 5$ = 199.39⨯0.699 = 139.37 minutes.

Prob 8. Find the overall rate constant k for the following hypothetical reaction $\mathrm{A}\underset{{\mathrm{k}}_2}{\overset{{\mathrm{k}}_1}{\rightleftharpoons }}\mathrm{B};$   $\mathrm{B} \underset{\mathrm{slow}}{\overset{{\mathrm{k}}_3}{\to }}\mathrm{C}$

Sol: for the reversible process  $\mathrm{A}\underset{{\mathrm{k}}_2}{\overset{{\mathrm{k}}_1}{\rightleftharpoons }}\mathrm{B}$

Rate of forward reaction = k₁[A]

Rate of backward reaction = k₂[B]

At equilibrium; rate of forward reaction = rate of backward reaction.

$\therefore {\mathrm{k}}_1\left[\mathrm{A}\right]={\mathrm{k}}_2\left[\mathrm{B}\right]\text{ or }\left[\mathrm{B}\right]=\frac{{\mathrm{k}}_1\left[\mathrm{A}\right]}{{\mathrm{k}}_2}$

From the slowest step, over all rate of reaction

$={\mathrm{k}}_3\left[\mathrm{B}\right]=\frac{{\mathrm{k}}_3{\mathrm{k}}_1\left[\mathrm{A}\right]}{{\mathrm{k}}_2}=\mathrm{k}\left[\mathrm{A}\right]$

Thus overall rate constant $\mathrm{k}=\frac{{\mathrm{k}}_3{\mathrm{k}}_1}{{\mathrm{k}}_2}$

Prob 9. The rate constant of a first order reaction is 60 s^–1.  How much time will it take to reduce the initial concentration 1/16^th value.

Sol:  Half life of reaction = $\frac{0.6931}{k}=\frac{0.6931}{60}=0.01155 \sec$

If N₀. is initial concentration and N is the concentration after ‘n’ half lives, then

$\mathrm{N}=\mathrm{No}{\left(\frac{1}{2}\right)}^{\mathrm{n}}$

or     $\frac{{\mathrm{N}}_0}{16}={\mathrm{N}}_0{\left(\frac{1}{2}\right)}^{\mathrm{n}}\text{ or }\mathrm{n}=4$

Thus total time required for the concentration to become

$\frac{1}{16}=\mathrm{n}\times {\mathrm{t}}_{1/2}=4\times 0.01155$ = 0.0462 sec = 4.62 ⨯ 10^-2  sec

Prob 10. The half life period for a first order reaction is 100 sec.  How long will it take for two third of the reaction to be completed?

Sol:  t_1/2 = 100 sec

$\therefore \mathrm{k}=\frac{0.693}{100}=6.93\times {10}^{-3}{\sec }^{-1}$

Remaining concentration of reactants = $1-\frac{2}{3}=\frac{1}{3}$

∴ Time required for the completion of 2/3^rd of the reaction,

$\mathrm{t}=\frac{2.303}{\mathrm{k}}\log \frac{\left[{\mathrm{A}}_{\circ }\right]}{\left[\mathrm{A}\right]}=\frac{2.303}{\mathrm{k}}\log \frac{\left[{\mathrm{A}}_0\right]}{\left[{\mathrm{A}}_0\right]/3}=$$\frac{2.303}{6.93\times {10}^{-3}}\log 3=158.55\sec$.

SOLVED PROBLEMS-2

Prob 1. The following data are for the decomposition of ammonium nitrite in aqueous solution   

Volume of N₂ in c.c.            Time (minutes)

6.25                                                   10

9.00                                                  15

11.40                                                 20

13.65                                                 25

35.05                                                $\infty$

The order of the reaction is

(A) Zero                 (B)  One                 (C) Two                 (D) Three

Sol: (B)  Suppose the reaction is of first order. Applying $\mathrm{k}=\frac{2.303}{\mathrm{t}}\log \frac{{\mathrm{V}}_{\mathrm{\infty }}}{{\mathrm{V}}_{-\mathrm{\infty }}-{\mathrm{V}}_{\mathrm{t}}}$

Value of k comes constant from the data. Hence, reaction is of first order.

Prob 2. The rate of reaction is doubled for every 10^oC rise in temperature. The increase in reaction rate as a result of temperature rise from 10^oC to 100^oC is

(A) 112                 (B) 512                 (C) 400                 (D) 614

Sol: (B)  Temperature coefficient $\left(\mu \right)$ = 2

Number of times the rate doubles = $\frac{100-10}{10}=9\Rightarrow \frac{R_{\text{new }}}{R}=2^9=512$

Prob 3. The conversion of $A\to B$ follows second order kinetics. Doubling the concentration of A will increase the rate of formation of B by a factor of

(A)  1/4               (B)  2               (C)  1/2               (D)  4

Sol: (D). ${\mathrm{R}}_1=\mathrm{k}[\mathrm{A}{]}^2$

${\mathrm{R}}_2=\mathrm{k}[2\mathrm{A}{]}^2=4{\mathrm{R}}_1$

Prob 4. Consider the following statements

The rate law for the acid catalysed hydrolysis of an ester is given by

Rate = k[H⁺][ester] If the acid concentration is doubled at constant ester concentration

(1)  The second order rate constant, k is doubled

(2)  The pseudo first order rate constant, k is doubled

(3)  The rate of the reaction is doubled

Which of the above statements are correct?

(A)  1 and 2               (B)  2 and 3            (C)  1 and 3               (D) 1, 2 and 3

Sol: (B)  R = k [ester] [H⁺]

Hence, on doubling the [H⁺], the initial rate and will be doubled.

Prob 5. For the reaction, $\mathrm{B}+2\mathrm{D}⟶3\mathrm{T}$, given that $\frac{-{\mathrm{dC}}_{\mathrm{B}}}{\mathrm{dt}}={\mathrm{kC}}_{\mathrm{B}}{\mathrm{C}}_{\mathrm{D}}^2$. The expression for $\frac{-{\mathrm{dC}}_{\mathrm{D}}}{\mathrm{dt}}$ will be

(A) $2{\mathrm{kC}}_{\mathrm{B}}{\mathrm{C}}_{\mathrm{D}}^2$               (B) $\frac{1}{2}{\mathrm{kC}}_{\mathrm{B}}{\mathrm{C}}_{\mathrm{D}}^2$               (C) $4{\mathrm{kC}}_{\mathrm{B}}{\mathrm{C}}_{\mathrm{D}}^2$               (D) ${\mathrm{kC}}_{\mathrm{B}}{\mathrm{C}}_{\mathrm{D}}^2$

Sol: (A)  $\frac{-{\mathrm{dC}}_{\mathrm{B}}}{\mathrm{dt}}=\frac{-{\mathrm{dC}}_{\mathrm{D}}}{2\mathrm{dt}}={\mathrm{kC}}_{\mathrm{B}}{{\mathrm{C}}_{\mathrm{D}}}^2$

$\frac{{\mathrm{dC}}_{\mathrm{D}}}{\mathrm{dt}}=2{\mathrm{kC}}_{\mathrm{B}}{{\mathrm{C}}_{\mathrm{D}}}^2$

Prob 6. The time taken for 90% of a first order reaction to complete is approximately

(A)  1.1 times that of half–life

(B)  2.2 times that of half–life

(C)  3.3 times that of half–life

(D) 4.4 times that of half–life

Sol: (C) $t_{90}=\frac{2.303}{0.693}\times t_{1/2}\times \log \frac{100}{10}$

Prob 7. At 373 K, a gaseous reaction $\mathrm{A}⟶2\mathrm{B}+\mathrm{C}$ is found to be of first order. Starting with pure A, the total pressure at the end of 10 minutes was 176 mm and after a long time when A was completely dissociated, it was 270 mm. The pressure of A at the end of 10 minutes was

(A)  94 mm              (B)  47 mm              (C)  43 mm              (D)  90 mm

Sol: (B)

$$\begin{gathered} \mathrm{A}\to 2\mathrm{B} + \mathrm{C} \\ \mathrm{At} \mathrm{t}=0 \mathrm{P}° 0 0 \\ \mathrm{At} \mathrm{t}=10 \min . \mathrm{P}°–\mathrm{P} 2\mathrm{P} \mathrm{P} \\ \mathrm{At} \mathrm{t}=\infty 0 2\mathrm{P}° \mathrm{P}° \end{gathered}$$

Given that,

$$\begin{gathered} {\mathrm{P}}^0-\mathrm{P}+2\mathrm{P}+\mathrm{P}={\mathrm{P}}^{\circ }+2\mathrm{P}=176 ............ \left(1\right) \\ \mathrm{and} 2\mathrm{P}°+\mathrm{P}°=3\mathrm{P}°=270 ..............\left(2\right) \end{gathered}$$

Solving (1) and (2), we get

${\mathrm{P}}^{\circ }-\mathrm{P}=47\mathrm{mm}$

Prob 8. In the sequence of the reaction

$\mathrm{A}\stackrel{{\mathrm{k}}_1}{⟶}\mathrm{B}\stackrel{{\mathrm{k}}_2}{⟶}\mathrm{C}\stackrel{{\mathrm{k}}_3}{⟶}\mathrm{D}$,   given that ${\mathrm{k}}_1<{\mathrm{k}}_2<{\mathrm{k}}_3$ then the rate determining step of the reaction is

(A) A → D              (B) B → C              (B) C → D              (D) A → B

Sol: (D) Since k₁ is smallest hence slowest step is A → B

Prob 9. The rate law for a reaction between the substances A and B is given by

Rate = k[A]ⁿ [B]^m

On doubling the concentration of A and halving the concentration of B, the ratio of the new rate to the earlier rate of the reaction will be as

(A) $\frac{1}{2^{\left(\mathrm{m}+\mathrm{n}\right)}}$               (B) (m+n)              (C)  (n-m)              (D) $2^{\left(n–m\right)}$

Sol: (D)  Rate = k [A]ⁿ [B]^m

when A^‘ = 2A and B^‘  = 0.5 B

The new rate becomes Rate^‘ = [2A]ⁿ [0.5 B]^m

$\frac{\text{ Rate’ }}{\text{ Rate }}=\frac{\mathrm{k}{2}^{\mathrm{n}}\left[\mathrm{A}{]}^{\mathrm{n}}\right(0.5{)}^{\mathrm{m}}[\mathrm{B}{]}^{\mathrm{m}}}{\mathrm{k}\left[\mathrm{A}{]}^{\mathrm{n}}\right[\mathrm{B}{]}^{\mathrm{m}}}$

$=2^{\mathrm{n}}{\left(\frac{1}{2}\right)}^{\mathrm{m}}\Rightarrow \frac{\text{ Rate’}}{\text{ Rate }}=2^{(\mathrm{n}-\mathrm{m})}$

Prob10. The reaction A (g) + 2B(g) $\to$ C(g) + D(g) is an elementary process. In an experiment, the initial partial pressure of A & B are P_A = 0.60 and P_B = 0.80 atm. When P_C = 0.2 atm the rate of reaction relative to the initial rate is

(A) 1/48               (B) 1/24            (C) 9/16              (D) 1/6

Sol: (D)

$$\begin{gathered} \mathrm{A}\left(\mathrm{g}\right) + 2\mathrm{B}\left(\mathrm{g}\right) \to \mathrm{C}\left(\mathrm{g}\right) + \mathrm{D}\left(\mathrm{g}\right) \\ \mathrm{At} \mathrm{t}=0 0.6 0.8 0 0 \\ \mathrm{At} \mathrm{t}=\mathrm{t} 0.6–0.2 0.8–2\times 0.2 0.2 0.2 \end{gathered}$$

Initial rate (R₁) = k [A] [B]²

= k (0.6) (0.8)²

When P_C = 0.2

Rate (R₂) = k (0.6–0.2) (0.8–0.4)²

$\frac{{\mathrm{R}}_2}{{\mathrm{R}}_1}=\frac{1}{6}$.