Heron’s Formula

 EXERCISE-12.1

P1. A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ‘a’. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?

Sol. Side of traffic signal board = a

Perimeter of traffic signal board = 3 × a

$2s=3a\Rightarrow s=\frac{3}{2}a$

By Heron’s formula,

Area of triangle

$=\sqrt{s(s–a)(s–b)(s–c)}$

$=\sqrt{\frac{3}{2}a\left(\frac{3}{2}a–a\right)\left(\frac{3}{2}a–a\right)\left(\frac{3}{2}a–a\right)}$

$=\sqrt{\frac{3}{2}\mathrm{a}\left(\frac{\mathrm{a}}{2}\right)\left(\frac{\mathrm{a}}{2}\right)\left(\frac{\mathrm{a}}{2}\right)}$

$=\frac{\sqrt{3}}{4}{a}^2$

Perimeter of traffic signal board = 180 cm

Side of traffic signal board 

$\left(\mathrm{a}\right)=\left(\frac{180}{3}\right)\mathrm{cm}=60 \mathrm{cm}$

Using equation (1), area of traffic signal board $\frac{\sqrt{3}}{4}(60 \mathrm{cm}{)}^2$

$=\left(\frac{3600}{4}\sqrt{3}\right){\mathrm{cm}}^2=900\sqrt{3}{ \mathrm{cm}}^2$

P2. The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122m, 22m, and 120m (see the given figure). The advertisements yield an earning of Rs 5000 per m²per year. A company hired one of its walls for 3 months. How much rent did it pay?

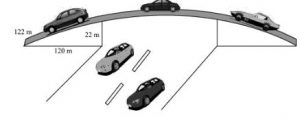
Sol. The sides of the triangle (i.e., a, b, c) are of 122 m, 22 m, and 120 m respectively.

Perimeter of triangle = (122 + 22 + 120) m

2s = 264 m

s = 132 m

By Heron’s formula,

Area of triangle

$=\sqrt{s(s–a)(s–b)(s–c)}$

$=\sqrt{132(132–122)(132–22)(132–120)}$

$\left[\sqrt{132\left(10\right)\left(110\right)\left(12\right)}\right]{\mathrm{m}}^2=1320{ \mathrm{m}}^2$

Rent of 1 m² area per year = Rs 5000

Rent of 1 m² area per month = Rs $\frac{5000}{12}$

Rent of 1320 m² area for 3 months = $Rs\left(\frac{5000}{12}\times 3\times 1320\right)$

= Rs (5000 × 330) = Rs 1650000

Therefore, the company had to pay Rs 1650000.

P3. There is a slide in the park. One of its side walls has been painted in the same colour with a message “KEEP THE PARK GREEN AND CLEAN” (see the given figure). If the sides of the wall are 15m, 11m, and 6m, find the area painted in colour.

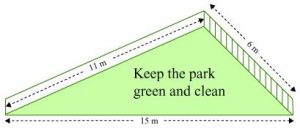
Sol. It can be observed that the area to be painted in colour is a triangle, having its sides as 11 m, 6 m, and 15 m.

Perimeter of such a triangle

= (11 + 6 + 15) m

2 s = 32 m

s = 16 m

By Heron’s formula,

Area of triangle

$=\sqrt{s(s–a)(s–b)(s–c)}$

$=\sqrt{16(16–11)(16–6)(16–15)}$

$=\left(\sqrt{16\times 5\times 10\times 1}\right){\mathrm{m}}^2$

$=20\sqrt{2}{ \mathrm{m}}^2$

Therefore, the area painted in colour is $20\sqrt{2}{m}^2$

P4.  Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.

Sol.  Let the third side of the triangle be x.

Perimeter of the given triangle = 42 cm

18 cm + 10 cm + x = 42

x = 14 cm

$s=\frac{\text{ Perimeter }}{2}=\frac{42 \mathrm{cm}}{2}=21 \mathrm{cm}$

By Heron’s formula,

Area of triangle

$=\sqrt{s(s–a)(s–b)(s–c)}$

Area of the given triangle= $\left(\sqrt{21(21–18)(21–10)(21–14)}\right){\mathrm{cm}}^2$

$=\sqrt{21\left(3\right)\left(11\right)\left(7\right)}{\mathrm{cm}}^2$

$=21\sqrt{11}{ \mathrm{cm}}^2$

P5.  Sides of a triangle are in the ratio of 12: 17: 25 and its perimeter is 540 cm. Find its area.

Sol.  Let the common ratio between the sides of the given triangle be x.

Therefore, the side of the triangle will be 12x, 17x, and 25x.

Perimeter of this triangle = 540 cm

12x + 17x + 25x = 540 cm

54x = 540 cm

x = 10 cm

Sides of the triangle will be 120 cm, 170 cm, and 250 cm.

$\mathrm{s}=\frac{\text{ Perimeter }}{2}=\frac{540 \mathrm{cm}}{2}=270 \mathrm{cm}$

By Heron’s formula,

Area of triangle

$=\sqrt{s(s–a)(s–b)(s–c)}$

$\left[\sqrt{270(270–120)(270–170)(270–250)}\right]{\mathrm{cm}}^2$

$=\left[\sqrt{270\times 150\times 100\times 20}\right]{\mathrm{cm}}^2$

=9000 cm²

Therefore, the area of this triangle is 9000 cm².

P6. An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.

Sol.  Let the third side of this triangle be x.

Perimeter of triangle = 30 cm

12 cm + 12 cm + x = 30 cm

x = 6 cm

$\mathrm{s}=\frac{\text{ Perimeter }}{2}=\frac{30 \mathrm{cm}}{2}=15 \mathrm{cm}$$=\sqrt{s(s–a)(s–b)(s–c)}$

By Heron’s formula,

Area of triangle

$=\sqrt{s(s–a)(s–b)(s–c)}$

$=\left[\sqrt{15(15–12)(15–12)(15–6)}\right]$

$=\left[\sqrt{15\left(3\right)\left(3\right)\left(9\right)}\right]{\mathrm{cm}}^2$

$=9\sqrt{15}{ \mathrm{cm}}^2$

EXERCISE-12.2

P1.  A park, in the shape of a quadrilateral ABCD, has ∠C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?

Sol. Let us join BD.

In ΔBCD, applying Pythagoras theorem,

BD² = BC² + CD²

= (12)² + (5)²

= 144 + 25

BD² = 169

BD = 13 m

$\text{Area of }\Delta \mathrm{BCD}=\frac{1}{2}\times \mathrm{BC}\times \mathrm{CD}$

$=\left(\frac{1}{2}\times 12\times 5\right){\mathrm{m}}^2=30{ \mathrm{m}}^2$

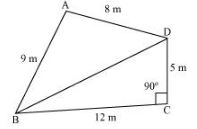
For ΔABD,

$s=\frac{\text{ Perimeter }}{2}=\frac{(9+8+13)\mathrm{cm}}{2}=15 \mathrm{cm}$

By Heron’s formula,

Area of triangle

$=\sqrt{s(s–a)(s–b)(s–c)}$

Area of ΔABD  $\left[\sqrt{15(15–9)(15–8)(15–13)}\right]{\mathrm{m}}^2$

$=\left(\sqrt{15\times 6\times 7\times 2}\right){\mathrm{m}}^2$

$=6\sqrt{35}{ \mathrm{m}}^2$

$=(6\times 5.916){\mathrm{m}}^2$

=35.496 m²

Area of the park = Area of ΔABD + Area of ΔBCD

= 35.496 + 30 m² = 65.496 m² = 65.5 m² (approximately)

P2. Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.

Sol.

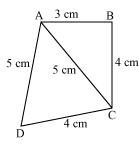
For ΔABC,

AC² = AB² + BC²

(5)² = (3)² + (4)²

Therefore, ΔABC is a right-angled triangle, right-angled at point B.

Area of ΔABC $\frac{1}{2}\times \mathrm{AB}\times \mathrm{BC}=\frac{1}{2}\times 3\times 4=6{ \mathrm{cm}}^2$

For ΔADC,

Perimeter = 2s = AC + CD + DA = (5 + 4 + 5) cm = 14 cm

s = 7 cm

By Heron’s formula,

Area of triangle

$=\sqrt{s(s–a)(s–b)(s–c)}$

This triangle is an isosceles triangle.

Perimeter = 2s = (5 + 5 + 1) cm = 11cm

$s=\frac{11 \mathrm{cm}}{2}=5.5 \mathrm{cm}$

Area of triangle

$=\sqrt{s(s–a)(s–b)(s–c)}$

$=\left[\sqrt{5.5(5.5–5)(5.5–5)(5.5–1)}\right]{\mathrm{cm}}^2$

$=\left[\sqrt{(5.5)(0.5)(0.5)(4.5)}\right]{\mathrm{cm}}^2$

$=0.75\sqrt{11}{ \mathrm{cm}}^2$

$=(0.75\times 3.317){\mathrm{cm}}^2$

$=2.488{ \mathrm{cm}}^2\text{ (approx.) }$

For quadrilateral II

This quadrilateral is a rectangle.

Area = l × b = (6.5 × 1) cm² = 6.5 cm²

For quadrilateral III

This quadrilateral is a trapezium.

Perpendicular height of parallelogram 

$=\left(\sqrt{1^2–(0.5{)}^2}\right)\mathrm{cm}$

$=\sqrt{0.75} \mathrm{cm}=0.866 \mathrm{cm}$

Area = Area of parallelogram + Area of equilateral triangle

$=(0.866)1+\frac{\sqrt{3}}{4}(1{)}^2$

= 0.866 + 0.433 = 1.299 cm²

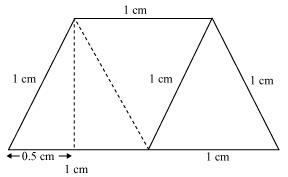
Area of triangle (IV)

= Area of triangle in (V)

$=\left(\frac{1}{2}\times 1.5\times 6\right){\mathrm{cm}}^2=4.5{ \mathrm{cm}}^2$

Total area of the paper used = 2.488 + 6.5 + 1.299 + 4.5 × 2

= 19.287 cm²

P4.  A triangle and a parallelogram have the same base and the same area. If the sides of triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.

Sol. For triangle

Perimeter of triangle

= (26 + 28 + 30) cm = 84 cm

2s = 84 cm

s = 42 cm

Area of triangle

$=\sqrt{s(s–a)(s–b)(s–c)}$

Area of triangle

$=\left[\sqrt{42(42–26)(42–28)(42–30)}\right]{\mathrm{cm}}^2$

$=\left[\sqrt{42\left(16\right)\left(14\right)\left(12\right)}\right]{\mathrm{cm}}^2=336{ \mathrm{cm}}^2$

Let the height of the parallelogram be h.

Area of parallelogram = Area of triangle

h × 28 cm = 336 cm²

h = 12 cm

Therefore, the height of the parallelogram is 12 cm.

P5. A rhombus shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, how much area of grass field will each cow be getting?

Sol.

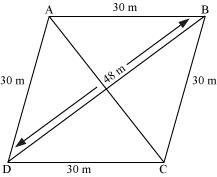
Let ABCD be a rhombus-shaped field.

For ΔBCD,

Semi-perimeter, $\mathrm{s}=\frac{(48+30+30)\mathrm{cm}}{2}=54$

Area of triangle

$=\sqrt{s(s–a)(s–b)(s–c)}$

Therefore, area of ΔBCD

$=\left[\sqrt{54(54–48)(54–30)(54–30)}\right]{\mathrm{m}}^2$

$\sqrt{54\left(6\right)\left(24\right)\left(24\right)}=3\times 6\times 24=432{ \mathrm{m}}^2$

Area of field = 2 × Area of ΔBCD

= (2 × 432) m² = 864 m²

Area for grazing for 1 cow $=\frac{864}{18}$

= 48 m²

Each cow will get 48 m² area of grass field.

P6.  An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see the given figure), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?

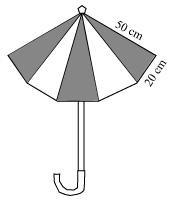
Sol. For each triangular piece,

Semi-perimeter, $s=\frac{(20+50+50)\mathrm{cm}}{2}=60 \mathrm{cm}$

By Heron’s formula,

Area of triangle

$=\sqrt{s(s–a)(s–b)(s–c)}$

Area of each triangular piece =

$\begin{array}{l}\left[\sqrt{60(60–50)(60–50)(60–20)}\right]{\mathrm{cm}}^2\\ =\left[\sqrt{60\left(10\right)\left(10\right)\left(40\right)}\right]{\mathrm{cm}}^2=200\sqrt{6}{ \mathrm{cm}}^2\end{array}$

Since there are 5 triangular pieces made of two different coloured cloths,

Area of each cloth required $(5\times 200\sqrt{6}){\mathrm{cm}}^2=1000\sqrt{6}{ \mathrm{cm}}^2$

P7.  A kite in the shape of a square with a diagonal 32 cm and an isosceles triangles of base 8 cm and sides 6 cm each is to be made of three different shades as shown in the given figure. How much paper of each shade has been used in it?

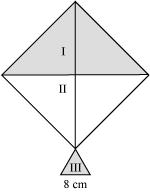
Sol. We know that

Area of square = $\frac{1}{2}$(diagonal)²

Area of the given kite 

$=\frac{1}{2}(32 \mathrm{cm}{)}^2=512{ \mathrm{cm}}^2$

Area of 1^st shade = Area of 2^nd shade

$=\frac{512{ \mathrm{cm}}^2}{2}=256{ \mathrm{cm}}^2$

Therefore, the area of paper required in each shape is 256 cm².

For III^rd triangle

Semi-perimeter, $s=\frac{(6+6+8)cm}{2}=10 \mathrm{cm}$

By Heron’s formula,

Area of triangle

$=\sqrt{s(s–a)(s–b)(s–c)}$

Area of III^rd triangle

$$\begin{gathered} \begin{array}{l}=\sqrt{10(10–6)(10–6)(10–8)}\\ =\left(\sqrt{10\times 4\times 4\times 2}\right){\mathrm{cm}}^2\\ =(4\times 2\sqrt{5}){\mathrm{cm}}^2\\ =8\sqrt{5}{ \mathrm{cm}}^2\end{array} \\ =(8\times 2.24){\mathrm{cm}}^2 \end{gathered}$$

=17.92 cm²

Area of paper required for III^rd shade = 17.92 cm²

P8. A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see the given figure). Find the cost of polishing the tiles at the rate of 50p per cm².

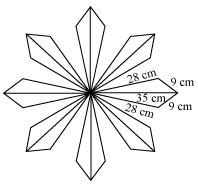
Sol.  It can be observed that

Semi-perimeter of each triangular-shaped tile, $s=\frac{(35+28+9)\mathrm{cm}}{2}=36 \mathrm{cm}$

By Heron’s formula,

Area of triangle

$=\sqrt{s(s–a)(s–b)(s–c)}$

Area of each tile 

$\begin{array}{l}=\left[\sqrt{36(36–35)(36–28)(36–9)}\right]{\mathrm{cm}}^2\\ =\left[\sqrt{36\times 1\times 8\times 27}\right]{\mathrm{cm}}^2\\ =36\sqrt{6}{ \mathrm{cm}}^2\\ =(36\times 2.45){\mathrm{cm}}^2\\ =88.2{ \mathrm{cm}}^2\end{array}$

Area of 16 tiles = (16 × 88.2) cm²= 1411.2 cm²

Cost of polishing per cm² area = 50 p

Cost of polishing 1411.2 cm² area = Rs (1411.2 × 0.50) = Rs 705.60

Therefore, it will cost Rs 705.60 while polishing all the tiles.

 P9. A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.

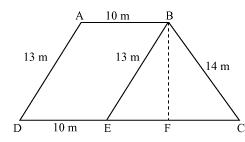
Draw a line BE parallel to AD and draw a perpendicular BF on CD.

It can be observed that ABED is a parallelogram.

BE = AD = 13 m

ED = AB = 10 m

EC = 25 − ED = 15 m

For ΔBEC,

Semi-perimeter,

$\mathrm{s}=\frac{(13+14+15)\mathrm{m}}{2}=21 \mathrm{m}$

By Heron’s formula,

Area of triangle

$=\sqrt{s(s–a)(s–b)(s–c)}$

Area of ΔBEC 

$\begin{array}{l}=\left[\sqrt{21(21–13)(21–14)(21–15)}\right]{\mathrm{m}}^2\\ =\left[\sqrt{21\left(8\right)\left(7\right)\left(6\right)}\right]{\mathrm{m}}^2=84{ \mathrm{m}}^2\end{array}$

Area of ΔBEC $\frac{1}{2}\times \mathrm{CE}\times \mathrm{BF}$

$\begin{array}{l}84{ \mathrm{cm}}^2=\frac{1}{2}\times 15 \mathrm{cm}\times \mathrm{BF}\\ \mathrm{BF}=\left(\frac{168}{15}\right)\mathrm{cm}=112 \mathrm{cm}\end{array}$

Area of ABED = BF × DE = 11.2 × 10 = 112 m²

Area of the field = 84 + 112 = 196 m²