NCERT TEXT BOOK EXERCISES
Q1. Classify the following as motion along a straight line, circular or oscillatory motion:
(i) Motion of your hands while running.
(ii) Motion of a horse pulling a cart on a straight road.
(iii) Motion of a child in a merry-go-round.
(iv) Motion of a child on a see-saw.
(v) Motion of the hammer of an electric bell.
(vi) Motion of a train on a straight bridge.
Ans. (i) Oscillatory motion
While running, the hands move to and fro and repeat their motion after a given interval of time. Hence, it is an oscillatory motion.
(ii) Straight line
The horse is pulling a cart on a straight road. Therefore, it has a motion along a straight line.
(iii) Circular motion
Merry-go-round has a circular motion. Therefore, a child sitting inside it will also have a circular motion.
(iv) Oscillatory motion
The child on a see-saw goes up and down continuously. It oscillates up-down. Therefore, it is an oscillatory motion.
(v) Oscillatory motion
The hammer hits the electric bell and vibrates rapidly. Therefore, it is an oscillatory motion.
(vi) Straight line
The train is moving on a straight bridge. Therefore, it has a motion along a straight line.
Q2. Which of the following are not correct?
(i) The basic unit of time is second.
(ii) Every object moves with a constant speed.
(iii) Distances between two cities are measured in kilometres.(iv) The time period of a given pendulum is not constant.
(v) The speed of a train is expressed in m/h.
Ans. (i) Correct
Second is the SI unit of time.
(ii) Not correct
An object can move with constant or variable speed.
(iii) Correct
The distance between two cities can be very large. Since kilometre is a bigger unit of distance, the distance between two cities is measured in kilometres.
(iv) Not correct
Time period of a pendulum depends on the length of the thread. Hence, it is constant for a particular pendulum.
(v) Not correct
The speed of a train is measured either in km/h or in m/s.
Q3. A simple pendulum takes 32 s to complete 20 oscillations. What is the time period of the pendulum?
Ans. Number of oscillations = 20
Total time taken to complete 20 oscillations = 32 s
Q4. The distance between two stations is 240 km. A train takes 4 hours to cover this distance. Calculate the speed of the train.
Ans. Distance between the two stations = 240 km
Time taken = 4 h
Q5. The odometer of a car reads 57321.0 km when the clock shows the time 08:30 AM. What is the distance moved by the car, if at 08:50 AM, the odometer reading has changed to 57336.0 km? Calculate the speed of the car in km/min during this time. Express the speed in km/h also.
Ans. Initial reading of the odometer of the car = 57321.0 km
Final reading of the odometer of the car = 57336.0 km
Distance covered by the car = Final reading of the odometer of the car − Initial reading of the odometer of the car
= 57336.0 − 57321.0 = 15 km
The given car starts at 8:30 a.m. and stops at 8:50 a.m.
Therefore, time taken by the car to cover the distance is (8:50 − 8:30) min = 20 min
Distance covered by the car = 15 km
Time taken by the car = 20 min
Again,
60 min = 1 h
Time taken by the car =
Q6. Salma takes 15 minutes from her house to reach her school on a bicycle. If the bicycle has a speed of 2 m/s, calculate the distance between her house and the school.
Ans. Time taken by Salma to reach her school from her home = 15 min = 15 60 = 900 s
Speed of her bicycle = 2 m/s
Distance covered = Speed Time taken = 2 900 = 1800 m
1000 m = 1 km
Q7. Show the shape of the distance-time graph for the motion in the following cases:
(i) A car moving with a constant speed.
(ii) A car parked on a side road.
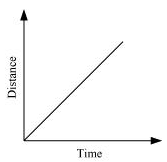
Ans. (i) A car moving with a constant speed covers equal distance in equal intervals of time. Such motion of car is represented in the given distance-time graph.
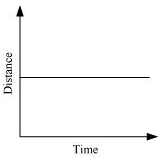
(ii) The distance-time graph of a car parked on a road side is such that with the increase in time, there is no change in distance, as shown in the given figure.
Q8. Which of the following relations is correct?
(i) Speed = Distance Time
(ii) Speed =
(iii)
(iv)
Ans. (ii) Speed of an object is given by the relation
Speed =
Q9. The basic unit of speed is:
(i) km/min
(ii) m/min
(iii) km/h
(iv) m/s
Ans. (iv) m/s
The basic unit of distance is metre (m).
The basic unit of time is second (s).
Therefore, the basic unit of speed is m/s.
Q10. A car moves with a speed of 40 km/h for 15 minutes and then with a speed of 60 km/h for the next 15 minutes. The total distance covered by the car is:
(i) 100 km
(ii) 25 km
(iii) 15 km
(iv) 10 km
Ans. (ii) 25 km
Case I
Speed of the car = 40 km/h
Distance covered, d1 = Speed Time taken = 40 0.25 = 10 km
Case II
Speed of the car = 60 km/h
Time taken = 15 min
Distance covered, d2 = Speed Time taken = 60 0.25 = 15 km
Total distance covered by the car, d = d1 d2 = 10 15 = 25 km
Therefore, the total distance covered by the car is 25 km.
Q11. Suppose the two photographs, shown in Figure 1 and Figure 2, had been taken at an interval of 10 seconds. If a distance of 100 metres is shown by 1 cm in these photographs, calculate the speed of the blue car.
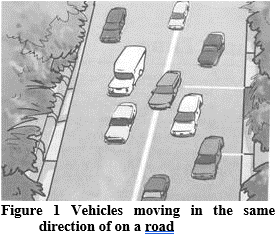
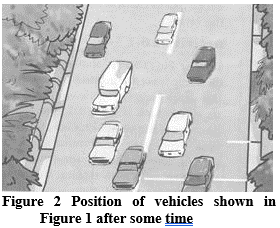
Ans. The distance covered by the blue car (as evident from the photograph) from one white strip to another, which is measured by scale is 1.4 cm.
It is given that 1 cm is equivalent to 100 m.
Therefore, 1.4 cm is equivalent to 140 m.
Distance travelled by the car = 140 m
Time interval between the two photographs = 10 s
Q12. Figure shows the distance-time graph for the motion of two vehicles A and B. Which one of them is moving faster?
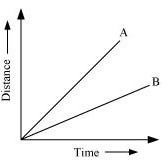
Distance-time graph for the motion of two cars
Ans. Vehicle A is moving faster than vehicle B.
Speed is given by the relation
This relation shows that speed of a vehicle is greater if it covers maximum distance in a given interval of time. To compare the distance, draw a line perpendicular to the time-axis, as shown in the following distance-time graph.
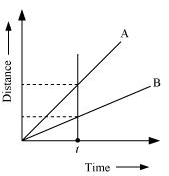
From the graph, it is evident that for a given time t, the distance covered by vehicle A is more than vehicle B. Hence, vehicle A is moving faster than vehicle B.
Q13. Which of the following distance-time graphs shows a truck moving with speed which is not constant?
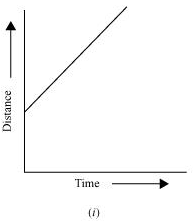
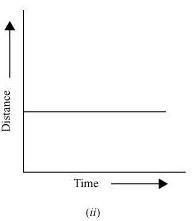
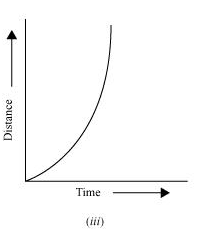
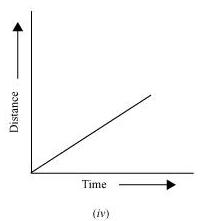
Ans. Graph (iii)
In a distance-time graph, the constant speed of a truck will be represented by a straight line.
In a distance-time graph, a straight line parallel to the time axis indicates that the truck is not moving.
A curved line on the distance-time graph indicates that the truck is moving with a speed which is not constant.








