Algebraic Expressions

EXERCISE-12.1

P1. Get the algebraic expressions in the following cases using variables, constants and arithmetic operations.

(i) Subtraction of z from y.

(ii) One-half of the sum of numbers x and y.

(iii) The number z multiplied by itself.

(iv) One-fourth of the product of numbers p and q.

(v) Numbers x and y both squared and added.

(vi) Number 5 added to three times the product of number m and n. (vii) Product of numbers y and z subtracted from 10.

(viii) Sum of numbers a and b subtracted from their product.

Sol. (i) y − z

(ii)$\frac{1}{2}\left(\mathrm{x}+\mathrm{y}\right)$

(iii)  z²

(iv)$\frac{1}{4}\left(\mathrm{pq}\right)$

(v) x² + y²

(vi) 5 + 3 (mn)

(vii) 10 − yz

(viii)  ab − (a + b)

P2. (i)Identify the terms and their factors in the following expressions Show the terms and factors by tree diagrams.

(a) x − 3

(b) 1 + x + x²

(c) y − y³

(d) $\mathbf{5}{\mathbf{xy}}^{\mathbf{2}}\mathbf{+}\mathbf{7}{\mathbf{x}}^{\mathbf{2}}\mathbf{y}$

(e) − ab + 2b² − 3a²

(ii) Identify terms and factors in the expressions given below:

(a) − 4x + 5

(b) − 4x + 5y 

(c) 5y + 3y²

(d) xy + 2x²y² 

(e) pq + q

(f) 1.2 ab − 2.4 b + 3.6 a 

(g) $\frac{\mathbf{3}}{\mathbf{4}}\mathbf{x}\mathbf{+}\frac{\mathbf{1}}{\mathbf{4}}$

(h) 0.1p² + 0.2 q²

Sol. (i) (a)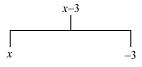

(b)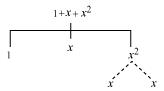

(c)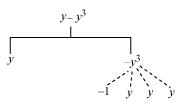

(d)

(e)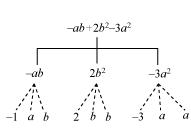

(ii)

Row	Expression	Terms	Factors
(a)	− 4x + 5	− 4x 5	− 4, x 5
(b)	− 4x + 5y	− 4x 5y	− 4, x 5, y
(c)	5y + 3y2	5y 3y2	5, y 3, y, y
(d)	xy + 2x2y2	xy 2x2y2	x, y 2, x, x, y, y
(e)	pq + q	pq q	p, q q
(f)	1.2ab − 2.4b + 3.6a	1.2ab − 2.4b 3.6a	1.2, a, b − 2.4, b 3.6, a
(g)	$\frac{3}{4}x+\frac{1}{4}$	$$\begin{gathered} \frac{3}{4}x \\ \frac{1}{4} \end{gathered}$$	$\frac{3}{4}$, x, $\frac{1}{4}$
(h)	0.1p2 + 0.2q2	0.1p2 0.2q2	0.1, p, p 0.2, q, q

 P3. Identify the numerical coefficients of terms (other than constants) in the following expressions:

(i) 5 − 3t²

(ii) 1 + t + t² + t³ 

(iii) x + 2xy+ 3y

(iv) 100m + 1000n 

(v) − p²q² + 7pq

(vi) 1.2a + 0.8b

(vii) 3.14 r²

(viii) 2 (l + b)

(ix) 0.1y + 0.01 y²

Sol.

Row	Expression	Terms	Coefficients
(i)	5 − 3t2	− 3t2	− 3
(ii)	1 + t + t2 + t3	t t2 t3	1 1 1
(iii)	x + 2xy + 3y	x 2xy 3y	1 2 3
(iv)	100m + 1000n	100m 1000n	100 1000
(v)	− p2q2 + 7pq	− p2q2 7pq	− 1 7
(vi)	1.2a +0.8b	1.2a 0.8b	1.2 0.8
(vii)	3.14 r2	3.14 r2	3.14
(viii)	2(l + b)	2l 2b	2 2
(ix)	0.1y + 0.01y2	0.1y 0.01y2	0.1 0.01

P4. (a) Identify terms which contain x and give the coefficient of x.

(i) y²x + y

(ii) 13y²− 8yx 

(iii) x + y + 2

(iv) 5 + z + zx 

(v) 1 + x+ xy

(vi) 12xy² + 25

(vii) 7x + xy²

(b) Identify terms which contain y² and give the coefficient of y².

(i) 8 − xy² 

(ii) 5y² + 7x 

(iii) 2x²y −15xy² + 7y²

Sol. (a)

Row	Expression	Terms with x	Coefficient of x
(i)	y2x + y	y2x	y2
(ii)	13y2 − 8yx	− 8yx	−8y
(iii)	x + y + 2	x	1
(iv)	5 + z + zx	zx	z
(v)	1 + x + xy	x xy	1 y
(vi)	12xy2 + 25	12xy2	12y2
(vii)	7x+ xy2	7x xy2	7 y2

(b)

Row	Expression	Terms with y2	Coefficient of y2
(i)	8 − xy2	−xy2	− x
(ii)	5y2 + 7x	5y2	5
(iii)	2x2y + 7y2 −15xy2	7y2 −15xy2	7 −15x

 P5. Classify into monomials, binomials and trinomials.

(i) 4y − 7z

(ii) y²

(iii) x + y − xy

(iv) 100

(v) ab − a − b

(vi) 5 − 3t

(vii) 4p²q − 4pq²

(viii) 7mn

(ix) z² − 3z + 8

(x) a² + b²

(xi) z² + z

(xii) 1 + x + x²

Sol. The monomials, binomials, and trinomials have 1, 2, and 3 unlike terms in it respectively.

(i) 4y − 7z $\Rightarrow$ Binomial

(ii) y² $\Rightarrow$ Monomial

(iii) x + y – xy $\Rightarrow$ Trinomial

(iv) 100 $\Rightarrow$Monomial

(v) ab − a – b $\Rightarrow$ Trinomial

(vi) 5 − 3t $\Rightarrow$ Binomial

(vii) 4p²q − 4pq² $\Rightarrow$ Binomial

(viii) 7mn $\Rightarrow$ Monomial

(ix) z² − 3z + 8 $\Rightarrow$ Trinomial

(x) a² + b² $\Rightarrow$ Binomial

(xi) z² + z $\Rightarrow$ Binomial

(xii) 1 + x + x² $\Rightarrow$ Trinomial

P6. State whether a given pair of terms is of like or unlike terms.

(i) 1, 100

(ii) $\mathbf{-}\mathbf{7}\mathbf{x}\mathbf{,}\frac{\mathbf{5}}{\mathbf{2}}\mathbf{x}$ 

(iii) − 29x, − 29y

(iv) 14xy, 42yx

(v) 4m²p, 4mp²

(vi) 12xz, 12 x²z²

Sol. The terms which have the same algebraic factors are called like terms. However, when the terms have different algebraic factors, these are called unlike terms.

(i) 1, 100 $\Rightarrow$ Like

(ii) − 7x, $\frac{5}{2}$x $\Rightarrow$ Like

(iii) −29x, −29y $\Rightarrow$ Unlike

(iv) 14xy, 42yx $\Rightarrow$ Like

(v) 4m²p, 4mp² $\Rightarrow$ Unlike

(vi) 12xz, 12x²z² $\Rightarrow$ Unlike

P7. Identify like terms in the following:

(a) −xy², − 4yx², 8x², 2xy², 7y, − 11x², − 100x, −11yx, 20x²y, −6x², y, 2xy,3x

(b) 10pq, 7p, 8q, − p²q², − 7qp, − 100q, − 23, 12q²p², − 5p², 41, 2405p, 78qp, 13p²q, qp², 701p²

Sol. (a) −xy², 2xy²

−4yx², 20x²y

8x², −11x², −6x²

7y, y

−100x, 3x

−11xy, 2xy

(b) 10pq, −7qp, 78qp

7p, 2405p

8q, −100q

−p²q², 12p²q²

−23, 41

−5p², 701p²

13p²q, qp²

EXERCISE-12.2

P1. Simplify combining like terms:

(i) 21b − 32 + 7b − 20b

(ii) − z² + 13z² − 5z + 7z³ − 15z

(iii) p − (p − q) − q − (q − p)

(iv) 3a−2b−ab − (a − b + ab) + 3ab + b − a

(v) 5x²y − 5x² + 3y x² − 3y² + x² − y² + 8xy² −3y²

(vi) (3 y² + 5y − 4) − (8y − y² − 4)

Sol. (i) 21b − 32 + 7b − 20b = 21b + 7b − 20b − 32

= b (21 + 7 − 20) −32

= 8b − 32

(ii) − z² + 13z² − 5z + 7z³ − 15z = 7z³ − z² + 13z² − 5z − 15z

= 7z³ + z² (−1 + 13) + z (−5 − 15)

= 7z³ + 12z² − 20z

(iii)  p − (p − q) − q − (q − p)

= p − p + q − q − q + p

= p − q

(iv) 3a − 2b − ab − (a − b + ab) + 3ba + b − a

= 3a − 2b − ab − a + b − ab + 3ab+b− a

= 3a − a − a − 2b + b + b –ab −ab+ 3ab

= a (3 − 1 − 1) + b (− 2 + 1 + 1) + ab (−1 −1 + 3)

= a + ab

(v) 5x²y − 5x² + 3yx² − 3y² + x² − y² + 8xy² − 3y²

= 5x²y + 3yx² − 5x² + x² − 3y² − y² − 3y² + 8xy²

= x²y (5 + 3) + x² (−5 + 1)+ y²(−3−1− 3) + 8xy²

= 8x²y − 4x² − 7y² + 8xy²

(vi) (3y² + 5y − 4) − (8y − y² − 4)

= 3y² + 5y − 4 − 8y + y² + 4

= 3y² + y² + 5y − 8y − 4 + 4

= y² (3 + 1) + y (5 − 8) + 4 (1 − 1)

= 4y² − 3y

P2. Add:

(i) 3mn, − 5mn, 8mn, −4mn

(ii) t − 8tz, 3tz − z, z − t

(iii) − 7mn+5, 12mn+2, 9mn − 8, − 2mn − 3

(iv) a + b − 3, b − a + 3, a − b + 3

(v) 14x + 10y − 12xy − 13, 18 − 7x − 10y + 8xy, 4xy

(vi) 5m − 7n, 3n − 4m + 2, 2m − 3mn − 5

(vii) 4x²y, − 3xy², − 5xy², 5x²y

(viii) 3p²q² − 4pq + 5, − 10p²q², 15 + 9pq + 7p²q²

(ix) ab − 4a, 4b − ab, 4a − 4b

(x) x² − y² − 1 , y² − 1 − x², 1− x² − y²

Sol. (i) 3mn + (−5mn) + 8mn + (−4mn) = mn (3 − 5 + 8 − 4) = 2mn

(ii) (t − 8tz) + (3tz − z) + (z − t)

= t − 8tz + 3tz − z + z − t

= t − t − 8tz + 3tz − z + z

= t (1 − 1) + tz (− 8 + 3) + z (− 1 + 1)

= −5tz

(iii) (− 7mn + 5) + (12mn + 2) + (9mn − 8) + (− 2mn − 3)

= − 7mn + 5 + 12mn + 2 + 9mn − 8 − 2mn − 3

= − 7mn + 12mn + 9mn − 2mn + 5 + 2 − 8 − 3

= mn (− 7 + 12 + 9 − 2) + (5 + 2 − 8 − 3)

= 12mn − 4

(iv) (a + b − 3) + (b − a + 3) + (a − b + 3)

= a + b − 3 + b − a + 3 + a − b + 3

= a − a + a + b + b − b − 3 + 3 + 3

= a (1 − 1 + 1) + b (1 + 1 − 1) + 3 (− 1 + 1 + 1)

= a + b + 3

(v) (14x + 10y − 12xy − 13) + (18 − 7x − 10y + 8yx) + 4xy

= 14x + 10y − 12xy − 13 + 18 − 7x − 10y + 8yx + 4xy

= 14x − 7x + 10y − 10y − 12xy + 8yx + 4xy − 13 + 18

= x (14 − 7) + y (10 − 10) + xy (− 12 + 8 + 4) − 13 + 18

= 7x + 5

(vi) (5m − 7n) + (3n − 4m + 2) + (2m − 3mn − 5)

= 5m − 7n +3n−4m + 2 + 2m − 3mn − 5

= 5m − 4m +2m−7n + 3n − 3mn + 2 − 5

= m (5 − 4 + 2) + n (− 7 + 3) −3mn + 2 − 5

= 3m − 4n − 3mn − 3

(vii) 4x² y − 3xy² − 5xy² + 5x²y = 4x² y + 5x²y − 3xy² − 5xy²

= x² y (4 + 5) + xy² (− 3 − 5)

= 9x²y − 8xy²

(viii) (3p²q² − 4pq + 5) + (−10 p²q²) + (15 + 9pq + 7p²q²)

= 3p²q² − 4pq + 5 − 10 p²q² + 15 + 9pq + 7p²q²

= 3p²q² − 10 p²q² + 7p²q² − 4pq + 9pq + 5 + 15

= p²q² (3 − 10 + 7) + pq (− 4 + 9) + 5 + 15

= 5pq + 20

(ix) (ab − 4a) + (4b − ab) + (4a − 4b)

= ab − 4a + 4b − ab + 4a − 4b

= ab − ab − 4a + 4a + 4b − 4b

= ab (1 − 1) + a (− 4 + 4) + b(4 − 4)

= 0

(x) (x² − y² − 1) + (y² − 1 − x²)+(1 − x² − y²)

= x² − y² − 1 + y² − 1 − x² + 1 − x² − y²

= x² − x² − x² − y² + y² − y² − 1 − 1 + 1

= x²(1 − 1 − 1) + y² (−1 + 1 − 1) + (− 1 − 1 + 1)

= − x² − y² − 1

P3. Subtract:

(i) − 5y² from y²

(ii) 6xy from − 12xy

(iii) (a − b) from (a + b)

(iv) a (b − 5) from b (5 − a)

(v) − m² + 5mn from 4m² − 3mn + 8

(vi) − x² + 10x − 5 from 5x − 10

(vii) 5a² − 7ab + 5b² from 3ab − 2a² −2b²

(viii) 4pq − 5q² − 3p² from 5p² + 3q² − pq

Sol. (i) y² − (−5y²) = y² + 5y² = 6y²

(ii) − 12xy − (6xy) = −18xy

(iii) (a + b) − (a − b) = a + b − a + b = 2b

(iv) b (5 − a) − a (b − 5) = 5b − ab − ab + 5a = 5a + 5b − 2ab

(v) (4m² − 3mn + 8) − (− m² + 5mn) = 4m² − 3mn + 8 + m² − 5 mn

= 4m² + m² − 3mn − 5 mn + 8

= 5m² − 8mn + 8

(vi) (5x − 10) − (− x² + 10x − 5) = 5x − 10 + x² − 10x + 5

= x² + 5x − 10x − 10 + 5

= x² − 5x − 5

(vii) (3ab − 2a² − 2b²) − (5a²− 7ab + 5b²)

= 3ab − 2a² − 2b² − 5a² + 7ab − 5 b²

= 3ab + 7ab − 2a² − 5a² − 2b² − 5 b²

= 10ab − 7a² − 7b²

(viii) 4pq − 5q² − 3p² from 5p² + 3q² − pq

(5p² + 3q² − pq) − (4pq − 5q²− 3p²)

= 5p² + 3q² − pq − 4pq + 5q² + 3p²

= 5p² + 3p² + 3q² + 5q² − pq − 4pq

= 8p² + 8q² − 5pq

P4. (a) What should be added to x² + xy + y² to obtain 2x² + 3xy?

(b) What should be subtracted from 2a + 8b + 10 to get − 3a + 7b + 16?

Sol. (a) Let a be the required term.

a + (x² + y² + xy) = 2x² + 3xy
a = 2x² + 3xy − (x² + y² + xy)

a = 2x² + 3xy − x² − y² − xy

a = 2x² − x² − y² + 3xy − xy = x² − y² + 2xy

(b) Let p be the required term.

(2a + 8b + 10) − p = − 3a + 7b + 16

p = 2a + 8b + 10 − (− 3a + 7b + 16)

= 2a + 8b + 10 + 3a − 7b − 16

= 2a + 3a + 8b − 7b + 10− 16

= 5a + b − 6

P5. What should be taken away from 3x² − 4y² + 5xy + 20 to obtain − x² − y² + 6xy + 20?

Sol. Let p be the required term.

(3x² − 4y² + 5xy + 20) − p = − x² − y² + 6xy + 20

p = (3x² − 4y² + 5xy + 20) − (− x² − y² + 6xy + 20)

= 3x² − 4y² + 5xy +20+x²+ y² − 6xy − 20

= 3x² + x² − 4y² + y² + 5xy−6xy+20 − 20

= 4x² − 3y² − xy

P6. (a) From the sum of 3x − y + 11 and − y − 11, subtract 3x − y − 11.

(b) From the sum of 4 + 3x and 5 − 4x + 2x², subtract the sum of 3x² − 5x and  − x² + 2x + 5.

Sol. (a) (3x − y + 11) + (− y − 11)

= 3x − y + 11 − y − 11

= 3x − y − y + 11 − 11

= 3x − 2y

(3x − 2y) − (3x − y − 11)

= 3x − 2y − 3x + y + 11

= 3x − 3x − 2y + y + 11

= − y + 11

(b) (4 + 3x) + (5 − 4x + 2x²) = 4 + 3x + 5 − 4x + 2x²

= 3x − 4x + 2x² + 4 + 5

= − x + 2x² + 9

(3x² − 5x) + (− x² + 2x + 5) = 3x² − 5x − x² + 2x + 5

= 3x² − x² − 5x + 2x + 5

= 2x² − 3x + 5

(− x + 2x² + 9) − (2x² − 3x + 5)

= − x + 2x² + 9 − 2x² + 3x − 5

= − x + 3x + 2x² − 2x² + 9 − 5

= 2x + 4

EXERCISE-12.3

P1. If m = 2, find the value of:

(i) m − 2

(ii) 3m − 5

(iii) 9 − 5m

(iv) 3m² − 2m − 7

(v) $\frac{\mathbf{5}\mathbf{m}}{\mathbf{2}}\mathbf{-}\mathbf{4}$

Sol. (i) m − 2 = 2 − 2 = 0

(ii) 3m − 5 = (3 × 2) − 5 = 6 − 5 = 1

(iii) 9 − 5m = 9 − (5 × 2) = 9 −10 = −1

(iv) 3m² − 2m − 7 = 3 × (2 × 2) − (2 × 2) − 7 = 12 − 4 − 7 = 1

(v) $\frac{5\mathrm{m}}{2}-4=\left(\frac{5\times 2}{5}\right)-4=1$

P2. If p = −2, find the value of:

(i) 4p + 7

(ii) −3p² + 4p + 7

(iii) −2p³ − 3p² + 4p + 7

Sol. (i) 4p + 7 = 4 × (−2) + 7 = − 8 + 7 = −1

(ii) − 3p² + 4p + 7 = −3 (−2) × (−2) + 4 × (−2) + 7 = − 12 − 8 + 7 = −13

(iii) −2p³ − 3p² + 4p + 7

= −2 (−2) × (−2) × (−2) − 3 (−2) × (−2) + 4 × (−2) + 7

= 16 − 12 − 8 + 7 = 3

P3. Find the value of the following expressions, when x = − 1:

(i) 2x − 7

(ii) − x + 2

(iii) x² + 2x + 1

(iv) 2x² − x − 2

Sol. (i) 2x − 7 = 2 × (−1) − 7 = −9

(ii) − x + 2 = − (−1) + 2 = 1 + 2 = 3

(iii) x² + 2x + 1 = (−1) × (−1) + 2 × (−1) + 1 = 1 − 2 + 1 = 0

(iv) 2x² − x − 2 = 2 (−1) × (−1) − (−1) − 2 = 2 + 1 − 2 = 1

P4. If a = 2, b = − 2, find the value of:

(i) a² + b²

(ii) a² + ab + b²

(iii) a² − b²

Sol. (i) a² + b² = (2)² + (−2)² = 4 + 4 = 8

(ii) a² + ab + b² = (2 × 2) + 2 × (−2) + (−2) × (−2) = 4 − 4 + 4 = 4

(iii) a² − b² = (2)² − (−2)² = 4 − 4 = 0

P5. When a = 0, b = − 1, find the value of the given expressions:

(i) 2a + 2b 

(ii) 2a² + b² + 1

(iii) 2a² b + 2ab² + ab

(iv) a² + ab + 2

Sol. (i) 2a + 2b = 2 × (0) + 2 × (−1) = 0 − 2 = −2

(ii) 2a² + b² + 1 = 2 × (0)² + (−1) × (−1) + 1 = 0 + 1 + 1 = 2

(iii) 2a²b + 2ab² + ab = 2 × (0)² × (−1) + 2 × (0) × (−1) × (−1) + 0 × (−1) = 0 + 0 + 0 = 0

(iv) a² + ab + 2 = (0)² + 0 × (−1) + 2 = 0 + 0 + 2 = 2

P6. Simplify the expressions and find the value if x is equal to 2

(i) x + 7 + 4 (x − 5)

(ii) 3 (x + 2) + 5x − 7

(iii) 6x + 5 (x − 2)

(iv) 4 (2x −1) + 3x + 11

Sol. (i) x + 7 + 4 (x − 5) = x + 7 + 4x − 20

= x + 4x + 7 − 20

= 5x − 13

= (5 × 2) − 13

= 10 − 13 = −3

(ii) 3 (x + 2) + 5x − 7 = 3x + 6 + 5x − 7

= 3x + 5x + 6 − 7 = 8x − 1

= (8 × 2) − 1 = 16 − 1 =15

(iii) 6x + 5 (x − 2) = 6x + 5x − 10

= 11x − 10

= (11 × 2) − 10 = 22 − 10 = 12

(iv) 4 (2x − 1) + 3x + 11 = 8x − 4 + 3x + 11

= 11x + 7

= (11 × 2) + 7

= 22 + 7 = 29

P7. Simplify these expressions and find their values if x = 3, a = − 1, b = − 2.

(i) 3x − 5 − x + 9

(ii) 2 − 8x + 4x + 4

(iii) 3a + 5 − 8a + 1

(iv) 10 − 3b − 4 − 5b

(v) 2a − 2b − 4 − 5 + a

Sol. (i)3x − 5 − x + 9

= 3x − x − 5 + 9

= 2x + 4

= (2 × 3) + 4

= 10

(ii) 2 − 8x + 4x + 4

= 2 + 4 − 8x + 4x

= 6 − 4x = 6 − (4 × 3)

= 6 − 12 = −6

(iii) 3a + 5 − 8a + 1

= 3a − 8a + 5 + 1

= − 5a + 6 = −5 × (−1) + 6

= 5 + 6 = 11

(iv) 10 − 3b − 4 − 5b 

= 10 − 4− 3b − 5b

= 6 − 8b = 6 − 8 × (−2)

= 6 + 16 = 22

(v) 2a − 2b − 4 − 5 + a

= 2a + a − 2b − 4 − 5

= 3a − 2b − 9s

= 3 × (−1) − 2 (−2) − 9

= − 3 + 4 − 9 = −8

P7. Simplify these expressions and find their values if x = 3, a = − 1, b = − 2.

(i) 3x − 5 − x + 9

(ii) 2 − 8x + 4x + 4

(iii) 3a + 5 − 8a + 1

(iv) 10 − 3b − 4 − 5b

(v) 2a − 2b − 4 − 5 + a

Sol. (i) 3x − 5 − x + 9

= 3x − x − 5 + 9

= 2x + 4

= (2 × 3) + 4

= 10

(ii) 2 − 8x + 4x + 4

= 2 + 4 − 8x + 4x

= 6 − 4x 

= 6 − (4 × 3)

= 6 − 12 = −6

(iii) 3a + 5 − 8a + 1

= 3a − 8a + 5 + 1

= − 5a + 6

= −5 × (−1) + 6

= 5 + 6 = 11

(iv) 10 − 3b − 4 − 5b 

= 10 − 4− 3b − 5b

= 6 − 8b 

= 6 − 8 × (−2)

= 6 + 16

= 22

(v) 2a − 2b − 4 − 5 + a

= 2a + a − 2b − 4 − 5

= 3a − 2b − 9s

= 3 × (−1) − 2 (−2) − 9

= − 3 + 4 − 9 = −8

P9.What should be the value of a if the value of 2x² + x − a equals to 5, when x = 0?

Sol. 2x² + x − a = 5, when x = 0

(2 × 0) + 0 − a = 5

0 − a = 5

a = −5

P10. Simplify the expression and find its value when a = 5 and b = −3.

2 (a² + ab) + 3 − ab

Sol. 2 (a² + ab) + 3 − ab 

= 2a² + 2ab + 3 − ab

= 2a² + 2ab − ab + 3

= 2a² + ab + 3

= 2 × (5 × 5) + 5 × (−3) + 3

= 50 − 15 + 3 = 38

EXERCISE-12.4

P1. Observe the patterns of digits made from line segments of equal length. You will find such segmented digits on the display of electronic watches or calculators.

If the number of digits formed is taken to be n, the number of segments required to form n digits is given by the algebraic expression appearing on the right of each pattern.

How many segments are required to form 5, 10, 100 digits of the kind −

Sol. (a) It is given that the number of segments required to form n digits of the kind  is (5n + 1).

Number of segments required to form 5 digits = (5 × 5 + 1)

= 25 + 1 = 26

Number of segments required to form 10 digits = (5 × 10 + 1)

= 50 + 1 = 51

Number of segments required to form 100 digits = (5 × 100 + 1)

= 500 + 1 = 501

(b) It is given that the number of segments required to form n digits of the kind  is (3n + 1).

Number of segments required to form 5 digits = (3 × 5 + 1)

= 15 + 1 = 16

Number of segments required to form 10 digits = (3 × 10 + 1)

= 30 + 1 = 31

Number of segments required to form 100 digits = (3 × 100 + 1)

= 300 + 1 = 301

(c) It is given that the number of segments required to form n digits of the kind  is (5n + 2).

Number of segments required to form 5 digits = (5 × 5 + 2)

= 25 + 2 = 27

Number of segments required to form 10 digits = (5 × 10 + 2)

= 50 + 2 = 52

Number of segments required to form 100 digits = (5 × 100 + 2)

= 500 + 2 = 502

P2. Use the given algebraic expression to complete the table of number patterns.

S. No	Expression	Terms
		1st	2nd	3rd	4th	5th	…	10th	…	100th	…
(i)	2n − 1	1	3	5	7	9	–	19	–	–	–
(ii)	3n + 2	2	5	8	11	–	–	–	–	–	–
(iii)	4n + 1	5	9	13	17	–	–	–	–	–	–
(iv)	7n + 20	27	34	41	48	–	–	–	–	–	–
(v)	n2 + 1	2	5	10	17	–	–	–	–	10, 001	–

Sol.    The given table can be completed as follows.

S.No.	Expression	Terms
		1st	2nd	3rd	4th	5th	…	10th	…	100th	…
(i)	2n − 1	1	3	5	7	9	–	19	–	199	–
(ii)	3n + 2	2	5	8	11	17	–	32	–	302	–
(iii)	4n + 1	5	9	13	17	21	–	41	–	401	–
(iv)	7n + 20	27	34	41	48	55	–	90	–	720	–
(v)	n2 + 1	2	5	10	17	26	–	101	–	10,001-	–