Practical Geometry

EXERCISE-14.1

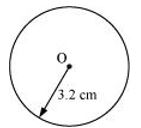
P1. Draw a circle of radius 3.2 cm.

Sol. The required circle can be drawn as follows.

Step 1

First, open the compasses for the required radius 3.2 cm.

Step 2

Mark a point ‘O’ where we want the centre of the circle to be.

Step 3

Place the pointer of compasses on O.

Step 4

Turn the compasses slowly to draw the circle.

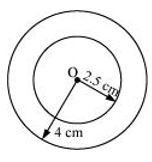
P2. With the same centre O, draw two circles of radii 4 cm and 2.5 cm.

Sol. The required circle can be drawn as follows.

Step 1

First, open the compasses for the required radius 4 cm.

Step 2

Mark a point ‘O’ where we want the centre of the circle to be.

Step 3

Place the pointer of compasses on O.

Step 4

Turn the compasses slowly to draw the circle.

Step 5

Now, open the compasses for 2.5 cm.

Step 6

Again put the pointer of the compasses on point ‘O’ and turn the compasses slowly to draw the circle.

P3. Draw a circle and any two of its diameters. If you join the ends of these diameters, what is the figure obtained ? What figure is obtained if the diameters are perpendicular to each other? How do you check your answer ?

Sol. A circle can be drawn of any convenient radius, also having its centre as O. Let AB and CD be two diameters of this circle. When we join the ends of these diameters, a quadrilateral ACBD is formed.

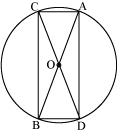
As we know that the diameters of a circle are equal in length, therefore, the quadrilateral so formed will have its diagonals of equal length.

Also, OA = OB = OC = OD = radius r and if a quadrilateral has its diagonals of same length which are bisecting each other, then it will be a rectangle.

Let DE and FG be two diameters of this circle such that these are perpendicular to each other. A quadrilateral is formed by joining the ends of these diameters.

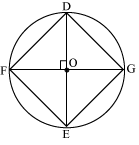
Here, OD = OE = OF = OG = radius r

In this quadrilateral DFEG, the diagonals are equal and perpendicular to each other. Also, since these are bisecting each other, it will be a square.

The length of the sides of the quadrilateral so formed can be measured to check our answers.

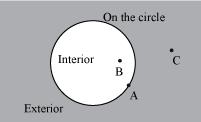
P4. Draw any circle and mark points A, B and C such that

(a) A is on the circle.

(b) B is in the interior of the circle.

(c) C is in the exterior of the circle.

Sol. A circle and three required points A, B, C can be drawn as follows.

P5. Let A, B be the centres of two circles of equal radii; draw them so that each one of them passes through the centre of the other. Let them intersect at C and D. Examine whether $\overline{AB}$ and $\overline{CD}$ are at right angles.

Sol. Let us draw two circles of same radius which are passing through the centres of the other circle.

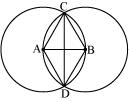
Here, point A and B are the centres of these circles and these circles are intersecting each other at point C and D.

In quadrilateral ADBC,

AD = AC (Radius of circle centered at A)

BC = BD (Radius of circle centered at B)

As radius of both circles are equal, therefore, AD = AC = BC = BD

Hence, $ADBC$ is a rhombus and in a rhombus, the diagonals bisect each other at 90°. Hence, $\overline{AB}$ and $\overline{CD}$ are at right angles.

EXERCISE-14.2

P1. Draw a line segment of length 7.3 cm using a ruler.

Sol. A line segment of length 7.3 cm can be drawn using a ruler as follows.

(1) Mark a point A on the sheet.

(2) Put 0 mark of ruler at point A.

(3) Mark a point B on the sheet at 7.3 cm on ruler.

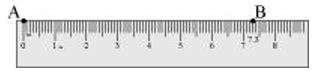
(4) Join A and B. $\overline{AB}$ is the required line segment.

P2. Construct a line segment of length 5.6 cm using ruler and compasses.

Sol. A line segment of length 5.6 cm can be drawn using a ruler and compasses as follows.

(1) Draw a line l and mark a point A on this line.

(2) Place the compasses on the zero mark of the ruler. Open it to place the pencil up to the 5.6 cm mark.

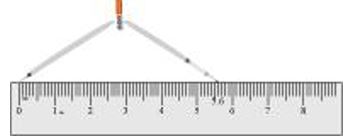
(3) Place the pointer of compasses on point A and draw an arc to cut l at B. AB is the line segment of 5.6 cm length.

P3. Construct $\overline{AB}$ of length 7.8 cm. From this, cut off $\overline{AC}$ of length 4.7 cm. Measure $\overline{BC}$.

Sol. (1) Draw a line l and mark a point A on it.

(2) By adjusting the compasses up to 7.8 cm, draw an arc to cut l on B, while putting the pointer of compasses on point A.

$\overline{AB}$ is the line segment of 7.8 cm.

(3) By adjusting the compasses up to 4.7 cm, draw an arc to cut l on C, while putting the pointer of compasses on point A.  $\overline{AC}$ is the line segment of 4.7 cm.

(4) Now, put the ruler along with this line such that 0 mark of the ruler will match with point C.

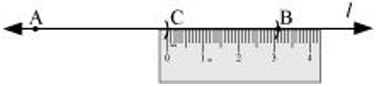
On reading the position of point B, it comes to 3.1 cm. $\overline{BC}$ is 3.1 cm.

P4. Given $\overline{AB}$ of length 3.9 cm, construct $\overline{PQ}$ such that the length of $\overline{PQ}$ is twice that of $\overline{AB}$. Verify by measurement.

(Hint : construct $\overline{PX}$ such that length of $\overline{PX}$ = length of $\overline{AB}$; then cut off $\overline{XQ}$ such that $\overline{XQ}$ also has the length of  $\overline{AB}$.)

Sol. A line segment $\overline{PQ}$ can be drawn such that the length of $\overline{PQ}$ is twice that of $\overline{AB}$ as follows.

(1) Draw a line l and mark a point P on it and let AB be the given line segment of 3.9 cm.

(2) By adjusting the compasses up to the length of AB, draw an arc to cut the line at X, while taking the pointer of compasses at point P.

(3) Again put the pointer on point X and draw an arc to cut line l again at Q.

$\overline{PQ}$ is the required line segment. By ruler, the length of $\overline{PQ}$ can be measured which comes to 7.8 cm.

P5. Given $\overline{AB}$ of length 7.3 cm and $\overline{CD}$ of length 3.4 cm, construct a line segment $\overline{XY}$ such that the length of $\overline{XY}$ is equal to the difference between the lengths of $\overline{AB}$ and $\overline{CD}$. Verify by measurement.

Sol. (1) Given that $\overline{AB}$, =7.3 cm and $\overline{CD}$ = 3.4 cm

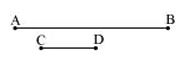
(2) Adjust the compasses up to the length of CD and put the pointer of the compasses at A. Draw an arc to cut AB at P.

(3) Adjust the compasses up to the length of PB. Now draw a line l and mark a point X on it.

(4) Now, putting the pointer of compasses at point X, draw an arc to cut the line at Y.

$\overline{XY}$ is the required line segment.

EXERCISE-14.3 

P1. Draw any line segment $\overline{PQ}$. Without measuring $\overline{PQ}$, construct a copy of $\overline{PQ}$.

Sol. The following steps will be followed to draw the given line segment $\overline{PQ}$ and to construct a copy of ­$\overline{PQ}$.

(1) Let $\overline{PQ}$ be the given line segment.

(2) Adjust the compasses up to the length of $\overline{PQ}$.

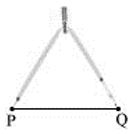
(3) Draw any line l and mark a point A on it.

(4) Put the pointer on point A, and without changing the setting of compasses, draw an arc to cut the line segment at point B.

$\overline{AB}$ is the required line segment.

P2. Given some line segment $\overline{AB}$, whose length you do not know, construct $\overline{PQ}$ such that the length of $\overline{PQ}$ is twice that of $\overline{AB}$.

Sol. The following steps will be followed to construct a line segment $\overline{PQ}$­ such that the length of $\overline{PQ}$ is twice that of $\overline{AB}$.

(1) Let $\overline{AB}$ be the given line segment.

(2) Adjust the compasses up to the length of $\overline{AB}$.

(3) Draw any line l and mark a point P on it.

(4) Put the pointer on P and without changing the setting of compasses, draw an arc to cut the line segment at point X.

(5) Now, put the pointer on point X and again draw an arc with the same radius as before, to cut the line l at point Q.

$\overline{PQ}$ is the required line segment.

EXERCISE-14.4 

P1. Draw any line segment $\overline{AB}$. Mark any point M on it. Through M, draw a perpendicular to $\overline{AB}$. (Use ruler and compasses)

Sol. (1) Draw the given line segment $\overline{AB}$ and mark any point M on it.

(2) With M as centre and a convenient radius, construct an arc intersecting the line segment $\overline{AB}$ at two points C and D.

(3) With C and D as centres and a radius greater than CM, construct two arcs. Let these be intersecting each other at E.

(4) Join EM. $\overline{EM}$ is perpendicular to $\overline{AB}$.

P2. Draw any line segment $\overline{PQ}$. Take any point R not on it. Through R, draw a perpendicular to $\overline{PQ}$. (Use ruler and set-square)

Sol. (1) Take the given line segment $\overline{PQ}$ and mark any point R outside $\overline{PQ}$.

(2) Place a set square on $\overline{PQ}$ such that one arm of its right angle aligns along $\overline{PQ}$.

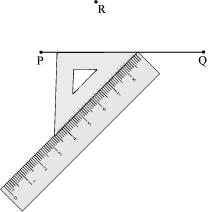
(3) Place the ruler along the edge opposite to the right angle of the set square.

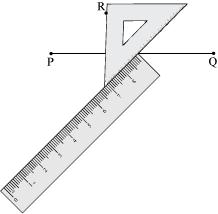
(4) Hold the ruler fixed. Slide the set square along the ruler till the point R touches the other arm of the set square.

(5) Draw a line along this edge of the set square which will be passing through R. It is the required line, which is perpendicular to $\overline{PQ}$.

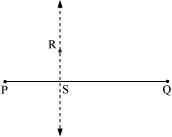
P3. Draw a line l and point X on it. Through X, draw a line segment $\overline{XY}$ perpendicular to l.

Now draw a perpendicular to $\overline{XY}$ at Y. (use ruler and compasses)

Sol. (1) Draw a line l and mark a point X on it.

(2) Taking X as centre and with a convenient radius, draw an arc intersecting line l at two points A and B.

(3) With A and B as centres and a radius more than AX, construct two arcs intersecting each other at Y.

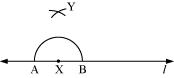
(4) Join XY. $\overline{XY}$ is perpendicular to l.

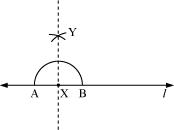
Similarly, a perpendicular to $\overline{XY}$ at the point Y can be drawn. The line $\overline{ZY}$ is perpendicular to $\overline{XY}$ at Y.

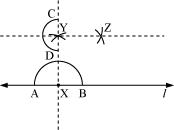
EXERCISE-14.4

P1. Draw $\overline{AB}$ of length 7.3 cm and find its axis of symmetry.

Sol. The below given steps will be followed to construct $\overline{AB}$ of length 7.3 cm and to find its axis of symmetry.

(1) Draw a line segment $\overline{AB}$ of 7.3 cm.

(2) Taking A as centre, draw a circle by using compasses. The radius of circle should be more than half the length of $\overline{AB}$.

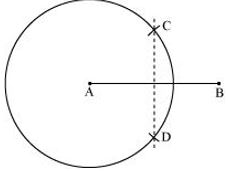
(3) With the same radius as before, draw another circle using compasses while taking point B as centre. Let it cut the previous circle at C and D.

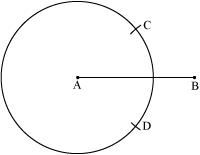
(4) Join $\overline{CD}$. $\overline{CD}$ is the axis of symmetry.

P2. Draw a line segment of length 9.5 cm and construct its perpendicular bisector.

Sol. The below given steps will be followed to construct a line segment of length 9.5 cm and its perpendicular bisector.

(1) Draw a line segment $\overline{PQ}$ of 9.5 cm.

(2) Taking P as centre, draw a circle by using compasses. The radius of circle should be more than half the length of $\overline{PQ}$.

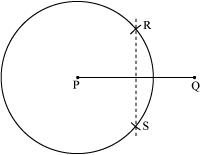
(3) With the same radius as before, draw another circle using compasses while taking point Q as centre. Let it cut the previous circle at R and S.

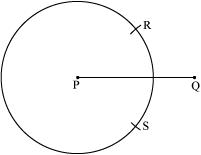
(4) Join RS. $\overline{RS}$ is the axis of symmetry i.e., the perpendicular bisector of line $\overline{PQ}$.

P3. Draw the perpendicular bisector of $\overline{XY}$ whose length is 10.3 cm.

(a) Take any point P on the bisector drawn. Examine whether PX = PY.

(b) If M is the mid point of $\overline{XY}$, what can you say about the lengths MX and XY ?

Sol. (1) Draw a line segment $\overline{XY}$ of 10.3 cm.

(2) Taking point X as centre, draw a circle by using compasses. The radius of circle should be more than half the length of $\overline{XY}$.

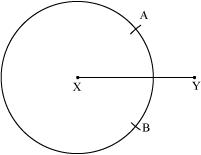
(3) With the same radius as before, draw another circle using compasses while taking point Y as centre. Let it cut the previous circle at A and B.

(4) Join $\overline{AB}$. $\overline{AB}$ is the axis of symmetry.

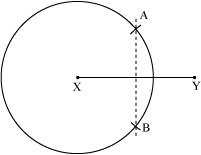
(a) Take any point P on $\overline{AB}$. We will find that the measures of the lengths of PX and PY are same.

It is because $\overline{AB}$ is the axis of symmetry. Hence, any point lying on $\overline{AB}$ will be at the same distance from both the ends of $\overline{XY}$.

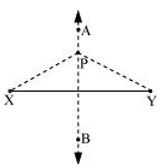
(b) M is the mid-point of $\overline{XY}$. Perpendicular bisector $\overline{AB}$ will be passing through point M. Hence, length of $\overline{AB}$ is just double of $\overline{MX}$.

Or, 2MX = XY

P4. Draw a line segment of length 12.8 cm. Using compasses; divide it into four equal parts. Verify by actual measurement.

Sol. (1) Draw a line segment $\overline{XY}$ of 12.8 cm.

(2) Draw a circle, while taking point X as centre and radius more than half of XY.

(3) With same radius and taking centre as Y, again draw arcs to cut the circle at A and B. Join AB which intersects $\overline{XY}$ at M.

(4) Taking X and Y as centres, draw two circles with radius more than half of $\overline{XM}$.

(5) With same radius and taking M as centre, draw arcs to intersect these circles at P, Q and R, S.

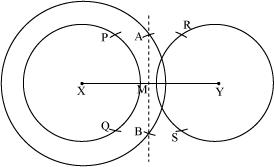
(6) Join PQ and RS. These are intersecting $\overline{XY}$ at T and U.

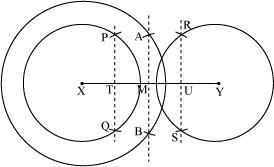
(7) Now, $\overline{\mathrm{XT}}=\overline{\mathrm{TM}}=\overline{\mathrm{MU}}=\overline{\mathrm{UY}}$. These are 4 equal parts of $\overline{XY}$.

By measuring these line segments with the help of ruler, we will find that each is of 3.2 cm.

P5. With $\overline{PQ}$ of length 6.1 cm as diameter draw a circle.

Sol. (1) Draw a line segment of 6.1 cm.

(2) Taking point P as centre and radius more than half of $\overline{PQ}$, draw a circle.

(3) With same radius and taking Q as centre, draw arcs to intersect this circle at points R and S.

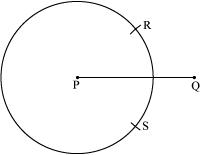
(4) Join RS which intersects $\overline{PQ}$ at T.

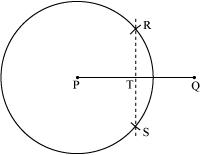
(5) Taking T as centre and with radius TP, draw a circle which will also pass through Q. It is the required circle.

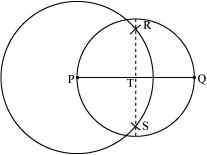
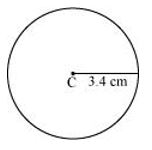
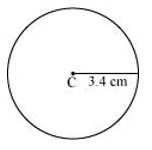
P6. Draw a circle with centre C and radius 3.4 cm. Draw any chord $\overline{AB}$. Construct the perpendicular bisector of $\overline{AB}$ and examine if it passes through C.

Sol. (1) Mark any point C on the sheet.

(2) By adjusting the compasses up to 3.4 cm and by putting the pointer of the compasses at point C, turn the compasses slowly to draw the circle. It is the required circle of 3.4 cm radius.

(3) Now, mark any chord $\overline{AB}$ in the circle.

(4) Taking A and B as centres, draw arcs on both sides of $\overline{AB}$. Let these intersect each other at D and E.

(5) Join DE, which is the perpendicular bisector of AB.

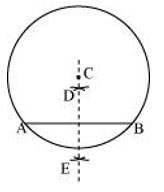
When $\overline{DE}$ is extended, it will pass through point C.

P7. Repeat P 6, if $\overline{AB}$ happens to be a diameter.

Sol. (1) Mark any point C on the sheet.

(2) By adjusting the compasses up to 3.4 cm and by putting the pointer of the compasses at point C, turn the compasses slowly to draw the circle. It is the required circle of 3.4 cm radius.

(3) Mark any $\overline{AB}$ diameter in the circle.

(4) Now, taking A and B as centres, draw arcs on both sides of $\overline{AB}$ taking radius more than $\overline{AB}$. Let these intersect each other at D and E.

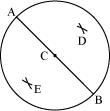
(5) Join DE, which is the perpendicular bisector of AB.

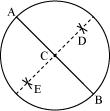
It can be observed that $\overline{DE}$ is passing through the centre C of the circle.

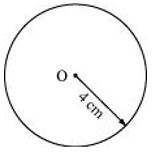
P8. Draw a circle of radius 4 cm. Draw any two of its chords. Construct the perpendicular bisectors of these chords. Where do they meet ?

Sol. (1) Mark any point C on the sheet. Now, by adjusting the compasses up to 4 cm and by putting the pointer of compasses at point C, turn the compasses slowly to draw the circle. It is the required circle of 4 cm radius.

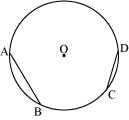
(2) Take any two chords $\overline{AB}$ and $\overline{CD}$ in the circle.

(3) Taking A and B as centres and with radius more than half of $\overline{AB}$, draw arcs on both sides of AB, intersecting each other at E, F. Join EF which is the perpendicular bisector of AB.

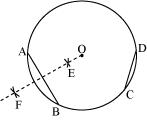
(4) Taking C and D as centres and with radius more than half of $\overline{CD}$, draw arcs on both sides of CD, intersecting each other at G, H. Join GH which is the perpendicular bisector of CD.

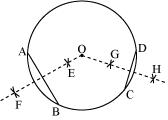
Now, we will find that when EF and GH are extended, they meet at the centre of the circle i.e., point O.

P9. Draw any angle with vertex O. Take a point A on one of its arms and B on another such that OA = OB. Draw the perpendicular bisectors $\overline{OA}$ of and $\overline{OB}$.

Let them meet at P. Is PA = PB ?

Sol. (1) Draw any angle whose vertex is O.

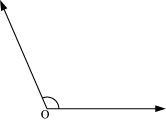
(2) With a convenient radius, draw arcs on both rays of this angle while taking O as centre. Let these points be A and B.

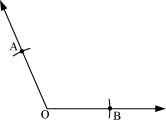
(3) Taking O and A as centres and with radius more than half of OA, draw arcs on both sides of OA. Let these be intersecting at C and D. Join CD.

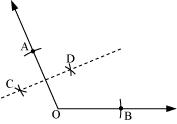
(4) Similarly, we can find the perpendicular bisector $\overline{EF}$ of $\overline{OB}$. These perpendicular bisectors $\overline{CD}$ and $\overline{EF}$ will intersect each other at P.

Now, PA and PB can be measured. These are equal in length.

EXERCISE-14.6

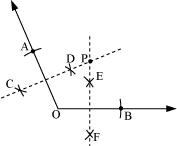
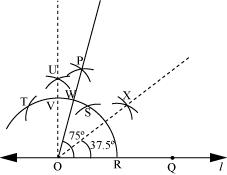
P1. Draw ÐPOQ of measure 75° and find its line of symmetry.

Sol. The below given steps will be followed to construct an angle of 75° and its line of symmetry.

(1) Draw a line l and mark two points O and Q on it, as shown in the figure. Draw an arc of convenient radius, while taking point O as centre. Let it intersect line l at R.

(2) Taking R as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at S.

(3) Taking S as centre and with the same radius as before, draw an arc intersecting the arc at T (see figure).

(4) Taking S and T as centre, draw an arc of same radius to intersect each other at U.

(5) Join OU. Let it intersect the arc at V. Now, taking S and V as centres, draw arcs with radius more than $\frac{1}{2}$SV. Let those intersect each other at P. Join OP, which is the ray making 75° with the line l.

(6) Let this ray be intersecting our major arc at point W. Now, taking R and W as centres, draw arcs with radius more than $\frac{1}{2}$RW in the interior of angle of 75º. Let these be intersecting each other at X. Join OX.

OX is the line of symmetry for ÐPOQ = 75°.

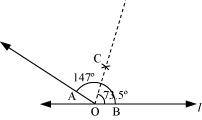
P2. Draw an angle of measure 147° and construct its bisector.

Sol. The below given steps will be followed to construct an angle of 147º measure and its bisector.

(1) Draw a line l and mark a point O on it. Place the centre of the protractor at point O and the zero edge along line l.

(2) Mark a point A at 147º. Join OA. OA is the required ray making 147º with line l.

(3) Draw an arc of convenient radius, while taking point O as centre. Let it intersect both rays of angle 147º at point A and B.

(4) Taking A and B as centres, draw arcs of radius more than $\frac{1}{2}$AB in the interior of angle of 147º. Let those intersect each other at C. Join OC. OC is the required bisector of 147º angle.

P3. Draw a right angle and construct its bisector.

Sol. The below given steps will be followed to construct a right angle and its bisector.

(1) Draw a line l and mark a point P on it. Draw an arc of convenient radius, while taking point P as centre. Let it intersect line l at R.

(2) Taking R as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at S.

(3) Taking S as centre and with the same radius as before, draw an arc intersecting the arc at T (see figure).

(4) Taking S and T as centres, draw arcs of same radius to intersect each other at U.

(5) Join PU. PU is the required ray making 90º with line l. Let it intersect the major arc at point V.

(6) Now, taking R and V as centres, draw arcs with radius more than $\frac{1}{2}$RV to intersect each other at W. Join PW.

PW is the required bisector of this right angle.

P4. Draw an angle of measure153° and divide it into four equal parts.

Sol. The below given steps will be followed to construct an angle of 153º measure and its bisector.

(1) Draw a line l and mark a point O on it. Place the centre of the protractor at point O and the zero edge along line l.

(2) Mark a point A at 153º. Join OA. OA is the required ray making 153º with line l.

(3) Draw an arc of convenient radius, while taking point O as centre. Let it intersect both rays of angle 153º at point A and B.

(4) Taking A and B as centres, draw arcs of radius more than $\frac{1}{2}$AB in the interior of angle of 153º. Let those intersect each other at C. Join OC.

(5) Let OC intersect the major arc at point D. Now, with radius more than $\frac{1}{2}$AD, draw arcs while taking A and D as centres, and D and B as centres. Let these be intersecting each other at point E and F respectively. Join OE, OF.

OF, OC, OE are the rays dividing 153º angle in 4 equal parts.

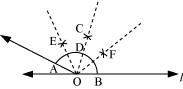
P5. Construct with ruler and compasses, angles of following measures:

(a) 60°

(b) 30°

(c) 90°

(d) 120°

(e) 45°

(f) 135°

Sol. (a) 60°

The below given steps will be followed to construct an angle of 60°.

(1) Draw a line l and mark a point P on it. Now, taking P as centre and with a convenient radius, draw an arc of a circle which intersects line l at Q.

(2) Taking Q as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at point R.

(3) Join PR which is the required ray making 60° with line l.

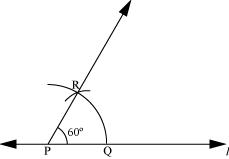
(b) 30°

The below given steps will be followed to construct an angle of 30°.

(1) Draw a line l and mark a point P on it. Now taking P as centre and with convenient radius, draw an arc of a circle which intersects line l at Q.

(2) Taking Q as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at point R.

(3) Now, taking Q and R as centre and with radius more than $\frac{1}{2}$RQ, draw arcs to intersect each other at S. Join PS which is the required ray making 30° with line l.

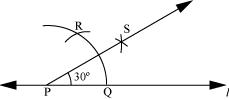
(c) 90º

The below given steps will be followed to construct an angle of 90°.

(1) Draw a line l and mark a point P on it. Now taking P as centre and with a convenient radius, draw an arc of a circle which intersects line l at Q.

(2) Taking Q as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at R.

(3) Taking R as centre and with the same radius as before, draw an arc intersecting the arc at S (see figure).

(4) Taking R and S as centre, draw an arc of same radius to intersect each other at T.

(5) Join PT, which is the required ray making 90° with line l.

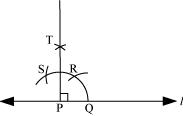
(d) 120º

The below given steps will be followed to construct an angle of 120°.

(1) Draw a line l and mark a point P on it. Now taking P as centre and with a convenient radius, draw an arc of a circle which intersects line l at Q.

(2) Taking Q as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at R.

(3) Taking R as centre and with the same radius as before, draw an arc intersecting the arc at S (see figure).

(4) Join PS, which is the required ray making 120° with line l.

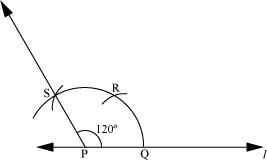
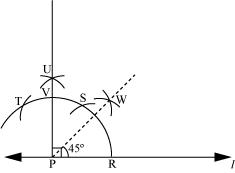
(e) 45º

The below given steps will be followed to construct an angle of 45°.

(1) Draw a line l and mark a point P on it. Now taking P as centre and with a convenient radius, draw an arc of a circle which intersects line l at Q.

(2) Taking Q as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at R.

(3) Taking R as centre and with the same radius as before, draw an arc intersecting the arc at S (see figure).

(4) Taking R and S as centres, draw arcs of same radius to intersect each other at T.

(5) Join PT. Let it intersect the major arc at point U.

(6) Taking Q and U as centres, draw arcs with radius more than $\frac{1}{2}$QU to intersect each other at V. Join PV.

PV is the required ray making 45° with the given line l.

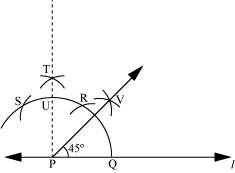
(f) 135°

The below given steps will be followed to construct an angle of 135°.

(1) Draw a line l and mark a point P on it. Now taking P as centre and with a convenient radius, draw a semi-circle which intersects line l at Q and R.

(2) Taking R as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at S.

(3) Taking S as centre and with the same radius as before, draw an arc intersecting the arc at T (see figure).

(4) Taking S and T as centre, draw arcs of same radius to intersect each other at U.

(5) Join PU. Let it intersect the arc at V. Now taking Q and V as centres and with radius more than $\frac{1}{2}$QV, draw arcs to intersect each other at W.

(6) Join PW which is the required ray making 135° with line l.

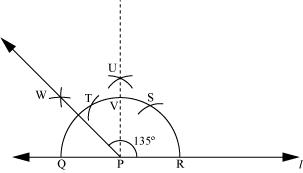
P6. Draw an angle of measure 45° and bisect it.

Sol. The below given steps will be followed to construct an angle of 45º and its bisector.

(1) ∠POQ of 45º measure can be formed on a line l by using the protractor.

(2) Draw an arc of a convenient radius, while taking point O as centre. Let it intersect both rays of angle 45º at point A and B.

(3) Taking A and B as centres, draw arcs of radius more than $\frac{1}{2}$AB in the interior of angle of 45º. Let those intersect each other at C. Join OC.

OC is the required bisector of 45º angle.

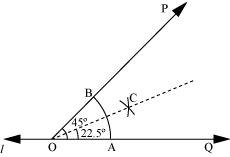
P7. Draw an angle of measure 135° and bisect it.

Sol. The below given steps will be followed to construct an angle of 135° and its bisector.

(1) $\angle POQ$ of 135º measure can be formed on a line l by using the protractor.

(2) Draw an arc of a convenient radius, while taking point O as centre. Let it intersect both rays of angle 135º at point A and B.

(3) Taking A and B as centres, draw arcs of radius more than $\frac{1}{2}$AB in the interior of angle of 135º. Let those intersect each other at C. Join OC. OC is the required bisector of 135º angle.

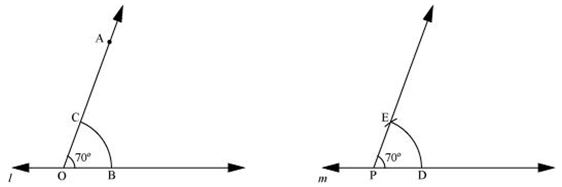
P8. Draw an angle of 70°. Make a copy of it using only a straight edge and compasses.

Sol. The below given steps will be followed to construct an angle of 70º measure and its copy.

(1) Draw a line l and mark a point O on it. Place the centre of the protractor at point O and the zero edge along line l.

(2) Mark a point A at 70º. Join OA. OA is the ray making 70º with line l. Draw an arc of convenient radius in the interior of 70º angle, while taking point O as centre. Let it intersect both rays of angle 70º at point B and C.

(3) Draw a line m and mark a point P on it. With the same radius as used before, again draw an arc while taking point P as centre. Let it cut the line m at point D.

(4) Now, adjust the compasses up to the length of BC. With this radius, draw an arc while taking D as centre, which will intersect the previously drawn arc at point E.

(5) Join PE. PE is the required ray which makes the same angle (i.e. 70º) with line m.

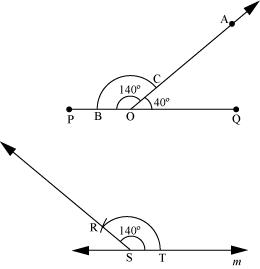
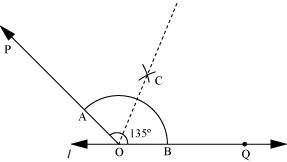
P9. Draw an angle of 40°. Copy its supplementary angle.

Sol. The below given steps will be followed to construct an angle of 40º measure and the copy of its supplementary angle.

(1) Draw a line segment $\overline{PQ}$ and mark a point O on it. Place the centre of the protractor at point O and the zero edge along line segment $\overline{PQ}$.

(2) Mark a point A at 40º. Join OA. OA is the required ray making 40º with $\overline{PQ}$. $\angle POA$ is the supplementary angle of 40º.

(3) Draw an arc of convenient radius in the interior of Ð POA, while taking point O as centre. Let it intersect both rays of Ð POA at point B and C.

(4) Draw a line m and mark a point S on it. With the same radius as used before, again draw an arc while taking point S as centre. Let it cut the line m at point T.

(5) Now, adjust the compasses up to the length of BC. With this radius, draw an arc while taking T as centre, which will intersect the previously drawn arc at point R.

(6) Join RS. RS is the required ray which makes the same angle with line m, as the supplementary of 40º is 140º.