Basic Geometrical Ideas

EXERCISE-4.1

P1. Use the figure to name :

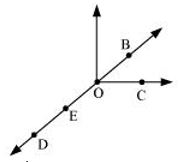
(a) Five points

(b) A line

(c) Four rays

(d) Five line segments

Sol. (a) The five points are D, E, O, B, and C.

(b) $\overline{BD}$

(c) $\overline{OD}, \overline{OB}, \overline{OC}, \overline{OE}$

(d) $\overline{\mathrm{DE}}, \overline{\mathrm{EO}}, \overline{OB}, \overline{OC}, \overline{\mathrm{BE}}$

P2. Name the line given in all possible (twelve) ways, choosing only two letters at a time from the four given.

Sol. $\overline{AB}, \overline{BC}, \overline{CD}, \overline{BA}, \overline{DC}, \overline{AD}, \overline{DA},\overline{AC}, \overline{CA}, \overline{BD}, \overline{DB}$

P3. Use the figure to name :

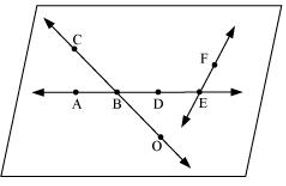
(a) Line containing point E.

(b) Line passing through A.

(c) Line on which O lies

(d) Two pairs of intersecting lines.

Sol. (a) $\overline{AE}$

(b) $\overline{AE}$

(c) $\overline{OC}$

(d) $\overline{OC}$ and $\overline{AE}, \overline{AE}$ and $\overline{EF}$

P4. How many lines can pass through (a) one given point ? (b) Two given points ?

Sol. (a) Infinite number of lines can pass through a single point.

(b) Only one line can pass through two given points.

P5. Draw a rough figure and label suitably in each of the following cases :

(a) Point P lies on $\overline{AB}$

(b) $\overline{XY}$ and $\overline{PQ}$ intersect at M.

(c) Line l contains E and F but not D.

(d) $\overline{OP} and \overline{OQ}$ meet at O.

Sol. (a)

(b)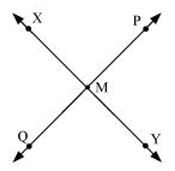

(c)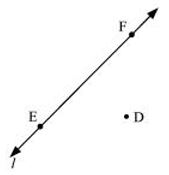

(d)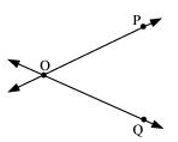

P6. Consider the following figure of line. Say whether following statements are true or false in context of the given figure.

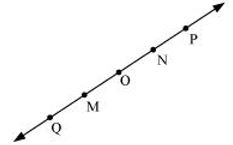
(a) Q, M, O, N, P are points on the line $\overline{MN}$.

(b) M, O, N are points on a line segment $\overline{MN}$.

(c) M and N are end points of line segment $\overline{MN}$.

(d) O and N are end points of line segment $\overline{OP}$.

(e) M is one of the end points of line segment $\overline{QO}$.

(f) M is point on ray $\overline{OP}$.

(g) Ray $\overline{OP}$ is different from ray $\overline{QP}$.

(h) Ray $\overline{OP}$ is same as ray $\overline{OM}$.

(i) Ray $\overline{OM}$ is not opposite to ray $\overline{OP}$.

(j) O is not an initial point of $\overline{OP}$.

(k) N is the initial point of $\overline{NP}$ and $\overline{NM}$.

Sol. (a) True

(b) True

(c) True

(d) False

(e) False

(f) False

(g) True

(h) False

(i) False

(j) False

(k) True

EXERCISE-4.2

P1. Classify the following curves as (i) Open or (ii) Closed.

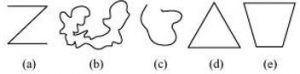
Sol. (a) Open

(b) Closed

(c) Open

(d) Closed

(e) Closed

P2. Draw rough diagrams to illustrate the following :

(a) Open curve

(b) Closed curve.

Sol. (a) Open curve

(b) Closed curve

P3. Draw any polygon and shade its interior.

Sol.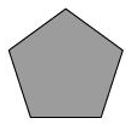

P4. Consider the given figure and answer the Ps :

(a) Is it a curve ?

(b) Is it closed ?

Sol. (a) Yes

(b) Yes

P5. Illustrate, if possible, each one of the following with a rough diagram :

(a) A closed curve that is not a polygon.

(b) An open curve made up entirely of line segments.

(c) A polygon with two sides.

Sol. (a)

(b)

(c) This is not possible as the polygon having the least number of sides is a triangle, which has three sides in it.

EXERCISE-4.3 

P1. Name the angles in the given figure.

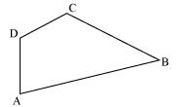
Sol. ∠BAD, ∠ADC, ∠DCB, ∠CBA

P2. In the given diagram, name the point (s)

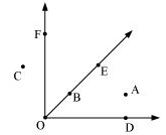
(a) In the interior of ∠DOE

(b) In the exterior of ∠EOF

(c) On ∠EOF

Sol. (a) A

(b) C, A, D

(c) B, E, O, F

P3. Draw rough diagrams of two angles such that they have

(a) One point in common.

(b) Two points in common.

(c) Three points in common.

(d) Four points in common.

(e) One ray in common.

Sol. (a)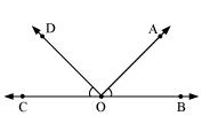

∠COD and ∠AOB have point O in common.

(b)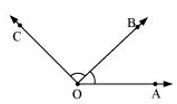

∠AOB and ∠BOC have points O and B in common.

(c)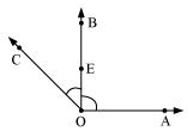

∠AOB and ∠BOC have points O, E, B in common.

(d)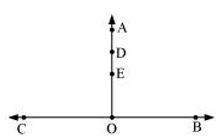

∠BOA and ∠COA have points O, E, D, A in common.

(e)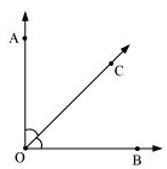

Ray $\overline{OC}$ is common between ∠BOC and ∠AOC.

EXERCISE-4.4 

P1. Draw a rough sketch of a triangle ABC. Mark a point P in its interior and a point Q in its exterior. Is the point A in its exterior or in its interior ?

Sol.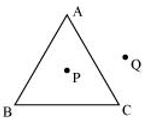

Point A lies on the given ΔABC.

P2.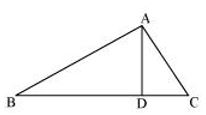

(a) Identify three triangles in the figure.

(b) Write the names of seven angles.

(c) Write the names of six line segments.

(d) Which two triangles have ∠B as common ?

Sol. (a) ΔABC, ΔACD, ΔADB

(b) ∠ABC, ∠ADB, ∠ADC, ∠ACB, ∠BAD, ∠CAD, ∠BAC

(c) $\overline{\mathrm{AB}}, \overline{\mathrm{BC}}, \overline{\mathrm{CA}}, \overline{\mathrm{AD}}, \overline{\mathrm{BD}}, \overline{\mathrm{CD}}$

(d) ΔABD and ΔABC

EXERCISE-4.5 

P1. Draw a rough sketch of a quadrilateral PQRS. Draw its diagonals. Name them. Is the meeting point of the diagonals in the interior or exterior of the quadrilateral ?

Sol.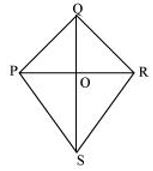

Diagonals are PR and QS. They meet at point O which is in the interior of &mnSq1PQRS.

P2. Draw a rough sketch of a quadrilateral KLMN. State,

(a) Two pairs of opposite sides,

(b) Two pairs of opposite angles,

(c) Two pairs of adjacent sides,

(d) Two pairs of adjacent angles.

Sol.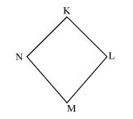

(a) $\overline{\mathrm{KL}}, \overline{\mathrm{NM}}\text{ and }\overline{\mathrm{KN}}, \overline{\mathrm{ML}}$

(b) ∠KLM and ∠KNM ; ∠LKN and ∠LMN

(c) $\overline{\mathrm{KL}}, \overline{\mathrm{KN}}\text{ and }\overline{\mathrm{NM}}, \overline{\mathrm{ML}} ; \overline{\mathrm{KL}}, \overline{\mathrm{LM}}\text{ and }\overline{\mathrm{NM}}\text{, }\overline{\mathrm{NK}}$

(d) ∠K, ∠L and ∠M, ∠N ; ∠K, ∠N and ∠L, ∠M

EXERCISE-4.6

P1. From the figure, identify :

(a) The centre of circle

(b) Three radii

(c) a diameter

(d) a chord

(e) Two points in the interior

(f) a point in the exterior

(g) a sector

(h) a segment

Sol. (a) O

(b) $\overline{OA}, \overline{OB}, \overline{OC}$

(c) $\overline{AC}$

(d) $\overline{ED}$

(e) O, P

(f) Q

(g) AOB (shaded region)

(h) DE (shaded region)

P2. (a) Is every diameter of a circle also a chord ?

(b) Is every chord of circle also a diameter ?

Sol. (a) Yes. The diameter is the longest possible chord of the circle.

(b) No

P3. Draw any circle and mark

(a) Its centre

(b) a radius

(c) a diameter

(d) a sector

(e) a segment

(f) a point in its interior

(g) a point in its exterior

(h) an arc

Sol.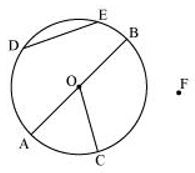

(a) O

(b) $\overline{OA}$

(c) $\overline{AB}$

(d) COA

(e)  DE

(f) O

(g) F

(h) AC

P4. Say true or false :

(a) Two diameters of a circle will necessarily intersect.

(b) The centre of a circle is always in its interior.

Sol. (a) True. They will always intersect each other at the centre of the circle.

(b) True