Coordinate Geometry

EXERCISE-7.1

P1. Find the distance between the following pairs of points:

(i) (2, 3), (4, 1)

(ii) (– 5, 7), (– 1, 3)

(iii) (a, b), (– a, – b)

Sol. (i) Distance between the two points is given by $\sqrt{{\left(x_1–x_2\right)}^2+{\left(y_1–y_2\right)}^2}$

Therefore, distance between (2, 3) and (4, 1) is given by

$l=\sqrt{(2–4{)}^2+(3–1{)}^2}=\sqrt{(–2{)}^2+(2{)}^2}$ $=\sqrt{4+4}=\sqrt{8}=2\sqrt{2}$

(ii) Distance between (-5, 7) and (-1, 3) is given by

$l=\sqrt{(–5–(–1){)}^2+(7–3{)}^2}=\sqrt{(–4{)}^2+(4{)}^2}$ $=\sqrt{(–5–(–1){)}^2+(7–3{)}^2}=\sqrt{(–4{)}^2+(4{)}^2}$

(iii) Distance between (a, b) and (-a, – b)is given by

$l=\sqrt{(a–(–a){)}^2+(b–(–b){)}^2}$ $=\sqrt{(2a{)}^2+(2b{)}^2}$ $=\sqrt{4a^2+4b^2}=2\sqrt{a^2+b^2}$

P2. Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns A and B.

Sol. Distance between points (0, 0) and (36, 15)

$=\sqrt{(36–0{)}^2+(15–0{)}^2}$

$=\sqrt{{36}^2+{15}^2}$

$=\sqrt{1296+225}$

$=\sqrt{1521}=39$

Yes, we can find the distance between the given towns A and B.

Assume town A at origin point (0, 0).

Therefore, town B will be at point (36, 15) with respect to town A.

And hence, as $\boxed{calculated}$ above, the distance between town A and B will be 39 km.

P3. Determine if the points (1, 5), (2, 3) and (– 2, – 11) are collinear.

Sol. Let the points (1, 5), (2, 3), and (−2, −11) be representing the vertices A, B, and C of the given triangle respectively.

Let  A = (1, 5), B= (2, 3), C = (-2, -11)

$\therefore \mathrm{AB}=\sqrt{(1–2{)}^2+(5–3{)}^2}=\sqrt{5}$

$\sqrt{(2–(–2){)}^2+(3–(–11){)}^2}=\sqrt{4^2+{14}^2}$ $=\sqrt{16+196}=\sqrt{212}$

$\mathrm{CA}=\sqrt{(1–(–2){)}^2+(5–(–11){)}^2}$ $=\sqrt{3^2+{16}^2}$ $=\sqrt{9+256}=\sqrt{265}$

Since AB + BC $\ne$ CA,

Therefore, the points (1, 5), (2, 3), and (−2, −11) are not collinear.

P4. Check whether (5, – 2), (6, 4) and (7, – 2) are the vertices of an isosceles triangle.

Sol. Let the points (5, −2), (6, 4), and (7, −2) are representing the vertices A, B, and C of the given triangle respectively.

AB = $\sqrt{(5–6{)}^2+(–2–4{)}^2}$ = $\sqrt{(–1{)}^2+(–6{)}^2}$ = $\sqrt{1+36}=\sqrt{37}$

BC = $\sqrt{(6–7{)}^2+(4–(–2){)}^2}$ = $\sqrt{(–1{)}^2+(6{)}^2}$ = $\sqrt{1+36}=\sqrt{37}$

CA = $\sqrt{(5–7{)}^2+(–2–(–2){)}^2}$ = $\sqrt{(–2{)}^2+0^2}=2$

Therefore, AB = BC

As two sides are equal in length, therefore, ABCis an isosceles triangle.

P5. In a classroom, 4 friends are seated at the points A, B, C and D as shown in below figure. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees.  Using distance formula,  find which of them is correct.

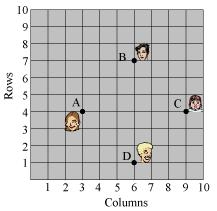
Sol. It can be observed that A (3, 4), B (6, 7), C (9, 4), and D (6, 1) are the positions of these 4 friends.

AB = $\sqrt{(3–6{)}^2+(4–7{)}^2}$ = $\sqrt{(–3{)}^2+(–3{)}^2}$ = $\sqrt{9+9}=\sqrt{18}=3\sqrt{2}$

BC = $\sqrt{(6–9{)}^2+(4–7{)}^2}$ = $\sqrt{(–3{)}^2+(–3{)}^2}$ = $\sqrt{9+9}=\sqrt{18}=3\sqrt{2}$

CB =  $\sqrt{(9–6{)}^2+(4–1{)}^2}$ = $\sqrt{(3{)}^2+(3{)}^2}$ = $\sqrt{9+9}=\sqrt{18}=3\sqrt{2}$

AD = $\sqrt{(3–6{)}^2+(4–1{)}^2}$ = $\sqrt{(–3{)}^2+(3{)}^2}$ = $\sqrt{9+9}=\sqrt{18}=3\sqrt{2}$

Diagonal AC = $\sqrt{(3–9{)}^2+(4–4{)}^2}$ = $\sqrt{(–6{)}^2+(0{)}^2}=6$

Diagonal BD = $\sqrt{(6–6{)}^2+(7–1{)}^2}$ = $\sqrt{(0{)}^2+(6{)}^2}=6$

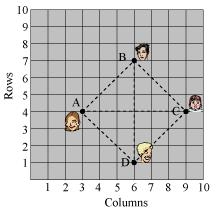
It can be observed that all sides of this quadrilateral ABCD are of the same length and also the diagonals are of the same length.

Therefore, ABCD is a square and hence, Champa was correct

P6. Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:

(i) (– 1, – 2), (1, 0), (– 1, 2), (– 3, 0)

(ii) (–3, 5), (3, 1), (0, 3), (–1, – 4)

(iii) (4, 5), (7, 6), (4, 3), (1, 2)

Sol. (i) Let the points (−1, −2), (1, 0), (−1, 2), and (−3, 0) be representing the vertices A, B, C, and D of the given quadrilateral respectively.

$\therefore$ AB = $\sqrt{(–1–1{)}^2+(–2–0{)}^2}$ = $\sqrt{(–2{)}^2+(–2{)}^2}$ = $\sqrt{4+4}=\sqrt{8}=2\sqrt{2}$

BC = $\sqrt{(1–(–1){)}^2+(0–2{)}^2}$ = $\sqrt{(2{)}^2+(–2{)}^2}$ = $\sqrt{4+4}=\sqrt{8}=2\sqrt{2}$

CD = $\sqrt{(1–(–3){)}^2+(2–0{)}^2}$ = $\sqrt{(2{)}^2+(2{)}^2}$ = $\sqrt{4+4}=\sqrt{8}=2\sqrt{2}$

AD = $\sqrt{(1–(–3){)}^2+(–2–0{)}^2}$ = $\sqrt{(2{)}^2+(–2{)}^2}$ = $\sqrt{4+4}=\sqrt{8}=2\sqrt{2}$

Diagonal AC = $\sqrt{(–1–(–1){)}^2+(–2–2{)}^2}$ = $\sqrt{0^2+(–4{)}^2}=\sqrt{16}=4$

Diagonal BD = $\sqrt{(1–(–3){)}^2+(0–0{)}^2}$ = $\sqrt{4^2+0^2}=\sqrt{16}=4$

It can be observed that all sides of this quadrilateral are of the same length and also, the diagonals   are of the same length. Therefore, the given points are the vertices of a square.

(ii) Let the points (− 3, 5), (3, 1), (0, 3), and (−1, −4) be representing the vertices A, B, C, and D of the given quadrilateral respectively.

AB = $\sqrt{(–3–3{)}^2+(5–1{)}^2}$ = $\sqrt{(–6{)}^2+(4{)}^2}$ = $\sqrt{36+16}=\sqrt{52}=2\sqrt{13}$

BC = $\sqrt{(3–0{)}^2+(1–3{)}^2}$ = $\sqrt{(3{)}^2+(–2{)}^2}=\sqrt{9+4}=\sqrt{13}$

CD = $\sqrt{(0–(–1){)}^2+(3–(–4){)}^2}$ = $\sqrt{(1{)}^2+(7{)}^2}=\sqrt{1+49}=\sqrt{85}$

AD = $\sqrt{(–3–(–1){)}^2+(5–(–4){)}^2}$ = $\sqrt{(–2{)}^2+(9{)}^2}=\sqrt{4+81}=\sqrt{85}$

It can be observed that all sides of this quadrilateral are of different lengths. Therefore, it can be said that it is only a general quadrilateral, and not specific such as square, rectangle, etc.

(iii) Let the points (4, 5), (7, 6), (4, 3), and (1, 2) be representing the vertices A, B, C, and D of the given quadrilateral respectively.

AB = $\sqrt{(4–7{)}^2+(5–6{)}^2}$ = $\sqrt{(–3{)}^2+(–1{)}^2}$ = $\sqrt{9+1}=\sqrt{10}$

BC $=\sqrt{(7–4{)}^2+(6–3{)}^2}$ = $\sqrt{(3{)}^2+(3{)}^2}=\sqrt{9+9}=\sqrt{18}$

CD = $\sqrt{(4–1{)}^2+(3–2{)}^2}$ = $\sqrt{(3{)}^2+(1{)}^2}=\sqrt{9+1}=\sqrt{10}$

AD = $\sqrt{(4–1{)}^2+(3–2{)}^2}$ = $\sqrt{(3{)}^2+(1{)}^2}=\sqrt{9+1}=\sqrt{10}$

Diagonal AC = $\sqrt{(4–4{)}^2+(5–3{)}^2}$ = $\sqrt{(0{)}^2+(2{)}^2}=\sqrt{0+4}=2$

Diagonal CD = $\sqrt{(7–1{)}^2+(6–2{)}^2}$ = $\sqrt{(6{)}^2+(4{)}^2}=\sqrt{36+16}$ = $\sqrt{52}=13\sqrt{2}$

It can be observed that opposite sides of this quadrilateral are of the same length. However, the diagonals are of different lengths. Therefore, the given points are the vertices of a parallelogram.

P7. Find the point on the x-axis which is equidistant from (2, –5) and (–2, 9).

Sol. We have to find a point on x-axis. Therefore, its y-coordinate will be 0.

Let the point on x-axis be (x, 0).

Distance between (x, 0) and (2, -5) = $\sqrt{(x–2{)}^2+(0–5{)}^2}$ = $\sqrt{(x–2{)}^2+(5{)}^2}$

Distance between (x,0) and (- 2, 9) = $\sqrt{(x–(–2){)}^2+(0–(–9){)}^2}$ = $\sqrt{(x+2{)}^2+(9{)}^2}$

By the given condition, these distances are equal in measure.

$\sqrt{(x–2{)}^2+(5{)}^2}=\sqrt{(x+2{)}^2+(9{)}^2}$

$(x–2{)}^2+25=(x+2{)}^2+81$

x² + 4 – 4x + 25 = x² + 4 + 4x + 81

8x = 25 – 81

8x = – 56

x = – 7

Therefore, the point is (− 7, 0).

P8. Find the values of y for which the distance between the points P(2, – 3) and Q(10, y) is 10 units.

Sol. It is given that the distance between (2, −3) and (10, y) is 10.

Therefore, $\sqrt{(2–10{)}^2+(–3–y{)}^2}$ = 10

$\sqrt{(–8{)}^2+(3+y{)}^2}=10$

64 + (y + 3)² = 100

(y + 3)² = 36

y + 3 = ±6

y + 3 = 6 or y – 3 = 6

Therefore, y = 3 or – 9

P9. If Q (0, 1) is equidistant from P(5, –3) and R(x, 6), find the values of x. Also find the distances QR and PR.

Sol. PQ = QR

$\sqrt{(5–0{)}^2+(–3–1{)}^2}=\sqrt{(0–x{)}^2+(1–6{)}^2}$

$\sqrt{(5{)}^2+(–4{)}^2}=\sqrt{(–x{)}^2+(–5{)}^2}$

$\sqrt{25+16}=\sqrt{{\mathrm{x}}^2+25}$

41 = x² + 25

16 = x²

x = ±4

Therefore, point R is (4, 6) or (−4, 6).

When point R is (4, 6),

PR = $\sqrt{(5–4{)}^2+(–3–6{)}^2}$ = $\sqrt{1^2+(–9{)}^2}=\sqrt{1+81}=\sqrt{82}$

QR = $\sqrt{(0–4{)}^2+(1–6{)}^2}$ = $\sqrt{(–4{)}^2+(–5{)}^2}=\sqrt{16+25}=\sqrt{41}$

When point R is (−4, 6),

PR = $\sqrt{(5–(4){)}^2+(–3–6{)}^2}$ = $\sqrt{(9{)}^2+(–9{)}^2}=\sqrt{81+81}=9\sqrt{2}$

QR = $\sqrt{(0–(–4){)}^2+(1–6{)}^2}$ = $\sqrt{(4{)}^2+(–5{)}^2}=\sqrt{16+25}=\sqrt{41}$

P10. Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (– 3, 4).

Sol. Point (x, y) is equidistant from (3, 6) and (−3, 4).

$\therefore \sqrt{(x–3{)}^2+(y–6{)}^2}=\sqrt{(x–(–3){)}^2+(y–4{)}^2}$

$\sqrt{(x–3{)}^2+(y–6{)}^2}=\sqrt{(x+3{)}^2+(y–4{)}^2}$

$(x–3{)}^2+(y–6{)}^2=(x+3{)}^2+(y–4{)}^2$

x² + 9 – 6x+ y² + 36 – 12y = x² + 9 + 6x + y² + 16 – 8y

36 -16 = 6x + 6x + 12y – 8y

20 = 12 x + 4y

3x + y = 5

3x + y – 5 = 0

EXERCISE-7.2

P1. Find the coordinates of the point which divides the join of (–1, 7) and (4,–3) in the ratio 2 : 3.

Sol. Let P(x, y) be the required point. Using the section formula, we obtain

$x=\frac{2\times 4+3\times (–1)}{2+3}=\frac{8–3}{5}=1$

$y=\frac{2\times (–3)+3\times 7}{2+3}=\frac{–6+21}{5}=\frac{15}{5}=3$

Therefore, the point is (1, 3).

P2. Find the coordinates of the points of trisection of the line segment joining (4, –1) and (–2, –3).

Sol.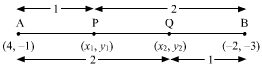

Let P (x₁, y₁) and Q (x₂, y₂) are the points of trisection of the line segment joining the given points i.e., AP = PQ = QB

Therefore, point P divides AB internally in the ratio 1:2.

$x_1=\frac{1\times (–2)+2\times 4}{1+2}$, $y_1=\frac{1\times (–3)+2\times (–1)}{1+2}$

$x_1=\frac{1\times (–2)+2\times 4}{1+2}$, $y_1=\frac{1\times (–3)+2\times (–1)}{1+2}$

Therefore, P(x₁, y₁) = $\left(2,–\frac{5}{3}\right)$

Point Q divides AB internally in the ratio 2:1.

${\mathrm{x}}_2=\frac{2\times (–2)+1\times 4}{2+1}$, $y_1=\frac{2\times (–3)+1\times (–1)}{2+1}$

$x_2=\frac{–4+4}{3}=0$, $y_2=\frac{–6–1}{3}=\frac{–7}{3}$

Q(x₂, y₂) = $\left(0,–\frac{7}{3}\right)$

P3. To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1m each. 100 flower pots have been placed at a distance of 1m from each other along AD, as shown in given figure. Niharika runs $\frac{1}{4}$^th the distance AD on the 2nd line and posts a green flag. Preet runs $\frac{1}{5}$th the distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag?

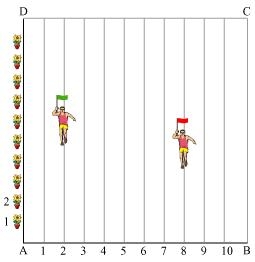
Sol. It can be observed that Niharika posted the green flag at $\frac{1}{4}$ of the distance AD i.e., $\left(\frac{1}{4}\times 100\right)\mathrm{m}$ = 25m from the starting point of 2^nd line.

Therefore, the coordinates of this point G is (2, 25).

Similarly, Preet posted red flag at $\frac{1}{5}$ of the distance AD i.e., $\left(\frac{1}{5}\times 100\right)\mathrm{m}$ = 20m from the starting point of 8^th line. Therefore, the coordinates of this point R are (8, 20).

Distance between these flags by using distance formula = GR

= $\sqrt{(8–2{)}^2+(25–20{)}^2}=\sqrt{36+25}=\sqrt{61} \mathrm{m}$

The point at which Rashmi should post her blue flag is the mid-point of the line joining these points. Let this point be A (x, y).

$x=\frac{2+8}{2}$, $y=\frac{25+20}{2}$

$x=\frac{10}{2}=5$, $y=\frac{45}{2}=22.5$

Hence, A(x, y) = (5.22.5)

Therefore, Rashmi should post her blue flag at 22.5m on 5^th line.

P4. Find the ratio in which the line segment joining the points (– 3, 10) and (6, – 8) is divided by (– 1, 6).

Sol. Let the ratio in which the line segment joining (−3, 10) and (6, −8) is divided by point (−1, 6) be k : 1.

Therefore, -1 = $\frac{6\mathrm{k}–3}{\mathrm{k}+1}$

– k – 1 = 6k – 3

7k = 2

k = $\frac{2}{7}$

Therefore, the required ratio is 2: 7.

P5. Find the ratio in which the line segment joining A(1, – 5) and B(– 4, 5) is divided by the x-axis. Also find the coordinates of the point of division.

Sol. Let the ratio in which the line segment joining A (1, −5) and B (−4, 5) is divided by x-axis be k : 1.

Therefore, the coordinates of the point of division is $\left(\frac{–4k+1}{k+1},\frac{5k–5}{k+1}\right)$.

We know that y-coordinate of any point on x-axis is 0.

$\therefore \frac{5k–5}{k+1}=0$

k = 1

Therefore, x-axis divides it in the ratio 1:1.

Division point = $\left(\frac{–4\left(1\right)+1}{1+1},\frac{5\left(1\right)–5}{1+1}\right)$ = $\left(\frac{–4+1}{2},\frac{5–5}{2}\right)=\left(\frac{–3}{2},0\right)$

P6. If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.

Sol.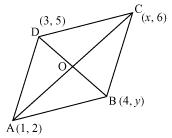

Let (1, 2), (4, y), (x, 6), and (3, 5) are the coordinates of A, B, C, D vertices of a parallelogram ABCD. Intersection point O of diagonal AC and BD also divides these diagonals.

Therefore, O is the mid-point of AC and BD.

If O is the mid-point of AC, then the coordinates of O are

$\left(\frac{1+x}{2},\frac{2+6}{2}\right)\Rightarrow \left(\frac{x+1}{2},4\right)$

If O is the mid-point of BD, then the coordinates of O are

$\left(\frac{4+3}{2},\frac{5+y}{2}\right)\Rightarrow \left(\frac{7}{2},\frac{5+y}{2}\right)$

Since both the coordinates are of the same point O,

$\therefore \frac{x+1}{2}=\frac{7}{2}$ and $4=\frac{5+y}{2}$

$\Rightarrow$ x + 1 = 7 and 5 + y = 8

$\Rightarrow$ x = 6 and y = 3

P7. Find the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, – 3) and B is (1, 4).

Sol. Let the coordinates of point A be (x, y).

Mid-point of AB is (2, −3), which is the center of the circle.

$\therefore (2,–3)=\left(\frac{x+1}{2},\frac{y+4}{2}\right)$

$\Rightarrow \frac{x+1}{2}=2$ and $\frac{y+4}{2}=–3$

$\Rightarrow$ x + 1 = 4 and y + 4 = – 6

$\Rightarrow$ x = 3 and y = – 10

Therefore, the coordinates of A are (3, -10)

P8. If A and B are (– 2, – 2) and (2, – 4), respectively, find the coordinates of P such that AP = $\frac{3}{7}$AB and P lies on the line segment AB.

Sol.

The coordinates of point A and B are (−2, −2) and (2, −4) respectively.

Since $\mathrm{AP}=\frac{3}{7}\mathrm{AB}$,

Therefore, AP: PB = 3:4

Point P divides the line segment AB in the ratio 3:4.

Coordinates of P = $\left(\frac{3\times 2+4\times (–2)}{3+4},\frac{3\times (–4)+4\times (–2)}{3+4}\right)$

= $\left(\frac{6–8}{7},\frac{–12–8}{7}\right)$

= $\left(–\frac{2}{7},–\frac{20}{7}\right)$

P9. Find the coordinates of the points which divide the line segment joining A(– 2, 2) and B(2, 8) into four equal parts.

Sol.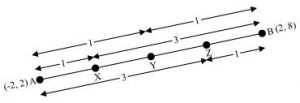

From the figure, it can be observed that points P, Q, R are dividing the line segment in a ratio 1:3,   1:1, 3:1 respectively.

Coordinates of P = $\left(\frac{1\times 2+3\times (–2)}{1+3},\frac{1\times 8+3\times 2}{1+3}\right)$ = $\left(–1,\frac{7}{2}\right)$

Coordinates of Q = $\left(\frac{2+(–2)}{2},\frac{2+8}{2}\right)$ = (0, 5)

Coordinates of R = $\left(\frac{3\times 2+1\times (–2)}{3+1},\frac{3\times 8+1\times 2}{3+1}\right)$ = $\left(1,\frac{13}{2}\right)$

P10. Find the area of a rhombus if its vertices are (3, 0), (4, 5), (– 1, 4) and (– 2, – 1) taken in order. [Hint: Area of a rhombus = $\frac{1}{2}$ (product of its diagonals)]

Sol.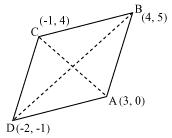

Let (3, 0), (4, 5), (−1, 4) and (−2, −1) are the vertices A, B, C, D of a rhombus ABCD.

Length of diagonal AC = $\sqrt{[3–(–1){]}^2+(0–4{)}^2}$ = $=\sqrt{16+16}=4\sqrt{2}$

Length of diagonal BD = $\sqrt{[4–(–2){]}^2+[5–(–1){]}^2}$ = $=\sqrt{36+36}=6\sqrt{2}$

Therefore, area of rhombus ABCD = $\frac{1}{2}\times 4\sqrt{2}\times 6\sqrt{2}$ = 24 square units          

EXERCISE-7.3

P1. Find the area of the triangle whose vertices are:

(i) (2, 3), (–1, 0), (2, – 4)

(ii) (–5, –1), (3, –5), (5, 2)

Sol. (i) Area of a triangle is given by

Area of a triangle = $\frac{1}{2}\left\{{\mathrm{x}}_1\left({\mathrm{y}}_2–{\mathrm{y}}_3\right)+{\mathrm{x}}_2\left({\mathrm{y}}_3–{\mathrm{y}}_1\right)+{\mathrm{x}}_3\left({\mathrm{y}}_1–{\mathrm{y}}_2\right)\right\}$

= $\frac{1}{2}\left\{2\right(0–(–4))+(–1\left)\right\{(–4)–\left(3\right)\}+2(3–0\left)\right\}$

= $\frac{1}{2}[8+7+6]=\frac{21}{2}\text{ square units }$

(ii) Area of given triangle = $\frac{1}{2}\left[\right(–5\left)\right[(–5)–(–2)]+3(2–(–1))+5(–1)–(–5\left)\right]$

= $\frac{1}{2}[35+9+20]=32\text{ square units }$

P2. In each of the following find the value of ‘k’, for which the points are collinear.

(i) (7, –2), (5, 1), (3, k)

(ii) (8, 1), (k, – 4), (2, –5)

Sol. (i) For collinear points, area of triangle formed by them is zero.

Therefore, for points (7, −2) (5, 1), and (3, k), area = 0

$\frac{1}{2}\left[7\right(1–\mathrm{k})+5(\mathrm{k}–(–2))+3((–2)–1\left)\right]=0$

7 – 7k + 5k + 10 – 9 = 0

– 2k + 8 = 0

k = 4

(ii) For collinear points, area of triangle formed by them is zero.

Therefore, for points (8, 1), (k, −4), and (2, −5), area = 0

$\frac{1}{2}\left[8\right(–4–(–5))+\mathrm{k}((–5)–\left(1\right))+2(1–(–4)\left)\right]=0$

8 – 6k + 10 = 0

6k = 18

k = 3

P3. Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.

Sol.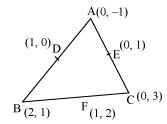

Let the vertices of the triangle be A (0, −1), B (2, 1), C (0, 3).

Let D, E, F be the mid-points of the sides of this triangle. Coordinates of D, E, and F are given by

$\mathrm{D}=\left(\frac{0+2}{2},\frac{–1+1}{2}\right)=(1,0)$

$\mathrm{E}=\left(\frac{0+0}{2},\frac{3–1}{2}\right)=(0,1)$

$\mathrm{F}\left(\frac{2+0}{2},\frac{1+3}{2}\right)=(1,2)$

Area of a triangle = $\frac{1}{2}\left\{{\mathrm{x}}_1\left({\mathrm{y}}_2–{\mathrm{y}}_3\right)+{\mathrm{x}}_2\left({\mathrm{y}}_3–{\mathrm{y}}_1\right)+{\mathrm{x}}_3\left({\mathrm{y}}_1–{\mathrm{y}}_2\right)\right\}$

Area of ΔDEF = $\frac{1}{2}\left[1\right(2–1)+1(1–0)+0(0–2\left)\right]$ = $\frac{1}{2}(1+1)=1\text{ square units }$

Area of ΔABC = $\frac{1}{2}\left[0\right(1–3)+2(3–(–1))+0(–1–1\left)\right]$ = $\frac{1}{2}\left[8\right]=4\text{ square units }$

Therefore, required ration = 1: 4

P4. Find the area of the quadrilateral whose vertices, taken in order, are (– 4, – 2), (– 3, – 5), (3, – 2) and (2, 3).

Sol.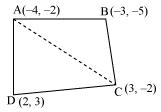

Let the vertices of the quadrilateral be A (−4, −2), B (−3, −5), C (3, −2), and D (2, 3). Join AC to form two triangles ΔABC and ΔACD.

Area of a triangle = $\frac{1}{2}\left\{{\mathrm{x}}_1\left({\mathrm{y}}_2–{\mathrm{y}}_3\right)+{\mathrm{x}}_2\left({\mathrm{y}}_3–{\mathrm{y}}_1\right)+{\mathrm{x}}_3\left({\mathrm{y}}_1–{\mathrm{y}}_2\right)\right\}$

Area of ΔABC = $\frac{1}{2}\left[\right(–4\left)\right\{(–5)–(–2)\}+(–3\left)\right\{(–2)–(–2)\}+3\{(–2)–(–5)\left\}\right]$

= $\frac{1}{2}(12+0+9)=\frac{21}{2}\text{ square units }$

Area of ΔACD = $\frac{1}{2}\left[\right(–4\left)\right\{(–2)–\left(3\right)\}+3\{\left(3\right)–(–2)\}+2\{(–2)–(–2)\left\}\right]$

= $\frac{1}{2}\{20+15+0\}=\frac{35}{2}$square units

Area of $\square \mathrm{ABCD}$ = Area of ΔABC + Area of ΔACD

= $\left(\frac{21}{2}+\frac{35}{2}\right)$square units = 28 square units

P5. You have studied in Class IX, (Chapter 9, and Example 3), that a median of a triangle divides it into two triangles of equal areas. Verify this result for Δ ABC whose vertices are A (4, – 6), B(3, –2) and C(5, 2).

Sol.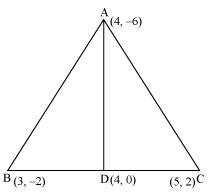

Let the vertices of the triangle be A (4, −6), B (3, −2), and C (5, 2).

Let D be the mid-point of side BC of ΔABC.

Therefore, AD is the median in ΔABC.

Coordinates of point D = $\left(\frac{3+5}{2},\frac{–2+2}{2}\right)=(4,0)$

Area of a triangle = $\frac{1}{2}\left\{{\mathrm{x}}_1\left({\mathrm{y}}_2–{\mathrm{y}}_3\right)+{\mathrm{x}}_2\left({\mathrm{y}}_3–{\mathrm{y}}_1\right)+{\mathrm{x}}_3\left({\mathrm{y}}_1–{\mathrm{y}}_2\right)\right\}$

Area of ΔABD = $\frac{1}{2}\left[\right(4\left)\right\{(–2)–\left(0\right)\}+(3\left)\right\{\left(0\right)–\left(6\right)\}+(4\left)\right\{(–6)–(–2)\left\}\right]$

= $\frac{1}{2}(–8+18–16)=–3\text{ square units }$

However, area cannot be negative. Therefore, area of ΔABD is 3 square units.

Area of ΔADC = $\frac{1}{2}\left[\right(4\left)\right\{0–\left(2\right)+\left(4\right)\left\{2\right\}–(–6)\}+(5\left)\right\{(–6)–\left(0\right)\left\}\right]$

$\frac{1}{2}(–8+32–30)=–3$ square units

However, area cannot be negative. Therefore, area of ΔADC is 3 square units.

Clearly, median AD has divided ΔABC in two triangles of equal areas.

EXERCISE-7.3

P1. Determine the ratio in which the line 2x + y − 4 = 0 divides the line segment joining the points A(2, − 2) and B(3, 7)

Sol. Let the given line divide the line segment joining the points A(2, −2) and B(3, 7) in a ratio k : 1.

Coordinates of the point of division $\left(\frac{3k+2}{k+1},\frac{7k–2}{k+1}\right)$

This point also lies on 2x + y − 4 = 0

$\therefore 2\left(\frac{3\mathrm{k}+2}{\mathrm{k}+1}\right)+\left(\frac{7\mathrm{k}–2}{\mathrm{k}+1}\right)–4=0$

$\Rightarrow \frac{6\mathrm{k}+4+7\mathrm{k}–2–4\mathrm{k}–4}{\mathrm{k}+1}=0$

$\Rightarrow 9\mathrm{k}–2=0$

$\Rightarrow \mathrm{k}=\frac{2}{9}$

Therefore, the ratio in which the line 2x + y − 4 = 0 divides the line segment joining the points A(2, −2) and B(3, 7) is 2:9.

P2. Find a relation between x and y if the points (x, y), (1, 2) and (7, 0) are collinear.

Sol. If the given points are collinear, then the area of triangle formed by these points will be 0.

Area of a triangle = $\frac{1}{2}\left\{{\mathrm{x}}_1\left({\mathrm{y}}_2–{\mathrm{y}}_3\right)+{\mathrm{x}}_2\left({\mathrm{y}}_3–{\mathrm{y}}_1\right)+{\mathrm{x}}_3\left({\mathrm{y}}_1–{\mathrm{y}}_2\right)\right\}$

Area = $\frac{1}{2}\left[\mathrm{x}\right(2–0)+1(0–\mathrm{y})+7(\mathrm{y}–2\left)\right]$

0 = $\frac{1}{2}[2x–y+7y–14]$

0 = $\frac{1}{2}[2\mathrm{x}+6\mathrm{y}–14]$

2x + 6y – 14 = 0

x + 3y – 7 = 0                                                    

This is the required relation between x and y.

P3. Find the centre of a circle passing through the points (6, − 6), (3, − 7) and (3, 3).

Sol. Let O (x, y) be the centre of the circle. And let the points (6, −6), (3, −7), and (3, 3) be representing the points A, B, and C on the circumference of the circle.

$\therefore \mathrm{OA}=\sqrt{(\mathrm{x}–6{)}^2+(\mathrm{y}+6{)}^2}$

$\mathrm{OB}=\sqrt{(\mathrm{x}–3{)}^2+(\mathrm{y}+7{)}^2}$

$\mathrm{OC}=\sqrt{(\mathrm{x}–3{)}^2+(\mathrm{y}–3{)}^2}$

However, OA = OB (Radii of the same circle)

$\Rightarrow \sqrt{(x–6{)}^2+(y+6{)}^2}$ $=\sqrt{(x–3{)}^2+(y+7{)}^2}$

$\Rightarrow$ x² +36 -12x + y² + 36 + 12y = x² + 9 -6x + y² + 49 + 14 y

$\Rightarrow$ – 6x – 2y + 14 = 0

$\Rightarrow$ 3x + y = 7                ^____ (1)

Similarly, OA = OC (Radii of the same circle)

$\Rightarrow \sqrt{(x–6{)}^2+(y+6{)}^2}$ $=\sqrt{(x–3{)}^2+(y–3{)}^2}$

$\Rightarrow$ x² + 36 -12 x + y² + 36 + 12y = x² + 9 -6x + y² + 9 -6y

$\Rightarrow$ – 6x + 18y + 54 = 0

$\Rightarrow$ – 3x + 9y = – 27       ^________ (2)

On adding equation (1) and (2), we obtain

10y = −20

y = −2

From equation (1), we obtain

3x − 2 = 7

3x = 9

x = 3

Therefore, the centre of the circle is (3, −2).

P4. The two opposite vertices of a square are (− 1, 2) and (3, 2). Find the coordinates of the other two vertices.

Sol.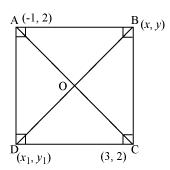

Let ABCD be a square having (−1, 2) and (3, 2) as vertices A and C respectively. Let (x, y), (x₁, y₁) be the coordinate of vertex B and D respectively.

We know that the sides of a square are equal to each other.

$\therefore$ AB = BC

$\Rightarrow \sqrt{(x+1{)}^2+(y–2{)}^2}$$=\sqrt{(x–3{)}^2+(y–2{)}^2}$

$\Rightarrow$ x²  + 2x + 1 + y² – 4y + 4 = x² + 9 – 6x + y² + 4 -4y

$\Rightarrow$ 8x = 8

$\Rightarrow$ x = 1

We know that in a square, all interior angles are of 90°.

In ΔABC,

AB² + BC² = AC²

$\Rightarrow {\left(\sqrt{(1+1{)}^2+(y–2{)}^2}\right)}^2+{\left(\sqrt{(1–3{)}^2+(y–2{)}^2}\right)}^2$ = ${\left(\sqrt{(3+1{)}^2+(2–2{)}^2}\right)}^2$

⇒ 4 + y² + 4 − 4y + 4 + y² − 4y + 4 =16

⇒ 2y² + 16 − 8 y =16

⇒ 2y² − 8 y = 0

⇒ y (y − 4) = 0

⇒ y = 0 or 4

We know that in a square, the diagonals are of equal length and bisect each other at 90°. Let O be the mid-point of AC.

Therefore, it will also be the mid-point of BD.

Coordinate of Point O = $\left(\frac{–1+3}{2},\frac{2+2}{2}\right)$

$\left(\frac{1+x_1}{2},\frac{y+y_1}{2}\right)=(1,2)$

$\frac{1+{\mathrm{x}}_1}{2}=1$

1 + x₁ = 2

x₁ = 1    and

$\frac{y+y_1}{2}=2$

⇒ y + y₁ = 4

If y = 0,

y₁ = 4

If y = 4,

y₁ = 0

Therefore, the required coordinates are (1, 0) and (1, 4).

P5. The class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is a triangular grassy lawn in the plot as shown in the following figure. The students are to sow seeds of flowering plants on the remaining area of the plot.

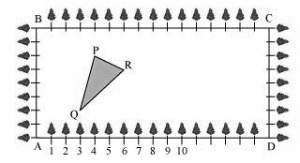
(i) Taking A as origin, find the coordinates of the vertices of the triangle.

(ii) What will be the coordinates of the vertices of Δ PQR if C is the origin?

Also calculate the areas of the triangles in these cases. What do you observe?

Sol. (i) Taking A as origin, we will take AD as x-axis and AB as y-axis. It can be observed that the coordinates of point P, Q, and R are (4, 6), (3, 2), and (6, 5) respectively.

Area of triangle PQR = $\frac{1}{2}\left[{\mathrm{x}}_1\left({\mathrm{y}}_2–{\mathrm{y}}_3\right)+{\mathrm{x}}_2\left({\mathrm{y}}_3–{\mathrm{y}}_1\right)+{\mathrm{x}}_3\left({\mathrm{y}}_1–{\mathrm{y}}_2\right)\right]$

= $\frac{1}{2}\left[4\right(2–5)+3(5–6)+6(6–2\left)\right]$

= $\frac{1}{2}[–12–3+24]$

= $\frac{9}{2}\text{ square units }$

(ii) Taking C as origin, CB as x-axis, and CD as y-axis, the coordinates of vertices P, Q, and R are (12, 2), (13, 6), and (10, 3) respectively.

Area of triangle PQR = $\frac{1}{2}\left[{\mathrm{x}}_1\left({\mathrm{y}}_2–{\mathrm{y}}_3\right)+{\mathrm{x}}_2\left({\mathrm{y}}_3–{\mathrm{y}}_1\right)+{\mathrm{x}}_3\left({\mathrm{y}}_1–{\mathrm{y}}_2\right)\right]$

= $\frac{1}{2}\left[12\right(6–3)+13(3–2)+10(2–6\left)\right]$

= $\frac{1}{2}[36+13–40]$

= $\frac{9}{2}\text{ square units }$

It can be observed that the area of the triangle is same in both the cases.

P6. The vertices of a ΔABC are A (4, 6), B (1, 5) and C (7, 2). A line is drawn to intersect sides AB and AC at D and E respectively, such that $\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\mathrm{AE}}{\mathrm{AC}}=\frac{1}{4}$. Calculate the area of the ΔADE and compare it with the area of ΔABC. (Recall Converse of basic proportionality theorem and Theorem 6.6 related to ratio of areas of two similar triangles)

Sol.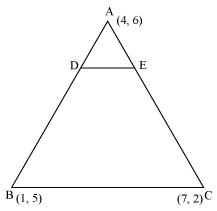

Given that, $\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\mathrm{AE}}{\mathrm{AC}}=\frac{1}{4}$

$\frac{\mathrm{AD}}{\mathrm{AD}+\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{AE}+\mathrm{EC}}=\frac{1}{4}$

$\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}=\frac{1}{3}$

Therefore, D and E are two points on side AB and AC respectively such that they divide side AB and AC in a ratio of 1:3.

Coordinates of Point D = $\left(\frac{1\times 1+3\times 4}{1+3},\frac{1\times 5+3\times 6}{1+3}\right)$ = $\left(\frac{13}{4},\frac{23}{4}\right)$

Coordinates of Point E = $\left(\frac{1\times 7+3\times 4}{1+3},\frac{1\times 2+3\times 6}{1+3}\right)$ = $\left(\frac{19}{4},\frac{20}{4}\right)$

Area of triangle = $\frac{1}{2}\left[{\mathrm{x}}_1\left({\mathrm{y}}_2–{\mathrm{y}}_3\right)+{\mathrm{x}}_2\left({\mathrm{y}}_3–{\mathrm{y}}_1\right)+{\mathrm{x}}_3\left({\mathrm{y}}_1–{\mathrm{y}}_2\right)\right]$

Area of ΔADE = $\frac{1}{2}\left[4\left(\frac{23}{4}–\frac{20}{4}\right)+\frac{13}{4}\left(\frac{20}{4}–6\right)+\frac{19}{4}\left(6–\frac{23}{4}\right)\right]$

$=\frac{1}{2}\left[3–\frac{13}{4}+\frac{19}{16}\right]=\frac{1}{2}\left[\frac{48–52+19}{16}\right]=\frac{15}{32}$ square units

Area of ΔABC =$\frac{1}{2}\left[4\right(5–2)+1(2–6)+7(6–5\left)\right]$ = $\frac{1}{2}[12–4+7]=\frac{15}{2}\text{ square units }$

Clearly, the ratio between the areas of ΔADE and ΔABC is 1:16.

Alternatively,

We know that if a line segment in a triangle divides its two sides in the same ratio, then the line segment is parallel to the third side of the triangle. These two triangles so formed (here ΔADE and ΔABC) will be similar to each other.

Hence, the ratio between the areas of these two triangles will be the square of the ratio between the sides of these two triangles.

Therefore, ratio between the areas of ΔADE and ΔABC = ${\left(\frac{1}{4}\right)}^2=\frac{1}{16}$

P7. Let A (4, 2), B (6, 5) and C (1, 4) be the vertices of ΔABC.

(i) The median from A meets BC at D. Find the coordinates of point D.

(ii) Find the coordinates of the point P on AD such that AP: PD = 2:1

(iii) Find the coordinates of point Q and R on medians BE and CF respectively such that BQ: QE = 2:1 and CR: RF = 2:1.

(iv) What do you observe?

(v) If A(x₁, y₁), B(x₂, y₂), and C(x₃, y₃) are the vertices of ΔABC, find the coordinates of the centroid of the triangle.

Sol.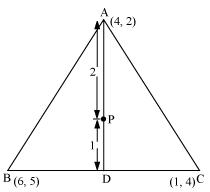

(i) Median AD of the triangle will divide the side BC in two equal parts.

Therefore, D is the mid-point of side BC.

Coordinates of D = $\left(\frac{6+1}{2},\frac{5+4}{2}\right)=\left(\frac{7}{2},\frac{9}{2}\right)$

(ii) Point P divides the side AD in a ratio 2:1.

Coordinates of P = $\left(\frac{2\times \frac{7}{2}+1\times 4}{2+1},\frac{2\times \frac{9}{2}+1\times 2}{2+1}\right)$ = $\left(\frac{11}{3},\frac{11}{3}\right)$

(iii) Median BE of the triangle will divide the side AC in two equal parts.

Therefore, E is the mid-point of side AC.

Coordinates of E = $\left(\frac{4+1}{2},\frac{2+4}{2}\right)=\left(\frac{5}{2},3\right)$

Point Q divides the side BE in a ratio 2:1.

Coordinates of Q = $\left(\frac{2\times \frac{5}{2}+1\times 6}{2+1},\frac{2\times 3+1\times 5}{2+1}\right)$ = $\left(\frac{11}{3}·\frac{11}{3}\right)$

Median CF of the triangle will divide the side AB in two equal parts. Therefore, F is the mid-point of side AB.

Coordinates of F = $\left(\frac{4+6}{2},\frac{2+5}{2}\right)=\left(5,\frac{7}{2}\right)$

Point R divides the side CF in a ratio 2:1.

Coordinates of R = $\left(\frac{2\times 5+1\times 1}{2+1},\frac{2\times \frac{7}{2}+1\times 4}{2+1}\right)$ = $\left(\frac{11}{3},\frac{11}{3}\right)$

(iv) It can be observed that the coordinates of point P, Q, R are the same.

Therefore, all these are representing the same point on the plane i.e., the centroid of the triangle.

(v) Consider a triangle, ΔABC, having its vertices as A(x₁, y₁), B(x₂, y₂), and C(x₃, y₃).

Median AD of the triangle will divide the side BC in two equal parts. Therefore, D   is the mid-point of side BC.

Coordinates of D = $\left(\frac{{\mathrm{x}}_2+{\mathrm{x}}_3}{2},\frac{{\mathrm{y}}_2+{\mathrm{y}}_3}{2}\right)$

Let the centroid of this triangle be O.

Point O divides the side AD in a ratio 2:1.

Coordinates of O = $\left(\frac{2\times \frac{{\mathrm{x}}_2+{\mathrm{x}}_3}{2}+1\times {\mathrm{x}}_1}{2+3},\frac{2\times \frac{{\mathrm{y}}_2+{\mathrm{y}}_3}{2}+1\times {\mathrm{y}}_1}{2+1}\right)$ = $\left(\frac{{\mathrm{x}}_1+{\mathrm{x}}_2+{\mathrm{x}}_3}{3},\frac{{\mathrm{y}}_1+{\mathrm{y}}_2+{\mathrm{y}}_3}{3}\right)$

P8. ABCD is a rectangle formed by the points A (− 1, − 1), B (− 1, 4), C (5, 4) and
D (5, − 1). P, Q, R and S are the mid-points of AB, BC, CD, and DA respectively. Is the quadrilateral PQRS is a square? a rectangle? or a rhombus? Justify your answer.

Sol.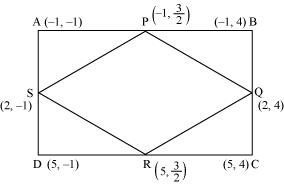

P is the mid-point of side AB.

Therefore, the coordinates of P are $\left(\frac{–1–1}{2},\frac{–1+4}{2}\right)=\left(–1,\frac{3}{2}\right)$

Similarly, the coordinates of Q, R and S are (2, 4), $\left(5,\frac{3}{2}\right)$ and (2, -1) respectively.

Length of PQ = $\sqrt{(–1–2{)}^2+{\left(\frac{3}{2}–4\right)}^2}$ = $\sqrt{9+\frac{25}{4}}=\sqrt{\frac{61}{4}}$

Length of QR = $\sqrt{(2–5{)}^2+{\left(4–\frac{3}{2}\right)}^2}$ = $\sqrt{9+\frac{25}{4}}=\sqrt{\frac{61}{4}}$

Length of RS = $\sqrt{(5–2{)}^2+{\left(\frac{3}{2}+1\right)}^2}$ = $\sqrt{9+\frac{25}{4}}=\sqrt{\frac{61}{4}}$

Length of SP = $\sqrt{(2+1{)}^2+{\left(–1–\frac{3}{2}\right)}^2}$ = $\sqrt{9+\frac{25}{4}}=\sqrt{\frac{61}{4}}$

Length of PR = $\sqrt{(–1–5{)}^2+{\left(\frac{3}{2}–\frac{3}{2}\right)}^2}=6$

Length of QS = $\sqrt{(2–2{)}^2+(4+1{)}^2}=5$

It can be observed that all sides of the given quadrilateral are of the same measure. However, the diagonals are of different lengths. Therefore, PQRS is a rhombus.