EXERCISE-8.1
P 1: In ΔABC right angled at B, AB = 24 cm, BC = 7 m. Determine
(i) sin A, cos A (ii) sin C, cos C
Sol. Applying Pythagoras theorem for ΔABC, we obtain
AC2 = AB2 + BC2
= (24 cm)2 + (7 cm)2
= (576 + 49) cm2
= 625 cm2
AC = cm = 25 cm
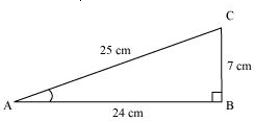
(i) sin A
cos A =
(ii) 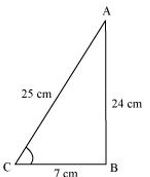
sin C =
cos C =
P2. In the given figure find tan P − cot R
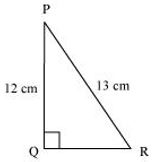
Sol. Applying Pythagoras theorem for ΔPQR, we obtain
PR2 = PQ2 + QR2
(13 cm)2 = (12 cm)2 + QR2
169 cm2 = 144 cm2 + QR2
25 cm2 = QR2
QR = 5 cm
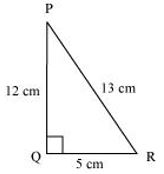
=
=
tan P − cot R =
P3. If sin A = , calculate cos A and tan A.
Sol. Let ΔABC be a right-angled triangle, right-angled at point B.
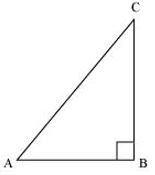
Given that,
Let BC be 3k.
Therefore, AC will be 4k, where k is a positive integer.
Applying Pythagoras theorem in ΔABC, we obtain
AC2 = AB2 + BC2
(4k)2 = AB2 + (3k)2
16k 2 − 9k 2 = AB2
7k 2 = AB2
AB =
P4. Given 15 cot A = 8. Find sin A and sec A
Sol. Consider a right-angled triangle, right-angled at B.

It is given that, cot A =
Let AB be 8k. Therefore, BC will be 15k, where k is a positive integer.
Applying Pythagoras theorem in ΔABC, we obtain
AC2 = AB2 + BC2
= (8k)2 + (15k)2
= 64k2 + 225k2
= 289k2
AC = 17k
=
P5. Given sec θ = , calculate all other trigonometric ratios.
Sol. Consider a right-angle triangle ΔABC, right-angled at point B.
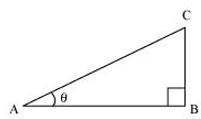
If AC is 13k, AB will be 12k, where k is a positive integer.
Applying Pythagoras theorem in ΔABC, we obtain
(AC)2 = (AB)2 + (BC)2
(13k)2 = (12k)2 + (BC)2
169k2 = 144k2 + BC2
25k2 = BC2
BC = 5k
P6. If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Sol. Let us consider a triangle ABC in which CD ⊥ AB.
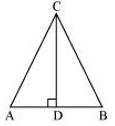
It is given that
cos A = cos B
… (1)
We have to prove ∠A = ∠B. To prove this, let us extend AC to P such that BC = CP.
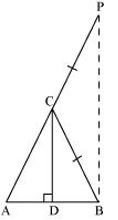
From equation (1), we obtain
(By construction we have BC = CP)
By using the converse of B.P.T, CD||BP
⇒ ∠ACD = ∠CPB (Corresponding angles) … (3)
And, ∠BCD = ∠CBP (Alternate interior angles) … (4)
By construction, we have BC = CP.
∠CBP = ∠CPB (Angle opposite to equal sides of a triangle) … (5)
From equations (3), (4), and (5), we obtain
∠ACD = ∠BCD … (6)
In ΔCAD and ΔCBD,
∠ACD = ∠BCD [Using equation (6)]
∠CDA = ∠CDB [Both 90°]
Therefore, the remaining angles should be equal.
∠CAD = ∠CBD
⇒ ∠A = ∠B
Alternatively,
Let us consider a triangle ABC in which CD ⊥ AB.
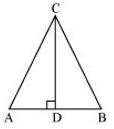
It is given that,
cos A = cos B
Let
⇒ AD = k BD … (1)
And, AC = k BC … (2)
Using Pythagoras theorem for triangles CAD and CBD, we obtain
CD2 = AC2 − AD2 … (3)
And, CD2 = BC2 − BD2 … (4)
From equations (3) and (4), we obtain
AC2 − AD2 = BC2 − BD2
⇒ (k BC)2 − (k BD)2 = BC2 − BD2
⇒ k2 (BC2 − BD2) = BC2 − BD2
⇒ k2 = 1 ⇒ k = 1
Putting this value in equation (2), we obtain
AC = BC
⇒ ∠A = ∠B (Angles opposite to equal sides of a triangle)
P7. If cot θ = , evaluate
(i)
(ii) cot2 θ
Sol. Let us consider a right triangle ABC, right-angled at point B.
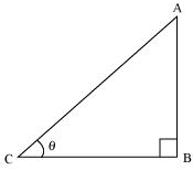
If BC is 7k, then AB will be 8k, where k is a positive integer.
Applying Pythagoras theorem in ΔABC, we obtain
AC2 = AB2 + BC2
= (8k)2 + (7k)2
= 64k2 + 49k2
= 113k2
AC =
(i)
(ii)
P8. If 3 cot A = 4, Check whether or not.
Sol. It is given that 3cot A = 4
Or, cot A =
Consider a right triangle ABC, right-angled at point B.
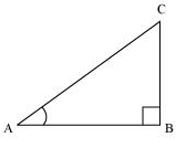
If AB is 4k, then BC will be 3k, where k is a positive integer.
In ΔABC,
(AC)2 = (AB)2 + (BC)2
= (4k)2 + (3k)2
= 16k2 + 9k2
= 25k2 AC
AC = 5k
cos2 A − sin2 A =
∴
P9. In ΔABC, right angled at B. If , find the value of
(i) sin A cos C + cos A sin C
(ii) cos A cos C − sin A sin C Sol.
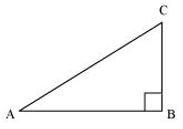
If BC is k, then AB will be , where k is a positive integer.
In ΔABC,
AC2 = AB2 + BC2
=
= 3k2 + k2
= 4k2
AC = 2k
(i) sin A cos C + cos A sin C
(ii) cos A cos C − sin A sin C
P10. In ΔPQR, right angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Sol. Given that,
PR + QR = 25
PQ = 5
Let PR be x.
Therefore, QR = 25 − x
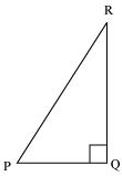
Applying Pythagoras theorem in ΔPQR, we obtain
PR2 = PQ2 + QR2
x2 = (5)2 + (25 − x)2
x2 = 25 + 625 + x2 − 50x
50x = 650
x = 13
Therefore, PR = 13 cm
QR = (25 − 13) cm = 12 cm
P11. State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = for some value of angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A
(v) , for some angle θ
Sol. (i) Consider a ΔABC, right-angled at B.
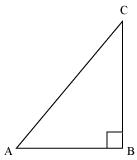
But
tan A > 1
So, tan A < 1 is not always true.
Hence, the given statement is false.
(ii)
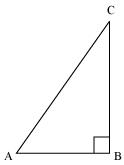
Let AC be 12k, AB will be 5k, where k is a positive integer.
Applying Pythagoras theorem in ΔABC, we obtain
AC2 = AB2 + BC2
(12k)2 = (5k)2 + BC2
144k2 = 25k2 + BC2
BC2 = 119k2
BC = 10.9k
It can be observed that for given two sides AC = 12k and AB = 5k,
BC should be such that,
AC − AB < BC < AC + AB
12k − 5k < BC < 12k + 5k
7k < BC < 17 k
However, BC = 10.9k.
Clearly, such a triangle is possible and hence, such value of sec A is possible.
Hence, the given statement is true.
(iii) Abbreviation used for cosecant of angle A is cosec A. And cos A is the abbreviation used for cosine of angle A. Hence, the given statement is false.
(iv) cot A is not the product of cot and A. It is the cotangent of ∠A.
Hence, the given statement is false.
(v) sin θ =
We know that in a right-angled triangle,
In a right-angled triangle, hypotenuse is always greater than the remaining two sides. Therefore, such value of sin θ is not possible.
Hence, the given statement is false
EXERCISE-8.2
P1. Evaluate the following
(i) sin60° cos30° + sin30° cos 60°
(ii) 2tan245° + cos230° − sin260°
(iii)
(iv)
(v)
Sol. (i) sin60° cos30° + sin30° cos 60°
(ii) 2tan245° + cos230° − sin260°
(iii)
(iv)
(v)
P2. Choose the correct option and justify your choice.
(i)
(A). sin60° (B). cos60° (C). tan60° (D). sin30°
(ii)
(A). tan90° (B). 1 (C). sin45° (D). 0
(iii) sin2A = 2sinA is true when
A = (A). 0° (B). 30° (C). 45° (D). 60°
(iv)
(A). cos60° (B). sin60° (C). tan60° (D). sin30°
Sol. (i)
Out of the given alternatives, only
Hence, (A) is correct.
(ii)
Hence, (D) is correct.
(iii) Out of the given alternatives, only A = 0° is correct.
As sin 2A = sin 0° = 0
2 sinA = 2sin 0° = 2(0) = 0
Hence, (A) is correct.
(iv)
Out of the given alternatives, only tan 60°
Hence, (C) is correct.
P3. If and ; 0° < A + B ≤ 90°, A > B find A and B.
Sol.
⇒
⇒ A + B = 60 … (1)
⇒ tan (A − B) = tan30
⇒ A − B = 30 … (2)
On adding both equations, we obtain
2A = 90
⇒ A = 45
From equation (1), we obtain
45 + B = 60
B = 15
Therefore, ∠A = 45° and ∠B = 15°
P4. State whether the following are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B
(ii) The value of sinθ increases as θ increases
(iii) The value of cos θ increases as θ increases
(iv) sinθ = cos θ for all values of θ
(v) cot A is not defined for A = 0°
Sol. (i) sin (A + B) = sin A + sin B
Let A = 30° and B = 60°
sin (A + B) = sin (30° + 60°) = sin 90° = 1
sin A + sin B = sin 30° + sin 60°
Clearly, sin (A + B) ≠ sin A + sin B
Hence, the given statement is false.
(ii) The value of sin θ increases as θ increases in the interval of 0° < θ < 90° as
sin 0° = 0
sin 90° = 1
Hence, the given statement is true.
(iii) cos 0° = 1
cos90° = 0
It can be observed that the value of cos θ does not increase in the interval of 0° < θ < 90°.
Hence, the given statement is false.
(iv) sin θ = cos θ for all values of θ.
This is true when θ = 45°
As
It is not true for all other values of θ.
As and ,
Hence, the given statement is false.
(v) cot A is not defined for A = 0°
As ,
= undefined
Hence, the given statement is true.
EXERCISE-8.3
P1. Evaluate
(I)
(II)
(III) cos 48° − sin 42°
(IV) cosec 31° − sec 59°
Sol. (I)
(II)
(III) cos 48° − sin 42° = cos (90°− 42°) − sin 42° = sin 42° − sin 42° = 0
(IV) cosec 31° − sec 59°= cosec (90° − 59°) − sec 59° = sec 59° − sec 59° = 0
P2. Show that
(I) tan 48° tan 23° tan 42° tan 67° = 1
(II) cos 38° cos 52° − sin 38° sin 52° = 0
Sol. (I) tan 48° tan 23° tan 42° tan 67°
= tan (90° − 42°) tan (90° − 67°) tan 42° tan 67°
= cot 42° cot 67° tan 42° tan 67°
= (cot 42° tan 42°) (cot 67° tan 67°)
= (1) (1)
= 1
(II) cos 38° cos 52° − sin 38° sin 52°
= cos (90° − 52°) cos (90°−38°) − sin 38° sin 52°
= sin 52° sin 38° − sin 38° sin 52°
= 0
P3. If tan 2A = cot (A− 18°), where 2A is an acute angle, find the value of A.
Sol. Given that, tan 2A
= cot (A− 18°) cot (90° − 2A)
= cot (A −18°) 90° − 2A
= A− 18° 108° = 3A
A = 36°
P4. If tan A = cot B, prove that A + B = 90°
Sol. Given that,
tan A = cot B
tan A = tan (90° − B)
A = 90° − B
A + B = 90°
P5. If sec 4A = cosec (A− 20°), where 4A is an acute angle, find the value of A.
Sol. Given that,
sec 4A = cosec (A − 20°)
cosec (90° − 4A) = cosec (A − 20°)
90° − 4A= A− 20°
110° = 5A
A = 22°
P6. If A, Band C are interior angles of a triangle ABC then show that
Sol. We know that for a triangle ABC,
∠ A + ∠B + ∠C = 180°
∠B + ∠C= 180° − ∠A
P7. Express sin 67° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Sol. sin 67° + cos 75° = sin (90° − 23°) + cos (90° − 15°) = cos 23° + sin 15°
EXERCISE-8.4
P1. Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Sol. We know that,
will always be positive as we are adding two positive quantities.
Therefore,
We know that,
However,
Therefore,
Also,
P2. Write all the other trigonometric ratios of ∠A in terms of sec A.
Sol. We know that,
Also, sin2 A + cos2 A = 1
sin2 A = 1 − cos2 A
tan2A + 1 = sec2A
tan2A = sec2A – 1
P3. Evaluate
(i)
(ii) sin25° cos65° + cos25° sin65°
Sol. (i)
= (As sin2A + cos2A = 1) = 1
(ii) sin25° cos65° + cos25° sin65°
= sin225° + cos225°
= 1 (As sin2A + cos2A = 1)
P4. Choose the correct option. Justify your choice.
(i) 9 sec2 A − 9 tan2 A =
(A) 1 (B) 9 (C) 8 (D) 0
(ii) (1+tan θ + sec θ) (1 + cot θ − cosec θ)
(A) 0 (B) 1 (C) 2 (D) −1
(iii) (secA + tanA) (1 − sinA) =
(A) secA (B) sinA (C) cosecA (D) cosA
(iv)
(A) sec2 A (B) −1 (C) cot2 A (D) tan2 A
Sol. (i) 9 sec2A − 9 tan2A
= 9 (sec2A − tan2A)
= 9 (1) [As sec2 A − tan2 A = 1]
= 9
Hence, alternative (B) is correct.
(ii) (1 + tan θ + sec θ) (1 + cot θ − cosec θ)
Hence, alternative (C) is correct.
(iii) (secA + tanA) (1 − sinA)
= cosA
Hence, alternative (D) is correct.
(iv)
=
Hence, alternative (D) is correct.
P5. Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
(i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
(viii)
(ix)
(x)
Sol. (i)
= R.H.S
(ii)
L.H.S =
=
=
=
=
= R.H.S
(iii)
L.H.S =
= 1+ secθ cosecθ
= R.H.S.
(iv)
L.H.S =
Using the identity cosec2 = 1 + cot2 A,
L.H.S =
= cosec A + cot A
= R.H.S
(vi)
L.H.S =
(vii)
L.H.S =
(viii)
L.H.S =
= R.H.S
(ix)
L.H.S =
R.H.S =
Hence, L.H.S = R.H.S
(x)
=








