Number System

EXERCISE-1.1 

P1. Is zero a rational number? Can you write it in the form $\frac{p}{q}$ , where p and q are integers and q≠0?

Sol. Yes. Zero is a rational number as it can be represented as $\frac{0}{1}\text{ or }\frac{0}{2}\text{ or }\frac{0}{3}$ etc.

P2. Find six rational numbers between 3 and 4.

Sol. There are infinite rational numbers in between 3 and 4.

3 and 4 can be represented as $\frac{24}{8}\text{ and }\frac{32}{8}$respectively.

Therefore, rational numbers between 3 and 4 are $\frac{25}{8},\frac{26}{8},\frac{27}{8},\frac{28}{8},\frac{29}{8},\frac{30}{8}$

P3. Find five rational numbers between $\frac{3}{5}\text{ and }\frac{4}{5}$.

Sol. There are infinite rational numbers between $\frac{3}{5}\text{ and }\frac{4}{5}$.

$\begin{array}{l}\frac{3}{5}=\frac{3\times 6}{5\times 6}=\frac{18}{30}\\ \frac{4}{5}=\frac{4\times 6}{5\times 6}=\frac{24}{30}\end{array}$

$\therefore$Rational numbers between $\frac{3}{5}\text{ and }\frac{4}{5}$ are $\frac{19}{30},\frac{20}{30},\frac{21}{30},\frac{22}{30},\frac{23}{30}$

P4. State whether the following statements are true or false. Give reasons for your answers.

(i) Every natural number is a whole number.

(ii) Every integer is a whole number.

(iii) Every rational number is a whole number.

Sol. (i) True; since the collection of whole numbers contains all natural numbers.

(ii) False; as integers may be negative but whole numbers are positive. For Example: −3 is an integer but not a whole number.

(iii) False; as rational numbers may be fractional but whole numbers may not be. For example: is a rational number but not a whole number.

EXERCISE-1.2

P1. State whether the following statements are true or false. Justify your answers.

(i) Every irrational number is a real number.

(ii) Every point on the number line is of the form $\sqrt{m}$, where m is a natural number.

(iii) Every real number is an irrational number.

Sol. (i) True; since the collection of real numbers is made up of rational and irrational numbers.

(ii) False; as negative numbers cannot be expressed as the square root of any other number.

(iii) False; as real numbers include both rational and irrational numbers. Therefore, every real number cannot be an irrational number.

P2. Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.

Sol. If numbers such as $\sqrt{4}=2,\sqrt{9=3}$ are considered,

Then here, 2 and 3 are rational numbers. Thus, the square roots of all positive integers are not irrational.

P3. Show how $\sqrt{5}$ can be represented on the number line.

Sol.    We know that, $\sqrt{4}=2$ and, $\sqrt{5}=\sqrt{(2{)}^2+(1{)}^2}$

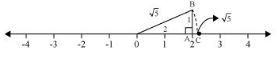
Mark a point ‘A’ representing 2 on number line. Now, construct AB of unit length perpendicular to OA. Then, taking O as centre and OB as radius, draw

an arc intersecting number line at C.

C is representing $\sqrt{5}$.

EXERCISE-1.3 [PAGE NO. 14] 

P1. Write the following in decimal form and say what kind of decimal expansion each has:

(i) $\frac{36}{100}$ 

(ii) $\frac{1}{11}$

(iii) $4\frac{1}{8}$

(iv) $\frac{3}{13}$

(v) $\frac{2}{11}$

(vi) $\frac{329}{400}$

Sol. (i) $\frac{36}{100}=0.36$

Terminating

(ii) $\frac{1}{11}=0.090909\dots =0.\overline{09}$   

Non-terminating repeating

(iii) $4\frac{1}{8}=\frac{33}{8}=4.125$  

Terminating

(iv) $\frac{3}{13}=0.230769230769\dots =0.\overline{230769}$  

Non-terminating repeating

(v) $\frac{2}{11}=0.18181818\dots =0\overline{18}$   

Non-terminating repeating

(vi) $\frac{329}{400}=0.8225$  

Terminating

P2. You know that $\frac{1}{7}=0.\overline{142857}$. Can you predict what the decimal expansion of $\frac{2}{7},\frac{3}{7},\frac{4}{7},\frac{5}{7},\frac{6}{7}$are, without actually doing the long division? If so, how?

[Hint: Study the remainders while finding the value of $\frac{1}{7}$carefully.]

Sol. Yes. It can be done as follows.

$\begin{array}{l}\frac{2}{7}=2\times \frac{1}{7}=2\times 0.\overline{142857}=0\overline{285714}\\ \frac{3}{7}=3\times \frac{1}{7}=3\times 0142857=0.\overline{428571}\\ \frac{4}{7}=4\times \frac{1}{7}=4\times 0.\overline{142857}=0571428\\ \frac{5}{7}=5\times \frac{1}{7}=5\times 0.\overline{142857}=0.\overline{714285}\\ \frac{6}{7}=6\times \frac{1}{7}=6\times 0.\overline{142857}=0.\overline{857142}\end{array}$

P3. Express the following in the form $\frac{p}{q}$ where p and q are integers and q ≠ 0.

(i) $0.\overline{6}$ (ii) $0.4\overline{7}$ (iii) $0.\overline{001}$

Sol. 

$\begin{array}{l}\left(i\right) 0.\overline{6}=0.666\dots \\ \text{ Let }x=0.666\dots \\ 10x=6.666\dots \\ 10x=6+x\\ 9x=6\Rightarrow x=\frac{2}{3}\\ \begin{array}{l}\left(ii\right) 0.\overline{47}=0.4777\dots \\ =\frac{4}{10}+\frac{0.777}{10}\\ \text{ Let }x=0.777\dots \\ 10x=7.777\dots \\ 10x=7+x\\ x=\frac{7}{9}\\ \frac{4}{10}+\frac{0.777\dots }{10}=\frac{4}{10}+\frac{7}{90}\\ =\frac{36+7}{90}=\frac{43}{90}\\ \begin{array}{l}\left(iii\right) 0.\overline{001}=0.001001\dots \\ \text{ Let }x=0.001001\dots \\ 1000x=1.001001\dots \\ 1000x=1+x\\ 999x=1\Rightarrow x=\frac{1}{999}\end{array}\end{array}\end{array}$

P4. Express 0.99999…in the form $\frac{p}{q}$. Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.

Sol.    Let x = 0.9999…

10x = 9.9999…

10x = 9 + x

9x = 9

x = 1

P5. What can the maximum number of digits be in the repeating block of digits in the decimal expansion of $\frac{1}{17}$? Perform the division to check your answer.

Sol. It can be observed that, $\frac{1}{17}=\overline{0.0588235294117647}$

There are 16 digits in the repeating block of the decimal expansion of  $\frac{1}{17}$.

P6. Look at several examples of rational numbers in the form $\frac{p}{q}$ (q ≠ 0), where p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?

Sol. Terminating decimal expansion will occur when denominator q of rational number $\frac{p}{q}$is either of 2, 4, 5, 8, 10, and so on…

$\begin{array}{l}\frac{9}{4}=2.25\\ \frac{11}{8}=1.375\\ \frac{27}{5}=5.4\end{array}$

It can be observed that terminating decimal may be obtained in the situation where prime factorisation of the denominator of the given fractions has the power of 2 only or 5 only or both.

P7. Write three numbers whose decimal expansions are non-terminating non-recurring.

Sol. 3 numbers whose decimal expansions are non-terminating non-recurring are as follows.

0.505005000500005000005…

0.7207200720007200007200000…

0.080080008000080000080000008…

P8. Find three different irrational numbers between the rational numbers $\frac{5}{7}\text{ and }\frac{9}{11}$.

Sol. $\frac{5}{7}=0.\overline{714285}$ 

$\frac{9}{11}=0.\overline{81}$            

3 irrational numbers are as follows.

0.73073007300073000073…

0.75075007500075000075…

0.79079007900079000079…

P9. Classify the following numbers as rational or irrational:

(i) $\sqrt{23}$ (ii) $\sqrt{225}$ (iii) 0.3796

(iv) 7.478478

(v) 1.101001000100001…

Sol.  (i) $\sqrt{23}=4.79583152331\dots$

As the decimal expansion of this number is non-terminating non-recurring, therefore, it is an irrational number.

(ii)  $\sqrt{225}=15=\frac{15}{1}$  

It is a rational number as it can be represented in $\frac{p}{q}$ form.

(iii) 0.3796

As the decimal expansion of this number is terminating, therefore, it is a rational number.

(iv) $7.478478\dots =7.\overline{478}$          

As the decimal expansion of this number is non-terminating recurring, therefore, it is a rational number.

(v) 1.10100100010000 …

As the decimal expansion of this number is non-terminating non-repeating, therefore, it is an irrational number.

EXERCISE-1.4

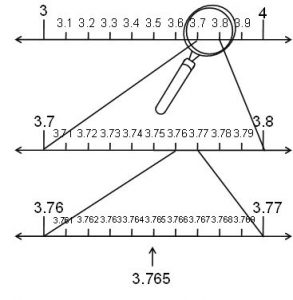
P1. Visualise 3.765 on the number line using successive magnification.

Sol. 3.765 can be visualised as in the following steps.

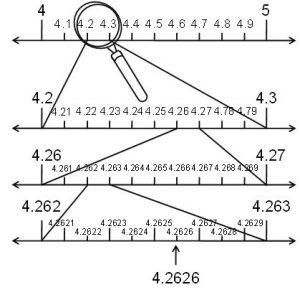
P2. Visualise $4.\overline{26}$ on the number line, up to 4 decimal places.

Sol. $4.\overline{26}$= 4.2626…

4.2626 can be visualised as in the following steps.

EXERCISE-1.5

P1. Classify the following numbers as rational or irrational:

(i) $2–\sqrt{5}$  

(ii) $(3+\sqrt{23})–\sqrt{23}$

(iii) $\left(\frac{2\sqrt{7}}{7\sqrt{7}}\right)$ 

(iv) $\frac{1}{\sqrt{2}}$ 

(v) 2π

Sol. (i) $2–\sqrt{5}=2–2.2360679\dots$ 

= − 0.2360679…

As the decimal expansion of this expression is non-terminating non-recurring, therefore, it is an irrational number.

(ii) $(3+\sqrt{23})–\sqrt{23}=3=\frac{3}{1}$ 

As it can be represented in $\frac{p}{q}$ form, therefore, it is a rational number.

(iii) $\frac{2\sqrt{7}}{7\sqrt{7}}=\frac{2}{7}$   

As it can be represented in $\frac{p}{q}$ form, therefore, it is a rational number.

(iv) $\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}=0.7071067811\dots$ 

As the decimal expansion of this expression is non-terminating non-recurring, therefore, it is an irrational number.

(v) 2π = 2(3.1415 …)

= 6.2830 …

As the decimal expansion of this expression is non-terminating non-recurring, therefore, it is an irrational number.

P2. Simplify each of the following expressions:

(i) $(3+\sqrt{3})(2+\sqrt{2})$      

(ii) $(3+\sqrt{3})(3–\sqrt{3})$    

(iii) $(\sqrt{5}+\sqrt{2}{)}^2$     

(iv) $(\sqrt{5}–\sqrt{2})(\sqrt{5}+\sqrt{2})$ 

Sol.

$\begin{array}{l}\left(i\right) (3+\sqrt{3})(2+\sqrt{2})\\ =3(2+\sqrt{2})+\sqrt{3}(2+\sqrt{2})\\ =6+3\sqrt{2}+2\sqrt{3}+\sqrt{6}\end{array}$    

(ii) $(3+\sqrt{3})(3–\sqrt{3})=(3{)}^2–(\sqrt{3}{)}^2$

= 9 − 3 = 6

(iii) $(\sqrt{5}+\sqrt{2}{)}^2$  

$=(\sqrt{5}{)}^2+(\sqrt{2}{)}^2+2\left(\sqrt{5}\right)\left(\sqrt{2}\right)$

$=5+2+2\sqrt{10}=7+2\sqrt{10}$

 (iv)  $(\sqrt{5}–\sqrt{2})(\sqrt{5}+\sqrt{2})$

$=(\sqrt{5}{)}^2–(\sqrt{2}{)}^2$

= 5 − 2 = 3

P3. Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, $\pi =\frac{c}{d}$. This seems to contradict the fact that π is irrational. How will you resolve this contradiction?

Sol. There is no contradiction. When we measure a length with scale or any other instrument, we only obtain an approximate rational value. We never obtain an exact value. For this reason, we may not realise that either c or d is irrational. Therefore, the fraction $\frac{c}{d}$ is irrational. Hence, π is irrational.

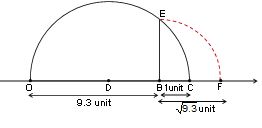
P4. Represent $\sqrt{9.3}$ on the number line.

Sol. Mark a line segment OB = 9.3 on number line. Further, take BC of 1 unit. Find the mid-point D of OC and draw a semi-circle on OC while taking D as its centre. Draw a perpendicular to line OC passing through point B. Let it intersect the semi-circle at E. Taking B as centre and BE as radius, draw an arc intersecting number line at F. BF is $\sqrt{9.3}$.

P5. Rationalise the denominators of the following:

(i) $\frac{1}{\sqrt{7}}$   

(ii) $\frac{1}{\sqrt{7}–\sqrt{6}}$      

(iii) $\frac{1}{\sqrt{5}+\sqrt{2}}$ 

(iv)  $\frac{1}{\sqrt{7}–2}$ 

Sol. (i) $\frac{1}{\sqrt{7}}=\frac{1\times \sqrt{7}}{1\times \sqrt{7}}=\frac{\sqrt{7}}{7}$

(ii) $\frac{1}{\sqrt{7}–\sqrt{6}}=\frac{1}{(\sqrt{7}–\sqrt{6})}\frac{(\sqrt{7}+\sqrt{6})}{(\sqrt{7}+\sqrt{6})}$

$=\frac{\sqrt{7}+\sqrt{6}}{(\sqrt{7}{)}^2–(\sqrt{6}{)}^2}$

$=\frac{\sqrt{7}+\sqrt{6}}{7–6}=\frac{\sqrt{7}+\sqrt{6}}{1}=\sqrt{7}+\sqrt{6}$

(iii) $\frac{1}{\sqrt{5}+\sqrt{2}}=\frac{1}{(\sqrt{5}+\sqrt{2})}\frac{(\sqrt{5}–\sqrt{2})}{(\sqrt{5}–\sqrt{2})}$

$=\frac{\sqrt{5}–\sqrt{2}}{(\sqrt{5}{)}^2–(\sqrt{2}{)}^2}=\frac{\sqrt{5}–\sqrt{2}}{5–2}$

$=\frac{\sqrt{5}–\sqrt{2}}{3}$

(iv) $\frac{1}{\sqrt{7}–2}=\frac{1}{(\sqrt{7}–2)}\frac{(\sqrt{7}+2)}{(\sqrt{7}+2)}$

$=\frac{\sqrt{7}+2}{(\sqrt{7}{)}^2–(2{)}^2}$

$=\frac{\sqrt{7}+2}{7–4}=\frac{\sqrt{5}+2}{3}$

EXERCISE-1.6 [PAGE NO. 26]

P1. Find:

(i) ${64}^{\frac{1}{2}}$

(ii) ${32}^{\frac{1}{5}}$

(iii) ${125}^{\frac{1}{3}}$

Sol. (i) ${64}^{\frac{1}{2}}={\left(2^6\right)}^{\frac{1}{2}}$

$=2^{6\times \frac{1}{2}}\left[{\left({\mathrm{a}}^{\mathrm{m}}\right)}^{\mathrm{n}}={\mathrm{a}}^{\mathrm{mn}}\right]$

$=2^3=8$

(ii) ${32}^{\frac{1}{5}}={\left(2^5\right)}^{\frac{1}{5}}$

$=(2{)}^{5\times \frac{1}{5}}\left[{\left({\mathrm{a}}^{\mathrm{m}}\right)}^{\mathrm{n}}={\mathrm{a}}^{\mathrm{mn}}\right]$

$=2^1=2$

(iii) ${125}^{\frac{1}{3}}={\left(5^3\right)}^{\frac{1}{3}}$

$=5^{3\times \frac{1}{3}}\left[{\left({\mathrm{a}}^{\mathrm{m}}\right)}^{\mathrm{n}}={\mathrm{a}}^{\mathrm{mn}}\right]$

$=5^1=5$

P2. Find:

(i) $9^{\frac{3}{2}}$ (ii) ${32}^{\frac{2}{5}}$ (iii) ${16}^{\frac{3}{4}}$ (iv) ${125}^{\frac{–1}{3}}$

Sol. (i) $9^{\frac{3}{2}}={\left(3^2\right)}^{\frac{3}{2}}$

$=3^{2\times \frac{3}{2}}\left[{\left({\mathrm{a}}^{\mathrm{m}}\right)}^{\mathrm{n}}={\mathrm{a}}^{\mathrm{mn}}\right]$

(ii) $(32{)}^{\frac{2}{5}}={\left(2^5\right)}^{\frac{2}{3}}$

$=(2{)}^{5\times \frac{2}{5}}\left[{\left({\mathrm{a}}^{\mathrm{m}}\right)}^{\mathrm{n}}={\mathrm{a}}^{\mathrm{mn}}\right]$

$=2^2=4$

(iii) ${16}^{\frac{3}{4}}={\left(2^4\right)}^{\frac{3}{4}}$

$=2^{4\times \frac{3}{4}}\left[{\left({\mathrm{a}}^{\mathrm{m}}\right)}^{\mathrm{n}}={\mathrm{a}}^{\mathrm{mn}}\right]$

$=2^3=8$

(iv) $(125{)}^{\frac{–1}{3}}=\frac{1}{(125{)}^{\frac{1}{3}}}\left[{\mathrm{a}}^{–\mathrm{m}}=\frac{1}{{\mathrm{a}}^{\mathrm{m}}}\right]$

$=\frac{1}{{\left(5^3\right)}^{\frac{1}{3}}} \mathrm{b}=\frac{1}{5^{3\times \frac{1}{3}}}\left[{\left({\mathrm{a}}^{\mathrm{m}}\right)}^{\mathrm{n}}={\mathrm{a}}^{\mathrm{mn}}\right]$

$=\frac{1}{5}$

P3. Simplify:

(i) $2^{\frac{2}{3}}·2^{\frac{1}{5}}$

(ii) ${\left(\frac{1}{3^3}\right)}^7$= 3³ = 27

(iii) $\frac{{11}^{\frac{1}{2}}}{{11}^{\frac{1}{4}}}$

(iv) $7^{\frac{1}{2}}·8^{\frac{1}{2}}$

Sol. (i) $2^{\frac{2}{3}}·2^{\frac{1}{5}}=2^{\frac{2}{3}+\frac{1}{5}}\left[{\mathrm{a}}^{\mathrm{m}}·{\mathrm{a}}^{\mathrm{n}}={\mathrm{a}}^{\mathrm{m}+\mathrm{n}}\right]$

$=2^{\frac{10+3}{15}}=2^{\frac{13}{15}}$

(ii) ${\left(\frac{1}{3^3}\right)}^7=\frac{1}{3^{3\times 7}}\left[{\left({\mathrm{a}}^{\mathrm{m}}\right)}^{\mathrm{n}}={\mathrm{a}}^{\mathrm{mn}}\right]=\frac{1}{3^{21}}$

$=3^{–21} \left[\frac{1}{{\mathrm{a}}^{\mathrm{m}}}={\mathrm{a}}^{–\mathrm{m}}\right]$

(iii) $\frac{{11}^{\frac{1}{2}}}{{11}^{\frac{1}{4}}}={11}^{\frac{1}{2}–\frac{1}{4}} \left[\frac{{\mathrm{a}}^{\mathrm{m}}}{{\mathrm{a}}^{\mathrm{n}}}={\mathrm{a}}^{m–\mathrm{n}}\right]$

$={11}^{\frac{2–1}{4}}={11}^{\frac{1}{4}}$

(iv) $7^{\frac{1}{2}}·8^{\frac{1}{2}}=(7\times 8{)}^{\frac{1}{2}}\left[a^m·b^n=(ab{)}^m\right]$

$=(56{)}^{\frac{1}{2}}$