EXERCISE-2.1
P1. Solve:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
Sol. (i)
(ii)
(iii)
(iv)
(v) =
(vi)
(vii)
P2. Arrange the following in descending order:
(i) (ii)
Sol. (i)
Changing them to like fractions, we obtain
Since 42 > 24 > 14,
(ii)
Changing them to like fractions, we obtain
As 49 > 30 > 14,
P3. In a “magic square”, the sum of the numbers in each row, in each column and along the diagonal is the same. Is this a magic square?
Sol. Along the first row, sum =
Along the second row, sum =
Along the third row, sum =
Along the first column, sum =
Along the second column, sum =
Along the third column, sum =
Along the first diagonal, sum =
Along the second diagonal, sum =
Since the sum of the numbers in each row, in each column, and along the diagonals is the same, it is a magic square.
P4. A rectangular sheet of paper is cm long and cm wide. Find its perimeter.
Sol. Length =
Breadth =
Perimeter = 2 × (Length + Breadth)
P5. Find the perimeters of (i) ΔABE (ii) the rectangle BCDE in this figure. Whose perimeter is greater?
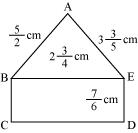
Sol. (i) Perimeter of ΔABE = AB + BE + EA
=
=
=
(ii) Perimeter of rectangle = 2 (Length + Breadth)
Perimeter of rectangle =
=
Perimeter of ΔABE =
Changing them to like fractions, we obtain
As 531 > 430,
Perimeter (ΔABE) > Perimeter (BCDE)
P6. Salil wants to put a picture in a frame. The picture is cm wide.
To fit in the frame the picture cannot be more thancm wide. How much should the picture be trimmed?
Sol. Width of picture =
Required width =
The picture should be trimmed by =
P7. Ritu ate part of an apple and the remaining apple was eaten by her brother Somu. How much part of the apple did Somu eat? Who had the larger share? By how much?
Sol. Part of apple eaten by Ritu =
Part of apple eaten by Somu = 1 − Part of apple eaten by Ritu =
Therefore, Somu ate part of the apple.
Since 3 > 2, Ritu had the larger share.
Difference between the 2 shares =
Therefore, Ritu’s share is larger than the share of Somu by .
P8. Michael finished colouring a picture in hour. Vaibhav finished colouring the same picture in hour. Who worked longer? By what fraction was it longer?
Sol. Time taken by Michael =
Time taken by Vaibhav =
Converting these fractions into like fractions,
we obtain
And,
Since 9 > 7,
Vaibhav worked longer.
Difference = hour
EXERCISE-2.2
P1. Which of the drawings (a) to (d) show:
(i) (ii) (iii) (iv)
(a) 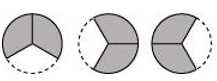
(b)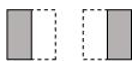
(c)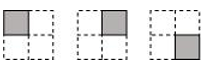
(d) 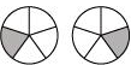
Sol. (i) represents addition of 2 figures, each representing 1 shaded part out of 5 equal parts.
Hence, is represented by (d).
(ii) represents addition of 2 figures, each representing 1 shaded part out of 2 equal parts.
Hence, is represented by (b).
(iii) represents addition of 3 figures, each representing 2 shaded parts out of 3 equal parts.
Hence, is represented by (a).
(iv) represents addition of 3 figures, each representing 1 shaded part out of 4 equal parts.
Hence, is represented by (c).
P2. Some pictures (a) to (c) are given below. Tell which of them show:
(i)
(ii)
(iii)
(a) 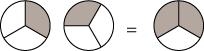
(b) 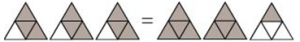
(c) 
Sol. (i) represents the addition of 3 figures, each representing 1 shaded part out of 5 equal parts and represents 3 shaded parts out of 5 equal parts.
Hence, is represented by (c).
(ii) represents the addition of 2 figures, each representing 1 shaded part out of 3 equal parts and represents 2 shaded parts out of 3 equal parts .
Hence, is represented by (a).
(iii) represents the addition of 3 figures, each representing 3 shaded parts out of 4 equal parts and represents 2 fully shaded figures and one figure having 1 part as shaded out of 4 equal parts.
Hence, is represented by (b)
P3. Multiply and reduce to lowest form and convert into a mixed fraction:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
(viii)
(ix)
(x)
Sol. (i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
(viii)
(ix)
(x)
P4. Shade:
(i) of the circles in box (a)
(ii) of the triangles in box (b)
(iii) of the squares in box (c)
(a) 
(b) 
(c) 
Sol. (i) It can be observed that there are 12 circles in the given box. We have to shade of the circles in it.
As , therefore, we will shade any 6 circles of it.

(ii) It can be observed that there are 9 triangles in the given box. We have to shade of the triangles in it.
As , therefore, we will shade any 6 triangles of it.

(iii) It can be observed that there are 15 squares in the given box. We have to shade of the squares in it.
As , therefore, we will shade any 9 squares of it.

P5. Find:
(a) of (i) 24 (ii) 46
(b) of (i) 18 (ii) 27
(c) of (i) 16 (ii) 36
(d) of (i) 20 (ii) 35
Sol. (a) (i)
(ii)
(b) (i)
(ii)
(c) (i)
(ii)
(d) (i)
(ii)
P6. Multiply and express as a mixed fraction:
(a)
(b)
(c)
(d)
(e)
(f)
Sol. (a)
(b)
(c)
(d)
(e)
(f)
P7. Find
(a) of (i) (ii)
(b) of (i) (ii)
Sol. (a) (i)
(ii)
(b) (i)
(ii)
P8. Vidya and Pratap went for a picnic. Their mother gave them a water bottle that contained 5 litres of water. Vidya consumed of the water. Pratap consumed the remaining water.
(i) How much water did Vidya drink?
(ii) What fraction of the total quantity of water did Pratap drink?
Sol. (i) Water consumed by Vidya = of 5 litres = litres
(ii) Water consumed by Pratap = of the total water
EXERCISE-2.3
P1. Find:
(i) of (a) (b) (c)
(ii) of (a) (b) (c)
Sol. (i) (a)
(b)
(c)
(ii) (a)
(b)
(c)
P2. Multiply and reduce to lowest form (if possible):
(i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
Sol. (i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
P3. Multiply the following fractions:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
Sol. (i)
This is an improper fraction and it can be written as a mixed fraction as .
(ii)
This is an improper fraction and it can be written as a mixed fraction as .
(iii)
This is a whole number.
(iv)
This is an improper fraction and it can be written as a mixed fraction as .
(v)
This is an improper fraction and it can be written as a mixed fraction as .
(vi)
This is an improper fraction and it can be written as a mixed fraction as .
(vii)
This is an improper fraction and it can be written as a mixed fraction as .
P4. Which is greater:
(i) of or of
(ii) of or of
Sol. (i)
Converting these fractions into like fractions,
Since
Therefore, of is greater.
(ii)
Since 3 > 2
Therefore, of is greater.
P5. Saili plants 4 saplings, in a row, in her garden. The distance between two adjacent saplings is m. Find the distance between the first and the last sapling.
Sol. 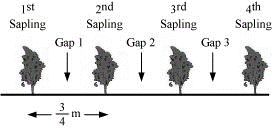 From the figure, it can be observed that gaps between 1st and last sapling = 3
From the figure, it can be observed that gaps between 1st and last sapling = 3
Length of 1 gap
Distance between I and IV sapling =
P6. Lipika reads a book for hours everyday. She reads the entire book in 6 days. How many hours in all were required by her to read the book?
Sol. Number of hours Lipika reads the book per day = hours
Number of days = 6
Total number of hours required by her to read the book =
P7. A car runs 16 km using 1 litre of petrol. How much distance will it cover using litres of petrol.
Sol. Number of kms a car can run per litre petrol = 16 km
Quantity of petrol =
Number of kms a car can run for litre petrol = = 44 km
It will cover 44 km distance by using litres of petrol.
P8. (a) (i) Provide the number in the box , such that .
(ii) The simplest form of the number obtained in is _______.
(b) (i) Provide the number in the box , such that ?
(ii) The simplest form of the number obtained in is _______.
Sol. (a) (i) As ,
Therefore, the number in the box , such that .
(ii) The simplest form of is .
(b) (i) As ,
Therefore, the number in the box , such that is .
(ii) As cannot be further simplified, therefore, its simplest form is
EXERCISE-2.4
P1. Find:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
Sol. (i)
(ii)
(iii)
(iv)
(v)
(vi)
P2. Find the reciprocal of each of the following fractions. Classify the reciprocals as proper fractions, improper fractions and whole numbers.
(i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
Sol. A proper fraction is the fraction which has its denominator greater than its numerator while improper fraction is the fraction which has its numerator greater than its denominator. Whole numbers are a collection of all positive integers including 0.
(i)
Reciprocal =
Therefore, it is an improper fraction.
(ii)
Reciprocal =
Therefore, it is an improper fraction.
(iii)
Reciprocal =
Therefore, it is a proper fraction.
(iv)
Reciprocal =
Therefore, it is a proper fraction.
(v)
Reciprocal =
Therefore, it is a proper fraction.
(vi)
Reciprocal =
Therefore, it is a whole number.
(vii)
Reciprocal =
Therefore, it is a whole number.
P3. Find:
Sol.
P4. Find:
Sol.
EXERCISE-2.5
P1. Which is greater?
(i) 0.5 or 0.05
(ii) 0.7 or 0.5
(iii) 7 or 0.7
(iv) 1.37 or 1.49
(v) 2.03 or 2.30
(vi) 0.8 or 0.88
Sol. (i) 0.5 or 0.05
Converting these decimal numbers into equivalent fractions,
And
It can be observed that both fractions have the same denominator.
As 50 > 5,
Therefore, 0.5 > 0.05
(ii) 0.7 or 0.5
Converting these decimal numbers into equivalent fractions,
It can be observed that both fractions have the same denominator.
As 7 > 5,
Therefore, 0.7 >0.5
(iii) 7 or 0.7
Converting these decimal numbers into equivalent fractions,
It can be observed that both fractions have the same denominator.
As 70 > 7,
Therefore, 7 > 0.7
(iv) 1.37 or 1.49
Converting these decimal numbers into equivalent fractions,
It can be observed that both fractions have the same denominator.
As 137 < 149,
Therefore, 1.37 < 1.49
(v) 2.03 or 2.30
Converting these decimal numbers into equivalent fractions,
It can be observed that both fractions have the same denominator.
As 203 < 230,
Therefore, 2.03 < 2.30
(vi) 0.8 or 0.88
Converting these decimal numbers into equivalent fractions,
and
It can be observed that both fractions have the same denominator.
As 80 < 88,
Therefore, 0.8 < 0.88
P2. Express as rupees using decimals:
(i) 7 paise
(ii) 7 rupees 7 paise
(iii) 77 rupees 77 paise
(iv) 50 paise
(v) 235 paise
Sol. There are 100 paise in 1 rupee. Therefore, if we want to convert paise into rupees, then we have to divide paise by 100.
(i) 7 paise =
(ii) 7 Rs 7 paise = = Rs 7.07
(iii) 77 Rs 77 paise = Rs 77.77
(iv) 50 paise Rs
(v) 235 paise
P3. (i) Express 5 cm in metre and kilometre
(ii) Express 35 mm in cm, m and km
Sol. (i) 5 cm
(ii) 35 mm
P4. Express in kg:
(i) 200 g
(ii) 3470 g
(iii) 4 kg 8 g
Sol. (i) 200 g = 0.2kg
(ii) 3470 g
(iii) 4 kg 8 g + 4kg kg = 4.008 kg
P5. Write the following decimal numbers in the expanded form:
(i) 20.03
(ii) 2.03
(iii) 200.03
(iv) 2.034
Sol. (i) 20.03 =
(ii) 2.03 =
(iii) 200.03 =
(iv) 2.034 =
P6. Write the place value of 2 in the following decimal numbers:
(i) 2.56
(ii) 21.37
(iii) 10.25
(iv) 9.42
(v) 63.352
Sol. (i) 2.56
Ones
(ii) 21.37
Tens
(iii) 10.25
Tenths
(iv) 9.42
Hundredths
(v) 63.352
Thousandths
P7. Dinesh went from place A to place B and from there to place C. A is 7.5 km from B and B is 12.7 km from C. Ayub went from place A to place D and from there to place C. D is 9.3 km from A and C is 11.8 km from D. Who travelled more and by how much?
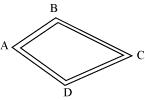
Sol. Distance travelled by Dinesh = AB + BC = (7.5 + 12.7) km
Therefore, Dinesh travelled 20.2 km.
Distance travelled by Ayub = AD + DC = (9.3 + 11.8) km
Therefore, Ayub travelled 21.1 km.
Hence, Ayub travelled more distance.
Difference = (21.1 − 20.2) km
Therefore, Ayub travelled 0.9 km more than Dinesh.
P8. Shyama bought 5 kg 300 g apples and 3 kg 250 g mangoes. Sarala bought 4 kg 800 g oranges and 4 kg 150 g bananas. Who bought more fruits?
Sol. Total fruits bought by Shyama = 5 kg 300 g + 3 kg 250 g
= 8 kg 550 g
= 8.550 kg
Total fruits bought by Sarala
= 4 kg 800 g + 4 kg 150 g
= 8 kg 950 g
= 8.950 kg
Sarala bought more fruits.
P9. How much less is 28 km than 42.6 km?
Therefore, 28 km is 14.6 km less than 42.6 km.
EXERCISE-2.6
P1. Find:
(i) 0.2 × 6
(ii) 8 × 4.6
(iii) 2.71 × 5
(iv) 20.1 × 4
(v) 0.05 × 7
(vi) 211.02 × 4
(vii) 2 × 0.86
Sol. (i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
P2. Find the area of rectangle whose length is 5.7 cm and breadth is 3 cm.
Sol. Length = 5.7 cm
Breadth = 3 cm
Area = Length × Breadth = 5.7 × 3 = 17.1 cm2
P3. Find:
(i) 1.3 × 10
(ii) 36.8 × 10
(iii) 153.7 ×10
(iv) 168.07 × 10
(v) 31.1 × 100
(vi) 156.1 × 100
(vii) 3.62 × 100
(viii) 43.07 × 100
(ix) 0.5 × 10
(x) 0.08 × 10
(xi) 0.9 × 100
(xii) 0.03 × 1000
Sol. We know that when a decimal number is multiplied by 10, 100, 1000, the decimal point in the product is shifted to the right by as many places as there are zeroes. Therefore, these products can be calculated as
(i) 1.3 × 10 = 13
(ii) 36.8 × 10 = 368
(iii) 153.7 × 10 = 1537
(vi) 168.07 × 10 = 1680.7
(v) 31.1 × 100 = 3110
(vi) 156.1 × 100 = 15610
(vii) 3.62 × 100 = 362
(viii) 43.07 × 100 = 4307
(ix) 0.5 × 10 = 5
(x) 0.08 × 10 = 0.8
(xi) 0.9 × 100 = 90
(xiii) 0.03 × 1000 = 30
P4. A two-wheeler covers a distance of 55.3 km in one litre of petrol. How much distance will it cover in 10 litres of petrol?
Sol. Distance covered in 1 litre of petrol = 55.3 km
Distance covered in 10litre of petrol = 10 × 55.3 = 553 km
Therefore, it will cover 553 km distance in 10 litre petrol.
P5. Find:
(i) 2.5 × 0.3
(ii) 0.1 × 51.7
(iii) 0.2 × 316.8
(iv) 1.3 × 3.1
(v) 0.5 × 0.05
(vi) 11.2 × 0.15
(vii) 1.07 × 0.02
(viii) 10.05 × 1.05
(ix) 101.01 × 0.01
(x) 100.01 × 1.1
Sol. (i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
(viii) = 10.5525
(ix) = 1.0101
(x) = 110.011
EXERCISE-2.7
P1. Find:
(i) 0.4 ÷ 2
(ii) 0.35 ÷ 5
(iii) 2.48 ÷ 4
(iv) 65.4 ÷ 6
(v) 651.2 ÷ 4
(vi) 14.49 ÷ 7
(vii) 3.96 ÷ 4
(viii) 0.80 ÷ 5
Sol.(i)
(ii) = 0.07
(iii) = 0.62
(iv) = 10.9
(v) = 162.8
(vi) = 2.07
(vii) = 0.99
(viii) = 0.16
P2. Find:
(i) 4.8 ÷ 10
(ii) 52.5 ÷ 10
(iii) 0.7 ÷ 10
(iv) 33.1 ÷ 10
(v) 272.23 ÷ 10
(vi) 0.56 ÷ 10
(vii) 3.97 ÷ 10
Sol. We know that when a decimal number is divided by a multiple of 10 only (i.e.,10, 100, 1000, etc.), the decimal point will be shifted to the left by as many places as there are zeroes. Since here we are dividing by 10, the decimal will shift to the left by 1 place.
(i) 4.8 ÷ 10 = 0 .48
(ii) 52.5 ÷ 10 = 5.25
(iii) 0.7 ÷ 10 = 0.07
(iv) 33.1 ÷ 10 = 3.31
(v) 272.23 ÷ 10 = 27.223
(vi) 0.56 ÷ 10 = 0.056
(vii) 3.97 ÷ 10 = 0.397
P3. Find:
(i) 2.7 ÷ 100
(ii) 0.3 ÷ 100
(iii) 0.78 ÷ 100
(iv) 432.6 ÷ 100
(v) 23.6 ÷ 100
(vi) 98.53 ÷ 100
Sol. We know that when a decimal number is divided by a multiple of 10 only (i.e., 10, 100, 1000, etc.), the decimal point will be shifted to the left by as many places as there are zeroes. Since here we are dividing by 100, the decimal will shift to the left by 2 places.
(i) 2.7 ÷ 100 = 0.027
(ii) 0.3 ÷ 100 = 0.003
(iii) 0.78 ÷ 100 = 0.0078
(iv) 432.6 ÷ 100 = 4.326
(v) 23.6 ÷ 100 = 0.236
(vi) 98.53 ÷ 100 = 0.9853
P4. Find:
(i) 7.9 ÷ 1000
(ii) 26.3 ÷ 1000
(iii) 38.53 ÷ 1000
(iv) 128.9 ÷ 1000
(v) 0.5 ÷ 1000
Sol. We know that when a decimal number is divided by a multiple of 10 only (i.e., 10, 100, 1000, etc.), the decimal point will be shifted to the left by as many places as there are zeroes. Since here we are dividing by 1000, the decimal will shift to the left by 3 places.
(i) 7.9 ÷ 1000 = 0.0079
(ii) 26.3 ÷ 1000 = 0.0263
(iii) 38.53 ÷ 1000 = 0.03853
(iv) 128.9 ÷ 1000 = 0.1289
(v) 0.5 ÷ 1000 = 0.0005
P5. Find:
(i) 7 ÷ 3.5
(ii) 36 ÷ 0.2
(iii) 3.25 ÷ 0.5
(iv) 30.94 ÷ 0.7
(v) 0.5 ÷ 0.25
(vi) 7.75 ÷ 0.25
(vii) 76.5 ÷ 0.15
(viii) 37.8 ÷ 1.4
(ix) 2.73 ÷ 1.3
Sol.(i)
(ii)
(iii) =
(iv) =
(v)
(vi) = 31
(vii) = 510
(viii)
(ix) =
P6. A vehicle covers a distance of 43.2 km in 2.4 litres of petrol. How much distance will it cover in one litre of petrol?
Sol. Distance covered in 2.4 litres of petrol = 43.2 km
Distance covered in 1 litre of petrol =
Therefore, the vehicle will cover 18 km in 1 litre petrol.








