2.1. INTRODUCTION
Most of the equations that we have worked with had integer coefficients and integer solutions. In this chapter, we shall deal with equations involving rational numbers as the coefficients and their solutions can also be rational numbers.
2.2. EQUATION
Equation A statement of equality which contains one or more unknown quantity or variable (literals) is called an equation.
Example
3x + 7 = 12, and are equations in one variable x.
2x + 3y = 15, are equations in two variables x and y.
2.3. LINEAR EQUATION
An equation involving only linear polynomials is called a linear equation.
Example
3x – 2 = 7, are linear equation in one variable, because the highest power of the variable in each equation is one whereas the equations.
3x2 – 2x + 1 = 0, y2 – 1 = 8 are not linear equations, because the highest power of the variable equation is not one.
2.4 SOLUTION OF A LINEAR EQUATION SOLUTION
A value of the variable which when substituted for the variable in an equation makes L.H.S. = R.H.S. is said to satisfy the equation and is called a solution or a root of the equation.
In other words, a value of the variable which makes the equation a true statement is called a solution or a root of the equation.
Example : Verify that x = 4 is a root of the equation 2x – 3 = 5.
Solution : Substituting x = 4 in the given equation,
We get L.H.S. = 2x – 3 = 2 × 4 – 3 = 8 – 3 = 5 = R.H.S.
Hence, x = 4 is a root of the equation 2x – 3 = 5.
2.5 SOLVING AN EQUATION
Solving an equation means determining its roots i.e., determining value of the variable which satisfies it.
Rules for Solving Linear Equations in One Variable
We learnt the rules for solving an equation in one variable. Let us recall them. They are :
Rule 1 : Same quantity (number) can be added to both sides of an equation without changing the equality.
Rule 2 : Same quantity can be subtracted from both sides of an equation without changing the equality.
Rule 3 : Both sides of an equation may be multiplied by the same non-zero number without changing the equality.
Rule 4 : Both sides of an equation may be divided by the same non-zero number without changing the equality. It should be noted that some complicated equations can be solved by using two or more of these rules together.
Solving Equations having variable terms on the side and number(s) on the other side
The following examples will illustrate the method of solving equations in one variable having variable terms on one side and numbers on the other side.
Example : Solve the equation and check the result.
Solution : We have
[Subtracting 11 from both sides]
[Multiplying both sides by 5]
Thus,
is the solution of the given equation.
2.6 TRANSPOSITION METHOD FOR SOLVING LINEAR EQUATIONS IN ONE VARIABLE
Sometimes the two sides of an equation contain both variable (unknown quantity) and constants (numerals).
In such cases, we first simplify two sides in their simplest forms and then transpose (shift) terms containing variable on R.H.S. to L.H.S. and constant terms on L.H.S. to R.H.S. By transposing a term from one side to the other side, we mean changing its sign and carrying it to the other side. In transposition the plus sign of the term changes into minus sign on the other side and vice-versa.
The transposition method involves the following steps :
Step I : Obtain the linear equation.
Step II : Identify the variable (unknown quantity) and constants (numerals).
Step III : Simplify the L.H.S. and R.H.S. to their simplest forms by removing brockets.
Step IV : Transpose all terms containing variable on L.H.S. and constant terms on R.H.S. Note that the sign of the terms will change in shifting them from L.H.S. to R.H.S. and vice-versa.
Step V : Simplify L.H.S. and R.H.S. in the simplest form so that each side contains just one term.
Step VI : Solve the equation obtained in step V by dividing both sides by the coefficient of the variable on L.H.S. Following examples will illustrate the above procedure.
Example : solve
Solution : We have,
The denominators on two sides are 2,5,3, and 4. Their LCM is 60.
Multiplying both sides of the given equation by 60, we get
2.7 CROSS-MULTIPLICATION METHOD FOR SOLVING EQUATIONS OF THE FORM
Consider the equation
Clearly, it is an equation of the form
, where a = 2, b = 5, c = 3, d = 7, m = 3 and n = 5.
Evidently, it is an equation in one variable x but it is not a linear equation, because the LHS is not a linear polynomial. However, it can be converted into a linear equation by applying the rules for solving an equation as discussed below.
We have,
As x represents a number, so 3x + 7 also represents a number. Multiplying both sides of (i) by (3x + 7) × 5 i.e., the product of numbers in the denominators on L.H.S. and RHS, we get
This is the required solution of equation .
Note that in solving this equation, we have first converted it into a linear equation given in (ii) by applying the rules of solving equations. Equation (ii) can also be obtained directly from equation (i) by equating the product of numerator of LHS and denominator of RHS to the product of denominator of LHS and numerator of RHS. This can be exhibited as follow :
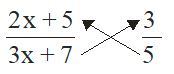
This process of multiplying the numerator on LHS with the denominator on RHS and equating it to the product of the denominator on LHS with the numerator on RHS is called cross-multiplication.
It is evident from the above discussion that by using cross-multiplication we can convert an equation of the form
To a linear equation n(ax + b) = m (cx + d)
This equation can now be solved by using the rules for solving equations.
2.8 APPLICATIONS OF LINEAR EQUATIONS TO PRACTICAL PROBLEMS
In this section, we sill study formulation and solution of some practical problems. These problems involve relations among unknown quantities (variables) and known quantities (numbers) and are often stated in words. That is why we often refer to these problems as word problems. A word problem is first translated in the form of an equation containing unknown quantities (variables) and known quantities (numbers or constants) and then we solve it by using any one of the methods discussed in the earlier section. The procedure to translate a word problem in the form of an equation is known as the formulation of the problem. Thus, the process of solving a word problem consists of two parts, namely, formulation and solution.
The following steps should be followed to solve a word problem:
Step I : Read the problem carefully and note what is given and what is required.
Step II : Denote the unknown quantity by some letters, say x, y, z etc.
Step III : Translate the statements of the problem into mathematical statements.
Step IV : Using the condition(s) given in the problem, form the equation.
Step V : Solve the equation for the unknown.
Step VI : Check whether the solution satisfies the equation.








