1. COMPOSITION OF THE NUCLEUS
The nucleus of an atom consists of two types of particles, protons and neutrons. A proton has a positive charge equal to 1.6 x 10-19 C and a mass equal to 1.6726 x 10-27 kg. A neutron has no charge and its mass is 1.6749 x 10-27 kg. Thus a neutron is slightly heavier than a proton. A proton or a neutron is called a nucleon. The total number of protons in the nucleus is called its atomic number (Z). The total number of nucleons in the nucleus is called its mass number (A). If N is the number of neutrons, then,
A = Z + N
If X is the chemical symbol of an element then its nucleus is represented as
Nuclear Radius: Assuming that the nuclei are spherical, their radii are fairly well represented by the empirical formula Where Ro is quantity which varies slightly from one nucleus to another nucleus (Ro=1.1 to 1.4 fermi), Generally, Ro = 1.1 fermi (fm) = 1.1⨯10–15 m.
Nuclear Charge: It is total positive charge carried by nucleus and is numerically equal to its atomic number times the electronic charge i..e.
Nuclear charge = Ze
Nuclear Density: The ratio of the mass of the nucleus to its volume is called nuclear density. Consider the nucleus of an atom having mass number A. It we neglect the mass of the orbital electron then mass of the nucleus of the atom = A amu = A ⨯ 1.660565 ⨯ 10–27 kg.
(1 amu = 1.660565 ⨯ 10-27 kg)
If R is the radius of the nucleus then volume of the nucleus
∴ Density of the nucleus ρ =
=
Nuclear density is independent of mass number A.
The nuclear force:
The force which binds the protons and neutrons inside the nucleus is neither electrical nor gravitational. It is an entirely different type of force called the strong nuclear force. This force is extremely complex in nature and is not fully understood. Some of its main characteristics are :
1. Short Ranged: the nuclear force has an extremely short range, of order 2-3 fm. Due to this reason, each nucleon can interact only with its immediate neighbours and not with all the nucleons. This property is called saturation.
2. Strongly Attractive with a Repulsive Core: The nuclear force is attractive but becomes strongly repulsive when the separation between the nucleons is fm. It is also called cohesive force.
3. Charge Independent: The nuclear force between two protons is the same as the force between two neutrons or that between a neutron and a proton.
In face, the nuclear force is an exchange force and arises due to the exchange of pions between the nucleons.
Yukawa’s theory of nuclear forces:
In 1935 Japanese scientist Yukawa attributed the origin to nuclear forces to a new particle called as π-Meson. The rest mass of π-Meson is found to be greater than that of an electron but less than that of a nucleon. The mesons may be neutral or may carry either a positive or negative charge equal to the electronic charge and are represented as and respectively. Yukawa’s put forward a theory involving these π-meson, called as the meson theory of unclear forces. According to this theory, all the nucleons consist of identical cores surrounded by a cloud of one or more π. The only difference between proton and neutron lies in the composition of their respective meson clouds. The mesons are being continuously exchanged between nearby nucleons due to which they continue to be converted into one another.
According to Yukawa, when a proton and a neutron interact, the proton emits a positively charged π-meson which is absorbed by the neutron. As a result, the proton is converted into neutron and the neutron is converted into proton.
Similarly when a neutron emits a negative charged π meson which is absorbed by a proton, then the neutron is converted into proton and proton is converted into neutron.
Thus the exchange of π– and π+ mesons between protons and neutron is responsible for the origin of nuclear forces between them. In the same way, the forces between two protons and those between two neutrons are generated due to the continues exchange of meson between them. Since mesons are continuously moving between the nucleons, so their mass is not added to mass of nucleus. The inter conversion of neutron to proton or vice-versa due to meson occurs 1024 times/sec.
2. MASS DEFECT
The rest mass of a nucleus is always less than the sum of the masses of the neutrons and protons is contains. The difference between the sum of the masses of the constituent nucleons and the mass of the nucleus is called mass defect.
Thus if a nucleus of mass M has Z protons and N neutrons, then its mass defect is
3. DIFFERENT TYPES OF NUCLEI
There are different types of nuclei depending upon the number of protons (atomic number) or number of nucleons (mass number) in them.
a) Isotopes: The atoms of an element having same atomic number but different mass number are called isotopes of that element. The isotopes of an element have the same place in the periodic table and therefore possess the same chemical properties.
The isotopes of the some elements are the following.
a) Hydrogen –
b) Oxygen –
c) Chlorine –
d) Uranium –
b) Isotones: Atoms where nuclei have same number of neutrons are called isotones. For them both the atomic number (Z) and atomic mass (A) are different but the value of difference (A-Z) is same. Examples of isotones are as under
a) b) c) d)
c) Isobars: Atoms of same mass number but different atomic number are called isobars. They have same number of nucleons (neutrons and protons) in their nuclei and hence they have same atomic weight. The number of protons in their nuclei as well as number of electrons revolving around their nuclei are different in each case. The chemical properties of isobars are different. Examples of isobars are as follows.
a) b) c) d)
The daughter nucleus left after the emission of β-particle is an isobar of the parent nucleus.
d) Isomers: Atoms having the same mass number A and the same atomic number Z but different radioactive properties are called isomers. A pair of isomers occurring in nature is uranium X2 and Uranium Z1 which are found in the uranium decay series.
4. MASS ENERGY RELATION
According to Einstein’s theory of relativity, the mass of a body is not constant but increases with the increase in the velocity of the body. In other words, when a body is given kinetic energy its mass is increased. This shows that mass depends upon energy. Therefore, mass and energy are inter convertible, i.e. they can be changed into each other. According to Einstein, a particle of mass m possesses an equivalent energy E given by
E = mC2 where C = velocity of light
The following points are worth nothing in mass-energy equivalence.
a) If an energy ΔE is given to some matter, then according to above relation its mass will increase by Δm, where . Since the value of C is very high. The increase in mass Δm is very small.
b) If a substance losses an amount Δm of its mass an equivalent amount ΔE of energy is produced, where ΔE = ΔmC2.
Illustration 1: Find the equivalent energy of (i) electron and (ii) proton and (iii) neutron at rest. Given that mass of electron = , mass of proton = and mass of neutron = .
Solution:
i) Equivalent energy E =
=
ii) Equivalent energy, E =
5. PACKING FRACTION
The divergence of the nuclear mass from nearest whole number (i.e. its mass number A) per nucleon is called Packing fraction i.e.
Packing fraction where M = actual mass of nucleus, A=mass number.
As M-A is the mass defect, packing fraction may also be expressed as
Packing fraction indicates that whereas individual nucleons have mass of A unit, when packed together, their mass will be different from A. It was to study the change in mass per nucleon from its nearest whole number that packing fraction was coined. The variation of packing fraction (f) with mass number (A) is shown in figure.
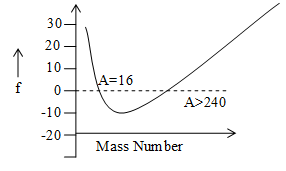
Illustration 2: What is the nuclear density and approximate radiant of .
Solution: Since nuclear density of an element is independent of mass number
∴ Nuclear density of Cu =
we know R =
6. FACTORS UPON WHICH STABILITY OF NUCLEUS DEPENDS
There are many factors upon which the stability of a nucleus depends
i) The larger the value of packing fraction, the greater is the stability of the nucleus.
ii) In general, the greater the value of binding energy per nucleon. The greater is the stability of the nucleus.
iii) Nuclei with so called magic value for their proton number (Z) and/or neutron number are much more stable than the average nucleus.
iv) Nuclei with even number of proton and/or neutrons are very stable.
7. BINDING ENERGY
When the neutrons and protons come together to form a nucleus, a small part of their mass is released in the form of electromagnetic radiation. This energy is called the binding energy of the nucleus.
When a nucleus is to be broken up, the same amount of energy has to be supplied. Therefore, the binding energy of a nucleus may also be defined as the minimum energy required to separate all the nucleons away from one another.
Let M = measured mass of the nucleus in kg.
A = mass number
Z = atomic number
MH = Mass of hydrogen atom or proton in kg.
Mn = Mass of the free neutron in kg.
∴ Number of protons = Z, and number of neutrons = A – Z.
Total mass of protons and neutrons in the nucleus =
Mass defect during the formation of nucleus
Total binding energy of the nucleus is
B.E. =
B.E. =
= 931.5 Δm MeV The ratio of binding energy of nucleus and total number of nucleons in the nucleus is called binding energy per nucleon. It is also called as binding fraction or average binding energy.
i.e. Binding energy/nucleon =
Binding Energy per Nucleon
The binding energy per nucleon (B.E./A) indicates how strongly the nucleons are held inside the nucleus. The variation of B.E/A with the mass number A for naturally occurring nuclei.
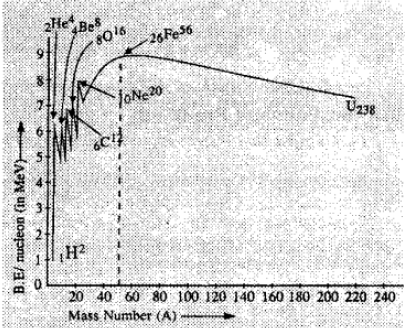
The following important observations are made
1. With the exception of some light nuclei, namely, , the values of B.E./A lie on or close to a smooth curve. These nuclei have exceptionally high binding as compared to their neighbors.
2. The binding energy per nucleon is about 8 MeV for nearly all nuclei except very light ones. The curve rises sharply in the beginning, has a broad maximum close to the value 8.5 MeV for nuclei in the mass number range from about 40 to 120, and then gradually decreases to about 7.6 MeV for heavy nuclei. Thus the elements in the intermediate range are the most stable.
The decreases in binding for heavy nuclei is due to the electrostatic repulsion between the protons, which becomes more and more significant as the number of protons increases because it is a long range force, whereas the attractive nuclear force is short ranged.
Illustration 3: Find (i) Mass defect (ii) Binding energy and binding energy per nucleon for helium nucleus. Given that mass of helium nucleus = 4.001509 amu, mass of proton = 1.007277 amu and mass of neutron = 1.008666 amu.
Solution: A helium nucleus has 2 protons and 2 neutrons
Actual mass of helium M = 4.001509 amu.
Mass number A = mass of proton + mass of neutrons
2⨯1.007277 + 2⨯1.008666 = 4.031886 amu
i) Mass defect ΔM = M – A = 4.001509 -4.031886 = -0.030377 amu
ii) Binding energy E =
Binding energy/nucleon =
Illustration 4: Obtain the binding energy of nuclei and in units of MeV from the following data. Mass of hydrogen atom = 1.007825 amu, mass of neutron = 1.008665 amu, Mass of atom = 55.934939 amu and mass of atoms = 208.980388 amu. Also calculate binding energy per nucleon in the two cases.
Solution: Given that
Mfe = 55.934939 amu, MBi = 208.980388 amu, Mn=1.008665
= 1.007825 amu
We know,
Binding energy =
For nucleus
Z = 26, A = 56
B.E. =
=
= 492.26 MeV
Binding energy per nucleus =
For nucleus
Z = 83, A = 209
∴
= 1640.26 MeV
Binding energy per nucleon =
Exercise 1:
(i) Show that the density of a nucleus does not depend upon its mass number.
(ii) Calculate the density of a nucleus taking the mass of a nucleon as m = 1.67 ⨯ 10–27 kg and R0 = 1.4 ⨯ 10–15m.
(iii) Calculate the mass defect, binding energy and binding energy per nucleon of an alpha particle.
8. ARTIFICIAL TRANSMUTATION OF ELEMENTS
Rutherford allowed α-particles to pass through different gases and studied the different processes that may happen. The radioactive substance emits α-particles whose range in air was found to be 8 cm. When the glass tube is filled with nitrogen gas, scintillations are observed, even when radioactive is at a distance of 40 cm from the foil. These particles producing scintillations can not be α-particles as they can not have such a long range. Further analysis prove that each of these particles had a mass nearly equal to that of hydrogen atom and carried a positive charge equal to that of an electron. The new particles were named as protons.
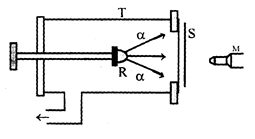
Rutherford concluded that nitrogen nucleus hit by an α particle disintegrates into oxygen nucleus and a proton . The nuclear reaction can be represented as
This process of producing a new stable nucleus from other stable nucleus is called artificial transmutation of elements. This is possible if atomic number of the element is less than 20. It was also observed that when lighter atoms are bombarded with α-particles, atom get radioactive nature. For example
Radio isotopes are not available in nature. They are to be produced by artificial means in nuclear reactors.
9. DISCOVERY OF NEUTRON
Neutron was discovered by Chadwick in 1932. He allowed α particles to bombard the Beryllium metal. The particles coming out from beryllium were allowed to incident on a paraffin block. It emits high energy protons. From energy calculations, Chadwick showed that the penetrating rays emerging from Beryllium metal were uncharged particles with mass approximately equal to protons. He named these uncharged particles as neutrons. The disintegration taking placed in the Beryllium metal is as follows:
(neutron)
Properties of neutron:
1) Neutron is a constituent of the nucleus.
2) Neutron is a neutral particle i.e. it has no charge on it.
3) The mass of neutron is about 1.6748⨯10–27 kg.
4) Neutron has very high penetrating power. Being neutral, it is neither attracted nor repelled by the nucleus of an atom, so it can penetrated deep into the atom.
5) Neutron has low ionizing power
6) Neutron inside the nucleus is stable.
7) A free neutron is unstable and decays according to the equation.
The half life period of a free neutron is about 12 minutes.
8) Thermal neutrons are most suitable for causing nuclear reactions
9) It has a spin equal to , where h is Planck’s constant.
10. NUCLEAR INSTABILITY
There are two major forces in a nuclear (i) the electrostatic force of repulsion between the protons (ii) the nuclear force is attractive and holds the nucleons inside the nucleus. The nuclear force is short-range force (i.e. about 10-15 m apart) and electrostatic force of repulsion is long range force. In a small or light nucleus, nuclear force is large as compared to electro-static force of repulsion, so light nuclei are stable. On other hand, in a large nucleus (having large number of nucleons > 20), the nuclear force is small as compared to the electrostatic force of repulsion. Hence, large nuclei are unstable.
A nucleus becomes stable if number of neutrons is equal to number of protons in it. Therefore, heavy nuclei become stable by converting a neutron into a proton by emitting β-particle and antineutrino till the number of neutrons is equal to the number of protons in the nucleus. Thus, large nuclei are unstable (i.e. radioactive)
11. NATURAL RADIOACTIVITY
The phenomenon of spontaneous disintegration of the nuclei of heavy element with the emission of certain types of radiations is known as natural radioactivity. The elements which show this phenomenon are called radioactive elements. E.g. uranium, radium etc. all heavy elements above Z = 82 show the phenomenon of radioactivity. The emission of radiation changes the radioactive element into an element of lower mass number. Radioactivity was discovered accidentally by Antonie Henri Becquerel in 1896. He noted that uranium element gave out some invisible rays that can penetrate through several thick black papers and affect a photographic plate placed on the other side. The same phenomenon was confirmed several months later by Pierie curie and Marie Curie. They named these penetrating rays as Becqueral rays.
The disintegration of unstable nuclei is involves the emission of α-particle or α-rays, or β-particles or β-rays and γ-rays or photons.
α-particle:
An α-particle is a helium nucleus () having two protons and two neutrons. They decay of radioactive nucleus by emitting α-particle is represented as follows.
is known as daughter nucleus which may or may not be radioactive in nature.
β-Particle:
β particle is a fast moving electron . The decay of radioactive nucleus by emitting β-particle is represented as follows.
It may be noted that β-particle and (antineutrino) do not exist inside the nucleus but they are created at the time of emission.
γ-rays:
γ rays are the packets of electromagnetic radiation and are known as photons. They do not have any charge and their rest mass is zero.
The decay of a radioactive nucleus by emitting γ-ray is represented by as follows
,
where represents the excited state and represents the ground state of the nucleus.
Note:
1. Neutrions and antinutrions emitted in β-decay
(i)
This type of decay is known as β-decay. It may be remembered that in -decay, electron is always accompanied by an antineutrino.
(ii)
This type of decay is known as β+ decay. It may be remembered that in β-decay, position is always accompanied by a neutrino.
2) Antineutrino is an anti particle of neutrino.
3) The mass of neutrino is zero.
4) The charge on neutrino is zero.
5) Neutrino and antineutrino are emitted to conserve energy and momentum during decay process.
6) In β-decay a proton is converted into a neutron and a neturon is converted into a proton as follows.
Properties of α particles:
1) An α-particle is equivalent to a helium nucleus consisting of two protons and two neutrons.
2) They have positive charge equal to +2e, where .
3) They are emitted with velocities ranging between to
4) They are deflected by electric and magnetic fields.
5) They cause fluorescence in certain materials like barium platinocyanide, zinc sulphide etc.
6) They have low penetrating power. Air of thickness 7.0 cm absorbs them completely. An aluminium foil of thickness 0.01 cm is able to absorb them.
7) They have rest mass equal to four times the mass of a proton i.e. mα = 4mp.
8) They have high ionising power. A single α-particle produces about 20,000 ion pairs per centimeter air, through which it passes.
9) They slightly affect the photographic plates.
10) The emission of α-particles from a radioactive nucleus is represented as follows
11) α-particles are capable of producing heating effecting when fall on a substance and they can cause skin burns.
12) α-particles are scattered by thin metallic foils.
Properties of β particles:
1) A β-particle is a fast moving electron
2) β-particle has a negative charge equal to the charge on an electron.
3) The rest mass of a β-particle is equal to the mass of an electron.
4) They are emitted with a velocity of the order of .
5) They are deflected by electric and magnetic fields.
6) They cause fluorescence in zinc sulphide and other fluorescent materials.
7) The ionising power of β-particles is about times the ionising power of α-particles. That is, their ionising power is less than that of α-particles.
8) The penetration power of β-particles is more than that of α-particles.
9) They affect the photographic plates.
10) The emission of β-particle from a radioactive nucleus is represented as follows
Properties of γ-rays:
1) They are the packets of energy of electromagnetic radiations
2) they have no charge.
3) The rest mass of γ-rays is zero.
4) They always travel with the speed of light in vacuum
5) They are not deflected by electric and magnetic fields.
6) They cause ionization but their ionising power is about times the ionising power of β-particles.
7) They have very high penetration power. Their penetration power is 100 times greater than that of β-particles.
8) They affect the photographic plates more than β-particles.
9) They cause less fluorescence (in substances like willimite).
10) The emission of γ-rays from a radioactive action is represented as follows
12. LAWS OF RADIOACTIVE DECAY
i) Radioactive decay is a spontaneous process and is not affected by the external conditions such as temperature, pressure etc.
ii) In any radioactive decay, either an α-particle or β-particle is emitted by the atom. Both the particles are not emitted simultaneously. Moreover, an atom does not emit more than one α-particle or more than one β-particle at a time. On emission of α-particle or β-particle, the neutron formed may emit γ-ray photon in case the nucleus is left in the excited state.
iii) When a radioactive element decays by emitting an α-particle, its nucleus loses four nucleus, two protons and two neutrons and its position goes down by two places in the periodic table.
iv) When an atom emits a β-particle there is no change in the total number of nucleons but its atomic number increases by 1.
i.e.
the position of daughter element is raised by one place in the periodic table.
v) When a radioactive element decays by emitting a γ-rays. Its position remain the same in the periodic table. The radioactive element in the excited state comes to its ground state by emitting the energy in the form of a photon or γ-ray.
i.e.
vi) The rate of disintegration of a radioactive substance is directly proportional to the number of atoms remained undecayed in the substance. This law is called radioactive decay law or disintegration law.
Suppose at the beginning of disintegration (at t = 0) the number of radioactive atoms present in a given sample is No. As the time passes the number of original radioactive atoms decreases due to disintegration. Suppose after time t, the number of radioactive left is N. Let us now suppose that dN atoms further disintegrate in a short interval of time dt.
Rate of disintegration =
According to decay law,
where λ is a constant called decay constant or disintegration constant.
Now equation (i) can be written as
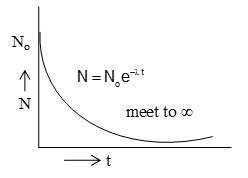
Integrating both sides we get
logN = -λt + C …… (ii)
when t = 0, N = No
∴
put the value of C in equation (ii)
log N = -λt + log No
………. (iii)
Equation (iii) is known as decay equation. It can be used to find the number of radioactive atom N present at any time t. It decays complete after infinite time as shown in figure.
13. RADIOACTIVE DECAY CONSTANT
We know
When
or
or
Thus radioactive decay constant is the reciprocal of the time during which the number of atoms in the radioactive substance reduces to 36.8% of the original number of atoms in it.
Units of decay constant: Decay constant is expressed in S–1 or min–1 or day–1 or year–1.
14. HALF LIFE OF A RADIOACTIVE SUBSTANCE
The time during which half of the atoms of the radioactive substance disintegrates is called half life of a radioactive substance.
Let half time of substance is T
We know
When
15. AVERAGE LIFE OF A RADIOACTIVE SUBSTANCE (MEAN LIFE)
Mean-life of a radioactive substance is defined as the sum of lives of all atoms divided by the total numbered atoms or reciprocal to the decay constant of the substance is called mean life. i.e. mean life, Tm or Tav = or
or
16. ACTIVITY OF A RADIOACTIVE SUBSTANCE
The activity of a radioactive substance is defined as the rate of disintegration of the substance.
i.e. Activity A = Number of atoms disintegrated per seoncd
we know,
∴ A = -λN
More is the half life, less is the activity of the substance and vice-versa.
Units of activity: The units of activity is Curie (Ci), Rutherford (rd) and Becquerel (Bq)
1 Curie (Ci) = disintegration/second
1 Rutherford (rd) = 106 disintegration/second
1 Becquerel (Bq) = 1 disintegration/second
Illustration 5: The mass number of radium is 226. It is observed that α-particles are emitted per second from 1g of radium. Calculate the half life of radium.
Solution: Given that
Mass number of radium = 226.
∴ Number of atoms in one gram radium =
N =
We know, A =
Illustration 6: The half-life of radius is 1500 years. After how many years will 1g of pure radium reduced to (i) 1 centigram (ii) lose 1 mg.
Solution: Given that
T = 1500 years, m0 = 1g.
1st case:
m = 1 centrigram = 1 centigram =
We know, N =
Since N m
∴
2 ⨯ 2.303 = λt
t =
=
= 9965.7 years
ii) Loss = 1 mg = .
Present m =
= 0.999
17. BASIC RULES FOR RADIOACTIVE DECAY
All radioactive decays are based on the following conservation rules
i) The nucleon number A must be conserved
ii) Electric charge must be conserved
iii) Energy must be conserved
iv) Liner momentum must be conserved
v) Angular momentum must be conserved.
Illustration 7: Consider the isotope of thorium which decays to radium isotope with emission of an α-particle. This radioactive decay can be written as
The masses of the various initial and final products are
mass of = 227.027706 amu
mass of = 223.0.18501 amu
mass of = 4.002603 amu
It is clear that in this decay there is a mass defect. This mass defect appears as K.E. of decay products. Let us now apply conservation law of radioactive decay to the above reaction equation.
i) The total nucleons number is 227 before and after the decay i.e. 227 = 223+4. Thus nucleon number conserved in decay.
ii) The total nuclear charge is 90e before and after the decay i.e. 90 e = 88e + 2e. Thus nuclear charge is conserved in decay.
iii) The difference in the mass before and after decay is
Δm = 227.027706 – 223.018501 – 4.002603 = 0.006602 amu.
Equivalent energy = 0.006602 ⨯ 931.5 MeV = 6.15 MeV.
This energy appears as K.E. and is shared by α particle and daughter nucleus. Thus energy is conserved.
iv) We can find the kinetic energy of the daughter product and α-particle by applying law of conservation of linear momentum and energy.
Since the initial momentum mass zero, the final momentum must be zero.
∴ D stands for daughter
…….. (1)
we know
18. ALPHA DECAY
The phenomenon of emission of α-particle from a radioactive nucleus is called α decay.
If difference between the initial and final mass energies is Q (it is called Q value of the reaction)
Then kinetic energy of α-particle is given by
and speed of α particle is given by
19. ARTIFICIAL RADIOACTIVITY
The process by which stable nuclei are made unstable by bombarding them with high energy particles and then these unstable nuclei are made to emit nuclear radiations is called artificial radioactivity.
The artificially made unstable nuclei are called radio-isotopes. Artificial radioactivity was discovered by Irene Curie Joliot and her husband Fredrick Joliot.
In artificial radioactivity, a stable nucleus can be made radioactive by disturbing its natural nucleon arrangement by bombarding it with external particles.
A few cases are discussed below:
i) Bombardment with α-particle
The half life of is 14 minutes.
ii) Bombardment with protons and deutrons
a)
b)
The half life on is 11 minutes
iii) Bombardment with neutrons
iv)
These radioactive isotopes are produced on large scale in atomic reactors.
20. RADIOACTIVE DATING – RADIOCARBON DATING
To find the age of objects that were once alive, we employ a technique called radiocarbon dating in which the radioactive isotope carbon-14 is used. Carbon has a radioactive isotope . It is formed when neutrons react with nitrogen in air. The neutron are produced by cosmic rays which enter the upper atmosphere and interact with air molecules.
The amount of the isotope absorbed in very small and it reaches a maximum concentration as long as they are living. The activity of the radioactive isotope in living material is about 19 decays per minute per gram. The half life of the isotope is T = 5600 years approximately.
∴ Normal activity Ao = 19 decays/min/gram.
When the plant dies, no more of the isotope is absorbed by it and the amount of radioactive isotope begins to decrease with the passage of time. Measuring the activity of the radioactive isotope in ancient wood is similar carbon materials can provide information about its age. This method is known as radiocarbon dating or carbon dating.
21. NUCLEAR REACTION
A reaction in which there is a successful attempt by an external bombarding particle to change the content of a nucleus is known as a nuclear reaction. Let a nucleus ‘X’ be bombarded by an energetic particle ‘a’. The resultant nucleus after the interaction between X and ‘a’ is ‘Y’ and an outgoing particle ‘b’ is emitted. The nuclear reaction may be represented as follows
Here ‘X’ and a are known as reactant and ‘Y’ and b are known as products. This reaction is known as (a, b) reaction and can be represented as X(a, b)Y.
E.g.
The reaction can be written as .
Q value of energy of nuclear reaction: The energy absorbed or released during nuclear reaction is known as Q value of nuclear reaction. Q value is measured by product of difference between mass of reactance and mass of products and square of velocity of light.
Q value = (mass of reactants – mass of products).C2 J
= (mass of reactants – mass of products) ⨯ 931 MeV
Q value of a nuclear reaction is also measured by difference between kinetic energy of reactants and products.
If Q < 0, the nuclear reaction is known as endothermic. The energy is absorbed in the reaction. If Q>0, the nuclear reaction is known as exothermic. The energy is released in the reaction.
Illustration 8: Find Q value of the following nuclear reaction.
Given mass of = 14.003 amu, mass of amu, mass of amu, mass amu.
Solution:
Mass of reactants = mass of + mass of
= 14.003 + 4.002 = 18.005 amu
mass of products = Mass of + mass of
= 16.999 + 1.008 = 18.007 amu
Q value of nucleon = (18.005 – 18.007) = – 0.002 amu
= -0.002 ⨯ 931 = -1.802 MeV
Since Q < 0, therefore reaction is endothermic
Exercise 2:
(i) The half – life of radium is 1600 years. How much time does 1g of radium take to reduce to 0.125 g?
(ii) The half – life of 58Co is 72 days. How much time does it take for 3/4th of the initial mass to disintegrate?
(iii) The half-life of radium is 1600 years. Find its average life.
22. NUCLEAR FISSION
Nuclear fission is a process of splitting a heavy nucleus into two nucleus of comparable masses along with the emission of large amount of energy. Nuclear fission was discovered by Otto Hahn and Strassman in 1939.
In nuclear fission the combined mass of the daughter nuclei is less than the mass of the parent nucleus. The difference is called the mass defect. Energy is released because the binding energy per nucleon of the daughter is about 1 MeV greater than that of the parent nucleus.
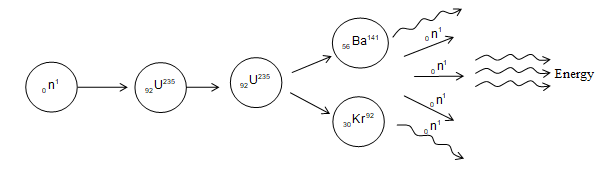
The fission of U235 by thermal neutrons can be represented by the equation
where is an intermediate excited state that lasts only for s before breaking into nuclei X and Y which are called fission fragments. In any fission equation there are many combinations of X and Y that satisfy the requirements of conservation of energy and charge with uranium.
Fission also results in the production of several neutrons, typically two or three on the average about 2.5 neutrons are released per event.
A typical fission reaction for uranium is
About 200 MeV is released in the fission of a heavy nucleus. The fission energy appears mostly as kinetic energy of the fission fragments which fly apart at great speed. Nuclear fission of when bombarded with a thermal neutron is shown in figure.
 23. NUCLEAR REACTOR
23. NUCLEAR REACTOR
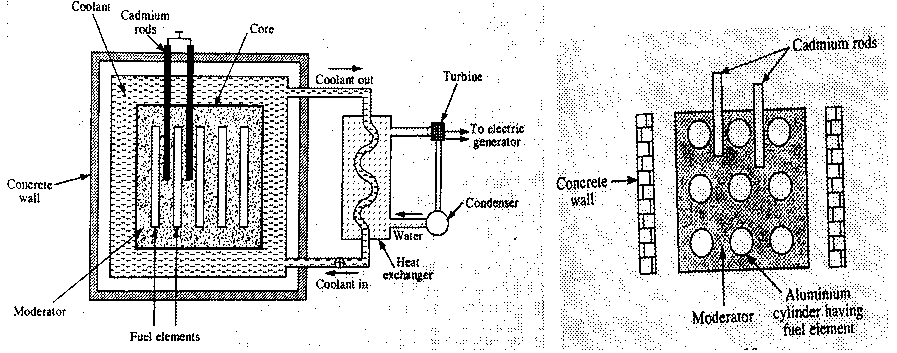
Nuclear reactor is a device in which the nuclear reaction is carried on as perfectly controlled chain reaction in a self sustained manner. It was formerly known as atomic pile. The main components in a nuclear reactor are the following.
i) Fissionable material (Fuel): The fissionable material used in the reactor is called the fuel of the reactor. Uranium isotope, Thorium isotope Th232 and plutonium isotopes are the most commonly used fuels in the reactor.
ii) Moderator: Moderator is used to slow down the fast moving neutrons. Most commonly used moderators are graphite and heavy water.
iii) Control material: Control material is used to control the chain reaction and to maintain a stable rate of reaction. This material controls the number of neutrons available for the fission. The neutrons available for fission are controlled by moving the cadmium rods in or out of the core of the reactor.
iv) Coolant: Coolant is a cooling material which removes the heat generated due to fission in the reactor. Commonly used coolants are water, CO2, nitrogen.
v) Protective shield: A protective shied is the form of a concrete thick wall surrounds the core of the reactor to save the persons working around the reactor from the hazardous radiations.
Working: A few nuclei undergo fission liberating fast neutrons. These fast neutrons are slowed down to an energy about 0.025 eV by the surrounding moderator (graphite) through elastic collisions when the reactor becomes critical, self sustained controlled chain reaction is achieved. The cadmium rods are used to control the chain reaction. The fission produces heat in the nuclear reactor core. The coolant transfers this heat from core to the heat exchanger, where steam is formed. This steam produced at a very high pressure runs a turbine and electricity is obtained at the generator. The dead steam from the turbine condenses into water and is returned to the heat exchange. The process repeats and we get continuous supply of energy in the form of electricity.
Radioactive isotopes:
The isotopes of an element which are also radioactive are called radioactive isotopes or simply radio isotopes. For examples, are the radio isotope of carbon and are the radio isotopes of sodium.
Radio isotopes are produced by bombarding stable elements with high energy α particle, deuteron etc.
Tracer technique: The process of adding a very small quantity of radio isotope to the same element is called labelling and the radio isotope used is called isotropic tracer. The technique of using radioactive tracers to study a certain phenomenon is called tracer technique. Tracer technique has proved to be very useful in the fields of agriculture, medicines, industry etc.
24. USES OF RADIOISOTOPES
Important uses of isotopes are given below.
i) Isotopes are used to test the wear and tear of engine parts like piston rings, gears, ball bearings and in deciding the efficiency of lubricants.
ii) Radioiodine has half life of 8 days and decay through β emission and is used in determining the size, activity and functioning of thyroid gland. So also by means of detecting the emitted radiation from the mixture of radio-isotope and organic dyes the radiologist gets information about the size and location of brain tumour.
iii) Restriction in blood circulation can be detected using radio sodium.
iv) Leukamea disease is found to respond to treatment by radiation from radio-isotopes of phosphorus.
v) By using a fertilizer in which radio-phosphorus is employed it is possible to know to what extent the plant absorbs phosphorus from a particular fertilizer.
vi) By measuring the ratio of concentration of C14 to C12 in the remnants of dead organisms and comparing it with the normal ratio in living organism it is possible to estimate, when the organism ceased to live. To find the age of ancient objects found during excavations, manuscripts, etc. this technique of ‘radio-carbon dating’ is used.
vii) Radio-isotopes are used to test the metal castings and welds without causing any damage to the material (called Non Destructive Testing).
25. CHAIN REACTION
The nuclear fission which once started continues till all the atoms of the fissionable material are disintegrates is known as chain reaction.
In a chain reaction, the neutrons keep on multiplying rapidly (in GP) during fission till the whole of the fissionable material is disintegrated. Since fission of one gives rise to about 3 neutrons, one could expect the initiation of chain reaction in process. Figure shows how chain reaction is initiated in uranium by a single neutron. When a single neutron initially causes the fission of nucleus 3 neutrons are released along with huge amount of energy.
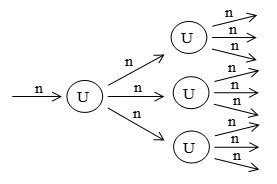
These 3 neutrons in turn cause three more nuclei to split, there by liberating a total of 9 neutrons and so on. A little reflection will show that for the fission to be self sustaining, the number of emitted fission neutrons should be more than the incident ones. Under such condition, the fission neutrons keep on increasing the maintaining the chain reaction. A very common term, called neutron multiplications, factor (or reproduction factor) is often used in chain reactions.
Reproduction factor K = .
If k = 1, i.e. the rate of production of neutron is equal to the rate of loss of neutron, the mass of the fissionable material is said to be critical and the chain reaction is sustained.
If 1 <<1, then chain reaction stops.
If K > 1, then chain reaction accelerated.
Types of chain reactions: There are two types of chain reactions
1) Explosive chain reaction: A nuclear chain reaction in which fission neutrons keep on increasing till the whole of the fissionable material is consumed (or disintegrated) is known as explosive chain reaction.
Conditions for explosive chain reaction: In order to produce explosive chain reaction, the following conditions must be fulfilled.
i) The mass and size of the fissionable material must not be less than the critical value called critical mass and critical size. It is because below these value, the neutron produced during fission will escape out of the material and hence the chain reaction would not take place.
ii) The fissionable material must be in the pure form because if an impurity like is present in , the secondary neutron produced would be captured by it and the chain reaction would stop.
2) Control chain reaction: A chain reaction that proceeds slowly without any explosion and in which energy released can be controlled is known as controlled chain reaction.
A chain reaction can be controlled by systematically removing same of the fission neutrons from the reaction vessel. The greater the number of fission neutrons removed. The lesser is the intensity of the energy released. The apparatus in which control chain reaction take place is called a nuclear reactor. In nuclear reactor, the reaction rate is adjusted by inserting neutron absorbing rods of boron steel into the uranium 20. Graphite core is used as a moderator to slow down the neutrons.
In the atomic bomb an increasing uncontrolled chain reaction occurs in a very short time when two pieces of Uranium-235 are rapidly brought together to form a mass greater that the critical size.
26. NUCLEAR FUSION
Binding energy for light nuclei (A<20) is much smaller than the binding energy for heavier nuclei. This suggest a process that is the reverse of fission. When two light nuclei combine to form a heavier nucleus, the process is called nuclear fusion. The union of light nuclei into heavier nuclei also lead to a transfer of mass and a consequent liberation of energy. Such a reaction has been achieved in hydrogen bomb and it is believed to be the principle source of the sun’s energy. Consider the formation of helium by the combination of 4 hydrogen nuclei.
The Q value of this reaction is about 25 MeV i.e. about 0.5 MeV/neutron. Very high temperatures and densities are required for fusion to take place because the proton have to be given sufficient energy to overcome the electrostatic repulsion.
How to cause fusion: Fusion is the process of combining two nuclei to form a heavy nucleus. But nuclei have positive charges and thus repel each other. However, if they can be brought close enough together (within 1014 m of each other). The attractive nuclear force can come into play, the latter can pull the nuclei together and fusion will occur. In order for the nuclei to get close enough together, they must have very high K.E. about 0.1 MeV. To impart energies to the nuclei as high as 0.1 MeV, the temperature should be of the order of 108 K. As high temperature is required to cause fusion, therefore, fusion is some time called thermonuclear reaction.
27. ENERGY AND SUN AND STARS
A fusion reaction is a powerful source of energy and is to be carried at a very high temperature. The temperatures of the sun and the stars are more than 106 K and they continuously emit energy without losing temperature. The emission of energy by sun and stars can be explained based on nuclear fusion. Depending upon the temperature, the energy released may be either through carbon-nitrogen cycle or proton-proton cycle.
Carbon – nitrogen cycle:
The cycle was proposed by H.A. Bethe in 1938 to account for the energy produced in the sun. It is believed that fusion reaction occurs in the very hot central region of the sun and stars.
The cycle is given below
…… (i)
…… (ii)
…… (iii)
…… (iv)
…… (v)
…… (vi)
By adding up, the net result is In the above reactions acts as a catalyst. The net energy released is 26.72 MeV. The conversion of hydrogen into Helium is a mass exchange reaction and would continue till the whole of hydrogen in the star is completely used.
Proton – Proton cycle:
Proton-proton cycle in which the direct collisions of protons result in the formation of heavy nuclei.
Proto-proton cycle takes place as follows
The above fusion reactions must occur twice to yield two nuclei. Therefore next reaction can be written as
The net result of the above reactions is that 4 protons are fused to produce an α particle and a few other particles and release of a total energy 27 MeV.
The proton-proton cycle is an important source of energy in the sun and in stars of comparatively lower temperatures. A conclusion that can be arrived from the above cycle is that the older starts have more Helium compared to the younger ones.
28. ELEMENTARY PARTICLES
Up to 1932 only four elementary (or fundamental) particles were known – electron, proton, neutron and photon. Subsequently, more and more elementary particles were discovered and the total number now is more than 200. Some of the important ones are as under:
Positron: It is a particle having the same mass as that of electron but positive charge. It was discovered in 1932 by Anderson in cosmic ray tracks. It is unstable.
Neutrino and antineutrino: the existence of these particles was postulated by pauli to explain the discrepancies with regard to the laws of conservation of energy and momentum in β – decay. These particles have zero (or negligible) mass and no charge. They can penetrate through large thickness of matter without appreciable interaction.
Muons : There are two types of muons-positive and negative . The mass of a muon is 207 me, where me, is the electronic mass. The muons interact feebly with matter and therefore have great penetrating power. They are unstable.
Pions : There are three types of pions, also called π-mesons and have mass 273 me and has mass 264 me. The existence of mesons was predicted by Yukawa to explain the nature of the nuclear force. They are unstable.
29. RADIATION HAZARDS
Radiation hazard means the risk to the living tissues exposed to the natural radioactivity, X-rays and nuclear radiations (α, β and γ-rays). The damage to the human body from nuclear radiations is due to the ionisation of atoms in the living cells. The ionization of atom completely destroys the living cell. Radiation hazards lead to the following disorders or diseases.
i) Radiation damage to the chromosomes in the reproductive organs can cause genetic disorder.
ii) Radiation damage to the blood producing cells in the spleen can increase the possibility of contracing leukemia.
iii) An acute exposure, to radiation weakens or even destroys the infection resistance mechanism and may lead to death.
iv) Long exposure to radiations causes cancer.
v) Long exposure to radiations causes blindness.
vi) Besides external exposure radiation damage can come form inhaling air containing radio-isotopes and eating food contaminated with radio-isotopes.
However the controlled exposure to radiations has number of uses:
i) The dangerous disease like cancer is cured by radiation therapy, γ-rays from are used for this purpose.
ii) Radiation are used to induce plant mutations which improves the varieties of many crops such as wheat, peas and rice.
iii) Radiation are also used to eliminate agriculture pests.
iv) Gamma rays or x-rays used to detect the defects in metal castings and welds.
Exercise 3:
(i) A radioactive sample has 2.0 ⨯ 1020 active nuclei at a certain instant of time. How many of them will still be in the same active state after three half-lives?
(ii) The half-life of 238U for α – decay is 4.5 ⨯ 109 years. How many disintegrations per second occur in 1g of 238U?
(iii) A radioactive substance has 6.0 ⨯ 1018 active nuclei initially. What time is required for the active nuclei of the same substance to become 1.0 ⨯ 1018 if its half life is 40 s.
(iv) Two radioactive substances X and Y initially contain an equal number of atoms. Their half-lives are 1 hour and 2 hours respectively. Calculate the ratio of their rates of disintegration after four hours.
Answer to Exercise
Exercise 1: (i) . (ii) 1.453 ⨯ 10–17 kg/m2 (iii) 7.075 MeV
Exercise 2: (i) 4800 years (ii) 144 days (iii) 103.9 days
Exercise 3: (i) 2.5⨯1019 (ii) 1.235⨯104 s–1 (iii) 103.4s (iv) 1/2
SOLVED PROBLEMS -1
Prob 1. How many electrons, protons and neutrons are there in 14 gram of ? Avogadro’s number is.
Sol: The symbol means that in one carbon atom,
there are 6 electrons, 6 protons and (14-6) = 8 neutrons.
Number of atoms in 14 gram =
∴ Number of electrons in 14 gram
Number of neutrons in 14 gram
Number of protons in 14 gram
Prob 2. Assuming that protons and neutrons have equal masses, calculate how many times nuclear matter is denser than water. Given that nuclear radius is given by R = meter and mass of nucleon =
Sol: Given that
Mass of proton = mass of neutron = kg
R =
Let mass number of an element is A
∴ Mass of nucleus =
Volume of the nucleus =
∴ Density of the nucleus
Density of water,
Prob 3. The neutron separation energy is defined to be the energy is defined to be the energy required to remove a neutron from a nucleus. Obtain the neutron separation energies of the nuclei and from the following data. mn = 1.008665 amu (or u), m = 39.96 2591 amu (or u), m = 40.96227 amu (or u), m = 25.986895 amu (or u) and M = 26.981541 amu (or u)
Sol: Neutron separation energy Sn at a nucleus is given by
(mass in amu)
∴
= (39.962591+1.008665 – 40.96278) ⨯ 931
= 0.008978 ⨯ 931 = 8.363 MeV
similarly
= (25.986895+1.008665-26.981541) ⨯ 931
= 0.014019 ⨯ 931 = 13.08 MeV
Prob 4. The nucleus is unstable against α-decay with a half-life of about years. Write down the equation of decay and estimate the kinetic energy of the emitted α-particle from the following data.
= 234.04363 amu
Sol: The equation representing the decay is
Where Q is the kinetic energy released.
Mass defect Δm =
= 238.5081 – 234.04363 – 4.00260
= 0.00458 amu
∴ Q = Δm ⨯ 931 MeV
= 0.00458 ⨯ 931 = 4.26 MeV
= 4.1884 MeV
Prob 5. What should be the speed of a body so that mass becomes three times its rest mass?
Sol: Let mv = mass of body moving at velocity v
By question mv = 3mo where mo = rest mass
We know
Prob 6. If the kinetic energy of a body is twice its rest mass energy, find its velocity.
Sol: Let mv = mass of body moving at velocity v
mo = rest mass of body
or …… (i)
Given that K.E. =
Now
Prob 7. Determine X in the following nuclear reactions.
i)
ii)
iii)
iv)
Sol:
i) can be written as
Z = 4+2 = 6, A = 9+4-1 = 12
∴ X =
ii) can be written as
Now Z = 20+1-20 = 1
and A = 42+1-41 = 2
iii) can be written as
Now Z = 39+2-1 = 40
And A = 87+4-1 = 90
∴
iv) can be written as
Now Z = 8+1-8 = 1
and A = 19+1 – 18 = 2
Prob 8. There is a stream of neutrons with a kinetic energy of 0.0327 eV. If the half life of neutron is 700 seconds. What fraction of neutrons will decay before they travel a distance of 10 m? Given that mass of neutron = 1.675 ⨯ 10–27 kg.
Sol: Given that
K.E. of neutron = 0.0327 eV, mn = 1.675 ⨯ 10–27
T = 700 sec, s = 10 m
∴
Time taken by neutrons to travel 10 m is
.
∴ Fraction of neutrons left behind in time t is
Fraction of neutron decayed = 1-0.999996
Prob 9. How many alpha and beta particles are emitted when uranium decay to lead .
Sol: Let a and b be the number of α and β particles emitted when decays to
We know total atomic number is conserve
∴ 238 = 206 + 4a
a =
and 92 = 82 + 2a – b
10 – 2a = -b
16 – 2⨯8 = -b
b = 6.
Number of emitted α-particle = 8
Number of emitted β-particles = 6
Prob 10. What is the power output of a reactor if it takes 30 days to use up 2 kg of fuel and if each fission gives 185 MeV usable energy? Avogadro’s number NA = 6.02⨯1026 per kilo mole.
Sol: Number of atoms in 2kg =
Rate of fission = number of atoms fissioned in one second
per second.
Each fission gives 185 MeV energy
∴ Energy obtain in one second P = 185 ⨯ fission rate
= 180 ⨯ 1.975 ⨯ 1018 MeV per second
= 58.46 ⨯ 106 J/s
= 58.46 Mw.
SOLVED PROBLEMS -2
Prob 1. Consider the following statements associated with the production of x-ray spectrum
1) The continuous X-ray spectrum is due to beams structuring
2) The characteristic sharp lines appearing in the spectrum depend on the nature of the target material
3) The x-ray spectrum is due to the rearrangement of nucleons
(A) 1 and 2 are correct
(B) 1 and 3 are correct
(C) 2 above is correct
(D) 1, 2 and 3 are correct
Sol: (D) 1, 2 and 3 are correct
Prob 2. If the wavelength of Kα line for silicon (X = 47) is 0.57 A°, then the value of wavelength for uranium (Z = 92) is
(A) 0.146 A° (B) 0.28 A° (C) 1.128 A° (D) 2.53 A°
Sol: (A)
or b = 1 for kα line
λu = 0.146 A°
Prob 3. When the number of electrons striking the anode of an X-ray tube is increased the …… of the emitted x-rays increase, while when the speeds of the electron striking the anode are increased the cut off wavelength of the emitted X-ray …………
(A) Intensity, decreases
(B) Current, increases
C) Intensity, increases
(D) Current, decreases
Sol: (A) Intensity, decreases
Prob 4. The potential difference applied to an X-ray tube is increased. As a result, in the emitted radiation.
(A) The intensity increases
(B) The minimum wavelength increases
(C) The intensity remains unchanged
(D) The minimum wavelength decreases
Sol: (C & D) The intensity remains unchanged and the minimum wavelength decreases
Prob 5. A – Gamma ray photon is produced from
(A) Atomic transitions
(B) Electronic transitions
(C) Rotational transitions
(D) Nuclear transitions
Sol: (D) Nuclear transitions
Prob 6. An electron cannot exist in the nucleus of an atom because
(A) It has a larger size than the other particles in the nucleus
(B) It has a negative charge
(C) It moves with a very large velocity
(D) Its de-Broglie wavelength is larger than the size of the nucleus
Sol: (D) Its de-Broglie wavelength is larger than the size of the nucleus
Prob 7. The kinetic energy of neutrons in a neutron beam is 0.0237 eV. If half life of neutrons is 700 sec, the fraction of neutrons decaying before traveling a distance 10 m is
(A) 5.7 ⨯ 10-3 (B) 4 ⨯ 10-6 (C) 5.7 ⨯ 10-4 (D) 6 ⨯ 10-5
Sol: (B) Velocity of neutrons =
=
Time taken by neutron to cover the distance 10 m
Now
where N is number of neutron after t seconds i.e. fraction of neutron decayed after t seconds will be
Prob 8. A nuclear reactor is operating at 600 M Watt level. If energy released per fission is 3⨯10-11 J, the number of nuclei consumed per minute will be
(A) 2 ⨯ 1019 (B) 1.2 ⨯ 1021 (C) 2 ⨯ 1013 (D) 3.3 ⨯ 1017
Sol: (D)
Energy per Hour = 600 ⨯ 106 Joules
Energy per minute = Joule
Number of nuclei consumed per minute
Prob 9. Rutherford’s alpha particle scattering experiment eventually led to the conclusion that
(A) Mass and energy are related
(B) Electrons occupy space around the nucleus
(C) Neutrons are buried deep in the nucleus
(D) The point of impact with matter can be precisely determined
Sol: (B) Electrons occupy space around the nucleus
Prob 10. Four physical quantities are listed in Column I. Their values are listed in Column II in a random order
Column I Column II
(a) Thermal energy of air (e) 0.02 eV molecules at room temperature
(b) Binding energy of heavy nuclei (f) 2 eV per nucleon
(c) X-ray photon energy (g) 3 KeV
(d) Photon energy of visible light (h) 7 MeV
The correct matching of column I and Ii is given by
(A) a-e, b-h, c-g, d-f
(B) a-e, b-g, c-f, d-h
(C) a-f, b-e, c-g, d-h
(D) a-f, b-h, c-e, d-g
Sol: (A)








