Elctromagnetic Waves

• According to Maxwell, an accelerated charge produces a sinusoidal time-varying magnetic field, which in turn produces a sinusoidal time varying electric field. The two fields so produced are mutually perpendicular. They constitute electro magnetic waves which can propagate through empty space.

1. DISPLACEMENT CURRENT

According to Ampere’s circuital Law, the magnetic field B is related to steady current I as $\oint \overrightarrow{\mathrm{B}}.\overrightarrow{\mathrm{dl}}={\mathrm{\mu }}_0\mathrm{I}$ ……….. (i)

where I is the current travelling through the surface bounded by closed loop.

In 1864, Maxwell showed that relation (i) is logically inconsistent. He accounted for this inconsistency as follows: Consider a parallel plate capacitor having plates P and Q being charged with battery B.

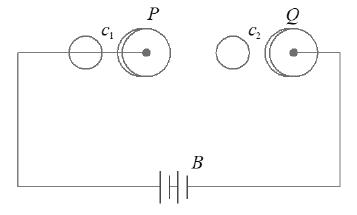
• During charging, a current I flows through the connecting wires which changes with time. This current will produce magnetic field around the wires which can be detected using a magnetic compass needle. Consider two loops $c_1$ and $c_2$ parallel to the plates P and Q of the capacitor. $c_1$ is enclosing only the connecting wire attached to the plate P of the capacitor and $c_2$ lies in the region between the two plates of capacitor. For the loop $c_1$ , a current I is flowing through it, hence Ampere’s circuital law for loop $c_1$ gives ${\oint }_{{\mathrm{C}}_1}\overrightarrow{\mathrm{B}}.\mathrm{d}\overrightarrow{\mathrm{l}}={\mathrm{\mu }}_0\mathrm{I}$ ……. (ii)

• Since the loop $c_2$ lies in the region between the plates of the capacitor, no current flows in this region. Hence Ampere’s circuital law for loop $c_2$ gives ${\oint }_{{\mathrm{C}}_2}\overrightarrow{\mathrm{B}}.\mathrm{d}\overrightarrow{\mathrm{l}}=0$……(iii)

• The relations (ii) and (iii) continue to be true even if two loops 1 c and 2 c are infinitesimally close to the plate P of the capacitor. In the other hand, as the loops $c_1 \& c_2$ are infinitesimally close, it is expected that ${\oint }_{{\mathrm{C}}_1}\overrightarrow{\mathrm{B}}.\mathrm{d}\overrightarrow{\mathrm{l}}={\oint }_{{\mathrm{C}}_2}\overrightarrow{\mathrm{B}}.\mathrm{d}\overrightarrow{\mathrm{l}}$……….(iv)

Thus, relation (iv) is in contradiction with relations (ii) and (iii). This led Maxwell to point out that Ampere’s circuital law as given by (i) is logically inconsistent.

2. IDEA OF DISPLACEMENT CURRENT

Maxwell predicted that not only a current flowing in a conductor produces magnetic field but also a timevarying electric field (i.e., changing electric field) in a vacuum/free space (or in a dielectric) produces a magnetic field. It means a changing electric field gives rise to a current which flows through a region so long as the electric field is changing there. Maxwell also predicted that this current produces the same magnetic field as a conduction current can produce. This current is known as ‘displacement current’.

• Thus, displacement current is that current which comes into play in the region in which the electric field and hence the electric flux is changing with time.
Maxwell defined this displacement current in space where electric field is changing with time as

${\mathrm{I}}_{\mathrm{D}}={\mathrm{\epsilon }}_0\frac{{\mathrm{d\varphi }}_{\mathrm{E}}}{\mathrm{dt}}$…….(v)

where ${\varphi }_E$ is the electric flux.

• Maxwell also found that conduction current (I) and displacement current (${\mathrm{I}}_{\mathrm{D}}$) together have the property of continuity, although, individually, they may not be continuous.
• This idea led Maxwell to modify Ampere’s circuital law in order to make the same logically consistent. He states Ampere circuital law in the form, ${\oint }_{\mathrm{C}}\overrightarrow{\mathrm{B}}.\overrightarrow{\mathrm{dl}}={\mathrm{\mu }}_0\left(\mathrm{I}+{\mathrm{I}}_{\mathrm{D}}\right)$

$={\mathrm{\mu }}_0\left(\mathrm{I}+{\mathrm{\epsilon }}_0\frac{{\mathrm{d\varphi }}_{\mathrm{E}}}{\mathrm{dt}}\right)$

It is now called as Ampere-Maxwell’s law.
• This means that out side the capacitor plates, we have only conduction current $i_c=i$ and no displacement current $i_d=0$. On the other hand, inside the capacitor, there is no conduction current $i_c=0$ and there is only displacement current $i_d=i$

3. MAXWELL’S EQUATIONS

• Maxwell, in 1862, gave the basic Laws of electricity and magnetism in the form of four fundamental equations which are known as Maxwell’s equations. In the absence of any dielectric and magnetic material may be stated in the integral form as below.

1. Gauss’s Law for electrostatics

This Law gives the total electric flux in terms of charge enclosed by the closed surface.
In the usual notations $\oint \overrightarrow{\mathrm{E}}.\overrightarrow{\mathrm{ds}}=\frac{{\mathrm{q}}_{\mathrm{in}}}{{\mathrm{\epsilon }}_0}$.

This Law states that electric lines of force start from positive charge and end at negative charge i.e., electric lines force do not form closed paths.

2. Gauss’s Law for magnetism

Mathematically $\oint \overrightarrow{B}.\overrightarrow{dS}=0$

• This Law shows that the no. of magnetic lines of force entering a closed surface is equal to no. of magnetic lines of force leaving that closed surface.

• This law tells that the magnetic lines of force form a continuous closed path.

• This Law also predicts that the isolated magnetic monopoles does not exist.

3. Faraday’s Law of electro magnetic induction

Mathematic cally $\oint \overrightarrow{E}.\overrightarrow{dl}=\frac{–d{\varphi }_B}{dt}$ = induced emf.

• This law gives a relation between electric field and changing magnetic flux.

• This law tells that changing magnetic field is a source of electric field.

4. Amper’s-Maxwell’s Law

Mathematically $\oint \overrightarrow{\mathrm{B}}.\overrightarrow{\mathrm{dl}}={\mathrm{\mu }}_0\left({\mathrm{i}}_{\mathrm{c}}+{\mathrm{i}}_{\mathrm{d}}\right)$

= ${\mu }_0\left(i_c+{\epsilon }_0\frac{d{\varphi }_E}{dt}\right)$

• This law states that magnetic field can be produced by a conduction current as well as by displacement current.

• At any instant in a circuit, conduction current is equal to displacement current.

5. Lorentz Force : Force acting on a charge ‘q’ moving in a region where electric and magnetic fields similar to

EM waves are existing simultaneously is $\overrightarrow{\mathrm{F}}=\mathrm{q}(\overrightarrow{\mathrm{E}}+\overrightarrow{\mathrm{v}}\times \overrightarrow{\mathrm{B}})$

4. SOURCE OF EM WAVES

• Accelerated charges radiate energy in the form of EM waves. So it is source of EM waves

• An oscillating charge produces an oscillating electric field inturn which produces an oscillating magnetic field.

• The oscillating electric and magnetic fields regenerate each other and propagate through space as waves called EM waves.

• An electric charge oscillating harmonically with frequency ‘$\nu$ ‘ produces EM waves of same frequency.

5. CHARACTERISTICS OF EM WAVES

1) EM waves are transverse in nature whose speed is same as that of speed of light

2) The two fields $\overrightarrow{E} and \overrightarrow{B}$ have same frequency of oscillation and they are in phase with each other.

3) Keeping these features in mind, we can assume that if EM wave is travelling along positive direction along xaxis, the electric field is oscillating parallel to the y-axis and that magnetic field is parallel to z-axis, then we can write the electric and magnetic fields as sinusoidal functions of position ‘x’ and time ‘t’

$E=E_{0}Sin(kx–wt); B=B_0\sin (kx–wt)$

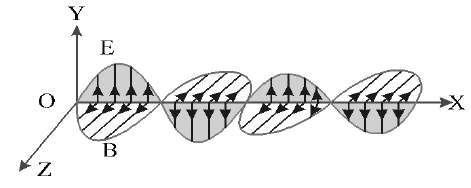
In this, $E_0 \& B_0$ are the amplitudes of the fields

4) EM waves can be polarised.

5) EM waves are self-sustaining oscillations of electric and magnetic fields in free space or vaccum. EM waves travel through vaccum with speed of light ‘C’ where. $C=\frac{1}{\sqrt{{\epsilon }_0{\mu }_0}}=3\times {10}^8 \mathrm{m}/\mathrm{Sec}$

6) The speed of EM waves in any other medium of permittivity $\epsilon$ and permeability $\mu$ is

$C_{med}=\frac{1}{\sqrt{\mu \epsilon }}=\frac{1}{\sqrt{{\mu }_r{\mu }_0{\epsilon }_r{\epsilon }_0}}=\frac{C_0}{\sqrt{{\mu }_r{\epsilon }_r}}$

$\sqrt{{\mu }_r{\epsilon }_r}=\frac{C_0}{C_{med}}=n$ R.I.of medium

7) In vaccum, EM waves are of different wavelengths, but velocity is same.

6. ENERGY DENSITY OF EM WAVES

• Consider a plane electro magnetic wave propagating along x-axis. The electric and magnetic fields in a plane

EM wave can be given by $E=E_0\sin (kx–\omega t)\text{ and }B=B_0\sin (kx–\omega t)$

• In any small volume ‘dV’, the energy of electric field is $U_E=\frac{1}{2}{\epsilon }_0{E}^{2}dV$ and energy of the magnetic field in volume ‘dV’ is $U_B=\frac{B^2}{2{\mu }_0}dV$

• Thus total energy of EM wave is $u=\frac{1}{2}{\epsilon }_0{E}^{2}dV+\frac{B^2}{2{\mu }_0}dV$

• Energy density of EM wave is $U=\frac{1}{2}{\epsilon }_0{E}^2+\frac{B^2}{2{\mu }_0}$

$=\frac{1}{2}{\epsilon }_0{E}_0^2{\sin }^2(kx–wt)+\frac{B_0^2}{2{\mu }_0}{\sin }^2(kx–\omega t)$

If we take average over a long time, the ${\sin }^2$ terms have an average value of $\frac{1}{2}$

Thus $u_{aV}=\frac{1}{4}{\epsilon }_0{E}_0^2+\frac{B_0^2}{4{\mu }_0}$

Now  $E_0=C{B}_0\text{ and }{\mu }_0{\epsilon }_0=\frac{1}{C^2}$

$\therefore u_E=\frac{1}{4}{\epsilon }_0{E}_0^2=\frac{1}{4}{\epsilon }_0\left(C^2{B}_0^2\right)=\frac{1}{4}{\epsilon }_0\frac{1}{{\mu }_0{\epsilon }_0}{B}_0^2=\frac{B_0^2}{4{\mu }_0}=u_B$

Hence is an EM wave, average energy density of electric field is equal to average energy density of magnetic field.

Thus units of $u_E \& u_B$ are $J{m}^{–3}$

$\therefore$ average energy density of EM wave

$u=u_E+u_B=2u_E=2u_B=\frac{1}{2}{\epsilon }_0{E}_0^2=\frac{B_0^2}{2{\mu }_0}$

INTENSITY OF ELECTRO MAGNETIC WAVE

Intensity of EM wave is defined as the energy crossing per second per unit area of a source perpendicular to the direction of propagation of the wave. It is denoted by I.

i.e. $\text{ Intensity }I=\frac{\text{ total }EM\text{ wave energy }}{\text{ Surface area }\times \text{ time }}$

$\frac{u_{aV}\times \Delta V}{A\Delta t}=\frac{u_{aV}\times Ac\Delta t}{A\Delta t}$

Interms of electric fields $I=\frac{1}{2}{\epsilon }_0{E}_0^{2}C$ …….. (1)

Interms of magnetic field $I=\frac{B_0^2}{2{\mu }_0}C$………… (2)

Either eq (1) or (2) may be used to find intensity of EM waves

ii) The intensity of EM radiation from an isotropic point source at a distance r is $I=\frac{P}{4\pi r^2}$ where P is power of source

Note: The rate of flow of energy crossing a unit area in an EM wave is described by the vector ‘S’ called poynting vector which is described by the expression.

$\overrightarrow{S}=\frac{1}{{\mu }_0}(\overrightarrow{E}\times \overrightarrow{B})$

Since $\overrightarrow{E} and \overrightarrow{B}$ are mutually perpendicular

$|\overrightarrow{E}\times \overrightarrow{B}|=EB$

Thus magnitude of Poynting vector

$S=\frac{EB}{{\mu }_0}=\frac{E^2}{{\mu }_{0}C}$

SI unit of S is $J{\sec }^{–1}{ \mathrm{m}}^{–2}\text{ (or) }{\mathrm{Wm}}^{–2}$

This relation shows that the value of electric vector at any instant in the EM wave is about 377 times the value of magnetic vector. It is because of this reason, optical properties of light is due to electric field. Average of Poynting vector is given by

$I=S_{aV}=\frac{E_0{B}_0}{2{\mu }_0}=\frac{1}{2}\epsilon E_0^{2}C=\frac{C{B}_0^2}{2{\mu }_0}$

8. MOMENTUM AND RADIATION PRESSURE

i) Electro magnetic waves have linear momentum as well as energy. When EM waves strike a surface, pressure is exerted on it, called radiation pressure.

ii) When EM waves are incident on a surface and the total energy transferred to the surface in a time t is U then magnitude of momentum transferred to surface is $p=\frac{U}{C}$ (total absorption)

$\left[E=m{C}^2=\left(mC\right)C\Rightarrow mC=\frac{E}{C}\Rightarrow P=\frac{E}{C}\right]$

iii) When radiation incident on a surface is entirely reflected back along its original path, magnitude of momentum delivered to the surface is $p=\frac{2U}{C}$ where ‘C’ is velocity of light.

iv) When the radiation incident on a surface (Perfect absorber) radiaton pressure

$P_r=\frac{F}{A}=\frac{1}{A}\frac{dp}{dt}=\frac{1}{A}\frac{d}{dt}\left(\frac{U}{C}\right)=\frac{1}{AC}\frac{dU}{dt}=\frac{S}{C}$

$\frac{dU/dt}{A}$ is called average value of Poynting vector.

If the surface is perfect reflector radiation pressure $P_r=\frac{2S}{C}$

9. ELECTRO MAGNETIC SPECTRUM

• The array obtained on arranging all the electromagnetic waves in an order on the basis of their wavelength is called the electromagnetic spectrum

In the order of increasing wavelength, these waves are (i) Gamma rays, (ii) X-rays, (iii) Ultraviolet rays, (iv) Visible light, (v) infrared waves, (vi) Microwaves and (vii) Radio waves.

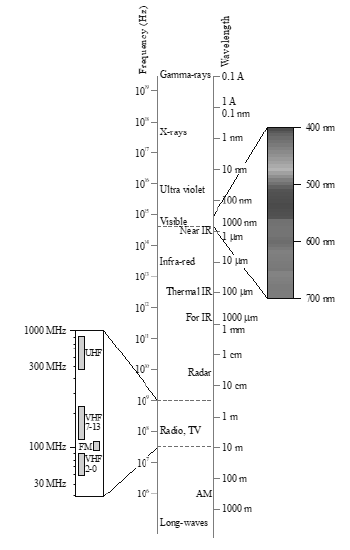
The figure illustrates the general spectrum of the electromagnetic radiations, in which the wavelength is expressed in metre.
1) Gamma rays : They were discovered by Becquerel and Curie in 1896. Their wavelength is of the order of ${10}^{–14} to {10}^{–10}$m . The main sources are the natural and artificial radioactive substances. These rays affect the photographic plate. These rays are mainly used in the treatment of cancer disease.

2) X-rays : They were discovered by Roentgen in 1895. Their wavelength is of the order of ${10}^{–12}$m to ${10}^{–18}$m . Xrays are produced when highly energetic cathode rays are stopped by a metal target of high melting point. They affect the photographic plate and can penetrate through the transparent materials. They are mainly used in
detecting the fracture of bones, hidden bullet, needle, costly material, etc., inside the body and also used in the study of crystal structure.
3) Ultraviolet rays : They were discovered by Ritter in 1801. Their wavelength is of the order ${10}^{–9}$m to $4\times {10}^{–7}$m .
In the radiations received from sun, major part is that of the ultraviolet radiation. Its other sources are the electric discharge tube, carbon arc etc. These radiations are mainly used in excitation of photoelectric effect and to kill the bacteria of many diseases.
4) Visible light : This was first studied in 1666 by Newton. The radiations in the range of wavelength from $4\times {10}^{–7}$m to $7\times {10}^{–7}$m fall in the visible region. The wavelength of the light of violet colour is the shortest and that of red colour is the longest. Visible light is obtained from the glowing bodies, while they are white hot.
The light obtained from the electric bulbs, sodium lamp, fluorescent tube is the visible light.
5) Thermal or infrared waves: They were discovered by Herchell in 1800. Their wavelength is of the order of $7\times {10}^{–7}$m to ${10}^{–3}$m . A body on being heated, emits out the infrared waves. These radiations have the maximum heating effect. The glass absorbs these radiations, therefore for the study of these radiations rock salt prism is
used instead of a glass prism. These waves are mainly used for therapeutic purpose by the doctors because of their heating effect.

6) Microwaves: They were discovered by Hertz in 1888. Their wavelength is in the range of nearly ${10}^{–4}$m to 1m. These waves are produced by the spark discharge or magnetron valve. They are detected by the crystal or semiconductor detector. These waves are used mainly in radar and long distance communication.
7) Radiowaves: They were first discovered in 1895 by Marconi. Their wavelength is in the range of 0.1m to 105m. They can be obtained by the flow of high frequency alternating current in an electric conductor. These waves are detected by the tank circuit in a radio receiver or transmitter.

Application of EM waves
1) Radio and microwave radiations are used in radio and TV communication system. Microwave radiations are mainly used in radar and TV communication.

2) Infrared radiations are used
i) in green houses to keep the plants warm
ii) in revealing the secret writings on the ancient walls
iii) for looking through haze, fog and mist during war time, as these radiations can pass through them.

3) Ultraviolet radiations are used
i) in preserving the food stuffs.
ii) in the detection of invisible writing, forged documents, finger prints in forensic laboratory.
iii) Ultraviolet radiations are also used for knowing the structure of the molecules and arrangement of electrons in the external shells.

4) X-rays many applications these rays provide us valuable information
i) about the structure of atomic nuclei
ii) in the study of crystal structure
iii) in the fracture of bones etc.

5) $\gamma –$ rays were used
i) in treatment of cancer and tumours
ii) to produce nuclear reactions.

SOLVED EXAMPLES

1. What is the instantanuous displacement current in space between plates of parallel plate capacitor of capacitor 1$\mu$ F which is charging at rate of ${10}^6$ V / S

Sol. As $I_d={\epsilon }_0\frac{d{\varphi }_E}{dt}={\epsilon }_{0}A\frac{d}{dt}\left(E\right)={\epsilon }_{0}A\frac{d}{dt}\left(\frac{V}{d}\right)$

$=\frac{{\epsilon }_{0}A}{d}\frac{dV}{dt}=C\frac{dV}{dt};I_d={10}^{–6}\times {10}^6=1A$

2. Electro magnetic waves travel in a medium with speed of 2$\times$10⁸ m/ sec . The relative permeability of the medium is 1 find relative permittivity.

Sol. Given $C=2\times {10}^8 \mathrm{m}/\sec , {\mu }_r=1$

Speed of EM waves in medium

$C_{med}=\frac{1}{\sqrt{{\mu }_r{\mu }_0{\epsilon }_r{\epsilon }_0}}=\frac{C_0}{\sqrt{{\mu }_r{\epsilon }_r}}; {\epsilon }_r=\frac{c_0^2}{c^2{\mu }_r}=\frac{{\left(3\times {10}^8\right)}^2}{{\left(2\times {10}^8\right)}^2\times 1}=2.25$

3. Suppose that the electric field amplitude of an EM wave is E₀ = 120 N /C and that its frequency v = 50$\mu$HZ. Determine (a) $B_0, \omega , \lambda$ and K (b) Find expressions for E and B

Sol. a) i) Using $C=\frac{E_0}{B_0}$ we get

$B_0=\frac{E_0}{C}=\frac{120}{3\times {10}^8}=4\times {10}^{–7}T=400nT$

ii) $\omega =2\pi v=2\times \pi \times 50\times {10}^6=3.14\times {10}^8 \mathrm{rad}/\mathrm{Sec}$

iii) $c=v\lambda \Rightarrow \lambda =\frac{C}{v}=\frac{3\times {10}^8}{50\times {10}^6}=6m$

iv) $K=\frac{2\pi }{\lambda }=\frac{2\pi }{6}=\frac{2\times 3.14}{6}=1.05{ \mathrm{m}}^{–1}$

b) $\overrightarrow{E}=E_0\sin (kx–\omega t)$

$=120\sin \left(1.05x–3.14\times {10}^{8}t\right)$

$B=B_0\sin (kx–\omega t)$

$=400\times {10}^{–9}\sin \left(1.05x–3.14\times {10}^{8}t\right)$

4. The electric field of an electro magnetic wave is given by $E=50\sin \omega \left(t–\frac{x}{c}\right)N/C$. Find energy contained in a cylinder of cross-section $10 c{m}^2$ and length 50cm along x-axis

Sol. Average volume of energy density $u_{aV}=\frac{1}{2}{\epsilon }_0{E}_0^2$

Total volume of cylinder V = Al

Total energy of contained in cylinder $U=\left(U_{aV}\right)V=\left(\frac{1}{2}{\epsilon }_0{E}_0^2\right)\left(Al\right)=5.5\times {10}^{–12}J$.

5. Light with an energy flux of 18W /cm² falls on a non reflecting surface at normal incidence. If the surface has an area of 20cm² then find average force exerted on the surface during a 30 minute time span.

Sol. Total energy falling on the surface is

$U=\left(18\times {10}^4\right)\left(20\times {10}^{–4}\right)(30\times 60)=6.48\times {10}^5 \mathrm{J}$

Total momentum delivered (complete absorption)

$p=\frac{U}{C}=\frac{6.48\times {10}^5}{3\times {10}^8}=2.16\times {10}^{–3} \mathrm{kg} \mathrm{m}/\sec$

average force exerted

$F=\frac{p}{t}=\frac{2.16\times {10}^{–3}}{30\times 60}=1.2\times {10}^{–6}N$

6. The rms value of electric field of light coming from sun is 720 N/C . Find average energy density of em wave.

Sol. Total average energy density = $\frac{1}{2}{\epsilon }_0{E}_0^2={\epsilon }_0{E}_{ms}^2$

$\left(\therefore E_{rms}=\frac{E_0}{\sqrt{2}}\right)=8.85\times {10}^{–12}\times (720{)}^2=4.58\times {10}^{–6}J{m}^{–3}$