1. INTRODUCTION
In the chapter Newton’s laws, force has played a central role as the quantity determining motion. This chapter is devoted to the very important concept of energy and the closely related concept of work which are scalar quantities and have no direction associated with them. The capacity of doing work is defined as energy. The energy of an object changes if an exchange of energy occurs between the object and its environment. Hence we discuss the transfer of energy via a force, a process known as doing work. The change in kinetic energy of an object when subjected to force is due to transfer of energy between the object and the one that applies the force. The chapter is not concerned with the common meaning of the word ‘work’ which implies any physical or mental labour.
By combining the Newton’s second law and the principle of kinematics, two additional methods of analysis are possible.
(a) One of these methods is Work – Energy Method. The advantage of this method is that the determination of the acceleration of the particle is not necessary. The method of work -energy relates force, mass, velocity and In this method, the work done by the forces acting on a particle is related to the change in kinetic energy of the particle.
(b) Law of conservation of energy is another method for solving The concept of energy is very important because, energy is conserved. The total energy remains constant in any process. There are many situations for which an analysis based on Newton’s laws would be difficult but which can be dealt with using the law of conservation of energy.
2. WORK DONE BY A FORCE
Work is said to be done by a force when a body undergoes displacement parallel to the line of action of the force or parallel to one of the components of force applied.
Work done by the force acting on a body can be calculated as follows.
Case – I : When body gets displaced along the direction of force then work done is equal to the product of force and displacement.
Case – II : When body gets displaced in a direction making some angle θ with the direction of force then work done by the force is equal to product of force and component of displacement along the force (or) product of displacement and component of force along the displacement (or) dot product of force and displacement.
Work is a scalar
Explanation:
Consider a body of mass ‘m’ at rest at point A on a horizontal surface as shown. Let a force acts on the body making an angle ‘ θ ‘ with the horizontal. Due to which the body undergoes displacement and travels from A to B. The component of force along the displacement is . Now
Work done
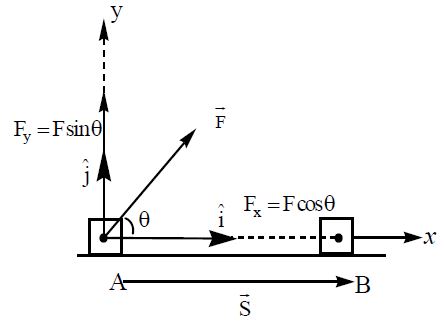
Note: If and
Dimensions and units of work
The dimensional formula of work is [ML2T-2]. Its unit in SI is joule and is denoted by J.
joule : Work is said to be one joule if a force of 1 newton displaces a body through a distance of 1 m along the direction of force.
1 J = 1 N ´1 m
In CGS system, the unit of work is erg
erg : Work done is said to be one ‘erg’ if a force of one dyne displaces the body through a distance of 1 cm along the direction of force.
1 erg = 1 dyne ´ 1 cm
Relation between joule and erg
1 J=1N´m = 105 dyne´100 cm = 107 dyne cm
1 J = 107 erg
Nature of work :
Work done by a force may be positive, negative or zero.
* Positive work : Positive work means that force (or one of its components) is parallel to If ‘θ’ is the angle between force and displacement, then, .
Examples :
(i) When a person lifts a body from the ground, the work done by the lifting force (upward) is positive
(ii) When a spring is stretched, work done by the external (stretching) force is positive
* Negative work :
Negative work means that force (or one of its components) is opposite to displacement. If ‘θ’ is the angle between force and displacement, then, .
Examples :
(i) When a person lifts a body from the ground, the work done by the force of gravity (downward) is negitive
(ii) When a body is made to slide over a rough surface, the work done by the frictional force is negitive
* Zero Work :
Under three conditions, work done becomes zero.
1. If the force is perpendicular to the displacement (θ = 90°)
Examples :
(i) When a body moves in a circle the work done by the centripetal force is always zero.
(ii) When a porter travels on a horizontal platform with a load on his head, work done by him against gravity by the porter is zero
(iii) When the bob of a pendulum swings, the work done by the tension in the string is
2. If there is no displacement [s = 0]
Examples :
1) When a person tries to displace a wall by applying a force and if it does not move the work done by him is zero.
2) Work done in holding bob of simple pendulum at its extreme position is zero.
3. If resultant force acting on the body becomes zero. (F = 0).
Examples:
1) The work done by all forces acting on a raindrop falling down with terminal velocity is zero.
2) If body is moving with uniform velocity on a horizontal frictionless surface, then work done on the body is zero.
Work done by a force
a) Work done by a constant force
If a constant force displaces a body by , then work done by the force
By using force–displacement graph, the area enclosed by the graph on displacement axis gives the amount of work done by the force.
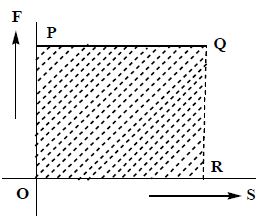
Force displacement curve of a constant force is shown in fig. OPQR
Area OPQR = OP ´ OR = F ´ S = work
b) Work Done by a Variable Force
When the magnitude and direction of a force varies with position, the work done by such a force for an infinitesimal displacement is given by
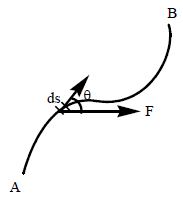
The total work done in going from A to B as shown in the figure is
In terms of rectangular component
or
By using force- displacement graph the above Work done is represented as follows.
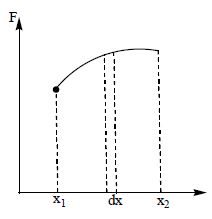
Let a body, whose initial position is x1, is acted upon by a variable force and finally the body acquires its final position x2.
For a small displacement ‘dx’ the work done will be the area of the strip of width dx.
dW = F dx
W = (Sum of Areas of various strips of width dx between x1 and x2)
W = Area under curve between x1 and x2
WORK DONE BY A FORCE IN VARIOUS SITUATIONS
Case-1
A body of mass ‘m’ is lifted from ground to a height ‘h’ by using a minimum force F.
The minimum Work done by the lifting force is
Work done by the gravitational force is
Case-2
One end of a string is fixed to a support and a body of mass ‘m’ is attached to the other end of the string. If the point of support moves with acceleration ‘a’ in the upward direction, Work done by tension in the string when the body moves upward through a distance ‘h’ is
In the above case if the body moves downward with acceleration ‘a’ then work done by the tension in the string is . Here work done is negative as force and displacement are opposite to each other.
Case-3
a). A body of mass ‘m’ is placed on a friction less horizontal surface. A force F acts on the body parallel to the surface, such that it moves with an acceleration ‘a’. The work done by the force acting on the body when its displacement is S, is given by .
b) If body moves with uniform velocity on a horizontal friction less surface. The Work done on the body is W = 0.
c) If frictional force is considered between the body and the surface then the Work done by the force to move the body with uniform velocity is .
d) In the above case if the body moves with uniform acceleration a Work done by the force is
Case-4
A body of mass ‘m’ and of density ‘d1‘ lies in a non viscous liquid of density ‘d2‘. The minimum Work done to lift the body with uniform velocity through a height ‘h’ in the liquid is
Case-5
A bucket full of water of total mass ‘M’ is lifted up with uniform velocity using a uniform rope of mass ‘m’ and length ‘ ‘
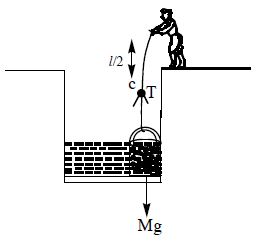
Work done by the lifting force in lifting the bucket full of water by means of the rope is
Case-6
A pendulum of length ‘L’ carries a bob of mass ‘m’ . The bob is pulled aside through an angle θ with the lower vertical by a horizontal force F.
Work done by the gravitational force
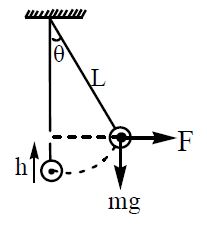
Work done by the horizontal force F is
Case-7
A uniform rod of mass ‘m’ and length ‘L’ is suspended vertically. If it is pulled aside through an angle ‘θ’ to lower vertical,
work done by gravitational force
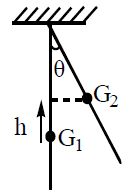
Case-8
A ladder of mass ‘m’ and length ‘‘ resting on a level floor is lifted and held against a wall at an angle ‘θ’ with the floor.
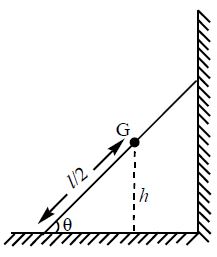
Work done by the gravitational force is
Where ‘h’ is the height gained by centre of gravity.
Case-9
A uniform chain of mass ‘m’ and length ‘‘ is suspended vertically. The lower end of the chain is lifted upto the point of suspension.
Work done by gravitational force is Wg = – mgh.
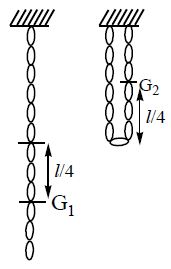
Where ‘h’ is the height gained by center of gravity of the lower half of chain, with respect to its initial position G1.
Work done by the gravitational force is
Case-10
A uniform chain of mass ‘m’ and length ‘L’ rests on a table, having part of its length hanging down from the edge of table. The work done by the pulling force to bring the hanging part of chain on to the table is
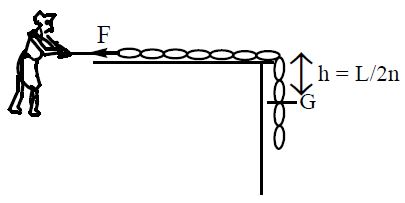
Where ‘h’ is the height gained by C.G. of hanging chain with respect to the edge of table.
Case-11
A uniform chain of mass ‘m’ and length ‘L’rests on a smooth horizontal table with part of its length is hanging from the edge of the table. Work done in pulling the chain partially, such that part is hanging from the edge of the table is given by
Case-12
A body of mass ‘m’ is on a smooth inclined plane of inclination ‘θ’ to horizontal. If ‘l‘ is the length of incline,
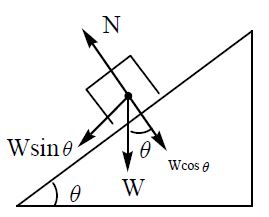
Work done by gravitational force in pulling the block down from top to bottom of the incline is
Here Work done by normal reaction is zero
Case-13
A body of mass ‘m’ is sliding down a rough inclined plane of inclination θ to horizontal. If ‘l‘ is the length of incline and is the coefficient of kinetic friction
Work done by gravitational force in pulling the block down to the incline is Wg = mg sin θl .
Work done by frictional force is
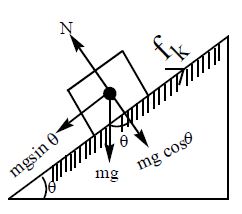
∴ Net work done by the resultant force on the body,
Case-14
Work done in compressing a gas in a cylinder, by a piston
Consider a gas at a pressure ‘P’ enclosed in a piston–cylinder arrangement
The force exerted by the gas in the cylinder on the piston of area ‘A’ is F = PA
The work done by the gas in producing a small displacement ‘dy’ of the piston is, dW = F dy
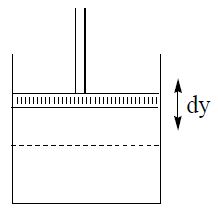
= PA dy
= P dV.
(where dV=change in volume of the gas)
Total work done by the gas during the change in its volume from
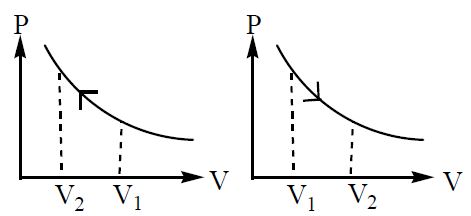
During compression ‘W’ is negative
During expansion ‘W’ is positive
Note: If ‘P’ is constant then
3. ENERGY
“Energy of a body is its capacity to do work”
Greater the amount of energy possessed by the body, greater the work it will be able to do. All the agents which are able to do work are said to be energetic.
i) A bullet fired into a wall is able to penetrate into the wall by doing work against friction due to its energy.
ii) Fast blowing wind is able to turn a wheel.
iii) A moving vehicle possess energy since it does work against friction and air resistance before coming to rest after the engine is switched off.
iv) Water stored in a dam has energy since it can run the turbines when the water flows down onto the turbines.
The different forms of energy are mechanical energy, light energy, heat energy, sound energy. electrical energy, nuclear energy etc.
In mechanics, we divide mechanical energy into two types, namely (1) Kinetic Energy (2) Potential Energy.
The dimensional formula for energy is ML2T-2 same as that of work.
SI unit of energy is joule (J)
C.G.S unit is erg.
1J = 107 erg.
Note: The other units of energy are:
Note: Many students think that KWH is the unit of power. But it is the unit of energy. Usually electrical energy is measured in KWH.
4. KINETIC ENERGY
Kinetic energy is the energy possessed by a body by virtue of its motion.
It is measured by the amount of work that the body can do against an opposing force acting on it before coming to rest.
Examples for bodies having Kinetic Energy :
(1) A vehicle in motion.
(2) Water flowing along a river.
(3) A bullet fired from a gun.
(4) A satellite going around the earth.
Expression for kinetic energy : Consider a body of mass ‘m’ is moving with a velocity ‘v’. A uniform force opposes its motion to bring the body to rest in a displacement S.The uniform retardation of the body due to the force is ‘a’ which is obtained by the kinematic equation.
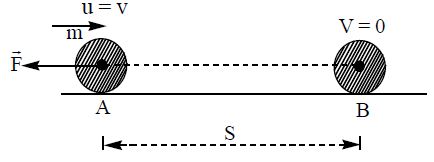
Here initial velocity = v, final velocity,V=0
,
The opposing force on the body is
.
From Newton’s third law of motion. Force applied by the body =
As the body moves against the applied force, its displacement is along the force applied by the body hence work done by the body against the opposing force acting on it is
∴ Kinetic energy of the body .
5. POTENTIAL ENERGY
Potential energy of a body is the energy possessed by a body by virtue of its position or configuration
* It is measured by the work that the body can do in position or configuration.
* Potential energy is defined only for conservative forces.
It does not exist for non – conservative forces.
* In case of conservative forces
Where dU is the change in potential energy.
Expression for gravitational potential energy
Consider a body of mass ‘m’ is on the ground. It is lifted vertically upwards through a height ‘h’. Considering the height to be very small compared to the radius of the earth (R) i.e., h<<R, we can neglect the variation of g. The gravitational force ‘mg’ on the body can be taken to be constant. The work done by the external agency against gravitational force is
W = Fs = mgh.
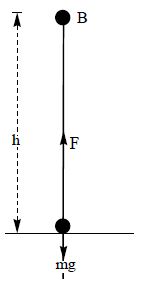
This work gets stored as potential energy of the body. Potential energy of the body
The above expression actually represents the increase in the stored energy from the reference position (earth surface) to the final position at a height ‘h’.
Note
1). By definition the negative of the work done by gravitational force is defined as the change in potential energy of the body.
2). Work done, potential energy and kinetic energy depend on frame of reference selected to observe the motion of the body.
6. SPRING FORCE
Spring force is an example of a variable force which is conservative. The figure shows one end of a massless spring attached to a rigid vertical support and the other end to a block of mass ‘m’ which can move on a smooth horizontal surface. Let X = 0, denote the position of block when the spring is at its natural length. In an ideal spring, the spring force Fs is directly proportional to ‘x’ where ‘x’ is the displacement of the block from equilibrium
position. (i.e. X = 0). This force law for the spring is called Hooke’s law and is mathematically expressed as Fs = –Kx.
The constant ‘K’ is called the spring constant. Its S.I unit Nm-1, and is a measure of the stiffness of the spring.
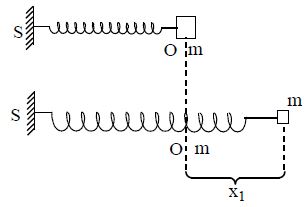
To calculate the work done on the block by the spring force as the block moves from undeformed position X = 0 to X = x1
* The work done by the spring force is always negative.
* If the block moves from, the work done by spring force is
* Similar is the result of the work done by spring force when it is compressed through ‘x’ from its natural length.
Potential energy stored in a spring
We define the change in potential energy of a system corresponding to a conservative internal force as
∴ dU = -(work done by the spring force)
Since we take Ui as zero when spring is at its natural length
Points to remember regarding potential energy
1. Potential energy can be positive or negative or zero.
2. A moving body may or may not have potential energy
3. Potential energy should be considered to be a property of the entire system , rather than kinetic it to any specific particle.
* If potential energy of the system is negative then the particles are bounded to the system.
* If potential energy of the system is positive the particles are not bounded to the system.
For example, in hydrogen atom, when electron is revolving round the nucleus potential energy of the atom is negative. i.e., electron is bounded to the nucleus of the atom.
When an electron is taken from K–shell to L–shell its potential energy increases.
4. The absolute value of potential energy has no physical significance.
Relation between Kinetic Energy and Linear Momentum
When a body of mass m moves with a velocity ‘v’ its kinetic energy is
This is the relation between kinetic energy and linear momentum
When a bullet is fired from a gun the momenta of the bullet and gun are equal and opposite. It can be seen from the above expression that the ratio of the kinetic energies of two bodies having the same magnitude of momenta is in the inverse ratio of their masses i.e.,
Hence, the kinetic energy of the bullet is greater than that of the gun.
Points to remember regarding Kinetic energy
1. As mass ‘m’ and v2 are always positive, kinetic energy is always a positive scalar
2. The kinetic energy depends on frame of reference . The kinetic energy of a person of mass ‘m’ sitting in a train moving with speed ‘v’ is zero in the frame of train but 1/2mv2 in the frame of earth
3. The relation kinetic energy K = p2/2m shows that a body cannot have kinetic energy without having momentum and vice versa.
7. WORK – ENERGY THEOREM
Statement : “The work done on a particle by the net force is equal to the change in its kinetic energy”.
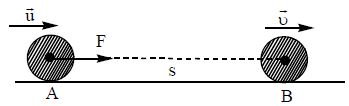
Proof : Consider a particle of mass ‘m’ is moving with an initial velocity ‘u’. When it is under the action of a constant net force F, let it gain uniform acceleration ‘a’. Its velocity becomes ‘v’ after a displacement S. Work done by the net force
W = FS = maS (∴ F = ma)
where Kf and Ki are the final and initial kinetic energies of the particle. Kf – Ki is the change in kinetic energy of the particle
Hence, the theorem is proved.
Note
1) The theorem is applicable not only for a single particle but also for a system. When it is applied to a system of two or more particles, change in the kinetic energy of the system is equal to work done on the system by the external as well as the internal forces.
2) Work-energy theorem can also be applied to a system under the action of variable forces, conservative as well as non conservative forces.
Special cases in work energy theorem
1. A particle of mass ‘m’ is thrown vertically up with a speed ‘u’. Neglecting the air friction , the work done by gravitational force, as particle reaches maximum height is
2. A particle of mass ‘m’ falls freely from a height ‘h’ in air medium onto the ground. If ‘V’ is the velocity with which it reaches the ground , the work done by air friction is Wf and work done by gravitational force Wg = mgh
3. A block of mass ‘m’ slides down a frictionless smooth incline of inclination ‘θ’ to the horizontal . If ‘h’ is the height of incline , the velocity with which the body reaches the bottom of incline is
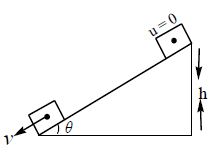
4. A body of mass ‘m’ starts from rest from the top of a rough inclined plane of inclination ‘ θ’ and length ‘l‘ . The velocity ‘v’ with which it reaches the bottom of incline if is the coefficient of kinetic friction is
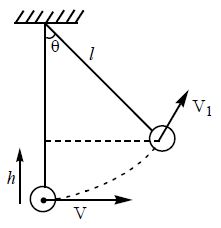
5. Bob of pendulum of length ‘l‘ is projectile horizontally with a speed ‘u’ at its lowest position then the speed of the bob when it makes an angle θ with the lower vertical is thus
6. A block of mass ‘m’ attached to a spring of spring constant ‘k’ oscillates on a smooth horizontal table . The other end of the spring is fixed to a wall . It has a speed ‘V’ when the spring is at natural length . The distance it moves on table before it comes to instantaneous rest is
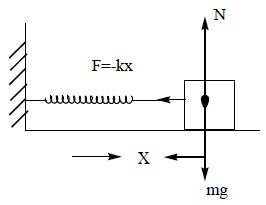
Let the mass be oscillating with amplitude x on compressing the spring.
since no work is done by gravity and normal reaction (N)
7. A bullet of mass ‘m’ moving with velocity ‘v’ stops in a wooden block after penetrating through a distance x . If ‘F’ is the resistance offered by the block to the bullet
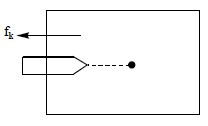
8. A pile driver of mass ‘m’ is dropped from a height ‘h’ above the ground. On reaching the ground it pierces through a distance ‘s’ and then stops finally. If ‘R’ is the resistance offered by ground, then
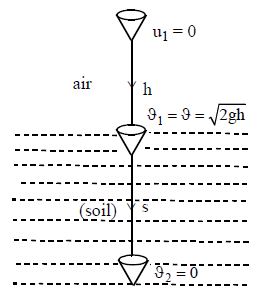
or
Here time of penetration is given by impulse equation
or
9. A bullet of mass ‘m’ is fired horizontally with a velocity ‘V’ which strikes a wooden block of mass ‘M’ suspended vertically . If the bullet is embedded in the block , the height ‘h’ to which the system would rise is By the principle of conservation of linear momentum mv = (M+m)V1 or V1 = mv/M+m
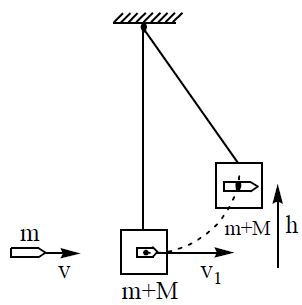
where V1 is the common velocity of bullet + block system
By work energy theorem
10. A body of mass ‘m’ is initially at rest. By the application of a constant force, its velocity changes to in time . The kinetic energy of the body at any time ‘t’ is
since
8. POWER
The time rate of doing work is called power.
If ‘W’ is the total work done by a force in a timeinterval ‘t’, then the average power is
Instantaneous power is the dot product of force and velocity of body, provided the force does not change with time. The instantaneous power is.
Where ‘v’ is the instantaneous velocity
Note If the work done is constant then .
Relation between average power and instantaneous power
A particle starts from rest and moving with uniform acceleretion and gains a velocity ‘V’ in time ‘t’
we know instantaneous power is
From the above it can be concluded that
Dimensions and units of Power
(a) Power is a scalar quantity with dimensions [ML2T-3].
(b) S.I unit of power is J/sec (or) watt (w).
CGS unit of power is erg/sec.
(c) Practical unit of power is horse power(hp)
1hp = 746W.
Watt : The power of an agent is said to be one watt, if one joule of work is done in one second.
(d) The slope of W-t curve gives instantaneous power.
(as shown in fig.(a))
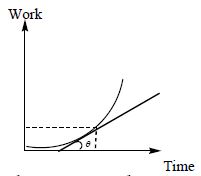
(e) The area under P-t graph gives Work done as
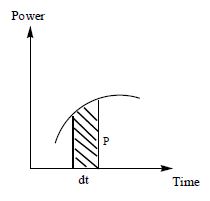
Efficiency of Crane or Motor
The ratio of output power to the input power is called efficiency.
Total input power
Applications to power
1) if a machine gun fires ‘n’ bullets per second such that mass of each bullet is ‘m’ and comming out with a velocity ‘v’ then the power of the machine gun is
(where N bullets are fired in time ‘t’ then n = N/t)
2) A conveyor belt moves horizontally with a constant speed ‘v’ Gravel is falling on it at a rate of ‘dm/dt’ then,
a) Extra force required to drive the belt is
b) Extra power required to drive the belt is
3) A car of mass ‘m’ is moving on a horizontal road with constant acceleration ‘a’. If R is the resistanceoffered to its motion, then the instantaneous power of the engine when its velocity is ‘v’
Net force on the car is F – R = ma
driving force of the engine is F = R + ma
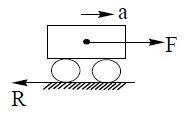
Instantaneous power P = F. V
4) The car moves on a rough horizontal road with a constant speed ‘V’ then the instantaneous power of engine is
P = F.V (V constant)
But F = f
P = fV (Here f = frictional force on rough horizontal surface) V
5) A body of mass ‘m’ is initially at rest. By the application of constant force its velocity changes to “” in time ‘ ‘ then
v = u + at
acceleration of the body is
a) Find instantaneous power at an instant of time ‘t’ is
P = F.V = (ma) (at) = m a2 t
b) Average power during the time ‘t’ is
6) A motor pump is used to deliver water at a certain rate from a given pipe. To obtain ‘n’ times water from the same pipe in the same time by what amount (a) force and (b) power of the motor should be increased.
If a liquid of density ‘ρ’ is flowing through a pipe of cross section ‘A’ at speed ‘V ‘, the mass coming out per second will be
To set ‘n’ times water in the same time
As the pipe and liquid are same
a) Now as F =
b) and as P = F.V
To get ‘n’ time of water. force must be increased n2 times while power n3 times
Position and velocity of an automobile w.r.t.time
An automobile of mass ‘m’ accelerates, starting from rest, while the engine supplies constant power, its position and velocity changes w.r.t time is
a) Velocity : As FV = P = constant
i.e
or
on integrating both sides, we get
As initially the body in at rest i. e
b) Position : From the above expression
i:e
By integrating both sides we get
Now as at t =0, s = 0
9. CONSERVATIVE AND NON–CONSERVATIVE FORCES
a. Conservative force
* If work done by the force around a closed path is zero and it is independent of the path, such a force is called conservative force.
* Work done by the conservative force is stored in the form of potential energy.
Example : Gravitational force, electrostatic force, and spring force
Under conservative force
Example-1 : In the absence of air resistance, a body is projected vertically up then work done by the gravitational force in moving the body through a height ‘h’ is Wg = –mgh and in return journey the work done by the gravitational force is Wg = + mgh, on reaching the ground the net work done by the gravitational force in a round trip is zero.
Example -2 : In the absence of air resistance, when a body of mass ‘m’ is projected vertically up with a velocity ‘u’, then it reaches the ground with a velocity ‘–u’. The work done by the gravitational force in a round trip is zero.
i.e
Example -3 : A body of mass ‘m’ lifted to a height ‘h’ from the ground level in different paths in between the points A & B as shown the figure. The work done by the gravitational force in all paths is same i.e., W1 = W2 = W3 = mgh. So work done by the conservative force depends on initial and final points, but not on the path followed by the body.
Non – conservative force
* If work done by the force around a closed path is not equal to zero and it is dependent on the path, such a force is called non – conservative force
Ex : Frictional force, viscous force
* Work done by the non conservative force will not be stored in the form of potential energy.
Example-1 : In the presence of air resistance, when a body is projected up then it reaches a maximum height ‘h’. Work done by the air friction in upward journey is –fh and in return journey is also, it is –fh. On reaching the ground net work done by the air friction is negative. so work done by the air friction in a round trip is non – zero.
Example-2 : A block mass ‘m’ is dragged on a rough horizontal surface through distance ‘s’ from the point ‘p’ to point ‘q’ and then back to the point ‘p’. Work done by the frictional force from p to q is negative and from q to p is negative. So the work done by the frictional force around a closed path is negative not equal to zero.
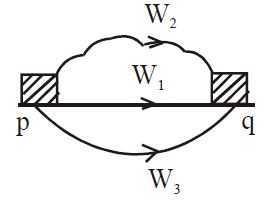
Example-3 : In the above case instead of moving the block from p to q along a straight line, if it follow different paths, the work done by the friction is still negative but its magnitude is different in different paths. So work done by the frictional force is dependent on the path.
10. LAW OF CONSERVATION OF ENERGY
“The total mechanical energy of a system is constant if the internal forces are conservative and external forces do no work”
Mechanical energy (E) = PE + KE
E = U + K = constant
Under only conservative forces mechanical energy of system is constant.
i.e.,
K + U = constant
Mechanical energy E = constant ΔE = 0
i.e., if kinetic energy of the body increases its potential energy will decrease by an equal amount and vice versa
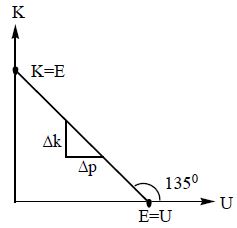
K + U = const.(c); K = –U + C; y = mx + c
hence slope m =
∴ gain in KE = loss in PE
Note
Under external and non – conservative forces mechanical energy of system is not conserved.
According to work energy theorem, work done by all forces external, and internal
(conservative and non – conservative) forces acting on the body is equal to change in kinetic energy.
We know work done by conservative force is equal to negative of change in potential energy
For example, some non–conservative force like friction is also acting on the particle, the total mechanical energy is no more constant, it changes by the amount of work done by the frictional force, i.e,
Where Wf is the work done against friction. The lost energy is transformed into heat
the heat energy developed is exactly equal to mechanical energy dissipated. We can therefore, write
where Q is heat produced.
Law of Conservation of Energy in case of Freely Falling Body
A body of mass ‘m’ is at a height ‘h’ from the ground. As the body falls freely under gravity its potential energy decreases and kinetic energy increases
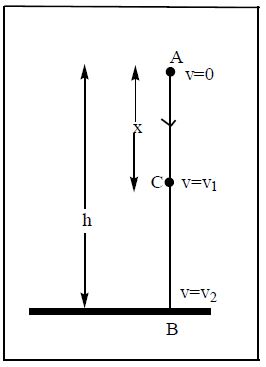
At point A: The highest point
P.E. of the body = mgh
Velocity of the body, ‘v’=0
∴ K.E. of the body
Total energy at A = P.E.+ K.E.
= mgh + 0 = mgh ________ (1)
At point C : As the body falls freely consider any point ‘C’ in its path where AC = x.
P.E. of the body = mg (h-x) = mgh – mgx
Let v1 be the velocity of the body at ‘C’.
Initial velocity u = 0 (at A)
Velocity at C = v = v1 (Say)
Acceleration a = g
Distance travelled = s = x
Using the formula
K.E. of the body at
Total energy at C = P.E.+K.E.
= mgh – mgx + mgx = mgh __ (2)
At point B : The body touches the ground at ‘B’ with a velocity ‘v2’.
P.E. at B = mg x 0 = 0
Again u=0; v=v2; a=g and s = h
∴ K E at B
At ‘B’ the total energy of the body =
P.E. + K.E.=0+mgh = mgh _______ (3)
Thus at any point on the path of a freely falling body the total energy is ‘mgh’.
Thus the law of conservation of energy is verified.
Law of Conservation of Energy in case of Vertically Projected Body
Consider a body of mass ‘m’ is projected vertically upwards from the ground with velocity ‘u’ so that it reaches a maximum height ‘h’ from the ground. As the body moves up against gravity its potential energy increases and kinetic energy decreases
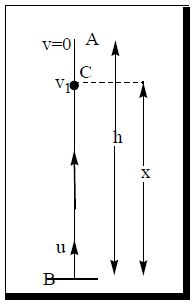
At ground B, as the height of the body is zero, the P.E. of the body = mgx 0 = 0
The K.E. of the body =
∴ T.E=P.E.+K.E =
At point C : During its motion, consider a point C where the velocity of the body is v1.
Let BC = x
At C, the P.E. of the body = mgx
But
The K.E. of the body
∴ The T.E. of the body = P.E. +K.E. =
………(2)
At point A : When the body reaches the maximum heigh ‘h’ above the ground, its final velocity becomes zero.
In the equation, v2 – u2 = 2as. v = 0, u = u, a =–g and s = h.
Then
∴ The P.E. of the body = ………(4)
Thus the total energy at all points A, B and C remains constant and equal to .
Hence the law of conservation of energy is verified in the case of a body projected vertically upwards.
COLLISIONS
11. INTRODUCTION
The strong physical interaction among bodies involving exchange of momenta in small interval of time, is called a collision.
In collision particles may or may not come in real physical contact.
Example.1 : In a collision between two billiard balls there is physical contact.
Example.2 : In the collision of α – particle with nucleus, due to electromagnetic interaction, α – Particle is scattered away without any physical contact.

In a collision, before and after the impact, interaction forces between the colliding particles becomes effectively zero, while during impact, the interaction forces are very large. In a collision the effect of external forces such as gravity or friction are not taken into account as due to small duration of collision, average impulsive force responsible for the collision is much larger than external forces acting on the system.
In case of collision, as the impulsive force acting during collision is internal, total momentum of the system always remains conserved, i.e.
In a collision, “total energy” is always conserved.
12. CLASSIFICATION OF COLLISIONS ON THE BASIS OF DIRECTION OF MOTION OF
COLLIDING BODIES
On the basis of direction of motion of colliding bodies, collisions are classified into two types.
a) Head on (or) one dimensional (or) direct collision
b) Oblique collision.
a) Head on (or) one dimensional (or) direct Collision
In a collision, if the motion of colliding particles before and after the collision are along the same straight line, then the collision is said to be head on (or) one dimensional (or) direct collision.
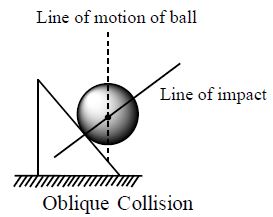
b) Oblique Collision
In a collision, if the motion of colliding particles before and after the collision are not along the initial line of motion, then the collision is said to be oblique collision. In an oblique collision, if the particles before and after the collision are in the same plane, then the collision is called two dimensional otherwise, the collision is called three dimensional.
13. TYPES OF COLLISIONS ON THE BASIS OF LAW OF CONSERVATION OF KINETIC ENERGY
On the basis of conservation of total kinetic energy of colliding particles, collisions are classified into two types.
a) Elastic collisions and
b) Inelastic collisions.
a) Perfectly elastic Collisions
The collisions, in which both momentum and kinetic energy remain constant or unchanged are known as elastic collisions. In this type of collision, the colliding particles regain their shape and size completely after collision i.e. no fraction of mechanical energy is stored as deformation potential energy in the bodies.
Examples of perfectly elastic collisions are
i) Collision between atomic particles
ii) Collision of α -particle with nucleus.
b) Inelastic (or semi elastic) Collisions
The collisions, in which kinetic energy is not conserved but law of conservation of momentum holds good are known as inelastic collisions. However, total energy is conserved in this type of collisions. In an inelastic collision, the colliding particles do not regain their shape and size completely after collision. Some fraction of mechanical energy is retained by the colliding particles in the form of deformation potential energy.
Examples of inelastic collisions are
i) Collision between two billiard balls.
ii) Collision between two automobiles on a road.
(c) Perfectly Inelastic (or plastic) Collision
If in a collision, the two colliding bodies stick together and move with a common velocity, then the collision is called perfectly inelastic collision. In perfectly inelastic collision linear momentum is conserved, kinetic energy is not conserved. But total energy is conserved.
Examples of perfectly inelastic collision are
i) Collision between bullet and block of wood into which it is fired, when the bullet remains embedded in the block.
14. LINE OF IMPACT
The line passing through the common normal to the surfaces in contact during impact is called line of impact.
The force during collision acts along this line on both bodies. Direction of Line of impact can be determined by
a) Geometry of colliding objects like spheres, discs, wedge etc.
b) Direction of change of momentum.
If one particle is stationary before the collision then the line of impact will be along its motion after collision.
Examples of line of impact
1) Two balls A and B are approaching each other such that their centres are moving along line CD.
2) Two balls A and B are approaching each other such that their centres are moving along dotted lines as shown in figure.
3) Ball is falling on a stationary wedge.
15. ELASTIC COLLISION IN ONE DIMENSION (OR) PERFECTLY ELASTIC HEAD-ON COLLISION
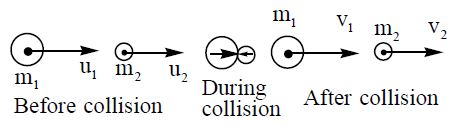
Let us consider an elastic one-dimensional (head on) collision between two particles of masses m1 and m2. Suppose u1, u2 and v1, v2 be their velocities before and after the collision respectively along the same straight line as shown in figure.
Applying the law of conservation of linear momentum, we have
Momentum of the system before collision = Momentum of the system after collision
or ………(1)
According to law of conservation of kinetic energy, we have
or ………(2)
Dividing eq. (2) by eq. (1), we get
or
or
or ………..(3)
Thus in head – on and elastic collision, the relative velocity of approach before collision is equal to the relative velocity of separation after collision.
From eq. (3),
Substituting this value of in eq.(1), we get
or
or
∴ …….(4)
Further from eq. (3),
Substituting this value of in eq. (1), we get
or
or
or
∴ …….(5)
Special cases : Here we consider the following special cases :
1) When, then from eq. (4) and (5)
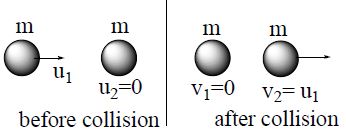
Hence in case of head – on elastic collision of two bodies of equal masses, the bodies simply exchange their velocities after collision.
2) When u2 = 0, i.e., the second body is at rest, we have
Now, in this case we consider the following conditions :
a) If , then
In this case, the colliding particle comes to rest and the other particle (initially at rest) moves with the original velocity u1of the colliding particle.
b) If , then
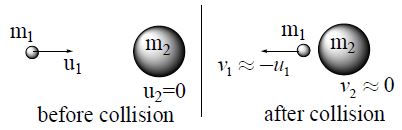
Thus when a lighter particle undergoes head – on elastic collision with a much heavier particle at rest, then the lighter particle rebounds with the same velocity while the heavier particle remains approximately at rest.
c) If , then
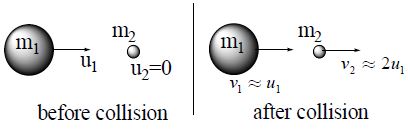
Thus, when a heavy particle collides head – on and elastically with a much lighter particle at rest, the velocity of the heavy particle remains practically unchanged but the lighter particle moves with double the velocity of the heavier particle.
Application.1 : A body of mass m1 moves with kinetic energy K undergoes head on elastic collision with another body of mass m2 at rest :
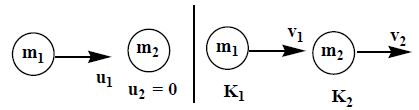
v1 = velocity of m1 after collision.
v2 = velocity of m2 after collision
P1 & K1 = Momentum and kinetic energy of m1 after collision
P2 & K2 = Momentum and kinetic energy of m2 after collision
i)
ii) KE of m1 after collision.
∴ Fraction of KE retained by m1 is
iii) KE of m2 after collision,
∴ Fraction of KE transferred by m1 to m2 is
iv) Fraction of momentum retained by m1
=
v) Fraction of momentum transferred by m1 to m2
=
Note.: Transfer of K.E. or momentum in a head – on elastic collision is maximum (100%) when m1 = m2 and m2 is initially at rest.
16. COEFFICIENT OF RESTITUTION (e)
Let u1 and u2 be the velocities of the bodies respectively before collision and v1 and v2 are their final velocities after collision and acting along same line in the same direction.
Then the coefficient of restitution (e) is defined as the ratio of the relative velocity of separation (v2 – v1) after the collision to the relative velocity of approach (u1 – u2) before collision.
Note. :
u1, u2 are the components of the velocities of m1 and m2 before collision along the line of impact and v1, v2 are the components of the velocities of m1 and m2 after collision along the line of impact.
i) The value of coefficient of restitution (e) is independent of the masses and velocities of the colliding bodies. It depends only on the nature of their materials.
ii) e has no units and no dimensions.
iii) For a perfectly elastic collision, e = 1
For a perfectly inelastic collision, e = 0
For other collisions, e lies between 0 and 1
iv) Coefficient of restitution is termed as degree of elasticity
a. Determination of coefficient of restitution
To find the coefficient of restitution between two bodies of different materials, take one of them in the form of a very heavy plate and the other body in the form of a small sphere.
The small sphere is dropped on to the plate from a height ‘H1’. It hits the plate with a velocity ‘u1’. Let the sphere rebounds to a height ‘H2’ after collision with the plate. Assuming the velocity of the plate before and after collision to be zero since the plate is very heavy.

But
when the ball rebounds with a velocity v1 it reaches a height H2, so that
v1 is in opposite direction to u1.
Thus ‘e’ is a number and has no units and is dimensionless.
Note : If a body falls from a height H1 and strikes the level ground with velocity of magnitude ‘V1‘ in a time ‘t1‘ seconds and rebounds with velocity of magnitude V2 upto a height H2 in a time t2 seconds.
Then the coefficient of restitution is given by
For a perfectly elastic collision, H2 = H1
For a perfectly inelastic collision, H2 = 0
For other collisions, H2 < H1
For any collision, H2 cannot be greater than H1
b. Equation for the height attained by a freely falling body after number of rebounds on the floor
A ball is dropped from a height H0 . The ball strikes the ground and it rebounds to a height H1. It again falls from that height and rebounds to a height H2 and so on.

The velocity with which it strikes the ground is
Let the ball rebounds to a height H1
Similarly after 2nd rebounce the ball rises to a height H2 which is given by
Similarly, 3rd rebounding height is given by
The height to which the body rebounds after the nth rebounce is given by
Application.2 : Total distance travelled by the ball before it stops bouncing:
Application.3 : Total time taken by the ball to stop bouncing:
Application.4 : Average speed of the ball during its entire journey is given by
=
Application.5: Average velocity of the ball during its entire journey is given by
=
Application.6: Magnitude of the velocity with which it rebounds from the ground after nth collision.
If V is the magnitude of velocity with which the ball hits the ground, then the magnitude of velocity with which it rebounds after first collision from the ground is V1.
As
The magnitude of the velocity with which the ball rebounds from the ground after second collision is
Similarly the magnitude of the velocity with which the ball rebounds from the ground after nth collision is
17. INELASTIC HEAD ON COLLISION
Consider two bodies of masses m1 and m2 moving along a straight line with velocities . They collide and as a result of this collision, their velocities change to v1 and v2 respectively, as shown in figure.
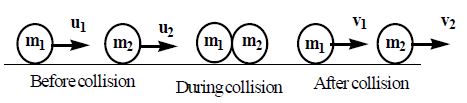
Applying law of conservation of momentum, we have ……(1)
From the definition of coefficient of restitution, we have
(or)
……(2)
(or) ……(3)
Substituting v2 and v1 from (2) and (3) in (1) and on simplification we have,
Note : If , then
and
Note : Loss in kinetic energy of the system in inelastic collision is
18. PERFECTLY INELASTIC HEAD ON COLLISION
Consider two bodies of masses m1 and m2 moving with velocities u1 and u2 ( u1 > u2 ) along a straight line undergo perfect inelastic collision. Let they move with a common velocity ‘v’ after the collision as shown in figure.
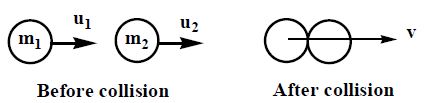
Applying law of conservation of linear momentum,
we have
∴ Common velocity,
Initial total K.E of the system =
Final total K.E of the system =
Loss of K.E (Δ K.E) of the system = Initial total K.E – Final total K.E
The ratio of loss of energy of the system and its initial energy, if u2 is zero, is given by
∴ Fractional loss in K.E of the system is given by
The ratio of final energy to initial energy of the system, if u2 is zero, is given by
Note: In the above case, if the two bodies move in opposite directions before collision, then Loss in KE of the system is given by
Note: If the two bodies undergoing plastic collision are not moving in the same direction before they collide, then the common velocity of the compound body after collision is given by
19. BALLISTIC PENDULUM
It is an arrangement used to determine the velocities of bullets. A log of wood of mass ‘M’ is suspended by a string of length ‘l’ as shown in the figure. A bullet of mass ‘m’ is fired horizontally into the wooden block with a velocity ‘u’.
Case I : Let the bullet gets embedded in the block and the system rises to a height ‘h’ as shown in the figure.
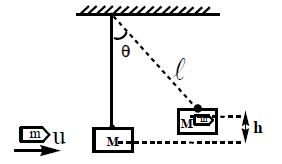
Applying law of conservation of linear momentum, we have
i.e.,
∴ Common velocity,
K.E of the system after collision is given by
P.E at highest point = (m + M) gh
K.E. at lowest point = P.E at highest point
i.e.,
i.e.,
∴ Velocity of the bullet,
Loss of K.E of the system =
Case II : If the bullet emerges out of the block with velocity ‘v’ then
mu = mv + MV where
20. OBLIQUE COLLISION
Oblique collision is the collision in which relative velocity of approach of the colliding bodies is not along the line of impact.
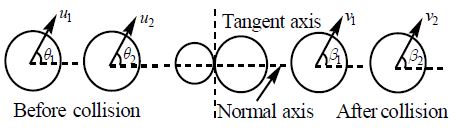
Procedure for solving the problems
Draw tangential- axis and normal – axis at the point of impact.
Apply the law of conservation of the momentum of the system, along and perpendicular to the line of impact, i.e., along normal – axis and tangential – axis. We obtain.
and ….. (1)
If the colliding bodies are smooth, no force is acting on m1 and m2 along the tangent ; the momentum of m1 and m2 remains conserved along tangential – axis
i.e., ……….. (2)
and ……….. (3)
Coefficient of restitution is defined along line of impact only.
……….. (4)
Now we have four equations and four unknowns . Solving four equations for the four unknowns, we obtain
Similarly we can find
SOLVED EXAMPLES
1. Find the work done in liftin g a stone of mass 10 kg and specific gravity 3 from the bed of a lake to a height of 6 m in water.
Sol. Weight in air = 10 kg.wt
Specific gravity =
2. Two identical cylindrical vessels with their bases at the same level, contain a liquid of density ρ . The height of the liquid in one vessel is h1 and that in the other is h2. The area of either base is A. What is the work done by gravity in equalising the levels when the vessels are connected ?
Sol. As the total volume of water is constant, the height ‘h’ in each vessel after inter–connection will be given by:
The level in the left vessel shown in the figure, drops from A to C and that in the right vessel rises from B to D.
The mass of water descended is
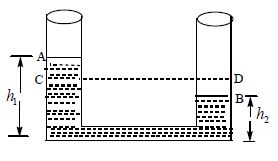
The height descended by this water is
So work done by the force of gravity in equalising the level
3. Consider “n” number of identical cubes each of mass “m” and side “a” lying on a level ground. Find the work done in piling them one above the other.
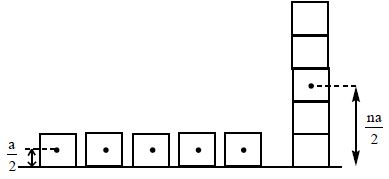
Sol. The initial total potential energy of all the blocks lying on the ground is
The potential energy, when the blocks are piled to form a single column is
∴ Work done in arranging the blocks one above the other is
or
4. A spring of force constant ‘k’ is stretched by a small length ‘x’. Find the work done in stretching it further by a small length ‘y’.
Sol. Let W1 is the work done in stretching a spring of force constant ‘K’ through a length “x”. Then
Let “W2” is the work done in stretching the spring through a length (x+y). Then
∴ Additional work done, to increase the elongation by “y” is
∴
5. The momentum of a body is doubled. By what percentage does its kinetic energy increase?
Sol.
Let
% increase in kinetic energy =
6. A 2kg block is connected with two springs of force constants K1 = 100 N/m and K2 = 300 N/m as shown in figure. The block is released from rest with the springs unstretched. Find the acceleration of the block in its lowest position (g = 10 m/s2)
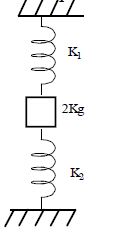
Sol. Let ‘x’ be the maximum displacement of block downwards. Then from conservation of mechanical energy : decrease in potential energy of 2 kg block = increase in elastic potential energy of both the springs
or
Acceleration of block in this position is
(upwards)
upwards
7. A particle of mass ‘m’ is moving in a horizontal circle of radius r, under a centripetal force equal to -(K/r2), where K is constant. What is the total energy of the particle ?
Sol. As the particle is moving in a circle
[ for circular motion ]
———- (1)
Now as ,
——— (2)
So Total energy E = U +K
8. Under the action of force, 2kg body moves such that its position x as a function of time t is given by , x is in metre and t in second. Calculate the work done by the force in the first 2 second.
Sol. From work-energy theorem, W = ΔKE
∴ velocity
At t = 0,
At t = 2,
work done
9. A lorry and a car moving with the same kinetic energy are brought to rest by the application of brakes, which provide equal retarding forces. Which of them will come to rest in shorter time? Which will come to rest in less distance?
Sol. a) Initial kinetic energy of each vehicle is K and when they come to rest their final kinetic energy is zero. The change in kinetic energy of both the car and lorry is K. By work–energy theorem
FS = change in kinetic energy
where F is the retarding force. As K and F are same for both the vehicles, they come to rest after travelling the same distance.
b) To find the time in which each vehicle comes to rest, we have to consider the momentum,
since . The initial momentum of the car is less than that of the lorry as K is same for both but mass of the car is less than that of the lorry. Final momentum is zero for both the vehicles. So, change in momentum is less for the car. By Newton’s second law,
Since ‘F’ is same,
As car has smaller momentum, the car comes to rest earlier.
10. An electric pump on the ground floor of a building taken 15 minutes to fill a tank of volume 30m3 with water. If the tank is 40m above the ground and the efficiency of the pump is 30%, find the electric power consumed by the pump in filling the tank. [density of water = 103 kg/m3
Sol. mass of the water to be filled =
(volume of the tank) × density of water m =
h = 40m, t=15 × 60 =900sec.
Efficiency = 30%
Input power
= 43.56KW
11. A machine gun fires 240 bullets per minute with certain velocity . If the mass of each bullet is 10-2 kg and the power of the gun is 7.2 kW, find the velocity with which each bullet is fired.
Sol. Mass of each bullet m = 10-2 kg
Power = 7.2 kW =
bullets / min = bullets / sec.
Power =
=
v = 600 m/s
12. A ball of mass 50 g falls from rest vertically downwards through a distance of 40 m and hits the ground. Find the kinetic energy and final velocity of the ball before it hits the ground (g = 9.8ms-2).
Sol. m = 50 gm = 50 ⨯ 10-3 kg ,
h = 40 m; g = 9.8 ms-2
From law of conservation of energy
loss in P.E = gain in K.E.
Final velocity,
13. Two blocks are connected by a string as shown in figure . They are released from rest. Show that after they moved a distance L, their common speed is given by.
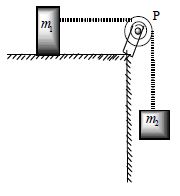
where is the coefficient of friction
Solution : In moving a distance L by m1 and m2 the PE will be lost by m2 only and will be m2gL, while work done by friction will be only on m1 and will be m1gL. Now as the string is inextensible and so, the gain in KE will be = (1/2) (m1+m2) v2. By conservation of energy.
Loss in PE = Gain in KE + WD against friction
i.e,.
14. A uniform chain of length ‘L’ and mass ‘m’ is on a smooth horizontal table, with th part of its length hanging from the edge of the table. Find the kinetic energy of the chain as it completely slips off the table.
Sol. With respect to the top of the table, the initial potential energy of the chain,
U1 = PE of the chain lying on the table + PE of the hanging part of the chain
=
P.E of the chain, when it just slips off the table,
From law of conservation of energy
If ‘V’ is the velocity of the chain, then,
∴
If ‘l‘ is the initial length of the hanging part, then
or and
15. A block of mass m hangs on a vertical spring. Initially the spring is unstretched, it is now allowed to fall from rest. Find (a) the distance the block falls if the block is released slowly; (b) the maximum distance the block falls before it begins to move up.
Sol. a) When the block falls slowly, it comes to rest at a distance , which is referred to as the equilibrium position.
From, condition of equilibrium,
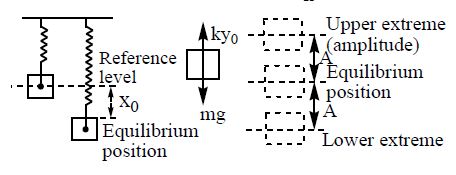
b) When the block is released suddenly, it oscillates about the equilibrium position. Initially the speed of the block increases then reaches maximum value and then decreases to zero at the lowest position. In this situation the block oscillates about the equilibrium position. The block is released from rest, therefore its total mechanical energy initially,
= 0 + 0 + 0
Final total mechanical energy,
From conservation of energy
16. Two bodies of masses m1 and m2 are moving with velocities 1 ms-1 and 3ms-1 respectively in opposite directions.
If the bodies undergo one dimensional elastic collision, the body of mass m1 comes to rest. Find the ratio of m1 and m2.
Sol.
17. A body ‘A’ with a momentum ‘P’ collides with another identical stationery body ‘B’ one dimensionally. During the collision, ‘B’ gives an impulse ‘J’ to the body ‘A’ . Then the coefficient of restitution is
Sol. According to law of conservation of linear momentum,
i.e.,
∴ Coefficient of restitution,
18. A bullet of mass m moving with velocity u passes through a wooden block of mass M = nm as shown in figure.
The block is resting on a smooth horizontal floor. After passing through the block, velocity of the bullet becomes v . Its velocity relative to the block is
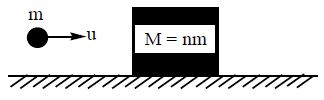
Sol. Let v’ be the velocity of block. Then from conservation of linear momentum.
velocity of bullet relative to block will be
19. A bullet of mass 2g travelling with a velocity of 500 ms-1 is fired into a block of wood of mass 1kg suspended from a string of 1 m length. If the bullet penetrates the block of wood and comes out with a velocity of 100 ms-1, find the vertical height through which the block of wood will rise (assuming the value of g to be 10 ms-2).
Sol. Let the masses of the bullet and the block be ‘m’ and ‘M’ respectively. Let their velocities after the impact be v and V respectively. Let the initial velocity of the bullet be ‘u’.
According to the law of conservation of linear momentum.
mu = mv + MV
Here
When the block rises to a height of ‘h’, according to the law of conservation of energy.
20. A ball A is falling vertically downwards with velocity v1. It strikes elastically with a wedge moving horizontally with velocity v2 as shown in figure. What must be the ratio v1 / v2, so that the ball bounces back in vertically upward direction relative to the wedge
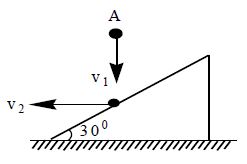
Sol. In the figure = velocity of ball w.r.t. wedge before collision and = velocity of ball w.r.t wedge after collision, which must be in vertically upward direction as shown.
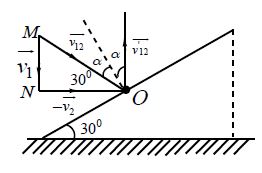
In elastic collision, and will make equal angles say with the normal to the plane.
We can show that ;
Now








