Waves

1. INTRODUCTION

A wave is any disturbance from normal or equilibrium condition that propagates without the transport of matter.  In general, a wave transports both energy and momentum. Wave occur when a system is disturbed from its equilibrium position and this disturbance travels or propagates from one region of the system to other.   Energy can be transmitted over considerable distance by wave motion.  The waves requiring a medium are called mechanical waves and their do not require a medium are called non-mechanical waves.  Light waves and all other electromagnetic waves are non-mechanical.

“Wave motion can be defined as a form of disturbance which travels through the medium due to repeated periodic motion of the particles of the medium about their mean positions”.

2. CLASSIFICATION OF WAVE MOTION

These are two distinct classes of wave motion

i) transverse ii) longitudinal

Transverse wave motion

In this, wave motion the particles of the medium oscillates about their mean partition at right angles to the direction of propagation of wave motion itself. This form of wave motion travels in the form of crests and troughs as for example wave traveling along a stretched string.

“If the direction of propagation of the waves is perpendicular to the direction of vibration of the particles, the waves are said to be Transverse waves”.

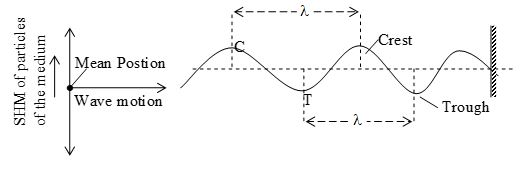
Longitudinal wave motion

In this, wave motion the particles of the medium oscillates about their mean position along the direction of propagation of the wave motion itself.  This type of wave motion travels in the form of compressions (C) and rarefaction (R).  Sound waves in a gas are longitudinal in nature.

“If the particles of the medium vibrate parallel to the direction of propagation of the waves, the waves are called Longitudinal waves”.

Waves may be one dimensional, two dimensional or three dimensional according as they propagate energy in just one, two or three dimensions.

Transverse waves along a string are one dimensions ripples on water surface are two dimensional and sound waves proceeding radically from point source are three dimensional.

Important points

i) Transverse or longitudinal nature of a wave decided by “Polarisation” as transverse wave can be polarized while a longitudinal wave cannot be.

ii) All non-mechanical waves are transverse.

iii)  If a wave is longitudinal, It is a mechanical wave, but if a wave is mechanical It may or may not be longitudinal.

iv) if a wave is non-mechanical, it is transverse wave. But if a wave is transverse it may or may not be non mechanical.

v) In string mechanical waves are always transverse.

vi) In gases and liquids mechanical waves are always longitudinal (because fluids cannot sustain shear) e.g. sound waves in air or water.

vii) In solids mechanical waves (may be sound) can be either transverse or longitudinal depending on the mode of excitation. viii) In solids longitudinal waves travel faster than transverse waves.

ix) Some waves are neither transverse nor longitudinal but a combination of two. These waves are called ripples.  Waves on free surface of liquid.

x) Transverse waves can be setup on the surface of liquids. But they cannot be transmitted inside liquids and gases. The longitudinal waves can be transmitted through solids, liquids and gases.

The following are the parameters of a progressive wave motion.

i) Amplitude (A) : The maximum displacement of any particle on the wave from its mean position in either direction is known as the amplitude of the wave.  The SI unit of amplitude is ‘metre’.

ii) Phase ($\mathit{\varphi }$): The phase of the wave at any instant at a point is the state of vibration of the particle at that point, with regards to its position and direction.  The SI unit of phase is “radian”, as it is represented as phase angle.  For example, if the phase of a particle at the crest (or at the compression) is $\frac{\mathrm{\pi }}{2}$ radian, the phase at the next trough (or at next rarefaction) is  $\frac{3\mathrm{\pi }}{2}$  Therefore the phase difference between a crest and the next through, or between a compression and the next rarefaction is $\mathrm{\pi }$ radian.  That is, the phase difference between two consecutive crests or troughs (compressions or rare factions) is 2$\mathrm{\pi }$.

iii)  Wavelength ($\mathit{\lambda }$):  The distance between two successive particles which are in the same phase of vibration on the wave is known as the wavelength.  The SI unit of wave length is “metre”.  On a transverse wave it can be identified as the linear separation between two consecutive crests of troughs.  Similarly the separation between two consecutive compressions or rarefactions is equal to the wavelength of a longitudinal wave.  Actually the phase difference between the particles separated by $\lambda$ is 2$\mathrm{\pi }$ and they are said to be “in phase”.

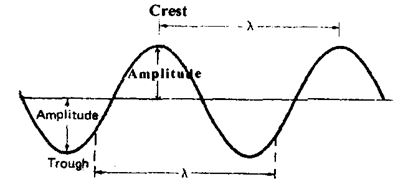
iv) Time period (T): It is the time taken by the disturbance to advance through a distance of one wavelength in the direction of propagation.  It is equal to the period of oscillation of any particle on the wave.  Its SI unit is ‘second’.

v) Frequency ($\mathit{\nu }$): It is equal to the number of vibrations per second completed by any particle on the wave.  In other words it is the number of wavelengths that take place in unit time (second) along the direction of propagation of the wave.  Its SI unit is ‘hertz’.  If ‘T’ is the period of the wave we can write .

vi) Velocity (v): It is the distance, through which the disturbance is propagated per second (per unit time) along the wave.  The SI unit of speed of the wave is “metre per second”.  It depends on the nature of the medium in which the wave travels.  Crests and troughs or compressions and rarefactions advance through a distance of one wavelength ($\lambda$) in a time period (T).

$\therefore$ The velocity of the wave $\mathrm{v}=\frac{\lambda }{\mathrm{T}}\text{ or }\mathrm{v}\lambda$    $\therefore v=\nu \lambda$

This velocity is not the velocity of the oscillating particle on the wave.  The particle velocity changes every moment during the oscillation, but the wave velocity is constant for a progressive wave and the energy is transmitted in the medium with this velocity.       

3. GENERAL EQUATION OF WAVE MOTION

In a wave motion, some physical quantity (say y) is made to oscillate at one place and these oscillations by y propagate to other places.  Then y may be

i) displacement of particles from their mean position in case of transverse wave in a rope or longitudinal sound wave in a gas.

ii) Pressure difference (dP) or density difference (dρ) incase of sound wave or

iii) electric and magnetic fields in case of electromagnetic waves.

The oscillations of y may or may not be simple harmonic in nature.  Now Let us consider a one dimensional wave traveling along x-axis.  In this case y is a function of position (x) and time (t).  the reason is that one may be interested in knowing the value of y at a general point x at any time t.

We can say that,

y = y (x,t )

But only those functions of x and t, represent a wave motion which satisfy the differential equation.

$\frac{{\partial }^{2}y}{\partial t^2}=v^2\frac{{\partial }^{2}y}{\partial x^2}$………….(i)

where, v = wave speed.

The general solution of this equation is of the form y (x,t) = f(ax $\pm$bt)  ………… (ii)

Thus any function of x and t which satisfies equation (i) or which can be written as equation (ii) represents a energy where and at all times.

Speed of wave (v) is given by, $\mathrm{v}=\frac{\text{ coefficient of }\mathrm{t}}{\text{ coefficient of }\mathrm{x}}=\frac{\mathrm{b}}{\mathrm{a}}$.

The (+) sign between ax and bt implies that the wave is traveling along negative x-direction and (-) sign shows that it is traveling along positive x-direction. 

4. PLANE PROGRESSIVE HARMONIC WAVE

The simplest form of a progressive wave is the one resulting from the simple harmonic oscillations of the particles of the medium.  Such a wave is known as a simple harmonic wave.  All the phases of vibration of any particle can be found on the consecutive particles in order, along the direction of propagation of the wave form, and the wave form advances with constant velocity.  Therefore the progressive wave equation should simultaneously represent the displacements of all the particles at any given instant and the phases of vibration of a particle at a given point along the direction of propagation.  Hence, the required wave equation should periodic in time as well as in position.

When y (x,t) is a sine or cosine functions such as

y (x,t) = asin k(x-vt)  or y (x,t) = A cosk(x-vt)

It is called plane progressive harmonic wave.  In plane progressive harmonic wave oscillations of  y are simple harmonic in nature.

The equation of a plane progressive harmonic wave moving along positive x-direction can be written as, y = A = Asin(kx-ωt)

= $\mathrm{Asin}\frac{2\pi }{\lambda }(\mathrm{x}–\mathrm{vt})=\mathrm{Asin}2\pi \left(\frac{\mathrm{x}}{\lambda }–\frac{\mathrm{t}}{\mathrm{T}}\right)$

5. PARTICLE VELOCITY (V_P) AND ACCELERATION (A_P)

Suppose the wave function is

y (x,t) = A sin (kx – ωt)      . . . (i)  

Differentiating w.r.t time,

$\frac{\mathrm{dy}}{\mathrm{dt}}$=particle velocity (v_p) = -ωA cos(kx-ωt). . . . (ii)

= $\mathrm{\omega }\sqrt{{\mathrm{A}}^2–{\mathrm{y}}^2}$

Then, $\frac{\mathrm{dy}}{\mathrm{dx}}=–\left(\frac{\mathrm{\omega }}{\mathrm{k}}\right).\frac{\mathrm{dy}}{\mathrm{dx}}$.

or ${\mathrm{v}}_{\mathrm{p}}=–\mathrm{v}\left(\text{ slope }\right)$, v = wave speed      . . . . (iii)

Differentiating equation  (ii) w.r.t time,

$\frac{d^{2}y}{d{t}^2}$= particle acceleration = ${\mathrm{a}}_{\mathrm{p}}=–{\mathrm{\omega }}^2\mathrm{Asin}(\mathrm{kx}–\mathrm{\omega t})$ 

= $–{\mathrm{\omega }}^2\mathrm{y}(\mathrm{x},\mathrm{t})$   . . . . (iv)

Note :

(a) Slope of the curve is positive.  Hence from equation.  (iii) particle velocity is negative or downwards. Similarly displacement of the particle is positive, so from equation (iv) acceleration will be negative or down words

(b)  Slope is negative while displacement is positive. 

6. CHARACTERISTICS OF WAVE MOTION

1)  When a wave motion passes through a medium, particles of the medium only vibrate simple harmonically about their mean position.  They do leave their position and move with the disturbance.

2)  In wave motion, the phase of particles of medium keeps on changing.

3)  The velocity of the particle during their vibration is different at different position.

4)  The velocity of wave motion through a particular medium is constant.  It depends only on the nature of medium not on the frequency, wavelength or intensity.

5)  Energy is propagated along with the wave motion without any net transport of the medium.

6)  For the propagation of wave, a medium should have following characteristics.

(i) Elasticity :  So that particles can return to their mean position.

(ii) Inertia : So that particles can store energy and overshoot their mean position.

(iii) Minimum friction amongst the particles of the medium. (iv)  Uniform density of the medium. 

7. PRINCIPLE OF SUPERPOSITION

Two or more wave can travel simultaneously in a medium without affecting the motion of one another.  Therefore the resultant displacement of each particle of the medium at any instant is equal to the vector sum of the displacements produced by two waves separately.  The principle is called principle of superposition.

“Principle of superposition of waves states that when two or more waves are simultaneously impressed on the particles of the medium, the resultant displacement of any particle is equal to the algebraic sum of displacements of all the waves.

If y₁, y₂, y₃ etc., are the displacements due to the overlapping waves, the resultant displacement of any particle is given by y = y₁ + y₂ + y₃ +….

Thus the resultant wave form can b obtained by the principle of superposition of waves.

Consider the superposition of two sinusoidal waves of same frequency at a point.  Let us assume that the two waves are traveling in  same direction with the same velocity.  The equation of the two waves reaching at a point can be written as.

${\mathrm{y}}_1={\mathrm{A}}_1\sin (\mathrm{kx}–\mathrm{\omega t})$

and ${\mathrm{y}}_2={\mathrm{A}}_2\sin (\mathrm{kx}–\mathrm{\omega t}+\mathrm{\varphi })$

The resultant displacement of the point where the waves meet is y = y₁ + y₂

= ${\mathrm{A}}_1\sin (\mathrm{kx}–\mathrm{\omega t})+{\mathrm{A}}_2\sin (\mathrm{kx}–\mathrm{\omega t}+\mathrm{\varphi })$

= ${\mathrm{A}}_1\sin (\mathrm{kx}–\mathrm{\omega t})+{\mathrm{A}}_2\sin (\mathrm{kx}–\mathrm{\omega t})\mathrm{cos\varphi }+{\mathrm{A}}_2\cos (\mathrm{kx}–\mathrm{\omega t})\mathrm{sin\varphi }$

= $\left({\mathrm{A}}_1+{\mathrm{A}}_2\mathrm{cos\varphi }\right)\sin (\mathrm{kx}–\mathrm{\omega t})+{\mathrm{A}}_2\mathrm{sin\varphi cos}(\mathrm{kx}–\mathrm{\omega t})$

or   $\mathrm{y}=\mathrm{Asin}(\mathrm{kx}–\mathrm{\omega t}+\mathrm{\varphi })$

Here  ${\mathrm{A}}_1+{\mathrm{A}}_2\mathrm{cos\varphi }=\mathrm{Acos\varphi }\text{ and }{\mathrm{A}}_2\mathrm{sin\varphi }=\mathrm{Asin\varphi }$

Then $\mathrm{A}=\sqrt{{\mathrm{A}}_1^2+{\mathrm{A}}_2^2+2{ \mathrm{A}}_1{ \mathrm{A}}_2\cos \varphi }$ and $\mathrm{tan\theta }=\frac{\mathrm{Asin\theta }}{\mathrm{Acos\theta }}=\frac{{\mathrm{A}}_2\mathrm{sin\varphi }}{{\mathrm{A}}_1+{\mathrm{A}}_2\mathrm{cos\varphi }}$

8. INTERFERENCE OF WAVES

Resulting amplitude is given by,

${\mathrm{A}}^2={\mathrm{A}}_1^2+{\mathrm{A}}_2^2+2{\mathrm{A}}_1{\mathrm{A}}_2\mathrm{cos\varphi }$….. (1)

If Intensity, $\mathrm{I}\propto {\mathrm{A}}^2$

Then , I = ${\mathrm{I}}_1+{\mathrm{I}}_2+2\sqrt{{\mathrm{I}}_1{\mathrm{I}}_2}\cos \varphi$      ……(2)

From equation (1) and (2), we see that the resulting amplitude A and intensity I depends on phase difference $\varphi$ between the interfering cases.

When, $\cos \varphi =1$

A_max = ${\mathrm{A}}_1+{\mathrm{A}}_2$ and, ${\mathrm{I}}_{\max }={\left(\sqrt{{\mathrm{l}}_1}+\sqrt{{\mathrm{l}}_2}\right)}^2$

This type of waves are said to be constructive interference.

Similarly, where, cosθ = -1,

${\mathrm{A}}_{\min }={\mathrm{A}}_1~{\mathrm{A}}_2$

And ${\mathrm{I}}_{\max }={\left({\sqrt{\mathrm{l}}}_1–\sqrt{{\mathrm{l}}_2}\right)}^2$

This type of waves are said to be destructive interference. 

9. REFLECTION AND TRANSMISSION OF WAVE

Progressive waves traveling in a medium get reflected when the medium ends abruptly at any point.  Such a discontinuity may be found even if the density and rigidity of the medium changes at any point.  Waves get reflected partially even when they refract into the next medium.

If a medium is denser for one type of wave then at the same time the same medium can be rare for the other type of wave.  For example, glass is denser for electromagnetic waves compared to air, because the speed of electromagnetic waves is less in glass than air.  At the same time for sound wave, glass is a rare medium because speed of sound wave in glass is more.

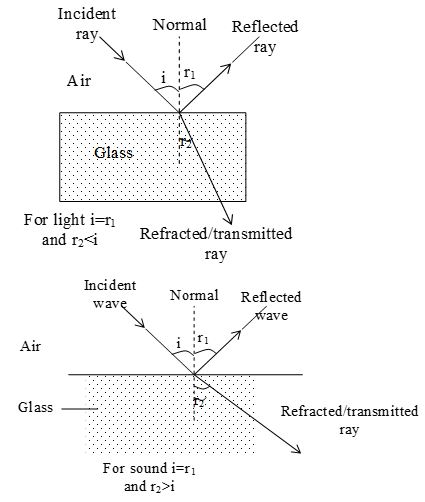
These physical quantities may be or may not be change when reflection or refraction takes place. The results in tabular form are given below

Wave property	Reflection	Transmission (refraction)
v	Does not change	Changes
f, T, ω	Do not change	Do not change
$\lambda$, k	Do not change	Change
A, I	Change	Change
$\varphi$	$∆\varphi =0$ from a rarer medium	Does not change
	$∆\varphi =\mathrm{\pi }$ from a denser medium

Note:

i) The reflection of the waves takes place at the fixed (rigid) end with the phase reversed by $\mathrm{\pi }$.

ii) The incident and reflected waves have a phase difference of 2$\mathrm{\pi }$. (i.e., they will be in phase) at the open end.

Important points in reflection and transmission

1) Suppose the equation of incident wave reflected and transmitted wave are

${\mathrm{y}}_{\mathrm{i}}={\mathrm{A}}_{\mathrm{i}}\sin \left({\mathrm{k}}_1\mathrm{x}–\mathrm{\omega t}\right), {\mathrm{y}}_{\mathrm{r}}={\mathrm{A}}_{\mathrm{r}}\sin \left({\mathrm{k}}_1\mathrm{x}+\mathrm{\omega t}\right)$ and ${\mathrm{y}}_{\mathrm{t}}={\mathrm{A}}_{\mathrm{t}}\sin \left({\mathrm{k}}_2\mathrm{x}–\mathrm{\omega t}\right)$

then, ${\mathrm{y}}_{\mathrm{i}}={\mathrm{y}}_{\mathrm{r}}+{\mathrm{y}}_{\mathrm{t}}$   ………… (i)

$\frac{{\mathrm{dy}}_{\mathrm{i}}}{\mathrm{dx}}=\frac{{\mathrm{dy}}_{\mathrm{r}}}{\mathrm{dx}}+\frac{{\mathrm{dy}}_{\mathrm{t}}}{\mathrm{dx}}$………… (ii)

By solving equation (i) and (ii) at x = 0.

We get ${\mathrm{A}}_{\mathrm{r}}=\frac{{\mathrm{v}}_2–{\mathrm{v}}_1}{{\mathrm{v}}_1+{\mathrm{v}}_2}{\mathrm{A}}_{\mathrm{i}}\text{ and }{\mathrm{A}}_{\mathrm{t}}=\frac{2{\mathrm{v}}_2}{{\mathrm{v}}_1+{\mathrm{v}}_2}{\mathrm{A}}_{\mathrm{i}}$

${\mathrm{A}}_{\mathrm{r}}=\frac{{\mathrm{k}}_1–{\mathrm{k}}_2}{{\mathrm{k}}_1+{\mathrm{k}}_2}{\mathrm{A}}_{\mathrm{i}}\text{ and }{\mathrm{A}}_{\mathrm{t}}=\frac{2{\mathrm{k}}_1{\mathrm{A}}_{\mathrm{i}}}{{\mathrm{k}}_1+{\mathrm{k}}_2}$

Under special conditions

Case (i) v₁ > v₂ i.e. medium (1) is rare and (2) is denser.

A_t = + ve & A_r = -ve and |A_r| and |A_t| both are less than |A_i|. Negative value of A_r indicates wave suffers a phase change of $\mathrm{\pi }$

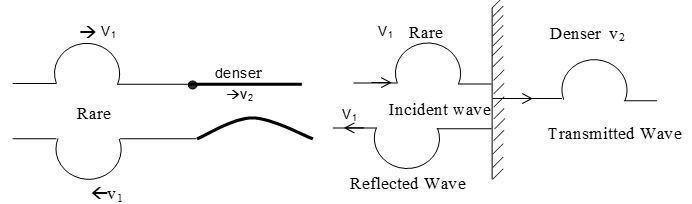
Case (ii): v₁ < v₂ i.e. medium (1) is denser and (2) is rare A_t and A_r  are both positive.  Also |A_t| > |A|  

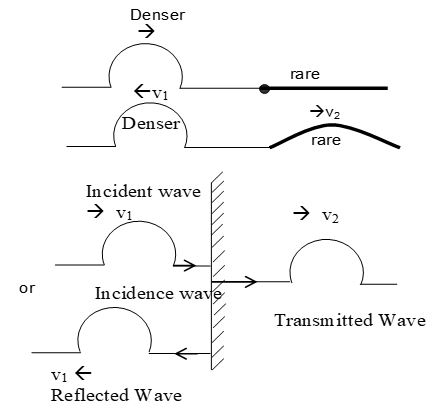
Case iii: Fixed end of a string: Since the fixed end is equivalent to a string of infinite linear mass density.

${\mathrm{v}}_2=\sqrt{\frac{\mathrm{T}}{\mu }}=0$ we obtain A_t = 0 and A_r = – A_i

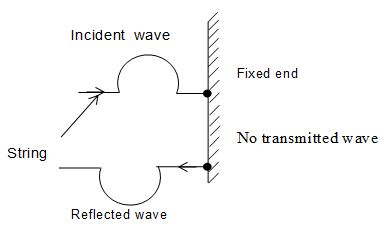
Case iv: Free end of a string:  In this case $\mu \to 0$, so $v_2\to \infty$ and we can show that A_t = 0 and A_r = A_i  

10. FORMATION OF STATIONARY WAVES IN STRETCHED STRING

A stretched string fixed at both the ends vibrates transversely, when plucked perpendicular to its length.  The transverse pulses travel either way along the length of the string and get reflected at the fixed ends.  These reflected waves, traveling in opposite directions with the same amplitude and frequency overlap along the length of the string.  The resultant wave is known as the standing wave or stationary wave.  It can be analytically obtained from the principle of superposition of waves.

Let two transverse progressive waves with the same amplitude A, wavelength $\lambda$ and frequency ‘$\nu$’, traveling in opposite directions along a stretched string be given by ${\mathrm{y}}_1=\mathrm{Asin}(\mathrm{kx}–\mathrm{\omega t})\text{ and }{\mathrm{y}}_2=–\mathrm{Asin}(\mathrm{kx}+\mathrm{\omega t})$, where $\mathrm{\omega }=\left(2\mathrm{\pi v}\right)\text{ and }\mathrm{k}=(2\mathrm{\pi }/\mathrm{\lambda })$.

Applying the principle of superposition of waves, the resultant wave is given by $\mathrm{y}={\mathrm{y}}_1+{\mathrm{y}}_2$

or $\mathrm{y}=\mathrm{Asin}(\mathrm{kx}–\mathrm{\omega t})–\mathrm{Asin}(\mathrm{kx}+\mathrm{\omega t})$

or  $\mathrm{y}=2\mathrm{Asinkxcos\omega t}$  ……. (1)

From the equation we find that the amplitude of the resultant wave (2A sin kx) is no more constant.  It depends on the value of kx.

When  $\mathrm{x}=0,\frac{\mathrm{\lambda }}{2},\frac{2\mathrm{\lambda }}{2},\frac{3\mathrm{\lambda }}{2}$ …… etc, the amplitude becomes zero.

These positions of zero amplitude are known as “Nodes”.

When $x=\frac{\lambda }{4},\frac{3\lambda }{4},\frac{5\lambda }{4}$ ….. etc., the amplitude becomes 2A (maximum)

These points of maximum amplitude are known as ‘Antinodes’:

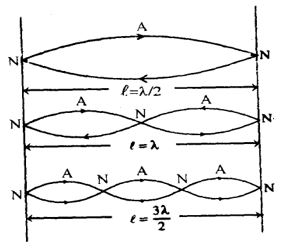
The amplitudes of the particles lying between a node and the next antinode are gradually in the increasing order.  Similarly the amplitudes between an antinode and the next node are successively decreasing.  However, the time period and frequency is the same for all particles.  Since each vibrating particle on the string has its own amplitude, the energy is not conveyed from one particle to the other.  Energy remains localized with the particles and the wave appears still.  Hence it is known as a standing wave or a stationary wave.  The separation between two consecutive nodes or antinodes is equal to half the wavelength of the overlapping waves.  The standing wave pattern is sustained as long as the string vibrates and can be diagrammatically represented in the form of loops or segments as shown in the fig. 

11. MODES OF VIBRATIONS OF A STRETCHED STRING

A stretched string can vibrate in different frequencies and form stationary wave pattern, in a given length.  These modes of vibrations are known as ‘harmonics’.  The first harmonic will have minimum number of nodes and antinodes and it vibrates in one segments (or loop).  This is known as the fundamental harmonic.  The higher harmonics are called the overtones of the fundamental.  Thus the second harmonic is known as the first overtone and if vibrates in two segments.  Similarly the third harmonic is the second overtone vibrating in three loops, and so on.  The patterns of vibrations are shown in the fig.

If ‘l’ is the length of the string vibrating in ‘p’ segments, the length of each segment is equal to $\frac{\mathcal{l}}{\mathrm{p}}$ and it corresponds to half the wavelength $\frac{\lambda }{2}$

$\therefore \frac{\ell }{\mathrm{p}}=\frac{\lambda }{2}\text{ or }\lambda =\frac{2\ell }{\mathrm{p}}$

$\therefore$ The frequency of the harmonic is given by $\mathrm{v}=\frac{\mathrm{vp}}{\mathrm{\lambda }}=\frac{\mathrm{vp}}{2\mathrm{\ell }}$   ……. (2)

If ‘T’ is the stretching force (Tension) in the string and ‘m’ is the mass per unit length (linear density) of the string, the velocity of transverse vibrations in the string is given by

$\mathrm{v}=\sqrt{\frac{\mathrm{T}}{\mathrm{m}}}$……. (3)

Using equations (2) & (3) the frequency of the harmonic in the string can be written as

$\mathrm{v}=\frac{\mathrm{p}}{2\mathrm{t}}\sqrt{\frac{\mathrm{T}}{\mathrm{m}}}$……. (4)

Thus the frequency of the fundamental or first harmonic ( p = 1),

${\mathrm{v}}_0=\frac{1}{2\mathcal{l}}\sqrt{\frac{\mathrm{T}}{\mathrm{m}}}$……. (5)

The frequency of the first overtone or second harmonic (p – 2) is given by ${\mathrm{v}}_1=\frac{2}{2\mathrm{\ell }}\sqrt{\frac{\mathrm{T}}{\mathrm{m}}}=2{\mathrm{v}}_0$

Similarly the frequency of the second overtone or third harmonic (p – 3) is given by

${\mathrm{v}}_2=\frac{3}{2\mathrm{\ell }}\sqrt{\frac{\mathrm{T}}{\mathrm{m}}}=3{\mathrm{v}}_0$ and so on.   

12. LAWS OF VIBRATING STRINGS

From the above equation  the laws of vibrating string can be stated as follows.

First law (Law of length)

When the tension (T) and linear density (m) are constant, the frequency of vibration (n) of a stretched string vibrating in one segment is inversely proportional to its length ($\mathcal{l}$)

i.e. $\mathrm{n\alpha }\frac{1}{\mathcal{l}}$

or $n\mathcal{l}$= constant or ${\mathrm{n}}_1{\mathrm{\ell }}_1={\mathrm{n}}_2{\mathrm{\ell }}_2$ = constant

Second law (law of tension)

When the length ($\mathcal{l}$) and the linear density (m) are constant, the frequency of vibration (n) of a stretched string vibrating in one segment is proportional to the square root of the tension (T) in the wire.

i.e., $\mathrm{n\alpha }\sqrt{\mathrm{T}}$

or $\frac{\mathrm{n}}{\sqrt{\mathrm{T}}}=\text{ const. i.e. },\frac{{\mathrm{n}}_1}{{\mathrm{n}}_2}=\sqrt{\frac{{\mathrm{T}}_1}{{ \mathrm{T}}_2}}$

Third law (law of mass)

When the length (l) and tension (T) are constant the frequency of the vibrations of a stretched a string vibrating in one segment is inversely proportional to the square root of linear density.

i.e, $\mathrm{n}\alpha \frac{1}{\sqrt{\mathrm{m}}}$

or  $\mathrm{n}\sqrt{\mathrm{m}}$= constant

i.e.  $\frac{{\mathrm{n}}_1}{{\mathrm{n}}_2}=\sqrt{\frac{{\mathrm{m}}_2}{{\mathrm{m}}_1}}$  ……………(6) 

13. EXPERIMENTAL VERIFICATION BY SONOMETER

The three laws of vibrating strings can be verified as given below.

The laws of vibration of strings are easily verified by means of a Sonometer.  It consists of a rectangular hollow wooden box, having holes on the sides for free vibrations of air inside.  A thin wire is stretched over two movable bridges ( by means of a weight hanging over a pulley. One end of the wire will be usually fixed and the other end carries a weight hanger .  the length of the wire can conveniently changed by moving the bridges.  The vibrations in the wire are set up by striking a tuning fork of standard frequency with a hammer and placing its stem on the sounding board of the Sonometer.  The length of the vibrating segment ($\mathcal{l}$) is adjusted till resonance occurs when the frequency of the vibrating string becomes equal to the frequency of the tuning fork.  This can be observed by placing a light paper rider in the middle of the wire.  When resonance occurs the paper rider is thrown off the wire

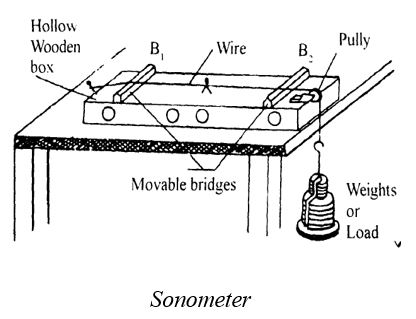
Verification of first law

Keep certain minimum weight such that the wire is free from kinks.  This tension is kept constant throughout the experiment.  A tuning fork of known frequency is excited and placed on the wooden box.  The distance between the bridges is adjusted until the paper rider falls down in resonance condition.  The corresponding vibrating length $\mathcal{l}$ is measured.  The experiment is repeated for different frequencies by changing the tuning forks and corresponding lengths of the same wire are measured and if the product $‘\mathrm{n}\mathcal{l}‘$  is found to be a constant, the first law is said to be verified.

It is difficult to verify the second and third laws directly.  These two laws are equivalent to prove respectively that $\frac{\sqrt{\mathrm{T}}}{\mathcal{l}} \mathrm{and} \mathcal{l}\sqrt{\mathrm{m}}$  are constants for verifying second and third laws.  

Verification of second law

In this part of the experiment for a given tuning fork and for a given wire the tension is changed in steps, the resonating length corresponding to the different tensions used are measured and if the ratio $\frac{\sqrt{\mathrm{T}}}{\mathcal{l}}$ is found to be a constant, the second law is said to be verified.

Verification of third law

The same tuning fork is used for the wires made of different materials under constant tension.  The resonating lengths corresponding to different wires are measured and if the product $\mathcal{l}\sqrt{\mathrm{m}}$ is found to be a constant, the third law is said to be verified

Precautions

1) Paper rider must be placed on the wire exactly at the centre between the bridges.

2) Weight  hanger should not touch the experimental bench

3) The thickness of the wire should be uniform

4) Tension applied should be within the elastic limit.

5) The tuning fork must always be held at its stem only.

6) The tuning fork is placed on wooden box such that the prongs of it may not touch the wire. The above precautions are to be observed while doing the sonometer experiment.  In this way the laws of transverse waves along a stretched string can be verified

Used of Sonometer

1) To determine the velocity of transverse waves along a stretched string.

2) To measure the frequency of alternating current in a circuit.

3) To determine the unknown frequency of the tuning fork.

4) To verify the laws of transverse waves along a stretched string. 

14. SOUND

Speed of wave:

i) Speed of transverse wave on a string is given by, v = $\sqrt{\frac{\mathrm{T}}{\mathrm{\mu }}}$

Where, $\mu$ = mass per unit length of the string = $\frac{\mathrm{m}}{\mathcal{l}}$.

= ρA,  Here, A = area of cross-section

                       ρ = density of string.

Then, $\mathrm{v}=\sqrt{\frac{\mathrm{T}}{\mathrm{\rho A}}}$

ii) Speed of longitudinal wave through a gas (or a liquid) is given as, $\mathrm{v}=\sqrt{\frac{\mathrm{B}}{\mathrm{\rho }}}$

Here, B = Bulk modulus and ρ = density of the gas or liquid.

Now, Newton’s who first deduced this relation for v assumed that during the passage of a sound wave through a gas (or air), the temperature of the gas is constant i.e., sound wave travels under isothermal conditions, then, isothermal bulk modulus = B=P.

Therefore, Newton’s   formula for the velocity of a sound wave (or a longitudinal wave) in a gaseous medium becomes, v = $\sqrt{\frac{\mathrm{p}}{\mathrm{\rho }}}$  at NTP, v = 280 m/s

(if ρ = 1.01⨯${10}^5 \mathrm{N}/{\mathrm{m}}^2$  and ρ =1.4 kg/${\mathrm{m}}^3$ ).  But velocity of sound (in air at NTP (experimentally) is 332 m/s.

La’place

correctly argued that a sound wave passes through a gas (or air) very rapidly.  So adiabatic conditions are developed.

Then, adiabatic bulk modulus = B = γp.  Where, γ is the ratio of ${\mathrm{C}}_{\mathrm{p}}$ and ${\mathrm{C}}_{\mathrm{v}}$.

Then, v = $\sqrt{\frac{\mathrm{\gamma P}}{\mathrm{\rho }}}$

For air, γ = 1.41, v = 331.6m/s.

iii) Speed of longitudinal wave in a thin rod or wire is given by,

v = $\sqrt{\frac{\mathrm{\gamma }}{\mathrm{\rho }}}$, here, Y is the young’s  modulus of elastically.   

15. FACTORS AFFECTING SPEED OF SOUND

i) Effected of temperature:

Velocity of sound in a gas

v = $\sqrt{\frac{\mathrm{\gamma RT}}{\mathrm{m}}}$ or $\mathrm{v}\propto \sqrt{\mathrm{T}}$, at constant γ and m.

i.e. with rise in temperature velocity of sound in a gas increases.

ii) Effect of relative humidity

Effect of relative humidity with increase in humidity density of air decreases

Here v = $\sqrt{\frac{\mathrm{\gamma P}}{\mathrm{\rho }}}$ or, $\mathrm{v}\propto \frac{1}{\sqrt{\mathrm{\rho }}}$, at const. P and γ.

i.e. with rise in humidity velocity of sound increases.

iii)  Effect of pressure:

Pressure has no effect on velocity of sound  in a gas long as temperature remains constant.

iv) Effect of wind velocity:

The velocity of sound in air is effected by the velocity of wind because wind drifts the medium along its direction of motion.

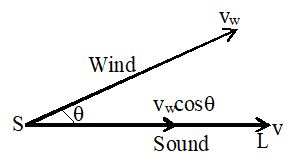
Let   v = velocity of sound emitted by source ‘S’

v_w = Velocity of wind,  θ = angle between v  and v_w.

component of wind velocity along SL = v_wcos θ.

∴ Resultant velocity of sound along SL

v_r = v + v_wcosθ.

16. ENERGY, POWER AND INTENSITY OF WAVES

If a sound wave given by y = Asin(ωt-kx) is propogating through a medium, the particle velocity will be,

${\mathrm{V}}_{\mathrm{p}}=\frac{\mathrm{dy}}{\mathrm{dt}}=\mathrm{a\omega cos}(\mathrm{\omega t}–\mathrm{kx})$

Kinetic energy of the wave per unit volume = $\frac{1}{2}\mathrm{\rho }{\left(\frac{\mathrm{dy}}{\mathrm{dt}}\right)}^2=\frac{1}{2}{\mathrm{\rho \omega }}^2{\mathrm{A}}^2{\cos }^2(\mathrm{\omega t}–\mathrm{kx})$

Here, ρ = the density of the medium

Then we know that,

K.E._max = P.E._max = E

i.e. energy density = u = $\frac{1}{2}{\mathrm{\rho A}}^2{\mathrm{\omega }}^2$.

So, the energy associated with a volume (S $∆x$) will be, $\mathrm{\Delta E}=\mathrm{u\Delta V}=\frac{1}{2}{\mathrm{\rho A}}^2{\mathrm{\omega }}^2 \mathrm{S\Delta x}$

So, power (rate of transmission of energy) will be

P = $\frac{\mathrm{\Delta E}}{\mathrm{\Delta t}}=\frac{1}{2}{\mathrm{\rho V\omega }}^2{ \mathrm{A}}^2 \mathrm{S} \left(\because \frac{\mathrm{\Delta x}}{\mathrm{\Delta t}}=\mathrm{v}\right)$

Now, Intensity (average energy transmitted per unit normal area per sec) will be

I = $\frac{\mathrm{\Delta E}}{\mathrm{S\Delta t}}=\frac{1}{2}{\mathrm{\rho V\omega }}^2{ \mathrm{A}}^2$

or $\mathrm{I}\propto {\mathrm{A}}^2$

Note : with increase in distance from the  source the total energy or power transmitted remain the same but intensity decreases.

For a isotropic point source of power P, intensity I at a distance r from it will be

$\mathrm{I}=\frac{\mathrm{p}}{\mathrm{s}}=\frac{\mathrm{p}}{4{\mathrm{\pi r}}^2}\text{ or }\mathrm{I\alpha }\frac{1}{{\mathrm{r}}^2}$

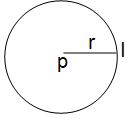
For spherical wave, $\mathrm{I}\alpha \frac{1}{{\mathrm{r}}^2}\text{ and }\mathrm{A}\propto \frac{1}{\mathrm{r}}$

17. PRESSURE WAVES

A longitudinal sound wave can be expressed either in terms of the longitudinal displacement of the particles of he medium or in terms of excess pressure produced due to compression or rarefaction, (at compression, the pressure is more than the normal pressure of the medium and at rarefaction the pressure is lesser than the normal). The first type is called the displacement wave and the second type the pressure wave.

If the displacement wave is represented by y = Asin (ωt – kx) then the corresponding pressure wave will be represented by $\mathrm{\Delta P}=–\mathrm{B}\frac{\mathrm{dy}}{\mathrm{dx}}$ (B = Bulk modulus of elasticity of medium)

Where ΔP₀ = pressure amplitude = AkB.

Pressure waves is $\left(\frac{\mathrm{\pi }}{2}\right)$ out of phase with displacement wave i.e., pressure is maximum when displacement is minimum and vice versa.

18. CHARACTERISTICS OF SOUND WAVES

Sound is a form of energy propagated in the form of longitudinal waves.  This energy causes the sensation of hearing on reaching the ear.  Any vibrating body could be a source causes the sensation of hearing on reaching the car.  Any vibrating body could be a source of sound.  An excited tuning fork, the plucked wire of a stringed instrument, a bell struck with a hammer, a vibrating air column in a trumpet could be some of the examples.  The sound produced by the source is propagated through a medium in the form of compressions and rarefactions.

Sound can not be transmitted through vacuum.  Sound can travel in solids, liquids and gases.  All the frequencies of the vibrating bodies can not produce the sensation of hearing.  The frequencies between 20 Hz and 20,000 Hz that produce the sensation of hearing are known as audible sounds.  Sounds with frequencies above 20,000 Hz are known as ultrasonics.  They can not be heard but still affect the cardrums and can cause acute pain.  They have greater penetrating power and can be used to detect mines in the sea and babies in the womb.  Many animals can hear the ultrasonic sounds.  Dogs can hear up to 50,000 Hz.  Bats can detect up to 1,00,000 Hz.  Sounds below 20 Hz are called Infrasonics.  Waves of earth quakes, volcanoes are some examples.  Infrasonic waves also can cause damage to the human bodies, causing irritation in the internal organs of the body.  Continuous exposure to the noise can bring down the range of audibility of a person.  The safest and healthiest sounds are the musical sounds which lie in the range of about 30 Hz to 5000 Hz.  The characteristics of sound notes are (i) intensity (ii) pitch, (iii) loudness and (iv)  quality (or timbre).

i) Intensity of wave:  The amount of energy flowing per unit area and per unit time is called intensity of wave.  It is represented by I.  Its units are watt/m² or J/m² (v = velocity of sound with respect to source)

I = 2$\mathrm{\pi }$²f²A²ρv

i.e.        I $\propto$f²  and I $\propto$ A²

If P is the power of an isotropic point source, intensity at a distance r is given by

$\mid =\frac{\mathrm{P}}{4{\mathrm{\pi r}}^2}, \mathrm{I}\propto \frac{1}{{\mathrm{r}}^2}$   for point source.

If P is the power of a line source, then intensity at distance r is given by

$\mathrm{I}=\frac{\mathrm{P}}{2\mathrm{\pi rl}}=\mathrm{I}\propto \frac{1}{\mathrm{r}}$  for a line source

Therefore

$\mathrm{A}\propto \frac{1}{\mathrm{r}}$  for point source 

$\mathrm{A}\propto \frac{1}{\sqrt{\mathrm{r}}}$ for line source

(ii) Pitch:  The pitch of the note is determined by its frequency.  The pitch of the buzzing of a bee is higher than the roar of a lion.  The sound produced by a violin has a higher pitch than the bass of a drum.  The lower the frequency the lower is the pitch.  Pitch is the subjective sensation of hearing while frequency is physically measurable quantity.

It is the sensation received by ear due to frequency.  It is depend on the frequency.  It determine the shrillness or graveness (sharp) of sound.  Smaller the frequency smaller is the pitch.  Greater the frequency greater is pitch.

(iii) Loudness:  The loudness of a note depends on the intensity of the wave.  The greater the intensity the greater the loudness.  The roar of a lion is louder than the buzz of a bee.  The intensity of the wave is directly proportional to the square of the amplitude of the wave.  Loudness is the subjective sensation of hearing while intensity is physically measurable quantity.  To produce a sound twice as loud requires a sound wave of about ten times greater in intensity.

However the energy of a sound wave is directly proportional to the squares of both frequency and amplitude.

L $\propto$ logI  or   $\mathrm{L}=10{\log }_{10}\frac{\mathrm{I}}{{\mathrm{I}}_0}=20\log \frac{\mathrm{P}}{{\mathrm{P}}_0}$     (here, I₀ = 10^–11 watt/m²)

The unit of loudness in Phon which is equal to the intensity level in dB of equally loud sound of 1 KHz.  

(iv) Quality or timbre:  It is the quality of a note which enables us to distinguish a note produced on one musical instrument from a note of the same pitch and intensity produced on another.  This is due to the difference in number, order and relative intensities of the overtones which accompany the note.  We can distinctly recognize the voice of a person due to the timbre of the characteristic notes from his vocal chords. 

19. ULTRASONIC, INFRASONIC AND AUDIBLE SOUND

Sound wave can be classified in three groups according to their range of frequencies. Infrasonic:  The sound wave having frequencies less than 20Hz are called infrasonic.  They cannot be heard by human beings.  They produced during earth quakes.  It can be heard by snakes.

Audible or sonic:  The sound wave having frequencies lying between 20-20,000 Hz are called audible wave. Ultrasonic: The sound wave having frequencies greater than 20,000 Hz are called ultrasonic wave. They are produced and heard by bats.

Ultrasonic wave can be used

i) to find internal cracks in metal

ii) to determining depth of the sea.

iii) To detect submarines, ice bergs.

iv) to clean clothes, fine machinery parts

v) to kill smaller animals.

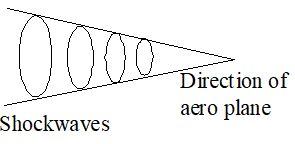
Shock waves:  If speed of the body in air is greater than the speed of the sound then it is called supersonic speed. Such body leaves behind a conical region of disturbance which spreads continuously.  Such disturbance is called “shock waves”.

This wave carries large amount of energy if it strikes a building.  Then the building may be damage.

Musical scale:  The arrangement notes having definite ratio in respective fundamental frequencies is called a musical scale. Musical scales are of two types.

a) Diatonic scale: It is known as “sargam” in Indian system. It contains eight notes with definite ratio in their frequencies.  The note of lowest frequency is called key note and the highest (which is double of first) is called a octave.  Harmonium, Piano etc are based on this scale.

b) Tempered scale: It contains 13 notes. The ratio of successive notes is 2^1/2.

Musical Interval: The ratio between the frequencies of two notes is called musical intervals.

i) Unison $\frac{{\mathrm{n}}_2}{{\mathrm{n}}_1}=1$

ii) octave = $\frac{{\mathrm{n}}_2}{{\mathrm{n}}_1}=2$

iii) major tone = $\frac{{\mathrm{n}}_2}{{\mathrm{n}}_1}=\frac{9}{8}$

iv) minor tone $\frac{{\mathrm{n}}_2}{{\mathrm{n}}_1}=\frac{10}{9}$

v) Semi tone $\frac{{\mathrm{n}}_2}{{\mathrm{n}}_1}=\frac{16}{15}$

vi) Fifth tone $\frac{{\mathrm{n}}_2}{{\mathrm{n}}_1}=\frac{3}{2}$

Standing Wave in a Organ Pipe

An organ pipe is a cylindrical tube having an air column.  If both ends of the tube are open, it is known as an open organ pipe.  If one end is closed and the other is open, it is known as a closed organ pipe.  When a compressional wave (sound wave) is sent through an organ pipe, the wave gets reflected at the ends of the pipe.  These incident and reflected waves which are in the same frequency, traveling in the opposite directions are superimposed along the length of the pipe and form longitudinal stationary waves.  At the open end, where the particles of the medium are free to vibrate, always an antinode is forced.  Here the two waves will be in the phase and the particles will have maximum displacement.  If  the reflection takes place at the closed end, the two waves will be in opposite phase and hence the superposition of the waves gives zero displacement to the particles.  Therefore always a node is formed at the closed end. 

20. HARMONICS AND OVERTONES

The possible frequencies in which the standing waves can be formed are called harmonics.  A harmonic in a vibrating length with minimum number of nodes and antinodes is known as the fundamental harmonic. 

If the also known as the first harmonic. A ‘harmonic’ is defined as a ‘tone’ of sound having a frequency which is an integral multiple of the fundamental frequencies.  The tones of sound other (higher) than the fundamental frequency are known as ‘overtones’.

1) Closed organ pipe:

(i) The first of the harmonics in a closed pipe should have a node at the closed end and an antinode at the open end, the length of the pipe (l) vibrating in one fourth of the wavelength.

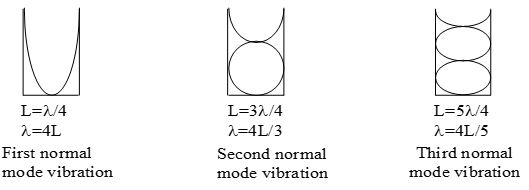
i.e., $\ell =\frac{{\lambda }_1}{4}$

∴ The fundamental frequency ${\mathrm{v}}_1=\frac{\mathrm{v}}{{\lambda }_1}=\frac{\mathrm{V}}{4\ell }$

(ii) The next possible harmonic with node at the closed end and antinode at the open end is only the third harmonic, since one more node and antinode should be included.  The length of the pipe becomes equal to $\frac{3}{4}$ of the wave length i.e.,  $\mathcal{l}=\frac{3{\lambda }_3}{4}$ where $\lambda$₃ is the wavelength of third harmonic.

The frequency of the third harmonic or first overtone is given by ${\mathrm{v}}_3=\frac{\mathrm{v}}{{\lambda }_3}=\frac{3\mathrm{v}}{4\ell }=3{\mathrm{v}}_1$.

(iii) Similarly the next overtone in the closed pipe is only the fifth harmonic.  It will have there nodes and three antinodes between the closed end and the open end of the pipe.  The length ‘l’ of the pipe adjusts itself to  of the wave length ($\lambda$₅) i.e., $\mathcal{l}=\frac{5}{4}{\lambda }_5$ and the frequency of this (second) over tone is given by ${\mathrm{v}}_5=\frac{\mathrm{v}}{{\mathrm{\lambda }}_5}=\frac{5\mathrm{v}}{4\mathrm{\ell }}=5{\mathrm{v}}_1$. 

The frequencies of the higher harmonics can be derived in the same way.

It can be observed that in the case of an organ pipe open at both ends all the harmonics can be formed, but in the case of closed organ pipes only odd harmonics are possible.

End correction:  The antinodes do not occur precisely at the open ends of the pipes, due to the pressure from outside the pipe.  Their position depends on the diameter of the pipe.  Generally the diameter is smaller compared to the length and the antinode will be very close to the open end.  Hence the vibrating length of the air column is extended slightly beyond the open end.  This correction ‘e’ to the vibrating length to be applied at the open end is called end correction.  The end correction should be applied at every open end.

2) Open organ pipe:

(i) The first harmonic or the fundamental should at least have an antinode at each end, with a node included between them.  Therefore the vibrating length (l) is equal to half the wavelength i.e., l = $\lambda$_1/2.

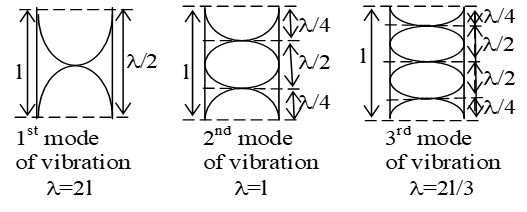
$\therefore$ The frequency of the fundamental ${\mathrm{v}}_1=\frac{\mathrm{v}}{{\mathrm{\lambda }}_1}$, where ‘v’ is the speed of sound in air.

$\therefore {\mathrm{v}}_1=\frac{\mathrm{v}}{2\mathcal{l}}$

(ii) The second harmonic or the first overtone will at least have one more node and natinode than the fundamental.

If $\lambda$₂ is the corresponding wavelength, $\ell =\frac{2{\lambda }_2}{2}={\lambda }_2$

$\therefore$  The corresponding frequency, ${\mathrm{v}}_2=\frac{\mathrm{v}}{{\mathrm{\lambda }}_2}=\frac{2\mathrm{v}}{2\mathcal{l}}=2{\mathrm{v}}_1$

(iii) Similarly the third harmonic or second overtone will have three nodes and four antinodes as shown in fig.  and if $\lambda$₃ is the wave length, $\mathrm{\ell }=\frac{3{\mathrm{\lambda }}_3}{2}$.

$\therefore$ The frequency of the second overtone The frequencies of the higher harmonics can also be derived in the same way.

21. FREE AND FORCED VIBRATIONS

If a body with elastic properties is given an initial impulse and let to itself, it vibrates with a definite frequency.  The frequency of vibrations depends on the classic constants, the dimensions and the mode of vibration of the body.  Such vibrations are known as free vibrations or natural vibrations of the body. The frequency of vibrations is known as natural frequency or characteristic frequency of the body.

For example, a tuning fork struck with a rubber hammer vibrates with its natural frequency (generally labeled on it). The natural frequency of the fork depends on the elastic nature of the material, the mass distribution and the dimensions of the prongs of the fork.

Similarly, if a loaded spring is initially given a push, it oscillates with a frequency of its own given by $\mathrm{v}=\frac{1}{2\mathrm{\pi }}\sqrt{\frac{\mathrm{k}}{\mathrm{m}}}$ where ‘k’ is the force constant of the spring and ‘m’ is the oscillating mass on the spring.  This is the natural frequency of the loaded spring.

The amplitude of free vibrations gradually decreases and the oscillations may die down due to the resistance of the surrounding medium.  Such oscillations are said to be damped oscillations. In order to overcome this damping effect, an external periodic force may be applied to the vibrating body to sustain the vibrations.  Then the body vibrates with the frequency of the periodic force.  Thus when a body is made to vibrate by an external periodic force such that the body vibrates with the frequency of the periodic force impressed on it, the oscillations are said to be forced vibrations.  As such, the natural frequency of the vibrating body need not be equal to the frequency of the periodic force.

For example, when the stem of a vibrating tuning fork is held on the top of a table a much louder sound is heard due to the forced vibrations.  These vibrations exist as long as the tuning fork vibrates and the frequency is equal to the frequency of the tuning fork.

Similarly when the strings on a musical instrument like veena or violin are vibrated, the sounding board and the air in the hollow box under it are also set into forced vibrations.  The force vibrations cease when the periodic force is removed. 

22. RESONANCE

If a body vibrates under the influence of a periodic force impressed on it, and if the natural frequency of the body coincides with the frequency of the periodic force on it, the body vibrates with increasing amplitude.  The phenomenon is called ‘Resonance’.

Resonant forced vibrations are also known as sympathetic vibrations.

Examples:

(i) Consider a child in a swing.  On giving a periodic push to the swing in the same direction every time it passes the extreme position, the amplitude of the swing goes on increasing and soon becomes very large.  Since the natural frequency of the of the swing is equal to the frequency of the periodic force, resonance occurs between the two and hence the amplitude increases.

(ii) Let us consider five pendulums A, B, C, D, E suspended from a common rigid support (a thin rod) X Y as shown in fig.  The pendulums B and D have the same length.  A is shorter and C, E are longer comparatively.  Let one of the pendulums B or D be set into oscillations.  These are free oscillations.  The forced oscillations take place in all the pendulum s through the common support.  Thus all the pendulums start oscillating initially but eventually only the pendulums B and D will have sustained oscillations with larger amplitudes.  The oscillation in A, C and E die down faster.  The two pendulums B and D are said to be in resonance since both of them have the same natural frequency and hence their amplitude increases.  The other three pendulums (A, C, E) have their natural frequencies deviated since their lengths are different.  Hence the forced osicllations die down faster.

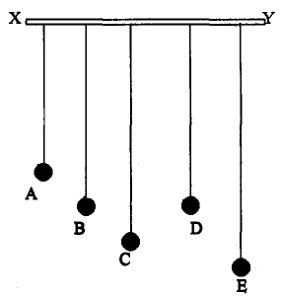
(iii) Another useful example of resonance is the tuning circuit in a radio set.  Radio waves of all frequencies strike the aerial of the radio set.  In the receiver set there will be a local electronic oscillator whose frequency is variable.  When the radio is tuned the frequency of the local oscillator is varied.  If the frequency of the local oscillator, incidentally, becomes equal to the frequency of a particular signal striking the aerial, resonance sets in at that frequency and the amplitude of vibrations becomes maximum.  This can be observed when the signal is heard in large volume.

(iv) Resonance is not desirable always.  For example, when a band of soldiers are marching on a bridge, they are commended to go out of step.  If they were to go marching in step, and if the natural frequency of the bridge happens to be equal to the frequency of the “in step” marching, resonance occurs between the two.  Due to resonance the amplitude of vibrations may increase enormously.  The bridge may vibrate violently and collapse.  Hence they are asked to go out of step.

(v) The phenomenon of resonance is applied in producing harmonics on stretched strings and air columns.  The frequency of natural vibrations of the strings and air columns depend on the vibrating length.  Let a tuning fork of the given frequency be excited and held on a sonometer with a stretched string or at the open end of air column in a pipe and the vibrating length be adjusted.  For a particular length resonance occurs and a harmonic in that frequency takes place with a loud sound.

23. BEATS

The phenomenon in which, two sound waves of nearly equal frequencies moving in the same direction interfere with each other and produce the waxing and waning of sound at regular intervals of time is called `beats’ the number of beats heard per second is called the `beat frequency’ and is equal to the difference between the two frequencies involved $\left({\mathrm{n}}_1–{\mathrm{n}}_2\right)$. Here ${\mathrm{n}}_1$ and ${\mathrm{n}}_2$ are the respective frequencies of the two waves.  Beats can be recognized by the human ear when the difference does not exceed 10.  The time interval between two successive maxima or minima is $\left(\frac{1}{{\mathrm{n}}_1–{\mathrm{n}}_2}\right)\sec$

The phenomenon, in which two sound notes of nearly same frequency traveling in the same direction interfere to produce a regular waxing and waning in the intensity of the combined note, is known as the “Beats”. Note: loading or filling of one of the prong of known or unknown (by wax) tuning fork, so frequency changes (decreases after loading, increases after filling).

Applications of beats

Beats can be used

1) To detect the presence of dangerous gases in mines.

2) To determine an un-known frequency of a sound note.

3) In ‘tuning’ an instrument to give a sound note and in heterodyne receivers the phenomenon of beats is used.

4) To determine the frequency of a given tuning fork.

24. DOPPLER EFFECT

The frequency of sound produced by the source and the frequency of sound heard by the observer will be the same, when there is no relative motion between them.  If the observer and the source of sound are in relative motion, the frequency of sound heard by him  is not the same as the actual frequency  of the source.  The relative motion can be discussed in two ways.  First, observer is at rest and source of sound is moving and second, source of sound is at rest and observer is moving.  For example, when a whistling rail engine approaches an observer standing on a platform, the frequency of sound appears to increase, and when it moves away, the frequency appears to be less than the actual frequency.  The same effect is observed if the engine is at rest and the observer moves towards or away from it.  But the observer in the moving train hears the same sound with constant frequency because, the train as well as the observer are moving with the same velocity.  So, the above example illustrates that when the observer and the source of sound are in relative motion then only the change in frequency can be observed.  It was first observed by C.  Doppler. Hence, this phenomenon is known as “Doppler effect “. The apparent change in the frequency of the source of sound due to relative motion between the observer and the source of sound is called “Doppler effect”.

Derivation of formula for apparent frequency in specific cases:

(a)  Source in motion, listener and medium at rest:

Let `S’ and `O’ be the positions of the source and the observer respectively in the beginning in a stationary medium.  Let the frequency of the sound emitted by the source be `n’, the velocity of source towards the observer be , and the velocity of the sound wave be denoted by `v’.

If the source were stationary, the `n’ waves emitted by it will occupy a length `v’ in one second.  But as it is moving towards the right a distance $‘{\mathrm{v}}_{\mathrm{s}}‘ \left({\mathrm{SS}}^{‘}\right)$  in one second, then `n’ waves produced by it per second are crowded in the space length $\left(\mathrm{v}–{\mathrm{v}}_{\mathrm{s}}\right)$ as shown in fig. (a) and as a result the wave length of the sound heard by the observer will be  reduced from $‘\lambda ‘$  to $‘ \lambda ‘ ‘$

Hence = ${\mathrm{\lambda }}^{‘}=\left(\mathrm{v}–{\mathrm{v}}_{\mathrm{s}}\right)/\mathrm{n}$

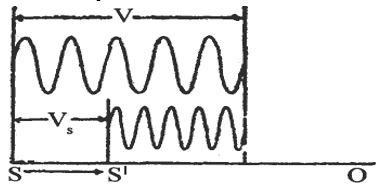
Now, the number of waves received per second or apparent frequency

$\mathrm{n}=\frac{\mathrm{v}}{\text{ new wavelength }}=\frac{\mathrm{v}}{{\mathrm{\lambda }}^{‘}}$

Substitution the value of $\lambda$’, we get

$\mathrm{n}‘=\frac{\mathrm{v}}{\left(\mathrm{v}–{\mathrm{v}}_{\mathrm{s}}\right)/\mathrm{n}}=\left(\frac{\mathrm{v}}{\mathrm{v}–{\mathrm{v}}_{\mathrm{s}}}\right)\mathrm{n}$

If the source is moving away from the observer the sign of $‘{\mathrm{V}}_{\mathrm{s}}‘$  should be reversed with the result that $\mathrm{n}‘=\left(\frac{\mathrm{v}}{\mathrm{v}+{\mathrm{v}}_{\mathrm{s}}}\right)\mathrm{n}$

b) Observer in motion and source and medium at rest:

Let the observer be moving with a velocity v₀ towards the stationary source in a stationary medium as shown. .  There is no crowding of the waves but the ear receives in one second not only `n’ waves but also an additional number of waves $\left(\frac{{\mathrm{v}}_0}{\mathrm{\lambda }}\right)$ during one second.  Therefore the increase in the frequency of the sound note heard is equal to $\frac{{\mathrm{v}}_0}{\mathrm{\lambda }}$.  That is,

$\frac{{\mathrm{v}}_0}{\mathrm{\lambda }}=\frac{{\mathrm{v}}_0}{\mathrm{v}}\mathrm{n} \left(\because \mathrm{\lambda }=\frac{\mathrm{v}}{\mathrm{n}}\right)$and the apparent frequency $‘\mathrm{n}‘$ of the sound heard is

$\mathrm{n}‘=\mathrm{n}+\frac{{\mathrm{v}}_0}{\mathrm{v}}\mathrm{n} \text{ or } \mathrm{n}‘=\left(1+\frac{{\mathrm{v}}_{\circ }}{\mathrm{v}}\right)\mathrm{n}=\left(\frac{\mathrm{v}+{\mathrm{v}}_{\mathrm{o}}}{\mathrm{v}}\right)\mathrm{n}$

When the observer is moving away from the stationary source, the sign of  should be reversed and therefore the apparent frequency of the source is $\mathrm{n}‘=\left(\frac{\mathrm{v}–{\mathrm{v}}_{\circ }}{\mathrm{v}}\right)\mathrm{n}$

(c) Source and observer both in motion and approaching each other in a stationary medium:

Combining the two results obtained above, we can get an expression for the frequency of the note heard when both source and observer are approaching each other.

Let the velocities $‘{\mathrm{v}}_{\mathrm{s}}‘$ and $‘{\mathrm{v}}_0‘$ of the source and observer respectively be estimated positive when the motion is from left to right.

Then, if the source is moving towards the stationary observer the frequency heard (n’) is

$\mathrm{n}‘=\left(\frac{\mathrm{v}}{\mathrm{v}–{\mathrm{v}}_{\mathrm{s}}}\right)\mathrm{n}$

In case the observer is also moving towards the source, we have

$\mathrm{n}“=\left(\frac{\mathrm{v}+{\mathrm{v}}_0}{\mathrm{v}}\right){\mathrm{n}}^{‘}$   [taking n’ =n’’ and n = n’]

Substituting the value of n’ is the equation of n’’ above, we get

n’’ = $\left(\frac{\mathrm{v}+{\mathrm{v}}_0}{\mathrm{v}–{\mathrm{v}}_{\mathrm{s}}}\right)\mathrm{n}$

When the both source and observer are moving away from each other, then the sign of  and  should be reversed.  Thus the apparent frequency can be written as

n’’  $\left(\frac{\mathrm{v}–{\mathrm{v}}_0}{\mathrm{v}+{\mathrm{v}}_{\mathrm{s}}}\right)\mathrm{n}$

d) Effect of motion of the medium on the frequency of sound:

If  the medium (air) is moving with a velocity “W” in the same direction, the effective velocity of sound waves is (v + W). If the medium moves opposite to the direction of sound waves, the effective velocity is (v-W).

When the source of sound, air or medium and observer all move, the apparent frequency received by the observer is given by

$\mathrm{n}“=\left[\frac{\mathrm{v}\pm \mathrm{W}\pm {\mathrm{v}}_{\mathrm{o}}}{\mathrm{v}\pm \mathrm{W}\pm \mathrm{vs}}\right]\mathrm{n}$

Appropriate sign is be taken depending on the direction of motion.

Applications  of Doppler effect

1) this effect is used in accurate navigation of aircraft and it is the basis of accurate target bombing techniques.

2) The speed of an automobile can be measured using this principle.

3) Velocities of stars are determined, relative to the earth.

4) Doppler’s effect is used for tracking an artificial satellite.

5) The rotation of Saturn’s rings and of double stars has been detected using Doppler effect.

Some important points concerning Doppler effect

(i) The Doppler effect is not symmetrical with respect to the motion of the source and the motion of the    observer.  The change in frequency is more when the source is in motion.

(ii) When a moving source passes a stationary observer.

The charge in frequency is given by,  $\mathrm{\Delta n}=\mathrm{n}‘–\mathrm{n}“=\frac{\mathrm{v}}{\mathrm{v}–{\mathrm{v}}_{\mathrm{s}}}\times \mathrm{n}–\frac{\mathrm{v}}{\mathrm{v}+{\mathrm{v}}_{\mathrm{s}}}\times \mathrm{n}=\frac{2{\mathrm{vv}}_{\mathrm{s}}}{{\mathrm{v}}^2–{\mathrm{v}}_{\mathrm{s}}^2}\times \mathrm{n}$

If ${\mathrm{v}}_{\mathrm{s}}<<\mathrm{v}$, then, $\mathrm{\Delta n}=\frac{2{\mathrm{v}}_{\mathrm{s}}}{\mathrm{v}}\times \mathrm{n}\text{ and }\mathrm{\Delta \lambda }=\frac{2{\mathrm{v}}_{\mathrm{s}}}{\mathrm{v}}\mathrm{\lambda }$

(iii) When, a moving observer passes a stationary source

The change in frequency is given by $\mathrm{\Delta n}=\mathrm{n}‘–\mathrm{n}“=\frac{\mathrm{v}+{\mathrm{v}}_0}{\mathrm{v}}\times \mathrm{n}–\frac{\mathrm{v}–{\mathrm{v}}_0}{\mathrm{v}}\times \mathrm{n}=\frac{2{\mathrm{v}}_0}{\mathrm{v}}\times \mathrm{n}$

and $\mathrm{\Delta \lambda }=\frac{2{\mathrm{v}}_0}{\mathrm{v}}\mathrm{\lambda }$

Limitation of Doppler effect

Doppler effect is applicable when the velocities of the source of sound and observer are much less than the velocity of sound i.e. ${\mathrm{v}}_{\mathrm{s}}<<\mathrm{v}$ and ${\mathrm{v}}_0<<\mathrm{v}$.

25. ECHOES

Echo is produced when sound is reflected from a surface.  The sound produced by the source is heard by listener by two ways.  First he receives the sound directly and after wards he listens the reflected sound.  The reflected sound is called `echo’.  The echo and the original sound have the same frequency but differs in intensity.

When a source of sound produces a sound note and an observer close to source listens it after reflection from an obstacle, the reflected sound is called an `Echo’.

Echoes are heard due to reflection of sound from

1. the reflecting surfaces or buildings.

2. the  surface of water in a well and

3. the surface of a mountain or cliff.

In the fig,`PQ’ is the reflecting surface that is placed in the path of the sound.  Let the source and the listener be at `O’.  When source emits sound, `OB’ is the path of the incident sound wave and `BO’ is the path of the reflected sound wave.  If reflecting surface `PQ’ is at a distance `d’ from `O’ and if `t’ is the time of echo we can write.

$\mathrm{t}=\frac{\text{ distance travelled }}{\text{ velocity of sound }}=\frac{(\mathrm{OB}+\mathrm{BO})}{\mathrm{v}}=\frac{(\mathrm{d}+\mathrm{d})}{\mathrm{v}}$

= $\frac{2\mathrm{d}}{\mathrm{v}}$ …………..(1.24)

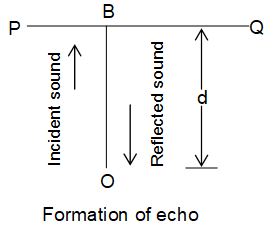
As the persistence of hearing is 0.1s, the sound remains in the ear for a time equal to 0.1 second only.  Within this time interval if another sound reaches the ear, it cannot be distinguished.  So, at least 0.1 second time interval is to be maintained to hear an echo. If the velocity of sound is taken as $330 {\mathrm{ms}}^{–1}$ (in air), this sound travels a distance equal to (v⨯t) =330⨯0.1=33m in 0.1 second i.e. 2d=33m and d = $\frac{33}{2}=16.5\mathrm{m}$. Hence reflecting surface must be at a distance of 16.5m from the observer.

Application of echoes:

1. The velocity  of sound  may be estimated making use of an echo.

2. Using the concept of an echo height of an aero plane and the depth of oceans may also be determined.

3. Megaphone and ear trumpet work on the principle of reflection of sound.

4. Sonar (Sound Navigation and Ranging)

To detect the presence of sub-marines in the seas, ultrasonic sound signals are sent and reflected sound waves are received.  Observing the echo characteristics, the position and direction of motion of the objects can be determined.

26. REVERBERATION

When, a man standing in an open space produces a sound it is hear by a listener after a time interval t = $\frac{\mathrm{x}}{\mathrm{v}}$; where `x’ is the distance between the source of sound and listener and `v’ is the velocity of sound in air.

If the sound is absorbed in the medium before reaching the listener, it can not be heard.  The absorption effect will be different if the sound is produced in a closed room `KLMN’ as

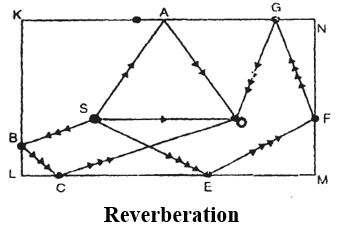
Let `S’ represents the source of sound (say a loud speaker) and `O’ represents the position of the observer in the closed room.  Then, observer receives the direct sound along the path `SO’ and also hears the same sound along the path `SAO’ after one reflection at A, along the path `SBCO’ after two reflections at B and  along the path `SEFGO’ after three reflections.  Though these four sounds started at `S’ at the same time they have traveled different distances due to reflection at the walls, reach the listener one by one with the decrease in intensity.  The intensity of the direct sound is greater than that of the second one after one reflection (SAO).  Thus, the intensity gradually decreases due to multiple reflections and there by some loss of sound energy in each reflection.  The intensity of sound that has traveled along the path `SBCO’ is still smaller due to two reflection at the walls.  When the sounding by source `S’ is stopped the listener hears the same sound for some more time with decreasing intensity.  This phenomenon is called `Reverberation’.

Reverberation is the persistence of sound in an enclosure as a result of multiple reflections of sound at the walls even after the source of sound is turned off.

Even if the source of sound is cut off, the listener hears the sound for some time till it reaches the threshold of audibility’.  The minimum intensity level of sound below which it becomes inaudible is called threshold of audibility

Reverberation time

Sabine defined the standard reverberation time (T) of a room as the time interval required by the sound intensity of a continuous note to decrease to threshold level of audibility from an initial intensity level of  times the threshold level after the source of sound is turned off.

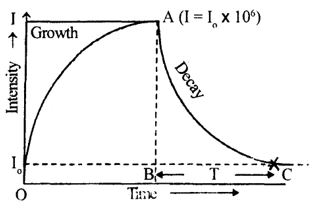
The growth and decay of sound in a room is shown in the fig. and the time of reverberation is T equal to BC. The reverberation time will depend on the size of the room or auditorium, the nature of the reflecting material used on the wall, the ceiling and the area of the reflecting surfaces.

The reverberation time should not be too large or too small.  Before pronouncing the second syllable, the intensity of the first syllable should fall well below threshold of audibility.  Otherwise, the listener receives the combined effect of the two syllables at the same time and hence, the clarity is lost.

If the reverberation time is too small then, sounds produced by less energetic sources become inaudible at some places of the room.  Reverberation time is selected keeping the above points in view. 

27. ABSORPTION OF SOUND WAVES

When a sound wave is incident on any surface, a part of the incident energy is absorbed.  Different substances absorb sound energy to different levels. The remaining energy is generally reflected.  Thick screens or curtains, mats, carpets, wood, card boards, are some of the examples for the sound absorbers.  Open windows and doors are good absorbers because the sound energy is transmitted through them completely.  The amount of sound absorbed by a material can be determined by comparing it with an open window of the same area.

If $‘{\mathrm{E}}_{\mathrm{s}}‘$ and $‘{\mathrm{E}}_{\mathrm{w}}‘$ are the amounts of sound energy absorbed by a surface and an open window of the same area in the same time then ${\mathrm{E}}_{\mathrm{s}}/{\mathrm{E}}_{\mathrm{w}}$ is called the absorption coefficient of the surface.

Absorption coefficient

The absorption co-efficient of surface is the ratio of the sound energy absorbed by it $\left({\mathrm{E}}_{\mathrm{s}}\right)$ to the sound energy absorbed by an open window of equal area $\left({\mathrm{E}}_{\mathrm{w}}\right)$ in the same time.

$\therefore \mathrm{a}=\frac{{\mathrm{E}}_{\mathrm{s}}}{{\mathrm{E}}_{\mathrm{w}}}$

28. FUNDAMENTALS OF BUILDING ACOUSTICS

The branch of physics dealing with production and controlling the factor relating to the design and construction of cinema theatres, auditoria, concert hall etc, so that the speech, music and songs are clearly reproduced to give a pleasing effect to the audience is called acoustics of building.  The subject that deals with the construction of good auditoria is called `Architectural acoustics”.

Architectural acoustics deals with controlling reverberation, elimination of extraneous noises, uniform distribution of sound in the room and overcoming echoes.  The fundamentals of architectural acoustics were laid by W.C sabine.

The sound produced in a closed room at a point, undergoes multiple reflections at various surfaces present with in the room.

Thus, there exists reverberation of sound.  Hence especially in the construction of large rooms, some conditions are to be fulfilled.

The following are some of the conditions:

i) The intensity of sound must be the same in different parts of the building. Loud speakers are used for the uniform distribution of sound and they are kept a little above the speakers head at different positions in the hall.

ii) There should not be any confusion due to overlapping of successive sounds (which means the decay of each syllable should be quick enough)

iii) Extraneous unwanted sounds (noise), such as sounds of automobiles, and loudspeakers should not enter into the hall or building.

iv) There should not be unnecessary echoes of sound.

v) The sound energy should be equally distributed inside the room. Sound focusing is the concentration of sound at a point in the enclosure due to reflection of sound from the surfaces.  The presence of cylindrical or spherical surfaces on the walls or the ceiling gives rise to undesirable focusing.  This effect should be eliminated by constructing parabolic surfaces inside the room.

vi) The sharp sound produced by a person in front of stairs may produce a musical note and the phenomenon is called `echelon effect’. This  is due to regular succession of echoes.  This is to be avoided by covering the stair cases with carpets.

Statement of Sabine’s formula

W.C. sabine, after conducting some experiments deduced a formula.  It is found that the reverberation time varies directly as the volume of the enclosure and varies inversely as the total absorption

If `T’ is the reverberation time of a building and `V’ is the volume of the building  containing the total absorption. `A’ then according to Sabine’s law.

$\mathrm{T\alpha V}$ and $\mathrm{T\alpha }\frac{1}{\mathrm{A}} or \mathrm{T\alpha }\frac{\mathrm{V}}{\mathrm{A}} \therefore \mathrm{T}=\mathrm{K}\frac{\mathrm{V}}{\mathrm{A}}$

Where `K’ is a constant.  This reverberation time does not depend on the shape of the enclosure and is also independent of the positions of sounding source and the listener.

When `a’ is the absorption co-efficient of the substance and `s’ the surface area of absorbing substance in the enclosure, then the total absorption due to all absorbing substances (A) is A = $\sum {\mathrm{a}}_{\mathrm{i}}{\mathrm{s}}_{\mathrm{i}}$

The value of reverberation time from the experiments is T = $\frac{0.17 \mathrm{V}}{\Sigma {\mathrm{a}}_{\mathrm{i}}{\mathrm{S}}_{\mathrm{i}}}$

Where `V’ is the volume of the enclosure, ${\mathrm{s}}_1, {\mathrm{s}}_2\text{ and }{\mathrm{s}}_3$ are the surface area of walls, floors, ceiling and  ${\mathrm{a}}_1, {\mathrm{a}}_2\text{ and }{\mathrm{a}}_3$ are their respective absorption co-efficient.  Reverberation time `T’ can be determined knowing other quantities.

SOLVED EXAMPLES  

1. Which of the following function represent a wave

(i) (x-vt)          ii) lx (x+vt)          iii) ${\mathrm{e}}^{–(\mathrm{x}–\mathrm{vt}{)}^2}$          iv) $\frac{1}{\mathrm{x}+\mathrm{vt}}$

Sol. Although all the four function are written in the form $\mathrm{f}(\mathrm{ax}\pm \mathrm{bt})$, only  (iii) among the four functions in finite everywhere at all slimes.  Hence only  (iii) represents a wave.  

2. The equation of the wave is y (x,t) = 0.05 sin$\left(\frac{\mathrm{\pi }}{2}(10\mathrm{x}–40\mathrm{t})–\frac{\mathrm{\pi }}{4}\right)\mathrm{m}$ .

Find i) The wave length, the frequency and the wave velocity

ii) The particle velocity and acceleration at x =0.5m and t = 0.05s

Sol.  i)  The equation may be written,

y(x,t) = 0.05 sin$\left(5\mathrm{\pi x}–20\mathrm{\pi t}–\frac{\mathrm{\pi }}{4}\right)\mathrm{m}$

Comparing this with equation of plane progressive harmonic wave,

y (x,t) = A sin(kx-ωt+t)

We have, wave number, k = $\frac{2\mathrm{\pi }}{\mathrm{x}}=5\mathrm{\pi rad}/\mathrm{m}$

Therefore, $\lambda$ = 0.4 m.

We know that, angular frequency = ω = 2$\mathrm{\pi }$f = 20$\mathrm{\pi }$

$\therefore$ f = 10Hz

The wave velocity is v = f$\lambda$ = 0.4⨯10 = 4 m/s in the x direction

ii) ${\mathrm{v}}_{\mathrm{p}}=–\mathrm{\omega A}$ cos (kx-ωt)

= $–\left(20\mathrm{\pi }\right)(0.05)\cos \left(\frac{5\mathrm{\pi }}{2}–\mathrm{\pi }–\frac{\mathrm{\pi }}{4}\right)$  (Here, x=0, .5m t = 0.05S]

= 2.22 m/s

and a_p = ${\mathrm{\omega }}^2\mathrm{A}$ sin (kx-ωt)

= – $\left(20\mathrm{\pi }{)}^2\right(0.05)\sin \left(\frac{5\mathrm{\pi }}{2}–\mathrm{\pi }–\frac{\mathrm{\pi }}{4}\right)$ = 140 m/${\mathrm{s}}^2$

3. Two waves of equal frequency have their amplitudes in the ratio of 3:5. They are superimposed on each other.  Calculate the ratio of maximum and minimum intensities of the resultant wave.

Sol. Given, $\frac{{\mathrm{A}}_1}{{\mathrm{A}}_2}=\frac{3}{5} \therefore \sqrt{\frac{{\mathrm{l}}_1}{{\mathrm{I}}_2}}=\frac{3}{5}$

maximum intensity is obtained, where, $\mathrm{cos\varphi }=1\text{ and }{\mathrm{I}}_{\max }={\left(\sqrt{{\mathrm{l}}_1}+\sqrt{{\mathrm{I}}_2}\right)}^2$

minimum intensity is obtained, where, $\mathrm{cos\varphi }=–1,\text{ and }{\mathrm{I}}_{\min }={\left(\sqrt{{\mathrm{I}}_1}–\sqrt{{\mathrm{I}}_2}\right)}^2$ 

Hence, $\frac{{\mathrm{I}}_{\max }}{{\mathrm{I}}_{\min }}=\frac{\left(\sqrt{{\mathrm{I}}_1}+\sqrt{{\mathrm{I}}_2}\right)}{{\left(\sqrt{{\mathrm{l}}_1}–\sqrt{{\mathrm{I}}_2}\right)}^2}={\left(\frac{\sqrt{\frac{{\mathrm{I}}_1}{{\mathrm{I}}_2}}+1}{\sqrt{\frac{{\mathrm{I}}_1}{{\mathrm{I}}_2}–1}}\right)}^2=\left(\frac{\frac{3}{5}+1}{\frac{3}{5}–1}\right)=\frac{16}{1}$

4. Wave y_i = 0.7 cos$\mathrm{\pi }$(3x – 60t) travels along a string towards a boundary at x = 0 with a second string. The wave speed on the second string is 50 m/sec.  Write expressions for reflected and transmitted waves.

Assume SI units.

Sol. Give equation is

y_i = 0.7 cos$\mathrm{\pi }$ (3x – 60t)

Here A_i = 0.7, ω = 60$\mathrm{\pi }$, k₁ = 3$\mathrm{\pi }$ $\Rightarrow$${\mathrm{v}}_1=\frac{\omega }{\mathrm{k}}=\frac{60\pi }{3\pi }$ , v₂ = 50 m/sec

$\therefore {\mathrm{A}}_{\mathrm{r}}=\frac{{\mathrm{v}}_2–{\mathrm{v}}_1}{{\mathrm{v}}_1+{\mathrm{v}}_2}{ \mathrm{A}}_{\mathrm{i}}=\frac{50–20}{50+20}\times 0.7=\frac{30}{70}\times 0.7=+0.3$

${\mathrm{A}}_{\mathrm{t}}=\frac{2{\mathrm{xv}}_2}{{\mathrm{v}}_1+{\mathrm{v}}_2}{\mathrm{A}}_{\mathrm{i}}=\frac{2\times 50}{70}\times 0.7=1$

${\mathrm{k}}_2=\frac{\mathrm{\omega }}{{\mathrm{V}}_2}=\frac{60\mathrm{\pi }}{50}=1.2\mathrm{\pi }$

Equation of reflected and transmitted waves are

${\mathrm{y}}_{\mathrm{r}}={\mathrm{A}}_{\mathrm{r}}\mathrm{cos\pi }(3\mathrm{x}+60\mathrm{t})=0.3\mathrm{cos\pi }(3\mathrm{x}+60\mathrm{t})$

${\mathrm{y}}_{\mathrm{t}}={\mathrm{A}}_{\mathrm{t}}\mathrm{cos\pi }(1.2\mathrm{x}–60\mathrm{t})=\mathrm{cos\pi }(12\mathrm{x}–60\mathrm{t})$

5. A wire of uniform cross-section is stretched between two points 100cm apart. The wire is fixed at one end and a weight is hung over a pulley at the other end.  A weight of 9 kg produces a fundamental frequency of 750 Hz.

a) What is the velocity of the wave in wire?

b) If the weight is reduced to 4 kg, what is the velocity of wave?  What is the wavelength and frequency?

Sol. (a) L = 100 cm, f₁ = 750 Hz

${\mathrm{v}}_1=2{\mathrm{Lf}}_1=2\times 100\times 750$

= 150000 cms^–1 = 1500 ms^–1

(b)  ${\mathrm{v}}_1=\sqrt{\frac{{\mathrm{T}}_1}{ \mathrm{m}}}\text{ and }{\mathrm{v}}_2=\sqrt{\frac{{\mathrm{T}}_2}{ \mathrm{m}}}$

$\frac{{\mathrm{v}}_2}{{\mathrm{v}}_2}=\sqrt{\frac{{\mathrm{T}}_2}{{ \mathrm{T}}_1}}\Rightarrow \frac{{\mathrm{v}}_2}{1500}=\sqrt{\frac{4}{9}}$

${\mathrm{V}}_2=1000{ \mathrm{ms}}^{–1}$

${\mathrm{\lambda }}_2=\text{ wavelength }–2\mathrm{L}=200\mathrm{cm}=2\mathrm{m}$

6. A wave moves with speed 300 m/s on a wire which is under a tension of 500 N. Find how much the tension must be changed to increase the speed to 312 m/s.

Sol. Speed of a transverse wave on a wire is , $\mathrm{v}=\sqrt{\frac{\mathrm{T}}{\mathrm{\mu }}}$   ……. (i)

Differentiating with respect to tension, we have $\frac{\mathrm{dv}}{\mathrm{dT}}=\frac{1}{2\sqrt{\mathrm{\mu T}}}$  ……. (ii)

Dividing Eq. (ii) by Eq. (i), we have $\frac{\mathrm{dv}}{\mathrm{v}}=\frac{1}{2}\frac{\mathrm{dT}}{\mathrm{T}}$

or  $\mathrm{dT}=\left(2\mathrm{T}\right)\frac{\mathrm{dv}}{\mathrm{v}}$

Substituting the proper values, we have $\mathrm{dT}=\frac{\left(2\right)\left(500\right)(312–300)}{300}=6.67 \mathrm{N}$

i.e., tension should be increased by 6.67 N.

7. Determine the speed of sound waves in water, the find the wavelength of a wave having a frequency of 242 Hz. Take B water = 2⨯10⁹Pa.

Sol. Speed of sound wave,

$\mathrm{v}=\sqrt{\frac{\mathrm{B}}{\mathrm{\rho }}}=\sqrt{\frac{2\times {10}^9}{{10}^3}}=1414 \mathrm{m}/\mathrm{s}$

Wavelength, $\mathrm{\lambda }=\frac{\mathrm{v}}{\mathrm{f}}=5.84 \mathrm{m}$.

8. Find the speed of sound in a mixture of 1mol of helium and 2 mol of oxygen at .

Sol. Molar mass of mixture = ${\mathrm{M}}_{\text{mix }}=\frac{{\mathrm{n}}_1{\mathrm{M}}_1+{\mathrm{n}}_2{\mathrm{M}}_2}{{\mathrm{n}}_1+{\mathrm{n}}_2}$

$=\frac{1\times 4+2\times 32}{1+2}=\frac{68}{3}\times {10}^{–3} \mathrm{kg}/\mathrm{mol}$

= (C_v) mix = $\frac{{\mathrm{n}}_1{\mathrm{c}}_{{\mathrm{V}}_1}+{\mathrm{n}}_2{\mathrm{c}}_{{\mathrm{V}}_2}}{{\mathrm{n}}_1+{\mathrm{n}}_2}=\frac{1\times \frac{3}{2}\mathrm{R}+2\times \frac{5}{2}\mathrm{R}}{1+2}=\frac{13}{6}\mathrm{R}$

(Cp) mix = $\left({\mathrm{C}}_{\mathrm{v}}\right)\mathrm{mix}+\mathrm{R}=\frac{13}{6}\mathrm{R}+\mathrm{R}=\frac{19}{6}\mathrm{R}$.  

$\therefore (\gamma {)}_{\text{mix }}=\frac{C_{\text{p }}}{C_V}=\frac{19}{6}R\times \frac{6}{13\mathrm{R}}=\frac{19}{13}$

The speed of sound, v = $\sqrt{\frac{\mathrm{\gamma RT}}{\mathrm{m}}}$

= $\sqrt{\frac{19}{13}\times \frac{8.31\times 300}{\left(68/3\times {10}^{–3}\right)}}=400.9 \mathrm{m}/\mathrm{s}$

9. Speed of sound in air is 332 m/s at NTP. What will be the speed of sound in Hydrogen at NTP if the density of hydrogen at NTP is 1/16 that of air

Sol. Given that

V_air = 332        ${\mathrm{P}}_{\text{air }}={\mathrm{P}}_{{\mathrm{H}}_2}={\mathrm{P}}_{\mathrm{a}}$

$\frac{{\mathrm{\rho }}_{\text{air }}}{{\mathrm{\rho }}_{{\mathrm{H}}_2}}=16$         ${\mathrm{T}}_{\mathrm{air}}={\mathrm{T}}_{{\mathrm{H}}_2}=273 \mathrm{K}$

                            ${\gamma }_{\text{air }}={\gamma }_{{\mathrm{H}}_2}=1.4$

We known      $\mathrm{V}\propto \sqrt{\frac{1}{\mathrm{\rho }}}$

$\frac{{\mathrm{V}}_{\text{air }}}{{\mathrm{V}}_{{\mathrm{H}}_2}}=\sqrt{\frac{{\mathrm{\rho }}_{{\mathrm{H}}_2}}{{\mathrm{\rho }}_{\text{air }}}}=\sqrt{\frac{1}{16}}=\frac{1}{4}$

${\mathrm{V}}_{{\mathrm{H}}_2}$ = 4×332 = 1328 m/sec.

10. A stretched string is forced to transmit transverse waves by means of an oscillator coupled to one end.  The string has a diameter of 4mm.  The amplitude of the oscillation is ${10}^{–4}\mathrm{m}$ and the frequency is 10Hz.  Tension in the string is 100N and mass density of wire is .  Find

a) the equation of the waves along the string.

b) the energy per unit volume of the wave

c) the average energy flow per unit time across an section of the string and

d) power required to derive the oscillator

Sol. a) speed of transverse wave on the string is

$\mathrm{v}=\sqrt{\frac{\mathrm{T}}{\mathrm{\rho S}}}=\sqrt{\frac{100}{\left(4.2\times {10}^3\right)\left(\frac{\mathrm{\pi }}{4}\right){\left(4\times {10}^{–3}\right)}^2}}$

v = = 43.53 m/s

$\mathrm{\omega }=2\mathrm{\pi f}=20\mathrm{\pi ad}/\mathrm{s}$ = 62.83 rad/s

$\mathrm{k}=\frac{\mathrm{\omega }}{\mathrm{v}}=1.44{ \mathrm{m}}^{–1}$

$\therefore$ k= Equation of the waves along the string,

y(x,t) = A sin(kx – $\omega$t)

= $\left({10}^{–4} \mathrm{m}\right) \sin \left(1.44{ \mathrm{m}}^{–1}\right)\mathrm{x}–(62.83)\mathrm{rad}/\mathrm{s}$

b) Energy per unit volume = u

= $\frac{1}{2}{\mathrm{\rho \omega }}^2{\mathrm{A}}^2$

= $\frac{1}{2}\left(4.2\times {10}^3\right)(62.83{)}^2{\left({10}^{–4}\right)}^2$

$=8.29\times {10}^{–2} \mathrm{J}/{\mathrm{m}}^3$.

c) Average energy flow per unit time

= $\mathrm{p}=\left(\frac{1}{2}{\mathrm{\rho \omega }}^2{ \mathrm{A}}^2\right)\left(\mathrm{sv}\right)$

= $\left(8.29\times {10}^{–2}\right)\left(\frac{\mathrm{\pi }}{4}\times {\left(4\times {10}^{–3}\right)}^2\times 43.53\right)$

$=4.53\times {10}^{–5} \mathrm{J}/\mathrm{s}$

d) Power required to derive the oscillator

= $\mathrm{p}=4.53\times {10}^{–5}\text{ watt. }$

11. The faintest sound the human car can detect at frequency 1 kHz corresponds to an intensity of about 10^–12 W/m². Determine the pressure amplitude and the maximum displacement associated with this sound assuming the density of the air = 1.3 kg/m³ and velocity of sound in air = 332 m/s.

Sol. $\mathrm{I}=\frac{{\mathrm{P}}^2}{2\mathrm{\rho v}}\Rightarrow \mathrm{P}=\sqrt{\mathrm{I}\times 2\mathrm{\rho v}}$

$=\sqrt{{10}^{–12}\times 2\times 1.3\times 332}=2.94\times {10}^{–5}\mathrm{N}/{\mathrm{m}}^2$

Again, $\mathrm{P}=\mathrm{\rho v\omega A}\Rightarrow \mathrm{A}=\frac{\mathrm{P}}{\mathrm{\rho v\omega }}=\frac{2.94\times {10}^{–5}}{1.3\times 332\times 2\mathrm{\pi }\times {10}^3}=1.084\times {10}^{–11}\mathrm{m}$.

12. A flute which we treat as a pipe open at both ends is 60cm long.

a) What is the fundamental frequency when all the holes are covered?

b) How far from the mouthpiece should a hole be uncovered for the fundamental frequency to be 330Hz?  Take speed of sound in air as 340 m/s.

Sol. (a) Fundamental frequency when the pipe is open at both ends is

${\mathrm{f}}_1=\frac{\mathrm{v}}{2\mathcal{l}}=\frac{340}{2\times 0.6}=283.33\mathrm{Hz}$

(b) Suppose the hole is uncovered at a length $\mathcal{l}$ from the mouthpiece, the fundamental frequency will be ;

${\mathrm{f}}_1=\frac{\mathrm{v}}{2\mathcal{l}}; \mathcal{l}=\frac{\mathrm{v}}{2{\mathrm{f}}_1}=\frac{340}{2\times 330}=0.515\mathrm{m}=51.5\mathrm{cm}$

Note: Opening holes in the side effectively shortens the length of the resonance column, thus increasing the frequency.

13. The first overtone of an open organ pipe beats with the first overtone of a closed organ pipe with a heat frequency of 2.2Hz. The fundamental frequency of the closed organ pipe is 110Hz.  Find the lengths of the pipes.  Speed of sound in air v=330 m/s.

Sol. Let ${\ell }_1\text{ and }{\ell }_2$ be the lengths of closed and open pipes respectively.

Fundamental frequency of closed organ pipe is given by ${\mathrm{f}}_1=\frac{\mathrm{v}}{4{\ell }_1}$

v = speed of sound in air = 330 m/s

But   f₁ = 110Hz is given

Therefore,   $\frac{\mathrm{v}}{4{\mathrm{\ell }}_1}=110 \mathrm{Hz}$

$\therefore {\ell }_1=\frac{\mathrm{v}}{4\times 100}=\frac{330}{4\times 110} \mathrm{m}=0.75 \mathrm{m}$

First overtone of closed organ pipe will be ${\mathrm{f}}_3=3{\mathrm{f}}_1=3\left(110\right)\mathrm{Hz}=330 \mathrm{Hz}$

This produces a beat frequency of 2.2 Hz with first overtone of open organ pipe.

Therefore, first overtone frequency of open organ pipe is either

(330 + 2.2) Hz = 332.2 Hz

or    (330 – 2.2) Hz = 327.8 Hz

If it is 332.2 Hz,

Then, $2\left(\frac{\mathrm{v}}{2{\mathrm{\ell }}_2}\right)=332.2 \mathrm{Hz}$

or ${\mathrm{\ell }}_2=\frac{\mathrm{V}}{332.2}=\frac{330}{332.2} \mathrm{m}=0.99 \mathrm{m}$  and

if it is 327.8 Hz.

$2\left(\frac{\mathrm{v}}{2{\ell }_2}\right)=327.8 \mathrm{Hz}$   or ${\mathrm{\ell }}_2=\frac{\mathrm{V}}{327.8} \mathrm{m}=\frac{330}{327.8} \mathrm{m}=1.0067 \mathrm{m}$

Therefore, length of the closed organ pipe is  while length of open pipe is either  or 1.0067m.

14. For a certain organ pipe, three successive resonance frequencies are observed of 425, 595 and 765 Hz respectively. Taking the speed of sound in air to be 340 m/s.

(a) Explain whether the pipe is closed at one end or open at both ends.

(b)  determine the fundamental frequency and length of the pipe.

Sol. a)  The given frequencies are in the ratio 5 : 7 : 9.  As the frequencies are odd multiple of 85 Hz the pipe must be closed at one end.

b) Now the fundamental frequency is the lowest i.e., 85 Hz.

$\therefore 85=\frac{\mathrm{V}}{4\mathrm{\ell }}\Rightarrow \mathrm{\ell }=\frac{340}{4\times 85}=1\mathrm{m}$

15. Two organ pipes each closed at one end gives 5 beat/sec, when emitting their fundamental notes. If their length are in the ratio of 50:51, determine their fundamental frequencies.

Sol. We known, with increasing the length of organ pipe, frequency decreased.

Net frequency of shorter length organ pipe is f and the bigger length organ pipe (f-5).

Then,  $\mathrm{f}\propto \frac{1}{\mathrm{I}}$   

$\therefore \frac{{\mathrm{f}}_1}{{\mathrm{f}}_2}=\frac{{\mathrm{I}}_2}{{\mathrm{I}}_1}\Rightarrow \frac{\mathrm{f}}{\mathrm{f}–5}=\frac{51}{50}$

f₁ = 255 Hz,      f₂ = 255 – 5 = 250 Hz  

16. Two tuning forks A and B sounded together give 8 beats per second. With an air resonance tube closed at one end, the two forks give resonance when the two air columns are 32 cm and 33 cm respectively.  Calculate the frequency of forks.

Sol. Let the frequency of the first fork be f₁ and that of second be f₂.

We then have, ${\mathrm{f}}_1=\frac{\mathrm{V}}{4\times 32}\text{ and }{\mathrm{f}}_2=\frac{\mathrm{V}}{4\times 33}$

We also see that f₁ > f₂

F₁ – f₂ = 8        ……. (i)

and   $\frac{{\mathrm{f}}_1}{{\mathrm{f}}_2}=\frac{33}{32}$ ……. (ii)

Solving Eq. (i) and (ii), we get

F₁ = 264 Hz and f₂ = 256 Hz.

17. A wire of density 9×10³ kg/m³ is stretched between two clamps 1m apart and is subjected to an extension of 4.9×10^-4 m. What will be the lowest frequency of transverse vibration in the wire. ($\gamma$ = 9×10¹⁰ N/m²)

Sol. Given

$\rho$ = 8×10³ kg/m³, l = 1m, $∆$x = 4.9×10^-4 m,  $\gamma$ = 9×10¹⁰ N/m²

stress = $\gamma$ x strain

Velocity of wave (v) =  $\sqrt{\frac{\mathrm{T}}{\mathrm{m}}}=\sqrt{\frac{\mathrm{T}}{\mathrm{\rho }\times \mathrm{A}}}$

$=\sqrt{\frac{\text{ stress }}{\mathrm{\rho }}}=\sqrt{\frac{\mathrm{\gamma }\times \text{ strain }}{\mathrm{\rho }}}$

$=\sqrt{\frac{9\times {10}^9\times 49\times {10}^{–4}}{9\times {10}^3}}=70 \mathrm{m}/\mathrm{s}$

Minimum frequency in string f

$=\frac{\mathrm{v}}{2\ell }=\frac{70}{2\times 1}=35 \mathrm{Hz}$

18. A siren emitting a sound of frequency 1000Hz moves away from you towards a cliff at a speed of 10 m/s.

a) What is the frequency f the sound you heat coming directly from the siren.

b) What is the frequency of sound you hear reflected off the cliff.  Speed of sound in air is 330 m/s.

Sol. a)  Sound heard directly, ${\mathrm{f}}_1={\mathrm{f}}_0\left(\frac{\mathrm{v}}{\mathrm{v}+{\mathrm{v}}_{\mathrm{s}}}\right)$

v_s = 10 m/s

$\therefore {\mathrm{f}}_1\left(\frac{330}{330+10}\right)\times 1000=\frac{33}{34}\times 1000 \mathrm{Hz}$

b) The frequency of the reflected sound is given by ${\mathrm{f}}_2={\mathrm{f}}_0\left(\frac{\mathrm{v}}{\mathrm{v}–{\mathrm{v}}_{\mathrm{s}}}\right)$

${\mathrm{f}}_2=\left(\frac{330}{330–10}\right)\times 1000=\frac{33}{32}\times 1000 \mathrm{Hz}$

19. An aluminium rod 80 cm clumed at the middle is used to create standing waves in a Kundt’s tube experiment. If the tube is 1m long and the dust heaps accommiate at 6cm, intervals and velocity of sound in air is 330 m/s.  Then determine the velocity of sound in the rod.

Sol. For Kundt’s tube

$\frac{{\mathrm{V}}_{\text{rod }}}{{\mathrm{V}}_{\text{air }}}=\frac{{\mathrm{I}}_{\text{rod }}}{{\mathrm{I}}_{\text{air }}}=\frac{80}{6}$

${\mathrm{v}}_{\text{rod }}=\frac{80}{6}{\mathrm{XV}}_{\text{air }}=\frac{80}{6}\times 330$ = 4400 m/s.

20. A train moves towards stationary observer with speed 34 m/s. The train sounds a whistle and its frequency registered by the observer is f₁.  If the train’s speed is reduced to 17 m/s, the frequency registered is f₂.  If the speed of sound is 340 m/s than, ratio $\frac{{\mathrm{f}}_1}{{\mathrm{f}}_2}$ is

(A)  18/19      (B)  1/2

(C)  2             (D)  19/18

Sol. (D)

Here, In 1^st case,  ${\mathrm{f}}_1={\mathrm{f}}_0\left(\frac{\mathrm{v}+0}{\mathrm{v}–{\mathrm{v}}_{\mathrm{s}}}\right)={\mathrm{f}}_{\mathrm{o}}\left(\frac{340}{340–34}\right)$  ……. (1)

and in case,  ${\mathrm{f}}_2={\mathrm{f}}_0\left(\frac{\mathrm{v}+0}{\mathrm{v}–{{\mathrm{v}}_{\mathrm{s}}}^1}\right)={\mathrm{f}}_0\left(\frac{340}{340–17}\right)$   ……. (2)

from (1) and (2), we get,

$\frac{f_1}{f_2}=\frac{(340–17)}{(340–74)}=\frac{323}{306}=\frac{19}{18}$