1. INTRODUCTION
A ‘Characteristic’, whose magnitude can be measured, directly or indirectly, is called a physical dimension or physical quantity. The entire set of physical quantities is divided into order or ranks of tensor. Tensor of zeroth-order is called scalar and of first order is called vector. A second order tensor is generally represented by a matrix. Stress and moment of inertia is second order tensor. These are called dyadics. There are higher order tensors also. However, all the tensors as such are not in your course. Only zeroth and first order tensors i.e. classification of scalar and vector quantities is in your course.
Those which can be measured directly and indirectly are called physical quantity. It is convenient to understand physical quantities with the following type of classification.
Scalar Quantities
If a physical quantity can be described fully by its magnitude alone, it is called a scalar quantity are simply scalar example mass, length, distance, time, density, work, specific heat, temperature, electric charge etc. Scalar quantities follow the rules of ordinary algebra.
Vectors quantities
If a physical quantity gets completely defined just by its magnitude and direction only; and in addition also follows the triangle law of vector addition, it is called a vector e.g. velocity, torque, etc. Usually a vector is represented by a bold letter with an arrow vector etc.
The magnitude of a vector is represented by A or .
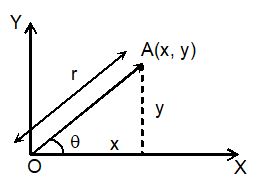
Graphical Representation of a Vector Graphically a vector is represented by an arrow drawn to a chosen scale, parallel to the direction of the vector. The length and the direction of the arrow thus represented the magnitude and the direction of the vector respectively. Thus, the arrow shown in the figure represents a vector in x-y plane making an angle θ with x-axis.
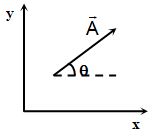
To determine the angle between two vectors. Both the vectors are drawn from a point in such a manner that arrows of both the vectors are outward from that point. Now the smaller angle is called the angle between two vectors
2. TYPES OF VECTORS
i. Equal Vector
Two vectors whose magnitudes are same and direction are either same or parallel are called equal vectors. Negative of a vector means a vector of same magnitude but opposite in direction.
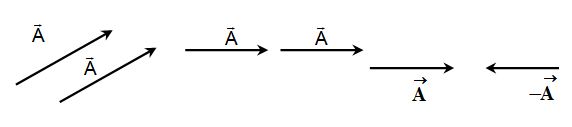
ii. Null vector or zero vector
A vector whose magnitude is zero and direction is arbitrary or unspecified is called a zero or null vector. If a particle starts moving from a point A, but come back to A, then its displacement is a null vector.
Properties of Null Vector
(1) When a vector is multiplied by zero, the result is a null vector, i.e.
(2) The result of addition of a vector to its own negative vector is a null vector i.e.
(3) The addition or subtraction of zero vector from a given vector is a null vector, i.e.
4. The multiplication of a non-zero real number n with a zero vector is again called a null vector. Thus,
For example, the velocity vector of a stationary particle is zero vectors, always.
iii) Unit vector
It is a vector whose magnitude is unity and whose direction is as specified. represents a unit vector whose magnitude is unity and direction is same as that of .
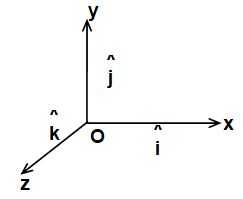
The only importance of unit vector is that it gives or indicated direction. The unit vectors in the directions of x, y and z-axes are represented as respectively
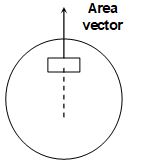
iv. Area vector
The area-vector of a plane figure is a vector whose magnitude is equal to the area of the plane figure and whose direction is from inside towards outside (in case of areas lying on closed figures) when areas are represented by their area vectors, they follow the triangle rule of vector addition.
v. Position Vector
It specifies the position of a point with reference the given set of co-ordinate axes. If we join the origin O with the given point A, then is called position vector of A. It is generally represented by .
magnitude of and
direction of
vi. Displacement vector
If a particle moves from position A to position B, we call as displacement vector. Suppose the particle was originally at the origin O. It moves first to A, then to B, then is called final displacement vector. Symbolically, we state it as;
From the triangle, triangle law of vector addition;
Displacement vector = Final position vector – initial position vector.

vii. Real or polar vectors:
Vectors with inherent direction, such as displacement, force, momentum, velocity, acceleration etc., the direction of real vectors is independent of coordinate system.
viii. Pseudo or axial vectors
Vectors whose direction is fixed by arbitrary rules (such as right hand screw rule). Eg: Angular velocity, all cross products such as torque etc,. When a right handed coordinate system is changed to a left handed coordinate system, a pseudo vector is reversed in direction.
3. ADDITION OF VECTORS
Triangle law
According to this law if the tail of one vector be placed at the head of the other, their sum or resultant is drawn from the tail end of the first to the head end of the other.
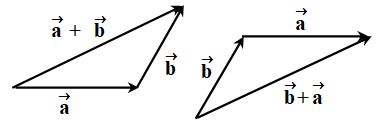
Thus
Polygon laws:
If a number of vectors can be represented fully by the successive sides of a polygon taken in order, then the closing side of that polygon, taken in opposite order, represent their resultant.
i.e., = resultant vector.
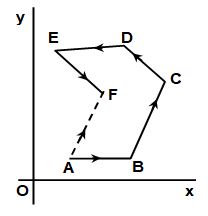
Parallelogram Law of Vector Addition:
According to parallelogram law of vector addition, the resultant is the diagonal of which and are adjacent sides as shown in figure
Magnitude of is given by,
Where θ = angle between . The direction can be found by angle α or β of .
Then,
If θ = 0°, R = maximum = A + B
θ = 180°, R = minimum = A – B
and θ = 90°, R =
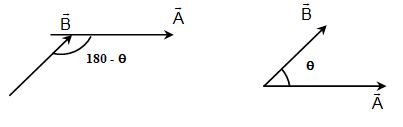
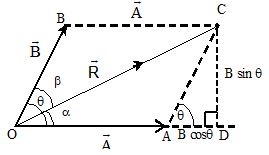
4. SUBTRACTION OF VECTORS
If angle between two vectors is θ. Then angle between will be (180° – θ) as shown in the figure.
Magnitude of
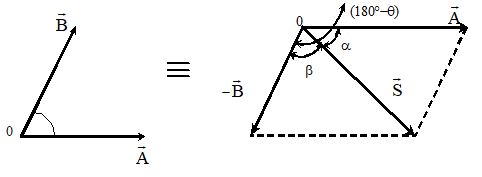
For direction of ,
Then, and
5. COMPONENT OF VECTOR
Two or more vectors which, when compounded in accordance with parallelogram law of vector are said to be components of vector . The most important components with which we are concerned are mutually perpendicular ones along the three co-ordinates axis ox, oy and oz respectively.
Thus, a vector can be written as,
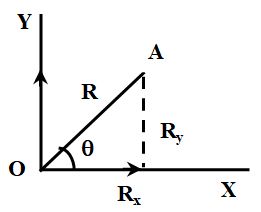
where Rx, Ry, and RZ are the components of in x, y and z axis respectively and , and are the unit vectors along these directions. Therefore the magnitude of resultant,
In case of a vector in x-y plane divided in two components like Rx and Ry. Thus, Rx = R cos θ and Ry = R sin θ
Magnitude of vector is R and direction is unit vector
6. LAMI’S THEOREM FOR FORCES IN EQUILIBRIUM
Sometimes vector has been resolved in two axes x and y not perpendicular to each other. Applying Lami’s theorem, we have,
or,
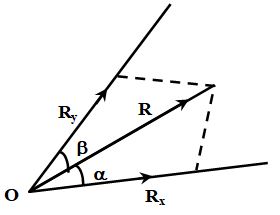
Note: Magnitude of vector components or resultant divided by the sine of the angle between the other two.
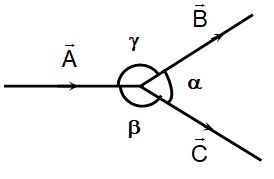
7. PRODUCT OF TWO VECTORS
Vector products are of two types
i) Dot product or scalar product.
ii) Cross product or vector product.
i. Dot Product or Scalar Product
It is called scalar product because the result is a scalar quantity.
Let and are the two vectors and θ is the angle between them. Then scalar product or dot product of is denote by .
where
θ = angle between and .

Properties of Scalar Product:
i) It is commutative
i.e.
ii) It is distributive
i.e.
iii) where m is scalar quantity
iv) In case of unit vector
so,
v) In case of orthogonal
vii) Angle θ between can be calculated as follows
ii. Cross Product or Vector Product
It is called vector product because the result is a vector quantity. Let are two vector and θ is the smaller angle between them. Then the vector product or cross product of , denoted by is defined as = AB sinθ
where is the unit vector perpendicular to the plane containing i.e. perpendicular to the plane containing . Its sense of direction is given by right hand screw rule.
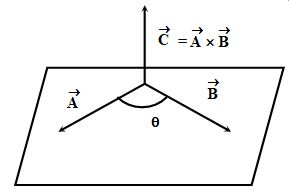
Properties of vector product:
i) ; i.e. commutative law does not hold good. Here,
ii) The vector product is distributive, when the order of the vectors is strictly maintained i.e.
iii)
, where m is scalar quantity.
iv)
v) In case of orthogonal unit vectors in accordance with right hand screw rule,
Application of Product of Two Vectors
1. The area of a parallelogram with adjacent sides .
2. The area of a triangle with adjacent sides .
3. The area of a parallelogram with diagonals
4. Lagrange’s identity: If and are any two vectors, then,
Work Done
In linear motion:
The force applied on a body and it changes its linear position from .
Then, work done = , a scalar quantity
In rotational motion:
The torque applied on a body and it changes its angular position from
Then, work done , a scalar quantity
Energy
In linear motion:
The body is moving linearly with velocity , then kinetic energy of a body is
K = , a scalar quantity =
In rotational motion:
The body is rotating with angular velocity , then kinetic energy of a body is
K = , a scalar quantity
Torque
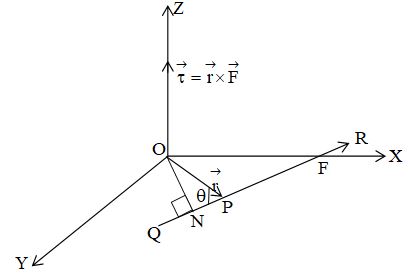
Moment ( ) of a force about a given point O is given by the rotation
where is position vector of any point situated in the direction of the force with reference to the point O taken as origin. Torque is a vector quantity.
Angular Momentum
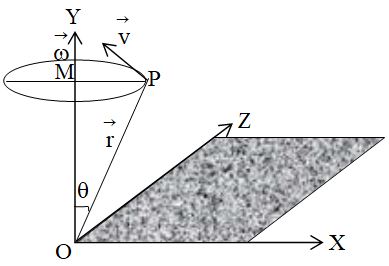
Angular momentum () of a momentum about a given point O is given by the relation , where is position vector of any point situated in the direction of with reference to the point O taken as origin. Angular momentum is a vector quantity.
SOLVED PROBLEMS
1. A vector has a component along the x-axis equal to 4 units and along the y-axis equal to 3 units. Find the magnitude and direction of the vector.
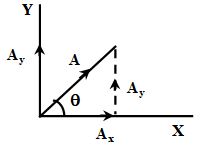
Sol. The given vector in the resultant of two perpendicular vectors.
The resultant has a magnitude A is given by,
= 5 units
The angle θ between and x-axis is given by
vector represented by,
2. Find the resultant of three vectors , as shown in the figure. Radius of the circle is R.
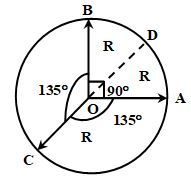
Sol.
is along and its magnitude is 2R cos 45° = R
is along
Hence, its magnitude =
3. Write the unit vector in direction of .
Sol.
The required unit vector is
4. The resultant of two forces is of magnitude P. If be doubled the resultant will be inclined to Q at an angle
(1)0° (2) 30° (3) 60° (4) 90°
Sol. In the figure

= (initially)
If gets doubled,
Then,
From the geometry, diameter (CA) formed angle at circumference is equal to 90° CBA = 90°
Correct choice is (D)
5. A force a body is displaced from position vector to the position vector . Find the work done by this force.
Sol. The body is displace from . Therefore, displacement of the body is
Now, work done by the force is
= 2(-1)+3(-2)+(4)(-3) = -2 – 6 – 12 = -20 J
6. Given and . Find the torque of this force.
Sol. We know that,








