1. TEMPERATURE AND SCALES OF TEMPERATURE
All substances whether they are in the term of solids, liquids or gases expand on heating except water between and and some aqueous solutions. This is known as thermal expansion.
In the case of solids, the increase will be in length, area and volume.
In liquid and gases, only expansion in volume is possible as they don’t possess any fixed shape. In the case of gases, the state of a gas at any instant is represented in terms of its volume, pressure and temperature. Thus, a gas can be heated at constant volume or at constant pressure.
The thermal expansion is different for different substances and it also depends on the state of substance. Thus thermal expansion is an important effect of heat and hence, it has many practical applications, namely the construction of thermometers which are based on the property of expansion of liquids or gases.
Temperature
Temperature is defined as degree of hotness or coldness of a body and its measurement is called thermometry. Temperature may be defined on the thermal condition of body which determines its ability to prompt heat to other bodies.
Important points
(i) Temperature is one of the seven fundamental quantities with dimensions . It is a scalar physical quantity with SI unit Kelvin.
(ii) Two bodies are said to be in Thermal equilibrium if and only if they are at same temperature.
(iii) When heat is given to a body and its state does not change, the temperature of body rises and if heat is taken from a body its temperature falls.
(iv) The temperature of a body can be raised without limit, it cannot be lowered without limit and theoretically limiting low temperature is taken to be zero of the Kelvin scale.
(v) Temperature determines the thermal state of a body whether it can give or receive heat.
Scales of temperature
There are various temperature scales such as Celsius, Fahrenheit, Reaumur, Rankine, Kelvin etc.
In nearly all countries of the world the Celsius scale is used for all popular and commercial and most scientific measurements. Conversion from one scale to other may be made by using the identity.
Where, ‘Z’ is any temperature scale with lower and upper fixed points and respectively
Thermometers and its types
Thermometers
A thermometer is an instrument used to measure temperature of a body. It works by absorbing some heat from the body, so the temperature recorded by it is lesser than actual unless the body is at constant temperature.
Different Types of Thermometers
Thermometers are classified depending upon the physical property of substance as given below.
1. Liquid thermometers based on the thermal expansion of liquids.
2. Gas thermometers which depend on the thermal expansion of gases.
3. Resistance thermometers based on the variation of electrical resistance of metals with temperature.
4. Thermoelectric thermometers which depend on the variation of thermo emf of a thermo couple with the temperature difference between the hot and cold junctions of the thermocouple..
5. Radiation thermometers based on the measurement of the thermal radiation emitted by a body to determine the temperature of the body.
6. Vapour pressure thermometers which depend on the variation of vapour pressure with temperature.
1. Liquid Thermometers
Liquid thermometers depend on the thermal expansion of liquids such as mercury, alcohol etc. The commonly used liquid thermometer is mercury thermometer which uses mercury as the thermometric liquid. The thermometer consists of a cylindrical glass bulb containing mercury to which a graduated capillary tube of uniform bore is attached. The change in temperature is shown by the apparent expansion of mercury in glass and the resulting movement of the mercury meniscus in the system of the thermometer. Suppose V is the volume of the bulb at a given temperature and γ is the coefficient of apparent expansion of mercury in glass i.e., apparent increase in volume per unit volume per unit rise in temperature. If the temperature of the bulb and mercury increases by 10C, the apparent increase in volume of mercury in the bulb = Vγ. The rise in the level of the meniscus in the stem of cross –sectional area A is x so that
As mercury freezes at – 38.80C and boils at 3560C, the mercury thermometer cannot be used for very low or very high temperature measurements. A mercury thermometer can be used to measure temperature up to 3000C. By filling nitrogen gas at high pressure above mercury column, it can be used up to 5000C. Alcohol thermometer is suitable for low temperature measurements as it remains a liquid up to -1120C and has large coefficient of expansion. The measure down to – 2000C, liquid pentane is used.
2. Gas Thermometers
Gases as thermometric substances possess several advantages over liquids. The advantages are
i) They expand much more than liquids for the same rise in temperature.
ii) Gases have much lower thermal capacity than liquids making them more sensitive for changes of temperature.
iii) The expansion of a gas is uniform over a much wider range of temperature than liquids.
iv) Gases have low density.
v) Gases can be obtained of the same purity anywhere.
vi) The scale furnished by different gases are almost identical, since the volume and pressure coefficients of all permanent gases are nearly equal.
Thus, the gas thermometers are taken as primary standards whereas all other thermometers are compared with them for calibration and hence called secondary thermometers.
Principle of Gas Thermometers:
The use of gas as a thermometric substance is based on perfect gas equation. For one mole of a perfect gas, PV = RT is the perfect gas equation. This equation indicates two ways of measuring temperature.
i) Constant Volume Thermometer: Keeping the volume constant, the changes in pressure are noted and the temperature of the body is found. It is found that the change of pressure at constant volume of hydrogen at ordinary temperature is far more uniform than in the case of any other gas. If P0 and P1 are the pressures of hydrogen gas filled in a thermometric bulb at 00C and t0C respectively and β is the pressure coefficient of the gas, then by the definition of the pressure coefficient of a gas (it is the increase in pressure per unit original pressure at 00C per unit rise in temperature), we get
…….. (1)
If the pressure of the gas is P100 at 1000C, then the pressure coefficient can also be given as
…….. (2)
From equation (1) and (2)
where t is the temperature to be measured.
ii) Constant Pressure Thermometer: Keeping pressure constant, the changes in volume are measured to determine the temperature. With air as thermometric substance Callendar developed a constant pressure air thermometer which can be used to measure temperatures up to 6000C
But constant volume hydrogen thermometers can be used over a wide range of temperature from -2000C to 5000C with platinum thermometric bulb. It can be used upto11000C with glazed porcelain bulb. For still higher temperatures up to 15000C nitrogen is used as thermometric substance and for low temperatures below – 2000C helium is often used.
3. Resistance Thermometers
The electrical resistance of a platinum wire increases gradually and uniformly with temperature over a wide range. If R0, R100 and R1 are the resistances of a platinum wire at 00C and t0C respectively, then
…….. (3)
…….. (4)
Where α is the temperature coefficient of resistance which is defined as the increase in resistance per unit original resistance at 00C per unit rise in temperature and t is the final temperature.
From Eq. (3)
…….. (5)
From equation (4)
…….. (6)
From equation (5) and (6)
…….. (7)
Electrical resistance thermometers can be used over a wide range of -2720C to 12000C.
4. Thermoelectric Thermometers
When the junctions of two dissimilar metals are maintained at different temperatures an emf is generated. This effect is called thermoelectric effect or Seebeck effect. The pair of metals used to generate the emf is referred to as a thermocouple. The emf causes a current in the circuit as shown by the deflection produced in a galvanometer G introduced in the circuit in fig.
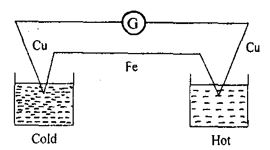
The emf increases with the temperature difference between the hot and cold junctions of a thermocouple. It reaches a maximum value at a certain temperature of the hot junction called neutral temperature. Thermoelectric thermometer is based on the thermoelectric effect. Keeping the cold junction in melting ice and heating the hot junction to different temperatures determined by a constant volume hydrogen thermometer, the emf at each temperature is measured. A calibration curve is drawn plotting emf against temperature. Then the temperature of any body can be found from the graph by measuring the emf, keeping the body in contact with the hot junction.
Thermocouples are used to measure temperatures in the range of -2500C to 30000C.
5. Radiation Thermometers
Thermal radiation can be used to measure high temperatures since the radiation from a body depends only on its temperature. Such devices are called radiation pyrometers. Radiation thermometers are used to measure temperatures above 30000C.
6. Vapour Pressure Thermometers
These depend on the fact that the saturation pressure of a pure liquid is a function of its temperature only. Such thermometers can be used below -2680C to about -2720C.
2. EXPANSION OF SOLIDS
Thermal Expansion
In general, atom are arranged in regular order in the form of lattice in solids. The inter atomic force of attraction depends on the distance between them. For a particular distance these attractive forces are maximum and potential energy curve indicates minimum value. In the state of equilibrium, the atom vibrate about a fixed point, called as equilibrium position in the lattice. At any particular temperature, the atoms are in specific state of vibration and the interatomic distances also have specific values.
Then a solid can be considered as an assembly of vibrators, vibrating about a periodic array of equilibrium positions.
It is clear that as the temperature increases, the amplitude of their vibration increases. This may not lead to thermal expansion of solids. If the oscillators are purely harmonic, the potential energy of an oscillator or vibrator is a parabolic function of its position as shown in the figure and symmetric. As temperature increases the vibrational energy and amplitude of oscillation of the oscillation increases, but their mean position remains the same, so that the average inter atomic spacing () remains the same. If there is no change in the average inter atomic distance with the increase of temperature, there is no thermal expansion. Thus, if the lattice vibrations are purely harmonic, the potential energy curve is parabola indicating that there is no thermal expansion.
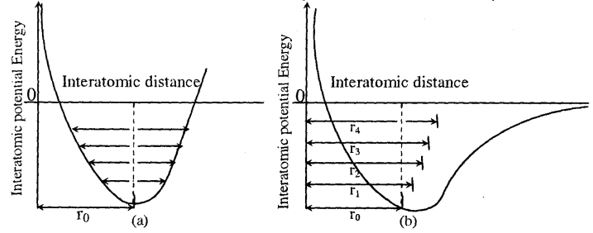
Interatomic potential energy as a function of interatomic distance for (a) a harmonic oscillator (b) and for an anharmonic oscillator r0 being average interatomic spacing at zero temperature.
In the given figure, inter atomic potential energy as a function of inter atomic distance for a harmonic oscillator (a) and for an anharmonic oscillator (b).
Here, = the average inter atomic spacing at zero temperature
If the oscillators are anharmonic, that is, if the potential energy of an oscillator is an asymmetric function of its position, the average position of oscillator increases with increase in temperature. The average inter atomic distance also increases from with increase in temperature. Hence the thermal expansion is observed. It can be concluded that the thermal expansion of anharmonicity of the lattice oscillations. If the anharmonicity were not there in the lattice oscillations, there would be no thermal expansion.
Coefficient of linear expansion (α)
The coefficient of linear expansion of the material of a solid is the ratio of the increase in its length to its original length per rise of temperature. Thus, the coefficient of linear expansion (α) is
Where, is the length at temperature at (initial length) is final length at temperature and is the rise in temperature, is the change in length. Then,
Note: α does depends slightly on the temperature but its variation is usually small enough to be negligible, even over a temperature range of . We will always assume that is constant.
Coefficient of Areal Expansion (β)
Suppose that the temperature of a metallic sheet of area ‘ ’ is changed from to . It is found experimentally that, if is not too large, the corresponding change in area of the rod is directly proportional to and .
Then,
and or,
introducing a proportionality constant or coefficient of areal expansion (β) of a metallic sheet.
or,
Coefficient of Volume Expansion (γ)
Similarly, the coefficient of cubical expansion or volume expansion (γ) of a metallic cube is the ratio of increase in its volume to its original volume per or rise to temperature.
Thus the coefficient of volume expansion (γ) is given by,
Relation between α, β and γ
For an isotropic solid,
We can write, and
Hence,
α values of different materials
Table shows the values of the coefficient of linear expansion ‘α’ for different materials.
| Material | |
| Aluminium | 23 |
| Lead | 29 |
| Brass | 19 |
| Bronze | 18 |
| Copper | 17 |
| Gold | 14 |
| Nickel | 13 |
| Concrete | 12 |
| Iron | 12 |
| Pyrex glass | 3.3 |
| Invar | 0.9 |
| Silicon | 0.5 |
Examples for expansion of Solids
1. In laying down a railway track a small gap is given between the ends of two consecutive rails. This is to allow for linear expansion of rails in summer.
2. The telegraphic wires between the two poles are loosely stretched to allow for their contraction in the winter season.
3. The diameter of the iron rim is slightly less than the wooden cart wheel on which it has to be fixed. The iron rim is heated and then slipped over the cart wheel and is allowed to cool. The iron rim controls and grips the wheel tightly.
4. When a wire is fused into glass it should have the same coefficient of linear expansion as that of the glass. The wire is fused into the glass and scaled at temperature where it becomes soft. When it is cooled, if the glass contracts more than that of the wire the glass breaks, on the other hand if the wire contracts more than that having the same value of ‘ ’ as that of the glass is fused into glass.
5. All the measuring tapes and rods are made up of steel because of its least coefficient of expansion with the change in temperature.
6. When a drop of water falls on a hot glass chimney the portion of the spot where the water falls contracts and due to uneven contraction glass breaks.
3. EXPANSION OF LIQUIDS
The Real and apparent expansion of liquids
When a liquid in a container is heated, both the liquid and the container expand. Hence, in case of liquids, there are two types of expansions. They are
(i) apparent expansion and
(ii) absolute or real expansion
When a liquid is heated in a container, the observed change in volume of the liquid relative to the container is called the apparent expansion of the liquid. If the real change in volume of the liquid is considered, then it is called the real or absolute expansion of the liquid. In general, the apparent expansion is always less than the real expansion of the liquid.
(i) Coefficient of apparent expansion of a liquid
The coefficient of apparent expansion of a liquid is the ratio of the apparent increase in volume to its original volume per rise of temperature.
If and are the apparent volumes of a liquid at temperatures and respectively, then the coefficient of apparent expansion of the liquid is
or,
or,
(ii) Coefficient of real or absolute expansion of a liquid
The coefficient of real expansion of a liquid is the ratio of the real increase in volume to its original volume per rise of temperature.
If and are the real volumes of a liquid at temperatures and respectively, then the coefficient of real expansion of the liquid is
or,
or,
Derivation of the relationship between coefficients of apparent and real expansions of a liquid
As shown in figure a round bottom end flask with a long neck is filled with a liquid of volume ‘v’ at room temperature up to the mark A. When the liquid is heated to , the flask and the liquid expand simultaneously. Considering the expansion of flask only, the level of the liquid falls from A to B. Thus the length AB represents the expansion of the flask. Now if the liquid alone expands, the liquid level rises from B to C. Hence the length BC represents the real expansion of the liquid.
But in the experiment we observe the expansion of the liquid from A to C. Thus the length AC represents the apparent expansion of the liquid. If ‘a’ is the area of cross section of the neck, then,
Coefficient of volume expansion of the flask
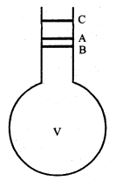
or,
Coefficient of apparent expansion of the liquid
or,
and, coefficient of real expansion of the liquid
or,
But from figure, we know that,
BC = AB + AC
Then,
Hence,
From this equation, we can write that the coefficient of real expansions of liquid is the sum of the coefficients of volume expansion of the glass container and the apparent expansion of the liquid.
| Liquid | |
| Mercury | 1.8 |
| Water | 2.1 |
| Glycerol | 4.7 |
| Olive oil | 7.0 |
| Turpentine | 9.7 |
| Carbon disulphide | 11.9 |
| Ether | 16.3 |
Variation of the density of a liquid with temperature
The volume of a liquid increases when it is heated but its mass does not change. Hence, the density (ρ) decreases with increase in temperature.
i.e.
If and are the volumes and and are the densities of a liquid of mass ‘m’ at temperature and respectively, then,
Then,
But the coefficient of real expansion of a liquid is
or,
or,
or,
For small values of and small temperature difference,
Determination of Determination of γa by specific gravity bottle method
A dry empty specific gravity bottle of volume ‘v’ is taken and its mass is determined using a common balance. The specific gravity bottle is completely filled with the given liquid at the room temperature and its mass is determined. The bottle with the filled liquid is now held in the water bath with the neck and the stopper projecting above the water level as shown in figure. The bottle with the liquid is now heated to a temperature which remains constant for about ten minutes. The temperature is noted using a thermometer. Since the temperature is raised from , the liquid expands and oozes out of the stopper. The expelled liquid is removed using a piece of blotting paper. The bottle is heated to until no more liquid oozes out. Then the bottle is taken out of the water bath and is cooled till it attains the room temperature . The outer surface of the bottle is cleaned with blotting paper and its mass with the remaining liquid is determined. The coefficient of the apparent expansion of the liquid is determined using the formula
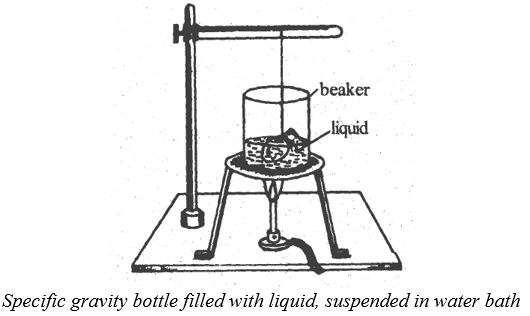
Theory
Mass of specific gravity bottle =
Mass of the bottle + liquid at =
Mass of the liquid =
Initial temperature =
Density of the liquid at
volume of the liquid at
The liquid expands to a volume = at
The coefficient of apparent expansion of the liquid,
Thus, the coefficient of apparent expansion of the given liquid can be determined.
Anomalous Expansion of water
Generally liquids expand on heating. But water at 00C on heating contracts up to 40C . It expands beyond 40C like any other liquid. On cooling, water contracts from 1000C to 40C and expands from 40C to 00C. This is called anomalous expansion of water.
When water freezes into ice it expands. A few other substances such as iron, bismuth, antimony expand when they solidify and such substances are useful for costing.
The anomalous expansion of water is demonstrated by Hope’s apparatus.
4. EXPANSION OF GASES
Gases have no definite shape, therefore gases have only volume expansion. Since the expansion of container is negligible in comparison to the gases, therefore gases have only real expansion.
Volume and pressure coefficient of a gas
When heat is given to a gas, both its volume and pressure undergo changes. Pressure remaining constant, the volume of a gas increases with increase in temperature. Similarly volume remaining constant, the pressure of a gas increases with increase in temperature. Thus, a gas has two different coefficient of expansion,
1. The coefficient of expansion of a gas at constant pressure called volume coefficient and
2. The coefficient of expansion of a gas at constant volume called pressure coefficient
1. Volume coefficient of a gas
The volume coefficient of a gas is the ratio of the increase in its volume per rise of temperature, to its volume at at constant pressure.
Let and be the volumes of a gas at temperatures and respectively at constant pressure.
Hence, the increase in the volume of the gas for rise in temperature =
The increase in the volume of the gas per
According to the definition, the volume coefficient of the gas is
or,
or, …….. (1)
Let be the volumes of a gas at temperatures , respectively at constant pressure.
Then from eq(1) we can write,
and
or,
or,
or,
…….. (2)
2. Pressure coefficient (β) of a gas
The pressure coefficient (β) of a gas is the ratio of the increase in its pressure per rise of temperature to its pressure at at constant volume.
Let be the pressures of a gas at constant volume and at temperatures respectively.
Hence, the increase in the pressure of the gas for rise in temperature =
The increase in the pressure of gas per
According to definition, the pressure coefficient (β) of the gas is,
…….. (1)
Thus,
or, …….. (2)
Let be the pressures of a gas at constant volume and at temperature respectively. Then from equation (2), we can write,
and,
Then,
or,
or,
or,
…….. (3)
Relation between the α and β
Let and be the volume and pressure of a given mass of gas at .
Keeping pressure constant, if the temperature is raised to , then assume that the volume changes to .
Thus, …….. (1)
Where, α is the volume coefficient of the gas.
Since, pressure is constant, at , we can write
….. (2)
Similarly, keeping the volume constant at v, if the temperature of the gas is increased from , assuming that the pressure of gas changes to p, thus
…….. (3)
Where, β is the pressure coefficient of the gas.
Since, the volume is constant at , the volume of the gas
….. (4)
From equation (2) and (4), we get,
or,
or,
Hence, for gases,
Volume coefficient (α) = Pressure coefficient (β)
Note:
Experimental Determination Of Volume Coefficient (α)
As shown in figure, the Regnault’s apparatus consists of a bulb (A) of about 700 cc. The bulb is connected to a manometer BCD through a narrow horizontal tube (capillary tube) F. The manometer is placed in a constant temperature water bath. It is calibrated to give the volume of the gas. The manometer has a tap T at its bottom which is used for leveling mercury in the manometer limbs.
The bulb with the capillary tube is filled with a gas using the side tube E. The bulb is kept in a container with melting ice (0oC). It is allowed for some time so that the gas attains a temperature 0oC. The levels of mercury in BC and CD of manometer are made equal by taking out mercury through T at 0oC.
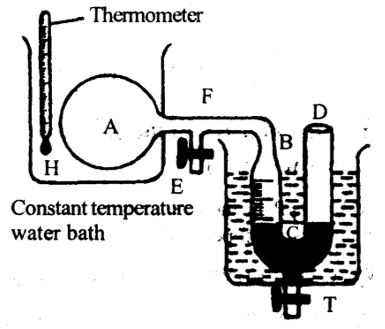
Thus, the pressure of the gas inside the bulb is equal to atmospheric pressure. From the calibrations the volume of the gas can be obtained
Now, the gas in the bulb is heated. Hence, the gas expands and pushes the mercury level in BC down. At a given temperature toC, the mercury levels in the manometer are again made equally by taking out mercury through T. Thus, the pressure of the gas in the bulb A is equal to the atmospheric pressure which is constant. the volume of the gas V at toC can be estimated from calibration on the manometer. Thus, the volume coefficient (α) of air can be calculated using the formula
Conducting the experiment for different gases it can be shown that volume coefficient is same for all gases.
Experimental Determination Of Pressure Coefficient (β) Of A Gas By Jolly’s Bulb Apparatus
Figure shows the Jolly’s bulb apparatus. In this a glass bulb B is attached to a glass tube bent at C and D. The other end of the glass tube is connected to a reservoir R by a rubber tubing. The system is fitted to a wooden plank which contains a metre scale. The reservoir can be raised or lowered and can be fixed at any position with the help of screw arranged to the stand. A part of the bent tube, the rubber tubing and the reservoir R are filled with mercury.
The volume of the gas in the bulb can be kept constant by bringing the mercury level up to the mark M in the narrow tube during the experiment. The levels of mercury can be noted using the meter scale.
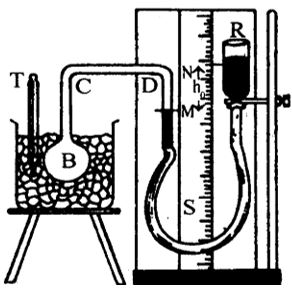
The glass bulb is immersed in an ice bath containing ice cubes (at 0oC). Then the reservoir R is adjusted such that the mercury level in the closed limb is at the mark M. The difference of levels, NM = ho is noted. Thus the pressure (Po) of the gas at 0oC is Po=H ho where ‘H’ is the atmospheric pressure. That is Po = H + ho if N is above M and Po = H – ho if N is below M.
Now, the glass bulb is heated to a fixed temperature toC. Hence, the gas expands and the mercury level in the closed limb is pushed down of the mark M. Again, the reservoir is adjusted such that the mercury level is brought back to the mark M, thus keeping the volume of the gas constant. The difference of levels of mercury h1 is noted. Thus, the pressure (Pt) of the gas in the bulb is .
Finally the pressure coefficient (β) of the gas is calculated using the formula
It can be shown that the value of the pressure coefficient is same for all gases by conducting the experiment for a number of different gases.
CALORIMETRY
HEAT
1. The form of energy which is exchanged among various bodies or system on account of temperature difference is defined as heat.
2. We can change the temperature of a body by giving heat (temperature rises) or by removing heat (temperature falls) from body.
3. The amount of heat (Q) is given to a body depends upon it’s mass (m), change in it’s temperature and nature of material i.e. ; where c = specific heat of material.
4. Heat is a scalar quantity. It’s units are joule, erg, cal, kcal etc.
5. The calorie (cal) is defined as the amount of heat required to raise the temperature of 1 gm of water from 14.5°C to 15.5°C.
Also 1 kcal = 1000 cal = 4186 J and 1 cal = 4.18 J
6. British Thermal Unit (BTU) : One BTU is the quantity of heat required to raise the temperature of one pound (1lb ) of water from 63°F to 64°F
1 BTU = 778 ft. lb = 252 cal = 1055 J
7. In solids thermal energy is present in the form of kinetic energy, in liquids, in the form of translatory energy of molecules. In gas it is due to the random motion of molecules.
8. Heat always flows from a body of higher temperature to lower temperature till their temperature becomes equal (Thermal equilibrium).
9. The heat required for a given temperature increase depends only on how many atoms the sample contains, not on the mass of an individual atom.
6. SPECIFIC HEAT
When a body is heated it’s temperature rises (except during a change in phase).
1. Gram specific heat : The amount of heat energy required to raise the temperature of unit mass of a body through 1°C (or K) is called specific heat of the material of the body.
If Q heat changes the temperature of mass m by then specific heat
(i) Units : Calorie/gm ⨯ °C (practical), J/kg ⨯ K (S.I.) Dimension :
(ii) For an infinitesimal temperature change d and corresponding quantity of heat dQ. Specific heat
2. Molar specific heat : Molar specific heat of a substance is defined as the amount of heat required to raise the temperature of one gram mole of the substance through a unit degree it is represented by (capital) C.
Molar specific heat (C) = M⨯Gram specification (c)
(M = Molecular mass of substance)
Units : calorie/mole ⨯ °C (practical); J/mole ⨯ kelvin (S.I.) Dimension :
7. SPECIFIC HEAT OF SOLIDS
When a solid is heated through a small range of temperature, its volume remains more or less constant. Therefore specific heat of a solid may be called its specific heat at constant volume CV.
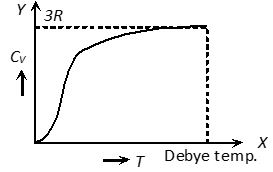
1) From the graph it is clear that at T = 0, CV tends to zero
2) With rise in temperature, CV increases and at a particular temperature (called Debey’s temperature) it becomes constant = 3R = 6 cal/mole ⨯ kelvin = 25 J/mole ⨯ kelvin
3) For most of the solids, Debye temperature is close to room temperature.
4) Dulong and Petit law : Average molar specific heat of all metals at room temperature is constant, being nearly equal to 3R = 6 cal. mole–1 K–1 = 25 J mole–1 K–1, where R is gas constant for one mole of the gas. This statement is known as Dulong and Petit law.
5) Debey’s law : It was observed that at very low temperature molar specific heat (exception are Sn, Pb and Pt)
6) Specific heat of ice : In C.G.S. In S.I. cice .
Specific heat of some solids at room temperature and atmospheric pressure
| Substance | Specific heat (J-kg–1 K–1) | Molar specific heat (J-g mole–1 K–1) |
| Aluminium | 900.0 | 24.4 |
| Copper | 386.4 | 24.5 |
| Silver | 236.1 | 25.5 |
| Lead | 127.7 | 26.5 |
| Tungsten | 134.4 | 24.9 |
8. SPECIFIC HEAT OF LIQUID (WATER)
(1) Among all known solids and liquids specific heat of water is maximum i.e. water takes more time to heat and more time to cool w.r.t. other solids and liquids.
(2) It is observed that by increasing temperature, initially specific heat of water goes on decreasing, becomes minimum at 37°C and then it start increasing. Specific heat of water is –
(This value is obtained between the temperature 14.5°C to 15.5°C)
(3) The variation of specific heat with temperature for water is shown in the figure. Usually this temperature dependence of specific heat is neglected.
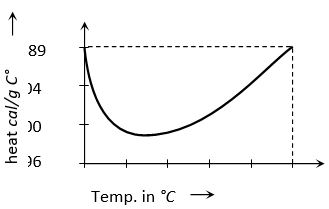
(4) As specific heat of water is very large; by absorbing or releasing large amount of heat its temperature changes by small amount. This is why, it is used in hot water bottles or as coolant in radiators.
9. SPECIFIC HEAT OF GASES
(1) In case of gases, heat energy supplied to a gas is spent not only in raising the temperature of the gas but also in expansion of gas against atmospheric pressure.
(2) Hence specific heat of a gas, which is the amount of heat energy required to raise the temperature of one gram of gas through a unit degree shall not have a single or unique value.
(3) If the gas is compressed suddenly and no heat is supplied from outside i.e. Q = 0, but the temperature of the gas raises on the account of compression.
(4) If the gas is heated and allowed to expand at such a rate that rise in temperature due to heat supplied is exactly equal to fall in temperature due to expansion of the gas. i.e. = 0
(5) If rate of expansion of the gas were slow, the fall in temperature of the gas due to expansion would be smaller than the rise in temperature of the gas due to heat supplied. Therefore, there will be some net rise in temperature of the gas i.e. T will be positive.
Positive
(6) If the gas were to expand very fast, fall of temperature of gas due to expansion would be greater than rise in temperature due to heat supplied. Therefore, there will be some net fall in temperature of the gas i.e. will be negative.
= Negative
Hence the specific heat of gas can have any positive value ranging from zero to infinity. Further it can even be negative. The exact value depends upon the mode of heating the gas. Out of many values of specific heat of a gas, two are of special significance, namely CP and CV , in the chapter “Kinetic theory of gases” we will discussed this topic in detail.
Specific heat of steam :
10. PHASE CHANGE AND LATENT HEAT
(1) Phase : We use the term phase to describe a specific state of matter, such as solid, liquid or gas. A transition from one phase to another is called a phase change.
(i) For any given pressure a phase change takes place at a definite temperature, usually accompanied by absorption or emission of heat and a change of volume and density.
(ii) In phase change ice at 0°C melts into water at 0°C. Water at 100°C boils to form steam at 100°C.
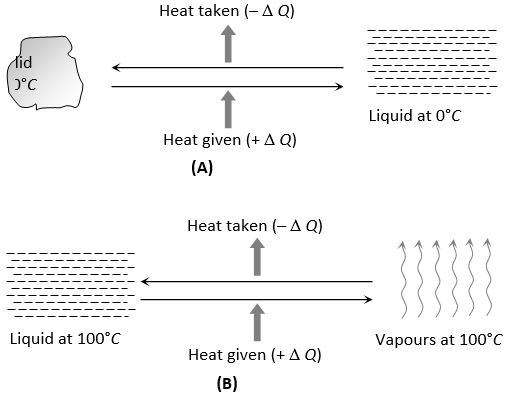
(iii) In solids, the forces between the molecules are large and the molecules are almost fixed in their positions inside the solid. In a liquid, the forces between the molecules are weaker and the molecules may move freely inside the volume of the liquid. However, they are not able to come out of the surface. In vapours or gases, the intermolecular forces are almost negligible and the molecules may move freely anywhere in the container. When a solid melts, its molecules move apart against the strong molecular attraction. This needs energy which must be supplied from outside. Thus, the internal energy of a given body is larger in liquid phase than in solid phase. Similarly, the internal energy of a given body in vapour phase is larger than that in liquid phase.
(iv) In case of change of state if the molecules come closer, energy is released and if the molecules move apart, energy is absorbed.
(2) Latent heat : The amount of heat required to change the state of the mass m of the substance is written as : Q = mL, where L is the latent heat. Latent heat is also called as Heat of Transformation. It’s unit is cal/gm or J/kg and Dimension:
(i) Latent heat of fusion : The latent heat of fusion is the heat energy required to change 1 kg of the material in its solid state at its melting point to 1 kg of the material in its liquid state. It is also the amount of heat energy released when at melting point 1 kg of liquid changes to 1 kg of solid. For water at its normal freezing temperature or melting point (0°C), the latent heat of fusion (or latent heat of ice) is
(ii) Latent heat of vaporisation : The latent heat of vaporisation is the heat energy required to change 1 kg of the material in its liquid state at its boiling point to 1 kg of the material in its gaseous state. It is also the amount of heat energy released when 1 kg of vapour changes into 1 kg of liquid. For water at its normal boiling point or condensation temperature (100°C), the latent heat of vaporisation (latent heat of steam) is
(iii) Latent heat of vaporisation is more than the latent heat of fusion. This is because when a substance gets converted from liquid to vapour, there is a large increase in volume. Hence more amount of heat is required. But when a solid gets converted to a liquid, then the increase in volume is negligible. Hence very less amount of heat is required. So, latent heat of vaporisation is more than the latent heat of fusion.
11. THERMAL CAPACITY AND WATER EQUIVALENT
(1) Thermal capacity : It is defined as the amount of heat required to raise the temperature of the whole body (mass m) through 0°C or 1K.
Thermal capacity= mc =
The value of thermal capacity of a body depends upon the nature of the body and its mass.
Dimension : , Unit : cal/°C (practical) Joule/k (S.I.)
(2) Water Equivalent : Water equivalent of a body is defined as the mass of water which would absorb or evolve the same amount of heat as is done by the body in rising or falling through the same range of temperature. It is represented by W.
If m = Mass of the body, c = Specific heat of body, = Rise in temperature.
Then heat given to body ….. (i)
If same amount of heat is given to W gm of water and its temperature also rises by . Then heat given to water … (ii) [As ]
From equation (i) and (ii)
Water equivalent (W) = mc gm
(i) Unit : Kg (S.I.) Dimension :
(ii) Unit of thermal capacity is J/kg while unit of water equivalent is kg.
(iii) Thermal capacity of the body and its water equivalent are numerically equal.
(iv) If thermal capacity of a body is expressed in terms of mass of water it is called water-equivalent of the body.
12. SOME IMPORTANT TERMS
(1) Evaporation : Vaporisation occurring from the free surface of a liquid is called evaporation. Evaporation is the escape of molecules from the surface of a liquid. This process takes place at all temperatures and increases with the increase of temperature. Evaporation leads to cooling because the faster molecules escape and, therefore, the average kinetic energy of the molecules of the liquid (and hence the temperature) decreases.

(2) Melting (or fusion)/freezing (or solidification) : The phase change of solid to liquid is called melting or fusion. The reverse phenomenon is called freezing or solidification.

When pressure is applied on ice, it melts. As soon as the pressure is removed, it freezes again. This phenomenon is called regelation.
(3) Vaporisation/liquefication (condensation) : The phase change from liquid to vapour is called vaporisation. The reverse transition is called liquefication or condensation.
(4) Sublimation : Sublimation is the conversion of a solid directly into vapours. Sublimation takes place when boiling point is less than the melting point. A block of ice sublimates into vapours on the surface of moon because of very very low pressure on its surface. Heat required to change unit mass of solid directly into vapours at a given temperature is called heat of sublimation at that temperature.
(5) Hoar frost : Direct conversion of vapours into solid is called hoar frost. This process is just reverse of the process of sublimation, e.g., formation of snow by freezing of clouds.

(6) Vapour pressure : When the space above a liquid is closed, it soon becomes saturated with vapour and a dynamic equilibrium is established. The pressure exerted by this vapour is called Saturated Vapour Pressure (S.V.P.) whose value depends only on the temperature – it is independent of any external pressure. If the volume of the space is reduced, some vapour liquefies, but the pressure is unchanged.
A saturated vapour does not obey the gas law whereas the unsaturated vapour obeys them fairly well. However, a vapour differs from a gas in that the former can be liquefied by pressure alone, whereas the latter cannot be liquefied unless it is first cooled.
(7) Boiling : As the temperature of a liquid is increased, the rate of evaporation also increases. A stage is reached when bubbles of vapour start forming in the body of the liquid which rise to the surface and escape. A liquid boils at a temperature at which the S.V.P. is equal to the external pressure. It is a fast process. The boiling point changes on mixing impurities.

(8) Dew point : It is that temperature at which the mass of water vapour present in a given volume of air is just sufficient to saturate it, i.e. the temperature at which the actual vapour pressure becomes equal to the saturated vapuor pressure.
(9) Humidity : Atmospheric air always contains some water vapour. The mass of water vapour per unit volume is called absolute humidity.
The ratio of the mass of water vapour (m) actually present in a given volume of air to the mass of water vapour (M) required to saturate the same volume at the same temperature is called the relative humidity (R.H.). Generally, it is expressed as a percentage, i.e.,
R.H. May also be defined as the ratio of the actual vapour pressure (p) of water at the same temperature, i.e.
Thus R.H. may also be defined as
(10) Variation of melting point with pressure : For those substances with contract on melting (e.g. water and rubber), the melting point decreases with pressure. The reason is the pressure helps shrinking and hence melting. Most substances expand on melting. (e.g. max, sulphur etc.)
An increase of pressure opposes the melting of such substances and their melting point is raised.
(11) Variation of latent heat with temperature and pressure : The latent heat of vapourization of a substance varies with temperature and hence pressure because the boiling point depends on pressure. It increases as the temperature is decreased. For example, water at 1 atm boils at 100°C and has latent heat 2259 Jg–1 but at 0.5 atm it boils at 82°C and has latent heat 2310 Jg–1
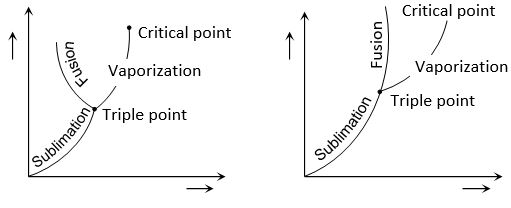
The latent heat of fusion shows similar but less pronounced pressure dependence.
The figures show the P-T graphs for (a) a substance (e.g., water) which contracts on melting an (b) a substance (e.g. wax) which expands on melting. The P–T graph consists of three curves.
(i) Sublimation curve which connects points at which vapour (V) and solid (S) exist in equilibrium.
(ii) Vapourization curve which shows vapour and liquid (L) existing in equilibrium.
(iii) Fusion curve which shows liquid and solid existing in equilibrium.
The three curves meet at a single point which is called the triple point. It is that unique temperature-pressure point for a substance at which all the three phases exist in equilibrium.
(12) Freezing mixture : If salt is added to ice, then the temperature of mixture drops down to less than 0°C. This is so because, some ice melts down to cool the salt to 0°C. As a result, salt gets dissolved in the water formed and saturated solution of salt is obtained; but the ice point (freeing point) of the solution formed is always less than that of pure water. So, ice cannot be in the solid state with the salt solution at 0°C. The ice which is in contact with the solution, starts melting and it absorbs the required latent heat from the mixture, so the temperature of mixture falls down.
13. JOULE’S LAW (HEAT AND MECHANICAL WORK)

Whenever heat is converted into mechanical work or mechanical work is converted into heat, then the ratio of work done to heat produced always remains constant. i.e.
This is Joule’s law and J is called mechanical equivalent of heat.
(1) From W = JQ if Q = 1 then J = W. Hence the amount of work done necessary to produce unit amount of heat is defined as the mechanical equivalent of heat.
(2) J is neither a constant, nor a physical quantity rather it is a conversion factor which used to convert Joule or erg into calorie or kilo calories vice-versa.
(3) Value of J =4.2 .
.
(4) When water in a stream falls from height h, then its potential energy is converted into heat and temperature of water rises slightly.
From W = JQ mgh = J (mc )
[where m = Mass of water, c = Specific heat of water, = temperature rise]
Rise in temperature
(5) The kinetic energy of a bullet fired from a gun gets converted into heat on striking the target. By this heat the temperature of bullet increases by .
From W = JQ
[where m = Mass of the bullet, v = Velocity of the bullet, c = Specific heat of the bullet]
Rise in temperature
If the temperature of bullet rises upto the melting point of the bullet and bullet melts then.
From W = J(QTemperature change + QPhase change)
; L = Latent heat of bullet
Rise in temperature
(6) If m kg ice-block falls down through some height (h) and melts partially (m’ kg) then its potential energy gets converted into heat of melting.
From W = JQ
If ice-block melts completely then m‘ = m
14. PRINCIPLE OF CALORIMETRY
Calorimetry means ‘measuring heat’.
When two bodies (one being solid and other liquid or both being liquid) at different temperatures are mixed, heat will be transferred from body at higher temperature to a body at lower temperature till both acquire same temperature. The body at higher temperature releases heat while body at lower temperature absorbs it, so that
Heat lost = Heat gained
i.e. principle of calorimetry represents the law of conservation of heat energy.
(1) Temperature of mixture (θmix) is always ≥ lower temperature (θL) and ≤ higher temperature (θH), i.e., .
It means the temperature of mixture can never be lesser than lower temperatures (as a body cannot be cooled below the temperature of cooling body) and greater than higher temperature (as a body cannot be heated above the temperature of heating body). Furthermore usually rise in temperature of one body is not equal to the fall in temperature of the other body though heat gained by one body is equal to the heat lost by the other.
(2) Mixing of two substances when temperature changes only : It means no phase change. Suppose two substances having masses , gram specific heat , temperatures and are mixed together such that temperature of mixture at equilibrium is θmix
Hence, Heat lost = Heat gained
Temperature of mixture in different cases
| Condition | Temperature of mixture |
| If bodies are of same material i.e. c1 = c2 | |
| If bodies are of same mass m1 = m2 | |
| If m1 = m2 and c1 = c2 |
(3) Mixing of two substances when temperature and phase both changes or only phase changes:
A very common example for this category is ice-water mixing.
Suppose water at temperature θW°C is mixed with ice at 0i°C, first ice will melt and then it’s temperature rises to attain thermal equilibrium. Hence; Heat given = Heat taken
(i) If then
(ii) By using this formulae if then take
15. HEATING CURVE
If to a given mass (m) of a solid, heat is supplied at constant rate P and a graph is plotted between temperature and time, the graph is as shown in figure and is called heating curve. From this curve it is clear that
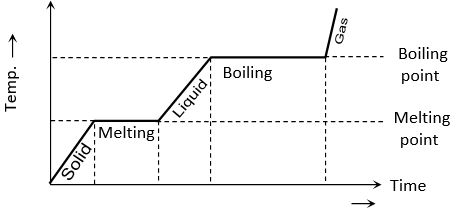
(1) In the region OA temperature of solid is changing with time so, [as Q = PΔt] But as (ΔT/Δt) is the slope of temperature-time curve
i.e. specific heat (or thermal capacity) is inversely proportional to the slope of temperature-time curve.
(2) In the region AB temperature is constant, so it represents change of state, i.e., melting of solid with melting point T1. At A melting starts and at B all solid is converted into liquid. So between A and B substance is partly solid and partly liquid. If LF is the latent heat of fusion.
[as ]
or LF length of line AB
i.e. Latent heat of fusion is proportional to the length of line of zero slope. [In this region specific heat ]
(3) In the region BC temperature of liquid increases so specific heat (or thermal capacity) of liquid will be inversely proportional to the slope of line BC
i.e.,
(4) In the region CD temperature is constant, so it represents the change of state, i.e., boiling with boiling point T2.
At C all substance is in liquid state while at D in vapour state and between C and D partly liquid and partly gas. The length of line CD is proportional to latent heat of vaporisation
i.e., LV Length of line CD [In this region specific heat ]
(5) The line DE represents gaseous state of substance with its temperature increasing linearly with time. The reciprocal of slope of line will be proportional to specific heat or thermal capacity of substance in vapour state.
SOLVED EXAMPLES
1. At what temperature, if any do the following pairs of scales gives the same reading
a) Celsius and Fahrenheit
b) Fahrenheit and Kelvin
c) Kelvin and Celsius?
Sol. If the temperature is at which the reading of two scales coincides, then from
a)
or,
or, i.e. reading of Celsius and Fahrenheit scale coincides at .
b)
or, θ = 574.6
i.e. reading of Fahrenheit and Kelvin scale coincides at 574.6°.
c) which is not possible
So, reading of celsius and Kelvin scale can never coincide.
2. State and explain three reasons why water is considered unsuitable for use in thermometers?
Sol. Water is unsuitable in thermometers because
(i) Due to anomalous behaviour its expansion is not uniform, so the temperature scale will not be uniform.
(ii) Due to large specific heat and low thermal conductivity it will not respond quickly to change in temperature.
(iii) Its freezing point is while boiling point , so the temperature range over which it can be used will be small i.e. from to .
It is transparent, sticks to glass wall and has high rate of evaporation.
3. The length of the railway line between two stations is 20km. It is laid with 300 rails of equal length with 2000 equal gaps between them. The temperature in the winter and summer are and respectively. Find how much gap is to be left between two railings.
Sol. We know that,
or,
Where, length of the railway line for iron
for iron =
and,
then, = 3.6 m
The gap to be left between two railings =
4. The volume of lead at is . At its volume is 100.85 . Find the linear coefficient of lead.
Sol. Given that,
Initial temperature =
Initial volume =
Final volume =
Final temperature =
Then, we know that,
Coefficient of volume expansion of lead = =
Hence, Coefficient of linear expansion of lead
5. A glass bulb contains 100gm of mercury at . When bulb is heated to , what is the amount of mercury expelled out?
Sol.
But,
or,
or,
or,
Mass of mercury expelled
=
6. Density of mercury is at . Coefficient of real expansion of mercury is . Calculate its density at
Sol. Density of mercury at is
7. At constant pressure, dry air occupying 2 litres of volume at is heated to . What would be the volume at .
Sol. We know that,
Where,
Then,
or,
8. How much should the temperature of a brass rod be increased so as to increase its length by 1%? Given α for brass is 0.000020C–1.
Sol. Here,
α = 0.000020C–1
As
or
9. The volume of a metal sphere is 1000 cm3 at 272 K. What would be its volume at 373K? Coefficient of linear expansion of the metal is 18 ⨯ 10–6 K–1.
Sol. Here, V = 1000 cm3 = 10–3m3;
(T2 – T1) = 3737 – 273 = 100K.
As
=
10. Calculate the length of the brass rod at if its length at in 10m ( for brass = )
Sol. From the given problem
Initial length of the rod
Initial temperature
Final temperature
Coefficient of linear expansion of brass
The length of the rod at
The length of the rod at is 10.018m
11. 50 gm of copper is heated to increase its temperature by 10°C. If the same quantity of heat is given to 10 gm of water, the rise in its temperature is (Specific heat of copper = 420 Joule-kg–1 °C–1)
(A) 5°C (B) 6°C (C) 7°C (D) 8°C
Sol. A
Same amount of heat is supplied to copper and water so
12. A beaker contains 200 gm of water. The heat capacity of the beaker is equal to that of 20 gm of water. The initial temperature of water in the beaker is 20°C. If 440 gm of hot water at 92°C is poured in it, the final temperature (neglecting radiation loss) will be nearest to
(A) 58°C (B) 68°C (C) 73°C (D) 78°C
Sol. B
Heat lost by hot water = Heat gained by cold water in beaker + Heat absorbed by beaker
13. A bullet moving with a uniform velocity v, stops suddenly after hitting the target and the whole mass melts be m, specific heat S, initial temperature 25°C, melting point 475°C and the latent heat L. Then v is given by
(A)
(B)
(C)
(D)
Sol. B
Firstly the temperature of bullet rises up to melting point, then it melts. Hence according to .
14. A lead bullet of 10 g travelling at 300 m/s strikes against a block of wood and comes to rest. Assuming 50% of heat is absorbed by the bullet, the increase in its temperature is
(Specific heat of lead = 150J/kg, K)
(A) 100°C (B) 125°C (C) 150°C (D) 200°C
Sol. C
Since specific heat of lead is given in Joules, hence use W = Q instead of W = JQ.
15. 1 g of a steam at 100°C melt how much ice at 0°C? (Latent heat of ice = 80 cal/gm and latent heat of steam = 540 cal/gm)
(A) 1 gm (B) 2 gm (C) 4 gm (D) 8 gm
Sol. D
Suppose m gm ice melted, then heat required for its melting =
Heat available with steam for being condensed and then brought to 0°C
Heat lost = Heat taken








