Motion in a Straight

Motion in a straight line deals with the motion of an object which changes its position with time along a straight line.

• The study of the motion of objects without considering the cause of motion is called kinematics.

1. REST AND MOTION

• If the position of a body does not change with time with respect to the surroundings then it is said to be at rest, if not it is said to be in motion.

2. DISTANCE AND DISPLACEMENT

• Distance is the actual path covered by a moving particle in a given interval of time while displacement is the change in position vector, i.e., a vector joining initial to final position. If a particle moves from A to B as shown in Fig. the distance travelled is $∆$s while displacement is

$\Delta \overrightarrow{r}=\overrightarrow{r_f}–{\overrightarrow{r}}_i$

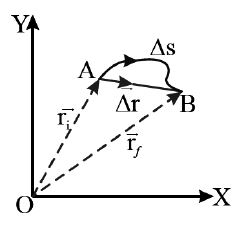
• Distance is a scalar while displacement is a vector, both having same dimensions[L] and SI unit is metre.

• The magnitude of displacement is equal to minimum possible distance between two positions; so
Distance $\ge$ |Displacement|
• For motion between two points displacement is single valued while distance depends on actual path and so can
have many values.
• For a moving particle distance can never decrease with time while displacement can.
• Decrease in displacement with time means body is moving towards the initial position.
• For a moving particle distance can never be negative or zero while displacement can be negative.
• In general, magnitude of displacement is not equal to distance. However, it can be so if the motion is along a
straight line without change in direction.
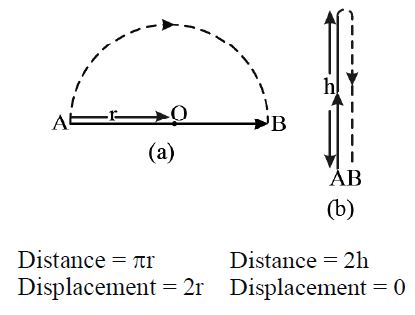
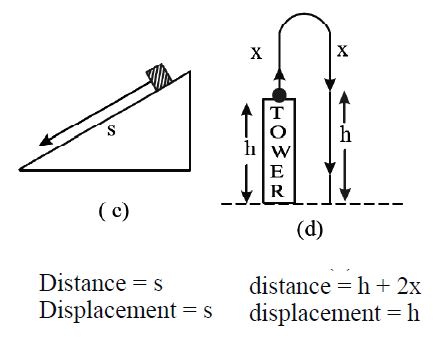
• Magnitude of displacement is less than the distance travelled in case of curvilinear motion.
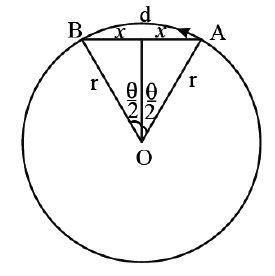
Ex : If an object turns through an angle $\theta$ along a circular path of radius r from point A to point B then
i) distance d = r $\theta$
ii) displacement $2x=2r\sin (\theta /2)$   $\left[\because \sin \frac{\theta }{2}=\frac{x}{r}\right]$

3. AVERAGE SPEED AND AVERAGE VELOCITY
• Average speed or velocity is a measure of overall ‘fastness’ of motion during a specified interval of time.
• The average speed of a particle for a given ‘interval of time’ is defined as the ratio of distance travelled to the time taken while average velocity is defined as the ratio of displacement to time taken.
• Thus, if a particle in time interval $∆$t after travelling distance $∆$r is displaced by $∆\overrightarrow{r}$

Average speed = $\frac{\text{ Distance travelled }}{\text{ Time taken }}$

i.e., $V_{\text{avg }}=\frac{\Delta r}{\Delta t}$…..(i)

Average velocity = $\frac{\text{ Displacement }}{\text{ Time }}$,

i.e., $\overrightarrow{V_{avg}}=\frac{\Delta \overrightarrow{r}}{\Delta t}$…..(ii)

• Average speed is a scalar while average velocity is a vector both having same units (m/s) and dimensions $\left[{\mathrm{LT}}^{–1}\right]$.
• For a given time interval average velocity is single valued while average speed can have many values depending on path followed.
• During the motion if the body comes back to its initial position.

${\overrightarrow{V}}_{\text{avg }}=0 (\because \Delta \overrightarrow{r}=0)$

but $V_{\text{avg }}>0$ and finite $(\because \Delta r>0)$

• For a moving body average speed can never be negative or zero while average velocity can be negative.

• If a graph is plotted between distance (or displacement) and time, the slope of chord during a given interval of time gives average speed (or ) average velocity avg
$V_{\mathrm{avg}}=\frac{\Delta \mathrm{r}}{\Delta \mathrm{t}}=\tan \varphi$ = slope of chord

4. INSTANTANEOUS SPEED AND INSTANTANEOUS VELOCITY
• Instantaneous velocity is defined as rate of change of position of the particle with time. If the position $\overrightarrow{r}$ of a particle at an instant ‘t’ changes by $∆\overrightarrow{r}$ in a small time interval $∆$t

$\overrightarrow{V}=\underset{\Delta t\to o}{\lim }\frac{\Delta \overrightarrow{r}}{\Delta t}=\frac{d\overrightarrow{r}}{dt}$

• The magnitude of velocity is called speed,i.e

Speed = |velocity| i.e, V $\left|\overrightarrow{V}\right|$

• Velocity is a vector while speed is a scalar , both having same units (m/s) and dimensions $\left({\mathrm{LT}}^{–1}\right)$.

• If during motion velocity remains constant throughout a given interval of time, then the motion is said to be uniform and for uniform motion, $\overrightarrow{V}$=constant=${\overrightarrow{\mathrm{V}}}_{\mathrm{avg}}$

• If velocity is constant, speed will also be constant. However , the converse may or may not be true,i.e, if speed=constant,velocity may or may not be constant as velocity has a direction in addition to magnitude which may or may not change,e.g, in case of uniform rectilinear motion

V = constant and $\overrightarrow{V}$= constant

While in case of uniform circular motion

V=constant but $\overrightarrow{V}$ is not constant , due to change in direction.

• velocity can be positive or negative as it is a vector but speed can never be negative as it is magnitude of velocity, i.e, $V=\left|\overrightarrow{V}\right|$

• As by definition $V=\frac{dr}{dt}$, the slope of displacement-versus time graph gives velocity , i.e,

$V=\frac{dr}{dt}=\tan \theta$ = slope of r – t curve

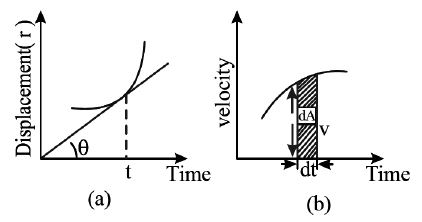
• As by definition $V=\frac{dr}{dt} ;\text{ i.e, } dr=Vdt$

and from fig. Vdt = dA

So, dA = dr i.e, $r=\int dA=\int Vdt$

i.e, area under velocity-time graph gives displacement while without sign gives distance.

• Average speed is the total distance divided by total time

${\mathrm{v}}_{\text{avg }}=\frac{\text{ Total distance travelled }}{\text{ Total time taken }}$

• If a body travels a distance s₁ in time t₁ , s₂ in time t₂ and s₃ in time t₃ then the average speed is ${\mathrm{V}}_{\mathrm{avg}}=\frac{s_1+{\mathrm{s}}_2+{\mathrm{s}}_3}{{\mathrm{t}}_1+{\mathrm{t}}_2+{\mathrm{t}}_3}$

• If an object travels distances ${\mathrm{S}}_1,{ \mathrm{S}}_2,{ \mathrm{S}}_3$ etc. with speeds ${\mathrm{V}}_1,{ \mathrm{V}}_2,{ \mathrm{V}}_3$ respectively in the same direction. Then Average speed = $\frac{{\mathrm{S}}_1+{\mathrm{S}}_2+{\mathrm{S}}_3}{\frac{{\mathrm{S}}_1}{{ \mathrm{V}}_1}+\frac{{\mathrm{S}}_2}{{ \mathrm{V}}_2}+\frac{{\mathrm{S}}_3}{{\mathrm{V}}_3}}$

• If an object travels first half of the total journey with a speed V₁ and next half with a speed 2 v then its average speed is

${\mathrm{v}}_{\mathrm{avg}}=\frac{\mathrm{s}+\mathrm{s}}{\frac{\mathrm{s}}{{\mathrm{v}}_1}+\frac{\mathrm{s}}{{\mathrm{v}}_2}}=\frac{2\mathrm{s}}{\frac{\mathrm{s}}{{\mathrm{v}}_1}+\frac{\mathrm{s}}{{\mathrm{v}}_2}}=\frac{2}{\frac{1}{{\mathrm{v}}_1}+\frac{1}{{\mathrm{v}}_2}}=\frac{2{\mathrm{v}}_1{\mathrm{v}}_2}{{\mathrm{v}}_1+{\mathrm{v}}_2}$

• If a body travels first 1/3 rd of the distance with a speed V₁ and second 1/3rd of the distance with a speed V₂ and last 1/3rd of the distance with a speed V₃, then the average speed

${\mathrm{v}}_{\text{avg }}=\frac{\frac{\mathrm{s}}{3}+\frac{\mathrm{s}}{3}+\frac{\mathrm{s}}{3}}{\frac{\mathrm{s}}{3{\mathrm{v}}_1}+\frac{\mathrm{S}}{3{\mathrm{v}}_2}+\frac{\mathrm{s}}{3{\mathrm{v}}_3}}$

$v_{\text{avg }}=\frac{3v_1{v}_2{v}_3}{v_1{v}_2+v_2{v}_3+v_3{v}_1}$

• If an object travels with speeds V₁, V₂, V₃ etc., during time intervals t₁, t₂, t₃ etc.,
then its average speed = $=\frac{{\mathrm{V}}_1{\mathrm{t}}_1+{\mathrm{V}}_2{\mathrm{t}}_2+{\mathrm{V}}_3{\mathrm{t}}_3+\dots }{{\mathrm{t}}_1+{\mathrm{t}}_2+{\mathrm{t}}_3+\dots }$

If t₁ = t₂ = t₃ = …. = t, then

${\mathrm{V}}_{\mathrm{avg}}=\frac{{\mathrm{V}}_1\mathrm{t}+{\mathrm{V}}_2\mathrm{t}+{\mathrm{V}}_3\mathrm{t}+\dots .}{\mathrm{nt}}=\frac{{\mathrm{V}}_1+{\mathrm{V}}_2+\dots }{\mathrm{n}}$

i.e.The average speed is equal to the arithmetic mean of individual speeds.

• The actual path length traversed by a body is called distance.

Note : If  $\overrightarrow{\mathrm{V}}={\mathrm{V}}_{\mathrm{x}}\hat{\mathrm{i}}+{\mathrm{V}}_{\mathrm{y}}\hat{\mathrm{j}}+{\mathrm{V}}_{\mathrm{z}}\hat{\mathrm{k}}$  varies with time t then $\overrightarrow{\mathrm{dr}}=\overrightarrow{\mathrm{v}}\mathrm{dt}\left(\because \overrightarrow{\mathrm{v}}=\frac{\overrightarrow{\mathrm{dr}}}{\mathrm{dt}}\right)$

Integrating on both sides then ${\int }_{{\overrightarrow{r}}_i}^{\overrightarrow{r_f}}\overrightarrow{dr}={\int }_{t_1}^{t_2}\overrightarrow{V}dt$

$\Rightarrow$ displacement of the particle from time ${\mathrm{t}}_1 \mathrm{to} {\mathrm{t}}_2$ is given by

$\overrightarrow{\mathrm{s}}=\overrightarrow{{\mathrm{r}}_{\mathrm{f}}}–{\overrightarrow{\mathrm{r}}}_{\mathrm{i}}={\int }_{{\mathrm{t}}_1}^{{\mathrm{t}}_2}{\mathrm{v}}_{\mathrm{x}} \hat{\mathrm{i}}\mathrm{dt}+{\int }_{{\mathrm{t}}_1}^{{\mathrm{t}}_2}{\mathrm{v}}_{\mathrm{y} }\hat{\mathrm{j}}\mathrm{dt}+{\int }_{{\mathrm{t}}_1}^{{\mathrm{t}}_2}{\mathrm{v}}_{\mathrm{z}} \hat{\mathrm{k}}\mathrm{dt}$

5. ACCELERATION
• The rate of change of velocity is equal to acceleration.

Average and Instantaneous acceleration
• If the velocity of a particle changes ( either in magnitude or direction or both) with time the motion is said to be accelerated or non-uniform. In case of non-uniform motion if change in velocity is $∆\overrightarrow{V}$ in time interval $∆t$ , then

$\overrightarrow{{\mathrm{a}}_{\text{avg }}}=\frac{\Delta \overrightarrow{\mathrm{v}}}{\Delta \mathrm{t}}=\frac{\overrightarrow{{\mathrm{v}}_2}–\overrightarrow{{\mathrm{v}}_1}}{{\mathrm{t}}_2–{\mathrm{t}}_1}$…….(1)

Instantaneous acceleration or simply acceleration is defined as rate of change of velocity with time at a given instant. So if the velocity of a particle $\overrightarrow{v}$ at time t changes by $∆\overrightarrow{V}$ in a small time interval $∆$t then

$\overrightarrow{\mathrm{a}}=\underset{\Delta t\to 0}{\lim }\frac{\Delta \overrightarrow{\mathrm{V}}}{\Delta \mathrm{t}}=\frac{\mathrm{d}\overrightarrow{\mathrm{V}}}{\mathrm{dt}}$………..(2)

Regarding acceleration it is worth noting that:

• It is a vector with dimensions $\left[L{T}^{–2}\right]$ and SI units $\left[\mathrm{m}/{\mathrm{s}}^2\right]$ .

• If acceleration is zero, velocity will be constant and the motion will be uniform. However, if acceleration is constant(uniform), motion is non-uniform and if acceleration is not constant then both motion and acceleration are non-uniform.

• As by definition $\overrightarrow{V}=(\overrightarrow{ds}/dt)$

So, $\overrightarrow{\mathrm{a}}=\frac{\mathrm{d}\overrightarrow{\mathrm{v}}}{\mathrm{dt}}=\frac{\mathrm{d}}{\mathrm{dt}}\left(\frac{\mathrm{d}\overrightarrow{\mathrm{s}}}{\mathrm{dt}}\right)=\frac{{\mathrm{d}}^2\overrightarrow{\mathrm{s}}}{{\mathrm{dt}}^2}$…….. (3)

i.e., if $\overrightarrow{s}$ is given as a function of time, second derivative of displacement w.r.t. time gives acceleration.
• If velocity is given as a function of position, then by chain rule

$\mathrm{a}=\frac{\mathrm{dv}}{\mathrm{dt}}=\frac{\mathrm{dv}}{\mathrm{dx}}·\frac{\mathrm{dx}}{\mathrm{dt}}$ or $\mathrm{a}=\mathrm{v}\frac{\mathrm{dv}}{\mathrm{dx}}$ $\left[\text{ as }\frac{dx}{dt}=v\right]$

• As acceleration $\overrightarrow{\mathrm{a}}=(\overrightarrow{\mathrm{dv}}/\mathrm{dt})$, the slope of velocity-time graph gives acceleration.

Velocity – Time Graph

${\overrightarrow{\mathrm{a}}}_{\text{avg }}=\frac{\Delta \overrightarrow{\mathrm{V}}}{\Delta \mathrm{t}}=\tan \varphi$

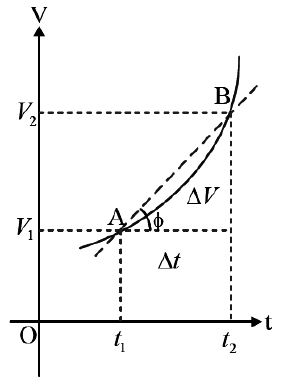
${\overrightarrow{\mathrm{a}}}_{\text{avg }}$= slope of the line joining two points in v-t graph.

• The slope of a versus t curve, i.e, $d\overrightarrow{a}/dt$ is a measure of rate of non-uniformity of acceleration(usually it is known as JERK).
• Acceleration can be positive or negative. Positive acceleration means velocity is increasing with time while negative acceleration called retardation means velocity is decreasing with time.

Equations of motion

• If a particle starts with an initial velocity u, acceleration a and it gains velocity v in time t then

$\mathrm{a}=\frac{\mathrm{dv}}{\mathrm{dt}}\text{ or }\mathrm{dv}=\mathrm{adt}$

or ${\int }_u^{v}dv=a{\int }_0^{t}dt\text{ or }[V{]}_u^v=a[t{]}_0^t$

or v = u + at …….(1A)

In vector form $\overrightarrow{\mathrm{v}}=\overrightarrow{\mathrm{u}}+\overrightarrow{\mathrm{a}}\mathrm{t} .....\left(1\mathrm{B}\right)$

• Now again by definition of velocity, Eqn. (1A) reduces to $\frac{\mathrm{ds}}{\mathrm{dt}}=\mathrm{u}+\mathrm{at}$

or ${\int }_0^{s}ds={\int }_0^t(u+at)dt$

or  $\mathrm{s}=\mathrm{ut}+\frac{1}{2}{\mathrm{at}}^2$   …….(2A)

In vector form $\overrightarrow{\mathrm{s}}=\overrightarrow{\mathrm{ut}}+\frac{1}{2}{\overrightarrow{\mathrm{at}}}^2$ ……………….(2B)

From eqns. (1A) and (2A), we get

$\mathrm{s}=\mathrm{u}\frac{(\mathrm{v}–\mathrm{u})}{\mathrm{a}}+\frac{1}{2}\mathrm{a}{\left[\frac{(\mathrm{v}–\mathrm{u})}{\mathrm{a}}\right]}^2$

or $2as=2uv–2u^2+v^2+u^2–2uv$

i.e., ${\mathrm{v}}^2={\mathrm{u}}^2+2\mathrm{as}$…….(3)

• In scalar form

$\overrightarrow{\mathrm{v}}·\overrightarrow{\mathrm{v}}=\overrightarrow{u}.\overrightarrow{u}+2\overrightarrow{a}.\overrightarrow{s}\text{ or }{\mathrm{v}}^2={\mathrm{u}}^2+2\overrightarrow{a}.\overrightarrow{s}$

• Distance travelled = average speed $\times$ time

$S=\left(\frac{u+v}{2}\right)t$…………(4)

• Distance travelled in ${\mathrm{n}}^{\mathrm{th}}$ second

${\mathrm{S}}_{\mathrm{n}}=\mathrm{u}+\mathrm{a}\left(\mathrm{n}–\frac{1}{2}\right)$………..(5)

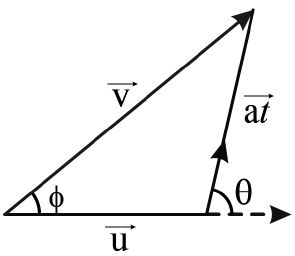
• If acceleration and velocity are not collinear, v can be calculated using

$\mathrm{v}={\left[{\mathrm{u}}^2+(\mathrm{at}{)}^2+2\text{ uat }\cos \theta \right]}^{1/2}$

with $\tan \varphi =\frac{\text{ at }\sin \theta }{\mathrm{u}+atcos\theta }$………..(6)

7. GRAPHS
Characteristics of s-t and v-t graphs
• Slope of displacement time graph gives velocity.
• Slope of velocity-time graph gives acceleration.
• Area under velocity-time graph gives displacement
Let us plot v-t and s-t graphs of some standard results. To draw the following graphs assume that the particle has got either a one-dimensional motion with uniform velocity or with constant acceleration.

6. EQUATIONS OF MOTION
• If a particle starts from rest and moves with uniform acceleration ‘a’ such that it travels distances $S_m$ and $S_n$ in the $m^{th}$ and $n^{th}$ seconds

then ${\mathrm{S}}_{\mathrm{n}}=0+\frac{\mathrm{a}}{2}(2\mathrm{n}–1)\to \left(1\right)(u=0)$

${\mathrm{S}}_{\mathrm{m}}=0+\frac{\mathrm{a}}{2}(2 \mathrm{m}–1)\to \left(2\right)$

subtracting eq (2) from eq (1) $a=\frac{S_n–S_m}{(n–m)}$

• A particle starts from rest and moves along a straight line with uniform acceleration. If ‘s’ is the distance travelled by it in n seconds and $S_n$ is the distance travelled in the $n^{th}$ second, then $\frac{{\mathrm{S}}_{\mathrm{n}}}{\mathrm{s}}=\frac{(2\mathrm{n}–1)}{{\mathrm{n}}^2}$(fraction of distance fallen in nth second during free fall )
• Moving with uniform acceleration, a body crosses a point ‘x’ with a velocity ‘u’ and another point ‘y’ with a velocity ‘v’. Then it will cross the midpoint of ‘x’ and ‘y’ with velocity

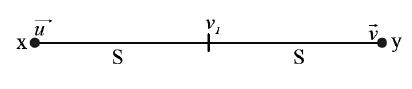
In this case acceleration a = $\frac{{\mathrm{v}}_1^2–{\mathrm{u}}^2}{2 \mathrm{S}}=\frac{{\mathrm{V}}^2–{\mathrm{v}}_1^2}{2 \mathrm{S}}$

$\therefore$ on solving, $v_1=\sqrt{\frac{{\mathrm{v}}^2+{\mathrm{u}}^2}{2}}$.

• If a bullet looses ${\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{n}$}\right.\right)}^{\mathrm{th}}$ of its velocity while passing through a plank, then the minimum no. of such planks required to just stop the bullet is.

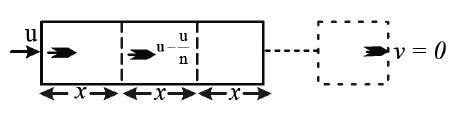
Let m be the no of planks required to stop the bullet

$\therefore {\left(\mathrm{u}–\frac{\mathrm{u}}{\mathrm{n}}\right)}^2–{\mathrm{u}}^2=2\mathrm{ax}\to \left(1\right)$

$0^2–{\mathrm{u}}^2=2\mathrm{amx} \to \left(2\right)$

Dividing eq (2) with eq (1)

$\frac{0^2–{\mathrm{u}}^2}{{\left(\mathrm{u}–\frac{\mathrm{u}}{\mathrm{n}}\right)}^2–{\mathrm{u}}^2}=\frac{2\mathrm{amx}}{2\mathrm{ax}}$

$\to m=\frac{u^2}{u^2–{\left(u–\frac{u}{n}\right)}^2}=\frac{1}{1–{\left(1–\frac{1}{n}\right)}^2}$

$\to m=\frac{1}{1–{\left(\frac{n–1}{n}\right)}^2}=\frac{n^2}{n^2–n^2–1+2n}$

$m=\frac{n^2}{2n–1}$

• The velocity of a bullet becomes $\frac{1}{\mathrm{n}}$ of the initial velocity while penetrating a plank. The number of such planks required to stop the bullet.

$\therefore {\left(\frac{\mathrm{u}}{\mathrm{n}}\right)}^2–{\mathrm{u}}^2=2\mathrm{ax} \to \left(1\right)$

$0^2–{\mathrm{u}}^2=2\mathrm{amx} \to \left(2\right)$

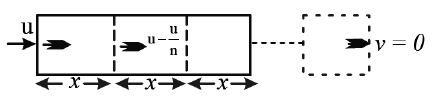
From eq (1) and eq (2) ;

$m=\frac{n^2}{n^2–1}$

• A bullet loose $\frac{1}{\mathrm{n}}$ of its velocity while penetrating a distance x into the target. The further distance travelled before coming to rest.

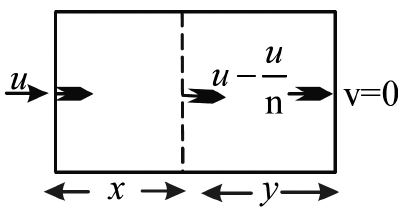
Let x is the distance covered by the bullet to lose the $\frac{1}{n}th$ of initial velocity

$\therefore {\mathrm{v}}^2–{\mathrm{u}}^2=2\mathrm{as}$

${\left(u–\frac{u}{n}\right)}^2–u^2=2ax\to \left(1\right)$

Let y is the further distance covered by the bullet to come to rest

$\therefore 0^2–{\mathrm{u}}^2=2\mathrm{a}(\mathrm{x}+\mathrm{y})\to \left(2\right)$

$\therefore$ From eq (1) and (2)

$y=x\left(\frac{(n+1{)}^2}{2n}\right)$

• If the velocity of a body becomes ${\left(\frac{1}{n}\right)}^{th}$ of its initial velocity after a displacement of ‘x’ then it will come to rest after a further displacement of

$\Rightarrow {\left(\frac{\mathrm{u}}{\mathrm{n}}\right)}^2–{\mathrm{u}}^2=2\mathrm{ax} \to \left(1\right)$

$\Rightarrow 0^2–{\left(\frac{\mathrm{u}}{\mathrm{n}}\right)}^2=2\mathrm{ay} \to \left(2\right)$

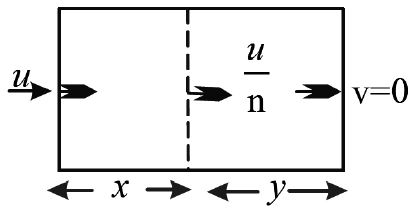
From eq. (1) and eq (2) ; $y=\frac{x}{n^2–1}$

8. EQUATIONS OF MOTION FOR VARIABLE ACCELERATION

• When acceleration ‘a’ of the particle is a function of time i.e., a = f(t)

$\Rightarrow \frac{\mathrm{dv}}{\mathrm{dt}}=\mathrm{f}\left(\mathrm{t}\right)\Rightarrow \mathrm{dv}=\mathrm{f}\left(\mathrm{t}\right)\mathrm{dt}$

Integrating both sides within suitable limits, we have

${\int }_u^{v}dv={\int }_0^{t}f\left(t\right)dt\Rightarrow v=u+{\int }_0^{t}f\left(t\right)dt$

• When acceleration ‘a’ of the particle is a function of distance a = f(x)

$\Rightarrow \frac{\mathrm{d}v}{\mathrm{dt}}=\mathrm{f}\left(\mathrm{x}\right)\Rightarrow \frac{\mathrm{dv}}{\mathrm{dx}}\frac{\mathrm{dx}}{\mathrm{dt}}=\mathrm{f}\left(\mathrm{x}\right)$

${\int }_u^{v}vdv={\int }_{x_0}^{x}f\left(x\right)dx\Rightarrow v^2=u^2+2{\int }_{x_0}^{x}f\left(x\right)dx$

9. ACCELERATION DUE TO GRAVITY
• The uniform acceleration of a freely falling body towards the centre of earth due to earth’s gravitational force is called acceleration due to gravity
• It is denoted by ‘g’
• Its value is constant for all bodies at a given place. It is independent of size, shape, material, nature of the body.
• Its value changes from place to place on the surface of the earth.
• It has maximum value at the poles of the earth. The value is nearly 9.83 m/s2.
• It has minimum value at equator of the earth. The value is nearly 9.78 m/s2.
• On the surface of the moon, earth moon ${\mathrm{g}}_{\mathrm{moon}}=\frac{{\mathrm{g}}_{\text{earth }}}{6}$
• The acceleration due to gravity of a body always directed downwards towards the centre of the earth, whether a body is projected upwards or downwards.
• When a body is falling towards the earth, its velocity increases, g is positive.
• The acceleration due to gravity at the centre of earth is zero.

10. MOTION UNDER GRAVITY
Equation of motion for a body projected
vertically downwards
• When a body is projected vertically downwards with an initial velocity u from a height h
then a = g, s = h

a) v = u + gt

b) $\mathrm{h}=\mathrm{ut}+\frac{1}{2}{\mathrm{gt}}^2$

c) $v^2–u^2=2gh$

d) ${\mathrm{S}}_{\mathrm{n}}=\mathrm{u}+\frac{\mathrm{g}}{2}(2\mathrm{n}–1)$

• In case of freely falling body u = 0, a = +g

a) v = gt

b) $\mathrm{S}=\frac{1}{2}{\mathrm{gt}}^2$

c) ${\mathrm{v}}^2=2\mathrm{gS}$

d) ${\mathrm{S}}_{\mathrm{n}}=\mathrm{g}\left(\mathrm{n}–\frac{1}{2}\right)$

• For a freely falling body, the ratio of distances travelled in 1 second, 2seconds, 3 seconds, …. = 1 : 4 : 9 : 16….
• For a freely falling body, the ratio of distances travelled in successive seconds = 1 : 3 : 5 : 9 ….
• A freely falling body passes through two points A and B in time intervals of $t_1$ and $t_2$ from the start, then the distance between the two points A and B is = $\frac{g}{2}\left(t_2^2–t_1^2\right)$

• A freely falling body passes through two points A and B at distances $h_1$ and $h_2$ from the start, then the time taken by it to move from A to B is

$\mathrm{T}=\sqrt{\frac{2{ \mathrm{h}}_2}{ \mathrm{g}}}–\sqrt{\frac{2{ \mathrm{h}}_1}{ \mathrm{g}}}=\sqrt{\frac{2}{ \mathrm{g}}}\left(\sqrt{{\mathrm{h}}_2}–\sqrt{{\mathrm{h}}_1}\right)$

• Two bodies are dropped from heights h1 and h2 simultaneously. Then after any time the distance between them is equal to $\left({\mathrm{h}}_2~{\mathrm{h}}_1\right)$.
• A stone is dropped into a well of depth ‘h’, then the sound of splash is heard after a time of ‘t’.

Time taken by the body to reach water, $t_1=\sqrt{\frac{2h}{g}}$

Time taken by sound to travel a distance ‘h’, $t_2=\frac{h}{V_{\text{sound }}}$

$\therefore$ Time to hear splash of sound is t = $t_1+t_2=\sqrt{\frac{2 \mathrm{h}}{ \mathrm{g}}}+\frac{\mathrm{h}}{{\mathrm{v}}_{\text{sound }}}$

• A stone is dropped into a river from the bridge and after ‘x’ seconds another stone is projected down into the river from the same point with a velocity of ‘u’. If both the stones reach the water simultaneously, then ${\mathrm{S}}_{1\left(\mathrm{t}\right)}={\mathrm{S}}_{2(\mathrm{t}–\mathrm{x})}$

$\frac{1}{2}{\mathrm{gt}}^2=\mathrm{u}(\mathrm{t}–\mathrm{x})+\frac{1}{2} \mathrm{g}(\mathrm{t}–\mathrm{x}{)}^2$

• A body dropped freely from a multistoried building can reach the ground in $t_1$ sec. It is stopped in its path after $t_2$ sec and again dropped freely from the point. The further time taken by it to reach the ground is ${\mathrm{t}}_3=\sqrt{{\mathrm{t}}_1^2–{\mathrm{t}}_2^2}$

We know that ${\mathrm{H}}_1={\mathrm{H}}_2+{\mathrm{H}}_3$

$\Rightarrow \frac{1}{2}{\mathrm{gt}}_1^2=\frac{1}{2}{\mathrm{gt}}_2^2+\frac{1}{2}{{\mathrm{gt}}_3}^2$

$\Rightarrow {\mathrm{t}}_1^2={\mathrm{t}}_2^2+{\mathrm{t}}_3^2 \therefore {\mathrm{t}}_3=\sqrt{{\mathrm{t}}_1^2–{\mathrm{t}}_2^2}$

Equations of motion of a body Projected
Vertically up :
• Acceleration (a) = -g

a) v = u – gt

b) $\mathrm{s}=ut–\frac{1}{2}{\mathrm{gt}}^2$

c) ${\mathrm{v}}^2–{\mathrm{u}}^2=–2\mathrm{gh}$

d) ${\mathrm{S}}_{\mathrm{n}}=\mathrm{u}–\frac{\mathrm{g}}{2}(2\mathrm{n}–1)$

• Angle between velocity vector and acceleration vector is $180°$ until the body reaches the highest point.
• At maximum height, v = 0 and a = g

• ${\mathrm{H}}_{\max }=\frac{{\mathrm{u}}^2}{2 \mathrm{g}}\Rightarrow {\mathrm{H}}_{\max }\propto {\mathrm{u}}^2$ (independent of mass of the body)

• A body is projected vertically up with a velocity ‘u’ from ground in the absence of air resistance ‘R’. then.

$\left(t_a=t_d\right)$

i) ${\mathrm{t}}_{\mathrm{a}}={\mathrm{t}}_{\mathrm{d}}=\frac{\mathrm{u}}{\mathrm{g}}$

ii) Time of flight $\mathrm{T}={\mathrm{t}}_{\mathrm{a}}+{\mathrm{t}}_{\mathrm{d}}=\frac{2\mathrm{u}}{\mathrm{g}}$

• A body is projected vertically up with a velocity ‘u’ from ground in the presence of constant air resistance ‘R’.
If it reaches the ground with a velocity ‘v’, then
a) Height of ascent = Height of descent

b) Time of ascent ${\mathrm{t}}_{\mathrm{a}}=\frac{\mathrm{mu}}{\mathrm{mg}+\mathrm{R}}$

c) Time of descent $t_d=\frac{mv}{mg–R}$

d) ${\mathrm{t}}_{\mathrm{a}}<{\mathrm{t}}_{\mathrm{d}}$

e) $\frac{v}{u}=\sqrt{\frac{mg–R}{mg+R}}(v<u)$

f) For a body projected vertically up under air resistance, retardation during its motion is > g
• At any point of the journey, a body possess the same speed while moving up and while moving down.

• Irrespective of velocity of projection, all the bodies pass through a height $\frac{g}{2}$in the last second of ascent.
Distance traveled in the last second of its journey  $u–\frac{g}{2}$.

• If a vertically projected body rises through a height ‘h’ in nth second, then in ${\left(n–1\right)}^{th}$ second it will rise through a height (h+g) and in ${\left(n+1\right)}^{th}$ second it will rise through height (h-g).
• If velocity of body in $n^{th}$ second is ‘v’ then in ${\left(n–1\right)}^{th}$ second it is (v + g) and that in ${\left(n+1\right)}^{th}$ second is (v – g)
while ascending
• A body is dropped from the top edge of a tower of height ‘h’ and at the same time another body is projected vertically up from the foot of the tower with a velocity ‘u’.

a) The separation between them after ‘t’ seconds is = (h – ut)
b) The time after which they meet $\mathrm{t}=\frac{\mathrm{h}}{\mathrm{u}}$

c) The height at which they meet above the ground = $\left(\mathrm{h}–\frac{{\mathrm{gh}}^2}{2{\mathrm{u}}^2}\right)$

d) The time after which their velocities are equal in magnitudes is $t=\frac{u}{2g}$

e) If they meet at mid point, then the velocity of thrown body is u = $\sqrt{gh}$ and its velocity of meeting is zero
f) Ratio of the distances covered when the magnitudes of their velocities are equal is 1 : 3.

• A body projected vertically up crosses a point P at a height ‘h’ above the ground at time ‘$t_1$’ seconds and at time $t_2$ seconds ( $t_1$ and $t_2$ are measured from the instant of projection) to same point while coming down.

$h=ut–\frac{1}{2}g{t}^2; g{t}^2–2ut+2h=0$

This is quadratic equation in t

Sum of the roots, $t_1+t_2=\frac{2u}{g}$ (time of flight)

Velocity of projection, $\mathrm{u}=\frac{1}{2} \mathrm{g}\left({\mathrm{t}}_1+{\mathrm{t}}_2\right)$

Product of the roots, $t_1{t}_2=\frac{2h}{g}$

Height of P is $\mathrm{h}=\frac{1}{2}{\mathrm{gt}}_1{\mathrm{t}}_2$

Maximum height reached above the ground $\mathrm{H}=\frac{1}{8} \mathrm{g}{\left({\mathrm{t}}_1+{\mathrm{t}}_2\right)}^2$

Magnitude of velocity while crossing P is $\frac{g\left(t_2–t_1\right)}{2}$

• A body is projected vertically up with velocity $u_1$ and after ‘t’ seconds another body is projected vertically up with a velocity $u_2$.

a) If $u_2>u_1$ , the time after which both the bodies will meet with each other is $h_1=h_2$

$u_{1}x–\frac{1}{2}g{x}^2=u_2(x–t)–\frac{1}{2}g(x–t{)}^2$

$\mathrm{x}=\frac{{\mathrm{u}}_2\mathrm{t}+\frac{1}{2}{\mathrm{gt}}^2}{\left({\mathrm{u}}_2–{\mathrm{u}}_1\right)+\mathrm{gt}}$ for the first body.

b) If ${\mathrm{u}}_1={\mathrm{u}}_2=\mathrm{u}$, the time after which they meet is $\left(\frac{u}{g}+\frac{t}{2}\right)$ for the first body and $\left(\frac{u}{g}–\frac{t}{2}\right)$ for the second body.

Height at which they meet = $\frac{u^2}{2g}–\frac{g{t}^2}{8}$

• A rocket moves up with a resultant acceleration a . If its fuel exhausts completely after time ‘t’ seconds, the maximum height reached by the rocket above the ground is $h=h_1+h_2$

$=\frac{1}{2}a{t}^2+\frac{1}{2g}{a}^2{t}^2\left[h_2=\frac{v^2}{2g}=\frac{a^2{t}^2}{2g}\right], [v=at]$

$\mathrm{h}=\frac{1}{2}{\mathrm{at}}^2\left(1+\frac{\mathrm{a}}{\mathrm{g}}\right)$

• An elevator is accelerating upwards with an acceleration a. If a person inside the elevator throws a particle vertically up with a velocity u relative to the elevator, time of flight is $\mathrm{t}=\frac{2\mathrm{u}}{\mathrm{g}+\mathrm{a}}$

• In the above case if elevator accelerates down, time of flight is $\mathrm{t}=\frac{2\mathrm{u}}{\mathrm{g}–\mathrm{a}}$

• The zero velocity of a particle at any instant does not necessarily imply zero acceleration at that instant. A particle may be momentarily at rest and yet have non-zero acceleration.
For example, a particle thrown up has zero velocity at its uppermost point but the acceleration at that instant continues to be the acceleration due to gravity.
• Three bodies are projected from towers of same height as shown. 1st one is projected vertically up with a velocity ‘u’. The second one is thrown down vertically with the same velocity and the third one is dropped as a freely falling body. If ${\mathrm{t}}_1,{\mathrm{t}}_2,{\mathrm{t}}_3$ are the times taken by them to reach ground, then,

For 1^st body,   $h=–u{t}_1+\frac{1}{2}g{t}_1^2 \to \left(1\right)$

For 2^nd body,  $h=u{t}_2+\frac{1}{2}g{t}_2^2 \to \left(2\right)$

For 3^rd body,   $h=\frac{1}{2}g{t}_3^2 \to \left(3\right)$

from $\left(1\right)\times t_2+\left(2\right)\times t_1$

$\Rightarrow h\left(t_1+t_2\right)=\frac{1}{2}g{t}_1{t}_2\left(t_1+t_2\right)$

i) Height of the tower $h=\frac{1}{2}g{t}_1{t}_2\to \left(4\right)$

ii) From eq (3) & (4),

$t_3=\sqrt{t_1{t}_2} \to \left(5\right)$

iii) Equating R.H.S of (1) & (2),

velocity of projection $\mathrm{u}=\frac{1}{2} \mathrm{g}\left({\mathrm{t}}_1–{\mathrm{t}}_2\right)\to \left(6\right)$

iv) Time difference between first two bodies to reach the ground $\Delta t=\frac{2u}{g}\to \left(7\right)$

11. RELATIVE MOTION IN ONE DIMENSION
• Velocity of one moving body with respect to other moving body is called Relative velocity.
• A and B are two objects moving uniformly with average velocities ${\mathrm{V}}_{\mathrm{A}}$ and $V_B$ in one dimension, say along x-axis having the positions ${\mathrm{x}}_{\mathrm{A}}\left(0\right)\text{ and }{\mathrm{x}}_{\mathrm{B}}\left(0\right)\text{ at }\mathrm{t}=0$.
• If ${\mathrm{x}}_{\mathrm{A}}\left(\mathrm{t}\right)\text{ and }{\mathrm{x}}_{\mathrm{B}}\left(\mathrm{t}\right)$ are positions of objects A and B at time t then

${\mathrm{x}}_{\mathrm{A}}\left(\mathrm{t}\right)={\mathrm{x}}_{\mathrm{A}}\left(0\right)+{\mathrm{v}}_{\mathrm{A}}\mathrm{t}; {\mathrm{x}}_{\mathrm{B}}\left(\mathrm{t}\right)={\mathrm{x}}_{\mathrm{B}}\left(0\right)+{\mathrm{v}}_{\mathrm{B}}\mathrm{t}$

• The displacement from object A to B is given by

${\mathrm{x}}_{\mathrm{BA}}\left(\mathrm{t}\right)={\mathrm{x}}_{\mathrm{B}}\left(\mathrm{t}\right)–{\mathrm{x}}_{\mathrm{A}}\left(\mathrm{t}\right)$

$=\left[{\mathrm{x}}_{\mathrm{B}}\left(0\right)–{\mathrm{x}}_{\mathrm{A}}\left(0\right)\right]+\left({\mathrm{v}}_{\mathrm{B}}–{\mathrm{v}}_{\mathrm{A}}\right)\mathrm{t}$

$={\mathrm{X}}_{\mathrm{BA}}\left(0\right)+\left({\mathrm{V}}_{\mathrm{B}}–{\mathrm{v}}_{\mathrm{A}}\right)\mathrm{t}$

Velocity of A w.r.t B is ${\overrightarrow{\mathrm{V}}}_{\mathrm{AB}}={\overrightarrow{\mathrm{V}}}_{\mathrm{A}}–{\overrightarrow{\mathrm{V}}}_{\mathrm{B}}$

$\left|{\overrightarrow{\mathrm{V}}}_{\mathrm{AB}}\right|=\sqrt{{\mathrm{v}}_{\mathrm{A}}^2+{\mathrm{v}}_{\mathrm{B}}^2–2{\mathrm{v}}_{\mathrm{A}}{\mathrm{v}}_{\mathrm{B}}\cos \theta }$

• Two bodies are moving in a straight line in same direction then, $\left|{\overrightarrow{\mathrm{V}}}_{A \mathrm{B}}\right|=\left|{\overrightarrow{\mathrm{V}}}_{\mathrm{A}}\right|–\left|{\overrightarrow{\mathrm{V}}}_{\mathrm{B}}\right|\left(\because \theta =0°\right)$

• Two bodies are moving in a straight line in opposite direction then, $\left|{\overrightarrow{\mathrm{V}}}_{\mathrm{AB}}\right|=\left|{\overrightarrow{\mathrm{V}}}_{\mathrm{A}}\right|+\left|{\overrightarrow{\mathrm{V}}}_{\mathrm{B}}\right|,\left(\because \theta =180°\right)$

• If two bodies move with same velocity and in same direction, then position between them does not vary with time.
• If two bodies move with unequal velocity and in same direction, then position between them first decreases to minimum and then increases.
• If the particles are located at the sides of n sided symmetrical polygon with each side a and each particle moves towards the other, then time after which they meet is

$\mathrm{T}=\frac{\text{ Initial separation }}{\text{ Relative velocity of approach }}$

$\mathrm{T}=\frac{\mathrm{a}}{\mathrm{v}–\mathrm{vcos}\left(\frac{2\pi }{\mathrm{n}}\right)}\Rightarrow \mathrm{T}=\frac{\mathrm{a}}{\mathrm{v}\left(1–\cos \left(\frac{2\pi }{\mathrm{n}}\right)\right)}$

and $\mathrm{T}=\frac{\mathrm{a}}{2{\mathrm{vsin}}^2\left(\frac{\pi }{\mathrm{n}}\right)}$

SOLVED EXAMPLES

1. An athlete completes one round of a circular track of radius R in 40 s. What will be his displacement at the end of 2 min 20 s?

Sol. The time = 2 min 20s = 140s

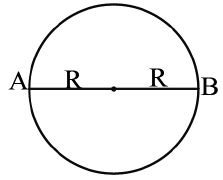
In 40 seconds athlete completes = 1 round
In 140 seconds athlete will completes

$=\frac{140}{40}$round =3.5 rounds

The displacement in 3 rounds = 0

So net displacement =2R

2. A particle starting from point A, travelling up to B with a speed S, then up to point ‘C’ with a speed 2S and
finally up to ‘A’ with a speed 3S, then find its average speed.

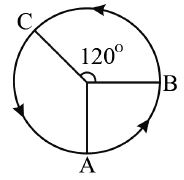
Sol. Average speed = $\frac{\text{ Total distance travelled }}{\text{ Total time taken }}$

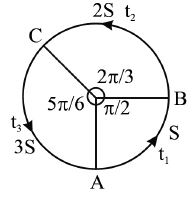
Total distance travelled

= AB + BC + CA = 2$\mathrm{\pi }$r

3. A particle is at x = +5 m at t = 0, x = -7m at t = 6s and x = +2m at t = 10s. Find the average velocity of the
particle during the interval (a) t = 0 to t = 6s; (b) t = 6s to t = 10s, (c) t = 0 to t = 10s.

Sol. ${\mathrm{x}}_1=+5\mathrm{m}, {\mathrm{t}}_1=0, {\mathrm{x}}_2=–7\mathrm{m}; {\mathrm{t}}_2=6\mathrm{s}, {\mathrm{x}}_3=+2\mathrm{m}$, ${\mathrm{t}}_3=10 \mathrm{s}$

a) The average velocity between the times t = 0 to t = 6s is

$\left|{\overrightarrow{\mathrm{v}}}_1\right|=\frac{\left|{\mathrm{x}}_2–{\mathrm{x}}_1\right|}{{\mathrm{t}}_2–{\mathrm{t}}_1}=\frac{|–7–5|}{6–0}=2 \mathrm{m}/\mathrm{s}$

b) The average velocity between the times ${\mathrm{t}}_2=6\mathrm{s}\text{ to }{\mathrm{t}}_3=10\mathrm{s}$ is

$\left|{\overrightarrow{\mathrm{v}}}_2\right|=\frac{{\mathrm{x}}_3–{\mathrm{x}}_2}{{\mathrm{t}}_3–{\mathrm{t}}_2}=\frac{2–(–7)}{10–6}=\frac{9}{4}=2.25 \mathrm{m}/\mathrm{s}$

c) The average velocity between times ${\mathrm{t}}_1=0\text{ to }{\mathrm{t}}_3=10 \mathrm{s}$ is

$\left|{\overrightarrow{\mathrm{v}}}_3\right|=\frac{{\mathrm{x}}_3–{\mathrm{x}}_1}{{\mathrm{t}}_3–{\mathrm{t}}_1}=\frac{2–5}{10–0}=0.3 \mathrm{m}/\mathrm{s}$

4. A body covers 100cm in first 2 seconds and 128cm in the next four seconds moving with constant acceleration.
Find the velocity of the body at the end of 8sec?
Sol. distance in first two seconds is

${\mathrm{S}}_1={\mathrm{ut}}_1+\frac{1}{2}{\mathrm{at}}_1^2$

$100=2\mathrm{u}+\frac{1}{2}\mathrm{a}\left(4\right)\dots \dots \left(1\right)$

distance in (2+4)sec from starting point is

${\mathrm{s}}_1+{\mathrm{s}}_2=\mathrm{u}\left({\mathrm{t}}_1+{\mathrm{t}}_2\right)+\frac{1}{2}\mathrm{a}{\left({\mathrm{t}}_1+{\mathrm{t}}_2\right)}^2$

$228=6\mathrm{u}+\frac{1}{2}\mathrm{a}\left(36\right)......\left(2\right)$

from eq (1) and (2)
We get a = -6 cm/s², sub a=-6 in eq – (1)
$\Rightarrow 100=2\mathrm{u}–\frac{1}{2}\times 6\times 4$

2u = 112                 u = 56 cm/s

$\mathrm{v}=\mathrm{u}+\mathrm{at}=56–6\times 8\Rightarrow \mathrm{v}=8 \mathrm{cm}/\mathrm{s}$

5. A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps
forward and 3 steps backward, and so on. Each step is 1m long and requires 1sec. How long the drunkard takes to
fall in a pit 13m away from the start?
Sol. Distance of the pit from the start =13-5=8m
Time taken to move first 5m = 5sec
5 steps (i.e., 5m) forward and 3steps(i.e.,3m) backward means that net distance moved =5-3=2m
and time taken during this process =5+3=8sec

$\therefore$ Time taken in moving 8m = $\frac{8\times 8}{2}$= 32sec

$\therefore$ Total time taken to fall in the pit = 32+5 = 37sec

6. A car starts from rest and moves with uniform acceleration of 5 m/s² for 8 sec. If the acceleration ceases after 8
seconds then find the distance covered in 12s starting from rest.

Sol. The velocity after 8 sec v = 0 + 5 x 8 = 40 m/s
Distance covered in 8 sec

${\mathrm{s}}_0=0+\frac{1}{2}\times 5\times 64=160 \mathrm{m}$

After 8s the body moves with uniform velocity and distance covered in next 4s with uniform velocity.
s = vt = 40 x 4 = 160 m
The distance covered in12 s =160 +160 =320m.

7. A bus accelerates from rest at a constant rate ‘$\alpha$’ for some time, after which it decelerates at a constant rate
‘$\beta$’ to come to rest. If the total time elapsed is t seconds. Then evaluate following parameters from the given
graph
a) the maximum velocity achieved
b) the total distance travelled graphically and
c) Average velocity

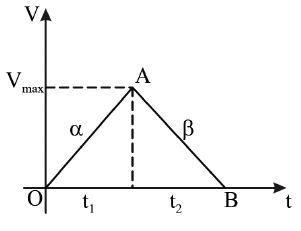
Sol. a) $\alpha$ = Slope of line OA = $\frac{{\mathrm{V}}_{\max }}{{\mathrm{t}}_1}\Rightarrow {\mathrm{t}}_1=\frac{{\mathrm{V}}_{\max }}{\alpha }$

b) $\beta$ = Slope of line AB = $\frac{{\mathrm{V}}_{\max }}{{\mathrm{t}}_2}\Rightarrow {\mathrm{t}}_2=\frac{{\mathrm{V}}_{\max }}{\beta }$

$\mathrm{t}={\mathrm{t}}_1+{\mathrm{t}}_2=\frac{{\mathrm{v}}_{\max }}{\alpha }+\frac{{\mathrm{V}}_{\max }}{\beta }={\mathrm{v}}_{\max }\left(\frac{\alpha +\beta }{\alpha \beta }\right)$

${\mathrm{v}}_{\max }=\left(\frac{\alpha \beta }{\alpha +\beta }\right)\mathrm{t}$

b) Displacement = area under the v-t graph  = area of $∆$OAB

$=\frac{1}{2}\times \text{ base }\times \text{ height }$ = $\frac{1}{2}\left({\mathrm{t}}_1+{\mathrm{t}}_2\right){\mathrm{v}}_{\max }=\frac{1}{2}{\mathrm{tv}}_{\max }=\frac{1}{2}\left(\frac{\alpha \beta }{\alpha +\beta }\right){\mathrm{t}}^2$

${\mathrm{V}}_{\text{avg }}=\frac{\text{ total displacement }}{\text{ total time }}=\frac{1}{2}\left(\frac{\alpha \beta }{\alpha +\beta }\right)\mathrm{t}=\frac{{\mathrm{v}}_{\max }}{2}$

8. Velocity-time graph for the motion of a certain body is shown in Fig. Explain the nature of this motion. Find
the initial velocity and acceleration and write the equation for the variation of displacement with time. What
happens to the moving body at point B ? How will the body move after this moment ?

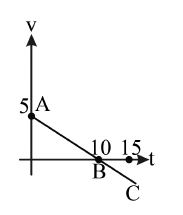
Sol. The velocity -time graph is a straight line with -ve slope, the motion is uniformly retarding one up to point B
and uniformly accelerated after with -ve side of velocity axis .
At point B the body stops and then its direction of velocity reversed.

The initial velocity at point A is ${\mathrm{v}}_0=7{\mathrm{ms}}^{–1}$

The acceleration

$\mathrm{a}=\frac{\Delta \mathrm{v}}{\Delta \mathrm{t}}=\frac{{\mathrm{v}}_{\mathrm{t}}–{\mathrm{v}}_0}{\Delta \mathrm{t}}=\frac{0–7}{11}=–0.6364{ \mathrm{ms}}^{–2}\approx –0.64{ \mathrm{ms}}^{–2}$

The equation of motion for the variation of displacement with time is

$\mathrm{s}=7\mathrm{t}–\frac{1}{2}0.64{\mathrm{t}}^2=7t–0.32t^2$

9. The acceleration (a) of a particle moving in a straight line varies with its displacement (S) as a = 2S. The
velocity of the particle is zero at zero displacement. Find the corresponding velocity-displacement equation.

Sol. $\mathrm{a}=2\mathrm{S}\Rightarrow \mathrm{v}\frac{\mathrm{dv}}{\mathrm{ds}}=2\mathrm{S}\Rightarrow \mathrm{vdv}=2\mathrm{SdS}$

$\Rightarrow {\int }_0^{\mathrm{v}}\mathrm{vdv}={\int }_0^{\mathrm{s}}2\mathrm{SdS}\Rightarrow {\left(\frac{{\mathrm{v}}^2}{2}\right)}_0^{\mathrm{v}}=2{\left(\frac{{\mathrm{S}}^2}{2}\right)}_0^{\mathrm{S}}$

$\Rightarrow \frac{{\mathrm{v}}^2}{2}={\mathrm{S}}^2\Rightarrow \mathrm{v}=\pm \sqrt{2} \mathrm{S}$

10. A body falls freely from a height of 125m (g = 10 m/s²). After 2 sec gravity ceases to act Find time taken by it to reach the ground ?
Sol. 1) Distance covered in 2s under gravity

${\mathrm{S}}_1=\frac{1}{2}{\mathrm{gt}}^2=\frac{1}{2}\left(10\right)(2{)}^2=20 \mathrm{m}$

Velocity at the end of 2s

$\mathrm{V}=\mathrm{gt}=10\times 2=20 \mathrm{m}/\mathrm{s}$

Now at this instant gravity ceases to act,
there after velocity becomes constant.
The remaining distance which is 125 – 20 = 105m
is covered by body with constant velocity20 m/s
Time taken to cover 105 m with constant velocity is given by

${\mathrm{t}}_1=\frac{\mathrm{S}}{\mathrm{V}}\Rightarrow {\mathrm{t}}_1=\frac{105}{20}=5.25 \mathrm{s}$

Total time taken = 2 + 5.25 = 7.25 s

11. If a freely falling body covers half of its total distance in the last second of its journey. Find its time of fall
Sol. Suppose t is the time of free fall

$S_n=\frac{g}{2}(2n–1)\text{ and } S=\frac{g}{2}\left(n^2\right)$

$\frac{S_n}{S}=\frac{(2n–1)\times \frac{g}{2}}{n^2\times \left(\frac{g}{2}\right)}=\frac{1}{2}$

$n^2–4n+2=0\text{ and }n=(2+\sqrt{2})\sec$

12. A ball is thrown vertically upwards from the top of a tower. Velocity at a point ‘h’ m vertically below the point
of projection is twice the downward velocity at a point ‘h’ m vertically above the point of projection. The
maximum height reached by the ball above the top of the tower is
Sol. If AB is the tower then according to the problem, velocity at ‘P’ is given as twice the velocity at ‘Q’

$V_P=\sqrt{\left(u^2+2gh\right)}; V_Q=\sqrt{\left(u^2–2gh\right)}; {\mathrm{V}}_{\mathrm{p}}=2\left({ \mathrm{V}}_{\mathrm{Q}}\right)$

$\sqrt{\left(u^2+2gh\right)}=\sqrt[2]{\left(u^2–2gh\right)}\Rightarrow u^2=\frac{10gh}{3}$

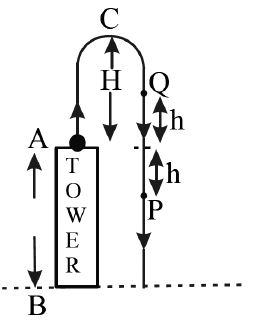
From the top of the tower maximum height reached $\mathrm{H}=\frac{{\mathrm{u}}^2}{2 \mathrm{g}}\Rightarrow \mathrm{H}=\frac{\left(\frac{10\mathrm{gh}}{3}\right)}{2 \mathrm{g}}=\frac{5 \mathrm{h}}{3}$

13. A balloon starts from rest, moves vertically upwards with an acceleration g/8 ms^-2. A stone falls from the
balloon after 8 s from the start. Further time taken by the stone to reach the ground (g = 9.8 ms^-2) is
Sol. The distance of the stone above the ground about which it begins to fall from the balloon is

$\mathrm{h}=\frac{1}{2}\left(\frac{\mathrm{g}}{8}\right)8^2=4 \mathrm{g}$

The velocity of the balloon at this height can be obtained from v = u + at; $\mathrm{v}=0+\left(\frac{\mathrm{g}}{8}\right)8=\mathrm{g}$

This becomes the initial velocity (u) of the stone as the stone falls from the balloon at the height h.
$\therefore$ u ‘ = g

For the total motion of the stone $\mathrm{h}=–{\mathrm{u}}^1\mathrm{t}+\frac{1}{2}{\mathrm{gt}}^2$

$\therefore –4 \mathrm{g}=\mathrm{gt}–\frac{1}{2}{\mathrm{gt}}^2\text{ and }{t}^2–2t–8=0$

Solving for ‘t’ we get t = 4 and -2s. Ignoring negative value of time, t = 4s.

14. Two trains, each travelling with a speed of 37.5kmh^-1 , are approaching each other on the same straight track.
A bird that can fly at 60kmph flies off from one train when they are 90 km apart and heads directly for the other
train. On reaching the other train, it flies back to the first and so on. Total distance covered by the bird before
trains collide is

Sol. Relative speed trains = 37.5 + 37.5 = 75kmh^-1

Time taken by them to meet $t=\frac{S_r}{u_r}=\frac{90}{75}=\frac{6}{5} \mathrm{h}$

Distance travelled by the bird, $x=V_{\text{bird }}\times t=60\times \frac{6}{5}=72 \mathrm{km} \left(\because V_{\text{bird }}=60{\mathrm{kmh}}^{–1}\right)$,

15. A particle has an initial velocity $3\hat{i}+4\hat{j}$ and an acceleration of $0.4\hat{i}+0.3\hat{j}$ . It speed after 10s is

Sol. $\overrightarrow{\mathrm{v}}=\overrightarrow{\mathrm{u}}+\overrightarrow{\mathrm{at}}$

$=(3\hat{i}+4\hat{j})+(0.4\hat{i}+0.3\hat{j})10$

$=3\hat{i}+4\hat{j}+4\hat{i}+3\hat{j}=7\hat{i}+7\hat{j}$

$\left|\overrightarrow{\mathrm{v}}\right|=\sqrt{49+49}=7\sqrt{2}$

16. A frictionless wire is fixed between A and B inside a circle of radius R. A small bead slips along the wire. Find
the time taken by the bead to slip from A to B.

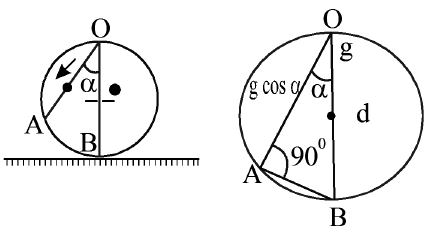
Sol. $\mathrm{S}=\frac{1}{2}{\mathrm{at}}^2$

$\text{ i.e. }AB=\frac{1}{2}\left(g\cos \alpha \right)t^2\dots \dots \dots \text{ (1) }$

From diagram AB = 2Rcos$\alpha$ ……….(2)

From eq (1) and eq (2)  $t=2\sqrt{\frac{R}{g}}$

17. The coordinates of a body moving in a plane at any instant of time t are $x=\alpha t^2\text{ and }y=\beta t^2$ . The speed of
the body is.

Sol. $\mathrm{x}=\alpha {\mathrm{t}}^2\Rightarrow {\mathrm{v}}_{\mathrm{x}}=\frac{\mathrm{dx}}{\mathrm{dt}}=2\alpha \mathrm{t}$

$\mathrm{y}=\beta {\mathrm{t}}^2\Rightarrow {\mathrm{v}}_{\mathrm{y}}=\frac{\mathrm{dy}}{\mathrm{dt}}=2\beta \mathrm{t}$

$\text{∴ speed }\mathrm{v}=\sqrt{{\mathrm{v}}_{\mathrm{x}}^2+{\mathrm{v}}_{\mathrm{y}}^2}=2\mathrm{t}\sqrt{{\alpha }^2+{\beta }^2}$

18. A person walks up a stationary escalator in time $t_1$. If he remains stationary on the escalator, then it can take
him up in time $t_2$. How much time would it take for him to walk up the moving escalator?
Sol. Let L be the length of escalator .

Speed of man w.r.t. escalator is ${\mathrm{V}}_{\mathrm{ME}}=\frac{\mathrm{L}}{{\mathrm{t}}_1}$

Speed of escalator ${\mathrm{v}}_{\mathrm{E}}=\frac{\mathrm{L}}{{\mathrm{t}}_2}$

Speed of man with respect to ground would be

${\mathrm{v}}_{\mathrm{M}}={\mathrm{v}}_{\mathrm{ME}}+{\mathrm{v}}_{\mathrm{E}}=\mathrm{L}\left(\frac{1}{{\mathrm{t}}_1}+\frac{1}{{\mathrm{t}}_2}\right)$

$\therefore$ The desired time is $\mathrm{t}=\frac{\mathrm{L}}{{\mathrm{v}}_{\mathrm{M}}}=\frac{{\mathrm{t}}_1{\mathrm{t}}_2}{{\mathrm{t}}_1+{\mathrm{t}}_2}$.