Mechanical Properties of Fluids

SURFACE TENSION

Introduction

Surface tension is one of the properties of matter in liquid state which will be discussed in this chapter. Surface tension is a molecular phenomenon.  It is due to the electromagnetic force between the molecules.  The forces between the molecules are of two types:  i)  Cohesive forces and ii)  adhesive forces. The force of attraction between the molecules of the same substance is called cohesive force.  The force of attraction between the molecules of different substance is called adhesive force.

Surface tension

It has been found that a liquid in small quantity (i.e. a liquid drop) at rest, free from external forces like gravity, always tends to have a spherical shape.  Since for a given volume, a sphere has the least surface area, hence it shows that the free surface of every liquid at rest has a tendency to have a least surface area. While doing so, the free surface behaves as if covered by a stretched membrane, having tension in all directions parallel to the surface.  This tension in the free surface of liquid at rest is called the surface tension.

Thus surface tension is the property of the liquid by virtue of which the free surface of liquid at rest tends to have minimum area and as such it behaves as if covered with a stretched membrane.

Measurement of surface tension

Imagine a line AB drawn tangentially anywhere on the liquid surface, the force of surface tension acts at right angles to this line on both its sides and also along the tangent to the liquid surface.  The force acting per unit length of such a line gives the quantitative measure of surface tension.

Therefore, surface tension of a liquid is measured as the force acting on unit length of a line imagined to be drawn tangentially anywhere on the free surface of the liquid at rest.  It acts at right angles to this line on both the sides and along tangent to the liquid surface.

Let F be the total force acting on an imaginary line of length l, drawn tangentially on the liquid surface at rest, the force of surface tension S, by definition, is

S = $\frac{\mathrm{F}}{\mathrm{I}}$   . . . .      (4)

Units of surface tension are dyne/cm in cgs system and Nm^-1 in S.I. The dimensional formula of surface tension is [ML^OT²].  Surface tension is a scalar quantity because it has no specific direction for a given liquid.  

Illustrations of surface tension

1. Rain drops are spherical in shape because each drop tends to acquire minimum surface area due to surface tension, and for a given volume, the surface area of sphere is minimum.

2. When mercury is split on a clean glass plate, it forms globules. Tiny globules are spherical on account of surface tension because force of gravity is negligible.  The bigger globules get flattened from the middle but have round shape near the edges.

The globule takes spherical shape due to surface tension but in case of big mercury globule, the force gravity is large.  The centre of gravity of the big globule is lowered due to its heavy weight.  As a result, the big globule gets flattened from the middle.

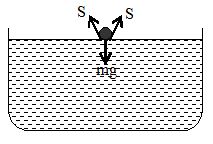
3. When a greased iron needle is placed gently on the surface of water at rest, so that it does not prick the water surface, the needle floats on the surface of water despite its being heavier. A slight depression, on the surface of water is observed just below the needle, indicating that the water surface behaves like a stretched membrane.  The forces of surface tension (S, S) act in the inclined manner as shown in the adjoining figure.  The weight of the needle is balanced by the vertical components of the forces of surface tension.  If the water surface is pricked by one end of the needle, the needle sinks down.

2. SURFACE ENERGY

The additional potential energy due to the molecular forces per unit surface area is called surface energy.  (or)  The excess potential energy per unit area of the surface film is called surface energy.

$\text{ Surface energy }=\frac{\text{ Potential energy due to molecular forces }}{\text{ Surface area }}$

Its SI unit is J/m².  Its CGS unit is erg/cm².

Its dimensional formula = $\left[\frac{{\mathrm{ML}}^2{ \mathrm{T}}^{–2}}{{ \mathrm{L}}^2}\right]=\left[{\mathrm{ML}}^0{ \mathrm{T}}^{–2}\right]$

A system in equilibrium has a tendency to acquire lowest possible potential energy.  For minimum potential energy in the surface film, minimum number of molecules must be present in it.  This is possible by decreasing the surface area of the surface film.  Hence, the free surface of a liquid always tends to have minimum possible area which is a consequence of surface tension.

Relation between surface tension and Surface Energy: Consider rectangular wire frame PQRS with a sliding wire of length l on its arms QP and RS.  Assume that there is no friction between the arms and the sliding wire.  A soap film is formed between RQ and the sliding wire by dipping it in a soap solution.  The wire is kept in horizontal position as shown in fig.  The soap film formed appears to be thin but it may have several hundred thousands molecular layers across its thickness.  So, it has two surfaces in contact with the sliding wire and hence exert forces due to surface tension on the sliding wire.  If T is the surface tension of the soap solution, each surface of the soap will pull the sliding wire parallel to itself with a force Tl, since the surface tension  

$\mathrm{T}=\frac{\text{ force }}{\text{ length }}$

The resultant force on the sliding wire due to the two surfaces in contact is given by F = 2Tl.  This force acts into the soap film and the sliding wire will be pulled inwards.  To keep the sliding wire in equilibrium an equal and opposite force F is to be applied wire a shown in fig.  Suppose the sliding wire is slowly pulled by the force F through a distance x so that the area of the soap film increases by lx.  The new surface area of the soap film created is 2l x, since there are two surfaces of the soap film in contact with the air.  When the soap film expands molecules from inside move on to the surface for which work is to be done.  The work done is given by

Work done = Force $\times$ displacement

= Fx

= T(2lx)

The work done by the external force is stored as the additional potential energy of the new surface, since there is no change in kinetic energy.

$\text{ Surface energy }\frac{\text{ Additional Potential energy }}{\text{ Surface area }}=\frac{\mathrm{T}\left(2l\mathrm{x}\right)}{2l\mathrm{x}}$

E = T. 

3. CALCULATION EXCESS PRESSURE

Excess of pressure on curved surface of liquid

We know that a liquid molecule on the surface of liquid is attracted by forces of cohesion in all directions and force of surface tension acts tangentially to the liquid surface at rest.  The direction of resultant force on a molecule on the surface of liquid depends upon the shape of the liquid surface.

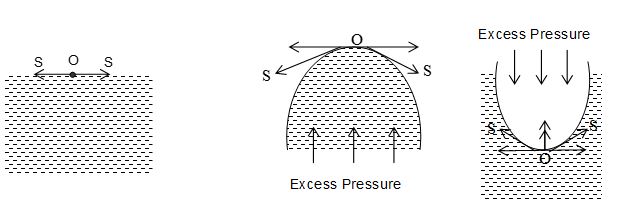
If liquid surface is plane, then the molecule O on the liquid surface will be equally attracted on all the sides, and the forces (S, S) of surface tension will be acting tangentially to the liquid surface in opposite directions.  Hence, no resultant force is acting on the molecule O.  It means the resultant force is acting normally to the liquid surface is zero.  As a result, no extra pressure is communicated to the inner side or outer side of liquid surface.  Thus the pressure on the liquid side is equal to the pressure on the vapour side in case of a plane liquid surface.

If the liquid surface is curved, the molecule O on the liquid surface is acted upon, by the forces (S, S) due to surface tension along the tangents to the surface.  Resolving these forces into horizontal and vertical components, horizontal components cancel each other whereas vertical components add up.  Thus a resultant force would be acting on the curved surface of the liquid which acts towards its centre of curvature.  It means, the resultant force is directed inwards in case of convex surface and is directed outwards in case of concave surface.  In order that the curved surface of liquid may be in equilibrium, there must be an excess of pressure on its concave side over that on the convex side, so that the forces of excess pressure may balance the resultant forces due to surface tension.  Hence, for the curved surface of liquid in equilibrium the pressure on concave side of liquid will be greater than pressure on its convex side.

Excess pressure inside a liquid drop

Consider a liquid drop of radius R.  The molecules lying on the surface of liquid drop, due to surface tension will experience a resultant force acting inwards, perpendicular to the surface.  Since the size of liquid drop cannot be reduced to zero due to force of surface tension, therefore, the pressure inside the drop must be greater than the pressure outside it.  This excess of pressure inside the drop will provide a force acting outwards perpendicular to the surface, to counter balance the resultant force due to surface tension.

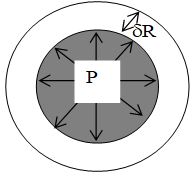
Let,      S = surface tension of liquid drop,

             P = excess of pressure inside the drop

Due to excess of pressure, let there be increase in the radius of the drop by a small quantity $\delta$R.  Then work done by the excess pressure

W = force $\times$ displacement = (excess pressure $\times$ area) $\times$ increase in radius

= $\mathrm{P}\times 4{\mathrm{\pi R}}^2\times \mathrm{\delta R}$   . . . .      (6)

Increase in surface area of the drop = final surface area – initial surface area

= $4\mathrm{\pi }(\mathrm{R}+\mathrm{\delta R}{)}^2–4{\mathrm{\pi R}}^2$

= $4\pi \left[{\mathrm{R}}^2+2\mathrm{R}\left(\delta \mathrm{R}\right)+(\delta \mathrm{R}{)}^2–{\mathrm{R}}^2\right]$

= $8\mathrm{\pi R\delta R}$

[Neglecting, ($\delta$R)² being very very small]

$\therefore$ Increase in potential energy = increase in surface area $\times$ surface tension

= $8\mathrm{\pi R}\left(\mathrm{\delta R}\right)\times \mathrm{R}$     . . . .      (6a)

As the increase in potential energy is at the cost of work done by the excess pressure, therefore from (6) and (6a), we get

$\mathrm{P}\times 4{\mathrm{\pi R}}^2\times \mathrm{\delta R} 8\mathrm{\pi R\delta R}\times \mathrm{S}$

or  $\mathrm{P}=\frac{2\mathrm{S}}{\mathrm{R}}$

Excess pressure inside a soap bubble

Consider soap bubble of radius R.  The molecules, lying on the surface of liquid bubble will experience a resultant force acting inwards perpendicular to the surface due to surface tension.  Since the size of soap bubble cannot be reduced to zero, therefore, the pressure inside the soap bubble must be greater than the pressure outside it.  This excess of pressure inside the bubble will provide a force acting outwards perpendicular to the surface of bubble to counter balance the resultant force to the surface tension.

Let,      S = surface tension of the soap solution,

             P = excess of pressure inside the bubble

Due to it, let there be increase in the radius of the bubble by a small amount $\delta$R.  Then, work done by the excess pressure W = force $\times$ distance

= (excess pressure $\times$ area) $\times$ increase in radius

= $\mathrm{P}\times 4{\mathrm{\pi R}}^2\times \mathrm{\delta R}$                       . . . .      (7)

The soap bubble has two free surfaces, one outside the bubble and the other inside the bubble where soap solution and air are in contact.

$\therefore$ The effective increase in surface area of the bubble

= 2[final surface area – initial surface area]

= $2\left[4\pi (\mathrm{R}+\delta \mathrm{R}{)}^2–4\pi {\mathrm{R}}^2\right]$

= $2\times 4\mathrm{\pi }\left[{\mathrm{R}}^2+2\mathrm{R}\left(\mathrm{\delta R}\right)+(\mathrm{\delta R}{)}^2–{\mathrm{R}}^2\right]$

= $8\pi \times 2\mathrm{R}\left(\delta \mathrm{R}\right)$  [Neglecting ($\delta$R)², being very small] = $16\pi \mathrm{R}\left(\delta \mathrm{R}\right)$

$\therefore$ Increase in potential energy = increase in surface area $\times$ surface tension

= 16 $\mathrm{\pi R\delta R}\times \mathrm{S}$  . . . .      (8)

As the increase in potential energy is at the cost of work done by the excess pressure, therefore from (7) and (8), we get

$\mathrm{P}\times 4{\mathrm{\pi R}}^2\times \left(\mathrm{\delta R}\right)=16\mathrm{\pi R}\left(\mathrm{\delta R}\right)\times \mathrm{S}$

or  $\mathrm{P}=\frac{4\mathrm{S}}{\mathrm{R}}$    . . . .  (9)

Excess pressure inside an air bubble in a liquid

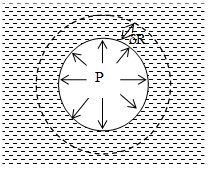
Consider an air bubble of radius R just inside a liquid of surface tension S.  the air bubble will have only one free surface as shown in figure given below. Proceeding as discussed above, it can be shown that the excess pressure inside the air bubble is given by P = 2S/R.

Note:

1. When an air bubble of radius r is at depth h below the free surface of liquid of density $\rho$ and surface tension S, then the excess of pressure inside bubble P = $\frac{2\mathrm{S}}{\mathrm{r}}+\mathrm{h\rho g}$

2. If r₁ and r₂ are the radii of the curved liquid surface then excess pressure inside the liquid surface is given by $\mathrm{P}=\mathrm{S}\left(\frac{1}{{\mathrm{r}}_1}+\frac{1}{{\mathrm{r}}_2}\right)$

3. For a single spherical surface such as a liquid drop or an air bubble in water, r₁ = r₂ = r, then $\mathrm{P}=\frac{2\mathrm{S}}{\mathrm{r}}$

4. If the surface is a liquid film, it has two free surfaces, then excess of pressure inside the liquid surface is $\mathrm{P}=25\left(\frac{1}{{\mathrm{r}}_1}+\frac{1}{{\mathrm{r}}_2}\right)$ for a soap bubble, r₁ = r₂ = r, then  P = $\frac{4S}{r}$

5. For a cylindrical liquid surface, r₁ = r and r₂ = $\infty$ then excess of pressure inside the surface is $\mathrm{P}=\frac{\mathrm{S}}{\mathrm{r}}$

6. In case of a liquid between two plates and separation ‘d’, we have r = $\frac{\mathrm{d}}{2}$. Then excess pressure p, given by, $\mathrm{P}=\frac{\mathrm{S}}{\mathrm{r}}=\frac{\mathrm{S}}{( \mathrm{d}/2)}=\frac{2\mathrm{S}}{ \mathrm{d}}$.

If A is the area over which the liquid wets the plate, then the force required to separate the plate is $\mathrm{F}=\mathrm{P}\times \mathrm{A}=\frac{2\mathrm{S}}{ \mathrm{d}}\times \mathrm{A}$

4. ANGLE OF CONTACT

Consider two tubes with different liquid in them, say water and mercury.  The liquid meniscus is concave in the tube containing water and convex in other tube containing mercury.  Let A be one of the points of contact of the liquid with the tube.  Through A, draw a tangent AX to the liquid surface and another tangent AY to the solid surface in contact with the liquid.  The $\angle$XAY=$\theta$ (say) is called the angle of contact of liquid with the given solid.

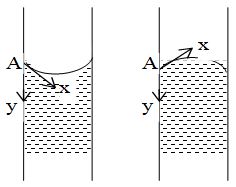
Therefore, angle of contact between a liquid and a solid is defined as the angle enclosed between the tangents to the liquid surface and the solid surface inside the liquid, both the tangents being drawn at the point of contact of the liquid with the solid.

For example, when a glass strip is dipped in water and mercury, the angle of contact $\theta$ in both the cases is as shown figure.

The value of angle of contact

1. Depends upon the nature of the liquid and solid in contact

2. Depends upon the medium which exists above the free surface

3. Is independent of the inclination of the solid to liquid surface

4. Is fixed for a given pair of solid and liquid and surrounding medium.

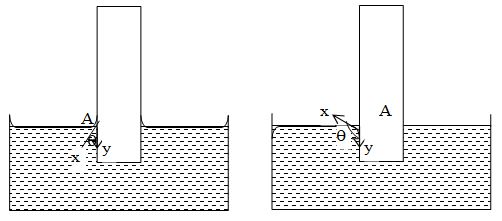
Those liquids which wet the walls of the container (e.g. water and glass) and have a meniscus concave upwards, the value of angle of contact is acute (i.e. $\theta$ < 90^o).  Those liquids which do not wet the walls of the container (e.g. mercury and glass) and have meniscus convex upwards, the value of angle of contact is obtuse (i.e. $\theta$ > 90^o)

The angle of contact of mercury with glass is about 140^o, whereas the angle of contact of water with glass is about 8^o.  However, for pure water in a glass tube, the angle of contact  is taken as 0^o. 

5. CAPILLARITY

When a capillary tube (capillary tube is a tube of very fine bore) open at both ends is dipped into a liquid vertically, the liquid inside the capillary tube either rises or falls due to surface tension.  This phenomenon is called capillary action.  This is also called capillarity.

A tube with a fine and uniform bore throughout its length is called a capillary tube.

When one end of a glass capillary tube open at both ends is dipped in a liquid like water which wets the tube, the liquid level in the tube rises to a certain height above the liquid level in the container.  However the liquid level in the tube falls below its level in the container, in case of liquids like mercury which do not wet the glass tube.

The phenomenon of rise or fall of liquid in a capillary tube is called capillarity.  

Examples of Capillarity

Common examples of capillarity are as follows:

1. The fine pores of a blotting paper act like capillary tubes. Ink rises in them leaving the paper dry.

2. A towel soaks water on account of capillary action

3. Oil rises in the long narrow spaces between threads of a wick, because they act as fine capillaries.

4. Swelling of wood in rainy season is due to rise of moisture from air, in the pores of wood.

5. Ploughing of fields is essential for preserving moisture in the soil. By ploughing, the fine capillaries in the soil are broken.  Water from within the soil shall not rise and evaporate off.

6. Sand is drier soil than clay. This is because holes between the sand particles are not so fine as compared to that of clay, as to draw up water by capillary action.

Rise of liquid in a capillary tube (ascent formula)

When one end of capillary tube of radius r is immersed into a liquid of density $\rho$ which wets the sides of the capillary tube (say water and capillary tube of glass), the shape of the liquid meniscus in the tube becomes concave upwards.

Let       R = radius of curvature of liquid meniscus

             P = atmospheric pressure

             S = surface tension of the liquid

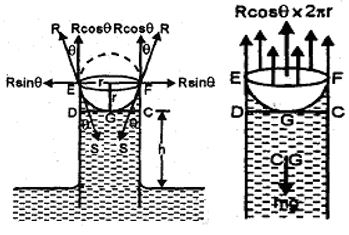
The pressure at point A just above the liquid meniscus in the capillary tube is atmospheric pressure = P. The pressure at point B, just below the liquid meniscus (on convex side) = P – 2S/R.

Pressures at points C and D, just above and below the plane surface of liquid in the vessel is also P (i.e. atmospheric pressure).  The points B and D are in the same horizontal plane in the liquid but the pressure at these points is different.  Hence there will be no equilibrium.

In order to maintain equilibrium, the liquid level rises in the capillary tube up to a height h so that the pressures at points D and E which are in the same level in liquid may become equal.

Now, pressure at E = pressure at B + pressure due to height h (=BE) of the liquid column = $\left(\mathrm{P}–\frac{2\mathrm{S}}{\mathrm{R}}\right)+\mathrm{h\rho g}$

As there is an equilibrium, therefore, pressure at E = pressure at D

i.e.        $\mathrm{P}–\frac{2\mathrm{S}}{\mathrm{R}}+\mathrm{h\rho g}=\mathrm{P}$

or         $\mathrm{h\rho g}=\frac{2\mathrm{S}}{\mathrm{R}}$

or     $\mathrm{h}=\frac{2\mathrm{S}}{\mathrm{R\rho g}}$    . . . .  (10)

Calculation of R:  Let l be the centre of curvature of liquid meniscus GXY in the tube and GS be the tangent to the liquid surface at point G.  In future

GI = R; GO = r

$\angle$ IGO = $\theta$ = angle of contact

In $∆$IGO, cos$\theta$ = $\frac{\mathrm{GO}}{\mathrm{GI}}=\frac{\mathrm{r}}{\mathrm{R}}$

or     $\mathrm{R}=\frac{\mathrm{r}}{\mathrm{cos\theta }}$

Putting this value in (10), we get

$\mathrm{h}=\frac{2\mathrm{Scos\theta }}{\mathrm{r\rho g}}$ . . . .      (11)

It is called ascent formula.  From equation (11), it is clear that $\mathrm{h}\propto \frac{1}{\mathrm{r}}$. It means, the smaller is the value of r, the larger will be the value of h and vice versa.  Thus liquid raises more in a narrow tube and less in wider tube.

Note: If the end of the capillary tube is immersed in a liquid which does not wet the sides of the tube (e..g mercury and glass tube), then liquid meniscus in the tube will be convex upwards.  The angle of contact $\theta$ is obtuse, cos$\theta$ will be negative and from (11), h will be negative.  In this situation, the liquid level gets depressed in the capillary tube.  In that case, equation (11) will be called descent formula. 

6. EXPERIMENT TO DETERMINE SURFACE TENSION OF A LIQUID

To determine the surface tension of the liquid a clean dry glass capillary tube is taken.  A long wire bent twice at right angles is taken and is attached to the capillary tube with the help of a rubber band.  This tube is vertically dipped in a glass beaker containing the liquid as shown in the fig.  The liquid rises into the tube upto certain extent.

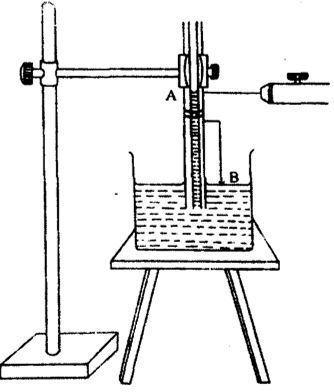
The height of the capillary tubes is so adjusted that the tip ‘B’ of the wire wound round the capillary tube just touches the surface of the liquid in the beaker.

A traveling microscope is focused on the meniscus of the liquid in the capillary tube and the horizontal cross wire to be adjusted tangential to the lower meniscus of the liquid and reading of the microscope ‘R₁’ is noted.  The beaker containing liquid is removed without disturbing the capillary tube and wire.  Now the microscope is focused against the tip ‘B’ of the wire and the reading of microscope ‘R₂’ is noted.

The difference between the two readings of microscope gives the height (h) of liquid in the capillary i.e., R₁ – R₂ = h.  The diameter of the capillary tube is measured using microscope by keeping the tube horizontal and radius is determined.  The surface tension ‘T’ of the given liquid can be determined on substituting the values of h.r.d and ‘g’ in the equation 

7. RISE OF LIQUID IN TUBE OF INSUFFICIENT LENGTH

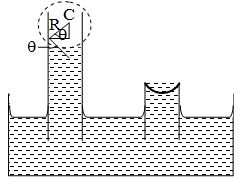
When the height to which a liquid can rise in a capillary tube is more than the length of the tube, the liquid does not overflow.  This is because radius of curvature of the liquid meniscus in the tube increases as discussed below: We know that the height h to which the liquid of density $\rho$, surface tension S, radius of curvature of liquid meniscus R in a capillary tube (when liquid wets the sides of the capillary tube) rises in a capillary tube is given by equation (10), as

$\mathrm{h}=\frac{2 \mathrm{S}}{\mathrm{R\rho g}}$

or  $\mathrm{hR}=\frac{25}{\mathrm{\rho g}}$

or   hR = a finite constant       $[\because \mathrm{S}, \mathrm{\rho }\text{ and }\mathrm{g}\text{ are constants }]$

Hence, when the tube is of insufficient length, radius of curvature of the liquid meniscus increases so as to maintain the product Rh a finite constant, i.e. as h decreases, R increases and the liquid meniscus becomes more and more flat, but the liquid does not over flow.  this is shown in figure.

1. The presence of impurities either on the liquid surface or dissolved in it, considerably affect the force of surface tension, depending upon the degree of contamination. A highly soluble substance like sodium chloride when dissolved in water, increases the surface tension of water.  But the sparingly soluble substances like phenol when dissolved in water, decreases the surface tension of water.

2. The surface tension of liquid decreases with rise of temperature. The surface tension of liquid is zero at its boiling point and it vanishes at critical temperature.  At critical temperature, intermolecular forces for liquid and gases become equal and liquid can expand without any restriction.  For small temperature differences, the variation in surface tension with temperature is linear and is given by the relation S_t = S_o (1 – $\alpha$t)

where S_t, S₀ are the surface tensions at t^oC and 0^oC respectively and $\alpha$ is the temperature coefficient of surface tension. 

8. DETERGENT AND SURFACE TENSION

The dirty greasy stains on the clothes cannot be cleaned by simply washing the clothes in water.  This is so because water does not find its contact with greasy dirt and hence can not wet such surfaces.  By adding detergent or soap to water, the greasy dirt from cloth can be easily cleaned which has been explained below:

1. The molecules of the soap or detergent are hair pins shaped.

2. When soap or detergent is dissolved in water, then heads of the hair pins shaped molecules get attracted to water surface.

3. When clothes with greasy stains are dipped in detergent or soap mixed water, then the pointed ends of the hair pins shaped molecules get attached to the molecules of the greasy stain. As a result of which, the water comes into contact with greasy stain and thus a water greasy dirt interface is formed.  Due to which the greasy dirties held suspended.  It happens so because detergent molecules reduce the surface tension between water and greasy stain.

4. When clothes are rinsed in water, then the greasy dirt is washed away by the running water.

9. APPLICATIONS OF SURFACE TENSION

1. Since surface tension of soap solution is low, it can spread over large area. Hence it can wash clothes more effectively.  Hot soap solution proves still better as surface tension decreases further on heating.

2. For the same reason, surface tension of all lubricating oils and paints is kept low.

3. Oil spreads, over the surface of water, as surface tension of oil is smaller than that of water.

4. Stormy waves at sea are calmed by pouring oil on sea water.

5. In soldering addition of ‘flux’ reduces the surface tension of molten tin, hence it spreads.

6. Antiseptics like detol have low surface tension, so they spread faster.

10. CALCULATION OF RADIUS OF A NEW BUBBLE

Radius of the new bubble formed when two bubbles coalesce

Consider two soap bubbles of radii r₁ and r₂ respectively.  If V₁ and V₂ are the volumes of two soap bubbles, then

${\mathrm{V}}_1=\frac{4}{3}\left[{\mathrm{\pi r}}_1^3\right]\text{ and }{\mathrm{V}}_2=\frac{4}{3}{\mathrm{\pi r}}_2^3$

Let S be the surface tension of the soap solution.  If P₁ and P₂ are the excess of pressure inside the two soap bubbles, then

${\mathrm{P}}_1=\frac{4\mathrm{S}}{{\mathrm{r}}_1}\text{ and }{\mathrm{P}}_2=\frac{4\mathrm{S}}{{\mathrm{r}}_2}$

Let r be the radius of the new soap bubble formed when two soap bubbles coalesce under isothermal conditions. If V and P be the volume and excess of pressure inside this new soap bubble, then

$\mathrm{V}=\frac{4}{3}{\mathrm{\pi R}}^3 \text{ and } \mathrm{P}=\frac{4\mathrm{S}}{\mathrm{r}}$

as the new bubble is formed under isothermal conditions, so Boyle’s law holds good

i.e. ${\mathrm{P}}_1{\mathrm{V}}_1+{\mathrm{P}}_2{\mathrm{V}}_2=\mathrm{PV}$

or $\frac{4\mathrm{S}}{{\mathrm{r}}_1}\times \frac{4}{3}{\mathrm{\pi r}}_1^3+\frac{4\mathrm{S}}{{\mathrm{r}}_2}\times \frac{4}{3}{\mathrm{\pi r}}_2^3=\frac{4\mathrm{S}}{\mathrm{r}}\times \frac{4}{3}{\mathrm{\pi r}}^3$

or ${\mathrm{r}}_1^2+{\mathrm{r}}_2^2={\mathrm{r}}^2$

or $\mathrm{r}=\sqrt{{\mathrm{r}}_1^2+{\mathrm{r}}_2^2}$

Radius of interface when two soap bubbles of different radii are in contact

Consider two soap bubbles of radii r₁ and r₂ in contact with each other as shown in figure.  Let r be the radius of the common boundary.  If P₁ and P₂ are the excess pressures on the two sides of the interface then the resultant excess pressure is

$\mathrm{P}={\mathrm{P}}_1–{\mathrm{P}}_2$

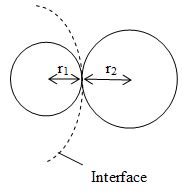
or $\frac{4\mathrm{S}}{\mathrm{r}}=\frac{4\mathrm{S}}{{\mathrm{r}}_1}–\frac{4\mathrm{S}}{{\mathrm{r}}_2} \text{ or }\frac{1}{\mathrm{r}}=\frac{1}{{\mathrm{r}}_1}–\frac{1}{{\mathrm{r}}_2}$

or $\mathrm{r}=\frac{{\mathrm{r}}_1{\mathrm{r}}_2}{{\mathrm{r}}_2–{\mathrm{r}}_1}$

FLUID DYNAMICS

11. FLUID & DENSITY OF A FLUID

Fluid

A fluid is a substance that deforms continuously under the application of a shear (tangential) stress no matter how small the shear stress may be.

Thus, fluids comprise the liquid and gas (or vapour) phases of the physical forms in which matter exists. The distinction between a fluid and the solid state of matter is clear if you compare fluid and solid behaviour. A solid deforms when a shear stress is applied but it does not continue to increase with time. However if a shear stress is applied to a fluid, the deformation continues to increases as long as the stress is applied. We may alternatively define a fluid as a substance that cannot sustain a shear stress when at rest.

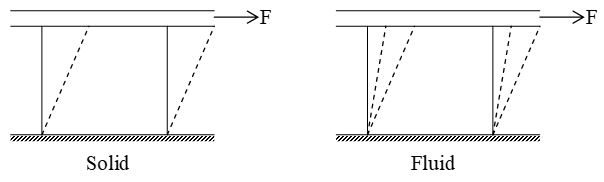
An ideal liquid is incompressible and non viscous in nature. An incompressible liquid means the density of the liquid is constant; it is independent of the variations in pressure. A nonviscous liquid means that parts of the liquid in contact do not exert any tangential force on each other.  Thus, there is no friction between the adjacent layers of a liquid.  The force by one part of the liquid on the other part is perpendicular to the surface of contact.  

Density of a liquid

Density ($\rho$) of any substance is defined as the mass per unit volume

$\therefore \mathrm{\rho }=\frac{\text{ mass }}{\text{ volume }}$

Relative Density (R.D.)

In case of a liquid, sometimes another term relative density is defined.  It is the ratio of density of the substance to the density of water at 4^oC.  Hence 

$\text{ Relative density }=\frac{\text{ Density of substance }}{\text{ Density of water at }4°\mathrm{C}}$

R.D. is a pure ratio.  So, it has no units.  It is also some times referred as specific gravity. Density of water at 4^oC in cgs is 1 gm/cm³.  Therefore, numerically the R.D. and density of substance (in CGS) are equal.  In SI units the density of water at 4^oC is 1000 kg/m³.  

Density of a mixture of two or more liquids

Case 1: Suppose two liquids of densities ${\mathrm{\rho }}_1$ and ${\mathrm{\rho }}_2$ having masses m₁ and m₂ are mixed together.  Then the density of the mixture will be

$\mathrm{\rho }=\frac{\text{ Total mass }}{\text{ Total volume }}=\frac{\left({\mathrm{m}}_1+{\mathrm{m}}_2\right)}{\left({\mathrm{V}}_1+{\mathrm{V}}_2\right)}=\frac{\left({\mathrm{m}}_1+{\mathrm{m}}_2\right)}{\left(\frac{{\mathrm{m}}_1}{{\mathrm{\rho }}_1}+\frac{{\mathrm{m}}_2}{{\mathrm{\rho }}_2}\right)}$

if  m₁ = m₂, then

$\mathrm{\rho }=\frac{2\mathrm{\rho }+{\mathrm{\rho }}_2}{{\mathrm{\rho }}_1+{\mathrm{\rho }}_2}$

Case 2: If two liquids of densities ${\mathrm{\rho }}_1$ and ${\mathrm{\rho }}_2$ having volumes V₁ and V₂ are mixed, then the density of the mixture is

$\mathrm{\rho }=\frac{\text{ Total mass }}{\text{ Total volume }}=\frac{{\mathrm{m}}_1+{\mathrm{m}}_2}{{\mathrm{V}}_1+{\mathrm{V}}_2}=\frac{{\mathrm{\rho }}_1{\mathrm{V}}_1+{\mathrm{\rho }}_2{\mathrm{V}}_2}{{\mathrm{V}}_1+{\mathrm{V}}_2}$

if    V₁ = V₂, then

$\mathrm{\rho }=\frac{{\mathrm{\rho }}_1+{\mathrm{\rho }}_2}{2}$

Effect of Temperature on Density

As the temperature of a liquid is increased, the mass remains the same while the volume is increased and hence, the density of the liquid decreases $\left(\text{ as }\mathrm{\rho } \infty \frac{1}{\mathrm{V}}\right)$.  Thus,

$\frac{{\mathrm{\rho }}^{‘}}{\mathrm{\rho }}=\frac{\mathrm{V}}{{\mathrm{V}}^{‘}}=\frac{\mathrm{V}}{\mathrm{V}+\mathrm{dV}}=\frac{\mathrm{V}}{\mathrm{V}+{\mathrm{V}}_{\mathrm{\gamma }}\mathrm{\Delta \theta }}$

or $\frac{{\mathrm{\rho }}^{‘}}{\mathrm{\rho }}=\frac{1}{1+\mathrm{\gamma \Delta \theta }}$

Here,    $\gamma$ = thermal coefficient of volume expansion

And      $∆\theta$ = rise in temperature

${\mathrm{\rho }}^{‘}=\frac{\mathrm{\rho }}{1+\mathrm{\gamma \Delta \theta }}$

Effect of pressure on Density

As pressure is increased, volume decreases and hence density will increase.  Thus,

$\mathrm{\rho }\propto \frac{1}{\mathrm{V}}$

$\frac{{\mathrm{\rho }}^{‘}}{\mathrm{\rho }}=\frac{\mathrm{V}}{{\mathrm{V}}^{‘}}=\frac{\mathrm{V}}{\mathrm{V}+\mathrm{dV}}=\frac{\mathrm{V}}{\mathrm{V}–\left(\frac{\mathrm{dp}}{\mathrm{B}}\right)\mathrm{V}}$

or Here,   dp = change in pressure

And           B = Bulk modulus of elasticity of the liquid

Therefore,    $\mathrm{\rho }‘=\frac{\mathrm{\rho }}{1–\frac{\mathrm{dp}}{\mathrm{B}}}$

12. PRESSURE IN A FLUID

When a fluid (either liquid or gas) is at rest, it exerts a force perpendicular to any surface in contact with it, such as a container wall or a body immersed in the fluid.

While the fluid as a whole is at rest, the molecules that makes up the fluid are in motion, the force exerted by the fluid is due to molecules colliding with their surroundings.

If we think of an imaginary surface within the fluid, the fluid on the two sides of the surface exerts equal and opposite forces on the surface, otherwise the surface would accelerate and the fluid would not remain at rest. Consider a small surface of area dA centered on a point on the fluid, the normal force exerted by the fluid on each side is dF₁. The pressure P is defined at the point as the normal force per unit is i.e.

P = $\frac{{\mathrm{dF}}_1}{\mathrm{dA}}$.

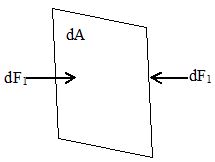
If the pressure is the same at all points of a finite plane surface with area A, then

  $\mathrm{P}=\frac{{\mathrm{F}}_1}{\mathrm{A}}$

where F₁ is the normal force on the side of the surface.  The SI unit of pressure is Pascal, where

1 Pascal = 1Pa = 1.0 N/m².

One unit used principally in meteorology is the Bar which is equal to 10⁵ Pa.

1 Bar = 10⁵ Pa.

Atmospheric Pressure (P_o)

It is pressure of the earth’s atmosphere.  This changes with weather and elevation, Normal atmospheric pressure at sea level (an average value) is 1.013$\times$10⁵ Pa.  Thus,

1 atm = 1.013$\times$10⁵ Pa.

Note: Fluid pressure acts perpendicular to any surface in the fluid no matter how that surface is oriented.  Hence, pressure has no intrinsic direction of its own, it’s a scalar.  By contrast, force is a vector with a definite direction.

Absolute pressure and Gauge Pressure

The excess pressure above atmospheric pressure is usually called gauge pressure and the total pressure is called absolute pressure.  Thus,

Gauge pressure = absolute pressure – atmospheric pressure.

Absolute pressure is always greater than or equal to zero. While gauge pressure can be negative also.

Variation in Pressure with depth

If the weight of the fluid can be neglected, the pressure in a fluid is the same throughout its volume.  But often the fluid’s weight is not negligible and under such condition pressure increases with increasing depth below the surface.

Let us now derive a general relation between the pressure P at any point in a fluid at rest and the elevation y of that point.  We will assume that the density $\mathrm{\rho }$ and the acceleration due to gravity g are the same throughout the fluid.  If the fluid is in equilibrium. Every volume element is in equilibrium.

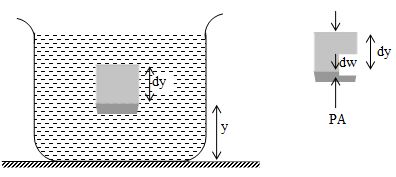
Consider a thin element of fluid with height dy.  The bottom and top surfaces each have area A and they are at elevations y and y+dy above some reference level where y=0.  The weight of the fluid element is

dW = (volume)(density)(g) = (Ady)($\rho$)(g)

or dW = $\mathrm{\rho }$gAdy

What are the other forces in y-direction on this fluid element?  Call the pressure at the bottom surface P, the total y component of upward force is PA.  The pressure at the top surface is P+dP and the total y-component of downward force on the top surface is (P+dP)A.  the fluid element is in equilibrium, so that total y-component of force including the weight and the forces at the bottom and top surfaces must be zero.

$\sum {\mathrm{F}}_{\mathrm{y}}=0$

$\therefore \mathrm{PA}–(\mathrm{P}+\mathrm{dP})\mathrm{A}–\mathrm{\rho gAdy}=0$

or $\frac{\mathrm{dP}}{\mathrm{dy}}=–\mathrm{\rho g}$

This equation shows that when y increases, P decreases i.e. as we move upward in the fluid, pressure decreases.

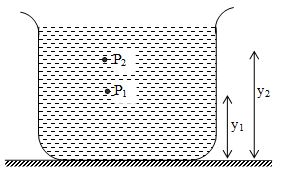
If P₁ and P₂ be the pressure at elevations y₁ and y₂ and if ρ and g are constant, then integrating equation (1), we get  

${\int }_{{\mathrm{P}}_1}^{{\mathrm{P}}_2}\mathrm{dP}=–\mathrm{\rho g}{\int }_{{\mathrm{y}}_1}^{{\mathrm{y}}_2}\mathrm{dy}$

or  ${\mathrm{P}}_2–{\mathrm{P}}_1=–\mathrm{\rho g}\left({\mathrm{y}}_2–{\mathrm{y}}_1\right)$  ……… (ii)

It is often convenient to express equation (ii) in terms of the depth below the surface of a fluid.  Take point 1 at depth h below the surface of fluid and let P represents pressure at this point.  Take point 2 at the surface of the fluid, where the pressure is P_o (subscript zero for zero depth).  The depth of point 1 below the surface is

h = y­₂ – y₁

and eq.(ii) becomes

P_o-P = ρg(y₂-y₁) = -ρgh

P = P_o+ρgh       …….. (iii)

Thus, pressure increases linearly with depth, if ρ and g are uniform.  A graph between P and h is shown below.

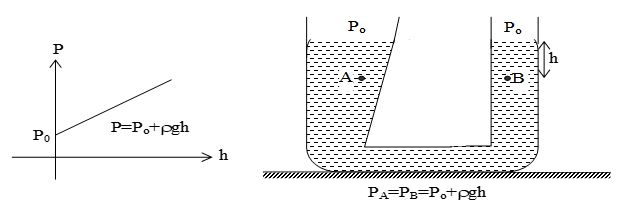
Further, the pressure is the same at any two points at the same level in the fluid. The shape of the container does not matter. 

13. PASCAL’S LAW

It states that “pressure applied to an enclosed fluid is transmitted undiminished to every portion of the fluid and the walls of the containing vessel”.

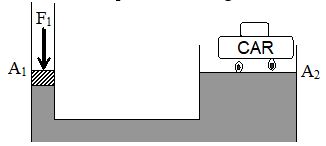
A well known application of Pascal’s law is the hydraulic lift used to support or lift heavy objects.

A piston with small cross section area A₁ exerts a force F₁ on the surface of a liquid such as oil.  The applied pressure P = $\frac{{\mathrm{F}}_1}{{\mathrm{A}}_1}$ is transmitted through the connecting pipe to a larger piston of area A₂.  The applied pressure is the same in both cylinders, so

$\mathrm{P}=\frac{{\mathrm{F}}_1}{{\mathrm{A}}_1}=\frac{{\mathrm{F}}_2}{{\mathrm{A}}_2}$

or ${\mathrm{F}}_2=\frac{{\mathrm{A}}_2}{{ \mathrm{A}}_1}.{\mathrm{F}}_1$

Now, since A₂ > A₁, therefore, F₂ > F₁.  Thus, hydraulic lift is a force multiplying device with a multiplication factor equal to the ratio of the area of the two pistons.  Dentist’s chairs, car lifts and jacks, many elevators and hydraulic brakes all use this principle.

14. ARCHIMEDES’ PRINCIPLE

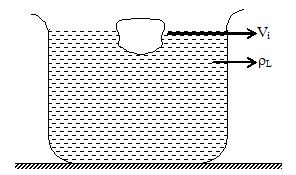
If a heavy object is immersed in water, it seems to weightless than when it is in air.  This is because the water exerts an upward force called buoyant force.  It is equal to the weight of the fluid displaced by the body.

A body wholly or partially submerged in a fluid is buoyed up by a force equal to the weight of the displaced fluid. This result is known as Archimedes’s principle.

Thus, the magnitude of buoyant force (F) is given by

F = V_iρ_Lg

Here,   V_i = immersed volume of solid

             ρ_L = density of liquid and      

             g = acceleration due to gravity. 

15. LAW OF FLOATATION

Consider an object of volume V and density ρ_s floating in a liquid of density ρ_L.  Let V_i be the volume of object immersed in the liquid.

For equilibrium of object,

Weight = Upthrust

Vρ_sg = V_iρ_Lg ………. (i)

This is the fraction of volume immersed in liquid.

Percentage of volume immersed in liquid = $\frac{{\mathrm{V}}_{\mathrm{l}}}{\mathrm{V}}\times 100$

$=\frac{{\mathrm{\rho }}_{\mathrm{s}}}{{\mathrm{\rho }}_{\mathrm{L}}}\times 100$

Three possibilities may now arise.

(i) If ρ_s < ρ_L, only fraction of body will be immersed in the liquid.  This fraction will be given by the above equation.

ii) If ρ_s = ρ_L, the whole of the rigid body will be immersed in the liquid. Hence, the body remains floating in the liquid wherever it is left.

iii) If ρ_s > ρ_L, the body will sink.  

Apparent weight of a Body inside a liquid

If a body is completely immersed in a liquid its effective weight gets decreased.  The decrease in its weight is equal to the upthrust on the body.  Hence,

              W_app = W_actual – Upthrust

or          W_app = Vρ_sg – Vρ_Lg

here,     V = total volume of the body

              ρ_s = density of body

and       ρ_L = density of liquid

Thus,    W_app = $Vg\left({\mathrm{\rho }}_{\mathrm{s}}–{\mathrm{\rho }}_{\mathrm{L}}\right)$

If the liquid in which body is immersed, is water, then

$\frac{\text{ weight in air }}{\text{ decrease in weight }}=\text{ Relative density of body(RD) }$

This can be shown as below

$\frac{\text{ weight in air }}{\text{ Decrease in weight }}=\frac{\text{ weight in air }}{\text{ Upthrust }}$

$=\frac{{\mathrm{V}}_{\mathrm{\rho }}\mathrm{g}}{{\mathrm{V\rho }}_{\mathrm{w}}\mathrm{g}}=\frac{{\mathrm{\rho }}_{\mathrm{s}}}{{\mathrm{\rho }}_{\mathrm{w}}}$ = R.d.

Buoyant Force in Accelerating Fluids

Suppose a body is dipped inside a liquid of density ρ_L placed in an elevator moving with an acceleration .  The buoyant force F in this case becomes

F = Vρ_L g_eff

Here,    g_eff = $|\overline{\mathrm{g}}–\overline{\mathrm{a}}|$

For example, if the lift is moving upwards with an acceleration a, the value of g_eff is g+a and if it is moving downwards with acceleration a, the g_eff is g-a.  In a freely falling lift g_eff is zero (as a=g) and hence, net buoyant force is zero.  This is why, in a freely falling vessel filled with some liquid, the air bubbles do not rise up( which otherwise move up due to buoyant force).  The above result can be derived as follows.

Suppose a body is dipped inside a liquid of density ρ_L in an elevator moving up with an acceleration a. Replace the body into the liquid by the same liquid of equal volume.  The replaced liquid is at rest with respect to the elevator.  Thus, this replaced liquid is also moving up with an acceleration a together with the rest of the liquid.

The forces acting on the replaced liquid are,

i) the buoyant force F and

ii) the weight mg of the substituted liquid.

From Newton’s second law,

F – mg = ma

F = m(g+a)

Here,    m = Vρ_L

$\therefore$ F= Vρ_L(g+a) = Vρ_Lg_eff

where   g_eff = g+a   

16. STREAMLINE, LAMINAR AND TURBULENT FLOW

Streamline flow

Consider a liquid flowing through a tube AB as shown in Fig. Let ${\overrightarrow{\mathrm{v}}}_1, \overrightarrow{{\mathrm{v}}_2}, \overrightarrow{{\mathrm{v}}_3}$ be the velocities of a particle of the liquid at points P, Q and R respectively on its path. If the velocities of the successive particles of the liquid remain unchanged i.e. if all other particles of the liquid pass through P with velocity $\overrightarrow{{\mathrm{v}}_1}$, through Q with the same velocity $\overrightarrow{{\mathrm{v}}_2}$, and through R, again with the same velocity $\overrightarrow{{\mathrm{v}}_3}$, the flow of liquid is said to be orderly and is called steady flow or streamline flow. In this flow every particle of liquid follows the path of its preceding particle and velocity of all the particles crossing a particular point is the same. But the velocity of the particles at different points in their path may not necessarily be the same.

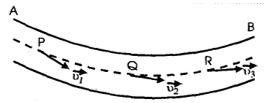
Thus streamline flow of a liquid is that flow in which every particle of the liquid follows exactly the path of its preceding particle and has the same velocity in magnitude and direction as that of its preceding particle while crossing through that point.

The stream line flow is accompanied by stream lines.

A stream line is the actual path followed by the procession of particles in a steady flow, which may be straight or curved such that tangent to it at any point indicates the direction of flow of liquid at that point.

Important properties of stream lines

i) In a streamline flow, no two streamlines can cross each other. If they do so, the particles for the liquid at the point of intersection will have two different directions for their flow, which will destroy the steady nature of the liquid flow.

ii) The greater is the crowding of stream lines at a place, the greater is the velocity of liquid particles at that place and vice versa.

Tube of low

A tube of flow is the bundle of streamlines having the same velocity of the liquid particles over any cross section perpendicular to the direction of flow of liquid.

It has been seen that the flow of liquid will be stream lined if the velocity of liquid flow is always less than the critical velocity of the liquid.  The value of critical velocity is different for different liquids. 

b. Laminar flow

If a liquid is flowing over a horizontal surface with a steady flow and moves in the form of layers of different velocities which do not mix with each other, then the flow of liquid is called laminar flow.  Thus a flow, in which the liquid moves in layer, is called a laminar flow.  In this flow, one layer slides over the other layer of liquid.  In this flow, the velocity of liquid flow is always less than the critical velocity of the liquid.  In general, laminar flow is a streamline flow. 

c. Turbulent flow

When a liquid moves with a velocity greater than its critical velocity, the motion of the particles of liquid becomes disorderly or irregular.  Such a flow is called turbulent flow.

In a turbulent flow, the path and the velocity of the particles of the liquid change continuously and haphazardly with time from point to point.  In a turbulent flow, most of the external energy maintaining the flow is spent in producing eddies in the liquid and only a small fraction of energy is available for forward flow.  For example, eddies are seen by the sides of the pillars of a river bridge,.

In order to visualize practically the stream line and turbulent flow, take a horizontal narrow tube. Connect its one end to water tap. Open the tap so that water flows out of the tube drop by drop.  Put a speck of potassium permanganate at the entrance of the tube. A coloured line along the axis of the tube is observed.  The flow of liquid through the tube is stream line flow. Now open tap to full-flow. It is observed that the coloured line is broken and entire liquid in tube is filled with colour. The flow of liquid through the tube now becomes a turbulent flow.

17. CRITICAL VELOCITY& REYNOLD’S NUMBER

Critical velocity

The critical velocity is that velocity of liquid flow, up to which its flow is streamlined and above which its flow becomes turbulent.

The critical velocity v_c of a liquid flowing through a tube depend upon (i) coefficient of viscosity of liquid ($\eta$) (ii) density of liquid (ρ) and (iii) the radius of the tube (r). Using the method of dimensions, we can obtain an expression for critical velocity.  Let

${\mathrm{v}}_{\mathrm{c}}={\mathrm{K\eta }}^{\mathrm{a}}{\mathrm{\rho }}^{\mathrm{b}}{\mathrm{r}}^{\mathrm{c}}$

where K is a dimensionless constant and a, b and c are the dimensions of v_c in terms of $\eta$, ρ and r. In dimensional form, the equation (11) can be written as

$\left[{\mathrm{M}}^0 \mathrm{L}{ \mathrm{T}}^{–1}\right]={\left[{\mathrm{ML}}^{–1}{ \mathrm{T}}^{–1}\right]}^{\mathrm{a}}{\left[{\mathrm{ML}}^{–3}\right]}^{\mathrm{b}}{\left[\mathrm{L}\right]}^c=\left[\mathrm{M}\mathrm{a}+\mathrm{b} \mathrm{L}–\mathrm{a}–3 \mathrm{b}+\mathrm{c} \mathrm{T}–\mathrm{a}\right]$

Applying the principle of homogeneity of dimensions, we get

Power of M,   a + b = 0

or                     b = -a

Power of L,    – a – 3b + c = 1

or                     – a + 3a + c = 1

or                     2a + c = 1

Power of T,       – 1 = – a or         a = 1

                              b = – 1

                              c = 1 – 2a = 1 – 2 x 1 = -1

Putting these values, we get

${\mathrm{v}}_{\mathrm{c}}={\mathrm{K\eta }}^1{\mathrm{\rho }}^{–1}{\mathrm{r}}^{–1}=\frac{\mathrm{K\eta }}{\mathrm{\rho r}}$

For the flow to be streamline value of v_c should be as large as possible.  For this, $\eta$ should be large ρr should be small.

Reynolds number

Reynolds number is a pure number which determines the nature of flow of liquid through a pipe.  According to Reynolds, the critical velocity v_c of a liquid flowing through a tube of diameter D is given by

${\mathrm{v}}_{\mathrm{c}}=\frac{{\mathrm{N}}_{\mathrm{R}}\mathrm{\eta }}{\mathrm{\rho D}}\text{ or }{\mathrm{N}}_{\mathrm{R}}=\frac{{\mathrm{\rho Dv}}_{\mathrm{c}}}{\mathrm{\eta }}$

where $\eta$ is the coefficient of viscosity of the liquid, ρ is the density of liquid and N_R is constant called Reynolds number.

The value of Reynolds number N_R is independent of the system of units used for the measurement of various quantities in equation.

If the value of Reynolds number lies between 0 to 2000, the flow of liquid is stream line or laminar.  For values of N_R above 3000, the flow of liquid is turbulent and for values of N between 2000 to 3000, the flow of liquid is unstable changing from streamline to turbulent flow.

Physical significance of Reynolds’s number

Reynolds’s number describes the ratio of the inertial force per unit area to the viscous force per unit area for a flowing fluid.

Consider a tube of small area of cross-section A, through which a fluid of density ρ is flowing with velocity v. The mass of fluid flowing through the tube per second,

$∆$m = volume flowing per second $\times$ density = Av$\times$ρ

$\therefore$  Internal force per unit are = $\frac{\text{ rate of change of momentum }}{\text{ area }}$

$=\frac{\left(\mathrm{\Delta m}\right)\mathrm{v}}{\mathrm{A}}=\frac{\left(\mathrm{Av\rho }\right)}{\mathrm{A}}\mathrm{v}={\mathrm{v}}^2\mathrm{\rho }$

viscous force, F = $\eta \mathrm{A}\frac{\mathrm{v}}{\mathrm{r}}$(in magnitude)

where r is the radius of the tube and v/r is the velocity gradient between the layers of the liquid flow.

$\therefore$ Viscous force per unit area = $\frac{\mathrm{F}}{ \mathrm{A}}=\frac{\mathrm{\eta v}}{\mathrm{r}}$

Thus, Reynolds’s number

${\mathrm{N}}_{\mathrm{R}}=\frac{\text{ inertial force per unit area }}{\text{ viscous force per unit area }}=\frac{{\mathrm{v}}^2\mathrm{\rho }}{\mathrm{\rho v}/\mathrm{r}}=\frac{\mathrm{v\rho r}}{\mathrm{\eta }}$

18. EQUATION OF CONTINUITY& ENERGY OF A LIQUID

Equation of continuity

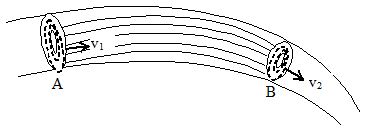
Consider a non-viscous liquid in streamline flow through a tube AB of varying cross-section.  Let a₁,a₂ = area of cross-section of the tube A and B respectively

v₁, v₂ = velocity of flow of liquid at A and B respectively.

ρ₁, ρ₂ = density of liquid at A and B respectively

$\therefore$ Volume of liquid entering per second at A = a₁v₁

Mass of liquid entering per second at A = a₁v₁ρ₁

Similarly, mass of liquid leaving per second at B = a₂v₂ρ₂.

If there is no loss of liquid in the tube  and the flow is steady, then

Mass of liquid entering per second at A = mass of liquid leaving per second at B

or   a₁v₁ρ₁ = a₂v₂ρ₂

If the liquid is incompressible,

Then  ρ₁ = ρ₂

Hence,  a₁v₁ = a₂v₂

or   av = constant

This is known as equation of continuity.

Here v $\propto$ 1/a.  It means the larger is the area of cross-section, the smaller will be he velocity of liquid flow and vice versa.  This is due to this reason that (a) deep water runs slow or slow water runs deep (b) The jet of falling water becomes narrow as it goes down.

Energy of a liquid

A liquid in motion may possess three types of energy.

1) Pressure energy

2) Potential energy

3) Kinetic energy

1) Pressure energy: It is the energy possessed by a liquid by virtue of its pressure.  It is the measure of work done in pushing the liquid against pressure without imparting any velocity to it.

Consider a liquid of density ρ contained in a wide tank T provided with a side tube S, filled with a frictionless piston of area of cross section a.

Let h = height of free surface of the liquid in the tank above the axis of the tube.

The hydrostatic pressure on the piston,

P = hρg

Let the liquid be pushed in with force F in the tank by moving the piston very slowly to the left through a small distance x.  Since the process is very slow, hence the kinetic energy acquired by the liquid in this process is negligible.

Volume of the liquid pushed into the tank = ax

Mass of the liquid pushed into the tank = axρ

Now, force on the piston, f= P$\times$a

Work done in pushing the liquid into tank  = force $\times$ distance = (P$\times$a) $\times$ x

This work done in pushing the liquid against the pressure P into the tank without imparting it any velocity becomes the pressure energy of mass axρ and of volume ax of the liquid.

$\therefore$ Pressure energy per unit mass = $\frac{\mathrm{Pax}}{\mathrm{axp}}=\frac{\mathrm{P}}{\mathrm{\rho }}$

$\therefore$ Pressure energy per unit volume of the liquid = $\frac{Pax}{\mathrm{ax}}=\mathrm{P}$

Hence, pressure energy per unit volume of the liquid is equal to the hydrostatic pressure due to the liquid.

2) Potential energy: It is the energy possessed by liquid by virtue of its height or position above the surface of earth or any reference level taken as zero level.

Let m be the mass of a liquid at a height h above the zero level and V be its volume.

$\therefore$ Potential energy of the liquid = mgh

Potential energy per unit volume of liquid =  $\frac{\mathrm{mgh}}{\mathrm{V}}=\mathrm{\rho gh}$ where ρ is the density of liquid.  

3) Kinetic energy:  It is the energy possessed by a liquid by virtue of its motion or velocity.

Let v be the velocity of a liquid of mass m, density ρ and volume V.

K.E. of the liquid = $\frac{1}{2}{\mathrm{mv}}^2$

K.E. per unit mass of the liquid = $\frac{1}{2}{\mathrm{mv}}^2/\mathrm{m}=\frac{1}{2}{\mathrm{v}}^2$

K.E. per unit volume of the liquid = $\frac{\frac{1}{2}{\mathrm{mv}}^2}{\mathrm{V}}=\frac{1}{2}{\mathrm{\rho v}}^2$

Note: The three types of energy possessed by a liquid in motion are mutually convertible from one from to the other.

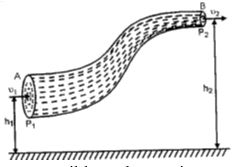
19. BERNOULLI’S THEOREM

Bernoulli’s theorem is an outcome of the principle of conservation of energy applied to a liquid in motion.  This theorem states that for the streamline flow of an ideal liquid, the total energy (the sum of the pressure energy, potential energy and kinetic energy) per unit mass remains constant at every cross-section through the flow.

An ideal liquid is one which is perfectly incompressible and non-viscous

Proof:  consider a tube AB of varying cross-section through which an ideal liquid is in stream line flow.

Let  P₁ = pressure applied on the liquid at A

P₂ = pressure at the end B, against which liquid is to move out.

a₁, a₂ = area of cross-section of the tube at A and B respectively.

h₁, h₂ = mean height of section A and B from the ground or a reference level.

v₁, v₂ = normal velocity of the liquid flow at section A and B respectively.

ρ = density of the ideal liquid flowing through the tube.

The liquid flows from A to B, therefore, P₁ > P₂.

The mass of the liquid crossing per second through any section of the tube in accordance with the equation of continuity is

           a₁v₁ρ = a₂v₂ρ = m

or        a₁v₁ = a₂v₂ = m/p = V (say)

as         a₁ > a₂

$\therefore$         v₂ > v₁

now force on the liquid at section A = P₁a₁ and force on the liquid at section B = P₂a₂.

Work done/second on the liquid at section A

= P₂a₁$\times$v₂ = P₂V

Work done/second by the liquid at section B

= P₂a₁$\times$v₂ = P₂V

Net work done/second on the liquid by the pressure energy in moving the liquid from section A to B = ${\mathrm{P}}_1\mathrm{V}–{\mathrm{P}}_2\mathrm{V}$.

When the mass m of the liquid flows in one second from A to B, its height increases from h₁ to h₂ and its velocity increases from v₁ to v₂.

$\therefore$ Increase in potential energy/sec of the liquid from A to B = mgh₂ – mgh₁

Increase in kinetic energy/sec of the liquid from A to B = $\frac{1}{2}{\mathrm{mv}}_2^2–\frac{1}{2}{\mathrm{mv}}_1^2$

According to work energy principle

Work done/sec by the pressure energy = increase in P.E./sec + increase in K.E/sec

or     P₁V – P₂V = (mgh₂ – mgh₁) + $\left(\frac{1}{2}{\mathrm{mv}}_2^2–\frac{1}{2}{\mathrm{mv}}_1^2\right)$

or     ${\mathrm{P}}_1{\mathrm{V}}_1+{\mathrm{mgh}}_1+\frac{1}{2}{\mathrm{mv}}_1^2={\mathrm{P}}_2\mathrm{V}+{\mathrm{mgh}}_2+\frac{1}{2}{\mathrm{mv}}_2^2$

dividing throughout by m, we get

$\frac{{\mathrm{P}}_1\mathrm{V}}{\mathrm{m}}+{\mathrm{gh}}_1+\frac{1}{2}{\mathrm{v}}_1^2=\frac{{\mathrm{P}}_2\mathrm{V}}{\mathrm{m}}+{\mathrm{gh}}_2+\frac{1}{2}{\mathrm{v}}_2^2$

or  $\frac{{\mathrm{P}}_1}{\mathrm{\rho }}+{\mathrm{gh}}_1+\frac{1}{2}{\mathrm{v}}_1^2=\frac{{\mathrm{P}}_2}{\mathrm{\rho }}+{\mathrm{gh}}_2+\frac{1}{2}{\mathrm{v}}_2^2$          $\left(\because \mathrm{\rho }=\frac{\mathrm{m}}{\mathrm{V}}\right)$

Hence $\frac{\mathrm{P}}{\mathrm{\rho }}+\mathrm{gh}+\frac{1}{2}{\mathrm{v}}^2=\text{ constant }$

Now  $(\mathrm{P}/\mathrm{\rho })$ = pressure energy per unit mass

                gh = potential energy per unit mass,     $\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right){\mathrm{v}}^2$  = K.E per unit mass

Thus we have

Pressure energy per unit mass + P.E. per unit mass + K.E. per unit mass = a constant.

i.e. the sum of pressure energy, potential energy and kinetic energy per unit mass is constant at all cross-section in the streamline flow of an ideal liquid.

This proves Bernoulli’s theorem.

Multiplying both the sides, by ρ we get

$\mathrm{P}+\mathrm{\rho gh}+\frac{1}{2}{\mathrm{\rho v}}^2$ = a constant

This gives us another statement of Bernoulli’s theorem

In a stream line flow of an ideal liquid, the sum of pressure energy per unit volume, potential energy per unit volume and kinetic energy per unit volume is always constant at all cross-section of the liquid.

Other Forms of Bernoulli’s Theorem

a) Dividing by g, we get

$\frac{\mathrm{P}}{\mathrm{\rho }.\mathrm{g}}+\mathrm{h}+\frac{1}{2}\frac{{\mathrm{v}}^2}{\mathrm{g}}$ = another constant

Here, $\frac{\mathrm{P}}{\mathrm{\rho g}}$ is called pressure head, h is called gravitational head and $\frac{{\mathrm{v}}^2}{2\mathrm{g}}$ is called velocity head.

($\therefore$ all the three quantities have the dimensions of distance, hence the name ‘head’).  Equation enables us to state Bernoulli’s theorem as under: In the streamline flow of an ideal liquid, the sum of pressure head, gravitational head and velocity head at every cross-section of liquid is constant.  

b) If the liquid is flowing through a horizontal tube the two ends of the tube are at the same level. Therefore, there is no gravitational head (level difference) i.e. h = 0

From (10) = $\mathrm{P}+\frac{1}{2}{\mathrm{\rho v}}^2$ = constant

This shows that if P increases, v decreases and vice versa.  Thus Bernoulli’s theorem also states that in the streamline flow of an ideal liquid through a horizontal tube, the velocity increases where pressure decreases and vice versa.  This is also called Bernoulli’s principle.  

Limitations of Bernoulli’s theorem

1) While deriving the Bernoulli’s equation, it is assumed that velocity of every particle of liquid across any cross-section of tube is uniform.  Practically it is not correct.  In fact the particles of the liquid in the inner most (i.e. central layer) have maximum velocity and those on a layer in contact with the tube have least velocity.  Therefore, we should take the mean velocity of the liquid.

2) The viscous drag of the liquid which comes into play when the liquid is in motion has not been taken into account.

3) While deriving the above equation, it is assumed that there is no loss of energy when liquid is in motion.  Infact some K.E. is converted into heat and is lost.

4) If the liquid is flowing along a curved path, the energy due to centrifugal force should also be considered. 

20. TORRICELLI’S THEOREM

According to this theorem, velocity of efflux i.e. the velocity with which the liquid flows out of on orifice (i.e. a narrow hole) is equal to that which a freely falling body would acquire in falling through a vertical distance equal to the depth of orifice below the free surface of liquid.

Consider an ideal liquid of density ρ contained in a tank provided with a narrow orifice (hole) at O.

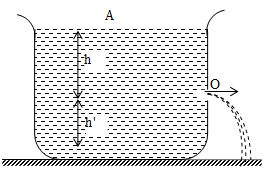
Let h = height of the surface of liquid above O,

h’ = height of the orifice above the bottom of the tank,

P = atmospheric pressure

v = velocity with which the liquid comes out of O.  (i.e. velocity of efflux)

Let h = height of free surface of liquid above O,

h’ = height of the orifice above the bottom of the tank,

P = atmospheric pressure,

v = velocity with which the liquid comes out of O.  (i.e. velocity of efflux).

Velocity of the liquid at the free surface A is zero.

Applying Bernoulli’s theorem at A and O, we get

$[\mathrm{P}+\mathrm{\rho gh}+0{]}_{\mathrm{at} \mathrm{A}}={\left[\mathrm{P}+0+\frac{1}{2}{\mathrm{\rho v}}^2\right]}_{\mathrm{at} \mathrm{O}}$

or $\mathrm{P}+\mathrm{\rho gh}=\mathrm{P}+\frac{1}{2}{\mathrm{\rho v}}^2\text{ or }\mathrm{\rho gh}=\frac{1}{2}{\mathrm{\rho v}}^2\text{ or } \mathrm{v}=\sqrt{2\mathrm{gh}}$

If a body falls freely through a vertical height, the velocity acquired by the body would be .  Thus Torricelli’s theorem is established.

As the liquid escapes through the orifice, it has zero initial velocity in vertical direction at O.  It flows out in the form of a parabolic jet and strikes the ground at a distance S from the tank after a time t.  The vertical distance covered by jet in time t = h’.

Using the relation $\mathrm{S}=\mathrm{ut}+\frac{1}{2}{\mathrm{at}}^2$

In vertical direction, $\mathrm{h}‘=0+\frac{1}{2} {\mathrm{gt}}^2\text{ or }\mathrm{t}=\sqrt{\frac{2 \mathrm{h}‘}{\mathrm{g}}}$

In horizontal direction, Horizontal range,

S = vt = $\sqrt{2\mathrm{gh}}\times \sqrt{2\mathrm{h}‘}/\mathrm{g}=2\sqrt{\mathrm{hh}‘}$

21. VISCOSITY

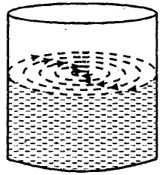
Just as surface tension is the property of a liquid at rest, viscosity is the property of liquid in motion.

Viscosity is the property of a fluid (liquid or gas) by virtue of which an internal frictional force comes into play when the fluid is in motion and opposes the relative motion of its different layers. It is also called fluid friction.

To understand it, let us stir water in a beaker with a glass rod. The water rotates in coaxial cylindrical layers, In fig. Put some pieces of paper on the surface of rotating water. Their movements show that the speed of the inner most cylindrical layer is maximum. The speed of successive Layers goes on decreasing as we approach the walls of the beaker. Thus there exists a relative motion amongst different layers of water. If we stop stirring, water continues rotating for some time and then stops. According to Newton’s first law of m only when an opposing force is acting on the layers which destroy their relative motion. Since no force is applied from outside, the opposing force must be arising from within the liquid. This opposing force is called internal frictional force or viscous force and this property of liquid is called viscosity.

Cause of viscosity

Viscosity is due to the intermolecular forces which are effective when the different layers of the liquid are moving with different velocities. These forces are of Vander Waal type and vary inversely as the seventh power of intermolecular distance. Due to these forces, every fast moving liquid layer tends to accelerate the adjoining slow moving layer and every slow moving layer tends to retard the adjoining fast moving layer of liquid. As a result a backward dragging force called viscous drag comes into play which accounts for viscosity of liquid.

Coefficient of Viscosity

Consider a liquid flowing steadily over a fixed horizontal surface. It flows in the form of layers. The layer immediately in contact with the surface moves with the minimum velocity due to force of adhesion between liquid and solid surface. The velocity of other layers goes on increasing as the distance from the fixed surface increases. Thus the topmost layer moves with maximum velocity.

Consider two adjoining layers P and Q. The layer 0 moving faster than F, tries to accelerate P. The layer P, moving at a slower rate tries to retard 0. Thus two layers tend to destroy their relative motion as if there is a backward dragging force acting tangentially on the layers’. Therefore to maintain the flow of the liquid, an external force equal and opposite to backward dragging force (also called viscous drag) must be applied.

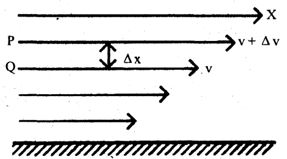
Newton observed that a backward tangential force (viscous drag), F acting between two layers of liquid moving with relative velocity dv with respect to each other, separated by a distance dx is given by

(i)  $\mathrm{F}\propto \mathrm{A}$      (A = area of each layer)

(ii) $\mathrm{F}\propto \mathrm{d}v/\mathrm{dx}$    ( dv/dx = velocity gradient between the layers)  

Thus   $\mathrm{F}\propto \mathrm{Adv}/\mathrm{dx}$

or  $\mathrm{F}=–\mathrm{\eta A}\frac{\mathrm{dv}}{\mathrm{dx}}$  ………(1)

where $\eta$ is a constant and is called the coefficient of viscosity of the liquid. The negative sign shows that the direction of F is opposite to the direction of velocity.

If  A = 1, dv/dx = 1

then from (1), $\mathrm{F}=–\mathrm{\eta }$

or $\mathrm{\eta }=–\mathrm{F}$

Thus coefficient of viscosity of a liquid is defined as the tangential force (= backward viscous drag) required to maintain a unit velocity gradient between two parallel layers each of unit area.

Dimension formula for $\mathit{\eta }$

From (1), $\mathrm{\eta }=\frac{\mathrm{F}}{\mathrm{A} \mathrm{dv}/\mathrm{dx}}=\frac{\left[{\mathrm{MLT}}^{–2}\right]}{\left[{\mathrm{L}}^2\right]\left[{\mathrm{LT}}^{–1}/\mathrm{L}\right]}=\left[{\mathrm{ML}}^{–1}{\mathrm{T}}^{–1}\right]$

In cgs system, the unit of  is called poise.

$\text{ 1poise }=\frac{\text{ 1dyne }}{1{ \mathrm{cm}}^2\times \left(1{\mathrm{cms}}^{–1}/\mathrm{cm}\right)}=\text{ dyne }{\mathrm{cm}}^{–2}\text{ sec }$

Thus coefficient of viscosity of a liquid is said to be one poise, if 1 dyne tangential force (= backward viscous drag) is required to maintain a velocity gradient of 1 cm sec^-1/cm between two parallel layers each of area 1 sq. cm. The S.I. unit of  is Pa s (Pascal-second) or decapoise.

$\text{ 1decapoise }=\frac{1\text{ newton }}{1{ \mathrm{m}}^2\mathrm{x}\left(1{ \mathrm{ms}}^{–1}/\mathrm{m}\right)}=1{\mathrm{Nsm}}^{–2}$

Thus coefficient of viscosity of a liquid is said to be 1 deca poise or 1 Pa-s, if 1 newton tangential force (backward viscous drag) is required to maintain a velocity gradient of 1ms^-1/m between two parallel layers each of area 1 sq. m.

Relation between deca poise and poise

1 deca poise = 1Nsm^-2

$={10}^5\text{ dynes }x{\left({10}^2\right)}^{–2}{ \mathrm{cm}}^{–2}=10\text{ poise }$

Distinction between Viscosity and Solid Friction

Viscosity is similar to the solid friction (friction among the solid surfaces in contact) in the respect that

i) both come into play whenever there is a relative motion.

ii) both oppose relative motion and

iii) both are due to molecular forces

Viscosity differs from the solid friction in the respect that the viscous force acting between two layers of the liquid depends upon

i) the area of the layers

ii) the relative velocity of two layers and

iii) distance between two layers.

The friction between two solid surfaces is independent of

i) the area of surfaces in contact and

ii) the relative velocity between them

22. POISEULLE’S FORMULA

When a liquid flows through a horizontal tube with a steady flow under some external pressure, the liquid moves in cylindrical layers coaxial with the axis of the tube.  The velocity of the cylindrical layer is maximum along the axis of the tube and it goes on decreasing towards the wall of the tube. The velocity is minimum for the layer in contact with the wall of the tube. 

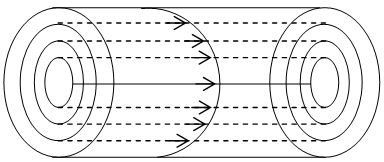
Poiseuille studied the rate of flow of a liquid through a horizontal capillary tube and concluded that the volume (V) of the liquid flowing per second through a capillary tube varies

(i) directly as the pressure difference (p) across the two ends of the tube

i.e. V $\propto$ p

(ii) Directly as the fourth power of radius (r) of the tube i.e. V $\propto$ r⁴

(iii) Inversely as the length (l) of the tube i.e. V $\propto \frac{1}{\mathcal{l}}$

(iv) Inversely as the coefficient of viscosity of the liquid i.e. V $\propto \frac{1}{\eta }$

Combining these factors, we get

$\mathrm{V}\propto \frac{{\mathrm{pr}}^4}{\eta \ell } \text{ or } \mathrm{V}=\frac{\pi }{8}\frac{{\mathrm{pr}}^4}{\eta \ell }$ … (3)

where $\mathrm{\pi }$/8 is a constant of proportionality.  This equation is called poiseuille’s equation and is true only for the steady flow of liquid through a horizontal capillary tube.

Derivation of Poiseuille’s Formula by Dimensional Analysis

Poiseuille studied the rate of flow of liquid through a horizontal capillary tube and concluded that the volume (V) of the liquid flowing per second through the capillary tube depends upon

(i) pressure gradient (P/l) [i.e. the rate of change of pressure with length],

(ii) radius of the capillary tube (r),

(iii) coefficient of viscosity of the liquid ($\eta$)

Let   $\mathrm{V}=\mathrm{K}{\left(\frac{\mathrm{P}}{l}\right)}^{\mathrm{a}}{\mathrm{r}}^{\mathrm{b}}{\mathrm{\eta }}^{\mathrm{c}}$    ……… (4)

where a, b, c are the dimensions of V in terms of (P/l), r and $\eta$ and K is a dimensionless constant. The dimensional formula of

$\mathrm{V}=\left[{\mathrm{L}}^3{\mathrm{T}}^{–1}\right]$

The dimensional formula of  

$\frac{P}{\ell }=\frac{\left[{\mathrm{ML}}^{–1}{ \mathrm{T}}^{–2}\right]}{\mathrm{L}}=\left[{\mathrm{ML}}^{–2}{ \mathrm{T}}^{–2}\right]$

The dimensional formula of r = [L]

The dimensional formula of $\eta =\left[{\mathrm{ML}}^{–1}{ \mathrm{T}}^{–1}\right]$

Putting in (4), we get

$\left[{\mathrm{L}}^3{ \mathrm{T}}^{–1}\right]={\left[{\mathrm{ML}}^{–2}{ \mathrm{T}}^{–2}\right]}^a[ \mathrm{L}{]}^{\mathrm{b}}\left[{\mathrm{ML}}^{–1}{ \mathrm{T}}^{–1}\right]°$

or $\left[{\mathrm{M}}^0{\mathrm{L}}^3{\mathrm{T}}^{–1}\right]=\left[{\mathrm{M}}^{\mathrm{a}+\mathrm{c}}{\mathrm{L}}^{–2\mathrm{a}+\mathrm{b}–\mathrm{c}}{\mathrm{T}}^{–2\mathrm{a}–\mathrm{c}}\right]$

Applying the principle of homogeneity of dimensions, we get

Power of M,      a +c = 0 or a = – c ……… (5)

Power of L,       – 2a + b – c = 3 ……… (6)

Power of T,       – 2a – c  = – 1

or                     – 2 ( – c ) – c = – 1

or                     2c – c = – 1 or c = – 1

From (5),          a = – ( – 1) = 1

From (6),          – 2 ( 1 ) + b – ( – 1 ) = 3

or                     – 2 + b + 1 = 3   or     b = 4

Putting the values in (4), we get

$\mathrm{V}=\mathrm{K}{\left(\frac{\mathrm{P}}{\ell }\right)}^1(\mathrm{r}{)}^4{\eta }^{–1}=\mathrm{K}\frac{{\mathrm{Pr}}^4}{\eta \ell }$

The value of K, when calculated experimentally, is found to be  $\raisebox{1ex}{$\mathrm{\pi }$}\!\left/ \!\raisebox{-1ex}{$8$}\right.$

Note:

1. According to Poiseuille’s formula

$\mathrm{V}=\frac{{\mathrm{\pi pr}}^4}{8\mathrm{\eta \ell }}=\frac{\mathrm{p}}{\mathrm{R}}$

Where $\mathrm{R}=\frac{8\eta \ell }{\left(\pi r^4\right)}$ is called liquid resistance.

2. When two capillary tubes of lengths $l_1$ and $l_2$, radius $r_1$ and $r_2$ are joined in series, through which a liquid is flowing, then the equivalent liquid resistance $\left({\mathrm{R}}_{\mathrm{s}}\right)$ is

${\mathrm{R}}_{\mathrm{s}}={\mathrm{R}}_1+{\mathrm{R}}_2=\frac{8{\mathrm{\eta \ell }}_1}{{\mathrm{\pi r}}_1^4}+\frac{8{\mathrm{\eta \ell }}_2}{{\mathrm{\pi r}}_2^4}$

3. When two capillary tubes are joined in parallel through which the liquid is flowing, then the effective liquid resistance is

$\frac{1}{{\mathrm{R}}_{\mathrm{p}}}=\frac{1}{{\mathrm{R}}_1}+\frac{1}{{\mathrm{R}}_2} \text{ or } {\mathrm{R}}_{\mathrm{p}}=\frac{{\mathrm{R}}_1{\mathrm{R}}_2}{{\mathrm{R}}_1+{\mathrm{R}}_2}$

23. STOKE’S LAW & TERMINAL VELOCITY

Stoke’s Law

When a small spherical body moves through a viscous medium at rest, the layers of the body touching the medium are dragged along with it.  But the layers of the medium away from the body are at rest.  This causes a relative motion between different layers of medium.  As a result of this, a backward dragging force (i.e. viscous drag) comes into play, which opposes the motion of the body.  This backward dragging force increases with the increase in velocity of the moving body.

Stoke found that the backward dragging force F acting on a small spherical body of radius r, moving through a medium of coefficient of viscosity , with velocity v is given by

$\mathrm{F}=6\pi \mathrm{\eta rV}$         …… (7)

This is called Stoke’s law of viscosity. The relation (7) can be easily derived by the method of dimensions. Stoke observed that viscous drag (F) depends upon

(i) coefficient of viscosity $\left(\eta \right)$ of the medium,

(ii) velocity$\left(\nu \right)$of the body,

(iii) radius (r) of the spherical body

Let     $\mathrm{F}=\mathrm{K}{\eta }^{\mathrm{a}}{v}^{\mathrm{b}}{\mathrm{r}}^{\mathrm{c}}$  ……… (8)

Where a, b and c are the dimensions of F in terms of $\eta , \nu$ and r, and K is a dimensionless constant. In dimensional form, the relation (8) can be written as

$\left[{\mathrm{MLT}}^{–2}\right]={\left[{\mathrm{ML}}^{–1}{ \mathrm{T}}^{–1}\right]}^a{\left[{\mathrm{LT}}^{–1}\right]}^{\mathrm{b}}\left[\mathrm{L}\right]°=\left[{\mathrm{M}}^{\mathrm{a}}{\mathrm{L}}^{–\mathrm{s}+\mathrm{b}+\mathrm{c}}{\mathrm{T}}^{–\mathrm{a}–\mathrm{b}}\right]$

Applying the principle of homogeneity of dimensions, we get

Power of M,                  a = 1

Power of L,                   – a + b + c = 1

or                                 – 1 + b + c = 1

or                                   b + c = 2……… (9)

Power of T,                   – a – b  = – 2

or                                 – 1 – b = – 2       or         b = 1

From (9),                      1 + c = 2           or         c = 1

Substituting the values of a, b and c in (8), we get  

$F=K\eta rv$

The value of K was found to be $6\mathrm{\pi }$, experimentally

$F=6\pi \eta rv$

Importance of Stoke’s law

1. This law is used in the determination of electronic charge with the help of Millikan’s experiment.

2. This law accounts the formation of clouds.

3. This law accounts, why the speed of rain drops is less than that of a body falling freely with a constant velocity from the height of clouds.

4. This law helps a man coming down with the help of a parachute.

Terminal velocity

It is maximum constant velocity acquired by the body while falling freely in a viscous medium. When a small spherical body falls freely through a viscous medium, three forces act on it.

i) Weight of the body acting vertically downwards.

ii) Upward thrust due to buoyancy equal to weight of liquid displaced.

iii) Viscous drag acting in the direction opposite to the motion of body.  According to Stoke’s law, F $\propto$ v i.e. the opposing viscous drag goes on increasing with the increasing velocity of the body.

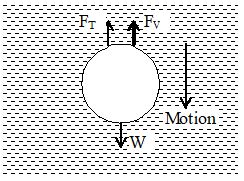
As the body falls through a medium, its velocity goes on increasing due to gravity.  Therefore, the opposing viscous drag which acts upwards also goes on increasing.  A stage reaches when the true weight of the body is just equal to the sum of the upward thrust due to buoyancy and the upward viscous drag.  At this stage, there is no net force to accelerate the body.  Hence it starts falling with a constant velocity, which is called terminal velocity.

Let $\rho$ be the density of the material of the spherical body of radius r and $\rho$_o be the density of the medium

$\therefore$ True weight of the body

W = volume $\times$ density $\times$ g = $\frac{4}{3}\pi r^3\rho g$

Upward thrust due to buoyancy,

F_T = weight of the medium displaced

$\therefore$ F_T = volume of the medium displaced $\times$ density $\times$ g = $\frac{4}{3}{\mathrm{\pi r}}^3{\mathrm{\rho }}_0\mathrm{g}$

If v is the terminal velocity of the body, then according to Stoke’s law.

Upward viscous drag, F_v= 6$\mathrm{\pi \eta }$rv

When body attains terminal velocity, then

F_T+F_V = W

$\therefore \frac{4}{3}{\mathrm{\pi r}}^3{\mathrm{\rho }}_0\mathrm{g}+6\mathrm{\pi \eta rv}=\frac{4}{3}{\mathrm{\pi }}^3\mathrm{\rho g}$

or  $6\mathrm{\pi \eta rV}=\frac{4}{3}{\mathrm{\pi r}}^3\left(\mathrm{\rho }–{\mathrm{\rho }}_0\right)\mathrm{g}$

or  $\mathrm{v}=\frac{2{\mathrm{r}}^2\left(\mathrm{\rho }–{\mathrm{\rho }}_0\right)\mathrm{g}}{9\mathrm{\eta }}$ …… (10)

The following results follow from (4)

i) The terminal velocity varies directly as the square of the radius of the body and inversely as the coefficient of viscosity of the medium. It also depends upon densities of the body and the medium.

ii) If $\rho <{\rho }_0$, the value of v is negative i.e. the body will move up with a constant velocity. It is due to this reason that the gas bubbles rise up through soda water bottle.

iii) By knowing r, $\mathrm{\rho }, {\mathrm{\rho }}_0$ and terminal velocity v(by noting the time taken by the body to cover a known distance in the liquid), the coefficient of viscosity of the liquid can be calculated

24. VARIATION & PRACTICAL USES OF VISCOSITY

Variation of viscosity

i) With increase in temperature, the viscosity of liquid decreases. The variation of viscosity of liquid with temperature as given by Slotte is

${\mathrm{\eta }}_1=\frac{{\mathrm{\eta }}_0}{\left(1+\mathrm{\alpha t}+{\mathrm{\beta t}}^2\right)}$,

where $\eta$_t and $\eta$_o are the coefficient of viscosities at t^oC and 0^oC respectively and $\alpha$ and $\beta$ are constants. The viscosity of all gases increases with increase in temperature, since the viscosity of a gas is directly proportional to the square root of the absolute temperature i.e. $\mathrm{\eta }\propto \sqrt{\mathrm{T}}$ .  This result is obtained from kinetic theory of gases.

ii) With increase in pressure, the viscosity of liquids increases but the viscosity of water decreases, whereas the viscosity of gases remains unchanged.

Practical uses of the knowledge of viscosity

i) The knowledge of viscosity and its variation with temperature helps us to select a suitable lubricant for a given machine.

ii) The knowledge of viscosity of some organic liquids such as proteins, cellulose etc helps us in determining their shape and molecular weight.

iii) At railway terminals, the liquids of high viscosity are used as buffers.

iv) Motion of some instruments is damped by using the viscosity of air or liquid.

v) The knowledge of viscosity helped Millikan in determining charge on an electron.

vi) The phenomenon of viscosity plays an important role in the circulation of blood through arteries and veins of human body.

SOLVED EXAMPLES

1. A rectangular plate of dimensions 6cm$\times$4cm and thickness 2 mm is placed with its largest face flat on the surface of water.  Find the downward force on the plate due to surface tension.  Surface tension of water is

Sol. Here, l = 6⨯10^–2 m;

b = 4⨯10^–2m;  d = 2⨯19^–3 m;

S = 7.0⨯10^–2 Nm^-1.

Force on the plate due to surface tension is

F = 2(l+b)S = 2(6⨯10^–2) + 4⨯10^–2) ⨯ 7.0⨯10^–2   = 1.4⨯10^–2 N

2. There is an air bubble of radius 1.0 mm in a liquid of surface tension 0.075 N/m and density 10³ kg/m³. The bubble is at depth 10.0 cm below the free surface.  By what amount is the pressure inside the bubble greater than the atmospheric pressure.

Sol. Here, r = 1.0 mm = 10^–3 ; S = 0.075 N/m;

ρ = 10³ kg/m³;  h = 10 cm = 0.1 m

the pressure inside the bubble which is greater than the atmospheric pressure is  

$\frac{2\mathrm{S}}{\mathrm{r}}+\mathrm{h\rho g}=\frac{2\times 0.075}{{10}^{–3}}+0.10\times {10}^3\times 9.8$

= 150 + 980 = 1130 Nm^–2.

3. The lower end of a capillary tube is dipped into water and it is seen that water rises through 7.5 cm in the capillary.  Given surface tension of water is 7.5⨯10^–2 N/m and angle of contact between water and glass capillary tube is zero.  Find the diameter of the capillary tube.  Given g=10ms^-2.

Sol. Here, h = 7.5 cm = 7.5⨯10^-2 m;     S = 7.5⨯10^-2 N/m; $\theta$ = 0^o, 2r = ?

As $\mathrm{h}=\frac{2\mathrm{Scos\theta }}{\mathrm{r\rho g}}$;

so $2\mathrm{r}=\frac{4 \mathrm{Scos}\theta }{\mathrm{h}\rho \mathrm{g}}=\frac{4\times 7.5\times {10}^{–2}\times \cos 0°}{7.5\times {10}^{–2}\times {10}^3\times 10}$

$=4\times {10}^{–4} \mathrm{m}=0.4 \mathrm{mm}$

4. A tube of 1mm bore is dipped into a vessel containing a liquid of density $\delta$=800kg m^-3 and of surface tension, S=49⨯10^-3 Nm^-1 and angle of contact, $\theta$ = 0^o.  The tube is held inclined to the vertical at an angle of 60^o, find the height to which the liquid can rise and the length which the liquid will occupy in the tube.

Sol. Here, r = $\frac{1}{2}$mm = $\frac{1}{2}\times {10}^{–3}$m;   ρ = 800 kg/m³;   S=4⨯10^-3 N/m;   $\theta$=0^o;   h=?;

Angle with the horizontal of inclined tube ($\alpha$) = 90^o – 60^o = 30^o.

Also, $\mathrm{h}=\frac{2 \mathrm{Scos}\theta }{\mathrm{r}\rho \mathrm{g}}=\frac{2\times 49\times {10}^{–3}\times \cos 0°}{\left(1/2\times {10}^{–3}\right)\times 800\times 9.8}$ = 0.025 m = 2.5 cm.

If l is the length occupied by the liquid in the tube, then sin$\alpha$ = h/l or cm.

or $\ell =\frac{\mathrm{h}}{\sin \alpha }=\frac{2.5}{\sin 30°}=2.5\times 2=5 \mathrm{cm}.$

5. Water rises to a height of 10cm in a capillary tube and mercury falls to a depth of 3.42 cm in the same capillary tube. If the density of mercury is 13.6 and the angle of contact of mercury and water are 135° and 0° respectively, then find the ratio of surface tensions of water and mercury.

Sol. $\mathrm{h}=\frac{2\mathrm{S} \mathrm{cos\theta }}{\mathrm{r\rho g}}\text{ or }\mathrm{S}=\frac{\mathrm{hr\rho g}}{2\mathrm{cos\theta }}$

or  $\mathrm{S}\propto \frac{\mathrm{h\rho }}{\mathrm{cos\theta }}$

$\frac{{\mathrm{S}}_{\mathrm{W}}}{{\mathrm{S}}_{\mathrm{Hg}}}=\frac{{\mathrm{h}}_1}{{ \mathrm{h}}_2}\times \frac{{\mathrm{cos\theta }}_2}{{\mathrm{cos\theta }}_1}\times \frac{{\mathrm{\rho }}_1}{{\mathrm{\rho }}_2}$

Putting the values, we obtain 1 : 6.5

6. Relative density of an oil is 0.8. Find the absolute density of oil in cgs and SI units.

Sol. Density of oil (in cgs) = (R.D.) gm/cm³

                                                = 0.8 g/cm³

                                                = 800 kg/m³

7. Two vessels have the same base area but different shapes. The first vessel takes twice the volume of water that the second vessel requires to fill up to a particular common height.  Is the force exerted by water on the base of the vessel the same in the two cases?  If so, why do the vessels filled with water to that same height give different readings on a weighing scale?

Sol. Pressure (and therefore force) on the two equal base areas are identical.  But force is exerted by water on the sides of the vessels also, which has non-zero vertical component when the sides of the vessel are not perfectly normal to the base.  This net vertical component of force by water on the sides of the vessel is greater for the first vessel than the second.  Hence, the vessels weigh different when force on the base is the same in the two cases.

8. A piece of ice is floating in a glass vessel filled with water. How will the level of water in the vessel change when the ice melts.

Sol. Let m be the mass of ice piece floating in water.

In equilibrium, weight of ice piece = up thrust

or           mg = V_iρ_wg

or    ${\mathrm{V}}_{\mathrm{i}}=\frac{\mathrm{m}}{{\mathrm{\rho }}_{\mathrm{w}}}$   . . . .     (i)

Here, V_i is the volume of the ice piece immersed in water

When the ice melts, let V be the volume of water formed by m mass of ice. 

Then $\mathrm{V}=\frac{\mathrm{m}}{{\mathrm{\rho }}_{\mathrm{w}}}$  . . . .     (ii)

Hence, the level will not change.

9. An orifice of area 10 square mm is made at the bottom of a vessel containing water to a height of 10m above the orifice. What is the force on the vessel?

Sol. Volume of water flowing out per second = v a

$\mathrm{v}=\sqrt{2\mathrm{gh}}=\sqrt{2\times 9.8\times 10}=14 \mathrm{m}/\mathrm{s}$

$\therefore$ volume of water flowing out/sec

$=14\times \frac{10}{{10}^6}{ \mathrm{m}}^3$

Mass of water flowing out/sec

$=\frac{14\times 10}{{10}^6}\times {10}^3\mathrm{Kg}=\frac{14}{100}\mathrm{Kg}$

$\therefore$ rate of change of momentum = $\frac{14}{100}\times 14$ Force = 1.96 N

10. Find the terminal velocity of a steel ball (density = $7.8\times {10}^3 {\mathrm{Kgm}}^{–3}$) of radius 2mm falling through a fluid of density = $1.2\times {10}^3 {\mathrm{Kgm}}^{–3}$ and coefficient viscosity $\eta =0.83N {\mathrm{Sm}}^{–2}$.

Sol. We know ${\mathrm{v}}_{\mathrm{t}}=\frac{2}{9}\mathrm{x}\frac{{\mathrm{r}}^2\mathrm{g}\left(\mathrm{p}–{\mathrm{\rho }}_0\right)}{\mathrm{\eta }}$

${\mathrm{v}}_{\mathrm{t}}=\frac{2}{9}\times \frac{{\left(2\times {10}^{–3}\right)}^2\times 9.8\left(7.8\times {10}^3–1.2\times {10}^3\right)}{0.83}$ = 0.069 ms^-1