Gravitation

1. Introduction

Gravitation is one of the four classes of interactions found in nature.  These classes are

i. The gravitational force
ii. The electromagnetic force
iii. The strong nuclear forces
iv. The weak nuclear forces

Although, gravitational force is weakest force in nature, it is of great importance, mainly in case of large objects.  It is the force of gravitation that holds the universe together.  In this chapter we will learn the basic laws that govern gravitational intersections.

Gravitational Force

Gravitational force is responsible for the attraction between particles of various bodies having some mass. Gravitational force is always an attractive force and is believed to be communicated through a particle called gravitation.

Electromagnetic Force

The electromagnetic force is dominant on the atomic level and is responsible for holding the atoms together that make up the molecules.  This force is either attractive or repulsive depending upon the type of charge of the interacting particles. Electromagnetic force is communicated through particles called photons.

Strong Nuclear Force

Strong nuclear force is responsible for holding the protons and neutrons in the nucleus.  The force acting between the nucleons is called the strong nuclear force.  Nuclear force does not extend outside the nucleus.  Nuclear force is basically attractive in nature.

Weak Nuclear Force 

Weak nuclear force is responsible for a type of radioactive decay known as beta decay and other similar decay processes involving fundamental particles.  It acts between all leptons (electrons, positrons, $\mu$ -mesons and neutrinos) and hadrons (mesons and baryons).  It is also a short range force.  It is communicated through weak bosons.

Relative strengths of basic forces between protons:

Basic Force	Relative strength	Range
Gravitational	1	Long Range, Infinite
Weak Nuclear	1031	Extremely short range << 1 fermi
Electromagnetic	1030	Long Range, Infinite
Strong force	1038	Short Range, 1 fermi

2. New ton’s Universal Law gravitation

Along with his three laws of motion, Newton also gave a very important law in gravitation which is called Newton’s law of gravitation or Universal law of gravitation.  According to this law, every particle of matter in the universe attracts every other particle with a force that is directly proportional to the product of the masses of the particles and inversely proportional to the square of the distance between them.

If m₁ and m₂ be the masses of two particles and r be the distance between them, then the magnitude of gravitational force between them is given by

$\mathrm{F}\propto \frac{{\mathrm{m}}_1{ \mathrm{m}}_2}{{\mathrm{r}}^2}\text{ or }\mathrm{F}=\frac{{\mathrm{Gm}}_1{ \mathrm{m}}_2}{{\mathrm{r}}^2}$ . . . .      (1)

Here, G is the constant of proportionality, called universal gravitational constant.

Magnitude of G in S.I. system is,

G = $6.67\times {10}^{–11} \mathrm{N}–{\mathrm{m}}^2/{\mathrm{kg}}^2$

The direction of the force is along the line joining the two particles.

Unit of G:  SI unit: Nm²/kg², CGS unit: dyne cm²/g².

Dimensions of G: $\mathrm{G}=\frac{{\mathrm{Fr}}^2}{{ \mathrm{m}}_1{ \mathrm{m}}_2}; \left[\mathrm{G}\right]=\left[\frac{{\mathrm{MLT}}^2{ \mathrm{L}}^2}{\mathrm{MM}}\right]=\left[{\mathrm{M}}^{–1}{ \mathrm{L}}^3{ \mathrm{T}}^{–2}\right]$  

Universal gravitational constant (G) does not depend upon the medium between the particles or any other factors.  It is constant every where in the universe.  So it is called universal gravitational constant.

Note:  The force of attraction of the first body of mass m₁ on the second body of mass m₂ is in the direction of the position vector r₁₂ of the first body with respect to the second body. In the vector form

${\overrightarrow{\mathrm{F}}}_{12}=\frac{{\mathrm{Gm}}_1{ \mathrm{m}}_2}{{\mathrm{r}}^2}{\hat{\mathrm{r}}}_{12}$

where ${\hat{\mathrm{r}}}_{12}$ is the unit vector in the direction of r₁₂ and r is the distance between the two bodies.

$\therefore {\overrightarrow{\mathrm{F}}}_{12}=\left(\frac{{\mathrm{Gm}}_1{\mathrm{m}}_2}{{\mathrm{r}}^3}\right){\overrightarrow{\mathrm{r}}}_{12}$

($\therefore$ unit vector = Vector/Magnitude of the vector; ${\hat{\mathrm{r}}}_{12}={\overrightarrow{\mathrm{r}}}_{12}/\mathbf{r}$)

Important points about gravitational force

1. It expresses the force between two point masses. However, for external points of rigid bodies, the whole mass can assumed to be concentrated at its COM.

2. It is conservative in nature.

3. It is independent of the medium between the particles.

4. It is independent of presence or absence of other bodies.

5. Gravitational force does not depend on the nature of attracting bodies and is always attractive.

6. Gravitational force between a pair of bodies is a central force i.e., it acts along the line joining their centers of mass.

7. Gravitational force is a conservative force i.e., it does not depend upon the path traversed.

8. Gravitational force results out of the distortion of space-time due to the presence of matter in it.

9. Gravitational force is believed to be communicated by mass less particles called ‘gravitons’.

10. Gravitational force has a universal nature i.e., it applies every where. It applies right from minute particles of gigantic stars.

3. Acceleration due to gravity

According to Newton’s law of gravitation, gravitation is the force of attraction between any two bodies.  If one of the bodies is earth then the gravitation is called gravity.  Hence gravity can be defined as the force with which earth attracts a body towards its centre.  It is a special case of gravitation.

Acceleration due to gravity

When a body is dropped from a certain height above the ground, it begins to fall towards the earth under the effect of gravity.  The acceleration produced in the body due to gravity is called acceleration due to gravity.  It is denoted by g.

Suppose that the mass of the earth is M, its radius is R, then the force of attraction, acting on the body of mass m close to the surface of earth is  

$\mathrm{F}=\frac{\mathrm{GMm}}{{\mathrm{R}}^2}$

According to Newton’s second law of motion, the acceleration due to gravity

$\mathrm{g}=\frac{\mathrm{F}}{\mathrm{m}}=\frac{\mathrm{GM}}{{\mathrm{R}}^2}$

This expression is free from m.  Hence if two bodies of different masses are allowed to fall freely, they will have same acceleration.

Near the surface of earth, the magnitude of g is constant, as G, M and R all are constants.  Its value near the surface of earth is 9.8 ms^-2. 

4. Variation of acceleration due to gravity

The value of acceleration due to gravity changes with height (i.e altitude), depth, shape of the earth and rotation of earth about its own axis.  The effect of each of the above factors on the value of g has been discussed below. 

a. Effect of altitude

Consider earth to be a sphere of mass M, radius R with centre at O.  Let g be the value of acceleration due to gravity at a point A on the surface of earth.

$\therefore \mathrm{g}=\frac{\mathrm{GM}}{{\mathrm{R}}^2}$      . . . .      (8)

If g’ is the acceleration due to gravity at a point B, at a height h above the surface of earth, then

${\mathrm{g}}^{‘}=\frac{\mathrm{GM}}{(\mathrm{R}+\mathrm{h}{)}^2}$  . . . .      (9)

Dividing (9) by (8), we get

$\frac{{\mathrm{g}}^{‘}}{\mathrm{g}}=\frac{\mathrm{GM}}{(\mathrm{R}+\mathrm{h}{)}^2}\times \frac{{\mathrm{R}}^2}{\mathrm{GM}}=\frac{{\mathrm{R}}^2}{(\mathrm{R}+\mathrm{h}{)}^2}$

$=\frac{{\mathrm{R}}^2}{{\mathrm{R}}^2(1+\mathrm{h}/\mathrm{R}{)}^2}={\left(1+\frac{\mathrm{h}}{\mathrm{R}}\right)}^{–2}$= . . . .(10)

If h<<R the h/R is very small as compared to 1.  Expanding the R.H.S. of above equation by Binomial theorem and neglecting the square and higher powers of $\frac{\mathrm{h}}{\mathrm{R}}$, we get

$\frac{{\mathrm{g}}^{‘}}{\mathrm{g}}=1–\frac{2\mathrm{h}}{\mathrm{R}}$

or  ${\mathrm{g}}^{‘}=\mathrm{g}\left(1–\frac{2\mathrm{h}}{\mathrm{R}}\right)$ . . . .      (11)

From (10) and (11), we note that the value of acceleration due to gravity decreases with height.

Note:

1. The relation (10) is used to find the value of acceleration due to gravity at height when h is comparable to the radius of earth R and relation (11) is used to find g’ when h is very small as compared to R.

2. With height h, the decrease in the value of g is $\mathrm{g}–{\mathrm{g}}^{‘}=\frac{2\mathrm{hg}}{\mathrm{R}}$

$\therefore$ Fractional decrease in the value of

g = $\frac{\mathrm{g}–{\mathrm{g}}^{‘}}{\mathrm{g}}=\frac{2\mathrm{h}}{\mathrm{R}}$

$\therefore$ % decrease in the value of

g = $\left(\frac{\mathrm{g}–{\mathrm{g}}^{‘}}{\mathrm{g}}\right)\times 100=\frac{2\mathrm{h}}{\mathrm{R}}\times 100$

b. Effect of depth

Consider earth to be a homogeneous sphere of radius R and mass M with centre at O.  Let g be the value of acceleration due to gravity at a point A on the surface of earth, then

$\mathrm{g}=\frac{\mathrm{GM}}{{\mathrm{R}}^2}$

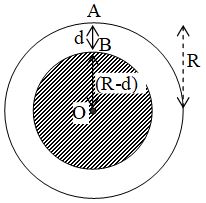
If $\rho$ is uniform density of material of the earth then

$\mathrm{M}=\frac{4}{3}{\mathrm{\pi R}}^3\mathrm{\rho }$

$\therefore \mathrm{g}=\frac{\mathrm{G}\times \frac{4}{3}{\mathrm{\pi R}}^3\mathrm{\rho }}{{\mathrm{R}}^2}=\frac{4}{3}\mathrm{\pi GR\rho }$      . . . .      (12)

Let g’ be the acceleration due to gravity at the point B at a depth d below the surface of earth.  The body at B will experience gravity pull due to shaded portion of earth whose radius is (R-d) and mass is M’.

$\therefore {\mathrm{g}}^{‘}=\frac{{\mathrm{GM}}^{‘}}{(\mathrm{R}–\mathrm{d}{)}^2}$

and ${\mathrm{M}}^{‘}=\frac{4}{3}\mathrm{\pi }(\mathrm{R}–\mathrm{d}{)}^3\mathrm{\rho }$

$\therefore {\mathrm{g}}^{‘}=\frac{\mathrm{G}\times \frac{4}{3}\mathrm{\pi }(\mathrm{R}–\mathrm{d}{)}^3\mathrm{\rho }}{(\mathrm{R}–\mathrm{d}{)}^2}$

= $\frac{4}{3}\mathrm{\pi G}(\mathrm{R}–\mathrm{d})\mathrm{\rho }$  . . . .      (13)

Dividing (13) by (12), we get

$\frac{{\mathrm{g}}^{‘}}{\mathrm{g}}=\frac{\frac{4}{3}\mathrm{\pi G}(\mathrm{R}–\mathrm{d})\mathrm{\rho }}{\frac{4}{3}\mathrm{\pi GRg\rho }}=\frac{\mathrm{R}–\mathrm{d}}{\mathrm{R}}=\frac{\mathrm{R}}{\mathrm{R}}–\frac{\mathrm{d}}{\mathrm{R}}$

or  ${\mathrm{g}}^{‘}=\mathrm{g}\left(1–\frac{\mathrm{d}}{\mathrm{R}}\right)$  . . . .      (14)

From (14), we note that the value of acceleration due to gravity decreases with depth. At the centre of the earth,

d  = R, g’ = g_o (say).

From (14), we get

g₀ = $\mathrm{g}\left(1–\frac{\mathrm{R}}{\mathrm{R}}\right)=0$

It means the acceleration due to gravity is zero at the centre of earth.  Therefore the weight of the body of mass m at the centre of earth = mg_o = 0, but the mass of the body will not be zero. Thus the value of acceleration due to gravity is maximum at the earth’s surface and becomes zero at the centre of the earth.

Note: Decrease in the value of g with depth d is = g-g’ = $\frac{\mathrm{dg}}{\mathrm{R}}$

$\therefore$ Fractional decrease in the value of g with depth = $\frac{\mathrm{g}–{\mathrm{g}}^{‘}}{\mathrm{g}}=\frac{\mathrm{d}}{\mathrm{R}}$

$\therefore$ % decrease in the value of

g = $\frac{\mathrm{g}–{\mathrm{g}}^{‘}}{\mathrm{g}}\times 100=\frac{\mathrm{d}}{\mathrm{R}}\times 100$

c. Effect of shape of earth

Earth is not a perfect sphere.  It is flattened at the poles and bulges out at the equator.  Equatorial radius R_e of the earth is about 21 km greater than the polar radius R_p

Now, g = $\frac{\mathrm{GM}}{{\mathrm{R}}^2}$

 

Since G and M are constants

$\therefore \mathrm{g}\propto \frac{1}{{\mathrm{R}}^2}$

Thus we conclude that the value of g is least at the equator and maximum at the poles.  It means the value of acceleration due to gravity increases as we go from equator to the pole.

At sea level, the value of g at pole is greater than its value at equator by 1.80 cms^-2. 

d. Effect of latitude

Latitude at a place is defined as the angle which the line joining the place to the centre of the earth makes with the equatorial plane.  It is generally denoted by the letter $\lambda$. In the figure latitude at a place P = $\angle$POE = $\lambda$.  It is clear from the figure that, $\lambda$ = 90^o at poles and $\lambda$ = 0^o at equator.

Consider earth to be a perfect sphere of mass M, radius R with centre O.  The whole mass of earth can supposed to be concentrated at the centre O.  As earth rotates about its polar axis from west to east, every particle lying on its surface moves along a horizontal circle with same angular velocity as that of earth.  The centre of each circle lies on the polar axis.

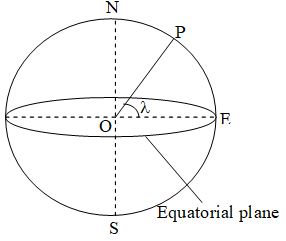
Consider a particle of mass m at a place P of latitude $\lambda$.  If earth is rotating about its polar axis NS with constant angular velocity $\omega$, then particle at P also rotates and describes a horizontal circle of radius r, where r = PC = OP cos$\lambda$ = Rcos$\lambda$ . . . .      (15)

The centrifugal force acting on the particle at P is ${\mathrm{mr\omega }}^2$.  It acts along PA, directed away from the centre C of the circle of rotation.

Suppose g is the acceleration due to gravity when earth were at rest, then the gravity pull on the particle (i.e. true weight of the particle) = mg; which acts towards the centre of the earth i.e. along PO.

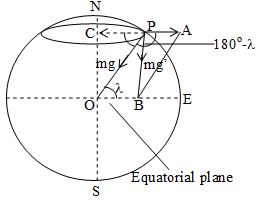
Let g’ be the acceleration due to gravity at P when rotation of earth is taken into account.  Then apparent weight of the particle at P = mg’.

This is the resultant of the true weight and centrifugal force acting on the particle at P and hence must be represented by the diagonal PB of parallelogram PABO.  Here $\angle$APO = (180^o–$\lambda$).

Using parallelogram law of forces, we have

$\mathrm{mg}‘=\sqrt{(\mathrm{mg}{)}^2+{\left({\mathrm{mr\omega }}^2\right)}^2+2(\mathrm{mg})\left({\mathrm{mr\omega }}^2\right)\cos \left(180°–\mathrm{\lambda }\right)}$

or  ${\mathrm{g}}^{‘}=\sqrt{{\mathrm{g}}^2+{\mathrm{r}}^2{\mathrm{\omega }}^4–2{\mathrm{gr\omega }}^2\mathrm{cos\lambda }}$

$=\sqrt{{\mathrm{g}}^2+{\mathrm{R}}^2{\cos }^2{\mathrm{\lambda \omega }}^4–2{\mathrm{gRcos\lambda \omega }}^2\mathrm{cos\lambda }}$

$=\mathrm{g}{\left(1+\frac{{\mathrm{R}}^2{\mathrm{\omega }}^4}{{\mathrm{g}}^2}{\cos }^2\mathrm{\lambda }–\frac{2{\mathrm{R\omega }}^2}{\mathrm{g}}{\cos }^2\mathrm{\lambda }\right)}^{1/2}$ …  (16)

We know that,       R = 6.4$\times$10⁶ m,  g = 9.8 ms^-2

and ${\mathrm{\omega }}^2=\frac{2\mathrm{\pi }}{\mathrm{T}}=\frac{2\mathrm{\pi }}{24\times 60\times 60}{\mathrm{rads}}^{–1}$

$\frac{\mathrm{R}{\omega }^2}{ \mathrm{g}}=6.4\times {10}^8\times \left(\frac{2\pi }{24\times 60\times 60}\right)\times \frac{1}{9.8}=\frac{1}{289}$

Since the value of $\frac{\mathrm{R}{\omega }^2}{ \mathrm{g}}$ is very small, therefore the terms with its squares and of higher powers can be neglected.  Hence (16), becomes

${\mathrm{g}}^{‘}=\mathrm{g}{\left(1–\frac{2{\mathrm{R\omega }}^2{\cos }^2\mathrm{\lambda }}{\mathrm{g}}\right)}^{1/2}$

Expanding it by Binomial theorem, we get

${\mathrm{g}}^{‘}=\mathrm{g}\left(1–\frac{1}{2}\times \frac{2{\mathrm{R\omega }}^2{\cos }^2\mathrm{\lambda }}{\mathrm{g}}\right)=\mathrm{g}\left(1–\frac{{\mathrm{R\omega }}^2{\cos }^2\mathrm{\lambda }}{\mathrm{g}}\right)$

or  ${\mathrm{g}}^{‘}=\mathrm{g}–Rg{\mathrm{\omega }}^2{\cos }^2\mathrm{\lambda }$     . . . .      (17)

As, cos$\lambda$ and $\omega$ are positive, therefore g’ < g.

Thus from (17), it is clear that acceleration due to gravity

i) Decreases on account of rotation of earth

ii) Increases with the increase in latitude of the place.

At equator,   $\lambda$ = 0^o, cos$\lambda$ = cos0^o = 1,

                        g’ = g_e (say)

Then from (17), g_e = g – R$\omega$²

Clearly, g_e is minimum

At poles,     $\lambda$ = 90^o,

cos$\lambda$ = cos90^o = 0, g’ = g_p (say)

Then from (17), g_p = g – R$\omega$² (0) = g

Clearly,  g_p is maximum.

Hence the value of acceleration due to gravity is minimum at the equator and maximum at the poles.

Note:

The difference in the value of acceleration due to gravity at pole and equator is given by  ${\mathrm{g}}_{\mathrm{p}}–{\mathrm{g}}_{\mathrm{e}}=\mathrm{g}–\left(\mathrm{g}–{\mathrm{R\omega }}^2\right)={\mathrm{R\omega }}^2$

When a body of mass m is moved from equator to pole, its weight increases by an anoint $=\mathrm{m}\left({\mathrm{g}}_{\mathrm{p}}–{\mathrm{g}}_{\mathrm{e}}\right)={\mathrm{mR\omega }}^2$.

The value of  ${\mathrm{g}}_{\mathrm{p}}–{\mathrm{g}}_{\mathrm{e}}={\mathrm{R\omega }}^2=6.4\times {10}^6\times {\left(\frac{2\mathrm{\pi }}{24\times 60\times 100}\right)}^2$= 0.034 m/s². 

5. Gravitational field Strength

Gravitational field strength at a point in a gravitational field is defined as the gravitational force per unit mass placed at that point.

If E is gravitational field strength, F is force exerted by the field on the body and m is the mass of the body placed in the field then,; $\mathrm{E}=\frac{\mathrm{F}}{\mathrm{m}}$

Gravitational field strength is also known as intensity of gravitational field.

Let us consider a body of mass m placed close to the surface of the earth.  Let the acceleration due to gravity ‘g’.

Force exerted by the earth on the body F = mg.

Gravitational field strength = $\frac{\mathrm{F}}{\mathrm{m}}=\frac{\mathrm{mg}}{\mathrm{m}}$

$\therefore$ Gravitational field strength = g  

Therefore gravitational field strength near the surface of the earth is equal to the acceleration due to gravity.  It should be kept in mind that the gravitational field strength and acceleration due to gravity are two separate physical quantities having equal magnitudes and the same directions. 

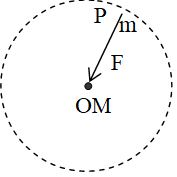
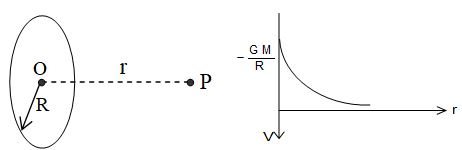
a. Field due to a point Mass

Suppose, a particle of mass M is placed at point O, we want to find the intensity of gravitational field  at a point P, a distance r from O.  Magnitude of a force F acting on a particle of mass m placed at P is

$\mathrm{F}=\frac{\mathrm{GMm}}{{\mathrm{r}}^2}$

$\mathrm{E}=\frac{\mathrm{F}}{\mathrm{m}}=\frac{\mathrm{GM}}{{\mathrm{r}}^2}$

$\mathrm{E}=\frac{\mathrm{GM}}{{\mathrm{r}}^2}$

The direction of the force F and hence E is from P to O as shown in figure.

b. Gravitational field due to a uniform solid sphere

Field at an external point:

A uniform sphere may be treated as a single particle of same mass placed at its centre for calculating the gravitational field at an external point.  Thus,

$\mathrm{E}\left(\mathrm{r}\right)=\frac{\mathrm{GM}}{{\mathrm{r}}^2}$ for $r\ge R$

$\mathrm{E}(\mathrm{r})\propto \frac{1}{{\mathrm{r}}^2}$

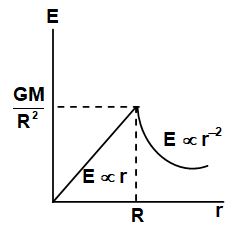
Here, r is the distance of the point from the centre of the sphere and R the radius of sphere.  

Field at an internal point

The gravitational field due to a uniform sphere at an internal point is proportional to the distance of the point from the centre of the sphere.  At the centre itself, it is zero and at surface it is $\frac{\mathrm{GM}}{{\mathrm{R}}^2}$, where R is the radius of the sphere.  Thus,

$\mathrm{E}\left(\mathrm{r}\right)=\frac{\mathrm{GM}}{{\mathrm{R}}^3}\mathrm{r}$   for   $\mathrm{r}\le \mathrm{R}$

Hence, E versus r graph is as shown in the figure.

c. Field due to a uniform Spherical shell

At an external point

For an external point the shell may be treated as a single particle of same mass placed at its centre.  Thus, at an external point the gravitational field is given by

$\mathrm{E}\left(\mathrm{r}\right)=\frac{\mathrm{GM}}{{\mathrm{r}}^2} \text{ for }\mathrm{r}\ge \mathrm{R}$

and otherwise  $\mathrm{E}\propto \frac{1}{{\mathrm{r}}^2}$

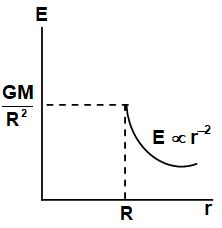
At an internal point

The field inside a uniform spherical shell is zero.  Thus, E versus r graph is as shown in the figure. 

d. Field due to a uniform circular ring at a point on its axis

Field strength at a point P on the axis of a circular ring of radius R and mass M is given by  

$\mathrm{E}\left(\mathrm{r}\right)=\frac{\mathrm{GMr}}{{\left({\mathrm{R}}^2+{\mathrm{r}}^2\right)}^{3/2}}$

This is directed towards the centre of the ring.  It is zero at the centre of the ring and maximum at r = $\frac{\mathrm{R}}{\sqrt{2}}$ (can be obtained by putting $\frac{\mathrm{d}E}{\mathrm{dr}}=0$).  Thus, E-r graph is as shown.

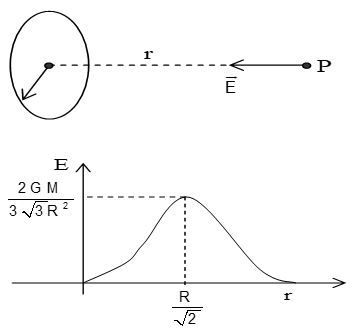
The maximum value is ${\mathrm{E}}_{\max }=\frac{2\mathrm{GM}}{3\sqrt{3{\mathrm{R}}^2}}$.

6. Gravitational potential

If a body is moved in a gravitational field from one place to the other, either work is done against the gravitational attraction or it is obtained.

The work done in bringing a unit mass from infinity to a point in the gravitational field is called the ‘gravitational potential’ at that point.

This work is obtained (not done) by the agent in bringing the mass.  The gravitational potential is denoted by V.  So, let W joule of work is obtained in bringing the mass m from infinity to some point, and then gravitational potential at that point will be $\mathrm{V}=\frac{\mathrm{W}}{\mathrm{m}}$.

Since, work is obtained, it is negative.  Hence, gravitational potential is always negative. 

a. Potential due to a point mass

Suppose a point mass M is situated at a point O.  We want to find the gravitational potential due to this mass at a point P a distance r from O.  For this let us find work done in taking the unit mass from P to infinity.  This will be

$\mathrm{W}={\int }_{\mathrm{r}}^{\infty }\mathrm{Fdr}={\int }_{\mathrm{r}}^{\infty }\frac{\mathrm{GM}}{{\mathrm{r}}^2}.\mathrm{dr}=\frac{\mathrm{GM}}{\mathrm{r}}$

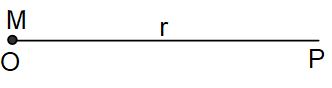
Hence, the work done in bringing unit mass from infinity to P will be $–\frac{\mathrm{GM}}{\mathrm{r}}$.  Thus, the gravitational potential at P will be,

$\mathrm{V}=–\frac{\mathrm{GM}}{\mathrm{r}}$

b. Potential due to a uniform solid sphere

Potential at an external point:

The gravitational potential due to a uniform sphere at an external point is same as that due to a single particle of same mass placed at its centre.  Thus,

$\mathrm{V}\left(\mathrm{r}\right)=\frac{\mathrm{GM}}{\mathrm{r}} \mathrm{r}\ge \mathrm{R}$

at the surface,        r = R and V =  $–\frac{\mathrm{GM}}{\mathrm{R}}$      

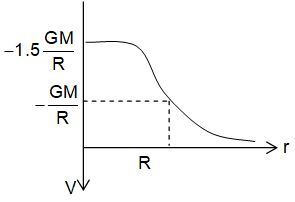
Potential at Internal point

At some internal point, potential at a distance r from the centre is given by,

If r $\le$ R     $\mathrm{V}\left(\mathrm{r}\right)=–\frac{\mathrm{GM}}{{\mathrm{R}}^3}\left(1.5{\mathrm{R}}^2–0.5{\mathrm{r}}^2\right)$ ,

At r = R,     $\mathrm{V}=–\frac{\mathrm{GM}}{\mathrm{R}}$

While at r = 0,   $\mathrm{V}=–\frac{1.5\mathrm{GM}}{\mathrm{R}}$

i.e., at the centre of the sphere the potential is 1.5 times the potential at surface.  The variation of V versus r graph is as shown in the given figure below. 

c. Potential due to a uniform thin spherical shell

Potential at an External Point

To calculate the potential at an external point, a uniform spherical shell may be treated as a point mass of same magnitude at its centre.  Thus, potential at a distance r is given by

If r $\ge$ R,    $\mathrm{V}\left(\mathrm{r}\right)=–\frac{\mathrm{GM}}{\mathrm{r}}$

At r = R,      $\mathrm{V}=–\frac{\mathrm{GM}}{\mathrm{R}}$

Potential at an internal point

The potential due to a uniform spherical shell is constant throughout any point inside the shell and this is equal to $–\frac{\mathrm{GM}}{\mathrm{R}}$.  Thus, V-r graph for a spherical shell is as shown below.

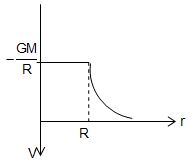
d. Potential due to a uniform ring at a point on its axis

The gravitational potential at a distance r from the centre on the axis of a ring of mass M and radius R is given by

When $0\le \mathrm{r}\le \infty \mathrm{V}\left(\mathrm{r}\right)=–\frac{\mathrm{GM}}{\sqrt{{\mathrm{R}}^2+{\mathrm{r}}^2}}$

At r=0,         $\mathrm{V}=–\frac{\mathrm{GM}}{\mathrm{R}}$,

i.e. at the centre of the ring gravitational potential is $–\frac{\mathrm{GM}}{\mathrm{R}}$.

The V-r graph is as shown in the figure.

Relation between gravitational field and potential

Gravitational potential is a field function.  It depends on the position of the point where potential is desired.  Gravitational field and the gravitational potential are related by the following relation.

$\overrightarrow{\mathrm{E}}=–\text{ gradient }\mathrm{V}$

    = – grad V

$=–\left[\frac{\partial V}{\partial x}\hat{i}+\frac{\partial V}{\partial y}\hat{j}+\frac{\partial V}{\partial z}\hat{k}\right]$

or   $\overrightarrow{\mathrm{E}}=–\left[\frac{\partial \mathrm{V}}{\partial \mathrm{x}}\hat{\mathrm{i}}+\frac{\partial \mathrm{V}}{\partial \mathrm{y}}\hat{\mathrm{j}}+\frac{\partial \mathrm{V}}{\partial \mathrm{z}}\hat{\mathrm{k}}\right]$   . . . .      (18)

Here, $\frac{\partial V}{\partial x}=$Partial derivative of potential function V w.r.to x i.e. differentiate V w.r.to. x assuming y and z to be constant.

Eq. (18) can be written in following different forms.

i)  $\mathrm{E}=–\frac{\mathrm{dV}}{\mathrm{dx}}$, if gravitational field is along x-direction only.

ii) $\mathrm{dV}=–\overrightarrow{\mathrm{E}}.\mathrm{d}\overrightarrow{\mathrm{r}}$

Here, $\mathrm{d}\overrightarrow{\mathrm{r}}=\mathrm{dx}\hat{\mathrm{i}}+\mathrm{dy}\hat{\mathrm{j}}+\mathrm{dz}\hat{\mathrm{k}}$

and  $\overrightarrow{\mathrm{E}}={\mathrm{E}}_{\mathrm{x}}\hat{\mathrm{i}}+{\mathrm{E}}_{\mathrm{y}}\hat{\mathrm{j}}+{\mathrm{E}}_{\mathrm{z}}\hat{\mathrm{k}}$

7. Gravitational potential energy

The concept of potential energy has already been discussed in the chapter of work, energy and power.   The word potential energy is defined for a conservative force field only.  There we have discussed that the change in potential energy (dU) of a system corresponding to a conservative internal force is given by

$\mathrm{dU}=–\overrightarrow{\mathrm{F}}.\mathrm{d}\overrightarrow{\mathrm{r}}$

or ${\int }_{\mathrm{Ui}}^{\mathrm{Uf}}\mathrm{dU}=–{\int }_{\overrightarrow{{\mathrm{r}}_{\mathrm{i}}}}^{\overrightarrow{{\mathrm{r}}_{\mathrm{f}}}} \overrightarrow{\mathrm{F}}\circ \mathrm{d}\overrightarrow{\mathrm{r}}$

or  ${\mathrm{U}}_{\mathrm{f}}–{\mathrm{V}}_{\mathrm{i}}=–{\int }_{\overrightarrow{{\mathrm{r}}_{\mathrm{i}}}}^{\overrightarrow{{\mathrm{r}}_{\mathrm{f}}}}\overrightarrow{\mathrm{F}}.\overrightarrow{\mathrm{dr}}$

We generally choose the reference point at infinity and assume potential energy to be zero there, i.e. if we take r₁ = $\infty$ (infinite) and U_i = 0 we can write  

$\mathrm{U}=–{\int }_{\infty }^{\overline{\mathrm{r}}}\overrightarrow{\mathrm{F}}·\overrightarrow{\mathrm{dr}}=–\mathrm{W}$

or potential energy of a body or system is negative of work done by the conservative forces in bringing it from infinity to the present position.

Gravitational potential energy of a two particle system:

The gravitational potential energy of two particles of masses m₁ and m₂ separated by a distance r is given by

$\mathrm{U}=\frac{{\mathrm{Gm}}_1{\mathrm{m}}_2}{\mathrm{r}}$

This is actually the negative of work done in bringing those masses from infinity to a distance r by the gravitational forces between them.

Gravitational potential energy for a system of particles

The gravitational potential energy for a system of particles (say m₁, m₂, m₃ and m₄) is given by

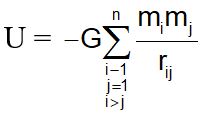
Thus, for a n particle system there are $\frac{\mathrm{n}\left(\mathrm{n}–1\right)}{2}$ pairs and the potential energy is calculated for each pair and added to get the total potential energy of the system.

Gravitational potential energy of a body on earth’s surface:

The gravitational potential energy of mass m in the gravitational field of mass M at a distance r from it is,  

$\mathrm{U}=–\frac{\mathrm{GMm}}{\mathrm{r}}$

The earth behaves for all external points as if its mass M were concentrated at its centre.   Therefore, a mass m near earth’s surface may be considered at a distance R (the radius earth) from M.  Thus, the potential energy of m due to earth will be

$\mathrm{U}=–\frac{\mathrm{GMm}}{\mathrm{R}}$

8. Escape velocity

Binding Energy

Therefore, the total mechanical energy of the particle is,

$\mathrm{E}=\mathrm{K}+\mathrm{U}=0–\frac{\mathrm{GMm}}{\mathrm{R}}$

or $\mathrm{E}=–\frac{\mathrm{GMm}}{\mathrm{R}}$

$\therefore$ Binding energy = |E| = $\frac{\mathrm{GMm}}{\mathrm{R}}$

It is due to this energy, the particle is attached with the earth.  If minimum this much energy is supplied to the particle in any form (normally kinetic) the particle no longer remains bound to the earth.  It goes out of the gravitational field of earth.

Escape velocity

The minimum vertical velocity required for an object to escape from the gravitational influence of a planet is known as escape velocity.

As we discussed the binding energy of a particle on the surface of earth kept at rest is $\frac{\mathrm{GMm}}{\mathrm{R}}$. If this much energy in the form of kinetic energy is supplied to the particle, it leaves the gravitational field of the earth. So, if v_e is the escape velocity of the particle, then

$\frac{1}{2}{\mathrm{mv}}_{\mathrm{e}}=_2\frac{\mathrm{GMm}}{\mathrm{R}}$ 

or ${\mathrm{V}}_{\mathrm{e}}=\sqrt{\frac{2\mathrm{GM}}{\mathrm{R}}}$

or ${\mathrm{V}}_{\mathrm{e}}=\sqrt{2\mathrm{gR}}$

as $\mathrm{g}=\frac{\mathrm{GM}}{{\mathrm{R}}^2}$

Substituting the value of g (9.8 m/s²) and R (6.4$\times$10⁶ m), we get

${\mathrm{V}}_{\mathrm{e}}=11.2$ km/s

Thus, the minimum velocity needed to take a particle infinitely away from the earth is called the escape velocity.  On the surface of earth its value is 11.2 km/s. 

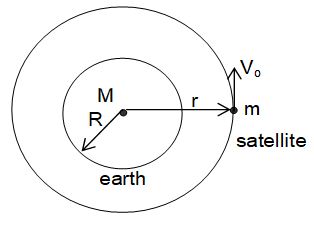
9. Motion of satellites & Orbital speed

Motion of satellites

Just as the planets revolve around the sun, in the same way few celestial bodies revolve around these planets.  These bodies are called ‘satellites.  For example moon is a satellite of earth.  Artificial satellites are launched from the earth. Such satellites are used for telecommunication, weather forecast and other applications.  The path of these satellites are elliptical with the centre of earth at a focus.  However the difference in major and minor axes is so small that they can be treated as nearly circular for not too sophisticated calculations.  Let us derive certain characteristics of the motion of satellites, assuming the orbit to the perfectly circular.

Orbital Speed

The horizontal velocity required for an object to revolve around a planet in a circular orbit is called orbital velocity.  It is denoted by v₀.

The necessary centripetal force to the satellite is being provided by the gravitational force exerted by the earth on the satellite.  Thus,

$\frac{{\mathrm{mv}}_0^2}{\mathrm{r}}=\frac{\mathrm{GMm}}{{\mathrm{r}}^2}$

$\therefore {\mathrm{v}}_0=\sqrt{\frac{\mathrm{GM}}{\mathrm{r}}}$

or  ${\mathrm{v}}_0\propto \frac{1}{\sqrt{\mathrm{r}}}$

hence, the orbital speed (v_o) of the satellite decreases as the orbital radius (r) of the satellite increases.  Further, the orbital speed of a satellite close to the earth’s surface (r=R) is,

${\mathrm{v}}_{\circ }=\sqrt{\frac{\mathrm{GM}}{\mathrm{R}}}=\sqrt{\mathrm{gR}}=\frac{{\mathrm{v}}_{\mathrm{e}}}{\sqrt{2}}$

substituting   ${\mathrm{v}}_{\mathrm{e}}=11.2 \mathrm{km}/\mathrm{s}$

${\mathrm{v}}_0=7.9 \mathrm{km}/\mathrm{s}$

Period of revolution

The period of revolution (T) is given by

$\mathrm{T}=\frac{2\mathrm{\pi r}}{{\mathrm{v}}_{\circ }}$

or  $\mathrm{T}=\frac{2\pi \mathrm{r}}{\sqrt{\frac{\mathrm{GM}}{\mathrm{r}}}}$   or   $\mathrm{T}=2\mathrm{\pi }\sqrt{\frac{{\mathrm{r}}^3}{\mathrm{GM}}}$  or $\mathrm{T}=2\mathrm{\pi }\sqrt{\frac{{\mathrm{r}}^3}{{\mathrm{gR}}^2}}$

From this expression of T, we can make the following conclusions

1. T $\propto$ ${\mathrm{r}}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$or  ${\mathrm{T}}^2\propto {\mathrm{r}}^3$  (which is also the Kepler’s third law)

2. Time period of a satellite very close to earth’s surface (r = R) is substituting the values, we get T = 84.6 minutes

3. Suppose the height of a satellite is such that the time period of the satellite is 23 hrs and moves in the same sense as the earth. The satellite will always be overhead a particular place on the equator.  As seen from the earth, this satellite will appear to be stationary.  Such a satellite is called geostationary satellite.  Putting T=24 hrs in the expression of T, the radius of geostationary satellite comes out to be r = 4.2$\times$10⁴ km.  The height above the surface of earth is about 3.6$\times$10⁴ km.

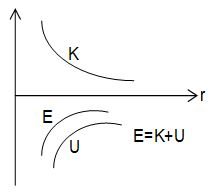
Energy of satellite

The potential energy of the system is  

$\mathrm{U}=–\frac{\mathrm{GMm}}{\mathrm{r}}$

The kinetic energy of the satellite is

$\mathrm{K}=\frac{1}{2}{\mathrm{mv}}_0^2=\frac{1}{2} \mathrm{m}\left(\frac{\mathrm{GM}}{\mathrm{r}}\right)\text{ or }\mathrm{K}=\frac{1}{2}\frac{\mathrm{GMm}}{\mathrm{r}}$

The total energy is,

$\mathrm{E}=\mathrm{K}+\mathrm{U}=–\frac{\mathrm{GMm}}{2\mathrm{r}}\text{ or } \mathrm{E}=–\frac{\mathrm{GMm}}{2\mathrm{r}}$

This energy is constant and negative, i.e. the system is closed.  The farther the satellite from the earth the greater its total energy.  

     

10. Kepler’s Laws of Planetary Motion

Kepler’s Laws

Kepler discovered three empirical laws that accurately described the motion of the planets.  The three laws may be stated as,

First Law

Each planet moves in an elliptical orbit, with the sun at one focus of the ellipse.  This law is also known as the law of elliptical orbits and obviously gives the shape of the orbits of the planets round the sun.

Second Law

The radius vector, drawn from the sun to a planet, sweeps out equal areas in equal time, i.e. its areal velocity (or the area swept out by it per unit time) is constant.  This is referred to as the law of areas and gives the relationship between the orbital speed of the planet and its distance from the sun.

Third Law

The square of the planet’s time period is proportional to the cube of the semi-major axis of its orbit.  This is known as the harmonic law and gives the relationship between the size of the orbit of a planet and its time of revolution.

Mathematically, this law can be expressed as  

${\mathrm{T}}^2\propto {\mathrm{R}}^3$

Where T= Time period of revolution of the planet and R= Semi-major axis of the elliptical orbit 

11. Geostationary Satellite & Black Holes

Geostationary Satellite

If the period of revolution of an artificial satellite is equal to the period of rotation of earth then such a satellite is called geostationary satellite. In other words a geostationary satellite takes 24 hours to complete on revolution around the earth. The term geostationary comes from the fact that such a satellite appears to be stationary for an observer on the earth.  Therefore, its relative velocity with respect to earth is zero. It revolves round the earth at a constant speed once per day over the equator from west to east in equatorial plane. Such a satellite is to be placed at a height of about 35,800 km with an orbital radius of about 42,250 km.

Uses of Geostationary Satellites

Geo stationary satellites can be used to

1) Study the upper layers of the atmosphere.

2) Forecast the changes in the atmosphere.

3) Know the shape and size of the earth.

4) Identify the minerals and natural resources present inside and on the surface of the earth.

5) Transmit the T.V. programmers to distant places.

6)Study the properties of radio waves in the upper layers of the atmosphere.

7) Under take space research i.e., to know about the planets, satellites and comets etc.          

Black Holes

The birth, life and death of a star is determined by interplay of nuclear reactions and the gravitational forces.  The nuclear reactions that take place in the interior of the star will create a radiation pressure which in turn tries to push the star outward.  However the gravitational forces between the particles of the star will try to pull it inward towards the centre.  When there is a balance between the outward radiation pressure and the inward gravitational pressure the star attains stability.  However, when the nuclear fuel inside the core of a massive star gets exhausted, the star collapses under its own enormous gravitational force.  As a result the star shrinks to a smallest size.  This collapsed star will be so dense that even light can not escape from it.  Such an entity in the cosmos is called ‘Black hole’

Formation of Black Holes

SOLVED EXAMPLES

1. Two identical spherical bodies of mass M and radius R are placed with their surfaces R distance apart. Find the force of gravitation between two bodies.

Sol.  Mass of bodies

m₁ = m₂ = M

Distance between centre of bodies

r = R+R+R = 3R

According to Newton’s law of gravitation

$\mathrm{F}=\frac{{\mathrm{Gm}}_1{ \mathrm{m}}_2}{{\mathrm{r}}^2}=\frac{{\mathrm{GM}}^2}{(3\mathrm{R}{)}^2}=\frac{{\mathrm{GM}}^2}{9{\mathrm{R}}^2}$

2. Three point masses m, 2m and 4m are placed at three vertices A, B and C of a right angled triangle, right angled at B. If AB = BC = l , find the magnitude of resultant gravitational pull on the body at A due to bodies at B and C.

Sol.  The situation is shown in the given figure.

Gravitational force on body at A due to body at B  

${\mathrm{F}}_{\mathrm{AB}}=\frac{\mathrm{G}\left(\mathrm{m}\right)\left(2\mathrm{m}\right)}{(\mathrm{AB}{)}^2}=\frac{2{\mathrm{Gm}}^2}{{\mathrm{\ell }}^2}$

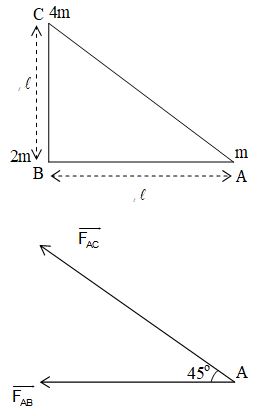
Gravitational force on body at A due to body at C

${\mathrm{F}}_{\mathrm{AC}}=\frac{\mathrm{G}\left(\mathrm{m}\right)(4 \mathrm{m})}{(\mathrm{AC}{)}^2}=\frac{4{\mathrm{Gm}}^2}{{\mathrm{AB}}^2+{\mathrm{BC}}^2}=\frac{4{\mathrm{Gm}}^2}{2{\mathrm{\ell }}^2}$

or ${\mathrm{F}}_{\mathrm{AC}}=\frac{2{\mathrm{Gm}}^2}{{\ell }^2}$

Directions of F_AB and F_AC are shown in the given figure.

Hence net force on A  

$\mathrm{F}=\sqrt{{\mathrm{F}}_{AB}{}^2+{\mathrm{F}}_{AC}{}^2+2{ \mathrm{F}}_{AB}{ \mathrm{F}}_{\mathrm{AC}}\cos 45°}$

$=\sqrt{{\left(\frac{2\mathrm{GM}}{{\mathrm{\ell }}^2}\right)}^2+{\left(\frac{2\mathrm{GM}}{{\mathrm{\ell }}^2}\right)}^2+2{\left(\frac{2\mathrm{GM}}{{\mathrm{\ell }}^2}\right)}^2\times \frac{1}{\sqrt{2}}}$

= 3.696 $\frac{{\mathrm{Gm}}^2}{{\ell }^2}$

3. If the radius of earth shrinks by 2%, mass remaining same, then how would the value of acceleration due to gravity change?

Sol.  Let M and R be the mass and radius of earth, and g be the acceleration due to gravity, near the surface of the earth, then $\mathrm{g}=\frac{\mathrm{GM}}{{\mathrm{R}}^2}$

Taking log on both sides we get, log g = logG + log M – logR²

Differentiation above equation, we get $\frac{\mathrm{dg}}{\mathrm{g}}=0+0–\frac{2\mathrm{dR}}{\mathrm{R}}$

When radius shrinks by 2%, $\frac{\mathrm{dR}}{\mathrm{R}}=–\frac{2}{100}$

$\therefore \frac{\mathrm{dg}}{\mathrm{g}}=–2\left(\frac{–2}{100}\right)=\frac{4}{100}=4\%$

Hence g increases by 4%.

4. How much above the surface of earth does the acceleration due to gravity reduces by 64% of its value on the surface of earth. Radius of earth = 6400 km.

Sol. Since the acceleration due to gravity reduces by 64%, then the value of acceleration due to gravity there is 100 – 64 = 36%. 

It means,   ${\mathrm{g}}^{‘}=\frac{36}{100}\mathrm{g}.$

If h is the height of location above the surface of earth, then

${\mathrm{g}}^{‘}=\mathrm{g}\frac{{\mathrm{R}}^2}{(\mathrm{R}+\mathrm{h}{)}^2}$   or  $\frac{36}{100} \mathrm{g}=\mathrm{g}\frac{{\mathrm{R}}^2}{(\mathrm{R}+\mathrm{h}{)}^2} \text{ or } \frac{6}{10}=\frac{\mathrm{R}}{\mathrm{R}+\mathrm{h}}$ or 6R + 6h = 10R

or $\mathrm{h}=\frac{4\mathrm{R}}{6}=\frac{2\mathrm{R}}{3}=\frac{2\times 6.4\times {10}^8}{3}$ = 4.27$\times$10⁶ m.

5. Find the percentage decrease in the weight of the body when taken to a depth of 16 km below the surface of earth. Radius of the earth is 6400 km.

Sol.  Here d= 16 km; R = 6400 km

Weight of the body at depth d is

mg’ = $\mathrm{mg}\left(1–\frac{\mathrm{d}}{\mathrm{R}}\right)$

% decrease in weight = $\frac{\mathrm{mg}–{\mathrm{mg}}^{‘}}{\mathrm{mg}}=\frac{\mathrm{d}}{\mathrm{R}}\times 100=\frac{16}{6400}\times 100=0.25\%$

6. Determine the speed with which the earth have to rotate on its axis so that a person on the equator would weigh 2/5^th as much as at present. Take the equatorial radius as 6400 km.

Sol.  True weight at equator, W = mg;

Observed weight at equator,

W’ = mg’ = $\frac{2}{5}\mathrm{mg}$

At equator latitude $\lambda$ = 0

As mg’ = mg – mR$\omega$²cos²$\lambda$

$\frac{2}{5}\mathrm{mg}=\mathrm{mg}–{\mathrm{mgR\omega }}^2{\cos }^{2}0=\mathrm{mg}–{\mathrm{mR\omega }}^2$

or  ${\mathrm{mR\omega }}^2=\frac{3}{5}\mathrm{mg}$

or $\mathrm{\omega }={\left(\frac{3}{5}\frac{\mathrm{g}}{\mathrm{R}}\right)}^{1/2}=\left(\frac{3\times 9.8}{5\times 6.4\times {10}^8}\right)=9.6\times {10}^{–4}\mathrm{rad}/\mathrm{s}$ = 9.1875 $\times$10^–5 rad/s

7. Two concentric spherical shells have masses m₁ and m₂ and radii r₁ and r₂ (r₂ > r). What is the force exerted by this system on a particle of mass m₃ if it is placed at a distance r(r₁<r<r₂) from the centre?

Sol.  The outer shell will have no contribution in the gravitational field at P  

${\mathrm{E}}_{\mathrm{P}}=\frac{{\mathrm{Gm}}_1}{{\mathrm{r}}^2}$

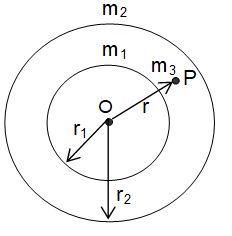
Thus, force on mass m₃ placed at P is,

$\mathrm{F}=\left({\mathrm{m}}_3{\mathrm{E}}_{\mathrm{P}}\right)=\frac{{\mathrm{Gm}}_1{ \mathrm{m}}_3}{{\mathrm{r}}^2}$

The field ${\overrightarrow{\mathrm{E}}}_{\mathrm{P}}$ and the force $\overrightarrow{\mathrm{F}}$ both are towards centre O.

8. A particle of mass 1 kg is kept on the surface of a uniform sphere of mass 30kg and radius 2.0m. Find the work to be done against the gravitational force between them to take the particle away from the sphere.

Sol.  Potential at the surface of sphere,

$\mathrm{V}=\frac{\mathrm{GM}}{\mathrm{R}}=–\frac{\left(6.67\times {10}^{–11}\right)\left(30\right)}{2} \mathrm{J}/\mathrm{kg}$

= = -1.0$\times$10^–9 J/kg

i.e. 1.0$\times$10^–9 J work is obtained to bring a mass of 1 kg from infinity to the surface of sphere.  Hence, the same amount of work will have to be done to take the particle away from the surface or sphere.  Thus, W = 1.334$\times$10^–9 J

9. Three masses of 2 kg, 3kg and 4kg are placed at the vertices of an equilateral triangle of side 2m. Find the gravitational potential energy of this system.  Take G=6.67$\times$10^–11 N-m²/kg²

Sol.  $\mathrm{U}=–\mathrm{G}\left(\frac{{\mathrm{m}}_3{\mathrm{m}}_2}{{\mathrm{r}}_{32}}+\frac{{\mathrm{m}}_3{\mathrm{m}}_1}{{\mathrm{r}}_{31}}+\frac{{\mathrm{m}}_2{\mathrm{m}}_1}{{\mathrm{r}}_{21}}\right)$

Here,   r₃₂ = r₃₁ = r₂₁ = 2.0m,

m₁ = 2kg, m₂=3kg and m₃ = 4kg.

Substituting in above, we get  

$\mathrm{U}=–\left(6.67\times {10}^{–11}\right)\left(\frac{4\times 3}{2}+\frac{4\times 2}{2}+\frac{3\times 2}{2}\right)$

or U = -8.67$\times$10^–10 J.  

10. Calculate the escape velocity from the surface of moon. The mass of the moon is 7.4$\times$10²² kg and radius = 1.74$\times$10⁶ m.

Sol. Escape velocity from the moon is  

${\mathrm{V}}_{\mathrm{e}}=\sqrt{\frac{2{\mathrm{GM}}_{\mathrm{m}}}{{\mathrm{R}}_{\mathrm{m}}}}$

Substituting the values, we have

${\mathrm{v}}_{\mathrm{e}}=\sqrt{\frac{2\times 6.67\times {10}^{–11}\times 7.4\times {10}^{22}}{1.74\times {10}^8}}$

= 2.4$\times$10³ m/s or 2.4 km/s  

11. A particle is projected from the surface of earth with an initial speed of 4.0 km/s. Find the maximum height attained by the particle.  Radius of earth = 6400 km and g = 9.8 m/s².

Sol.  From the principle of conservation of M.E.

$–\frac{\mathrm{GMm}}{\mathrm{R}}=\frac{1}{2}{\mathrm{mv}}^2–\frac{\mathrm{GMm}}{\mathrm{R}+\mathrm{h}}\Rightarrow \mathrm{h}=\frac{{\mathrm{v}}^2}{2 \mathrm{g}–\frac{{\mathrm{v}}^2}{\mathrm{R}}}$

substituting the values, we have $\mathrm{h}=\frac{{\left(4.0\times {10}^3\right)}^2}{2\times 9.8–\frac{{\left(4.0\times {10}^3\right)}^2}{6.4\times {10}^8}}$

= 9.35$\times$10⁵ m = 935 km                  

12. A spaceship is launched into a circular orbit close to the earth’s surface. What additional velocity has now to be imparted to the space-ship in the orbit to overcome the gravitational pull.  Radius of earth = 6400 km, g = 9.8 m/s².

Sol.  The speed of the space ship in a circular orbit close to the earth’s surface is given by

${\mathrm{v}}_{\mathrm{o}}=\sqrt{\mathrm{gR}}$

and escape velocity is given by,

${\mathrm{v}}_e=\sqrt{2 \mathrm{gR}}$

Additional velocity required to escape  ${\mathrm{v}}_{\mathrm{e}}–{\mathrm{v}}_0=\sqrt{2 \mathrm{gR}}–\sqrt{\mathrm{gR}}=(\sqrt{2}–1)\sqrt{\mathrm{gR}}$

Substituting the values of g and R, we get $v_e–v_0=3.278\times {10}^3 \mathrm{m}/\mathrm{s}$.