Trogonometric Functions

1. MEASUREMENT OF ANGLES

Angle

An angle is considered as figure obtained by rotating a given ray about its initial point. The original ray (before rotation) is known as initial side and the final position of the ray (after rotation) is known as terminal side of the angle, the point of rotation is known as vertex. The angle is said to be positive or negative as the rotation is anti-clockwise or clockwise.

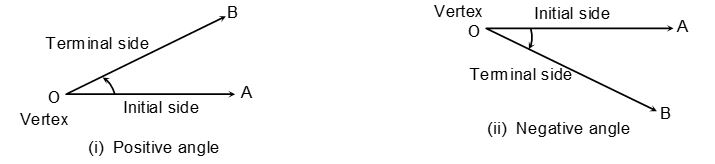
There are two methods used in measuring angles.

Sexagesimal System (Degree Measure)

The measure of an angle will be one degree, if the rotation from initial side to terminal side is ${\left(\frac{1}{360}\right)}^{\mathrm{th}}$ of a revolution.

1 right angle = 90 degrees   (= 90°)

1 degree = 60 minutes   (= 60’)

1 minute = 60 seconds   (= 60”)

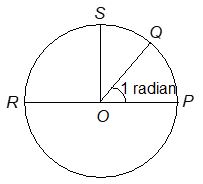
Circular System (Radian Measure)

One radian is the angle subtended at the centre of any circle by an arc of the circle equal in length to the radius.

Relation between Degrees and Radians

The angle subtended by a circle at its centre = $2{\mathrm{\pi }}^{\mathrm{c}}=360°$

$\Rightarrow$ p radians = 180 degrees or ${\mathrm{\pi }}^{\mathrm{c}}$ = 180°

$\Rightarrow 1^c={\left(\frac{180}{\pi }\right)}^0=57°{16}^{‘}$  (Approx)

LENGTH OF AN ARC OF A CIRCLE

$\Rightarrow$ Length of arc = (radius of the circle) × (angle subtended by that arc at the centre of circle)

arc PQ =r if the length of arc PS = l,

then $l=r \theta$

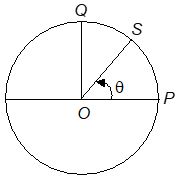
Illustration-1:

Find the radian measure corresponding to –37° 30‘.

Solution:

$60‘=1°\Rightarrow 30‘={\left(\frac{1}{2}\right)}^{°}\Rightarrow –37°30‘=–37{\frac{1}{2}}^{°}=–\frac{75°}{2}$

$360°=2\mathrm{\pi }\text{ radians }\Rightarrow \frac{–75°}{2}=–\frac{2\mathrm{\pi }}{360}\times \frac{75}{2}\text{ radians }=\frac{–5\mathrm{\pi }}{24}\text{ radians }$

Illustration-2:

The minute hand of a clock is 10 cm long. How far does the tip of the hand move in 20 minutes ?

Solutio :

The minute hand moves through 120° in 20 minutes or moves through $\frac{2\mathrm{\pi }}{3}$ radians.

Since the length of the minute hand is 10 cm, the distance moved by the tip of the hand is given by the formula l = $\mathrm{r\theta }=10\times \frac{2\mathrm{\pi }}{3}=\frac{20\mathrm{\pi }}{3} \mathrm{cm}$

2. TRIGONOMETRIC FUNCTIONS OF AN ANGLE

The six trigonometric ratios sine, cosine, tangent, cotangent, secant and cosecant of an angle θ, 0° < θ < 90° are defined as the ratios of two sides of a right-angled triangle with θ as one of the angles.

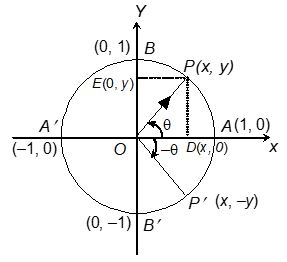
cosθ = x, the x coordinate of P

sinθ = y, the y coordinate of P

tanθ = $\frac{y}{x}, x\ne 0$

cotθ = $\frac{x}{y}, y\ne 0$

$\sec \theta =\frac{1}{x}, x\ne 0$

$cosec\theta =\frac{1}{y}, y\ne 0$

Angles measured anticlockwise from the initial line OX are deemed to be positive and angles measured clockwise are considered to be negative.  

The range and sign of the trigonometric ratios in the four quadrants are depicted in the following table.

1. TRIGONOMETRIC FUNCTIONS OF (-θ)

sin(-θ) = -sin(-θ)
cos(-θ) = cosθ
tan(-θ) = -tanθ

2. CIRCULAR FUNCTIONS OF ALLIED ANGLES

When θ is an acute angle, 90° – θ is called the angle complementary to θ.  When θ is acute, θ and 180° – θ are called supplementary angles.

TABLE OF FORMULAE FOR ALLIED ANGLES  

	180° – θ	180° + θ	360° – θ	– θ	90° – θ	90° + θ	270° – θ	270° + θ
Sin	sinθ	– sinθ	– sinθ	– sinθ	cosθ	cosθ	– cosθ	– cosθ
Cos	– cosθ	– cosθ	cosθ	cosθ	sinθ	-sinθ	-sinθ	sinθ
Tan	-tanθ	+tanθ	-tanθ	-tanθ	cotθ	-cotθ	cotθ	-cotθ

3. SOME IMPORTANT FACTS

(i) For any power n, (sin A)ⁿ is written as sinⁿA. Similarly for all trigonometric ratios.
(ii) sin²A + cos²A = 1; 1 + tan²A = sec²A and 1 + cot²A = cosec²A.
(iii) |sinA| $\le$ 1 $\Rightarrow$ -1 $\le$ sinA $\le$ 1
        |cosA| $\le$ 1 $\Rightarrow$ -1 $\le$ cosA $\le$ 1
(iv) The trigonometric ratios are also called as trigonometric functions. They are also sometimes called circular functions.

ANGLE/ RATIO	0°	30°	45°	60°	90°
sine	0	$\frac{1}{2}$	$\frac{1}{\sqrt{2}}$	$\frac{\sqrt{3}}{2}$	1
cosine	1	$\frac{\sqrt{3}}{2}$	$\frac{1}{\sqrt{2}}$	$\frac{1}{2}$	0
tangent	0	$\frac{1}{\sqrt{3}}$	1	$\sqrt{3}$	undefined
cotangent	undefined	$\sqrt{3}$	1	$\frac{1}{\sqrt{3}}$	0
secant	1	$\frac{2}{\sqrt{3}}$	$\sqrt{2}$	2	undefined
cosecant	undefined	2	$\sqrt{2}$	$\frac{2}{\sqrt{3}}$	1

Illustration-3:

Evaluate: cos(–3030°).

Solution:

cos(-3030°) = cos(3030°) (using cos(-θ) = cosθ) = cos(8 × 360° + 150°)

                       = cos150° = cos(180° – 30°) = – cos30° =$–\frac{\sqrt{3}}{2}$.

Illustration-4:

Find the values of the other five trigonometric functions if .

Solution:

cos θ is negative in II^nd and III^rd quadrant only

In II^nd quadrant sine and cosecant is positive and other trigonometric ratios are negative.
Now construct a right angle triangle with base BC = 1 and hypotenuse AC = 2
$\Rightarrow$ perpendicular AB = $\sqrt{3}$

$\Rightarrow \sin \theta =\frac{AB}{AC}=\frac{\sqrt{3}}{2}\Rightarrow cosec\theta =\frac{AC}{AB}=\frac{2}{\sqrt{3}}$

$\Rightarrow \tan \theta =–\frac{AB}{BC}=–\sqrt{3}\Rightarrow \cot \theta =–\frac{BC}{AB}=–\frac{1}{\sqrt{3}}$

and  $\sec \theta =–\frac{AC}{BC}=–2$

In III^rd quadrant only tangent and cotangent are positive and rest are negative

$\Rightarrow \sin \theta =–\frac{\sqrt{3}}{2}, \tan \theta =\sqrt{3}, \cot \theta =\frac{1}{\sqrt{3}}, \sec \theta =–2\text{ and }cosec\theta =–\frac{2}{\sqrt{3}}$

Illustration-5:

Simplify: $\frac{\sin \left(\frac{3\mathrm{\pi }}{2}–\mathrm{\theta }\right)\cos \left(\frac{\mathrm{\pi }}{2}+\mathrm{\theta }\right)}{\tan \left(\frac{\mathrm{\pi }}{2}+\mathrm{\theta }\right)}–\frac{\sin \left(\frac{3\mathrm{\pi }}{2}–\mathrm{\theta }\right)}{\sec (\mathrm{\pi }+\mathrm{\theta })}$.

Solution:

The expression = $\frac{(–\cos \theta )(–\sin \theta )}{–\cot \theta }–\frac{(–\cos \theta )}{(–\sec \theta )}=–{\sin }^2\theta –{\cos }^2\theta =–\left({\sin }^2\theta +{\cos }^2\theta \right)=–1$.  

Illustration-6:

Prove that cosec⁴θ(1 – cos⁴θ) = 1 + 2cot²θ.

Solution:

cosec⁴θ(1 – cos⁴θ) – 2cot²θ

= $\frac{{cosec}^2\mathrm{\theta }\left(1–{\cos }^2\mathrm{\theta }\right)\left(1+{\cos }^2\mathrm{\theta }\right)}{{\sin }^2\mathrm{\theta }}$ – 2cot²θ = $\cos e{c}^2\theta \left(1+{\cos }^2\theta \right)–2co{t}^2\theta$

= cosec²θ + cot²θ – 2cot²θ = 1 + 2 cot²θ – 2cot²θ = 1 

3. CIRCULAR FUNCTIONS OF COMPOUND ANGLES

1. Addition and subtraction formulae

•  cos(θ + ϕ) = cosθ cosϕ – sinθ sinϕ
• cos(θ + ϕ) = cosθ cosϕ + sinθ sinϕ

• sin(θ + ϕ) = sinθ cosϕ + cosθ sinϕ

• sin(θ – ϕ) = sinθ cosϕ – cosθ sinϕ

• $\mathbf{tan}\mathbf{(}\mathbf{\theta }\mathbf{+}\mathbf{\varphi }\mathbf{)}\mathbf{=}\frac{\mathbf{tan\theta }\mathbf{+}\mathbf{tan\varphi }}{\mathbf{1}\mathbf{–}\mathbf{tan\theta tan\varphi }}$
• $\mathbf{tan}\mathbf{(}\mathbf{\theta }\mathbf{–}\mathbf{\varphi }\mathbf{)}\mathbf{=}\frac{\mathbf{tan\theta }\mathbf{–}\mathbf{tan\varphi }}{\mathbf{1}\mathbf{+}\mathbf{tan\theta tan\varphi }}$
• $\mathbf{cot}\mathbf{(}\mathbf{\theta }\mathbf{+}\mathbf{\varphi }\mathbf{)}\mathbf{=}\frac{\mathbf{cot\theta cot\varphi }\mathbf{–}\mathbf{1}}{\mathbf{cot\varphi }\mathbf{+}\mathbf{cot\theta }}$
• $\mathbf{cot}\mathbf{(}\mathbf{\theta }\mathbf{–}\mathbf{\varphi }\mathbf{)}\mathbf{=}\frac{\mathbf{cot\theta cot\varphi }\mathbf{+}\mathbf{1}}{\mathbf{cot\varphi }\mathbf{–}\mathbf{cot\theta }}$

Illustration-7:

If sinθ = $\frac{\mathbf{8}}{\mathbf{17}}$ and cosβ = $\frac{\mathbf{9}}{\mathbf{41}}$, find sin(θ + β), cos(θ + β), sin(θ – β) and cos(θ – β), where q is an obtuse angle and β is an acute angle.

Solution :

Since sinθ = $\frac{8}{17}$, cos²θ = $1–\frac{64}{289}=\frac{225}{289}$

∴ cosθ = ±$\frac{15}{17}$.  As θ is obtuse, cosθ is negative.

∴ $\cos \theta =–\frac{15}{17}$

${\sin }^2\mathrm{\beta }=1–\frac{81}{1681}=\frac{1600}{1681}$

$\therefore \mathrm{sin\beta }=\pm \frac{40}{41}$

As β is acute, sinβ is positive

$\therefore \mathrm{sin\beta }=+\frac{40}{41}$

Now sin(θ + β) = sinθ cosβ + cosθ sinβ = $\frac{8}{17}.\frac{9}{41}+\left(–\frac{15}{17}\right)\frac{40}{41}=\frac{72–600}{697}=–\frac{528}{697}$

cos(θ + β) = cosθ cosβ – sinθ sinβ = $\left(–\frac{15}{17}\right)\left(\frac{9}{41}\right)–\left(\frac{8}{17}\right)\left(\frac{40}{41}\right)=–\frac{455}{697}$

sin(θ – β) = sinθ cosβ – cosθ sinβ = $\left(\frac{8}{17}\right)\left(\frac{9}{41}\right)–\left(–\frac{15}{17}\right)\left(\frac{40}{41}\right)=\frac{672}{697}$

cos(θ – β) = cosθ cosβ + sinθ sinβ = $\left(–\frac{15}{17}\right)\left(\frac{9}{41}\right)+\left(\frac{8}{17}\right)\left(\frac{40}{41}\right)=\frac{185}{697}$.

Illustration-8:

Show that $\mathbf{cos\theta }\mathbf{+}\mathbf{sin}(270°+\theta )\mathbf{–}\mathbf{sin}(270°–\theta )\mathbf{+}\mathbf{cos}(180°+\theta )\mathbf{=}\mathbf{0}$.

Solution:

L.H.S = $\cos \theta +\sin \left(270°+\theta \right)–\sin \left(270°–\theta \right)+\cos \left(180°+\theta \right)$
            = $\cos \theta –\cos \theta +\cos \theta –\cos \theta$ = 0 = R.H.S

2. MULTIPLE ANGLE FORMULAE

(a) Functions of 2A

(i) sin2A = 2sinA cosA

(ii) cos2A = cos²A  – sin²A = 2 cos²A – 1 = 1  – 2sin²A

(iii) tan2A = $\frac{2\tan A}{1–{\tan }^{2}A}$

(b) Functions of 3A

(i) sin3A = 3sinA – 4sin³A

(ii) cos3A = 4cos³A – 3 cosA

(iii) tan3A = $\frac{3\tan A–{\tan }^{3}A}{1–3{\tan }^{2}A}$

Illustration-9:

Prove that $\frac{\mathbf{tan}\mathbf{(}\mathbf{\pi }\mathbf{/}\mathbf{4}\mathbf{+}\mathbf{A}\mathbf{)}}{\mathbf{tan}\mathbf{(}\mathbf{\pi }\mathbf{/}\mathbf{4}\mathbf{–}\mathbf{A}\mathbf{)}}\mathbf{=}\frac{\mathbf{2}\mathbf{cosA}\mathbf{+}\mathbf{sinA}\mathbf{+}\mathbf{sin}\mathbf{3}\mathbf{A}}{\mathbf{2}\mathbf{cosA}\mathbf{–}\mathbf{sinA}\mathbf{–}\mathbf{sin}\mathbf{3}\mathbf{A}}$

Solution:

L.H.S. = $\frac{{\displaystyle \frac{1+\mathrm{tanA}}{1–\mathrm{tanA}}}}{{\displaystyle \frac{1–\mathrm{tanA}}{1+\mathrm{tanA}}}}=\frac{(1+\mathrm{tanA}{)}^2}{(1–\mathrm{tanA}{)}^2}=\frac{1+{\tan }^2\mathrm{A}+2\mathrm{tanA}}{1+{\tan }^2\mathrm{A}–2\mathrm{tanA}}$

$=\frac{1+\frac{2\tan A}{1+{\tan }^{2}A}}{1–\frac{2\tan A}{1+{\tan }^{2}A}}=\frac{1+\sin 2A}{1–\sin 2A}$

R.H.S.= $\frac{2\cos A+2\sin 2A·\cos A}{2\cos A–2\sin 2A\cos A}=\frac{2\cos A(1+\sin 2A)}{2\cos A(1–\sin 2A)}=\frac{1+\sin 2A}{1–\sin 2A}$

Both sides reduce to the same result. 

3. EXPRESSING PRODUCTS OF TRIGONOMETRIC FUNCTIONS AS SUM OR DIFFERENCE

(i) 2sinA cosB = sin(A + B) + sin(A – B)
(ii) 2cosA sinB = sin(A + B) – sin(A – B)
(iii) 2cosA cosB = cos(A + B) + cos(A – B)
(iv) 2sinA sinB = cos(A – B) – cos(A + B)

Illustration-10:
Show that 8 sin 10° sin 50° sin 70° = 1.
Solution:

L.H.S. = 4 (2sin 50° sin 10°) sin70°

             = 4 {cos(50° – 10°) – cos (50° + 10°)} sin70°, using 2 sinA sinB

             = 2{sin110° + sin30°} -2 sin70° since cos60° = 1/2.

             = cos(A – B) – cos(A + B)

             = 4(cos40° –  cos60°) sin70°

              = 2.(2sin70°. cos40°) – 4cos60°  sin70°= 2sin70° + 2sin30° – 2sin70°

               = 2sin30° = 1. 

4. EXPRESSING SUM OR DIFFERENCE OF TWO SINES OR TWO COSINES AS A PRODUCT

sinC + sinD = $2\sin \frac{\mathrm{C}+\mathrm{D}}{2}.\cos \frac{\mathrm{C}–\mathrm{D}}{2}$

sinC – sinD = $2\cos \frac{\mathrm{C}+\mathrm{D}}{2}.\sin \frac{\mathrm{C}–\mathrm{D}}{2}$

cosC + cosD = $2\cos \frac{\mathrm{C}+\mathrm{D}}{2}.\cos \frac{\mathrm{C}–\mathrm{D}}{2}$

cosD – cosC = $2\sin \frac{\mathrm{C}+\mathrm{D}}{2}.\sin \frac{\mathrm{C}–\mathrm{D}}{2}$

Illustration-11:

Show that $\frac{\mathbf{sin}\mathbf{7}\mathbf{x}\mathbf{–}\mathbf{sin}\mathbf{3}\mathbf{x}\mathbf{–}\mathbf{sin}\mathbf{5}\mathbf{x}\mathbf{+}\mathbf{sinx}}{\mathbf{cos}\mathbf{7}\mathbf{x}\mathbf{+}\mathbf{cos}\mathbf{3}\mathbf{x}\mathbf{–}\mathbf{cos}\mathbf{5}\mathbf{x}\mathbf{–}\mathbf{cosx}}\mathbf{=}\mathbf{tan}\mathbf{2}\mathbf{x}$

Solution:

Numerator = (sin7x + sinx) – (sin5x + sin3x)

                     = 2sin4x  . cos3x – 2sin4x . cosx                {using C.D. formula}

                     = 2sin4x (cos3x – cosx)

Denominator  = (cos 3x – cos5x) – (cosx – cos7x)

                           = 2sin4x sinx – 2sin4x sin3x  = 2sin4x (sinx – sin3x)

∴  the given expression = $\frac{\cos 3x–\cos x}{\sin x–\sin 3x}=\frac{\cos x–\cos 3x}{\sin 3x–\sin x}=\frac{2\sin 2x\sin x}{2\cos 2x\sin x}=\tan 2x$

4. GRAPH OF TRIGONOMETRIC FUNCTIONS

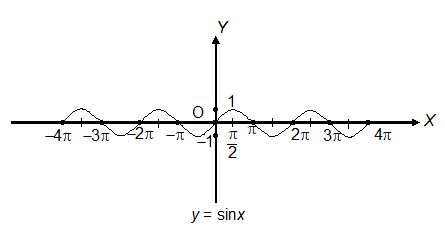
1. Graph of y = sin x

Domain : R

Range : [–1, 1]

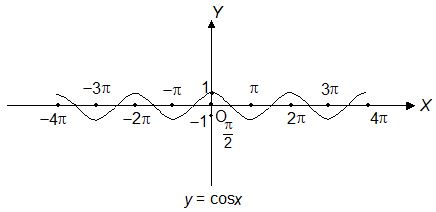
2. Graph of y = cos x

Domain : R

Range : [–1, 1]

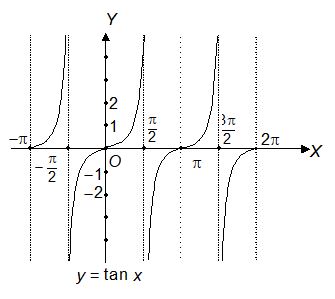
3. Graph of y = tan x

Domain : $\mathrm{R}–\left\{(2\mathrm{n}+1)\frac{\mathrm{\pi }}{2}:\mathrm{n}\in \mathrm{I}\right\}$

Range : R

TRIGONOMETRIC EQUATIONS

5. BASIC TRIGONOMETRIC EQUATIONS

  Consider the following:

cosθ – sinθ = 1        …(i)

|sec(θ –$\mathrm{\pi }$/4)|  = 2  …(ii)

sin²θ + cos²θ = 1    …(iii)

Equation (i) is satisfied if we put θ = 0, 2$\mathrm{\pi }$, 4$\mathrm{\pi }$,…….etc. in it. Equation (ii) is satisfied if we put $\theta =\frac{7\pi }{12},\frac{11\pi }{12},–\frac{\pi }{12}$, etc. in it. But equation (iii) is satisfied for any value of θ. Equations (i) & (ii) are called trigonometric equations while (iii) is a trigonometric identity.

A trigonometric equation has three kinds of solutions:

1. Principal solution : Numerically smallest value of the unknown angle satisfying the given equation.

2. Particular solution : Any value of angle satisfying the given equation.

3. General solution : Collection of all particular solutions.

Illustration-12:

Find the principal solutions of following equations:

(i) $\tan \theta =\frac{1}{\sqrt{3}}$     (ii) $sec\theta =2$     (iii) $\mathrm{cot\theta }=–\sqrt{3}$     (iv) $\cos ec\theta =–2$

Solution:

(i) tanθ is positive in Ist and IIIrd quadrant.

$\Rightarrow \tan \frac{\pi }{6}=\frac{1}{\sqrt{3}}\text{ and }\tan \left(\pi +\frac{\pi }{6}\right)=\frac{1}{\sqrt{3}}$

Also, $\frac{\pi }{6},\left(\pi +\frac{\pi }{6}\right)\in [0,2\pi )$

∴ Principal solutions are $\frac{\mathrm{\pi }}{6},\frac{7\mathrm{\pi }}{6}$.

(ii) secθ is positive in Ist and IVth quadrant.

$\Rightarrow \sec \frac{\pi }{3}=2\text{ and }\sec \left(2\pi –\frac{\pi }{3}\right)=2$

Also, $\frac{\mathrm{\pi }}{3}, 2\mathrm{\pi }–\frac{\mathrm{\pi }}{3}\in [0,2\mathrm{\pi })$

∴  Principal solutions are $\frac{\mathrm{\pi }}{3}, \frac{5\mathrm{\pi }}{3}$.

(iii) cotθ is negative in IInd and IVth quadrant.

Now, $\cot \frac{\pi }{6}=\sqrt{3}\Rightarrow \cot \left(\pi –\frac{\pi }{6}\right)=–\sqrt{3}\text{ and }\cot \left(2\pi –\frac{\pi }{6}\right)=–\sqrt{3}$    

$\Rightarrow \cot \frac{5\pi }{6}=–\sqrt{3}\text{ and }\cot \left(\frac{11\pi }{6}\right)=–\sqrt{3}$

Also,    $\frac{5\pi }{6},\frac{11\pi }{6}\in [0,2\pi )$

∴ Principal solutions are  $\frac{5\pi }{6},\frac{11\pi }{6}$

(iv) cosec θ is negative in IIIrd and IVth quadrant.

Now, $cosec\frac{\mathrm{\pi }}{6}=2\Rightarrow cosec\left(\mathrm{\pi }+\frac{\mathrm{\pi }}{6}\right)=–2\text{ and }cosec\left(2\mathrm{\pi }–\frac{\mathrm{\pi }}{6}\right)=–2$

$\Rightarrow cosec\left(\frac{7\pi }{6}\right)=–2\text{ and }cosec\left(\frac{11\pi }{6}\right)=–2$

Also, $\frac{7\pi }{6},\frac{11\pi }{6}\in [0,2\pi )$

∴ Principal solutions are $\frac{7\pi }{6},\frac{11\pi }{6}$.

1. GENERAL SOLUTION OF SOME SIMPLE TRIGONOMETRIC EQUATIONS

(i) sinθ = 0  $\Rightarrow$ θ = n$\mathrm{\pi }$

(ii) cosθ = 0  $\Rightarrow$ $\theta =(2n+1)\frac{\pi }{2}$

Illustration-13:  

Solve $\mathbf{sin}\mathbf{2}\mathbf{x}\mathbf{+}\mathbf{cosx}\mathbf{=}\mathbf{0}$.

Solution:

$\sin 2\mathrm{x}+\mathrm{cosx}=0$ $\Rightarrow \mathrm{cosx}\{2\mathrm{sinx}+1\}=0$

$\Rightarrow \cos x=0 \text{ or }\sin x=–\frac{1}{2}=\sin \frac{7\pi }{6}$

$\Rightarrow \mathrm{x}=(2\mathrm{n}+1)\frac{\mathrm{\pi }}{2}$  or  $\mathrm{x}=\mathrm{m\pi }+(–1{)}^{\mathrm{m}}\frac{7\mathrm{\pi }}{6},\mathrm{m},\mathrm{n}\in \mathrm{I}$

Illustration-14:

Solve sinx = tanx.

Solution:

$\sin x=\tan x\Rightarrow \sin x–\frac{\sin x}{\cos x}=0\Rightarrow \sin x\left(\frac{\cos x–1}{\cos x}\right)=0$

$\Rightarrow \sin x(\cos x–1)=0 \therefore \sin x=0\text{ or }\cos x=1$

$\Rightarrow \mathrm{sinx}=0\Rightarrow \mathrm{x}=\mathrm{n\pi }, \mathrm{n}\in \mathrm{I}$

$\Rightarrow \cos x=1\Rightarrow \cos x=\cos 0$ $\Rightarrow \mathrm{x}=2\mathrm{m\pi }\pm 0, \mathrm{m}\in \mathrm{I}\text{ or }\mathrm{x}=2\mathrm{m\pi }, \mathrm{m}\in \mathrm{I}$

These solutions are included in the solutions $\mathrm{x}=\mathrm{n\pi }, \mathrm{n}\in \mathrm{I}$ because 2m is also an integer.

∴ The solution is  $x=n\pi , n\in I$

2. GENERAL SOLUTION OF sinθ = sinα

θ = np + (-1)ⁿα, n ∈ l 

Illustration-15:

Solve the equations: (i)  $\mathbf{cosec}\mathbf{ }\mathbf{m\theta }\mathbf{=}\mathbf{2}$   (ii)  $\mathit{s}\mathit{i}\mathit{n}\mathbf{2}\mathit{\theta }\mathbf{=}\frac{\sqrt{\mathbf{5}}\mathbf{–}\mathbf{1}}{\mathbf{4}}$

Solution:

$\text{ (i) }cosec\mathrm{m\theta }=2$

or   $\mathrm{sinm\theta }=\frac{1}{2}=\sin \frac{\mathrm{\pi }}{6}$

$\therefore \mathrm{m\theta }=\mathrm{n\pi }+(–1{)}^{\mathrm{n}}\frac{\mathrm{\pi }}{6}, \mathrm{n}\in \mathrm{I}$   $\Rightarrow \mathrm{\theta }=\frac{\mathrm{n}}{\mathrm{m}}\mathrm{\pi }+(–1{)}^{\mathrm{n}}\frac{\mathrm{\pi }}{6\mathrm{m}}, \mathrm{n}\in \mathrm{I}$

(ii)   $\sin 2\theta =\frac{\sqrt{5}–1}{4}$

$\therefore \sin 2\theta =\sin 18°=\sin \frac{\pi }{10}$

$\therefore 2\theta =n\pi +(–1{)}^n\frac{\pi }{10},n\in I$   $\Rightarrow \theta =\frac{n\pi }{2}+(–1{)}^n\frac{\pi }{20},n\in I$

3. GENERAL SOLUTION OF cosθ = cosα

$\mathrm{\theta }=2\mathrm{n\pi }\pm \mathrm{\alpha }, \mathrm{n}\in \mathrm{I}$

Illustration-16:

Solve the equation $\mathbf{sin}\mathbf{3}\mathbf{x}\mathbf{+}\mathbf{cos}\mathbf{2}\mathbf{x}\mathbf{=}\mathbf{0}$.

Solution:

We have, $\sin 3x+\cos 2x=0$ $\Rightarrow \cos 2x=–\sin 3x\Rightarrow \cos 2x=\cos \left(\frac{\pi }{2}+3x\right)$

$\therefore 2\mathrm{x}=2\mathrm{n\pi }\pm \left(\frac{\mathrm{\pi }}{2}+3\mathrm{x}\right), \mathrm{n}\in \mathrm{I}$

Taking positive sign $\mathrm{x}=–2\mathrm{n\pi }–\frac{\mathrm{\pi }}{2}, \mathrm{n}\in \mathrm{I}$

Taking negative sign  $\mathrm{x}=\frac{2\mathrm{n\pi }}{5}–\frac{\mathrm{\pi }}{10}, \mathrm{n}\in \mathrm{I}$

4. GENERAL SOLUTION OF tanθ = tanα

$\mathrm{\theta }=\mathrm{n\pi }+\mathrm{\alpha },\mathrm{n}\in \mathrm{I},\text{ where }\mathrm{\alpha }\ne (2\mathrm{m}+1)\frac{\mathrm{\pi }}{2},\forall \mathrm{m}\in \mathrm{I}$

Illustration-17:

Solve the equation $\mathbf{tan}\mathbf{2}\mathbf{x}\mathbf{=}\mathbf{–}\mathbf{cot}(x+\frac{\pi }{6})$.

Solution: $\tan 2\mathrm{x}=–\cot \left(\mathrm{x}+\frac{\mathrm{\pi }}{6}\right)\Rightarrow \tan 2\mathrm{x}=\tan \left(\frac{\mathrm{\pi }}{2}+\mathrm{x}+\frac{\mathrm{\pi }}{6}\right)$$\Rightarrow \tan 2x=\tan \left(\frac{2\pi }{3}+x\right)$

$\therefore 2\mathrm{x}=\mathrm{n\pi }+\left(\frac{2\mathrm{\pi }}{3}+\mathrm{x}\right), \mathrm{n}\in \mathrm{I}\Rightarrow \mathrm{x}=\mathrm{n\pi }+\frac{2\mathrm{\pi }}{3},\mathrm{n}\in \mathrm{I}$