1. FUNDAMENTAL PRINCIPLE OF COUNTING AND FACTORIAL NOTATION
1. MULTIPLICATION PRINCIPLE
If one experiment has n possible outcomes and another experiment has m possible outcomes, then there are m ⨯ n possible outcomes when both of these experiments are performed.
2. ADDITION PRINCIPLE
If one experiment has n possible outcomes and another has m possible outcomes, then there are (m + n) possible outcomes when exactly one of these experiments is performed. In other words, if a job can be done by n different methods and for the first method there are a1 ways, for the second method there are a2 ways and so on . . . for the nth method, an ways, then the number of ways to get the job done is (a1 + a2 + … + an).
3. THE BIJECTION PRINCIPLE
Let A = { a1 , a2 , ….. an } and B = {b1 , b2 , … , bm }.
If f : A → B is an injective function then n m.
If f : A → B is a surjective function then m n.
If f : A → B is injective and surjective then f is known to be a bijective function. For a bijective function, n = m.
Total number of possible functions (f : A → B) is mn and (f : B → A) is nm
Illustration-1
A college offers 7 courses in the morning and 5 in the evening. Find the possible number of choices with the student if he wants to study one course in the morning and one in the evening.
Solution
The student has seven choices from the morning courses out of which he can select one course in 7 ways.
For the evening course, he has 5 choices out of which he can select one in 5 ways.
Hence the total number of ways in which he can make the choice of one course in the morning and one in the evening = 7 ⨯ 5 = 35.
Illustration-2
A person wants to go from station A to station C via station B. There are three routes from A to B and four routes from B to C. In how many ways can he travel from A to C?
Solution
A → B in 3 ways
B → C in 4 ways
⇒ A → C in 3 ⨯ 4 = 12 ways
Remark:
The rule of product is applicable only when the number of ways of doing each part is independent of each other i.e. corresponding to any method of doing the first part, the other part can be done by any method.
Illustration-3
How many (i) 5-digit (ii) 3-digit numbers can be formed by using 1, 2, 3, 4, 5 without repetition of digits.
Solution
(i) Making a 5-digit number is equivalent to filling 5 places.

The first place can be filled in 5 ways using anyone of the given digits.
The second place can be filled in 4 ways using any of the remaining 4 digits.
Similarly, we can fill the 3rd, 4th and 5th place.
No. of ways of filling all the five places = 5 ⨯ 4 ⨯ 3 ⨯ 2 ⨯ 1 = 120
⇒ 120 5-digit numbers can be formed.
(ii) Making a 3-digit number is equivalent to filling 3 places.

Number of ways of filling all the three places = 5 ⨯ 4 ⨯ 3 = 60
Hence the total possible 3-digit numbers = 60.
Illustration-4
A Hall has 3 gates. In how many ways can a man enter the hall through one gate and come out through a different gate?
Solution
Suppose the gates are A, B and C. Now there are 3 ways (A, B or C) of entering into the hall. After entering into the hall, the man come out through a different gate in 2 ways. Hence, by the multiplication principle, total number of ways is
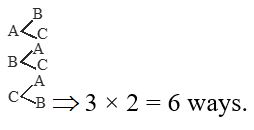
Illustration-5
A college offers 7 courses in the morning and 5 in the evening. Find the number of ways a student can select exactly one course, either in the morning or in the evening.
Solution
The student has seven choices from the morning courses out of which he can select one course in 7 ways.
For the evening course, he has 5 choices out of which he can select one course in 5 ways.
Hence he has total number of 7 + 5 = 12 choices.
Illustration-6
Find the number of two digit numbers (having different digits) which are divisible by 5.
Solution
Any number of required type either ends in 5 or in 0. Number of two digit numbers (with different digits) ends in 5 is 8 and that of ending in 0 is 9.
Hence, by addition principle the required number of numbers is 8 + 9 = 17.
4. FACTORIAL NOTATION
Let n be a positive integer. Then, the continued product of first n natural numbers is called factorial n, to be denoted by n !or n . Also, we define 0 ! = 1.
when n is negative or a fraction, n ! is not defined.
Thus, n ! = n (n – 1) (n – 2) ……3.2.1.
Deduction: n ! = n(n – 1) (n – 2) (n – 3) ……3.2.1
Thus, and ; Also,
Illustration-7
If . Find x.
Solution
We have,
.
Illustration-8
If are in the ratio 2 : 1, find the value of n.
Solution
We have,
⇒ 12 = 2(n – 2) (n – 3) ⇒ 6 = n2 – 5n + 6 ⇒ n2 – 5n = 0
⇒ n(n – 5) = 0 ⇒ n = 0 or 5.
when, n = 0, (n – 2)! and (n – 4)! are not defined, Rejecting n = 0, we have n = 5.
2. NUMBER OF PERMUTATIONS WITHOUT REPETITION
1. DEFINITIONS
Permutation
An arrangement that can be formed by taking some or all of a finite set of things (or objects) is called a Permutation.
Order of the things is very important in case of permutation.
Linear Permutation
A permutation is said to be a Linear Permutation if the objects are arranged in a line. A linear permutation is simply called as a permutation.
2. NUMBER OF PERMUTATIONS WITHOUT REPETITION
(1) Arranging n objects, taken r at a time equivalent to filling r places from n things.
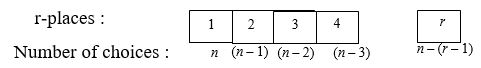
The number of ways of arranging = The number of ways of filling r places.
(2) The number of arrangements of n different objects taken all at a time =
(i)
(ii)
Illustration-9
If = 1320 then find n.
Solution
We know that = n(n – 1) (n – 2)
= 1320 = 132 ⨯ 10
= 12 ⨯ 11 ⨯ 10
comparing on both sides, we get n = 12
Illustration-10
If (n+1)P5 : nP6= 2 : 7, find n.
Solution
7n + 7 = 2 [ n2 – 9n + 20]
2n2– 18n + 40
2n2 – 25n + 33 = 0
2n2 – 22n – 3n + 33 = 0
2n(n – 11) – 3(n – 11) = 0
(2n – 3) (n – 11) = 0
n = 3/2 or 11
since n is a positive integer, n = 3/2 is impossible.
n = 11 only
Illustration-11
If = 9 : 7 then find r.
Solution
By data,
Illustration-12
How many different signals can be given using any number of flags from 5 flags of different colours?
Solution
The signals can be made by using one or more flags at a time.
The total number of signals when r flags are used at a time from 5 flags is equal to the number of arrangements of 5, taking r at a time i.e., 5Pr.
Since r can take the values 1, 2, 3, 4, 5, hence, by the fundamental principle of addition, the total number of signals is
5P1 + 5P2 + 5P3 + 5P4 + 5P5 = 5 + (5 × 4) + (5 × 4 × 3) + (5 × 4 × 3 × 2) + (5 × 4 × 3 × 2 × 1) = 5 + 20 + 60 + 120 + 120 = 325
Illustration-13
If there are 30 Railway stations on a Railway line, how many number of single second class tickets must be printed so as to enable a passenger to travel from one station to another.
Solution
Let the stations be . We know that a ticket will be printed to travel from one station to another. So, r = 2. Total number of tickets to be printed by Railway Department will include return tickets also.
We have to select 2 of these 30 and then we have to arrange them in order.
Total number of tickets to be printed
= number of permutations of 30 different things taken 2 at a time when repetitions are not allowed = 30P2 = 870
Illustration-14
Find the number of 5 letter words that can be formed using the letters of the word CONSIDER. How many of them begin with “C” , how many of them end with “R” , and how many of them begin with “C” and end with “R”
Solution
The number of letters in the word CONSIDER are 8.
The number of 5 letter words formed is = 8⨯7⨯6⨯5⨯4 = 6720. C- – – .
If the words begin with C, then there are four gaps after it and they can be filled with the remaining 7 letters in = 7⨯6⨯5⨯4 = 840 ways.
– – – R .
If the words end with R, then also there are four gaps before R and they can be filled with the remaining
7 letters in = 7⨯6⨯5⨯4 = 840 ways.
If the words begin with C and end with R then, there are three gaps between them and they can be filled with the remaining 6 letters in = 6⨯5⨯4 = 120 ways.
Illustration-15
How many 4 letter words can be formed using the letters of the word ‘ARTICLE’. Find the number of words if i) that begin with an vowel ii) containing A
Solution
Word ARTICLE contains 7 letters
i) Since each 4 – letter word must begin with a vowel, fill up the first blank place with any one of the 3 vowels i.e., A, I, E in 3 ways only.
The remaining 3 places can be filled with any one of the remaining six letters (2 vowels and 4 consonants) in ways.
By fundamental principle, required number of 4 – letter words = = 3⨯6⨯5⨯4 = 360
ii) Here n = 7 and r = 4 The number of 4 letter words containing A is 4 × = 4 × 6 × 5 × 4 = 480 using
Illustration-16
Find the number of ways to arrange 5 boys and 5 girls in a row such that
i) all the girls must sit together
ii) no two girls sit together
iii) all the boys sit together and all girls sit together
iv) no two of the same sex sit together or boys and girls sit alternately
Solution
i) Since all the girls must sit together, treat all the 5 girls as one unit. Now there are 5 boys + 1 unit of girls i.e., 6 different objects. They can be arranged along a row by taking all of them at a time in ways. The 5 girls can be rearranged among themselves in ways.
By fundamental principle, number of arrangements such that all girls sit together = Note :
This method of treating all the objects to be together or one unit is known as STRING METHOD
ii) First arrange the 5 boys in a row. It can be done in Then we get 6 gaps denoted by ‘X’ as shown below.
X B X B X B X B X B X
Since, no 2 girls come together, the 5 girls can be arranged by selecting 5 gaps from these six gaps in ways
By fundamental principle,
The number of arrangements such that no two girls come together =
Note :
This method of creating gaps is known as GAPS METHOD
iii) Since boys and girls must sit together,
Consider all the boys as a unit and all the girls as another unit. These two units can be arranged between themselves in ways i.e., ways. Now the 5 boys can be arranged among themselves in ways and the 5 girls can be arranged among themselves in ways.
By fundamental principle, the required number of arrangements =
iv) The row may begin either with a boy or a girl i.e two different ways. If the row begins with a boy, all the odd places {1, 3, 5, 7, 9} will be occupied by boys and the even places {2,4,6,8,10}by girls. If the row begins with a girl, odd places will be occupied by girls and even places by boys. Five boys in 5 odd places can be arranged in 5! ways and 5 girls in five even places can be arranged in 5! ways. Hence the number of arrangements that begins with a boy is ( 5! )2. Similarly the number of arrangements that begins with a girl is (5!)2. Thus number of arrangements in which boys and girls sit alternately is 2(5!)2
Illustration-17
In how many ways 6 boys and 5 girls can be arranged along a row so that
i) all the girls come together
ii) all the girls do not come together
iii) no two girls come together
iv) no two of the same sex come together
Solution
i) Treat 5 girls as 1 unit. So we have 6 boys + one unit of girls = 7 different units. They can be arranged in a line in 7! ways and the 5 girls can be arranged among themselves in 5! ways.
Required number of arrangements = 7! × 5!
ii) The number of ways in which all 5 girls do not come together = total no.of unrestricted permutations – no.of permutations in which all girls come together is (11!) – 7! × 5!
iii) Now we use gaps method. First arrange 6 boys in a line in 6! ways – B – B – B – B – B – B –. Now there are 7gaps for 5 girls so that they can be arranged in 7p5 ways.
∴ Required no.of arrangements = 6! × 7p5.
iv) First arrange 5 girls in a line in 5! ways – G – G – G – G – G –. Now there are 6 gaps for 6 boys so that they can be arranged in a line in 6! ways.
Required no.of arrangements =5 ! × 6!
Illustration-18
Find the number of ways of arranging the letters of the word ‘FATHER’ so that the relative positions of vowels and consonants are not disturbed.
Solution
Since the relative positions of vowels and consonants are not disturbed, we have to arrange the 4 consonants F, T, H, R among themselves and the 2 vowels A, E between themselves. This can be done in 4p4 2p2 i.e., 24⨯2 = 48 ways
Illustration-19
Find the number of ways of arranging the letters of the word ‘KRISHNA’ so that
i) all the vowels come together
ii) no two vowels come together
iii) relative positions of vowels and consonants are not disturbed.
Solution
There are 2 vowels and 5 consonants in the word KRISHNA
i) Treat the two vowels as one unit. So we have 5 consonants + 1 unit of vowels = 6 different units. They can be arranged in a line in 6! ways and 2 vowels can be arranged between themselves in 2! ways.
Hence the required number of arrangements 6 ! 2! = 720 × 2 = 1440 .
ii) Now we use gaps method. First arrange 5 consonants in a line in 5!
ways – C–C–C–C–C–. Now there are 6 gaps for 2 vowels and they can be arranged in 6p2 ways.
Therefore, required number of arrangements is 5! 6p2
iii) If the relative positions of vowels and consonants remain unchanged the two vowels can be arranged between themselves in 2! ways and 5 consonents can be arranged among themselves in 5! ways. Hence required number of arrangements is 2! × 5! = 2 × 120 = 240.
Illustration-20
Find the number of ways of arranging 10 persons A1, A2, ……….A10 in a row if no two of A1, A2 and A3 come together.
Solution
First arrange A4, A5, ……………, A10 in a line in 7! ways.
– A4 – A5 – A6 – A7 – A8 – A9 – A10 . Then there are 8 gaps for three objects A1, A2 and A3 so that they can be arranged in 8P3 ways.
Required no.of arrangements = 7! × 8P3
Illustration-21
Find the number of ways of arranging 15 students A1, A2, …..,A15 in a row such that A1, A2 and A3 sit together in a specified order
Solution
Consider A1, A2 and A3 as one unit.
Now there are 12 persons + 1 unit of A1, A2 and A3
i.e., 13 things to be arranged in a row by taking all at a time. It can be done in 13P13 i.e., ways.
Here we need not arrange the three persons A1, A2 and A3 among themselves because they must be seated together in a specified order. Required number of ways =
Illustration-22
How many numbers between 6000 and 10000 can be formed using the digits 2, 3, 4, 6, 7, 9 without repetition.
Solution
We require 4 digit numbers begining with 6,7 and 9 when repetitions are not allowed.
6 – – – 5P3
Number of 4 digit numbers begining with 6 = 54 3 = 60
Similarly number of 4 digit numbers begining with 7 and 9 is also 60 ways each.
Required numbers of 4 digited numbers = 360 = 180
3. NUMBER OF PERMUTATIONS WITH REPETITION
(1) The number of permutations (arrangements) of n different objects, taken r at a time, when each object may occur once, twice, thrice,……..upto r times in any arrangement = The number of ways of filling r places where each place can be filled by any one of n objects.

The number of permutations = The number of ways of filling r places = (n)2.
(2) The number of arrangements that can be formed using n objects out of which p are identical (and of one kind) q are identical (and of another kind), r are identical (and of another kind) and the rest are distinct is .
CONDITIONAL PERMUTATIONS
(1) Number of permutations of n dissimilar things taken r at a time when p particular things always occur = .
(2) Number of permutations of n dissimilar things taken r at a time when p particular things never occur = .
(3) The total number of permutations of n different things taken not more than r at a time, when each thing may be repeated any number of times, is .
(4) Number of permutations of n different things, taken all at a time, when m specified things always come together is .
(5) Number of permutations of n different things, taken all at a time, when m specified things never come together is .
(6) Let there be n objects, of which m objects are alike of one kind, and the remaining objects are alike of another kind. Then, the total number of mutually distinguishable permutations that can be formed from these objects is .
The above theorem can be extended further i.e., if there are n objects, of which p1 are alike of one kind; p2 are alike of another kind; p3 are alike of 3rd kind;……;p, are alike of rth kind such that ; then the number of permutations of these n objects is .
Illustration-23
Find the number of three digited numbers that can be formed using 7,6,8 and 9 when each digit may be used any number of times ?
Solution
Since repetitions are allowed the first, second and third places can be filled with any one of the given 4 digits in 4 ways. Hence required number of 3 digit numbers formed = 43 = 64.
Illustration-24
Find the number of six digited numbers that can be formed using 1, 7, 8.
Solution
Clearly, here repetitions are to be allowed
Each of the six places can be filled with 3 ways . Required no. of ways are 36.
Illustration-25
Find the number of 5 letter words that can be formed using the letters of the word ‘MIXTURE’ which begin with an vowel when repetitions are allowed.
Solution
First place can be filled in 3 ways with an vowel from I, U, E
The remaining 4 places each can be filled in 7 ways since repetitions are allowed.
Required number of arrangements = 3 ⨯ 74
Illustration-26
How many 4 digited numbers can be formed using 0, 1, 2, 3, 4 when repetition is allowed.
Solution
Consider 4 blank places. __, __, __, __
The first place i.e., 1000th place can be filled in 4 ways (Since zero can not be used in first place)
Since repetition is allowed, the remaining 3 places each can be filled in 5 ways.
The number of 4-digited numbers = 4 ⨯ 53.
Illustration-27
Find the number of 4 letter words that can be formed using the letters of the word ‘ARTICLE’ in which atleast one letter is repeated.
Solution
We know that the number of 4 letter words that can be formed using 7 letters = 74 (if repetition is allowed) These 74 words can be divided into two exclusive categories.
i) The 4 letter words without repetition
ii) The 4 letter words with atleast one letter repeated.
The 4 letter words without repetition will be 7P4.
The 4 letter words with atleast one letter repeated = Total number of 4 letter words formed – no of 4 letter words without repetition = 74 – 7P4
Illustration-28
10 different letters of an alphabet are given. Find the number of 5 letter words that can be formed using 10 letters which have
i) no letter repeated
ii) atleast one letter repeated
Solution
i) The number of 5 letter words formed out of 10 different letters if no letter is repeated = 10P5 = 30,240.
ii) Number of 5 letter words formed having atleast one letter is repeated = 105 – 10P5 = 69,760.
Illustration-29
Find the number of 3 digit numbers that can be formed using using the digits 1,2, 3, 4, 5, 6 with an odd digit in the middle place when repetition is allowed.
Solution
The middle place can be occupied in 3 ways using anyone of 1 or 3 or 5.
The first and third place can be filled in 6 ways each. Required number of 3 digit number = 6⨯3⨯6 = 108
Illustration-30
If a set A has 6 elements, find the number of elements in the power set of A.
Solution
Number of elements in the power set of A is P(A) = 26 = 64
Illustration-31
There are six periods in each working day of a school. Find the number of ways in which 5 subjects can be arranged if each subject is allotted at least one period and no period remains vacant.
Solution
Let the five subjects are a, b, c, d, e.
Since numbers of subjects are less than the number of periods, any one of the five subjects will occur twice.
If subject ‘a’ occur twice (a, a, b, c, d, e), then six subjects can be arranged in ways.
Similar number of ways when subject b, c, d and e occur twice.
Hence total number of ways are
Illustration-32
Find the number of permutation of all the letters of the word “MATHEMATICS” which starts with consonants only.
Solution
(M M), (A A), (T T), H, E, I, C, S
Words starting with M or A or T are
Words starting with H, E, I, C, S are
Hence number of words, are
Illustration-33
How many 4-digit numbers can be formed by using the digits 1, 2, 3, 4, 5, 6, 7 if at least one digit is repeated?
Solution
The numbers that can be formed when repetition of digits is allowed are 74.
The numbers that can be formed when all the digits are distinct when repetition is not allowed are 7P4.
Therefore, the numbers that can be formed when at least one digit is repeated are 74 – 7P4.
Illustration-34
How many 3 digit numbers can be formed using the digits 0, 1,2,3,4,5 so that
(a) digits may not be repeated
(b) digits may be repeated
Solution
(a) Let the 3-digit number be XYZ
Position (X) can be filled by 1,2,3,4,5 but not 0. So it can be filled in 5 ways.
Position (Y) can be filled in 5 ways again. (Since 0 can be placed in this postion).
Position (Z) can be filled in 4 ways.
Hence, by the fundamental principle of counting, total number of ways is 5 x 5 x 4 = 100 ways.
(b) Let the 3 digit number be XYZ
Position (X) can be filled in 5 ways
Position (Y) can be filled in 6ways.
Position (Z) can be filled in 6 ways.
Hence by the fundamental principle of counting, total number of ways is 5 x 6 x 6 = 180.
Illustration-35
Find the number of ways of arranging (all) the letters of the following words.
i) SWIMMING ii) MISSAMMA
iii) BROOKE BOND iv) DECEMBER
Solution
i) Number of letters in SWIMMING = 8
Number of Is = 2, Number of Ms = 2
Hence number of arragnements =
ii) Number of letters in MISSAMMA = 8
Number of Ms = 3, Number of As = 2
Number of Ss= 2
Hence number of arragnements=
iii) Number of letters in BROOKE BOND = 10
Number of Os = 3, Number of Bs = 2
Hence number of arragnements =
iv) Number of letters in DECEMBER is 8
Number of Es = 3
Hence number of arrangements =
Illustration-36
Find the number of different words that can be formed using 4 A’s, 3 B’s, 2 C’s and one D.
Solution
Total number of letters = 4 + 3 + 2 + 1 = 10
Number of A’s= 4, Number of B’s = 3
Number of C’s = 2, Number of D’s = 1
Required number of arrangements
Illustration-37
Find the number of ways of arranging the letters of the word a4b3c5 in expanded form.
Solution
a4b3c5 contains 12 letters of which 4 are alike of one kind, 3 are alike of second kind and 5 are alike of 3rd kind.
So, they can be arranged in ways
Illustration-38
There are 5 copies each of 4 different books. Find the number of ways of arranging these books in a shelf.
Solution
Total number of books = 20
Number of arrangements =
Illustration-39
A book store has m copies each of n different books. Find the number of ways of arranging these books in a shelf.
Solution
In the book store there are ‘mn’ books and n sets where each set contains malike books.
They can be arranged in = ways
Illustration-40
How many numbers can be formed using all the digits 1, 2, 3, 4, 3, 2, 1 such that even digits always occupy even places.
Solution
Let us consider 7 places
![]()
Among these 7 places there are 3 even places in which we have to arrange the even digits 2, 4 and 2. They can be arranged in ways i.e., 3 ways.
The 4 odd digits 1, 3, 3, 1 can be arranged in the remaining 4 places in ways i.e. 6 ways.
By product rule, required number of arrangements = 3⨯6 = 18
Illustration-41
Find the number of 5 digited numbers that can be formed using the digits 2, 2, 3, 3, 4. How many of them are greater than 30000.
Solution
Number of 5 digit numbers formed is
Number of 5 digit numbers greater than 30,000 may begin with 3 or 4
No. of 5 digit numbers beging with 3 _ _ _ _ in = 12
No. of 5 digit numbers beging with 4 _ _ _ _ in = 6
Required number of numbers = 12 + 6 = 18
Illustration-42
In how many ways, can the letters of the word CHEESE be arranged so that no two E’s come together?
Solution
There are 3E’s and 3 non E’s (C, H, S). First arrange C, H, S in a line in 3! ways – C – H – S –
Then there are 4 gaps for 3 E’s Hence they can be arranged in ways
Hence required number of arrangements is
Illustration-43
Find the number of ways of arranging the letters of the word ‘SHIPPING’ such that
i) 2 P’s will come together
ii) 2 I’s do not come together
Solution
i) The word ‘SHIPPING’ contains 2 P’s, 2 I’s and S, H, N, G one each.
Since P’s must come together, consider 2 P’s as a unit.
Now it will have 7 letters of which there are 2I’s.
They can be arranged in ways.
We need not rearrange the 2P’s among them selves because they are alike.
∴ Required number of arrangements =
ii) Since the 2I’s do not come together, arrange the remaining letters at first.
In the remaining six letters there are 2 P’s, it can be done in ways.
Now we get 7 gaps in which 2I’s can be arranged.
It can be done
Total number of arrangements = = 180⨯42 = 7560
Illustration-44
Find the number of ways of arranging the letters of the word SINGING so that
i) they begin and end with I
ii) the two G’s come together
Solution
i) There are seven letters in the word SINGING. If the words begin and end wtih I
I – – – – I . The five gaps between them and the remaing four letters can be arranged in
ii) Treat 2G’s as one unit. So we have 5 others + 1 unit of G’s = 6 objects out of which there are two 2I’s and 2 N’s so that they can be arranged in
= 180 ways.
(The 2 G’s can be arranged between themselves in = 1way only)
Illustration-45
Find the number of ways of arranging the letters of the word ARRANGE so that
i) the two R’s come together
ii) A occurs at the beginning and at the end
Solution
i) Treat the 2 R’s as one unit so we have 5 others + 1 unit of R’s = 6 letters out of which there are A’s so that they can be arranged in
ii) If A occurs at the beginning and at the end A – – – – – A then there are 5 gaps between them and the remaining 5 letters can be arranged in = 60 ways
Illustration-46
If the letters of the word ‘AJANTA’ are permutated in all possible ways and the words thus formed are arranged in dictionary order. Find the rank of ‘JANATA’.
Solution
The order of letters is A, A, A, J, N, T
The number of words which begin with A = = 60
The number of words which begin with JAA = = 6
The number of words which begin with JANAA = 1
The next word is JANATA
Rank = 60 + 6 + 1 + 1 = 68
4. CIRCULAR PERMUTATIONS
In circular permutations, what really matters is the position of an object relative to the others. Thus, in circular permutations, we fix the position of the one of the objects and then arrange the other objects in all possible ways.
There are two types of circular permutations :
(i) The circular permutations in which clockwise and the anticlockwise arrangements give rise to different permutations, e.g. Seating arrangements of persons round a table.
(ii) The circular permutations in which clockwise and the anticlockwise arrangements give rise to same permutations, e.g. arranging some beads to form a necklace.
1. DIFFERENCE BETWEEN CLOCKWISE AND ANTI-CLOCKWISE ARRANGEMENT
If anti-clockwise and clockwise order of arrangement are not distinct e.g., arrangement of beads in a necklace, arrangement of flowers in garland etc. then the number of circular permutations of n distinct items is .
(i) Number of circular permutations of n different things, taken r at a time, when clockwise and anticlockwise orders are taken as different is .
(ii) Number of circular permutations of n different things, taken r at a time, when clockwise and anticlockwise orders are not different is .
2. THEOREMS ON CIRCULAR PERMUTATIONS
Theorem 1
The number of circular permutations of n different objects is
Theorem 2
The number of ways in which n persons can be seated round a table is
Theorem 3
The number of ways in which n different beads can be arranged to form a necklace, is .
Theorem 4
The number of circular permutations of ‘n’ different things taken ‘r’ at a time
Case 1: If clockwise and anticlockwise orders are taken as different, then the required number of circular permutation =
Case 2: If clockwise and anticlockwise orders are taken as same , then the required number of circular permutation
Note: When the positions are numbered, circular arrangement is treated as a linear arrangement. In a linear arrangement, it does not make difference whether the positions are numbered or not.
Illustration-47
Find the number of ways to arrange 8 persons around a circle by taking 4 at a time.
Solution
We know that the number of circular permutations of n distinct things taken r at a time =
∴ The required number of arrangements is
Illustration-48
Find the number of ways of arranging 5 boys and 5 girls around a circle ?
Solution
Total number of persons = n = 10 (boys and girls put together)
Therefore, number of circular permutations = (n – 1)! = 9!
Illustration-49
Find the number of ways of preparing a chain with 6 different coloured beads.
Solution
The number of ways of preparing a chain with 6
different coloured beads =
Illustration-50
A round table conference is attended by 3 Indians , 3 Chinese, 3 Canadians and 2 Americans. Find the number of ways of arranging them at the round table so that the delegates belonging to same country sit together.
Solution
Since the delegates belonging to the same country to be together, treat 3 Indians as one unit, 3 Chinese as 2nd unit, 3 Canadians as third unit and 2 Americans as fourth unit and the four units can be arranged among themselves at a round table in 3! ways. Now 3 Indians can be arranged among themselves in 3! ways, 3 Chinese can be arranged among themselves in 3! ways, 3 Canadians can be arranged among themselves in 3! ways and 2 Americans can be arranged among themselves in 2! ways.
Required number of arrangements = 3! × 3! × 3 ! × 3! × 2! = 6 × 6 × 6 × 6 × 2 = 2592
Illustration-51
Find the number of ways of arranging 6 red roses and 3 yellow roses of different sizes into a garland. In how many of them, all the yellow roses come together.
Solution
The nine different roses can be arranged along a circle in ways.
Since, it is hanging type circular arrangement, we consider only one direction.
Therefore the number of garlands =
Since all the 3 different yellow roses come together, treat them as a unit.
The number of roses are 6 + 1 unit = 7 units. They can be arranged in ways.
The yellow roses can be arranged among themselves in ways. The number of garlands =
Illustration-52
Find the number of ways of arranging 6 boys and 6 girls around a circle so that
(i) all the girls come together (ii) no two girls come together.
Solution
i) Since all the girls come together, consider 6 girls as a unit. Now we can arrange 6 boys + 1 unit of girls = 7 persons around a circle in The girls can be arranged among themselves in ways. Therefore the required number of arrangements =
ii) Since no two girls come together, first arrange 6 boys along a circle in ways
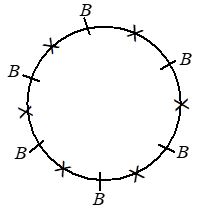
We get exactly 6 gaps denoted by ‘X’ as shown above in which the girls can be arranged in ways.
Therefore, the required number of arrangements =
Illustration-53
Find the number of ways of arranging 8 men and 4 women around a circular table. In how many of them
i) all the women come together.
ii) no two women come together.
Solution
Total 12 persons can be arranged around a circular table in (11)! ways
i) Treat all the women as one unit. So, we have 8 + one unit of women = 9 different persons and they can be arranged around a circle in 8! ways and 4 women can be arranged among themselves in 4! ways.
Required number of arrangement = 8! ⨯ 4!
ii) First arrange 8 men around circle in 7! ways. Then there are 8 gaps for 4 women so that they can be arranged in 8P4 Hence, required number of arrangements = 7!⨯8P4
Illustration-54
Find the number of ways of arranging 5 men and 3 women around a round table so that
i) two particular women sit together.
ii) no two women sit together.
iii) all the three women sit together.
Solution
i) Treat the two particular women W1and W2as one unit. So we have 5 men +1 remaining woman + one unit of particular women = 7 objects and they can be arranged around table in 6! ways and the two particular women can be arranged between themselves in 2! ways. Hence, required number of arrangements is 6! 2! = 720⨯2 = 1440
ii) First arrange 5 men arround table in 4! ways. Now there are 5 gaps for 3 women so that they can be arranged in 5P3 Hence, required number of arrangements = 4!⨯5P3.
iii) Treat all the 3 women as one unit. So we have 5 men + 1 unit of women = 6 persons and they can be arranged around a table in 5! ways and the 3 women can be arranged among them selves in 3 ! ways.
Hence, required number of arrangements = 5!⨯3! = 120⨯6 = 720
Illustration-55
A family consists of father, mother, 2 daughters and 2 sons. In how many different ways, can they sit at a round table if 2 daughters wish to sit on either side of the father.
Solution
Let the father, mother, two daughters and two sons be denoted by F, M, D1, D2, S1 and S2 respectively.
Treat as one unit. So that we have 3 others +1 unit = 4 different units and they can be arranged around a circle in 3! ways and the two daughters D1 and D2 can be interchanged in 2! ways. So by product rule, the required number of arrangements = .
Illustration-56
Garlands are formed using 4 red roses and 4 yellow roses of different sizes. In how many of them
i) all 4 red roses come together.
ii) red roses and yellow roses come alternately.
Solution
i) Treat the 4 red roses as one dunit. So, we have 4 yellow roses + one unit of red roses = 5 objects and they can be arranged in the form of a garland in 4! ways and the 4 red roses can be arranged among themselves in 4! ways. Hence, required number of arrangements
= ⨯4!⨯4! = ⨯24⨯24 = 288
ii) First arrange 4 red roses in the form of a garland in ⨯3! ways. Then there are 4 gaps for 4 yellow roses and they can be arranged in 4!ways.Henec required number of arrangements
=
Illustration-57
Let 15 toys be distributed among 3 children subject to the condition that any child can take any number of toys. Find the required number of ways to do this if
(i) toys are distinct. (ii) toys are identical.
Solution
(i) Toys are distinct Here we have 3 children and we want the 15 toys to be distributed to the 3 children with repetition. In other words, it is same as selecting and arranging children 15 times out of 3 children with the condition that any child can be selected any no. of time, which can be done in 315 ways (n = 3, r = 15).
(ii) Toys are identical Here we only have to select children 15 times out of 3 children with the condition that any child can be selected any number of times which can be done in 3 + 15 – 1C15 = 17C2 ways (n = 3, r = 5).
5. NUMBER OF COMBINATIONS WITHOUT REPETITION
1. COMBINATION
Each of the different groups or selections which can be formed by taking some or all of a number of objects, irrespective of their arrangements, is called a combination.
Suppose we want to select two out of three persons A, B and C.
We may choose AB or BC or AC.
Clearly, AB and BA represent the same selection or group but they give rise to different arrangements. Clearly, in a group or selection, the order in which the objects are arranged is immaterial.
Notation: The number of all combinations of n things, taken r at a time is denoted by C(n, r) or .
Difference between a permutation and combination
(i) In a combination only selection is made whereas in a permutation not only a selection is made but also an arrangement in a definite order is considered.
(ii) In a combination, the ordering of the selected objects is immaterial whereas in a permutation, the ordering is essential. For example A, B and B, Aare same as combination but different as permutations.
(iii) Practically to find the permutation of n different items, taken r at a time, we first select r items from n items and then arrange them. So usually the number of permutations exceeds the number of combinations.
(iv) Each combination corresponds to many permutations. For example, the six permutations ABC, ACB, BCA, BAC, CBA and CAB correspond to the same combination ABC.
Note : Generally we use the word ‘arrangements’ for permutations and word “selection” for combinations.
2. NUMBER OF COMBINATIONS WITHOUT REPETITION
The number of combinations (selections or groups) that can be formed from n different objects taken
at a time is
Let the total number of selections (or groups) = x. Each group contains r objects, which can be arranged in r !ways. Hence the number of arrangements of r objects = . But the number of arrangements = nPr. .
Important Tips
- nCr is a natural number.
- If n is even then the greatest value of is nCr is nCn/2.
- If n is odd then the greatest value of nCr is .
Note : Number of combinations of n dissimilar things taken all at a time , .
Illustration-58
If 12Cr = 495, find the possible values of ‘r’.
Solution
12Cr = 495 = 5 × 99 = 11 × 9 × 5
=
=
Hence possible values of r = 4 or 8.
Illustration-59
i) If , find s.
ii) If then find t.
Solution
i) If then,
eithers + 1 = 2s – 5 or s + 1 + 2s – 5 = 12
⇒ s = 6 or 3s = 16
∴ s = 6 only Since s = , a non-integer is not possible
ii) Since
we have 2t + 1 = 3t – 5 (or) 2t + 1 + 3t – 5 = 17
⇒ t = 6 or 5t = 21 ⇒ t = 6 or t = 21/5
But if t=21/5 then 2t+1 = which is not an integer.
∴
∴ t = 6
Illustration-60
In a class there are 50 students. If each student plays a game of chess with each other student, then find the total number of games played by them.
Solution
For every selection of 2 students from 50, a game will be conducted.
By interchanging these two selected students we are not going to conduct another game.
Therefore, the number of games = = = 1225
Illustration-61
Find the number of ways of selecting 4 boys and 3 girls from a group of 8 boys and 5 girls.
Solution
4 boys out of 8 and 3 girls out of 5 can be selected in ways = 700 ways.
Illustration-62
Find the number of ways of forming a committee of 5 members from 6 gents and 3 ladies.
Solution
Since there is no restriction to form the committee, we have to select 5 members from 9 members. This can be done in 9C5 ways i.e., in 9C4 ways.
Illustration-63
If n persons are sitting in a row, find the number of ways of selecting 2 persons so that they are not adjacent to each other.
Solution
Let the n persons be arranged in the following order. a1, a2, a3, …..,an-1, an
The number of ways to select 2 persons with out any restriction = nC2
Among these nC2 selections we do not accept the following (n – 1)selections which are (a1, a2), (a2, a3), ….., (an-1, an) as they are adjacent to each other.
So, the required number of selections =
Note :
If ‘n’ different objects are arranged along a line, then the number of pairs of objects which are consecutive or adjacent is (n – 1).
Illustration-64
If 30 persons are sitting around a circle. In how many ways can 2 persons out of them be selected so that they are not adjacent.
Solution
Suppose the circular arrangement of 30 persons
a1, a2, a3, ….. , a29, a30 is as shown below
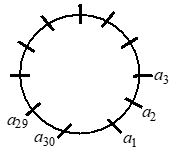
Without any restriction we can select 2 persons in 30C2 ways. Among these selections we do not accept the following 30 selections.
a1, a2, a3, ….. , a29, a30 a1 which are adjacent to each other
Required number of selections = 30C2 – 30
Note :
If n different objects are arranged along a circle, then the number of pairs of objects which are consecutive or adjacent is n.
Illustration-65
i) If a set A has 8 elements, find the number of subsets of A containing at least 6 elements.
ii) A set A has 10 elements. Find the number of subsets of A with atmost 4 elements.
Solution
The number of elements in set A = 8
i) The number of subsets of A containing atleast
6 elements = number of 6 elements subsets + number of 7 elements subsets + number of 8 elements subsets =
= 28 + 8 + 1 = 57.
ii) At most means maximum. So required number of subsets = number of subsets of A containing 0 elements + number of subsets of A containing exactly one element + number of subsets of A containing exactly two elements + number of subsets of A containing exactly three elements + number of subsets of A containing exactly four elements is
= 1+10+45+120+210 = 386
Illustration-66
A teacher wants to take 20 students to a park. He can take exactly 5 students at a time and will not take the same group more than once. Find the number of times that
i) a particular student can go to the park
ii) the teacher can go to the park
Solution
i) Number of times that a particular student goes is same as the number of ways of forming groups with 5 students containing that particular student =
ii) Since the teacher has to accompany each and every group, the number of times that teacher goes = number of different groups of 5 formed from 20 =
Illustration-67
Find the number of ways of forming a committee of 5 persons from a group of 4 Indians and 3 Russians such that there are atleast 3 Indians in the committee.
Solution
Different possible committees are
Indians Russians
(4) (3)
3 2
4 1
Required number of selections = 43 + 13 = 12+3 = 15
Illustration-68
A double decker bus has 15 seats in the lower deck and 13 seats in the upper deck. In how many ways can a marriage party of 28 persons be arranged if 4 old people refuse to go to the upper deck and 4 children wish to travel in the upper deck only.
Solution
If 4 old people refuse to go to the upper deck allow them sit them in the lower deck and if 4 children wish to travel in the upper deck only, let them sit as they wish. Now from the remaining 20 people select 11 in ways to the lower deck and the remaining 9 go to the upper deck in ways. Hence, number of selections = .
Each selection gives rise to (15)! (13)! permutations or arrangements. Hence, total number of arrangements = ⨯ (15)! (13)!
6. NUMBER OF COMBINATIONS WITH REPETITION AND ALL POSSIBLE SELECTIONS
(1) The number of combinations of n distinct objects taken r at a time when any object may be repeated any number of times.
= coefficient of xr in = coefficient of xr in
(2) The total number of ways in which it is possible to form groups by taking some or all of n things at a time is .
(3) The total number of ways in which it is possible to make groups by taking some or all out of things, when n1 are alike of one kind, n2 are alike of second kind, and so on is .
(4) The number of selections of r objects out of n identical objects is 1.
(5) Total number of selections of zero or more objects from n identical objects is n+1.
(6) The number of selections taking at least one out of objects, where a1 are alike (of one kind), a2 are alike (of second kind) and so on…… an are alike (of nth kind) and k are distinct = .
CONDITIONAL COMBINATIONS
(1) The number of ways in which r objects can be selected from n different objects if k particular objects are
(i) Always included =
(ii) Never included =
(2) The number of combinations of n objects, of which p are identical, taken r at a time is , if and
, if r > p.
Illustration-69
There are 4 oranges, 5 apples and 6 mangoes in a fruit basket. In how many ways can a person make a selection of fruits from among the fruits in the basket if
(i) all fruits of the same type are identical.
(ii) all fruits of the same type are different
Solution
(i) Zero or more oranges can be selected out of 4 identical oranges in 4 + 1 = 5 ways.
zero or more apples can be selected out of 5 identical apples in 5 + 1 = 6 ways.
zero or more mangoes can be selected out of 6 identical mangoes in 6 + 1 = 7 ways
Total number of selections when all the three types of fruits are selected = 5 × 6 × 7 = 210.
But in one of these selections number of each type of fruit is zero and hence this selection must be excluded.
Required number = 210 – 1 = 209.
(ii) Number of selections = 215 – 1 (as any fruit is either to be included or excluded in the selection)
Illustration-70
If nCr = 84, nCr–1 = 36 and nCr+1 = 126, then find the value of n.
Solution
14r – 6 = 9r + 9 or r = 3 ∴ n = 9
Illustration-71
Twenty-eight games were played in a football tournament with each team playing once against each other. How many teams were there?
Solution
Let the number of teams be n. Then number of matches to be played is nC2 = 28.
⇒ n2 – n – 56 = 0
⇒ (n – 8) (n + 7) = 0
⇒ n = 8 as n -7
Illustration-72
In how many of the permutations of n things taken r at a time will there given things occur?
Solution
According to the condition of the problem, we have to select r – 3 things from remaining n – 3 things and permute these r things. So, the number of permutations is
Illustration-73
In a certain algebraical exercise book there are 4 examples on arithmetical progressions, 5 examples on permutation and combination and 6 examples on binomial theorem. Find the number of ways a teacher can select for his pupils at least one but not more than 2 examples from each of these sets.
Solution
Number of ways teacher can select examples from arithmetic progression = (4C1 + 4C2)
Number of way teacher can select examples from permutation and combinations = (5C1 + 5C2)
Number of ways teacher can select examples from binomial theorem = (6C1 + 6C2)
Hence total number of ways = (4C1 + 4C2) (5C1 + 5C2) (6C1 + 6C2)
Illustration-74
A delegation of four students is to be selected from a total of 12 students. In how many ways can the delegation be selected
(a) If all the students are equally willing.
(b) If two particular students have to be included in the delegation.
(c) If two particular students do not wish to be together in the delegation.
(d) If two particular students wish to be included together only.
(e) If two particular students refuse to be together and two other particular student wish to be together only in the delegation.
Solution
(a) Formation of delegation means selection of 4 out of 12. Hence the number of ways = 12C4 = 495.
(b) If two particular students are already selected. Here we need to select only 2 out of the remaining 10.
Hence the number of ways = 10C2 = 45.
(c) The number of ways in which both are selected = 45. Hence the number of ways in which the two are not included together = 495 – 45 = 450.
(d) There are two possible cases
(i) Either both are selected. In this case, the number of ways in which the selection can be made = 45.
(ii) Or both are not selected. In this case all the four students are selected from the remaining ten students.
This can be done in 10C4 = 210 ways.
Hence the total number of ways of selection = 45 + 210 = 255.
(e) We assume that students A and B wish to be selected together and students C and D do not wish to be together. Now there are following 6 cases.
(i) (A, B, C) selected, (D) not selected
(ii) (A, B, D) selected (C) not selected
(iii) (A, B) selected (C, D) not selected
(iv) (C) selected (A, B, D) not selected
(v) (D) selected (A, B, C) not selected
(vi) A, B, C, D not selected
For (i) the number of ways of selection = 8C1 = 8
For (ii) the number of ways of selection = 8C1 = 8
For (iii) the number of ways of selection = 8C2 = 28
For (iv) the number of ways of selection = 8C3 = 56
For (v) the number of ways of selection = 8C3 = 56
For (vi) the number of ways of selection = 8C4 = 70
Hence total number of ways = 8 + 8 + 28 + 56 + 56 + 70 = 226.
Illustration-75
A box contains 5 different red and 6 different white balls. In how many ways can 6 balls be selected so that there are at least two balls of each other?
Solution
The selection of 6 balls, consisting of at least two balls of each colour from 5 red and 6 white balls, can be made in the following ways:
| Red balls (5) | White balls (6) | Number of ways |
| 2 | 4 | 5C2 × 6C4 = 150 |
| 3 | 3 | 5C3 × 6C3 = 200 |
| 4 | 2 | 5C4 × 6C2 = 75 |
| Total | 425 |
7. DIVISION INTO GROUPS
Case I
(1) The number of ways in which n different things can be arranged into r different groups is or n! according as blank group are or are not admissible.
(2) The number of ways in which n different things can be distributed into r different group is or Coefficient of is n! .
Here blank groups are not allowed.
(3) Number of ways in which m × n different objects can be distributed equally among n persons (or numbered groups) = (number of ways of dividing into groups) × (number of groups) ! = .
Case II
(1) The number of ways in which (m+n) different things can be divided into two groups which contain m and n things respectively is, .
Corollary:
If m = n, then the groups are equal size. Division of these groups can be given by two types.
Type I : If order of group is not important : The number of ways in which 2n different things can be divided equally into two groups is .
Type II : If order of group is important : The number of ways in which 2n different things can be divided equally into two distinct groups is
.
(2) The number of ways in which (m + n + p) different things can be divided into three groups which contain m, n and p things respectively is
= .
Corollary : If m = n = p, then the groups are equal size. Division of these groups can be given by two types.
Type I : If order of group is not important : The number of ways in which 3p different things can be divided equally into three groups is .
Type II : If order of group is important : The number of ways in which 3p different things can be divided equally into three distinct groups is .
(i) If order of group is not important : The number of ways in which mn different things can be divided equally into m groups is .
(ii) If order of group is important: The number of ways in which mn different things can be divided equally into m distinct groups is .
Illustration-76
In how many ways can a pack of 52 cards be
(i) distributed equally among four players in order?
(ii) divided into 4 groups of 13 cards each?
(iii) divided into four sets of 20, 15, 10, 7 cards?
(iv) divided into four sets, three of them having 15 cards each and the fourth having 7 cards?
Solution
(i) From 52 cards of the pack, 13 cards can be given to the first player in 52C13 ways.
From the remaining 39 cards, 13 cards can be given to the second player in 39C13 ways.
From the remaining 26 cards, 13 cards can be given to the second player in 26C13 ways.
The remaining 13 cards can be given to the fourth player in 13C13 = 1 way.
By fundamental theorem, the number of ways of dividing 52 cards equally among four players = =
(ii) By standard result, the number of ways of forming 4 groups, each of 13 cards = .
(iii) Here the sets have unequal number of cards, hence the required number of ways = =
(iv) By standard result, the required number of ways = .
DERANGEMENT
As another application of the principle of inclusion and exclusion, number of derangement of n objects (number of ways in which n numbered balls (from 1 to n) can be placed in n numbered boxes (from 1 to n), one in each box, so that no ball goes to its corresponding numbered box) is given by n!.
Also
Illustration-77
A person writes letters to six friends and address the corresponding envelopes. In how many ways can the letters be placed in the envelopes so that
(i) at least two of them are in the wrong envelopes
(ii) all the letters are in the wrong envelopes
Solution
(i) The number of all the possible ways of putting 6 letters into 6 envelopes is 6!. There is only one way of putting all the letters correctly into the corresponding envelopes. Hence if there is a mistake, at least 2 letters will be in the wrong envelope.
Hence the required answer is 6! – 1 = 719.
(ii) Using the result of derangements, the required number of ways
=
= 360 – 120 + 30 – 6 + 1 = 265.
Illustration-78
Murthy writes letters to his five friends and addresses the corresponding. The number of ways can the letters be placed in the envelopes so that atleast two of them go into the wrong envelopes is
Solution
Required ways=total ways-all correct ways
(one letter will never go into wrong envelope) = 5! – 1 = 119
Illustration-79
Find the number of permutations of 1, 2, 3, 4, 5 in which exactly one number occupies its natural position.
Solution
Choose the number which should occupy its natural position (5C1)
The number of arrangements of the others is D4.
Hence the required number = 5C1. D4 = 45.
9. SOME IMPORTANT RESULTS FOR GEOMETRICAL PROBLEMS
(1) Number of total different straight lines formed by joining the n points on a plane of which m (<n) are collinear is .
(2) Number of total triangles formed by joining the n points on a plane of which m (<n) are collinear is .
(3) Number of diagonals in a polygon of n sides is .
(4) If m parallel lines in a plane are intersected by a family of other n parallel lines. Then total number of parallelograms so formed is
(5) Given n points on the circumference of a circle, then
(i) Number of straight lines = nC2
(ii) Number of triangles = nC3
(iii) Number of quadrilaterals = nC4.
(6) If n straight lines are drawn in the plane such that no two lines are parallel and no three lines are concurrent. Then the number of part into which these lines divide the plane is = .
(7) Number of rectangles of any size in a square of n⨯n is and number of squares of any size is .
(8) In a rectangle of number of rectangles of any size is and number of squares of any size is .
(9) n straight lines are drawn in the plane such that no two lines are parallel and no three lines are concurrent. Then the number of parts into which these lines divide the plane is equal to 1 + .
(10) The number of triangles whose angular points are at the angular points of a given polygon of n sides, but none of whose sides are the sides of the polygon is n(n-4) (n-5).
(11) There are n straight lines in a plane, no two of which are parallel and no three passes through the same point. Their points of intersection are joined. Then the number of fresh lines thus introduced is n(n – 1) (n – 2) (n – 3).
(12) Number of points of intersections of diagonals of a polygon of n sides which lie completely inside the polygon are nC4
Illustration-80
There are 20 points in a plane out of which 7 points are collinear and no three of the points are collinear unless all the three are from these 7 points. Find the number of different straight lines.
Solution
From the given 20 points, by selecting 2 of them and joining, we are supposed to get 20C2 lines. But since 7 points are collinear, by selecting 2 points from these 7 points, we get only one line instead of getting 7C2 lines. Hence 7C2 lines will be lost and only one line in its place will be obtained. Number of different lines formed = 20C2 – 7C2 + 1
Illustration-81
Find the number of sides of the polygon having 90 diagonals.
Solution
Let the number of sides be n
We know that number of diagonals of n sided polygon =
∴ n = 15 (or) –12.
But n cannot be negative integer.
∴ n = 15 only.
Illustration-82
Find the number of triangles that can be formed by choosing the vertices from a set of 12 points, seven of which lie on the same straight line.
Solution
Required number of ways = = 220 – 35 = 185
Illustration-83
The straight lines are parallel and lie in the same plane. A total number of m points are taken on points on points on . The maximum number of triangles formed with vertices at these points are
(a)
(b)
(c)
(d) None of these
Solution (b)
Total number of points are m+n+k, the formed by these points =
Joining 3 points on the same line gives no triangle, such are
Required number .
10 MULTINOMIAL THEOREM AND NUMBER OF DIVISOR
1. MULTINOMIAL THEOREM
Let be integers. Then number of solutions to the equation …..(i)
Subject to the condition
…..(ii)
is equal to the coefficient of in
….…..(iii)
This is because the number of ways, in which sum of m integers in (i) equals n, is the same as the number of times comes in (iii).
(1) Use of solution of linear equation and coefficient of a power in expansions to find the number of ways of distribution : The number of integral solutions of where is the same as the number of ways to distribute n identical things among r persons.
This is also equal to the coefficient of xn in the expansion of
= coefficient of xn in
= coefficient of xn in
= coefficient of xn in
.
(2) The number of integral solutions of where is same as the number of ways to distribute n identical things among r persons each getting at least 1. This also equal to the coefficient of xn in the expansion of .
= coefficient of xn in
= coefficient of xn in
= coefficient of xn in
= coefficient of xn in
= = .
2. NUMBER OF DIVISOR
Let , where are different primes and are natural numbers then :
(1) The total number of divisors of N including 1 and N is = .
(2) The total number of divisors of N excluding 1 and N is = .
(3) The total number of divisors of N excluding 1 or N is = .
(4) The sum of these divisors is …..
(5) The number of ways in which N can be resolved as a product of two factors is
(6) The number of ways in which a composite number N can be resolved into two factors which are relatively prime (or co-prime) to each other is equal to where n is the number of different factors in N.
Illustration-84
If, then n =
(A) 6 (B) 7 (C) 8 (D) 9
Solution
(C)
.
Illustration-85
If P(n, r) = 1680 and C(n, r) = 70, then
(A) 128 (B) 576 (C) 256 (D) 625
Solution
(B) …..(i)
…..(ii)
, [From (i) and (ii)]
Now = 576.
Illustration-86
An n-digit number is a positive number with exactly n digits. Nine hundred distinct n-digit numbers are to be formed using only the three digits 2, 5 and 7. The smallest value of n for which this is possible is
(A) 6 (B) 7 (C) 8 (D) 9
Solution (B)
Since at any place, any of the digits 2, 5 and 7 can be used, total number of such positive -digit numbers are .
Since we have to form 900 distinct numbers, hence .
Illustration-87
If , then the value of n is
(A) 10 (B) 15 (C) 9 (D) 5
Solution
(C)
Given, .
Therefore,
=
.
Illustration-88
If nPr = 720. nCr , then r is equal to
(A) 6 (B) 5 (C) 4 (D) 7
Solution
(A)
Illustration-89
The sum , is maximum when m is
(A) 5 (B) 15 (C) 10 (D) 20
Solution
(B) For m = 5,
= ,
for m = 10,
= ,
for m = 15,
=
and for m = 20,
=
Clearly, the sum is maximum for m = 15.
Note that 10Cr is maximum for r = 5 and 20Cr is maximum for r = 10. Note that the single term
(in case m = 15) is greater than the sum
(in case m = 10).
Also the sum in case m = 10 is same as that in case m = 20.
Illustration-90
The number of divisors of 9600 including 1 and 9600 are
(A) 60 (B) 58 (C) 48 (D) 46
Solution
(C)
Since
Hence, number of divisors = .
Illustration-91
Number of divisors of n = 38808 (except 1 and n) is
(A) 70 (B) 68 (C) 72 (D) 74
Solution
(A)
Since, 38808 = 8 × 4851
= =
So, number of divisors
= (3 + 1) (2 + 1) (2 + 1) (1 + 1) = 72.
This includes two divisors 1 and 38808. Hence, the required number of divisors = 72 – 2 = 70.
Illustration-92
The sum of all positive divisors of 960 is
(A) 3048 (B) 3087 (C) 3047 (D) 2180
Solution
(A)
Given number is 960, we know that . Therefore bases are and powers . Thus sum of all the positive divisors of 960.
= (127)(4)(6) = 3048.
Illustration-93
There is a rectangular sheet of dimension (2m-1)×(2m-1), (where m>0; n>0). It has been divided into square of unit area by drawing lines perpendicular to the sides. Find number of rectangles having sides of odd unit length
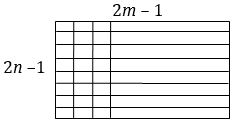
(A) (B) (C) (D)
Solution
(D)
Along horizontal side one unit can be taken in (2m–1) ways and 3 unit side can be taken in ways.
∴ The number of ways of selecting a side horizontally is
Similarly the number of ways along vertical side is .

∴ Total number of rectangles
= = .
11. MISCELLANEOUS CONCEPTS AND PROBLEMS
1. THE INCLUSION – EXCLUSION PRINCIPLE
Consider properties P1 , P2 , … , Pn. Let ak be the number of objects satisfying the property Pk , k = 1, 2, … , n. A commonly asked question is “ how many elements satisfy atleast one of the properties P1 , P2 , … , Pn ” ?
This question is answered by the inclusion-exclusion principle which is stated below :
Let A1 , A2 , … , An be finite sets, their cardinalities being denoted by
|Ai|, i = 1, 2, … , n. Then
Illustration-94
1. In how many ways can 5 cards be drawn from a complete deck (of 52 cards) so that all the suites are present ? (Do not simplify.)
Solution
Consider the notation : In a selection of 5 cards,
C : the set of selections in which clubs are absent
D : the set of selections in which diamonds are absent
S : the set of selections in which spades are absent
H : the set of selections in which hearts are absent
We have | C | = | D | = | S | = | H | = 39C5 ,
|C D| = … = 26C5 ,
|C D S | = … = 13C5,
and |C D S H | = 0
Now |C D S H | =
Finally, the required number is
.
Illustration-95
In how many ways can 6 distinguishable objects be distributed in four distinguishable boxes such that there is no empty box ?
Solution
The number of distributions such that : –
i) atleast one box is empty, is 4C1 . 36
ii) atleast two boxes are empty, is 4C2 .26
iii) atleast three boxes are empty, is 4C3 .16
The totality of distributions is 46.
Hence the required number is
Note : If there should be exactly one empty box, then the number of distributions is = 2160
2. DIVISIBILITY PROBLEMS
The product of n consecutive natural numbers is divisible by n!
A number is divisible by 2, if the last digit is even.
A number is divisible by 3, if the sum of the digits in the number is divisible by 3.
A number is divisible by 4, if the last two digits of the number formed is divisible by 4.
A number is divisible by 5, if the last digit is either 0 or 5.
A number is divisible by 6, if the number is divisible by 2 and 3. (Even numbers whose sum of digits is divisible by 3).
A number is divisible by 7, if the difference between twice the digit in the units place and the number formed by the other digits is either 0 or a multiple of 7.
A number is divisible by 8, if the number formed by the last three digits is divisible by 8. Example : 2192,9128
A number is divisible by 9, if the sum of its digits is divisible by 9. Example : 6453, 8640
A number is divisible by 10, if the last digit is 0.
A number is divisible by 11, if the sum of the digits in the odd places and the sum of the digits in the even places are equal or differ by a multiple of 11. Example : 209, 3564
Illustration-96
The number of 4 – digit numbers that can be formed using the digits 2, 3, 5, 6, 8 (without repetition), which are divisible by 3
Solution
A number is divisible by 3, if the sum of digits in it is a multiple of 3. Since the sum of the given 5 digits is 24, we have to leave either 3 or 6 and use the digits 2, 5, 6, 8 or 2, 3, 5, 8. In each case, we can permute them in 4! ways. Thus the number of 4-digit numbers divisible by 3 is 2 x 4! = 48.
Illustration-97
The number of 4 digit numbers which are divisible by 6 by using the digits 2, 3, 5, 8.
Solution
Given digits are 2, 3, 5, 8. A number is divisible by 6 means it is divisible by 2 and 3. A number is divisible by 3, if the sum of the digits is multiple of three.
Here 2 + 3 + 5 + 8 = 18 = 3 x 6.
A number is divisible by 2, if the units digit is even number
(2, 8)
_ _ _ _
(2 ways)
Here unit’s place filled in 2 ways (2 or 8).
Now remaining ‘3’ gaps are filled in ways.
required numbers which are divisible by 6 are = .
Illustration-98
Is this number 3675 is divisible by 7.
Solution
Let the number is 3675
Here units place digit is 5
Twice the unit’s place = 2 x 5 = 10
Now the remaining number is ‘367’
Then the difference between 367 and 10 is 357 clearly 357 is divisible by ‘7’ 3675 is divisible by ‘7’.
Illustration-99
Find the number of 4 digit numbers divisible by 5 that can be formed using the digits 1, 2, 3, 4, 5 when repetition of digits is allowed.
Solution
A number is divisible by 5 if it ends with 5. The three gaps before it can be filled in 5 ways each. Hence number of 4 digit numbers ending with 5 is 53 = 125.
Illustration-100
Find the number of 4 digited numbers that can be formed using the digits 0, 1, 2, 3, 4, 5 which are divisible by 6 when repetition of digits is allowed
Solution
Consider 4 blank places
X X X X
The extreme left place i.e. 1000th place can be filled in 5 ways (since 0 cannot be used)
Since repetition is allowed, the remaining 3 places each can be filled in 6 ways (either 0, 1, 2, 3, 4 or 5)
So, by fundamental principle, we can prepare 5 ⨯ 6 ⨯ 6 ⨯ 6 i.e., 5 ⨯ 63 numbers having 4 digits which may or may not be divisible by 6.
By fixing first 3 places with a1, a2, a3 where a1 0 and varying the unit place with 0, 1, 2, 3, 4, 5 we get the following six consecutive integers.
a1 a2 a3 0
a1 a2 a3 1
a1 a2 a3 2
a1 a2 a3 3
a1 a2 a3 4
a1 a2 a3 5
Among these six consecutive integers exactly one is divisible by 6.
∴ The number of 4 digited numbers when repetition is allowed which are divisible by
= 180 = 1/6 (Total number of 4 digit numbers formed)
3. SUM OF NUMBERS
• Sum of the numbers formed by taking all the given n digits (excluding 0) is
(Sum of all the n digits) x (n-1)! x (111 … n times).
• Sum of the numbers formed by taking all the given n digits (including 0) is (sum of all the n digits) [(n-1)! x (111 …. n times) – (n-2)! (111 …. (n-1) times)]
• Sum of all the r-digit numbers formed by taking the given n digits (excluding 0) is (sum of all the n digits) x (n-1)4Pr-1 x (111 …… r times).
• Sum of all the r-digit numbers formed by taking the given n digits (including 0) is (sum of all the n digits) [(n-1)4Pr-1 x (111 …. r times) – (n-2)4Pr-2 x (111 … (r-1) times)].
• The sum of the digits in any place of all the numbers formed with the help of a1, a2, …. an (excluding zero) taken all at a time is
• When n digits are given excluding zero, then the sum of the value of digits in any place of n digited number is (n – 1)! x sum of the numbers x {its place value}.
Illustration-101
Find the sum of all 4 digited numbers that can be formed using the digits 0, 2, 4, 7, 8 without repetition.
Solution
Put n = 5, r = 4
=
Illustration-102
The sum of the digits at the 100’s place of all the numbers formed with the digits of 5,6,7,8 taken all at a time is
Solution
The sum of the digits at the 100’s place of all the numbers formed with the digits of 5, 6, 7, 8 taken all at a time is
= (n-1)! x (sum of the given digits)
= (n-1)! x (5+6+7+8) = 3!⨯26 = 156
Illustration-103
The sum of the ‘value’ of the digits at the 100’s place of all the numbers formed with digits of 5, 6, 7, 8 taken all at a time is
Solution
Sum of the value of the digits at the 100’s place of all the numbers formed with digits of 5, 6,7, 8 taken all at a time is
(n-1)! x (sum of the given digits) x 100
= (4-1)! x (5 + 6 + 7 + 8) x 100
= 3! x 26 x 100 = 6 x 26 x 100 = 15600
4. NUMBER OF FUNCTIONS
• The number of mappings that can be defined from set A containing ‘m’ elements to set B containing ‘n’ elements is nm.
• The number of injections (one one functions) that can be defined from set A containing ‘m’ elements to set B containing ‘n’ elements is nPm where
• The number of surjections (on to functions) that can be defined from set A containing ‘m’ elements to set B containing ‘2’ elements is
• The number of bijections (one one and onto functions) that can be defined from set ‘A’ containing ‘n’ elements to set B containing ‘n’ elements is n!
• The number of many to one functions that can be defined from set A containing ‘m’ elements to set B containing ‘n’ elements is
• Number of constant functions that can be defined from set A containing ‘m’ elements to set B containing ‘n’ elements is ‘n’.
• The number of surjections (onto functions) that can be defined from set A containing ‘m’ elements to set B containing ‘n’ elements is
• The Number of into functions that can be defined from set A containing ‘m’ elements to set B containing ‘n’ elements is Total number of functions – Number of onto functions
• Number of identity functions that can be defined from set ‘A’ to itself is ‘’one’’
Illustration-104
The number of constant mappings from A = {1, 2} to B = {a, b,…..,z} is
Solution
The number of constant functions is equal to n(B)
The number of constant functions is 26
Illustration-105
The number of into functions that can be defined from A = {x, y, z, w, t} to B = {} is
Solution
n(A) = m = 5, n(B) = n = 3
The number of into functions = (Total no. of functions) – (number of onto functions)
=
= 93
Illustration-106
If a set A has 3 elements and B has 5 elements, find the number of injections from A to B.
Solution
Here m = 3 and n = 5
Number of injections from A to B is nPm = 5P3 = 60
Illustration-107
If a set X has 5 elements, then find the number of bijections from X onto itself.
Solution
The number of bijections from X onto itself = 5! = 120
5. PALINDROME
A number or a word which reads same either from left to right or from right to left is called a Palindrome. Some examples of palindromes are ATTA, ROTOR, 12321, 120021 etc.,
Note: The number of palindromes with ‘r’ distinct letters that can be formed using given ‘n’ distinct letters is i) if r is even ii) if r is odd.
Illustration-108
The number of Palindromes with 6 digits that can be formed using the digits 1, 3, 5, 7, 9.
Solution
n = 5, r = 6 (even)
number of Palindromes =
Note: The number of palindromes with ‘r’ distinct digits that can be formed using given ‘n’ distinct digits (including ‘0’) is
i) if r is even ii) if r is odd.
Illustration-109
The number of Palindromes with ‘6’ digits that can be formed using the digits 0, 2, 4, 6, 8 is
Solution
Given digits 0, 2, 4, 6, 8.r = 6 (even), n = 5
Required 6 digits Palindromes are =
6. RANK OF A WORD
If all the arrangements formed with all the letters of the given word are put in alphabetical order then the numerical place of the given word is called it’s “Rank”.
Illustration-110
Find the rank of the word ‘RAMESH’
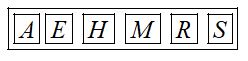
Solution
Write the letters in boxes as alphabetical order
Write all factorials begining with one less than number of boxes i.e., 5! 4! 3! 2! 1! 0!
In RAMESH first letter is R. Then multiply first factorial with number of letters before R. In alphabetical order and this process will continue till end.
By adding the above factorials we get the rank.
The rank of the word ‘RAMESH’ is
4 x 5! + 0 x 4! + 2 x 3! + 0 x 2! + 1 x 1! + 0! = 494
7. VANDERMONDE’S THEOREM
……..+
Illustration-111
The sum is maximum when m is
Solution
…….+
is maximum when
IMPORTANT TIPS
• is divisible by ‘n’ only if ‘n’ is prime number. As 6C2 is not divisible by 6 but 7C4 is divisible by 7.
• The number of combinations of ‘n’ things taken ‘r’ at a time in which
a) ‘s’ particular things will always occur is
b) ‘s’ particular things will never occur is
c) ‘s’ particular things always occur and ‘p’ particular things never occur is .
• If ‘n’ different objects are in a row then the number of ways of selecting ‘r’ objects at a time so that no two of these ‘r’ objects are consecutive is
• If ‘n’ different objects are on a circle then the number of ways of selecting ‘r’ objects at a time so that no two of these ‘ r’ objects are consecutive is
Illustration-112
In how many ways can a cricket eleven be chosen out of a batch of 15 players if
(a) There is no restriction on the selection
(b) a particular player is always chosen
(c) a particular player is never chosen?
Solution
(i) The total number of ways of selecting 11 players out of 15 is
= =
(ii) if a particular player is always chosen. This means that 10 players are selected out of the remaining 14 players. Hence Required number of ways =
(iii) If a particular player is never chosen. This means that 11 players are selected out of the remaining 14 players. Hence Required number of ways =
Illustration-113
The number of ways in which a team of eleven players can be selected from 22 players always including 2 of them and excluding 4 of them is
Solution
Required number of ways
8. EXPONENT OF PRIME P IN n!
Let p be a prime number and n be a positive integer. Then the last integer amongst 1, 2, 3, …….(n – 1), n which is divisible by p is , where denote the greatest integer less than or equal to .
For example: etc.
Let denotes the exponent of the prime p in the positive integer n. Then,
= =
[ Remaining integers between 1 and n are not divisible by p]
Now the last integer amongst 1, 2, 3,…..which is divisible by p is
because the remaining natural numbers from 1 to are not divisible by p =
Similarly we get where S is the largest natural number. Such that .
Illustration-114
If 2n divides 33! then find maximum value of n.
Solution
E2 (33!) =
= 16 + 8 + 4 + 2 = 30
∴ maximum value of n = 30.








