BASIC PRINCIPLES AND NOMENCLATURE
Introduction:
The element carbon forms different types of compounds as it has the unique property called catenation (the ability to form bonds with itself) due to which it forms single as well as multiple covalent bonds with other carbon atoms. It is further supplemented by the fact that it also forms covalent bonds with atoms of other elements like hydrogen, oxygen, nitrogen, sulphur, phosphorus and halogens in a variety of ways (i.e., single and multiple bonds).
The branch of chemistry dealing with these compounds, which are widely distributed in nature and play an important role in our daily lives, is called organic chemistry.
In the earlier period of development of chemistry, compounds were classified into two types:
i) Organic compounds derived from ‘living matter’ (plants and animals).
ii) Inorganic compounds prepared from ‘non-living matter’ (mineral sources).
Berzelius, a Swedish chemist proposed the mistaken notion that a ‘vital force’ present in living matter was essential for the synthesis of organic compounds. However, the synthesis of urea an organic compound present in urine, from ammonium cyanate, an inorganic compound by F. Wohler in 1828 effectively destroyed the myth of organic compounds being associated with a ‘vital force’.
Soon afterwards the pioneering work of Herman Kolbe who synthesized acetic acid and of Berthelot who synthesized methane showed conclusively that organic compounds are essentially the compounds formed by carbon with itself and other elements and that they can be synthesized in a laboratory as easily as inorganic compounds.
The chemistry of hydrocarbons and their derivatives constitutes organic chemistry.
Shapes of organic compounds
Tetravalency of carbon and the formation of single and multiple covalent bonds by it can be explained in terms of its excited state valence shell electronic configuration:
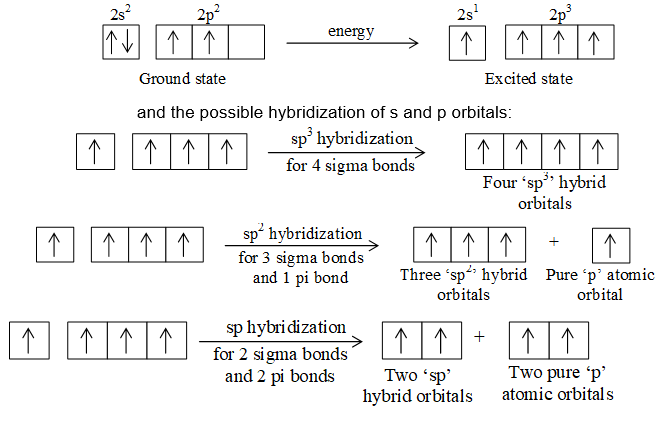
Orbital hybridization is a mathematical approach that involves the combining of individual wave functions for s and p orbitals to obtain wave functions for new orbitals.
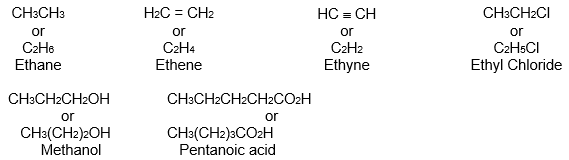
The formation of sigma and pi bonds in terms of these hybridization schemes helps to understand the formation and the structures plus shapes of molecules of alkanes (e.g., methane, CH4), alkenes (e.g., ethene, C2H4) and alkynes (e.g., ethyne, C2H2). The formation of methane and ethane are easily explained in terms of sp3 hybridization as shown in figure.
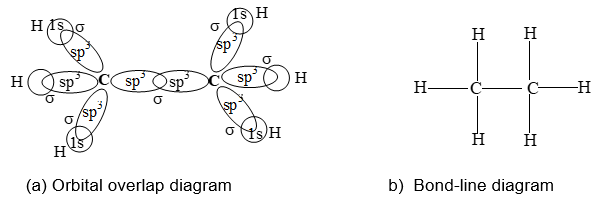
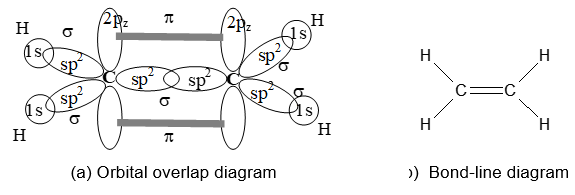
The formation of ethene, C2H4, is easily explained in the terms of sp2 hybridization as shown:
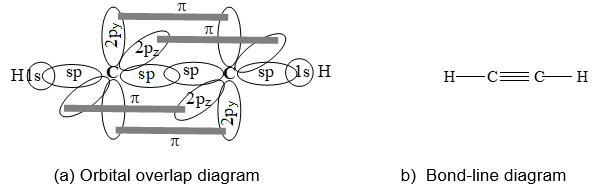
The formation of ethyne, C2H2, is easily explained in terms of sp hybridization as shown below
Scheme of hybridization influences the bond length and hence the bond strength (or bond enthalpy) in organic molecules. The more the ‘s’ character in the hybrid orbital, the more the probability of finding the bonded electrons closer to the nucleus and hence the shorter and the stronger the bond. Thus 1) sp3 hybridization > sp2 hybridization > sp hybridization.

For example:
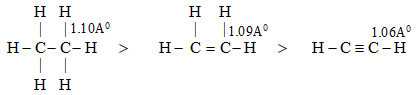
The shortest C–H bonds are associated with those carbon orbitals which have the greatest ‘s’ character.
2) sp hybridization > sp2 hybridization > sp3 hybridization.
For example:
Scheme of hybridization also affects the electronegativity of the bonded carbon. The greater the ‘s’ character of the hybrid orbital, the higher the probability of finding the bonded electrons near the carbon nucleus and hence the greater is the electronegativity. 3) sp hybridization > sp2 hybridization > sp3 hybridization.
This relative change in electronegativity is reflected in many physical and chemical properties of the compounds concerned. For example, the acidic character of the hydrogen atom bonded to carbon follows the order:
In orbital hybridization, we combine orbitals, not electrons.
Some characteristic features of bonds:
Sideways overlap of the two p orbitals on adjacent carbon atoms leads to the formation of a pi (p) bond. The necessary and sufficient condition for an effective sideways overlap is the parallel orientation of the two p orbitals. This demands that, in ethene (H2C = CH2) molecule, all the atoms must be in the same plane so that both the p orbitals are mutually parallel and are perpendicular to the plane of the molecule.
Rotation of one CH2 bonding unit relative to other prevents the maximum possible overlap of p orbitals and, therefore, such a rotation about carbon–carbon double bond [C = C] is restricted.
Estimates based on thermochemical calculations indicate that the strength of the p bond is 264 kJ mol–1. This barrier to rotation of the double bond is markedly higher than the rotational barrier of groups joined by carbon–carbon single bonds (13 – 26 kJ mol–1).
While group joined by single bonds rotate relatively freely at room temperature, those joined by double bonds do not.
Consequently, a disubstituted ethene such as C2H2Br2 can exist in two different forms (I and II) as show below because of the restricted rotation around the C = C bond.

In ‘I’ called the cis form, the two Br atoms are on the same side of the double bond while in ‘II’ called the trans form, the two Br atoms are on the opposite sides.
Rotation of one CH3 bonding unit relative to another in an ethane (C2H6) molecule does not affect the extent of overlap of orbitals forming the sigma bond. Consequently, free rotation around a sigma () bond is practically allowed.
Rotation about the carbon–carbon sigma bond results in different arrangements of bonded atoms (or groups of atoms) in space resulting into different interconvertible forms of the molecule known as conformations.
The electron charge cloud of the bond is placed equally above and below the plane of bonding atoms. As a result the pi electrons become easily available to the attacking (oxidizing) reagents. Consequently, ethene (C2H4) readily reacts with commonly used oxidizing reagents like potassium permanganate (KMnO4) or potassium dichromate (K2Cr2C7) at ordinary temperature, whereas ethane (C2H6) lacking pi electrons remains totally unaffected by these reagents at ordinary temperature.
In general, pi () bonds are the most reactive centres in the molecules of unsaturated compounds.
Illustration 1: How many sigma (s) and pi (p) bonds are present in each of the following molecules?
a) CH2 = C = CH2 b) CH3 – CH = CH – C C – CH3
Solution: Every single bond is a s bond, every double bond contains one s- and one p-bond while every triple bond consists of one – and two -bonds. Thus
a) b)
Illustration 2: Predict the shape of each of the following molecules.
a) HC CH b) CH3Cl c) H2C = O
Solution: sp3 hybridization can always be correlated to tetrahedral shape, sp2 to trigonal planar and sp to linear. Thus,
a) sp hybridized carbon atoms, linear
b) sp3 hybridized carbon, tetrahedral
c) sp2 hybridized carbon, trigonal planar
Representation of Structural Formulae
Structural formula (or just called the structure) is the sequence in which different atoms constituting the molecule are bonded to one another. Structures of molecules of organic compounds can be described in various ways. The most common types of representations are:
1) Lewis structure (or electron dot structure) Here dots are used to represent all of the valence electrons of all the bonded atoms in the molecule:
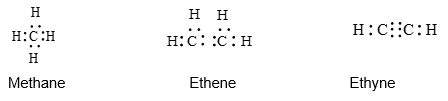
Writing dot structure is tedious and time–consuming. The other representations are more convenient and are, therefore, more often used.
2) Dash structural formula
The Lewis structure can be simplified by representing a shared electron pair by a ‘stick’ (dash, -) between the bonded atoms. When there is one dash between two atoms, the atoms are said to be bonded by a single covalent bond. A double covalent bond, in which two pairs of electrons are shared, is shown by two dashes between the atoms. A triple bond is represented by three dashes between the atoms.
The valence electrons that are not included in covalent bonds are called nonbonding electrons. These are assigned to specific atoms and are represented by dots drawn next to the symbols for these atoms.
Non bonding electrons, like bonding electrons, almost always come in pairs called lone pairs.
Lone pair of electrons on hetero atoms (e.g. oxygen, nitrogen, sulphur, phosphorus, halogens) may or may not be shown. Such structural formulae which focus only on the valence electrons involved in bond formation are called complete structural formulae.
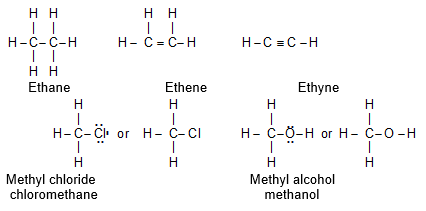
3) Condensed structural formula Complete structural formulae can be shortened by leaving out some or all of the covalent bonds and by denoting the number of identical groups attached to an atom by a subscript. The resulting description of the molecule is called a condensed structural formula. Thus,
Condensed structural formulae are easier to write than dash formulae. In condensed formulae all of the hydrogen atoms that are attached to a particular carbon are usually written immediately after the carbon. In fully condensed formulae, all of the atoms that are attached to the carbon are usually written immediately after that carbon, listing hydrogens first.
For example, the condensed formula for isopropyl alcohol can be written in four different ways:
If we look at the dash and condensed formulae, we find that the chain of atoms is straight in these formulae. In the actual shape of the molecule, the chain of atoms is not at all straight.
Notice that in these formulae we represent the bond angles as being 900, not 109.50. This convention is followed simply for convenience in printing.
Sometimes we even omit unshared pairs when we write formulae. However, when we write chemical reactions, we see that it is necessary to include the unshared electron pairs when they participate in the reaction.
It is a good idea, therefore, to get into the habit of writing the unshared (nonbonding) electron pairs in the structures we draw.
Proper use of condensed structural formulae is one essential tool in organic chemistry
Bond-line structural formula: For further simplification only lines are used to represent the structures of organic molecules. In this bond-line structural formula of organic molecule, carbon and hydrogen atoms are not shown. The lines denoting the carbon – carbon bonds are drawn in a zig – zag fashion. The only atoms especially written are the hetero atoms (oxygen, nitrogen etc). They are neither carbon nor hydrogen bonded to carbon. The termini describe methyl (CH3 – ) groups (unless denoted otherwise by a functional group). The line junctions indicate carbon atoms bonded to suitable number of hydrogens needed to satisfy the covalency of the carbon atoms: Thus
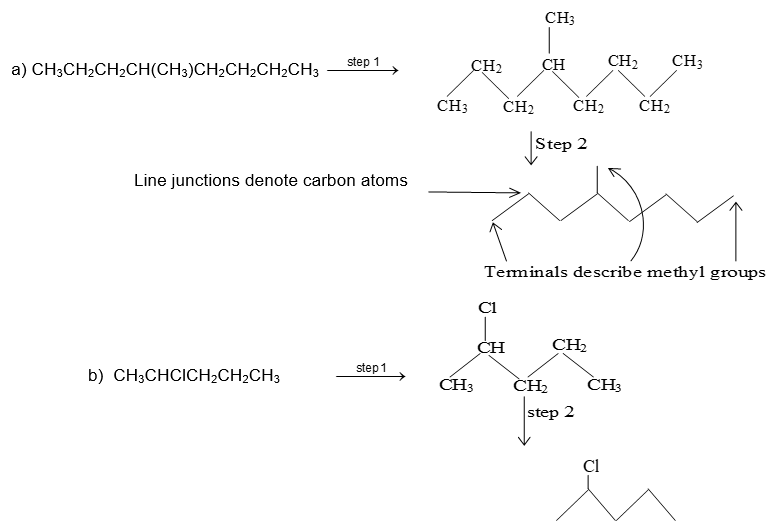
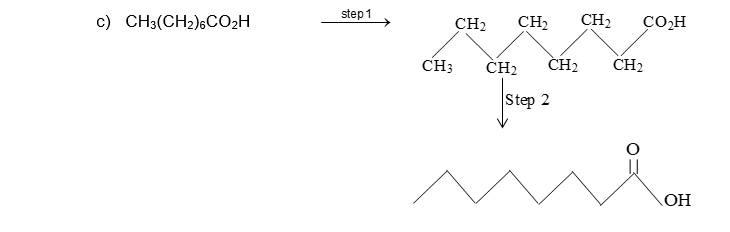
The bond-line representation is the quickest of all to write because it shows only the carbon skeleton. Organic compounds not only have their carbon atoms arranged in chains, they can also have them arranged in rings. An organic compound in which carbon atoms are not bonded in chain but are bonded in closed structures called rings are known as cyclic compounds. Such a compound containing one or more rings is represented by drawing the suitable ring (polygon) without indicating the carbon and hydrogen atoms. The corner of the polygon denotes a carbon atom and its sides represent a carbon – carbon bond. An atom or a group of atoms (other than hydrogen) bonded to the carbon is however shown in the structure.
Bond–line formulae of some cyclic compounds are:
Multiple bonds are also indicated in bond-line formulae. For example:
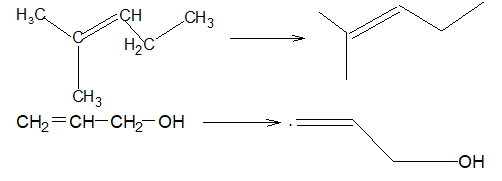
Illustration 3: Convert each of the following Lewis structures into complete structural formulae:
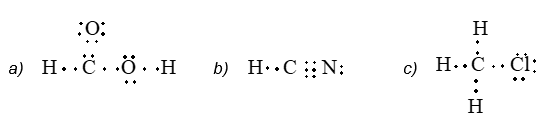
Solution: Use the dash to represent the shared electron pair.
a)
b) H – C N: or H – C N
c)
Illustration 4: Convert each of the following complete structural formulae into condensed formulae.
a)
b)
c)
d)
Solution: Omitting some or all of the dashes and indicating the number of identical group by a subscript we get
a) HO(CH2)2NH2
b) CH3C C(CH2)3CH3
c) H3CCOCH3
d) CH3(CH2)3NO2
Illustration 5: Write the condensed structural formulae for the compound that follows in different ways.
Solution:
or
Illustration 6: Write the bond–line formula for
Solution: First, outline the carbon skeleton, including the OH group as follows:
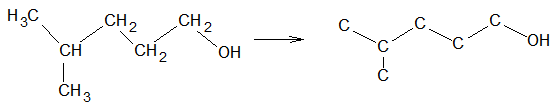
Thus, the bond–line formula is
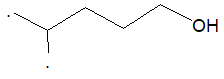
Illustration7: For each of the following condensed formulae write the corresponding bond-line formula.
a) (CH3)2CH(CH2)2CH2OH
b) CH3(CH2)4CHICH2CHO
c) (CH3)2CHCH3CH(CH2)3NO2
d) (CN)2CHCH2COCl
Solution: In bond-line formula carbon and hydrogen atoms except those that are part of the functional groups are not shown. We show only the carbon skeleton. The number of hydrogen atoms necessary to fulfill the carbon atoms’ valences are assumed to be present, but we do not write them in. Other atoms (e.g., Cl, O, N) are written in. Each intersection of two or more lines and the end of a line represent a carbon atom unless some other atom is written in.
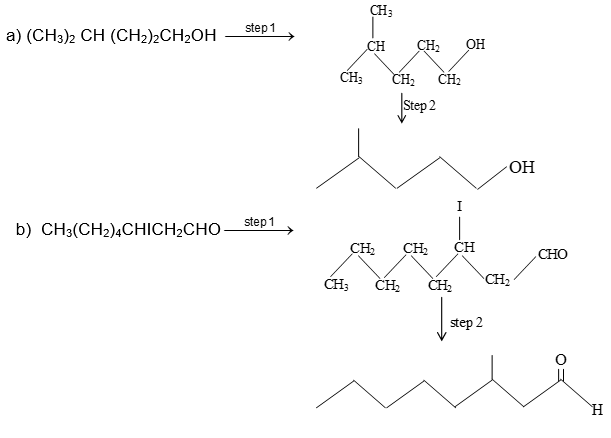
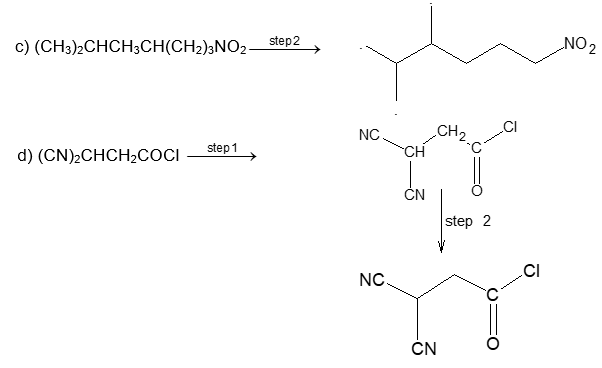
Illustration8: Draw all possible bond-line formulae for a cyclic compound, C5H10.
Solution: Start with the maximum number of carbon atoms in the ring and move towards the ring of 3 carbon atoms. Explore all sorts of possibilities on this route:

Three dimensional representation of organic molecules
None of the formulae that we have described so far conveys any information about how the atoms of a molecule are arranged in space. Shape or the three-dimensional (3-D) structure of organic molecules can be described on a paper (two-dimensional) by exploring certain conventions. For instance, by using

the 3–D image of an organic molecule can be perceived on a two-dimensional paper.
In solid-wedge and dashed-wedge description the solid-wedge denotes a bond projecting out of the plane of the paper towards the viewer. The dashed-wedge depicts the bond projecting behind the plane of the paper and going away from the viewer. Both the wedges are drawn in such a way that the broad end of the wedge is near the viewer. The other two bonds lying in the plane of the paper are shown by using a normal line ( – ).
For tetrahedral atoms, we first draw the two bonds that are in the plane of the paper with an angle of approximately 1090 between them. Next step (to provide the proper three-dimensional perspective) then requires the solid-wedge and dashed-wedge bonds to be drawn near each other on the paper (i.e., the atom in front nearly eclipses the atom behind).
We can draw trigonal planar atoms either with all bonds in the plane of the paper separated by approximately 1200 or with one of the three bonds in the plane of the paper, one behind and one in front. Atoms with linear bonding geometry are best drawn with all bonds in the plane of the paper. Generally, we only use three dimensional formula when it is necessary to convey information about the shape of the molecule.
Let’s consider the wedge- and dashed-wedge representation of methane (CH4) molecule:

The two carbon-hydrogen bonds represented by normal lines are in the plane of paper, whereas the carbon-hydrogen bond represented with a solid wedge is aimed to be in front of the plane of paper. The hydrogen bonded to carbon by dashed wedge is intended to be behind the plane of paper. Note that the carbon atom is lying in the plane of paper.
Wedge and dashed-wedge formulae are an important tool for clearly showing three dimensions.
Bonds that project upward out of the plane of the paper are indicated by a solid wedge
 ,
,
those that lie behind the plane are indicated with a dashed wedge
 ,
,
and those bonds that lie in the plane of the paper are indicated by a line (-).
Molecular models are physical tools that impart, if available, a better visualization and perception of 3-dimensional shapes of organic molecules. Usually three types of molecular models are used:
Ball-and-stick model Here balls describe atoms while a stick denotes a single covalent bond. Multiple bonds are best represented by springs leading to ball-and-spring model.
Framework model shows only the bonds (not the atoms) connecting the different atoms of the organic molecule. It emphasizes the pattern of bonds of molecule while ignoring the atoms.
Space-filling model highlights the relative size of each atom using its van der Waals radius. It thus, conveys the volume occupied by each atom in the molecule. Bonds are not shown in this model.
Projection techniques are also used to describe the 3-D arrangement of atoms of organic molecules on the plane of paper. For this purpose the 3-D model of organic molecule is projected in paper using a light ray and then, according to certain conventions, the 2-D image of the molecule is drawn on paper. For projection purpose the molecule may be oriented in different ways relative to the plane of paper. Usually three different types of projection formulae are employed:
Sawhorse projection formulae to depict the conformations.
Newman projection formulae also to represent the different conformations of an organic molecule. Fischer projection formulae to describe the possible stereoisomers of chiral molecules having at least one chiral carbon atom. They are frequently employed for carbohydrates and amino acids. These will be discussed in details at suitable stages.
Classification of organic compounds
To handle the existing large number of organic compounds and their ever increasing numbers it is needed to broadly classify them on the basis of their skeletons as outlined below:
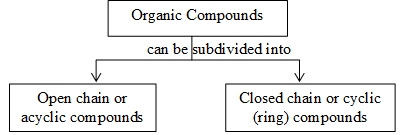
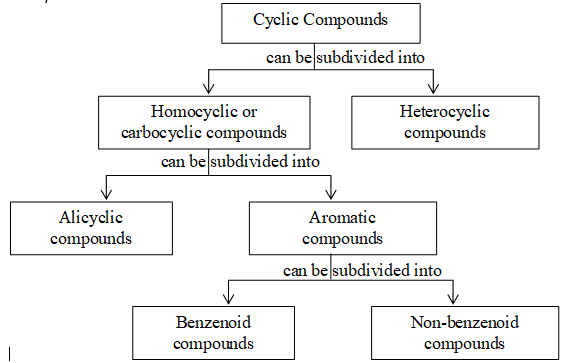
Depending on the nature of atoms forming the ring structure and also on the basis of their behavior, the cyclic compounds are further classified as follows:
Acyclic (or open chain) compounds are also known as aliphatic compounds. The name aliphatic arises from the fact that the first compounds of this class to be studied were the fatty acids (Greek: aliphos, fat). Their molecules consist of straight or branched chains of carbon atoms:
Homocyclic (or carbocyclic) compounds consist of carbon atoms joined in the form of a ring. Alicyclic compounds are those carbocyclic compounds which exhibit some of the properties similar to those of aliphatic compounds. Some typical examples are: ’
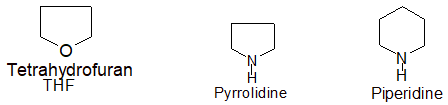
Heterocyclic compounds consist of carbon atoms and atoms other than carbon (e.g., oxygen, nitrogen, sulphur etc) joined in the form of a ring. Some typical examples are :
During the latter part of the nineteenth century organic compounds were placed in either of two broad categories: aliphatic or aromatic. To be classified as aliphatic meant then that the chemical behavior of a compound was “fatlike” (Now it means that the compound reacts like an alkane, an alkene, an alkyne or one of their derivatives). To be classified as aromatic meant then that the compound had a low hydrogen/carbon ratio and that it was “fragrant”.
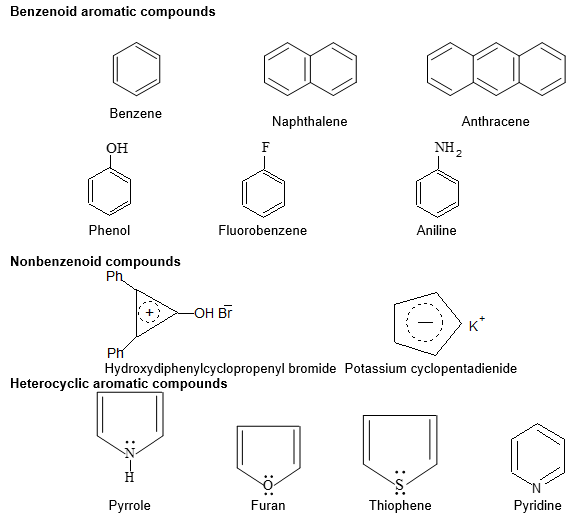
Aromatic compounds are special types of organic compounds. Benzenoid aromatic compounds include benzene and other related ring compounds while non benzenoid aromatic compounds include compounds carrying no benzene nucleus.
Aromatic compounds may also have hetero atoms in the ring. Such compounds are called heterocyclic aromatic compounds. Some typical examples are :
Further classification of organic compounds, on the basis of functional group, leads to families or homologous series.
Functional groupsi
Using structural theory one can classify the vast number of organic compounds into a relatively small number of families based on their structures. Most important families of organic compounds are listed below:
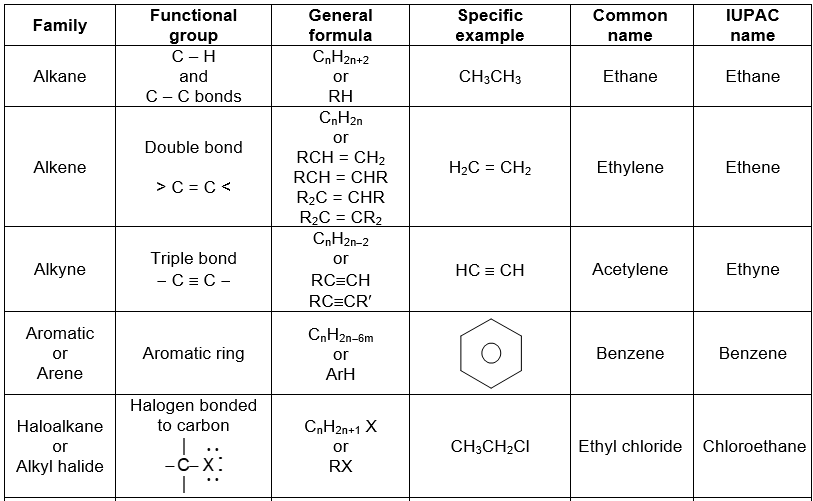
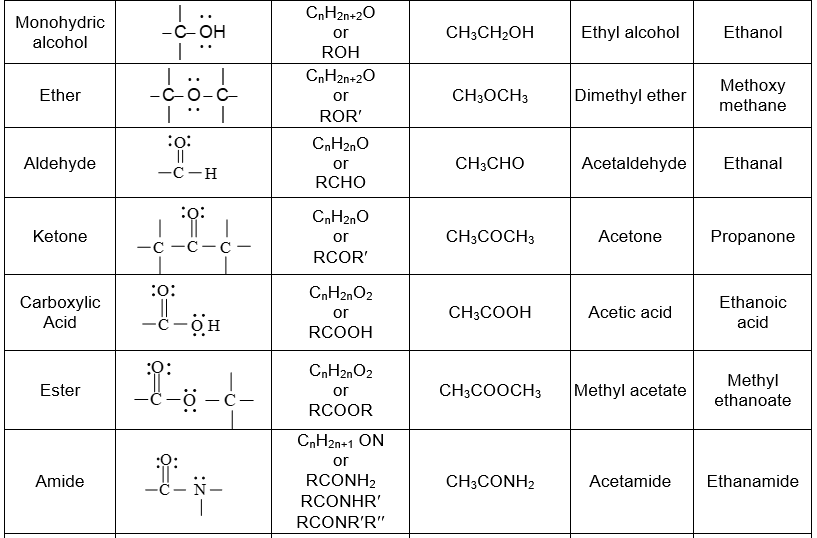
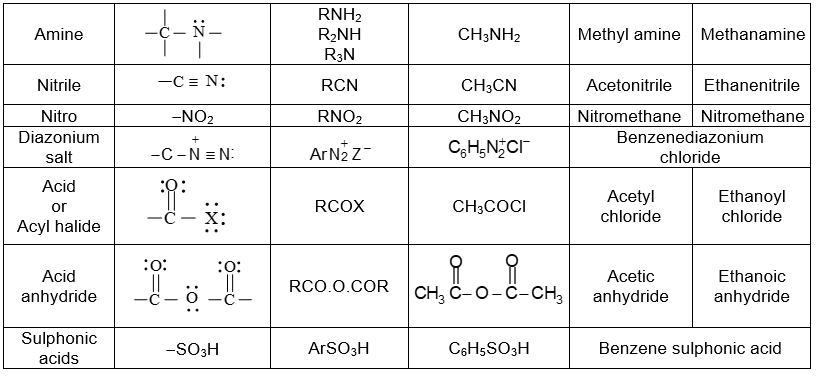
The molecules of organic compounds in a particular family are characterized by the presence of a specific arrangement of atoms called a functional group.
The functional group, which may be defined as a group of atoms joined in a specific manner, is that part of an organic molecule where most of its characteristic chemical reactions occur. It is that part which defines the structure of a particular family of organic compounds and at the same time effectively determines the compounds’ chemical properties and also many of its physical properties. For instance, the functional group of an alkyne is its carbon – carbon triple bond. Thus, most of the chemical reactions of alkynes are the chemical reactions of the carbon – carbon triple bond. Similarly, in alkyl halides, the functional group is the halogen atom attached to the carbon of an alkyl group.
Thus, the characteristic reactions of this family occur at the bond.
Alkanes do not have a functional group. Their molecules have carbon-carbon single bonds and carbon-hydrogen bonds, but such bonds are present in molecules of almost every organic compound. Moreover, the C-C and C–H bonds are usually much less reactive than common functional groups.
The Homologous series
Organic compounds, while large in number are classified into a relatively small number of families whose behavior are defined by their functional groups. A family of organic compounds, such as the alkenes, each containing a characteristic functional group forms a homologous series, and the members of the series are called homologues. Some typical examples of homologous series of organic compounds are alkanes, alkenes, alkynes, arenes haloalkanes etc.
Members of a homologous series have similar chemical structures/reactions and graded physical properties. In homologous series each member differs from the next member by a constant structural unit. The family of alkanes forms such a homologous series, the constant difference between successive members being CH2. Each homologous series has it own characteristic general formula.
Nomenclature of organic compounds
Organic chemists, dealing with millions of compounds, can communicate with one another about their work just by writing suitable structures and equations, a slow process. For more rapid and efficient communication one needs to have systematic names for compounds. Before the development of a formal system for naming organic compounds, many organic compounds were known. They were assigned names based on their source or sometimes their properties as illustrated below:
| Compound | Common name | Basis |
| CH3CO2H | Acetic acid | Can be obtained from vinegar, thus takes its name from the Latin word for vinegar, acetum. |
| CH3COCH3 | Acetone | Formed by strong heating of the calcium salt of acetic acid. |
| HCOOH | Formic acid | Can be obtained from some ants, thus named from the Latin word for ants, formicae. |
| CH3(CH2)2CO2H | Butyric acid | Gives rancid butter its typical smell (Latin: butyrum, butter |
| CH3(CH2)4CO2H CH3(CH2)6CO2H CH3(CH)8CO2H | Caproic acid Caprylic acid Capric acid | All found in goat fat, thus take their name from the Latin word for goat, caper |
| CH3CH2CH | Grain alcohol | Obtained by the fermentation of grains |
| Citric acid | It is found in citrus fruits. |
These traditional names for organic compounds are now called “common’ or “trivial” names. Many of these names are still widely used. Thus, it is still essential to learn the common names for some of the every day use compounds. Most of the time, the names used will be those called IUPAC names. Lemon juice contains about 6‑10 percent citric acid.
The formal system of nomenclature used today is one proposed by the International Union of Pure and Applied Chemistry (IUPAC). This system, first developed in1892 is being revised at regular intervals to keep it up to date. The fundamental objective behind the IUPAC system of nomenclature for organic compounds is: each different compound should have a unique name so that one is able to derive the correct structure of a given compound from its IUPAC name.
Organic compounds containing only two elements, carbon and hydrogen are known as hydrocarbons.
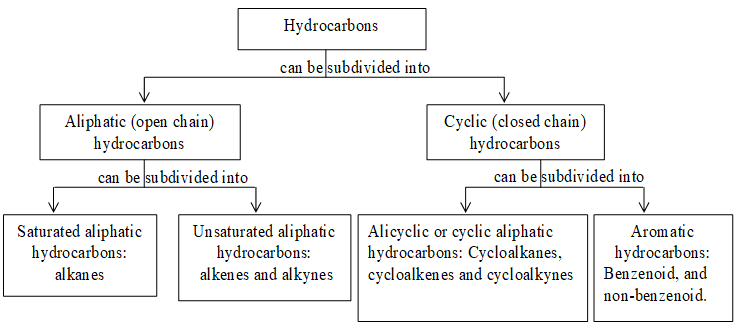
Saturated hydrocarbons contain only carbon – carbon single bonds while unsaturated hydrocarbons contain at least one carbon–carbon double or triple bond. For convenience, open chain or aliphatic hydrocarbons can be subclassified into two types depending on their carbon skeleton: straight chain hydrocarbons and branched chain hydrocarbons.
Nomenclature of Alkanes
Alkane is the IUPAC name of saturated aliphatic hydrocarbons. Paraffin (Latin: little affinity) was the earlier name given to these compounds. Alkanes have no double or triple bonds, or rings and conform to the general formula CnH2n+2.
Alkanes are labelled as “straight chain” alkanes (i.e., unbranched) if all the carbon atoms in the chain are linked to just one or two other carbons or “branched chain” alkanes if at least one carbon atom is linked to more than two other carbons:
CH3 – CH2 – CH2 – CH3 (Straight chain alkane)
(Branched chain alkane)
The first four straight chain alkanes do not have systematized names. The higher members, beginning with pentane, are named systematically with
a numerical prefix (pent-, hex-, hept-, etc.,) to indicate the number of carbon atoms and with the ending (–ane) to label the compound as a saturated paraffin hydrocarbon as illustrated below.
Table 1: IUPAC names of unbranched alkanes
| No. of carbon atoms | Molecular formula | Molecular structure | IUPAC name |
| 1 | CH4 | CH4 | Methane |
| 2 | C2H6 | CH3CH3 | Ethane |
| 3 | C3H8 | CH3CH2CH3 | Propane |
| 4 | C4H10 | CH3(CH2)2CH3 | Butane |
| 5 | C5H12 | CH3(CH2)3CH3 | Pentane |
| 6 | C6H14 | CH3(CH2)4CH3 | Hexane |
| 7 | C7H16 | CH3(CH2)5CH3 | Heptane |
| 8 | C8H18 | CH3(CH2)6CH3 | Octane |
| 9 | C9H20 | CH3(CH2)7CH3 | Nonane |
| 10 | C10H22 | CH3(CH2)8CH3 | Decane |
| 11 | C11H24 | CH3(CH2)9CH3 | Undecane |
| 12 | C12H26 | CH3(CH2)10CH3 | Dodecane |
| 20 | C20H42 | CH3(CH2)18CH3 | Icosane |
| 30 | C30H62 | CH3(CH2)28CH3 | Triacontane |
| 40 | C40H82 | CH3(CH2)38CH3 | Tetracontane |
To specify a straight-chain alkane, the prefix n-(for normal) is used some times. However, in the absence of any prefix, the alkane is supposed to be unbranched.
CH3 – CH2 – CH2 – CH3 Butane or n-Butane
Alkyl groups
Alkyl groups are the groups that constantly appear as structural units of organic molecules. These are derived, from an alkane, by removing a hydrogen atom bonded to carbon. These groups (known collectively as alkyl groups) are named simply by dropping –ane from the name of the corresponding alkane and replacing it by –y1. The general formula for an alkyl group is CnH2n+1, because it contains one less hydrogen atom than the parent alkane, CnH2n+2.
| Alkane | Alkyl group | Abbreviation |
| Methane, CH4 | Methyl, CH3– | Me- |
| Ethane, CH3CH3 |
Ethyl, CH3CH2– or C2H5– n – propyl, CH3CH2CH2– |
Et – |
| Propane, CH3CH2CH3 |
Isopropyl, n-Butyl, CH3CH2CH2CH2– |
n-Pr – or Pr – i-Pr- |
| n-Butane, CH3CH2CH2CH3 |
sec – Butyl, Isobutyl, |
n-Bu– or Bu– s-Bu– i-Bu– |
| Isobutane, | tert–Butyl, | t-Bu- |
Among the alkyl groups we encounter the problem of isomerism. While only one alkyl group can be derived from methane (the methyl, CH3-) and ethane (the ethyl, CH3CH2-), two or more alkyl groups can be derived from higher alkanes.
From propane (C3H8), two alkyl groups can be derived. Removal of one of the hydrogens from one of the end carbon atoms gives an alkyl group that is called the propyl group.
n-Propyl
Removal of one of the hydrogens from the middle carbon atom gives an alkyl group that is called the isopropyl group.
Both these alkyl groups contain the propane chain, but differ in the point of attachment of the group to the rest of the molecule.
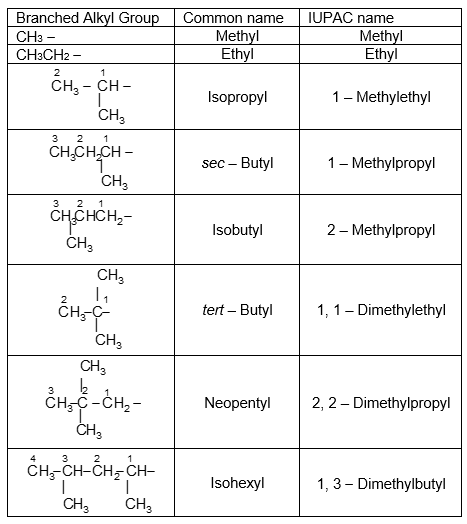
There are four butyl groups, two derived from the straight–chain n-butane, and two derived from the branched–chain isobutane. These are given the designations: n– (normal), sec– (secondary), iso– and tert– (tertiary) as shown below:
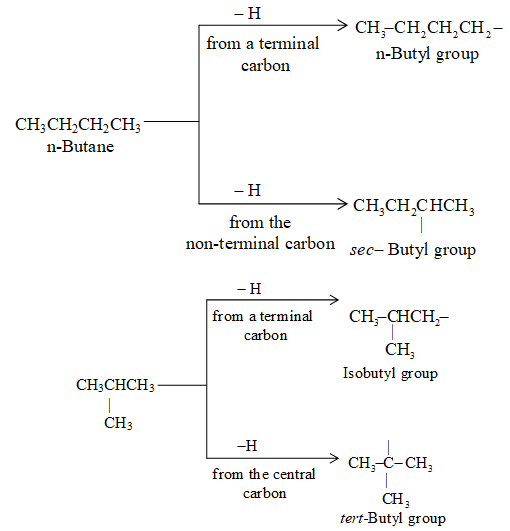
Again the difference between n–butyl and sec–butyl and between isobutyl and tert-butyl lies in the point of attachment of the alkyl group to the rest of the molecule. Beyond butane the number of isomeric alkyl groups derived from every possible alkane becomes so large that it is impracticable to designate them all by various available prefixes.
There is one five-carbon alkyl group commonly called the neopentyl group:
Sometimes the smaller alkyl groups are written using abbreviation. For example, methyl as Me-, ethyl as Et– and so on.
The symbol R is used as a general symbol to describe any possible alkyl group. For instance, R may be a methyl group, an ethyl group, a propyl group, or an isopropyl group. Thus, the general formula for an alkane is R – H.
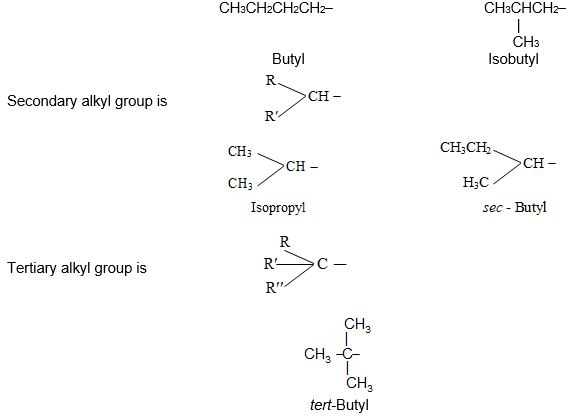
An alkyl group is described as primary if the carbon at the point of attachment is bonded to only one other carbon, as secondary if bonded to two other carbons, and tertiary if bonded to three other carbons. Thus, if R is any hydrocarbon radical, the different kinds of alkyl groups are
RCH2– R2CH- R3C-
Primary Secondary Tertiary
Illustration 9: Classify each of the following alkyl groups as primary, secondary or tertiary: Butyl, Isopropyl, Isobutyl, sec-Butyl and tert-Butyl.
Solution: Primary alkyl group is RCH2 –
In future discussion, the prefix n-will be used to describe any alkyl group in which all the carbons make a single continuous chain and in which the point of attachment is the terminal carbon. For example:
CH3CH2CH2CH2CH2– CH3(CH2)4CH2–
n-Pentyl n–Hexyl
The prefix iso– will be used to describe any alkyl group (of 6 carbons or fewer) that has a single one-carbon branch on the second last carbon of a chain and has the point of attachment at the opposite end of the chain. For example
Nomenclature of Branched–Chain Alkanes
In branched chain alkanes, all the carbon atoms are not present in a continuous sequence rather, one or more carbons are attached to the chain at one or more points:
The prefixes n–, iso-, and neo–are sufficient to identify the different butanes and pentanes, but after this point unworkable number of prefixes would be required.
The prefix n-could be used for any alkane, no matter how large, in which all the carbon atoms make a continuous chain with no branches:
An alkane of six or less carbons in which all the carbons except one form a continuous chain and that left out carbon is attached to the second last carbon is called an isoalkane.
To name any other of the higher alkanes, it is better to make use of the IUPAC system. The possibility of having branched–chain alkanes that are structural isomers of the continuous – chain alkanes starts with butane (n = 4). A systematic name of a branched chain alkane is derived by identifying the parent alkane.
The IUPAC rules for the systematic naming of these alkanes are:
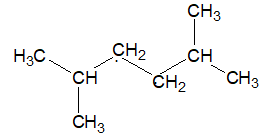
IUPAC Rule 1: To determine the parent alkane, identify the longest continuous chain of carbon atoms. The parent chain is the framework on which the various substituent groups are attached and thus the compound is considered to have been derived from this parent structure by the replacement of one or more hydrogens by various alkyl groups. Thus, the following branched – chain alkane is a substituted pentane rather than a substituted butane because the longest continuous chain has five carbons:
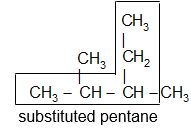
Similarly the following hydrocarbon will be regarded as a substituted hexane because the longest continuous carbon chain (parent chain/ root chain) contains six carbon atoms.
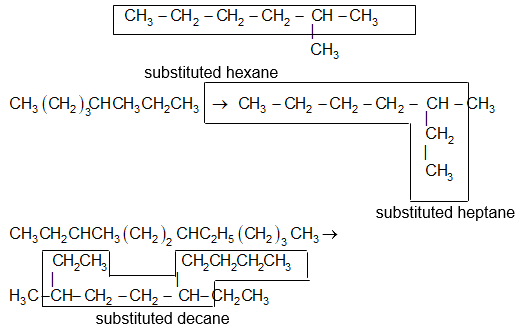
Illustration10: Is the following selection of the parent chain correct? Comment.
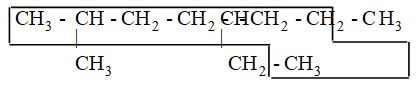
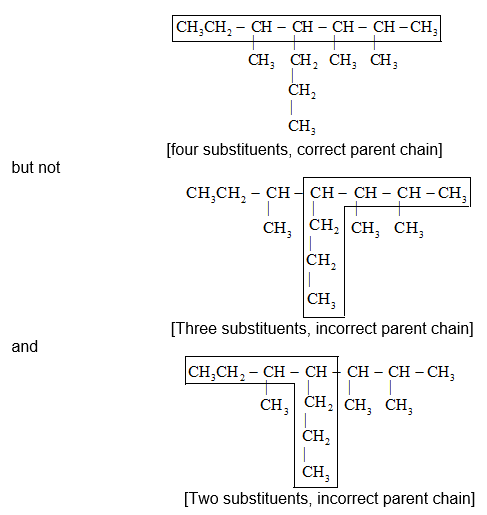
Solution: In the given alkane, the longest chain has nine carbons as shown below, hence the parent (root) alkane is nonane:

Previous selection of parent chain is not correct because it has just eight carbons. If in a given alkane two or more continuous chains of equal length compete for selection as the parent chain, select the chain with the maximum number of substituents (side chains) as the base stem chain. Thus, select
IUPAC Rule 2: The substituent groups attached to the parent chain are named by replacing the ending –ane of the corresponding alkane by –yl. In other words, all the substituent groups attached to the parent chain should be named as the alkyl groups (or alkyl radicals), the simplest examples being the methyl (CH3-) and ethyl (CH3CH2-) groups. If the substituent chain is branched, then the same IUPAC rules apply to such complex substituents: first, find the longest continuous chain in the substituent; next name all its substituents.
IUPAC Rule 3: To locate the positions of the carbon atoms at which branching takes place due to the substitution of alkyl groups in place of hydrogen atoms, the parent chain is numbered starting from one of the ends of the chain. The substituent groups are assigned numbers corresponding to their positions on the chain.
For a single substituent, numbering begins with the end of the parent chain that is closest to the substituent. For two substituents the numbering is done in such a way that the carbon atoms carrying the side chain substituents get the lowest possible numbers. Thus

If the two substituents are at equal distance from the two ends of the chain, use the alphabet to decide how to number. The substituent coming first in alphabetical order is given the lower number.
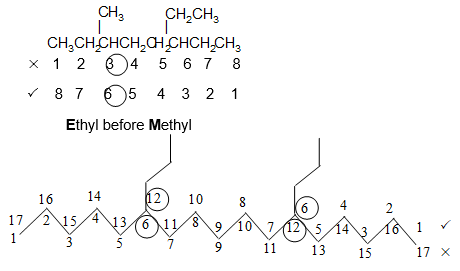
If there are three or more substituents, then number the stem chain in the direction that gives the lower number at the first difference between the two possible numbering schemes. In other words, when the series of substituent locants are compared term by term, the “lowest” series has the lowest number at the first point of difference. This procedure follows the principle of the first point of difference.
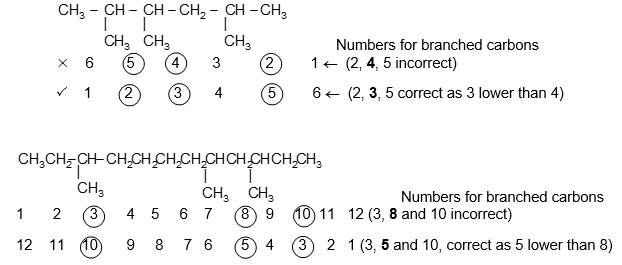
Branched substituent groups are numbered outward from the main chain, thus, the carbon attached to the main stem, becomes the C1 of the group.
The above examples clearly highlight the fact that the systematic nomenclature for branched alkyl groups is similar to that for branched – chain alkanes, with the provision that numbering always starts at the point where the group is attached to the main chain.
The common names isopropyl, isobutyl, sec-butyl, tert-butyl and neopentyl are approved by the IUPAC system provided these groups are not substituted further.
IUPAC Rule 4:
Write the name of the branched–chain alkane by first naming the substituent group, preceded by the number (obtained by applying rule 2) denoting its location on the parent chain, and then adding the name of the parent alkane without any break. Numbers designating the location of the substituent group are separated from words by a hyphen.
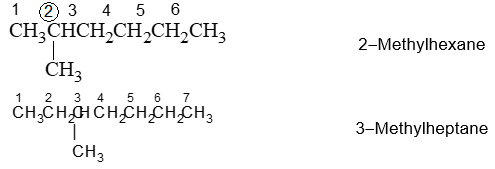
If two or more different substituents are present, then each possible substituent is given a number designating its location on the parent chain. Arrange all the substituents in an alphabetical order (each preceded by the carbon number to which it is attached and a hyphen) and then add the name of the stem.
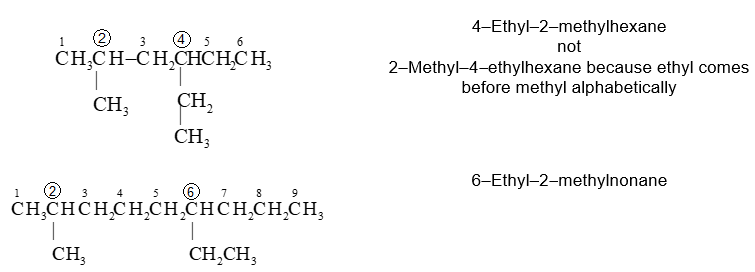
If two different substitutents are present on the same carbon atom of the parent chain, then use the number designating the location twice.
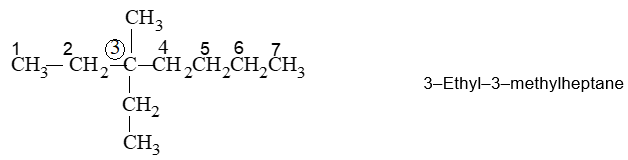
If two or more identical substituents are present in a molecule, then the name of the particular substituent should be preceded by the prefixes: di- (for 2), tri- (for 3), tetra- (for 4), penta- (for 5), hexa- (for 6) and so forth. The positions of attachment to the parent chain are written collectively before the substituent name and are separated by commas :

The numerical prefixes as well as the prefixes sec– and tert– are not considered in the alphabetical ordering, except when they are part of a complex substituent name. However, the prefixes iso and neo– are considered in the alphabetical ordering.
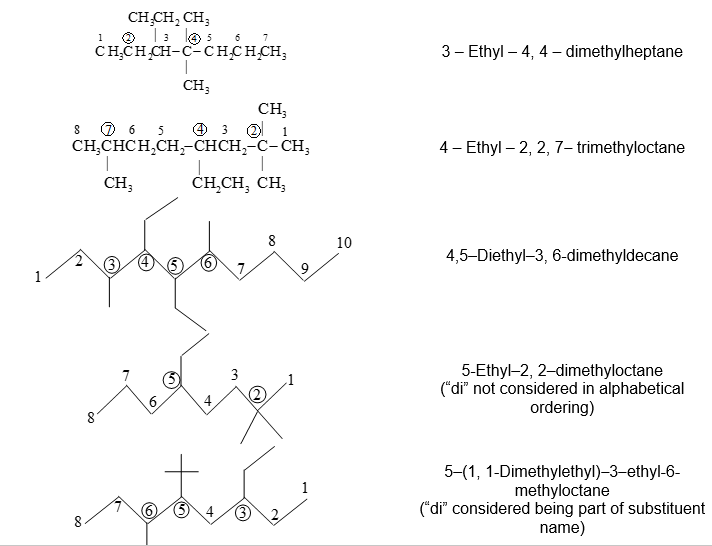
As discussed above the name of branched chain alkyl group is placed in parenthesis while naming the compound.
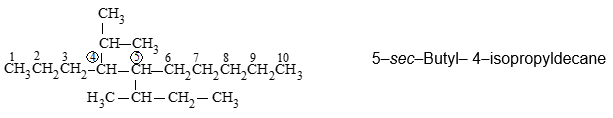
As described above the use of iso and related common prefixes for describing alkyl groups, along the parent chain, are allowed by the IUPAC system as long these are not further substituted.
Although the common group names are permitted by IUPAC, it is preferable to use the systematic names. Such complex names are usually enclosed in parentheses to avoid possible ambiguities:
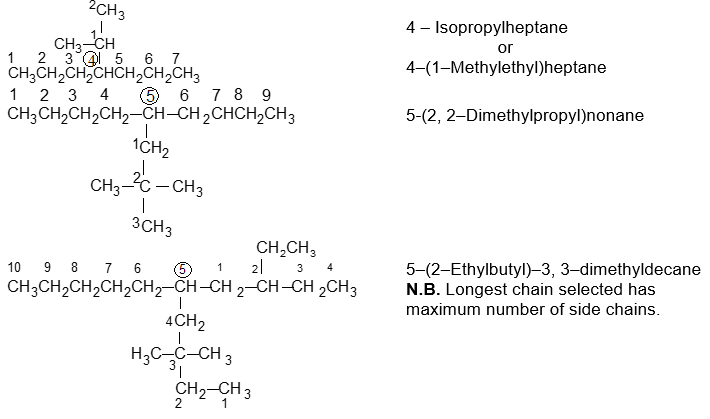
Illustration 11: Write the IUPAC names of the following compounds.
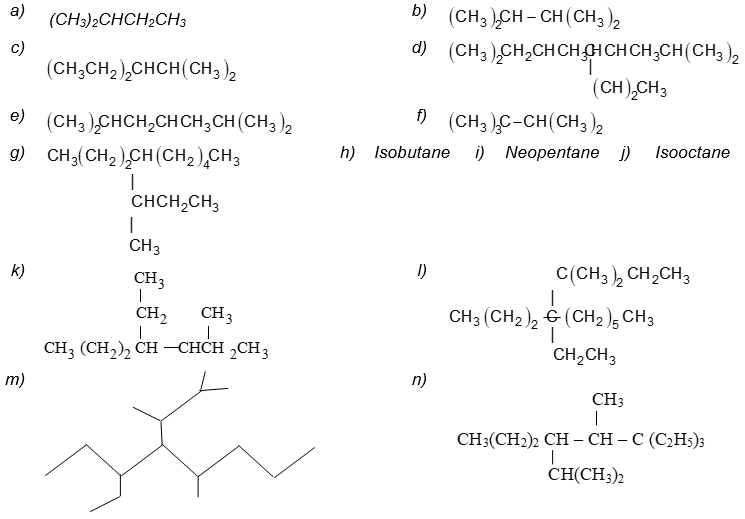
Solution:
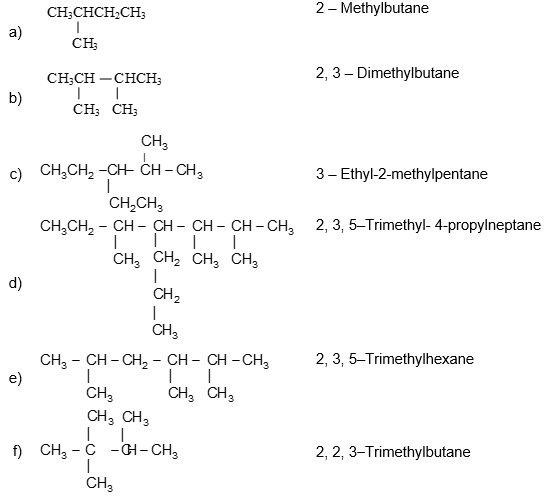
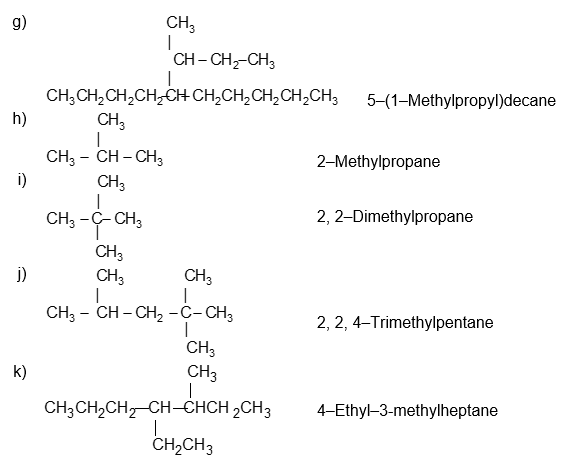
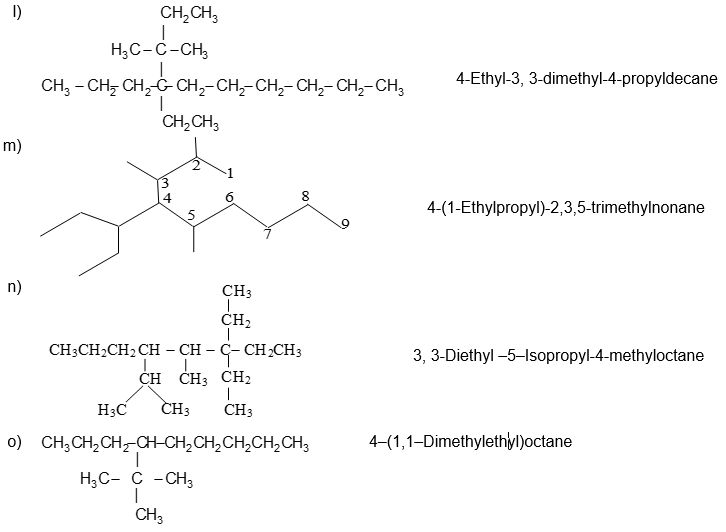
If a specific complex substituent is present more than once, its name is preceded by the prefix bis (for 2), tris – (for 3), tetrakis – (for 4), pentakis – (for 5), and so on.
5, 8 – Bis (1 – methylethyl)dodecane
Classification of carbon and hydrogen atoms
It is extremely useful to classify each carbon atom of an organic molecule with respect to the number of other carbon atoms to which it is bonded. A primary (10) carbon atom is bonded directly to only one other carbon atom; a secondary (20) carbon atom is bonded directly to two other carbon atoms; a tertiary (30) carbon is bonded to three others and a quaternary (40) is bonded to four others. For example:
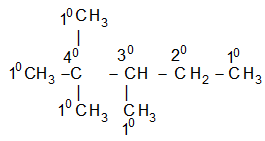
The hydrogen atoms of an organic molecule are classified on the basis of the carbon atoms to which they are attached. A hydrogen atom attached to a primary carbon atom is a primary (10) hydrogen atom. Similarly secondary (20) hydrogen atom is attached to a secondary carbon and tertiary (30) hydrogen atom is attached to a tertiary carbon. For example, 2–methylbutane has primary (10), secondary (20), and tertiary (30) hydrogen atoms.
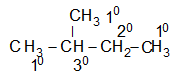
There is no quaternary (40) hydrogen atom!
Illustration 12: Which of the following pentanes has only primary hydrogen atoms?
a) n-pentane b) Isopentane c) Neopentane
Solution: Make their structures
a) CH3CH2CH2CH2CH3 has 10 and 20 hydrogen atoms.
b)
c) .
Cycloalkanes and their nomenclature
In open–chain compounds, the carbon atoms are attached to one another to form straight chains as well as branched chains. In cyclic compounds, the carbon atoms are arranged to form rings.
Cyclic compounds which contain closed rings comprised of carbon atoms only are known collectively as carbocyclic or homocyclic compounds.
Cyclic compounds in which the rings contain more than one kind of atom are known collectively as heterocyclic compounds.
Carbocyclic compounds which resemble the aliphatic compounds in many ways are often called alicyclic compounds (aliphatic cyclic compounds).
Saturated alicyclic hydrocarbons, containing singly bonded carbon atoms arranged in rings are known as cyclic alkanes or cycloalkanes. (Alkanes in which all or some of the carbon atoms are arranged in a ring.)
Alkanes have the general formula CnH2n+2; cycloalkanes containing a single ring have two fewer hydrogen atoms and thus have the general formula cnH2n or (CH2)n. [The same as that of the alkenes, they do not contain a double bond but possess a ring structure]. When the molecular formula of a saturated alicyclic hydrocarbon corresponds to the general formula CnH2n-2, then the compound contains two rings; if to cnH2n-4, three rings, etc.
Since the cyclic alkanes contain a number of methylene groups joined together to form a ring, they are known as the polymethylens, the number of carbon atoms in the ring being indicated by a Greek or Latin prefix, e.g.,
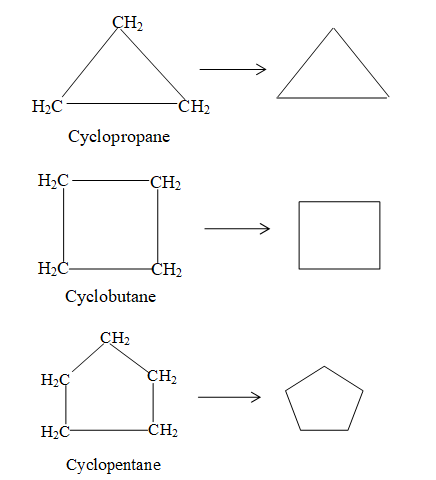
According to the IUPAC system, the saturated alicyclic hydrocarbons with one ring are named by adding the prefix cyclo– to the name of the corresponding open–chain saturated hydrocarbon (continuous – chain alkane) having the same number of carbon atoms as the ring. Thus, they are known collectively as the cycloalkanes or cycloparaffins things. For example:
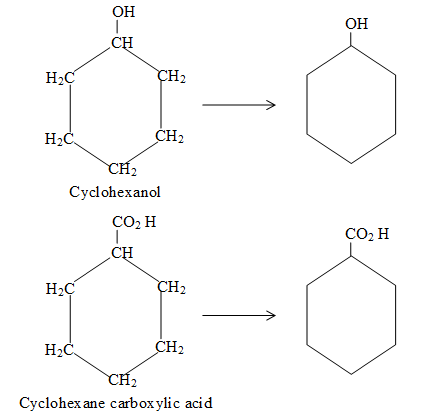
For convenience, aliphatic rings are often represented by simple geometric figures: a triangle for cyclopropane, a square for cyclobutane, a pentagon for cyclopentane, a hexagon for cyclohexane, and so on. It is understood that two hydrogens are located at each corner of the figure unless some other group is indicated.
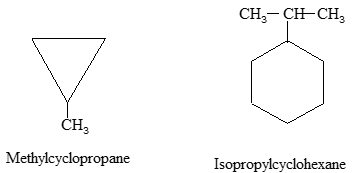
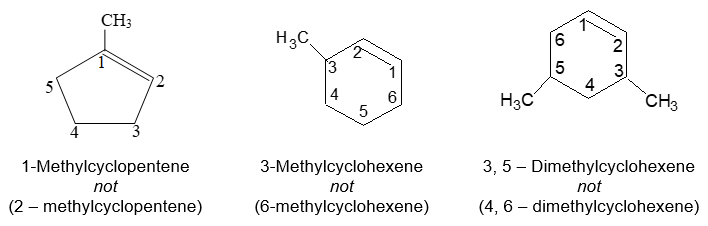
Naming substituted cycloalkanes is straightforward: we name them as alkylcycloalkanes (halocycloalkanes, alkylcycloalkanols and so on). Naming a substituted cycloalkane requires the numbering of the individual ring carbons only if more than one substituent is attached to the ring.
a) If only one substituent is present it is not necessary to designate its position as the carbon of attachment is always defined as carbon 1 of the ring. For example:
b) When two substituents are present, we number the ring carbons in the direction that gives the lowest possible numbering sequence.
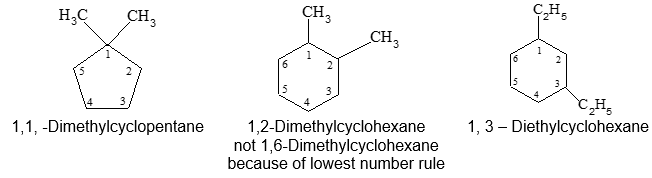
c) When two different substituents are present, we number the ring beginning with the substituent first in the alphabetical order and number in the direction that gives the next substituent the lower possible number. For example
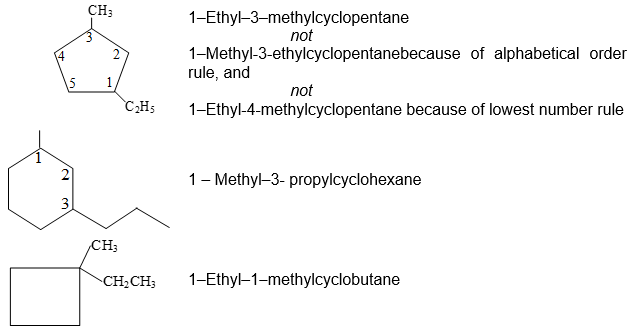
d) When 3 or more substituents are present, we begin at the substituent that leads to the lowest set of locants. When two such sequences are possible, the alphabetical order of the substituent names takes precedence.

e) The substituent groups (or radicals) derived from cycloalkanes by removal of a hydrogen atom are named by replacing the ending –ane of the hydrocarbon with –yl to give cycloalkyl (radicals). Thus cyclopropane becomes cyclopropyl, cyclobutane becomes cyclobutyl, cyclopentane becomes cyclopentyl and so on.
Substituted cycloalkanes are therefore sometimes named as cycloalkylderivatives. Remember, the numbering of the cycloalkyl substituent starts at the point of attachment, and larger rings take precedence over smaller rings.

f) When a cycloalkane has an alkyl substituent the compound could be called either an alkylcycloalkane or a cycloalkylalkane. When a single ring system is attached to a single chain with a greater number of carbon atoms, or when more than one ring system is attached to a single chain, then it is appropriate to name the compound as cycloalkylalkanes.

In general, the smaller unit is treated as a substituent to the larger one.
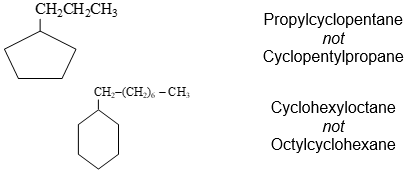
Polycycloalkanes and their Nomenclature
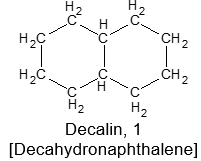
There are many hydrocarbons and hydrocarbon derivatives with two or more rings having common carbon atoms. These polycyclic compounds containing two or more rings share two or more carbon atoms. One such a substance is decalin, which has ten carbons arranged in two six-membered rings:
Another common example is norbornane:
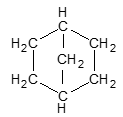
According to the IUPAC system, polycycloalkanes of this type containing two fused or bridged rings are named by attaching the prefix bicyclo to the name of the open-chain alkane containing the same total number of carbon atoms as in the rings. Thus, they are collectively known as bicycloalkanes. For example, decalin containing 10 carbon atoms is a bicyclodecane while norbornane containing 7 carbon atoms is a bicycloheptane.
Molecular models of polycyclic alkanes can be readily constructed by linking the carbon atoms of two alkyl substituents in a monocyclic alkane.
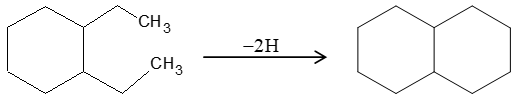
For example, if we remove two hydrogen atoms from the methyl groups in 1, 2-diethylcyclohexane and link the resulting two open valences, the result is decalin.
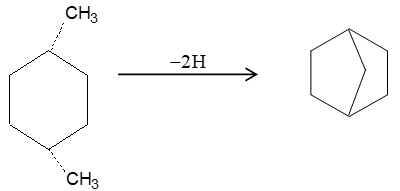
If we treat a molecular model of cis–1, 3–dimethylcyclopentane in the same way, we obtain norbornane.
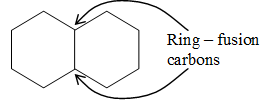
In decalin, two cyclohexanes share two adjacent carbon atoms and the two rings are said to be fused. Bicyclic compounds constructed in this way are called fused bicyclic ring systems, and the shared carbon atoms are called the ring fusion carbons. Groups attached to ring-fusion carbons are called ring-fusion substituents.
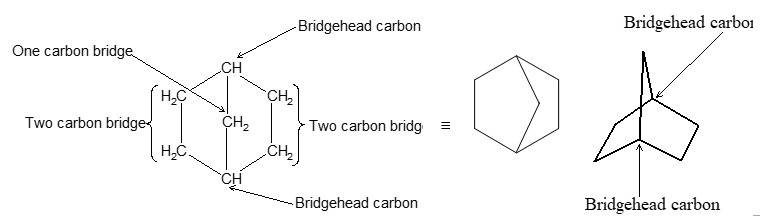
Norbornane is an example of a bridged bicyclic ring system. In bridged bicyclic systems, two nonadjacent carbon atoms common to both rings are called the bridgehead carbons, and each bond, or each chain of atoms, connecting the bridgehead atoms is called a bridge.
Next, we need a way to specify the sizes of the rings, which is done by counting the number of carbon atoms in each of the chains connecting the two tertiary carbon atoms that constitute the ring junctions or bridge heads. Decalin has four carbons in each of the two chains and none in the third. Therefore, decalin is bicyclo [4.4.0] decane.
Notice that the numbers indicating the number of carbon atoms in each of the three bridges connecting the two tertiary carbon atoms are enclosed in square brackets after the prefix “bicyclo” and before the name of the hydrocarbon. The numbers are listed in order of decreasing magnitude and are properly separated by periods, not commas. Some other examples follow:
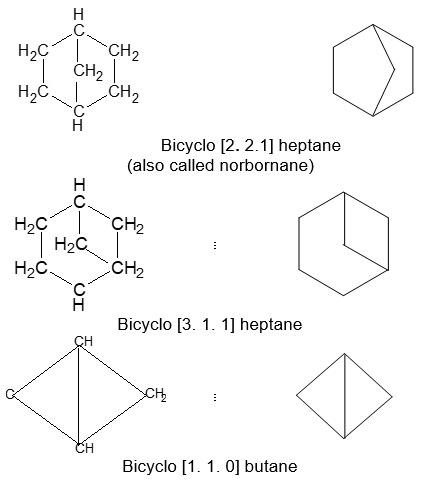
Illustration13: Give IUPAC name for each of the following bicyclic alkanes.

Solution:
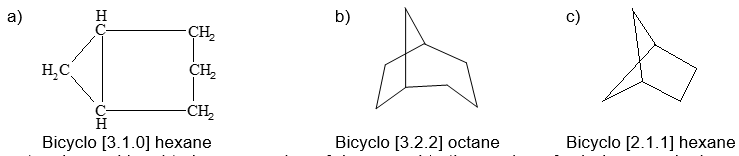
A bridged system is considered to have a number of rings equal to the number of scissions required to convert the system into an acyclic compound.
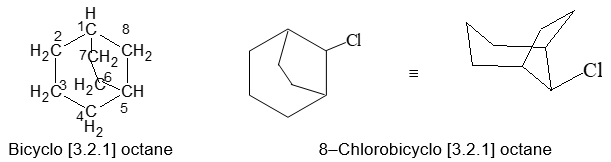
To name substituted polycycloalkanes a suitable numbering system is required. In the IUPAC system the main ring is the one that contains the largest number of carbon atoms. Two of the carbons in the main ring serve as junctions for the main bridge, which is chosen to be as large as possible, consistent with the choice of the main ring. In numbering bicyclic ring systems that have two ring junctions, one of the bridgehead carbons is chosen as C1. The numbering proceeds along the longest chain of carbons to the second bridgehead carbon, then continues from this atom along the next longest chain back to the first bridgehead, and finally is completed along the shortest chain. For example
Here, the main ring has seven carbons (C1 to C7) and there is one-carbon bridge (C8). When the hydrocarbon rings have only one carbon in common, they are called spiranes and are given systematic names in accord with the following examples:
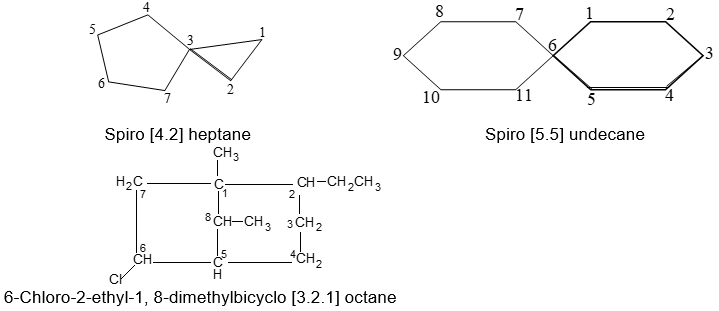
Notice that for spiranes the numbering starts next to the junction point in the smaller ring.
To determine whether a given bridged polycyclic ring system should be bicyclo, tricyclo, and so on, use the rule that the number of rings is equal to the minimum number of bond cleavages needed to convert the ring system into an acyclic hydrocarbon having the same number of carbons.
Nomenclature of alkenes, cycloalkenes and alkadienes
The open – chain hydrocarbons whose molecules have just one carbon – carbon double bond are called alkenes. They are the unsaturated hydrocarbons having the general formula CnH2n (the same as that for the cycloalkanes). The carbon–carbon double bond is often called the “olefinic bond” or “ethylenic bond” and the alkenes designated as olefins (Oil – formers).
The name olefin arose from the fact that ethylene was called ‘olefiant gas’ (oil – forming gas), since it formed oily liquids on treatment with chlorine or bromine.
Like other organic compounds, some alkenes are still known by common names, in which the suffix –ane of the corresponding alkane is replaced by –ylene. For example
N.B. Ethylene occurs in nature as a plant hormone. It is produced naturally by fruits such as tomatoes and bananas and is involved in the ripening process of these fruits. Now most of the ethene is used in the commercial fruit industry to bring about the ripening of tomatoes and bananas picked green because the green fruits are less susceptible to damage during shipping. Propylene is used in making the polymer polypropylene (plastic).
Substituent names are added as prefixes. Isomers differing only in the position of the double bond are prefixed by Greek letters or numbers which indicate the position of the double bond, and the number (or Greek letter) indicates the first of the two carbon atoms that are joined together by the double bond. For example
CH3CH2CH = CH2 1 – Butylene or – butylene
CH3CH = CHCH3 2 – Butylene or – butylene
3 – Methyl – 2- pentylene
Another method of nomenclature is to consider ethylene as the parent substance and the higher members as derivatives of ethylene. If the compound is a monosubstituted derivative of ethylene, then no difficulty is encountered in naming it, if the compound is a disubstituted derivative of ethylene, isomerism is possible, since the alkyl groups can be attached to the same or different carbon atoms. When the groups are attached to the same carbon atom, the olefin is named as the asymmetrical or unsymmetrical compound (abbreviated to as or – unsym); when attached to different carbon atoms, the olefin is named as the symmetrical (sym or s – ) compound:
According to the IUPAC system of nomenclature, the class suffix of the olefins is –ene, and thus the homologous series becomes the alkene series. If the simpler ending –ene is used instead of –ylene, then the two simplest alkenes ethylene and propylene will be named as ethene and propene respectively. More complicated systems require adaptations and extensions of the rules for naming alkanes.
Rule 1 : To determine the parent name (i.e., to name the stem) select the longest continuous chain that includes both the carbons making up the double bond (The molecule may have longer carbon chains, but ignore them) and change the ending of the name of the alkane of identical length from –ane to –ene. Thus, if the parent chain contains five carbons, the parent name for the alkene is pentene; if it contains six carbons, the parent name is hexene, and so on. For example:
Rule 2 : To indicate the location of the double bond number the parent chain. Start numbering from that end of the chain which is closer to the double bond. Designate the location of the double bond by using the number of the first atom of the double bond as a prefix.
Cycloalkenes do not require the numerical prefix, but the carbons making up the double bond are assigned the numbers 1 and 2.
Alkenes that have the same molecular formula but differ in the location of the double bond (such as but-1-ene and but-2-ene) are called double – bond isomers.
An alk-1-ene is also referred to as a terminal alkene; the others are called internal. Note that alkenes are easily depicted in the line notation.
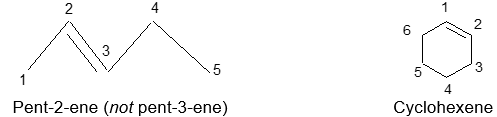
Rule 3: To indicate the locations of the substituent groups use the numbers of the carbon atoms to which they are attached. To complete the name, add names of the substituents and their positions to the parent alkene name as prefixes:
Rule 4: If the alkene stem is symmetrical, begin from the end that gives the first substituent along the chain the lowest possible number.
Rule 5: When there are several chains of equal length containing the double bond, then the same principles apply as for the alkanes:
Rule 6: Cycloalkenes are named by the system used for the open – chain alkenes, except that the numbering always is started at one of the carbons of the double bond and continued around the ring through the double bond so as to keep the index numbers as small as possible.
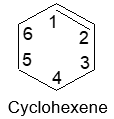
Rule 7 : To name the substituted cycloalkenes, number the structure in such a way that the carbon atoms of the double bond get the 1 and 2 positions and also the substituted groups get the lower numbers at the first point of difference. Note that with substituted cycloalkenes it is not necessary to specify the position of the double bond since it will always begin with C1 and C2. For example:
Rule 8: The names of univalent hydrocarbon groups derived from alkenes have the ending –enyl (alkene alkenyl) and the carbon atom with the free valence is numbered 1. For example :
A few alkenyl groups have trivial names that commonly are used in place of systematic names. These are
Rule 9 : Use the suffix – ylidene to give alkylidene when a hydrocarbon group is doubly – bonded to a single carbon of a cycloalkane ring:

Rule 10 : In a 1, 2 – disubstituted ethene, the two substituents may be on the same side of the molecule or on opposite sides. Thus, there is a need to identify the stereoisomers. The first stereochemical arrangement in which the two substituents are on the same side of the double bond is designated cis, and the second, in which the two substituents are on opposite sides, is designated trans:
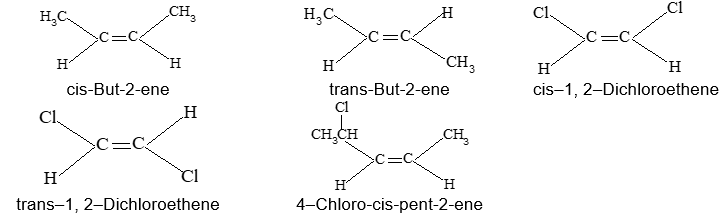
Two alkenes of the same molecular formula differing only in their stereochemistry are called cis – trans isomers and are typical examples of diastereomers: stereoisomers that are not mirror images of each other.
Rule 11 : To label more complex diastereomers, a more general method, the E, Z system is used. The labels cis- and trans- cannot be applied when three or four different substituents are attached to the double-bond carbons. To name such alkenes, IUPAC has adopted an alternative system: the E, Z system: In this convention, the sequence rules devised for establishing priority in R, S names are applied separately to the two groups on each double – bond carbon.
When the two groups of higher priority are on opposite sides, the molecule is of the E configuration (E from entgegen, German, opposite). When the two substituents of higher priority appear on the same side, the molecule is a Z isomer (Z from zusammen, German, together).
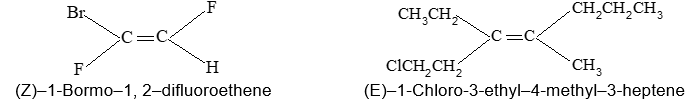
Rule 12 : Name the compounds containing a double bond and an alcohol group as alkenols. Give the hydroxyl functional group precedence over the double bond in numbering the parent chain i.e. the stem incorporating both functional groups is numbered so as to give the carbon bearing the – OH group the lowest possible arrangement.
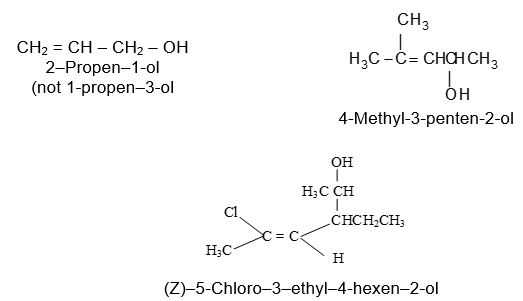
The last e in alkene is dropped in the naming of alkenols.
Rule 13: An alkene containing halogen is usually named as a haloalkene, that is, as an alkene containing halogen as a side chain.
CH2 = CH – Cl CH2 = CH – CH2 – Br
Chloroethene 3–Bromopropene
Rule 14: In the smaller substituted cycloalkenes, the double bond can exist only in the cis configuration. The trans arrangement is prohibited due to strain. However, in larger cycloalkenes, trans isomers are stable.
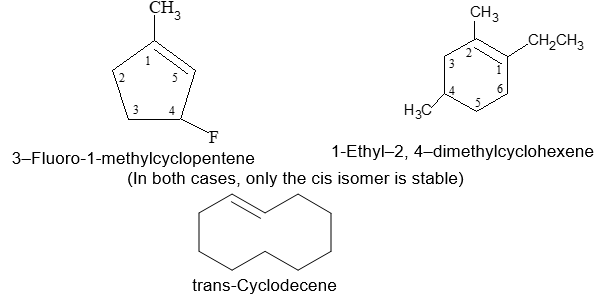
Rule 15: Name cyclic compounds containing a double bond and an alcohol group as cycloalkenols and give the alcohol carbon the lower number.
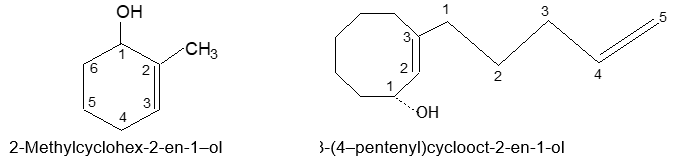
The numbering of a substituent chain begins at the point of attachment to the basic stem.
Unsaturated acyclic hydrocarbons with more than one double bond
When the aliphatic hydrocarbon contains two double bonds, it is known as a diolefin or alkadiene and has the general formula CnH2n-2; when there are three double bonds present, the compound is known as a triolefin or alkatriene, and has the general formula CnH2n-4; etc.
Rule 16: To name diolefin, triolefin, etc. select the longest continuous carbon chain containing the maximum number of double bonds as the parent chain, and number the main chain so as to give the lowest possible numbers to the double bonds. Finally, the location of each double bond is specified by suitable numbers, as illustrated below:
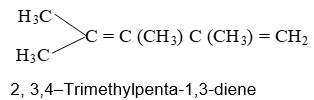
There are three different types of alkadienes on the basis of the relationship of the double bonds to each other:
1, 2–Alkadienes and similar substances containing the arrangement > C = C = C < are said to have cumulated double bonds. The simplest compound of this type is allene or propadiene :
H2C = C = CH2
Propadiene (allene)
1,3–Alkadienes and similar compounds containing single and double bonds arranged alternately are said to have conjugated double bonds.
The simplest member of this group of compounds is buta–1,3–diene:
CH2 = CH – CH = CH2
Other typical examples are:
Compounds with two double bonds that are neither cumulated nor conjugated are classified as having isolated double – bond systems:
Typical examples:
CH2 = CH – CH2 – CH = CH2 CH2 = CH – CH2 – CH2 – CH = CH2
1,4–Penta-1,4-diene Hexa-1,5-diene (diallyl)
Illustration 14: Give IUPAC names for the following:
a)
b)

d) CH2= C(CH2CH2CH3)2
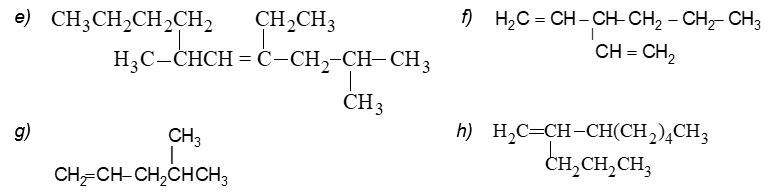
Solution:
a) 3–Methylbut–1-ene b) 2,8–Dimethyldeca-3,6-diene
c) Octa-1,3,5,7–tetraene d) 2–(1–Propyl)pent-1-ene
e) 4–Ethyl-2,6-dimethyldec-4-ene f) 3–n-Propylpenta-1,4–diene
g) 4–Methylpent-1-ene h) 3–Propylocta-1-ene
i) 5–Ethyl-6-methyl-dec-5-ene j) 2,3-Dimethylhept-2-ene
k) trans–Hept-3-ene l) Bromoethene
m) 3–Chloropropene n) 1,3–Dimethylcyclohexene
o) 3–n-Propylhept-1-ene p) 2,3–Dimethylbut–2-ene
q) 4–Ethyl–2-methylhex-1-ene r) 4–Methylpent–4-ene–2-ol
s) 3,5-Dimethylcyclohexene
The locant for double bond may be written preceding or following the name of the parent alkene or following the root name followed by the suffix ene or diene or triene. For example, all the three names i.e., 1, 3–butadiene, butadiene–1, 3 or buta – 1, 3 –diene are correct for butadiene.
Nomenclature of Alkynes
Alkynes are unsaturated acyclic (or aliphatic) hydrocarbons that contain just one carbon – carbon triple bond. They have the general formula CnH2n-2, the same as that for the cycloalkenes. Alkynes occur in nature and can be synthesized in the laboratory.
Like the alkanes and alkenes, the alkynes form a homologous series, the increment again being CH2. Acetylene is the common name of the simplest and smallest alkyne, C2H2.
Two systems of nomenclature are in use. In the common (or trivial) system, higher homologues are considered to be derived from acetylene by replacement of one or both hydrogen atoms by alkyl groups. Thus the common names for the higher alkynes are the alkylacetylenes.
Common names for alkynes
For more complicated alkynes, the IUPAC names are used. The rules of the IUPAC system are :
Rule 1: Select as the parent structure the longest continuous carbon chain that contains the carbon – carbon triple bond; then treat the compound to have been derived from this structure by replacement of hydrogen by suitable substituents.
The parent structure is known as ethyne, propyne, butyne, pentyne, and so on, depending upon the number of carbon atoms, each name is derived by changing the ending –ane of the corresponding alkane name to –yne.
Rule 2: Indicate by a number the position of the triple bond in the parent chain. Although the triple bond involves two carbon, atoms designate its position by the number of the first triply bonded carbon encountered when numbering starts from the end of the chain which is closest the triple bond:
CH3CH2C CH CH3C CCH3 CH3CH2C CCH3
But-1-yne But-2-yne Pent-2-yne
Rule 3 : Indicate by numbers the positions of the alkyl groups attached to the parent chain.
Monosubstituted acetylenes or 1-alkynes having the general structure RC CH are called terminal alkynes, whereas those with structure of RC º CR are called internal alkynes.
The hydrogen attached to the carbon of the triple bond is called the acetylenic hydrogen.
R – C C – H Acetylenic hydrogen
A terminal alkyne
The anion obtained when the acetylenic hydrogen is removed is known as an alkynide ion or acetylide ion. These ions are quite useful in synthesis:
An alkynide ion The propynide ion
(an acetylide ion)
Rule 4 : The univalent hydrocarbon substituents derived from alkynes have the endings ynyl and hence are called alkynyl groups. As usual, the numbering of the substituent chain begins at the point of attachment to the basic stem:
CH C- CH3 – C C- CH C – CH2–
Ethynyl Propynyl 2-Propynyl
(Propargyl)
Like alkanes and alkenes, alkynes can also be depicted in bond–line notation.
Rule 5: An alkyne containing halogen is usually named as a haloalkyne, that is, as an alkyne containing halogen as a side chain.
CH3CCCHBrCH2CH3 Cl – CH2CCH CH3CCCH2Cl
4-Bromohex–2–yne 3 – Chloropropyne 1-Chlorobut–2–yne
Rule 6: Alkynes incorporating the hydroxyl function are named alkynols, with numbers to indicate the positions of the double bond and the hydroxyl group. Note that an – OH group has priority over the triple bond when numbering the chain of an alkynol:
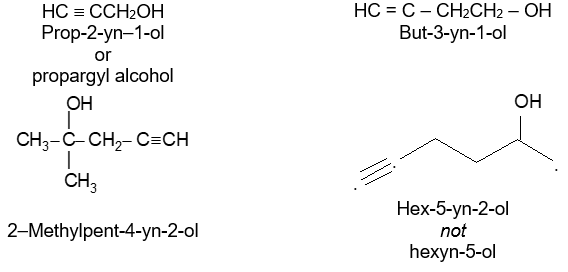
Note that –ol takes priority over –yne, –ol appears last in the name. Also note the omission of the final e of –yne in –ynol.
Rule 7: Hydrocarbons with more than one triple bond are called alkadiynes, alkatriynes, and so on, according to the number of triple bonds. The longest continuous carbon chain containing the maximum number of triple bonds is chosen as the parent hydrocarbon, and the parent chain is so numbered as to give the lowest possible numbers to the triple bonds.
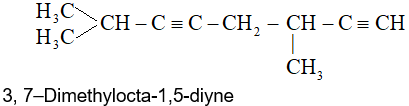
Rule 8: In IUPAC system, hydrocarbons containing both double and triple bonds are named systematically as alkenynes (not alkynenes). The parent chain always should be numbered to give the multiple bonds the lowest possible numbers (i.e., the chain is numbered starting from the end closest to either of the functional groups).
When a double bond and a triple bond are at equidistant positions from either turminus, the double bond is given the lower number.
CH2 = CH – CH CH CH2 = CH – C C – CH = CH2
But-1-en-3-yne Hexa-1,5-dien-3-yne
(vinylacetylene) (divinylacetylene)
CH3 – CH = CH – C CH CH3CH2CH = CH – C CH
Pent-3-en-1-yne Hex-3-en-1-yne
not not
pent-2-en-4-yne hex-3-en-5-yne
Note the omission of the final e of –ene in –enyne.
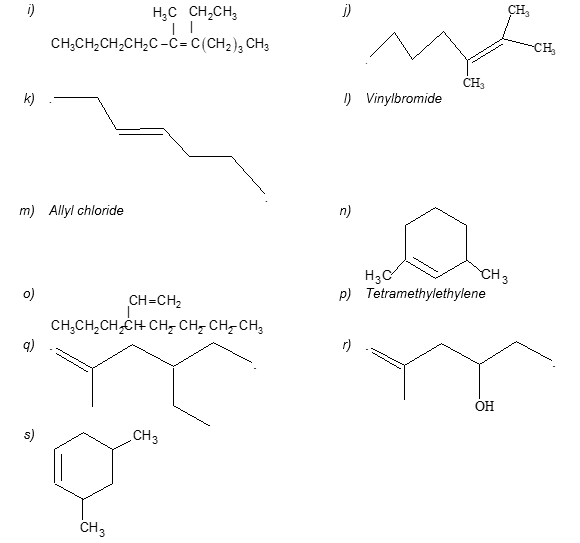
Illustration 15: Give the IUPAC names for the following :
a)
b) CH2 = CH – CH2 – C º CH
c) CH3CH= CH– C º CH
Solution:
a) 3,3-Dimethylbut-1-yne
b) Pent-1-en-4-yne (not pent-4-ene-1-yne)
c) 5-Ethynylhepta-1,3,6-triene
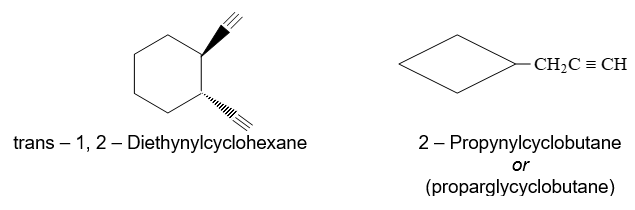
Illustration 16: Draw structures for the following
a) Hexa-1,3-diene-5-yne b) Cyclodec-1-en-4-yne c) 5-Ethynylhepta-1,3,6-triene
Solution:
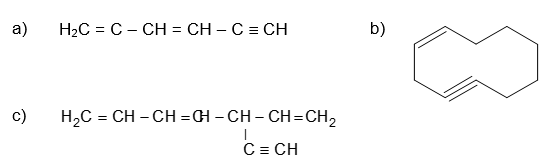
Nomenclature of arenes and their derivatives
Arenes the so called aromatic hydrocarbons are cyclic unsaturated compounds that have such strikingly different chemical properties from conjugated alkenes (polyenes) that it is convenient to consider them as a separate class of hydrocarbons.
Benzene and its derivatives were originally called aromatic compounds because many of them have a strong aroma. Benzene (a colorless liquid, m.p. 5.50, b.p. 800c), even though its order is not particularly pleasant, is viewed as the ‘parent’ aromatic molecule.
Frequently, the simplest member benzene, is represented as a cyclic conjugated molecule of three single and three double bonds:
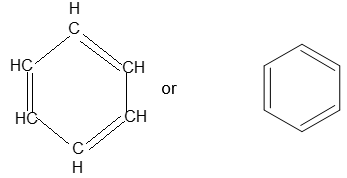
Actually, all the carbon – carbon bonds are equivalent but it is convenient to represent the structure in the manner shown above.
Wherever the symbol for the benzene ring with its three double bonds is written it should be understood to represent only one of contributing resonance forms. Alternatively, the benzene ring is sometimes drawn as a regular hexagon with an inscribed circle.

A variety of substituted benzenes are known that have one or more of the hydrogen atoms of the ring replaced with other atoms or groups. In almost all of these compounds the special properties associated with the benzene nucleus are retained.
Rule 1: Two systems are used in naming monosubstituted benzenes. In certain compounds, benzene is the parent name and the substituent is simply indicated by a prefix. Thus, to name such derivatives we simply prefix the name of the substituent group to the word – benzene as, for example:
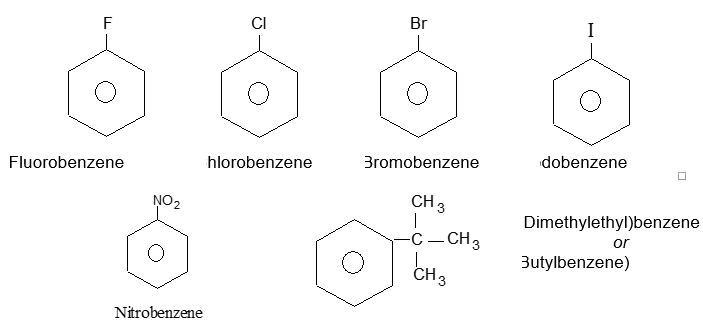
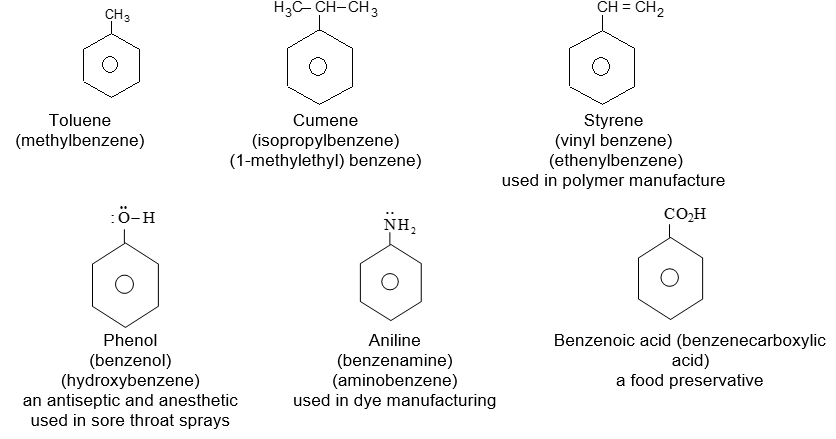
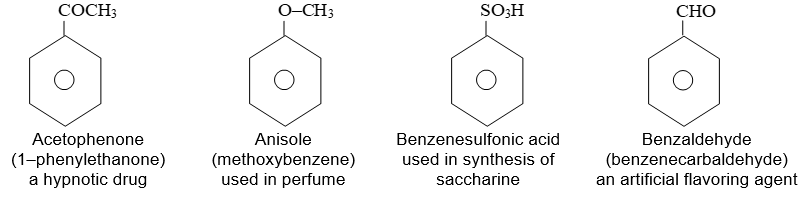
For other compounds, the substituent and the benzene ring taken together form a new parent name (special name) which may show no resemblance to the name of the attached substituent group. For example
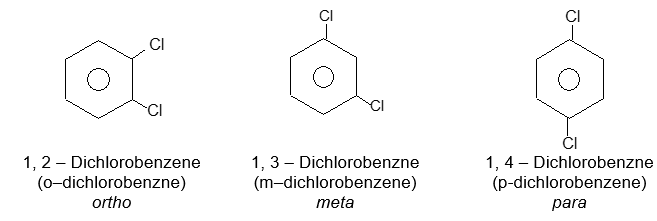
Rule 2: When there are two or more substituents on a benzene ring, position isomerism arises. There are three possible arrangements of disubstituted benzenes. These arrangements are designated by the prefixes or by the use of numbers: 1, 2– (ortho, or o- ) for adjacent substituents, 1, 3– (meta-, or m-) for alternate substituents, and 1, 4- (para – , or p-) for diagonally opposite substituents. For example:
If one of the two groups is the kind that gives a special name to the molecule, then the compound is named as a derivative of that special compound. For example :
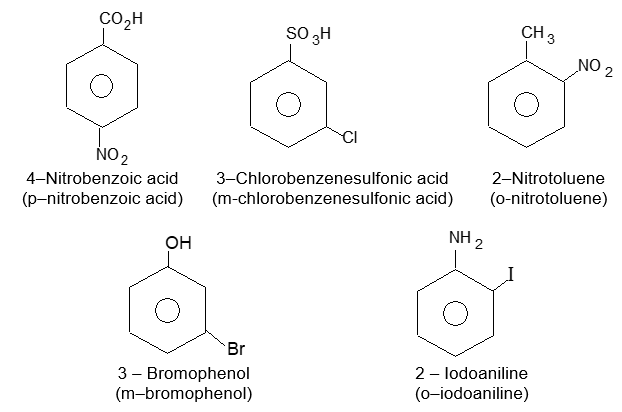
If the two groups are different, and neither is a group that gives a special name to the molecule, we simply list them in alphabetical order and assign their positions on the ring with the lowest possible numbers. Finally, end the word with benzene as, for example:
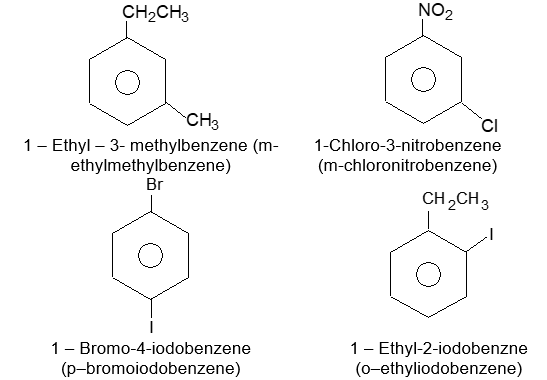
Sometimes both the groups impart special names which may show no resemblance to the name of the attached substituent groups, for example, the dimethylbenzenes are often called xylenes :
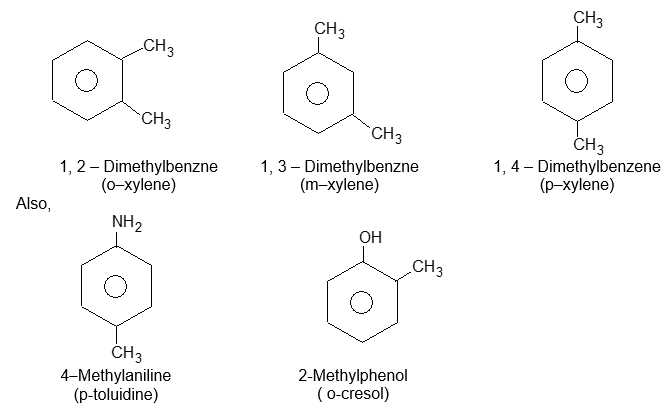
Xylenes are common industrial and laboratory solvents. Rule 3: To name tri – and more highly substituted derivatives, the positions of the substituents must be indicated by the use of numbers. For this purpose the six carbons of the benzene ring are numbered so as to give the substituents the lowest set of numbers, as in cyclohexane nomenclature. For example:

Notice that the benzene ring is numbered so as to give the lowest possible numbers to the substituents.
When more than two substituents are present and the substituents are different, they are listed in alphabetical order.
Substituent positions on the ring are identified by the lowest locant rule.

If one of the substituents that gives a special name is present, then the compound is named as having the special substituent in position 1. For example:
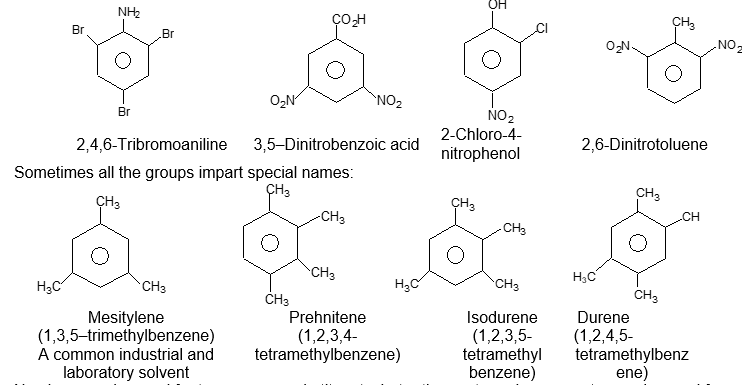
Numbers can be used for two or more substituents, but ortho, meta and para must never be used for more than two.
Rule 4: When the univalent hydrocarbon group from benzene itself (C6H5–) is named as a substituent, it is called a phenyl group. It is represented in several ways:
Ways of representing a phenyl group
Rule 5: A hydrocarbon composed of one saturated chain and one benzene ring is usually named as a derivative of the larger structural unit:
Rule 6: However, if the chain is unsaturated, the compound should be named as a derivative of that chain, regardless of ring size:
Rule 7: Compounds containing more than one phenyl group on a saturated chain are nearly always named as derivatives of alkanes:

The common names phenol, benzaldehyde and benzoic acids will be used in place of their systematic counter parts.
Ring – substituted derivatives of these compounds are named either by numbering the ring positions or by using the prefixes o- , m- and p- . The substituent that gives the compound its base name is placed at carbon 1.
A number of the common names for aromatic compounds refer to their fragrance and natural sources. Several of them have been accepted by IUPAC.
Aromatic Flavoring Agents:
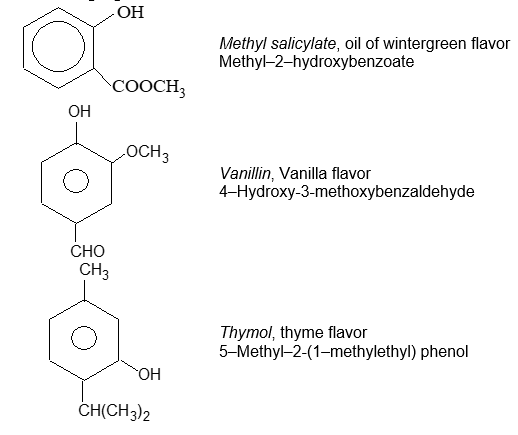
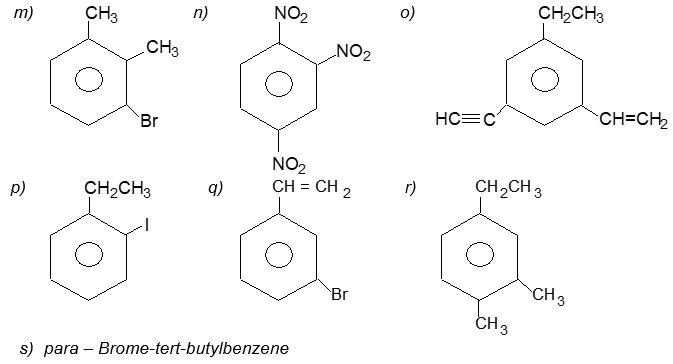
Illustration 17: Write systematic names of the following :
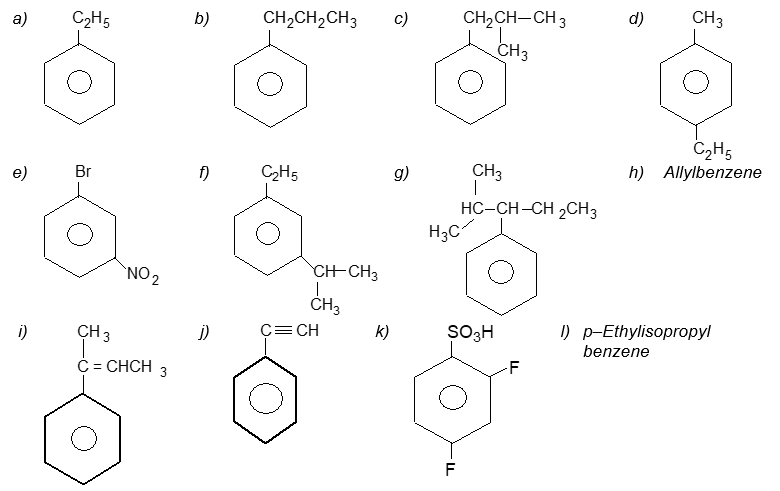
Solution:
| a) | Ethylbenzene | b) | n–Propylbenzene |
| c) | (2–Methylpropyl)benzene (or isobutylbenzne) | d) | p–Ethyltoluene |
| e) | 1–Bromo–3-nitrobenzene (or m–bromonitrobenzene) | f) | m–Ethylisopropylbenzene |
| g) | 2–Methyl–3-phenylpentane | h) |
|
| i) | 2–Phenyl–but-2-ene | j) | 2–Phenylethyne (or phenylacetylene) |
| k) | 2, 4–Difluorobenzenesulfonic acid | l) | 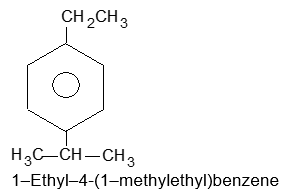 |
| m) | 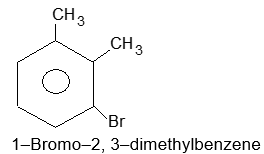 |
n) | 1,2,4–Trinitrobenzene |
| o) | 1–Ethenyl–3–ethyl–5–ethylnylbenzene | p) | 1–Iodo–2-methylbenzene ( or o–iodotoluene ) |
| q) | 1–Bromo–3-ethenylbenzene (or m–bromostyrene) | r) | 4–Ethyl–1, 2–dimethylbenzene (not 1–ethyl–3, 4–dimethylbenzene) |
| s) | 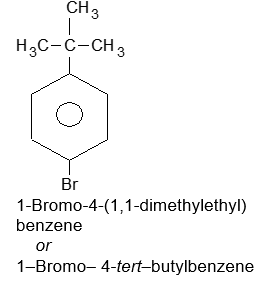 |
Illustration18: Draw the structures of
| a) | m–Bromochlorobenzene (or 1–bromo–3-chlorobenzene) | b) | p–Chlorotoluene |
| c) | 4–Bromo–o–xylene | d) | p–Iodo–o–cresol (or 4–iodo -2-methylphenol) |
| e) | 3–Bromo–p–hydroxybenzoic acid (or 3–bromo–4-hydroxybenzoic acid) | f) | 2–Nitro–p–toluidine (or 4–amino–3-nitrotoluene or 1–amino-4–methyl–2–nitrobenzene) |
| g) | 2–Chloro–1-methyl–4-nitrobenzene |
Solution:
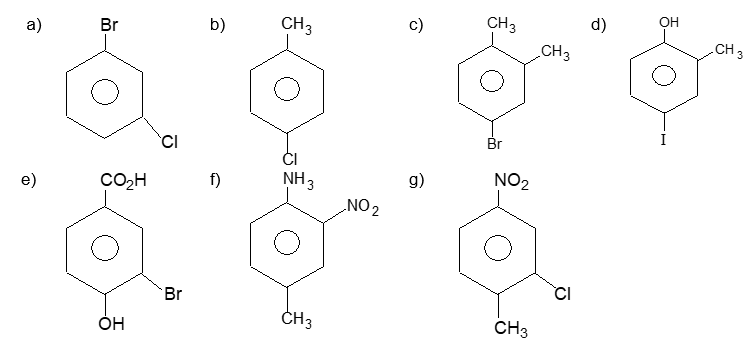
Illustration 19: Give IUPAC names of the following:

Solution:
| a) | 2–Chloro–4-methylanisole | b) | p–Nitroaniline |
| c) | 4–Ethyl–2-methylaniline | d) | 2, 3–Dibromo–1-phenylpentane |
| e) | 3, 4–Dimethylphenol | f) | 4–Ethyl-1–fluoro–2-nitrobenzene |
| g) | o–Ethylanisole |
Rule 8: When several benzene rings are fused together to give more extended p systems, the molecules are called polycyclic benzenoid or polycyclic aromatic hydrocarbons (PAHs). In these structures two or more benzene rings share two or more carbon atoms. Two benzene rings that share a pair of carbon atoms are said to be fused.
The more complex ring systems having two or more fused benzene rings have nonsystematic names and illogical numbering systems. As there is no simple system for naming these structures, we shall use their common names. The fusion of one benzene ring to another in the o – position results in the simplest and most important of these fused ring hydrocarbons, naphthalene.
Positions in the naphthalene ring system are designated as shown below:
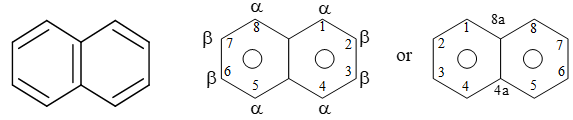
There are two carbons in naphthalene (C4a and C8a) that are common to both rings. These two atoms are said to be at the points of ring fusion. They direct all of their bonds toward other carbon atoms and do not bear hydrogen atoms.
Notice that in naphthalene, the positions 1, 4, 5 and 8 are identical (a – positions), as are positions 2, 3, 6 and 7 (b – positions).
Two isomeric monosubstituted naphthalene are differentiated by the Greek letters a – and b – or more preferably by 1– and 2- .
The arrangement of groups in more highly substituted naphthalenes is indicated by numbers. For example:
Illustration20: Name the following compounds systematically:
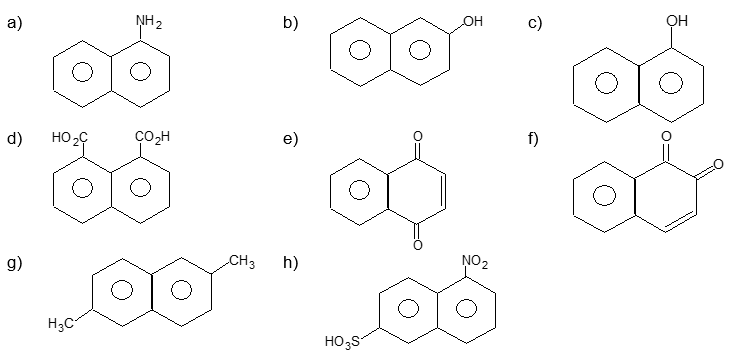
Solution:
| a) |
1 – Naphthylamine (or -naphthylamine) |
b) |
2 – Naphthol (or -naphthol) |
| c) |
1 – Naphthoic acid (or naphthalene–1-carboxylic acid) |
d) |
Naphthalene–1, 8–dicarboxylic acid (or naphthalic acid) |
| e) |
1, 4–Naphthoquinone (or -naphthoquinone or 1, 4–dihydronaphthalene–1, 4–dione) |
f) |
1, 2–Naphthoquinone (-naphthoquinone) |
| g) | 2, 6 – Dimethylnaphthalene | h) | 5–Nitro–2–naphthalenesulfonic acid |
Further fusion can occur in a linear manner to give anthracene, tetracene, pentacene and so on, a series called the acenes, Positions in the anthracene ring system are designated as shown below:
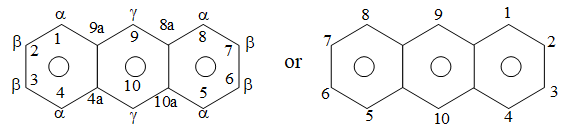
Notice that in anthracene, the positions 1, 4, 5, and 8 are identical ( – positions) as are positions 2, 3, 6, and 7 ( – positions) and positions 9, and 10 ( – positions).
Illustration 21: Name the following compounds systematically:
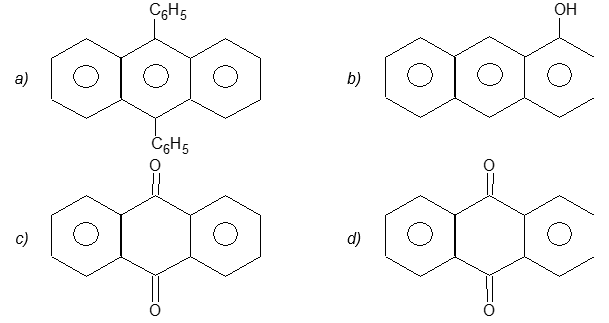
Solution:
a) 9, 10 – Diphenylanthracene
b) 1 – Anthrol (or 1- hydroxyanthracene)
c) Anthraquinone (or 9, 10–dihydroanthracene–9, 10–dione
d) 2–Aminoanthraquinone
Angular fusion (“annulation”) results in phenanthrene, which can be further annulated to a variety of other benzenoid polycycles. Positions in the phenanthrene ring system are designated as shown below:
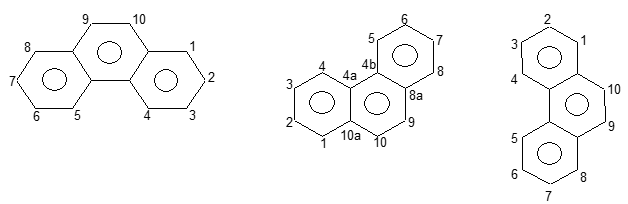
Phenanthrene, C14H10, is isomeric with anthracene. It is an example of an angular polynuclear hydrocarbon.
Illustration 22: Give IUPAC names for the following:
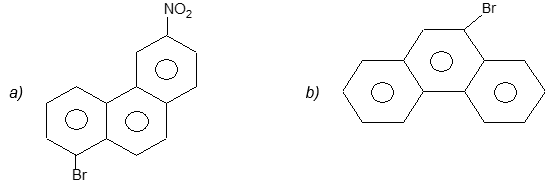
Solution:
a) 1–Bromo–6-nitrophenanthrene
b) 9–Bromophenanthrene
Each system has its own numbering system around the periphery.
Illustration23: Draw the structures of the following:
a) -Naphthol b) 1-Methylanthracene c) 9-Methylphenanthrene
Solution:

A fused carbon (or a quaternary carbon as it bears no H atom) is given the number of the preceding carbon in the sequence followed by the letters a, b and so on, depending on how close it is to that carbon.
There are some polynuclear hydrocarbons in which the benzene rings are isolated. For example:
Rule 9 : Organic halides derived from arenas are of two kinds. If the halogen is attached directly to the aromatic ring, the compound is an aryl halide; its general formula is ArX, where Ar = phenyl or substituted phenyl. If the halogen is not attached directly to the ring, the compound is an aralkyl halide, an alkyl halide that happens to contain an aromatic group.
An aryl or aralkyl halide is named according to the pattern: we name the parent compound, and then prefix this with chloro– , bromo– , etc.
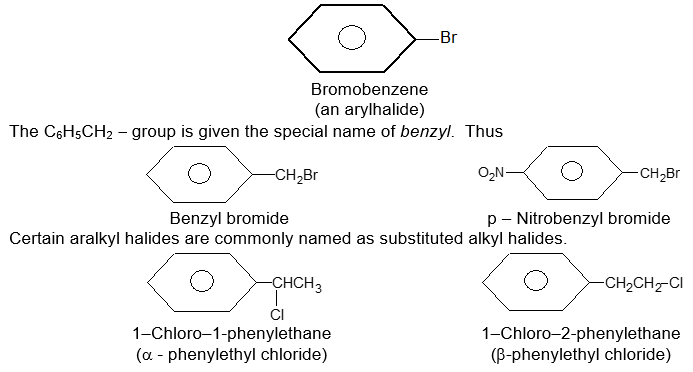
Rule 10 : Similarly, hydroxyl compounds derived from arenas are of two kinds. If –OH is attached directly to the aromatic ring, the compound is a phenol. If –OH is not attached directly to the ring, the compound is an aryl-substituted alcohol.

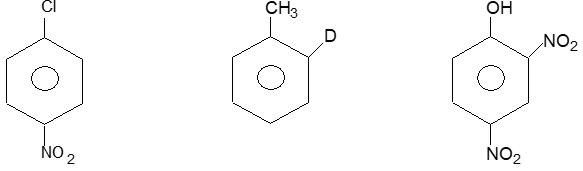
Illustration 24: Write systematic and common names of the following:
Solution:
a) 1 – Chloro – 4- nitrobenzene (p – chloronitrobenzene)
b) 1–Deuterio – 2- methylbenzene (o – deuteriotolyene)
c) 2, 4 – Dinitrophenol
Illustration 25: Draw the structures of
a) 2–Methyl–1, 3, 5–trinitrobenzene
b) 1–Ethenyl–4-nitrobenzene
c) (1 – Methyl(butyl) benzene
Solution:

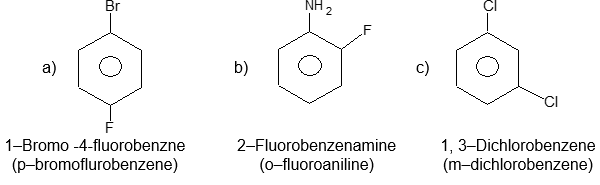
Illustration26: The following names are incorrect, write the correct form.
a) p – Fluorobromobenzene
b) o–Aminophenyl fluoride
c) 3, 5 – Dichlorobenzene
Solution:
Nomenclature of halogen derivatives of alkanes:
Halogen derivatives of the alkanes are classified on the basis of the number of halogen atoms in the molecule into mono- , di-, tri-, etc. substitution products.
Monohalogen derivatives are usually called the alkyl halides. Thus, alkyl halides are compounds in which a halogen atom (chlorine, bromine or iodine) replaces a hydrogen atom of an alkane. For example, CH3Br and CH3CH2Cl are typical alkyl halides.
Alkyl halides have the general formula RX, in which R is an alkyl or substituted alkyl group and X the halogen atom (Cl, Br, or I).
Alkyl halides are classified as being primary (10), secondary (20) and tertiary (30):
R, R’ and R” may or may not be same.
This classification is simply based on the nature of carbon atom to which the halogen is directly attached. If the carbon atom bearing the halogen is attached to only one other carbon, the carbon atom is said to be a primary carbon atom and the alkyl halide is classified as a primary alkyl halide (RCH2X). If the carbon that bears the halogen is itself attached to two other carbon atoms, then the carbon is a secondary carbon and the alkyl halide is a secondary alkyl halide (R2CHX). If the carbon that carries the halogen atom is directly attached to three other carbons, then the carbon is a tertiary carbon and the alkyl halide is a tertiary alkyl halide (R3CX).
Although we use the symbols 10, 20, 30 we do not say first degree, second degree and third degree; we say primary, secondary and tertiary.
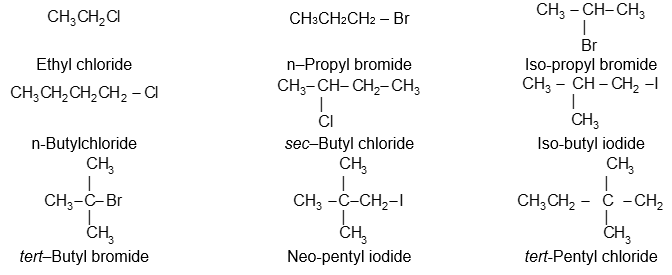
These compounds can be given two kinds of names:
Common names (for the simpler homologues). This method of naming RX is straight forward. In the common nomenclature system, called radicofunctional nomenclature, the compounds are usually named as the halide of the corresponding alkyl group i.e., we simply name the alkyl group attached to the halogen and add the word chloride, bromide or iodide. For example :
IUPAC names : In the systematic system of nomenclature, the compound RX, is simply named as a haloalkane, i.e., an alkane with a halogen attached as a side chain. For example
CH3I CH3CH2Cl
Iodomethane Chloroethane
Rule 1 : As usual, the longest (stem) chain carrying the halogen is numbered so that the substituent (halogen) receives the lowest number.
1–Bromopropane 2–Bromopropane
Rule 2 : When the parent chain has both an alkyl and a halo substituent attached to it, number the chain from the end nearer the first substituent regardless of whether it is halo or alkyl (i.e., the longest stem chain is numbered so that the first substituent from either end receives the lowest number). Substituents are listed alphabetically:
Ruler 3 : If two substituents are at equal distance from the either end of the chain, then number the chain from the end nearer the substituent that has alphabetical precedence.
Rule 4 : Complex appendages (attachments) are named according to the rules used for complex alkyl groups:
Illustration 27: Draw the structure of 5–Butyl–3-chloro–2, 2, 3–trimethyldecane.
Solution: First make the parent skeleton then attach the substituents at their respective positions:
or
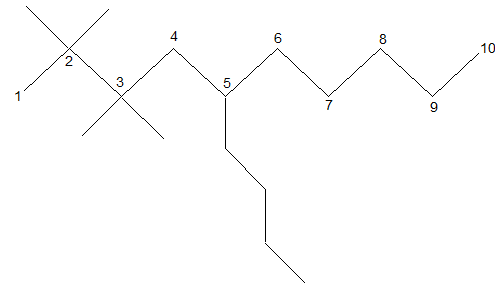
Illustration28: Give the IUPAC names of the following and label them as primary (10), secondary (20) or tertiary (30):
a) tert – Pentyliodide
b)
c) Isobutyl chloride
d) n – Butyl bromide
e)
f) Isopropyl chloride
Solution:
a) b) c)
d) e) f)
Dihalogen derivatives of the alkanes are compounds in which two halogen atoms (same or different) substitution the two hydrogen atoms of an alkane. For example:
CH3CHCl2 and ClCH2CH2Br
i) When both halogen atoms are attached to the same carbon atom of an alkane they are said to be in the geminal (gem- ) position. Thus,
is a geminal dihalide
Since the loss of two hydrogen atoms from the same carbon atom gives the alkylidene group, gemdihalides are commonly named as the alkylidene dihalides. For example
Rule 5 : In the IUPAC system, the geminal dihalide are simply named as an alkane with halogens attached as side chains. For example:
ii) When the two halogen atoms are on adjacent carbon atoms they are said to be in the vicinal (vic-) position. For example
is a vicinal dihalide.
In the trivial system these dihalides are named as the dihalide of the alkene from which they may be prepared by the addition of halogen (alkylene dihalide or simply halide). For example:
CH2ClCH2Cl (CH3)2CBrCH2Br
Ethylene dichloride Isobutylene dibromide
Rule 6 : In the IUPAC system, we treat the halogens of vicinal dihalides as substituents to the alkane framework:
iii) When there is a halogen atom on each of the terminal carbon atoms of the chain, i.e., in the a, w – position, the compound is commonly named as the polymethylene dihalide. For example:
ClCH2CH2CH2Cl CH2ClCH2CH2CH2Cl
Trimethylene dichloride Tetramethylene dichloride
iv) When the two halogen atoms occupy positions other than those mentioned above, the compounds have no common names.
Rule 7: In the IUPAC system, they are named as dihalogen derivatives of the parent hydrocarbon, the positions of the halogen atoms being indicated by numbers in accordance with the principle of lowest numbers. For example:
2, 4–Dichlorohexane
(not 3, 5–dichlorohexane)
Rule 8: Polyhalogen derivatives containing three or more halogens per molecule are best named by the IUPAC system, and the names of the different halogens (and any other substituents present) are arranged alphabetically:
Some polyhalogen derivatives used as solvents have common names: Trihalomethanes are named as haloforms while tetrahalomethanes are named as carbontetrahalides. Fully halogenated hydrocarbons are called perhaloalkanes (per = thoroughly)
Compounds having several halogen atoms and other more complex halogen compounds are usually named according to the IUPAC system.
Nomenclature of alcohols
An alcohol is an organic compound containing one or more hydroxyl ( -OH) groups, i.e., alcohols are hydroxy derivatives of the alkanes.
They are classified on the basis of the number of hydroxyl groups present in the molecule. Monohydric alcohols contain one hydroxyl group, dihydric, two; trihydric, three; etc. When the molecules of alcohols contain four or more hydroxyl groups, they are usually called polyhydric alcohols. For example :
The monohydric alcohols constitute an homologous series with the general formula CnH2n+2O. Methyl alcohol (more systematically called methanol) is the simplest member of monohydric alcohols. It has the structural formula CH3OH. The most common example of a monohydric alcohol is ethyl alcohol, CH3CH2OH (also called ethanol).
Since the characteristic functional group of this family is the hydroxyl (- OH) group attached to an sp3 – hybridized carbon atom, their general formula is more satisfactorily written as CnH2n+1OH or ROH, where R is any alkyl or substituted alkyl group.
Monohydric alcohols may be viewed structurally in two different ways:
1) as monohydroxy derivatives of alkanes and
2) as monoalkyl derivatives of water.
For example, methyl alcohol can be seen as a methane molecule in which one of the hydrogens has been substituted by a hydroxyl ( – OH) group, or as a water molecule in which one of the hydrogens has been substituted by a methyl group.
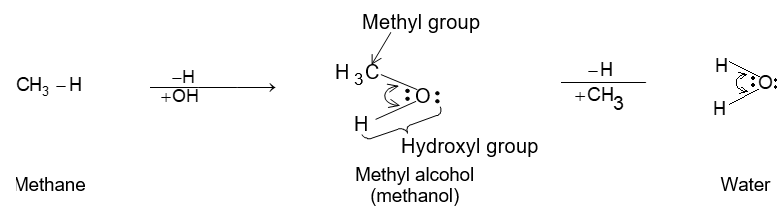
As with alkyl halides, monohydric alcohols are subdivided into primary (10), secondary (20) and tertiary (30) alcohols according as the alkyl group attached to the hydroxyl group is a primary, secondary or tertiary group, respectively. [In other words, this classification is based on the degree of substitution of the carbon to which the hydroxyl group is directly attached]. If the carbon atom bearing the hydroxyl group has only one other carbon attached to it, the carbon is said to be a primary carbon and the alcohol is a primary alcohol.
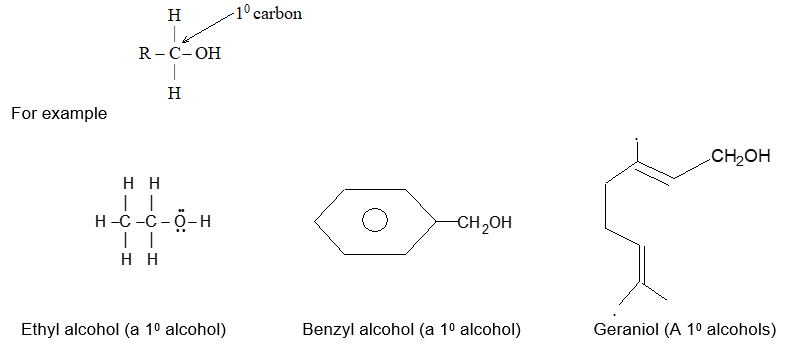
Notice that primary alcohols contain the primary alcoholic group: −CH2OH.
Geraniol is a major component of the oil of roses.
If the carbon atom that bears the –OH group has two other carbon atoms attached to it, the carbon is said to be a secondary carbon, and the alcohol is a secondary alcohol: Secondary (20) alcohol (R and R’ may be same or different)
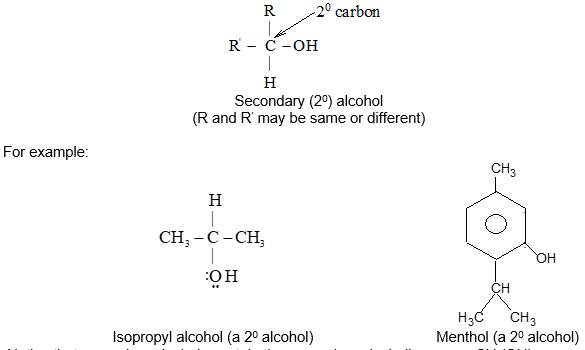
Notice that secondary alcohols contain the secondary alcoholic group: -CH (OH) – Menthol is found in peppermint oil.
If the carbon atom that carries the hydroxyl group also has three other carbon atoms attached to it, the carbon is called a tertiary carbon, and the alcohol is a tertiary alcohol:
Notice that tertiary alcohols contain the tertiary alcoholic group: C (OH)
Norethindrone is an oral contraceptive that contains a 30 alcoholic group as well as a ketone group and carbon-carbon double and triple bonds.
Monohydric alcohols are named by three systems:
1) Trivial system: The simpler alcohols are most often called by their common or trivial names [radicofunctional nomenclature] that are also approved by the IUPAC. These names are obtained by naming the alcohol as a derivative of the alkyl group attached to the hydroxyl group, i.e., a common name consists simply of the common name of the alkyl group followed by the word alcohol. For example :
2) Carbinol system: This system of nomenclature considers the alcohols as derivatives of methyl alcohol, which is named carbinol. For example:
| Methylcarbinol | Dimethylcarbinol | Ethylmethylcarbinol |
3) IUPAC system: This is the most versatile system. It treats alcohols as derivatives of alkanes. The ending –e of the parent alkane is replaced by –ol. Thus, an alkane is converted into an alkanol. For example, the simplest alcohol derived from methane is named as methanol. Ethanol stems from ethane, propanol from propane and so on. In more complicated, branched systems, the name of the alcohol may have as many as four features. locants, prefixes, parent compound and one suffix.
Let’s consider the following compound as an illustration [without, for the time being, worrying as to how the name arises]: The locant 5 – tells that the substituent methyl group named as a prefix, is attached to the parent compound at C5. The parent compound contains seven carbon atoms and no multiple bonds, hence the parent name heptane, and it is an alcohol, therefore, it has the suffix –ol. The locant 1 – tells that C1 bears the hydroxyl group (-OH).
In general, numbering of the parent chain always beings at the end nearer the group named as a suffix.
The following process should be followed to impart alcohols their IUPAC names:
Rule 1: Select as the parent structure the longest continuous carbon chain to which the hydroxyl (-OH) group is directly attached. (It need not be the longest chain in the molecule). Change the name of the alkane corresponding to this main chain by dropping the terminal e and adding the suffix – ol. The parent structure is thus known as ethanol, propanol, butanol, etc., depending upon the number of carbon atoms in the stem:
By the IUPAC system, the suffix –ol for OH is added to the name of the parent hydrocarbon. Notice that alkane + –ol becomes alkanol, with the –e omitted.
Rule 2: Consider the compound to have been derived from this parent alkane by substitution of hydrogens by various groups.
Rule 3: To locate substituent positions along the parent chain, number each carbon atom beginning from the end closest to the OH group.
Rule 4: Indicate the position of the – OH group in the parent chain by using the lowest possible number as a locant.
Rule 5: Add the names of other substituents attached to the parent chain (alkanol stem) as prefixes. Indicate their positions by using the numbers corresponding to their positions along the parent chain as locants.
Examples:
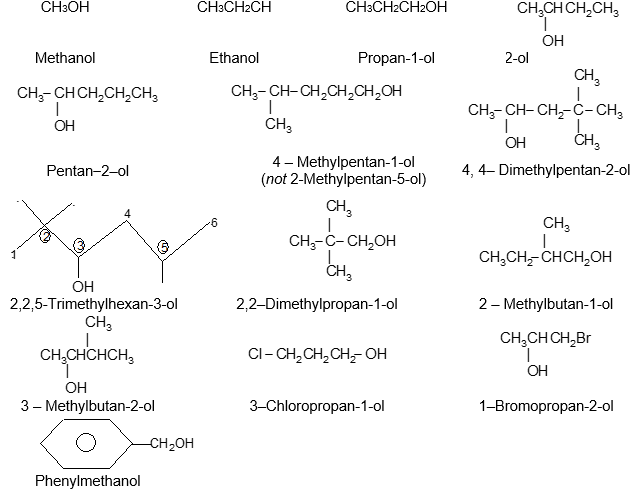
Rule 6 : Complex alkyl attachments are named according to the IUPAC rules for hydrocarbons:
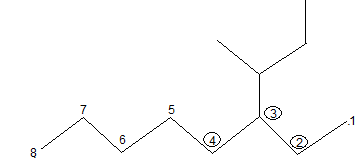
Rule 7 : Cyclic alcohols are called cycloalkanols. Here the carbon carrying the – OH group automatically receives the number 1.
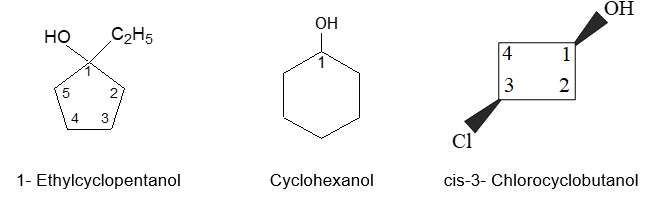
Rule 8 : When named as a substituents, the –OH group is called hydroxy. This occurs when a functional group taking higher precedence is present.
The substituent name for the –OH group should be used whenever the –OH group is not the parent (or principal) functional group. Notice how the precedence rules apply – hydroxyl below carboxylic acid and hydroxyl below ketone.

Dihydric alcohols containing two hydroxyl groups are commonly called glycols. They are classified as , , … glycols, according to the relative positions of the two hydroxyl groups: is the 1, 2 – glycol ; , 1, 3; , 1, 4 …. The commonest glycols are the -glycols.
The common names of the a – glycols are derived from the corresponding alkene from which they may be prepared by direct hydroxylation:
-, – ….. glycols are named as the corresponding polymethylene glycols:
Rule 9 : In the IUPAC system of nomenclature, the class suffix of dihydric alcohols is –diol, thus, they are named as alkanediols. Numbers are used to indicate the positions of side – chains and the two hydroxyl groups:
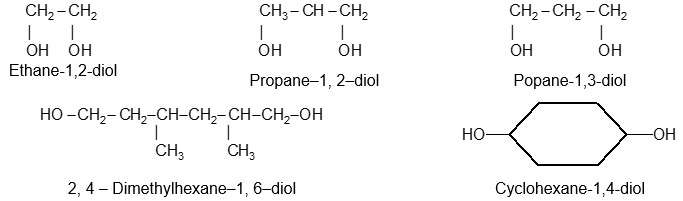
Ethylene glycol, the simplest glycol, is often called glycol.
The only important trihydric alcohol is glycerol :
For arene alcohols (phenols) and aromatic alcohols, trivial names are often used:
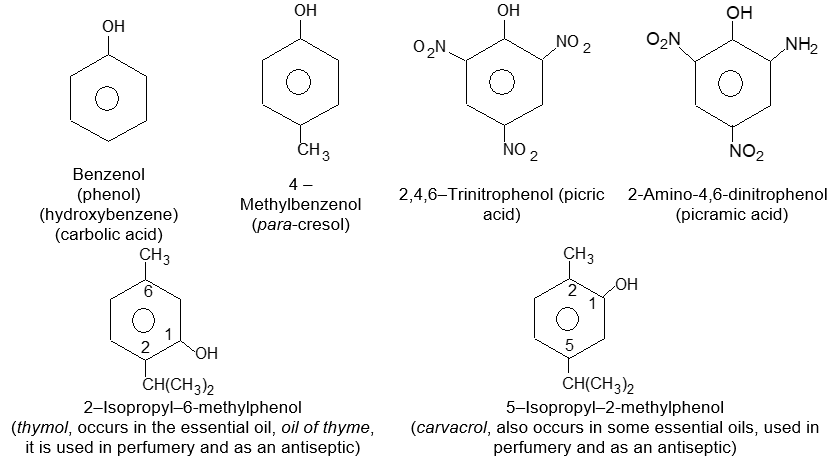
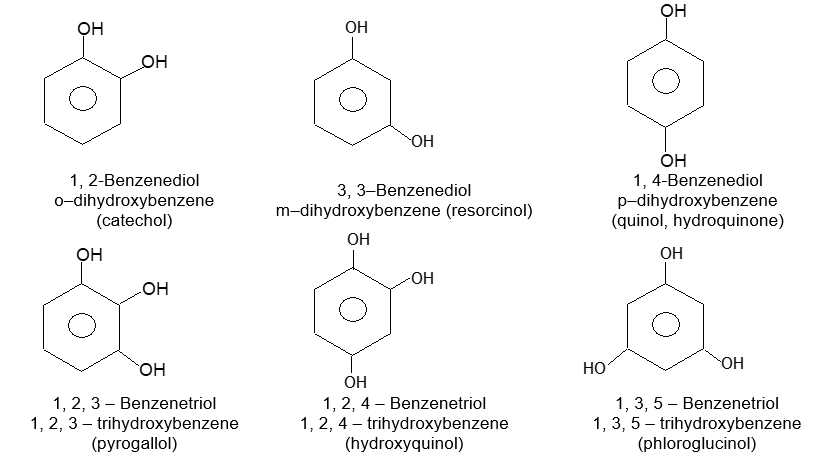
Illustration 29: Draw the structures of the following alcohols.
a) Neopentyl alcohol
b) trans – 2- Bromocyclopentanol
c) 3 – Methylhexan-3-ol
Solution:
Alcohols are compounds whose molecules have a hydroxyl group attached to a saturated [sp3 hybridized] carbon atom. The saturated carbon atom may be that of a simply alkyl group, as in methyl alcohol, isopropyl alcohol, tert–butyl alcohol etc. The alcohol carbon atom may also be a saturated carbon atom of an alkenyl or alkynyl group, or the carbon atom may be a saturated carbon atom that is attached to a benzene ring:
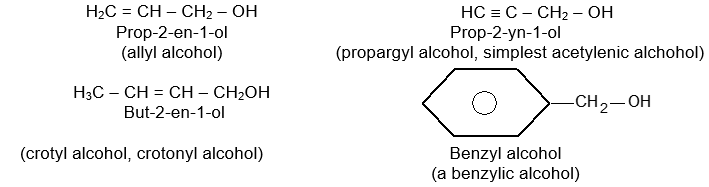
The hydroxyl group has precedence over double bonds and triple bonds in deciding which functional group to name as the suffix.
Compounds in which a hydroxyl group is directly attached to an unsaturated carbon atom of a double bond, i.e., C = C – OH, are called enols.
Illustration30: Give IUPAC substitutive names for the following alcohols.
a)
b)
c)
Solution: The longest continuous chain to which the hydroxyl group is attached gives us the base name. The ending is – ol. Number the parent chain from the end that gives the carbon bearing the hydroxyl group, the lowest possible number. Thus, the names are
a) 2, 4–Dimethylpentan-1-ol
b) Pent – 4-en–2–ol
c) 4-Phenylpentan–2-ol
Nomenclature of ethers
Aliphatic ethers are compounds of the general formula CnH2n+2O (which is the same as that of the monohydric alcohols). They have the general structure R–O–R¢ where R¢ may be an alkyl group different from R.
On account of their general structure, aliphatic ethers can be thought of as derivatives of water in which both hydrogen atoms have been replaced by same or different alkyl groups. The bond angle at the oxygen atom of an ether is only slightly larger than that of water:
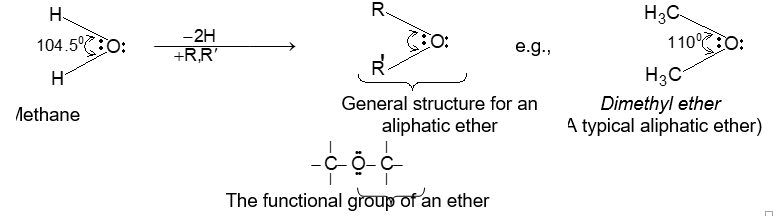
Aliphatic ethers may also be thought of as derivatives of alcohols in which the hydroxyl hydrogen has been substituted by an alkyl group. Thus, they may be regarded as alkyl oxides or the anhydrides of the alcohols.
Aliphatic ethers differ from monohydric alcohols in that the oxygen atom of an ether is bonded to two carbon atoms.
When the two alkyl groups in an ether are the same, the ether is said to be symmetrical or simple, e.g., diethyl ether, C2H5 –O –C2H5. When the two alkyl groups are different the ether is said to be unsymmetrical or mixed, e.g., ethyl methyl ether, H3C – O – C2H5.
Aliphatic ethers are named by two systems:
1) Common or Trivial system: In this system of nomenclature, all the members are known as ethers and the individuals are named according to the alkyl groups attached to the oxygen atom. If the two groups are different, name the two alkyl groups attached to the oxygen atom in alphabetical order and add the word ether:
If the two alkyl groups are the same, use the prefix di– (for simple groups) or bis– (for substituted groups):
Diethyl ether is more commonly called ethyl ether because with simple ethers the prefix di is often omitted.
2) IUPAC system:
In this system of nomenclature, the ethers are treated as alkanes in which one of the hydrogen atoms has been substituted by an alkoxy group, ( -OR).
R and R’ may be same or different
Rule 1 : For unsymmetrical ethers(R ≠ R¢), the smaller alkyl group is considered part of the alkoxy group, and the larger group being chosen as the parent alkane. Thus in the IUPAC system, ethers are alkoxyalkanes:
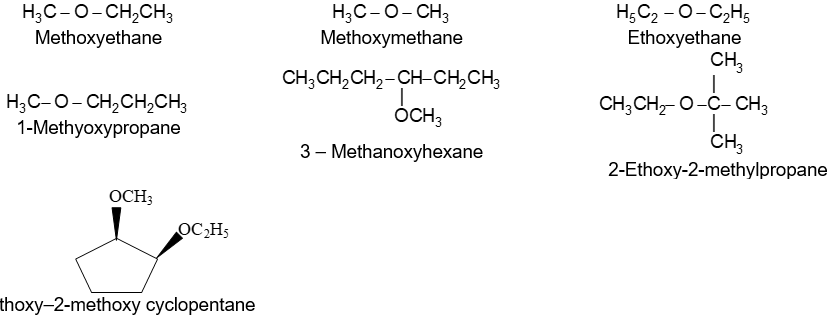
Rule 2: The hydroxyl group has precedence over alkoxy group in deciding which functional group to name as the suffix:
In aliphatic ethers, the hydrocarbon groups may be alkenyl, alkynyl, or vinyl:
The double and triple bonds have precedence over the alkoxy group in deciding which functional group to name as the suffix.
Aromatic ethers may be divided into two groups, the phenolic ethers (alkaryl ethers), which are of the type, and the diaryl ethers which are of the type Ar – O – Ar¢ where Ar¢, may be an aryl group different from Ar.
Examples of phenolic ethers:
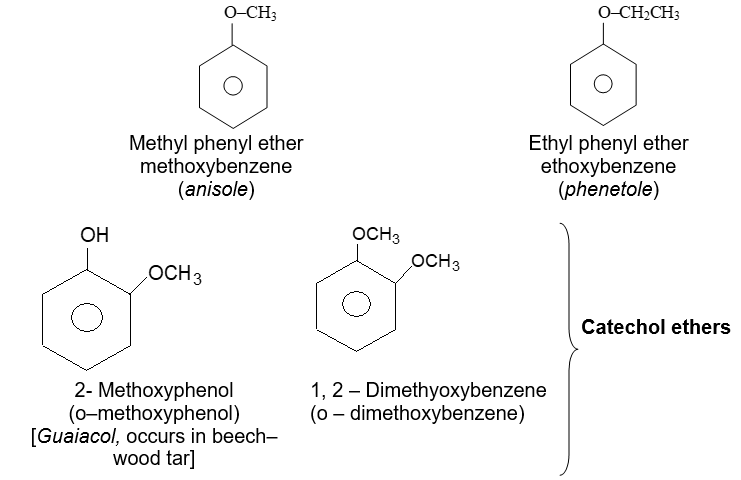
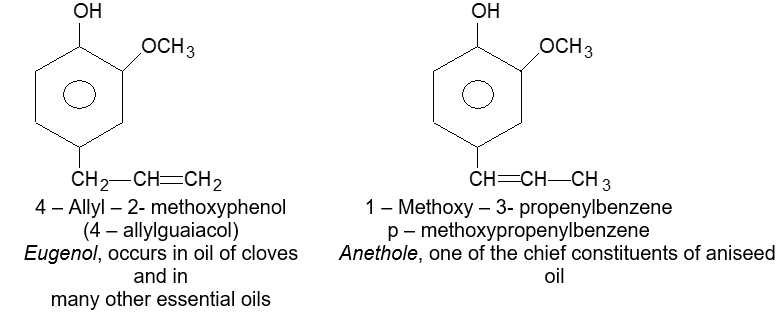
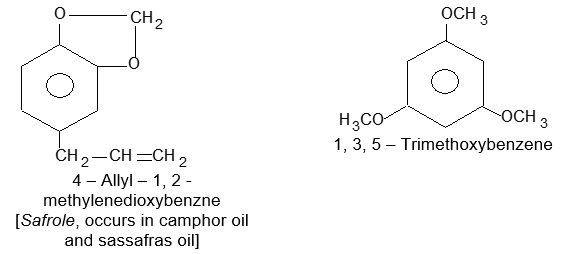
Examples of diaryl ethers:

Methyl ethers of o– and p–aminophenols are known as o–anisidine and p–anisidine:
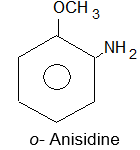
They are used in the preparation of azo–dyes.
Ethyl ethers of the aminophenols are known as phenetidines:
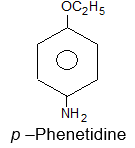
These are also used in the preparation of azo – dyes.
Acetyl derivative of p–phenetidine is known as phenacetin :
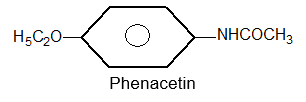
It is replacing acetanilide in medicine, it is a very good analgesic (i.e., promotes relief from pain) and antipyretic (i.e., fever – reducing).
Carbamyl derivative of p–phenetidine is known as Dulcin:
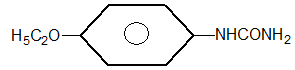
It is about 200 times as sweet as sugar, thus, used commercially as a sweetening agent.
Cyclic ethers are members of a class of cycloalkanes in which one or more carbons have been replaced by oxygen – a heteroatom. [A heteroatom is defined as any atom except carbon and hydrogen]. Cyclic compounds of this type, are called heterocycles.
The simplest system for naming cyclic ethers is based on the oxacycloalkane stem, in which the prefix oxa, indicates the replacement of carbon by oxygen in the ring. Thus, three-membered cyclic ethers are oxacyclopropanes. (Other names used are oxiranes, epoxides and ethylene oxides), four–membered systems are oxacyclobutanes and the next two higher homologous are oxacyclopentanes (tetrahydrofurans) and oxacyclohexanes (tetrahydropyrans). The compounds are numbered by starting at the oxygen and proceeding around the ring:
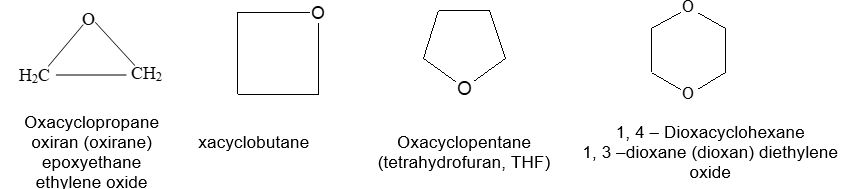
Rule 3:There are alternate IUPAC ring names for the cyclic ethers, (CH2)nO, where n=2,3,4…
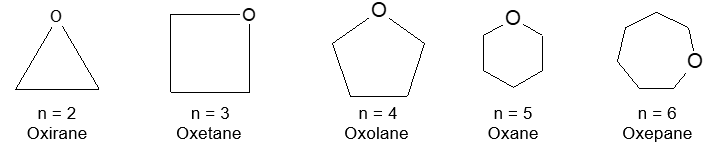
The italicized portions of these names are the suffixes used to represent the size of saturated heterocyclic rings other than those with N atoms.
Rule 4 : The oxa method can be extended to noncyclic ethers also. The method pretends that the O of the longest continuous chain (or ring) is a C and it is thus counted to determine the parent chain (or the parent ring). Its presence is indicated by the prefix oxa – and a number to designate its position in the chain:
The two O’s and four C’s are taken as six C’s and the parent hydrocarbon is hexane.
Bis ( – methoxyethyl) ether, diglyme
Rule 5 : Cyclic polyethers which contain multiple ether functional groups (usually with at least four O atoms) based on the 1, 2–ethanediol unit are called crown ethers, so called because their molecules adopt a crown like conformation in the crystalline state and, presumably, in solution.
Two typical examples are :

The first of two numbers in the name of crown ethers refers to the total number of atoms in the ring, the second to the number of O atoms. Thus, the structure (I) has 12 atoms, including 4 O’s, while there are 18 atoms, including six O’s in the structure (II). Notice that a structural unit – O – CH2 – CH2 – O – is repeated around the ring.
Nomenclature of aldehydes and ketones
Aldehydes and ketones both contain the carbonyl (oxo) group – a group in which a carbon atom has a double bond to oxygen atom.
![]()
The carbonyl group
Both aldehydes and ketones are thus often referred to collectively as carbonyl compounds. Except for formaldehyde, the simplest aldehyde, the carbon atom of the carbonyl group in all aldehydes is bonded to at least one hydrogen atom. Hence the functional group of aldehydes is –CHO.
The aldehyde functional group always occurs at the end of a chain.
In ketones, the carbon atom of the carbonyl group is bonded to two carbon atoms. Thus, the functional group of ketones (the keto group) occurs within a chain except ketens.
Ketens (ketenes) are compounds which are characterized by the presence of the grouping.
![]()
Both aliphatic aldehydes and ketones have the general formula CnH2nO. Using R, we can designate the general structure for an aliphatic aldehyde as
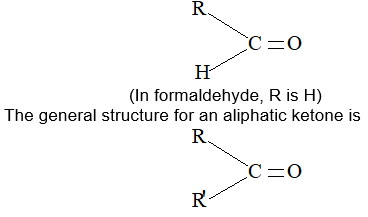
where R’ is an alkyl group different from R
Aromatic aldehydes fall into two groups: those in which the aldehyde group (-CHO) is directly attached to the benzene nucleus, and those in which it is attached to the side-chain. The former group comprises the typical aromatic aldehydes (ArCHO); the latter, which behave as aliphatic aldehydes, are best regarded as aryl-substituted aliphatic aldehydes.
Aromatic ketones may be either alkaryl ketones or diaryl ketones
where Ar’ may be an aryl group different from Ar
Aliphatic aldehydes are named by two systems
1) Trivial (or common) system: The lower members are commonly named after the carboxylic acids that they form on oxidation. For this purpose the ending –ic acid of the common name of the corresponding carboxylic acid is replaced by –aldehyde. For example
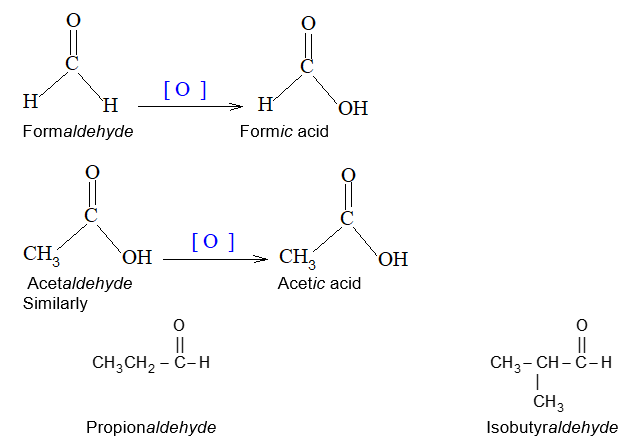
Branched-chain aldehydes are named as derivatives of straight-chain aldehydes. The positions of side chains or substituents are indicated by Greek letters, -, -, -, -, etc., the carbon atom being the one bearing the -CHO group:
used in common names
For example:

IUPAC system: According to this system of nomenclature, aldehydes are designated by the class suffix –al, which is added to the name of the alkane from which they are derived. An alkane thus becomes an alkanal.
Rule 1: The longest continuous carbon chain carrying the aldehyde group (–CHO) is chosen as the parent alkane and is named by replacing the –C of the corresponding alkane by –al. The positions of side – chains or substituents are indicated by numbers, the aldehyde group carbon is always given the number 1, which may be omitted from the name if it is the only functional group present in the compound. For example
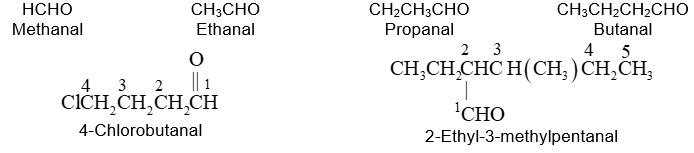
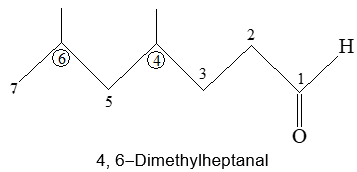
Some examples of unsaturated aldehydes are:
The aldehyde group is given preference over C = C and C C functional groups.
Rule 2: Aldehydes in which the –CHO group is attached to a ring system are named by adding the suffix carbaldehyde, to the name of the parent hydrocarbon. For example
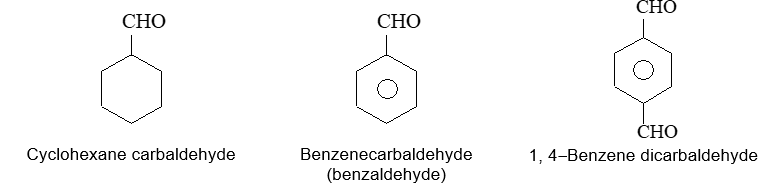
The parent aromatic aldehyde is benzenecarbaldehyde, although its common name, benzaldehyde, is far more frequently used. Common names of aromatic aldehydes are derived from the common name of the corresponding carboxylic acid, with the ending –ic or oic acid replaced by –aldehyde.
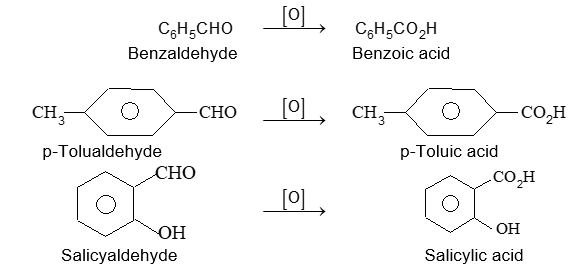
Rule 3: Dialdehydes are named as –dials. For instance
OHC – CHO OCHCH2CH2CHO
Ethanedial Butanedial
[glyoxal, oxaldehyde] (Succinaldehyde, succindialdehyde)
Rule 4: When the -CHO group is a substituent on the parent chain or ring and it ranks below another functional group, it is designated by the prefix methanoyl. However, the prefix formyl is also used:
Like aldehydes, ketones are also named by two systems:
1) Trivial (or common) system The simplest aliphatic ketone has the common name of acetone. Common (radicofunctional) names for other ketones are obtained simply by separately naming the two groups that are attached to carbonyl carbon, and adding the word ketone as a separate word. Note that names of different groups should be listed alphabetically. If the groups are identical then use the prefix di– or bis- .
If the two alkyl groups in a ketone are the same, the ketone is said to be simple or symmetrical; if unlike, mixed or unsymmetrical.
A ketone in which the carbonyl group is attached to a benzene ring is named as a –phenone:
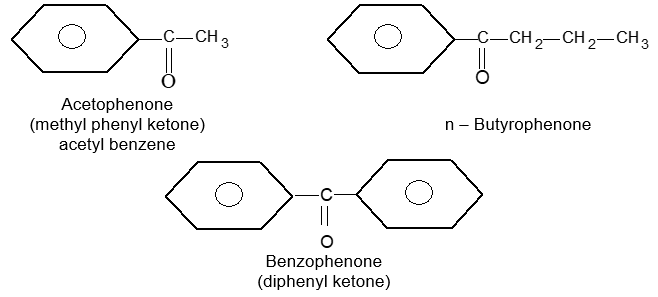
Branched–chain ketones are named as derivatives of straight–chain ketones. To indicate the point of attachment of side–chains or substituents, the Greek letters, -, -, – , -, etc., are used; the a-carbon atom being the one adjacent to the keto group. For instance
, ‘-Dichlorodiethyl ketone
2) IUPAC system:
According to this system of nomenclature, ketones should be treated as derivatives of the alkanes, with the ending –e of the alkane replaced with –one. An alkane thus becomes an alkanone.
Rule 1 : The longest continuous carbon chain containing the keto group is considered the parent alkane, and is named by replacing the –e of the corresponding alkane with –one. The positions of various side–chains or substituents are indicated by numbers. The carbonyl carbon (or keto carbon) being given the lowest possible number:
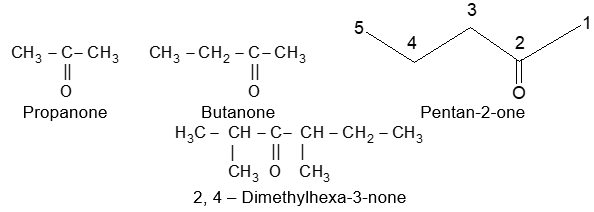
Examples of unsaturated ketones:
The carbonyl carbon is given preference over the C = C or C º C functional groups.
Rule 2 : Aromatic ketones are named as aryl–substituted alkanones:
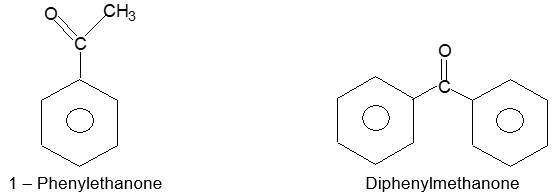
Rule 3 : Ketones, unlike aldehydes, may also be part of a ring, giving compounds called cycloalkanones.
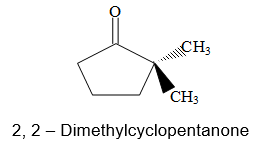
We assign the number 1 to the carbonyl carbon when it is in a ring.
Rule 4 : Diketones are named as –diones:
Rule 5 : When the ketone carbonyl group is regarded as a substituent along the parent chain or ring, it is called an oxo group.
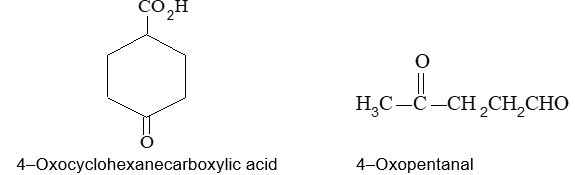
The aldehyde function takes precedence over that of ketones.
The systematic name for the fragment is alkanoyl, although the common name acyl is widely used.
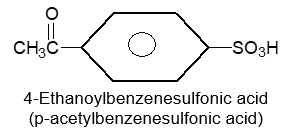
Illustration31: Give IUPAC names of the following compounds:
| a) | o–Bromobenzaldehyde | b) | Diethyl ketone |
| c) | 4–Hydroxy–3-methoxybenzaldehyde | d) | 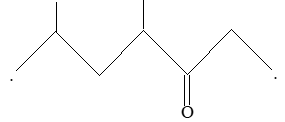 |
| e) | Propargylaldehyde | f) | |
| g) | 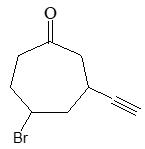 |
h) | 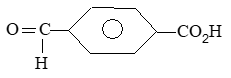 |
| i) | j) | o–Formylbenzoic acid | |
| k) | l) | Phenylacetaldehyde | |
| m) |  |
n) | Allyl methyl ketone |
| o) | Cyclohexyl ethyl ketone | p) |
Salicylaldehyde (o–hydroxybenzaldehyde) |
| q) | p–Nitrobenzaldehyde | r) | Isopropyl methyl ketone |
| s) | Benzyl methyl ketone | t) | 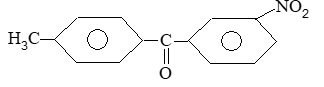 |
Solution:
| a) | 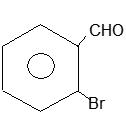 |
b) | |
| 2 – Bromobenzenecarbaldehyde | Pentan-3-one | ||
| c) |
4–Hydroxy–3-methoxybenzenecarbaldehyde |
d) | 4 – Chloro-6-methylheptan-3-one |
| e) | , Propynal | f) | 7–Hydroxy–7-methyl– 4-octen–2-one |
Note that, e of –ene and –yne is dropped in –enone and –ynal.
| g) | 5–Bromo–3-ethynylcycloheptanone | h) | 4–Formylcyclohexanecarboxylic acid |
| i) | 5–Oxobutanal | j) |
2–Methanoylbenzenecarboxylic acid |
| k) | 5–Chloropentanal | l) |
Phenylethanal |
| m) | 2–Naphthalenecarbaldehyde | n) |
Pent-4-en–2-one (not pent-1-en–4-one) |
| o) | 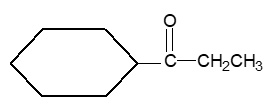 |
p) | 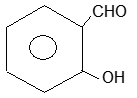 |
| 1 – Cyclohexylpropan–1-one | 2 – Hydroxybenzenecarbaldehyde | ||
| q) | 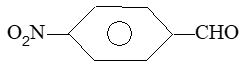 |
r) | |
| p–Nitrobenzenecarbaldehyde | 3–Methylbutanone | ||
| s) | 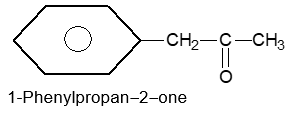 |
t) | 4–Methyl–3-nitrobenzophenone |
There are various ways of drawing aldehydes and ketones. As usual, condensed formulae or the zig – zag (bond – line) notation may be used. Note that the condensed formulae for aldehydes are written as RCHO, ArCHO, and never as RCOH, ArCOH to prevent confusion with the hydroxyl group of alcohols.
Various ways of writing aldehyde and ketone structures:
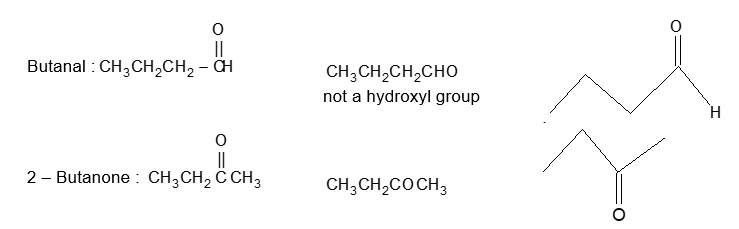
Illustration 32: Name and or draw the structures of the following compounds:
a) Cinnamaldehyde
b) Anisaldehyde(p–methoxy benzaldehyde)
c) 4–Bromocyclohexanone
d) 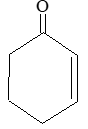
e) 4–Octyn–3-one
f) 3–Hydroxybutanal
g) 
Solution:
| a) |
3 – Phenylpropenal |
b) |
4-Methoxybenzenecarbaldehyde |
| c) |  |
d) | 2 – Cyclohexenone |
| e) |  |
||
| f) | 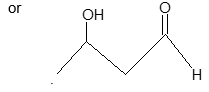 |
||
| g) | (E)–4-Methyl–4-hexenal |
Nomenclature of carboxylic acids
Carboxylic acids are characterized by the presence of the carboxyl (carbonyl + hydroxyl) or the carboxy group, a functional group containing a hydroxyl unit attached to a carbonyl carbon. The carboxyl group, , is usually abbreviated as –COOH or –CO2H.
Monocarboxylic acids contain the carboxyl group attached to hydrogen (HCOOH), an alkyl group (RCOOH), or an aryl group (ArCOOH):

Whether the group is aliphatic or aromatic, saturated or unsaturated, substituted or unsubstituted, the properties of the carboxyl group are essentially the same.
The saturated monocarboxylic acids are also referred to as the fatty acids, because of the fact that some of the higher members, especially palmitic (C15H31CO2H) and stearic (C17H35CO2H) acids, occur in natural fats. Their general formula is CnH2nO2 but, they are more aptly expressed as CnH2n+1 CO2H or RCO2H, since these illustrate the nature of their functional group, the carboxyl group.
As usual, the carboxylic acids are named by two systems:
1) Trivial (or common) system : Like other organic compounds, many aliphatic monocarboxylic acids have common names that are derived from Latin or Greek words that are used frequently in the literature. These names often refer to their natural sources (from which the acids were first isolated) rather than to their chemical structures. Chemical Abstracts retains the common names for the two simplest, formic and acetic acids.
Names and natural sources of carboxylic acids
| Structure | Common name | Natural source |
| HCOOH | Formic acid | From the “destructive distillation” of ants (formica, Latin, ant) |
| CH3COOH | Acetic acid | Vinegar (acetum, Latin, vinegar) |
| CH3CH2CO2H | Propionic acid | Dairy products (pion, Greek, fat) |
| CH3CH2CH2CH2CO2H | Butyric acid | Butter (particularly if rancid) (butyrum, Latin, butter) |
| CH3(CH2)3CO2H | Valeric acid | Valerian root |
| CH3(CH2)4CO2H | Caproic acid | Odor of goats (caper, Latin, goat) |
Another system of nomenclature considers the acids, except formic acid, as derivatives of acetic acid, e.g.,
| CH3CH2CO2H | (CH3)3CCO2H | (CH3)2CHCH2CO2H |
| Methylacetic acid | Trimethylacetic acid | Isopropylacetic acid |
In the above two systems the branched – chain acids and substituted acids are named as derivatives of the straight–chain acids. The positions of substituents in the chain are indicated by Greek letters, – , -, -, -, etc, the – carbon atom being the one joined to the carboxyl group:
used in common names
For example :
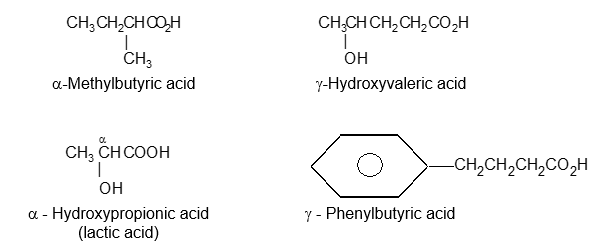
Illustration33: Write common names for each of the following structures:
a)
b)
c)
Solution:
a) – Chloro – – methylbutyric acid
b) – Dimethylvaleric acid
c) – Chloro – – methylbutyric acid
Aromatic acids, ArCOOH, are compounds containing carboxyl group, which is directly attached to the benzene nucleus. They are usually named as derivatives of the parent acid, benzoic acid, C6H5CO2H.
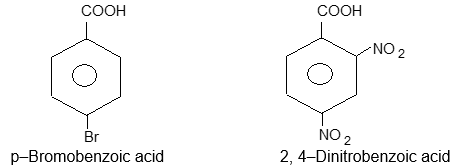
Some of these are given the special names:
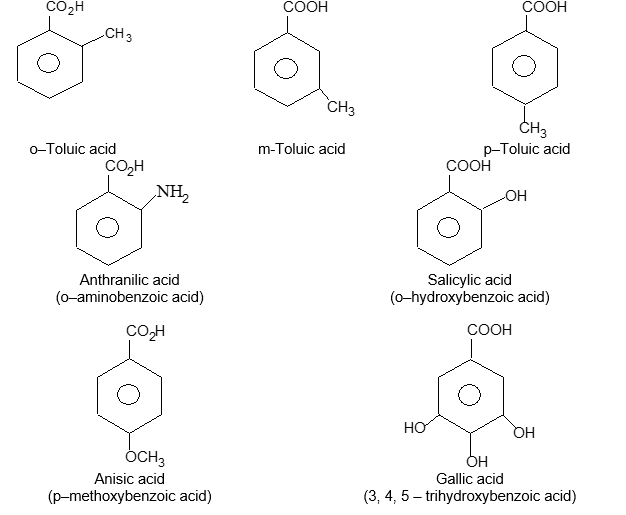
2-Hydroxybenzoic (salicyclic) acid has been known for over 2000 years as an analgesic (pain killing) folk remedy present in willow bark (salix, Latin, willow). The acetic acid ester of salicylic acid is better known as aspirin.
Gallic acid occurs in the free state in tea plants.
2) IUPAC system: The IUPAC names follow the usual pattern.
Rule 1 : The systematic names for saturated monocarboxylic acids are obtained by dropping the ending –e in the name of the alkane corresponding to the longest continuous chain incorporating the –CO2H group and by adding –oic acid. The alkanoic stem is always numbered by assigning the number 1 to the carboxy carbon. Any substituent along the stem is labelled by numbers designated to them. For example:
Illustration34: Give IUPAC names for the following:
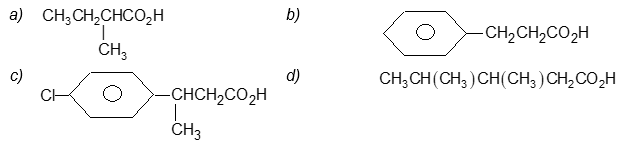
Solution:
a) 2 – Methylbutanoic acid
b) 3 – Phenylpropanoic acid
c) 3 – (p – chlorophenyl) butanoic acid
d) 3, 4 – Dimethylpentanoic acid
The carboxyl functional group takes precedence over carbon – carbon multiple bonds.
Some examples of unsaturated acids are:
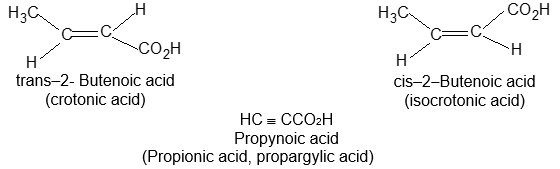
Illustration 35: Give IUPAC names of the following:
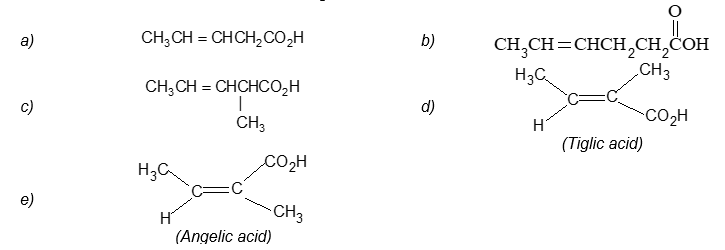
Solution :
a) 3–Pentenoic acid (or pent–3-enoic acid)
b) 4–Hexenoic acid
c) 2–Methyl–3-pentenoic acid
d) cis–2-Methylbutenoic acid
e) trans–2-Methylbutenoic acid
Rule 2: In multiply functionalized carboxylic acids, the main chain is chosen to include other functional groups as much as possible.
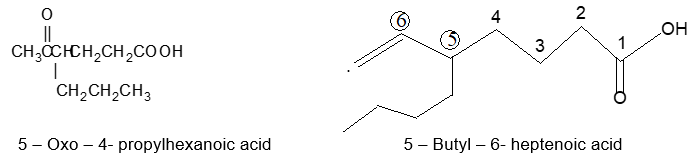
Rule 3 : Saturated cyclic acids are named as cycloalkanecarboxylic acids:
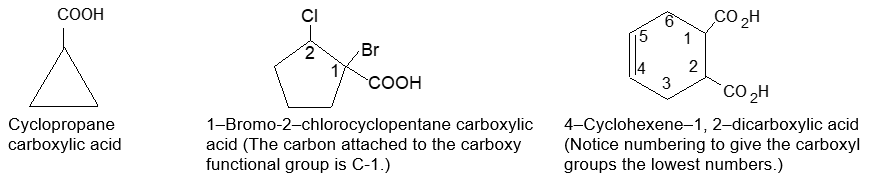
Rule 4 : Dicarboxylic acids should be referred to as –dioic acids. The general formula of the saturated dicarboxylic acids is CnH2n (CO2H)2 and the best–known examples are those which have the two carboxyl groups at the opposite ends of the carbon chain.
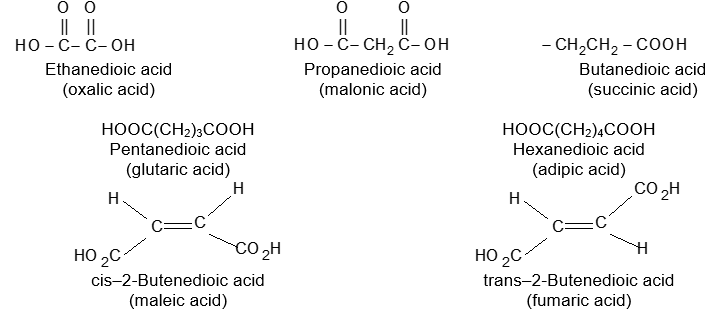
Their common names again derive from their natural origins. For example, oxalic acid occurs in shubarb, in sorrel and other plants of the oxalis group. Succinic acid was originally obtained by the distillation of amber (Latin: succinum, amber). Glutaric acid got its name due to relationship to glutamic acid and tartaric acid. Adipic acid received its name from the fact that it was first obtained by the oxidation of fats Latin: adeps, fat), and fumaric acid is found in the plant Fumaria which was burned in ancient times to ward off evil sprits (Latin: fumus, smoke).
Rule 5 : When all the carboxyl groups can’t be included in the parent chain, then we regard each of the carboxyl group as a substituent, and the name of the acid is then obtained by adding the suffix carboxylic acid to the name of the parent chain.
Rule 6 : For salts of carboxylic acids, the name of the acid with the ending – ic acid changed to –ate and the counter ion (the cation) is named as a separate word:

Illustration 36: Give IUPAC names or write the structure, as appropriate, of the following compounds:
| a) | b) | Benzoic acid | |
| c) | d) | 4 – Hydroxypentanoic acid |
| e) |  |
f) | 2, 2–Dibromohexanedioic acid |
| g) |  |
h) | 4–(1,1-Dimethylethyl)benzoic acid |
| i) | HCOONH4 | j) | |
| k) | , – Dimethylvaleric acid | l) | Phthalic acid |
| m) | Isophthalic acid | n) | Terephthalic acid |
Solution:
| a) | 2 – Nitrobutanedioic acid | b) | Benzenecarboxylic acid |
| c) | Sodium 2–aminopropanoate | d) | |
| e) | 5–Bromo–3-chloroheptanoic acid | f) | |
| g) | 4-Oxocyclohexanecarboxylic acid | h) | 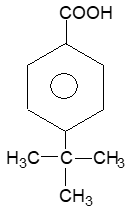 |
| i) | Ammonium formate | j) | Potassium 2, 3–dibromopropanoate |
| k) |
2, 3–Dimethylpentanoic acid |
l) |
Benzene–1, 2–dicarboxylic acid |
| m) |
Benzene–1, 3–dicarboxylic acid |
n) |
Benzene–1, 4–dicarboxylic acid |
Nomenclature of compounds containing Acyl groups
Rule 1 : The function is called an acyl group and is named systematically by adding the suffix –oyl to the appropriate hydrocarbon prefix. That is,
Alkane- + -oyl alkanoyl
For example:
Rule 2 : Acyl groups containing cyclic structures are called alkanecarbonyl or cycloalkanecarbonyl groups:

When an acyl group replaces the hydrogen of alcohols, carboxylic acids, hydrogen halides, ammonia or amines, we have the acyl compounds known as esters, anhydrides, halides and amides respectively.
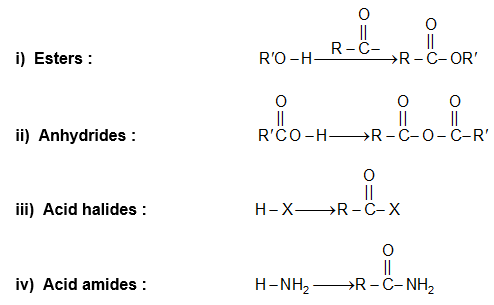
These compounds, which are closely related to the carboxylic acids and to each other, are collectively known as functional derivatives of carboxylic acids.
Each of these types of compounds are named as follows:
Carboxylic esters
Esters are compounds which are formed when the hydroxylic hydrogen atom in oxygen acids is substituted by an alkyl or aryl group; the acid may be organic or inorganic. The most important esters are derived from the carboxylic acids. The general molecular formula of the carboxylic esters is CnH2nO2, which is the same as that of the carboxylic acids.
Carboxylic esters have the general structural formula RCO2R’ (or RCOOR’) where a carbonyl group is bonded to an alkoxyl group:
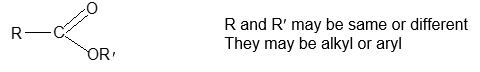
Carboxylic esters can be made from, a carboxylic acid and an alcohol through the acid – catalyzed loss of a molecule of water. For example:
Rule 1 : The names of esters are taken in simple ways from either the common name or the IUPAC name of the corresponding carboxylic acid. The name of the parent carboxylic acid (alkanoic acid) is changed to alkanoate ( -ic acid to –ate) and is preceded, in a separate word, by the name of the ester alkyl group R‘ (alcohol or phenol group):
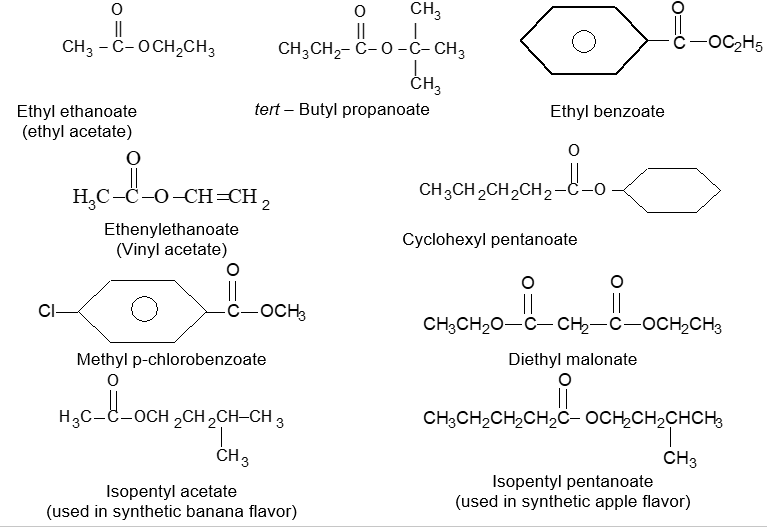
Thus, the names of esters are derived from the names of the alcohol (with the ending -yl) and the acid (with the ending –ate or –oate). The portion of the name derived from the alcohol comes first
Common name of ester: Change -ic acid of common name of carboxylic acid into – ate and precede it by the name of alkyl group of alcohol or phenol.
IUPAC name of ester: Change –ic acid of IUPAC name of carboxylic acid into –ate and precede it by the name of alkyl group of alcohol or phenol.
Rule 2 : When appropriate, esters also are named as carboxylates:
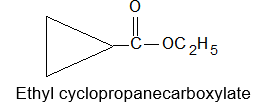
Rule 3 : When it is necessary to name the -CO2R’ function as a substituent, it becomes alkoxycarbonyl, (Notice that it is structurally different from ).
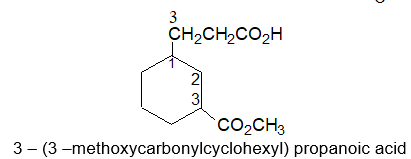
Notice the use of parentheses to separate the numbering of C3 of the cyclohexane ring from the numbering of the chain.
Rule 4 : It also may be essential at times to name the group as a substituent, in which case it becomes acyloxy or –carbonyloxy -. For example:

Acid anhydrides
The acid anhydrides may be regarded theoretically as being derived from an acid by the removal of one molecule of water from two molecules of the acid. The most important anhydrides are derived from the carboxylic acids:
Thus, carboxylic anhydrides have the general structural formula
R and R’ may be same or different
R and R’ may be alkyl or aryl groups
They are named by dropping the word acid from the name of the carboxylic acid and then adding the word anhydride.
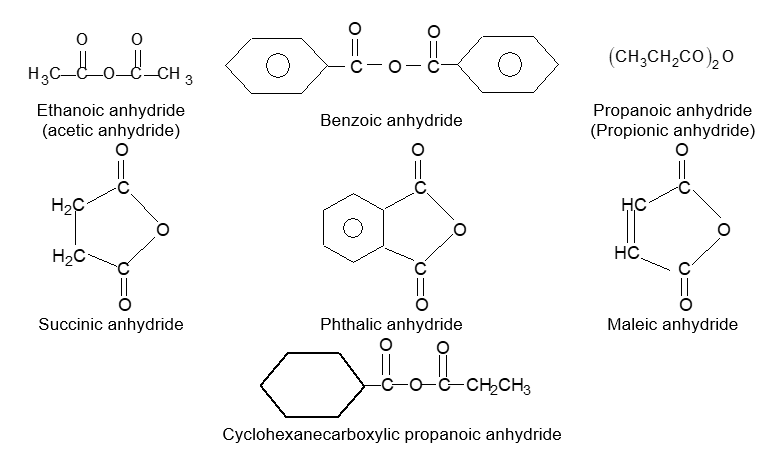
Notice that symmetrical anhydrides (R = R’) are named after the parent acid; unsymmetrical or “mixed anhydrides (R ≠ R’) cite each of the parent acids.
Acyl Halides
Acyl halides may be prepared by the replacement of the hydroxyl in the carboxyl group by halogen. The general structural formula of the acyl halides is
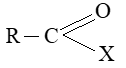
Rule 1 : According to the IUPAC system the class suffix of the acyl halides is – oyl; the common names are formed by changing the suffix –ic of the trivial name of the acid into –yl. For example:
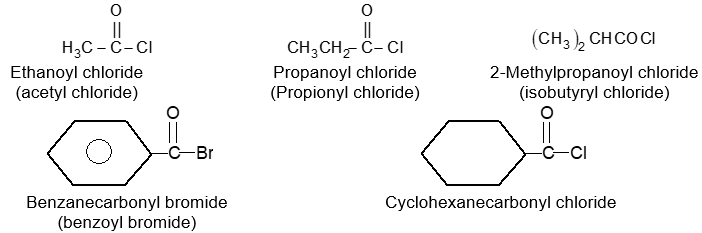
The acyl group, , and the halogen (as halide) are cited separately.
Acyl halides are named by dropping –ic acid from the common (or IUPAC) name of the acid and then adding –yl chloride.
Change: -ic acid to -yl chloride.
Rule 2 : If the carboxyl group is considered as a substituent, then according to the IUPAC system, the nomenclature of all substances containing acyl groups is in all cases based on the name ‘carbonyl’ for the CO group e.g.
CH3CH2CH2COCl
Propane-1-carbonyl chloride
Amides
Acid amides are compounds in which the hydroxyl of the carboxyl group has been replaced by the amino-group, NH2 (or substituted amino group, NHR’, or NR’R”), to form the amido group, -CONH2 (or substituted amido group, -CONHR’, or -CONR’R”).
Thus, acid amides have the general formulae RCONH2, RCONHR’ or RCONR’R” when a carbonyl group is bonded to a nitrogen atom bearing hydrogen and /or alkyl groups.
Rule 1 : Amides that have no substituent on nitrogen are named by dropping –ic acid from the common name of the acid (or –oic acid from the IUPAC name) and then adding amide.
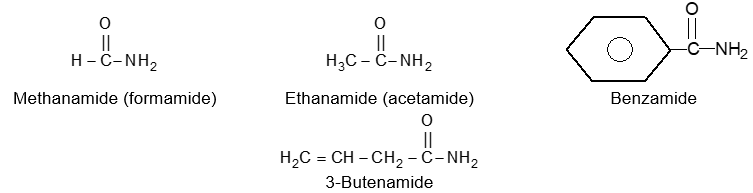
For IUPAC names replace –oic acid of the parent acid by amide but for common names replace –ic acid of the parent acid by amide.
Alternatively, the suffix amide is appended to the name of the hydrocarbon corresponding to the carbon chain that includes the carbonyl group. That is,
Alkan(e) + amide = alkanamide
A one-carbon chain is a carboxamide:
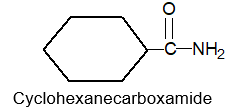
Rule 2 : When the amide nitrogen is substituted with lower-ranking groups than the acyl group, the substituents are designated as prefixes. The letter N is used to show that the substitution is on nitrogen:
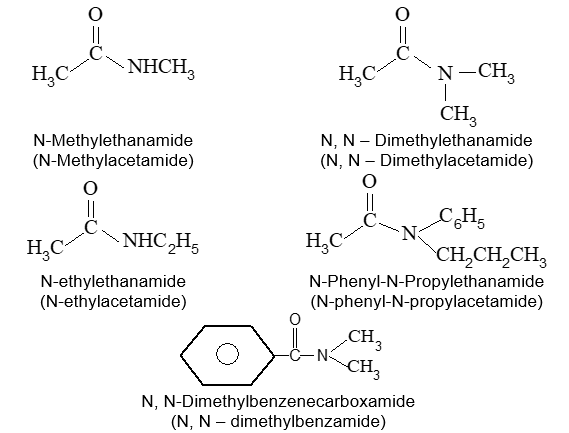
Thus, alkyl groups on the nitrogen atom of amides are named as substituent, and the named substituent is prefaced by N- or N, N-.
Rule 3 : Names for amides as substituents include the following:
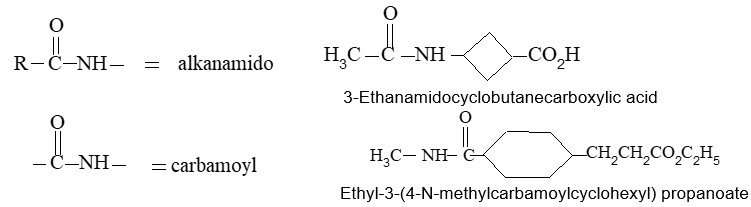
Nomenclature of amines
Just as alcohols and ethers may be regarded as organic derivatives of water, amines may be considered as organic derivatives of ammonia thus amines are organic derivatives of ammonia in which one or more H atoms have been substituted by alkyl groups or aryl groups.
An anime has the general structural formula RNH2, R2NH, or R3N, where R is any alkyl or aryl group:
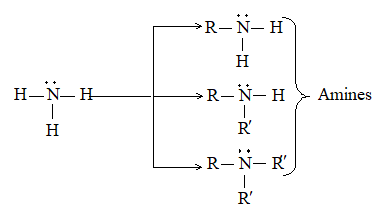
For example
Amines are classified as primary, secondary, or tertiary amines. This calssfiication is based on the number of organic groups (alkyl or aryl groups) that are directly attached to the nitrogen atom. Thus the general structural formulae of primary, secondary and tertiary amines may be written as:

the tertiary nitrogen atom , respectively.
Notice that this classification is quite different from the way alcohols and alkyl halides are classified. For example, isopropyl amine is a primary amine (but isopropyl halide is a secondary halide) even though its – NH2 group is attached to a secondary carbon atom. It is a primary amine because only one organic group is attached to the nitrogen atom:

Rule 1 : In common nomenclature most primary amines are named as alkylamines. In systematic nomenclature (IUPAC names) they are named by adding the suffix –amine to the name of the chain or ring system to which the NH2 group is attached with replacement of the final – e.
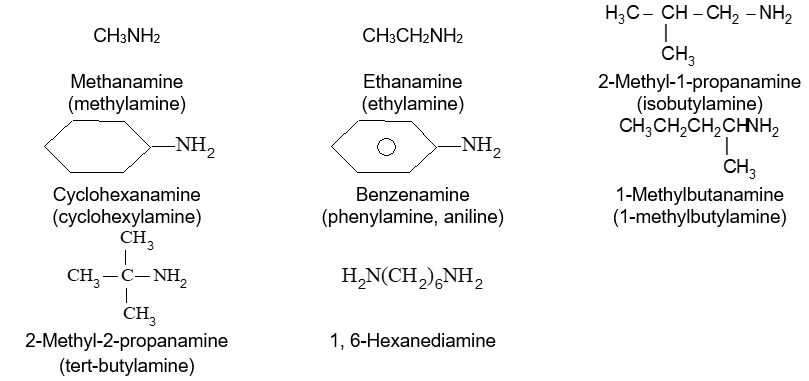
The word “amine” is derived from ammonia and the class of compounds known as amines. Therefore are commonly named as substituted ammonias. In this system, primary amines, having only one substituent on nitrogen, are named with the substituent as a prefix.
More systematic nomenclature appends –amine to the longest chain, as for alcohols.
Rule 2: Most secondary and tertiary amines are named in the same general way. In common nomenclature we either designate the organic groups individually if they are different or use the prefixes di- or tri- if they are the same.
In systematic nomenclature we use the locant N to designate substituents attached to a nitrogen atom.
Secondary amines:
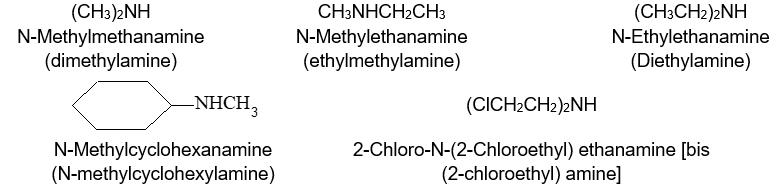
Notice that, alphabetical order puts chloro -ahead of chloroethyl– .
Tertiary amines:
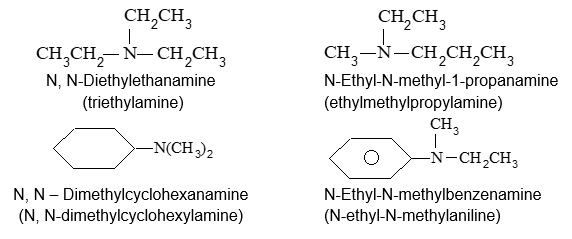
Secondary and tertiary amines, which have two or three substituents on nitrogen, commonly are named as N – substituted amines.
As for substituted amides, N is included to indicate that the substituent is on the nitrogen atom unless there is no ambiguity as to where the substituent is located.
Systematic nomenclature of secondary and tertiary amines is related to the systematic ether nomenclature.
Rule 3 : Aromatic amines – those in which nitrogen is attached directly to an aromatic ring – are generally named as derivatives of the simplest aromatic amine, aniline.
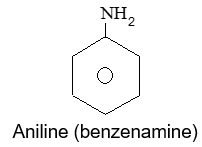
For example:
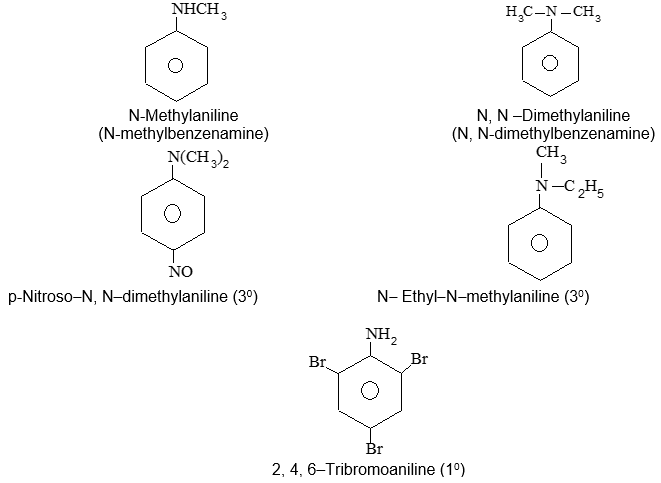
An aminotoluene is given the special name of toluidine.
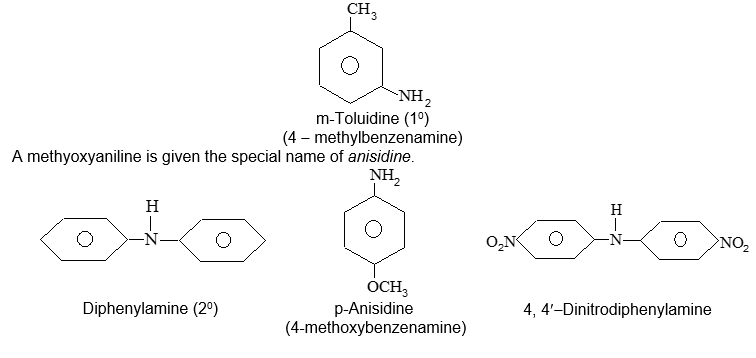
Rule 4: The important heterocyclic amines all have common names. In IUPAC system of nomenclature (or systematic replacement nomenclature) the pretixes aza–, diaza–, and triaza– are used to indicate that nitrogen atoms have replaced carbon atoms in the corresponding hydrocarbon. A nitrogen atom in the ring (or the highest atomic weight heteroatom, as in the case of thiazole) is designated position 1 and numbering proceeds to give the lowest overall set of locants to the heteroatoms.
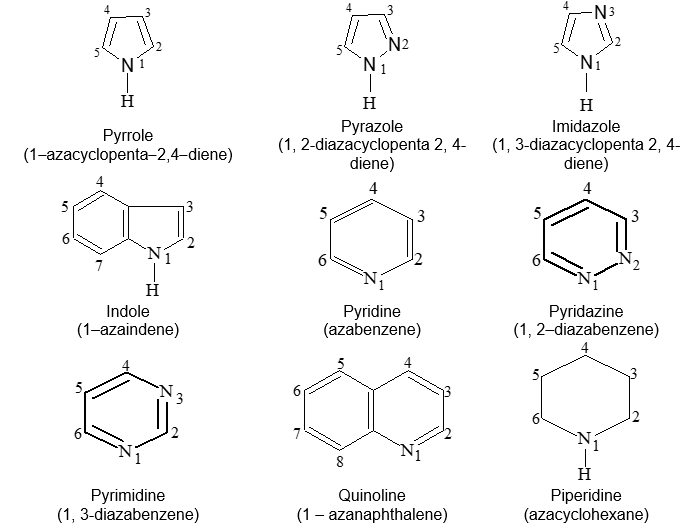
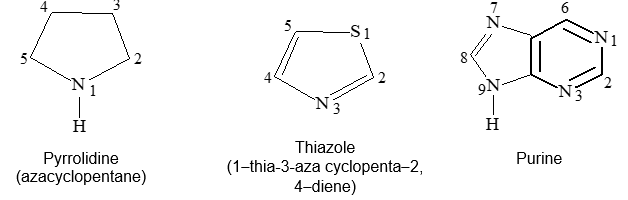
Rule 5: As a substituent, the -NH2 group is systematically called amino. N-substituted amino groups are named accordingly:
We often use this system for naming amines containing an OH group or a CO2H group:
Salts of amines are generally named by replacing –amine by –ammonium (or – aniline by – anilinium), and adding the name of the anion (chloride, nitrate, sulfate, etc.). For example
The method of naming a quaternary ammonium hydroxide is illustrated by the following examples:
Nomenclature of nitriles
A nitrile has the general structural formula,
or RCN
where R may be an alkyl or an aryl group.
The carbon and the nitrogen of a nitrile are sp hybridized.
Rule 1 : In IUPAC systematic nomenclature, acyclic nitriles (compounds with the N function) are named by adding the suffix nitrile to the name of the main-chain hydrocarbon that includes the carbon linked to the nitrile (N) function. The chain is numbered so the CN carbon is C1:
In the common system of nomenclature, nitriles are either named as alkyl cyanides (i.e. the alkyl derivatives of hydrogen cyanide) or as the nitrile of the acid which is produced on their hydrolysis.
They are named by dropping –ic acid from the common name of the acid and adding –nitrile; usually for euphony an “O” is inserted between the root and the ending. For example:
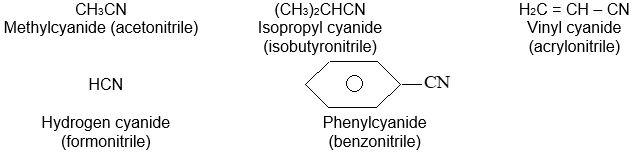
Nitriles can be regarded as derivatives of carboxylic acids because the acid, RCO2H, usually can be obtained from the nitrile, RCN.
Rule 2 : Cyclic nitriles are named by adding the suffix carbonitrile, to the name of the ring system to which the -CN group is attached:

Rule 3 : The substituent name for -CN is cyano. For example,

Nomenclature of isonitriles
An isonitrile has the general structural formulae
or RNC
where R may be an alkyl or an aryl group.
The carbon and the nitrogen of a na isonitrile are sp hybridized.
In IUPAC systematic nomenclature, acyclic isonitriles are named by adding the suffix isonitrile to the name of the corresponding hydrocarbon:
Notice that the carbon of the NC group is not considered while naming the hydrocarbon. In the common system of nomenclature isonitriles are either named as alkyl isocyanides or alkyl carbylamines:
Nomenclature of nitroalkanes
A nitroalkane has the general structural formula
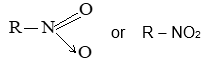
where R may be an alkyl or aryl group.
In the IUPAC system, the nitroalkanes are named as the nitro-derivative of the corresponding alkane, the positions of the nitro-groups being indicated by numbers. For example:
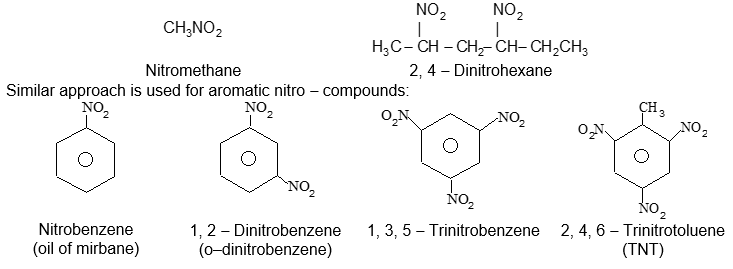 General approaches to naming organic compounds
General approaches to naming organic compounds
There are two aspects to consider:
a) how to derive the name from the given structure, and
b) how to derive the structure from the given name.
Naming a compound of known structure:
Step 1 : First decide what type of compound it is. The decision usually is straight forward for hydrocarbons, which fall in one or the other of the categories alkanes, alkenes, alkynes, arenes, cycloalkanes, and so on.
But when the compound has more than one functional group it is not always obvious which is the parent function. For example, compound 1 could be named as an alkene (because of the double-bond function) or as an alcohol (because of the OH function):
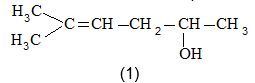
Step 2: To name a compound which contains more than one functional group, it is necessary to choose one as the principal function. The compound is then named by using the suffix of the principla function and the prefixes of the other functions.
Step 3 : Use the order of precedence of functional groups set by Chemical Abstracts to decide which is the parent function.
Classification of compounds in order of decreasing priority for citation as principal function.
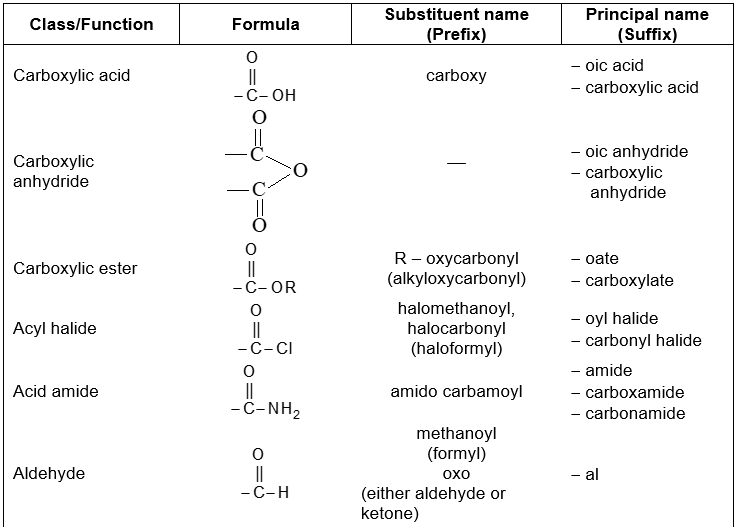
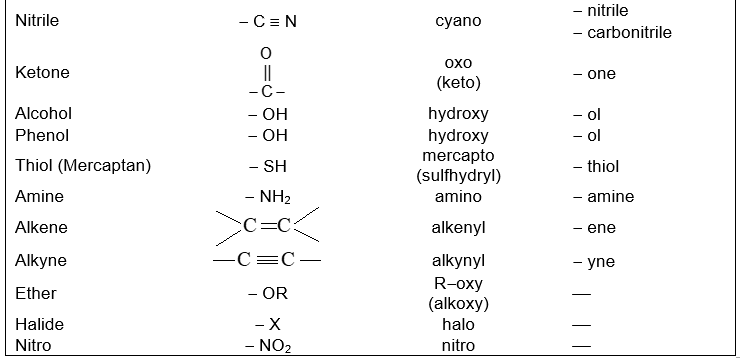
By this system, the OH group takes precedence over hydrocarbons, and compound 1 therefore is named as an alcohol, not as an alkene.
Step 4 : Having decided on the main classification, our next step is to identify the longest, carbon chain that includes the principal functional group. Then this chain is numbered, starting at the end that gives the main function the lowest possible number. The remaining groups, functional or nonfunctional, are taken as substituents and are assigned numbers according to their positon along the chain. Thus for compound 1 :
a) The longest continuous carbon chain carrying the OH group is a sex-carbon unit. The prefix for a six-carbon hydrocarbon is hex-.
b) The chain is numbered so the OH group is at C2, the lowest possible number. Therefore, the IUPAC suffix is -2-ol, in which ol signifies alcohol.
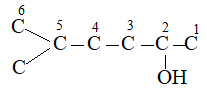
c) The remaining functions are –en(e) (at C4) and methyl (at C5). The complete name is

Notice that the final e is dropped from the suffix -ene when followed by another suffix beginnig with a vowel.
Now consider acetoacetic ester or ethyl acetoacetate.
It contains a ketonic group and a carboxyl group, and since the latter is the principal function, acetoacetic acid is named as a ketonic acid, viz., – ketobutyric acid, 3-ketobutanoic acid, or 3-oxobutanoic acid.
Acetoacetic acid may also be named propan-2-one-1-carboxylic acid – each functional group is indicated by its appropriate suffix.
Let’s consider CH2OHCH2CHO.
This is both an alcohol and an aldehyde, so that, bearing in mind the order of preference, the name of the compound will be b-hydroxypropionaldehyde or 3-hydroxypropionaldehyde or 3-hydroxypropanal.
Translating a name into its chemical structure:
Step 1 : Identify the parent function, which usually is determined from the suffix or word at the end of the name.
Suppose, for example, that a structure is to be written for a compound having the name 3-methoxybutanal. The suffix –al is the IUPAC suffix for aldehyde; therefore the compound is an aldehyde and the principal function is -CHO.
Step 2 : Set up the carbon chain that includes the aldehyde carbon. The prefix butan– denotes a saturated four – carbon chain. Thus, a partial structure with numbering may be written to place the aldehyde function at C1:
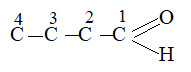
butanal
Step 3 : The rest of the name which generally precedes the parent name, describes the substituent and its position on the parent chain. In our example, 3-methoxy means a CH3O- group at C3. Thus the complete structure of 3-methoxybutanal is
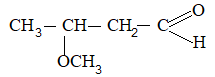
Naming compounds from structures or deducing structures from names requires knowledge of both the parent names and the substituent names of the important types of functional and nonfunctional groups.
The use of Greek Letters to denote substituent positions
In the older literature, considerable use is made of the Greek letters a, b, g, and so on, to designate successive positions along a hydrocarbon chain.
The carbon directly attached to the principal functional group is denoted as a, the second carbon is b, and so on down the chain:
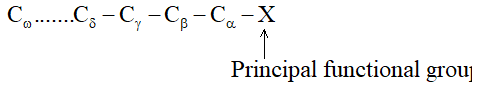
The omega (w) position sometimes is used to designate the last position along the chain regardless of its length. Thus 6-bromohexanoic acid is w-bromohexanoic acid.
In general, the use of Greek letters in the naming of compounds is to be avoided. Because the usage is widespread, knowledge and understanding of the system is important, but systematic naming and numbering systems should be used whenever possible.
Single – or multiple – word names
A troublesome point in naming chemical compounds concerns the rules governing when a compound is to be written as a single word (as methylamine) or as two or more, words (as methyl chloride). To solve this problem, you must determine whether the principal (or parent function) is an element or a compound in its own right. If it is either one, then the name is written as a single word. The following examples should help to clarify the system. In each name, the part of the name that denotes the parent compound is italicized:
The parent compounds designated here as amine carbaldehyde, and sulfonic acid are properly ammonia, methanal, and sulfurous acid (HSO3H) when no substituent groups are attached.
However, if the parent function can’t be constructed as being a real compound, the name is correctly written as two or more words. For example, CH3Cl could be named as a chloride, in which case we use two words, methyl chloride to describe it. A chloride, or any halide, is a class of compound, not a specific compound. To identify a specific halide, the adjective that describes the halide is written as a separate word preceding the class name.
Examples follow in which the class name is italicized:

These word – separated names sometimes are called radicofunctional names.
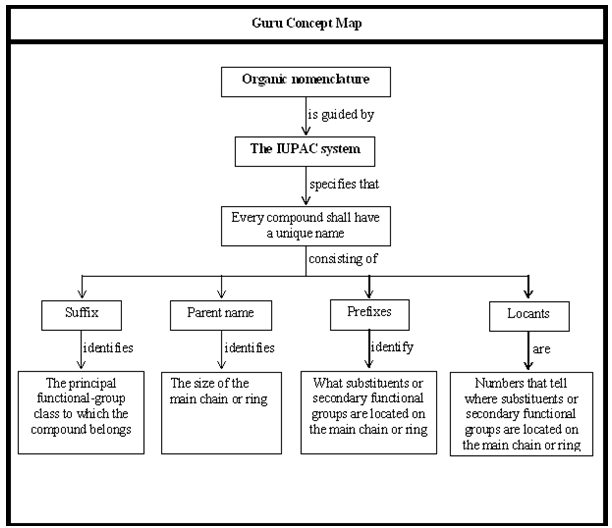
ISOMERISM The concept of isomerism illustrates (especially well) the fundamental importance of molecular structure. Let’s consider two substances, ethyl alcohol and dimethyl ether, which have the same molecular formula, C2H6O but are quite clearly different compounds because they have different physical and chemical properties as discussed below.
| Ethyl Alcohol | Dimethyl Ether |
| 1) It is a liquid boiling at 78.50C. | 1) It is a gas with a boiling point of –24.90C. |
| 2) Its melting point is – 117.30C. | 2) Its melting point is – 1380C. |
| 3) It contains carbon, hydrogen and oxygen in the proportions 2C: 6H: 1O. | 3) It contains carbon, hydrogen and oxygen in the same proportion as ethyl alcohol, 2C: 6H: 1O |
| 4) Measurement of its mass spectrum shows that it has a molecular weight of 46. | 4) It has the same molecular weight as ethyl alcohol. |
| 5) It is a quite reactive compound. | 5) It is a quite unreactive compound. |
| 6) If a piece of sodium metal is dropped into a test tube containing ethyl alcohol, there is a vigorous bubbling. The sodium metal is consumed, hydrogen gas is evolved and a compound of formula C2H5ONa is left behind. | 6) It does not react at all with sodium metal. |
| 7) It reacts with hydriodic acid to form water and a compound of formula C2H5I. | 7) Like ethyl alcohol, it reacts with hydriodic acid, but it yields a compound of formula CH3I. |
We can account for the existence of these two compounds by the fact that they differ in molecular structure: ethyl alcohol is represented by structure I while dimethyl ether is represented by structure II.
One glance at the structural formulae for these two compounds reveals their difference. The two compounds differ in their connectivity. The atoms of carbon, hydrogen and oxygen in ethyl alcohol are connected in a way that is different from that of dimethyl ether. In ethyl alcohol there is a C – C – O linkage while in dimethyl ether the linkage is C – O – C. Ethyl alcohol has a hydrogen atom attached to oxygen while in dimethyl ether all of the hydrogen atoms are attached to carbon. It is the hydrogen atom covalently bonded to oxygen (in ethyl alcohol) that accounts for the fact that ethyl alcohol is a liquid at room temperature.
Hydrogen atom attached to oxygen allows molecules of ethyl alcohol to form hydrogen bonds to one another and gives ethyl alcohol a boiling point much higher than that of dimethyl ether.
The differences in physical and chemical properties of these two compounds can easily be explained on the basis of the difference in structure. Different compounds that have same molecular formula are called isomers (Greek: isos, equal, meros, part).
The phenomenon of existence of two or more compounds possessing the same molecular formula but different properties is known as isomerism. Ethyl alcohol and dimethyl ether contain the same numbers of the same kinds of atoms, but the atoms are attached to one another in different ways. These two compounds are typical examples of what are now called constitutional isomers. An older term for isomers of this type was structural isomers. The international union of pure and applied chemistry (IUPAC) now recommends that use of the term “structural” when applied to isomers of this type be abandoned.
Constitutional isomers are different compounds that have the same molecular formula, but differ in the sequence in which their atoms are bonded together, that is in their connectivity. Constitutional isomers are different compounds because, they have different molecular structures. This difference in molecular structure gives rise to a difference in properties.
Constitutional isomers usually have different physical properties (e.g., melting point, boiling point, and density) and different chemical properties. It is the difference in properties which tells us that we are dealing with different compounds. In some cases, for example, ethyl alcohol and dimethyl ether, the difference in structure and hence the difference in properties is so large (marked) that the isomers belong to different chemical families.
In other cases the difference in structure is so minute (subtle) that it can be described only in terms of three dimensional models.
Other kinds of isomerism fall between these two extremes.
The following flow chart shows different types of isomerism.
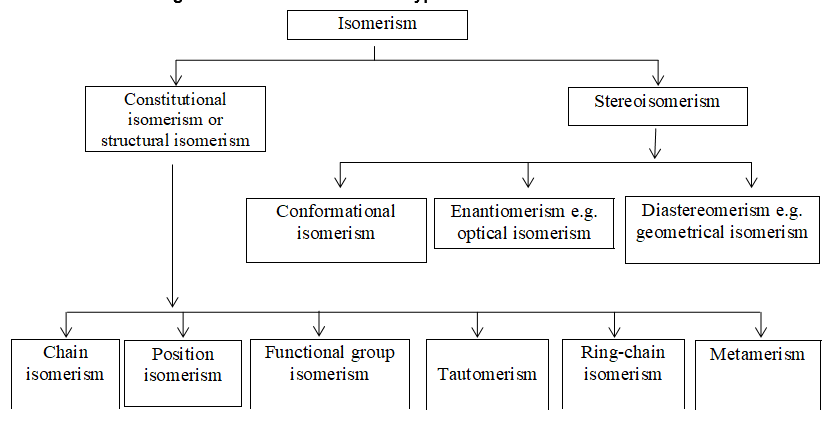
Constitutional Isomerism
The phenomenon of existence of two or more different compounds possessing the same molecular formula but different molecular structures is called constitutional (or structural) isomerism. Thus constitutional isomers are those isomers that differ because their atoms are connected in a different order. They are said to have a different connectivity.
Depending upon the exact cause of the difference in molecular structure, the constitutional isomerism is subclassified into following types:
1. Chain (or nuclear or skeletal) isomerism
The phenomenon of existence of two or more different compounds having the same molecular formula but different carbon skeletons is called chain (nuclear) isomerism. The different compounds are called chain (or nuclear) isomers. Thus this type of isomerism arises due to the difference in the connectivity of carbon atoms in the carbon chain. The essential requirement of chain isomerism is that the molecule of the compound should contain at least three carbon atoms.
This type of isomerism is nicely illustrated by alkanes. All the alkanes can be derived formally from methane by substituting hydrogen atoms by methyl groups (-CH3). When the alkane contains three or more carbon atoms, substitution gives rise to chain isomerism. For example, propane, C3H8, gives rise to two butanes, C4H10.
(I) by substitution at a terminal carbon atom, and
(II) by substitution at the central carbon atom
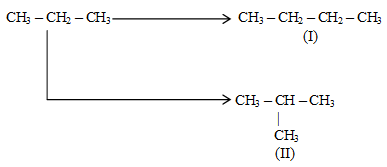
(I) has a straight carbon chain, and (II) has a branched carbon chain. Both isomers are known. This is a typical example of chain (or nuclear) isomerism as it is characterized by the manner of linking of the carbon chain.
Thus butane is the first alkane to exhibit constitutional isomerism. (I) is known as normal butane and (II) as isobutane.
Three pentanes, C5H12, may be derived from the butanes:

As the number of carbon atoms in the alkane increases, the number of possible chain isomers increases rapidly. Thus, there are 5 hexanes, 9 heptanes, 18 octanes, 35 nonanes and 75 decanes. The alkane C15H32 can exist in 4347 isomeric forms and for the twenty – carbon icosane, there are 366319 possible isomeric structures!
The number of isomers of a given alkane may be calculated by means of mathematical formulae. In most cases very few have actually been prepared.
Each isomer has a distinctive name. If two structural formulae have the same (correct) names, they are identical even if they are drawn differently.
Illustration37: Write the condensed structural formulae for the octane (C8H18) and undecane (C11H24) with the maximum number of methyl groups.
Solution: Octane : ; Undecane
2. Position Isomerism
The phenomenon of existence of two or more different compounds having the same molecular formula but different position of substituent or functional group on the same carbon skeleton is termed as position isomerism.
Thus the following compounds can exhibit position isomerism:
(a) Alkenes (b) Alkynes (c) Arenes d) Alkyl halides
(e) Aryl halides (f) Alcohols (g) Amines and h) Nitro compounds
a) Alkenes containing four or more carbon atoms can exhibit position isomerism due to the difference in the position of double bond on the same carbon skeleton, For example:
i)
ii)
iii)
b) Alkynes containing four or more carbon atoms can exhibit position isomerism due to the difference in the position of triple bond on the same carbon skeleton. For example:
i)
ii)
c) Arenes containing eight or more carbon atoms exhibit position isomerism due to the difference in the position of alkyl groups on the benzene ring. For example:
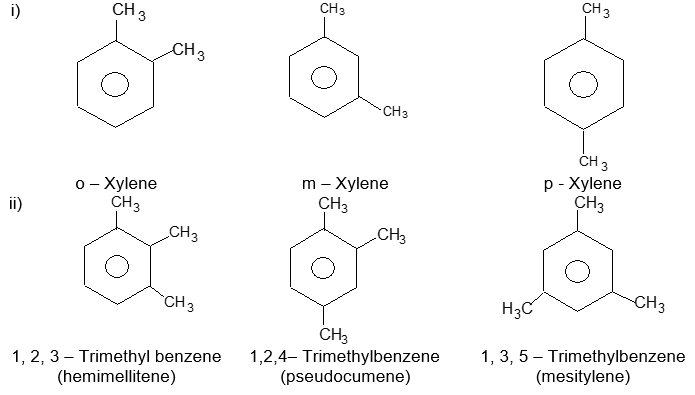
d) Alkyl halides containing three or more carbon atoms can exhibit position isomerism due to the difference in the position of halogen atom on the same carbon skeleton. For example
i) C3H7Cl has two position isomers:
ii) n – Pentane on monochlorination gives three isomeric chloropentanes:
Polyhalogen derivatives containing two or more carbon atoms can also exhibit position isomerism. For example:
CH3CHCl2 1, 1 – Dichloroethane ClCH2CH2Cl 1, 2 – Dichloroethane
e) Aryl halides containing two or more benzene rings can exhibit position isomerism due to the difference in the position of halogen atom. For example:

Polyhalogen compounds containing just one benzene ring can also exhibit position isomerism. For example:

f) Alcohols containing three or more carbon atoms exhibit position isomerism due to the difference in the position of functional group ( -OH). For example :
i) The molecular formula C3H8O represents two isomeric alcohols:
ii) Four monohydric alcohols differing in the position of – OH group can be derived from isopentane:
g) Primary amines (RNH2) containing three or more carbon atoms can exhibit position isomerism due to the difference in the position of amino group on the same carbon skeleton. For example:
h) Nitro compounds (RNO2) containing three or more carbon atoms can exhibit position isomerism due to the difference in the position of nitro group on the same carbon skeleton. For example:
3. Functional group Isomerism:
The phenomenon of existence of two or more different compounds possessing the same molecular formula but different functional groups is known as functional group isomerism such compounds are called as functional isomers. Unlike chain and position isomers, functional isomers belong to different chemical families. The following are typical examples of functional isomers:
a) Both alkynes and dienes have the same molecular formula, CnH2n-2, but have different properties due to different functional groups. For example, the molecular formula, C4H6, represents the following alkynes and dienes:
| Alkynes | Dienes |
| CH3CH2C CH | H2C = C = CH – CH3 |
| But – 1- yne | Buta – 1, 2 – diene (an allene) |
| CH3C CCH3 | CH2 = CH – CH = CH2– |
| But – 2- yne | Buta – 1, 3 – diene |
Notice that but-1-yne and buta-1, 2-diene are functional isomers. Similarly but -1-yne and buta-1,3-diene are functional isomers, etc.
b) Both monohydric alcohols (ROH) and ethers (R–O–R’) have the same molecular formula CnH2n+2O, but have different properties due to different functional groups. For example, the molecular formula C4H10O represent the following monohydric alcohols and ethers.
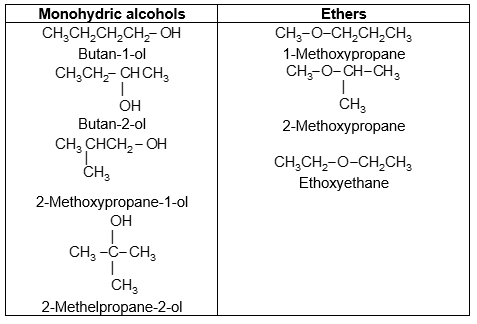
Notice that butan-1-ol and 1-methoxypropane are functional isomers. Similarly, butan-1-ol and 2-methoxypropane are functional isomers, etc.
c) Aldehydes, ketones, unsaturated alcohols, unsaturated ethers, epoxy alkanes and cyclic alcohols all have the same molecular formula, CnH2nO, but possess different properties due to different functional groups. For example, the molecular formula, C3H6O, represents the following functional isomers:
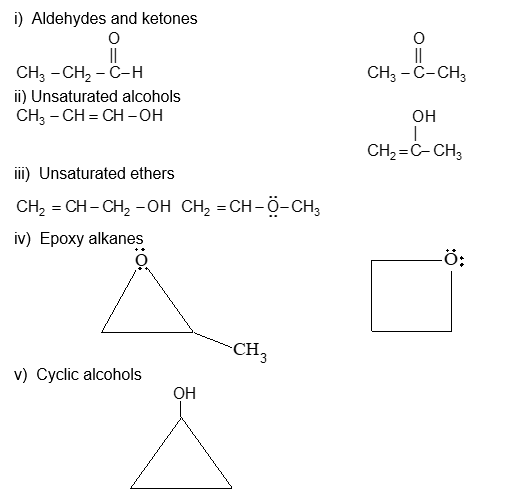
While writing the structural isomers for any given molecular formula, tautomers are neglected unless asked for.
Illustration 38: Write all possible structural isomers of molecular formula, C3H6O.
Solution: Here we consider the stable as well as the unstable structures i.e. tautomers are also included.
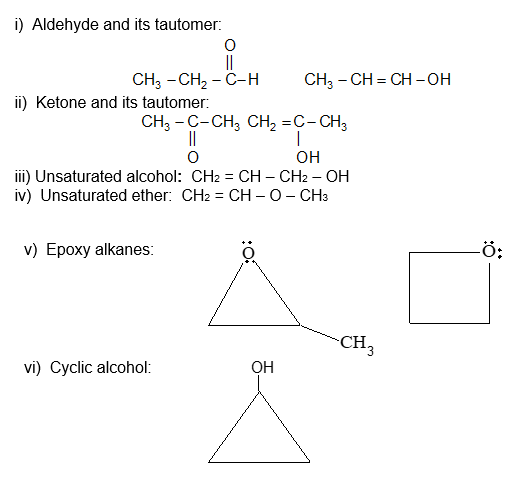
Illustration 39: How many carbonyl compounds (only structural isomers) are possible for molecular formula, C5H10O?
Solution: Aldehydes (RCHO) :
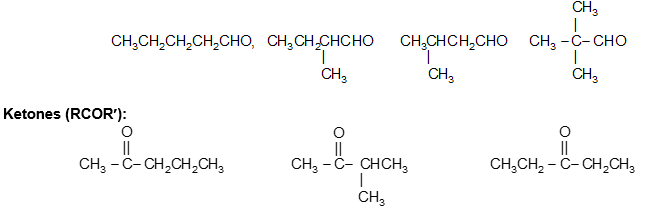
d) Saturated monocarboxylic acids (RCO2H), esters (RCO2R/) and hydroxyl carbonyl compounds have the same molecular formula CnH2nO2, but have different properties due to different functional groups. Thus the molecular formula, C4H8O2, represents the following carboxylic acids and esters as functional isomers:
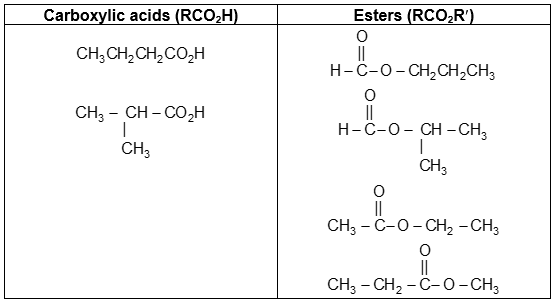
Illustration 40: How many isomeric carboxylic acids (only structural isomers) are possible corresponding to molecular formula, C5H10O2?
Solution: Possible carboxylic acids are :
Illustration 41: How many isomeric esters (only structural isomers) are possible corresponding to molecular formula, C5H10O2?
Solution: Possible carboxylic esters are:
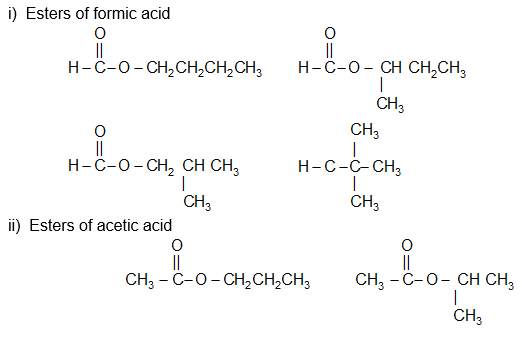
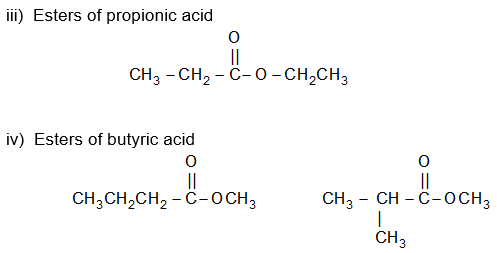
e) Both nitroalkanes and alkyl nitrites have the same molecular formula, (CnH2n+1NO2), but possess different properties due to different functional groups. Thus the molecular formula, C3H7NO2, represents the following functional isomers:
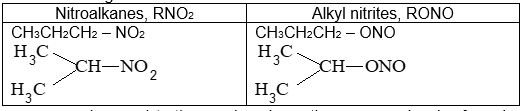
f) Primary, secondary and tertiary amines have the same molecular formula, CnH2n+3N, but carry different functional groups. Thus, the molecular formula, C4H11N, represents the following functional isomers:
Primary amines, RNH2
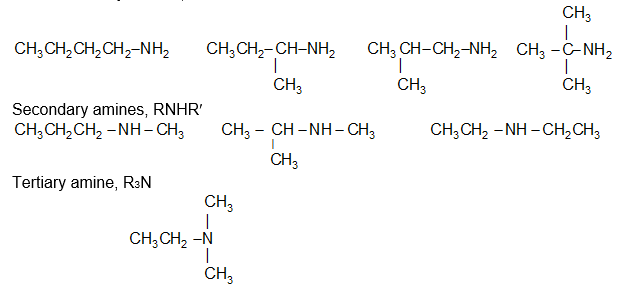
g) Both cyanides (R-CºN) and isocyanides () have the same molecular formula but possess different properties dept to different functional groups. For example, the molecular formula, C2H3N, represents the following functional isomers:
4. Metamerism
The phenomenon of existence of two or more different compounds having the same molecular formula but different number and arrangement of carbon atoms on either side of the functional group is called metamerism. Such compounds are known as metamers.
Metamerism is never possible in compounds possessing the univalent functional group. Metamerism is due to the difference in the nature of alkyl groups attached to the same polyvalent functional group such as
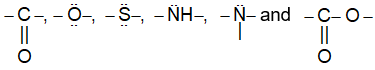
Metamerism is exhibited by compounds of the same homologous series.
a) Ethers, R–O–R¢, exhibit metamerism due to difference in the nature of the alkyl groups attached to the oxygen atom. Thus, the molecular formula, C4H10O, represents the following metamers:
b) Ketones, , exhibit metamerism due to the difference in the nature of the alkyl groups attached to the carbonyl group. Thus, the molecular formula, C5H10O, represents the following metamers:
c) Thioethers, R–S–R¢, exhibit metamerism due to the difference in the nature of the alkyl groups attached to the sulphur atom. Thus, the molecular formula, C4H10S, represents the following metamers:
d) Secondary and tertiary amines exhibit metamerism due to the difference in the nature of the alkyl groups attached to the – NH – group and the atom respectively. Thus the molecular formula, C4H11N, represents the following metamers:
e) Esters, , exhibit metamierism due to the difference in the nature of the alkyl groups attached to the Thus, the following esters are metamers:
If same polyvalent functional group is present in two or more organic compounds, then instead of chain or position isomerism, treat the phenomenon as metamerism.
(i) Pentan – 2- one and pentan – 3- one are metamers and not position isomers. They can be included in position isomerism, if metamerism is not mentioned.
(ii) Similarly, pentan – 2- one and 3 – methylbutan-2-one are metamers and not chain isomers.
Metamers may be considered as position isomers. For instance, pentan – 2- one and penta-3- one may be regarded as position isomers as well as metamers.
5. Tautomerism
Ethyl acetoacetate (E. A.A) or acetoacetic ester (A. A. E) is the ethyl ester of acetoacetic acid, ketonicacid.
Acetocetic ester was first discovered by Geuther (1863), who suggested the formula
and prepared it by the action of sodium on ethyl acetate.
Frankland and Duppa (1865) also prepared (independently of Geuther) acetoacetic aster by the action of sodium on ethyl acetate but proposed the formula of a -ketobutyric ester:
Evidence in favour of the Geuther formula:
The Geuther formula, an unsaturated alcohol, is supported by the following chemical reactions:
i) When acetoacetic ester is treated with an ethanolic solution of bromine, the colour of the latter is immediately discharged. This indicates the presence of an olefinic double bond, >C=C<
ii) When acetoacetic ester is treated with sodium metal, dihydrogen gas is evolved and the sodium derivative is formed. This indicates the presence of a hydroxyl group, –
iii) When acetoacetic ester is treated with ferric chloride, a reddish – violet colour is produced. This is characteristic of compounds containing the group.
Evidence in favour of the Frankland – Duppa formula:
The Frankland – Duppa formula, a ketone, is supported by the following chemical reactions:
i) Acetoacetic ester forms a bisulphite compound with sodium hydrogen sulphite.
ii) Acetoacetic ester forms a cyanohydrin with hydrogen cyanide.
Here we have a compound which has two different formulae, each of which supported by a number of particular reactions.
In 1910, chemists came to the conclusion that both formulae were correct because the two compounds existed together in dynamic equilibrium in solution.
When a reagent which reacts with ketones is added to the equilibrium system, the ketone form of acetoacetic ester is consumed. This upsets the equilibrium. In order to restore the equilibrium, the hydroxyl – form of the acetoacetic ester changes into the ketone form.
Thus, on addition of sufficient amount of reagent, acetoacetic ester reacts completely as the ketone form. Similarly, on addition of sufficient quantity of a reagent which reacts with alkenes or with hydroxyl – compounds, acetoacetic ester reacts completely as the hydroxyl – form.
In 1911, Knorr, succeeded in isolating both forms of acetoacetic ester, the pure hydroxyl – form corresponding to the Geuther formula and the pure ketone form corresponding to the Frankland–Duppa formula.
Thus acetoactic ester is a substance that plays the dual role of two structural (or constitutional isomers) which exist together in equilibrium.
This is a case of dynamic isomerism as each isomer changes rapidly into the other when the equilibrium is disturbed, for example, by the addition of certain reagents.
The name tautomerism (Greek : same parts) was given by Laar (1885) to describe this equilibrium phenomenon.
The two forms are known as tautomers or tautomerides. Since the ketone isomer is called the keto form of acetoacetic ester, and the hydroxyl isomer the enol form, this type of tautomerism is known as keto-enol tautomerism.
In the IUPAC system of nomenclature the suffix – en indicates the presence of a double bond, and the suffix-ol, a hydroxyl group.
The word enol is a combination of these suffixes and indicates the structure of the non ketonic isomer.
Thus, taumerism, a case of dynamic isomerism, may be defined as an isomerism in which a single compound exists in two easily and rapidly interconvertible structures that differ markedly in arrangement of atoms.
Structures that differ markedly in arrangement of atoms, but which exist in easy and rapid equilibrium are called tautomers.
Tautomerism is a special type of functional isomerism where the isomers exist simultaneously in dynamic equilibrium with each other.
Sometimes the form tautomerism is also refered to as desmotropism (Greek : desmos – bond; tropos – turn), since the interconversion of the two forms involves a change in the position of a pi ( bond). It is also called as dynamic isomerism as the tautomers are in dynamic equilibrium with each other. Other uncommon names used for tautomerism are:
Kryptomerism, allelotropism and mesotropy. However, tautomerism is the most widely used term.
The most common kind of tautomerism involves structures that differ in the point of attachement of hydrogen. Keto-enol tautomerism is the typical example of this kind.
The most widely studied and investigated example of keto –enol tautomerism is that of acetoacetic ester.
When one tautomer is more stable than the other (under normal conditions) the former is known as the stable form, and the latter as the labile form.
In practice, it is usually difficult to say which is the stable form, because very often a slight change in the conditions such as temperature or nature of solvent, shifts the equilibrium easily and rapidly from keto to enol or vice versa. In the solid state, the possibility of tautomerism is rare. Hence, in the solid state, one or other tautomer is normally stable, for example, only the keto form of acetoacetic ester is stable in the solid state.
However, in the liquid or gaseous state, or in solution, the two forms usually exist as an equilibrium mixture.
The enol form is more volatile than the keto, and the change from enol to keto is extremely sensitive to catalysts.
Traces of basic compounds are very effective catalysts. Thus, soft glass vessels are unsuitable for the separation of the keto and enol forms. Because, when fractionated, the more volatile enol form rapidly changes into the original keto – enol mixture under the catalytic influence of the walls of the containing vessel.
One can successfully separate the enol form from the keto form by carrying out the fractional distillation under reduced pressure in silica apparatus which has been thoroughly cleaned i.e., freed from dust, moisture, etc. Distillation under these conditions is known as aseptic distillation.
In general, in tautomerism there may be an equilibrium between two or more forms. Either all may be present to about the same extent or one may predominate. The concentration of each form depends on the temperature and the solvent (if in solution).
Although it may not be possible to separate tautomers owing to
i) the ease and rapidity of their interconversion or,
ii) as in many cases, due to one form being almost completely absent.
iii) the presence of more than one compound may be shown by special properties of each isomer.
Experiments using deuterium exchange reactions have shown the presence of keto-enol mixtures. For example, hydrogen is exchanged slowly by deuterium when acetaldehyde is dissolved in D2O. Since the C – H bond in alkanes is stable under these conditions, the inference is that a hydroxyl group is present in acetaldehyde, i.e., some enol form is present.
Acetone undergoes this exchange more rapidly.
The various methods used for the quantitative estimation of each form in any tautomeric equilibrium (of which the keto – enol system is only one example) fall into two distinct groups, physical and chemical.
| Compound | Per cent enol (in ethanol) |
| Aldehydes of type RCH2CHO | Trace |
| Ketones of type RCH2COCH2R | Trace |
| 4.8 | |
| 7.5 | |
| 31.0 | |
| 76.0 | |
| 96.0 |
Enolisation:
The ability of a compound to form the enol form is called enolisation. The phenomenon of enolisation is exhibited by compounds containing either a methylene group, –CH2– , or a methyne group, adjacent to a carbonyl group.
The actual amount of >CH- enol form present depends on a number of factors:
When the methylene or methyne group is attached to two or three carbonyl groups, the hydrogen atom should migrate equally well to one or other carbonyl group.
This does not happen for unsymmetrical compounds as one enol form is either present exclusively, or largely predominating. For example, in acetoacetic ester the hydrogen atom migrates exclusively to the acetyl carbonyl group:
When two or more enols forms are possible (theoretically), ozonolysis may be used to as certain the structure of the form present. For example, in hexane-2,4-dione, , the two possible enols are:
Ozonolysis of (I) will give CH3CO2H and CH3CH2COCHO while ozonolysis of (II) will give CH3COCHO and CH3CH2CO2H. Identification of these compounds can easily decide whether the enol is (I) or (II), or a mixture of both.
The kind of tautomerism described above is known as the keto-enol triad system, because in this system a hydrogen atom migrates from atom 1 (oxygen) to atom 3 (carbon) or vice versa:
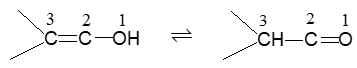
Enols and phenols resemble each other in a number of ways:
both give characteristic colerations with ferric chloride
both form soluble sodium salts
both couple with diazonium salts.
The keto–enol kind of tautomerism is just one example of a triad system. Another important example of a triad system is nitro-acinitro (psuedonitro) system:
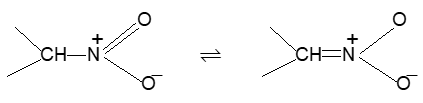
The triad system is the most important class of tautomeric systems.
In addition to the ‘open’ systems of tautomerism, there is also ring – chain tautomerism:
Recent work suggests that aldol is an equilibrium mixture of – hydroxylbutyraldehyde and the cyclic hemiacetal:
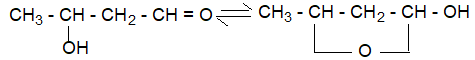
This is an example of ring – chain tautomerism.
Carbohydrates such as glucose also exhibit ring – chain tautomerism.
If during tautomerisation the hydrogen atom oscillates between two polyvalent atoms joined together, the tautomeric system is a diad.
A typical example of diad system is hydrocyanic acid in which hydrogen atom oscillates between carbon and nitrogen atoms:
Theory of tautomerism:
Base – catalysed enolisation of a ketone proceeds through an enolate anion (I) whose formation is controlled largely by the inductive effects of the alkyl groups:
Acid–catalysed enolisation involves the removal of a proton from the conjugate acid of the ketone (II) :
This process depends mainly on the hyperconjugation by the alkyl groups in the transition state for the formation of the carbon – carbon double bond.
Evidence for these mechanisms is that alkyl groups depress base – catalysed reaction rates.
The mechanisms described above are stepwise mechanisms. They appear to operate in certain cases. In other cases, acid and base – catalysis of enolisation take place by a concerted mechanism, i.e., the molecule undergoing change is attacked simultaneously at two places.
Enolisation of acetone proceeds by the simultaneous removal of a proton from an – carbon and the addition of a proton to the oxygen of the carbonyl group:
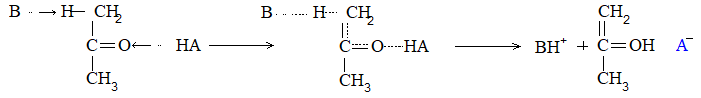
Note: B is a base and HA is an acid.
In this type of mechanism, the solvent water molecules are supposed to be involved, one acting as a proton acceptor and the other as a proton donor.
The tremendous increase in speed by acid and base catalysts is supported by the fact that the pure keto and enol forms of ethyl acetoacetate change very slowly into the equilibrium mixture (several weeks), whereas the latter is obtained rapidly (several minutes) by the addition of acid or base catalysts.
Illustration 42: Using the following bond energy data:
E (C – H) = 414.2 kJ/mol E (C – C) = 347.3 kJ/mol
E (C = C) = 606.7 kJ/mol E (C = O) = 694.5 kJ/mol
E (C – O) = 334.7 kJ/mol E (O – H) = 464.4 kJ/mol
show that keto form is usually more stable.
Solution: Find the sum of the bond energies of the and groups
This implies that the enthalpy of formation of the CH2CO group is – 1870 kJ and that of the CH = C(OH) – group is – 1820 kJ.
Thus the keto form is usually more stable than the enol by 50kJ mol–1. Hence there must be some driving force to bring about enolisation.
Illustration 43: Show that a difference of 22.84 kJ mol–1 in G shifts the equilibrium from 1 percent enol to 99 per cent enol.
Solution: GӨ = – RT ln K
If the equilibrium mixture contains 1 percent enol, then
GӨ =
If the equilibrium mixture contains 99 percent enol, then
Thus, a difference of 22.84 kJ mol–1 in G shifts the equilibrium from 1 percent enol to 99 percent enol.
This also implies that small changes in G will have large effects on the position of the equilibrium.
Factors deciding the position of keto–enol equilibrium
i) Nature of the solvent: If one form is more solvated than the other, then there is considerable entropy effect connected with the nature of the solvent.
Any solvent that can form hydrogen bonds with the carbonyl group of the keto form will lead to a decrease in entropy.
Since the enol form forms an intramolecular hydrogen bond, it is largely prevented from forming hydrogen bonds with the solvent. Consequently, there is a smaller decrease in entropy.
Since, GӨ = H Ө – TSӨ = – RT ln K
the term SӨ becomes important in deciding the position of keto – enol equilibrium.
Thus, polar protic solvents such as water, methanol, acetic acid etc, which form H – bonds with the carbonyl group of the keto form tend to reduce the enol content.
On the other hand in aprotic solvents such as hexane, benzene, etc., (or in the absence of polar protic solvent), the enol content will be larger. For instance, enol content of acetylacetone in ethanol is 76% but in hexane is 92%.
The enol content of E.A.A. (pure liquid) decreases as the pressure increases. This implies that the molar volume of the enol form is greater than that of the keto.
ii) Steric factor: Consider the enol content of acetylacetone and a-methylacetone in the gas phase:
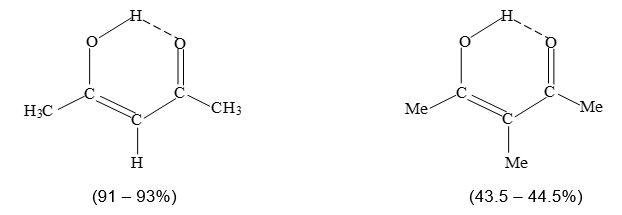
We find that, although both the enols are stabilized by H – bonding, less enol is present in the latter equilibrium mixture than in the former. In -methylacetylacetone, there is much greater steric repulsion due to the presence of the – methyl group. Thus, the a – methyl enol form has greater internal strain than the enol of acetylacetone and so the former is less favourable energetically than the latter.
iii) Hydrogen bonding: Higher the stability of the enol form, greater is the enol content. Thus, the amount of enolic form is relatively higher if the enol form is stabilized by intramolecular hydrogen bonding (chelation):
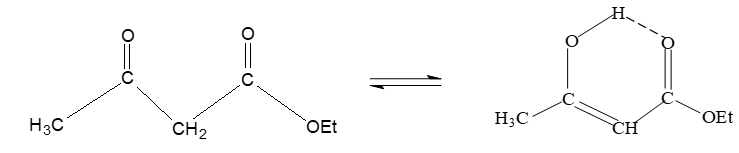
In simple carbonyl compounds such as acetaldehyde and acetone, the amount of enolic form is negligibly small. However, in 1,3–dicarbonyl compounds, the amount of enolic form is relatively higher on account of intramolecular hydrogen bonding.
iv) Resonance stabilization: Higher the stability of the enol form, greater is the enol content. Thus, the amount of enolic form is relatively higher, if the enol form is more stabilized by resonance. For example, the enol form of E.A.A. is less stabilized by resonance than that of acetylacetone and thus is present in small amount.
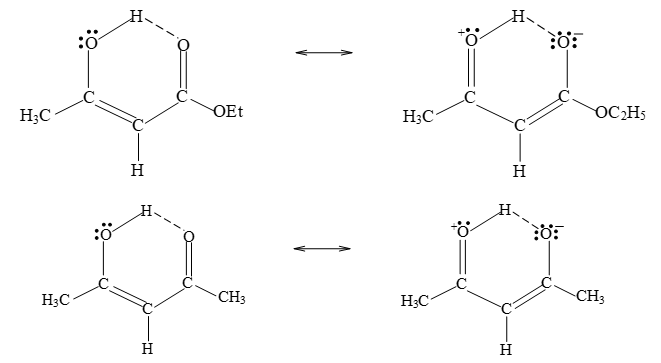
Necessary and Sufficient Condition to exhibit Tautomerism
i) Molecule of compound should have at least one acidic (or active) hydrogen atom, i.e., hydrogen atom directly attached to a highly electronegative element such as nitrogen or oxygen, and a – hydrogen atom of carbonyl compounds.
ii) The negative ion formed after the loss of acidic hydrogen atom as proton should be resonance stabilized.
Difference between Resonance and Tautomerism Notice that keto – enol tautomers are not resonance structures. They are constitutional isomers in equilibrium (usually favoring the keto form as keto forms are generally more stable then enol forms). Some of the important differences between resonance and tautomerism are summarized in the tabular format:
| Tautomerism | Resonance | ||
| 1) | Tautomers are definite compounds. They can be separated and characterized by suitable methods. | 1) | Resonating structures are the imaginary structures of the same compound. Hence, they can’t be isolated. |
| 2) | Tautomerism (cationotropism) involves the migration of an atom (usually hydrogen) between two polyvalent atoms present in the molecule. Thus, tautomers differ in the position of that mobile atom. | 2) | Resonance involves a change in the position of pi (p) electrons or unshared electrons. Thus, resonating structures have identical atomic arrangement. |
| 3) | Tautomers are in dynamic equilibrium with each other i.e. they are inter convertible. Thus tautomerism is indicated by ‘’. | 3) | Resonating structures are not in dynamic equilibrium with each other i.e. they are not interconvertible. Thus, resonance is indicated by ‘’. |
| 4) | Tautomers have different functional groups and hence have different structures. | 4) | Various resonating structures have the same functional group and hence have the same structure. |
| 5) | Tautomerism has no effect on bond length. | 5) | Resonance affects the bond length. It is accompanied by an increase in bond length of a double bond and decrease in the bond length of a single bond. |
| 6) | Tautomerism does not lower the energy of the molecule and hence has no contribution in stabilizing the molecule. | 6) | Resonance lowers the (internal) energy of the molecule and hence increases the stability of the molecule. |
| 7) | Tautomerism occurs in planar as well as in non-planar molecules | 7) | Resonance occurs only in planar molecules. |
6. Ring – chain isomerism
The phenomenon of existence of two or more compounds having the same molecular formula but possessing open chain and closed chain (cyclic structure) is called ring – chain isomerism. This type of isomerism arises due to different modes of linking of carbon atoms. Thus ring-chain isomers possess open chain or closed chain structures as illustrated by the following examples: Examples:
i) Two ring-chain isomers are possible corresponding to the molecular formula C3H6:
ii) Six pairs of ring-chain isomers are possible for the molecular formula C4H8:
iii) The molecular formula C3H4 represents the two ring – chain isomers:
Ring chain isomerism, can be included in functional isomerism, if not considered separately. The problems based on structural isomerism (and structure determination of organic molecules) can be easily tackled by the concept of degree (or element) of unsaturation, which is defined as the number of pairs of hydrogen atoms a molecular formula lacks to be an alkane (CnH2n+2). Thus it is sometimes called index of hydrogen deficiency or double bond equivalents (D.B.E.).
Thus, the degree of unsaturation for C6H14 is zero as this molecular formula fits the alkane series. A molecule with four carbon atoms needs 10 hydrogen atoms to be an alkane. Thus, the formula, C4H6, with six hydrogen atoms lacks four hydrogen atoms or two pairs of hydrogen atoms. It has 20 of unsaturation.
Similarly a formula, C6H6, with six carbon atoms and only six hydrogen atoms lacks eight hydrogen atoms or four pairs of hydrogen atoms. It also has 40 of unsaturation. The following structural features induce degree of unsaturation:
i) multiple bonds
ii) rings (or cyclic structures)
Thus, the total number of D.B.E. is the sum of multiple bonds and rings present in the molecule: D.B.E = (Number of double bonds) + (Number of rings) + 2 (Number of triple bonds). It is also given by the following relation:
where n = number of atoms of each kind present in the molecule
V = valency of each atom
For example, the molecular formula C4H6 has
= 1 + 1 = 2
This means that C4H6 has 20 of unsaturation as follows:
i) Two double bonds: H2C = CH – CH = CH2 H2C = C = CH – CH3
ii) One triple bond:
iii) One ring and one double bond:

iv) Two rings:
Similarly 4 D.B.E implies
i) Four double bonds or (ii) two triple bonds or (iii) two double bonds + one triple bond or (iv) three double bonds + one ring, etc.
Illustration 44: Write down the cyclic isomers having the molecular formula, C3H6O.
Solution: First calculate the degree of unsaturation or double bond equivalents.
D.B.E =
= 1
Thus, various cyclic isomers of C3H6O contain just one ring :
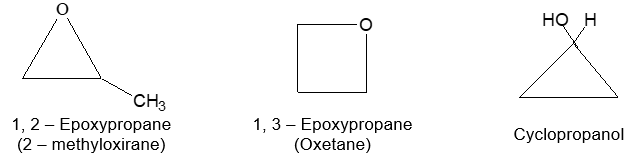
Illustration 45: Write down structural isomeric ethers corresponding to the molecular formula, C5H12O.
Solution: First calculate the degree of unsaturation or double bond equivalents:
= 0
This implies that only saturated acyclic ethers are to be considered:
Illustration 46: Write down polygon formulae (structural isomers) for the molecular formula, C5H10
Solution: Here polygon formulae mean cyclic formulae. They are:

Double bond equivalent is also called the index number.
Chemistry is primarily a molecular science as chemists try to explain observable phenomena in terms of molecular structure of the changing material.
Whenever a chemist is faced with a problem he will often ask “ what is the structure of the material”? Molecular structures are models or shorthand descriptions of molecules which convey considerable information.
Molecular structure provides a basis for
i) understanding observed properties,
ii) predicting new properties not yet reported,
iii) suggesting methods of synthesis,
iv) if the compound is a natural product speculating about its method of production (biosynthesis) and
v) its reactions in living systems (metabolism)
Every compound has its own distinct structure. If two compounds differ in only a single property, though identical in all other respects, then their molecules are different in some way. This must be reflected in their different structures.
Stereoisomerism
In 1874 Le Bel and van’t Hoff made an independent suggestion that molecules exist in a three – dimensional form.
Two or more different compounds whose molecules have the same molecular formula and the same atomic connectivities but differ in the three-dimensional arrangement of their constituent atoms are called stereoisomers.
Stereoisomers are not constitutional isomers.
Stereoisomers have the same constitution, i.e., their atoms are connected in the same sequence, but they differ in the arrangement of their atoms in space.
Thus, stereoisomerism is the subtle kind of isomerism which can be understood only in three dimensional terms.
Tartaric acid has been known for centuries. It is readily obtained from a crystalline deposit which separates in wine vats in the form of a potassium salt.
About 1819 a second acid was obtained during the crystallization of the above potassium salt. It was called racemic acid (racemus, bunch of grapes).
In 1853, Pasteur made yet another compound called mesotartaric acid differing from the others, but having the same structure when represented in the linear form.
The three acids have the same chemical properties and can be represented as HOOC.CH(OH).CH(OH).COOH
but they differ in physical properties such as their crystalline form, melting point, and water – solubility.
The prefix “stereo” is derived from the Greek word stereos which means “solid”. Stereochemistry is the study of spatial arrangements of atoms or groups of atoms in molecules. Thus, stereochemistry deals with how various atoms or groups of atoms in a molecule are arranged relative to one another in three-dimensional space.
A century has passed since van’t Hoff and Le Bel gave stereochemistry its surging start with their statement that molecules have three dimensional structures.
They independently proposed that the four sigma bonds formed by a carbon atom are directed towards the four corners of a regular tetrahedron with the carbon atom sitting at the centre of the tetrahedron.
Because of this three-dimensional arrangement, the given two compounds with the same constitution may differ if the arrangement of their atoms in space is different.
Stereoisomers are of two types:
i) Configurational isomers, and
ii) Conformational isomers
There are three different staggered conformations of n – butane, each of which lies at the bottom of an energy valley (i.e., at an energy minimum) separated from the others by energy hills. Different conformations corresponding to energy minima are called conformational isomers or conformers.
Since conformational isomers differ from each other only in the way their atoms are oriented in space, they too, are stereoisomers.
Interconversion of conformational isomers involves rotation about single bonds. In most cases, the rotational barrier is a very low one and interconversion is easy and fast.
The interconversion of conformational isomers does not require breaking and remaking of covalent bonds.
Configurational isomers or inversional isomers differ from one another in configuration about a stereogenic center.
These stereoisomers arise due to certain types of rigidity within the molecule.
These stereoisomers can be interconverted only by breaking and re-making of covalent bonds and not simply by rotation about sigma bonds.
There is a very high energy barrier: ~50 Kcal mol–1 or more for the interconversion of configurational stereoisomers, as it involves the breaking of a covalent bond.
Thus, unless one deliberately provides conditions to bring it about, interconversion of configurational stereoisomers is difficult and is negligibly slow.
| Conformational isomers | Configurational isomers |
| 1) Differ from one another in conformation. | 1) Differ from one another in configuration. |
| 2) Interconverted by rotations about single bonds. | 2) Interconverted by inversion (turning – inside – out) at a stereogenic centre. |
| 3) Do not possess any rigidity in the molecules. | 3) Possess certain types of rigidity in the molecules |
Configurational stereoisomers (or just called stereoisomers) can be subdivided into two general categories:
i) Enantiomers and ii) Diastereoisomers or diastereomers
Enantiomers are those stereoisomers whose molecules are nonsuperposable mirror images of each other. Optical isomers are typical examples of enantiomers.
Diastereomers are those stereoisomers whose molecules are not mirror images of each other. Geometrical isomers cis-but-2-ene and trans-but-2-ene are typical examples of diastereomers.
Two objects are superposable if, when one object is placed on top of the other, all parts of each coincide. To be superposable is different than to be superposable. Any two objects can be superimposed simply by putting one object one top of the other, whether or not all parts coincide. The condition of superposability must be met for two things to be identical.
| Enantiomers | Diastereomers |
| 1) They are nonsuperposable mirror images. | 1) They are not mirror images. |
| 2) They differ only in their ability to rotate plane polarized light in an equal and opposite direction. | 2) They may or may not be able to rotate plane polarized light or not. |
Tetrahedral nature of carbon atom
The experimental evidence of electron diffraction, X-ray diffraction, and spectroscopy shows that when carbon is bonded to four other atoms its bonds are directed towards the corners of a tetrahedron:
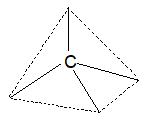
The tetrahedral nature of the carbon atom was proposed by Joseph Achille Le Bel and Jacobus Henricus van’t Hoff as early as 1874 (years before the direct determination of molecular structure was possible). Their proposal was based upon the concept and evidence of isomer number.
Isomer number is the number of isomeric compounds that are possible on the basis of given arrangement of atoms.
Any compound, simple or complex, that contains carbon atom bonded to four other atoms can be considered to be a derivative of methane, the simplest possible stable hydrocarbon.
Whatever we learn about the shape of the methane molecule can be applied to the shapes of vastly more complicated molecules.
Fact 1: For any atom or a group of atoms (unless the group is so complicated that in itself it brings about isomerism) X, only one compound with the general formula CH3X has ever been found. Thus, fluorination of methane yields only one compound of formula CH3F, chlorination yields only one compound of formula CH3Cl. Similarly, only one CH3Br is known, and only one CH3I. Also, there is only one CH3OH, only one CH3COOH and only one CH3SO3H.
What does this suggest about the arrangement of atoms in methane?
It suggests that every hydrogen atom in methane is identical (equivalent) to rest of the hydrogen atoms (i.e., to every other hydrogen atom). Thus, substitution of any one of them gives rise to the same product.
If the hydrogen atoms of methane were not identical, then substitution of different hydrogen atoms would yield different compounds. This way isomeric substitution products would be obtained.
In what ways can the atoms of methane be arranged in space so that the four hydrogen atoms are identical. There are three possible arrangements:
i) Planar arrangement (I) in which carbon is at the centre of a square (or rectangle) and a hydrogen atom is at each corner.
ii) Pyramidal arrangement (II) in which carbon is at the apex of a pyramid and a hydrogen atom is at each corner of a square base.
iii) Tetrahedral arrangement (III) in which carbon is at the centre of a tetrahedron and a hydrogen atom is at each corner.
How do we know that each of these arrangements could give rise to only one substance of formula CH3YH?
To see whether each of these arrangements could give rise to just one substance of formula CH3YX, we make two identical models of each of these arrangements. In one model we substitute any of the four H’s with a different atom X, represented by a differently colored ball.
In the other model we similarly substitute one of the four H’s (this time a different one, if it was the upper left – hand H in one of the models of arrangement I, then this time it could be the lower left – hand H).
Now we see whether or not the two resulting models are superposable. In other words, we see whether or not we can make the two models coincide in all their parts by any manipulations except bending or breaking the bonds.
If the two models are superposable, they correspond to two molecules of the same compound. If the two models are not super imposable, they correspond to molecules of two different compounds, which are basically isomers as they have the same molecular formula.
Whichever hydrogen we substitute in any of the three arrangements (I or II or III), we get the same compound. From any arrangement other than these three, we get more than one compound on monosubstitution.
If methane were a pyramid with a rectangular base, two stereoisomers of formula CH3X would be possible. These are nonsuperposable mirror images i.e., they are enantiomers.
Thus, as far as compounds of formula CH3X are investigated, the evidence of isomer number limits the arrangement of atoms in methane to one of these three possibilities.
Fact 2 Only one compound with the general formula CH2X2 or CH2XY has ever been found . For instance, dihalogenation of methane with the same or different halogens yields only one compound of formula CH2Br2, only one compound of formula CH2Cl2 and only one compound of formula CH2ClBr.
Of the three possible arrangements of methane, only the tetrahedral one survives with this evidence, i.e., only one compound of formula CH2XY is possible if methane is tetrahedral.
If methane were rectangular, three stereoisomers of formula CH2XY would be possible
If methane were square, two stereoisomers of formula CH2XY would be possible.
If methane were a pyramid with a square base, three stereoisomers of formula CH2XY would be possible. Two of these are nonsuperposable mirror images.
Thus, only the tetrahedral arrangement for methane agrees with the evidence of isomer number.
One may say that this is negative evidence by arguing that isomers exist even for tetrahedral arrangement but they have never been isolated or detected simply because the experimental techniques are not good enough. But any compound that contains carbon bonded to four other atoms can be regarded as a derivative of methane. The number of isomers obtained, in the preparation of hundreds of thousands of compounds of this type, has always been consistent with the concept of the tetrahedral carbon atom.
There is additional (positive) evidence for the tetrahedral carbon atom: compounds of formula CQRST exhibit enantiomerism”. It was the existence of enantiomers that convinced van’t Hoff and Le Bel that the carbon atom is tetrahedral.
In order to understand the behavior of enantiomers, we need to learn about the property called optical activity. We also need to understand the nature of plane–polarized light and how an instrument called a polarimeter operates.
Plane – polarized light and optical activity:
Light has dual character – particle character and wave character.
Light possesses certain properties that are best understood it we consider it to be an electromagnetic wave.
Thus, a beam of light consists of two mutually perpendicular oscillating fields: an oscillating electric field and an oscillating magnetic field. Both the fields are perpendicular to the direction of propagation.
Light is an electromagnetic wave in which vibrations (of mutually perpendicular fields) occur at right angles to the direction in which the light travels.
There are an infinite number of planes passing through the line of propagation. If we view a beam of ordinary light from one end, and if we actually see the planes in which the electrical oscillations are occurring, we find that oscillations of the electric field are occurring in all possible planes perpendicular to the direction of propagation. The same is true of the magnetic field.
Ordinary light vibrates in all of the infinite number of planes passing through the line of propagation.
When ordinary light passes through a polarizer, the polarizer interacts with the oscillating electric field in such a way that the electric field of the light that emerges out from the polarizer is oscillating only in one plane. (The same is true of the magnetic field). Such light is called plane – polarized light.
In plane – polarized light is light whose osciallations (of electric field and magnetic field) take place in only one of the possible planes.
Polarizer is a lens made of the material known as Polaroid.
Ordinary light is turned into plane – polarized light, more traditionally, by passing it through suitably cut pieces of calcite (a particular crystalline form of CaCO3) so arranged as to constitute what is called a Nicol prism.
Some crystals and some other compounds in the solid, liquid or gaseous state rotate plane– polarized light in a clockwise or anticlockwise manner, i.e., the light emerges from such materials vibrating in a different plane. These are referred to as optically active substances.
An optically active substance is one that rotates the plane of polarized light.
When polarized light vibrating in a certain plane, is passed through an optically active substance, it emerges vibrating in a different plane.
Crystalline inorganic compounds such as quartz and sodium chlorate deviate the plane of polarization only in the crystalline form.
Organic compounds such as oil of turpentine or cane-sugar or camphor are optically active in the solid, liquid (whether molten or in solution), and gaseous state.
The polarimeter
The device that is used for detecting the rotation of the plane of polarized light by the optically active compound is called the polarimeter. The angle of rotation by which the plane – polarized light is rotated can also be measured by polarimeter.
The principal working parts of a polarimeter are:
1) an ordinary light source (usually a sodium lamp, emitting the sodium D line 589.3 nm),
2) a polarizer,
3) a tube to hold the substance (in the light beam) that is being examined for optical activity,
4) an analyzer, and
5) a scale for measuring the number of degrees that the plane of polarized light has been rotated.
These are arranged so that the light passes through the polarizer, then the tube, then the analyzer, and finally reaches the eye of the observer.
The analyzer of a polarimeter is nothing more than another polarizer.
When the tube of the polarimeter is empty or when an optically inactive substance is placed into the tube, the observer will detect the maximum amount of light passing through, when the polarizer and analyzer are so arranged that they pass light vibrating in the same plane.
This is possible if the axes of the plane polarized light and the analyzer are exactly parallel i.e., when the instrument reads 00. If we rotate the analyzer, we notice that the light dims and reaches a minimum when the analyzer is at right angles to its previous position.
Two pieces of Polaroid or two Nicol prisms (polarizer and analyzer) will transmit plane polarized light only when suitably aligned.
The amount of light transmitted decreases to zero as one prism is rotated through 900 and then increases to the original value during rotation through another 900.
If on the other hand the polarimeter tube contains an optically active substance (for example, a solution of one enantiomer) the plane of polarization of the light gets rotated as it passes through the tube.
In order to detect the maximum brightness of the polarized light, the observer needs to rotate the axis of the analyzer in either a clockwise or counterclockwise direction. If the rotation of the plane of polarization and hence rotation of the analyzer is to the right (i.e., in a clockwise direction), the rotation, (measured in degrees), is said to be positive (+).
The optically active substance that rotates plane polarized light in the clockwise direction is said to be dextrorotatory (Latin: dexter, right) or d– form. It is indicated by placing a positive (+) sign before the degrees of rotation. If the rotation is to the left (i.e., counterclockwise), the rotation is said to be negative (-).
The optically active substance that rotates plane polarized light in a counterclockwise direction is said to be levorotatory (Latin: laevus, left) or the l– form and a negative (-) sign is placed before the degrees of rotation.
Nowadays, dextro and levo rotations are represented by algebraic signs of (+) for dextro and (-) for levo, instead of d and l.
Thus, using polarimeter, one can determine not only that the substance has rotated the plane and in which direction, but also by how much.
With modern photoelectric polarimeters the angles can be measured with a precision of one ten thousandth of a degree.
The amount of rotation is simply the number of degrees that one must rotate the analyzer to restore the position of maximum (or minimum) passage of plane – polarized light. The symbols (+ ) and (-) are used to indicate rotations to the right and to the left, respectively.
In practice, it is easier to detect a minimum than a maximum; the principle remains the same. The lactic acid that is extracted form muscle tissue (meat extract) rotates polarized light to the right, and hence is known as dextrorotatory lactic acid, or (+)-lactic acid. This acid is also know as sarcolactic acid (Greek: sarkos, flesh)
The lactic acid obtained by the fermentation of lactose (the suger in milk) by Bacillus acidi laevolactiti rotates light to the left and is known as levorotatory lactic acid, or (-)-lactic acid.
Specific rotation
Rotation of the plane of polarized light is caused by individual molecules of the optically active compound. Thus, the number of degrees (i.e. the amount of rotation) by which the plane of polarization is rotated depends upon how many molecules the light encounters in passing through the tube. This definitely depends on
i) the length of the polarimeter tube, and
ii) the concentration of the solution of optically active compound.
The polarized light will encounter thrice as many molecules in a tube 30cm long as in a tube 10cm long, and the rotation will be thrice as large.
If the optically active compound is in solution, the number of molecules encountered by the light will depend upon the concentration. For a given tube length, light will encounter thrice as many molecules in a solution of 3g per 100mL of solvent as in a solution containing 1g per 100mL of solvent, and the rotation will be thrice as large.
The degree of rotation depends not only on the material being investigated, the length of the polarimeter tube, the concentration of the solution but also on the temperature, the solvent, and on the wavelength of the light employed. When allowances are made for the length of tube and the concentration, it is observed that the amount of rotation as well as its direction becomes a characteristic of each individual optically active compound.
In order to compare measured rotations on a standard basis, chemists calculate a quantity called the specific rotation, [].
Specific rotation, [], is the number of degrees of rotation observed if one decimeter (or 10 centimeters) long tube is used, and the compound being examined is present to the extent of oneg/mL.
This is usually calculated from experimental observations made with tubes of other lengths and solutions of different concentrations by means of the following equation:
where [] = specific rotation in degrees
= experimentally observed angle of rotation i.e., the observed optical rotation in degrees
c = concentration of the solution in grams per milliliter of solution or density in g/mL for neat (pure) liquids
= length of the polarimeter tube in decimeters (1 dm = 10 cm)
Since the specific rotation depends on the temperature and the wavelength of light (thus monochromatic light is used, generally the sodium D line) that is employed, specific rotations are reported so as to incorporate these quantities as well.
Thus, while reporting [a], the wavelength of light used is given as a subscript and the temperature (in degree Celsius) as a superscript, i.e., a specific rotation might be given as follows:
This implies that the D line of a sodium lamp ( = 589.6nm) was used for the light, that a temperature of 250C was maintained, and that a sample containing 1.00 g mL–1 of the optically active substance, placed in a 1 dm tube, produced a rotation of 3.120 in a counterclockwise direction.
It is also customary to designate the solvent and concentration. Thus, (c.0.50 ethanol) means that when was measured the sample concentration was 0.50 g/mL in ethanol.
The specific rotation is as much a property of a compound as its melting point, boiling point, density or refractive index.
Optical activity (or rotatory power) may be measured at different wavelengths. A graph showing the variation of a as a function of the wavelength , is called an optical rotatory dispersion curve.
The sign and/or value of the specific rotation of a molecule can’t be deduced from its structure.
Discovery of enantiomerism
The discovery of the polarization of light by Malus in 1808 was followed by the discovery of optical activity in 1813 by the physicist J.B. Biot. The crystallographer Haüy had shown that quartz crystals were of two kinds, which differed in their effect on polarized light.
One type of crystal produced a clockwise, deviation and the other type of crystal an anticlockwise deviation. Up to 1848, no organic compound was known to exist in two forms corresponding to the two types of quartz.
In 1848, the young chemist Louis Pasteur made an important and exciting discovery. To gain some experience in crystallography, he was repeating another chemist’s earlier work on salts of tartaric acid when he saw something that no one had noticed before: optically inactive sodium ammonium tartrate existed as a mixture of two different kinds of crystals, which were mirror images of each other.
Using a hand lens and a pair of tweezers, he carefully and laboriously separated the mixture into two tiny piles – one of right handed crystals and the other of left handed crystals – much as one might separate right-handed and left-handed gloves lying jumbled together on a shop counter. Each set of crystals was dissolved in water to form aqueous solutions of equal concentration. Although the original mixture was optically inactive, the aqueous solutions of both types of the crystals showed optical activity.
Furthermore, the specific rotations of the two solutions of equal concentration were exactly equal but of opposite sign, i.e., one solution rotated plane–polarized light to the right and the other solution an equal number of degrees to the left. In all other properties the two substances were identical.
Rotation was no longer observed when the two types of crystals were mixed in equal amounts. Since the difference in optical rotation was observed in solution, Pasteur concluded that it was characteristic, of the molecules, but not of the crystals.
Pasteur proposed that, like the two sets of crystals themselves, the molecules making up the crystals were mirror images of each other. This was the first ever proposal of the existence of a pair of isomers whose structures differ only in being mirror images of each other, and whose properties differ only in the direction of rotation of plane polarized light.
Pasteur believed that this difference in optical activity was associated with the three dimensional arrangement of atoms in the two types of crystals.
Based on many observations that led van’t Hoff and Le Bel concluded that spatial orientation of groups around carbon atoms is tetrahedral when a carbon atom is bonded to four other groups. They pointed out that a tetrahedral carbon atom could account for the following facts:
1) absence of isomers of general formula CH3X
2) absence of isomers of general formula CH2X2 or CH2XY
3) existence of mirror–image isomers (enantiomers) of general formula CHXYZ like Pasteur’s tartaric acids
Tetrahedral carbon and Enantiomerism
To convince that mirror–image isomers do exist, we can start with the actual, tetrahedral arrangement for methane. We make a model of a compound CHXYZ, using a ball of a different color for each different atom or group represented as H, X, Y, and Z.
Imagine that we are holding this model before a mirror. We construct a second model of its mirror image. Using wedge formulae, we can represent the two models as :
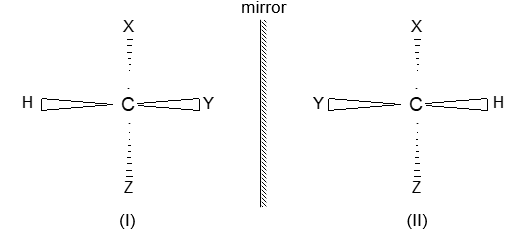
A solid wedge represents a bond coming out of the plane of the paper and towards the viewer. A broken wedge represents a bond behind the plane of the paper and going away from the viewer. An ordinary line would represent a bond lying in the plane of the paper.
We may twist and turn the two models as much as we please. We notice that, as long as no bonds are broken, although two atoms (or groups) of each may coincide, the other two do not.
We can do the same thing with the wedge formula, in our mind’s eye.
We therefore conclude that the two models are not superposable on each other, and therefore they represent different but isomeric molecules of formula CHXYZ.
Because models represented as I and II are nonsuperposable mirror images of each other, the molecules that they represent are enantiomers.
This exercise clearly indicates that mirror–image isomers do exist. Thousands of examples besides the tartaric acids are known. Thus, there are two enatiomeric:
i) Butan-2-ols, CH3CH(OH)CH2CH
ii) Lactic acids, CH3CH(OH)CO2
iii) Chlorobromomethanesulfonic acids, CHClBrSO3
iv)2–Methylbutan-1-ols,
Since the models we made for CHXYZ can stand for any of these, the 3–dimensional structures of each pair are nonsuperposable and therefore represent enantiomers.
At this point, we only need to tell when atoms or groups are the same as or different from each other, and whether or not a model can be superposed on its mirror image.
Even two isotopes of the same element, like ordinary hydrogen, H (protium) and heavy hydrogen, D (deuterium), are different enough to permit detectable enantiomerism. Thus, a – deuterioethylbenzene [C6H5CH(D)CH3] exists as enantiomers.
All the molecules have a mirror image. However, most molecules are superposable on their mirror images (e.g. bromochloromethane, CH2ClBr) and do not show this mirror–image isomerism.
Mirror-image isomers are called enantiomers. They belong to the general class called stereoisomers because they differ from one another only in the way the atoms are oriented in space.
Stereiosomers that are not mirror images of each other are called diastereomers.
Any two stereoisomers are classified either as enantiomers or as diasteromers, depending upon whether or not they are mirror images of each other.
Optical activity and enantiomerism
One can easily see that the non-superposability of mirror images that brings about the existence of enantiomers also gives them their optical activity. Thus, enantiomers are often referred to as optical isomers.
Optically active compounds do not belong to a particular chemical family, since such compounds are found in all families.
When a beam of plane polarized light passes through a sample of a single pure compound, its plane is rotated by a tiny amount due to interaction with the charged particles of the individual molecule, the beam passes through in nearly every instance.
The direction and magnitude of rotation varies with the orientation of the particular molecule in the beam. For most compounds, for every molecule that the light encounters, there is another (identical) molecule oriented as the mirror image of the first, which exactly cancels its effect.
This is because of the random distribution of the large number of molecules that make up even the smallest sample of a single pure compound.
The net result is optical inactivity, i.e., no rotation. Thus, optical inactivity is not a property of individual molecules, but rather of the random distribution of molecules (in the bulk) that serve as mirror images of each other.
Both the molecule and its mirror image (another identical molecule) co-exist in the same sample of pure optically inactive compound. In other words, optical inactivity requires that one molecule of a compound acts as the mirror image of another.
However, in the case of an optically active compound of general formula CHXYZ, we have a molecule, whose mirror image is not just another identical molecule, but rather a molecule of a different isomeric compound.
In a pure sample of one of the enantiomers, no molecule can play the role of the mirror image of another molecule. Thus, there is not 100% canceling out of the rotations. Consequently, the net result is optical activity.
The non-superposability of mirror images that gives rise to enantiomerism is also the necessary and sufficient condition of optical activity.
Chirality and prediction of enantiomerism
A molecule that is nonsuperposable on its mirror image is defined as a chiral molecule. Enantiomers occur only with compounds whose molecules are chiral. Thus, chirality is the necessary and sufficient condition for the existence of enantiomers.
A compound whose molecules are chiral can exist as enantiomers.
An achiral molecule has a superposable mirror image.
A compound whose molecules are achiral (without chirality) can’t exist as enantiomers.
When we say that a molecule and its mirror image are superposable, we mean that if (in our mind’s eye) we bring the mirror image from behind the mirror where it is created and superpose on the molecule then it coincides in all its parts with the molecule.
To decide whether or not a molecule is chiral, we need to make a model of it and a model of its mirror image. Finally, see if we can superpose them.
This is the safest way as it always gives the right answer provided it is properly handled.
You should always use this method until you become quite familiar with the things involved.
In spite of this, we should use this technique whenever we come across a new compound.
After we become familiar with the models, we should draw wedge formulae to represent them, and mentally try to superpose these.
We find some of the wedge formulae like those of chlorobromomethanesulfonic acid are not superposable:
Therefore, these molecules are chiral and the compound chlorobromomethanesulfonic acid exists as enantiomers.
Others are superposable, like those of isopropyl alcohol:
Thus, these molecules are achiral and the compound isopropyl alcohol can’t exist as enantiomers.
A chiral molecule and its mirror image are called a pair of enantiomers. The relationship between them is defined as enantiomeric.
The same is true of your feet and also of your gloves and shoes. A right-hand glove fits your right hand but not your left and we learn early in life that it is desirable to have our shoes correctly placed on our feet.
This illustrates an important principle that one chiral object (the hand or the foot) can distinguish another chiral object (the glove or the shoe) with which it is designed to interact. This is equally true at the molecular level for a drug or an enzyme.
The symmetry and asymmetry are also observed in many day-to-day objects: a sphere, a cube, a cone, a tetrahedron, a fork, a spoon are all identical to their mirror images, and can thus be superposed (point for point) on their mirror images. Such objects whose projections are superposable on their mirror images are called symmetrical objects.
Many familiar objects such as a tree, a glove, shoes, right and left hands are non-superposable on their mirror images. The word chiral (Greek cheir, hand; pronounced kiral) implies the property of “handedness,” i.e., the object and mirror–image relationship of a left and right hand.
This is an important concept which must be clearly grasped.
Your two hands are similar but not identical. Your left hand is (more or less) the mirror image of your right hand and vice versa but the one cannot be superposed on the other. The general property of handedness is called chirality.
Objects that are non-superposable on their mirror images are called chiral, while the objects that are superposable on their mirror images are called achiral (meaning not chiral). For example, shoes are chiral, whereas most socks are achiral.
Many familiar objects are chiral, while other objects can be shown to be chiral only by applying the universal test for chirality – the non–superposability of the object and its mirror image.
Illustration 47: Classify each of the following objects as to whether it is chiral or achiral.
a) A screwdriver b) An ear
c) A nail d) A baseball bat
e) A tennis shoe f) A car
g) A hammer h) A golf club
i) A wood screw j) A cup
k) An empty spool l) A filled spool of thread
Solution:
a) b) Chiral
c) Achiral d)
e) Chiral f)
g) Achiral h)
i) j) Achiral
k) Achiral l) Chiral
Notice that a spool of thread has the thread wound on it in either clockwise or counterclockwise fashion.
In geometry, an object that is not superposable on its mirror image is called dissymmetric object where ‘dis’ signifies an opposite quantity. In stereochemistry the word used for dissymmetric is chiral. It is non-superposability on mirror image that is necessary and sufficient condition for enantiomerism. It is also a necessary but not sufficient condition, for optical activity.
The chiral center
How do you know when to expect the possibility of enantiomers?
So far, all the chiral molecules we have mentioned about have one thing in common. They are all of the type CHXYZ, that is, each molecule carries a carbon (C*) that holds four different atoms or groups of atoms.
In butan-2-ol this carbon atom is C2.
The four different atoms or groups that are attached to C2 are a methyl group, a hydrogen atom, an ethyl group and a hydroxy group.
The other examples are :
One way (but not the only way) is to recognize that a pair of enantiomers is always possible for molecules that contain just one tetrahedral atom (usually a C atom) with four different groups attached to it. An atom bonded tetrahedrally to four different atoms or groups of atoms (ligands) is a chiral center.
A chiral center is usually a C atom, but may be N, S, P, Si, etc.
Chiral centers are often designated with an asterisk ( *).
Sometimes a carbon atom to which four different groups are attached is called a chiral carbon, when it is necessary to distinguish it from chiral nitrogen, chiral phosphorus.
Chiral carbon is also called asymmetric carbon.
The following are examples of Si, N and P serving as chiral centres similar to C:
An important property of enantiomers such as these is that interchanging any two groups at the tetrahedral atom that bears four different groups converts one enantiomer into the other.
In the following figure
it is easy to see that interchanging the hydroxy group and the hydrogen atom converts one enantiomer into the other. Now convince yourself (may be with models) that interchanging any other two groups has the same result.
Interchanging any two groups of a model or three – dimensional formula is a useful test for determining whether structures of two chiral molecules are the same or different.
If two ligands (atoms or groups) attached to an atom are switched resulting in a new stereoisomer, the atom is called a stereocentre or stereogenic atom. If the new stereoisomer is an enantiomer, the stereocenter is a chiral centre.
Not all stereocenters are chiral centers but all chiral centers are stereocenters.
Let’s consider the compound butan-2-ol. Because interchanging two groups at C2 converts one stereoisomer into another, C2 is an example of a stereogenic carbon.
A stereogenic carbon is defined as a carbon atom bearing groups of such nature that an interchange of any two groups will produce a stereoisomer.
Carbon-2 of butan-2-ol is an example of a tetrahedral stereogenic carbon.
Not all stereogenic carbons are tetrahedral
The carbon atoms of cis– and trans–1, 2–dichloroethene

are examples of trigonal planar stereogenic carbons because an interchange of groups at either carbon atom produces a stereoisomer (a diastereomer).
In general, any location where an interchange of groups leads to a stereoisomer is called a stereogenic centre or stereocenter.
The of a carbocation can’t be a chiral center because C+ uses sp2 HO’s and has a flat geometry (Thus, it has a plane of symmetry).
A carbon radical can’t be a chiral center because radicals are also sp2 hybridized and have a plane of symmetry.
The following kinds of sp2 hybridized C’s cannot be chiral centers: C = C in alkenes, C = O in aldehydes, ketones, acids and acid derivatives, C = N in imines and oximes.
You must take care to notice that when you interchange groups like this you do something to a molecular model or you do something on paper.
An interchange of groups in a real molecule (if it can de done) requires breaking of covalent bonds, and this definitely requires a large input of energy. This implies that enantiomers such as the butan-2-ol enatiomers do not interconvert spontaneously.
At one time, tetrahedral atoms with four different groups were called chiral atoms or asymmetric atoms.
Chirality is a geometric property that pervades and affects all parts of a chiral molecule. All of the atoms of butan-2-ol are in a chiral environment and therefore all are said to be chirotopic.
When we consider an atom such as C–2 of butan-2-ol, we are considering it as a stereogenic carbon and not as a chiral atom.
Thus, the most common indicator of chirality is the presence of a tetrahedral carbon bonded to four different ligands.
Enantiomeric compounds necessarily result whenever a molecule contains a single tetrahedral stereogenic carbon.
Note that enantiomers are also possible for molecules that contain more than one tetrahedral atom with four different groups attached to it, but some of these molecules do not exist as enantiomers.
Common examples of such chiral molecules are
i) Glyceraldehyde, OHC – *CHOH – CH2OH, 2, 3 – dihydroxypropanal
ii) Lactic acid, CH3 – *CHOH – CO2H, 2- hydroxypropanoic acid
iii) Bromochloroiodomethane, BrCl*CHI
Illustration 48: Write the structural formulae for the simplest chiral (a) alkane (b) alkene, (c) alkyne (d) alcohol (e) aldehyde, (f) ketone, (g) Carboxylic acid and (h) amine.
Solution : Just create one tetrahedral stereogenic carbon for every chemical family.
a)
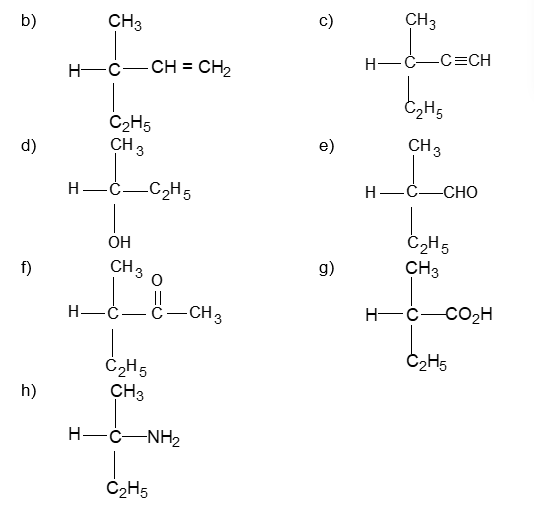
If all of the tetrahedral atoms in a molecule have two or more groups attached that are the same, the molecule does not have a stereogenic carbon. Such a molecule is superposable on its mirror image and is achiral.
Propan-2-ol is a typical example of this type of molecule:
Carbon atoms 1 and 3 bear three identical hydrogen atoms and the central atom bears two identical methyl groups. Experimentally only one form of propan-2-ol has ever been found. Many (but not all) molecules that contain a chiral center are chiral. Many (but not all) chiral molecules contain a chiral center.
There are molecules that contain chiral centers and yet are achiral. Such achiral molecules always contain more than one chiral center.
If there is only one chiral center in a molecule, it is certain that the molecule is chiral. There are chiral molecules that contain no chiral centres.
The presence or absence of a chiral center is thus no critersion of chirality.
Most of the chiral molecules that we shall discuss do contain chiral centers. Thus, it will be useful for us to look for such centers. If we find a chiral center, then we should consider the possibility that the molecule is chiral, and hence can exist in enantiomeric forms.
The kind of molecules that may be achiral, in spite of the presence of chiral centers, contain more than one chiral center.
Fisher Projection Formulae
In writing structures for chiral molecules so far, you have used only three – dimensional formulae. The reason: three – dimensional formulae are unambiguous and can be manipulated on paper in any way that you wish, as long as you do not break the bonds. Moreover, their use teaches us to see molecules (in our mind’s eye) in three dimensions.
After we become familiar with the use of models and of wedge formulae, we can make use of even simpler representations of molecules containing chiral centres, which can be drawn much faster. Chemists sometimes represent structures for chiral molecules with two–dimensional formulae called Fischer projection formulae.
Thus, the Fischer projection formula is a convenient way of depicting three–dimensional structures in two–dimensions.
It is particularly useful for simpler representation of the stereochemistry of compounds that contain one or more chiral centres.
In this formula, the molecule is simply drawn as a cross with the chiral carbon at the intersection of the horizontal and vertical lines. The chiral carbon (usually one that is a stereogenic center) is not explicitly shown by atomic symbol in the Fischer projection. The four atoms (or groups) that are attached to the chiral carbon are placed on the four ends of the cross.
The use of Fischer projection formulae requires a rigid adherence to certain conventions. Used carelessly, these projection formulae can easily lead to incorrect conclusions.
Chemists have agreed that such a diagram stands for a particular description : the horizontal lines represent the bonds that project out of the plane of the paper and coming toward the viewer, whereas the vertical lines represent the bonds that project behind the plane of the paper (or that lie in it) and going away from the viewer.
A Fischer projection formula for bromochlorofluoromethane that contains one chiral carbon is shown as:
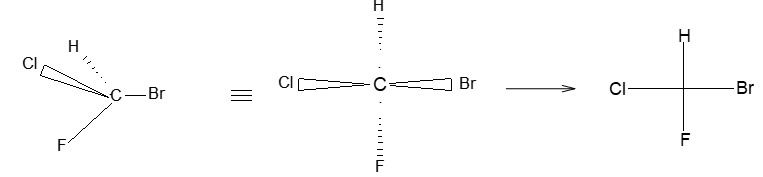
Similarly
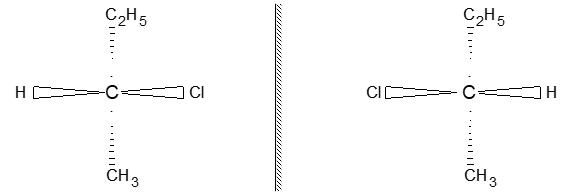
can be represented by
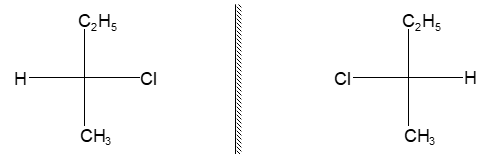
In testing the superposability of two of these flat, two dimensional representations of three – dimensional objects, we must follow a certain procedure and obey certain rules.
In other words, if Fisher projections are to be used certain rules must be obeyed and certain conventions clearly understood, otherwise the structure will be misinterpreted.
i) Use Fisher projections only for molecules that contain at least one chiral center.
ii) The structure of the molecule is written in a vertical rather than a horizontal form. For this purpose, the carbon atom bearing the lowest number (in standard nomenclature terms) is written upper most. For example, in glyceraldehyde (2,3–dihydroxypropanal), the aldehyde group -CHO is placed at the top of the Fischer projection because this is C–1 according to nomenclature rules.
iii) In a Fischer projection the chiral atom under consideration lies in the plane of the paper.
iv) Although all bonds are represented by plain lines it is understood that atoms (or groups) vertically linked to the chiral atom project below the paper and that atoms (or groups) horizontally linked to the chiral atom project above the paper. This must be clearly understood when visualizing Fischer projections.
v) To test the superposability of two structures of a given compound, you draw Fischer projection of one of them and then draw the other as its mirror image.
Drawing these formulae at random can lead to some interesting but quite wrong conclusions about isomer number.
vi) In using Fischer projections to test the superposability for two structures, we are permitted (in our mind’s eye) to slide these formulae or rotate them (in the plane of the paper) end for end i.e., by 1800 but by no other angle.
vii) We must always keep them in the plane of the paper but we must not remove them from the plane of the paper, i.e., we are not allowed to flip them over.
Used with caution, this method of representation is convenient. It is not fool proof, thus, in doubtful cases models or wedge formulae should be used. It is safest to cheek our conclusion by drawing cross formulae or, better, wedge formulae or, best of all, by making models.
The two – dimensional formulae called Fischer projection formulae are especially useful for compounds with several stereogenic carbons because they have space and are easy to write. They are widely used to depict acyclic forms of simple carbohydrates.
By not writing the carbon at the intersections in a Fischer projection, we know that we can interpret the formula as indicating the three – dimensional aspects of the molecule. If the carbons were shown, the formula would not be a Fischer projection and we could not ascertain the stereochemistry of the molecule.
Properties of enantiomers and the biological importance of chirality
The configurational stereoisomers that are related to each other as nonsuperposable mirror images are called enantiomers.
Compounds whose molecules contain just one chiral centre always exist in two enantiomeric forms. Thus two different lactic acids are enantiomers (Greek: enantio, opposite).
Enantiomers have identical physical properties except their different influence on plane – polarized light which they rotate in opposite directions but to an equal extent.
Thus, enantiomers such as two 2–methylbutan-1-ols have identical melting points, boiling points, densities, refractive indices, solubilities, infrared spectra, and any other physical constant one might measure, except for the direction of rotation of the plane of polarized light. One rotates plane polarized light to the right, the other to the left. Only the direction of rotation is different, the amount of rotation is the same, the specific rotation of one being + 5.900, the other – 5.900.
This fact is not surprising, since the interactions of both kinds of molecules with their fellows should be the same.
It is reasonable that these molecules, being so similar, can rotate light by the same amount. The molecules are mirror images and so are their properties: the mirror image of a clockwise rotation is a counterclockwise rotation and of exactly the same magnitude.
The two enantiomers also have identical chemical properties except in the presence of chiral reagents (i.e., in reactions with other optically active compounds which may be simple chemicals or complex substances like enzymes).
For examples, the two different lactic acids are acids of exactly the same strength. Both ionize to exactly the same degree when dissolved in water at the same concentration and temperature.
The two different 2-methylbutan-1-ols form the same products (alkenes on treatment with hot sulphuric acids, alkyl bromides on treatment with HBr, esters on treatment with acetic acid) at exactly the same rate.
The atoms undergoing attack in each case are influenced in their reactivity by exactly the same combination of substituents. The reagent approaching either kind of molecule encounters the same environment except that one environment is the mirror image of the other.
There is only one way in which enantiomers may differ in their reactions with ordinary optically inactive reagents: sometimes they give products (at exactly the same rate) that are not identical but enantiomeric.
On the other hand, when the reagent is optically active, the influences exerted, on the reagent, in the attack on the two enantiomers are not identical.
The reaction rates will be different. In some cases, the rates are so different that reaction with one isomer does not take place at all.
In biological systems, such stereochemical specificity is the rule rather than the exception. This is because of the fact that the enzymes, and most of the compounds they work on, are optically active.
The origin of biological properties relating to chirality is often linked to the specificity of our hands for their respective gloves. The binding specificity for a chiral molecule (like a hand) at a chiral receptor site (a glove) is only favorable in one way.
If either the molecule or the biological receptor site had the wrong handedness, the natural physiological response (e.g. neural impulse, reaction catalysis) would not occur. Chiral molecules can show their different handedness in many ways, including the way they affect human beings:
a) The sugar (+)-glucose plays a unique role in animal metabolism and is the basis of a multimillion – dollar fermentation industry; yet (–)-glucose is neither metabolized by animals nor fermented by yeasts.
b) When the mold Penicillium glaucum feeds on a mixture of enantiomeric tartaric acids, it consumes only the (+)-enantiomer and leaves (–)-tartaric acid
c) The hormonal activity of (–)-adrenaline is many times that of its enatiomer.
d) Only one stereoisomer of chloromycetin is an antibiotic.
e) (+)-Ephedrine not only has no activity as a drug, but actually interferes with the action of its enantiomer.
f) Among amino acids, only one asparagine, and one leucine are sweet, and only one glutamic acid enhances the flavor of food.
g) They may also smell differently: One enantiomeric form of a compound called (+)-limonene smells of oranges and is primarily responsible for the odor of oranges. The other enantiomer, (-)-limonene smells of lemons and is primarily responsible for the odor of lemons.
h) One enantiomer of a compound called (-)-carvone isolated from spearmint oil gives oil of spearmint its characteristic odor and the other enantiomer, (+)-carvone, isolated from caraway seed oil, is the essence of the caraway.
Let’s consider a crude analogy, a right and left hand of equal strength (the enantiomers) hammering a nail (an optically inactive reagent) or alternatively inserting a right – handed screw (an optically active reagent).
Hammering requires exactly corresponding sets of muscles in the two hands, and can be done at identical rates. Inserting the screw uses different sets of muscles: the right thumb pushes, whereas the left thumb pulls.
Let’s consider reactivity (in the most precise way) by the transition state approach: First consider the reactions of two enantiomers with an optically inactive reagent. The reactants in both cases (one enantiomer plus the reagent and the other enantiomer plus the same reagent) are of exactly the same energy.
The two transition states for the reactions are nonsuperposable mirror images i.e. they are enantiomeric. Hence, they are also of exactly the same energy.
Consequently, the energy differences between reactants and transition states (the Eact values) are identical, and so are the rates of reaction.
Now consider the reactions of two enantiomers with an optically active reagent. Here also the reactants are of the same energy.
However, the two transition states are not mirror images of each other, they are diastereomeric.
Hence, they are of different energies. Consequetnly, the Eact values are different and so are the rates of reaction.
Enantiomers show different physical or chemical properties only in a chiral medium. Plane polarized light provides such a medium. Thus, in it enantiomers differ in direction of the rotation of the light, a physical property.
Enantiomers may also differ in solubility in an optically active solvent, or in adsorption on an optically active surface.
For enantiomers to react at different rats, the necessary chiral medium can be provided in a number of ways:
a) by an optically active reagent,
b) by a chiral solvent,
c) by the chiral surface of a catalyst,
d) by irradiation with circularly polarized light (for light – catalyzed reactions).
For simplicity, we often use the term “Optically active reagent” or “chiral reagent” in speaking of reaction under any of these chiral conditions.
On the other hand, we use the term “optically inactive reagent” or “achiral reagent” or even “ordinary conditions” in speaking of reaction in the absence of a chiral medium.
Enantiomers are distinguished by prefixing their name with the symbols (+)- or (-)-as appropriate. The alternative symbols d– and l– are now hardly ever used.
The racemic mixture
A sample that consists exclusively or predominantly of one enantiomer causes a net rotation of plane–polarized light.
The plane of polarization rotates slightly in clockwise direction when the light encounters a molecule of (+)- lactic acid. Each additional molecule of (+)- lactic acid that the beam encounters would cause further rotation in the same direction.
If, on the other hand, the sample contains molecules of (-)- lactic acid, each molecule of this enantiomer would cause the plane of polarization to rotate in the opposite direction.
If the (+)- and (-)- lactic acids were present in equal amounts in the sample, there would be no net rotation of the plane of polarized light. An equimolar mixture (i.e., a 1 : 1 mixture or a mixture of equal parts) of two enantiomers is called a racemic mixture (or racemic form or racemic modification or racemate).
A racemic mixture causes no net rotation of plane-polarized light. It is optically inactive, due to external compensation.
When two enantiomers are mixed together in equal proportions, the rotation caused by each molecule of one enantiomer is exactly canceled by an equal and opposite rotation caused by each of the other enantiomer, resulting in no net optical activity.
To specify the racemic nature of the given sample, the prefix (±) is used. Thus, a racemic mixture of two lactic acids is designated as
Let’s compare a racemic modification with an achiral compound (that is, a compound whose molecules are superposable on their mirror images):
Both are optically inactive for exactly the same reason. On account of the random distribution of the large number of molecules, for every molecule that the light encounters there is a second molecule, a mirror image of the first. It is aligned just right to cancel the effect of the first one. In a racemic modification this second molecule happens to be an isomer of the first whereas for an achiral compound it is not an isomer, but another, identical molecule.
For an optically active substance, uncontaminated by its enantiomer, such cancellation of rotation cannot occur since no other molecule can serve as the mirror image of another, no matter how random the distribution.
Let’s compare chemical and physical properties of an enantiomer and its racemic form:
The chemical properties of an enantiomer and its racemic from are the same towards achiral reagents, but chiral reagents react with them at different rates.
Enantiomers are optically active while the racemate is optically inactive.
Other physical properties, such as crystalline form, melting point, and solubility of an enantiomer and its racemate may differ. For example, lactic acid melts at 530 in either of its enantiomeric forms but at 170 in its racemic form.
The process of conversion of an enantiomer into a racemic mixture is known as racemisation.
Consequence of the identity of most physical properties of enantiomers has great practical significance.
The two enantiomers cannot be separated by ordinary methods:
a) not by fractional distillation, because their boiling points are identical.
b) not by fractional crystallization, because their solubilities in a given solvent (unless the solvent is optically active) are identical
c) not by chromatography, because they are held equally strongly on a given adsorbent (unless it is optically active).
The method of separation of a racemic modification into its enantiomeric constituents is called the resolution of a racemic modification.
Resolution is a special kind of job, and requires a special kind of approach.
A closer look at optical activity
Optical activity, like enantiomerism, results from (and only from) chirality, that is, the nonsuperposability of certain molecules on their mirror images. Thus, whenever we observe (molecular) optical activity, we know we are dealing with chiral molecules.
However, the reverse is not true. Whenever we deal with chiral molecules (i.e. with compounds that exist as enantiomers) we need not always observe optical activity. For example, a 50 : 50 mixture of two enantiomers is optically inactive.
This clearly indicates that we can observe optical activity provided the material we are dealing with contains an excess of one enantiomer (enough of an excess that the net optical rotation can be detected by the particular polarimeter at hand).
Furthermore, this excess of one of the enantiomers must persist long enough, so that optical activity can be measured.
If the enantiomers are rapidly interconvertible, then before one can measure the optical activity due to one enantiomer, it will be converted into an equilibrium mixtre.
Since enantiomers have exactly the same stability, the equilibrium mixture must be a 50:50 mixture and hence optically inactive.
Even if all these conditions are met, the magnitude and hence the detectability of the optical rotation depends on the structure of the particular molecule concerned.
In the following compound (A) the four alkyl groups attached to the chiral center differ only in chain length.
Calculations showed that this compound should have the tiny specific rotation of 0.000010 – far below the limits of the detection by any existing polarimeter. In 1965, enantiomerically pure samples of both enantiomers of (A) were prepared, and each was found to be optically inactive.
At the present level of study, the matter of speed of interconversion is not going to trouble. Nearly all the chiral molecules we come across during the discussion lie at either of two extremes:
a) Molecules which owe their chirality to chiral centers. Here interconversion of enantiomers (configurational enantiomers) is so slow (because of breaking of bonds) that one need not concern at all about interconversion.
b) Molecules whose enantiomeric forms (conformational enantiomers) are interconvertible simply by rotations about single bonds. Here interconversion is so fast that one need not concern at all about the existence of the enantiomers.
Tests for chirality: Elements of symmetry
The necessary and sufficient condition for chirality is not just the presence of asymmetric carbon atoms but asymmetry of the molecule as a whole.
The ultimate way to test for molecular chirality is to construct models of the molecule and its mirror image and then determine whether they are superposable.
If the two models are superposable, the molecule that they represent is achiral.
If the models are not superposable, then the molecules that they represent are chiral.
We can apply this test with actual models or we can apply it by drawing three dimensional structures and attempting to superpose them in our minds.
However, there are other aids that will assist we in recognizing chiral molecules: one of these has already been mentioned – it is the presence of a single tetrahedral stereogenic carbon.
The other aids are based on the absence (in the molecule) of certain symmetry elements. A molecule as a whole will be chiral if it does not possess any element of symmetry such as
i) a plane of symmetry,
ii) a centre of symmetry,
iii) an axis of symmetry, and
iv) an alternating axis of symmetry.
However, at our present level of study, only first two kinds of symmetry elements are relevant to the discussion. Thus, a molecule will not be chiral if it possesses a plane of symmetry or a centre of symmetry or even both.
A plane of symmetry (also called a sigma (s) plane or mirror plane) is defined as an imaginary plane that bisects a molecule in such a way that one-half of the molecule is the mirror image of the other half. The plane of symmetry may pass through atoms, between atoms, or both.
2-Chloropropane has a plane of symmetry and is thus achiral, whereas 2-Chlorobutane does not possess a plane of symmetry (and also a centre of symmetry) and is chiral.
All molecules with a plane of symmetry are achiral.
The center of symmetry is defined as that point (atom) in a given molecule from which if a straight line is drawn to any part of the molecule and extended to an equal distance by a straight line on the other side, an identical point (or atom) is encountered.
In other words, a line extended from any point (or atom) in the object (or molecule) through the center meets an identical point (or atom) in the object (or molecule) at an equal distance from the center.
The center (or point) of symmetry is invariably a point (atom) in the center of an object (or molecule). It is symbolized as Ci and is also called the centre of inversion.
All molecules with a centre of symmetry are achiral.
Enantiomeric excess (optical purity)
A sample of an optically active substance is said to be enantiomerically pure or to have an enantiomeric excess of 100% if it consists of a single enantiomer.
An enantiomerically pure sample of (+)-butan-2-ol shows a specific rotation of + 13.520,
i.e. ,.
On the other hand, a sample of (+)-butan-2-ol that contains less than an equimolar amount of (–)-butan-2-ol will show a specific rotation that is less than +13.520 but greater than 00. Such a sample is said to have an enantiomeric excess less than 100%.
Thus, enantiomeric excess is a defined as follows:
Enantiomeric excess =
The enantiomeric excess can also be calculated from optical rotations:
% Enantiomeric excess =
This calculation should be applied to a single enantiomer or to mixtures of enantiomers only. It should not be applied to mixtures in which some other compound is present.
Suppose that a mixture of the butan-2-ol enantiomers shows a specific solution of + 6.760. We then say that the enantiomeric excess of the (+)–buton-2-ol is
Enantiomeric excess =
The fact, that the enantiomeric excess of this mixture is 50%, means that 50% of the mixture consists of the (+)-enantiomer (the excess) and the other 50% consists of the racemic form.
Since the optical rotations cancel one another out for the 50% of the mixture (that is racemic), only the 50% of the mixture that consists of the (+)-enantiomer contributes to the observed specific rotation. The observed optical rotation is, therefore, 50% (or one half) of what it would have been if the mixture had only the (+)-enantiomer.
Let’s work out the actual stereoisomeric composition of the mixture:
Of the total mixture, 50% consists of the racemic form, which contains equal amounts of the two enantiomers. Therefore, half of this 50%, or 25% is the (+)-enantiomer and the rest half or 25% is the (–)-enantiomer.
The other 50% of the mixture (the excess) is the (+)-enantiomer. Thus, the mixture is 25% (–)-enantiomer and 75% (+)-enantiomer.
Illustration 49: If pure sample of (+) enantiomer shows a specific rotation of +120 a) what is the optical purity (OP) of a sample isolated from a reaction having a specific rotation of +6.00? b) Assume all measurements are taken in a 1.0 dm tube at the same concentrations and with the same wavelength, calculate the molar % composition.
Solution: Optical purity
= 50%
b) 50% optical purity means that the mixture has 50% (+) and 50% (±), which is equivalent to, 75% (+) and 25% (–).
Illustration 50: The specific rotation of a pure enantiomer is + 120. What is the % composition of a mixture of the two enantiomers whose observed specific rotation is – 9.00.
Solution: Optical purity =
= 75%
Of the total mixture, 75% consists of (–)-enantiomer and 25% consists of the racemic form. Thus, total % of (–)-enantiomer is = 87.5%. The remaining 12.5% is (+)-enantiomer.
Assigning of configuration
The spatial arrangement of atoms that characterizes a particular (configurational) stereoisomer is called its configuration.
There are two stereoisomeric sec-butyl chlorides having nonsuperposable mirror image relationship. They have the configurations I and II.
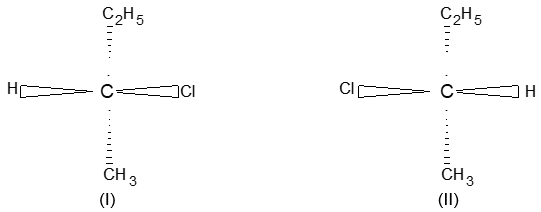
Suppose by suitable methods, we have obtained in the laboratory samples of two compounds of formula C2H5CHClCH3. We find that one of these rotates the plane of polarized light to the right, and the other to the left. We place them into two separate containers, one labeled “(+)-sec–butyl chloride” and the other “(–)-sec-butyl chloride”.
We have isolated two isomeric sec–butyl chlorides and we also have made two models to represent the two different configurations of the chloride. Now the big question arises, which configuration describes which isomer? That is to say, how do we assign configuration?
In 1951, J.M. Bijvoet reported that, using a special kind of X–ray analysis (the method of anomalous scattering) he had determined the actual arrangement in space of the atoms of an optically active compound. The compound was a salt of (+)-tartaric acid.
Over the years prior to 1951, the relationships between the configuration of (+)-tartaric acid and the configurations of hundreds of optically active compounds were known by certain methods.
Thus, when the configuration of (+)-tartaric acid became known, these other configurations too immediately became known. For example, the (-) isomer of the sec–butyl chloride is known to have configuration I, and the (+) isomer configuration II.
Specification of configuration (Nomenclature of enantiomers) : The R, S – system
After assigning of configuration, a further problem arises. If you name the two enantiomers of the sec–butyl chloride using only the IUPAC system of nomenclature that we have learned so far, both enantiomers will have the same name: 2–chlorobutane. This is unacceptable because each compound must have its own distinct name.
Moreover, the name (that is given to a compound) should allow a chemist, who is familiar with the rules of nomenclature, to write the structure of the compound from its name alone. Given the name 2–chlorobutane, a chemist could write either configuration I or configuration II.
Moreover, how can you specify a particular configuration in some simpler, more convenient way than by always drawing its picture?
Three chemists, R.S. Cahn (London), Sir Christopher Ingold (London), and V. Prelog (Zurich), devised a system of nomenclature (the most generally useful way yet suggested) that, when added to the IUPAC system, solves all of these problems.
This system, called the R, S – system or the Cahn – Ingold – prelog system, is now widely used and is part of the IUPAC rules.
According to this system, one enantiomer of 2–chlorobutane should be designated (R)-2-chlorobutane and the other enantiomer should be designated (S)-2-chlorobutane. (R ) and (S) are form the Latin words rectus and sinister, meaning right and left respectively. Thus, the two enantiomers of 2–chlorobutane are said to have opposite configurations at C2.
The (R) and (S) configurations are assigned on the basis of the following steps:
Step 1: Identify the centre(s) of chirality.
Step 2 : Assign a sequence of priority or preference 1, 2, 3 or 4 to the four atoms or groups of atoms (ligands) attached to the chiral center. This is done by following a set of sequence rules.
Step 3 : Orient the molecule (by visualization) so that the ligand with lowest priority (i.e., 4) is directed away from the viewer. Now observe the arrangement of the remaining ligands by tracing a path from (1) to (2) to ( 3).
If, in proceeding from the ligand of highest priority (1) to the ligand of second priority (2) and finally to the third (3), the direction of our eye (or finger or pencil) is clockwise, the configuration of the enantiomer is specified R (Latin : rectus, right). If the direction is counterclockwise, the configuration of the enantiomer is designated S (Latin: sinister, left).
A complete name for an optically active compound should reveal both configuration and direction of rotation (if they are known), for example. (S) – (+) -sec-butyl chloride.
A racemic modification can be specified by the prefix RS, for example, (RS) –sec–butyl chloride. One must not confuse the direction of optical rotation of a compound (a physical property of a real substance, like melting point or boiling point) with the direction in which the eye or the finger happens to travel when one imagines a molecule held in an arbitrary manner.
Unless one happens to know what has been established experimentally for a specific compound, one has no idea whether (+) or (-) rotation is associated with the R or the S configuration.
Sequence rules or Cahn – Ingold – Prelog (CIP) priority rules
Each of the four groups attached to the stereogenic carbon is assigned a priority or preference 1(a), 2(b), 3(c), and 4(d).
Sequence Rule (or CIP priority rule) 1:
Priority is first assigned on the basis of the atomic number of the atom that is directly attached to the stereogenic carbon.
If all the four atoms attached to the stereogenic center are different, priority depends on their atomic number only. The group with the atom of lowest atomic number is given the lowest priority, 4(d); the group with the atom of next higher atomic number is given the next higher priority, 3(c); and so on.
One can understand the application of the rule with the help of an enantiomer of chloroiodomethanesulphonic acid.
Iodine has the highest atomic number of the four atoms directly attached to the stereogenic carbon and is assigned the highest priority, 1(a). Hydrogen has the lowest atomic number and is assigned the lowest priority, 4 (d).
Thus, according to rule 1, the order of decreasing priority of groups is as follows:
I > Cl > SO3H > H
If two atoms are isotopes of the same element, the atom of higher mass number has the higher priority, that is, in the case of isotopes, the isotope of greatest atomic mass has highest priority. Thus, in – deuterioethyl bromide :
The sequence is
Br > C > D > H.
Sequence Rule 2:
Consider the butan-2-ol enantiomer:
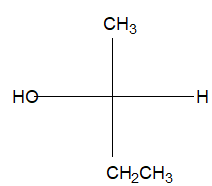
Oxygen has the highest atomic number of the four atoms directly attached to the stereogenic carbon and is assigned the highest priority, 1(a). Hydrogen has the lowest atomic number and is assigned the lowest priority, 4(d).
A priority cannot be assigned for the methyl group and the ethyl group by the rule 1 because the atom that is directly attached to the stereogenic carbon is a carbon atom in both groups.
If the relative priority of two groups cannot be decided by Rule 1 it shall be determined by a similar comparison of the next atoms in the groups and so on (if necessary), working outward from the chiral center.
That is to say, when a priority cannot be assigned on the basis of the atomic number of the atoms that are directly attached to the stereogenic carbon, then the next set of the atoms in the unassigned groups is examined. This process is continued until a decision can be made.
In other words, if two atoms attached to the chiral center are the same, you compare the atoms attached to each of these first atoms.
We assign a priority at the first point of difference.
When we examine the methyl group of the butan-2-ol enantiomer, we find that the next set of atoms consists of three hydrogen atoms (H, H, H). In the ethyl group of the enantiomer the next set of atoms consists of one carbon atom and the two hydrogen atoms (C, H, H). Since carbon has a higher atomic number than hydrogen, we assign the ethyl group the higher priority, 2 (b), and the methyl group the lower priority, 3 (c ), that is to say (C, H, H) > (H, H, H). Similarly for sec–butyl chloride, a complete sequence of priority is: Cl, C2H5, CH3, H. In 3–chloro-2-methylpentane:
The (C, C, H) of isopropyl takes priority over the (C, H, H) of ethyl. Thus, the complete sequence of priority is
Cl > isopropyl > ethyl > H
In 1, 2-dichloro-3-methylbutane:
The (Cl, H, H) of CH2Cl takes priority over the (C, C, H) of isopropyl because chlorine has a higher atomic number than carbon.
The fact that there are two C’s and only one Cl does not matter. One higher number is worth more than two or three – of a lower number.
The rules for a branched chain require that we follow the chain with the highest priority atom.
The first two rules of the Cahn – Ingold – Prelog system allow us to make an (R) or (S) designation for most compounds containing single bonds. For compounds containing multiple bonds one other rule is necessary:
Sequence Rule 3:
Where there is a double or triple bond, both bonded atoms are considered to be duplicated or triplicated. In other words, groups containing double or triple bonds are assigned priorities as if both atoms were duplicated or triplicated, that is
and
where the symbols in parentheses are duplicate or triplicate representations of the atoms at the other end of the multiple bond.
Thus, the vinyl group, -CH=CH2, is of higher priority than the isopropyl group, because
-CH = CH2, equals , while isopropyl group is
At the first set of atoms both groups are the same: C, C, H. But at the second set of atoms out, the vinyl group (see the structure) is C, H, H, whereas the isopropyl group along either branch is H, H, H.
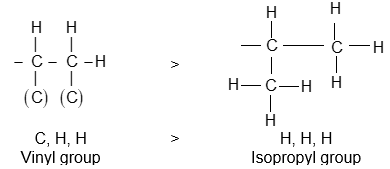
In glyceraldehyde the OH group has the highest priority of all,

And the (O, O, H) of –CHO takes priority over the (O, H, H) of –CH2OH. The complete sequence is then – OH > -CHO > -CH2OH > -H.
To handle the phenyl group, C6H5-, we take the help of one of the Kekule structures:

Thus, in 1–amino-2-methyl-1-phenylpropane,

the (C, C, C) of phenyl takes priority over the (C, C, H) of isopropyl, but not over N, which has a higher atomic number. The entire sequence is then NH2, C6H5, C3H7, H.
Illustration 51: Draw cross formulae for the enantiomers of
a) Chloroiodomethane sulfonic acid
b) – Deuterioethylbromide
Also label them as (R) and (S).
Solution: Keep the lowest priority atom (or group of atoms) at the bottom:
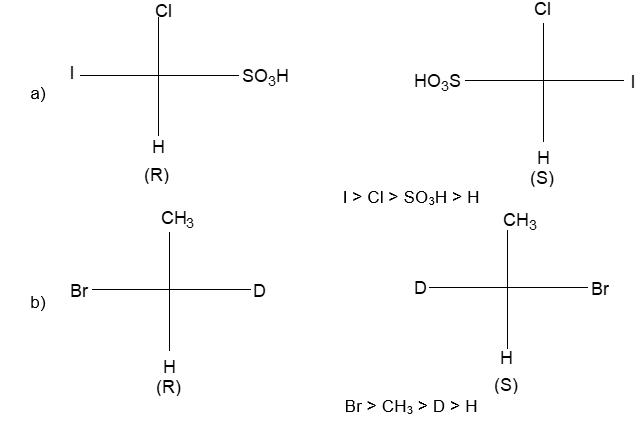
Illustration52: Convert the following structures into Fischer projection formulae:

Solution: In the Fischer formula, the chiral atom is not drawn; it is at the crossing of a horizontal and a vertical line. The horizontal bonds project out of the plane of the paper and toward the viewer, the vertical bonds project behind the plane of the paper and away from the viewer.
Tip the Cl back so that H and Cl are behind the plane with the Cl on top and the H below. The Me and Br both project in front of the paper on the horizontal.
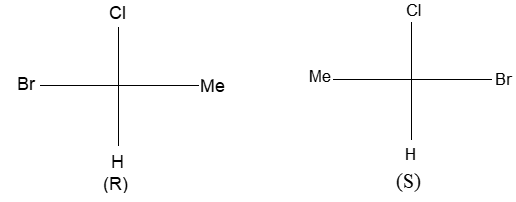
Compounds with more than one stereogenic (or chiral) centre – Diastereomers and meso compounds.
All of the chiral molecules that we have considered so far have contained only one stereogenic carbon. We found that there are two stereoisomers (i.e., the R and S enantiomers) for a molecule that contains one centre of chirality.
Many organic molecules, especially those important in biology, contain more than one streogenic centre.
We must learn what stereosiomers are possible for compounds whose molecules contain, not just one, but more than one chiral centre.
Here we have a very useful rule that gives the maximum number of stereoisomers:
In compounds whose stereoisomerism is because of tetrahedral stereogenic centres such as chiral carbons, the total number of stereoisomers never exceeds 2n, where n is equal to the number of tetrahedral stereogenic centres.
Thus, for 2, 3 – dichloropentane
that has two stereogenic centres in the form of two chiral carbon atoms, we should not expect more than four stereoisomers (22 = 4).
Cholesterol, having eight stereogenic centres, hypothetically could exist in 28 (256) stereoisomeric forms, yet biosynthesis via enzymes produces only one stereoisomer!
To write three–dimensional formulae for the stereoisomers of the compound, we begin by writing a three–dimensional formula for one possible stereoisomer and then we write the 3–D formula for its mirror image [We can also use models].
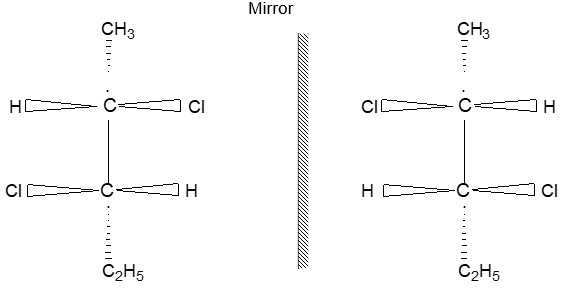
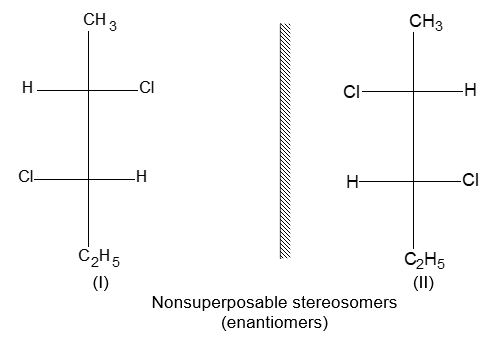
It is quite helpful to follow certain conventions when we write these three–dimensional formulae. For instance, we usually write our structures in eclipsed conformations. This should not imply that eclipsed conformations are the most stable ones – they most certainly are not.
We write eclipsed conformations because planes of symmetry, when they are present, are easy to recognize through them. We also write the longest carbon chain in a generally vertical orientation on the page. This makes the direct comparison of the structures that we write.
While doing these things, we must remember that
i) molecules can rotate as a whole rather than in parts, and
ii) that normal temperatures rotations about all single bonds are also possible.
If rotations of the structure itself or rotations of groups joined by single bonds make one structure superposable with another, then the structures do not represent different compounds. Instead they represent different orientations or different conformations of two molecules of the same compound.
We may represent the structures by wedge formulae and mentally try to superpose these. Or we may use the simple “cross” representations, being careful, as before, not to remove the drawings from the plane of the paper or board.
We find that structures I and II are not superposable, and hence they represent different compounds. Since structures I and II differ only in the arrangement of their atoms in space, they must be stereoisomers. Structures I and II are also mirror images of each other. Thus, they represent enantiomers.
Do we have any other stereoisomers of 2,3–dichloropentane? The answer is yes. Structures I and II are not the only possible structures. We find that we can make (or write) a structure III, which is different from either I or II because it is nonsuperposable on either I or II. Moreover, it is not the mirror image of either.
Using models, we make its mirror image, structure IV, and find that this is not superposable on (or interconvertible with) III.
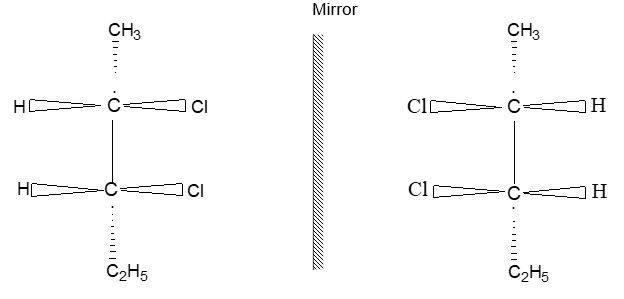
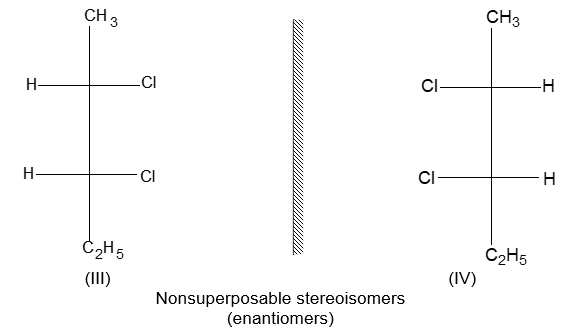
Thus, structures III and IV represent (or correspond to) a second pair of enantiomers.
Since structures I – IV are all different, there are (in total) four stereoisomers (22) of 2, 3– dichloropentane.
Essentially what we have done above is to write all the possible structures that result by successively interchanging two groups at all stereogenic carbons.
At this point one should convince that there are no other stereoisomers by writing other structural formulae.
One should notice that rotation about the single bonds (or of the entire structure) of any other arrangement of the atoms will cause the structure to become superposable with one of the structures that we have written here. All the compounds represented by structures I – IV are optically active compounds. Thus, any one of them, when placed separately in a polarimeter, would show optical activity.
The compounds represented by structures I and II are enantiomers. The compounds represented by structures III and IV are also enantiomers. But what is the isomeric relationship between the compounds represented by I and III or between II and III? We can answer this question by observing that I and III are stereoisomers but not enantiomers as they are not mirror images of each other.
Stereoisomers that are not mirror images of each other are called diastereomers. Therefore, compound III is a diastereomer of I, and similarly of II. Also, compound IV is a diastereomer of I, and similarly of II. Finally, we can say that there are 4 pairs of diastereomers.
Diastereomers have different physical properties:
Unlike enantiomers, they have different melting points, boiling points, solubilities in a given solvent, densities, refractive indexes and so on.
Diastereomers differ in specific rotation as they may have the same or opposite signs of rotation, or some may be inactive like diastereomeric alkenes such as cis and trans-but-2-ene.
Diasteromers have similar chemical properties:
It is so because they are members of the same family. However, their chemical properties are not identical. In the reaction of two diastereomers with a given chemical reagent, neither the two sets of reactants nor the two transition states are mirror images, and hence (except by sheer coincidence) do not carry the same energies. The Eact values will be different and so will the rates of reactions.
Diastereomers can (in principle at least) be separated from each other by fractional distillation or fractional crystallization, as a result of their differences in boiling point and in solubility.
As a result of differences in molecular shape and polarity, diastereomers differ in adsorption. Thus, they can be separated by chromatography.
If we are given a mixture of all four stereoisomeric 2, 3 – dichloropentanes, then by distillation, we could separate it into two fractions only. One fraction would be the racemic modification of I plus II, the other fraction would be the racemic modification of III plus IV.
Further separation would require resolution of the racemic modification by use of optically active reagents.
Thus, the presence of two stereogenic centers can lead to the existence of as many as four stereoisomers. For compounds containing three stereogenic centers, there could be as many as eight stereoisomers; for compounds containing four stereogenic centers, there could be as many as sixteen stereoisomers and so on. The maximum number of stereoisomers that can exist is equal to 2n, where n is the number of stereogenic centers.
A compound with n stereogenic centres does not always have 2n stereoisomers. In any case, where meso compounds exist, there will be fewer than this maximum number.
By far the most important and abundant of the carbohydrates is the sugar (+)–glucose.
It is the compound oxidized in our cells to provide energy, it is the building block making up starch, from which our food ultimately comes, and cellulose, the framework of the plants that synthesize this starch. Glucose contains five stereogenic centres. This could and does give rise to 25 or 32 stereoisomers. Of these only one, -D–glucose, is the unit of starch, and only one, -D–Glucose, is the unit of cellulose.
Meso compounds
A compound (or a structure) with two stereogenic carbons does not always have four possible stereoisomers. Sometimes there are only three. This occurs because some molecules are achiral even though they contain stereogenic carbons. As an example, let us consider 2, 3–dichlorobutane, which has two stereogenic carbons:
Let us write stereochemical formulae for the compound. As we did before, we first write the formulae for one possible stereoisomer and its mirror image.
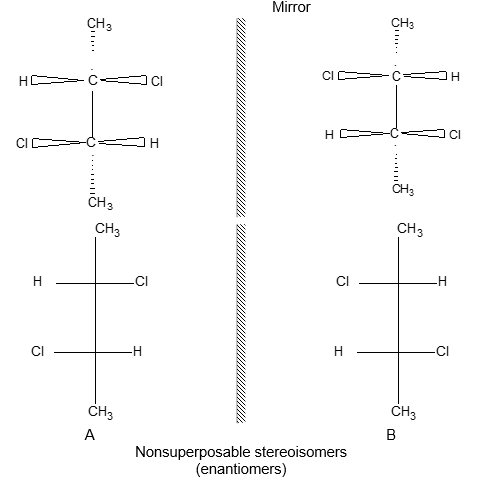
These structures A and B are mirror images that are nonsuperposable or not interconvertible. They represent a pair of enantiomers. Therefore, each should be capable of optical activity. Next, we write structure C, which we notice to be a diastereomer of A and of B. If we write structure D, the mirror image of C.
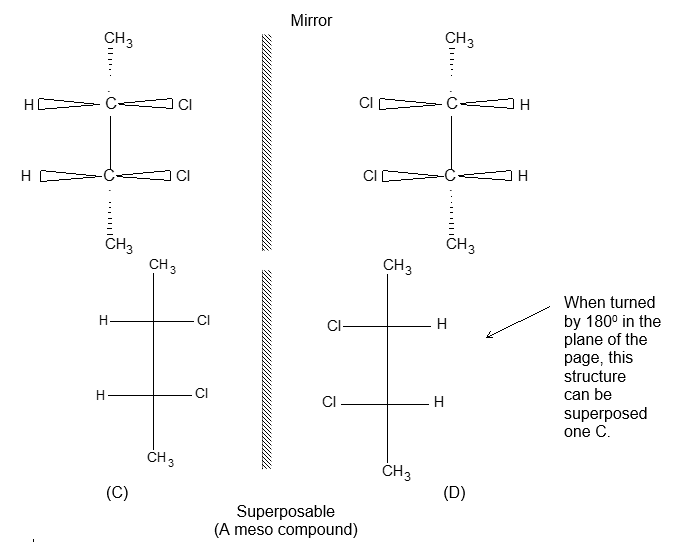
we find the two structures to be superposable. Turned end-for-end, D coincides in every respect with C. This means that C and D do not correspond to a pair of enantiomers. Actually, formulae C and D represent two different orientations of the same compound.
The compound described by structure C (or D) is not chiral in spite of the fact that it contains chiral centres, i.e., it contains tetrahedral C atoms with 4 different attached atoms and groups. It can’t exist in two enantiomeric forms, and it can’t be optically active. Such compounds are called meso compounds. Because they are achiral, meso compounds are optically inactive.
A meso compound is that compound whose molecules are achiral (i.e., superposable on their mirror images) even though they contain chiral centres.
The ultimate test for molecular chirality is to construct a model (or write the structure) of the molecule and then test whether or not the model (or structure) is superposable on its mirror image. If it is, the molecule is achiral. If it is not, the molecule is chiral.
A meso compound is optically inactive for the same reason as any other compound whose molecules are achiral: the rotation caused by any one molecule is cancelled by an equal and opposite rotation caused by another molecule that is the mirror image of the first.
One can easily recognize a meso compound on sight by the fact that (in at least one of its conformations) one half of the molecule is the mirror image of the other half. This can be easily seen for meso– 2, 3–dichlorobutane
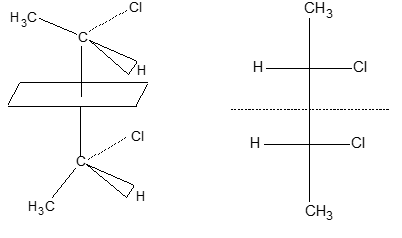
if we imagine the molecule to be cut by a plane lying where the dottled line is drawn. Since the molecule has a plane of symmetry, it can’t be chiral. If we do not see a plane of symmetry, however, this does not essentially mean that the molecule is chiral.
Specification of absolute configuration of compounds with more than one stereoganic carbon:
Compounds which contain more than one stereogenic center, present no special problem toward specification of configuration.
If a compound has more than one tetrahedral stereogenic carbon, we simply analyze each centre separately and specify the configuration about it, that is decide whether it is (R) or (S). Then by using numbers, we tell, which designation (or specification) refers to which carbon atom.
Let’s consider the stereoisomers of the 2, 3–dichloropentane:
Step 1: Take each of the chiral centres, C–2 and C–3, in turn, ignoring for the moment the existence of the other.
Step 2: In order of priority, the four ligands attached to C-2 are. On C–3, they are Cl > CH3CHCl > CH3CH2, H.
Step 3: Now we take in our hands or in our mind’s eye, a model of the particular stereoisomer we are interested in. First we focus our attention on C-2 (ignoring C–3), and then on C–3 (ignoring C-2). Stereisomer I (page 101) is specified as (2S, 3S)–2, 3–dichloropentane. Similarly, II is designated as (2R, 3R), III as (2S, 3R), and IV as (2R, 3S).
These designations help us to analyze the relationships among the stereoisomers : Since I and II are enantiomers, they have opposite, that is, mirror–image configurations about both chiral centres: 2S, 3S and 2R, 3R. Since I and III are diastereomers, they have opposite configurations about one chiral center, and the same configuration about the other : 2S, 3S and 2S, 3R.
We can handle 2, 3 – Dichlorobutane in exactly the same way.
Here, the two stereogenic carbons occupy equivalent positions along the chain. Thus, it is not essential to use numbers in the designations.
Enantiomers A and B (page 105) are designated (S, S) – and (R, R) – 2, 3 – Dichlorobutane, respectively.
We can also specify them as (2S, 3S) – 2, 3 – Dichlorobutane and (2R, 3R) –2, 3 – Dichlorobutane respectively.
The mesoisomer, C (or D), can be designated as either (R, S) – or (S, R) –2, 3– Dichlorobutane. Notice that the absence of numbers emphasizes the equivalence of the two Designations.
The mirror – image relationship between the two ends of meso molecule is consistent with the opposite designations of R and S for the two chiral centres.
Not all R, S isomers are meso structures. Only those whose two halves are chemically equivalent.
Chloramphenicol is a potent antibiotic, isolated from Streptomyces venezuelae, that is particularly effective against typhoid fever. It was the first naturally occurring substance shown to contain a nitro (-NO2) group attached to an aromatic ring. Both stereogenic carbons in chloramphenicol are known to have the (R) configuration.

Conformational stereoisomers
There are 3 different staggered conformations of n – butane, each of which lies at the bottom of an energy valley (i.e., at an energy minimum) separated from the others by energy hills.
Different conformations of a compound corresponding to energy minima are called conformational isomers, or conformers.
Conformational isomers are stereoisomers because they differ from each other only in the way their atoms are oriented in space. Like stereoisomers of any kind, a pair of conformers can either be mirror images of each other or not. n–Butane has 3 conformational isomers, one anti (I) and two gauche (II and III). The gauche conformers, II and III, are nonsuperposable mirror images of each other, and hence are (conformational) enantiomers. On the other hand, conformers I and II (or I and III) are not mirror images of each other, and hence are (conformational) diastereomers.
Although the energy barrier to rotation in n-butane is a little higher than in the ethane, it is still low enough that (at ordinary temperatures) interconversion of conformers is easy and rapid.
The system is at equilibrium, which favors a higher population of the more stable anti conformer. However, the populations of the two gauche conformers (which are mirror images and hence of exactly equal stability) are equal.
In other words, any given molecule of n – butane spends the greater part of its life time as the anti conformer, and divides the smaller part equally between the two gauche conformers.
On account of the rapid interconversion these isomers can’t be separated. Rapid and easy interconversion is the characteristic of almost every set of conformational isomers.
It is this quality in which such isomers differ most, from the kind of stereoisomers, we have discussed so far in this chapter. This difference in interconvertibility is due to a difference in height of the energy barrier separating stereoisomers, which is (in turn) due to a difference in origin of the barrier.
By definition, interconversion of conformational stereoisomers involves rotation about single bonds. In most cases, the rotational energy barrier is a very low one and thus, inter conversion is easy and fast. Configurational stereoisomers (or inversional stereoisomers), the other kind of stereoisomers, differ from one another in configuration about a stereogenic center.
Their interconversion involves the breaking of a covalent bond for which there is a very high barrier: 50 kcal mol–1 or more.
Thus, unless one deliberately provides conditions to bring it about, interconversion is difficult and negligibly slow.
Interconvertibility of stereoisomers is of great practical significance because it limits their isolability:
i) Hard-to-interconvert stereoisomers can be separated (with special methods for resolution of enantiomers) and studied individulally. Among other things, their optical activity can be measured.
ii) Easy-to-interconvert stereoisomers cannot be separated. Thus, single isolated isomers can’t be studied. Since any chiral molecules are present only as non –resolvable reacemic modifications, optical activity cannot be observed.
Thus, two stages are involved in our general approach to stereoisomers.
i) First, we test the superposability of possible isomeric structures, and then
ii) we test their interconvertibility.
Both the tests are best carried out with models. We make models of the two molecules and we try to superpose them without allowing any rotations about single bonds. If they cannot be superposed, they represent isomers.
Next we do all possible rotations about single bonds in the models, and repeatedly try to superpose them. It they still can’t be superposed they are non interconvertible and represent configurational stereoisomers.
But it they can be superposed after rotation, they are interconvertible and represent conformational stereoisomers.
We can ignore the existence of easy–to–interconvert isomers which means most conformational isomers, while dealing with those aspects of stereochemistry that depend on
i) isolation of stereoisomers (isomer number)
ii) optical activity
iii) study of the reactions of a single stereoisomer.
For convenience the following “ground rule” will hold:
Unless specifically indicated otherwise, the terms “stereoisomers”, “enantiomers”, and “diastereomers” will refer only to configurational isomers, including geometric isomers and will exclude conformational isomers. The latter will be referred to as “conformational stereoisomers”, “conformers”, “conformational enantiomers and “conformational diastercomers”.
There is no sharp boundary between easy–to–interconvert and hard–to–interconvert stereoisomers. Although we can be sure that interconversion of configurational isomers will be hard, we can’t be sure that interconversion of conformational isomers will be easy. Depending upon the size and nature of substituents, the barrier to rotation about single bonds can be of any height, from the low one in ethane to one comparable to that for breaking a covalent bond.
Some conformational isomers exist that are readily isolated, kept and studied. Study of such isomers, called atropisomers, makes up a large and extremely important part of stereochemistry.
Other conformational isomers exist that can be isolated, not at ordinary temperatures, but at lower temperatures, where the average collision energy is lower.
The conformational stereoisomers that we shall discuss in our syllabus have low rotational barriers. We may assume (until we learn otherswise) that when we classify stereoisomers as configurational or conformational, we at the same time classify them as hard to–interconvert or easy-to-interconvert.
Conversion of an achiral molecule into a chiral molecule (Generation of a chiral center)
One of the products of monochlorination of n-butane is the chiral compound, sec-butyl chloride:
Due to just one stereogenic centre, it can exist as two enantiomers, I and II. They are specified as S and R, respectively.

Each enantiomer is optically active. Now, if we put the sec-butyl chloride actually prepared by the chlorination of n – butane into a polarimeter, it does not rotate the plane of polarized light. It is because of the fact that sec–butyl chloride prepared by the above method is not a pure substance but a mixture, the racemic modification.
Why is the racemic modification formed?
Step 1: A chlorine atom abstracts hydrogen to yield hydrogen chloride and a sec–butyl free radical:
The carbon atom carrying the odd e– in the free radical is sp2–hybridized (trigonal). Thus, a part of the radical is flat, i.e., the sp2–hybridized (trigonal) carbon and the three atoms directly attached to it are lying in the same plane.
Step 2: The free radical abstracts chlorine atom from a chlorine molecule to yield sec-butyl chloride:
In this process, the incoming chlorine atom may be attached to either face of the flat radical. This yields either of two enantiomers: R or S, depending upon which face takes chlorine.
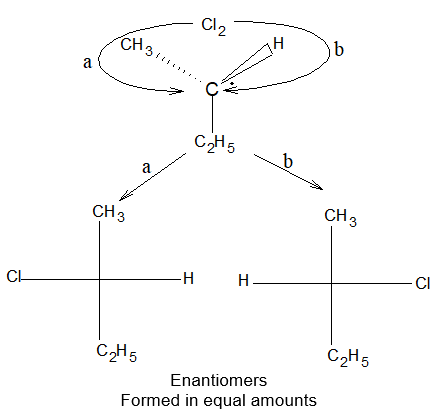
Since the probability of attack at one face is exactly identical to that of attack at the other face, the two enantiomers are obtained in exactly equal amounts. Thus, the product is the racemic modification.
As long as neither the starting material nor the reagent (even, nor the environment) is optically active, we should obtain an optically inactive product.
In such situations at some stage of the reaction sequence, there will be two alternative paths, one of which yields one enantiomer and the other the opposite enantiomer. The two paths will always be equivalent. The selection between them will be random.
The facts agree with these predictions.
Synthesis of chiral compounds from achiral reactants always yields the racemic modification. In more general sence: Optically inactive reactants yield optically inactive products
Whenever a racemic modification is formed in a reaction, we will only isolate a racemic modification, by ordinary methods:
a) Since the enantiomeric sec-butyl chlorides have exactly the same boiling point, they can’t be separated, by carrying out a fractional distillation. Thus, they are collected in the same distillation fraction.
b) Since their solubilities in every (optically inactive) solvent are identical, no separation is possible through recrystallization.
How do we know that the product obtained during an ordinary chemical synthesis is a racemic modification? The answer is the product is optically inactive.
How do we know that it is actually made up of a mixture of two optically active substance as this can’t be separated by our usual methods of distillation, crystallization, etc. The answer is the separation of enantiomers (called resolution) can be accomplished by special methods. These involve the use of optically active reagents.
Reactions of chiral molecules involving bond – breaking
When sec–Butyl chloride undergoes free – radical chlorination, a number of isomeric dichlorobutanes are formed, corresponding to attack at various positions in the molecule:
Try to work out the other isomers.
Let us consider (S) –sec–butyl chloride, which rotates light to the right and take only the part of the reaction that yields 1, 2–Dichlorobutane.
Using a single ball for –C2H5 but a separate ball for each atom in –CH3, let’s make a model (I) of the starting molecule. In accordance with the familiar steps of the mechanism, we remove an –H from –CH3 and replace it with a –Cl.
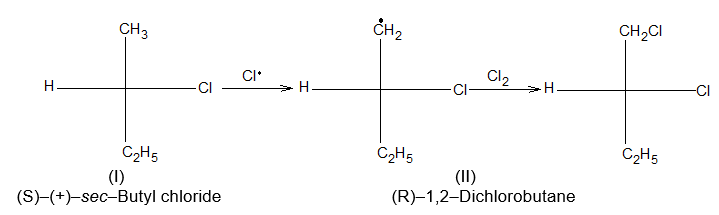
Since no bond to the stereogenic center is broken in either step, the spatial arrangement about the stereogenic center is unchanged. In other words, we say, configuration is retained, with –CH2Cl now occupying the same relative position that was previously occupied by –CH3. Thus, the model we arrive at necessarily has configuration II.
A reaction that does not involve the breaking of a bond to a stereogenic center proceeds with retention of configuration about that chiral center.
If a bond to a chiral center is broken in a reaction, configuration can be changed. Just what happens depends on the mechanism of the particular reaction.
Relating configurations through reactions of chiral molecules (in which no bonds to the stereogenic carbon are broken):
The configuration of a particular enantiomer can be determined directly by a special kind of X–ay diffraction. But the procedure is difficult and time consuming, and can be applied only to certain compounds.
This method was first applied in 1951 by Bijvoet to (+)–tartaric acid.
However, in spite of this limitation, the configurations of thousands of other compounds are now known, since they were related by chemical methods to (+)–tartaric acid.
Most of these relationships were established by applying the following axiom:
The configurational relationship between two optically active compounds can be determined by converting one into the other by reactions that do not involve breaking of a bond to a stereogenic center.
If a reaction takes place in such a way that no bonds to the stereogenic carbon are broken, the product will necessarily have the same general configuration of groups around the stereogenic carbon as the reactant.
Such a reaction is said to proceed with retention of configuration.
Let us consider as an example (-)–2-methylbutan-1-ol (the enantiomer found in fusel oil). Accept for the moment, that it has configuration III, specified as S.
Now, as an example, consider the reaction that take place when (S) –(-)2–methylbutan-1-ol is heated with concentrated hydrochloric acid to form the alkyl chloride, 1-chloro-2-methylbutane.

Without knowing the mechanism of this reaction one can see that the reaction must involve breaking the carbon-oxygen bond (the CH2 – OH bond) of the alcohol because the – OH group is replaced by a -Cl .
Since no bonds to the stereogenic carbon are broken, the reaction must take place with retention of configuration. The product of the reaction must have the same configuration of groups around the stereogenic carbon that the reactant had.
By saying that the two compounds have the same configuration, it is meant that comparable or identical groups in the two compounds occupy the same relative positions in space around the stereogenic carbon.
In this particular situation the – CH2OH group and the – CH2Cl group are comparable, and they occupy the same relative position in both compounds. All the other groups are identical and they occupy the same positions.
When we put the chloride into a polarimeter tube, we find that the plane of polarized light is rotated to the right, that is, the product is (+) -1-chloro-2- methylbutane.
Since (-)-2-methylbutan-1-ol has configuration III, (+)-1-chloro-2-methylbutane must have configuration IV, that is, must be specified as S.
Note that in this particular example while the R, S designation does not change (as both reactant and product are specified as ‘S’), the direction of optical rotation does change (as the reactant is (-) but the product is (+). Neither occurrence is a necessity when a reaction proceeds with retention of configuration.
There are examples of reactions in which configurations are retained but the direction of optical rotation does not change.
The following reaction is an example of a reaction that proceeds with retention of configuration but involves a change in the R, S designation.
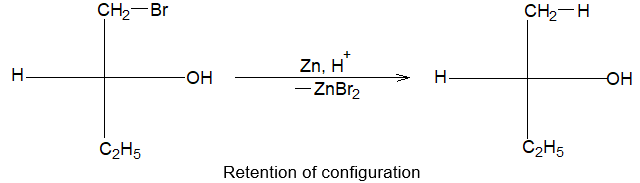
In this example the R, S–designation changes because the –CH2Br group of the reactant changes to a –CH3 group in the product. Note that –CH2Br has a higher priority than -CH2CH3, and –CH3 has a lower priority than –CH2CH3.
If we oxidize (-)-2-methylbutan-1-ol with potassium permanganate, we get the corresponding acid, 2-methylbutanoic acid which rotates light to the right.
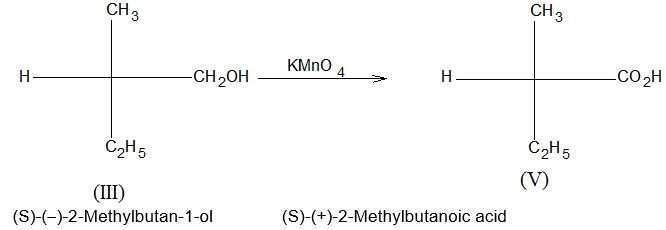
Again, no bond to the stereogenic centre is broken. Thus, we assign configuration V to (+)-2-Methylbutatnoic acid.
We can nearly always tell whether or not a bond to a chiral center is broken by simple inspection of the formulae of the reactant and product and without a knowledge the reaction mechanism.
Reactions in which no bonds to the stereogenic carbon are broken are useful in relating configurations of chiral molecules. In other words, they allow us to demonstrate that certain compounds have the same relative configuration.
In each of the examples that we have just discussed, the products of the reactions have the same relative configurations as the reactants.
But how do we come to know that (-)-2-methylbutan-1-ol has configuration III?
Its configuration was related in this same manner to that of another compound, and that one to the configuration of still another, and so on, going back ultimately to (+)-tartaric acid and Bijvoet’s X-ray analysis.
Before 1951 only relative configurations of chiral molecules were known. No one prior to that time was able to demonstrate with certainty what the actual spatial arrangement of groups was in any chiral molecule.
To say this another way, no one was able to determine the absolute configuration of an optically active compound.
The fact that two compounds happen to have the same sign or opposite sign of rotation means little because they may or may not have similar configurations.
We can’t tell whether two compounds have the same or opposite configurations by simply looking at the letters used to specify their configurations. We must work out and compare the absolute configurations indicated by those letters.
Configurations of chiral molecules were related to each other through reactions of known stereochemistry. Attempts were also made to relate all configurations to a single compound that was chosen arbitrarily to be the standard.
The D, L system of configurational designation
The simplest carbohydrates, those that cannot be hydrolyzed into simpler carbohydrates, are called monosaccharides.
The compounds glyceraldehyde and dihydroxyacetone are the simplest monosaccharides:
Of these two compounds, only glyceraldehyde (2,3-dihydroxypropanal) contains a stereogenic center. Therefore, glyceraldehyde exists in two enantiomeric forms that are known to have the following absolute configurations:
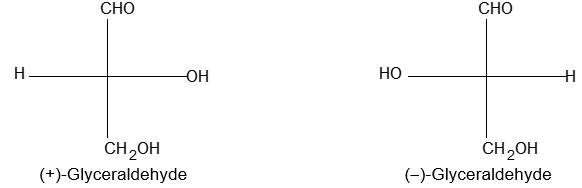
According to the Cahn–Ingold–Prelog convention (+)-glyceraldehyde should be designated (R)-(+)-glyceraldehyde and (-)-glyceraldehyde should be designated (S)-(-)-glyceraldehyde.
Early in the 20th century, before the absolute configurations of any organic compounds were known, another system of stereochemical designations was introduced.
According to this system (first suggested by M.A. Rosanoff of New York University in 1906) (+)-glyceraldehyde is designated D-(+)-glyceraldehyde and (-)-glyceraldehyde is designated L-(-)-glyceraldehyde.
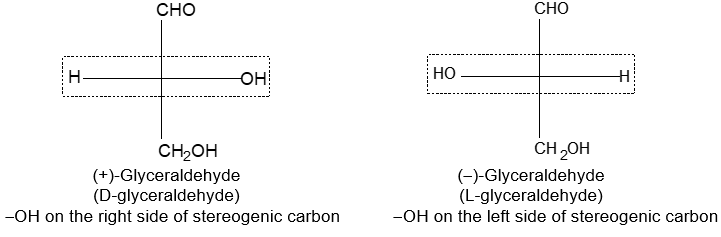
Now it is possible to determine absolute configuration by means of crystallographic procedures. In the case of the two glyceraldehyde structures Rosanoff made a guess. He assumed that structure with the OH group to the right represented (+)-glyceraldehyde and the structure with the OH group to the left represented (-)-glyceraldehydes. At a later date these were also designated D-glyceraldehyde and L-glyceraldehyde respectively.
These two compounds serve as configurational standards for all monosaccharides. A monosaccharide whose highest numbered stereogenic centre (the penultimate carbon) has the same configuration as D-(+)-glyceraldehyde is designated as a D sugar while one whose highest numbered stereogenic center has the same configuration as L-glyceraldehyde is designated as an L-sugar.
All molecules, which could be chemically related to D-glyceraldehyde are assigned the D-configuration and those related to L-glyceraldehyde are all designated L-configuration.
While assigning D, L configuration, we take the help of the Fischer projections. In Fischer projections, by convention, horizontal lines project out of the plane of the page toward the reader, vertical lines project behind the plane of the page and away from the reader.
When we use Fischer projections, however, we must not (in our mind’s eye) remove them from the plane of the page in order to test their superposability and we must not rotate them by 900.
The Fischer projection of the molecule is drawn in such a way that the main longest carbon chain becomes vertical with the most highly oxidized carbon at or nearest the top.
The D, L system is commonly used in assigning stereochemistry to carbohydrates and amino acids. By convention, acyclic forms of monosaccharide are drawn vertically with the aldehyde or keto group at or nearest the top.
When drawn in this way, D sugars have the -OH on their penultimate carbon on the right while L sugars have the – OH on their penultimate carbon on the left.
The D and L designations are like (R) and (S) designations in that they are not necessarily related to the optical rotations of the sugars to which they are applied. Thus, one may encounter other sugars that are D-(+)- or D-(-) and ones that are L-(+)- or L-(-)-.
There is no direct relation between D, L configuration with d and l or ( + ) or (-) notations.
The D, L – system of stereochemical designations is thoroughly established in the literature of carbohydrate chemistry. Even though it has the disadvantage of specifying the configuration of only one stereogenic center, we shall employ the D, L – system in our designations of carbohydrates.
Illustration 53: Specify the configuration of the following compounds as D or L.
Solution
a) Since –OH on C–3 is on right, it is D-configuration.
b) Since –OH on C–3 is on left side, it is L-configuration.
To apply the D, L-system of stereochemical designations to -amino acids, the configurational arrangement of –NH2, -COOH, -R, and -H groups at alpha carbon atom is related to that of the –H, -CHO, -CH2OH, and -H groups respectively of glyceraldehyde.
Thus, (D)–glyceraldehyde and (D)-a-amino acids are said to have the same configuration. Similarly (L)–glyceraldehyde and (L)-a-amino acids are said to have the same relative configurations.
Illustration54: Specify the configuration of the following compounds as D or L.
Solution:
a) Since H2N on a-carbon is on left side, it is L configuration.
b) Since H2N on a-carbon is on left side, it is L configuration.
c) First convert to Fischer projection,

since H2N on – carbon is on left, it is L-configuration.
Relative stereochemistry gives specification of the stereochemical relation between two molecules.
Before 1951, no one could be sure which configuration belonged to which enantiomer. Chemists decided arbitrarily to assign the (R ) configuration to the ( + ) – enantiomer. Then, configurations of other molecules were related to one glyceraldehyde enantiomer or the other through reactions of known stereochemistry.
For example, the configuration of (-)-lactic acid can be related to (+)-glyceraldehyde through the following sequence of reactions in which no bond to the stereogenic carbon is broken.
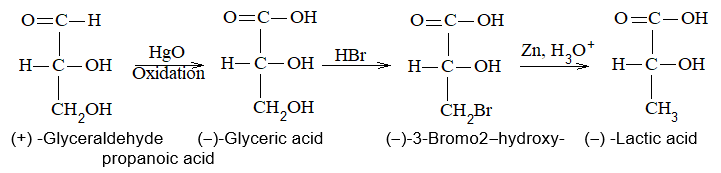
The stereochemistry of all of these reactions is known. Because none of the bonds to the stereogenic carbon has been broken during the sequence, its original configuration is retained. If the assumption is made that the configuration of (+)-glyceraldehyde is
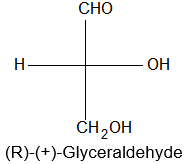
then the configuration of (-)-Lactic acid is
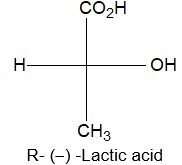
The configuration of (-)-glyceraldehyde was also related through reactions of known stereochemistry to (+) -tartaric acid:
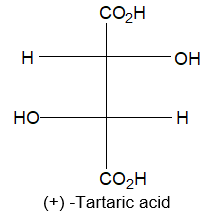
In 1951, J.M. Bijvoet using a special technique of X–ray diffraction, was able to show conclusively that (+) -tartaric acid had the absolute configuration shown above. This meant that the original arbitrary assignment of the configurations of (+)-and (-)-glyceraldehyde was also correct. It also meant that the configurations of all of the compounds that had been related to one glyceraldehyde enantiomer or the other were now known with certainty and were now absolute configurations.
The prefixes threo– and erythro–:
The simplest C3 sugar – glyceraldehydes – was a useful example for discussing several factors about the stereochemistry of compounds with one chiral centre.
The next members of this series – C4 sugars provide a convenient starting point for compounds with two different chiral centres.
A molecule with one stereogenic centre exists in two enantiomeric forms which together form a racemic mixture.
In general, molecules with ‘n’ different stereogenic centres exist in 2n enantiomeric forms which can be combined in appropriate pairs to form half that number (2n-1) of racemic mixtures.
Therefore, the C4 sugars with two different stereogenic centres, should exist in four enantiomeric forms and as two racemic mixtures.
These are known as erythrose and threose and have the Fischer projections I – IV.
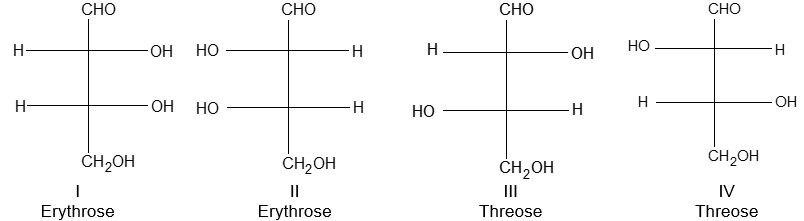
Erythrose exists in two enantiomeric forms (I) and (II) so does threose (III) and (IV). The compounds represented by I and say III are diastereomers. They are stereoisomers which are not enantiomeric.
The enantiomers I and II differ from one another in only one physical property – the direction in which they rotate plane polarized light – and in no chemical property except those with chiral reagents.
The same statement is true of III and IV but the properties of I and (say) III will be similar but not identical. The two racemic C4 sugars will also have similar but not identical properties.
Illustration 55: To name the compounds represented by structures I – IV, each chiral centre must be designated (R ) or (S ). Each will then be of a form such as (R)–2, (S)–3, 4–trihydroxybutanal.
Name each structure in this way.
Solution:
I) (R)–2, (R)–3, 4–trihydroxybutanal
II) (S)–2, (S)–3, 4–trihydroxybutanal
III) (R)–2, (S)–3, 4–trihydroxybutanal
IV) (S)–2, (R)–3, 4–trihydroxybutanal
Other molecules with two different stereogenic centres, not necessarily on adjacent carbon atoms, are frequently designated by the prefix threo or erythro. This implies that erythro stereoisomer contains two identical (or similar) groups on the same side of the carbon chain when expressed as a Fischer projection. On the other hand, threo stereoisomer contains two identical (or similar groups) on opposite side of the carbon chain when expressed as a Fisher projection. The following examples illustrate the application:
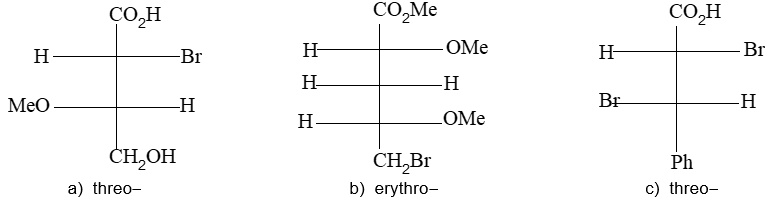
It is important to realize that the Fischer projection represents a structure according to an agreed convention and does not necessarily indicate the conformation which the molecule will assume in the crystalline state, in the liquid state, or in a solvated form.
It does not follow, for example, that two hydroxyl groups on adjacent carbon atoms are closer together in the erythro-isomer than in the threo-isomer.
Reactions of chiral molecules (Generation of a second chiral center)
Let’s consider the free-radical chlorination of sec-butyl chloride:
Let’s focus our attention on one of the products in which a second stereogenic centre is generated: 2,3-dichlorobutane. This compound exists as three stereoisomers, a pair of enantiomers and a meso. By fractional distillation we separate the 2,3-dicholorobutanes from all the other products (the 1,2 isomer, 2,2-isomer, etc). Which stereoisomers can we expect to have?
Three important points are illustrated by the course of reaction:
1) Since no bond to the original stereogenic center, C – 2, is broken, its configuration is retained in all the products. This must apply in all cases where a second chiral center is generated in the way.
2) There are two possible configurations about the new chiral center, C–3. In this particular case, both of these appear from attacks (a) and (b) on opposite sides of the flat portion of the free radical, giving the diastereomeric S, S and R, S (or meso) products.
In some reactions, both configurations may not actually be generated, but we must always consider the possibility that they will be.
3) The diastereomeric products will be formed in unequal amounts because in this case attack (a) and attack (b) are not equally likely. This must apply in all cases where diastereomeric products are formed.
Initially, we saw that generation of the first stereogenic center in a compound yields equal amounts of enantiomers, that is, yields an optically inactive racemic modification.
Now, we see that generation of new chiral center in a compound that is already optically active yields an optically active product containing unequal amounts of diastereomers.
Suppose that the products from (S)–sec–butyl chloride show an S, S: meso ratio of 29:71. Chlorination of (R)–sec–butyl chloride would give R, R and meso products, and the R, R : meso ratio would be exactly 29:71. Whatever factor favors meso product over S, S product will also favor meso product over R, R product, and to exactly the same extent.
If optically inactive, racemic sec-butyl chloride is subjected to chlorination, then the S isomer that is present would yield S, S and meso products in the ratio of 29:71; the R isomer would yield R, R and meso products in the same ratio of 29:71.
Since there are exactly equal quantities of S and R reactants, the two sets of products would exactly balance each other, to give racemic and meso products in the ratio of 29 : 71.
Optically inactive reactants yield optically inactive products.
The diastereomeric products are formed in unequal amounts because the intermediate 3–chloro–2- butyl radical already contains a chiral center. The free radical is chiral and lacks the symmetry that is necessary for attack at the two faces to be equally likely.
Resolution : (Reaction of chiral molecule with optically active reagent:
It is a well known fact that when optically inactive reactants form a chiral compound, the product is the racemic modification.
How are enantiomers separated?
We know that the enantiomers making up a racemic modification have identical physical properties (except for direction of rotation of polarized light) i.e., they have identical solubilities in ordinary solvents, and they have identical boiling points.
Consequently, the conventional methods for separating organic compounds such as fractional crystallization and fractional distillation, fail when applied to a racemic form.
Living organisms usually produce only one enantiomer of a pair. Thus, many (pure) optically active compounds are obtained from natural sources.
Compounds which contain stereogenic centres are usually produced in the racemic form by chemical synthesis but in an enantiomeric form from natural sources.
We deal with optically active substances to an extent that we may not realize we eat optically, active bread and optically active meat, live in houses, wear clothes, and read books made of optically active cellulose.
The proteins that make up our muscles and other tissues, the glycogen in our liver and glucose in our blood, the enzymes and hormones that enable us to grow and that regulate our bodily processes are all optically active.
Naturally occurring compounds are optically active because the enzymes that bring about their formation and often the raw materials from which they are made are themselves optically active.
Other optically active compounds can be made from these naturally occurring compounds, for example, (-)-2-methylbutan-1-ol, can be conversed without loss of configuration into the corresponding chloride or acid. These optically active compounds can, in turn, be converted into many others.
Most optically, active compounds are obtained by the separation of racemic modification into enantiomers, i.e., by the resolution of a racemic modification.
1) Mechanical separation: In this method the enantiomorphous crystals are actually separated by hand provided that the crystals are sufficiently well defined.
This method used by Pasteur in 1848 is mainly of historical interest. Using tweezers and a magnifying glass, Pasteur, separated the two kinds of crystals of the sodium ammonium salt of racemic tartaric acid.
Unfortunately, few organic compounds give chiral crystals as do the (+)- and (-) -tartaric acid salts. Few organic compounds crystallize into separate crystals (containing separate enantiomers) that are visibly chiral like the crystals of the sodium ammonium salt of tartaric acid.
Pasteur’s method, therefore, is not generally applicable to the separation of enantiomers.
2) Biochemical separation: This method was also used by Pasteur in 1858. When, certain, bacteria and moulds, grow in a dilute solution of a racemic modification, destroy one enantiomer more rapidly than the other. For example, Penicillium glaucum (a mould), attacks the D-form leaving the L-, when grown in a solution of ammonium racemate.
Another biochemical separation is done by enzymes, whereby an enzyme selectively converts one enantiomer in a racemic mixture to another compound, after which the unreacted enantiomer and the new compound are separated.
3) By means of salt-formation: This method, which is the best of all the methods of resolution, was also developed by Pasteur in 1858.
Most such resolutions are accomplished through the use of reagents that are themselves optically active. These reagents are usually obtained from natural sources.
This method, which is one of the most useful procedures for separating enantiomers, is based on allowing a racemic form to react with a single enantiomer of some other compound. This changes a mixture of enantiomers (present in a racemic modification) into a mixture of diastereomers. Because of their different melting points, different boiling points, and different solubilities, these diastereomers can be separated by conventional means.
Diastereomeric recrystallization is one such process.
The majority of resolutions that have been carried out depend upon the reaction of organic bases with organic acids to yield salts:
For example, suppose that we have prepared the racemic acid, (±)-HA. Now, think of very complicated bases called alkaloids (that is, alkali-like), which are isolated from various plants. Some typical examples are cocaine, morphine, strychnine, and quinine.
Most, alkaloids are produced by plants in only one of two possible enantiomeric forms, and hence they are optically active.
Now take one of these optically active bases, a dextrorotatory, (+)-B, and mix it with the racemic acid (±)-HA.
Acid + base salt
Due to the chemical reaction, we get crystals of two different salts:
[(+)-BH+(+)-A–] and [(+)-BH+ (-)-A–]
because the acid is present in two configurations, but the base is present in only one configuration.
Let’s find the stereochemical relationship between these two salts:
i) They are not superposable, since the acid parts are not superposable.
ii) They are not mirror images, since the base parts are not mirror images.
Therefore, the salts are stereoisomers that are not enantiomers, that is, they are diastereomers. These diastereomeric salts having different physical properties including solubility in a given solvent can be separated by fractional crystallization.
After the separation of the two salts, optically active acid can be separated from each salt by adding a strong mineral acid which displaces the weaker organic acid.
If the salts have been carefully purified by repeated crystallizations to remove all traces of its diastereomer, then the acid obtained from it is optically pure.
Among the alkaloids commonly used for this purpose are (-)-brucine, (-)- quinine, (-)- strychnine, and (+)-cinchonine.
Resolution of organic bases is carried out by reversing the process just described above, that is, by mixing with naturally occurring optically acid, for example, (-)-malic acid.
Resolution of alcohols poses a special problem: since alcohols are neither appreciably basic nor acidic, they can’t be resolved by direct formation of salts.
Yet they can be resolved by a rather ingenious adaptation of the method: one attaches to them an acidic ‘handle’, which permits the formation of salts, and then removing it when it is no longer needed. Thus, racemic alcohols are converted into the acid ester derivative with phthalic anhydride:
The acid ester, consisting of equimolecular quantities of the D- and L- forms, may now be resolved by method used for acids.
Compounds other than organic acids, bases, or alcohols can also be resolved. Although the particular chemistry may differ from the salt formation just described, the principle remains the same:
A racemic modification is converted by an optically active reagent into a mixture of diastereomers which can then be separated.
4) Selective adsorption: Optically active substances may be relatively adsorbed by some optically active adsorbent. For example, a racemic modification of a camphor derivative can be resolved on D-Lactose as adsorbent.
5) Channel complex formation: This method is based on the fact that the complexes of each enantiomer have different solubilities. For example (±)-2-chloro-octane can be resolved by means of channel complex formation with urea.
Geometrical Isomerism
When malic acid (2-hydroxybutanedioic acid) is heated, it is dehydrated as indicated:
This representation, however, is not entirely satisfactory because the product is a mixture of two compounds designated fumaric and maleic acids.
The actual product is a mixture of fumaric acid and maleic anhydride but on treatment with water the latter becomes maleic acid.
Both have the molecular formula C4H4O4, both are reduced to succinic acid (butanedioic acid):
They show other similar properties also. Nevertheless they also show some distinctive properties indicating they are clearly two different compounds. Thus, they have to be represented differently.
Many fatty compounds contain oleic acid as a major component. Its structure is represented as:
Under, certain conditions this low-melting solid (mp 130 when pure) is converted to a higher melting form designated elaidic acid (mp 450).
Oleic and elaidic acids have similar but not identical properties yet both are equally well represented by the same structure.
It immediately follows that the above representation is not entirely adequate since it can’t describe two acids which however similar are yet different compounds.
These are two early examples of stereoisomeric compounds which are now discussed in terms of geometrical isomerism (or cis-trans isomerism).
There are a number of possible arrangements for the butylenes, C4H8:
i) A straight-chain skeleton as in n-butane, or a branched-chain skeleton as in isobutane.
ii) For the straight –chain skeleton, there are two possible arrangements that differ in position of the double bond in the chain.
Thus, we get a total of three structures:
However, experiments show that not three but four alkenes of the formula C4H8 exist, having the following physical properties:
| Name | B.P., 0C | M.P., 0C |
| cis-But-2-ene | + 4 | -139 |
| trans-But-2-ene | +1 | -106 |
| But-1-ene | -6 | < -195 |
| 2-Methylpropene | -7 | -141 |
Let’s consider the designation of these isomers:
i) The isomer of b.p. -70C contains a branched chain because on hydrogenation, it yields isobutane. Thus, it has the structure designated isobutylene.
ii) The other three isomers have straight –chain skeleton because on hydrogenation, they all yield the same compound, n-butane. Through a technique called ozonolysis, one can break an alkene molecule apart at the double bond, and from the fragments obtained deduce the position of the double bond in the molecule.
Through this procedure it was found that the isomer of b.p. -60C carries the double bond at the end of the chain. Thus it has the structure designated but-1-ene.
Through the same procedure it was found that both remaining isomers carry the double bond in the middle of the chain as both yielded the same mixture of products.
From the products of hydrogenation and the products of cleavage, we conclude that the butylenes of b.p. + 10C and + 40C both have the structure designated but-2-ene.
However, the differences in boiling point, melting point, and other physical properties clearly show that they are not the same compound, that is, they are isomers.
Origin of geometrical isomerism
To understand the nature of isomerism that gives rise to two but-2-enes, one needs to examine more closely
a) the structure of alkenes and
b) the nature of the carbon-carbon double bond.
Ethylene is a flat molecule as a result of the geometric arrangement of the hybrid orbitals, and the overlap giving rise to the -bond.
For the same reasons, the two doubly bonded carbons and the four atoms directly attached to them all lie in the same plane, that is, a portion of every alkene is always flat.
If one examines the flat portion more closely, one finds that there are two quite different ways, I and II, in which the atoms (or groups) directly attached to the doubly bonded carbons can be arranged.
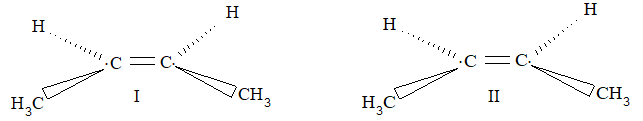
Besides these two arrangements, the infinite number of possibilities arise from rotation about the single bonds!
In one of the arrangements (I), the two methyl groups (or two H atoms) lie on the same side of the molecule whereas in the other arrangement (II) they lie on opposite sides of the molecule.
Can one isolate two isomeric but-2-enes corresponding to these two different arrangements or are they two readily interconvertible like the conformations of alkanes?
Rotation of one part of the molecule about the carbon-carbon double bond can convert I into II. Thus, the amount of energy required for this rotation will decide the possibility of isolating isomers.
Overlap of the p-orbitals that lie above and below the plane of the bonds (orbitals) leads to the formation of the bond. For the maximum possible strength of the bond, the overlapping p-orbitals must be exactly parallel to each other.
The molecule must be twisted to move from I to II or the other way. Consequently, the p orbitals are no longer parallel. Thus rotation prevents overlap of the p-orbitals and ultimately breaks the bond.
About 70 kcal of energy is required to break the bond. At room temperature, the rate of this interconversion (III or III) is extremely small because an insignificant proportion of molecular collisions possess this required energy.
Thus, there is hindered rotation about the carbon-carbon double bond because of this 70 kcal energy barrier. Two isomeric but-2-enes of b.p. + 40C and b.p. + 10C can thus be isolated because of this hindered rotation.
When two atoms are linked by a single bond the barrier to free rotation about this bond is quite small.
When two atoms are multiply bonded then the barrier to free rotation is very much higher and where such compounds exist in two different arrangements the passage from one to the other requires so much energy that each isomer has a stable and independent existence.
In short, free rotation about a carbon to carbon double bond can’t occur without description of the pi bond.
The two isomeric but-2-enes are actually stereoisomers because
a) they are like one another with respect to connectivity of atoms (i.e. which atoms are attached to which other atoms).
b) they differ from one another only in the way the atoms are oriented in space.
They are not enantiomers because they are not nonsuperposable mirror images of each other. They are called diastereomers, the stereoisomers that are not mirror images of each other. Diastereomers which may or may not be optically active and owe their existence to hindered rotation about double bonds (or cyclic structures) are called geometric isomers.
The isomeric but-2-enes are diastereomers, and more accurately, geometric isomers.
In optical isomerism, all (or at least some) of the isomers are optically active.
Optical activity is not a criterion for geometrical isomerism but is (by definition) a criterion for optical isomerism.
The space arrangement of atoms that characterizes a particular (configurational) stereoisomer is called its configuration.
The configurations of the isomeric but-2-enes are the arrangements I and II. Traditionally the two configurations are differentiated in their names by the prefixes cis– (Latin: on this side) and trans-(Latin: across).
The cis-isomer is the one which has one or two pairs of identical atoms (or groups) on the same side of the double bond; in the trans-isomer the identical atoms (or groups) are on opposite sides of the double bond.
For the arrangements I and II, the prefixes cis- and trans- indicate that the methyl groups are on the same side or on opposite sides of the double bond (or molecule).
Measurement of dipole moment frequently enables us positively to designate a particular isomer as cis or trans.
Through dipole moment measurements, the isomer of higher b.p. + 40C has been assigned the cis configuration, and the isomer of lower b.pt. + 10C has born assigned the trans configuration.
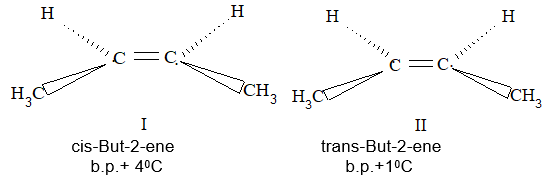
In the trans isomer, the methyl groups are well separated, however, in the cis isomer the methyls are thrown closely enough together to cause crowding. This makes the cis isomer to be less stable than the trans.
Several types of compounds are capable of exhibiting geometrical isomerism, but right now we have focused the one in which molecule contains a double bond.
There is hindered rotation of the molecule about every carbon-carbon double bond, but geometric isomerism is not possible in every alkene.
Any carbon-carbon double bond gives rise to geometric isomerism provided a certain relationship among the atoms (or groups) attached to the doubly bonded carbons is satisfied.
If the alkene is designated as abC = Ccd then it will exist in two diastereomeric forms so long as a b and c d, that is, each of the doubly bonded carbons should be directly attached to two different atoms (or groups).
It does not matter whether a and / or b are the same as c and / or d.
Geometrical isomerism can’t exist in alkenes if either carbon carries two identical groups.
Thus, double bond is not the only condition for geometrical isomerism; the groups attached to the unsaturated carbon atoms must also be taken into consideration.
Illustration 56: Examine the following arrangements:
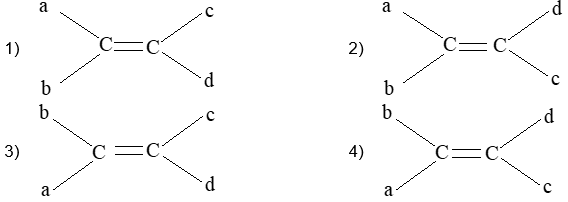
How many different compounds are represented?
Solution: The symbols represent atoms which lie in one plane and that rotation about C = C bond only occurs under special circumstances which can be neglected for the present.
These four arrangements represent only two different compounds. Arrangement (1) is the same as (4) and arrangements (2) and (3) are also identical. If (3) or (4) is turned over it is seen to be the same as (2) or (1) respectively.
Arrangements (1) and (2), however, are different. In (1) the atoms (or groups) a and c are on one side of the double bond and the atoms (or groups) b and d are on the other side.
In arrangement (2) a and d lie on one side whereas b and c on the other.
Illustration 57: Which of the arrangements 3 to 6 represent compounds able to show geometric isomerism?
Formulate the stereoisomer in these cases and state whether the stereoisomeric pair is correctly described as enantiomeric or diastereomeric.
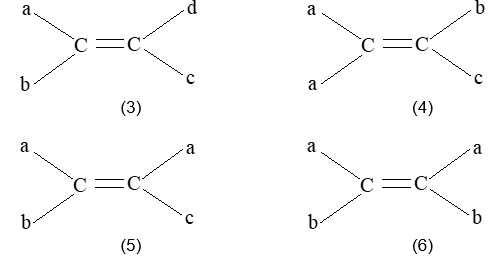
Solution: Inspection of these formulae shows that the compound of arrangement (4) does not show geometric isomerism, because one olefinic carbon atom carries two identical atoms (or groups).
The remainder will have diastereomers represented by (3’), (5’), and (6’)
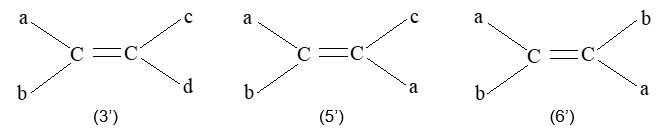
The phenomenon of geometric isomerism is a general one and can be found in any class of compounds that contain carbon-carbon double bonds (or even double bonds of other kinds). The two terms conformation and configuration often lead to confusion, since both are concerned with spatial arrangement.
They may be differentiated as follows: change from one configuration to another involves breaking and making of bonds, whereas change from one conformation to another involves rotations (or twisting) about a single bond of one part of the molecule with respect to another part.
Let’s look again at the maleic/fumaric and oleic acid pairs. Now, it is easy to formulate arrangements to correspond to the two pairs of compounds:
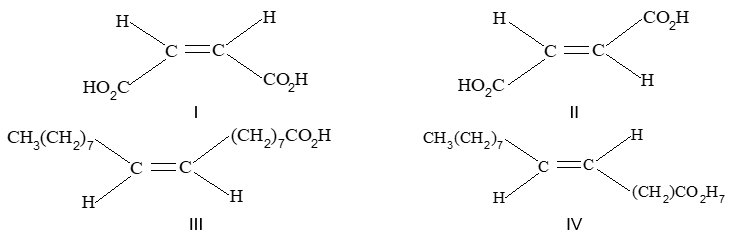
Arrangements I and III represent cis-isomers and II and IV represent trans-isomers. This system fails when there are no identical groups and a more general system of nomenclature is then applied.
Which compound has which arrangement?
Ans. The allocation of structures I and II to the maleic/fumaric acid pair is based on the following observations
1) Maleic acid (mp 1300C) loses water when heated to ~1400 to form an anhydride (C4H2O3) which on hydration reforms maleic acid.
2) Fumaric acid (mp 2700) is more stable on heating and loses water only at ~ 2750C to form an anhydride (C4H2O3) which is identical with that from maleic acid and which on hydration gives not fumaric acid but maleic acid. That is to say : maleic acid readily forms an anhydride on heating, fumaric acid forms an anhydride only with difficulty and then it is maleic anhydride.
An assignment of arrangement can now be made on the assumption that in the cyclic anhydride the two carbonyl groups must be on the same side of the alkene double bond system. The alternative would be a highly strained system. Hence maleic acid has its two carbonyl groups on the same side and is the cis-isomer and fumaric acid is the trans-isomer.
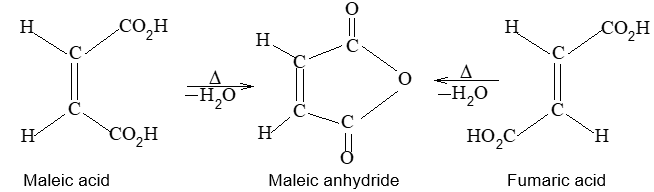
This type of argument must be undertaken with care, especially if the mechanism of the reaction under consideration is not fully known.
Though originally thought to be the trans-isomer, oleic acid is now known to have the cis-configuration on the basis of several different lines of argument. One of these involves the use of stereospecific reactions (i.e., reactions of known stereochemical pattern).
The suitable alkynoic acid (which exists in only a single isomeric form) can be partially reduced to oleic or elaidic acids under reaction conditions now known to furnish a particular stereoisomer:
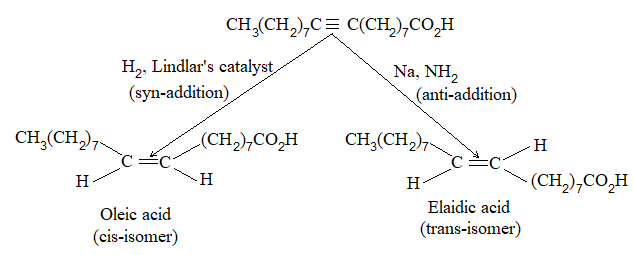
What happens when the terms cis and trans cannot be used? The symbols (E) and (Z).
The terms cis and trans, used to designate the stereochemistry of alkene diastereomers, are unambiguous only when applied to disubstituted alkenes.
If the alkene is trisubstituted or tetrasubstituted, the terms cis and trans are ambiguous and hence do not apply at all.
Consider the following alkene as an example.
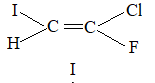
It is impossible to decide whether (I) is cis or trans because no two atoms are identical.
Difficulty in assigning the terms cis and trans arises when there is no pair of identical groups.
This problem is now solved by an alternative description which can always be applied. This system, called the (E)–(Z) system that works in all cases and applies to alkene diastereoisomers of all types, is based on the priorities of atoms (or groups) in the Cahn-Ingold-Prelog convention.
The new terms (E) and (Z) replace the older terms though it seems likely that cis and trans will continue to be used to describe alkene diastereomers whenever possible.
Under the new (E)-(Z) system,
Step 1 : Examine the two atoms (or groups) directly attached to one of the doubly bonded carbon atoms and decide which one has higher priority. In other words, arrange the two atoms (or groups) in their Cahn-Ingold-Prelog sequence. Then repeat that operation at the other doubly bonded carbon:
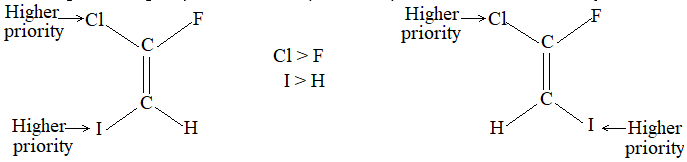
Step 2 : Take the atom (or group) of higher priority on the one doubly bonded carbon and compare it with the atom (or group) of higher priority on the other doubly bonded carbon.
Step 3 : Tell whether they are on the same side of the molecule or on opposite sides. If the two atoms (or groups) of higher priority are on the same side of the double bond, the alkene is designated (Z) [from the German word zusammen, meaning together]. If the two atoms (or groups) of higher priority are on opposite sides of the double bond, the alkene is designated (E) [from the German word entgegen, meaning opposite].
The appropriate letter then becomes part of the name of such an alkene. The following examples illustrate this
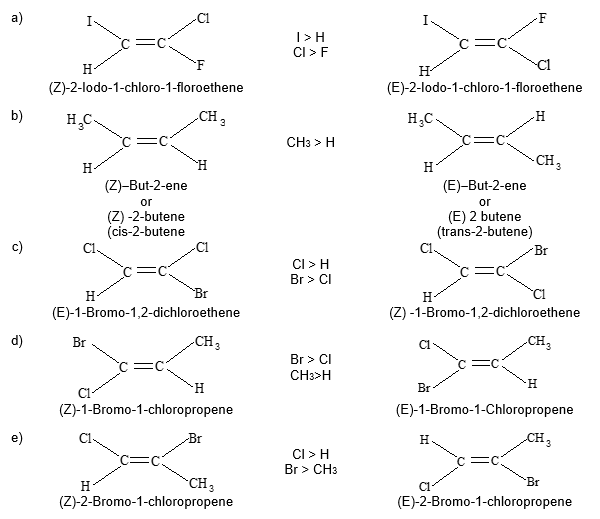
Illustration 58: Write configurations for (i) maleic and fumaric acids and (ii) oleic and elaidic acids and designate each as (E) or (Z) isomers.
Solution: Under the new system the two ligands (atoms or groups) attached to each olefinic carbon atom are put in order of precedence by application of the Sequence Rules and the symbols (E) and (Z) are then used to describe those diastereomers in which the ligands of higher precedence are on the opposite or the same side.
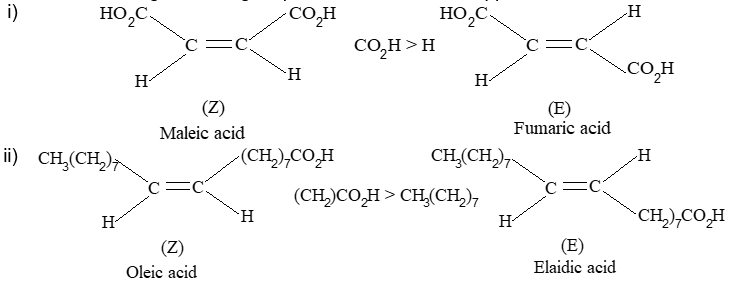
Illustration 59: Allocate the symbols (E) or (Z) to each of the following:
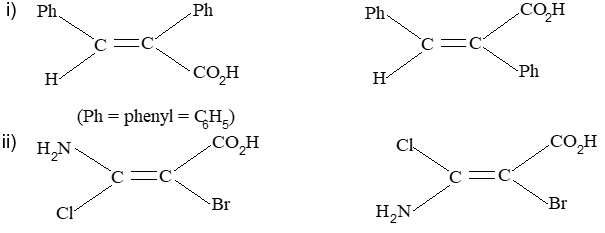
Solution: (i) Since Ph > H and CO2H > Ph

In many cases, but by no means all, the old term cis corresponds to (Z) and the term trans corresponds to (E). This correspondence should never be used without checking. The above case is an example where the simple correspondence between cis and (Z) does not apply.
ii) since Cl > N and Br > C

The properties of geometric isomers
Geometric isomers exhibit the same relationship (in chemical and physical properties) to each other as do the other diastereomers:
i) They show similar chemical properties because they contain the same functional group. Since their arrangements are neither identical nor mirror images, their chemical properties are not identical. Therefore, they react with the same reagents, but at different rates.
In biological systems, geometric isomers can vary widely in their chemical behavior.
ii) They have different physical properties: different melting points, boiling points, refractive indicies, solubilities, densities, and so on. On the basis of these different physical properties, they can be distinguished from each other and identified. Moreover, on the basis of these differences in physical properties they can be separated.
Is geometric isomerism confined to C = C compounds?
One or both carbon atoms can be replaced by another doubly bonded atom. Most commonly this is nitrogen in which one sp2 hybrid orbital contains only a lone pair. Thus, oximes and azo compounds can exist in diastereomeric forms:
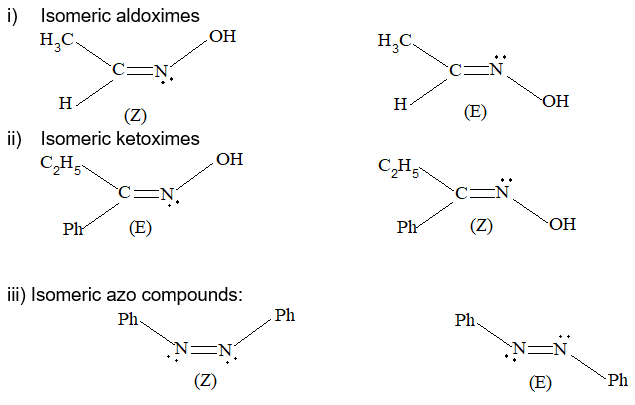
The lone pair comes below H in precedence order.
Symmetrical carbonyl compounds, having identical atoms (or groups) attached to the >C = O group, form oximes which can’t exist as geometric isomers. The only aldehyde to meet this requirement is formaldehyde (H2C = O) but there are many symmetrical ketones of which acetone (Me2C = O) is the simplest.
Illustration 60: Formulate the (Z) isomers of the following compounds:
(i) But-2-enoic acid
(ii) 4, 4¢-Diaminoazobenzene
(iii) 1, 2- Difloroethene
(iv) 2-Ethyl-3-methylpent-2-enoic acid
(v) 3, 3-Diphenylpropenoic acid
Solution: So for we have designated diastereomers as (E) or (Z). It is also necessary to be able to write a configuration from a name. First write the structure and then orient the ligands according to their priorities.
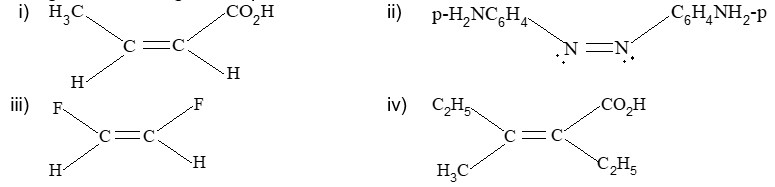
v) This compound, Ph2C = CHCO2H, does not exist in stereoisomeric forms!
Geometric isomerism in cyclic compounds
Geometric isomerism occurs in any molecule in which four suitable groups (ligands) are held in one plane by some element of rigidity within the molecule.
So far our compounds have involved a double bond such as C = C, C = N, or N = N to achieve this, but it also happens in cyclic compounds in which the ring (though having some flexibility) nevertheless restricts the freedom of movement of groups attached to it.
In the following illustration the cyclohexane system is treated as planar. This is not so, but its non-planarity does not weaken the argument. Rather, it is simpler at this stage to accept this slight deception.
Cyclohexane-1,4- dicarboxylic acid can be written as.
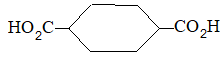
With the understanding that all the carbon atoms carry as many H atoms as is required for them to have the usual tetravalency.
However, this compound exists in two forms (m.p. 1620 and 3000) of which only the lower melting isomer readily forms an anhydride. When hydrated, the anhydride furnishes the original low melting dibasic acid.
This is another typical example of geometric isomerism. The cyclohexane ring can be regarded as planar and the four groups (H, CO2H, H, CO2H) attached to C1 and C4 lie in one plane. The two possible arrangements are shown:
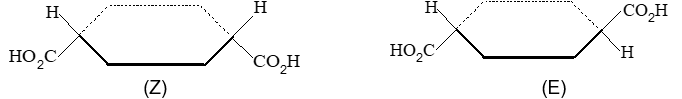
By analogy with maleic acid it is expected that anhydride formation will occur most readily when the two CO2H groups are closest together, i.e., the (Z) isomer.
The above structures contain 3 types of lines which are used in a standard way when tying to indicate 3-dimensional models in a 2-dimentional picture. Light lines ____ are interpreted as being in the plane of the paper, heavy lines ___ project forward from this paper toward the reader, and dashed lines —– or —– project backward from the paper away from the reader.
What are the possibilities of stereoisomerism in compounds with more than one C = C group?
The possibilities of stereoisomerism increase when the molecule contains more than one C=C (or C=N, etc.) group. Each double bond can give rise to an independent set of isomers except that in certain symmetrical molecules some isomers may be identical.
Thus the unsymmetrical diene, octa-2,5-diene exists in four stereoisomeric forms and the symmetrical hepta -2, 5 diene in only three:
i) (Octa-2, 5-diene)
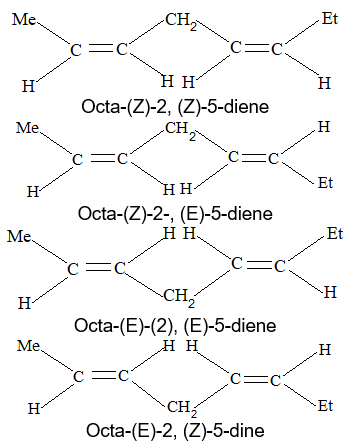
ii) (hepta-2,5-diene)symmetrical diene.
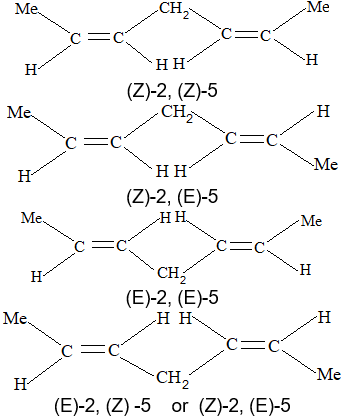
Notice that the second and fourth arrangements are the same.
Illustration 61: The two isomers of 1, 2-dichloroethene have dipole moments of 0.00 and 1.89 D. Formulate each of these and relate them with their dipole moment.
Solution: Dipole moments are very satisfactory for structural assignments.
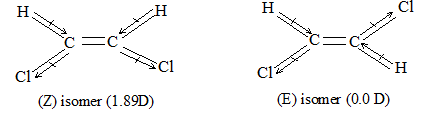
The dipole moment in these molecules is the vector sum of the bond dipoles. In the (E) isomer these cancel so that it has a zero dipole moment.
Illustration 62: An acid of structure Cl3CCH = CHCO2H can be reduced to CH3CH = CHCO2H and hydrolysed to fumaric acid. What is the configuration of each of the acids formulated?
Solution: If it is assumed that these changes:
occur without any change in configuration of the alkene then all the compounds will have the same configuration as fumaric acid i.e. trans or (E).

Exercise 1: (i) How many isomers are possible for C7H8O?
(A) 5 (B) 3 (C) 4 (D) 2
(ii) Which of the following compounds can exhibit both geometrical isomerism and enantiomerism?
(iii) The two configurations given below are

(A) enantiomers
(B) diastereomers
(C) stereoisomers
(D) both (A) and (C)
(iv) The number of possible enantiomeric pairs that can be produced during monochlorination of 2-methylbutane is
(A) 2 (B) 3 (C) 4 (D) 1
(v) Tautomerism is not exhibited by
(vi) An enantiomerically pure acid is treated with racemic mixture of an alcohol having one chiral carbon. The ester formed will be
(A) optically active mixture
(B) pure enantiomer
(C) meso compound
(D) racemic mixture
Can geometric isomers be interconversed?
Early in the discussion, it was pointed out that geometric isomerism is found among alkenes and certain related nitrogen-containing compounds because the double bond provides a considerable barrier to rotation about its axis.
The conversion of cis- to trans- isomers or the reverse process – known as stereomutation – can be effected in two ways:
i) either by a series of chemical reactions by which the alkene is converted to the compounds from which the alkene can be regenerated as the alternative isomer, or
ii) by a reversible procedure converting the double bond compound to a single bond compound in which free rotation is possible before regeneration of the alkene as a mixture of the two isomeric forms.
This reversible process may be effected by vigorous heating, by photolysis, or, usually under milder conditions, by a free radical species such as those resulting from iodine, thiols or other sulphur compounds, or nitrogen tetroxide: R’
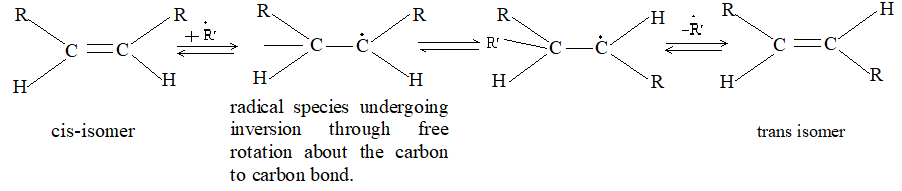
The product is eventually an equilibrium mixture of the two isomers. The trans-isomer, being the more stable, usually predominates but pure compounds have to be separated from the reaction mixture.
Stereospeceific and stereoselective reactions
A reaction is stereospecific, when a particular stereoisomer of the reactant reacts in such a way that it gives a specific stereoisomer of the product.
The anti addition of a halogen to an alkene is a typical example of a stereospecific reaction:
Reaction 1 : When trans-but-2-ene adds bromine, the product is the meso compound, (2R, 3S)-2, 3-dibromobutane.
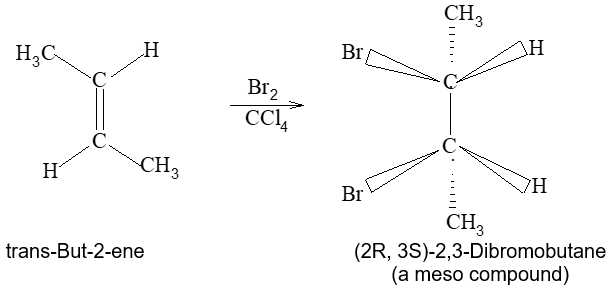
Reaction 2: When cis-But-2-ene adds bromine, the product is a racemic form of (2R, 3R)- 2, 3- dibromobutane and (2S, 3S)-2,3-dibromobutane.
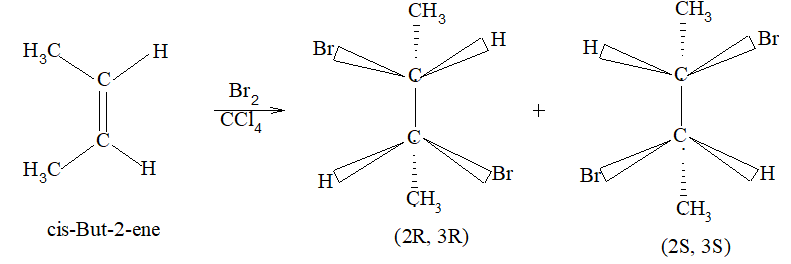
The reactants cis-but-2-ene and trans-but-2-ene are stereoisomers and more specifically, they are diastereomers.
The product of reaction 1 is a meso compound. It is a stereoisomer of both the products (the enantiomeric 2, 3 dibromobutanes) of the reaction 2. Thus, by definition, both reactions are stereospecific as one stereoisomeric form of the reactant (e.g. trans-but-2ene) gives one product (the meso compound) whereas the other stereoisomeric form of the reactant (cis-but-2-ene) gives a stereoisomerically different product (the enantiomers).
One can better understand the results of these two reactions if one examines their mechanism. A reaction is stereoselective when the reactant is not essentially stereoisomeric but produces predominantly or exclusively one stereoisomeric form of the product. The anti (or syn) addition of hydrogen to but-2-yne is a typical example of a stereoselective reaction:
Reaction 1:
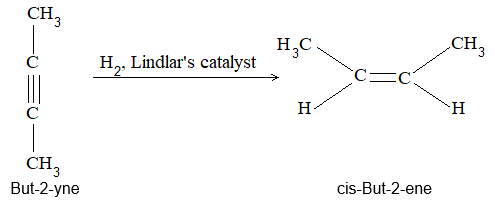
Reaction 2:
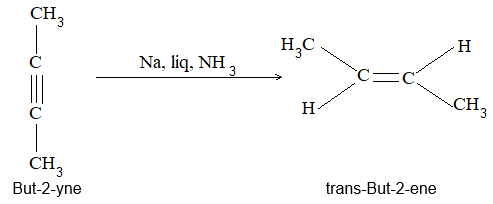
Note the difference between setereoselective and stereospecific:
A stereospecific reaction is one that produces predominantly or exclusively one stereoisomer of the product when a specific stereoisomer of the reactant is used.
All stereospecific reactions are stereoselective, but the reverse is not essentially true.

Exercise 2: (i) How many cyclic isomers of C5H10 are possible?
(A) 4 (B) 3 (C) 2 (D) 5
(ii) Hydrogenation of the following compound
in the presence of poisoned palladium catalyst gives
(A) a racemic mixture
(B) a diastereomeric mixture
(C) an optically active compound
(D) an optically inactive compound
(iii) The number of isomers for the compound with molecular formula C2BrClFl is
(A) 3 (B) 4 (C) 5 (D) 6
(iv) The configurations given below are
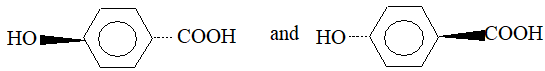
(A) enantiomers
(B) identical
(C) stereoisomers
(D) diastereomers
(v) The total number of chiral compounds obtained on monochlorination of 2-methylbutane is
(A) 2 (B) 4 (C) 6 (D) 8
(vi) Correct designation of the following configuration
is
(A) 1S, 2S (B) 1S, 2R (C) 1R, 2S (D) 1R, 2R
Exercise 3: (i) Consider the following configuration
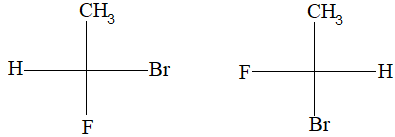
they are
(A) enantiomers
(B) diasteromers
(C) conformational isomers
(D) identical compounds
(iii) Number of primary amines of the formula, C4H11N, is
(A) 1 (B) 2 (C) 3 (D) 4
(iv) Match the list I and list II and select the correct answer using the code given below the lists
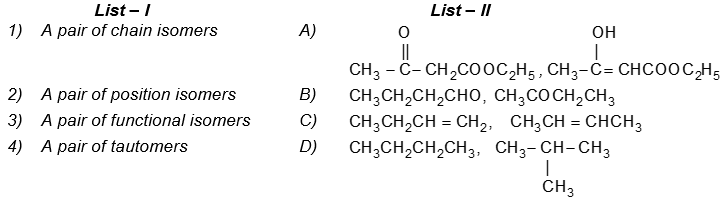
Codes :
(A) 1-A, 2-B, 3-C, 4-D
(B) 1-D, 2-C, 3-B, 4-A
(C) 1-B, 2-D, 3-A, 4-C
(D) 1-C, 2-A, 3-D, 4-B
(v)
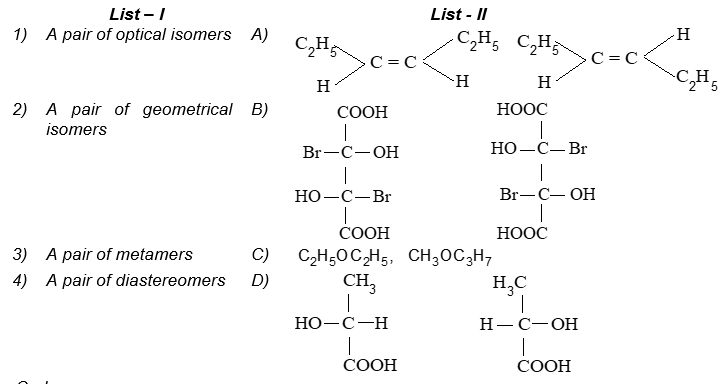
Codes:
(A) 1-D, 2-A, 3-C, 4-B
(B) 1-A, 2-B, 3-D, 4-C
(C) 1-C, 2-D, 3-B, 4-A
(D) 1-B, 2-C, 3-A, 4-D
Exercise 4:
| (i) | List – I | List – II | |
| 1) | Conformation | A) | Polarimeter |
| 2) | Meso form | B) | Optically inactive |
| 3) | Specific rotation | C) | Eclipsed and staggered forms |
| 4) | Nonsuperposable mirror images | D) | Enantiomers |
Codes:
(A) 1-A, 2-D, 3-B, 4-C
(B) 1-D, 2-A, 3-C, 4-B
(C) 1-B, 2-C, 3-D, 4-A
(D) 1-C, 2-B, 3-A, 4-D
(ii) Which of the following structures cannot exhibit geometrical isomerism?
(A)
(B)
(C)
(D)
(iii) Which of the following configurations are designated as (Z)?
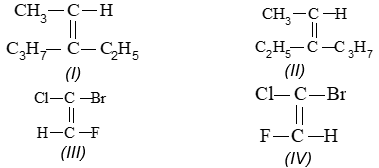
(A) (I), (III)
(B) (II), (IV)
(C) (III), (II)
(D) (IV), (I)
(iv) Keto-enol tautomerism is observed in
I) C6H5 – CHO II) C6H5COCH3 III) C6H5COC6H5 IV) C6H5COCH2COCH3
(A) II, III, IV
(B) III, IV
(C) II, IV
(D) II, III
ANALYSIS OF ORGANIC COMPOUNDS
Purification of Organic Compounds:
Organic compounds prepared (synthesized) in laboratory or extracted from nature are mostly impure. To separate the desired compound/products from others (impurities), their physical and/or chemical properties are explored. The point of difference in any of these properties leads to the path of their separation and hence purification.
In general, we may use separation & purification synonymously but, in fact, separation is the obtaining of each component present in the mixture (often known to us) while purification employs obtaining the desired and generally only one component from the impurities (often unknown to us).
The most common methods employed are: sublimation, crystallization, distillation, differential extractions, and chromatography.
1) Sublimation (for solids)
The solid substances which vaporize on heating without melting (sublimable substances) are separated by this method from those impurities which don’t sublime. The vapours of only the sublimate obtained by heating the impure substance are collected and when cooled solidify without appearance of the liquid phase and giving the pure compound.
Camphor, naphthalene, benzoic acid, anthracene, ammonium chloride, iodine etc. can be purified by this method.
2) Crystallization (for solids)
The method is based upon the solubility differences of the compounds. It is the most convenient method for purification of solid compounds. Whenever a crystal is formed, it leaves impurities into the solution allowing only the ions of its type to grow on its surface. For this purpose suitable solvents are to be selected for which the compound is less soluble and impurities are more soluble. So that impurities may remain in the solution and the compound crystallizes out.
Depending on the degree/purity of separation, it could be classified into:
a) Simple crystallization Impurities of upto 5% are removed using this method.
The impure compound is dissolved in minimum amount of solvent (heated if required; but it should not change the chemical structure or reactivity of compound). The mixture is then filtered and kept for crystallization to set in. The crystals are separated after sometime from the left solution (called mother liquor containing impurities).
e.g., sugar + NaCl mixture: NaCl can be crystallized using hot ethanol (as NaCl is less soluble in alcohol in comparison to sugar).
benzoic acid + naphthalene : benzoic acid dissolves in hot water, naphthalene doesn’t.
If the compound is highly soluble in a solvent but little soluble in another, the mixture of the two solvents can be used satisfactorily for purification.
The impurities that impart colour to the solution should be removed beforehand by adsorbing them over activated charcoal.
b) Fractional crystallization
Separation of two or more compounds from a mixture by repeated crystallization processes is called fractional crystallization. It is used in the cases where the impurities have nearly the same solubilities to that of the compound for the given solvent. Each crystallization retains some impurities with the compound every time. After separation and repeated crystallizations, they become almost pure.
3) Distillation (for volatile liquids)
It’s the boiling of a liquid to vaporize the more volatile component followed by cooling to liquefy it and thus obtaining in the pure form as the impurities remain either unvolatite or have more bp & hence the desired compound can be separated from the other one.
The process is based upon the difference in boiling points (bp’s) of the liquids to be separated.

a) Simple distillation
It’s used to separate volatile liquids from non-volatile solids or the two liquids having a larger difference in their bp’s.
The mixture on heating produces vapours of more volatile liquids. These vapours are collected & cooled to condense, giving the liquid in pure form.
e.g., (i) Ethanol from ethanolic inorganic chlorides (LiCl, NaCl, KCl, BeCl2 etc.) easily be distilled off to give pure alcohol.
(ii) Chloroform (610C) and aniline (1840C) be separated using distillation (Chloroform will distill out and collected in the receiver leaving the aniline back in the distillation flask).
b) Fractional distillation
When bp’s of two liquids differ only by 10-150C, the vapours of the liquid having high bp also begins to come out at the bp of the low boiling liquid. By simple distillation both compounds will come off and condense together; no separation will take place.
The separation is hence achieved by using a fractionating column, which is placed over the mouth of round bottom flask (RBF) or boiling container. Fractionating column is a tall (vertical) column having a large surface area allowing the maximum vapours to cool & condense. This sends the less volatile compound back into the RBF by condensing the vapours of high boiling liquid, which start to evaporate at the bp of low boiling solid. The mixture of vapours enters it and the one having low volatility (higher bp) condenses to send them back to the RBF. The vapours going to the consendor are only with (of) high volatility. The fractionating columns are available in various sizes and designs to meet with the requirement of desired separation.
Still, the distillate (liquid obtained in the receiver after distillation) may contain some impurities. The process is repeated in such a case to separate them completely.
e.g. Fractional distillation of crude oil in petrochemistry is of great importance to yield gasoline, kerosene, diesel, lubricating oil etc.
c) Azeotropic distillation
Azeotrops are the constant boiling mixture which can’t be separated by even fractional distillation, as both the components distill together in the same composition. e.g., 95.87 part ethanol and 4.13 part water (by weight) boils at 78.10C.
In azeotropic distillation a third component is added to the mixture. This component has depressing effect on either of the liquids. As a result, the effective bp of one component is decreased, so it distills earlier.
For ethanol water azeotrop compounds with lower bp than water (benzene, ether, CCl4 etc.) decrease the bp of ethanol, while those with high bp (glycerol, glycol etc.) decrease the bp of water.
d) Vacuum distillation
It is used for the liquids with high bp and liquids which decompose at or below their bp. Reducing pressure by vacuum pump in the distillation set-up lowers down the bp of a liquid. The liquid now starts to boil at lower temperature than its bp without decomposing and can easily be purified.
In fact, the pressure is decreased upto the extent that liquid starts to boil at a temperature at which it doesn’t decompose.
e.g. (i) Glycerol decomposes at its bp (2900C). It can be distilled at 1800 without decomposition at 12 mm Hg.
(ii) Sugarcane juice in sugar industry is concentrated using the same method. (Fuel economy)
e) Steam distillation
The liquids which are water immiscible & steam volatile are purified by steam distillation. Such compounds should possess high vapour pressure at bp of water (10–15mm-Hg at 1000C).
If Pw = vapour pressure of water
PL = vapour pressure of liquid and
PT = vapour pressure of the mixture of vapours,
PW + PL = 760mm-Hg (PT)
PL = 760 – PW (PL < 760)
The liquid will know vaporize at a temp. lower than its actual bp.
Water vapours are passed through the mixture to be separated. The vapour miscible component vaporizes leaving the others (impurities or components) into mixture itself. These vapours on cooling give water and the immiscible liquid, which can be separated using separating funnel.
Proportion of organic substance that distills over with the steam is related to its vapour pressure as well as molecular weight.
w1 & w2 masses of water and the organic compound respectively, similarly
p1 & p2 vapour pressures at the temperature of distillation, and
m1 & m2 molar masses
e.g., Aniline (bp 1800C ) is purified by steam distillation at 98.50C in the presence of steam. Essential oils, o-nitrophenol, o-hydroxyacetephenone, salicylaldehyde, nitrobenzene, chlorobenzene, naphthalene etc. are also purified by this method.
4) Differential extractions (solvent extraction)
Solvent extraction is used to extract traces of organic compounds from aqueous solutions. An organic solvent, immiscible with H2O and having more solubility of the organic compound in it is used for the purpose. To the aqueous solution having the organic compound, an organic solvent is added in the separating funnel. The compound, which is more soluble in organic solvent, passes into it. The two layers (aqueous and organics) are separated. Organic solvent is distilled off to obtain the pure compound.
If the compound is less soluble in organic solvent, a large amount of solvent will be required; continuous extraction technique is used in such cases where, the same solvent is repeatedly used. Multiple extractions are more efficient than single extraction.
e.g., if 200 ml organic solvent is to be used, it will give more amount of separated compound if used in aliquots of 20 ml each for 10 times in comparison to 200 mL 1 time.
Aqueous solution of benzoic acid can be extracted with benzene.
I2 can be extracted from dil. aq. solution (slightly soluble in water) using CCl4.
5) Chromatography
(Greak, chroma = colour, graphein = to write)
Since, for the first time it was used for the separation of coloured compounds (chlorophylls) from plants by a Russian botanist Mikhail Tswett (1903), hence assigned the name.
The objectives of chromatography are:
To separate mixtures into compounds (Separation)
To purify them (Purification)
To check their presence/identity (Identification)
It is efficient for even very small concentrations (upto mg L–1).
The mixture is applied onto a stationary phase (adsorbent). Suitable solvents or a mixture of solvents (mobile phase) is passed over it slowly. The components of the mixture get separated gradually one after another in the order of their degree of interaction with adsorbent and mobile phase.
Broadly chromatography can divided into:
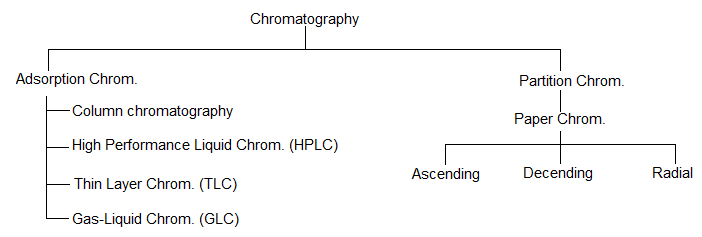
| Type of chromatography | Stationary phase | Mobile phase | Uses |
| Column Chrom. | Solid | Liquid | Large scale separation |
| HPLC | Solid | Liquid | Qualitative & quantitative analyses |
| TLC | Liquid | Gas | Quantitative analysis |
| GLC | Liquid | Gas | Qualitative & quantitative |
| Paper | Liquid | Liquid | Qualitative & quantitative analyses of polar organic & inorganic compounds |
a) Column Chromatography
The mixture to be separated is made to absorb over a column of adsorbent (stationary phase), packed in a glass tube. Some adsorbents are alumina, silica gel, calcium carbonate, magnesium oxide, cellulose paper etc.
Appropriate solvent or mixture of solvents (mobile phase called eluent) is allowed to flow down the adsorbed mixture slowly.
The combination of degree of adsorption of a compound onto adsorbent and its solubility in the element makes them separated and purified completely. The weakly adsorbed compound will move down the column (elute) more rapidly than those adsorbed strongly. More soluble compound in the eluent will move down faster than the others.
b) Thin Layer Chromatography
In TLC an adsorbent is spread in the form of very thin layer (~0.2 mm) supported by a glass plate or metal foil (generally aluminium) and is called TLC plate or chromaplate.
The mixture to be analyzed is taken in solution form and applied as a dot at one end of the TLC plate. The plate is then put into a closed jar (chromatography chamber) having some eluent in it. As the eluent rises up, the more soluble and poorly adsorbed component moves up along with the solvent, followed by the others in the order of their interactions.
The relative adsorption of each component is given in the terms of retardation or retention factor or value
Coloured compounds give visible spots on the TLC plate. The spots of colourless compounds are identified by either of following methods:
Putting the plate under U.V. light where it may fluoresce
Placing it in I2 jar, where some compounds give brown spots due to adsorption of I2 By spraying the plate with suitable reagent to produce coloured spots (e.g., amino acid on spraying with ninhydrin solution)
Partition Chromatography
The principle of partition chromatography is the continuous differential partitioning of components of a mixture between stationary and mobile phases.
In Paper chromatography a special paper is used called chromatography paper, which contains water trapped in it. This water works as stationary phase and continuous partition between water and organic solvent used takes place during the chromatographic separation. The paper so obtained having coloured bands is called chromatogram.
Depending upon the method of development of chromatogram it can be ascending, descending or radial (circular) chromatography.
Exercise 5: (i) Naphthalene can be purified by
(A) sublimation
(B) crystallization
(C) distillation
(D) extraction with solvent
(ii) The separation of mixture of two compounds by chromatographic technique is based upon
(A) differential solubilities
(B) different densities
(C) different absorption
(D) differential adsorption
(iii) Steam distillation is applied for the separation of those compounds which are
(A) steam volatile and soluble in water
(B) steam volatile and decompose in water
(C) steam volatile and insoluble in water
(D) capable of chemical reaction with steam
(iv) The process of differential extraction is based upon
(A) different solubilities
(B) different molecular masses
(C) different boiling points
(D) different chemical properties
Exercise 6: (i) Which of the following method of separation can be applied to the mixture of liquids having different boiling points?
(A) solvent extraction
(B) differential crystallization
(C) fractional distillation
(D) steam distillation
(ii) Two solids A and B have appreciable different solubilities in water but their melting points are very close. The mixture of A and B can be separated by
(A) sublimation
(B) fractional crystallization
(C) distillation
(D) specific method
Qualitative Analysis
Organic compounds have carbon and hydrogen, in most cases. Other elements present in organic compounds are oxygen, nitrogen, halogen, sulphur and sometimes phosphorus.
Detection of Carbon and Hydrogen
Heating the compound with CuO (Cupric oxide) decomposes and then oxidizes the organic compound Carbon of organic compound is oxidized to CO2, which is tested by lime water, as it turns turbid.
Hydrogen is converted into H2O which turns anhydrous CuSO4 blue due to complexation.
Detection of other elements
N, S, X & P are detected by Lassaigne’s test.
Elements are converted into ionic form by fusing the compound with sodium metal.
In an ignition tube small amounts of compound are put in the form of layers between Na, followed by several such other layers. This is heated gently, then upto red hot, followed by breaking it into a petridish having distilled water. Depending on the elements present in the compound the following changes take place:
(if nitrogen is present, carbon from org compound)
(if sulphur is present)
(if halogen is present)
The above solution is filtered to give a clear solution called sodium fusion extract or simply sodium extract.
Soda extract is used in inorganic qualitative analysis where the inorganic mixture is fused with Na2CO3.
Fusion should be complete else left Na will react with water to give NaOH.
The fusion mixture should be concentrated enough otherwise it will not respond to any test. Li & K can’t be used in place of Na; Li reacts slowly & gives covalent compounds while K reacts violently.
Detection of Nitrogen
Sodium extract is boiled with freshly prepared FeSO4 and then acidified with conc. H2SO4. Prussian blue colour confirms the presence of nitrogen.
Freshly prepared is required as it converts into on standing.
Diazo compounds don’t respond to this test, as on heating N2 is evolved without any chances of formation of NaCN.
Prussian blue sometimes turns green either due to small amount of N or yellow colour of FeCl3.
Detection of Sulphur
(a) Sodium fusion extract is acidified with CH3COOH followed by addition of the lead acetate solution to it; a black precipitate of PbS indicates the presence of sulphur.
(b) Treating sodium extract with sodium nitroprusside gives violet colour in case of S compounds.
Detection of N & S both in same compound
Sodium extract on treating with FeCl3 gives blood red colour & not the Prussian blue if nitrogen and sulphur both are present in the organic compound.
However, if excess of Na metal is used NaCNS is decomposed into NaCN & Na2S.
Detection of Halogens
Sodium extract is acidified with nitric acid and then treated with AgNO3. The colour of precipitate and its solubility in NH4OH gives the result about the halogen present.
| Colour of Precipitate | Solubility in | Soluble compound | Inference |
| White (AgCl) | Soluble | Cl present | |
| Light Yellow (AgBr) | Soluble in excess of | Br present | |
| Dark Yellow (AgI) | Insoluble | —- | I present |
If N and S are also present along with halogen, the sodium extract must be boiled with conc. HNO3 to decompose cyanide or sulphide, else there is no interpretable result.
Beilstein test for Halogens
The organic compounds having halogen, on heating over Cu wire loop imparts green or blue flame to it due to formation of volatile halides.
The test is sensitive, but not reliable, since many compounds having no halogen at all, respond to it. (e.g., urea, thiourea, pyridine, -COOH)
Layer test for and
To sodium extract dil. is added followed by an organic layer of or . When water is added to it, or is liberated from aqueous solution on shaking and is dissolved into organic layer giving it a characteristic colour.
Brown layer Br
Violet layer I
Detection of Phosphorus
Treating the organic compound with an oxidizing agent converts P into .
The solution is then boiled with conc. followed by addition of ammonium molybdate. A yellow ppt. is obtained.
Quantitative Analysis:
The determination of amount of elements present in a compound is called quantitative analysis.
Estimation of Carbon and Hydrogen
In the same experiment as that used in the detection of carbon and hydrogen, the known mass of organic compound is burnt in excess of and CuO. C & H are oxidized to & respectively.
The mass of water is determined by passing the mixture through a ‘U’ tube, containing weighed anhydrous CaCl2 or Mg(ClO4)2 or anhydrous CuSO4 which traps the water molecules. CO2 is absorbed in another ‘U’ tube having conc. KOH or ascarite (NaOH + CaO) or saphnolite resin. Both these tubes are connected in series.
The increase in mass of anhyd. CaCl2 gives the amount of H2O and that of KOH gives the amount of CO2.
Let the mass of organic compound be M and mass of water & CO2 be m1 and m2 respectively, then
% of carbon =
% of hydrogen =
The method is devised for the comp. having only C & H. If other elements are also present, they will also give their oxides which will be absorbed in KOH. Following modification should be made
1) If N is present: The gaseous oxide mixture is passed over heated Cu gauze, which reduces all nitrogen oxides into N2.
2) If halogen is present : A roll of silver gauze is placed over exit of oxides (AgX).
3) If sulphur is present: A layer of fused lead chromate is placed over exit of combustion tube to trap S as PbSO4
Estimation of Nitrogen:
a) Duma’s method
b) Kjeldahl’s method
a) Duma’s method
The compound is heated with CuO in an atmosphere of CO2. Free N2, CO2 and water are formed. If any oxide of nitrogen is formed, it is converted back to free N2 by passing over a hot reduced copper gauge.
Oxides of Nitrogen
The mixture of gases so formed is collected over KOH to remove CO2 and drying agent to remove moisture (H2O).
Dry N2 is thus collected in Nitrometer and its value is calculated for STP by applying gas equation:
b) Kjeldahl’s Method:
The compound is heated with conc. H2SO4 along with K2SO4 (boiling point elevator) and CuSO4 or Hg (as a catalyst) whereupon N is converted into ammonium sulphate. The acidic mixture is then heated with excess of NaOH, when ammonia is evolved.
Organic compound + H2SO4 (NH4)2SO4
(NH4)2SO4 + 2NaOH Na2SO4 + 2NH3 + 2H2O
The ammonia liberated is absorbed in excess of standard H2SO4 solution. The exact amount of amount of NH3 liberated is calculated by titrating the residual acid against a standard alkali.
+ acid (residual v1 ml)
acid » standard alkali
N1v1 = N2V2
Amount of acid used to neutralize ammonia = (V – v1) ml
% of N =
= Volume of acid used against NH3
Not useful for nitro and azo groups and those where N is present in the rings (e.g., pyridine). Since they don’t give (NH4)2SO4 under these conditions.
Estimation of Halogens
Carius Method
Known amount of compound is heated with excess of fuming HNO3 and few crystals of AgNO3 in a sealed tube called Carius tube. As a result C converts into CO2; H into H2O; halogens into silver halides. The ppt of AgX formed is filtered, washed, dried & weighed.
Estimation of Sulphur
The organic compound is treated in Carius tube to produce H2SO4 which is treated with excess of BaCl2 to produce BaSO4.
Estimation of Phosphorus
In Carius tube under similar conditions H3PO4 is formed, when treated with magnesia mixture (MgCl2, NH4Cl, NH4OH) it results into ppt. of magnesium ammonium phosphate.
This ppt. after filtering, drying & igniting gives magnesium pyrophosphate.
Estimation of Oxygen
In a given problem if the sum of all other elements doesn’t correspond to 100%, it means that the rest is oxygen and is calculated by the difference method.
O% = 100 – (Sum of the percentage of all other elements)
An Alternate Method
Organic compound is decomposed by beating it in the stream of N2 gas; when the O is evolved as O2. The gaseous mixture is passed over red hot coke (11000C).
When all the O2 is converted into CO, the mixture is then passed through warm I2O5, which converts CO into CO2 and produces I2.
% of O can be derived from amount of CO2 or iodine produced.
MOLECULAR MASS DETERMINATION
Physical Methods
A) For volatile compounds
1) Victor Mayer Method
The organic volatile substance is vaporized and the volume of vapours so produced is calculated for NTP, using gas equation, followed by the relation:
Mol. mass =
Similarly are used
2) Duma’s method and
3) Hofmann’s method
B) For non-volatile compounds
1) Ebullioscopic method
where, = elevation in boiling point
= molal elevation constant
w, W = masses of organic compound and solvent
2) Cryoscopic method
where, = depression in freezing point
= molal freezing constant
Chemical Methods
1) Volumetric method
By titrating a known weight of an acid or base with the standard solution of its counterpart. Since equivalent amounts are neutralized by acids & bases, it gives E, the equivalent weight and,
N1V1 (acid) = N2V2 (base)
Molecular mass of an acid = Equivalent weight of an acid basicity of the acid
Mol. mass of a base = Equivalent weight of base acidity of the base
2) Silver salt method
Organic (carboxylic) acids form insoluble silver salts which upon heating decompose to give silver metal.
Let x g Ag metal is obtained from silver salt of the acid
108g Ag metal will be obtained from silver salt
Mass of RCOOH = mass of RCOOAg – mass of Ag + Mass of H
General formula:
Mol. mass of the acid =
3) Platinum chloride method
Organic bases combine with chloroplatinic acid to form the salts in the form of insoluble solids. These salts, give metallic platinum when heated.
Mol. mass of base = acidity of base
Drying & Dehydration:
1) All acidic oxides (of non-metals of CO2, NO2, SO2, P2O5 etc.) are absorbed in alkali (NaOH, KOH, Ca (OH)2 etc.)
2) All basic oxides (of metal e.g., Na2O, K2O, CaO etc.) are dissolved in acids.
3) Acidic substances are not dehydrated by basic dehydrating agent, but by acidic dehydrants. However, if an acidic substances reacts with the acidic anhydrating agent, it cannot be dried using this one.
4) Similarly basic compounds are dehydrated by basic dehydrating agents.
5) In general, a dehydrating agent must not react with the substance to be dehydrated.
Illustration 64: 0.858g of an organic compound on complete combustion gave 2.63g CO2 and 1.28g H2O. Determine the amount of C & H present in it.
Solution:
or,
Amount of H =
Illustration 65: In Duma’s method 0.5g of an organic compound gave 75 mL N2 at 270C and 725 mm Hg. If aq. tension at 270C = 15 mm Hg) what is the % of N in the compound? Actual pressure = 725 – 15 = 710 mm Hg
Solution: (Since at the given temperature some pressure will always be exerted by the water vapours, which shall be present along with the N2 collected in the sample)
Volume of N2 at STP =
Illustration 66: During estimation of N by Kjeldahl’s method, 0.5g of org. compound evolved some ammonia, which was completely neutralized by 250 mL N/20 H2SO4. Find the % of N in the compound.
Solution:
Illustration 67: In Carius method of estimation of halogens, 0.2 g of org. compound gave 0.15g AgCl. Calculate the % of Cl.
Solution:
Illustration 68: 0.15g organic compound upon treatment with excess of BaCl2 gave 0.56g BaSO4. What will be the percentage of sulphur?
Solution:
Illustration 69: In estimation of P 0.132g of compound gave 0.23g Mg2P2O7. What is the % of P in the compound?
Solution:
Exercise 7: (i) In Lassaigne’s test, the organic compound is fused with sodium metal so as to
(A) burn the compound
(B) form a sodium derivative
(C) convert N, S or halogen into soluble ionic compound
(D) None of the above
(ii) Which of the following compound will give blood red colour while doing the Lassaigne’s test for N?
(A)
(B)
(C)
(D)
(iii) The violet colour in the Lassaigne’s test of sulphur is due to
(A)
(B)
(C)
(D)
(iv) The function of boiling the sodium extract with concentrated nitric acid before testing halogens is
(A) to make solution clear
(B) to destroy CN– and S2– ion
(C) to make the solution acidic
(D) to bring common ion effect
(v) The blue colour developed during the Lassaigne’s test for nitrogen is due to
(A)
(B)
(C)
(D)
Exercise 8: (i) In Kjeldahl’s method, the nitrogen present in the organic compound is converted into
(A) gaseous ammonia
(B) ammonium sulphate
(C) ammonium phosphate
(D) ammonium nitrate
(ii) In Kjeldahl’s method, CuSO4 acts as
(A) oxidizing agent
(B) catalytic agent
(C) reducing agent
(D) hydrolyzing agent
(iii) 0.59g of an organic substance when treated with caustic soda evolved ammonia, which required 20 c.c. of N/2 sulphuric acid for neutralization. The percentage of nitrogen is
(A) 40 % (B) 53.6% (C) 63.6% (D) 23.7%
(iv) Kjeldahl’s method cannot be used for the estimation of nitrogen in
(A) Pyridine
(B) Nitro compounds
(C) Azo compounds
(D) All the three above
Exercise 9: (i) An organic compound is found to contain C = 40.0%, H = 6.66%. The empirical formula is
(A) CH2O (B) CHO2 (C) CHO (D) C2H6O
(ii) An organic compound is found to have the formula C5H10ONCl. The percentage of nitrogen in it is
(A) 20.36 (B) 10.3 (C) 44.05 (D) None of these
(iii) Complete combustion of a sample of hydrocarbon Q gives 0.66g of CO2 and 0.36g of H2O. The empirical formula of the compound is
(A) CH2 (B) C3H4 (C) C3H8 (D) C4H8
Answer to Exercise
Exerice 1: (i) A (ii) B (iii) D (iv) A (v) B (vi) A
Exerice 2: (i) D (ii) D (iii) D (iv) B (v) B (vi) A
Exerice 3: (i) D (ii) D (iii) B (iv) A
Exerice 4: (i) D (ii) D (iii) A (iv) C
Exercise 5. (i) A (ii) D (iii) C (iv) A
Exercise 6. (i) C (ii) B
Exercise 7. (i) C (ii) B (iii) C (iv) B (v) B
Exercise 8. (i) B (ii) B (iii) D (iv) D
Exercise 9. (i) A (ii) B (iii) C
FORMULAE AND CONCEPT AT A GLANCE
1. Organic compounds have been classified on the basis of carbon skeleton (structure) or functional group or the concept of homology.
2. Acyclic or open-chain compounds (Aliphatic compounds) may be straight or branched chains.
3. Cyclic or closed-chain compounds (Ring compounds) contain one or more closed-chains or rings of atoms in their molecules.
4. Homocyclic or carbocyclic compounds contain a ring or rings of carbon atom only in the molecules.
5. Alicyclic compounds (Cycloalkanes) are carbocyclic compounds which resemble aliphatic compounds in most of their properties. Examples are cyclopropane, cyclobutane, cyclopentane and cyclohexane etc.
6. Aromatic compounds consist of at least one benzene ring, i.e., a six-membered carbocyclic ring having alternate single and double bonds.
7. Heterocyclic compounds are cyclic compounds containing one or more hetero atoms (O, N, S, etc.) in the ring. Example are furan, thiophene, pyrrole, pyridine, indole and quinoline, etc.
8. Functional group is an atom or group of atoms present in a molecule which largely determines its chemical properties. For example, C=C, CºC, X(Cl, Br, I), -OH, -SH,
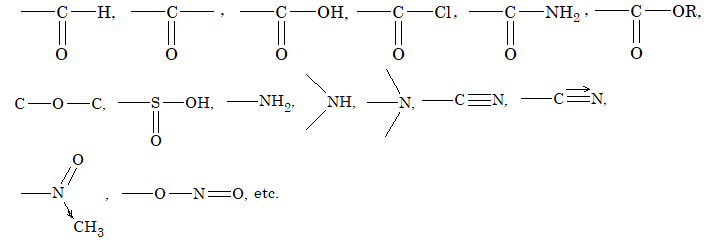
9. Nomenclature of aliphatic compounds having poly functional groups. The order of preference for the choice of principal functional group is
Carboxylic acids > sulphonic acids > acid anhydrides > esters > acid chlorides > acid amides > cyanides > aldehydes > Keotnes > alcohols, phenols, thiols > amines > ethers > alkenes, alkynes > halo, nitro, alkyl.
10. Isomerism due to differences in the order in which the atoms are joined together, is called structural isomerism.
11. Isomerism due to differences only in the spatial orientation of the atoms in the molecule, is called stereoisomerism.
12. Tautomerism is a special case of structural isomerism and also known as dynamic isomerism. In tautomerism, two isomers are directly interconvertible and exist in dynamic equilibrium with each other.
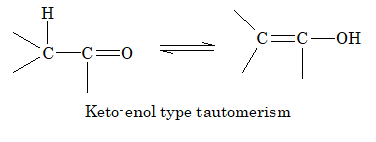
13. A carbon atom, which is attached to four different atoms or groups is called a chiral or an asymmetric carbon atom. For example,
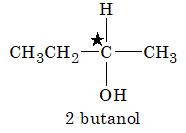
14. The separation of racemic mixture into its two enantiomorphic forms is known as resolution.
15. The compounds which do not show optical activity inspite of presence of chiral carbon atoms are called meso compounds.
16. Application of inductive effect
(a) Acidity of acid: If -I producing group are attached to carbon chain of carboxylic acid. e.g., Halogenated acids are much more strong acid than parent carboxylic acid.
(b) Basicity of Base: In general more alkylated base are more basic than parent base.
17. Application of mesomeric effect
Mesomeric effect in which e–s are transferred from multiple bond to an atom or from a multiple bond to a single covalent bond or lone pair of electron from an atom to the adjacent single covalent bond (conjugation effect).
In case of aniline the electron density of unshared pair does not reside entirely on the nitrogen atom but is spread over the ring. Thus decrease the electron of nitrogen atom.
18. Stability of intermediate
The order of stability can be explained on the basis of electron releasing inductive effect of alkyl groups.
Greater the number of alkyl group on the carbon atom carrying positive charge, greater will be dispersal of the charge and hence more stable be the carbon atom.
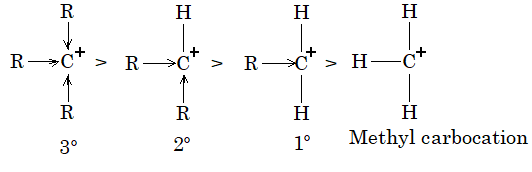
19. Stability of carbanions can be explained on the basis of +I effect of alkyl group. Greater the number of alkyl group on carbon atom carrying -ve charge greater will be intensity of -ve charge on carbon atom and hence less stable would be the carbanion.
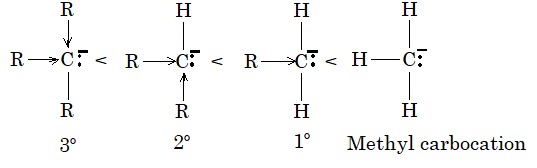
20. Stability of free radicals can be explained on the basis of hyperconjugation.
Greater the number of hyperconjugated structure greater will be stability.
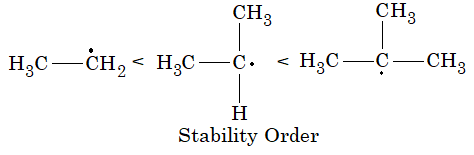
SOLVED PROBLEMS
Prob1: In column chromatography the moving phase is constituted of
(A) a substance which have to be separated
(B) eluent
(C) adsorbent
(D) mixture of eluent and substances to be separated
Sol: (D) The adsorbent material (stationary phase) is some inert substance like SiO2, Al2O3 on which the liquid (moving phase) having substance & element are passed on for separation.
Prob2: Simple distillation can be used to separate compound which
(A) are highly volatile and have very close boiling points
(B) are steam volatile
(C) decomposes on heating
(D) are volatile and have non volatile impurities
Sol: (D) Volatile impurities will come off & nonvolatile will left behind.
Prob3: A compound has simplest formula CH2. To which hydrocarbon series does it belong?
(A) Alkanes
(B) Cycloalkanes
(C) Alkynes
(D) None of these
Sol: (B) Cycloalkanes: CnH2n
Prob4: If empirical formula of an organic compound is CH2O and its 6.02 ´ 1023 molecules weigh 60g, then it can be
(A) CH3OH
(B) C2H5OH
(C) HCOOH
(D) HCOOCH3
Sol: (D) C2H4O2 or (CH2O)2 24 + 4 + 3 = 60 Mass of 6.02 ´1023 molecules is equal to molecular mass.
Prob5: Latest technique for purification, isolation and separation of organic substances is
(A) distillation
(B) crystallization
(C) sublimation
(D) chromatography
Sol: (D) Used for all of these purposes.
Prob6: Chromatography is used for the purification of
(A) solids
(B) gases
(C) liquids
(D) All the above
Sol: (D) Used for all of these purposes.
Prob7: Copper wire test is called
(A) Dumas test
(B) Leibig test
(C) Beilstein’s test
(D) Fusion test
Sol: (C) Taking a substance into Bunsen burner on the copper wire produces blue or green flame.
Prob8: The most satisfactory method to separate sugars is to use
(A) fractional crystallization
(B) sublimation
(C) chromatography
(D) Benedict’s reagent
Sol: (C) Sugars are non-sublimable and have almost same solubility; Benedict reagent reacts with carbonyl compounds.
Hence the only method possible for separation chromatography.
Prob9: Positive Beilstein test shows that
(A) halogen is surely present
(B) halogen is absent
(C) halogen may be present
(D) None of these
Sol: (C) Apart from halogen, urea & thiourea also give the same colour in flame.
Prob10: A mixture of naphthalene and benzoic acid can be separated by
(A) extraction with solvent
(B) sublimation
(C) fractional crystallization
(D) distillation
Sol: (A) Benzoic acid is soluble in hot water, naphthalene being almost insoluble. Dil NaHCO3 solution (being basic in nature) will dissolve only benzoic acid leaning behind the naphthalene.
Prob11: Which of the following carbocation is most stable?

Sol: (B) Stability of carbocation µ number of hyperconjugation structure.
Prob12: How many primary hydrogen atoms are there in the compound?
(A) 18
(B) 6
(C) 24
(D) 12
Sol: (A). Each primary carbon having three primary hydrogen atoms
Thus, total number of primary hydrogen = 63 = 18.
Prob13: Among the following which is the strongest base
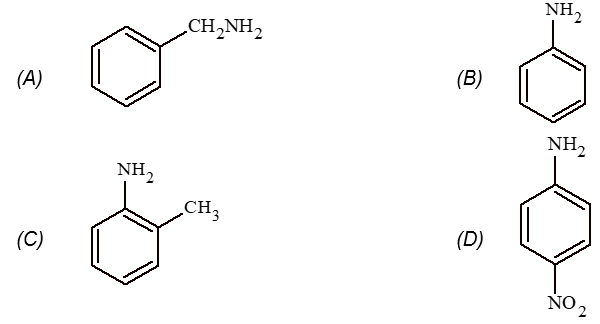
Sol: (A) Aliphatic amines are more basic than aromatic amines.
Prob14: Which of the following has the highest pKa value?
(A) CH3—CH2—OH
(B) Cl—CH2—CH2—OH
(C) F3C—CH2—OH
(D)
Sol: (D) The alcohol which is least acidic has highest pKa value.
Prob15: The no. of s and p bonds in 1-buten-3-yne are
(A) 5 , 5
(B) 7 , 3
(C) 8 , 6
(D) 6 , 4
Sol:
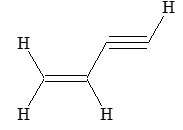
In double bond one s and one p bond. In triple bond one s and two p bond. All single bonds are s bond.
Prob16: IUPAC name of the compound
(A) 1, 2, 3 – tricyanopropane
(B) propane-1,2,3-tricarbonitrile
(C) 1, 2, 3 – cyanopopane
(D) propane tricarbylamine
Sol: (B).
Prob17: IUPAC name of the compound
![]()
is
(A) but – 2 – en – 1 ol
(B) 1 – hydroxy but – 1 – ene
(C) 4 – hydroxy but – 3 – ene
(D) but-1-en-1-ol
Sol. (D).
Prob18: IUPAC name of
is
(A) 2-ethyl-3-methylhex-1-en-4-yne
(B) 5-ethyl-4-methylhex-2-en-5-yne
(C) 3-ethyl-4-methylhex -5-yne
(D) 5-ethyl-5-ethyl–4–methylhepta–2–yne
Sol: (A).
Prob19: 2 – methyl – 2 butene will be represented as

Sol. (D).
Prob20: The IUPAC name of the compound having the formula Cl3CCHO
(A) chloral
(B) trichloroacetaldehyde
(C) 1, 1, 1 – trichloroethanal
(D) 2, 2, 2 – trichloroethanal
Sol: (D).