Equilibrium Part 1

CHEMICAL EQUILIBRIUM

Equilibrium is a state of a process in which the properties like temperature, pressure, concentration of the system do not change with the passage of  time.

In all processes which attain equilibrium two opposing processes are involved.  Equilibrium is attained when the rates of two opposing processes become equal.

• If the opposing processes involve only physical changes, the equilibrium is called physical equilibrium. It is a state of equilibrium between same chemical species in different phases.  For example liquid water may exist in equilibrium with water vapour, in both the phases (liquid and vapour) the chemical species is H₂O

Types of physical equilibria

1. Solid – Liquid equilibrium:

The state when solid and liquid phases of a substance coexist is called solid-liquid equilibrium.

The temperature at which the solid and liquid form of a pure substance are in equilibrium at the atmospheric pressure is called the normal freezing point or melting point of that substance.  If some ice cubes and water at 0⁰C and normal atmospheric pressure are placed in a thermos flask so that no heat can enter or leave the system, the mass of ice and water is found to remain constant.  However the two opposing processes going on at equilibrium are melting of ice and freezing of water. The equilibrium is represented as

${\mathrm{H}}_2\mathrm{O}\left(\mathrm{s}\right)\rightleftharpoons {\mathrm{H}}_2\mathrm{O}\left(\mathcal{l}\right)$

at equilibrium; rate of melting of ice = Rate of freezing of water.

• At 273 K and 1 atm pressure, ΔG = 0, i.e., ice and water are in equilibrium

             ${\mathrm{H}}_2\mathrm{O}\left(\mathrm{s}\right)\rightleftharpoons {\mathrm{H}}_2\mathrm{O}\left(\mathcal{l}\right)$

• At temperature higher than 273 K and 1 atm pressure ΔG < O, the process in forward direction would become favourable and ice will melt to give more water.
• At temperature less than 273 K and 1 atm pressure ΔG > O, the reverse reaction will become favourable and more ice will be formed from liquid water.

2. Liquid – gas equilibrium:

When a liquid is placed in a closed container and this container is placed at room temperature.  It is observed that in the beginning more and more of the water is changing into vapours.  After some time the amount of water vapours becomes constant i.e., as much water changes into vapours, the same amount of water vapours change back into liquid water.  Thus at equilibrium.

Rate of evaporation = Rate of condensation.

3. Equilibrium between a solid and its solution:

A solution containing maximum amount of solute at any fixed temperature and pressure is called a saturated solution.  A saturated solution cannot dissolve more solute.  Even if a small quantity of solute is added to a saturated solution, it does not dissolve in solution and there exists a dynamic equilibrium between the solid solute and solution phases.  For a saturated sugar solution in water, the equilibrium state, the number of sugar molecules going into the solution from the solid sugar is equal to the number of molecules precipitating out from the solution.  Thus at equilibrium.

Rate of dissolution of sugar = Rate of precipitation of sugar.

• The maximum mass (in grams) of a solute which can be dissolved in 100g of a solvent at any temperature and pressure is called its solubility at that temperature and pressure.

4. Equilibrium between a gas and its solution in a liquid (Henry’s Law):

The solubility of a gas in any liquid depends upon nature of the gas and that of the liquid, temperature of the liquid and pressure of the gas over the surface of solution.

The effect of pressure on the solubility of a gas in a liquid is described by Henry’s law.  This law states that “ The mass of a gas dissolved in a given mass of a solvent at any temperature is directly proportional to the pressure of the gas above the solvent”.

m $\propto$ P    or     m = kp

Where k is the proportionality constant.

• In the sealed soda water bottle, the pressure of CO₂ gas is very high above the liquid, so the mass of the CO₂ gas dissolved is also high. As soon as the bottle is opened under normal atmospheric condition, the dissolved gas escapes out to reach a new equilibrium state required by the lower pressure.  At lower pressure, the solubility of the gas in water decreases.
• Henry’s law is applicable to ideal gases only. Since the real gases behave like ideal gases at low pressure, hence Henry’s law should be applied only at low pressures.
• Henry’s law is not applicable to gases which react chemically with the solvent.

General characteristics of physical Equilibrium:

i. Physical equilibrium can be established only in closed systems.

ii. The state of equilibrium depends upon temperature and pressure. So, the temperature and pressure of the system at equilibrium must remain constant.

iii. Equilibrium is dynamic in nature i.e., there are two opposing processes taking place at equal rates.1

iv. At equilibrium, some observable properties of the system becomes constant.

v. The value of the equilibrium constant indicates the direction and extent of the process.

Equilibria in chemical Processes:

In certain reactions whole of the reactants gets converted into products, whereas in some others, only a part of the reactants gets converted into products, thus different reactions proceed to different extent.  The chemical reactions are classified on the basis of the extent to which type proceed into the following two classes.

1) Irreversible reactions :  The reactions which move in one direction i.e., forward direction only are called irreversible reaction.  In such reactions, products do not react together to produce reactants again, i.e., the reaction does not move in backward direction. Some examples of irreversible reactions are as follows:

(i). ${\mathrm{AgNO}}_3+\mathrm{NaC}l\to \mathrm{AgC}l+{\mathrm{NaNO}}_3$

(ii). $2\mathrm{KC}l{\mathrm{O}}_3\underset{\mathrm{Heat}}{\overset{{\mathrm{MnO}}_2}{\to }}2\mathrm{KC}l+3{\mathrm{O}}_2$

(iii). ${\mathrm{NH}}_4{\mathrm{NO}}_2⟶{\mathrm{N}}_2+2{\mathrm{H}}_2\mathrm{O}$

(iv). ${\mathrm{H}}_2{\mathrm{SO}}_4+2\mathrm{NaOH}⟶{\mathrm{Na}}_2{\mathrm{SO}}_4+2{\mathrm{H}}_2\mathrm{O}$

2)  Reversible reactions :  The chemical reactions which take place in both directions under similar conditions are called reversible reactions.  In such reactions products also react with each other and produce reactant again.  The reversible reactions proceed only to a limited extent and both the reactants and products are present in the reaction mixture.  The sign (ƒ $\rightleftharpoons$ ) represents the reversibility of the reaction.

e.g., When hydrogen is passed over heated magnetic oxide, metallic iron and water are produced.

${\mathrm{Fe}}_3{\mathrm{O}}_4+4{\mathrm{H}}_2⟶3\mathrm{Fe}+4{\mathrm{H}}_2\mathrm{O}$

If steam is passed over powdered iron at the same temperature, magnetic oxide of iron and hydrogen are formed.

$3\mathrm{Fe}+4{\mathrm{H}}_2\mathrm{O}\to {\mathrm{Fe}}_3{\mathrm{O}}_4+4{\mathrm{H}}_2$

If the reaction is carried out in closed vessel, then both of the above reactions can take place in the vessel.  After some time rate of both (forward and backward) reactions become equal.

Some other examples of reversible reactions are

(i) ${\mathrm{CaCO}}_3( \mathrm{s})\rightleftharpoons \mathrm{CaO}\left(\mathrm{s}\right)+{\mathrm{CO}}_2( \mathrm{g})$

(ii) ${\mathrm{CH}}_3\mathrm{COOH}\left(\ell \right)+{\mathrm{C}}_2{\mathrm{H}}_5\mathrm{OH}\left(\ell \right)\rightleftharpoons {\mathrm{CH}}_3{\mathrm{COOC}}_2{\mathrm{H}}_5\left(\ell \right)+{\mathrm{H}}_2\mathrm{O}\left(\ell \right)$

(iii) $2\mathrm{HI}\left(\mathrm{g}\right)\rightleftharpoons {\mathrm{H}}_2( \mathrm{g})+{\mathrm{I}}_2( \mathrm{g})$

(iv) ${\mathrm{PCl}}_5( \mathrm{g})\rightleftharpoons {\mathrm{PCl}}_3( \mathrm{g})+{\mathrm{Cl}}_2( \mathrm{g})$

(v) 2SO₂(g) + O₂ (g) ƒ $\rightleftharpoons$ 2SO₃(g)

(vi) ${\mathrm{N}}_2( \mathrm{g})+3{\mathrm{H}}_2( \mathrm{g})\rightleftharpoons 2{\mathrm{NH}}_3( \mathrm{g})$

(vii) N₂O₄(g) $\rightleftharpoons$ ƒ 2NO₂(g)

Reversible reactions do not proceed to completion. In a reversible reaction both reactant and products are present in equilibrium with each other.

State of chemical equilibrium:

For a general reversible reaction

$\mathrm{A}+\mathrm{B}\rightleftharpoons \mathrm{C}+\mathrm{D}$

In the beginning the concentrations of A and B are maximum and concentrations of C and D are minimum.  As the reaction proceeds, the concentrations of reactants are decreasing with the passage of time and the concentrations of products are increasing.  After some time rate of forward reaction, becomes equal to the rate of backward reaction.  At this state, the reaction is said to be in a state of chemical equilibrium.

Thus in reversible reactions, chemical equilibrium is a state at which both forward and backward reactions occur at the same speed. 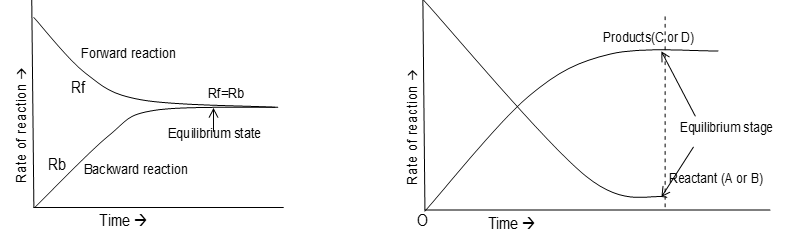Characteristics of equilibrium state:

(i) A chemical equilibrium can be established only in closed systems. If the system is not closed some of the products may escape and thus the backward reaction will not occur.

(ii) Chemical equilibrium can be attained from either direction i.e., from the side of reactants or products.

• In case of reversible reactions, the free energy of the system is minimum at the equilibrium state. The free energy decreases both in going from reactants to the equilibrium state and from products to the equilibrium state.
• Hence reactants will form the products and products will form the reactants until the state of equilibrium is reached.  At equilibrium (ΔG = 0)

(iii) A catalyst does not change the equilibrium but helps in attaining it rapidly.

(iv) At equilibrium, the concentrations of reactants and products may or may not be equal, but concentration remains unchanged with time. This does not mean that reaction has stopped at the equilibrium. At equilibrium state, both forward and backward reactions proceed at the same rate i.e., rate of formation of products becomes equal to the rate of formation of reactants.  Such a state of equilibrium is called dynamic equilibrium.

(v) Chemical equilibrium does not change with time so long as the external factors remain the same.

• The state of equilibrium is characterized by a constant called equilibrium constant.
• Reversible chemical reactions are classified into two types.

1) Homogenous reactions:  The reversible reactions in which all the reactants and products are in the same physical state.

e.g. (i) ${\mathrm{N}}_2( \mathrm{g})+3{\mathrm{H}}_2( \mathrm{g})\rightleftharpoons 2{\mathrm{NH}}_3( \mathrm{g})$

(ii) $2{\mathrm{NO}}_2( \mathrm{g})\rightleftharpoons {\mathrm{N}}_2{\mathrm{O}}_4( \mathrm{g})$

(iii) ${\mathrm{CH}}_3\mathrm{COOH}\left(\ell \right)+{\mathrm{C}}_2{\mathrm{H}}_5\mathrm{OH}\left(\ell \right)\rightleftharpoons {\mathrm{CH}}_3{\mathrm{COOC}}_2{\mathrm{H}}_5\left(\ell \right)+{\mathrm{H}}_2\mathrm{O}\left(\ell \right)$

2) Heterogeneous reactions : The reversible reactions in which various chemical species are present in two or more phases are called heterogeneous reactions.

e.g., (i) $3\mathrm{Fe}\left(\mathrm{s}\right)+4{\mathrm{H}}_2\mathrm{O}\left(\mathrm{g}\right)\rightleftharpoons {\mathrm{Fe}}_3{\mathrm{O}}_4( \mathrm{s})+4{\mathrm{H}}_2( \mathrm{g})$

(ii) ${\mathrm{CaCO}}_3( \mathrm{s})\rightleftharpoons \mathrm{CaO}\left(\mathrm{s}\right)+{\mathrm{CO}}_2( \mathrm{g})$

(iii) ${\mathrm{MgCO}}_3( \mathrm{s})\rightleftharpoons \mathrm{MgO}\left(\mathrm{s}\right)+{\mathrm{CO}}_2( \mathrm{g})$

Exercise 1:

(i) Which of the following is an example of a reversible reaction?

(A) AgNO₃(aq) + NaCl (aq) $\to$ AgCl(s) + NaNO₃(aq)

(B) 2Na(s) + 2H₂O(l) $\to$ 2NaOH(l) + H₂(g)

(C) 2KClO₃ (s) $\to$ 2KCl(s) + 3O₂(g)

(D) NH₄Cl(s) $\to$ NH₃(g) + HCl (g)

(ii) If a chemical reaction is at equilibrium, it means that

(A) the reactants are completely transformed into the products

(B) product formation is minimum

(C) equal amounts of reactants and products are present

(D) the rates of the forward and the backward reactions are equal

(iii) What are the characteristics of a chemical equilibrium?

(A) Permanency of equilibrium

(B) Approachability from either side

(C) Incompleteness of reaction

(D) All of these

(iv) The reaction which proceeds in the forward direction is

(A) Fe₂O₃ + 6HCl $\to$ 2FeCl₃ + 3H₂O

(B) NH₃ + H₂O + NaCl $\to$ NH₄Cl + NaOH

(C) SnCl₄ + Hg₂Cl₂ $\to$ SnCl₂ + 2HgCl₂

(D) 2CuI + I₂ + 4K⁺ $\to$ 2Cu²⁺ + 4KI

Law of chemical equilibrium (Equilibrium constant) : Consider a reversible homogenous reaction which has attained equilibrium state at a particular temperature.

$\mathrm{aA}+\mathrm{bB}\rightleftharpoons \mathrm{cC}+\mathrm{dD}$

According to law of mass action.

Rate of forward reaction $\alpha \left[\mathrm{A}{]}^{\mathrm{a}}\right[\mathrm{B}{]}^{\mathrm{b}}$

or  Rate of forward reaction = $k_f\left[\mathrm{A}{]}^{\mathrm{a}}\right[\mathrm{B}{]}^{\mathrm{b}}$

where k_f is the rate constant for forward reaction similarly,

rate of backward reaction = ${\mathrm{k}}_{\mathrm{b}}\left[\mathrm{C}{]}^{\mathrm{C}}\right[\mathrm{D}{]}^d$

(where k_b is rate constant for backward reaction)

At equilibrium,

Rate of forward reaction = Rate of backward reaction

i.e., R_f = R_b

or ${\mathrm{k}}_{\mathrm{f}}\left[\mathrm{A}{]}^{\mathrm{a}}\right[\mathrm{B}{]}^{\mathrm{b}}={\mathrm{k}}_{\mathrm{b}}\left[\mathrm{C}{]}^{\mathrm{c}}\right[\mathrm{D}{]}^d$ or $\frac{{\mathrm{k}}_{\mathrm{f}}}{{\mathrm{k}}_{\mathrm{b}}}=\frac{\left[\mathrm{C}{]}^{\mathrm{C}} \right[\mathrm{D}{]}^{\mathrm{d}}}{[\mathrm{A}{]}^{\mathrm{a}} [\mathrm{B}{]}^{\mathrm{b}}}$

Both k_f and k_b are constant.  The ratio $\frac{{\mathrm{k}}_{\mathrm{f}}}{{\mathrm{k}}_{\mathrm{b}}}$ is also a new constant (K_c)

K_c is known as equilibrium constant

Thus ${\mathrm{K}}_c=\frac{{\left[\mathrm{C}\right]}^{c }[\mathrm{D}{]}^{\mathrm{d}}}{[\mathrm{A}{]}^{\mathrm{a}} [\mathrm{B}{]}^{\mathrm{b}}}$

The above mathematical equation is known as law of chemical equilibrium.

Equilibrium constant may be defined as the ratio between the product of the molar concentrations of the products to the molar concentrations of the reactants with each concentration term is raised to a power equal to stoichiometric coefficient in the balanced chemical equation.

or

Equilibrium constant is the ratio of the rate constants of forward and backward reactions.

For homogenous chemical equilibrium, when the concentrations of the reactants and products are expressed in moles per litre, the equilibrium constant is written as K_c.

When the reactants and products are gaseous the equilibrium constant can be expressed either in terms of concentrations in moles per litre or in terms of partial pressure of reactants and products.  When equilibrium constant is expressed in terms of partial pressures of reactants and products; then it is denoted by K_b.

Thus, ${\mathrm{K}}_{\mathrm{p}}=\frac{{\left({\mathrm{p}}_{\mathrm{c}}\right)}^c\times {\left({\mathrm{p}}_{\mathrm{D}}\right)}^{\mathrm{d}}}{{\left({\mathrm{p}}_{\mathrm{A}}\right)}^{\mathrm{a}}\times {\left({\mathrm{P}}_{\mathrm{B}}\right)}^{\mathrm{b}}}$

Where p_A, p_B, p_C, p_D are the partial pressures of A, B, C and D respectively in the reaction mixture at equilibrium.  Pressures in the above equation are taken in atmospheres or bars or pascals.

Relationship between K_p and K_c

Consider the general reversible reaction

$\mathrm{aA}+\mathrm{bB}\rightleftharpoons \mathrm{cC}+\mathrm{dD}$

If the equilibrium constant for this reaction is expressed in terms of concentrations, then

${\mathrm{K}}_c=\frac{\left[\mathrm{C}{]}^{\mathrm{C}} \right[\mathrm{D}{]}^{\mathrm{d}}}{\left[\mathrm{A}{]}^{\mathrm{a}} \right[\mathrm{B}{]}^{\mathrm{b}}}$

Where [A], [B] and [C], [D] represent the molar concentration of reactants and products respectively.

If A, B, C and D are gaseous substances; the equilibrium constant for the above reaction may be expressed in terms of partial pressures.

${\mathrm{k}}_{\mathrm{p}}=\frac{{\mathrm{p}}_{\mathrm{C}}^{\mathrm{c}}{\mathrm{P}}_{\mathrm{D}}^{\mathrm{d}}}{{\mathrm{P}}_{\mathrm{A}}^{\mathrm{a}}{\mathrm{P}}_{\mathrm{B}}^{\mathrm{b}}}$.

If the gaseous components behave ideally, then we can apply the ideal gas equation.

i.e., pV = nRT or $\mathrm{p}=\frac{\mathrm{n}}{\mathrm{V}}\mathrm{RT}$ where $\frac{‘\mathrm{n}‘}{\mathrm{V}}$ represents moles per litre concentrations,

Thus, ${\mathrm{P}}_{\mathrm{c}}=\left[\mathrm{C}\right]\mathrm{RT}, {\mathrm{P}}_{\mathrm{D}}=\left[\mathrm{D}\right]\mathrm{RT}$

${\mathrm{P}}_{\mathrm{A}}=\left[\mathrm{A}\right]\mathrm{RT}, {\mathrm{p}}_{\mathrm{B}}=\left[\mathrm{B}\right]\mathrm{RT}$

Putting these values in the expression for K_p

${\mathrm{K}}_{\mathrm{p}}=\frac{{\mathrm{p}}_{\mathrm{C}}^{\mathrm{C}}{\mathrm{p}}_{\mathrm{D}}^{\mathrm{d}}}{{\mathrm{p}}_{\mathrm{A}}^{\mathrm{a}}{\mathrm{p}}_{\mathrm{B}}^{\mathrm{b}}}=\frac{\left(\right[\mathrm{C}]\mathrm{RT}{)}^{\mathrm{o}}\times (\left[\mathrm{D}\right]\mathrm{RT}{)}^{\mathrm{d}}}{\left(\right[ \mathrm{A}]\mathrm{RT}{)}^{\mathrm{a}}\times (\left[\mathrm{B}\right]\mathrm{RT}{)}^{\mathrm{d}}}$ = $\frac{\left[\mathrm{C}{]}^{\mathrm{c}} \right[\mathrm{D}{]}^{\mathrm{d}}}{\left[\mathrm{A}{]}^{\mathrm{a}} \right[\mathrm{B}{]}^{\mathrm{b}}}\times (\mathrm{RT}{)}^{(\overline{\mathrm{c}+\mathrm{d}}–\overline{\mathrm{a}+\mathrm{b}})}$

If Δn = No. of moles of products – NO. of moles of reactants.

= Change in no. of moles = $(\overline{\mathrm{c}+\mathrm{d}}–\overline{\mathrm{a}+\mathrm{b}})$

$\therefore {\mathrm{K}}_{\mathrm{p}}=\frac{{\left[\mathrm{C}\right]}^{\mathrm{c}} [\mathrm{D}{]}^{\mathrm{d}}}{\left[\mathrm{A}{]}^{\mathrm{a}} \right[\mathrm{B}{]}^{\mathrm{b}}}(\mathrm{RT}{)}^{\mathrm{\Delta n}}$

or  K_p = K_c (RT)^Δn

depending on the value of Δn.  Three cases may arise:

(i) When Δn = 0,    e.g., ${\mathrm{H}}_2( \mathrm{g})+{\mathrm{I}}_2( \mathrm{g})\rightleftharpoons 2\mathrm{Hl}\left(\mathrm{g}\right)$

K_p = K_c (RT)⁰ = K_C

(ii) Δn = + ve   or   Δn > 0

${\mathrm{K}}_{\mathrm{p}}>{\mathrm{K}}_{\mathrm{c}};\text{ e.g. }{\mathrm{PCl}}_5( \mathrm{g})\rightleftharpoons {\mathrm{PCl}}_3( \mathrm{g})+{\mathrm{Cl}}_2( \mathrm{g})$

(iii)  Δn = – ve     or   Δn < 0

K_p < K_c     e.g., ${\mathrm{N}}_2( \mathrm{g})+3{\mathrm{H}}_2( \mathrm{g})\rightleftharpoons 2{\mathrm{NH}}_3( \mathrm{g})$

Characteristics of equilibrium constant

(i) Equilibrium constant has a definite value for every chemical reaction at a given temperature.

(ii) Equilibrium constant of a reaction does not depend upon the concentrations of various species involved in the reaction.

(iii) The value of equilibrium constant for backward reaction is reciprocal of the equilibrium constant for forward reaction.

e.g., The equilibrium constant for the reaction.

${\mathrm{CH}}_3\mathrm{COOH}+{\mathrm{C}}_2{\mathrm{H}}_5\mathrm{OH}\rightleftharpoons {\mathrm{CH}}_3{\mathrm{COOC}}_2{\mathrm{H}}_5+{\mathrm{H}}_2\mathrm{O}$ is K, then equilibrium constant for the backward reaction.

${\mathrm{CH}}_3{\mathrm{COOC}}_2{\mathrm{H}}_5+{\mathrm{H}}_2\mathrm{O}\rightleftharpoons {\mathrm{CH}}_3\mathrm{COOH}+{\mathrm{C}}_2{\mathrm{H}}_5\mathrm{OH}$ will be ${\mathrm{K}}^{‘}=\frac{\left[{\mathrm{CH}}_3\mathrm{COOH}\right] \left[{\mathrm{C}}_2{\mathrm{H}}_5\mathrm{OH}\right]}{\left[{\mathrm{CH}}_3{\mathrm{COOC}}_2{\mathrm{H}}_5\right] \left[{\mathrm{H}}_2\mathrm{O}\right]}=\frac{1}{ \mathrm{K}}$

$\mathrm{K}‘=\frac{1}{\mathrm{K}}$ ; Thus equilibrium constant for backward reaction

= $\frac{1}{\text{ equilibrium constant for forward reaction }}$

(iv) The value of equilibrium constant depends upon the stoichiometry of chemical equation.  If the equation (having equilibrium constant K) is divided by 2, the equilibrium constant for the new equation is the square root of K i.e., $\left(\sqrt{\mathrm{K}}\right)$ .

For example the dissociation of NO₂ can be represented as

$2{\mathrm{NO}}_2\rightleftharpoons {\mathrm{N}}_2+2{\mathrm{O}}_2$    . . . . (1)

or ${\mathrm{NO}}_2\rightleftharpoons \frac{1}{2}{ \mathrm{N}}_2+{\mathrm{O}}_2$ . . . . (2)

For equation (1) ${\mathrm{K}}_{\mathrm{c}}=\frac{\left[{\mathrm{N}}_2\right]{\left[{\mathrm{O}}_2\right]}^2}{{\left[{\mathrm{NO}}_2\right]}^2}$

For equation (2) ${\mathrm{K}}_{\mathrm{C}}^{‘}=\frac{{\left[{\mathrm{N}}_2\right]}^{1/2}\left[{\mathrm{O}}_2\right]}{\left[{\mathrm{NO}}_2\right]}$   Thus ${\mathrm{K}}_c^{‘}=\sqrt{{\mathrm{K}}_c}$

When the coefficients of all the reactants and products are multiplied by 2, then the equilibrium constant for the new equation is equal to the square of the equilibrium constant for the original equation.

In general when a balanced equation having equilibrium constant K_c is multiplied by a certain value n, the equilibrium constant for the new equation will be equal to (K_c)ⁿ.

e.g., $\mathrm{A}+\mathrm{B}\rightleftharpoons \mathrm{C}+\mathrm{D} {\mathrm{K}}_{\mathrm{c}}=\frac{\left[\mathrm{C}\right] \left[\mathrm{D}\right]}{\left[\mathrm{A}\right] \left[\mathrm{B}\right]}$

$\mathrm{nA}+\mathrm{nB}\rightleftharpoons \mathrm{nC}+\mathrm{nD} {\mathrm{K}}_{\mathrm{c}}^{‘}=\frac{\left[\mathrm{C}{]}^{\mathrm{n}} \right[\mathrm{D}{]}^{\mathrm{n}}}{\left[\mathrm{A}{]}^{\mathrm{n}} \right[\mathrm{B}{]}^n}={\left({\mathrm{K}}_{\mathrm{c}}\right)}^{\mathrm{n}}$

v) If the equation (having equilibrium constant K) is written in two steps and equilibrium constant for 1^st and 2^nd steps are K₁ and K₂ respectively, then

K = K₁ $\times$ K₂

e.g., ${\mathrm{N}}_2( \mathrm{g})+{\mathrm{O}}_2( \mathrm{g})\rightleftharpoons 2\mathrm{NO}\left(\mathrm{g}\right)$ $K_1=\frac{[\mathrm{NO}{]}^2}{\left[{ \mathrm{N}}_2\right] \left[{\mathrm{O}}_2\right]}$

$2\mathrm{NO}\left(\mathrm{g}\right)+{\mathrm{Cl}}_2( \mathrm{g})\rightleftharpoons 2\mathrm{NOCl}\left(\mathrm{g}\right)$ ${\mathrm{K}}_2=\frac{[\mathrm{NOCl}{]}^2}{[\mathrm{NO}{]}^2\left[{\mathrm{Cl}}_2\right]}$

__________________________________________

${\mathrm{N}}_2( \mathrm{g})+{\mathrm{O}}_2( \mathrm{g})+{\mathrm{Cl}}_2( \mathrm{g})\rightleftharpoons 2\mathrm{NOCl}\left(\mathrm{g}\right)$

${\mathrm{K}}_1\times {\mathrm{K}}_2=\frac{[\mathrm{NO}{]}^2}{\left[{ \mathrm{N}}_2\right]\left[{\mathrm{O}}_2\right]}\times \frac{[\mathrm{NOCl}{]}^2}{[\mathrm{NO}{]}^2\left[{\mathrm{Cl}}_2\right]}=\frac{[\mathrm{NOCl}{]}^2}{\left[{ \mathrm{N}}_2\right]\left[{\mathrm{O}}_2\right]\left[{\mathrm{Cl}}_2\right]}=\mathrm{K}$ ____________________________________________

Similarly for three steps K = K₁ ⨯ K₂ ⨯ K₃ (vi) Prediction of extent of reaction: Large value of K shows that the reaction in forward direction is more favoured.  Very large value of K, e.g., K = 10¹⁰ or so means that the reaction proceed in the forward direction to almost completion.

Intermediate value of K (10^–3 to 10³) shows that the concentration of reactants and products are comparable.

e.g., For the reaction ${\mathrm{Fe}}^{3+}\left(\mathrm{aq}\right)+{\mathrm{SCN}}^{–}\left(\mathrm{aq}\right)\rightleftharpoons \left[\mathrm{Fe}\right(\mathrm{SCN}){]}^{2+}$    K_c = 138 at 25⁰C

Low value of K (< 10^–3) shows that backward reaction is favoured i.e., concentration of reactants is much larger then that of products.

(vii) In the case of endothermic reactions, the value of equilibrium constant is higher at higher temperature. In the case of exothermic reactions, the value of equilibrium constant is lower at higher temperature.

(viii) The value of equilibrium constant is not affected by the addition of a catalyst to the reaction.  This is because the catalyst increases the speed of the forward reaction and the backward reaction to the same extent.

Units of equilibrium constant :

Units of equilibrium constant of a reaction depends upon the number of moles of the reactants and products. ‘K’ has no units for a reaction in which total number of moles of reactants and products are the same, for example for the reaction ${\mathrm{H}}_2( \mathrm{g})+{\mathrm{I}}_2( \mathrm{g})\rightleftharpoons 2\mathrm{Hl}\left(\mathrm{g}\right); \mathrm{K}=\frac{[\mathrm{HI}{]}^2}{\left[{\mathrm{H}}_2\right]\left[{\mathrm{I}}_2\right]}=\frac{{\left({\mathrm{molL}}^{–1}\right)}^2}{\left({\mathrm{molL}}^{–1}\right)\left({\mathrm{molL}}^{–1}\right)}$ = No units.

Equilibrium constant has units for a reaction in which the total number of moles of reactants and products are different.  For the general reaction.

$\mathrm{aA}+\mathrm{bB}\rightleftharpoons \mathrm{cC}+\mathrm{dD}$

${\mathrm{K}}_{\mathrm{c}}=\frac{[\mathrm{C}{]}^{\mathrm{c}} [\mathrm{D}{]}^{\mathrm{d}}}{\left[\mathrm{A}{]}^4 \right[ \mathrm{B}{]}^{–1}}=\frac{{\left({\mathrm{molL}}^{–1}\right)}^{\mathrm{c}+\mathrm{d}}}{{\left({\mathrm{molL}}^{–1}\right)}^{\mathrm{ath}}}={\left({\mathrm{molL}}^{–1}\right)}^{(\mathrm{c}+\mathrm{d})–(\mathrm{a}+\mathrm{b})}$ = (mol L^–1)^Δn

Similarly for a reaction containing gaseous reactants and gaseous products

${\mathrm{K}}_{\mathrm{p}}=\frac{{\mathrm{p}}_{\mathrm{C}}^{\mathrm{c}} {\mathrm{p}}_{\mathrm{D}}^{\mathrm{d}}}{{\mathrm{p}}_{\mathrm{A}}^{\mathrm{a}} {\mathrm{p}}_{\mathrm{B}}^{\mathrm{b}}}=(\mathrm{atm}{)}^{(\mathrm{c}+\mathrm{d})–(\mathrm{a}+\mathrm{b})}=(\mathrm{atm}{)}^{\mathrm{\Delta n}}\text{ or }(\mathrm{bar}{)}^{\mathrm{\Delta n}}$

For the reaction

${\mathrm{N}}_2( \mathrm{g})+3{\mathrm{H}}_2( \mathrm{g})\rightleftharpoons 2{\mathrm{NH}}_3( \mathrm{g}) \mathrm{\Delta n}=2–4=–2$

Units of K_c = (mol L^–1)^–2; and units of Kp = (atm)^–2

similarly for the reaction

${\mathrm{PCl}}_5( \mathrm{g})\rightleftharpoons {\mathrm{PCl}}_3( \mathrm{g})+{\mathrm{Cl}}_2( \mathrm{g}) \mathrm{\Delta n}=2–1=1$

Units of K_c and K_p are mol L^–1 and atmosphere respectively.  Now a days activities are used in place of molar concentrations or pressures.  These represent concentrations or pressures with respect to a standard state concentration (C_o) of 1 mol L^–1 or standard state pressure (p₀) of 1 bar.  Thus a concentration of 0.5 mol L^–1 with respect to standard state of 1 mol L^–1 means 0.5 mol L^–1/1 mol L^–1 = 0.5, which is a dimensionless quantity.  Hence K_c or K_p are dimensionless.

Reaction Quotient:

For a reaction, aA + bB ƒ cC + dD ; the concentration ratio Q = $\frac{[\mathrm{C}{]}^{\mathrm{c}} [\mathrm{D}{]}^{\mathrm{d}}}{[\mathrm{A}{]}^{\mathrm{a}} [\mathrm{B}{]}^{\mathrm{b}}}$ at any stage of the reaction is called reaction quotient in terms of concentration Q is denoted as Q_C or Q_p depending upon whether the concentration is taken in terms of mol per litre or partial pressures respectively.

At any other stage of the reaction the value of Q_c or Q_p is different from the value of K_c or K_P.  If the value of Q_C or Q_P is not equal to K_C or K_P, the reaction is not at equilibrium.  Depending upon the conditions, the following three cases become possible.

(i) If, the products are present in larger amount as compared to those present at the equilibrium.  Therefore the reaction will be fast in backward direction. or Rate of backward reaction > Rate of forward reaction.

(ii) If Q_C = K_C or Q_P = K_P then the concentration of reactants and products are equal to those at the equilibrium i.e., rate of forward and backward reaction becomes equal.

(iii) If Q_C < K_C or Q_P < K_P; then the products are present in lesser amounts as compared to those present at the equilibrium. Therefore the reaction will be fast in forward direction i.e., reaction has a tendency to form products.

or rate of forward reaction > rate of backward reaction.

Equilibrium constant expressions for some reactions

(i)  Formation of HI:  Let ‘a’ moles of hydrogen and ‘b’ moles of I₂ are heated in a sealed bulb having a volume V litre.  If at equilibrium, x moles of each of H₂ and I₂ have reacted, 2x moles of HI will be formed.

$$\begin{gathered} {\mathrm{H}}_2\left(\mathrm{g}\right) + {\mathrm{I}}_2\left(\mathrm{g}\right) \rightleftharpoons 2\mathrm{HI}\left(\mathrm{g}\right) \\ \mathrm{a} \mathrm{b} 0 \mathrm{Initial} \mathrm{moles} \\ \left(\mathrm{a}–\mathrm{x}\right) \left(\mathrm{b}–\mathrm{x}\right) 2\mathrm{x} \mathrm{moles} \mathrm{at} \mathrm{equilibrium} \\ \left(\frac{\mathrm{a}–\mathrm{x}}{\mathrm{V}}\right) \left(\frac{\mathrm{b}–\mathrm{x}}{\mathrm{V}}\right) \frac{2\mathrm{x}}{\mathrm{V}} \mathrm{molar} \mathrm{concentration} \mathrm{at} \mathrm{equilibrium} \end{gathered}$$

Thus equilibrium constant ${\mathrm{K}}_{\mathrm{C}}=\frac{[\mathrm{HI}{]}^2}{\left[{\mathrm{H}}_2\right]\left[{\mathrm{I}}_2\right]}=\frac{{\left(\frac{2\mathrm{x}}{\mathrm{V}}\right)}^2}{\left(\frac{\mathrm{a}–\mathrm{x}}{\mathrm{V}}\right)\left(\frac{\mathrm{b}–\mathrm{x}}{\mathrm{V}}\right)}$

or ${\mathrm{K}}_{\mathrm{C}}=\frac{4{\mathrm{x}}^2}{(\mathrm{a}–\mathrm{x})(\mathrm{b}–\mathrm{x})}$

when a = b = 1, x becomes degree of formation of HI and ${\mathrm{K}}_{\mathrm{c}}=\frac{4{\mathrm{x}}^2}{(1–\mathrm{x}{)}^2}$

For the above reaction Δn = 0

$\therefore {\mathrm{K}}_{\mathrm{P}}={\mathrm{K}}_{\mathrm{c}}(\mathrm{RT}{)}^{\Delta \mathrm{n}}\text{ or }{\mathrm{K}}_{\mathrm{p}}={\mathrm{K}}_{\mathrm{c}}$

(ii) Formation of NH₃

N₂(g)   + 3H₂(g)$\rightleftharpoons$ 2NH₃(g)

 a              b                   0                                      initial moles

If x moles of nitrogen combines with 3x moles of hydrogen and produce 2x moles of ammonia, then at equilibrium, molar concentration of various reactants and products are

$\left[{\mathrm{N}}_2\right]=\frac{(\mathrm{a}–\mathrm{x})}{\mathrm{V}}$

(V is the volume of closed vessel in which reactants and products are present)

$\left[{\mathrm{H}}_2\right]=\frac{(\mathrm{b}–3\mathrm{x})}{\mathrm{V}}$

${\mathrm{NH}}_3=\frac{2\mathrm{x}}{\mathrm{V}}$

${\mathrm{K}}_{\mathrm{C}}=\frac{{\left[{\mathrm{NH}}_3\right]}^2}{\left[{ \mathrm{N}}_2\right]{\left[{\mathrm{H}}_2\right]}^3}=\frac{{\left(\frac{2\mathrm{x}}{\mathrm{V}}\right)}^2}{\frac{(\mathrm{a}–\mathrm{x})}{\mathrm{V}}{\left(\frac{\mathrm{b}–3\mathrm{x}}{\mathrm{V}}\right)}^3}=\frac{4{\mathrm{x}}^2{ \mathrm{V}}^2}{(\mathrm{a}–\mathrm{x})(\mathrm{b}–3\mathrm{x}{)}^3}$

(iii)  Dissociation of PCl₅  

${\mathrm{PCl}}_5( \mathrm{g})\rightleftharpoons {\mathrm{PCl}}_3( \mathrm{g})+{\mathrm{Cl}}_2( \mathrm{g})$

Let a moles of PCl₅ be taken in a closed vessel of volume V litre.  One mole of PCl₅ on dissociation gives one mole of PCl₃ and one mole of Cl₂.

Thus, x moles of PCl₅ will give x moles of PCl₃ and x moles of Cl₂.  At equilibrium, molar concentrations of various reactants and products are  

${\mathrm{PCl}}_5( \mathrm{g})\rightleftharpoons {\mathrm{PCl}}_3( \mathrm{g})+{\mathrm{Cl}}_2( \mathrm{g})$

    a               O                  O                             Initial moles,

(a – X)         x                    x                             moles at equilibrium

$\left(\frac{\mathrm{a}–\mathrm{x}}{\mathrm{V}}\right)$     $\frac{\mathrm{x}}{\mathrm{V}}$               $\frac{\mathrm{x}}{\mathrm{V}}$                             molar concentration at equilibrium 

Thus ${\mathrm{K}}_{\mathrm{c}}=\frac{\left[{\mathrm{PCl}}_3\right] \left[{\mathrm{Cl}}_2\right]}{\left[{\mathrm{PCl}}_5\right]}=\frac{\left(\frac{\mathrm{x}}{\mathrm{V}}\right)\left(\frac{\mathrm{x}}{\mathrm{V}}\right)}{\left(\frac{\mathrm{a}–\mathrm{x}}{\mathrm{V}}\right)}=\frac{{\mathrm{x}}^2}{(\mathrm{a}–\mathrm{x})\mathrm{V}}$

when a = 1, x becomes degree of dissociation and ${\mathrm{K}}_{\mathrm{c}}=\frac{{\mathrm{x}}^2}{(1–\mathrm{x})\mathrm{V}}$

Total number of moles at equilibrium = (a – x) + x + x = a + x

Let the total pressure at equilibrium be P, then partial pressure of PCl₅    

${\mathrm{p}}_{{\mathrm{PCl}}_5}=\left(\frac{\mathrm{a}–\mathrm{x}}{\mathrm{a}+\mathrm{x}}\right)\mathrm{P}, {\mathrm{p}}_{{\mathrm{PCl}}_3}=\frac{\mathrm{x}}{(\mathrm{a}+\mathrm{x})}\mathrm{P}$, ${\mathrm{p}}_{{\mathrm{Cl}}_2}=\left(\frac{\mathrm{x}}{\mathrm{a}+\mathrm{x}}\right)\mathrm{P}$

$\therefore K_p=\frac{p_{PC{l}_3}\times pC{l}_2}{p_{PC{l}_5}}=\frac{\left(\frac{x}{a+x}\right)P\times \left(\frac{x}{a+x}\right)·P}{\left(\frac{a–x}{a+x}\right)·P}$   or   $K_p=\frac{x^{2}P}{(a–x)(a+x)}$

Rules for writing equilibrium constant expression:

While writing expressions for the equilibrium constant following rules must be kept in mind.

1) Expression for the equilibrium constant of a reaction is written in the form of a ratio in which the numerator consists of molar concentrations of the product, each term raised to a power equal to its stoichiometric coefficient in the balanced chemical equation, and the denominator consists of molar concentration terms for the reactants, each term raised to a power equal to the stoichiometric coefficient in the balanced chemical equation.

For example ${\mathrm{H}}_2( \mathrm{g})+{\mathrm{I}}_2( \mathrm{g})\rightleftharpoons 2\mathrm{Hl}\left(\mathrm{g}\right)$

${\mathrm{K}}_{\mathrm{C}}=\frac{[\mathrm{HI}{]}^2}{\left[{\mathrm{H}}_2\right]\left[{\mathrm{I}}_2\right]};{\mathrm{K}}_{\mathrm{P}}=\frac{{\mathrm{p}}^2\mathrm{HI}}{{\mathrm{p}}_{{\mathrm{H}}_2}\times {\mathrm{p}}_{{\mathrm{l}}_2}}$

2) Active mass of a pure solid is constant irrespective of its amount.  If a pure liquid is present in excess its active mass is also constant. In both cases active mass is taken as unity.

e.g., (i)  For the reaction, ${\mathrm{CaCO}}_3( \mathrm{s})\rightleftharpoons \mathrm{CaO}\left(\mathrm{s}\right)+{\mathrm{CO}}_2( \mathrm{g})$

$\mathrm{K}=\frac{\left[\mathrm{CaO}\right(\mathrm{s}\left)\right] \left[{\mathrm{CO}}_2( \mathrm{g})\right]}{\left[{\mathrm{CaCO}}_3( \mathrm{s})\right]}$

But by convention [CaO(s)] = 1 and [CaCO₃(s)] = 1 hence K = [CO₂(g)].  Since the concentration of a gas is usually expressed in terms of partial pressures hence ${\mathrm{K}}_{\mathrm{P}}={\mathrm{P}}_{{\mathrm{CO}}_2}$

$3\mathrm{Fe}\left(\mathrm{s}\right)+4{\mathrm{H}}_2\mathrm{O}\left(\mathrm{g}\right)\rightleftharpoons {\mathrm{Fe}}_3{\mathrm{O}}_4( \mathrm{s})+4{\mathrm{H}}_2( \mathrm{g})$

Equilibrium constant for this reaction.

${\mathrm{K}}_{\mathrm{c}}=\frac{\left[{\mathrm{Fe}}_3{\mathrm{O}}_4( \mathrm{s})\right]{\left[{\mathrm{H}}_2( \mathrm{g})\right]}^4}{\left[\mathrm{Fe}\right(\mathrm{s}){]}^3{\left[{\mathrm{H}}_2\mathrm{O}\left(\mathrm{g}\right)\right]}^4}$

But by convention $\left[{\mathrm{Fe}}_3{\mathrm{O}}_4( \mathrm{s})\right]=\left[\mathrm{Fe}\right(\mathrm{s}\left)\right]=1$

Hence ${\mathrm{K}}_{\mathrm{c}}=\frac{{\left[{\mathrm{H}}_2\left(\mathrm{g}\right)\right]}^4}{{\left[{\mathrm{H}}_2\mathrm{O}\left(\mathrm{g}\right)\right]}^4}$

or  in terms of pressure ${\mathrm{K}}_{\mathrm{P}}=\frac{{\mathrm{p}}_{{\mathrm{H}}_2}^4}{{\mathrm{p}}_{{\mathrm{H}}_2\mathrm{O}}^4}$

(iii) ${\mathrm{HPO}}_4^{–2}\left(\mathrm{aq}\right)+{\mathrm{H}}_2\mathrm{O}\rightleftharpoons {\mathrm{H}}_3{\mathrm{O}}^{+}\left(\mathrm{aq}\right)+{\mathrm{PO}}_4^{–3}\left(\mathrm{aq}\right)$

${\mathrm{K}}_{\mathrm{c}}=\frac{\left[{\mathrm{H}}_3{\mathrm{O}}^{+}\right]\left[{\mathrm{PO}}_4^{–3}\right]}{\left[{\mathrm{HPO}}_4^{2–}\right]}$

(iv) $\mathrm{AgBr}\left(\mathrm{s}\right)\rightleftharpoons {\mathrm{Ag}}^{+}\left(\mathrm{aq}\right)+{\mathrm{Br}}^{–}\left(\mathrm{aq}\right)$

${\mathrm{K}}_{\mathrm{c}}=\frac{\left[{\mathrm{Ag}}^{+}\left(\mathrm{aq}\right)\right]\left[{\mathrm{Br}}^{–}\left(\mathrm{aq}\right)\right]}{\left[\mathrm{AgBr}\right(\mathrm{s}\left)\right]}$

But [AgBr] = 1   $\therefore$ K_c = [Ag⁺] [Br^–]

(v) ${\mathrm{CH}}_4( \mathrm{g})+2{\mathrm{O}}_2( \mathrm{g})\rightleftharpoons {\mathrm{CO}}_2( \mathrm{g})+2{\mathrm{H}}_2\mathrm{O}\left(\ell \right)$

${\mathrm{K}}_{\mathrm{c}}=\frac{\left[{\mathrm{CO}}_2( \mathrm{g})\right]{\left[{\mathrm{H}}_2\mathrm{O}\left(\ell \right)\right]}^2}{\left[{\mathrm{CH}}_4( \mathrm{g})\right]{\left[{\mathrm{O}}_2( \mathrm{g})\right]}^2}$

(vi) ${\mathrm{NH}}_3\left(\mathrm{aq}\right)+{\mathrm{H}}_2\mathrm{O}\left(\ell \right)\rightleftharpoons {\mathrm{NH}}_4^{+}\left(\mathrm{aq}\right)+{\mathrm{OH}}^{–}\left(\mathrm{aq}\right)$

${\mathrm{K}}_{\mathrm{c}}=\frac{\left[{\mathrm{NH}}_4^{+}\left(\mathrm{aq}\right)\right]\left[{\mathrm{OH}}^{–}\left(\mathrm{aq}\right)\right]}{\left[{\mathrm{NH}}_3\left(\mathrm{aq}\right)\right]\left[{\mathrm{H}}_2\mathrm{O}\left(\ell \right)\right]}$     As H₂O is present in excess therefore by convention, [H₂O] is constant and put equal to 1

Hence ${\mathrm{K}}_{\mathrm{c}}=\frac{\left[{\mathrm{NH}}_4^{+}\left(\mathrm{aq}\right)\right]\left[{\mathrm{OH}}^{–}\left(\mathrm{aq}\right)\right]}{\left[{\mathrm{NH}}_3\left(\mathrm{aq}\right)\right]}$

Illustration 1:

The equilibrium constant for the reaction ${\mathrm{H}}_2\left(\mathrm{g}\right)+{\mathrm{I}}_2\rightleftharpoons 2\mathrm{HI}\left(\mathrm{g}\right)$ at 426⁰c is 55.3, what will be the value of equilibrium constant

(i) if the reaction is reversed.

(ii)  If the given reaction is represented as $2{\mathrm{H}}_2+2{\mathrm{I}}_2\rightleftharpoons 4\mathrm{HI}\left(\mathrm{g}\right)$

Solution.

For the reverse reaction

$2\mathrm{HI}\left(\mathrm{g}\right)\rightleftharpoons {\mathrm{H}}_2\left(\mathrm{g}\right)+{\mathrm{I}}_2\left(\mathrm{g}\right)$ the equilibrium constant ${\mathrm{K}}^{‘}=\frac{1}{ \mathrm{K}}=\frac{1}{55.3}$

The reaction $2{\mathrm{H}}_2( \mathrm{g})+2{\mathrm{I}}_2( \mathrm{g})\rightleftharpoons 4\mathrm{Hl}\left(\mathrm{g}\right)$ is obtained by multiplying the reaction.

${\mathrm{H}}_2\left(\mathrm{g}\right)+{\mathrm{I}}_2( \mathrm{g})\rightleftharpoons 2\mathrm{HI} \left(\mathrm{g}\right)$

by 2; hence K^// = (K)² = (55.3)²

Illustration 2:

If one mole of H₂O and 1 mol of CO are taken in a 10 litre vessel and heated to 725 K.  At equilibrium 40% of water reacts with CO according to the equation.

${\mathrm{H}}_2\mathrm{O}\left(\mathrm{g}\right)+\mathrm{CO}\left(\mathrm{g}\right)\rightleftharpoons {\mathrm{H}}_2( \mathrm{g})+{\mathrm{CO}}_2( \mathrm{g})$

Calculate the equilibrium constant for the reaction.

Solution.

                                ${\mathrm{H}}_2\mathrm{O}\left(\mathrm{g}\right)$        +        $\mathrm{CO}\left(\mathrm{g}\right)$     $\rightleftharpoons$     ${\mathrm{H}}_2\left(\mathrm{g}\right)$     +     ${\mathrm{CO}}_2\left(\mathrm{g}\right)$

Initial moles.              1                           1                          0                    0

At equilibrium     = $\left(1–\frac{40}{100}\right)$          $\left(1–\frac{40}{100}\right)$         $\frac{40}{100}$              $\frac{40}{100}$

mols                         = 0.6                       = 0.6                 = 0.4              = 0.4

Molarity                  = $\frac{0.6}{10}$                      = $\frac{0.6}{10}$               = $\frac{0.4}{10}$            = $\frac{0.4}{10}$

                                  = 0.06                     = 0.06                 = 0.04           = 0.04

Equilibrium constant :

${\mathrm{K}}_{\mathrm{c}}=\frac{\left[{\mathrm{H}}_2( \mathrm{g})\right] \left[{\mathrm{CO}}_2( \mathrm{g})\right]}{\left[{\mathrm{H}}_2\mathrm{O}\left(\mathrm{g}\right)\right] \left[\mathrm{CO}\right(\mathrm{g}\left)\right]}=\frac{(0.04)(0.04)}{(0.06)(0.06)}=0.44$

Illustration3:

At a certain temperature, the equilibrium constant K_c is 16 for the gaseous reaction. ${\mathrm{SO}}_2+{\mathrm{NO}}_2\rightleftharpoons {\mathrm{SO}}_3+\mathrm{NO}$

If we take one mol of each of all the four gases in one litre container, what would be the equilibrium concentration of NO and NO₂?

Solution.

                                               $S{O}_2+N{O}_2 \rightleftharpoons S{O}_3+NO$

Initial mols.                         1                       1                       1                       1

At equilibrium, mols        (1 – x)               (1 – x)                (1+x)               (1+x)

Molarity                               $\frac{1–x}{1}$             $\frac{1–x}{1}$               $\frac{1+x}{1}$                $\frac{1+x}{1}$

${\mathrm{K}}_c=\frac{\left[{\mathrm{SO}}_3\right] \left[\mathrm{NO}\right]}{\left[{\mathrm{SO}}_2\right] \left[{\mathrm{NO}}_2\right]}=\frac{(1+\mathrm{x}{)}^2}{(1–\mathrm{x}{)}^2}=16$

or       $\frac{1+x}{1–x}=4 \text{ or } x=0.6$

Hence equilibrium concentration of

[NO] = (1 + x) = 1 + 0.6  = 1.6 mol/L

[NO₂] = (1-x) = 1- 0.6 = 0.4 mol/L

Illustration 4:

At 700 K, equilibrium constant for the reaction  is 54.8 if 0.5 mol L^–1 of HI(g) is present at equilibrium at 700K, what are the concentrations of H₂(g) and I₂(g) assuming that we initially started with HI(g) and allowed it to reach equilibrium at 700 K.

Solution.

$2\mathrm{Hl}\left(\mathrm{g}\right)\rightleftharpoons {\mathrm{H}}_2( \mathrm{g})+{\mathrm{I}}_2( \mathrm{g})$

Let, the concentrations of H₂ and I₂ at equilibrium be equal to x mol L^–1 and [HI] = 0.5 mol L^–1

$\therefore {\mathrm{K}}_{\mathrm{c}}=\frac{{\mathrm{x}}^2}{(0.5{)}^2}=\frac{1}{54.8}$

$x^2=\frac{(0.5{)}^2}{54.8}$   or   x = 0.068

Illustration 5:

At 448⁰c, the equilibrium constant (K_c) for the reaction. Predict the direction in which the reaction will proceed to reach equilibrium.  If at initiation of the reaction 4.0⨯10^–2 moles of HI, 2.0⨯10^–2 mols of H₂ and 3.0⨯10^–2 mols of I₂ are present in a 2.0L container.

Solution.

Initial concentrations are

$$\begin{gathered} \left[\mathrm{HI}\right]=\frac{4.0\times {10}^{–2}}{2}=2\times {10}^{–2} \mathrm{mol}{ \mathrm{L}}^{–1} \\ \left[{\mathrm{H}}_2\right]=\frac{2\times {10}^{–2}}{2}=1\times {10}^{–2}{\mathrm{molL}}^{–1} \\ {\mathrm{I}}_2=\frac{3\times {10}^{–2}}{2}=1.5\times {10}^{–2}{\mathrm{molL}}^{–1} \end{gathered}$$

Reaction Quotient, $\mathrm{Q}=\frac{[\mathrm{HI}{]}^2}{\left[{\mathrm{H}}_2\right]\left[{\mathrm{I}}_2\right]}=\frac{{\left(2.0\times {10}^{–2}\right)}^2}{\left(1\times {10}^{–2}\right)\left(1.5\times {10}^{–2}\right)}=2.67$

Q < K_c, hence the reaction will proceed in the forward direction to attain equilibrium.

Illustration 6:

The value of K_c for the reaction ${\mathrm{N}}_2( \mathrm{g})+3{\mathrm{H}}_2( \mathrm{g})\rightleftharpoons 2{\mathrm{NH}}_3( \mathrm{g})$ is 0.50 at 400⁰C find the value of Kp at 400⁰C when concentrations are expressed in mol L^–1 and pressure in atmosphere?

Solution.

${\mathrm{N}}_2\left(g\right)+3{\mathrm{H}}_2( \mathrm{g})\rightleftharpoons 2{\mathrm{NH}}_3\left(\mathrm{g}\right)$

Δn = 2 – (1 + 3) = – 2;

R = 0.082  L-atm degree^–1 mol ^–1; Kc = 0.50

$\therefore {\mathrm{K}}_{\mathrm{p}}={\mathrm{K}}_{\mathrm{c}}(\mathrm{RT}{)}^{\Delta \mathrm{n}}=0.50\times (0.082\times 673{)}^{–2}$ = $\frac{0.5}{\left(55.185\right)}=1.641\times {10}^{–4}$

Illustration 7:

For the reaction $\mathrm{A}\left(\mathrm{g}\right)+\mathrm{B}\left(\mathrm{s}\right)\rightleftharpoons \mathrm{C}\left(\mathrm{g}\right)+\mathrm{D}\left(\mathrm{g}\right)$ K_c = 49 mol L^–1 at 127⁰C.  Calculate K_p^.

Solution.

${\mathrm{K}}_{\mathrm{p}}={\mathrm{K}}_{\mathrm{c}}{\left(\mathrm{RT}\right)}^{∆\mathrm{n}}$

K_c = 49 mol L^–1, R = 0.0821 L-atm dig^–1 mol^–1

T = 127 + 273 = 400 K

Δn = 2 – 1 = 1

Exercise 2:

(i) If the equilibrium constant of the reaction $2\mathrm{Hl}\left(\mathrm{g}\right)\rightleftharpoons {\mathrm{H}}_2( \mathrm{g})+{\mathrm{I}}_2( \mathrm{g})$ is 0.25,  the equilibrium constant of the reaction H₂(g) + I₂ (g) ƒ 2HI(g) will be

(A) 2.0

(B) 4.0

(C) 1.0

(D) 3.0

(ii) The factor which changes the equilibrium constant of the reaction A₂(g) + B₂(g) ƒ 2 AB(g) is

(A) total pressure

(B) amounts of A₂ and B₂

(C) temperature

(D) catalyst

(iii) For the equilibrium NH₄HS(s) ƒ NH₃(g) + H₂S(g)

(A) ${\mathrm{K}}_{\mathrm{p}}=\frac{1}{2}\mathrm{p}$

(B) ${\mathrm{K}}_{\mathrm{p}}=\frac{1}{4}\mathrm{p}$

(C) ${\mathrm{K}}_{\mathrm{p}}=\frac{1}{4}{\mathrm{p}}^2$

(D) ${\mathrm{K}}_{\mathrm{p}}=\frac{1}{2}{\mathrm{p}}^2$

(iv) The equilibrium of the reaction ${\mathrm{N}}_2( \mathrm{g})+3{\mathrm{H}}_2( \mathrm{g})\rightleftharpoons 2{\mathrm{NH}}_3( \mathrm{g})$ will be shifted to the right when

(A) K_p > 1

(B) Q < K_P

(C) Q = K_P

(D) Q < 2K_P

(v) In which of the following chemical reactions at equilibrium is K_P ≠ K_C?

(A) ${\mathrm{N}}_2{\mathrm{O}}_4( \mathrm{g})\rightleftharpoons 2{\mathrm{NO}}_2( \mathrm{g})$

(B) ${\mathrm{PCl}}_5( \mathrm{g})\rightleftharpoons {\mathrm{PCl}}_3( \mathrm{g})+{\mathrm{Cl}}_2( \mathrm{g})$

(C) $2{\mathrm{SO}}_2( \mathrm{g})+{\mathrm{O}}_2( \mathrm{g})\rightleftharpoons 2{\mathrm{SO}}_3( \mathrm{g})$

(D)  All of these

(vi) Let K₁ and K₂ be the equilibrium constants for the reactions (1) and (2).

${\mathrm{N}}_2( \mathrm{g})+{\mathrm{O}}_2( \mathrm{g})\rightleftharpoons 2\mathrm{NO}\left(\mathrm{g}\right)$……. (1)

$\mathrm{NO}\left(\mathrm{g}\right)\rightleftharpoons \frac{1}{2}{ \mathrm{N}}_2( \mathrm{g})+\frac{1}{2}{\mathrm{O}}_2( \mathrm{g})$ ……. (2)

Then

A) ${\mathrm{K}}_1={\left(\frac{1}{{ \mathrm{K}}_2}\right)}^2$

(B) ${\mathrm{K}}_1={\mathrm{K}}_2^2$

(C) ${\mathrm{K}}_1=\frac{1}{{ \mathrm{K}}_2}$ 

(D) ${\mathrm{K}}_1={\left({\mathrm{K}}_2\right)}^0$

Le Chatelier’s principle:

The effect of concentration, temperature and pressure on a system in equilibrium can be predicted with the help of Le Chatelier’s principle.

According to this principle, “If a system at equilibrium is subjected to a change of concentration, temperature or pressure, the equilibrium shifts in the direction that tends to cancel the effect of applied change.

1. Effect of change in concentration :

If a system is at equilibrium and the concentration of one of the species involved in the reaction is increased then the system will readjust so as to decrease the concentration of that species.  Similarly if the concentration of some substance is decreased, the reaction proceed so as to make up the loss in the concentration.  In other words, if any of the reactant is added, the rate of forward reaction increases and if any of the products is added, the rate of backward reaction increases.

In general, In a chemical equilibrium increasing the concentration of reactants or decreasing the concentration of products results in shifting the equilibrium in favour of products.  Similarly increasing the concentration of products or decreasing the concentration of reactants shifts the equilibrium in backward direction i.e., toward the formation of reactants.

For example : (i)  The chemical equilibrium taking place in Haber’s process is ${\mathrm{N}}_2( \mathrm{g})+3{\mathrm{H}}_2( \mathrm{g})\rightleftharpoons 2{\mathrm{NH}}_3\left(\mathrm{g}\right)$.

(i) In this process an increase in the concentration of N₂ and H₂ shifts the equilibrium in the forward direction.  Similarly if NH₃ gas is removed from the reaction mixture, this removal of product also increases the rate of formation of NH₃.

(ii) In the decomposition of CaCO₃ to form quick lime (CaO) and CO₂.  If the gaseous, CO₂ which is one of the product is allowed to escape, the reaction continues to move in the forward direction.

(iii) Clothes dry quicker when there is a breeze because water vapour of the nearby air are removed and cloth loses more water vapour to re-establish equilibrium with the surrounding air.

2. Effect of change of pressure on Equilibrium:

Change of pressure has effect only on those equilibria which involve gaseous reactants or products and the reaction proceeds with a change in number of gaseous moles.

When the pressure on a reaction involving gases is changed, the equilibrium will shift in a direction, so as to cancel the effect of change in pressure.  If the pressure on the system is increased, the volume of the system will decrease proportionately.  Hence total number of moles per unit volume will now be more than before.  Therefore the equilibrium will shift in that direction in which the total number of moles decreases.

Similarly if the pressure on the system is decreased the equilibrium will shift in the direction which is accompanied by increase in total number of moles.

e.g., PCl₅ dissociates according to the reaction.

PCl₅ $\rightleftharpoons$ PCl₃ + Cl₂

When pressure is increased in this equilibrium, the system moves in the direction in which volume decreases.  Thus high pressure does not favour dissociation of PCl₅.

Illustration 8:

What is the effect of increasing pressure on the following physical equilibrium. Ice $\rightleftharpoons$ Water

Solution.

The volume of fixed mass of water is less than that of ice at its melting point.  Therefore an increase in pressure will favour the forward reaction i.e., when pressure is applied to a system containing ice and water at equilibrium more ice will melt.

Effect of pressure on solubility of gas:

When the pressure on the gas is increased, the equilibrium shifts in a direction so as to decrease the volume of the gas.  As a result more gas gets dissolved in the liquid, it means the solubility of gas in liquid increases with increase in pressure.

(ii) For the reaction : ${\mathrm{N}}_2+3{\mathrm{H}}_2\rightleftharpoons 2{\mathrm{NH}}_3$

The forward reaction is accompanied by a decrease in total number of moles.  If the pressure on the system is increased, the volume will decrease considerably.  Then according to Le Chatelier’s principle the equilibrium will shift in that direction in which decrease in the total number of moles takes place.  Thus higher the pressure better would be the yield of NH₃.

Effect of change of Temperature on Equilibrium:

A reversible chemical reaction involves two opposing reactions, forward and backward.  If the forward reaction is endothermic, the backward reaction will be exothermic and vice versa.  The change of temperature alters the state of equilibrium for only those reactions in which either heat is evolved or heat is absorbed.  According to Le chatelier’s principle.

a) An increase in the temperature of a chemical system at equilibrium favours the reaction that proceed with the absorption of heat i.e., an endothermic reaction is favoured.

b) A decrease in temperature of a system at equilibrium favours the reaction which proceed with the evolution of heat i.e., an exothermic reaction is favoured.

For example : (i)  the reaction  

${\mathrm{N}}_2( \mathrm{g})+3{\mathrm{H}}_2( \mathrm{g})\rightleftharpoons 2{\mathrm{NH}}_3( \mathrm{g}) \Delta \mathrm{H}=–93.6 \mathrm{kJ}/\mathrm{mol}$

is exothermic in the forward direction and endothermic in the backward direction.

• If the temperature is increased i.e., heat is supplied to the system, then according to Le chaterier’s principle, the equilibrium will shift to the side that absorbs heat i.e., in the backward direction. Similarly decrease in temperature will shift the equilibrium in the forward direction.

(ii)  Formation of NO from nitrogen and oxygen is one of the initial reaction for the Birkland – Eyde process for the manufacture of nitric acid.

${\mathrm{N}}_2+{\mathrm{O}}_2\rightleftharpoons 2\mathrm{NO} \Delta \mathrm{H}=+180.7 \mathrm{kJ}/\mathrm{mol}$

This reaction is endothermic i.e., heat is absorbed during the reaction. Due to endothermic nature of the reaction, an increase in temperature will favour the forward reaction i.e., more NO is formed at higher temperature.

4) Effect of catalyst on equilibrium:

Catalyst does not shift the position of equilibrium in any direction.  Positive catalyst increases the rate of both forward and backward reactions equally; i.e., the equilibrium is attained in less time.  On the other hand negative catalyst lowers the rate of both forward and backward reactions equally.  Same amount of product will be formed in more time in present of negative catalyst.  Thus presence of catalyst does not affect the equilibrium constant.

5) Effect of adding an inert gas at equilibrium:

(i)  Effect of adding an inert gas at constant pressure : Addition of the inert gas at constant pressure increases the total volume of the system.  Hence at equilibrium the molar concentration of each of the reactants and products will decrease.  As a result equilibrium will shifts towards larger number of gaseous molecule.

e.g.  For the dissociation of PCl₅,

PCl₅(g) $\rightleftharpoons$ PCl₃(g) + Cl₂ (g)

When inert gas is added at constant pressure, molar concentration (moles per unit volume) of both reactants and products decreases.

Hence to keep K_c constant the equilibrium will shift towards larger number of gaseous moles.  This can happen only if more of PCl₅ dissociates to give PCl₃ and Cl₂.  Hence, dissociation of PCl₅ increases with the addition of an inert gas at constant pressure.

(ii) Effect of adding an inert gas at constant volume: If the reaction takes place at constant volume i.e., the volume of reaction vessel is not allowed to increase, addition of inert gas will not change the molar concentration of the reactants and products.  Hence the state of equilibrium will remain unaffected.

Application of Le Chatelier’s Principle:

1. Manufacture of ammonia (Haber’s Process):

${\mathrm{N}}_2\left(\mathrm{g}\right)+3{\mathrm{H}}_2\left(\mathrm{g}\right)\rightleftharpoons 2{\mathrm{NH}}_3\left(\mathrm{g}\right) \Delta \mathrm{H}=–93.6 \mathrm{kJ}/\mathrm{mol}$

i) Effect of concentration : An increase in the concentration of reactants i.e., N₂ and H₂ or removal of NH₃ from reaction mixture would shift the equilibrium in forward direction i.e., formation of NH₃ would be favoured.  If concentration of only one reactant is raised than again equilibrium shifts in forward direction till the other reactant is available for reaction.

ii) Effect of pressure : The reaction proceeds with a decrease in volume.  Therefore an increase in pressure should favour the forward reaction.  The most favourable pressure range for the production of ammonia is found to be 200 – 900 atm pressure.

Effect of temperature:

The reaction is exothermic, therefore the Le Chaterier’s principle predicts lower temperature to be favourable for the forward reaction.  But at low temperature the reaction is very slow, if the temperature is kept low the reaction will take a long time to attain equilibrium state.  So an optimum temperature of 725 – 775K is used.  Finely divided iron is used as a catalyst to achieve equilibrium rapidly and molybdenum is used to increase the efficiency of the catalyst.

2. Industrial synthesis of SO₃ (contact process):

During the manufacture of sulphuric acid (contact process) SO₃ is prepared by the oxidation of SO₂.

i) Effect of concentration : Higher the concentration of SO₂ and O₂ greater would be the yield of  SO₃.  If the reaction is carried out under excess of oxygen the equilibrium shifts in a direction so as to give larger amount of SO₃ due to the effect of increased concentration of one of the reactant.

ii) Effect of pressure : The forward reaction takes place with decrease in number of moles or the decrease in volume.  If pressure on the system is increased, the volume will decrease correspondingly.  Hence the total number of moles per unit volume will now be more than before.  Therefore as per Le Chatelier principle, equilibrium will shift in that direction in which decrease in number of moles occurs i.e., in the forward direction.  But at high pressures, the towers used in the synthesis are corroded.  Therefore optimum pressure of 1.5 to 1.7 atmosphere serves the purpose.

(iii) Effect of temperature:  The forward reaction leading to the formation of SO₃ is an exothermic reaction.  Hence low temperature will be favourable for higher yield.  But at the low temperatures the reaction is slow.  Therefore an optimum temperature of 673K – 723K is used, and platinised asbestos or V₂O₅ is used as a catalyst to attain the equilibrium state rapidly.

3) Formation of Nitric oxide:

Formation of nitric oxide by direct combination of N₂ and O₂ is the initial reaction for the Birkland – Eyde process for the manufacture of nitric acid.

${\mathrm{N}}_2\left(\mathrm{g}\right)+{\mathrm{O}}_2\left(\mathrm{g}\right)\rightleftharpoons 2\mathrm{NO} \Delta \mathrm{H}=+180.7 \mathrm{kJ}$

i) Effect of concentration : When concentration of N₂ or O₂ is increased, the rate of forward reaction increases thereby increasing the concentration of NO.

ii) Effect of pressure : In the formation of NO, the number of moles remains the same, hence the equilibrium state is not affected by any change in pressure.

iii) Effect of temperature : Due to endothermic nature of the reaction, an increase in temperature will favour the forward reaction i.e., more NO is formed at higher temperature.

Exercise 3:

(i) On the basis of Le Chatelier’s principle, predict which of the following conditions would be unfavourable for the formation of SO₃?  Given that

$2{\mathrm{SO}}_2\left(\mathrm{g}\right)+{\mathrm{O}}_2\left(\mathrm{g}\right)\rightleftharpoons 2{\mathrm{SO}}_3\left(\mathrm{g}\right); \Delta \mathrm{H}=–42\mathrm{kcal}$

(A) Low temperature

(B) High temperature

(C) High pressure

(D) High concentration of SO₂

(ii) The conditions which favour the manufacture of ammonia by the reaction

${\mathrm{N}}_2( \mathrm{g})+3{\mathrm{H}}_2( \mathrm{g})\rightleftharpoons 2{\mathrm{NH}}_3( \mathrm{g}); \Delta {\mathrm{H}}^0=–92 \mathrm{kJ}$

(A) low temperature and high pressure

(B) low temperature and low pressure

(C) high temperature and low pressure

(D) high temperature and high pressure

(iii) Consider the following reaction in a closed container at equilibrium

CaCO₃(s) ƒ$\rightleftharpoons$ CaO (s) + CO₂(g)

What would be the effect of addition of CaCO₃ on the equilibrium concentrations of CO₂?

(A) Concentration of CO₂ will increase

(B) Concentration of CO₂ will decrease

(C) Concentration of CO₂ will remain unaffected

(D) Data insufficient to predict it

(iv) Which of the following gaseous reactions will be favoured by low pressure?

(A) ${\mathrm{H}}_2\left(\mathrm{g}\right)+{\mathrm{I}}_2\left(\mathrm{g}\right)\rightleftharpoons 2\mathrm{Hl}\left(\mathrm{g}\right)$

(B) ${\mathrm{PCl}}_5\left(\mathrm{g}\right)\rightleftharpoons {\mathrm{PCl}}_3\left(\mathrm{g}\right)+{\mathrm{Cl}}_2\left(\mathrm{g}\right)$

(C) ${\mathrm{N}}_2\left(\mathrm{g}\right)+3{\mathrm{H}}_2\left(\mathrm{g}\right)\rightleftharpoons 2{\mathrm{NH}}_3\left(\mathrm{g}\right)$

(D) ${\mathrm{N}}_2\left(\mathrm{g}\right)+{\mathrm{O}}_2\left(\mathrm{g}\right)\rightleftharpoons 2\mathrm{NO}\left(\mathrm{g}\right)$

(v) For the equilibrium

$2{\mathrm{NO}}_2( \mathrm{g})\rightleftharpoons {\mathrm{N}}_2{\mathrm{O}}_4( \mathrm{g})+14.6 \mathrm{kcal}$

increase in temperature would

(A) favour the formation of N₂O₄

(B) favour the decomposition of N₂O₄

(C) not alter the equilibrium

(D) stop the reaction

(vi) For the reaction

${\mathrm{CH}}_3\mathrm{COOH}+{\mathrm{H}}_2\mathrm{O}\rightleftharpoons {\mathrm{CH}}_3{\mathrm{COO}}^{–}+{\mathrm{H}}_3{\mathrm{O}}^{+}$

The equilibrium constant is most likely to be changed by

(A) the addition of acetic acid solution

(B) the addition of a suitable catalyst

(C) the addition of acetate ions

(D) heating the given mixture

Application of Le Chatelier’s principle to physical equilibrium:

1) Solubility of substances:  When solid substances are dissolved in water either heat is evolved or heat is absorbed. Certain salts like NH₄Cl, KCl dissolve with the absorption of heat.  The solubility of such salts increases with increase in temperature.

$\mathrm{KCl}+\mathrm{aq}\rightleftharpoons \mathrm{KCl}\left(\mathrm{aq}\right)–\text{ heat }$

On the other hand, certain salts like NaOH, KOH, (CH₃COO)₂Ca etc dissolve with the evolution of heat.

$\mathrm{KOH}+\mathrm{aq}\rightleftharpoons \mathrm{KOH}\left(\mathrm{aq}\right)+\text{ heat }$

In such cases solubility decreases with increase in temperature.

2)  Effect of pressure on melting point: 

i) Solids whose volume decrease on melting e.g. ice

$\underset{\left(\mathrm{More} \mathrm{volume}\right)}{\mathrm{Ice}} \stackrel{+\mathrm{Heat}}{\rightleftharpoons } \underset{\left(\mathrm{Less} \mathrm{volume}\right)}{\mathrm{Water}}$

On increasing the pressure on this system the equilibrium shifts in a direction in which volume decreases.  Thus increasing pressure favours change of ice into water i.e., more of ice melts.  This process of melting is facilitated at high pressure, thus melting point is lowered.

ii) The volume of some solids increases on melting e.g., iron silver, copper etc. In this case the process of melting become difficult at high pressure, thus melting point becomes high.

Effect of pressure on boiling point:

The change of water to water vapour is a reversible endothermic process. The reaction involves increase in volume.

$\underset{\mathrm{Less} \mathrm{volume}}{\mathrm{Water}}+\mathrm{Heat} \rightleftharpoons \underset{\mathrm{More} \mathrm{volume}}{\mathrm{Water} \mathrm{vapour}}$

On increasing the pressure on this system, the equilibrium shifts towards condensation of water vapour into water.  Thus more heat is required to equate vapour pressure with atmospheric pressure as a result of which boiling point increases.

Exercise 4:

(i) Which of the following factors will favour the reverse reaction in a chemical equilibrium?

(A) Increase in concentration of one of the reactants

(B) Increase in concentration of one of the products

(C) Removal of one of the products at regular intervals

(D) None of these

(ii) According to Le Chatelier’s principle, adding heat to a system of solid and liquid at equilibrium will cause the

(A) amount of solid to decrease

(B) amount of liquid to decrease

(C)  temperature to rise

(D)  temperature to fall

(iii) Le Chatelier’s principle is applicable only to a

(A) system not in equilibrium

(B) homogeneous system

(C) heterogeneous system

(D) system at equilibrium

(iv) Pure ammonia is placed in a vessel at a temperature at which its dissociation constant is appreciable. At equilibrium

(A) K_P does not change significantly with pressure

(B) the degree of dissociation does not change with pressure

(C) the concentration of NH₃ does not change

(D) the concentration of H₂ is less than that of N₂

Relationship between equilibrium constant and standard Free Energy change:

For any reversible reaction, A + B $\rightleftharpoons$ C + D, the free energy change and standard free energy change are related with each other by the following relation.

$\Delta \mathrm{G}=\Delta {\mathrm{G}}^0+{\mathrm{RTlog}}_{\mathrm{e}}\mathrm{Q}$

Where R is universal constant and Q is reaction quotient.

At equilibrium state ΔG = 0 and Q = K

$\therefore 0=\Delta {\mathrm{G}}^0+{\mathrm{RTlog}}_{\mathrm{e}}{\mathrm{K}}_{\mathrm{c}}$

or ${\mathrm{\Delta G}}^0=–{\mathrm{RTlog}}_{\mathrm{e}}{\mathrm{K}}_{\mathrm{c}}$

or $\Delta {\mathrm{G}}^0=–2.303\mathrm{RT} {\mathrm{logK}}_{\mathrm{c}}$

when ΔG⁰ = 0;   then K_c = 1

when ΔG⁰ > 0 then K_c < 1.  In this case reverse reaction is feasible i.e., less concentration of products at equilibrium state.

When ΔG⁰ < 0 then K_c > 1.  In this case forward reaction is feasible.  It represents large concentration of products at equilibrium.

Answer to Exercises

Exercise 1.

(i) D     (ii) D     (iii) D     iv) C

Exercise 2.

(i) B     (ii) C     (iii) C     (iv) B     (v) D     (vi) A

Exercise 3.

(i) B     (ii) A     (iii) C     (iv) B     (v) B     (vi) D

Exercise 4.

(i) B     (ii) A     (iii) D     (iv) A

FORMULAE AND CONCEPTS AT A GLANCE  

1. For a general reaction

aA + bB $\rightleftharpoons$ cC + dD

${\mathrm{K}}_{\mathrm{c}}=\frac{\left[\mathrm{C}{]}^{\mathrm{c}} \right[\mathrm{D}{]}^{\mathrm{d}}}{\left[\mathrm{A}{]}^{\mathrm{a}} \right[\mathrm{B}{]}^{\mathrm{b}}}$ {[A], [B], [C], [D] are molar con of A, B, C and D}

Unit of K_c = (mol L^–1)^{(c + d) – (a + b)}

${\mathrm{K}}_{\mathrm{p}}=\frac{{\left[{\mathrm{P}}_{\mathrm{C}}\right]}^{\mathrm{c}} {\left[{\mathrm{P}}_{\mathrm{D}}\right]}^{\mathrm{d}}}{{\left[{\mathrm{P}}_{\mathrm{A}}\right]}^{\mathrm{a}} {\left[{\mathrm{P}}_{\mathrm{B}}\right]}^{\mathrm{b}}}$ {Where P_A, P_B­, P_C and P_D are partial pressure of A, B, C and D]

Unit of K_p = (atm)^{(c + d) – (a + b)}

Catalysts donot shift the equilibria.

Only it helps to achieve equilibria earlier.

2. ${\mathrm{K}}_{\mathrm{p}}={\mathrm{K}}_{\mathrm{c}}[\mathrm{RT}{]}^{∆{\mathrm{n}}_{\mathrm{gaseous}}}$

$\begin{array}{ll}\Delta \mathrm{n}=\left[\right(\mathrm{c}+\mathrm{d})–(\mathrm{a}+\mathrm{b}\left)\right]& \\ \Delta \mathrm{n}=0,& { \mathrm{K}}_{\mathrm{p}}={\mathrm{K}}_{\mathrm{c}}\\ \Delta \mathrm{n}=+\mathrm{ve},& {\mathrm{K}}_{\mathrm{p}}>{\mathrm{K}}_{\mathrm{c}}\\ \Delta \mathrm{n}=–\mathrm{ve},& {\mathrm{K}}_{\mathrm{p}}<{\mathrm{K}}_{\mathrm{c}}\end{array}$

3. As catalyst increases rate of both forward and backward reaction upto same extant.

4. Reaction quotient and K

Q > K reaction goes backward;  Q < K reaction goes forward; Q = K equilibrium  

5. We already know,

As concentration of both reactants and products remains constant after attaining equilibrium, which is dynamic in nature. Hence the rate of conversion from reactant to product or vice-versa is equal to equilibrium. So, one should be with rate of reaction and rate law (law of mass action) in order to study chemical equilibrium in detail.  

6. Temperature coefficient of reaction = $\frac{{\mathrm{K}}_{\mathrm{t}+10°}}{{\mathrm{K}}_{\mathrm{t}}}\approx 2 \mathrm{to} 3$

where K_t and K_t+10 are rate constant at t and (t + 10)^oC respectively.

7. The value of equilibrium constant changes with temperature. The values of equilibria constants at two different temperature and related by the following equation:

$\log \frac{{\mathrm{K}}_2}{{ \mathrm{K}}_1}=\frac{\mathrm{\Delta H}}{2.303\mathrm{R}}\left[\frac{1}{{ \mathrm{T}}_1}–\frac{1}{{ \mathrm{T}}_2}\right]$

when ΔH = 0, i.e., heat of reaction at constant volume is zero,  K₂ = K₁

when ΔH = +ve, i.e., endothermic reaction, K₂ > K₁

and when ΔH = -ve, i.e., exothermic reaction,    K₂ < K₁  

8. Standard free energy change of a reaction and its equilibrium constant are related to each other at temperature T by the following relation:

$\mathrm{\Delta G}°=–2.303\mathrm{RT} {\mathrm{logK}}_{\mathrm{p}}$, when $\mathrm{\Delta G}°=–\mathrm{ve}$ the value of equilibrium constant will be large positive quantity and when $\mathrm{\Delta G}°=+\mathrm{ve}$ the value of K is less than 1.

SOLVED PROBLEMS-1

Prob 1.

K_C for the reaction, ${\mathrm{N}}_2+3{\mathrm{H}}_2\rightleftharpoons 2{\mathrm{NH}}_3$ is 0.5 mol^–2 litre² at 400 K.  Find K_P.  Given R = 0.082 litre atm degree^–1 mol^–1.

Sol.

K_P = K_C (RT)^Δn

${\mathrm{K}}_{\mathrm{p}}=0.5\times (0.082\times 400{)}^{–2}$

${\mathrm{K}}_{\mathrm{p}}=4.648\times {10}^{–4}( \mathrm{atm}{)}^{–2}$

Prob 2.

In which case does the reaction go farthest to completion.  K = I, K = 10¹⁰; K = 10^–10 and why?

Sol.

The ratio $\left[\frac{\mathrm{Product}}{\mathrm{Reactant}}\right]$ is maximum when K = 10¹⁰ and thus, reaction goes farthest to completion when K = 10¹⁰.

Prob 3.

For a gaseous phase reaction, $2\mathrm{HI}\rightleftharpoons {\mathrm{H}}_2+{\mathrm{I}}_2$ at equilibrium 7.8g, 203.2g and 1638.4g of H₂, I₂ and HI respectively were found in 5 litre vessel.  Calculate K_C.  If all the reactants and products are transferred to a 2 litre vessel, what will be the amount of reactants and products at equilibrium?

Sol.

Mole at equilibrium

$$\begin{gathered} 2\mathrm{HI} \rightleftharpoons {\mathrm{H}}_2 + {\mathrm{I}}_2 \\ \frac{1638.4}{128} \frac{7.8}{2} \frac{203.2}{254} \\ = 12.8 3.8 0.8 \end{gathered}$$

Let volume of container be V litre

$\left[{\mathrm{H}}_2\right]=\frac{3.9}{ \mathrm{V}}; \left[\mathrm{HI}\right]=\frac{12.8}{ \mathrm{V}}; \left[{\mathrm{I}}_2\right]=\frac{0.8}{ \mathrm{V}}$

$\therefore {\mathrm{K}}_{\mathrm{C}}=\frac{\left[{\mathrm{H}}_2\right] \left[{\mathrm{I}}_2\right]}{[\mathrm{H}{]}^2}=\frac{3.9\times 0.8}{ \mathrm{V}\times \mathrm{V}\times {\left(\frac{12.8}{ \mathrm{V}}\right)}^2}=0.019$

$\therefore$ K_C = 0.019

Prob 4.

At a certain temperature, K_C for ${\mathrm{SO}}_2\left(\mathrm{g}\right)+{\mathrm{NO}}_2\left(\mathrm{g}\right)\rightleftharpoons {\mathrm{SO}}_3\left(\mathrm{g}\right)+\mathrm{NO}\left(\mathrm{g}\right)$ is 16.  If we take one mole of each of all the four gases in one litre container, what would be the equilibrium concentration of NO and NO₂?

Sol.

                                        ${\mathrm{SO}}_2\left(\mathrm{g}\right)$      +         ${\mathrm{NO}}_2\left(\mathrm{g}\right)$   $\rightleftharpoons$     ${\mathrm{SO}}_3\left(\mathrm{g}\right)$       +           $\mathrm{NO}\left(\mathrm{g}\right)$

Mole at t = 0                      1                            1                            1                            1

Mole at equilibrium       (1 – x)                 (1 – x)                    (1 + x)                   (1 + x)

$\therefore {\mathrm{K}}_{\mathrm{C}}=\frac{\left(\frac{1+\mathrm{x}}{\mathrm{V}}\right)\left(\frac{1+\mathrm{x}}{\mathrm{V}}\right)}{\left(\frac{1–\mathrm{x}}{\mathrm{V}}\right)\left(\frac{1–\mathrm{x}}{\mathrm{V}}\right)}=\frac{(1+\mathrm{x}{)}^2}{(1–\mathrm{x}{)}^2}$

$\therefore \frac{(1+x{)}^2}{(1–x{)}^2}=16 \left(\because {\mathrm{K}}_{\mathrm{c}}=16\right)$

$\therefore \frac{(1+\mathrm{x})}{(1–\mathrm{x})}=4 \text{ or } \mathrm{x}=\frac{3}{5}=0.6$

$\because$ Volume = 1 litre

$\because \left[{\mathrm{SO}}_2\right]=\left[{\mathrm{NO}}_2\right]=1–\mathrm{x}=1–0.6=0.4 \mathrm{mol}{\text{ litre }}^{–1}$

$\left[{\mathrm{SO}}_3\right]=\left[\mathrm{NO}\right]=1+\mathrm{x}=1+0.6=1.6 \mathrm{mol}{\text{ litre }}^{–1}$

Prob 5.

For the reaction $\mathrm{A}+\mathrm{B} \rightleftharpoons 3\mathrm{C}$ at 25⁰C, a, 3 litre vessel contains 1, 2, 4 mole of A, B and C respectively.  Predict the direction of reaction if

a) K_C for the reaction is 10.

b) K_C for the reaction is 15.

c) K_C for the reaction is 10.66

Sol.

$\mathrm{A}+\mathrm{B} \rightleftharpoons 3\mathrm{C}$

Before reaction,     [A] = 1/3

                                  [B] = 2/3

                                  [C] = 4/3

Thus, $\mathrm{Q}=\frac{[\mathrm{C}{]}^3}{[ \mathrm{A}] \left[\mathrm{B}\right]}=\frac{4^3\times 3\times 3}{3^3\times 1\times 2}=\frac{64}{6}=10.66$

(a) Since K_C = 10, thus Q must decrease to attain K_C, value and thus, [C] must decrease or [A] and [B] should increases. Thus, reaction will occur in backward direction.

(b) Since K_C = 15, thus Q must increase to attain K_C value and thus, [C] must increase or [A] and [B] should decrease. Thus, reaction will occur in forward direction.

(c) Q = K_C; thus, reaction is in equilibrium.

Prob 6.

How much PCl₅ must be added to a one litre vessel at 250⁰C in order to obtain a concentration of 0.1 mole of Cl₂?  K_C for $PC{l}_5 \rightleftharpoons PC{l}_3+C{l}_2$ is 0.0414 mol/litre.

Sol.                               PCl₅      ƒ$\rightleftharpoons$      PCl₃           +        Cl₂

Initial mole                     a                    0                            0

Mole at equilibrium   (a – 0.1)            0.1                        0.1

${\mathrm{K}}_{\mathrm{C}}=\frac{\frac{0.1}{1}\times \frac{0.1}{1}}{\frac{\mathrm{a}–0.1}{1}}$ ($\because$ volume is 1litre)

or  $0.0414=\frac{0.01}{(a–0.1)}$   or    a = 03415 mole

Prob 7.

K_C for $\frac{3}{2}{\mathrm{H}}_2+\frac{1}{2}{ \mathrm{N}}_2\rightleftharpoons {\mathrm{NH}}_3$ are 0.0266 and 0.0129 atm^–1 at 350⁰C and 400⁰C respectively.  Calculate heat of formation of NH₃.

Sol.

$2.303{\log }_{10}\frac{{\mathrm{K}}_{{\mathrm{P}}_2}}{{ \mathrm{K}}_{{\mathrm{P}}_1}}=\frac{\mathrm{\Delta H}}{\mathrm{R}}\left[\frac{{\mathrm{T}}_2–{\mathrm{T}}_1}{{ \mathrm{T}}_1{ \mathrm{T}}_2}\right]$

$2.303{\log }_{10}\frac{0.0129}{0.0266}=\frac{\mathrm{\Delta H}}{2}\left[\frac{673–623}{673\times 623}\right]$

ΔH = – 12140 cal

= – 12.140 kcal

Prob 8.

For NH₄HS(s) ƒ$\rightleftharpoons$ NH₃(g) + H₂S(g), the observed pressure for reaction mixture in equilibrium is 1.12 atm at 106⁰C.  What is the value of K_P for the reaction?

Sol.

                                             ${\mathrm{NH}}_4\mathrm{HS}\left(\mathrm{s}\right)\rightleftharpoons {\mathrm{NH}}_3( \mathrm{g})+{\mathrm{H}}_2 \mathrm{S}( \mathrm{g})$

Pressure at equilibrium                               P                P

$\therefore$ Total pressure at equilibrium = 2P = 1.12 atm

$\therefore$ P = 1.12/2 atm

$\because {\mathrm{K}}_{\mathrm{P}}={\mathrm{P}}_{{\mathrm{NH}}_3}^{‘}\times {\mathrm{P}}_{{\mathrm{H}}_2\mathrm{s}}^{‘}$

$\because {\mathrm{K}}_{\mathrm{p}}=\frac{1.12}{2}\times \frac{1.12}{2}=0.3136{ \mathrm{atm}}^2$

Prob 9.

The heat of reaction at constant volume for an endothermic reaction in equilibrium is 1200 cal more than at constant pressure at 300 K.  Calculate the ratio of equilibrium constants K_P and K_C.

Sol.

Given that ΔE – ΔH = 1200 cal

Where ΔE is heat of reaction at constant volume and ΔH is heat of reaction at constant pressure.

Also, we have   ΔH = ΔE + ΔnRT

ΔnRT = – 1200

$\mathrm{\Delta n}=\frac{–1200}{2\times 300}=–2 (\mathrm{R}=2\mathrm{cal})$

Now    K_P = K_C (RT)^Δn

$\therefore \frac{{\mathrm{K}}_{\mathrm{P}}}{{\mathrm{K}}_{\mathrm{C}}}=(0.0821\times 300{)}^{–2}=1.648\times {10}^{–3}$

Prob 10.

At 273K and one atm, ‘a’ litre of N₂O₄ decomposes to NO₂ according to equation N₂O₄(g) ƒ $\rightleftharpoons$2NO₂(g). To what extent has the decomposition proceeded when the original volume is 25% less than that of existing volume?

Sol.

                                                 ${\mathrm{N}}_2{\mathrm{O}}_4\left(\mathrm{g}\right) \rightleftharpoons 2{\mathrm{NO}}_2\left(\mathrm{g}\right)$

Mole before equilibrium          a                      0

Mole at equilibrium                 (a – x)             2x

Given that original volume = $\frac{75}{100}\times$ existing volume at equilibrium

Since     mole $\propto$ volume      (at constant P and T)

Initial mole = $\frac{75}{100}\times$mole at equilibrium

$a=\frac{75}{100}\left(a+x\right)$

$\therefore \mathrm{x}=\frac{25}{75}\mathrm{a}=0.33\mathrm{a}$

Now % decomposition $\left(\alpha \right)=\frac{x}{a}=\frac{0.33a}{a}=0.33\text{ or }33\%$

SOLVED PROBLEMS-2

Prob 1.

Consider the following equilibrium in a closed container ${\mathrm{N}}_2{\mathrm{O}}_4( \mathrm{g})\rightleftharpoons 2{\mathrm{NO}}_2( \mathrm{g})$

At a fixed temperature, the volume of the reaction container is halved.  For this change, which of the following statements holds true regarding the equilibrium constant (K_P) and degree of dissociation ($\alpha$)?

(A) neither K_P nor α changes

(B) both K_P and α change

(C) K_P changes, but α does not change

(D) K_P does not change, but α changes

Sol.

(B)

For this reaction, ${\mathrm{K}}_{\mathrm{p}}=\frac{4{\alpha }^2\mathrm{P}}{\left(1–{\alpha }^2\right)}$

When the volume of the reaction container is halved, pressure get doubled.  As a result, the reaction proceeds  in the backward direction. This means, due to a decrease in the value of α, both P and α change.

Prob 2.

The equilibrium constant for the reaction N₂(g) + O₂(g) $\rightleftharpoons$ ƒ 2NO(g) at temperature t is 4 ⨯ 10^–4.  The value of K_C for the reaction $\mathrm{NO}\left(\mathrm{g}\right)\rightleftharpoons \frac{1}{2}{ \mathrm{N}}_2( \mathrm{g})+\frac{1}{2}{\mathrm{O}}_2( \mathrm{g})$ at the same temperature is                (A) 2.5 ⨯ 10²

(B) 0.02

(C) 4 ⨯ 10^–4

(D) 50

Sol.

(D)

For ${\mathrm{N}}_2( \mathrm{g})+{\mathrm{O}}_2( \mathrm{g})\rightleftharpoons 2\mathrm{NO}\left(\mathrm{g}\right)$     ${\mathrm{K}}_{\mathrm{C}}=\frac{[\mathrm{NO}{]}^2}{\left[{ \mathrm{N}}_2\right] \left[{\mathrm{O}}_2\right]}$

and

For $\mathrm{NO}\left(\mathrm{g}\right)=\frac{1}{2}{ \mathrm{N}}_2\left(\mathrm{g}\right)+\frac{1}{2}{\mathrm{O}}_2\left(\mathrm{g}\right)$     ${\mathrm{K}}_{\mathrm{C}}^{\mathrm{t}}=\frac{{\left[{\mathrm{N}}_2\right]}^{1/2} {\left[{\mathrm{O}}_2\right]}^{1/2}}{\left[\mathrm{NO}\right]}$

Comparing the two expressions, one can write

${\mathrm{K}}_{\mathrm{C}}^{‘}=\frac{1}{{\sqrt{\mathrm{K}}}_{\mathrm{C}}}=\frac{1}{{\left(4\times {10}^{–4}\right)}^{1/2}}=\frac{1}{2\times {10}^{–2}}=50$

Prob 3.

For the reaction $\mathrm{CO}\left(\mathrm{g}\right)+{\mathrm{Cl}}_2\left(\mathrm{g}\right)\rightleftharpoons {\mathrm{COCl}}_2\left(\mathrm{g}\right)$ the K_P/K_C is equal to

(A) 1/RT

(B)  1.0

(C) $\sqrt{RT}$

(D) RT

Sol.

(A)

In this reaction, $\Delta {\mathrm{n}}_g=1–(1+1)=–1\le$

For a reversible reaction  $\frac{{\mathrm{K}}_{\mathrm{P}}}{{\mathrm{K}}_{\mathrm{C}}}=(\mathrm{RT}{)}^{\Delta \mathrm{n}}=(\mathrm{RT}{)}^{–1}=\frac{1}{\mathrm{RT}}$

Prob 4.

For the reaction equilibrium,  N₂O₄(g) ƒ$\rightleftharpoons$ 2NO₂(g)

The concentrations of N₂O₄ and NO₂ at equilibrium are 4.8 ⨯ 10^–2 and 1.2 ⨯ 10^–2 mol L^–1 respectively.  The value of K_C for the reaction is

(A) 3.3 ⨯ 10² mol L^–1

(B) 3 ⨯ 10^–1 mol L^–1

(C) 3 ⨯ 10^–3 mol L^–1

(D)  3 ⨯ 10³ mol L^–1

Sol.

(C)

${\mathrm{K}}_{\mathrm{c}}=\frac{\left[{\mathrm{NO}}_2\right]}{\left[{\mathrm{N}}_2{\mathrm{O}}_4\right]}=\frac{{\left(1.2\times {10}^{–2} \mathrm{mol}{ \mathrm{L}}^{–1}\right)}^2}{4.8\times {10}^{–2} \mathrm{mol}{ \mathrm{L}}^{–1}}=3\times {10}^{–3} \mathrm{mol}{ \mathrm{L}}^{–1}$

Prob 5.    The equilibrium constant (K_C) of the reaction

${\mathrm{A}}_2( \mathrm{g})+{\mathrm{B}}_2( \mathrm{g})\rightleftharpoons 2\mathrm{AB}\left(\mathrm{g}\right)$

is 50.  If 1 mol of A₂ and 2 mol of B₂ are mixed, the amount of AB at equilibrium would be

(A) 0.934 mol

(B) 0.467 mol

(C) 1.866 mol

(D) 1.401 mol

Sol.

(C)

${\mathrm{A}}_2( \mathrm{g})+{\mathrm{B}}_2( \mathrm{g})\rightleftharpoons 2\mathrm{AB}\left(\mathrm{g}\right)$

1 mol – x             2 mol – x              2x

Since, ΔVg = 0, we will have K_c = K_p = K_n 

${\mathrm{K}}_{\mathrm{n}}=\frac{(2\mathrm{x}{)}^2}{(1 \mathrm{mol}–\mathrm{x}) (1 \mathrm{mol}+\mathrm{x})}$  that is ${\mathrm{K}}_{\mathrm{n}}=\frac{2\mathrm{x}}{(1 \mathrm{mol}–\mathrm{x}) (1 \mathrm{mol}+\mathrm{x})}=50$

Solving for x, we get x = 0.933 mol

Amount of AB = 2x = 1.866 mol

Prob 6.

For the reaction $\mathrm{CO}\left(\mathrm{g}\right)+{\mathrm{H}}_2\mathrm{O}\left(\mathrm{g}\right)\rightleftharpoons {\mathrm{CO}}_2( \mathrm{g})$ at a given temperature, the equilibrium amount of CO₂(g) can be increased by

(A) adding a suitable catalyst

(B) adding an inert gas

(C) decreasing the volume of the container

(D) increasing the amount of CO(g)

Sol.

(D)

By increasing the amount of CO(g), the reaction in the forward direction gets favoured.

Prob 7.

If concentration of reactants is increased by x, then the K becomes

(A) $e^{\raisebox{1ex}{$K$}\!\left/ \!\raisebox{-1ex}{$x$}\right.}$

(B) K

(C) K/x

(D) x/K

Sol.

(B)

The value of K is independent of the concentration of reactants.

Prob 8.

For the chemical reaction,  $3X\left(g\right)+Y\left(g\right)\rightleftharpoons X_{3}Y\left(g\right)$ the amount of X₃Y at equilibrium is affected by

(A) temperature and pressure

(B) temperature only

(C) pressure only

(D) temperature, pressure and catalyst

Sol.

(A)

The position of equilibrium, therefore, the relative concentrations of the reactants and products depend upon temperature and pressure.

Prob 9.

For the reaction

${\mathrm{N}}_2{\mathrm{O}}_4( \mathrm{g})\rightleftharpoons 2{\mathrm{NO}}_2( \mathrm{g})$

The relation connecting the degree of dissociation (α) of N₂O₄(g) with the equilibrium constant K_p is

(A) $\alpha =\frac{{\mathrm{K}}_{\mathrm{p}}/\mathrm{P}}{4+{\mathrm{K}}_{\mathrm{p}}/\mathrm{P}}$

(B) $\alpha =\frac{{\mathrm{K}}_{\mathrm{p}}}{4+{\mathrm{K}}_{\mathrm{p}}}$

(C) $\alpha ={\left(\frac{{\mathrm{K}}_{\mathrm{p}}/\mathrm{P}}{4+{\mathrm{K}}_{\mathrm{p}}/\mathrm{P}}\right)}^{1/2}$

(D) $\alpha ={\left(\frac{K_p}{4+K_p}\right)}^{1/2}$

Sol.

(C)

${\mathrm{N}}_2{\mathrm{O}}_4( \mathrm{g})\rightleftharpoons 2{\mathrm{NO}}_2( \mathrm{g})$

1 – α             2 – α;

$n_{total}=1+\alpha$

${\mathrm{PN}}_2{\mathrm{O}}_4=\frac{1–\alpha }{1+\alpha }\mathrm{P}$       ${\mathrm{P}}_{{\mathrm{NO}}_2}=\frac{2\mathrm{\alpha }}{1+\mathrm{\alpha }}\mathrm{P}$

${\mathrm{K}}_{\mathrm{p}}=\frac{{\mathrm{P}}_{{\mathrm{NO}}_2}}{{\mathrm{P}}_{{\mathrm{NO}}_2}}={\left(\frac{2\alpha }{1+\alpha }\mathrm{P}\right)}^2\left(\frac{1+\alpha }{1–\alpha }\frac{1}{\mathrm{P}}\right)=\frac{4{\alpha }^2}{1–{\alpha }^2}\mathrm{P}$

Rearranging, we get   $\alpha ={\left(\frac{{\mathrm{K}}_{\mathrm{p}}/\mathrm{P}}{4+{\mathrm{K}}_{\mathrm{p}}/\mathrm{P}}\right)}^{1/2}$

Prob 10.

Given the following reaction at equilibrium

${\mathrm{SO}}_2( \mathrm{g})+\frac{1}{2}{\mathrm{O}}_2( \mathrm{g})\rightleftharpoons {\mathrm{SO}}_3( \mathrm{g})$

The addition of an inert gas at constant volume would cause

(A) the formation of more of SO₃

(B) the formation of less of SO₃

(C) no affect on the equilibrium concentration of SO₃

(D) the system to move to a new equilibrium position which cannot be theoretically predicted

Sol.

(C)

The addition of inert gas at constant volume changes pressure. This will not affect equilibrium as equilibrium constant is independent of pressure.