Three Dimensional Geometry

1. COORDINATE OF A POINT IN SPACE

There are infinite number of points in space. We want to identify each and every point of space with the help of three mutually perpendicular coordinate axes OX, OY and OZ.

Three mutually perpendicular lines OX, OY, OZ are considered as the three axes.

The plane formed with the help of x and y axes is called x-y plane, similarly y & z axes form y-z plane and z and x axes form z – x plane.

Consider any point P in the space, Drop a perpendicular from that point to x -y plane, then the algebraic length of this perpendicular is considered as z-coordinate and from foot of the perpendicular drop perpendiculars to x and y axes. These algebraic lengths of perpendiculars are considered as y and x coordinates respectively.

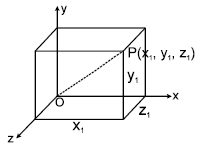
2. VECTOR REPRESENTATION OF A POINT IN SPACE

If coordinate of a point P in space is (x, y, z) then the position vector of the point P with respect to the same origin is $\mathrm{x}\hat{\mathrm{i}}+\mathrm{y}\hat{\mathrm{j}}+\mathrm{z}\hat{\mathrm{k}}$.

3. SIGNS OF CO-ORDINATES OF A POINT IN VARIOUS OCTANTS

Octant $\to$ Coordinates $\downarrow$	I	II	III	IV	V	VI	VII	VIII
x	+	–	–	+	+	–	–	+
y	+	+	–	–	+	+	–	–
Z	+	+	+	+	–	–	–	–

4. DISTANCE FORMULA

Distance between any two points (x₁, y₁, z₁) and (x₂, y₂, z₂) is given as $\sqrt{{\left(x_1–x_2\right)}^2+{\left(y_1–y_2\right)}^2+{\left(z_1–z_2\right)}^2}$

Vector method

We know that if position vector of two points A and B are given as $\overrightarrow{\mathrm{OA}}$ and $\overrightarrow{\mathrm{OB}}$ then

$\mathrm{AB}=|\overrightarrow{\mathrm{OB}}–\overrightarrow{\mathrm{OA}}|$

$\Rightarrow \mathrm{AB}=\left|\left({\mathrm{x}}_2\mathrm{i}+{\mathrm{y}}_2\mathrm{j}+{\mathrm{z}}_2\mathrm{k}\right)–\left({\mathrm{x}}_1\mathrm{i}+{\mathrm{y}}_1\mathrm{j}+{\mathrm{z}}_1\mathrm{k}\right)\right|$

$AB=\sqrt{{\left(x_2–x_1\right)}^2+{\left(y_2–y_1\right)}^2+{\left(z_2–z_1\right)}^2}$

5. DISTANCE OF A POINT P FROM COORDINATE AXES

Let PA, PB and PC are distances of the point P(x, y, z) from the coordinate axes OX, OY and OZ respectively then

$\mathrm{PA}=\sqrt{{\mathrm{y}}^2+{\mathrm{z}}^2}, \mathrm{PB}=\sqrt{{\mathrm{z}}^2+{\mathrm{x}}^2}, \mathrm{PC}=\sqrt{{\mathrm{x}}^2+{\mathrm{y}}^2}$

Illustration-1

Show that the points (0, 7, 10), (– 1, 6, 6) and (– 4, 9, 6) form a right angled isosceles triangle.

Solution

Let A $\equiv$ (0, 7, 10), B $\equiv$ (–1, 6, 6), C $\equiv$ (– 4, 9, 6)

AB² = (0 + 1)² + (7 – 6)² + (10 – 6)² = 18

$\therefore \mathrm{AB}=3\sqrt{2}$

Similarly

$\therefore \mathrm{BC}=3\sqrt{2}, \& \mathrm{AC}=6$

Clearly AB² +BC² = AC²

$\therefore \angle ABC=90°$

Also   AB = BC

Hence $∆\mathrm{ABC}$ is right angled isosceles.

Illustration-2

Show by using distance formula that the points (4, 5, –5), (0, –11, 3) and (2, –3, –1) are collinear.

Solution

Let A$\equiv$(4, 5, -5), B $\equiv$ (0, -11, 3), C $\equiv$ (2, -3, -1)

$\mathrm{AB}=\sqrt{(4–0{)}^2+(5+11{)}^2+(–5–3{)}^2}=\sqrt{336}=\sqrt{4\times 84}=2\sqrt{84}$

$\mathrm{BC}=\sqrt{(0–2{)}^2+(–11+3{)}^2+(3+1{)}^2}=\sqrt{84}$

$\mathrm{AC}=\sqrt{(4–2{)}^2+(5+3{)}^2+(–5+1{)}^2}=\sqrt{84}$

BC + AC = AB

Hence points A, B, C are collinear and C lies between A and B.

Illustration-3

Find the locus of a point which moves such that the sum of its distances from points A(0, 0, –$\alpha$) and B(0, 0, $\alpha$) is constant.

Solution

Let the variable point whose locus is required be P(x, y, z)

Given PA + PB = constant = 2a (say)

$\therefore \sqrt{(\mathrm{x}–0{)}^2+(\mathrm{y}–0{)}^2+(\mathrm{z}+\mathrm{\alpha }{)}^2}+\sqrt{(\mathrm{x}–0{)}^2+(\mathrm{y}–0{)}^2+(\mathrm{z}–\mathrm{\alpha }{)}^2}=2\mathrm{a}$

$\Rightarrow \frac{1}{2}=2\mathrm{a}–\sqrt{{\mathrm{x}}^2+{\mathrm{y}}^2+(\mathrm{z}–\mathrm{\alpha }{)}^2}$

$\Rightarrow {\mathrm{x}}^2+{\mathrm{y}}^2+{\mathrm{z}}^2+{\mathrm{\alpha }}^2+2\mathrm{z\alpha }=4{\mathrm{a}}^2+{\mathrm{x}}^2+{\mathrm{y}}^2+{\mathrm{z}}^2+{\mathrm{\alpha }}^2–2\mathrm{z\alpha }$$–4\mathrm{a}\sqrt{{\mathrm{x}}^2+{\mathrm{y}}^2+(\mathrm{z}–\mathrm{\alpha }{)}^2}$

$\Rightarrow 4\mathrm{z\alpha }–4{\mathrm{a}}^2=–4\mathrm{a}\sqrt{{\mathrm{x}}^2+{\mathrm{y}}^2+(\mathrm{z}–\mathrm{\alpha }{)}^2}$

$\Rightarrow \frac{{\mathrm{z}}^2{\mathrm{\alpha }}^2}{{\mathrm{a}}^2}+{\mathrm{a}}^2–2\mathrm{z\alpha }={\mathrm{x}}^2+{\mathrm{y}}^2+{\mathrm{z}}^2+{\mathrm{\alpha }}^2–2\mathrm{z\alpha }$

or,   ${\mathrm{x}}^2+{\mathrm{y}}^2+{\mathrm{z}}^2\left(1–\frac{{\mathrm{\alpha }}^2}{{\mathrm{a}}^2}\right)={\mathrm{a}}^2–{\mathrm{\alpha }}^2\text{ or, }\frac{{\mathrm{x}}^2+{\mathrm{y}}^2}{{\mathrm{a}}^2–{\mathrm{\alpha }}^2}+\frac{{\mathrm{z}}^2}{{\mathrm{a}}^2}=1$

This is the required locus.

Illustration-4

The point equidistant from the points A(a,0,0), B (0,b,0), C (0,0,c) and origin.

Solution

Let P (x, y, z) be the required point

OP² = PA²

$\Rightarrow {\mathrm{x}}^2+{\mathrm{y}}^2+{\mathrm{z}}^2=(\mathrm{x}–\mathrm{a}{)}^2+{\mathrm{y}}^2+{\mathrm{z}}^2$

$\Rightarrow 2\mathrm{ax}={\mathrm{a}}^2$

$\therefore x=\frac{a}{2}$, similarly  y =b/2, z= c/2

$\therefore$ P(a/2, b/2, c/2)

Illustration-5

The distance of the point ( 1,2,3) from the x-axis is

Solution

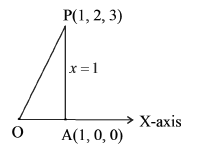
OA = 1,     $\mathrm{OP}=\sqrt{14}$

$\Rightarrow \mathrm{PA}=\sqrt{{\mathrm{OP}}^2–{\mathrm{OA}}^2}=\sqrt{14–1}=\sqrt{13}=\sqrt{{\mathrm{y}}^2+{\mathrm{z}}^2}$

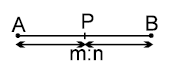
6. SECTION FORMULA

If point P divides the distance between the points $A\left(x_1,y_1,z_1\right)\text{ and }B\left(x_2,y_2,z_2\right)$ in the ratio of m : n, then coordinates of P are given as

$\left(\frac{{\mathrm{mx}}_2+{\mathrm{nx}}_1}{\mathrm{m}+\mathrm{n}},\frac{{\mathrm{my}}_2+{\mathrm{ny}}_1}{\mathrm{m}+\mathrm{n}},\frac{{\mathrm{mz}}_2+{\mathrm{nz}}_1}{\mathrm{m}+\mathrm{n}}\right)$

Mid point

$\left(\frac{{\mathrm{x}}_1+{\mathrm{x}}_2}{2},\frac{{\mathrm{y}}_1+{\mathrm{y}}_2}{2},\frac{{\mathrm{z}}_1+{\mathrm{z}}_2}{2}\right)$

7. CENTROID OF A TRIANGLE

$G\equiv \left(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3},\frac{z_1+z_2+z_3}{3}\right)$

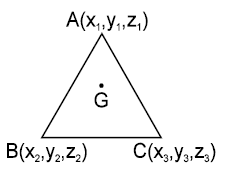
8. INCENTRE OF TRIANGLE ABC

$\left(\frac{a{x}_1+b{x}_2+c{x}_3}{a+b+c},\frac{a{y}_1+b{y}_2+c{y}_3}{a+b+c},\frac{a{z}_1+b{z}_2+c{z}_3}{a+b+c}\right)$

Where AB = c, BC = a, CA = b

9. CENTROID OF A TETRAHEDRON

A(x₁, y₁, z₁) B(x₂, y₂, z₂) C(x₃, y₃, z₃) and DC(x₄, y₄, z₄) are the vertices of a tetrahedron then coordinate of its centroid (G) is given as

$\left(\frac{\sum {\mathrm{x}}_{\mathrm{i}}}{4},\frac{\sum {\mathrm{y}}_{\mathrm{i}}}{4},\frac{\sum {\mathrm{z}}_{\mathrm{i}}}{4}\right)$

Illustration-6

Show that the points A(2, 3, 4), B(–1, 2, –3) and C(–4, 1, –10) are collinear. Also find the ratio in which C divides AB.

Solution

Given A $\equiv$ (2, 3, 4), B $\equiv$ (–1, 2, –3), C $\equiv$ (– 4, 1, –10).

Let C divide AB internally in the ratio k : 1, then

$\mathrm{C}\equiv \left(\frac{–\mathrm{k}+2}{\mathrm{k}+1},\frac{2\mathrm{k}+3}{\mathrm{k}+1},\frac{–3\mathrm{k}+4}{\mathrm{k}+1}\right)$

$\therefore \frac{–\mathrm{k}+2}{\mathrm{k}+1}=–4 \Rightarrow 3\mathrm{k}=–6 \Rightarrow \mathrm{k}=–2$

For this value of k, $\frac{2\mathrm{k}+3}{\mathrm{k}+1}=1,\text{ and }\frac{–3\mathrm{k}+4}{\mathrm{k}+1}=–10$

Since k < 0, therefore k divides AB externally in the ratio 2 : 1 and points A, B, C are collinear.

Illustration-7

The vertices of a triangle are A(5, 4, 6), B(1, –1, 3) and C(4, 3, 2). The internal bisector of $\angle$BAC meets BC in D. Find AD.

Solution

$\mathrm{AB}=\sqrt{4^2+5^2+3^2}=5\sqrt{2}$

$\mathrm{AC}=\sqrt{1^2+1^2+4^2}=3\sqrt{2}$

Since AD is the internal bisector of $\angle$BAC

$\therefore \frac{\mathrm{BD}}{\mathrm{DC}}=\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{5}{3}$

$\therefore$ D divides BC internally in the ratio 5 : 3

$\therefore \mathrm{D}\equiv \left(\frac{5\times 4+3\times 1}{5+3},\frac{5\times 3+3(–1)}{5+3},\frac{5\times 2+3\times 3}{5+3}\right)$

or,   $D=\left(\frac{23}{8},\frac{12}{8},\frac{19}{8}\right)$

$\therefore AD=\sqrt{{\left(5–\frac{23}{8}\right)}^2+{\left(4–\frac{12}{8}\right)}^2+{\left(6–\frac{19}{8}\right)}^2}$

$=\frac{\sqrt{1530}}{8}\text{ unit }$

Illustration-8

If the points P, Q, R, S are (4, 7, 8), (– 1, – 2, 1), (2, 3, 4) and (1, 2, 5) respectively, show that PQ and RS intersect. Also find the point of intersection.

Solution

Let the lines PQ and RS intersect at point A.

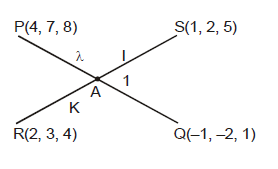
Let A divide PQ in the ratio $\lambda$ : 1, then

$\mathrm{A}\equiv \left(\frac{–\mathrm{\lambda }+4}{\mathrm{\lambda }+1},\frac{–2\mathrm{\lambda }+7}{\mathrm{\lambda }+1},\frac{\mathrm{\lambda }+8}{\mathrm{\lambda }+1}\right)....\left(1\right)$

Let A divide RS in the ratio k : 1, then

$A\equiv \left(\frac{k+2}{k+1},\frac{2k+3}{k+1},\frac{5k+4}{k+1}\right).....\left(2\right)$

From (1) and (2), we have,

$\frac{–\lambda +4}{\lambda +1}=\frac{k+2}{k+1}.....\left(3\right)$

$\frac{–2\lambda +7}{\lambda +1}=\frac{2k+3}{k+1}.....\left(4\right)$

$\frac{\lambda +8}{\lambda +1}=\frac{5k+4}{k+1}.....\left(5\right)$

From (3), $–\mathrm{\lambda k}–\mathrm{\lambda }+4\mathrm{k}+4=\mathrm{\lambda k}+2\mathrm{\lambda }+\mathrm{k}+2$

or   $2\lambda k+3\lambda –3k–2=0.....\left(6\right)$

From (4),  $–2\lambda k–2\lambda +7k+7=2\lambda k+3\lambda +2k+3$

or     $4\lambda \mathrm{k}+5\lambda –5\mathrm{k}–4=0.....\left(7\right)$

Multiplying equation (6) by 2, and subtracting from equation (7), we get

– $\lambda$ + k = 0 or,  $\lambda$ = k

Putting $\lambda$ = k in equation (6), we get

$2{\lambda }^2+3\lambda –3\lambda –2=0$

or,     $\lambda =\pm 1$

But $\lambda \ne –1$, as the co-ordinates of P would then be underfined and in this case

PQ || RS, which is not true.

$\therefore \lambda =1=k$.

Clearly $\lambda$ k = 1 satisfies eqn. (5).

Hence our assumption is correct

$\therefore A\equiv \left(\frac{–1+4}{2},\frac{–2+7}{2},\frac{1+8}{2}\right) \text{ or, } A\equiv \left(\frac{3}{2},\frac{5}{2},\frac{9}{2}\right).$

10. COLLINEAR POINTS

If the points $\mathrm{A}\left({\mathrm{x}}_1,{\mathrm{y}}_1,{\mathrm{z}}_1\right),\mathrm{B}\left({\mathrm{x}}_2,{\mathrm{y}}_2,{\mathrm{z}}_2\right)\text{ and }C\left(x_3,y_3,z_3\right)$ are collinear points then

AB : BC = $\left(x_1–x_2\right):\left(x_2–x_3\right)$ or $\left({\mathrm{y}}_1–{\mathrm{y}}_2\right):\left({\mathrm{y}}_2–{\mathrm{y}}_3\right)\text{ or }\left({\mathrm{z}}_1–{\mathrm{z}}_2\right):\left({\mathrm{z}}_2–{\mathrm{z}}_3\right)$ or $\frac{x_1–x_2}{x_2–x_3}=\frac{y_1–y_2}{y_2–y_3}=\frac{z_1–z_2}{z_2–z_3}$   or   $\left|\begin{array}{ccc}{x}_1& y_1& z_1\\ x_2& y_2& z_2\\ x_3& y_3& z_3\end{array}\right|=0$

11. COORDINATE PLANE DIVIDES LINE SEGMENT

If A(x₁, y₁, z₁) and B(x₂, y₂, z₂) are two points then

i) yoz plane divides the line segment AB in the ratio $–x_1:x_2$

ii) zox plane divides the line segment AB in the ratio $–y_1:y_2$

iii) x o y plane divides the line segment AB in the ratio $–z_1:z_2$

iv) The internal angular bisector of angle A of triangle ABC intersect the opposite side BC in D and I is incentre of the triangle then

i) BD : DC = AB:AC           ii) AI : ID = AB+AC : BC

12. LOCUS

i) The set of all points in the space satisfying given condition or a given property is called locus.

ii) If p(x, y, z) is any point in a Locus then the algebraic relation between x, y, z obtained by using geometrical condition is called the equation of the locus.

iii) The Locus of the point which is at a distance of k units from

XOY plane is |z| = k

YOZ plane is |x| = k

ZOX plane is |y| = k

iv) The Locus of the point which is equidistant from

a) XY- plane and YZ – plane is $z^2–x^2=0$

b)YZ- plane and XZ – plane is $x^2–y^2=0$

c) XZ- plane and XY – plane is $y^2–z^2=0$

13. TRANSLATION OF AXES

i) The transformation that obtained by shifting origin to some another point without changing the direction of axes is called Translation of axes.

ii) If we shift the origin to the point (h,k,l) without changing the directions of the coordinate axes and (x,y,z) and (X,Y,Z) are the coordinates of the point P with respect to the old axes, new axes
respectively, then

x = X + h, y = Y + k, z = Z + l

Illustration-9

The line passing through the points A (5,1,a) and B (3,b,1) crosses the yz – plane at the point $\left(0,\frac{17}{2},–\frac{13}{2}\right)$

Then the values of a, b are

Solution

YZ plane divides $\overline{AB}$ in the ratio = $–x_1:x_2$

$\left(0,\frac{–5b+3}{–2},\frac{–5+3a}{–2}\right)=\left(0,\frac{17}{2},\frac{–13}{2}\right)\Rightarrow a=6,b=4$

Illustration-10

The ratio in which the line joining the points A ( -3,4,8) and B( 5,-6,4) is divided by xoy plane and the point of intersection of the line with the plane.

Solution

Let P divides AB in the ratio $\lambda :1$

$\Rightarrow$ P is in xoy plane

$\Rightarrow \frac{4\lambda +8}{\lambda +1}=0 \Rightarrow \lambda =–2$

$\Rightarrow x o y$plane divides AB externally in the ratio 2:1, Point of intersection = ( 13,-16,0)

Illustration-11

If the vertices of a triangle are A( 3,2,0) B(5,3,2) C( -9,6,-3) , the internal bisector of angle A meets BC in D, then co-ordinates of D are

Solution

We know that $\frac{BD}{DC}=\frac{BA}{AC}=\frac{3}{13}$

$\therefore D=\left(\frac{3(–9)+13.5}{3+13},\frac{3.6+13.3}{3+13},\frac{3(–3)+13.2}{3+13}\right)=\left(\frac{38}{16},\frac{57}{16},\frac{17}{16}\right)$

Illustration-12

What is the locus of the equation $x^2+y^2+z^2+1=0$

Solution

Sum of positive numbers not equal to zero

Locus is an empty set