Atoms

1. RUTHERFORD’S α -PARTICLE SCATTERING EXPERIMENT

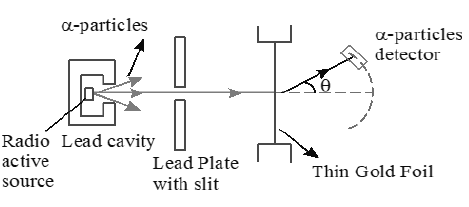
Experimental Observations:

a) Most of the α- particles were found to pass through the gold- foil without being deviated from their paths.

b) Some α- particles were found to be deflected through small angles θ < 90°.

c) Few α- particles were found to be scattered at fairly large angles from their initial path θ > 90°

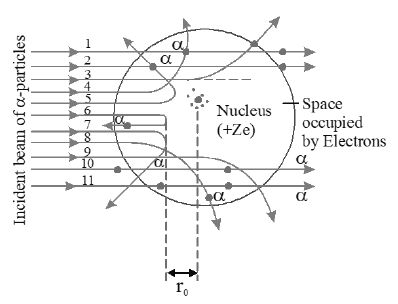
d) A very small number of α- particles about 1 in 8000 practically retracted their paths or suffered deflections of nearly 180°.

• The observation (a) indicates that most of the portion of the atom is hollow inside.

• Because α- particle is positively charged, from the observations (b), (c) and (d) atom also have positive charge and the whole positive charge of the atom must be concentrated in small space which is at the centre of the atom is called nucleus. The remaining part of the atom and electrons are revolving around the nucleus in circular
objects of all possible radii. The positive charge present in the nuclei of different metals is different . Higher the positive charge in the nucleus, larger will be the angle of scattering of α- particle.

2. DISTANCE OF CLOSEST APPROACH

• An α- particle which moves straight towards the nucleus in head on direction reaches the nucleus i.e, it moves close to a distance $r_0$ as shown the figure.

• As the α- particle approaches the nucleus, the electrostatic repulsive force due to the nucleus increases and kinetic energy of the alpha particle goes on converting into the electrostatic potential energy. When whole of the kinetic energy is converted into electrostatic potential energy, the α- particle cannot further move towards the
nucleus but returns back on its initial path i.e α- particle is scattered through an angle of 180°. The distance of α- particle from the nucleus in this stage is called as the distance of closest approach and is represented by $r_0$

• Let m_α and v_α be the mass and velocity of the α- particle directed towards the centre of the nucleus. Then kinetic energy of the α- particle $\mathrm{K}=\left(\frac{1}{2}\right){\mathrm{m}}_{\mathrm{\alpha }}{\mathrm{v}}^2\mathrm{\alpha }$

Because the positive charge on the nucleus is Ze and that on the α- particle 2e, hence the electrostatic potential energy of the α- particle, when at a distance ${\mathrm{r}}_0$ from the centre of the nucleus, is given by  $\mathrm{U}=\frac{1}{4\mathrm{\pi }{\in }_0}·\frac{\left(2\mathrm{e}\right)\left(\mathrm{Ze}\right)}{{\mathrm{r}}_0}$

Because at r = $r_0$ kinetic energy of the α- particle appears as its potential energy, hence, K=U

$\frac{1}{4\mathrm{\pi }{\in }_0}.\frac{\left(2\mathrm{e}\right)\left(\mathrm{Ze}\right)}{{\mathrm{r}}_0}=\frac{1}{2}{ \mathrm{m}}_{\mathrm{\alpha }}{\mathrm{v}}_{\mathrm{\alpha }}^2$

${\mathrm{r}}_0=\frac{1}{4\mathrm{\pi }{\in }_0}\frac{4{\mathrm{Ze}}^2}{{\mathrm{m}}_{\mathrm{\alpha }}{\mathrm{v}}_{\mathrm{\alpha }}^2}$

Note:

• When a mono energitic beam of α particles is projected towards a thin metal foil, some of the particles are found to deviate from their original path. This phenomenon is called α ray scattering

• It is caused by coulomb repulsive force between α particles and positive charges in atom.

• The number of α -particles scattered at an angle θ is given by $\mathrm{N}=\frac{{\mathrm{Qntz}}^2{\mathrm{e}}^4}{{\left(8{\mathrm{\pi \epsilon }}_0\right)}^2{\mathrm{r}}^2{\mathrm{E}}^2{\sin }^4\left(\frac{\mathrm{\theta }}{2}\right)}$

where

Q → Total number of α particles striking the foil
n → number of atoms per unit volume of the foil
r → distance of screen from the foil
t → thickness of the foil
z → Atomic number of the foil atoms
θ → angle of scettering
E → kinetic energy of α particles

$\mathrm{N}\alpha \mathrm{t}; \mathrm{N}\alpha {\mathrm{z}}^2 ; N\alpha \frac{1}{{\sin }^4\frac{\theta }{2}}$

$\mathrm{N\alpha }\frac{1}{{\mathrm{E}}^2}\text{ or }\mathrm{N\alpha }\frac{1}{{\mathrm{v}}^4}$

where $\vartheta$ is the velocity of α particles falling on the foil.

3. IMPACT PARAMETER(b)

The perpendicular distance of the initial velocity vector of the α- particle from centre of the nucleus is called “impact parameter”.

$\mathrm{b}=\frac{{\mathrm{Ze}}^2\cot \left(\frac{\mathrm{\theta }}{2}\right)}{4\mathrm{\pi }{\in }_0\times \frac{1}{2}{\mathrm{mv}}^2}$

4. BOHR’S MODEL OF HYDROGEN LIKE ATOMS

• Electron can revolve round the nucleus only in certain allowed orbits called stationary orbits and the Coulomb’s force of attraction between electron and the positively charged nucleus provides necessary centripetal force.

$\frac{\mathrm{k}\left(\mathrm{Ze}\right)\mathrm{e}}{{\mathrm{r}}^2}=\frac{{\mathrm{mV}}^2}{\mathrm{r}}$

• Suppose m is the mass of electron, V is the velocity and ‘r’ is the radius of the orbit, then in stationary orbits the angular momentum of the electron is an integral multiple of $\frac{h}{2\mathrm{\pi }}$, where h is the Planck’s constant. The angular momentum $\mathrm{L}=\mathrm{I\omega }=\mathrm{mVr}=\mathrm{n}\frac{\mathrm{h}}{2\mathrm{\pi }}$ where n is called principal quantum number.

• An electron in a stationary orbit has a definite amount of energy. It posses kinetic energy because of its motion and potential energy on account of the attraction of the nucleus. Each allowed orbit is therefore associated with a certain quantity of energy called the energy of the orbit, which equals the total energy of the electron in it. In
these allowed orbits electrons revolve without radiating energy.

• Energy is radiated or absorbed when an electron jumps from one stationary orbit to another stationary orbit. This energy is equal to the energy difference between these two orbits and emitted or absorbed as one quantum of radiation of frequency ν given by Planck’s equation ${\mathrm{E}}_2–{\mathrm{E}}_1=\mathrm{hv}=\frac{\mathrm{hc}}{\lambda }$. This is called Bohr’s frequency condition.

• Radius of Bohr’s orbit : When mass of the nucleus is large compared to revolving electron, then electron revolves around the nucleus in circular orbit. According to first postulate

$\frac{\mathrm{k}\left(\mathrm{Ze}\right)\mathrm{e}}{{\mathrm{r}}^2}=\frac{{\mathrm{mV}}^2}{\mathrm{r}}\left(\text{ where }\mathrm{k}=\frac{1}{4\pi {\mathrm{E}}_0}\right)$……..(1)

According to second postulate

$\mathrm{mVr}=\mathrm{n}\frac{\mathrm{h}}{2\pi }$ where n = 1, 2, 3, 4…..

(or) $\mathrm{V}=\frac{\mathrm{nh}}{2\mathrm{\pi mr}}$………..(2)

After solving the equations, radius of the orbit $\mathrm{r}=\frac{{\mathrm{n}}^2{ \mathrm{h}}^2}{4{\pi }^2{\mathrm{kZme}}^2}$ For ${\mathrm{n}}^{\mathrm{th}}$ orbit ${\mathrm{r}}_{\mathrm{n}}=\frac{{\mathrm{h}}^2}{4{\mathrm{\pi }}^2{\mathrm{ke}}^2}.\left(\frac{{\mathrm{n}}^2}{ \mathrm{mZ}}\right)$…………(3)

For hydrogen atom Z = 1, radius of the first orbit (n = 1) is given by ${\mathrm{r}}_1=0.529\times {10}^{–10} \mathrm{m}=0.53 \stackrel{\mathrm{o}}{\mathrm{A}}$

This value is called as Bohr’s radius and the orbit is called Bohr’s orbit. In general, the radius of the ${\mathrm{n}}^{\mathrm{th}}$ orbit of a hydrogen like atom is given by ${\mathrm{r}}_{\mathrm{n}}=0.53\left(\frac{{\mathrm{n}}^2}{\mathrm{Z}}\right) \stackrel{0}{\mathrm{A}}$ where n = 1, 2, 3, ……(4)

5. VELOCITY OF THE ELECTRON IN THE ORBIT

The velocity of an electron in $n^{th}$ orbit ${\mathrm{V}}_{\mathrm{n}}=\frac{\mathrm{nh}}{2\pi {\mathrm{mr}}_{\mathrm{n}}}$

hence ${\mathrm{V}}_{\mathrm{n}}=\frac{2{\mathrm{\pi ke}}^2}{ \mathrm{h}}·\left(\frac{\mathrm{Z}}{\mathrm{n}}\right)\left(\therefore {\mathrm{r}}_{\mathrm{n}}=\frac{{\mathrm{n}}^2{ \mathrm{h}}^2}{4{\mathrm{\pi }}^2{\mathrm{kZme}}^2}\right)$….(5)

i.e the velocity of electron in any orbit is independent of the mass of electron. The above equation can also be written as

$\therefore {\mathrm{V}}_{\mathrm{n}}=\left(\frac{\mathrm{c}}{137}\right)·\frac{\mathrm{Z}}{\mathrm{n}}\mathrm{m}/\mathrm{s}$ ……. (6)

Where ‘c’ is the speed of light in vacuum.

Time period of electron in the orbit :

Angular velocity of electron in $n^{th}$ orbit

${\omega }_{\mathrm{n}}=\frac{{\mathrm{V}}_{\mathrm{n}}}{{\mathrm{r}}_{\mathrm{n}}}=\frac{{\omega }_0{\mathrm{Z}}^2}{{\mathrm{n}}^3}$ where ${\omega }_0=\frac{8{\pi }^3{\mathrm{k}}^2{\mathrm{e}}^4 \mathrm{m}}{{ \mathrm{h}}^3}$…..(7) is the angular velocity of electron in first Bohr’s orbit. The time period of rotation of electron in $n^{th}$ orbit $\mathrm{T}=\frac{2\mathrm{\pi }}{{\mathrm{\omega }}_{\mathrm{n}}}=\frac{{\mathrm{n}}^3}{2{\mathrm{\pi \omega }}_0{\mathrm{Z}}^2}$ …… (8) i.e   $\mathrm{T}\propto \frac{{\mathrm{n}}^3}{{\mathrm{Z}}^2}$.

The time period of rotation increases as n increases and is independent on the mass of the electron.

6. ENERGY OF THE ELECTRON IN THE ORBIT

• The kinetic energy of the electron revolving round the nucleus in $n^{th}$ orbit is given by

${\mathrm{K}}_{\mathrm{n}}=\frac{1}{2}{\mathrm{mV}}^2=\frac{1}{2} \mathrm{m}{\left[\frac{2\pi {\mathrm{ke}}^2}{ \mathrm{h}}·\frac{\mathrm{Z}}{\mathrm{n}}\right]}^2$

${\mathrm{K}}_{\mathrm{n}}=\frac{2{\pi }^2{\mathrm{k}}^2{\mathrm{e}}^4}{{ \mathrm{h}}^2}·\left(\frac{{\mathrm{mZ}}^2}{{\mathrm{n}}^2}\right)\dots \dots .\left(9\right); {\mathrm{K}}_{\mathrm{n}}\alpha \frac{{\mathrm{mZ}}^2}{{\mathrm{n}}^2}$

If the reference level (zero potential energy level) is at infinity then the electrostatic potential energy is given by

${\mathrm{U}}_{\mathrm{n}}=–\frac{\mathrm{k}\left(\mathrm{Ze}\right)\mathrm{e}}{{\mathrm{r}}_{\mathrm{n}}}=–{\mathrm{kZe}}^2\left[\frac{4{\mathrm{\pi }}^2 {\mathrm{kmZe}}^2}{{\mathrm{n}}^2{ \mathrm{h}}^2}\right]$

${\mathrm{U}}_{\mathrm{n}}=–\frac{4{\pi }^2{\mathrm{k}}^2{\mathrm{e}}^4}{{ \mathrm{h}}^2}\left(\frac{{\mathrm{mZ}}^2}{{\mathrm{n}}^2}\right)$………..(10)

Total energy of the electron in $n^{th}$ orbit

${\mathrm{E}}_{\mathrm{n}}={\mathrm{K}}_{\mathrm{n}}+{\mathrm{U}}_{\mathrm{n}}=–\frac{2{\pi }^2{\mathrm{k}}^2 {\mathrm{mZ}}^2{\mathrm{e}}^4}{{\mathrm{n}}^2{ \mathrm{h}}^2}$

${\mathrm{E}}_{\mathrm{n}}=–\frac{2{\pi }^2{\mathrm{k}}^2{\mathrm{e}}^4}{{ \mathrm{h}}^2}\left(\frac{{\mathrm{mz}}^2}{{\mathrm{n}}^2}\right)$ …….. (11)

The expression of total energy for hydrogen like atom may be simplified as

${\mathrm{E}}_{\mathrm{n}}=–13.6\frac{{\mathrm{Z}}^2}{{\mathrm{n}}^2}$   eV, n = 1,2,3….. (12)

Where -13.6 eV is the total energy of the electron in the ground state of an hydrogen atom.

From the equations (9),(10)&(11) it is clear that

PE : K.E : T.E = -2 : 1 : -1

i.e U = – 2K and E = -K (or) E = -K = U / 2

• The state n = 1 is called ground state and n > 1 states are called excited states. When electron go from lower orbit to higher orbit speed and hence kinetic energy decrease, but both potential energy and total energy increases.

$\mathrm{E}\propto \frac{1}{{\mathrm{n}}^2}$ tells us that the energy gap between the two successive levels decreases as the value of n increases. At infinity level the total energy of the atom becomes zero.

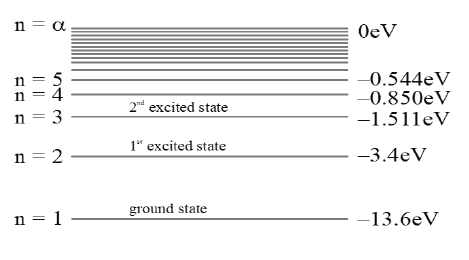
Energy level diagram of hydrogen atom (Z = 1) for normal and excited states as shown the figure.

The energy level diagram of hydrogen like atom with atomic number Z for normal and excited states as shown in Figure.

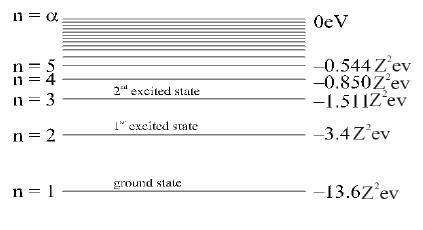
The total energy of the electron is negative implies the atomic electron is bound to the nucleus. To remove the electron from its orbit beyond the attraction of the nucleus , energy must be required.
The minimum energy required to remove an electron from the ground state of an atom is called its ionization energy and it is 13.6 ${\mathrm{Z}}^2$ eV.

• In hydrogen atom the ground state energy of electron is –13.6 eV, so 13.6 eV is the ionization energy of the Hydrogen atom.

7. EMISSION OF RADIATION

• When an electron jumps from higher energy level n2 to a lower energy level n1 in stationary atom, the difference in energy is radiated as a photon whose frequency ν is given by Planck’s formula.

${\mathrm{E}}_{{\mathrm{n}}_2}–{\mathrm{E}}_{{\mathrm{n}}_1}=\mathrm{h}\nu$

(or) $\mathrm{hv}={\mathrm{E}}_2–{\mathrm{E}}_1=13.6{\mathrm{Z}}^2\left[\frac{1}{{\mathrm{n}}_1^2}–\frac{1}{{\mathrm{n}}_2^2}\right]\mathrm{eV}$

$\left(\therefore E_n=–\frac{13·6Z^2}{n^2}\text{ e.V }\right)$ since 1eV = $1.6\times {10}^{–19}\mathrm{J}$ hence $\mathrm{h}\frac{\mathrm{c}}{\mathrm{\lambda }}=\left(12.8\times {10}^{–18}\right){\mathrm{Z}}^2\left[\frac{1}{{\mathrm{n}}_1^2}–\frac{1}{{\mathrm{n}}_2^2}\right]\mathrm{J}$

(or) wave number  $\overline{\mathrm{v}}=\frac{1}{\mathrm{\lambda }}={\mathrm{RZ}}^2.\left[\frac{1}{{\mathrm{n}}_1^2}–\frac{1}{{\mathrm{n}}_2^2}\right]{\mathrm{m}}^{–1}$

where R is called for “Rydberg constant”, when the nucleus is infinitely massive as compared to the revolving electron. In other words the nucleus is considered to be stationary. The numerical value of R is $1.097\times {10}^7{ \mathrm{m}}^{–1}$.

8. EMISSION SPECTRUM OF HYDROGEN ATOM

Electron in hydrogen atom, can be in excited state for very small time of the order of ${10}^{–8}$ second. This is because in the presence of conservative force system particles always try to occupy stable equilibrium position and hence minimum potential energy, which is least in ground state. Because of instability, when an electron in excited state makes a transition to lower energy state, a photon is emitted. Collection of such emitted photon frequencies is called an emission spectrum. This is as showing in figure.

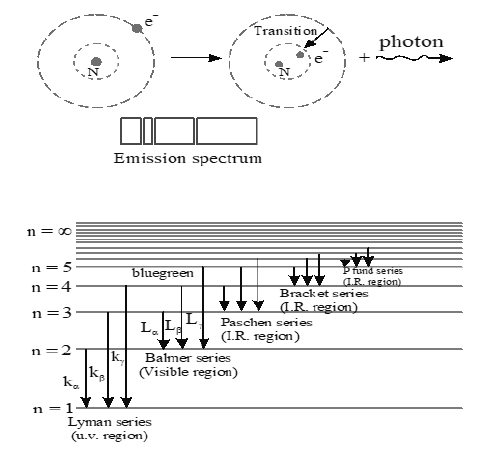
The Spectral Series of Hydrogen Atom as shown in figure, are explained below.

(a) Lyman Ser ies : Lines corresponding to transition from outer energy levels $n_2=2,3,4,......\infty$ to first orbit (${\mathrm{n}}_1$= 1) constitute Lyman series. The wave numbers of different lines are given by, $\overline{\mathrm{v}}=\frac{1}{\lambda }=\mathrm{R}\left[\frac{1}{l^2}–\frac{1}{{\mathrm{n}}_2^2}\right]$

• Line corresponding to transition from $n_2$ = 2 to $n_1$ = 1 is first line; its wavelength is maximum.

$\frac{1}{{\mathrm{\lambda }}_{\max }}=\mathrm{R}\left[\frac{1}{1^2}–\frac{1}{2^2}\right]=1.1\times {10}^7\left[\frac{1}{1}–\frac{1}{4}\right] \therefore {\mathrm{\lambda }}_{\max }=1212\stackrel{°}{\mathrm{A}}$   Similarly transition from ${\mathrm{n}}_2=\infty \text{ to }{n}_1=1$ gives line of minimum wavelength. $\frac{1}{{\lambda }_{\mathrm{m}\text{in }}}=\mathrm{R}\left[\frac{1}{1^2}–\frac{1}{{\infty }^2}\right]=1.1\times {10}^7$.

$\therefore {\mathrm{\lambda }}_{\min }=912\stackrel{°}{\mathrm{A}}$

• Lyman series lies in ultraviolet region of electro magnetic spectrum.

• Lyman series is obtained in emission as well as in absorption spectrum.

(b) Balmer Series: Lines corresponding to ${\mathrm{n}}_2=3,4,5,\dots \dots .\infty \text{ to }{\mathrm{n}}_1=2$ constitute Balmer series. The wave numbers of different lines are given by, $\overline{\mathrm{v}}=\frac{1}{\mathrm{\lambda }}=\mathrm{R}\left[\frac{1}{2^2}–\frac{1}{{\mathrm{n}}_2^2}\right]$

• Line corresponding to transition $n_2$=3 to $n_1$=2 is first line, wavelength corresponding to this transition is maximum.
Line corresponding to transition ${\mathrm{n}}_2=\infty \text{ to }{\mathrm{n}}_1=2$ is last line; wavelength of last line is minimum.

$\frac{1}{{\mathrm{\lambda }}_{\max }}=\mathrm{R}\left[\frac{1}{2^2}–\frac{1}{3^2}\right] \therefore {\mathrm{\lambda }}_{\max }=6568\stackrel{0}{\mathrm{A}}$     $\frac{1}{{\mathrm{\lambda }}_{\min }}=\mathrm{R}\left[\frac{1}{2^2}–\frac{1}{{\infty }^2}\right] \therefore {\mathrm{\lambda }}_{\min }=3636\stackrel{0}{\mathrm{A}}$

• Balmer series lies in the visible region of electromagnetic spectrum. The wavelength of L_α line is 656.8 nm (red). The wavelength of L_β line is 486 nm (blue green). The wavelength of L_γ line is 434 nm (violet). The remaining lines of Balmer series closest to violet light wavelength. The speciality of these lines is that in going from one end to other, the brightness and the separation between them decreases regularly.

• This series is obtained only in emission spectrum. Absorption lines corresponding to Balmer series do not exist, except extremely weakly, because very few electrons are normally in the state n = 2 and only a very few atoms are capable of having an electron knocked from the state n = 2 to higher states. Hence photons that correspond
to these energies will not be strongly absorbed. In highly excited hydrogen gas there is possibility for detecting absorption at Balmer-line wavelengths.

(c) Paschen Series: Lines corresponding to ${\mathrm{n}}_2=4,5,6,\dots \dots \infty \text{ to }{\mathrm{n}}_1=3$ constitute Paschen series. The wave number of different lines are given by $\overline{\mathrm{v}}=\mathrm{R}\left[\frac{1}{3^2}–\frac{1}{n_2^2}\right]$.

• Line corresponding to transition $n_2$ = 4 to $n_1$ = 3 is first line, having maximum wavelength. Line corresponding to transition $n_2=\infty \text{ to }{\mathrm{n}}_1=3$ is last line, having minimum wavelength

$\frac{1}{{\mathrm{\lambda }}_{\max }}=\mathrm{R}\left[\frac{1}{3^2}–\frac{1}{4^2}\right] \therefore {\mathrm{\lambda }}_{\max }=18747\stackrel{0}{\mathrm{A}}$

$\frac{1}{{\mathrm{\lambda }}_{\min }}=\mathrm{R}\left[\frac{1}{3^2}–\frac{1}{\infty }\right]=1.1\times {10}^7\times \left[\frac{1}{9}–0\right]$

$\therefore {\mathrm{\lambda }}_{\min }=8202\stackrel{0}{\mathrm{A}}$

• Paschen series lies in the infrared region of electromagnetic spectrum.

• This series is obtained only in the emission spectrum.

(d) Bracket Series: The series corresponds to transitions from ${\mathrm{n}}_2=5,6,7\dots \dots ,\infty \text{ to } {\mathrm{n}}_1=4$. The wave number are given by, $\overline{\mathrm{v}}=\frac{1}{\lambda }=\mathrm{R}\left[\frac{1}{4^2}–\frac{1}{{\mathrm{n}}_2^2}\right]$

• Line corresponding to transition from ${\mathrm{n}}_2=5\text{ to }{\mathrm{n}}_1=4$ has maximum wavelength and ${\mathrm{n}}_2=\infty$ to $n_1=4$ has minimum wavelength.

$\frac{1}{{\mathrm{\lambda }}_{\max }}=\mathrm{R}\left[\frac{1}{4^2}–\frac{1}{5^2}\right] \therefore {\mathrm{\lambda }}_{\max }=40477\stackrel{0}{\mathrm{A}}$

$\frac{1}{{\mathrm{\lambda }}_{\min }}=\mathrm{R}\left[\frac{1}{4^2}–\frac{1}{{\infty }^2}\right] \therefore {\mathrm{\lambda }}_{\min }=14572\stackrel{0}{\mathrm{A}}$

• This series lies in the infrared region of electromagnetic spectrum.

(e) Pfund Series: This series corresponds to transitions from ${\mathrm{n}}_2=6,7,8,\dots ,\infty \text{ to }{\mathrm{n}}_1=5$ The wave numbers are given by $\overline{\mathrm{v}}=\frac{1}{\mathrm{\lambda }}=\mathrm{R}\left[\frac{1}{5^2}–\frac{1}{{\mathrm{n}}_2^2}\right]$

• Line corresponding to transition from ${\mathrm{n}}_2=6\text{ to }{\mathrm{n}}_1=5$ has maximum wavelength and ${\mathrm{n}}_2=\infty \text{ to }{\mathrm{n}}_1=4$ has minimum wavelength. $\frac{1}{{\lambda }_{\max }}=\mathrm{R}\left[\frac{1}{5^2}–\frac{1}{6^2}\right]$

$\therefore {\mathrm{\lambda }}_{\max }=74563\stackrel{0}{\mathrm{A}} \frac{1}{{\mathrm{\lambda }}_{\min }}=\mathrm{R}\left[\frac{1}{5^2}–\frac{1}{{\infty }^2}\right]$

$\therefore {\mathrm{\lambda }}_{\min }=22768\stackrel{0}{\mathrm{A}}$

• This series lies in infrared region of electromagnetic spectrum.

Note : In an atom emission transition may start from any higher energy level and end at any energy level below of it. Hence in emission spectrum the total possible number of emission lines from some excited state ${\mathrm{n}}_2$ to another energy state

${\mathrm{n}}_1\left(<{\mathrm{n}}_2\right)\text{ is }\frac{\left({\mathrm{n}}_2–{\mathrm{n}}_1\right)\left({\mathrm{n}}_2–{\mathrm{n}}_1+1\right)}{2}$

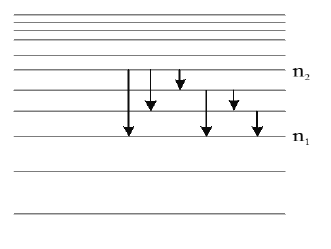
Note 1 : for n₂ = 4, and n₁ =1, the number of possible lines are 6.

Note 2 : If ΔE is the energy difference between two given energy states, then due to transition between these two states wavelength of emitted photon is $\mathrm{\lambda }\left(\stackrel{0}{\mathrm{A}}\right)=\frac{12400}{\mathrm{\Delta E}\left(\mathrm{eV}\right)}$.

9. LIMITATION OF BOHR’S MODEL

Despite its considerable achievements, the Bohr’s model has certain short coming.

• It could not interpret the details of optical spectra of atoms containing more than one electron.

• It involves the concept of orbit which could not be checked experimentally

• It could be successfully applied only to single-electron atoms (e.g., H, He⁺ , Li²⁺, etc.)

• Bohr’s model could not explain the binding of atoms into molecules.

• No justification was given for the “principle of quantization of angular momentum”.

• Bohr’s model could not explain the reason why atoms should combine to form chemical bonds and why do the molecules become more stable on such combinations.

• Bohr had assumed that an electron in the atom is located at definite distance from the nucleus and is revolving with a definite velocity around it. This is against the Heisenberg uncertainty principle. With the advancements in quantum mechanics, it be came clear that there are no well defined orbits; rather there are clouds of negative
charge.

S.No	Name of the series	Final State (n1)	Initial State (n2)	Formula	Series limit	Maximum wavelength	Region
1.	Lyman	n1 = 1	2,3,4,…∞	$\frac{1}{\mathrm{\lambda }}=\mathrm{R}\left(\frac{1}{1^2}–\frac{1}{{\mathrm{n}}_2^2}\right)$	$\lambda =\frac{1}{\mathrm{R}}=911 \mathrm{A}°$	$\lambda =\frac{4}{3\mathrm{R}}$	UV
2.	Balmer	n1 = 2	3,4,5.,…∞	$\frac{1}{\mathrm{\lambda }}=\mathrm{R}\left(\frac{1}{2^2}–\frac{1}{{\mathrm{n}}_2^2}\right)$	$\lambda =\frac{4}{\mathrm{R}}$	$\lambda =\frac{36}{5\mathrm{R}}$	Visible
3.	Paschen	n1 = 3	4,5,6.,…∞	$\frac{1}{\mathrm{\lambda }}=\mathrm{R}\left(\frac{1}{3^2}–\frac{1}{{\mathrm{n}}_2^2}\right)$	$\lambda =\frac{9}{\mathrm{R}}$	$\lambda =\frac{144}{7\mathrm{R}}$	Near IR
4.	Brackett	n1 = 4	5,6,7,…∞	$\frac{1}{\mathrm{\lambda }}=\mathrm{R}\left(\frac{1}{4^2}–\frac{1}{{\mathrm{n}}_2^2}\right)$	$\lambda =\frac{16}{\mathrm{R}}$	$\lambda =\frac{400}{9\mathrm{R}}$	Middle IR
5.	Pfund	n1 = 5	6,7,8,…∞	$\frac{1}{\mathrm{\lambda }}=\mathrm{R}\left(\frac{1}{5^2}–\frac{1}{{\mathrm{n}}_2^2}\right)$	$\lambda =\frac{25}{\mathrm{R}}$	$\lambda =\frac{9000}{11\mathrm{R}}$	Far IR

ADDITIONAL INFORMATION

10. RADIATION FORCE AND PRESSURE

(i) Electromagnetic waves (radiation) carry energy and momentum and exert force on the surface of a body when they get absorbed or reflected by that surface

(ii) Accoding to Einstein’s mass energy equivalence $\left(E=m{c}^2\right)$ linear momentum associated with energy E is $P=\frac{E}{c}$ (∵ E = mc⨯c and mc is linear momentum of a photon of energy E or linear momentum of a portion of the wave carrying an energy E)

(iii) According to qunatum theory of radiation, linear momentum associated with a photon is $P=\frac{E}{C}=\frac{hv}{C}=\frac{h}{C}\times \frac{C}{\lambda }=\frac{h}{\lambda }$ where

λ = wave length, ν = frequency, C = velocity of light

(iv) Intensity of eletromagnetic waves (or photons)I is the flow of energy through unit area

(perpendiculer o the flow) in unit time. i.e $\mathrm{I}=\frac{1}{\mathrm{A}}\left(\frac{\mathrm{dE}}{\mathrm{dt}}\right)\text{ Unit: }{\mathrm{Wm}}^{–2}$

Case (i):

(i) Consider a beam of eletro magnetic radiation of intensity I, and of cross sectional area A which falls on a surface of a body normally

(ii) If the surface absorbs the radiaction falling on it completely, force excerted by the radiation on the surface = Rate of change of linear momentum

$\text{ ie }\mathrm{F}=\frac{\mathrm{dp}}{\mathrm{dt}}=\frac{\mathrm{dE}}{\mathrm{C}}\times \frac{1}{\mathrm{dt}}=\frac{1}{\mathrm{C}}\left(\frac{\mathrm{dE}}{\mathrm{dt}}\right)=\frac{\mathrm{LA}}{\mathrm{C}}$

(iii) Pressure excerted on the surface ${\mathrm{P}}^{!}=\frac{\mathrm{F}}{\mathrm{A}}=\frac{\mathrm{I}}{\mathrm{C}}$

Case (ii):

(i) If the surface reflects the radiation completly (falling on it normally), force excerted on the surface

$F=\frac{dp}{dt}=2\left(\frac{dE}{C}\right)\times \frac{1}{dt}=\frac{2}{C}\left(\frac{dE}{dt}\right)=\frac{2LA}{C}$ and pressure on the surface ${\mathrm{P}}^{!}=\frac{\mathrm{F}}{\mathrm{A}}=\frac{2\mathrm{I}}{\mathrm{C}}$

Case (iii):

(i) If the radiation falls normally and the surface is partially reflecting and absorbing the remaining with reflection and absorption coefficients r and a respectively, then force on the surface

$F=r\times 2\left(\frac{dE}{C}\right)\times \frac{1}{dt}+a\left(\frac{dE}{C}\right)\times \frac{1}{dt}$

$=\frac{1}{C}\left(\frac{dE}{dt}\right)(2r+a)=\frac{IA}{C}(2r+1–r)=\frac{IA}{C}(1+r)$

$(\because a+r=1)$

Pressure $P^{!}=\frac{F}{A}=\frac{I}{C}(1+r)$

(ii) In this case if surface is partially transmitting with reflection ,absorption and transmission coefficients r,a and t respectively, then force on the surface

$F=r\times 2\left(\frac{dE}{C}\right)\times \frac{1}{dt}+a\left(\frac{dE}{C}\right)\times \frac{1}{dt}$

$=\frac{1}{C}\left(\frac{dE}{dt}\right)(2r+a)=\frac{IA}{C}(2r+a)$

and r + a + t = 1

Case (iv) :

Let a parallel beam of radiation falls on a plane surface at an angle θ with normal to the surface and A be the cross-sectional area of the beam

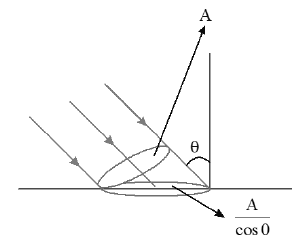
(i) If the radiation is absorbed by the surface completely, force on the surface normal to it is

$F_n=\left(\frac{dE\cos \theta }{C}\right)\times \frac{1}{dt}=\frac{1}{C}\left(\frac{dE}{dt}\right)\cos \theta =\frac{IA}{C}\cos \theta$

Force on the surface parallel to the surface is

$F_t=\left(\frac{dE\sin \theta }{C}\right)\times \frac{1}{dt}=\frac{1}{C}\left(\frac{dE}{dt}\right)\sin \theta =\frac{IA}{C}\sin \theta$

Resultant force on the surface $F=\sqrt{F_n^2+F_t^2}=\frac{IA}{C}$ at an angle θ with normal to the surface

$\text{ Pressure }=\frac{\text{ normal force }}{area}=\frac{F_n}{\left(\frac{A}{\cos \theta }\right)}=\frac{IA\cos \theta }{C\left(\frac{A}{\cos \theta }\right)}=\frac{I}{C}{\cos }^2\theta$

(ii) In this case if radiation is completely reflected at the same angle, then force on the surface

$\mathrm{F}=2\left(\frac{\mathrm{dEcos\theta }}{\mathrm{C}}\right)\times \frac{1}{\mathrm{dt}}=\frac{2}{\mathrm{C}}\left(\frac{\mathrm{dE}}{\mathrm{dt}}\right)\mathrm{cos\theta }=\frac{2\mathrm{IA}}{\mathrm{C}}\mathrm{cos\theta }$

and force parallel to the surface = 0 (∵ no change in linear momentum parallel to the surface)

$\text{ pressure }{P}^{!}=\frac{F}{\left(\frac{A}{\cos \theta }\right)}=\frac{2I{\cos }^2\theta }{C}$

(iii) In this case if the surface partially reflects (at same angle) and absorbs the remaining with reflection and absorption coefficients r and a respectively (r+a=1), then force on surface normal to it due to the reflected and absorbed parts of the radiation is

$F_n=r\times \frac{2dE\cos \theta }{C}\times \frac{1}{dt}+a\left(\frac{dE\cos \theta }{C}\right)\frac{1}{dt}$

$=\frac{1}{C}\times \left(\frac{dE}{dt}\right)\cos \theta (2r+a)=\frac{IA\cos \theta }{C}(2r+1–r)$

$=\frac{\mathrm{IAcos\theta }}{\mathrm{C}}(1+\mathrm{r})$

Force on the surface parallel to it ( this is due to the absorbed portion of the radiation only) is

$F_t=a\frac{dE\sin \theta }{C}\times \frac{1}{dt}=\frac{a}{C}\left(\frac{dE}{dt}\right)\sin \theta$

$=\frac{IA}{C}\sin \theta (1–r)$

Resultant force on th surface is

$F=\sqrt{F_n^2+F_t^2}=\frac{IA}{C}\sqrt{(1+r{)}^2{\cos }^2\theta +(1–r{)}^2{\sin }^2\theta }$

This force ats at an angle $\alpha ={\tan }^{–1}\left(\frac{F_t}{F_n}\right)$ with normal to the surface

ie. $\alpha ={\tan }^{–1}\left[\tan \theta \left(\frac{1–r}{1+r}\right)\right]$

$\text{ Pressure }{P}^{!}=\frac{\text{ normal force }}{\text{ area }}=\frac{F_A}{{\displaystyle \frac{A}{\cos \theta }}}$

$=\frac{\mathrm{IAcos\theta }}{\mathrm{C}}\frac{(1+\mathrm{r})}{\frac{\mathrm{A}}{\mathrm{cos\theta }}}=\frac{\mathrm{I}}{\mathrm{C}}{\cos }^2\mathrm{\theta }(1+\mathrm{r})$

11. EFFECT OF FINITE MASS OF NUCLEUS ON BOHR’S MODEL OF AN ATOM

(i) In the atomic spectra of hydrogen and hydrogen like atoms a very small deviation with Bohr’s model results

(ii) This is in the assuption that the nucleus is infinitely massive when compared to mass of eletron so that it remains stationary during the rotation of eletron around it

(iii) Infact the nucleus is not infinitely massive and hence both the nucleus and eletron revolve around their centre of mass with same angular velocity ω

(iv)

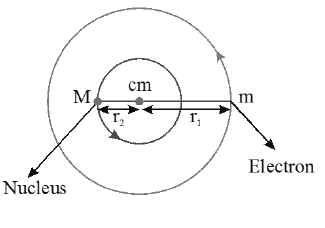
(iv) let m be the mass of eletron, M be the mass of the nucleus , Z be its atomic number and r be the separation between them. If ${\mathrm{r}}_1, {\mathrm{r}}_2$ are distances of centre of mass from electron and nucleus respectively then $r_1+r_2=r$ and

${\mathrm{r}}_1=\frac{\mathrm{Mr}}{\mathrm{M}+\mathrm{m}}, {\mathrm{r}}_2=\frac{\mathrm{mr}}{\mathrm{M}+\mathrm{m}}$

(v) For both the eletron and the nucleus the necessary centripetal force to revolve in circular orbits is provided by the electrostaic force between them.

$\text{ i.e., }m{r}_1{\omega }^2=\frac{1}{4\pi {\epsilon }_0}\frac{Z{e}^2}{r^2};m\frac{Mr}{M+m}{\omega }^2=\frac{1}{4\pi {\epsilon }_0}\frac{Z{e}^2}{r^2}$

$\text{ i.e., }\mu r^3{\omega }^2=\frac{Z{e}^2}{4\pi {\epsilon }_0}\text{…. (1) }$

where $\mu =\frac{Mm}{M+m}$ called reduced mass

(vi) From Bohr ’s theory of quantization of angular moentum, total angular momentum of the system

$L=I_1\omega +I_2\omega =\frac{nh}{2\pi }; m{r}_1^2\omega +M{r}_2^2\omega =\frac{nh}{2\pi }$

$m\frac{M^2{r}^2}{(M+m{)}^2}\omega +\frac{M{m}^2{r}^2}{(M+m{)}^2}\omega =\frac{nh}{2\pi }$

$\frac{mM{r}^2\omega }{(M+m{)}^{\cancel{2}}}\cancel{(M+m)}=\frac{nh}{2\pi }\text{ ie }\mu r^2\omega =\frac{nh}{2\pi }$………(2)

(vii) A system of this type is equalent a single particle of mass μ revolving around the position of the heavier particle(nucleus) in an orbit of radius r.

From (1) and (2) $r=\frac{{\epsilon }_0{n}^2{h}^2}{\pi z\mu e^2}$

(viii) Radius of orbit of such a particle in a quantum state n is $r_n=\frac{{\epsilon }_0{n}^2{h}^2}{\pi z\mu e^2}\Rightarrow r_n\propto \frac{n^2}{\mu z}$.

(ix) Potential energy of the system $PE=\frac{–Z{e}^2}{4\pi {\epsilon }_{0}r}$ and kinetic energy of the system

$\mathrm{KE}=\frac{1}{2}{\mathrm{I}}_1{\mathrm{\omega }}^2+\frac{1}{2}{\mathrm{I}}_2{\mathrm{\omega }}^2=\frac{1}{2}\left({\mathrm{I}}_1+{\mathrm{I}}_2\right){\mathrm{\omega }}^2$

$=\frac{1}{2}\left(m{r}_1^2+M{r}_2^2\right){\omega }^2$

$=\frac{1}{2}\left[\mathrm{m}\frac{{\mathrm{M}}^2{\mathrm{r}}^2}{(\mathrm{M}+\mathrm{m}{)}^2}+\mathrm{M}\frac{{\mathrm{m}}^2{\mathrm{r}}^2}{(\mathrm{M}+\mathrm{m}{)}^2}\right]{\mathrm{\omega }}^2$

$=\frac{1}{2}\frac{{\mathrm{mMr}}^2{\mathrm{\omega }}^2}{(\mathrm{M}+\mathrm{m}{)}^{\cancel{2}}}\cancel{(\mathrm{M}+\mathrm{m})}=\frac{1}{2}\left(\frac{\mathrm{mM}}{\mathrm{M}+\mathrm{m}}\right){\mathrm{r}}^2{\mathrm{\omega }}^2$

ie. $\mathrm{KE}=\frac{1}{2}{\mathrm{\mu r}}^2{\mathrm{\omega }}^2=\frac{1}{2}\frac{{\mathrm{Ze}}^2}{4{\mathrm{\pi \epsilon }}_0\mathrm{r}}\left(\because {\mathrm{\mu r}}^3{\mathrm{\omega }}^2=\frac{{\mathrm{Ze}}^2}{4{\mathrm{\pi \epsilon }}_0}\right)$

∴ Total energy of the system (or equivalent particle of mass μ) E = PE + KE

$\mathrm{E}=–\frac{{\mathrm{Ze}}^2}{8{\mathrm{\pi \epsilon }}_0\mathrm{r}}=–\frac{{\mathrm{Ze}}^2}{8{\mathrm{\pi \epsilon }}_0}\times \frac{{\mathrm{\pi Z\mu e}}^2}{{\mathrm{n}}^2{\mathrm{h}}^2{\mathrm{\epsilon }}_0}=–\frac{{\mathrm{Z}}^2{\mathrm{\mu e}}^4}{8{\mathrm{\epsilon }}_0^2{\mathrm{n}}^2{\mathrm{h}}^2}$

ie Energy of ${\mathrm{n}}^{\mathrm{th}}$ quantum state

${\mathrm{E}}_{\mathrm{n}}=\frac{–{\mathrm{Z}}^2{\mathrm{\mu e}}^4}{8{\mathrm{\epsilon }}_0^2{\mathrm{n}}^2{\mathrm{h}}^2}=\frac{–{\mathrm{mZ}}^2{\mathrm{\mu e}}^4}{8{\mathrm{\epsilon }}_0^2{\mathrm{n}}^2{\mathrm{h}}^2\times \mathrm{m}}=\frac{–{\mathrm{me}}^4}{8{\mathrm{\epsilon }}_0^2{\mathrm{h}}^2}\times \left(\frac{{\mathrm{Z}}^2\mathrm{\mu }}{{\mathrm{n}}^2\mathrm{m}}\right)$

${\mathrm{E}}_{\mathrm{n}}=–13.6\left(\frac{{\mathrm{z}}^2}{{\mathrm{n}}^2}\right)\times \frac{\mathrm{\mu }}{\mathrm{m}}\mathrm{eV}=–13.6\left(\frac{{\mathrm{Z}}^2}{{\mathrm{n}}^2}\right)\times \frac{\mathrm{M}}{\mathrm{M}+\mathrm{m}}\mathrm{eV}$

$=\frac{–13.6}{1+\frac{\mathrm{m}}{\mathrm{M}}}\left(\frac{{\mathrm{Z}}^2}{{\mathrm{n}}^2}\right)\mathrm{eV}$

The formulae for $r_n$ and $E_n$ can be obtained simply by replacing m by μ in the formulae for stationary nucleus, If λ is wave length of photon emitted due to transition from a quantum state $n_2$ to a quantum state $n_1$, then

$\frac{hc}{\lambda }=\frac{m{e}^4{z}^2}{8{\epsilon }_0^2{h}^2}\times \frac{1}{\left(1+\frac{m}{M}\right)}\left(\frac{1}{n_1^2}–\frac{1}{n_2^2}\right)$

$\frac{1}{\lambda }=\frac{m{e}^4{z}^2}{8{\epsilon }_0^2{h}^{3}c}\times \frac{1}{\left(1+\frac{m}{M}\right)}\left(\frac{1}{n_1^2}–\frac{1}{n_2^2}\right)$

$\frac{1}{\lambda }=\frac{R_0{Z}^2}{\left(1+\frac{m}{M}\right)}\left(\frac{1}{n_1^2}–\frac{1}{n_2^2}\right)$ where $R_0$ is Rydberg’s constant when the nucleus is stationary

12. EXCITATION BY COLLISION

(i) When an atom is bombarded by particles like electron, proton, neutron, α-particle etc, the loss in KE of the system during collision may be used in excitation of the atom

(ii) If loss in KE of the system during collision (during deformation phase)is less than the energy required to excite the eletron to next higher energy state, eletron can’t be excited and the loss of KE of the system during deformation phase again converts into KE of the system and totally there will be no loss of KE of of the system and hence the collision is elastic

(iii) If loss in KE of the system during deformation phase is more than or equal to the energy required to excite the electron to next higher state, excitation of the electron may take place and hence kinetic energy of the system may not be conserved hence the collision may be inelastic or even perfectly inelastic.

(iv) If loss in KE is sufficient even ionization may take place.Even though the possible loss in KE is greater than or equal to excitation energy of electron, excitation may not take place necessarily and hence collision may be elastic.

(v) Consider a particle of mass m moving with velocity u which strikes a stationary hydrogen like atom of mass M which is in ground state.

(vi) Loss in KE will be maximum in perfectly inelastic collision. In this case if V is common velocity after collision, from conservation of linear momentum $\mathrm{mu}+0=(\mathrm{M}+\mathrm{m})\mathrm{V}\Rightarrow V=\frac{mu}{M+m}$

∴  Maximum possible loss in KE is

$\Delta K=\frac{1}{2}m{u}^2–\frac{1}{2}(M+m)V^2$

i.e   $\Delta K=\frac{1}{2}\left(\frac{Mm}{M+m}\right)u^2$

(vii) If ΔE is minimum excitation energy (ex: n=1 to n=2 in ground state) and if ΔK < ΔE eletron can’t be excited hence there will be no loss of KE of the system hence the collision is elastic.

(viii)If ΔK > ΔE the electron may get excited and the collision may be perfectly in elastic.

(ix) If ΔK > ΔE the electron may get excited to higher energy states or even removed from the atom and may have some kinetic energy. In this case the collision may be inelastic or may be perfectly inelastic as there is loss in KE of the system, or even elastic if excitation dose not take place.

(x) If $K{E}_{min}$ is the minimum KE that should be pocessed by the colliding particle to excite the electron, ΔK $\ge$ ΔE for excitation

$\frac{1}{2}\frac{\mathrm{mM}}{\mathrm{M}+\mathrm{m}}{\mathrm{u}}^2\ge \mathrm{\Delta E}\Rightarrow \frac{1}{2}{\mathrm{mu}}^2\ge \mathrm{\Delta E}\left(\frac{\mathrm{M}+\mathrm{m}}{\mathrm{M}}\right)$

$\Rightarrow {\mathrm{KE}}_{\min }=\mathrm{\Delta E}\left(\frac{\mathrm{M}+\mathrm{m}}{\mathrm{M}}\right)=\mathrm{\Delta E}\left(1+\frac{\mathrm{m}}{\mathrm{M}}\right)$

In the same way we can calculate ${\mathrm{KE}}_{\min }$ in other cases where atom is also moving using the conservation of linear momentum.

SOLVED EXAMPLES

1. The electron in a hydrogen atom makes a transition ${\mathrm{n}}_1\to {\mathrm{n}}_2$ where n1 and n2 are the principal quantum numbers of the two states. Assume the Bohr model to be valid. The time period of the electron in the initial state is eight times that in the final state. What are the possible values of n₁ and n₂ ?

Sol. Since $\mathrm{T}\propto {\mathrm{n}}^3;\frac{{\mathrm{T}}_1}{{ \mathrm{T}}_2}=\frac{{\mathrm{n}}_1^3}{{\mathrm{n}}_2^3}$ ,

As ${\mathrm{T}}_1=8{ \mathrm{T}}_2,{\left(\frac{{\mathrm{n}}_1}{{\mathrm{n}}_2}\right)}^3=8\text{ (or) }{\mathrm{n}}_1=2{\mathrm{n}}_2$

Thus the possible values of n₁ and n₂ are ${\mathrm{n}}_1=2, {\mathrm{n}}_2=1, {\mathrm{n}}_1=4, {\mathrm{n}}_2=2, {\mathrm{n}}_1=6, {\mathrm{n}}_2=3;$ and so on.

2. Find the kinetic energy, potential energy and total energy in first and second orbit of hydrogen atom if potential energy in first orbit is taken to be zero.

Sol. E₁ = -13.60eV; K1 = -E₁ = 13.60eV

U₁ = 2E₁ = -27.20eV E₂ = -3.40eV K₂ = 3.40eV and U₂ = -6.80eV

Now, U₁ = 0, i.e., potential energy has been increased by 27.20eV. So, we will increase U and E in all energy states by 27.20eV while kinetic energy will remain unchanged.

Hence                      K(eV),   U(eV),   E(eV)

First orbit are           13.6,      0,          13.6

in Second orbit         3.40,     20.40,  23.80

3. A small particle of mass m moves in such a way that the potential energy U = ${\mathrm{ar}}^2$ where a is a constant and r is the distance of the particle from the origin. Assuming Bohr’s model of quantization of angular momentum and circular orbits, find the radius of ${\mathrm{n}}^{\mathrm{th}}$ allowed orbit.

Sol. The force at a distance r is, $\mathrm{F}=–\frac{\mathrm{dU}}{\mathrm{dr}}=–2\mathrm{ar}$ Suppose r be the radius of ${\mathrm{n}}^{\mathrm{th}}$ orbit. Then the necessary centripetal force is provided by the above force.

Thus,   $\frac{{\mathrm{mv}}^2}{\mathrm{r}}=2\mathrm{ar}$ ……. (i)

Further, the quantization of angular momentum gives, $\mathrm{mvr}=\frac{\mathrm{nh}}{2\mathrm{\pi }}$ ……….. (ii)

Solving Eqs. (i) and (ii) for r, we get $\mathrm{r}={\left(\frac{{\mathrm{n}}^2{\mathrm{h}}^2}{8{\mathrm{am\pi }}^2}\right)}^{1/4}$

4. Consider a hydrogen-like atom whose energy in ${\mathrm{n}}^{\mathrm{th}}$ excited state is given by ${\mathrm{E}}_{\mathrm{n}}=–\frac{13.6{\mathrm{Z}}^2}{{\mathrm{n}}^2}$ when this excited atom makes transition from excited state to ground state most energetic photons have energy ${\mathrm{E}}_{\max }=52.224\mathrm{eV}$ and least energetic photons have energy ${\mathrm{E}}_{\min }=1.224\mathrm{eV}$. Find the atomic number of atom and the state of excitation.

Sol. Maximum energy is liberated for transition ${\mathrm{E}}_{\mathrm{n}}\to 1$ and minimum energy for $E_n\to E_{n–1}$

Hence, $\frac{{\mathrm{E}}_1}{{\mathrm{n}}^2}–{\mathrm{E}}_1=52.224\mathrm{eV}$ ….. (1)

and $\frac{{\mathrm{E}}_1}{{\mathrm{n}}^2}–\frac{{\mathrm{E}}_1}{(\mathrm{n}–1{)}^2}=1.224\mathrm{eV}$ ……… (2)

Solving above equations simultaneously, we get

${\mathrm{E}}_1=–54.4\mathrm{eV} \mathrm{and} \mathrm{n}=5$ Now ${\mathrm{E}}_1=–\frac{13.6{\mathrm{Z}}^2}{1^2}=–54.4\mathrm{eV}$. Hence, Z = 2 i.e, gas is helium originally excited to n = 5 energy state.

5. A hydrogen-like atom (atomic number Z) is in a higher excited state of quantum number n. This excited atom can make a transition to the first excited state by successively emitting two photons of energies 10.20 eV and 17.00 eV respectively. Alternatively the atom from the same excited state can make a transition to the second excited state by successively emitting two photons of energies 4.25 eV and 5.95 eV respectively. Determine the values of n and Z (ionization energy of hydrogen atom = 13.6 eV)

Sol. The electronic transitions in a hydrogen-like atom from a state n₂ to a lower state n₁ are given by $\Delta \mathrm{E}=13.6{\mathrm{Z}}^2\left(\frac{1}{{\mathrm{n}}_1^2}–\frac{1}{{\mathrm{n}}_2^2}\right)$. For the transition from a higher state n to the first excited state ${\mathrm{n}}_1=2$, the total energy released is (10.2 + 17.0) eV or 27.2eV. Thus ΔE = 27.2 eV, ${\mathrm{n}}_1=2\text{ and }{\mathrm{n}}_2=\mathrm{n}$

We have $27.2=13.6{\mathrm{Z}}^2\left[\frac{1}{4}–\frac{1}{{\mathrm{n}}^2}\right]$………(1)

For the eventual transition to the second excited state ${\mathrm{n}}_1$ = 3, the total energy released is (4.25 + 5.95) eV or 10.2eV.

Thus  $10.2=13.6{\mathrm{Z}}^2\left[\frac{1}{9}–\frac{1}{{\mathrm{n}}^2}\right]$ …. (2)

Dividing the Eq. (1) by Eq. (2) we get $\frac{27.2}{10.2}=\frac{9{\mathrm{n}}^2–36}{4{\mathrm{n}}^2–36}$.

Solving we get ${\mathrm{n}}^2$ = 36 or n = 6

Substituting n = 6 in any one of the above equations, we obtain ${\mathrm{Z}}^2$ = 9 (or) Z = 3, Thus n=6 and Z=3.

6. A doubly ionized lithium atom is hydrogen like with atomic number Z = 3. Find the wavelength of the radiation required to excite the electron in Li²⁺ from the first to the third Bohr orbit. Given the ionization energy of hydrogen atom as 13.6 eV

Sol. The energy of n^th orbit of a hydrogen-like atom is given as ${\mathrm{E}}_{\mathrm{n}}=–\frac{13.6{\mathrm{Z}}^2}{{\mathrm{n}}^2}$ Thus for Li²⁺ atom, as Z = 3, the electron energies of the first and third Bohr orbits are For n = 1, E₁ = –122.4eV, for n = 3, E₃ = –13.6eV. Thus the energy required to transfer an electron from E₁ level to E₃ level is, E = E₃ – E₁ = -13.6 – (-122.4) = 108.8eV.

Therefore, the radiation needed to cause this transition should have photons of this energy. hv = 108.8 eV. The wavelength of this radiation is or $\mathrm{\lambda }=\frac{\mathrm{hc}}{108.8\mathrm{eV}}=114.25 \stackrel{0}{\mathrm{A}}$

7. A hydrogen atom in a state of binding energy 0.85 eV makes a transition to a state of excitation energy of 10.2eV.

(i) What is the initial state of hydrogen atom?
(ii)What is the final state of hydrogen atom ?
(iii) What is the wavelength of the photon emitted ?

Sol. (i) Let n₁ be initial state of electron. Then ${\mathrm{E}}_1=–\frac{13.6}{{\mathrm{n}}_1^2}\mathrm{eV}$ Here E₁ = – 0.85 eV, therefore $–0.85=–\frac{13.6}{{\mathrm{n}}_1^2}\text{ or }{\mathrm{n}}_1=4$

(ii) Let n2 be the final excitation state of the electron. Since excitation energy is always measured with respect to the ground state, therefore

$\mathrm{\Delta E}=13.6\left[1–\frac{1}{{\mathrm{n}}_2^2}\right]\text{ here }\mathrm{\Delta E}=10.2\mathrm{eV},\text{ therefore, }$

$10.2=13.6\left[1–\frac{1}{{\mathrm{n}}_2^2}\right]\text{ or }{\mathrm{n}}_2=2$ Thus, the electron jumps from n₁ = 4 to n₂ = 2.

(iii) The wavelength of the photon emitted for a transition between ${\mathrm{n}}_1=4\text{ to }{\mathrm{n}}_2=2$, is given by

$\frac{1}{\mathrm{\lambda }}={\mathrm{R}}_{\infty }\left[\frac{1}{{\mathrm{n}}_2^2}–\frac{1}{{\mathrm{n}}_1^2}\right]\text{ (or) }\frac{1}{\mathrm{\lambda }}=1.09\times {10}^7\left[\frac{1}{2^2}–\frac{1}{4^2}\right]=4860\stackrel{0}{\mathrm{A}}$.

8. A hydrogen atom initially in the ground level absorbs a photon, which excites it to the n = 4 level. Determine the wavelength and frequency of photon. To find the wavelength and frequency of photon use the relation of energy of electron in hydrogen atom is ${\mathrm{E}}_{\mathrm{n}}=–\frac{13.6}{{\mathrm{n}}^2}\mathrm{eV}$.

Sol. For ground state ${\mathrm{n}}_1=1\text{ to }{\mathrm{n}}_2=4$.

Energy absorbed by photon, E = E₂ – E₁

$=+13.6\left(\frac{1}{{\mathrm{n}}_1^2}–\frac{1}{{\mathrm{n}}_2^2}\right)\times 1.6\times {10}^{–19} \mathrm{J}$

$=13.6\left(\frac{1}{1}–\frac{1}{4^2}\right)\times 1.6\times {10}^{–19}$

$=13.6\times 1.6\times {10}^{–19}\left(\frac{15}{16}\right)=20.4\times {10}^{–19}$.

or E = hν = 20.4 ⨯ ${10}^{–19}$

Frequency $v=\frac{20.4\times {10}^{–19}}{ \mathrm{h}}=\frac{20.4\times {10}^{–19}}{6.63\times {10}^{–34}}$

$=3.076\times {10}^{15}=3.1\times {10}^{15} \mathrm{Hz}$

Wavelength of photon $\lambda =\frac{c}{v}=\frac{3\times {10}^8}{3.076\times {10}^{15}}=9.74\times {10}^{–8} \mathrm{m}$. Thus, the wavelength is $9.7\times {10}^{–8} \mathrm{m}$ nd frequency is $3.1\times {10}^{15} \mathrm{Hz}$

9. (a) Using the Bohr’s model calculate the speed of the electron in a hydrogen atom in the n = 1, 2 and 3 levels.

(b) Calculate the orbital period in each of these levels.

Sol. (a) Speed of the electron in Bohr’s nth orbit

$\mathrm{v}=\frac{\mathrm{c}}{\mathrm{v}}\mathrm{\alpha }\text{ where, }\mathrm{\alpha }=\frac{2{\mathrm{\pi Ke}}^2}{\mathrm{ch}}$

α = 0.0073          $\therefore \mathrm{v}=\frac{\mathrm{c}}{\mathrm{n}}\times 0.0073$

For   n=1,            ${\mathrm{v}}_1=\frac{\mathrm{c}}{1}\times 0.0073$

$=3\times {10}^8\times 0.0073=2.19\times {10}^6 \mathrm{m}/\mathrm{s}$

For   n=2              ${\mathrm{v}}_2=\frac{\mathrm{c}}{2}\times 0.0073$

$=\frac{3\times {10}^8\times 0.0073}{2}=1.095\times {10}^6 \mathrm{m}/\mathrm{s}$

For   n=3               ${\mathrm{V}}_3=\frac{\mathrm{c}}{3}\times 0.0073$

$=\frac{3\times {10}^8\times 0.0073}{3}=7.3\times {10}^5 \mathrm{m}/\mathrm{s}$

(b) Orbital period of electron is given by $\mathrm{T}=\frac{2\pi \mathrm{r}}{\mathrm{v}}$

Radius of nth orbit   $r_n=\left(\frac{n^2}{m}\right){\left(\frac{h}{2\pi }\right)}^2\frac{4\pi {\epsilon }_0}{e^2}$

$\therefore {\mathrm{r}}_1=\frac{(1{)}^2\times {\left(6.63\times {10}^{–34}\right)}^2}{\left.4\times 9.87\times (9\times 10{)}^9\times 9\times {10}^{–31}\times 6.6\times {10}^{–19}\right)}$

$=0.53\times {10}^{–10} \mathrm{m}$

For    n=1              ${\mathrm{T}}_1=\frac{2\pi {\mathrm{r}}_1}{{\mathrm{v}}_1}$

$=\frac{2\times 3.14\times 0.53\times {10}^{–10}}{2.19\times {10}^6}=1.52\times {10}^{–16} \mathrm{s}$

For n = 2, radius   $r_n=n^2{r}_1$

${\mathrm{r}}_2=2^2.{\mathrm{r}}_1=4\times 0.53\times {10}^{–10} \mathrm{m}$ and

velocity   ${\mathrm{v}}_{\mathrm{n}}=\frac{{\mathrm{V}}_1}{\mathrm{n}}$

$\therefore {\mathrm{v}}_2=\frac{{\mathrm{v}}_1}{2}=\frac{2.19\times {10}^6}{2}$

Time period   ${\mathrm{T}}_2=\frac{2\times 3.14\times 4\times 0.53\times {10}^{–10}\times 2}{2.19\times {10}^6}$

$=1.216\times {10}^{–15} \mathrm{s}$.

For n = 3, radius ${\mathrm{r}}_3=3^2$

${\mathrm{r}}_1=9{\mathrm{r}}_1=9\times 0.53\times {10}^{–10} \mathrm{m}$

and velocity  ${\mathrm{v}}_3=\frac{{\mathrm{v}}_1}{3}=\frac{2.19\times {10}^6}{3} \mathrm{m}/\mathrm{s}$

Time period ${\mathrm{T}}_3=\frac{2\pi {\mathrm{r}}_3}{{\mathrm{v}}_3}$

$=\frac{2\times 3.14\times 9\times 0.53\times {10}^{–10}\times 3}{2.19\times {10}^6}=4.1\times {10}^{–15} \mathrm{s}$.

10. The radius of the innermost electron orbit of a hydrogen atom is 5.3 ⨯ 10^-11 m. What are the radii of the n = 2 and n = 3 orbits?

Sol. Given, the radius of the innermost electron orbit of a hydrogen ${\mathrm{r}}_1=5.3\times {10}^{–11} \mathrm{m}$.

As we know that    ${\mathrm{r}}_{\mathrm{n}}={\mathrm{n}}^2{\mathrm{r}}_1$

For n = 2, radius   ${\mathrm{r}}_2=2^2$

${\mathrm{r}}_1=4\times 5.3\times {10}^{–11}=2.12\times {10}^{–10} \mathrm{m}$.

For n = 2, radius   ${\mathrm{r}}_3=3^2$

${\mathrm{r}}_1=9\times 5.3\times {10}^{–11}=4.77\times {10}^{–10} \mathrm{m}$.

11. A 12.5 eV electron beam is used to bombard gaseous hydrogen at room temperature. What series of wavelength will be emitted?

Sol. Energy of electron beam E=12.5 eV

$=12.5\times 1.6\times {10}^{–10} \mathrm{J}$

Planck’s constant h = $6.63\times {10}^{–34} \mathrm{J}–s$

Velocity of light c = $3\times {10}^8 \mathrm{m}/\mathrm{s}$

Using the relation $\mathrm{E}=\frac{\mathrm{hc}}{\lambda }=\frac{6.62\times {10}^{–34}\times 3\times {10}^8}{12.5\times 1.6\times {10}^{–19}}$

$=0.993\times {10}^{–7} \mathrm{m}=993\times {10}^{–10} \mathrm{m}=993{ \mathrm{A}}^0$

This wavelength falls in the range of Lyman series (912 $\mathrm{A}°$ to 1216 $\mathrm{A}°$)

thus, we conclude that Lyman series of wavelength 993 $\mathrm{A}°$ is emitted.

12. In accordance with the Bohr’s model, find the quantum number that characterises the earth’s revolution around the sun in an orbit of radius $1.5\times {10}^{11}$ m with orbital speed $3\times {10}^4$ m/s. (Mass of earth = $6.0\times {10}^{24}$ kg).

Sol. Given, radius of orbit r = 1.5 ⨯ 10¹¹ m

Orbital speed v = 3 ⨯ 10⁴ m/s;

Mass of earth M = 6 ⨯ 10²⁴ kg

Angulalr momentum, $\mathrm{mvr}=\frac{\mathrm{nh}}{2\mathrm{\pi }}\text{ or }\mathrm{n}=\frac{2\mathrm{\pi vrm}}{\mathrm{h}}$

[where, n is the quantum number of the orbit]

$=\frac{2\times 3.14\times 3\times {10}^4\times 1.5\times {10}^{11}\times 6\times {10}^{24}}{6.63\times {10}^{–34}}$

$=2.57\times {10}^{74}\text{ or }\mathrm{n}=2.6\times {10}^{74}$. Thus, the quantum number is 2.6 ⨯ 10⁷⁴ which is too large. The electron would jump from n=1 to n=3

${\mathrm{E}}_3=\frac{–13.6}{3^2}=–1.5\mathrm{eV}$

So, they belong to Lyman series.