The branch of chemistry which deals with the study of relationship between electrical energy and chemical energy and inter conversion of one form of energy into another is called electrochemistry.
ELECTROCHEMISTRY
The branch of chemistry which deals with the study of relationship between electrical energy and chemical energy and inter conversion of one form of energy into another is called electrochemistry.
This branch deals with the study of following two types of reactions.
i) Reactions in which chemical energy is converted into electrical energy (Electrochemical cell)
ii) Reactions in which electrical energy is required to bring about a chemical reaction (Electrolytic cell)
Conductors: The substances which allow the passage of electricity through them are called conductors. Conductors are further of two types, metallic conductors and electrolytes.
i) Metallic conductors: In these conductors the flow of electric current is due to the movement of free electrons in the metallic crystal without producing any chemical changes in the conductor.
e.g. Copper, Silver, Aluminium
Besides metals some minerals and a non-metal graphite also show conduction due to the movement of electrons.
They are collectively called electronic conductors.
ii) Electrolytic conductors: In these conductors, the flow of current is due to movement or migration of ions towards oppositely charged electrodes accompanied by chemical changes at the electrodes.
e.g. Fused salts (KCl, NaCl) and aqueous solution of salts (KCl, K2SO4 Solutions), acids and alkalies are some examples of electrolytes.
• The substances which do not conduct electricity in their molten state or in the form of their solutions are called non-electrolytes.
Some examples of non electrolytes are ethyl alcohol, sucrose, glucose, glycerine, urea etc. In general non-polar covalent carbon compounds are non- electrolytes. They do not contain ions.
• The electrolysis is carried out in a tank or cell called electrolytic cell and the electrical energy is used to cause chemical reaction to take place.
Depending upon their extent of ionization, electrolytes are of two types.
i) Strong electrolytes: These are almost completely ionized in their aqueous solutions.
e.g. HCl, H2SO4, NaOH, KOH and salts like CH3COONH4, NH4Cl,NaCl etc.
ii) Weak electrolytes: They ionise in aqueous solutions to the smaller extent. Their aqueous solutions contain ions in equilibrium with undissociated molecules. e. g. etc.,
In aqueous solution or molten state, the electrolytes split up into oppositely charged ions. These ions are free to move in solutions. The electrical conductivity of solution depends on the number of ions present in the solution. Some factors which affect the electrical conductivity of solution are
i) Larger the interionic attraction between ions lesser is freedom of movement and smaller will be the electrical conductivity.
ii) Larger the solute – solvent interactions greater is the extent of solvation and lower will be the electrical conductivity of the solution.
iii) Larger the solvent – solvent interactions, larger will be the viscosity and more will be the hinderance to the movement of ions, consequently lower will be the electrical conductivity.
iv) As the temperature of electrolyte solution is increased, kinetic energy of ions increases. This results in the increase in electrical conductivity of solutions.
Resistance:
It measures the obstruction to the flow of current. It is represented by the symbol `R’. Unit of resistance is ohm (Ω) which in terms of SI base units is equal to . Resistance can be measured with the help of a Wheatstone bridge.
Ohm’s law:
It states that the current (I) flowing through a conductor at a given temperature is proportional to the potential difference (V) and inversely proportional to resistance (R )
I = or V = IR
In other words, the ratio of potential difference across the conductor to the current flowing through it is constant and is called resistance of the conductor.
• Ohm’s law is obeyed by both the metallic as well as electrolytic conductors.
Specific Resistance or resistively: The electrical resistance of any object is directly proportional to its length `l’ and inversely proportional to its area of cross section `A’.
The constant of proportionality (rho) is called resistivity or specific resistance. Its SI units are ohm-metre (Ωm)
• IUPAC has recommended the use of the term resistivity over specific resistance.
• Physically the resistivity for a substance is its resistance when it is one metre long and its area of cross section is one e. if =1 m and A = 1
The S.I. units of resistivity are ohm-m 1 Ω-m = 100 Ω cm or 1 Ω cm = 0.01 Ω m
Conductance:
The inverse of resistance is called conductance `G’. It is a measure of the ease with which current flows through the conductor.
The units of conductance are i.e. OR mho. It is also expressed is siemens denoted by S
Conductivity or specific conductance:
The inverse of resistivity is called conductivity or specific conductance. It is represented by the symbol `κ’ (greek, kappa)
If = 1cm, and a = 1 cm2
Thus conductivity may also be defined as the conductance of one centimetae cube of the conductor. The SI units of conductivity are but quite often κ is expressed in S
IUPAC has recommended the use of term conductivity over specific conductance.
The conductivity of electrolytic solutions depends on :
i) The nature of the electrolyte added
ii) Size of the ions produced and their solvation
iii) The nature of the solvent and its viscosity
iv) Concentration of the electrolyte
v) Temperature (conductivity increases with increase of temperature)
Molar conductivity:
The conductivity of solutions of different electrolytes in the same solvent and at a given temperature differs due to charge and size of the ions in which the electrolytes dissociate. It also depends on the concentration of ions or ease with which the ions move under potential gradient. Therefore in case of electrolytic solutions, a more appropriate term, molar conductivity is used, which takes into account the concentration of the solution as well as its conductivity.
Molar conductivity is the conductance of a solution containing 1 mol or 1g molecule of electrolyte such that the entire solution is placed between the electrodes one centimeter apart. It is denoted by symbol Λ m
• If κ is the conductivity of solution and `V’ is the volume of solution in containing one mole of the electrolyte, Λ m is related to κ by the equation
If molarity of solution in `M’, it means volume of solution containing M g-mol of electrolyte = 1 L = 1000
Volume of solution containing 1 g-mol of electrolyte
And κ is expressed in
Units of Λ m in this case are
In SI units κ is expressed in and V is expressed in
Equivalent conductivity;
Equivalent conductivity is the conductance of the solution containing one g-equivalent of the electrolyte such that the entire solution is placed between two parallel electrodes one centimeter apart. It is denoted by symbol .
where κ is conductivity and V is the volume of the solution in containing one gram equivalent of the electrolyte.
If normality of solution is N, i.e. N g-equivalent of electrolyte are present in 1000 ml
volume of solution containing 1 g-equivalent of electrolyte =
If k is expressed in , then units of are
Measurement of the conductivity of ionic solutions:
Conductivity (κ) is related to the resistance (R)
Here, is the distance of separation of two electrodes and a is the area of cross-section of electrodes. The quantity is called cell constant. Knowing the value of cell constant and the resistance of the solution, the conductivity can be calculated
(i) Determination of Resistance.
The resistance of the electrolytic solution is measured with the help of wheat stone bridge method.
Wheatstone bridge consists of two fixed resistances and , a variable resistance and the conductivity cell containing solution of electrolyte is made the resistance .
The conductivity cell is made of pyrex glass and is fitted with two platinum electrodes. Finely divided metallic ppt is deposited on the electrodes electrochemically. There electrodes have area of cross-section equal to `a’ and are separated by a distance `’
solution confined between these electrodes is a column of length and area of cross section `a’
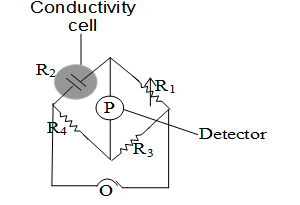
This Wheatstone bridge containing four resistances is fed by an oscillator which is a source of a.c power in the audio frequency range 550 to 5000 cycles per second. The resistances are so adjusted that a null point is obtained. The null point is indicated by a detector which may be a headphone or other electronic device. The bridge is balanced when no current passes through the detector. Under these conditions
• Direct current can not be used here because it causes electrolysis and results in the change in concentration of electrolytic solution near the electrodes resulting in polarisation effects.
ii) Determination of cell constant
Cell constant depends on the distance between the electrodes and their area of cross-section. It can be calculated if we know and a. Experimental determination of and a is not only inconvenient but also unreliable. The cell constant is usually determined by measuring the resistance of the cell containing a solution whose conductivity is already known. For this purpose a standard solution of KCl is used whose conductivity is known at different concentrations and temperatures.
Cell constant =
Once the cell constant is known, the conductivity can be calculated from the measured conductance or measured resistance of the electrolytic solution. κ =
• In conductance measurements, the solutions are always prepared in conductivity water which has no conductance due to dissolved impurities. It is prepared by distilling a number of times the distilled water to which a little and KOH have been added in a hard glass assembly. Such water has very low conductance of the order of ohm m–1. For ordinary purposes double distilled water may be used.
Variation of conductivity with concentration
The conductivity of a solution at any given concentration is the conductance of one unit volume of solution kept between two platinum electrodes with unit area of cross section and at a distance of unit length. With the increase in dilution the number of ions present in one centimeter cube of the solution decreases. Consequently, conductivity of the electrolytic solution also decreases as the dilution increases.
Variation of molar conductivity with concentration
Molar conductivity increases with decrease in concentration.
For weak electrolytes as the dilution increases, the degree of ionization also increases causing more and more ionization. As a result the value of Λm also increases significantly.
At infinite dilution or at zero concentration, the degree of ionization approaches unity i.e. the electrolyte almost undergo complete ionization.
This causes steep rise in the value of Λm near the infinite dilution. When conc approaches zero the molar conductivity is known as limiting molar conductivity and is represented by a symbol
The strong electrolytes are almost completely ionized in aqueous solution at all concentration. In concentrated solutions of strong electrolyte inter – ionic interactions are very high. On increasing dilution, inter ionic attractions are decreased. As a result the value of molar conductivity increases. For a strong electrolyte the variation of molar conductivity is given by Debye Huckel onsager equation. The equation in its simplified form can be written as
Where Λm is molar conductivity, is limiting molar conductivity or molar conductivity at infinite dilution, `b’ is a constant which depends upon the viscosity and dielectric constant of the solvent, and C is concentration of solution.
At infinite dilution, the concentration tends to be zero, i.e. (`C’ approaches zero or = Graphic representation of the variation of
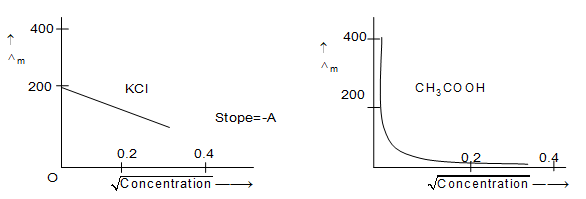
The graph reveals following fact
i) Molar conductivity of electrolytes generally increases with dilution.
ii) For the same concentration, Λm values of strong electrolytes is larger than those of weak electrolytes.
iii) Relative increase in value of Λm for strong electrolyte is quite small as compared to that for weak electrolytes.
iv) In the case of weak electrolyte, there is no indication that the limiting value can be attained because when concentration approaches zero the graph becomes almost parallel to the y-axis.
Therefore for, weak electrolytes, the value of limiting molar conductivity can not be obtained by extrapolating the graph to the zero concentration. It may be obtained indirectly by using Kohlrausch’s law.
v) For strong electrolytes, the value of is determined from the graph by extrapolating it to zero concentration.
Kohlrausch’s law:
According to this law, at infinite dilution, when the dissociation is complete, each ion makes a definite contribution towards molar conductivity of the electrolyte irrespective of the nature of the other ions present.
The law states that molar conductivity of an electrolyte at infinite dilution is the sum of the ionic conductivities of the cations and anions each multiplied by the number of ions present in one formula unit of the electrolyte. If represent the limiting molar conductivities of cation and anion respectively, then the limiting molar conductivity of electrolyte at infinite dilution is given by
Where represent the number of positive and negative ions present in one formula unit of the electrolyte.
e.g. if are limiting molar conductivity of sodium and chloride ions respectively then the limiting molar conductivity for NaCl is given by the equation
Applications of Kohlrausch’s law:
1) Determination of limiting molar conductivity of weak electrolyte:
The value of for weak electrolytes cannot be obtained directly by extrapolation of to zero concentration. At infinite dilution (i.e. concentration → 0) electrolyte dissociates completely but at such low concentration the conductivity of the solution is so low that it cannot be measured accurately. Therefore for weak electrolyte is obtained by using Kohlrausch law of independent migration of ions.
e.g. The value of for acetic acid can be calculated from values of strong electrolytes like HCl and NaCl
or
Similarly
ii) Calculation of Degree of Dissociation of weak Electrolytes
Weak electrolytes like acetic acid have lower degree of dissociation at higher concentration. As dilution increases, the degree of dissociation of weak electrolyte also increases and consequently molar conductivity of electrolyte increases. At infinite dilution the degree of dissociation approaches unity. At this stage, molar conductivity of electrolyte becomes maximum and attains the value of limiting molar conductivity of the electrolyte.
At any concentration `C’ if is α the degree of dissociation, then
iii) Calculation of dissociation constant of weak electrolyte
Weak electrolytes are not completely ionized when dissolved in water. There exists equilibrium between ions and unionized molecules
concept of chemical equilibrium and law of mass action can be applied to ionic equilibrium.
Where `C’ is concentration, is molar conductivity at concentration `C’ is molar conductivity at infinite dilution.
(iv) Determination of the solubility of sparingly soluble salt
The aqueous solution of sparingly soluble salt is infinitely dilute due to their extremely low solubility. At the same time, this solution is saturated also. Hence concentration of such salts in their aqueous solution pertains to their respective solubility and it can be calculated by the measurement of conductivity and molar conductivity of the aqueous solution.
Illustration 1: Electrolytic conductivity of 0.02 M solution of KCl at 298 K is 2.48 . Calculate its molar conductivity.
Solution. κ=2.48 S , molarity = 0.02 mol/L
volume of solution containing 0.02 mol of electrolyte (KCl) = 1 L =
Volume of solution containing 1 mole of electrolyte (KCl)
=
molar conductivity, Λm = κ V
Illustration 2 : The specific conductance of an KCl solution at . The resistance of the solution contained in the cell in found to be 65Ω. Calculate the cell constant ?
Solution. Specific conductance or conductivity
= conductance × cell constant;
Illustration 3 : The resistance of an aqueous solution containing 0.624g of per 100 of the solution in a conductance cell of cell constant 153.7 per metre is 520 Ω at 298 K. Calculate the molar conductivity (GMM of )
Solution. R = 520 Ω ; cell constant = 153.7 per metre
= 1.537 per cm
conductivity = ; molarity of solution = mol/L
molar conductivity,
= mho
Illustration 4: In a conductivity cell the two platinum electrodes, each of area 10 sq. cm, are fixed 1.5cm apart. The cell contained 0.05N solution of a salt. If the two electrodes are just half dipped into the solution which has a resistance of 50Ω. What will be the equivalent conductivity of the salt solution.
Solution. Since the electrodes of the cell are half dipped the effective area will be
conductivity
Equivalent conductivity
Illustration 5: The resistance of two electrolytes A and B were found to be 45 and 100 ohms respectively when equal volumes of both the solutions were taken in the same cell in two different experiments. If equal volumes of these solutions are mixed in the same cell, what will be the conductance of the mixture ?
Solution. Let and be the specific conductance’s of the solutions A and B respectively
conductivity = conductance cell constant
……………………………..(i)
………………………….(ii)
When equal volumes of A and B are mixed, both the solutions get doubly diluted, hence their individual contribution towards conductivity of the mixture will be respectively and conductivity of the mixture will be
If R is the resistance of mixture, then
Thus conductance = 0.016
Illustration 6: The resistance of 0.02M KCl solution was found to be 550 Ω at 298 K. The conductivity of this solution at same temperature is 0.002768 The resistance of 0.05M solution when measured in the same cell at 298K is found to be 72.18 Ω . Find the molar conductivity of solution
Solution.
Illustration 7 : Given the equivalent conductance of sodium butyrate, sodium chloride and hydrogen chloride as 83, 127 and 426 at 298 K respectively. Calculate the equivalent conductance of butyric acid at infinite dilution?
Solution. ……… (i)
……… (ii)
……… (iii)
Illustration 8: Conductivity of 0.00241M acetic acid is 7.896 . Calculate its molar conductivity if for acetic acid is . What is its dissociation constant?
Solution.
Illustration 9: The conductivity of saturated solution of AgBr is . The conductivity of pure water at the same temperature is . If molar conductivity of , are 137.0, 131 and 134 respectively. Calculate solubility of AgBr in g
Solution. The conductivity of AgBr solution (only due to and ions)
molar conductivity of AgBr solution at infinite dilution
= 134 + 137 – 131 = 140
Solubility of AgBr =
Solubility in gram per litre
ELECTROCHEMICAL CELLS
It is the device in which chemical energy is converted into electrical energy. It is also called galvanic cell or voltaic cell. In a galvanic cell the decrease in free energy during the spontaneous redox reaction is made to appear as electrical energy.
All galvanic cells consists of two half cells. Each half cell consists of a metallic electrode dipping into an electrolyte.
The half cell in which oxidation takes place is called anode and it has negative potential with respect to solution.
The other half cell in which reduction takes place is called cathode and has positive potential with respect to solution.
The two half cells are connected by a metallic wire through a voltmeter and a switch externally. The electrolytes of two half cells are connected through a salt bridge.
Daniel cell is an example of galvanic cell. Daniel cell converts the chemical energy liberated during the reaction, to electrical energy. This cell has an electrical potential equal to 1.1 volt when activity (nearly equal to molarity) of an ion is unity.
In its simple form, a zinc strip is dipped in the solution and a copper strip is dipped in the solution taken in separate beakers. The two metallic strips act as electrodes and are connected by a metallic wire through a voltmeter. The two solutions are joined by an inverted `U’ tube known as salt bridge. When the zinc and copper electrodes are joined by a wire, it is observed that the conventional current flows through the outer circuit from copper to zinc strip. It indicates that electron flow occurs from zinc to copper strip.
At the zinc electrodes, the zinc metal is oxidized to zinc ions which go into the solution.
(oxidation)
The electrons released at the electrode travel through the external circuit to the copper electrode where they are used in the reduction of ions to metallic copper which is deposited on the electrode
(Reduction)
Thus the overall redox reaction is
• At the zinc rod oxidation occurs. The half cell in which oxidation occurs is called oxidation half cell. It is the anode of the cell and is negatively charged.
• At the copper rod reduction occurs. The half cell in which reduction occurs is called reduction half cell. It is the cathode of the cell and is positively charged.
• In the external circuit electrons flow from anode to cathode.
Salt bridge and its function:
A salt bridge is a U-shaped tube containing conc solution of an inert electrolyte like etc. An inert electrolyte is one whose ions do not take part in the redox reaction and also do not react with electrolytes used. Salt bridge is prepared by dissolving gelatin or agar agar in a hot concentrated aqueous solution of an inert electrolyte and the solution thus formed is filled in the U-tube. On cooling the solution sets in the form of a gel in the U-tube.
Functions of salt bridge:
1) It helps to complete the electrical circuit
2) It maintains the electrical neutrality of the electrolytes in the two half cells.
In anodic half cell positive ions pass into the solution and accumulate around the anode which prevent the flow of electrons from anode. This does not happen because negative ions are provided by salt bridge. Similarly, in cathodic half cell negative ions accumulate around cathode due to deposition of positive ions by reduction, salt bridge neutralizes this negative charge by providing positive ions. Thus salt bridge maintains electrical neutrality.
• Salt bridge can be replaced by a porous partition which allows the migration of ions without allowing the solutions to intermix
Representation of electrochemical cell:
Electrochemical cell is a combination of two half cells i.e. oxidation half cell and reduction half cell. Conventionally a cell is represented by writing the cathode on the right hand side and anode on left hand side. While writing anode, metal or solid phase (or the gas) is written first followed by its ion which represents its oxidized state. The contact between solid and electrolytic solution is denoted by a vertical line or semicolon.
While writing cathode the ion is written first along with the concentration of solution in brackets followed by the symbol of the metal (or the gas).
The two vertical lines are put between the two half cells which indicate salt bridge. Sometimes the formula of the electrolyte used in the salt bridge is also written below the vertical lines.
e.g. Zinc – Copper sulphate cell is represented as follows :
Different types of electrodes.
1. Metal – metal ion electrode ⇒ In this electrode a metal rod is dipped in the solution of its own ions
e.g. , Electrode reaction
, electrode reaction
2. Amalgam electrodes ⇒ This electrode is generally used for active metals like Na,K,Zn etc. In this electrode the metal is used in the form of its amalgam with Hg.
e.g. Electrode reaction
3. Gas electrodes ⇒ In this type of electrode, an inert metal such as platinum or gold is dipped in the solution containing ions of the gaseous element. The arrangement is made in such a way that gas and its ions are brought in contact at the surface of the inert metal
e.g. i) Hydrogen electrode,
Electrode reaction
ii) Chlorine electrode,
Electrode reaction.
4. Metal – metal insoluble salt – salt anion electrodes ⇒ In this electrode, the metal and some sparingly soluble salt of metal is dipped in the aqueous solution of some other soluble salt whose anion is same as that of sparingly soluble salt of the metal
e.g. (i) Ag, AgCl (s) | KCl (aq)
Electrode reaction :
ii)
Electrode reaction :
5. Oxidation – reduction electrodes ⇒ These electrodes are prepared by dipping platinum wire in solution of two salts of same metal with different oxidation states.
e.g.
Electrode reaction :
• In the above electrodes reduction as well as oxidation half reaction can take place depending upon the second electrode combined to form the cell. Hence these electrodes are also called reversible electrodes.
Electrode Potential:
When a metal is placed in a solution of its ions, then there is one of the following three possibilities.
i) The metal ions may collide with the metallic strip and bounce back without any change.
ii) If metal has relatively higher tendency to get oxidized, then metal atoms will lose electrons and change into ions.
These electrons will accumulate on the metal rod and cause it to develop negative charge. This metal rod would retract the metal ions from solution to neutralize its charge. Ultimately an equilibrium is reached as follows :
iii) If metal ions have relatively higher tendency to get reduced, then metal ions will gain electrons from the metal rod. As a result metal rod will develop a positive charge with respect to the solution. Ultimately an equilibrium is established between the metal ions and the metal atoms at the interface.
The equilibrium between the metal and its ions leads to the separation of charges. This results in a potential difference between the metal rod and its solution.
Thus, electrical potential difference set up between the metal and solution of its ions is known as half cell electrode potential.
It may also be defined as the tendency of an electrode to either lose or gain electrons when it is in contact with the solution of its ions.
• If oxidation takes place at the electrode, the electrode potential is called oxidation potential.
• If reduction takes place at the electrode, the electrode potential is called reduction potential.
• Reduction potential and oxidation potential of an electrode are numerically equal but have opposite signs.
• The magnitude of electrode potential depends on the nature of the electrode, concentration of the ions in solution, and temperature
• Reduction potential increases with the increase in the concentration of ions and decreases with the decrease in the concentration of ions in solution
Standard electrode Potential
According to IUPAC convention, the half cell reactions are always written as reduction half reactions and electrode potentials are represented by reduction potentials.
The reduction potential of electrode when the concentration of the ions in solution is 1 and temperature is 298 K is called standard reduction potential and is represented by
Standard Hydrogen Electrode (Reference Electrode)
It is not possible to measure the absolute potential of an electrode individually because the oxidation half reaction or reduction half reaction can not occur alone. It can only be measured by connecting the half cell with a reference electrode of known potential.
It is only the difference of potentials between two electrodes that can be measured by combining them to give a complete cell. By arbitrarily fixing potential of one electrode as zero, it is possible to assign numerical values to potential of various other electrodes. Accordingly, the potential of a reversible hydrogen electrode in which the gas at one bar pressure is bubbled through a solution of hydrogen ions of unit activity (approximately 1M concentration) has been fixed as zero. This electrode is known as standard hydrogen electrode and is represented as :
If this electrode acts as anode, then oxidation will take place at it
If this electrode acts as cathode then reduction will take place at it.
Standard hydrogen electrode consists of a platinum wire sealed into a glass tube and carrying a platinum foil at one end. The platinum foil is coated with finely divide platinum. The electrode is placed in beaker containing an aqueous solution of some acid having one molar concentration of ions gas at 1 bar pressure is bubbled through the solution at 298K temperature. The platinum strip and glass tube is surrounded by an outer glass tube which has an inlet for gas at the top and many holes at the base for the escape of excess of hydrogen gas.
Measurement of standard Electrode potential
To measure the standard electrode potential of an electrode, the electrode in standard conditions is connected to SHE to constitute a cell. The emf of the cell is measured with the help of potentiometer or vacuum tube voltmeter. The direction of flow of conventional current in external circuit is noticed with the help of galvanometer.
• According to IUPAC convention, the electrode potential is given a positive sign if reduction occurs at the electrode when connected to the standard hydrogen electrode.
• The electrode potential is given a negative sign if oxidation occurs at the electrode when connected to the standard hydrogen electrode whose potential is taken arbitrarily as zero
e.g. When copper electrode (Cu rod dipped in solution) is connected with SHE, the voltmeter reading shows a potential difference of 0.34 volts. The electron flow occurs from SHE towards copper electrode … SHE acts as anode and copper electrode acts as cathode
hydrogen electrode : (oxidation)
Copper electrode : (Reduction)
The net reaction is
• If zinc electrode is connected with the standard hydrogen electrode, oxidation takes place at the zinc electrode. The voltmeter reading shows the potential difference of 0.76 volt. The electrode reactions are as follows :
Zinc electrode : (oxidation)
Hydrogen electrode : (Reduction)
The net reaction is
The standard reduction potentials of other electrodes including metals as well as non-metals can be determined in the similar way.
• It is not convenient to use the standard hydrogen electrode as the reference electrode because it is difficult to maintain the activity of ions in the solution at unity and to keep the pressure of the gas uniformly at one bar pressure. The hydrogen electrode gets poisoned even if traces of impurities are present.
To overcome these difficulties, SHE is usually replaced by other reference electrodes which are known as secondary reference electrodes like calomel electrode or silver – silver chloride electrode.
i) Calomel electrode ⇒ This electrode consists of mercury, solid mercurous chloride and a solution of KCl. The electrode is represented as
, and the electrode reaction may be represented as
The electrode is reversible with respect to ions.
The potential of the calomel electrode, on the hydrogen scale, has been measured by connecting it to a standard hydrogen electrode. Its electrode potential varies with concentration of ions or KCl (aq). The values for 0.1 M KCl, 1.0 M KCl and saturated solution of KCl are 0.3335 volt, 0.2810 volt and 0.2422 volt respectively at
• The calomel electrode with saturated KCl solution is most commonly used and is referred to as saturated calomel electrode.
ii) Silver – Silver Chloride electrode ⇒ It consists of a silver wire coated with a layer of AgCl. This is inserted in a solution of KCl or HCl of a known concentration. It is represented as Ag, AgCl(s)/KCl(aq). This electrode is also reversible with respect to ions.
EMF of the cell
Every voltaic cell is composed of two half cells, the oxidation half cell and the reduction half cell. The reduction potential of these half cells are always different. Due to this potential difference, the electrons flow from an electrode of lower reduction potential to the electrode of higher reduction potential i.e. from anode to cathode.
The difference between the electrode potential of the two half cells is called electromotive force of the cell.
Thus cell potential (EMF)= Reduction potential of cathode – Reduction potential of anode
EMF is potential difference between two electrodes when no current is flowing in the circuit. It is the maximum voltage that can be obtained from the cell. It is measured by a potentiometer. EMF corresponds to the maximum useful work obtained from the galvanic cell, EMF of the cell depends on the nature of the reactants, concentration of the solution in the two half cells, and temperature.
Reversible and Irreversible cells
A cell is said to work reversibly in the thermodynamic sense when it is generating infinitesimally small current so that the cell reaction always remains virtually in a state of equilibrium. The cell will be reversible if it satisfies the following conditions :
i) If an external opposing EMF (exactly equal to that of the cell itself) is applied to the cell, no current is given out by the cell and no chemical reaction takes place in the cell.
ii) If the opposing EMF is slightly greater than that of cell itself, an extremely small current flows through the cell in the opposite direction and the chemical reaction also takes place in reverse direction.
• In the determination of EMF of a cell potentiometrically, the current given out by the cell, at the time of taking the reading is almost zero. Thus the cell at that time is working in a reversible manner.
• Any other cell which does not obey the above two conditions is termed as irreversible cell.
e.g. A cell consisting of zinc and copper electrodes dipped into the solution of is irreversible.
Electrochemical series:
The arrangement of various element in the order of increasing values of standard reduction potentials is called electrochemical series. It is also known as activity series.
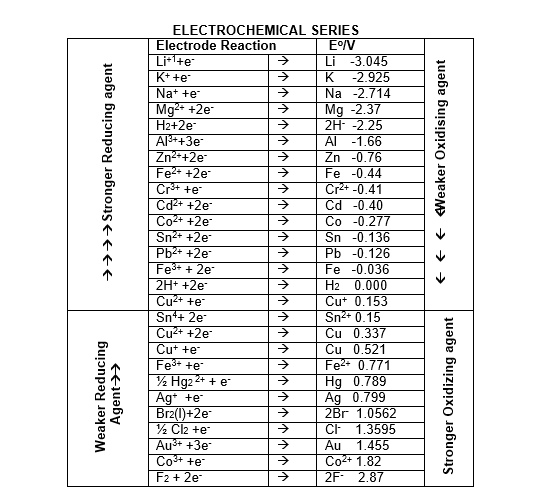
Characteristics of Electrochemical Series
1. By international convention, the standard potentials of electrodes are tabulated for reduction half reactions. It indicates the tendencies of the electrodes to behave as cathodes towards SHE.
2. The electrode with –Ve sign of reduction potential when connected with SHE acts as anode and oxidation occurs on this electrode. Similarly the +ve sign of standard reduction potential indicates that the electrode when connected with SHE acts as cathode and reduction occurs on this electrode.
3. In activity series metals on the top have high negative values of standard reduction potentials or high positive values of oxidation potential. These metals have high tendency to lose electrons. The substances which are stronger reducing agent than hydrogen, have –ve value of reduction potential and are placed above hydrogen in activity series.
4. The activity of metals decreases from top to bottom. The substances which are placed below hydrogen are stronger oxidizing agent then hydrogen these elements have high positive values of standard reduction potential. These elements have high tendency to accept electrons.
Application of Electrochemical series.
1. Greater the oxidation potential of a metal more easily it can lose electrons and hence greater is its reactivity. As a result, a metal with greater oxidation potential can displace metals with lower oxidation potentials from their salt solution.
2. Reducing nature of metals depends on the tendency of losing electrons. Higher value of negative reduction potential indicates high tendency to lose electrons. The reducing power of metals decreases from top to bottom in the electrochemical series.
e.g. Lithium is the strongest reducing agent.
3. Oxidizing nature of non metals depends on the tendency to accepts electrons. Higher the value of reduction potential, higher is the tendency to accept electrons. The oxidizing power of non metals increases as the value of reduction potential becomes more and more positive
e.g. has the highest reduction potential, it is reduced most easily or acts as strongest oxidizing agent.
4. All metals lying above hydrogen in the electrochemical series react with the acid to give hydrogen gas.
The metals which are below hydrogen in electrochemical series like Cu, Hg, Au, Pt etc. do not evolve hydrogen from dilute acids.
5. Iron and the metals above iron are capable of liberating hydrogen from water. Alkali and alkaline earth metals liberate hydrogen from cold water, Mg, Zn and Fe can liberate hydrogen from hot water, or steam.
6. In an electrochemical cell, the electrode with higher reduction potential acts as cathode while that with lower reduction potential acts as anode. Standard EMF of the cell can be calculated by applying the formula.
Where are standard reduction potential of cathode and anode and is EMF of cell under standard conditions.
7. Electrochemical series help to predict the feasibility of redox reaction in a given direction. For a redox reaction to be spontaneous, the EMF of the cell must be positive. If the EMF comes out to be negative, the direct reaction can not take place; the reverse reaction may take place.
8. The thermal stability of metal oxide depends on its electropositive nature. As the electropositive nature decreases from top to bottom the thermal stability of oxide also decreases from top to bottom. The metals which come below copper form unstable oxides.
e.g
9. The non-metal which possess high positive reduction potentials have the tendency to accept electrons readily. These electrons are provided by the ions of the non-metal having low value of reduction potential. Thus can displace , and from their salt solutions. Solutions can displace and whereas can displace from its solutions e.g.
10. A more electropositive metal can displace a less electropositive metal from its salt solution. This principle is applied for the extraction of silver and gold in Mac Arthur Forest cyanide process.
Zn can displace silver as it is more electropositive than silver.
Illustration 10 : Given that :
select strongest oxidant and reductant.
Solution. Higher is the value of reduction potential higher is the oxidizing power, thus is the strongest oxidant. Lower the value of reduction potential higher is the reducing power thus is strongest reductant
Illustration 11: In which of the following vessel 1M solution of be stored
i) Al vessel ii) Zn vessel iii) Cu vessel
Solution. Reduction potential of Al and Zn are more negative than that of Fe. These metals can displace iron from its aqueous solution. Reduction potential of Cu is greater than that of Fe. Thus solution can be stored in Cu Vessel.
Illustration 12: The standard EMF of the cell is 0.59 volt.
The standard reduction potential of copper electrode is 0.34 volt. Calculate the standard electrode potential of Nickel electrode.
Solution.
EMF of cell =
Effect of Electrolyte concentration and temperature on the electrode potential (Nernst equation):
The electrode potential and the emf depend upon the nature of the electrode, temperature and the activities (molarity) of the ions in solution.
The quantitative relationship between conc of ions and electrode potentials is given by Nernst equation. For a general electrode reaction.
Nernst equation can be written as
T = Temperature, It represents the activities of various species. The activity of a gas is assumed to be equal to its partial pressure and that of solution is taken to be its molarity.
n = No. of electrons involved in the electrode reaction
F = Faraday constant
R = gas constant (8.314 J ) at 298 K and substituting the values of R and F in Nernst equation, we get
For pure solids or liquids or gases at one atmospheric pressure the molar concentration is taken as unity .
e.g. in the above case [M] = 1
Nernst equation for EMF of a cell:
The reaction that occurs in Daniell cell is
For copper electrode.
Thus E depends on the concentration of both ions. It increases with increase in the conc. of ions and with the decrease in the conc. Of ions.
For a general electro chemical reaction of the type
• In this equation, the values of n,a,b,c,d are obtained from the balanced cell reaction. E.g. the balanced cell reaction for the cell
The Nernst equation can be written as :
[Ag] = [Ni] =1
Similarly, for the cell,
, the cell reaction is
Here n = 6
Concentration cell:
A cell in which both electrodes are of the same type but the solutions of electrolyte in which they dip have different concentrations is called concentration cell. The electrode which is placed in electrolyte of larger concentration acts as cathode. Whereas electrode which is placed in electrolyte of lower concentration acts as anode. For example,
In this cell standard electrode potentials of the two electrode cancel each other and the cell potential is given by the equation.
For cell potential to be positive
Equilibrium constant from Nernst equation:
In an electrochemical cell a reversible redox process takes place
e.g. in Daniell cell
As the time passes, the concentration of keeps on increasing while the concentration of keeps on decreasing. At the same time voltage of the cell as read on the voltmeter keeps on decreasing. After some time, there is no change in the concentration of and ions and at the same time, voltmeter gives zero reading. This indicates that the equilibrium has been attained. In this state the potential difference becomes zero and the flow of electrons stops.
Applying the Nernst equation for cell potential
Electrochemical cell And Gibb’s energy of the reaction:
The electrical work or the electrical energy is equal to the product of EMF of the cell and the electrical charge that flows through the external wire
Electrical work = (EMF) x (charge)
To obtain maximum work from a galvanic cell, the charge has to be passed reversibly. The reversible work done by a galvanic cell is equal to decrease in its Gibb’s energy
Thus ΔG = Electrical work
For the transference of one mole of electrons in the cell reaction, the quantity of electricity flowing through the wire is 1 faraday if n mole of electrons are transferred in the cell reaction, then charge flowing through the wire = nF, if E is the EMF of the cell, then electrical work = nF × E
or -ΔG = nFE
or ΔG = -nFE
standard Gibb’s energy change, =
Change in free energy helps in predicting the feasibility of the cell reaction. For cell reaction to be spontaneous ΔG must be negative, and for ΔG to be negative, the value of E must be positive.
• From the standard Gibbs energy, equilibrium constant can be calculated by the equation
Illustration 13: Calculate the reduction potential of zinc – zinc ion electrode in which the zinc ion activity is 0.001 M ?
Solution.
Illustration 14: At what pH of HCl solution will hydrogen gas electrode show electrode potential of -0.118volt? gas is bubbled at 298 K and 1 atm pressure.
Solution.
Illustration 15 : Write Nernst equation and find out the emf of the following cell
Solution. Nernst equation for this cell
EMF of this cell is negative, it means this cell reaction is not possible,
Illustration 16: Construct galvanic cell from the following pairs of half cells and calculate its EMF at
Solution. For the half cell reaction
At conc. 1M and 298 kelvin electrode potential is equal to standard reduction potential
For the half cell reaction
The reduction potential of second half cell is greater than that of first cell. Therefore first half cell undergoes oxidation and second half cell undergoes reduction. Thus the cell may be represented as
Illustration 17: The standard reduction potential of electrodes are +0.34 and +0.80 volt respectively. Construct a galvanic cell using these electrodes so that its standard emf is positive. For what concentration of will the emf of the cell at be zero if the concentration of is 0.01 M.
Solution. Reduction potential of is greater than that of . Silver electrode will act as cathode and copper electrode will act as anode. The representation of cell is
Illustration 18: For a Daniel cell
The standard reduction potentials are -0.763 volt for and +0.35 volt for . Write down the cell reaction. Is the cell reaction spontaneous or not ?
Solution. Reduction potential of is greater than that of the cell reaction will be
Illustration 19: A cell is constructed on the basis of following half reactions
Calculate the equilibrium constant for the reaction
Solution.
CORROSION :
Decay of the metal in presence of moisture and oxygen is known as corrosion. It slowly forms a coating on the metal surface with oxides.
e.g. rusting of iron tarnishing of silver, green coating on copper and bronze.
In corrosion, a metal is oxidized by loss of electron to oxygen and formation of oxides.
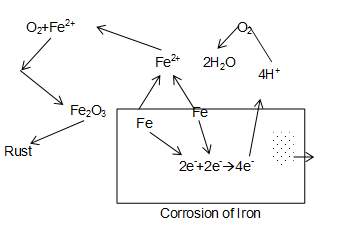
Rusting of iron occurs in presence of water and air. Mechanism of corrosion is complicated. It may, however, be considered as an electrochemical phenomenon.
A particular spot, of an iron piece, where the oxidation takes place is anode.
Anode reaction:
Electron released at anodic spot move through the metal and go to another spot on the metal and reduce oxygen in presence of (which is possibly available from , formed when is dissolved in water). This spot is a cathodes
Reaction at cathode:
Overall reaction
ions are further oxidized to Ferric ion by atmospheric oxygen and give rise to
FUEL CELLS
The efficiency of thermal plants for the production of electricity is about 40% and method is a measure source of pollution. In such plants the chemical energy of possible fuels (coal) is first used for converting water into steam of high pressure. This steam is used to run a turbine to produce electricity.
It is now possible to make such cells in which reactants are fed continuously to the electrodes and products are removed continuously from electrolyte compartment. The cells convert the energy of combustion of fuels directly into electrical energy are called Fuel cells.
H2O2 fuel cell →
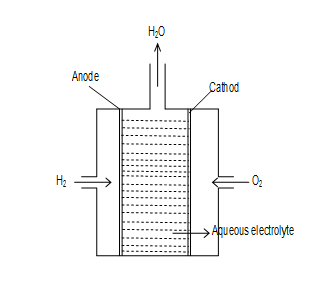
In the cell are bubbled through po rous carbon electrodes into conc. aq. NaOH solution. Finely divided platinum or palladium metal are incorporate into electrodes for increasing the rate of electrode reactions. (i.e. as catalyst)
Note : Efficiency of fuel cell is more than 70% and there has been tremendous progress in the development of new electrode materials, better catalysts and electrolytes for increasing the efficiency of fuel cells. These have been used in automobiles on experimental basis. Fuel cells are pollution free and in view of their importance in future a variety of fuel cells have been fabricated and tried.
BATTERIES
Any battery or cell that we use as a source of electrical energy is basically a galvanic cell where the chemical energy of the redox reaction is converted into electrical energy.
However, for a battery to be of practical use it should be reasonably light, compact and its voltage shuld ot vary appreciably during its use. There are mainly two types of batteries.
Primary Batteries:
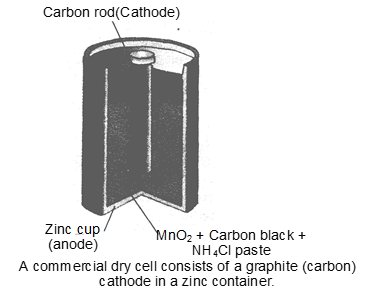
In the primary batteries, the reaction occurs only once and battery then becomes dead after use over a period of of time and cannot be reused again. The most familiar example of this type is the dry cell (known as Leclanche cell after its discoverer) which is used commonly in our transistors and clocks. The cell consists of a zinc container that also acts as anode and the cathode is a carbon (graphite) rod surrounded by powdered manganese dioxide and carbon (fig). The space between the electrodes is filled by a moist paste of . The electrode reactions are complex, but they can be written approximately as follows :
In the reaction at cathode, managanese is reduced from the +4 oxidation state to the +3 state. Ammonia produced in the reaction forms complex with . The cell has a potential of nearly 1.5V
Mercury cell: Suitable for the low current devices like hearing aids and camera, etc., consists of zinc-mercury amalgam as anode and a paste of HgO and carbon as the cathode. The electrolyte is a paste of KOH and ZnO. The electrode reactions for the cell are given below :
The overall reaction is represented by
Zn(Hg) + HgO(s) → ZnO(s) + Hg(l)
The cell potential is approximately 1.35V and remains constant during its life as the overall reaction does not involve any ion in solution whose concentration can change during its life time.
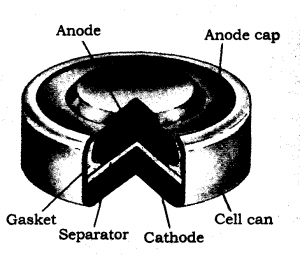
Commonly used mercury cell. The reducing agent is zinc and the oxidizing agent is mercury (II) oxide.
Secondary Batteries:
A secondary cell after use can be recharged by passing current through it in opposite direction so that it can be used again. A good secondary cell can undergo a large number of discharging and charging cycles. The most important secondary cell is the lead storage battery commonly used in automobiles and invertors. It consists of a lead anode and a grid of lead packed with lead dioxide as cathode. A 38% solution of sulphuric acid is used as an electrolyte.
The cell reactions when the battery is in use are given below:
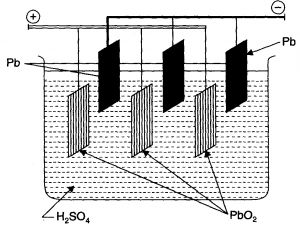
On charging the battery the reaction is reversed and on anode and cathode is converted into Pb and , respectively.
Another important secondary cell is the nickel-cadmium cell which has longer life than the lead storage cell but more expensive to manufacture. We shall not go into details of working of the cell and the electrode reactions during charging and discharging. The overall reaction during discharge is :
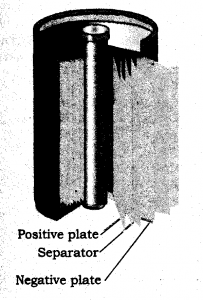
A reachargeable nickel cadmium cell in a jelly roll arrangement and separated by a layer soaked in moist sodium of potassium hydroxide.
ELECTROLYSIS
The process of chemical decomposition of an electrolyte by passage of electrical current through its solution is called electrolysis.
OR
Chemical change (oxidation and reduction) occurring at electrodes when electric current is passed through the electrolytic solution is called electrolysis.
ELECTROLYTIC CELLS:
The cell in which electrical energy is converted to chemical energy.
Anode: The electrode where Oxidation takes place.
Cathode: The electrode where reduction takes place.
Note: Sign of anode and cathode should not be made important point
Electrolysis of Molten NaCl:
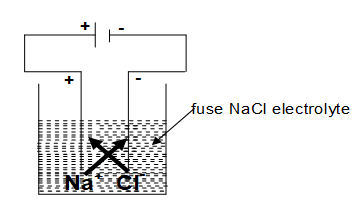
so Na metal gets deposited over cathode one gas is liberated at anode. This way Na is extracted from NaCl (Fused) which is not possible otherwise by any other method.
Note: In case if we take aq. NaCl solution, Na will not deposit over cathode rather gas is liberated at cathodes. Reason in case of aq. NaCl there are total four ions present in the solution now there is competition between to reach the cathode, since discharge potential of is higher so it reaches the cathode. at anode and in the cell NaOH solution is formed.
Faraday’s law of Electrolysis.
Faraday’s First law : When an electric current is passed through an electrolyte, the amount of substance deposited is proportional to the quantity of electric charge passed through the electrolyte.
or W∝Q Where W = mass of the substance deposited
W = ZQ Q = charge in coulomb
Since Q = current x time Z = electro chemical equivalent
= I x t I = current in ampere
hence W = Z x I x t t = time in seconds.
Electrochemical equivalent, Z, can be defined as the mass of substance deposited by one coulomb of charge or one ampere of current passed for one second.
Faraday’s second law:When the same quantity of charge is passed through different electrolytes, then the masses of different substances deposited at the respective electrodes will be in the ratio of their equivalent masses.
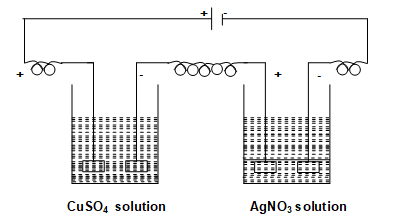
Hence for the above setup according to second law of Faraday.
Note:
1 Faraday (1F) is the charge in coulomb present on 1 mole of electrons.
Charge present on an electron = 1.6 x 10-19 C
No. of electrons present in 1 mole = 6.022 x 1023
So, 1F = 96500 C
Applications of electrolysis
i) Determination equivalent weight of a substance.
ii) Electrometallurgy
iii) Electro-refining of Metals → metals like copper, aluminium silver and gold etc. are refined by electrolysis.
iv) Electroplating: The process of coating an inferior metal by a superior metal by electrolysis is known as electroplating.
The advantages of electroplating
a) To prevent the metal from corrosion
b) To make it attractive.
Note: Electroplating of iron by zinc is called galvanization:
Illustration 20: How much charge in coulomb is required to reduce
i) 1 mole of to and (ii) 1 mole of .
Solution. i)
To reduce 1 mole of , 3 moles of are required
so charge = 3F = .
ii)
change of 5 units
to reduce 1 mole of , 5 moles of are required so the
charge = 5 F = 5 x 96500
Illustration 21: Exactly 0.4 faraday electric charge is passed through three electrolytic cells in series, first containing, solution.
How many grams of each metal will be deposited assuming only cathodic reaction in each cell ?
Solution. The reactions at cathode of each cell are
Illustration 22: How long has a current of 3 ampere of be applied through a solution of silver nitrate to coat a metal surface of 80 with 0.005 mm thick layer ? Density of silver is 10.5 g/ml
Solution. Mass of silver to be deposited
W = volume x density
= Area x thickness x density
= 80 x 0.005 x 0.1 x 10.5
= 0.42 g
for silver Z =
Let the current be passed for t seconds, then
W = Z x I x t
= 0.14 x 893.52
= 125.09 seconds.
FORMULA AND CONCEPTS AT A GLANCE
1. Specific conductance or conductivity (k) = 1/
or
2. is called cell constant. Its units are cm-1. Hence
Specific conductance (k) = observed conductance (C) ⨯ Cell constant
3. Equivalent conductance = Sp. Conductance ⨯ vol of sol. in cc containing 1 g eq. of the electrolyte i.e.
4. Molar conductance = Sp. Conductance´ Vol. of sol. in cc containing 1 mole of the electrolyte
i.e.
5. For a sparingly soluble salt like AgCl, BaSO4, PbSO4 etc
Solubility in mole L-1(S) =
6. According to Kohlrausch’s Law, for any electrolyte, AxBy
where are the ionic conductivities at infinity dilution for the cation and the anion respectively.
7. Degree of dissociation of an electrolyte at concentration C is given by
8. Eq. wt of substance is the weight deposited by 1 faraday (96500 coulombs) of electricity. Hence
Eq.wt =
9. Z = Eq. wt. of the substance/96,500
10. According to Faraday’s second law of electrolysis, for the same quantity of electricity passed through solutions of different electrolytes, (e.g. CuSO4 and AgNO3)
11. For a given reaction to be spontaneous, ECell must be postive
12. According to Nernst equation
(i) For the reduction half reaction (electrode reaction)
(ii) For the cell reaction
13.
14. Thermodynamic efficiency of a fuel cell
SOLVED PROBLEMS-1
Prob 1. A 100 watt, 110 volt incandescent lamp is connected in series with an electrolytic cell containing cadmium sulphate solution. What mass of cadmium will be deposited by the current flowing for 10 hours ?
Sol: We know, watt = ampere ⨯ volt
100 = ampere ⨯ 110
ampere =
Charge = ampere ⨯ second
reaction at cathode
112.4g 2F
Mass of cadmium deposited
W = Z x ⨯ t
= 19.06g
Prob 2. Calculate the electricity that would be required to reduce 12.3g of nitrobenzene to aniline, if the current efficiency for the process is 50%. Find out the energy consumed if the potential drop across the cell is 3 volts.
Sol:
Hydrogen required to reduce 0.1 mole of nitro benzene = 0.1 x 3 = 0.3 mole
Amount of charge required for the liberation of 0.3 mole of hydrogen
= 2 ⨯ 96500 ⨯ 0.3 = 57900 coulomb.
Actual amount of charge required as efficiency is 50% = 2 ⨯ 57900 = 115800 coulomb
Energy consumed = charge x potential difference = 115800 ⨯ 3 = 347400 J = 347.4 kJ
Prob 3. A current of 1.70 ampere is passed through 300ml of 0.16M solution of Zinc sulphate for 230 seconds, with a current efficiency of 90%. Find out the molarity of Zn2+ ions after the deposition of Zinc. Assume the volume of the solution to remain constant during electrolysis.
Sol: Amount of charge passed = 1.70 ⨯ 230 coulomb.
Amount of actual charge passed = 351.9 coulomb
No .of moles of zinc deposited by passing 351.9 C of charge
Molarity of ions after deposition of zinc.
= 0.154 M
Prob 4. At what pH of HCl solution will hydrogen gas electrode show electrode potential of -0.118V ? gas is bubbled at 298K and 1 atm pressure.
Sol: Electrode reaction
Ecell or emf =
– 0.118 = 0 + 0.59 log
Prob 5. Calculate the potential of the single electrode
Sol:
= – 0.762 + 0.0295 ⨯ (-1)
= – 0.762 – 0.0295
E = -0.792V
Prob 6. Calculate the electrode potential of the single electrode ?
Sol:
= 0.799 – 0.06⨯2
E = 0.799 – 0.120 = 0.679 V
Prob 7. Calculate the EMF of Zn/ (0.1M) ||
of ; of | Cu = +0.337 V
Sol:
Prob 8. Calculate the EMF of the cell formed from Ag and Ni electrodes
Sol: Cell is
= +0.799 – (– 0.250)
Prob 9. Calculate the electrode potential of
Sol:
E = 0.762 – 0.03 = -0.792 V
= 1.36 + 0.06 2 = 1.36 + 0.12
= 1.48 V
Ecell = E0cathode – E0anode 1.48 – (–0.792) = 2.272V
Prob 10. Calculate the EMF of the cell
Sol:
= +0.337 – 0.03 = +0.307
= 1.36 + 0.06 2 = 1.36 + 0.12 = 1.48 V
= 1.48 -0.307 = +1.073 V
SOLVED PROBLEMS-2
Prob 1. The main function of the salt bridge is :
(A) To allow ions to go from one cell to another
(B) To provide link between two half cells
(C) To keep the e.m.f. of the cell positive
(D) To maintain electrical neutrality of the solution in two half cells
Sol: (D) Salt bridge is used to remove or eliminate liquid junction potential arised at the junction of two electrolytes in an electrochemical cell. Thus salt bridge such as KCl is placed in between two electrolytes. A salt used for this purpose should have almost same speeds of its cation and anion, salt bridge maintains electrical neutrality of the solution in two half cells.
Prob 2. A dilute aqueous solution of sodium fluoride is electrolysed, the products at the anode and cathode are :
(A) (B) (C) (D)
Sol: (A) Reduction potential of hydrogen is greater than that of sodium, thus
at cathode
an anode
Prob 3. At pH = 2, will be
(A) 1.36 V (B) 1.30 V (C) 1.42 V (D) 1.20 V
Sol: (C) Given, , pH = 2
From Nernst equation
= 1.30 + 0.1182
= 1.4182
= 1.42
Prob 4. The metals that cannot be obtained by electrolysis of the aqueous solutions of their salts are :
(A) Ag and Mg (B) Ag and Al (C) Mg and Al (D) Cu and Cr
Sol: (C) Alkali metals, alkaline earth metals and aluminium can not be obtained by electrolysis of their aqueous salt solutions because of their strong electropositive nature i.e., high oxidation potential or less reduction potentials.
Prob 5. If the half cell reaction has a large negative reduction potential, it follows that :
(A) A is readily reduced
(B) A is readily oxidised
(C) is readily reduced
(D) is readily oxidised
Sol: (D) Large negative reduction potential means less E0red & more E0oxid. i.e.,
Hence, A– is readily oxidized.
Prob 6. graph is of the type as shown in fig. where OA=0.34 V then electrode potential of the half cell of Cu | (0.1M) will be
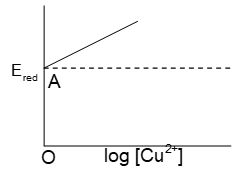
(A) (B) 0.34 + 0.0591 V (C) 0.34V (D) None of these
Sol : (A)
Prob 7. During the charging of lead storage battery, the reaction occurring at the cathode is represented by :
(A)
(B)
(C)
(D)
Sol: (B) During recharging the battery, the reaction may be written as
Prob 8. In an aqueous solution, hydrogen will not reduce :
(A) (B) (C) (D)
Sol: (C) Both Zn and Fe are lying above the H in electro chemical series, However Fe3+ can be reduced to Fe2+ by H. Therefore, Fe3+ can be reduced to Fe2+ by H. Therefore, Zn2+/Zn will not be reduced in aq. solution by H.
Prob 9. Consider the reaction, . The standard reduction potential values of the metals are -0.34 V, -3.05 V and -1.66V respectively. The order of their reducing power will be :
(A)
(B)
(C)
(D)
Sol: (D) Reducing power of metals E0oxid
Hence reducing power of
M2 > M3 > M1
-3.05v – 1.66 v – 0.34 E0red)
+3.05v – 1.66 v + 0.34 E0oxid)
Prob 10. The equilibrium constant for the reaction given below at 298K is :
(A)
(B)
(C)
(D)
Sol: (D)
Now








