Solutions

A solution is a homogenous mixtures of two or more pure substances.  Its composition may be varied within certain limits.  The solution of two components is called binary solution.  The solutions of three or four components are called ternary and quaternary solution respectively.  The two components of a binary solution are called a solvent and a solute. 
Solvent is that component whose physical state is the same as that of solution. But when solvent and solute are in the same physical state, then the component which is present in greater amount is called the solvent.

Depending on the state of solute or solvent, there may be nine types of binary solutions:

	Types of solution	Examples
1.	Gaseous solution
	i)  Gas in gas	a mixture of O2 and N2 in air.
	ii)  liquid in gas	Water vapours in air camphor vapours in N2 gas.
	iii)  solid in gas	Camphor vapours in N2 gas.
2.	Liquid solutions
	i)  Gas in liquid	Oxygen dissolved in water
	ii)  liquid in liquid	Ethanol dissolved in water
	iii)  solid in liquid	Sucrose in water salt in water
3.	Solid solutions
	i)  Gas in solid	Solution of hydrogen in palladium
	ii)  liquid in solid iii) Solid in solid	Amalgam of mercury with sodium. Homogeneous mixture of two or more metals (alloys).

• Generally in solution, the components do not lose their identity, they can be separated by some physical methods such as distillation, crystallization, and adsorption. 

Methods of expressing the concentration of a solution:
1) Mass percentage :  It is the amount of solute in grams present in 100 grams of the solution
mass percentage of solute = $\frac{\mathrm{Mass} \mathrm{of} \mathrm{solute}}{\mathrm{Mass} \mathrm{of} \mathrm{solute}+\mathrm{Mass} \mathrm{of} \mathrm{solvent}}\times 100$

• A 10 percent (W/W) solution of NaCl in water means that 10g of NaCl is present in 90 g of water so that total mass of solution is 100 g.

2) Volume percentage:  It is the volume of solute present in 100 parts by volume of solution.
Volume percentage of solute  = $\frac{\mathrm{Volume} \mathrm{of} \mathrm{solute}}{\mathrm{Volume} \mathrm{of} \mathrm{solute}+\mathrm{Volume} \mathrm{of} \mathrm{solvent}}\times 100$

• A 20% solution of ethanol (V/V) means that 20 ml of ethanol is present in 80 ml of water.

3) Strength of solution (Grams per litre): It is the amount of the solute in grams present in one litre of the solution.
$\mathrm{strength}=\frac{\mathrm{Mass} \mathrm{of} \mathrm{solute} \mathrm{in} \mathrm{grams}}{\mathrm{Volume} \mathrm{of} \mathrm{solution} \mathrm{in} \mathrm{liters}}$

4) Molarity:  It is the No. of moles of solute per litre of the solution.  It is designated by the symbol M.
$$\begin{gathered} \mathrm{Molarity} \left(\mathrm{M}\right) =\frac{\mathrm{Mols} \mathrm{of} \mathrm{solute}}{\mathrm{Volume} \mathrm{of} \mathrm{solution} \mathrm{in} \mathrm{liter}} \\ =\frac{\mathrm{Mass} \mathrm{of} \mathrm{solute} \mathrm{in} \mathrm{grams}}{\mathrm{GMM} \mathrm{of} \mathrm{solute}\times \mathrm{Volume} \mathrm{of} \mathrm{solution} \mathrm{in} \mathrm{liter}} \end{gathered}$$ 

0.2M aqueous solution of K₂SO₄ contains 0.2 mole of salt in 1 litre of solution.  The molarities of potassium and sulphate ions in solution are 0.4M and 0.2M respectively, as 1 mol K₂SO₄ gives 2 moles of potassium ions and 1 mol of sulphate ions on dissociation.

• Molarity of solution changes with temperature due to change in volume of the solution with temperature.

• When a solution is diluted, there is no change in moles of solute.
$\therefore$ moles of solute before dilution = moles of solute after dilution.
M₁V₁ = M₂V₂

• When two or more sample of solution (containing same solvent and solute) are mixed, then molarity of the resulting mixture can be given as :
${\mathrm{M}}_{\mathrm{R}}=\frac{{\mathrm{M}}_1{\mathrm{V}}_1+{\mathrm{M}}_2{\mathrm{V}}_2+{\mathrm{M}}_3{\mathrm{V}}_3}{{\mathrm{V}}_1+{\mathrm{V}}_2+{\mathrm{V}}_3}$
Where M_R = Resultant molarity.
Relation between molarity and mass percentage:
Molarity = $\frac{\mathrm{mass} \mathrm{percentage}\times \mathrm{density} \mathrm{of} \mathrm{solution} \times 10}{\mathrm{Gram} \mathrm{molecular} \mathrm{mass} \mathrm{of} \mathrm{solute}}$

• Relation between molarity and gram/litre strength
Molarity =$\frac{\mathrm{gram}/\mathrm{litre} \mathrm{strength} }{\mathrm{GMM} \mathrm{of} \mathrm{solute}}$

• In terms of molarity solutions are expressed as

Molar soltuion	1M	Centimolar	0.01 M
Semimolar	0.5 M	Millimolar	0.001M
Decimolar	0.1M

5) Normality :  It is the number of gram equivalents of solute present per litre of solution.  It is designated by ‘N’.
  $$\begin{gathered} \mathrm{Normality}=\frac{\mathrm{Number} \mathrm{of} \mathrm{gram} \mathrm{equivalents} \mathrm{of} \mathrm{solute}}{\mathrm{volume} \mathrm{of} \mathrm{solution} \mathrm{on} \mathrm{litres}} \\ =\frac{\mathrm{mass} \mathrm{of} \mathrm{solute} \mathrm{in} \mathrm{grams}}{\mathrm{gram} \mathrm{equivalent} \mathrm{mass}\times \mathrm{volume} \mathrm{of} \mathrm{solution} \mathrm{in} \mathrm{litres}} \end{gathered}$$

Gram equivalent mass ⇒ equivalent mass of a substance (element or compound) is the number of parts by mass of it, that will combine or displace 1.008 parts by mass of hydrogen, 8 parts by mass of oxygen, 35.5 parts by mass of chlorine, 108 parts by mass of silver or the equivalent parts by mass of any other elements.
Gram equivalent mass =  $\frac{\mathrm{GMM} \mathrm{or} \mathrm{GAM}}{\mathrm{n}}$
Where    n ⇒ Valency in case of an element
⇒  Basicity in case of an acid
⇒  Acidity in case of a base
⇒  Total + ve or – ve valency in case of a salt.
⇒  Change in oxidation number per molecule for an oxidant or a reductant.
⇒   Normality is expressed in terms of gram equivalents/L.
⇒  Both normality as well as molarity of a solution change with change in temperature.
Normality =$\frac{\mathrm{gram} \mathrm{per} \mathrm{litre} \mathrm{strength} }{\mathrm{gram} \mathrm{equivalent} \mathrm{mass} \mathrm{of} \mathrm{solute}}$
⇒   Relation between normality and molarity
Molarity × Mol. mass of solute = normality × equivalent mass of solute
or  $\frac{\mathrm{normality} }{\mathrm{molarity}}=\frac{\mathrm{molecular} \mathrm{mass}}{\mathrm{equivalent} \mathrm{mass}}=\mathrm{n}$

⇒   Relation between normality and mass percentage
Normality = $\frac{\mathrm{mass} \mathrm{percentage}\times \mathrm{density}\times 10}{\mathrm{gram} \mathrm{equivalent} \mathrm{mass} \mathrm{of} \mathrm{solute}}$

⇒ In terms of normality solutions are expressed as
Normal solution           1N                    centinormal                   N/100
Seminormal                  N/2                  millinormal                    N/1000
Decinormal                   N/10
⇒    Normality equation        (N₁V₁ = N₂V₂)

6) Molality: Molality is the number of moles of solute present in 1000g of solvent.  It is denoted by ‘m’.
Molality = $\frac{\mathrm{No}. \mathrm{of} \mathrm{mloes} \mathrm{of} \mathrm{solute}}{\mathrm{mass} \mathrm{of} \mathrm{solvent} \mathrm{in} \mathrm{kg}}$
$=\frac{\mathrm{mass} \mathrm{of} \mathrm{solute} \mathrm{in} \mathrm{gram}}{\mathrm{GMM} \mathrm{of} \mathrm{solute} \times \mathrm{mass} \mathrm{of} \mathrm{solvent} \mathrm{in} \mathrm{kg}}$
Molality is expressed in units of moles per kilogram.
⇒  Molality of a solution does not change with temperature.
⇒  Relation between molarity and molality.
$\mathrm{m}=\frac{1000\times \mathrm{m}}{\left(1000\times \mathrm{d}\right)–\left(\mathrm{M}\times \mathrm{GMM} \mathrm{of} \mathrm{solute}\right)}$

Where m → molality, d → density of solution in grams/ml, M → Molarity.

7) Formality :  It is the no. of gram formula masses of the ionic solute present in one litre of the solution. It is denoted by F.  Formality is used to express the concentration of ionic solids.  Ionic solids do not exist as molecules but exist as network of ions.  Like normality and molarity, formality of solution changes with change in temperature.
Formality = $\frac{\mathrm{mass} \mathrm{of} \mathrm{ionic} \mathrm{solute}\left(\mathrm{g}\right)}{\left(\mathrm{Gram} \mathrm{formula} \mathrm{mass} \mathrm{of} \mathrm{solute}\right)\times \mathrm{volume} \mathrm{of} \mathrm{solution} \mathrm{in} \mathrm{litre}}$

8) Mole fraction : It is the ratio of number of moles of one component to the total no. of moles of all components.
Suppose a solution contains three components, W₁ grams of A, W₂ grams of B, W₃ grams of C and their molecular masses are M₁, M₂, M₃ respectively, hence moles of A = $\frac{{\mathrm{W}}_1}{{\mathrm{M}}_1}$; moles of  B = $\frac{{\mathrm{W}}_2}{{\mathrm{M}}_2}$; Moles of C = $\frac{{\mathrm{W}}_3}{{\mathrm{M}}_3}$
Total no. of moles =  $\frac{{\mathrm{W}}_1}{{\mathrm{M}}_1}+\frac{{\mathrm{W}}_2}{{\mathrm{M}}_2}+\frac{{\mathrm{W}}_3}{{\mathrm{M}}_3}$
Thus mole fraction of $A, X_A=\frac{W_1/M_1}{\frac{{\mathrm{W}}_1}{{\mathrm{M}}_1}+\frac{{\mathrm{W}}_2}{{\mathrm{M}}_2}+\frac{{\mathrm{W}}_3}{{\mathrm{M}}_3}}$
Mol. fraction of  $B, X_B=\frac{W_2/M_2}{\frac{{\mathrm{W}}_1}{{\mathrm{M}}_1}+\frac{{\mathrm{W}}_2}{{\mathrm{M}}_2}+\frac{{\mathrm{W}}_3}{{\mathrm{M}}_3}}$
Mol. fraction of  $C, X_C=\frac{W_3/M_3}{\frac{{\mathrm{W}}_1}{{\mathrm{M}}_1}+\frac{{\mathrm{W}}_2}{{\mathrm{M}}_2}+\frac{{\mathrm{W}}_3}{{\mathrm{M}}_3}}$

• The sum of mol fractions of all the components in a solution is always unity i.e., X_A + X_B + X_C = 1.

• Mole fraction is independent of temperature.

9) Parts per million (ppm):  When the solute is present in very small amounts, its concentration is expressed in parts per million.  It is the quantity of the solute in grams present in 10⁶ grams of the solution.
Parts per million = $\frac{\mathrm{mass} \mathrm{of} \mathrm{solute}}{\mathrm{mass} \mathrm{of} \mathrm{solution}}\times {10}^6$

Illustration 1 : A solution is prepared by dissolving 16g of glucose in 64g water.  What will be the mass percent of each component of solution?
Solution. Mass percent of solute (glucose) = $\frac{\mathrm{mass} \mathrm{of} \mathrm{solute}\times 100}{\mathrm{mass} \mathrm{of} \mathrm{solute}+\mathrm{mass} \mathrm{of} \mathrm{solvent}}$

$=\frac{16\times 100}{16+64}=20$
$\therefore$ Mass percent of water = 80%

Illustration 2 : 200g of 25% solution of solute A, 300g of 40% solution of solute B and 400g of 30% solution of C are mixed.  Calculate the percentage composition in terms of mass.
Solution. Total mass of solution = 200 + 300 + 400 = 900g
Mass of solute A present in 200g of 25% solution = $\frac{200\times 25}{100}=50\mathrm{g}$
Mass of solute B present in 300g of 40% solution = $\frac{300\times 40}{100}=120\mathrm{g}$
Mass of solute C present in 400g of 30%  solution = $\frac{400\times 30}{100}=120\mathrm{g}$
Total mass of solute = 50 + 120 + 120 = 290g
Mass percentage of solute = $\frac{\mathrm{mass} \mathrm{of} \mathrm{solute}}{\mathrm{mass} \mathrm{of} \mathrm{solution} }\times 100$
= $\frac{290}{900}\times 100=32.22\%$
Mass percentage of solvent = 100 – 32.22 = 67.78% 

Illustration 3: How many grams of a dibasic acid are (mol. wt. 200) present in 100 ml of its aqueous solution to give decimolar strength?
Solution. Molarity of solution = $\frac{1}{10}\mathrm{mol}/\mathrm{litre}$
Molarity = $\frac{\mathrm{mass} \mathrm{of} \mathrm{solute} \mathrm{in} \mathrm{gram}}{\mathrm{GMM}\hspace{0.17em}\mathrm{of} \mathrm{solute}\times \mathrm{volume} \mathrm{of} \mathrm{solution} \mathrm{in} \mathrm{litre}}$
$\therefore$ Mass of solute in grams = molarity × GMM of solute  × V_{(L)
= $\frac{1}{10}\times 200\times \frac{100}{1000}=2\mathrm{grams}$}

Illustration 4: Calculate the quantity of sodium carbonate required to prepare 200ml of $\frac{\mathrm{M}}{10}$ solution.
Solution. Mass of solute in gram
= molarity × GMM × V_{(L)
= $\frac{1}{10}\times 106\times \frac{200}{1000}=2.12\mathrm{g}$}

Illustration 5 : Calculate the molarity and normality of a solution containing 4 g of NaOH dissolved in 100C.C. of solution.
Solution.
$$\begin{gathered} \mathrm{Molarity}=\frac{\mathrm{mass} \mathrm{of} \mathrm{solute}}{\mathrm{GMM} \mathrm{of} \mathrm{solute}\times {\mathrm{V}}_{\left(\mathrm{L}\right)}} \\ =\frac{4\times 1000}{40\times 100}=1\mathrm{M} \\ \mathrm{Normality}= \frac{\mathrm{mass} \mathrm{of} \mathrm{solute}}{\mathrm{GEM} \mathrm{of} \mathrm{solute}\times {\mathrm{V}}_{\left(\mathrm{L}\right)}} \\ =\frac{4\times 1000}{40\times 100}=1\mathrm{N} \end{gathered}$$

Illustration 6: Calculate the normality of a 2M sulphuric acid.
Solution. Molarity × GMM = Normality × GEM (solute)
$\therefore \frac{\mathrm{Normality}}{\mathrm{Molarity}}=\frac{\mathrm{GMM}}{\mathrm{GEM}}=\mathrm{n}$
Thus for H₂SO₄  N = n × Molarity
= 2 × 2 = 4N 

Illustration 7: Calculate the concentration of NaOH solution in g/mL, which has the same normality as that of a solution of HCl of concentration 0.04g/mL
Solution. Normality of HCl = $\frac{0.04\times 1000}{36.5\times 1}=1.096$
Normality of the HCl = Normality of NaOH
Normality of HCl = Normality of NaOH
$\therefore 1.096=\frac{\mathrm{mass} \mathrm{of} \mathrm{NaOH}\times 1000}{40\times 1}$
or mass of NaOH in 1 ml solution = 0.0438g
Thus conc. of NaOH = 0.0438g/ml

COLLIGATIVE PROPERTIES:
Dilute solutions of non-volatile solutes exhibit some properties which depend only on the number of the solute particles.  These properties do not depend upon the nature of solute particles.  These properties are collectively called colligative properties.
Dilute solutions have the following related properties:
i) Relative lowering of vapour pressure
ii) Elevation of boiling point
iii) Depression of freezing point
iv) Osmotic pressure
Vapour pressure of liquid:   When a liquid is placed in a closed air tight container.  The volume of container is greater than that of liquid.  At a certain temperature a part of liquid evaporates and its vapours fill the space available to them.  The vapours have a tendency to change back to the liquid state, this process is called condensation.  Initially rate of vapourisation is greater than rate of condensation.  After some time an equilibrium is established between liquid and vapour phase.
“The pressure exerted by the vapours above the liquid surface in equilibrium state at a give temperature is called vapour pressure of the liquid.
Factors influencing vapour pressure :
i) Nature of solvent : A solvent having higher attractions among their molecules has less tendency to get vapourise and thus has low vapour pressure. On the other hand solvents having weak intermolecular forces are volatile and have greater vapour pressure for example ether, methyl alcohol.
ii) Temperature : As the temperature of solvent increases, kinetic energy of solvent molecules increases.  As a result tendency to get vapourised increases thus vapour pressure of solvent increases.  The variation of vapour pressure of a liquid with temperature is given by clausius clapeyrons equation.
$2.303\log \frac{{\mathrm{P}}_2}{{\mathrm{P}}_1}=\frac{∆\mathrm{H}}{\mathrm{R}}\left[\frac{1}{{\mathrm{T}}_1}–\frac{1}{{\mathrm{T}}_2}\right]$
Where $∆$H ⇒ Enthalpy of vapourisation, P₁ and P₂ are vapour pressure at temperature T₁ and T₂.
R ⇒ Universal gas constant.
Vapour pressure of the solution containing non volatile solute: When a small amount of a non-volatile solute is added to the solvent to form a solution, then a part of the liquid surface is occupied by solute particles.  As a result surface area of liquid from which evaporation occurs decreases.  Thus rate of vapourisation is slowed down by addition of non-volatile solute.  This results in the decrease of vapour pressure of the solvent.
Hence vapour pressure of solution containing non volatile solute is less than that of pure solvent. The difference between the vapour pressure of pure solvent (P₀) and vapour pressure of solution (P_S) is known as lowering of vapour pressure
(P₀ – P_s) is the lowering of vapour pressure whereas $\left(\frac{{\mathrm{P}}_0–{\mathrm{P}}_{\mathrm{s}}}{{\mathrm{P}}_0}\right)$  is known as relative lowering of vapour pressure.

RAOULT’S LAW:
i) For solutions containing non volatile solute: The French chemist Francois Marie Raoult in (1886) observed that vapour pressure of solution containing non volatile solute is directly proportional to mole fraction of the solvent, in the solution.
Mathematically     P_solution = P⁰_solvent X_solvent      ………………….   (1)
P⁰_solvent is vapour pressure of pure solvent
P_solution is vapour pressure of solution
X_solvent is mole fraction of solvent

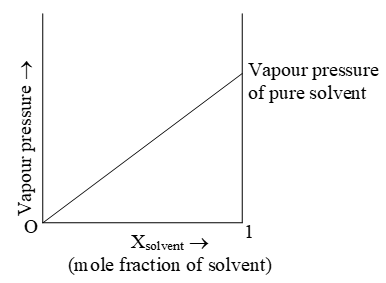
Equation (1) on rearrangement gives:-

$$\begin{gathered} \frac{{\mathrm{P}}_{\mathrm{solution}}}{{{\mathrm{P}}^0}_{\mathrm{solven}}}={\mathrm{X}}_{\mathrm{solvent}} \\ \mathrm{or} \\ 1–\frac{{\mathrm{P}}_{\mathrm{solution}}}{{{\mathrm{P}}^0}_{\mathrm{solven}}}=1–{\mathrm{X}}_{\mathrm{solvent}} \\ \mathrm{or} \frac{{{\mathrm{P}}^0}_{\mathrm{solven}}–{\mathrm{P}}_{\mathrm{solution}}}{{{\mathrm{P}}^0}_{\mathrm{solven}}}={\mathrm{X}}_{\mathrm{solvent}} \end{gathered}$$

Thus at a given temperature, the relative lowering of vapour pressure is equal to mole fraction of solute.
ii) Raoult’s law for solution of two volatile liquids : Raoult’s law can also be applied to a binary solution in which both components are volatile.  In this case, the partial vapour pressure of each component in the solution in directly proportional to its mole fraction.  If X_A and X_B represent the mole fraction of the two components A and B in liquid solution, then according to Raoult’s law,
Partial vapour pressure of component A, P_A = P⁰_AX_A
Partial vapour pressure of component B, P_B = P⁰_BX_B
Hence total pressure of solution;                                   
(According to Dalton’s law of partial pressure)
P=  P⁰_AX_A+P⁰_BX_B

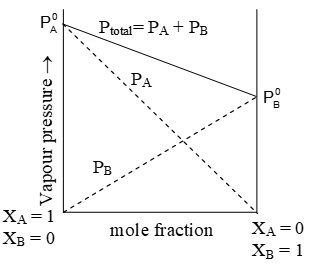
⇒  The law is applicable only when the two volatile liquids   form a homogenous mixture.
⇒   Raoult’s law is valid only for ideal solutions.
⇒  Mole fraction of each component is different in the liquid and its vapour

IDEAL SOLUTION : An ideal solution is formed by dissolving a very small amount of the nonvolatile solute in the solvent.  During the formation of an ideal solution, no change in volume and no change in enthalpy takes place.  An ideal solution obeys Raoult’s law over the entire range of concentration and temperature.  Thus the conditions for an ideal solution are:
(i) ΔH = 0                     (ii)  ΔV = 0                    (iii)  P_solution = P⁰_solvent X_solvent
No solution behave as an ideal solution, but, when solvent-solvent and solute-solute interactions are of the same type as solvent solute interaction, then solvent and solute on mixing foarm an ideal solution.  Generally most of the dilute solutions obey the Raoult’s law or behave as ideal solutions.  In ideal solutions interactions between molecules are almost same before and after mixing of solvent and solute.
Examples of ideal solutions:

(i) n-Butyl bromide and n-butyl chloride

(ii) Chlorobenzene and bromobenzene

(iii) n-Hexane and n-Heptane

(iv) Ethylene bromide and ethylene chloride

(v) Benzene and toluene

Non-Ideal solutions:  These solutions do not obey Raoult’s law.  In these solutions solute – solvent interations are of different magnitude then the interaction between solvent-solvent and solute-solute.  Thus conditions for a non-ideal solution:

(i) ΔH ≠ 0                      (ii)  ΔV ≠ 0                     (iii)  P_solution ≠ P⁰_solvent X_solvent
Types of non-ideal solutions:

(i) Solutions showing positive deviation from Raoult’s law.

(ii) Solutions showing negative deviation from Raoults law

(i) Solutions with positive deviations:  In these solutions vapour pressure of each component is greater than that expected from Raoult’s law P_A > P_A⁰ X_A and P_B > P_B⁰ .  This happens when solvent solute interactions are weaker than solvent-solvent and solute-solute interactions.  Because of weaker interactions, the escaping tendency of molecules increases which results in high vapour pressure than that expected from Raoult’s law.  Since interactions between molecules decreases. $\therefore$ΔH_mix > 0 and ΔV_mix > 0, that is heat is absorbed and volume is increased after dissolution.
Examples:

(i) Acetone and ethanol

(ii) Carbon tetrachloride + Ethanol

(iii) Water and Propyl alcohol

(iv) Ethyl alcohol and chloroform

(v) Acetaldehyde and carbon disulphide

A mixture of ethanol and acetone exhibits +ve deviation from ideal behaviour.  In pure ethanol, molecules are hydrogen bonded.  On adding acetone, these molecules get in between alcohol molecules, and break the hydrogen bonds of alcohol molecules, hence intermolecular forces becomes weaker.  This results in the increase in vapour pressure.
(ii) Solutions with negative deviation:  In these solutions vapour pressure of each component is less than that expected from Raoult’s law.
P_A < P_A⁰ X_a         P_B < P_B⁰X_B

This happens when solvent-solute interactions are stronger than solvent-solvent and solute-solute interaction.  Since interactions among molecules become stronger, their escaping tendency decreases which results in decrease in vapour pressure.
Since interaction between molecules increases, these solutions are accompanied by evolution of heat and decrease in volume, that is
ΔH_mix < 0 and ΔV_mix < 0
Examples:
(i)  Water – HCl               (ii)  Water – HNO₃               (iii)  Acetone – chloroform      
(iv)  Acetic acid – Pydridine               (v)  Chloroform – Benzene.  
A mixture of chloroform and acetone forms a solution with negative deviation.  In solution chloroform molecule is able to form hydrogen bond with acetone molecule.

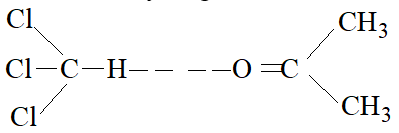
This decreases the escaping tendency of molecules, consequently the vapour pressure of each component decreases which results in negative deviation from Raoult’s law.
AZEOTROPIC MIXTURES
Azeotropic mixtures are binary mixtures having same composition in liquid and vapour phase and boil at a constant temperature without undergoing any change in composition.  In such cases, components of solution can not be separated by fractional distillation.
There are two types of azeotropes:
(i)  Minimum boiling azeotropes:  Solutions which show positive deviation from ideal behaviour form minimum boiling azeotropes. 
Example :  Ethanol-water mixtures that is rich in water, can be concentrated upto 95% by volume of ethanol, when this composition is achieved the two components can not be further separated.  The other methods have to be used for obtaining 100% alcohol.
(ii)  Maximum boiling azeotropes:  Solutions which show negative deviation from ideal behaviour form maximum boiling azeotropes.  Boiling points of these azeotropes are higher than either of the components.
Example:  H₂O and HNO₃ form maximum boiling azeotropes, the composition of this azeotrope is 68% HNO₃ and 32% H₂O by mass with a boiling point of 393 K.

• A liquid mixture which distils with a change in composition is called zeotropic mixture.

Calculation of molecular mass of solute from relative lowering of vapour pressure:
According to Raoult’s law, relative lowering of vapour pressure = mole fraction of solute
$$\begin{gathered} \frac{{{\mathrm{P}}^0}_{\mathrm{solvent}}–{\mathrm{P}}_{\mathrm{solution}}}{{{\mathrm{P}}^0}_{\mathrm{solvent}}}={\mathrm{X}}_{\mathrm{solute}} \\ \mathrm{or} \frac{{{\mathrm{P}}^0}_{\mathrm{solvent}}–{\mathrm{P}}_{\mathrm{solution}}}{{{\mathrm{P}}^0}_{\mathrm{solvent}}}=\frac{\mathrm{n}}{\mathrm{n}+\mathrm{N}}\left\{\begin{array}{c}\mathrm{n}\to \mathrm{moles} \mathrm{of} \mathrm{solute}\\ \mathrm{N}\to \mathrm{moles} \mathrm{of} \mathrm{solvent}\end{array}\right\} \end{gathered}$$

For dilute solutions n << N, and can be neglected in denominator.
thus,
$\frac{{{\mathrm{P}}^0}_{\mathrm{solvent}}–{\mathrm{P}}_{\mathrm{solution}}}{{{\mathrm{P}}^0}_{\mathrm{solvent}}}=\frac{\mathrm{n}}{\mathrm{N}}=\frac{\mathrm{W}\times {\mathrm{M}}_{\mathrm{solvent}}}{{\mathrm{M}}_{\mathrm{solute}}\times \mathrm{W}}$

${\mathrm{M}}_{\mathrm{solute}}=\frac{\mathrm{W}\times {\mathrm{M}}_{\mathrm{solvent}}}{\mathrm{W}}\left(\frac{{{\mathrm{P}}^0}_{\mathrm{solvent}}}{{{\mathrm{P}}^0}_{\mathrm{solvent}}–{\mathrm{P}}_{\mathrm{solution}}}\right)$

w → mass of solute, M_solute → molecular mass of solute
w → mass of solvent, M_solvent → molecular mass of solvent

Illustration 8: Vapour pressure of water at 300 K is 12.3 kPa.  What will be the vapour pressure of one molal solution of non volatile solute in water at 300K?

Solution. One molal solution means one mole of solute is present in 1 kg of water. 
$\therefore$ moles of solute = 1
Moles of water  = $\frac{1000}{18}=55.55$
Mole fraction of solvent i.e., water = $\frac{55.55}{56.55}=0.9823$
Vapour pressure of solution containing non volatile
Solute = vapour pressure of solvent × mole fraction of solvent
=  ${{\mathrm{P}}^0}_{\mathrm{solvent}}\times {\mathrm{X}}_{\mathrm{solvent}}$
= 12.3 × 0.9823 = 12.08 kPa

Illustration 9: Calculate the vapour pressure of a solution at 373K containing 3.42g of cane sugar in 36g of water.
Solution. Moles of sugar = $\frac{3.42}{342}= 0.01$
Moles of water = $\frac{36}{18}=2$
Vapour pressure of pure water at 373K  is 760 mm of Hg
$\therefore \frac{{\mathrm{P}}_0–{\mathrm{P}}_{\mathrm{s}}}{{\mathrm{P}}_0}=\frac{\mathrm{n}}{\mathrm{n}+\mathrm{N}}$
Where  P₀ → vapour pressure of pure solvent
P_s → vapour pressure of solution containing non-volatile solute.
n → moles of solute and N → moles of solvent

$$\begin{gathered} \frac{{\mathrm{P}}_0–{\mathrm{P}}_{\mathrm{s}}}{{\mathrm{P}}_0}=\frac{0.01}{0.01+2}=\frac{0.01}{2.01} \\ or \frac{{\mathrm{P}}_0}{{\mathrm{P}}_0}–\frac{{\mathrm{P}}_{\mathrm{s}}}{{\mathrm{P}}_0}=\frac{1}{201} or 1–\frac{{\mathrm{P}}_{\mathrm{s}}}{{\mathrm{P}}_0}=\frac{1}{201} \\ \frac{{\mathrm{P}}_{\mathrm{s}}}{{\mathrm{P}}_0}=1–\frac{1}{201} =\frac{200}{201} \\ {\mathrm{P}}_{\mathrm{s}} ={\mathrm{P}}_0\times \frac{200}{201}=760\times \frac{200}{201}=756.22 \mathrm{mm} 0\mathrm{f} \mathrm{Hg} \end{gathered}$$

Illustration 10: A solution of 30 g of non-volatile solute in 90g of water has vapour pressure of 2.8 kPa at 298 K.  Further addition of 18g of water causes vapour pressure to increase to 2.9 kPa at 298 K.  Calculate molar mass of solute and vapour pressure of pure water at 298 K.

Solution. Let the molar mass of solute be M and the vapour pressure of pure water at 298 k be P⁰ moles of solute = $\frac{30}{\mathrm{M}}$; moles of water,  i.e., solvent =$\frac{90}{18}=5$

$$\begin{gathered} \mathrm{Mole} \mathrm{fraction} \mathrm{of} \mathrm{water} = \frac{\mathrm{moles} \mathrm{of} \mathrm{water}}{\mathrm{moles} \mathrm{of} \mathrm{solute}+\mathrm{moles} \mathrm{of} \mathrm{water}} \\ =\frac{5}{{\displaystyle \frac{30}{\mathrm{M}}+5}}=\frac{\mathrm{M}}{\mathrm{M}+6} \end{gathered}$$
Vapour pressure of solution = vapour pressure of solvent × mole fraction of solvent
${\mathrm{P}}_{\mathrm{s}}={\mathrm{P}}_0\times {\mathrm{X}}_{{\mathrm{H}}_2\mathrm{O}}={\mathrm{P}}_0\times \frac{\mathrm{M}}{\mathrm{M}+6}$                            . . . . (i)
$\therefore$ Addition of 18g of H₂O to solution increases the vapour pressure of solution.
Thus, after adding 18g of water, mole fraction of H₂O
$$\begin{gathered} {{\mathrm{H}}^{\mathrm{I}}}_{{\mathrm{H}}_2\mathrm{O}}=\frac{6}{6+{\displaystyle \frac{30}{\mathrm{M}}} \\ }=\frac{\mathrm{M}}{\mathrm{M}+5} \end{gathered}$$

Vapour pressure of solution  ${{\mathrm{P}}^{\mathrm{I}}}_{\mathrm{s}}={\mathrm{P}}_0\times \frac{\mathrm{M}}{\mathrm{M}+5}$          . . . . (ii)
Dividing (ii) by (i)
$\frac{2.9}{2.8}=\frac{\mathrm{M}+6}{\mathrm{M}+5}$
or   29 ( M + 5) = 28 (M + 6)
or  M = 23g/mol 
Substituting the value of M in (i)
${\mathrm{P}}_0=\frac{{\mathrm{P}}_{\mathrm{s}}(\mathrm{M}+6)}{\mathrm{M}}=\frac{2.8(23+6)}{23}=\frac{2.8\times 29}{23}$

= 3.53 kPa

Elevation in Boiling point: The boiling point of a liquid is the temperature at which its vapour pressure becomes equal to the atmospheric pressure.
The vapour pressure of a liquid is lowered when a non volatile solute is added to it.  The temperature, at which vapour pressure of solution will be equal to atmospheric pressure, will be higher than the boiling point of pure solvent.
The difference in the boiling point of solution and boiling point of pure solvent is called elevation of boilng point.
The elevation of boiling point is directly proportional to the molality of the solution.
ΔT_b ∝ m  or  ΔT_b = k_bm
Here m is molality of solution, and constant of proportionality i.e., k_b is called molal elevation constant or molal ebullioscopic constant.
When 1 mole of solute is present in 1 kg of solvent then, molality = 1 : $\therefore$ ΔT_b = k_b.
Thus k_b is elevation in boiling point when one mole of non-volatile solute is dissolved in 1 kg of solvent.  The units of k_b are K. kg mol^–1.

Calculation of molecular mass of solute from elevation in boiling point:
If w gram of solute of molar mass M_solute  is present in W gram of solvent, then molality = $\frac{\mathrm{W}\times 1000}{{\mathrm{M}}_{\mathrm{solute}}\times \mathrm{W}}$
$\therefore ∆{\mathrm{T}}_{\mathrm{b}}=\frac{{\mathrm{K}}_{\mathrm{b}}\times \mathrm{W}\times 1000}{{\mathrm{M}}_{\mathrm{solute}}\times \mathrm{W}} \mathrm{or} {\mathrm{M}}_{\mathrm{solute}}=\frac{{\mathrm{K}}_{\mathrm{b}}\times \mathrm{W}\times 1000}{∆{\mathrm{T}}_{\mathrm{b}}\times \mathrm{W}}$
The value of k_b depends only upon the solvent and is independent of the nature of solute and concentration of the solution.
k_b is related to molar enthalpy of vapourisation of solvent according to the relation.
${\mathrm{K}}_{\mathrm{b}}=\frac{{\mathrm{M}}_{\mathrm{solvent}}{{\mathrm{RT}}_{\mathrm{b}}}^2}{∆{\mathrm{H}}_{\mathrm{vap}.}\times 1000}$
Here T_b is boiling point of pure solvent, ΔH_vap is enthalpy of vapourisation of solvent, R is universal gas constant.

• The method of determining molecular mass by the study of elevation in boiling point is known as ebullioscopic method. 

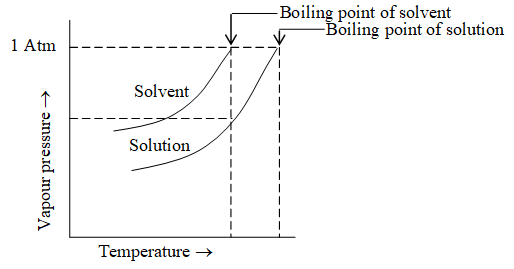
Illustration 11:  Boiling point of a solution containing 1.23 g of substance in 10g of water is 100.39⁰C.  Calculate the molecular weight of the substance (k_b = 0.52⁰C kg mol^–1)
Solution.                    
$\begin{array}{r}\text{ Elevation in boiling point i.e ; }\mathrm{\Delta }{T}_b=100.39-100={0.39}^{\circ }\mathrm{C}\\ \begin{array}{rl}{\mathrm{\Delta T}}_{\mathrm{b}}=& {\mathrm{k}}_{\mathrm{b}}\mathrm{m}=0.52\times \frac{\text{ moles of solute }}{\text{ mass of solventin }\mathrm{kg}}\\ \text{ or }\mathrm{\Delta }& {\mathrm{T}}_{\mathrm{b}}=\frac{0.52\times 1.23\times 1000}{\text{ GMMof solute }\times 10}\text{ or GMMof solute }=\frac{0.52\times 1.23\times 1000}{0.39\times 10}\\ & =164\mathrm{g}/\mathrm{mol}.\end{array}\end{array}$

Depression in freezing point:
The temperature at which vapour pressure of liquid phase is same as the vapour pressure of solid phase, is called freezing point of the substance. 
Or freezing point of a substance is the temperature at which solid and liquid phases of the substance coexist.
The addition of non-volatile solute always lowers the vapour pressure of solvent, therefore vapour pressure of solvent becomes equal to that of solid solvent at a lower temperature.  Thus the freezing point of a solution containing non-volatile solute is always less then the freezing point of a pure solvent. 
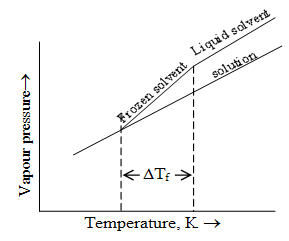
The difference between the freezing point of the pure solvent and its solution is called depression in freezing point (ΔT_f)
Similar to elevation in boiling point, depression in freezing point is directly proportional to molality (m) of the solution.  Thus  ΔT_f ∝ m     or    ΔT_f = K_f m
The constant of proportionality i.e., k_f is called molal depression constant or molal cryoscopic constant.  When 1 mol of solute is present in 1 Kg of solvent then molality = 1, hence ΔT_f = k_f.
Thus k_f is depression in freezing point when one mole of non-volatile solute is dissolved in 1 kg of solvent.
The units of k_f are K. kg mol^–1.

Calculation of molecular mass of solute from depression in freezing point:
If w gram of the solute, present in W gram of solvent produces the depression in freezing point DT_f of the solvent and molecular mass of solute is M_solute, then, molality of solution.
$$\begin{gathered} \mathrm{m}=\frac{\mathrm{w}\times 1000}{{\mathrm{M}}_{\mathrm{solute}}\times \mathrm{W}} \\ \therefore ∆{\mathrm{T}}_{\mathrm{f}}=\frac{{\mathrm{K}}_{\mathrm{f}}\times \mathrm{w}\times 1000}{{\mathrm{M}}_{\mathrm{solute}}\times \mathrm{w}} \mathrm{or} {\mathrm{M}}_{\mathrm{solute}}=\frac{{\mathrm{K}}_{\mathrm{f}}\times \mathrm{w}\times 1000}{∆{\mathrm{T}}_{\mathrm{f}}\times \mathrm{W}} \\ \therefore ∆{\mathrm{T}}_{\mathrm{f}}=\frac{{\mathrm{K}}_{\mathrm{f}}\times \mathrm{w}\times 1000}{{\mathrm{M}}_{\mathrm{solute}}\times \mathrm{W}} \mathrm{or} {\mathrm{M}}_{\mathrm{solute}}=\frac{{\mathrm{K}}_{\mathrm{f}}\times \mathrm{w}\times 1000}{∆{\mathrm{T}}_{\mathrm{f}}\times \mathrm{W}} \end{gathered}$$

• Depression in freezing point depends upon relative number of moles of solute and solvent but does not depend upon nature of solute, so it is a colligative property.

• k_f is related to molar enthalpy of fusion of solvent as;
${\mathrm{k}}_{\mathrm{f}}=\frac{{\mathrm{M}}_{\mathrm{solvent}}{{\mathrm{RT}}_{\mathrm{f}}}^2}{∆{\mathrm{H}}_{\mathrm{fusion}}\times 1000}$

The method of determining molecular mass by the study of depression in freezing point is called cryoscopic method.

Antifreeze solutions:  Addition of ethylene glycol to water decreases the freezing point of water.  This solution has freezing point lower than zero.  Freezing point can be lowered to the desired extent by changing the concentration.  The solution of ethylene glycol in water is used in radiators of vehicles at high altitude where temperature remains below zero.

• A mixture of NaCl and CaCl₂ is scattered on icy roads at higher altitudes. This mixture helps in melting the ice as long as the environmental temperature is above the lowest freezing point of salt-water mixture.

• CaCl₂ is more effective in melting the ice than NaCl.

Illustration 12: Freezing point of naphthalene is 80⁰C.  When 1.2g of sulphur is melted with 15g of naphthalene, the solution freezes at 77.2⁰C.  What will be the molar mass of this form of sulphur.
(k_f for naphthalene = 6.80 K. kg mol^–1)
Solution. Freezing point of naphthalene = 80⁰C
Freezing point of solution containing sulphur in naphthalene = 77.2⁰C
depression in freezing point = 80 – 77.2 = 2.8⁰C
$\begin{array}{r}\text{ depression in freezing point }\mathrm{\Delta }{T}_f=\frac{k_f\times w\times 1000}{M_{\text{solute }}\times W}\left(\begin{array}{c}\text{ where }w\to \text{ masso solute }\\ W\to \text{ mass of solvent }\end{array}\right)\\ \text{ or }{M}_{\text{solute }}=\frac{k_f\times w\times 1000}{W\times \mathrm{\Delta }{T}_f}=\frac{6.8\times 1.2\times 1000}{15\times 2.8}=194\end{array}$

Illustration 13: An aqueous solutions contains 5% by weight of glucose and 10% by weight of urea.  What will be the freezing point of this solution? (k_f for water is 1.86 K kg mol^–1)
Solution. 
$$\begin{gathered} \mathrm{Moles} \mathrm{of} \mathrm{glucose} =\frac{5}{180}=0.028 \\ \mathrm{Moles} \mathrm{of} \mathrm{urea} =\frac{10}{60}=0.167 \\ \mathrm{Total} \mathrm{moles} =0.028+0.167=0.195 \\ \mathrm{Mass} \mathrm{of} \mathrm{solvent} \mathrm{i}.\mathrm{e}., \mathrm{water} =100-(10+5)=85\mathrm{g} \\ \mathrm{Depression} \mathrm{in} \mathrm{freezing} \mathrm{point} {\mathrm{\Delta T}}_{\mathrm{f}}=\frac{{\mathrm{k}}_{\mathrm{f}}\times \text{ total mole s of solute }}{\text{ mass of solvent in kg }} \\ =\frac{1.86\times 0.195\times 1000}{85}=4.267 \\ \therefore \mathrm{freezing} \mathrm{point} \mathrm{of} \mathrm{solution} =0^{\circ }\mathrm{C}-4{.267}^{\circ }\mathrm{C}=-4{.267}^0\mathrm{C} \end{gathered}$$

OSMOSIS: When a solution is separated from pure solvent by a semipermeable membrane, it is observed that solvent molecules enter the solution and the volume of solution increases.  If two solutions of different concentrations are separated by a semipermeable membrane, the solvent molecules move from a solution of low concentration towards a solution of higher concentration.  This flow of solvent molecules from a pure solvent to a solution or from a dilute to a concentrated solution through semipermeable membrane is called osmosis.

• A semipermeable membrane allows solvent molecules to pass through it but does not allow the solute particles to pass through it. Parchment paper, cellophane membrane, freshly precipitated copper ferrocyanide, silicates of iron, cobalt are examples of artificial semipermeable membranes.  Animal bladder is an example of natural semipermeable membrane.

OSMOTIC PRESSURE:
The flow of solvent molecules from solvent side to solution side through semipermeable membrane can be stopped if some extra pressure is applied on the solution.  This pressure that just stops the flow of solvent is called osmotic pressure.  This pressure depends on the concentration of the solution.

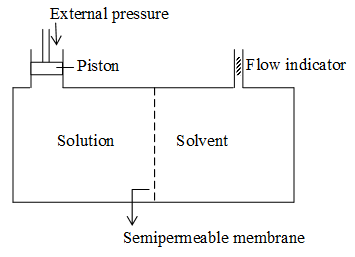
When a thistle funnel containing concentrated aqueous sugar solution and covered with semipermeable membrane, is placed in distilled water, then water flows from beaker into the funnel.  As a result of osmosis, the level of solution in funnel increases.  After a few days, the level becomes stationary.  At this stage hydrostatic pressure of column is sufficient enough to stop flow of solvent into solution.
Thus the hydrostatic pressure developed as a result of osmosis, is a measure of osmotic pressure.

• A solution having higher osmotic pressure than some other solution is called hypertonic with respect to the other solution.

• A solution having lower osmotic pressure relative to some other solution is called hypotonic with respect to other solution.

• The two solutions having equal osmotic pressure are called isotonic solutions.

• When a plant cell is placed in hypotonic solution, the water is drawn in and the cell swells.

• If the cell is placed in a hypertonic solution, water will diffuse out of the cell, and the cell will partially collapse.

• Solvent concentrations is greater in hypotonic solution and lower in hypertonic solution, hence osmosis takes place from hypotonic to hypertonic.

• 9% NaCl solution called normal saline solution is isotonic with respect to human blood. Therefore medicines are mixed with saline water before intravenous injection.  This prevents the blood cells from bursting or shrinking.

• Osmotic pressure is determined by the following methods
(i)  Pfeffer’s method      (ii)  Morse and Frazer’s method  (iii)  Berkely and Hartley’s method

Van’t Hoff’s Law of osmotic pressure:
A substance in dissolved state behaves as a gas and the osmotic pressure of the solution is equal to the pressure which the solute would exert if it were a gas at the same temperature and occupying the same volume as that of the solution.  This statement is known as Van’t Hoff theory of dilute solutions.

• For a given solvent the osmotic pressure depends only upon the molar concentration of solute but does not depend upon its nature. Thus osmotic pressure is a colligative property.

Determination of molecular mass from osmotic pressure:
Osmotic pressure is related to the number of moles of the solute by the following relation:
πV=nST
Where π → osmotic pressure; V → volume of solution.
T → Temperature; S → solution constant
 n → No. of moles of solute.
If w gram of the solute whose molecular mass is M_solute be present in solution then
$$\begin{gathered} \mathrm{n}=\frac{\mathrm{W}}{{\mathrm{M}}_{\mathrm{solute}}}; \mathrm{Thus} \mathrm{\pi }=\frac{\mathrm{wST}}{{\mathrm{M}}_{\mathrm{solute}}} \\ \mathrm{or} {\mathrm{M}}_{\mathrm{solute}}=\frac{\mathrm{wST}}{\mathrm{\pi V}} \end{gathered}$$

• For macromolecular substances such as polymers or proteins, osmotic pressure method is widely used to determine molecular masses. For macromolecules the freezing point depression and other colligative properties are too small to be measured.  However osmotic pressure for such substances can be easily measured.

• The osmotic pressure method has the advantage over other methods because pressure measurement can be done around room temperature.

• Osmotic pressure determination is particularly useful for biomolecules as they are not stable at higher temperature.

Reverse osmosis:

• The direction of osmosis can be reversed if a pressure greater than the osmotic pressure is applied to the solution side, it means that solvent starts passing from solution into solvent through semipermeable membrane. This phenomenon is called reverse osmosis.

• Reverse osmosis is used for purification of sea water or hard water. Sea water which is a solution of many undesirable salts, is placed is contact with pure water through semipermeable membrane.  When pressure more than osmotic pressure is applied on sea water, pure water is squeezed out of the sea water through the membrane.

• The pressure required for reverse osmosis is quite high. That’s why a workable porous membrane is achieved by a film of cellulose acetate placed over a suitable support.  Cellulose acetate is permeable to water but impermeable to impurities and ions present in sea water.

Difference between diffusion and osmosis:

• In diffusion, solvent as well as solute molecules move from one region to the other, while in osmosis the flow of solvent molecules occurs in one direction only.

• For osmosis semipermeable membrane is required, while for diffusion it is not required.

• Osmosis is limited to solutions only, while diffusion can take place in liquids, solutions and gases.

• Osmosis can be stopped or reversed by applying additional pressure on the solution side, but diffusion can neither be stopped nor reversed.

Illustration 14: What is the osmotic pressure of a solution of 4.48g of a substance of molecular mass 286 in 100 c.c. water at 298K (R = 0.0821 L atm/mol K)

Solution. Osmotic pressure $\pi =\frac{\text{wRT}}{M_{\text{solute}}V}$
Where   w → mass of solute
V → volume of solution
M_{solute →} gram molecular mass of solute

$\therefore \pi = \frac{4.48\times 0.0821\times 298\times 1000}{286\times 100}= 3.83 \text{atm}$                        

Illustration 15: A 5% solution of cane sugar is isotonic with 0.877% solution of urea.  Find the molecular mass of urea.
Solution. Osmotic pressure of cane sugar solution = osmotic pressure of urea solution.
i.e., π₁ = π₂
or $\begin{array}{r}\frac{{\mathrm{n}}_1\mathrm{RT}}{\mathrm{V}}=\frac{{\mathrm{n}}_2\mathrm{RT}}{\mathrm{V}}\\ \end{array}$  (Where n₁ and n₂ are moles of sugar and urea)
or  n₁ = n₂
$\begin{array}{r}\frac{5}{342}=\frac{0.877}{{\mathrm{M}}_{\mathrm{urea}}}\text{ or }{\mathrm{M}}_{\text{urea }}=\frac{0.877\times 342}{5}=60\mathrm{g}/\mathrm{mol}\end{array}$        

Illustration 16: x g of a non electrolyte compound with molecular mass (100) is dissolved in 1.0L of 0.05 M NaCl solution.  The osmotic pressure of this solution was found to be 4.92atm at 27⁰C.  Assuming complete dissociation of NaCl and ideal behaviour of solution, find the value of x.
Solution. There is complete dissociation of NaCl
$\begin{array}{l}\therefore \mathrm{i}=2\\ \text{Moles of }\mathrm{NaCl}=0.05\times 2=0.1\\ \text{Moles of non.electrolyte compound}=\frac{\mathrm{x}}{100}\\ \because \text{total mole}\mathrm{s}=(0.1+\frac{\mathrm{x}}{100})\therefore \pi =\frac{\mathrm{nRT}}{\mathrm{V}}\\ \text{or }4.92=\frac{(0.1+\frac{\mathrm{x}}{100})\times 0.0821\times 300}{1} \Rightarrow 0.1+\frac{\mathrm{x}}{100}=\frac{4.92}{0.0821\times 300}=\frac{4.92}{24.63}=0\\ \Rightarrow \frac{\mathrm{x}}{100}=0.2-01=0.1 \Rightarrow \mathrm{x}=100\times 0.1=10\mathrm{g}\end{array}$         

ABNORMAL COLLIGATIVE PROPERTIES
Colligative properties provide methods for determination of molecular mass of dissolved solutes.  The various relations between colligative properties and molecular mass are applicable only if the following three conditions are satisfied:

• The solution should be very dilute

• The solute should be non-volatile

• The solute should neither dissociate nor associate in the solution.

The colligative properties of solutions depend on the No. of solute particles present in solution.  In case the total number of particles of the solute changes in solution, the colligative property changes accordingly.  The number of particles in solution may change in any of following two ways:
(i)  Association of solute molecules                ii)  Dissociation of solute molecules
i) Association of solute molecules: When two or more molecules of the solute associate to form a single molecule, the number of particles decreases and consequently the value of collogative properties decreases.The colligative properties are inversely proportional to molecular mass.
Calligative properties ∝ $\frac{1}{\mathrm{molecular} \mathrm{mass}}$
Hence, higher values are obtained for associated molecules then normal values.
For example benzoic acid dissolved in benzene is found to have molecular mass double of its normal molecular mass because benzoic acid form dimers in solution due to hydrogen bonding.

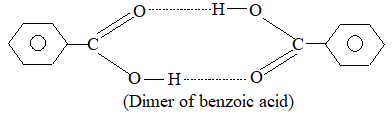
(ii) Dissociation of solute molecules:  When solute molecules ionize in solution, then number of particles in solution increases, consequently the value of colligative properties also increases.  Since colligative properties are inversely proportional to molecular masses, therefore molecular masses of such substances as calculated from colligative properties will be less than their normal values.

VAN’T HOFF’S FACTOR:
When the solute molecules dissociate or associate in solution, the number of particles in solution increases or decreases and thus colligative properties changes accordingly.
In 1886 Van’t Hoff introduced a factor ‘i’ to express the extent of association or dissociation of solute in solution.
$\begin{array}{rl}\text{Vant Hoff’s factor ‘i’}=& \frac{\text{observedcolligative property}}{\text{Normalor the oretical colligative property}}\\ & \\ =& \frac{\text{No.of particle safter association or dissociation}}{\text{No. of particle sbefore association or dissociation}}\\ & \\ & =\frac{\text{Normal molecular mass of the solute}}{\text{Observedmole cular mass of the solute}}\end{array}$

• In case of association observed molecular mass being more than normal, the factor ‘i’ is less than one. Suppose ‘n’ molecules associate to form one molecule and a is degree of association then, 
$$\begin{gathered} \begin{array}{l}\mathrm{total} \mathrm{number} \mathrm{of} \mathrm{particl} \mathrm{in} \mathrm{solution}=1-\mathrm{\alpha }+\frac{\mathrm{\alpha }}{\mathrm{n}}\\ =1+\mathrm{\alpha }(\frac{1}{\mathrm{n}}-1)\end{array} \\ \mathrm{Thus} \mathrm{Van}’\mathrm{t} \mathrm{Hoff}’\mathrm{s} \mathrm{factor} ‘\mathrm{i}’=\frac{1+\mathrm{\alpha }(\frac{1}{\mathrm{n}}-1)}{1} \\ \mathrm{If} \mathrm{n} \mathrm{is} 2 \mathrm{or} \mathrm{more}, \mathrm{then} \mathrm{i} < 1 \\ \mathrm{or} \mathrm{\alpha }=\frac{\mathrm{i}-1}{\frac{1}{\mathrm{n}}-1} \end{gathered}$$                             

• In case of dissociation, the Van’t Hoff’s factor is more than 1 because the observed molecular molecular mass has a lesser value than the normal molecular mass.
Suppose one molecule of an electrolyte gives ‘n’ ions on dissociation and ‘α’ is its degree of ionization
Thus number of ions produced = nα.
Number of unionized molecules = 1 – α.
Total number of particles in solution = 1 – α + nα = 1 + α (n -1)
Van’t Hoff’s factor ‘i’       =  1 + α (n -1)
If n is 2 or more; then i > 1      or   $\mathrm{\alpha }=\frac{\mathrm{i}-1}{\mathrm{n}-1}$                               

• For the electrolytes such as NaCl, KCl, the number of particles in solution ( n = 2)
$\therefore$ α = i – 1

• For the electrolytes of the type CaCl₂, MgCl₂ the number of particles in solution (n = 3).
$\therefore \mathrm{\alpha }=\frac{\mathrm{i}-1}{2}$

• Introduction of Van’t Hoff’s factor modifies the equations for the colligative properties as,

i) Osmotic pressure  $\mathrm{\pi }=\frac{\text{in ST}}{\mathrm{V}}$

ii) Relative lowering of vapour pressure $\frac{{\mathrm{P}}_{\text{solvent}}^0-{\mathrm{P}}_{\text{solution}}}{{\mathrm{P}}_{\text{solvent}}^0}={\mathrm{iX}}_{\text{solute}}$

iii) Elevation is boiling point ΔT_b = ik_bM

iv) Depression in freezing point ΔT_f = ik_fm 

Illustration 17:  0.2 molal aqueous solution of a weak acid (HX) is 20% ionized.  Calculate the freezing point of this solution.  (K_f = 1.86⁰C/m) for water.
Solution.             

$$\begin{gathered} \begin{array}{rl}\alpha =\frac{20}{100}=0.2;& \mathrm{for}HX \mathrm{n}=2\\ \alpha =\frac{\mathrm{i}-1}{\mathrm{n}-1} or 0.2=\frac{\mathrm{i}-1}{2-1}& \end{array} \\ or i=1.2; Depression in freezing point \mathrm{\Delta Tf}=\mathrm{ikm} \\ {\mathrm{\Delta T}}_{\mathrm{f}}=1.2\times 1.86\times 0.2=0.446 \\ \therefore \mathrm{Freezing} \mathrm{point} \mathrm{of} \mathrm{solution} 0^{\circ }\mathrm{C}-{0.446}^{\circ }\mathrm{C}=-{0.446}^{\circ }\mathrm{C} \end{gathered}$$

Illustration 18:  What is the ratio of the value of any colligative property for KCl solution to that for sugar solution?
Solution.   In case of sugar solution; there is neither association nor dissociation hence observed and normal colligative properties have the same value.  But in case of KCl which is an electrovalent compound, complete dissociation occurs in aqueous soltuion.  Hence Van’t Hoff’s factor ‘i’ for KCl

$\mathrm{i}=\frac{\text{No. of particles after dissociation}}{\text{No. of particles before dissociation}}$= 2

Thus the ratio of the values of colligative property for KCl to that for sugar solution = 2.0.

Illustration 19: Assuming complete dissociation calculate the expected freezing point of a solution prepared by dissolving 6.00g of Na₂SO₄.10 H₂O in 0.1 kg of water.
Solution. Molecular mass of Na₂SO₄. 10H₂O = 322.
Molality of solution = $\frac{6}{322\times 0.1}=\frac{60}{322}$
for complete dissociation α = 1
$\therefore \mathrm{\alpha }=\frac{\mathrm{i}-1}{\mathrm{n}-1}=\frac{\mathrm{i}-1}{3-1}$;  or i = 3
(Na₂ SO₄ →  2Na⁺ + SO₄^2–; hence n = 3)
k_f for water = 1.86
Depression in freezing point ΔT_f = ik_f m    =  $\frac{3\times 1.86\times 60}{322}=1.04$
Thus freezing point of solution = – 1.04⁰C

Illustration 20: 12.2g of Benzoic acid in 100g water has elevation in boiling point of 0.27.  If there is 100% association, then what is the number of molecules of benzoic acid in associated state.  (k_b = 0.54 K. Kg mol^–1).

Solution. Molecular mass of Benzoic acid (C₆H₅COOH). = 122 g
Molality of solution = $\frac{\text{mass of solute}}{\text{Grammolecular mass of solute}\times \text{mass of solvent in }\mathrm{kg}}$

$=\frac{12.2\times 1000}{122\times 100}=1\mathrm{mol}/\mathrm{kg}$
k_b for water = 0.54,    ΔT_b = 0.27      ΔT_b = i k_bm   or   i =  $\frac{{\mathrm{\Delta T}}_{\mathrm{b}}}{{\mathrm{k}}_{\mathrm{b}}\times \mathrm{m}}=\frac{0.27}{0.54\times 1}=\frac{1}{2}$
If association is 100%, then degree of association α = 1;   Thus  $1=\frac{\mathrm{i}-1}{\frac{1}{\mathrm{n}}-1}$
or  $\frac{1}{\mathrm{n}}-1=\frac{1}{2}-1$       or   n = 2.

Illustration 21:  The values of observed and calculated molecular mass of Ca(NO₃)₂ are 65.4 and 164 respectively.  What is the degree of ionization of the salt.
Solution. Van’t Hoff’s factor ‘i’ = $$$\frac{\text{Normal mole cular mass}}{\text{observed mole cular mass}}=\frac{164}{65.4}=2.5$

$\{\mathrm{Ca}{\left({\mathrm{NO}}_3\right)}_2\to {\mathrm{Ca}}^{2+}+2{\mathrm{NO}}_3^{- }\mathrm{thus} \mathrm{n}=3\}$
Degree of ionization   $\alpha =\frac{i-1}{n-1}=\frac{2.5-1}{3-1}=\frac{1.5}{2}=\frac{3}{4}=0.75$
Percentage ionization = 75%

SOLVED PROBLEMS-1

Prob 1. What approximate proportions by volume of water (d = 1g/c.c.) and ethylene glycol must be mixed to protect an automobile cooling system to -10⁰C.  (density of ethylene glycol = 1.12/cc).

Sol.  $\Delta {\mathrm{T}}_{\mathrm{f}}=10°\mathrm{C}$

Gram molecular mass of solute i.e., $\begin{array}{cc}\mathrm{C}& {\mathrm{H}}_2\mathrm{OH}\\ |& \\ \mathrm{C}& {\mathrm{H}}_2\mathrm{OH}\end{array}$ is 62.  Let the mass of ethylene glycol = V_g ⨯ d_g and mass of water = v_w ⨯ d_w

(where V_g and V_w are volume of ethylene glycol and water respectively.  Similarly d_y and d_w are densities of ethylene glycol and water respectively)

$$\begin{gathered} \therefore \mathrm{\Delta T}=\frac{{\mathrm{k}}_1\times \text{ mass of solute }\times 1000}{\text{ GMM of solute }\times \text{ mass of solve }\mathrm{nt}\left(\mathrm{g}\right)} \\ \mathrm{or} 10=\frac{1.86\times {\mathrm{V}}_{\mathrm{g}}\times 1.12\times 1000}{62\times {\mathrm{V}}_{\mathrm{w}}\times 1.0} \\ \mathrm{or} \frac{{\mathrm{V}}_{\mathrm{w}}}{{\mathrm{V}}_{\mathrm{g}}}=\frac{1.86\times 1.12\times 1000}{62\times 1.0\times 10}=3.36 \\ \mathrm{or} \frac{{\mathrm{V}}_{\mathrm{w}}}{{\mathrm{V}}_{\mathrm{g}}}\approx \frac{10}{3} \end{gathered}$$

Prob 2. An aqueous solution of glucose is labelled as 18 percent w/w.  If density of solution in 1.8g mL^-1, calculate the molarity and molality of solution.

Sol. GMM of glucose = 180g

Mass of solute = 18g

Mass of solvent = 100 – 18 = 82g

$\begin{array}{r}\text{ Volume of solution }=\frac{\text{ Mass }}{\text{ Density }}=\frac{100}{1.8}=55.55\mathrm{ml}\\ \text{ Molarity of solution }=\frac{\text{ mass of solute }}{\text{ GMM of solute }\times \text{ Volume of solutionin }\mathrm{L}}\\ =\frac{18\times 1000}{180\times 55.55}=1.8\mathrm{M}\\ \text{ Molality of solution }=\frac{18\times 1000}{180\times 82}=1.22\mathrm{m}\end{array}$

Prob 3. 100 ml of 0.6N H₂SO₄ and 200 ml of 0.3 N HCl were mixed together.  (a)  What will be the normality if the resulting solution?  (b)  What will be the normality if the resulting solution is diluted to 600 ml?

Sol :        H₂SO₄              HCl

$\begin{array}{r}{\mathrm{N}}_1{\mathrm{V}}_1+{\mathrm{N}}_2{\mathrm{V}}_2=\mathrm{N}\left({\mathrm{V}}_1+{\mathrm{V}}_2\right)\\ \mathrm{N}=\frac{{\mathrm{N}}_2{\mathrm{V}}_1+{\mathrm{N}}_2{\mathrm{V}}_2}{{\mathrm{V}}_1+{\mathrm{V}}_2}=\frac{0.6\times 100+0.3\times 200}{100+200}\\ =\frac{60+60}{300}=\frac{120}{300}=0.4\mathrm{N}\end{array}$

b) On dilution, miliequivalent of solution does not change. Thus 120 miliequivalent will be

present in 600 ml of resulting solution.

∴ Normality of resulting solution = $\frac{120}{600}=0.2\mathrm{N}$

Prob 4. Find the molarity and molality of a 18% solution of H₂SO₄.  Density of solution is 1.2 g/ml.

Sol:  Molar mass of H₂SO₄ = 98g/mol

mass of solution = 100;        mass of solute = 18g

mass of solvent = 100 – 18 = 82g

$\begin{array}{r}\text{ Volume of solution }=\frac{\text{ Mass }}{\text{ Density }}=\frac{100}{1.2}\\ \text{ Molarity of solution }=\frac{\text{ Mass of solute }}{\text{ GMM of solute }\times {\mathrm{V}}_{\left(\mathrm{L}\right)}}\\ =\frac{18\times 1.2\times 1000}{98\times 100}=2.2\mathrm{M}\\ \text{ Molality of solution }=\frac{\text{ Mass of solute }}{\mathrm{GMM}\times \text{ Mass of solventin }\mathrm{kg}}\\ =\frac{18\times 1000}{98\times 82}=2.24\mathrm{m}\end{array}$

Prob 5. What volume of 96% H₂SO₄ solution (density = 1.83 g/ml) is required to prepare 5 litre of 3.0 M H₂SO₄ solution?

Sol: Mass of solute = 96 g

Mass of solution = 100g

Volume of solution = $\frac{\text{ Mass }}{\text{ density }}=\frac{100}{1.83}\mathrm{ml}$

Molarity of solution = $\frac{\text{ Mass of solute }\times 1000}{\text{ GMMof solte }\times {\mathrm{V}}_{\text{mL }}}$

$=\frac{96\times 1000\times 1.83}{98\times 100}=17.93\mathrm{M}$

Let the volume of this solution to prepare 4 litre of 3.0 M H₂SO₄ solution be = V₁

∴  M₁V₁ = M₂V₂

17.93 ⨯ V₁ = 3.0 ⨯ 4

or   ${\mathrm{V}}_1=\frac{3.0\times 4}{17.93}=0.67\text{ litre }$

Prob 6. A 500g toothpaste sample has 0.2g fluoride concentration.  What will be the concentration of fluorine in terms of ppm?

Sol: Concentration in terms of ppm = $\frac{\text{ Mass of solute }}{\text{ Mass of solution }}\times {10}^6=\frac{0.2}{500}\times {10}^6=400\mathrm{ppm}$

Prob 7. A solution is prepared by mixing 50g sugar in 100g of water at 25⁰C.  Calculate the mole fractions of sugar and water.

Sol: GMM of sugar (C₁₂H₂₂O₁₁) = 342 g/mol

Mole of sugar = $\frac{\text{ Mass of sugar }}{\text{ GMM of sugar }}=\frac{50}{342}=0.146$

Mole of water = $\frac{100}{18}=5.55$

Mole of fraction of sugar = $\frac{0.146}{0.146+5.55}=\frac{0.146}{5.696}=0.0256$

Mole fraction of water = $\frac{5.55}{5.696}=0.974$

Prob 8. Molarity of H₂SO₄ is 0.8 and its density is 1.06g/c.c.  What will be its concentration in terms of molality and mole fraction.

Sol: Molarity of H₂SO₄ = 0.8

It means 1 litre of H₂SO₄ solution contains 0.8 moles

Mass of 1 litre of H₂SO₄ solution = volume ⨯ density

= 1000 ⨯ 1.06 = 1060g

Mass of solute i.e., H₂SO₄ = 0.8 ⨯ 98 = 78.4g

Mass of solvent = 1060 – 78.4 = 981.6

Molality of solution = $\frac{\text{ moles of solute }}{\text{ massof solvent in }\mathrm{kg}}=\frac{0.8\times 1000}{981.6}=0.815\mathrm{m}$

Moles of solvent = $\frac{981.6}{18}=54.53$

Mole fraction of H₂SO₄ = $\frac{0.8}{54.53+0.8}=\frac{0.8}{55.33}=0.0144$

Prob 9. 3g of acetic acid is added to 500 c.c. of water.  If 23% of acetic acid is dissociated what will be the depression in freezing point.

(density of water = 0.997 gcm^–3; kg = 1.86 k kg^–1 mol^–1)

Sol. Mass of solute = 3.0g

Molecular mass of solute (CH₃COOH) = 60

Mass of solvent = 500 ⨯ 0.997 = 498.5g

Degree of dissociation, $\alpha =\frac{i-1}{n-1}$

or    0.23 = $\frac{i-1}{2-1}$         or      i = 1.23

Depression in freezing point ${\mathrm{\Delta T}}_{\mathrm{f}}=\mathrm{i}\times \mathrm{kf}\times \mathrm{m}$

$\therefore {\mathrm{\Delta T}}_{\mathrm{f}}=1.23\times 1.86\times \frac{3\times 1000}{60\times 498.5}$ = 0.229

Prob 10. 3.1g of BaCl₂ is added to 250g of water.  This solution boils at 100.083⁰C.  Calculate the value of Van’t Hoff’s factor and molality of BaCl₂ in the solution (K_b for H₂O = 0.52 K.Kg mol^-1)

Sol. Gram molecular mass of BaCl₂ = (137.32 + 71) = 208.32

Molality = $\frac{3.1\times 1000}{208.32\times 250}$ 0.0595 mol/kg

Elevation in boiling point = 100.083 – 100.00 = 0.083

${\mathrm{\Delta T}}_{\mathrm{b}}=\mathrm{ikbm}\therefore \mathrm{i}=\frac{{\mathrm{\Delta T}}_{\mathrm{b}}}{{\mathrm{k}}_{\mathrm{b}}\mathrm{m}}$

Hence      $\mathrm{i}=\frac{0.083}{0.52\times 0.0595}=2.68$

SOLVED PROBLEMS-2

Prob 1. A compound X undergoes complete tetramerisation in a given organic solvent. The Van’t Hoff factor i is 

(A) 4.0               (B) 0.25               (C) 0.125               (D) 2.0

Sol. (B) $\mathrm{i}=\frac{\text{ Normal molecular mass }}{\text{ Observed molecular mass }}=\frac{1}{4}=0.25$

Prob 2. When a solute is added to a pure solvent. Which of the following statement is true?

(A) Vapour pressure of the solution becomes lower than the vapour pressure of the pure solvent.

(B) Rate of evaporation of the pure solvent is reduced.

(C) Solute does not affect the rate of condensation.

(D) All of these.

Sol. (D) All of these

Prob 3. The vapour pressures of ethanol and methanol are 42.0 mm and 88.5 mm Hg respectively. An ideal solution is formed at the same temperature by mixing 46.0 g of ethanol with 16.0 g of methanol. The mole fraction of methanol in the vapour is

(A)  0.467               (B)  0.502               (C)  0.513               (D) 0.556

Sol. (C)

${\mathrm{X}}_{\text{ethanol }}=\frac{\frac{46}{46}}{\frac{46}{46}+\frac{16}{32}}=\frac{2}{3}{\mathrm{X}}_{\text{methanol }}=1-\frac{2}{3}=\frac{1}{3}$

So, ${\mathrm{P}}_{\text{ethanol }}=42\times \frac{2}{3}=28{\mathrm{P}}_{\text{methanol }}=88.5\times \frac{1}{3}=29.5$

${\mathrm{y}}_{\text{methanol }}\left(\text{ vapour phase }\right)=\frac{{\mathrm{P}}_{\text{methanol }}}{{\mathrm{P}}_{\text{methanol }}+{\mathrm{P}}_{\text{ethanol }}}=\frac{29.5}{28+29.5}=0.513$

Prob 4. At a certain temperature pure liquid A and liquid B have vapour pressures 10 torr and 37 torr respectively. For a certain ideal solution of A and B, the vapour in equilibrium with the liquid has the components A and B in the partial pressure ratio P_A : P_B = 1 : 7. What is the mole fraction of A in the solution?

(A) 0.346               (B) 0.654               (C) 0.5               (D)  None of these

Sol. $\frac{1}{7}=\frac{{\mathrm{P}}_{\mathrm{A}}}{{\mathrm{P}}_{\mathrm{B}}}=\frac{{\mathrm{X}}_{\mathrm{A}}\times 10}{{\mathrm{X}}_{\mathrm{B}}\times 37}\Rightarrow \frac{10\times {\mathrm{X}}_{\mathrm{A}}}{\left(1-{\mathrm{X}}_{\mathrm{A}}\right)\times 37}=\frac{1}{7}\Rightarrow 70{\mathrm{X}}_{\mathrm{A}}=37-37{\mathrm{X}}_{\mathrm{A}};{\mathrm{X}}_{\mathrm{A}}=\frac{37}{107}=0.346$

Prob 5. If relative decrease in vapour pressure is 0.5 for a solution containing 1 mol CaCl₂ and 4 mol of H₂O then % ionization of CaCl­_­2 is

(A)  100%               (B)  60%               (C)  75%               (D)  50%

Sol. (C)

$\begin{array}{r}\frac{\mathrm{\Delta P}}{{\mathrm{P}}^{\circ }}=0.5=\frac{1}{1+4}\times \mathrm{i}\mathrm{i}=2.5\\ \text{Now, }\\ {\mathrm{CaCl}}_2\rightleftharpoons {\mathrm{Ca}}^{++}+2{\mathrm{Cl}}^{-}\\ 1-\alpha \alpha 2\alpha \\ \mathrm{i}=1+2\alpha =2.5;\alpha =0.75;\mathrm{\%}\text{ dissociation }=75\mathrm{\%}\end{array}$

Prob 6. 12.2 gm of benzoic acid (M = 122) in 100 gm H₂O has elevation of boiling point of If there is 100% polymerisation, number of molecules of benzoic acid in associated state is

(A)  1               (B)  2               (C)  3               (D) 4

Sol.  (B)

$\begin{array}{r}\begin{array}{rl}{\mathrm{\Delta T}}_{\mathrm{b}}={0.27}^{\circ }\mathrm{C}={\mathrm{iK}}_{\mathrm{b}}\mathrm{m}& \\ =\mathrm{i}\times 0.54\times \frac{\frac{12.2}{122}}{100}\times 1000\Rightarrow \mathrm{i}=\frac{0.27}{0.54}=\frac{1}{2}& \\ \mathrm{n}\left({\mathrm{C}}_6{\mathrm{H}}_5\mathrm{COOH}\right)={\left({\mathrm{C}}_8{\mathrm{H}}_5\mathrm{COOH}\right)}_n& \\ 1-1=0& \frac{1}{\mathrm{n}}\\ \frac{1}{\mathrm{n}}=\frac{1}{2}\Rightarrow \mathrm{n}=2& \end{array}\end{array}$

Prob 7. The ratio of the value of any colligative property for K₄[Fe(CN)₆] solution to that of Fe₄[Fe(CN)₆]₃ (Prussian blue), solution is nearly

(A)  1               (B)  0.71               (C)  1.4               (D)  Less than 1

Sol. (B)

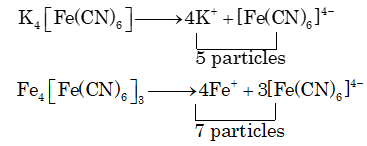
Ratio = $\frac{5}{7}=0.71$

Prob 8. 20 gm of a binary electrolyte (molecular weight = 100) is dissolved in 500 gm of water. The freezing point of the solution is – 0.74°C, K_f = 1.86 K molality^–1. The degree of ionisation of the electrolyte is

(A)  50%               (B)  75%               (C)  100%               (D)  zero

Sol. (D)

${\mathrm{\Delta T}}_{\mathrm{f}}={\mathrm{imK}}_{\mathrm{f}}$

 $0.74=\mathrm{i}\times \frac{20}{100/0.5}\times 1.86\Rightarrow \frac{0.74\times 2.5}{1.86}=1$

i = 1 ,So degree of dissociation is zero.

Prob 9. Distillate of vapours of a solution containing 2 moles of A (= 100 mm Hg) and 3 moles of B (= 150 mm Hg) will have total vapour pressure, approximately, on condensation:

(A)  135 mm               (B)  130 mm               (C)  140 mm               (D)  145 mm

Sol. (A)

${\mathrm{X}}_{\mathrm{A}}^{\mathrm{V}}=\frac{{\mathrm{X}}_{\mathrm{A}}^{\mathrm{L}}.{\mathrm{P}}_{\mathrm{A}}^{\circ }}{{\mathrm{X}}_{\mathrm{A}}^{\mathrm{L}}{\mathrm{P}}_{\mathrm{A}}^0+X_{\mathrm{B}}^{\mathrm{L}}\cdot {\mathrm{P}}_{\mathrm{B}}^{\circ }}=\frac{0.4\times 100}{0.4\times 100+0.6\times 150}=\frac{40}{40+90}=\frac{4}{13}$

${\mathrm{X}}_{\mathrm{B}}^{\vee }=1-\frac{4}{13}=\frac{9}{13}$   V.P. over the distillate upon condensation

${\mathrm{P}}_{\mathrm{mix}}=\frac{4}{13}\times 100+\frac{9}{13}\times 150$= 30.769 + 103.846 $\approx$ 134.6 $\approx$ 135 mm

Prob 10. Dry air was passed successively through a solution of 5 g solute in 180 g of water and then through pure water. The loss in weight of solution was 2.50 g and that of pure solvent is 0.04 g. The molecular weight of the solute is

(A)  31.25               (B)  3.125               (C)  312.5                (D)  None

Sol. (A)

$P^{\circ }-P_s\propto$ loss in weight of water chamber

$P_s\propto$ loss in weight of solution chamber

$\therefore \frac{{\mathrm{P}}^{\circ }-{\mathrm{P}}_{\mathrm{s}}}{{\mathrm{P}}^{\circ }}=\frac{\mathrm{n}}{\mathrm{N}}=\frac{\mathrm{w}/\mathrm{m}}{\mathrm{W}/\mathrm{M}}$ (for very dilute solution) $\frac{0.04}{2.54}=\frac{5/\mathrm{m}}{180/18}\Rightarrow \mathrm{m}=31.25$