The Solid State

Particles in solid state are held by stronger interparticle forces.  Hence, the particles in solid state do not possess translatory motion, they can only vibrate about their fixed position.  Therefore solids are rigid and possess definite shapes.  Solids have generally high density and low compressibility due to close packing of molecules.  The vapour pressure of solid is generally much less than vapour pressure of liquid at a definite temperature.
Solids can be classified into two types:
(i) Crystalline solids                      (ii) Amorphous solids

(i) Crystalline solids: These solids have definite and regular geometry due to definite and orderly arrangement of atoms, ions or molecules in three dimensional space.  They have sharp melting points and change abruptly into liquids.  Crystalline solids are anisotropic because some of their physical properties are different in different directions.  Crystalline solids are rigid and their shape is not distorted by mild forces.
Crystals are bound by plane faces.  The angle between any two faces is called interfacial angle.  For a given crystalline solid it is definite angle and remains always constant.  When a crystalline solid is hammered, it breaks up into smaller crystals of the same geometrical shape.  An important property of crystals is their symmetry.  There are three types of symmetry.
(i)  Plane of symmetry
(ii)  Axis of symmetry
(iii)  Centre of symmetry
Crystalline solids are considered as true solids.

(ii) Amorphous solids:  They do not have any pattern of arrangement of atoms, ions or molecules and thus do not have any definite geometrical shape.  Amorphous solids do not have sharp melting points and do not change abruptly into liquids.  These solids are isotropic because their physical properties are same in all directions.  These solids do not have well defined planes.  When an amorphous solid is broken, the surfaces of the broken pieces are generally not flat and intersect at random angles.  They do not have any symmetry.  These are considered pseudosolids or super cooled liquids.

Isotropy and Anisotropy: The substances which show same properties in all directions are said to be isotropic.  In amorphous solids, the properties such as electrical conductivity thermal conductivity, mechanical strength and refractive index are same in all directions.  Amorphous substances are therefore said to be isotropic.  Liquids and gases are also isotropic.  In amorphous solids and in liquids and gases, the arrangement of building constituents is random and disordered.  Hence all directions are equal and therefore properties are same in all directions. 
The physical properties of crystalline, solids are different in different directions within the crystal therefore crystalline solids are said to be anisotropic. 
For example, in the crystal of silver iodide the coefficient of thermal expansion is positive in one direction and negative in the other direction.  The phenomenon of anisotropy provides a strong evidence for the presence of ordered molecular arrangement in crystals.

Space lattice or Crystal lattice:
A space lattice may be defined as a regular three dimensional arrangement of identical points in space.  Each lattice point has the same environment as that of any other point in the lattice.  The constituent particle has always to be represented by a lattice point, irrespective of whether it contains a single atom or more than one atom.

Unit cells:
A space lattice can be subdivided into a number of small cells known as unit cells.  It can be defined as the smallest repeating unit in space lattice which when repeated over and over again, results in a crystal of the given substance.  A unit cell of a crystal possesses all the structural properties of the given crystal.  For example if a crystal is a cube, the unit cell must also have its atoms, molecules or ions arranged so as to give a cube.  Each unit cell has three vectors a, b and c.  The distances a, b and c are the lengths of the edges of the unit cell and angles α, β and γ are the angles between three imaginary axes OX, OY and OZ respectively.

Types of unit cells:

i) Simple, primitive or basic unit cell:
This unit cell has lattice points only at the corners.  Each particle at the corner of a unit cell is shared by eight unit cells in the lattice and hence contributes only 1/8^th to a particular unit cell.  Thus, the number of atoms per unit cell in primitive lattice is $8\times \frac{1}{8}= 1 \mathrm{atom}$.

ii) Face centred unit cell:
There are lattice points at the corners as well as at the centre of each of the six faces of the cube.  A face centred cubic unit cell has one atom at each corner (each shared by 8 unit cell) and one atom at each face centre.  An atom at the face centre is being shared by two unit cells and makes a contribution of only ½ to a particular unit cell.  Hence a face centred cubic unit cell has,
8(at corners)$\times \frac{1}{8}+6$(at face centres)$\times \frac{1}{2}=4 \mathrm{atoms}$

iii)  Body centred cubic unit cell:
This type of unit cell has eight atoms at corners and one at the body centre.  Each corner atom makes $\frac{1}{8}$contribution and the atom at the body centre belongs only to the particular unit cell.  Thus number of atoms per unit cell are
8(at corners)$\times \frac{1}{8}+1$(at body centre)$\times$1=2 atoms

(iv)  End centred unit cell:
In this unit cell, there are eight atoms at the corners and two atoms in the face centres of only one set of faces (end faces).  The number of atoms per unit cell is
8(at corners)$\times \frac{1}{8}+2$(at endfaces)$\times \frac{1}{2}$=2

A particle at the edge centre is shared by four unit cells in the lattice and hence contributes only ¼ to a particular unit cell.

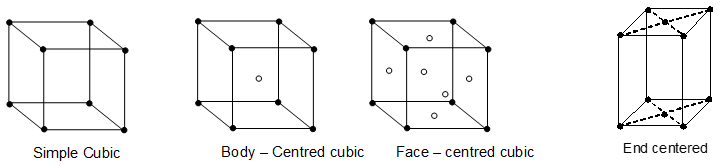
Illustration 1: In a cubic solid structure X atoms are located at the corners of the cube, Y atoms at the cube centres and O atoms at the edge centres.  What is the formula of the compound?

Solulution: No.of X atoms per unit cell = 8 x 1/8 =1
                         No.of Y atoms per unit cell = 1 x 1 = 1
                         No. of O atoms per unit cell = 12 x $\frac{1}{4}$ =3
                         So the formula of the compound is ${\mathrm{XYO}}_3$

Illustration 2: A compound formed by elements X and Y crystallizes in the cubic structure where Y atoms are at the corners of the cube and X atoms are at the centre of one set of opposite faces.  What is the formula of the compound?
Solulution: No. of atoms of Y = $8\times \frac{1}{8}=1$
                         No. of atoms of X = 2 (at face centres)$\times \frac{1}{2}=1$
                         Hence the formula of the compound is XY
Crystal systems:  Seven types of basic or primitive crystal systems have been recognized among crystals.  These are cubic, tetragonal, orthorhombic, monoclinic, triclinic, hexagonal and rhombohedral.

Table: SEVEN CRYSTAL SYSTEM

Crystal System	Axial distances or Edge lengths	Axial angles	Examples
Cubic	a=b=c	$\alpha =\beta =\gamma =90°$	Copper, ZnS, KCl
Tetragonal	a=b≠c	$\alpha =\beta =\gamma =90°$	White $\mathrm{Sn}, {\mathrm{SnO}}_2,{\mathrm{TiO}}_2$
Orthorhombic	a≠b≠c	$\alpha =\beta =\gamma =90°$	Rhombic S, CaCO3
Monoclinic	a≠b≠c	$\alpha =\gamma =90°, \beta \ne 90°$	Monoclinic $\mathrm{S}, {\mathrm{PbCrO}}_2$
Hexagonal	a=b≠c	$\mathrm{\alpha }=\beta =90°, \mathrm{\gamma }=120°$	Graphite, ZnO
Rhombohedral	a=b=c	$\alpha =\beta =\gamma \ne 90°$	CaCO3 (Calcite), HgS
Triclinic	a≠b≠c	$\alpha \ne \beta \ne \gamma \ne 90°$	${\mathrm{K}}_2{\mathrm{Cr}}_2{\mathrm{O}}_7,{\mathrm{CuSO}}_4.5{\mathrm{H}}_2\mathrm{O}$

Bravais Lattices:
Bravais showed from geometrical considerations that there can be only 14 different ways in which similar points can be arranged in a three dimensional space.  Thus the total number of space lattices belonging to all the seven basic crystal systems put together is only 14 (7 primitive, 3 body centred, 2 face centred and 2  end centred).  These 14 different types of lattices are known as Bravais lattices.

Exercise 1:

(i) Potassium metal crystallizes in the form of a body-centred cubic structure. The number of nearest neighbour atoms for each potassium atom in the solid is

(A) four               (B) six               (C) twelve               (D) eight

(ii) Which type of crystals contain one Bravais lattice?

(A) Hexagonal          (B) Triclinic          (C)  Rhombohedral          (D)  All of these

(iii) Which type of crystals contain the maximum number of Bravais lattices?

(A)  Cubic          (B)  Triclinic          (C)  Orthorhombic          (D)  Tetragonal

(iv) The number of molecules per unit cell for a compound that crystallizes in the form of an orthorhombic end-centred lattice with a molecule at each lattice site is

(A)  one          (B)  two          (C)  four          (D)  six

(v) A compound contains two types of atoms – X and Y. It crystallizes in a cubic lattice with atoms X at the corners of the unit cell and atoms Y at the body centres.  The simplest possible formula of this compound is

(A)  X₈Y          (B)  X₂Y          (C)  XY          (D)  XY₈

(vi) Because of anisotropy

(A)  mica cleaves into thin sheets and asbestos cleaves into long, rod-like pieces

(B)  mica cleaves into long, rod-like pieces and asbestos cleaves into thin sheets

(C)  mica as well as asbestos cleave into thin sheets

(D)  mica as well as asbestos cleave into long, rod-like pieces

Keys.

(i) D          (ii) D          (iii) C          (iv) B          (v) C          (vi) A

Crystallography and X-Ray diffraction (Determination of structure of solids):
Crystallography is the branch of science which deals with the geometry, properties and structure of crystals and crystalline substances.

In general the structure of solids is determined by diffraction methods.  X-ray diffraction has been used more extensively for this purpose.
From the diffraction pattern, it is possible to determine the arrangement of atoms or ions in a crystal.  The German physicist Max Von Laue in 1912 suggested that crystal should behave as a diffraction grating for X-rays and he obtained a diffraction pattern produced by passing X-rays through a crystal of copper sulphate.
W.L. Bragg and his father W.H. Bragg determined the cubic structure of NaCl using X-rays.  These days, the structures of extremely complex substances such as proteins and nucleic acids are determined using this technique.
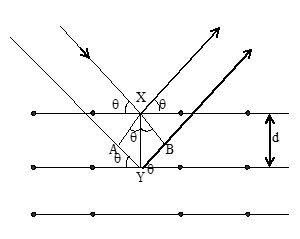
When X-rays are incident on the crystal plane, they undergo diffraction.  The atoms or ions are arranged in the regular places in a crystal.  When the waves are diffracted from the atoms or ions, they may have constructive interference or a destructive interference.
From the figure we can see that two waves (which are in phase) are approaching the crystal and after reflection, the ray emerging along XV is ahead of the ray emerging along YZ.
If the waves are in phase after reflection, the path difference must be equal an integral number of wavelength (nλ), for constructive interference.
Thus path difference = WY + YZ
                                       = XY sin$\mathrm{\theta }$ + XY sin$\mathrm{\theta }$
                                        = 2d sin$\mathrm{\theta }$
Where d is the distance between two planes.  Therefore for constructive interference of reflected X-rays.
nλ = 2d sinθ  Where n = 1, 2, 3 …. Any integral value.
This relation is known as Bragg equation.  For X-rays of a particular wavelength ‘λ’ and for a given value of d, maximum reinforcement will occur only at certain values of θ.  If we know value of θ and λ, we can calculate the distance ‘d’ between planes in the crystal.  It is to be noted that as ‘n values increase, ‘θ’ values increase. 
The X-ray diffraction techniques used in the study of crystals are of two types known as rotating crystal technique and powder technique.  Both the techniques make use of the X-rays spectrometer.

 

Rotating crystal technique:
In this technique X-rays generated in a tube are passed through a slit so as to obtain a narrow beam which is then allowed to strike a single crystal mounted on a turn table.  The crystal is rotated gradually by means of the turn table so as to increase the glancing angle at which the X-rays are incident at the exposed face of the crystal.  The intensities of the reflected rays are measured on a recording device such as photographic plate or an ionization chamber.  The angles for which reflections are maximum give the value of θ.  The lowest angle at which the maximum reflection occurs corresponds to n = 1.  The next higher angle at which max reflection occurs again corresponds to n = 2.
The values of θ for the 1^st order reflection from the three faces of NaCl crystal are found to be 5.9⁰, 8.4⁰ and 5.2⁰ respectively.
Applying the Bragg equation and knowing that n and λ are same in each case, the distance ‘d’ between successive planes in the three faces will be in the ratio
$\frac{1}{\sin 5.9}:\frac{1}{\sin 8.4}:\frac{1}{\sin 5.2}=100 : 0.70 : 1.14$
This ratio is very close to that exist between spacing along the three planes of a face centred cube.  Thus NaCl has FCC structure.

Powder technique:
This method is particularly used for crystals with simple structures.  The powder consists of many small crystals which are oriented in all possible directions.  As a result of this X rays are scattered from all sets of planes.  The scattered rays are detected by using a X-ray sensitive films. 
In this method the crystalline substance is ground to a fine powder.  It is packed into a thin walled capillary tube.  Sometimes the powder is coated on hair and it is used as a substitute for capillary tube.
A narrow beam of X ray is allowed to fall on the powder.  The diffracted X-rays strike a strip of photographic film arranged in the form of a circular arc.
In this method no rotation is necessary since the powder sample already contains microcrystals arranged in all possible orientation.  Hence a large number of them will have their lattice planes in correct positions for maximum X-ray reflection to occur.  As a result of this we get lighted areas in the form of arcs of lines at different distances from the incident beam.  These distances can be converted into scattering angles to be used in the Bragg equation for different planes of the crystals.

Illustration 3: X-rays of wavelength 154 pm strike a crystal and are observed to be reflected at an angle of 22.5^o.  If this is a first order reflection, calculate the distance between the parallel planes of atom that are responsible for this reflection.
Solution: Given λ=154  pm
θ = 22.5^o
n = 1
formula nλ = 2d sin θ
d = $\frac{n\lambda }{2 \sin \theta }=\frac{1\times 154}{2\times \sin \left(22.5^{°}\right)}$
= $\frac{154}{2\times 0.383}=201 \mathrm{pm}$

Close packing is two Dimensions:
In the formation of crystals the constituent particles try to pack as closely as possible so as to attain a state of maximum possible density and stability.  There are two possible arrangement of spheres in a plane (i) square close packing (ii)  Hexagonal close packing.
In square close packing each sphere is in contact with four other sphere.  In this arrangement only 52.4% of the space is occupied by spheres.  In hexagonal close packing, each sphere is in direct contact with six other spheres.  In this arrangement 60.4 percent of the space is occupied by spheres.  This arrangement is more efficient.  In this arrangement, the vacant spaces between three touching spheres is called triangular void.

Close packing in three Dimensions:
In three dimensional close packing, first layer is in hexagonal close packing because it is most efficient.  For close packing, spheres in the second layer rests in the depressions of the first layer. For the third layer there are two alternatives.

(i) Spheres are placed in the depressions of the second layer which are directly above the spheres of the first layer. In this scheme the third layer duplicates the first layer and fourth layer duplicates IInd layer and so on.  This leads to ABAB type arrangement which results in a hexagonal close packed structure.  This sort of arrangement of atoms is found in many metals like magnesium and zinc.

(ii) In the IInd alternative, the spheres of the third layer lie in the depressions of the second layer that do not lie directly over the atoms of the first layer. If we call this third layer ‘C’ then the resulting structure has an ABC, ABC pattern of layers to give a cubic close packed structure.  Copper, silver and gold crystallize in this structure.

• In a hexagonal close packed or in cubic close packed structure each sphere has three nearest neighbours in the plane below, six in its own plane and three in the one above, thus, there are 12 spheres in all at equal distances. This means, coordination number of each atom in this arrangement is 12.

• In either type of close packing 74.0 percent of the available space is occupied by spheres.

• It is impossible to pack identical spheres together with a co-ordination number greater than 12.

• In crystals with directional bond coordination number is lower as compared to crystals with non directional bonds.

Interstitial Voids:
In hcp as well as ccp only 74% of the available space is occupied by spheres.  The remaining space is vacant and constitutes interstitial voids or spaces.  There are two types of interstitial voids in three dimensional close packing.
(i)  Tetrahedral voids              (ii)  Octahedral voids
(i) Tetrahedral voids:  In a close packing arrangement each sphere in the second layer rests on the hollow triangular void in the three touching spheres in the first layer.  The vacant space between these four touching spheres is called tetrahedral void.  In a close packing, the number of tetrahedral voids is double the number of spheres.
(ii) Octahedral voids:  In a close packing, the interstitial void formed by combination of two triangular voids of the first and second layer is called octahedral void because this is enclosed between six spheres, centres of which occupy corners of a regular octahedron.

• In a close packing, the number of octahedral voids is equal to the number of spheres. Thus there is only one octahedral void associated with each sphere.

Exercise 2:

(i) NiO adopts a rock-salt structure. The coordination number of the Ni²⁺ ion is

(A) two               (B) four               (C) twelve               (D) six

(ii) Which of the following expressions is correct for a CsCl unit cell with lattice parameter a?

(A) ${\mathrm{r}}_{\mathrm{Cs}}^{+}+{\mathrm{r}}_{\mathrm{Cl}}=2\mathrm{a}$

(B) ${\mathrm{r}}_{{\mathrm{Cs}}^{+}}+{\mathrm{r}}_{\mathrm{cr}}=\frac{\mathrm{a}}{\sqrt{2}}$

(C) ${\mathrm{r}}_{{\mathrm{cs}}^{+}}+{\mathrm{r}}_{\mathrm{cr}}=\frac{\sqrt{3}}{\sqrt{2}}\mathrm{a}$

(D) ${\mathrm{r}}_{{\mathrm{Cs}}^{+}}+{\mathrm{r}}_{\mathrm{cl}}=\frac{3\mathrm{a}}{2}$

(iii) The molecules NaCl, MgO and NiO show 6 : 6 coordination, but BeO exhibits 4 : 4 coordination because

(A) BeO is covalent

(B) BeO is ionic

(C) BeO is amphoteric

(D) BeO is polymeric

(iv) When the radius ratios lie between 0.732 and 0.414, the arrangement of the crystal is

(A)  tetrahedral               (B) octahedral               (C)  linear               (D)  cubic

(v) Which of the following statements is incorrect for a two-dimensional hexagonal close-packed layer?

(A) Each sphere is surrounded by six sphere

(B) Each sphere is surrounded by six voids

(C) Each sphere has three voids

(D) Each void is surrounded by three spheres

Keys.

(i) D               (ii) C               (iii) A               (iv) B               (v) C

Radius ratio:  In crystals generally the anions (larger ions) form a close packed arrangement and the cations fit into the interstitial sites or voids.  The ratio of radius of cation to the radius of anion is known as radius ratio of the ionic solid.
OR radius ratio =$\frac{{\mathrm{r}}_{\mathrm{void}}}{{\mathrm{r}}_{\mathrm{sphere}}}=\frac{{\mathrm{r}}_{\mathrm{cation}}}{{\mathrm{r}}_{\mathrm{anion}}} \mathrm{or} \frac{{\mathrm{r}}^{+}}{{\mathrm{r}}^{–}}$
For tetrahedral void, $\frac{{\mathrm{r}}_{\mathrm{void}}}{{\mathrm{r}}_{\mathrm{sphere}}}=0.225$
For octahedral void, $\frac{{\mathrm{r}}_{\mathrm{void}}}{{\mathrm{r}}_{\mathrm{sphere}}}=0.414$

• If the ratio $\frac{{\mathrm{r}}^{+}}{{\mathrm{r}}^{–}}$ is 0.225, the cations would fit exactly into tetrahedral voids and would have coordination number four.

• If the radius ratio is 0.414, the cation would fit exactly into octahedral void and would have coordination number six.

• When the radius ratio is more than the minimum value, the close packed arrangement opens up slightly to accommodate the bigger cations.

• The minimum radius ratio that can give a specific co-ordination number and hence the shape of the compound is 0.15.

Radius ratios in crystals

Radius ratio ${\mathbf{r}}^{\mathbf{+}}\mathbf{/}{\mathbf{r}}^{\mathbf{–}}$	Structural Arrangement	Co-ordination Number	Structure type	Examples
0.732 and more	Cubic	8	Caesiumchloride	CsI, CsBr, Tl Br NH4Br
0.414-0.732	Octahedral	6	Sodium Chloride (rock salt)	NaBr,KBr, MgO, CaS, MnO
0.225-0.414	Tetrahedral	4	Sphalerite(ZnS)	BaS, HgS, CuCl,CuBr, CuI
0.155-0.225	Plane triangular	3	Boron Oxide	B2O3

Illustration 4: A solid  of atoms A and B has the following arrangement.
a) Atoms A have fcc arrangement
b) Atoms B occupy all the octahedral voids and half the tetrahedral voids.
What is the formula of compound  ?
Solution: In fcc structure no.of atoms are four so no.of A atoms = 4
and No.of octahedral holes  = 4
no.of tetrahedral holes = 2$\times$4=8
so no.of B atoms = octahedral holes + $\frac{1}{2}\times$ tetrahedral holes = 4+4 = 8
so formula of the compound = ${\mathrm{A}}_4 {\mathrm{B}}_8$
or = ${\mathrm{AB}}_2$

Illustration 5: Ferric oxide crystallizes in a hexagonal close packed array of oxide ions with two out of every three octahedral holes occupied by ferric ions.  Derive the formula of ferric oxide.
Solution: In hcp structure, no.of oxide ions = 6
So no.of octahedral holes  = 6
Two out of every three octahedral holes are occupied by ferric ion.
Means No.of ferric ions = 4
So formula of ferric oxide = $F{e}_4{O}_6$
or = $F{e}_2{O}_3$

Efficiency of packing in Face centred cubic structure:
In a face centred cubic unit cell, the spheres at corners are in contact with sphere at the face centre but are not touching each other.  Let ‘r’ be the radius of sphere and ‘a’ be the edge length of the cube.

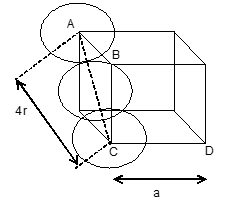
In $∆$ABC, $A{C}^2=B{C}^2+A{B}^2$
=$a^2+a^2=2a^2$
or     AC=$a\sqrt{2}$
and AC= 4r=$a\sqrt{2}$   0r $r=\frac{a\sqrt{2}}{4}=\frac{a}{2\sqrt{2}}$
In FCC unit cell, there are 4 spheres and total volume of 4 spheres is equal to $4\times \frac{4}{3}\pi r^3$
Volume of cube = $a^3 or {\left(2\sqrt{2}r\right)}^3$
Percentage of space occupied by spheres or
Percentage efficiency =$\frac{\mathrm{Volume} \mathrm{occupied} \mathrm{by} \mathrm{four} \mathrm{spheres} \mathrm{in} \mathrm{the} \mathrm{unit} \mathrm{cell} \times 100}{\mathrm{Total} \mathrm{volume} \mathrm{of} \mathrm{the} \mathrm{unit} \mathrm{cell}}$
= $\frac{4\times {\displaystyle \frac{4}{3}}{\mathrm{\pi r}}^3\times 100}{{\left(2\sqrt{2}r\right)}^3}=\frac{\left(16/3\right){\mathrm{\pi r}}^3\times 100}{16\sqrt{2}{r}^3}=74\%$

• Thus in both hcp and ccp arrangements 74% of the available space is occupied by spheres.

Efficiency of packing in body centred cubic unit cell:  In a BCC unit cell there are two spheres per unit cell.  Let ‘a’ be the side of the unit cell and ‘r’ be the radius of sphere.

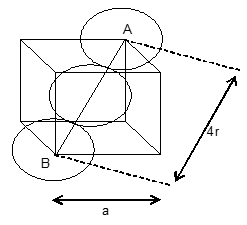
Volume of sphere = $\frac{4}{3}{\mathrm{\pi r}}^3$
Volume occupied by two spheres = $2\times \frac{4}{3}{\mathrm{\pi r}}^3$
In $∆$ABC,
Face diagonal AC= $\sqrt{A{B}^2+B{C}^2}=\sqrt{2a^2}$
In right angle triangle ACD
Body diagonal AD = $\sqrt{{\mathrm{AC}}^2+{\mathrm{CD}}^2}$
= $\sqrt{2a^2+a^2}=a\sqrt{3}$
In BCC unit cell, the spheres at the corners are not touching each other but are in contact with the sphere at the centre.

$\therefore$Body diagonal AD is equal to the four times of the radius of the sphere.
$\therefore AD=a\sqrt{3}=4r or a=\frac{4}{\sqrt{3}}r$
Volume of the cube =  $a^3={\left(\frac{4}{\sqrt{3}}r\right)}^3=\frac{64}{3\sqrt{3}}{r}^3$
Thus, percentage of space occupied by spheres or percentage efficiency
$$\begin{gathered} =\frac{Volume of spheres}{Volume of cube}\times 100 \\ =\frac{{\displaystyle \frac{8}{3}}{\mathrm{\pi r}}^3}{{\displaystyle \frac{64}{3\sqrt{3}}}{r}^3}\times 100 =68\% \end{gathered}$$
Thus, in this arrangement packing is not quite so close, only 68% of the space is occupied by spheres.

• In a simple cubic unit cell there is only one atom per unit cell.
$\therefore$ volume of sphere = $\frac{4}{3}{\mathrm{\pi r}}^3$

The spheres at the corners are touching each other, the edge length ‘a’ is equal to 2 r.
$\therefore$volume of the cube = a³ = (2r)³ = 8r³
Percentage of space occupied by spheres $=\frac{Volume of spheres}{Volume of cube}\times 100 =\frac{{\displaystyle \frac{4}{3}{\mathrm{\pi r}}^3}}{{\displaystyle 8r^3}}\times 100 =52.4\%$

• In a face centred cubic unit cell there is 1 octahedral void at the centre of the cube and 12 octahedral voids on the centres of the 12 edges of the cube. Each octahedral void on the edge centre is shared by four unit cells.

Thus number of octahedral voids per unit cell in a cubic close packing.
= 1 (at the centre of the cube) + 12 (at the edge centres) $\times \frac{1}{4}$
= 1 + 3 = 4

• In cubic close packing, there are eight tetrahedral voids per unit cell. These voids are located on the body diagonals.  There are two tetrahedral voids on each body diagonal, at one forth distance from each end.

Structures of simple ionic compounds:
The lattice points in ionic crystals are occupied by positively and negatively charged ions.  It is impossible for both cations and anions to have closed packed structures.  Generally the bigger ion constitute the space lattice with hcp or ccp type of arrangement whereas the smaller ion occupy the interstitial voids.

• For a binary compound if the negative ions constitute the space lattice and all octahedral voids are occupied then formula of ionic solid is AB.

• If all tetrahedral voids are occupied the formula of ionic solid is A₂B. (A is present in void)

• If half of the tetrahedral voids are occupied then the formula is AB.

Structure of sodium chloride (Rock salt structure):

(i) In NaCl, chloride ions are arranged in cubic close packing and sodium ions occupy all the octahedral voids.

(ii) There are six octahedral voids around each chloride ion, $\therefore$ each chloride ion is surrounded by six sodium ions. Similarly each Na⁺ ions is surrounded by 6 chloride ions.  Therefore co-ordination No. of Cl^– ion is 6 and that of Na⁺ ions is 6.  This is called 6 : 6 coordination.

(iii) For cations to fit into octahedral voids, the radius ratio $\frac{r_{N{a}^{+}}}{r_{C{l}^{–}}}$  should be equal to 0.414.  Actually, the ratio $\left(\frac{r_{N{a}^{+}}}{r_{C{l}^{–}}}\right)$  exceeds this value and to accommodate somewhat large sized Na⁺ ions, Cl^– ions move apart slightly.

(iv) Number of Na⁺ ions per unit cell
= 12(at edge centres)$\times \frac{1}{4}+1$(at body centre)
= 4
Number of Cl^– ions per unit cell
= 8(at corners)$\times \frac{1}{8}+6$(at face centres)$\times \frac{1}{2}$
= 4
Thus number of NaCl units per unit cell is 4.

(v) Most of the halides of alkali metals and oxides of alkaline earth metals have this type of structure.  Some examples are LiCl, KBr, AgCl, MgO, CaO, NaI, KCl, RbI and RbF.

• FeO also has rock-salt structure in which oxide ions are arranged in ccp and Fe²⁺ ions occupy octahedral voids. However in this oxide, some of the Fe²⁺ ions are replaced by two third as many Fe³⁺ ions in the octahedral void.  Thus, this compound in non-stoichiometric and has the composition Fe_0.95O (wustite)

Caesium chloride structure:

(i) In this structure, the Cl^– ions are at the corners of a cube whereas Cs⁺ ion is at the centre of the cube or vice-versa.

(ii) Each Cs⁺ ion is surrounded by eight Cl^– ions and each Cl^– ion is surrounded by eight Cs⁺ Thus, this structure has 8 : 8 co-ordination.

(iii) For exact fitting of cation in cubic voids the ratio $\frac{r_{+}}{r_{–}}$ should be equal to 0.732, actually the ratio is slightly larger i.e.,  $\frac{{r_{Cs}}^{+}}{r_{C{l}^{–}}}$=0.93  $\therefore$ packing of Cl^– ions slightly opens up to accommodate Cs⁺ ions.

(iv) No. of Cs⁺ ions per unit cell = 1 (at the body centre) $\times$ 1 = 1
No. of Cl^– ions = 8 (at corners) $\times \frac{1}{8}=1$
Thus no. of CsCl units per unit cell is 1.

(v) This type of structure is adopted by CsBr, CsI, TlCl, TlBr etc.

• Since co-ordination number of ions in CsCl (8 : 8) is higher than those in NaCl (6 : 6) it represents that CsCl lattice is slightly more stable than NaCl lattice.

• Temperature and pressure also affect the structure of an ionic solid. On application of high pressure NaCl type structure transforms to CsCl type structure ( 8 : 8 coordination).  Thus high pressure increases the co-ordination number.

• On the other hand, CsCl on heating at 760K transforms to the NaCl structure. Thus at higher temperature, co-ordination number decreases.

Structure of Zinc sulphide (ZnS):
It has two types of structures
1) Zinc blende structure

2) Wurtzite structure

1) Zinc Blende structure or Sphalerite structure (ZnS):
(i) In zinc Blende structure, sulphide ions are arranged in ccp arrangement i.e., at the corners of the cube and at the centre of each face.
(ii) Zinc ions occupy half of the tetrahedral voids.
(iii) Each sulphide ion is tetrahedrally surrounded by four zinc ions and each zinc ion is surrounded by four sulphide ions. Thus zinc sulphide has 4 : 4 co-ordination.
(iv) For exact fitting of Zn²⁺ ions in the tetrahedral voids, the radius ratio $\frac{{r_{zn}}^{2+}}{{r_s}^{2–}}$ should be 0.225.
(v) No. of S^2– ions per unit cell
= 8(at corners)$\times \frac{1}{8}+6$(at face centres)$\times \frac{1}{2}$
= 4
No. of Zn²⁺ per unit cell = 4 (within the body) $\times$1 = 4
Thus, the number of ZnS units per unit cell is 4.

(vi) The electronegativities of Zn and S are 1.6 and 2.5 respectively. On Pauling scale EN difference is 0.9 only.  Therefore the bond between Zn and S is more covalent than ionic even though Zn²⁺ and S^2– ions are supposed to give an ionic structure.

(vii) The structure of sphalerite is similar to that of diamond. In diamond all the positions of Zn²⁺ and S^2– are made of C atoms only.

• Some more examples having zinc blende structure are CuCl, CuBr, CuI, AgI, HgS.

2) Wurtzite structure:
i) The sulphide ions are arranged in a hexagonal close packed arrangement and zinc ions occupy half of the tetrahedral voids.
ii) The basic difference between zinc blends and Wurtzite structure is that, in the former case the sulphide ions are arranged in ccp and in the latter case sulphide ions are arranged in hcp type of packing.

Fluorite structure (CaF₂):

(i) In CaF₂, Ca²⁺ ions are arranged in ccp arrangement, so that there are Ca²⁺ ions at all the corners and at the centre of each face of the cube. The fluoride ions occupy all the tetrahedral voids.

(ii) Since there are two tetrahedral voids for each Ca²⁺ ion and F^– occupy all the tetrahedral voids, there will be two F^– ions for each Ca²⁺ Thus the stoichiometry of the compound is 1 : 2.

(iii) Each F^– ion is surrounded by 4 Ca²⁺ ions and each Ca²⁺ ion is surrounded by eight F^– Thus CaF₂ has 8 : 4 coordination.

(iv) No. of calcium ions = 8 (at corners) $\times \frac{1}{8}+6$(at face centre)$\times \frac{1}{2}$= 4
No. of fluoride ions = 8 (within the body)$\times$ 1 = 8
Thus number of CaF₂ units per unit cell is 4.

(v) Other example of compounds having fluorite structure are SrF₂, BaCl₂, BaF₂, PbF₂ and CdF₂. 

Antifluorite structure:

i) Anions are arranged in cubic close packing while the cations occupy all the tetrahedral voids.

ii) Na₂O has an antifluorite structure. In this case the O^2– ions constitute a ccp type of lattice and Na⁺ ions occupy all the tetrahedral voids.

iii) In this case, each O^2– ion is in contact with eight sodium ions whereas each Na⁺ ion is in contact with four oxide ions. Thus Na₂O has 4 : 8 coordination.  Other example of compounds having antifluorite structure are Li₂O, K₂O, Rb₂O and Rb₂

Normal spinel and Inverse spinel structure:
In normal spinel structure the negative ions constitute the ccp or fcc lattice whereas the positive ions occupy voids.  The low valency dipositive ions are present in tetrahedral voids and high valency tripositive ions are present in octahedral voids.
e.g., In spinel MgAl₂O₄ oxide ions are arranged in ccp with Mg²⁺ ions occupy tetrahedral voids and Al³⁺ ions in a set of octahedral voids.  Many Ferrites such as Zn Fe₂O₄ also possess spinel structure.  These are very important magnetic materials and are used in telephones and memory loops in computers.
In Inverse spinel structure oxide ions are arranged in FCC, dipositive ions are present in octahedral voids and tripositive ions are equally distributed between tetrahedral and octahedral voids.  The most common example is load stone or magnetite (Fe₃O₃).  In Fe₃O₄, Fe³⁺ and Fe²⁺ ions are present in the ratio 2 : 1.  It has the composition FeO.Fe₂O₃.  In Fe₃O₄ oxide ions are arranged in ccp.  Fe²⁺ ions occupy octahedral voids while Fe³⁺ ions are equally distributed between octahedral and tetrahedral voids.
e.g., MgFe₂O₄, in this compound Mg²⁺ ions are present in place of Fe²⁺ ions in Fe₃O₄.

Exercise 3:

(i) Which of the following statements is incorrect for sphalerite, a form of ZnS?

(A) It has the same structure as diamond, except that the alternate atoms are zinc and sulphur.

(B) Because the sulphide ion is larger than the zinc ion, only six rather than four or eight sulphide ions can be packed around a zinc ion.

(C) Because the sulphide ion is larger than the zinc ion, only four rather than six or eight sulphide ions can be packed around a zinc ion.

(D) ZnS is polar covalent molecule

(ii) Which of the following compounds represent an inverse 2 : 3 spinel structure?

(A) Fe^III (Fe^IIFe^III)O₄               (B) PbO₂               (C) Al₂O₃               (D) Mn₃O₄

(iii) All the positions in an fcc lattice are occupied by A atoms, and the bcc octahedral hole in it by a B atom of appropriate size. The formula of the compound is

(A) A₂B               (B) AB₄               (C) A₄B               (D) A₄B₃

(iv) Imagine the construction of an MX₂ structure from the bcc CsCl structure by the removal of the half the Cs⁺ ions so that there is tetrahedral coordination around each Cl^–. What is the structure of MX₂?

(A) An antifluorite (Na₂O) structure

(B) A fluorite (CaF₂) structure

(C) A rutil (TiO₂) structure

(D) A pyrolusite (MnO₂) structure

Keys.

(i) B               (ii) A               (iii) C               (iv) B

Density of cubic crystal ($\mathit{\rho }$):

Let ‘a’ be the edge length of the cube in cm and ‘z’ be the number of atoms in the unit cell.

$\therefore$volume of the unit cell = a³ cm³

Mass of the unit cell = Number of atoms in the unit cell $\times$mass of each atom.
= z × m
Mass of each atom = $\frac{\mathrm{Gram} \mathrm{atomic} \mathrm{mass}}{\mathrm{Avogadro} \mathrm{number}}$
Density of unit cell = $\frac{\mathrm{Mass} \mathrm{of} \mathrm{the} \mathrm{unit} \mathrm{cell}}{\mathrm{Volume} \mathrm{of} \mathrm{the} \mathrm{unit} \mathrm{cell}} \mathrm{\rho }=\frac{\mathrm{z}\times \mathrm{M}}{{\mathrm{a}}^3\times \mathrm{No}}$             
Density of the unit cell is same as the density of the substance.

Illustration 6: Calculate the percentage of space occupied by spheres in a simple cubic unit cell.
Solution: As in fig.

total no.of atom = 1
2r = a
Percentage efficiency.
$$\begin{gathered} \frac{Vol. occupied by 1 sphere\times 100}{Total volume of unit cell}\% \\ =\frac{1\times {\displaystyle \frac{4}{3}}{\mathrm{\pi r}}^3\times 100}{a^3}\% \\ =\frac{1\times {\displaystyle \frac{4}{3}}{\mathrm{\pi r}}^3\times 100}{8\times r^3}\% \\ =\frac{100\times 4\times 3.15}{8\times 3}\% =52.4\% \end{gathered}$$

Illustration 7: An element (density 6.8 g/${\mathrm{cm}}^3$ occurs in BCC structure with edge length 290 pm.  Calculate the number of atoms present in 200g of the element.
Solution: In bcc, no.of atoms = 2
Let M be the molecular mass.
Mass per unit cell = no. of atoms in a unit cell × mol. mass
= 2 × M
Vol. of the unit cell = $$\begin{gathered} {\mathrm{a}}^3={\left(290\times {10}^{–10}\right)}^3{\mathrm{cm}}^3 \\ =24.4\times {10}^{–24}{\mathrm{cm}}^3 \end{gathered}$$
Density =$\frac{\mathrm{Mass} \mathrm{of} \mathrm{unit} \mathrm{cell}}{\mathrm{Volume} \mathrm{of} \mathrm{unit} \mathrm{cell}}$
$$\begin{gathered} 6.8=\frac{2\times M}{24.4\times {10}^{–24}} \\ M=\frac{6.8\times 24.4\times {10}^{–24}}{2}=50 \end{gathered}$$

Thus No.of atoms in 200g =$\frac{200\times 6.022\times {10}^{23}}{50}$ = 24.09 x 10²³ atoms.

Classification of crystalline solids:
Crystalline solids can be classified into different categories depending upon the type of constituent particles and the nature of attractive forces operating between them.

1) Atomic solids:
In these solids constituent particles are atoms.  The attractive forces operating between atoms are van der Wall’s forces.  Such solids are soft, possess very low melting point and poor conductors of heat and electricity. e.g., Crystal of noble gases.

2) Molecular solids: 
In these solids the constituent particles are molecules.  These molecules may be polar or non polar.  In case of polar molecules (such as H₂O, HF, SO₂) the attractive forces between these molecules are dipole-dipole forces. E.g., Solid HCl, Solid SO₂.
In some solids with polar molecules, the interparticle forces are hydrogen bond. e.g., ice, solid HF, solid NH₃.
In case of non-polar molecules, the attractive forces between molecules are Van der Waal’s forces e.g., solid CO₂, iodine.
Molecular solids are generally soft.  They have low to moderately high melting points.  Solids with non-polar molecules have relatively low melting points as compared to solids with polar molecules.
These solids are generally bad conductors of heat and electricity.  They have low density.

3) Covalent solids:  
In these solids, the lattice points are occupied by neutral atoms either of same element or of different element.  For example, in diamond only carbon atoms constitute the covalent network while in carborundum covalent bond network is constituted by silicon and carbon atoms.  The interparticle forces operating in these solids are covalent bonds.  These solids are also called network solids because the covalent bonds extend in three dimensions forming a giant interlocking structure.  Covalent solids are very hard.  They have very high melting point and high heat of fusion.  Other example of covalent solids are aluminium nitride, quartz, and silica.

4) Metallic solids: 
In these solids, the constituent particles are metal atoms.  Interparticle forces are metallic bonds.  The metallic crystals have positive metal ions as lattice points surrounded by a sea of mobile electrons.  Positively charged part of metal atom without valence electrons is known as kernel.  The attractive force between the kernels and mobile valence electrons is termed as metallic bond.
Metallic crystals are good conductors of heat and electricity.  They are malleable and ductile.  They posses bright lustre.  Except alkali metals they have high melting and boiling point.

5) Ionic solids: 
In ionic solids, the constituent particles are ions of opposite charges.  The forces operating in ionic crystals are electrostatics.  The lattice points in such crystals are occupied by positively and negatively charged ions.  Each ion is surrounded by largest possible number of oppositely charged ions.  This number of oppositely charged ions surrounding each ion is termed its co-ordination numbers.  Co-ordination numbers of positive or negative ions may be same or different.
Some example of ionic solids are NaCl, CsCl, ZnS, CaF₂ etc.  Ionic solids are hard, brittle and have low volatility.  They have high melting points.  Ionic solids are poor conductors of electricity in solid state, however they are good conductors of electricity in molten state or in dissolved state.  Ionic solids are generally soluble in polar solvents like water.
In ionic crystals, the co-ordination numbers as well as geometrical shapes of the crystals depend mainly on the relative sizes of ions.

Imperfection in solids: 
An ideal crystal is the one which has the same unit cell and contains the same lattice points throughout the crystal.  At absolute zero, most of the ionic crystals are ideal but with rise in temperature, the crystals start deviating from the perfectly ordered arrangement.  Any deviation from the perfectly ordered arrangement constitutes a defect or imperfection.  These defects are sometimes called thermodynamic defects because the number of these defects depend on the temperature.  Crystals may also posses additional defects due to presence of impurities.  The defect may appear at a point (point defects), or extend along lines (line defects) or planes (plane defects).

• Line defects are also called dislocations. 

Point defects:  
If the deviation occurs because of missing atoms, displaced atoms or extra atoms, the imperfection is named as a point defect.  Such defects may arise due to imperfect packing during the original crystallization or they may arise from thermal vibration of atoms at elevated temperatures.  The most common point defects are the Schottky defect and the Frenkel defect.  Comparatively less common point defects are the metal excess defect and metal deficiency defects.   

Stoichiometric point defects:  Compounds in which the number of positive and negative ions are exactly in the ratios indicated by their chemical formulae are called stoichiometric compounds.  The defects that do not disturb the stoichiometry are called stoichiometric defects.  These are of following types:

i) Schottky Defects: These defects arise if some of the lattice points in a crystal are unoccupied.  The points which are unoccupied are called lattice vacancies.  In these defects crystal as a whole remains neutral because the number of missing positive and negative ions is the same.

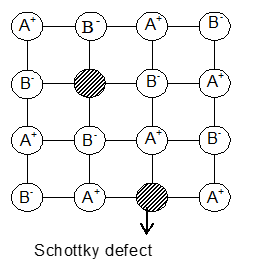
• Schottky defects appear generally in ionic crystals in which the positive and negative ions do not differ much in size. For example NaCl, KCl, CsCl and KBr.

• NaCl has one defect in 10¹⁵ lattice sites at room temperature. The number of defects increases with increase in temperature.  The number of defects increases to one in 10⁶ sites at 775 K.

• Because of Schottky defects, the crystal is in a position to conduct electricity to a small extent by an ionic mechanism. As an electric field is applied, a nearby ion moves from its lattice site to occupy a vacancy.  This results in creating a new vacancy and another nearby ion moves into it and so on.

• The existence of vacancies also enables easy movement of atoms or ions in the crystal, this accounts for the phenomenon of diffusion in solids.

• The presence of Schottky defects in solids also lowers their density.

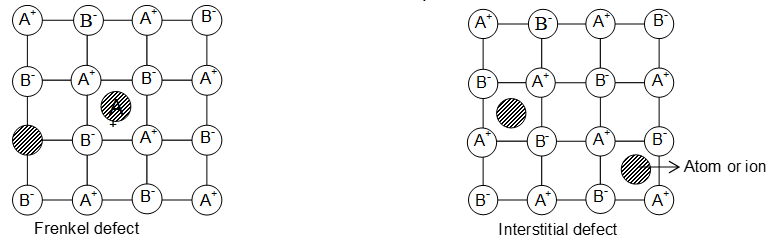
ii) Frenkel defect: This type of defect is created when an ion leaves its correct lattice site and occupies an interstitial site. These defects are common in ionic compounds which have low co-ordination number and in which there is large difference in size between positive and negative ions.  For example ZnS, AgCl, AgBr and AgI.
The crystal remains neutral since the number of positive ions is the same as the number of negative ions.

• Frenkel defects appear in crystals in which the negative ions are much larger than the positive ions.

• Like Schottly defects, the Frenkel defects are also responsible for the conduction of electricity in crystals and also for the phenomenon of diffusion in solids.

• The presence of ions in interstitial sites in the Frenkel defects increases the dielectric constant of the crystals.

• Frenkel defects also increase with increase in temperature.

Non stoichiometric defects:
The compounds in which, the number of positive and negative ions are different from those expected from their ideal chemical formulae are called non-stoichiometric or Berthollide compounds.
For example FeO also exists as non-stoichiometric compound having composition Fe_0.93O to Fe_0.95O.  In other words, there is excess of either positive charge or negative charge in the crystal.  However, the crystal as a whole is neutral. If positive charge is in excess, it is balanced by the presence of extra electrons.  If negative charge is in excess, it is balanced by the presence of extra positive ions.
This results in defects in the crystal structure.  The defects which disturb the stoichiometry of the compound are called non-stoichiometric defects.
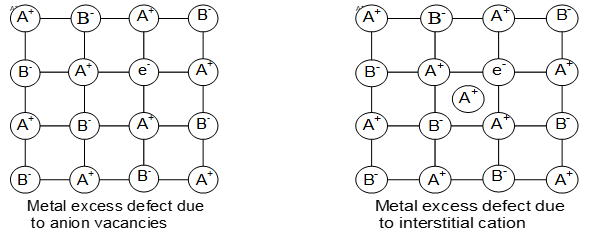
i) Metal excess defects: These defects may arise in two ways.
a) A negative ion may be missing from its lattice site leaving a vacancy or hole which is occupied by an extra electron to maintain the electrical balance. Evidently there is an excess of positive (metal) ions, although the crystal as a whole is neutral.
These type of defects are found in crystals which are likely to posses Schottky defects.  Anion vacancies in alkali halides are produced by heating the alkali halide crystals in an atmosphere of alkali metal vapours.
It has been observed that if a crystal of NaCl is heated in sodium vapour, it acquires a yellow colour.  This yellow colour is due to the formation of a non-stoichiometric compound of NaCl in which there is a slight excess of sodium ions.  In this case sodium metal atoms deposit on the surface of the NaCl crystal, Cl^– ions move to the surface and combine with Na⁺ ions.  The electron released during conversion of metal atoms into ions diffuse into the crystal and occupy the sites vacated by anions.  These sites occupied by extra electrons are known as colour centres.  These are also called F-centres.  This name comes from the German word Farbe meaning colour.

• Another example of metal excess defects is the formation of magenta coloured non-stoichiometric compound of potassium chloride by exposing the crystals of KCl to K vapour. The coloured compound contains an excess of K⁺ ions, the vacant Cl^– sites being filled by electrons obtained by the ionization of excess K-metal doped into the crystal.

• Greater the number of F-centres greater is the intensity of colour.

• Solids containing F-centres are paramagnetic because the electrons occupying the holes are unpaired.

b) Another way in which metal excess defect may occur is, if an extra positive ion occupies an interstitial position in the lattice and to maintain electrical neutrality, an electron also finds a place in the interstitial space.
This type of defects are exhibited by the crystals which are likely to exhibit Frenkel defect.  For example when ZnO is heated, it loses oxygen reversibly.  The excess metal is accommodated in interstitial sites with electron trapped in the neighborhood.    

• The yellow colour and the electrical conductivity of the non stoichiometric ZnO is due to these trapped electrons.

ii) Metal deficiency Defects: In certain cases one of the positive ions is missing from its lattice site and the extra negative charge is balanced by some nearby metal ions having higher positive charge.  Evidently, there is a deficiency of metal ions although the crystal as a whole is neutral.

• This type of defect is generally shown by compounds of transition metals which can exhibit variable valency.

• Crystals of FeO, FeS and NiO show this type of defects.

• Metal excess compounds as well as metal deficient compounds act as semi conductors. Metal excess compounds conduct electricity through normal electron conduction mechanism and are therefore n-type semiconductors.

• Metal deficient compounds conduct electricity through positive hole conduction mechanism and are therefore p-type semiconductors.

Impurity Defects: 
Certain defects in crystals arise from the presence of chemical impurities.  Foreign atoms can occupy interstitial or substitutional sites in a crystal.
Defects in the ionic solids may be introduced by adding impurity ions. If the impurity ions have different valence state than that of the host ions, vacancies are created.
For example addition of CdCl₂ to AgCl (or of SrCl₂ to NaCl) yields solid solutions where the divalent cation Cd²⁺ (or Sr²⁺) occupies the Ag⁺ or Na⁺ sites and produces cation vacancies equal in number to that of the divalent ions.

Exercise 4 :

(i) Crystals may be coloured by

(A)  the introduction of chemical impurities

(B)  X-ray, g-ray and electron bombardment

(C)  introducing an excess of the metal

(D)  all these methods

(ii) In AgCl, the silver ion is displaced from its lattice position to an interstitial position. Such a defect is called a

(A)  Schottky defect

(B)  Frenkel defect

(C)  Wadsley defect

(D)  colour centre

(iii) Which of the following mechanisms is incorrect for stoichiometrically pure compound AB?

(A) There is a displacement of A atoms to interstitial sites, leaving an equal number of A-type vacancies in the structure.

(B) There is a displacement of B atoms to interstitial sites, accompanied by the formation of an equal number of B-type vacancies.

(C) An equal number of A and B-type vacancies are created by the migration of atoms to the crystal surface.

(D)  An equal number of interstitial A and B atoms, and A and B-type vacancies, are created.

(iv) A solid solution of CdBr₂ in AgBr contains

(A)  Schottky defects

(B)  Frenkel defects

(C)  Frenkel as well as Schottky defects

(D)  Colour centres

Keys.

(i) D               (ii) B               (iii) D               (iv) C

Properties of solids:

1) Electrical properties:  On the basis of electrical conductivity the solid can be classified into three types: (i)  Conductors (ii)  Insulators (iii)  Semiconductors.
i) Conductors: Metals are good conductors and have conductivities in the order 10⁷ (W m)^–1.  In metals conductivity depends on the number of valence electrons available per atom.  A metal lattice has an extremely large number of atoms.  The atomic orbitals on these atoms with same symmetry and same energy overlap resulting in the formation of energy bands.
Depending upon different types of atomic orbitals which overlap, different energy bands are obtained.  The arrangement of electrons in different energy bands determines the properties of a metal.  The highest occupied energy band is called the valence band while the lowest unoccupied energy band is called the conduction band.  The energy gap between the top of the valence band and bottom of the conduction band is called the energy gap (E_g).

• In the case of metals, the valence band may be half filled or there may be an overlapping between the valence and the conduction bands. This makes it possible for the electrons to go into the vacant bands and is responsible for high electrical conductivity of metals.

• At laboratory temperatures conductivity of metals is nearly independent of impurities and lattice defects.

The concentration of electrons is determined by the nature of the metal i.e., the valence electrons, and the mobility of electrons is determined by lattice vibrations.  At low temperature, the lattice vibrations are negligible and as a result the conductivity should be infinitely large.  However this is not true because of the lattice imperfections and the impurities.  Then the purity of the metal can be measured by resistance ratio r_300K/r_4.2K. 
ii) Insulators: Such substances do not conduct electric current, their conductivity is very low ranging between 10^-10 and 10^–20 (Wm)^–1.  In case of insulators, the energy gap is very large and therefore the vacant conduction band is not available to the electrons of the completely filled valence band.  On heating they decompose but do not give free conducting electrons.
iii) Semiconductors:  Several solids have electrical properties intermediate between those of metals and insulators.  These are called semiconductors.  The energy gap in these substances is very small and increase in temperature gives thermal energy for some of the electrons in the valence band to move into the conduction band.  Therefore, electrical conductivity of semiconductors increases with increasing temperature.

• Diamond with a large energy gap is an insulator. Silicon and germanium have small energy gap between valence and conduction bands, and are called semiconductors.

• Electrical conductivity of semiconductors is substantially greater than that of insulators but far less than that of conductors. Their conductivities generally ranges from 10^–6 to 10⁴ (Ωm)^–1. 

Semiconductors are of two types:
a) Intrinsic semiconductors:
Pure substances that exhibit conducting behaviour like that of silicon and germanium are called intrinsic semiconductors.  Intrinsic semiconductor is a semiconductor in its own right i.e., no impurity has been added to it. In an intrinsic semiconductor, the valence band is full and the conduction band is empty at very low temperatures.  The energy gap between the two bands is so small that electrons can jump across it by the addition of a small amount of thermal energy alone i.e., only heating the material results in electrical conduction. 
The electrical conductivity increases with increase in temperature since more and more electrons are liberated with increase in temperature.  The smaller the value of Eg, the better is the semiconductor. Thus germanium is a better conductor than silicon. 
As an electron jumps from the valence band to the conductance band, it leaves behind a hole in the valence band.  The hole is positively charged and since an electron can jump into the hole from another part of valence band, it is as if the hole was moving.

• Conduction can occur either by the electrons moving within the conduction band or by positive holes moving within the valence band.

b) Extrinsic semiconductors:
For practical purposes, the conductivity of pure silicon and germanium is too low at room temperature.  In order to increase the number of electrons or number of holes, the pure substances are carefully doped with impurities.
Doping means introduction of small amount of impurities like phosphorus, arsenic or boron into the pure crystal of silicon or germanium.
Conductivity of silicon increases dramatically by doping it with certain other elements.
Extrinsic semiconductors are of two types.

1) n-type semiconductor:
In pure crystalline silicon at room temperature four valence electrons of each atom are used for forming four normal covalent bonds with four adjacent Si atoms.  When a silicon crystal is doped with a group 15 element such as P, As , Sb, Bi, the structure of the crystal lattice does not change, but some of the Si atoms are replaced by group 15 element.
15^th group element uses four of its valence electrons to form covalent bonds with silicon just as if it were a silicon atom.  Because the fifth electron is not needed for bonding, it becomes delocalized and is free to contribute to electrical conduction.
Silicon, doped with group 15^th element is known as n-type semiconductor.  ‘n’ is standing for ‘negative’ (since negatively charged electrons are responsible for conducting).

2) p-type semiconductor:
Doping a silicon crystal with a group 13 element such as B, Al, Ga or In results in the substitution of some silicon atoms in its structure by the dopant.  Group 13 elements have only three valence electrons.  The fourth valence electron is missing.  The place where the fourth valence electron is missing is called a hole.  Such holes can move through the crystal like a positive charge giving rise to electrical conductivity.  Direction of motion of the holes in an electric field is opposite to that of the electrons.
Group – 13 doped crystals of silicon are called p-type semiconductors because holes (positive in charge) appear to be responsible for conductivity.

• Various combinations of n-type and p-type semiconductors are used to make electronic components for example a diode is a combination of p and n-type semiconductors and is used as a rectifier.

• Transistors are pnp or npn semiconductors and are used to detect or amplify radio or audio signals.

• A solar cell is an efficient photo diode used for converting radiant energy into electrical energy.

• A large variety of solid state materials have been prepared by combination of elements of group 13 and 15 or 12 and 16 to simulate average valence of 4 as in Ge and Si.

• Examples of group 13-15 compounds are InSb AlP and GaAs. Gallium arsenide (GaAs) semiconductors have very fast responses and have revolutionized the design of semiconductor devices.

• Examples of group 12-16 compounds are ZnS, CdS, CdSe and HgTe. In these compounds, the bonds are not perfectly covalent and the ionic character depends on the electronegativities of the two elements.

• Transition metal oxides show marked differences in electrical properties. TiO, CrO₂ and ReO₃ behave like metals.  Rhenium oxide ReO₃ is like metallic copper in its conductivity and appearance.

• Certain other oxides like VO, VO₂, VO₃, TiO₃ show metallic or insulting properties depending on temperature.

Magnetic properties:
The magnetic properties of materials are a consequence of magnetic moments associated with individual electrons.  The overall magnetic moment of an atom originate from two sources.  The first one is related to the orbital motion of electrons around nucleus and is known as orbital magnetic moment.  The second one is related to the spin of electrons around their axis and is known as spin magnetic moment.
A moving electron may be considered to be a small current loop, generating a small magnetic field and having a magnetic moment along its axis of rotation.  The other type of magnetic moment originates from electron spin which is directed along the spin axis.
Thus each electron in an atom may be thought of as being a small magnet having permanent orbital and spin magnetic moments.
Due to the magnetic moment of the electrons, different substances behave differently towards the external applied magnetic field.  Bohr magneton (μ_B) is the fundamental unit of magnetic moment and is equal to 9.27 × 10^–24 Am².  For each electron in an atom, the spin magnetic moment is ±μ_B, depending on the two possibilities of the spins.  The contribution of the orbital magnetic moment is equal to m_l μ_B where m_l is the magnetic quantum number of the electron.

• Solids composed of atoms having completely filled electron shells or subshell are not capable of being permanently magnetized. This category includes the noble gases as well as some ionic materials.  Solids can be classified into different types depending upon their behaviour towards magnetic field.
i) Diamagnetic substances: These substances are weakly repelled by external magnetic field.  For example TiO₂, NaCl and Benzene.  Diamagnetic substances have all their electrons paired.
ii) Paramagnetic substances: In paramagnetic substances, there are permanent magnetic dipoles due to the presence of atoms, ions or molecules with unpaired electrons (e.g., O₂, Cu²⁺, Fe³⁺) and these substances are attracted by a magnetic field.  These substances lose their magnetism in the absence of a magnetic field.
For example TiO, VO₂ and CuO.
iii) Ferromagnetic substances:  The substances which are strongly attracted by magnetic field are called ferromagnetic substances.  These substances show permanent magnetism even when the external magnetic field is removed.  Once such a material is magnetised, it remains magnetised permanently.  Iron, cobalt and nickel are three elements which show ferromagnetism at room temperature.  Ferromagnetism arises due to spontaneous alignment of magnetic moments of ions or atoms in the same direction.
CrO₂ is a ferromagnetic substance, it is used to make magnetic tapes for use in audio recording.
iv) Antiferromagnetic substances: Alignment of magnetic moments in opposite direction in a compensatory manner and resulting in a zero magnetic moment (due to equal number of parallel and antiparallel magnetic dipoles) gives rise to antiferromagnetism. For example MnO, Mn₂O₃ and MnO₂ are antiferromagnetic.
v) Ferrimagnetic substances: Ferrimagnetism is found when the magnetic moments are aligned in parallel and antiparallel directions in unequal numbers resulting in a net magnetic moment.  For example Fe₃O₄ is ferrimagnetic.  Similarly, ferrites of the formula M²⁺ Fe₂O₄ are ferrimagnetic in nature (where M = Mg, Cu, Zn etc).

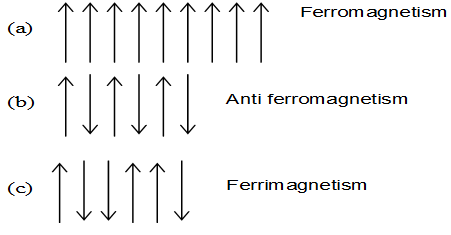
• All magnetically ordered solids (ferromagnetic and antiferromagnetic solids) transform to the paramagnetic state at high temperature due to randomisation of spins. Fe₃O₄ which is ferrimagnetic at room temperature becomes paramagnetic at 850 K.  V₂O₃, NiO change from antiferrimagnetic phase to paramagnetic phase at 150K and 523 K respectively.

Dielectric properties: A dielectric is a substance in which an electric field gives rise to no net flow of electric charge.  This is due to the reason that electrons in a dielectric are tightly held by individual atoms and they do not generally migrate under an applied electric field.  However, dipoles are created by a shift in charges resulting in polarization.  Besides that there may also be permanent dipoles in the crystal.
The alignment of these dipoles in different ways impart certain characteristic properties to solids.
1) Piezoelectricity:  Electric dipole may align themselves in an ordered manner such that there is a net dipole moment in the crystal.  The crystals where this situation is found exhibit piezoelectricity or pressure electricity.  When such crystals are subjected to a pressure or mechanical stress, electricity is produced.  Conversely if an electric field is applied to such a crystal, the crystal gets deformed due to generation of mechanical strain.  This is sometimes called inverse piezoelectric effect.

• Piezoelectric crystals are utilized in transducers devices that convert electrical energy into mechanical strains or vice versa. Piezoelectrics are also utilized in phonograph pickups, microphones, ultrasonic generators, strain gauges and sonar detectors.

• Piezoelectric materials include lead titanate, barium titanate, lead zirconate (PbZrO₃). Ammonium dihydrogen phosphate (NH₄H₂PO₄) and quartz.

2) Pyroelectricity:  Some of the piezoelectric crystals, when heated produce small electric potential, or acquire electric charges on opposite faces.  This property of crystals is known as pyroelectricity.

3) Ferro electricity:  In some of the piezoelectric crystals the dipoles are permanently lined up (spontaneously polarised) even in the absence of an electric field and the direction of polarisation can be changed by applying an electric field.  Such substances are called ferroelectric substances and phenomenon is called ferroelectricity.

• Barium titanate (BaTiO₃), sodium potassium tartrate (Rochelle salt) and potassium dihydrogen phosphate are ferroelectric solids.

• All ferroelectric solid materials are piezoelectric but the reverse is not true.

4) Antiferroelectricity:  If the alternate dipoles are in opposite direction, then the net dipole moment will be zero and the crystal is called antiferroelectric.  Lead zirconate (PbZrO₃) is an anti-ferroelectric solid.
Superconductivity:  The electrical resistance of metals decreases with decrease in temperature and becomes almost zero near the absolute zero.  Materials in this state are said to possess superconductivity.
Superconductivity was first discovered by H.  Kamerlingh-Onnes who was awarded the 1913 physics noble prize for his contributions to low temperature physics.  He found that mercury becomes superconducting at 4.15 K. The temperature at which a substance starts behaving as super-conductor is called transition temperature.  The critical temperatures for superconductivity lying between 0.1 K and 10K.  Since a superconductor has almost zero resistance, it can carry electric current without losing energy and, in principle the current can flow forever.
The highest temperature at which super conductivity was known till recently was 23K for alloys of niobium.  Many complex metal oxides have been found to possess superconductivity at somewhat higher temperature.  E.g.,.  This superconductor is called yttrium-barriumcuprate, this is 1-2-3 system because of the ratio of the metals present.
Super conducting materials can be used in electronics, in building magnets, in power transmission and in levitation transportation, levitation occurs when objects float in air.  This can be achieved by the mutual repulsion between a permanent magnet and a semiconductor.

FORMULAE AND CONCEPTS AT A GLANCE

1. Crystalline solids are anisotropic and amorphus solids are isotropic

2. Bragg’s equation is 2d sinθ = nλ
Where, λ = wavelength of X – ray
              d = inter planar distance
              θ = angel of incident X – ray

3. The no of atoms per unit cell for simple cubic = 1, for FCC =4, and for BCC = 2

4. Packing fraction =$\frac{\mathrm{Volume} \mathrm{of} \mathrm{atoms} \mathrm{per} \mathrm{unit} \mathrm{cell}}{\mathrm{Volume} \mathrm{of} \mathrm{unit} \mathrm{cell}}$

5. For cubic close packing
Number of octahedral voids = no. of atoms per unit cell
Number of tetrahedral voids = 2×number of atoms per unit cell

6. Radius ratio is the ratio of radius of cation and anion

7. Density of a cubic crystal is given by d =$\frac{Z\times M}{a^3\times N_A}$

8. NaCl has FCC structure and CsCl has BCC structure

9. Coordination number increases by increasing pressure and decreasing temperature.

10. In stoichiometric defects the formula of the compound remains same and in non stoichiometric defects the formula changes.

11. In Schottky defects the density of the crystal decreases and in Frenkel defects the density remains same.

12. The non stoichiometric compounds having F–centres appear coloured when heated e.g. NaCl appears yellow.

13. Addition of 15^th group element in pure semiconductor make it n – type semiconductor.

14. Addition of 13^th group element in pure semi conductor make it p– type semiconductord.

15. Compounds having zero resistance are called supper conductors.

SOLVED PROBLEMS-1

Prob 1: Calculate the number of atoms contained within (i) a primitive cubic unit cell (ii) a body – centred cubic (b.c.c) unit cell (iii) a face-centred cubic (f.c.c.) unit cell and (iv) the unit cell for the diamond lattice.

Sol. (i) The primitive cubic unit cell consists of one atom at each of the 8 corners.  Each atom is thus shared by 8 unit cells.  Hence, n = 8 ⨯ (1/8) = 1.

(ii) The b.c.c. unit cell consists of 8 atoms at the 8 corners and one atom at the centre.  At each corner only 1/8^th of the atom is within the unit cell.  Thus, the contribution of the 8 corners is 8 ´ (1/8) = 1 while that of the body centred atom is 1. Hence, n = 1 + 1 = 2.

(iii) The 8 atoms at the corners contribute 8 ⨯ (1/8) = 1.  There is one atom at each of the 6 faces, which is shared by 2 unit cells each.  Therefore, the contribution of 6 face-centred atoms = 6 ⨯ (1/2) = 3.  Hence, n = 1 + 3 = 4.

(iv) If we consider the unit cell of a diamond lattice, we find that there are 8 atoms on the 8 corners, each shared by 8 unit cells.  Also, there are 6 atoms on the faces, each shared by 2 unit cells.  In addition, there are 4 atoms inside the until cell.  Hence, n = 8 ⨯ (1/8) + 6 ⨯ (1/2) + 4 = 8.

Prob 2: A metallic element exists as a cubic lattice.  Each edge of the unit cell is 2.88 Å.  The density of the metal is 7.20g cm^-3.  How many unit cells there will be in 100g of the metal?

Sol. Volume of the unit cell = (2.88 Å)³ = 23.9 ⨯ 10^-24 cm³

Volume of 100g of the metal = $\frac{\mathrm{m}}{\mathrm{\rho }}=\frac{10 \mathrm{g}}{7.20{\mathrm{gcm}}^{–3}}=13.9{ \mathrm{cm}}^3$

Number of unit cells in this volume = $\frac{13.9{ \mathrm{cm}}^3}{23.9\times {10}^{–24}{ \mathrm{cm}}^3}=5.82\times {10}^{23}$

Prob 3: Iron ($\alpha$ – Fe) crystallizes in a b.c.c. system with a = 2.861 Å.  Molar mass M of iron is 55.85g mol^-1.  Calculate the density of iron

Sol.  $\rho =\frac{\mathrm{nM}}{{\mathrm{N}}_{\mathrm{A}}\mathrm{V}}=\frac{2\times \left(55.85{\mathrm{gmol}}^{–1}\right)}{\left(6.022\times {10}^{23}{ \mathrm{mol}}^{–1}\right){\left(2.861\times {10}^{–9} \mathrm{cm}\right)}^3}=7.92{\mathrm{gcm}}^{–3}$

Prob 4: Lithium borohydride, LiBH₄, crystallizes in an orthorhombic system with 4 molecules per unit cell.  The unit cell dimensions are : a = 6.81 Å, b = 4.43 Å and c = 7.17Å.  If the molar mass M of LiBH₄ is 21.76g mol^–1, calculate the density of the crystal.

Sol. $\rho =\left(\frac{\mathrm{nM}}{{\mathrm{N}}_{\mathrm{A}}\mathrm{V}}\right)=\frac{4\times \left(21.76{\mathrm{gmol}}^{–1}\right)}{\left(6.0222\times {10}^{23}{ \mathrm{mol}}^{–1}\right)\left(6.81\times 4.43\times 7.17\times {10}^{–24}{ \mathrm{cm}}^3\right)}=0.668{\mathrm{gcm}}^{–3}$

Prob 5:    Calculate the coordination number (C.N.) of an atom in (i) a primitive cubic unit cell (ii) a body-centred cubic unit cell and (iii) a face-centred cubic unit cell.

Sol. (i) A little consideration shows that in a primitive cubic unit cell, each atom has 6 equally-spaced nearest neighbour atoms.  Thus, C.N. = 6.            

(ii) Considering the atom in the centre of the unit cell, we find that it is surrounded by 8 nearest neighbour atoms situated at the corners of the cube.  Thus, C.N. = 8.

(iii) C.N. for a face – centred atom in an f.c.c. unit cell is, evidently, equal to 12.

Prob 6: Calculate the angle at which (a) first order reflection and (b) second order reflection will occur in an X-ray spectrometer when X-rays of wave length 1.54Å are diffracted by the atom of a crystal, given that the interplanar distance is 4.04Å.

Sol. (a) For first order reflection (n = 1), the Bragg equation is 2d sin q = l.

∴  θ = sin^–1 (l/2d) = sin^–1 (1.54Å/8.08Å) = sin^–1 (0.191) = 10⁰ 59′

(b) For second order reflection (n = 2), the Bragg equation is 2d sin θ = 2λ

∴ θ= sin^–1 (l/d) = sin^–1 (1.54/4.04) = sin^–1 (0.381) = 22⁰24′

Prob 7: In a close packed structure of mixed oxides, the lattice is composed of oxide ions, one eighth of tetrahedral voids are occupied by divalent cations while one half of octahedral voids are occupied by trivalent cations.  What is the formula of the oxide?

Sol. Number of oxide ions (O) per unit cell = 1

Number of tetrahedral voids per ion in lattice = 2

Number of divalent cation (A) = $\frac{1}{8}\times 2=\frac{1}{4}$

Number of octahedral voids per ion in lattice = 1

Number of trivalent cations (B) = $1\times \frac{1}{2}=\frac{1}{2}$

Formula = A₁/₄B_1/2O = AB₂O₄

Prob 8: In a crystal of an ionic compound the ions B form the close packed lattice and the ions A occupy all the tetrahedral voids.  What is the formula of the compound?

Sol. In closed packed array of B ions the number of tetrahedral voids per ion of B is two.  Since, tetrahedral voids are occupied by A ions, there are two A ions per B ion in the crystal.  Therefore, the formula of the compound is A₂B.

Prob 9: The edge length of unit cell of a metal having mol. wt. 75g mol^-1 is 5 Å which crystallizes in cubic lattice.  If the density is 2g.cm^-3, calculate the radius of metal atom (N_A = 6 ⨯ 10²³).

Sol. $\text{ Density }=\frac{\mathrm{n}\times \mathrm{mol}.\mathrm{wt}}{\mathrm{V}\times \mathrm{Av}.\mathrm{No}}$

a = 5 ⨯ 10^-8cm, d = 2 g/cm³

$\therefore 2=\frac{\mathrm{n}\times 75}{{\left(5\times {10}^{–8}\right)}^3\times 6\times {10}^{23}}$

∴   n = 2

i.e., the metal crystallizes in b.c.c. thus, radius =  $\frac{\sqrt{3}}{4}\times a=\frac{\sqrt{3}}{4}\times 5=2.165$ Å = 216.5 pm

Prob 10:  An element crystallizes in f.c.c. lattice having edge length 400 pm.  Calculate the maximum diameter which can be placed in interstitial sites without disturbing the structure.

Sol. Either octahedral voids $\left(\frac{{\mathrm{r}}_1}{{\mathrm{r}}_2}=0.414\right)$ or tetrahedral voids  $\left(\frac{r_1}{r_2}=0.225\right)$ are occupied by interstitial sites in f.c.c. where r₁ is radius of atom in interstitial sites and r₂ is radius of atom arranged in f.c.c.

Since in f.c.c. atoms along the face diagonal are touching, thus, $4r_2=\sqrt{2}a$

Required diameter of interstitial sites = $2{\mathrm{r}}_1=2\times 0.414{\mathrm{r}}_2$

$=\frac{2\times 0.414\times \sqrt{2}a}{4}$

$=\frac{2\times 0.414\times \sqrt{2}\times 400}{4}$ = 117.1 pm

SOLVED PROBLEMS-2

Prob 1: Which substance acts as superconductor at 4K

(A)  Hg               (B)  Cu               (C)  Na               (D)  Mg 

Sol. (A). Mercury

Prob 2: For orthorhombic system, axial ratios are a ¹ b ¹ c and the axial angles are

(A)  $\alpha =\beta =\gamma \ne 90°$

(B)  $\alpha =\beta =\gamma =90°$

(C)  $\alpha =\gamma =90°,\beta \ne 90°$

(D) $\alpha \ne \beta \ne \gamma =90°$

Sol. (B). $\alpha =\beta =\gamma =90°$

Prob 3: The existence of a substance in more than one solid modifications is known as

(A) isomorphism          (B) polymorphism          (C) amorphism          (D)  allotropy

Sol. (B). Polymorphism.

Prob 4: The ionic radii of Rb⁺ and I^– are 1.46 and  respectively. The most probable type of structure exhibited by it is.

(A)  CsCl type               (B)  NaCl type               (C)  ZnS type               (D)  CaF₂ type

Sol.  (B) $\frac{{\mathrm{r}}^{+}}{{\mathrm{r}}^{–}}=\frac{1.46}{2.16}=0.67$, hence octahedral.

Prob 5: In FCC lattice of NaCl structure, if the diameter of Na⁺ is x, and the diameter of Cl^– is y, then the bond length of NaCl in the crystal is

(A)  2x + 2y          (B) x + y          (C) $\frac{x}{2}+\frac{y}{2}$          (D) None

Sol. (C). Bond length = radius of Na⁺ + radius of Cl^–  = $\frac{x}{2}+\frac{y}{2}$

Prob 6: Frenkel defect is generally observed in

(A)  AgBr          (B)  Agl          (C)  ZnS          (D)  All of these

Sol. (D). All of these shows Frenkel defect.

Prob 7: In which of the following substances the carbon atoms are arranged in a tetrahedral structure.

(A)  Diamond               (B)  Benzene               (C)  Graphite               (D)  Carbon black

Sol. (D). Impure semiconductors are called extrinsic semiconductors.

Prob 8: A binary solid  has a rock salt structure. If the edge length is 400 pm, and radius of cation is 75 pm the radius of anion is

(A)  100 mm               (B)  125 pm               (C)  250 pm               (D)        325 pm

Sol. (B). Edge = $2\left(r^{+}+r^{–}\right)$

$\Rightarrow 400=2\left(75+r^{–}\right)$

$\therefore r^{–}=125\mathrm{pm}$

Prob 9: The substance which possesses zero resistance at zero kelvin is called

(A)  conductor

(B)  super conductor

(C)  insulator

(D)  semiconductor

Sol. (B). Superconductors have zero resistance.

Prob 10:  A compound crystallizes as follows

Ions A are at corners of a cubic unit cell and B ions at face centres of a cubic unit cell and C ions in 1/4^th of the total tetrahedral void. Assuming, if this is dissolved, only the ions in the tetrahedral voids are dissociated completely in water, which one of the following statements is true. (Assuming all are univalent ions) and also A and C are cations and B is an anions.

(A) Boiling point of same concentration of  solution (100% dissociation) will be greater than that of this solution.

(B) Boiling point of same concentration of ${\mathrm{Ca}}_3{\left({\mathrm{PO}}_4\right)}_2$ (100% dissociation) will be greater than that of this solution.

(C) Boiling point of same concentration of sucrose will be greater than this solution

(D) Data insufficient to predict.

Sol. (B). Compound is $A{B}_3{C}_2$

So, if C alone dissociates

${\mathrm{AB}}_3{\mathrm{C}}_2⟶{\left[{\mathrm{AB}}_3\right]}^{2–}+2[\mathrm{C}{]}^{+}$

A total number of 3 ions.