1. INTRODUCTION
A particle has oscillatory (vibrational) motion when it moves periodically about stable equilibrium position. The motion of a pendulum is oscillatory. When a weight is attached to a stretched spring, once it is released, it starts oscillating.
When the particle is moved away from the equilibrium position and released, a force comes into play to pull it back toward equilibrium. But by the time it gets there, it has picked up some kinetic energy, so it overshoots, stopping somewhere on the other side and is again pulled back toward equilibrium.
Of all the oscillatory motions, the most important is called simple harmonic motion (SHM). In this type of oscillatory motion, displacement, velocity, acceleration and force all vary (w.r.t. time) in a way that can be described by either the sine or the cosine function collectively called sinusoids. Any oscillatory motion that cannot be described so simply is called an harmonic oscillation.
Besides being the simplest motion to describe and analyze, it constitutes a rather accurate description of many oscillations found in nature.
Understanding periodic motion will be essential for our later study of waves, sound, alternating electric current and light.
2. SIMPLE HARMONIC MOTION
“A periodic motion, in which a body moves to and fro about a fixed mean position, is said to be simple harmonic, if its acceleration (a) is proportional to the displacement (x) of the body from its mean position and is always directed towards the mean position”. The simple harmonic motion can be described by the following relation.
a α – x
a = – 2 x …… (1)
Where 2 is the proportionality constant. The negative sign indicates that the acceleration and displacement are opposite in direction to each other. The following are the conditions to be obeyed for a body of execute simple harmonic motion.
i) Motion should be periodic.
ii) The object must move to and fro about mean position.
iii) Acceleration must be directly proportional to the displacement from mean position.
iv) Acceleration must always be directed towards the mean position.
v) Acceleration and displacement must always be opposite to each other.
If the to and fro motion is along a straight line it is called linear simple harmonic motion. The displacement is measured along the straight line. If the displacement is measured in terms of angles then it is called angular simple harmonic motion.
Examples of simple harmonic motion (SHM)
1) Linear simple harmonic motion
i) The oscillations of a simple pendulum with small displacements.
ii) The vibrations of the prongs of a tuned tuning fork.
iii) Motion of a loaded spring which is stretched and released.
iv) Motion of objects which float on water waves.
v) The oscillations of a swing with small displacement.
vi) The projection of uniform circular motion on any diameter of the reference circle.
2) Angular simple harmonic motion
i) The oscillations of a freely suspended magnet in the earth’s magnetic field.
ii) Oscillations of a torsional pendulum.
iii) Oscilaltions of a balancing wheel is a watch.
Derivation of expressions for displacement, velocity, acceleration, time period and frequency
The projection of uniform circular motion on any diameter of a circle is also defined as simple harmonic motion. Based on this we can derive equations for displacement, velocity, acceleration, time period and frequency of a particle executing simple harmonic motion.
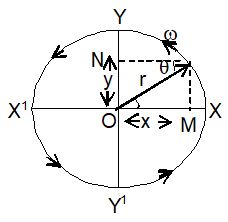
As shown in fig consider a particle ‘P’ moving on the circumference of a circle of radius ‘r’ with centre ‘O’ and with uniform angular velocity ‘’ in the anti-clockwise direction. This circle is known as reference circle. XX1 is the reference axis and YY1 is any diameter. Draw perpendiculars PM and PN on XX1 and YY1 respectively. Hence, M and N are the projections of ‘P’ on XX1 and YY1 respectively. As the particle moves along the circumference of the circle, its projections M and N move along the diameters XX1 and YY1 respectively, thus executing to and from motion.
Let the particle be at ‘X’ when the time t = 0
Let the particle be at ‘P’ represented by position vector after ‘t’ seconds. The angular displacement of the particle during this time is , (as shown in the fig).
For the particle ‘P’ to move on the circle the magnitude of centripetal acceleration that acts on it is r2 which is directed along PO. Thus, rω2 cosθ and rω2 sinθ are the components of this centripetal acceleration along XOX1 and YOY1 respectively. Hence, the projection N of P is acted on by an acceleration rω2sinθ along YOY1.
∴ Acceleration (a) =
From ΔONP,
If ON = y,
Then y = r sinθ
But θ = ωt
Y = r sin ωt …… (2)
This equation represents the displacement of N (projection of P on YOY1)
A = – ω2y …… (3)
Since uniform angular velocity (ω) is constant.
This implies that the acceleration (a) is proportional to displacement (Y) and is oppositely directed. Hence, the motion of the projection ‘N’ along YOY1 is simple harmonic.
Similarly, we can also prove that the motion of the projection ‘M’ is also simple harmonic. Hence, the uniform circular motion, in general can be described as a combination of two simple harmonic motions acting perpendicular to each other.
3. CHARACTERISTICS OF SHM
Here we shall discuss the physical meaning of constants A, ω and used to describe simple harmonic motion.
a) Amplitude A: It is defined as the maximum (positive or negative) value of displacement from equivalent position. Since maximum and minimum values of sine functions are respectively +1 and -1, the maximum and minimum values of y in the equation y = A sin(ωt+) are respectively +A and -A; A is called amplitude. Furthermore if S is the span of SHM, amplitude A will be (S/2).
b) Time period T: The smallest time interval after which the oscillation repeats itself is called the time period T of the oscillation. If y is the displacement of a particle executing SHM at any time t, it will achieve the same position again for the first time if time is advanced by (2/ω), i.e.
. . . . (4)
In other words, the displacement repeats itself after a time interval of (2/ω), after a time interval of (2/ω), so that
T = (2/ω).
c) Frequency f: Frequency in SHM is the number of oscillations completed in a unit time interval. Therefore, by definition, frequency is the reciprocal of time period, i.e.,
or
or Quantity ω is called angular frequency of the motion. The SI unit of T is s (second), of f is Hz (hertz) and of ω is rad/s. The period of frequency is the characteristic of the system executing SHM and is determined from its elastic and inertial properties. Furthermore out of T, f and ω only one is usually given and the others may be calculated by using the above equation.
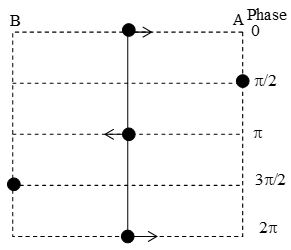
d) Phase: The argument (ωt+) of the sine function is called the phase of the motion. The phase of an oscillating system at any instant is its state as regards its position and direction of motion at that instant, e.g. if the phase is zero at a certain instant then from equation of SHM.
i.e. , , y = 0
This implies that the particle is crossing the equilibrium position and if (ωt + ) = (/2)
y = A and v = 0
i.e., the particle is at extreme position. Figure shows the state of a particle executing SHM in different phases.
e) Phase Constant : The constant in the equation of SHM is called epoch or phase constant or initial phase. This enables us to find the position from where time is considered in SHM, e.g., if we consider the motion from equilibrium position,
i.e. at t = 0, y = 0, the equation y=Asin(ωt+) gives
0 = Asin(ω ⨯ 0 + ),
i.e. sin = 0 or = 0.
i.e., if time is considered from equilibrium position, initial phase is zero and so equation of motion become y = Asinωt.
and if we consider the motion from extreme position, i.e., at t=0, y=A, then from equation
y=Asin(ωt+).
A = Asin(ω ⨯0+), i.e. sin = 1 or = /2.
i.e., if time is considered from extreme position, initial phase (/2) and equation of motion will become y=Asin[ωt+(/2)] = Acosωt.
4. SOME PHYSICAL QUANTITIES OF INTEREST IN SHM
a) Displacement: In SHM if time is considered from equilibrium position, displacement y at any time t is given by
. . . . (5)
regarding displacement it is worth nothing that
1) Its direction is always away from the equilibrium position either particle is moving away from or is coming towards the equilibrium position
2) If t is given it can be calculated and vice-versa, e.g., if , i.e. , and , if , , i.e., in traveling half the amplitude from the equilibrium position, the particle takes 1/12th of its time period while in time 1/8th of the period it travels times of its amplitude.
b) Velocity: In case of SHM when motion is considered from equilibrium position,
y = Asinωt
so . . . . (6)
or . . . . (7)
Equations (6) and (7) gave the velocity of a particle executing SHM at any instant and position respectively. From these equations it is clear that
1. v will be the minimum when ymax = A and vmin = 0, i.e. in SHM velocity is minimum at extreme position and is zero.
2. v will be maximum when ymin = 0 and vmax = Aω i.e., in SHM velocity is maximum at equilibrium position and is Aω.
3. Direction of velocity is either towards or away from equilibrium position.
c) Acceleration: In case of SHM when time is considered form equilibrium position, as
y = Asinωt
i.e.
so [as y = Asinωt] . . . . (8)
from this it is clear that
1. In SHM as |Acceleration| (=ω2y) is not constant so equation of translatory motion cannot be applied.
2. |Acceleration| will be minimum when |y|min = 0 and so |acc|min = 0, i.e., acceleration is minimum (=0) at equilibrium position where |velocity| is maximum (=ωA)
3. |Acceleration| will be maximum when |y|max = A and so |acc|max = ω2A i.e. acceleration is maximum at extreme position where velocity is minimum (=0).
4. Acceleration is always directed towards the equilibrium position and so is always opposite to displacement.
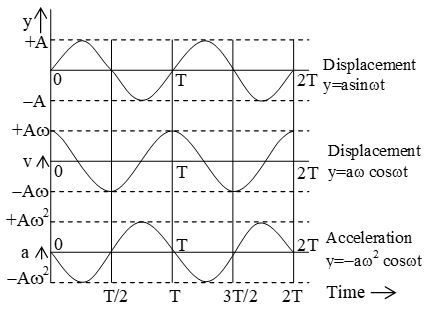
Figure and the table below give comparative study of displacement, velocity and acceleration in SHM.
| S.No. | Physical quantity | Equilibrium Position | Extreme position |
| 1. | Displacement y=Asinωt | Minimum = 0 | Maximum = A |
| 2. | Velocity v = | Maximum = ωA | Minimum = 0 |
| 3. | Acceleration |a|= ω2y | Minimum = 0 | Maximum = ω2A |
d) Energy E: in case of SHM as kinetic energy
while as F = – ky, potential energy
. . . . (9)
so mechanical energy
[as ω2 = k/m] . . . . (10)
equations (8), (9) and (10) are the desired equations and from these, it is clear that
1) With increase in y, i.e., when particle moves from equilibrium position to extreme position, PE increases, KE decreases and ME remains constant.
2) At equilibrium position as ymin = 0, so
KEmax = and PEmin = 0 while at extreme position as ymax = A.
KEmin = 0 and PEmax = .
The variation of KE, PE and ME as function of position are shown in figure.
3) As in SHM y = Asinωt
KE,
PE, U =
so that
and
with
and E = . . . . (11)
i.e. in SHM, KE and PE vary periodically with double the frequency of SHM (i.e. with time period = T/2). The variations of KE, PE and ME as functions of time are shown in figure.

4) In SHM, E = , i.e. energy is directly proportional to the square of amplitude and can also be expressed as
this equation, i.e., conservation of ME in SHM can be used to find time period, since E is constant (dE/dt) = 0 so that the above equation reduces to
,
i.e.
with
5. SIMPLE PENDULUM
A point mass suspended by a massless, inextensible string from a rigid support constitutes a simple pendulum. In reality neither point mass nor mass less string exist. So we can never construct a simple pendulum strictly according to its definition. A small heavy spherical mass suspended from a light inextensible string constitutes an approximate simple pendulum.
Now when the pendulum is pulled to one side and released, it will swing to and fro describing an arc of a circle in a vertical plane
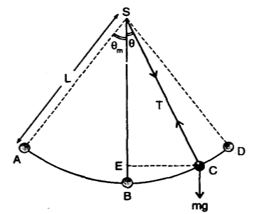
(as the string is inextensible), i.e., the displacement involved in the motion is angular. So the motion of a simple pendulum is angular and oscillatory. Here restoring torque about S is developed due to the weight of the pendulum as shown in figure.
i.e.
[negative sign is used as direction of torque is opposite to displacement)
If θ is small sinθ = θ,
so . . . . (12)
i.e. restoring torque is linear, so motion will be angular simple harmonic,
Now as in case of rotational motion:
. . . . (13)
so from equations (12) and (13)
or
or
with . . . . (14)
equation (14) is the standard equation of angular simple harmonic motion with the time period so here
. . . . (15)
This is the required result and from this it is clear that
1. The period of simple pendulum is independent of amplitude as long as its motion is simple harmonic.
2. Time period of simple pendulum is also independent of mass of the bob. This is why
a) If the solid bob is replaced by a hollow sphere by same radius but different mass, time period remains unchanged.
b) If a girl is swinging in a swing and another sits with her the time period remains unchanged.
6. SPRING PENDULUM
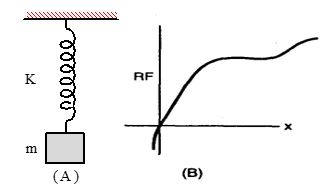
A point mass suspended from a massless spring constitutes a liner harmonic spring pendulum. In reality neither point mass nor massless spring exists, so the construction of a spring pendulum is never possible strictly according to its definition. A small heavy mass suspended from a light spring is an approximate spring pendulum.
The restoring force in a spring pendulum develops due to elasticity of the spring, i.e.
which in the limit of small displacement becomes F = -ky, i.e. restoring force becomes linear, so motion of spring pendulum is linear simple harmonic. However, if the displacement is not small the motion does not remain simple harmonic but becomes oscillatory.
Now for a spring pendulum, as
or ,
or
with
this is the standard equation of linear simple harmonic motion with time period T = (2/ω). So here
or . . . . (16)
This is the required result and from this we can conclude that
1. The period of a spring pendulum is independent of acceleration due to gravity. This is why a clock based on spring pendulum will keep proper time everywhere on a hill or moon or in a satellite and time period of a spring pendulum will not change inside a liquid if damping effects are neglected.
2. Time period of a spring pendulum depends on the mass suspended i.e.
i.e. greater the mass greater will be the inertia and so lesser will be the frequency of oscillations and greater will be time period.
3. The time period depends on the force constant k of the spring, i.e.
i.e. greater the force constant greater will be the frequency and lesser will be the time period. [The force constant k of a spring is inversely proportional to its natural length]
4. If the spring has a mass M and mass m is suspended from it, effective mass is given by
so that
5. If two masses of mass m1 and m2 are connected by a spring and made to oscillate on horizontal surface, the reduced mass m is given by
so that

Note: Composite-spring pendulum: If a spring pendulum is constructed by using two springs and a mass, the following three situations are possible.
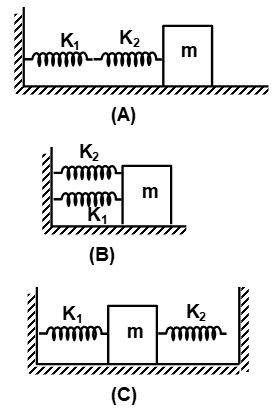
for the three cases shown above we have respectivel
(A) So
(B) So
(C) So
7. FLUID PENDULUM
a) Motion of a liquid in V-shape tube when it is slightly depressed and released: Here it is taken for granted that cross-section of the tube is uniform and the liquid is incompressible and nonviscous. Initially the level of liquid in the two limbs will be at the same height. If the liquid is depressed by y in one limb, it will rise by y along the length of the tube in the other limb. So here the restoring force will develop by hydrostatic pressure difference, i.e.
As the restoring force is linear, motion will be linear simple harmonic with force constant
so that
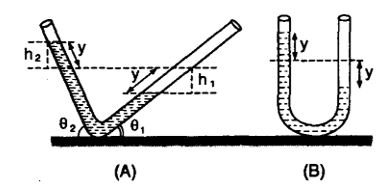
Note: If the tube is a U-tube and liquid is filled to a height h, θ1 = θ2 = 90o and m = hAd ⨯ 2,
so .
b) When a partially submerged floating body is slightly depressed and released: If a body of mass m and cross-section A is floating on a liquid of density with height h inside the liquid.
mg = Ahρg,
i.e. m = Ahρ
Now from this equilibrium position if it is depressed by y, the restoring force will develop due to extra thrust,
i.e. F = -Agy
As restoring force is linear, the motion will be linear simple harmonic with force constant
From this expression it is clear that if density of liquid decreases, the time period will increase and vice-versa. And also as from equation (1) m = Ah,
where h is the height of the body inside the liquid.
Note
If the body is floating fully submerged then on pressing it will remain at the displaced position as no net force acts on it.
Superposition of two SHMs of same frequency In the same direction
When a particle is superposed with more than one harmonic forces, each force tries to move the particle in its own direction with SHM. We call it interference of SHM.
First we consider two SHMs that produces displacement of the particle along same line. The displacement of the particle produced by each simple harmonic motion is given by
. . . . (17)
and . . . . (18)
where is phase difference between x1 and x2.
where is phase difference between x1 and x2.
Case (i) If =0, we say that the two motions are in phase. Then the resultant motion is x=A1cosωt + A2cosωt = (A1+A2)cosωt . . . . (19)
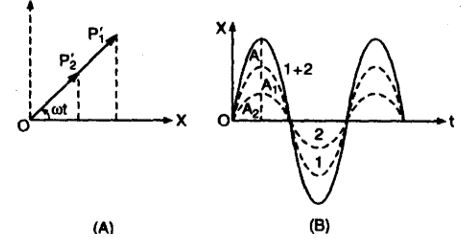
Resultant amplitude is A1+A2. The two rotating vectors and corresponding to the two motions are represented in the figure.
Case (ii): If =, from equation (18)
x2 = A2cos(ωt + ) = -A2cosωt
then resultant motion is
x = (A1 – A2) cosωt . . . . (20)
which shows that the resultant motion is SHM with the same angular frequency and resultant amplitude is A = A1 – A2
Hence we say that the motions are in opposite or for = the two SHMs are in opposite phase.
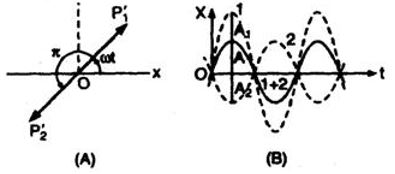
In general case, phase difference is arbitrary; the resultant motion is also SHM with the same angular frequency ω and an amplitude given by,
. . . . (21)
In the figure the rotating vectors and corresponding to x1 and x2 are drawn. Their resultant OP’ is the rotating vector corresponding to x. We use the law of vector addition to find magnitude of A. Angle of resultant OP’ with is given by
Hence resultant SHM is given by
SOLVED EXAMPLES
1. If two SHMs are represented by equations , find the ratio of their amplitudes.
Sol. As ,
So if 5 = Acos and
i.e. if A = and ,
i.e.
the above equation becomes
=
i.e.
so i.e. A1 : A2 = 1 : 1
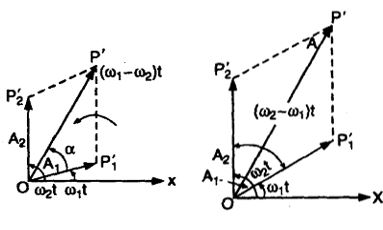
2. Two particles execute SHM of the same amplitude and frequency along the same straight line. They pass one another when going in opposite directions, each time their displacement is half of their amplitude. What is the phase difference between them?
Sol. In case of SHM, and as here y = A/2,
So,
or,
i.e.
so the phase of the two particles when they are crossing each other at y = A/2 in opposite directions are . So phase difference
3. A particle executed SHM of amplitude 4 cm and T=4 sec. What is the time taken by it to move from positive extreme position to half the amplitude?
Sol. The equation of motion of linear SHM is
y = Asin(wt + ). When time is counted from extreme position y=A at t=0, so that A=Asin(0+), i.e., sin = 1 or = /2, so the equation of motion becomes
Now as here by
or
or ,
or
4. A particle is executing SHM with amplitude A and has a maximum velocity vo. (a) At what displacement will its velocity be (vo/2)? (b) What is its velocity at displacement A/2?
Sol. In SHM velocity at any position y is given by
so v will be maximum when y2 = min = 0, i.e. vo = Aw.
(a) Given that .
So
i.e.
b) Given that y = A/2
so
i..e.
5. A point particle of mass 0.1 kg is executing SHM with amplitude of 0.1m. When the particle passes through the mean position, its kinetic energy is joule. Obtain the equation of motion of this particle if the initial phase of oscillation is 45o.
Sol. Given that A = 0.1 m; m =0.1 kg, = 45o = /4 rad, so the equation of SHM will be
. . . . (i)
Now as in SHM, KE is given by
which according to given problem is J for y=0
so ,
i.e. ω = 4 rad/s . . . . (ii)
substituting the value of ω from equation (ii) in (i), we get
6. The displacement of a particle executing periodic motion is given by . Find independent constituent simple harmonic motions.
Sol.
or y = 2(1 + cost) sin(1000t) (as 2cos2θ = (1+cos2θ)
or y = 2sin1000t + 2sin1000t ⨯ cost
or y = 2sin100t + sin1001t + sin999t [as 2sinAcosB = sin(A+B) + sin(A-B)] so the given expression is the resultant of 3 independent harmonics.
7. Two linear SHMs of equal amplitude and frequencies ω and 2ω are impressed on a particle along x and y-axes respectively. If the initial phase difference between them is (/2), find the resultant path followed by the particle.
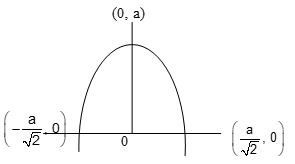
Sol. According to the given problem,
x = asinωt and
so that y = acos2ωt [as sin(θ + 90o) = cosθ]
or
[as cos2ωt = 1 – 2sin2ωt]
or
[as x= asinωt]
or
i.e. the resultant path is a parabola with vertex (0, a) and latus rectum as shown in figure.
8. A simple pendulum is made by attaching a bob of 1kg to a 5 m long copper wire of diameter 0.08 cm and it has a certain period of oscillation. Next a 10 kg bob is substituted for the 1kg bob. Calculate the change in the period if any. (Young’s modulus for copper = )
Sol.
So that
or
i.e.,
i.e. sec.
9. Figure shows a system consisting of a massless pulley, a spring of force constant k = 4000 N/m and a block of mass m = 1 kg. If the block is slightly displace vertically down from its equilibrium position and released, find the frequency of its vertical oscillation in case (A), (B) and (C).
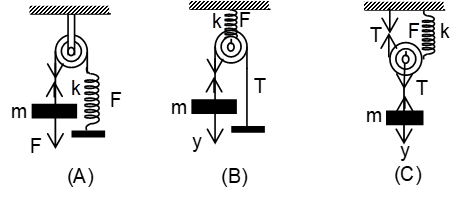
Sol. (A) As the pulley is fixed and the string is inextensible, if mass m is displaced by y the spring will stretch by y and as there is no mass between string and spring (as pulley is massless)
F = T = ky
i.e. restoring force is linear and so motion of mass m will be linear simple harmonic with frequency = 10 Hz
B) As the pulley is movable and string inextensible, if mass m moves down a distance y, the pulley will move down by (y/2). So the force in the spring F = k(y/2). Now as the pulley is masless, F=2T, i.e., T = F/2 = (k/4)y. So the restoring force on the mass m,
with
so .
C) In this situation if the mass m moves by y the pulley will also move by y and so the spring will stretch by 2y (as the string is inextensible) and so T’=F=2ky. Now as the pulley is massless, T = F+T’ , i.e. the restoring force on the mass m, T = 4ky = k’y with k’=4k
And so
When restoring force is due to Hydrostatic pressure or thrust
10. A force 6.4 N stretches a vertical spring by 0.1m. The mass that must be suspended from the spring so that it oscillates with a period of (p/4) sec is
(A) (p/4) kg (B) 1 kg
(C) (1/p) kg (D) 10 kg
Sol. (B)
According to the given question
F = kx = 64 N/m
Substituting it in the following equation
11. Two blocks of mass m and 2m are connected together by a spring of spring constant k and are kept on a smooth plane. The angular frequency of oscillation of the system is
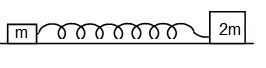
(A) (B) (C) (D)
Sol. (D)
Hence,
12. A particle of mass m is executing oscillations about the origin on the x – axis. Its potential energy is V(x) = k|x|3, where k is a positive constant. If the amplitude of oscillation is a, then its time period T is
(A) proportional to
(B) independent of a
(C) proportional to
(D) proportional to a3/2
Sol. (A)
U(x) = k|x|3
13. The displacement y in cm is given in terms of time t second by the equation,
y = 3 sin 314t + 4 cos 314t. The amplitude of the SHM is
(A) 7 cm (B) 3 cm (C) 4 cm (D) 5 cm
Sol. (D)
The equation can be rewritten as
Hence, the amplitude is 5 cm.
14. A clock ‘S’ is based on the oscillation of a spring and a clock ‘P’ is based on motion of the pendulum. Both clocks run at the same rate on the earth. On a planet having the same density as earth, but twice the radius
(A) S will run faster than P
(B) P will run faster than S
(C) they will both run at the same rate, as on the earth.
(D) none of these
Sol. (B)
Hence, P will run faster on the plant and S will run at the same rate, as time period will have no effect, even if acceleration due to gravity changes.
15. Two particles undergo SHM along the same line with the same line with the same time period (T) and equal amplitudes (A). At a particular instant one particle is at x =-A and the other is at x = 0. They move in the same direction. They will cross each other at
(A) (B) (C) (D)
Sol. B, C
x1 = -A cos ωt and x2 = A sin ωt
Equating x1 = x2
-A cos ωt = A sin ωt
or tan ωt = -1
or
or
or








