Laws of Motion

1. INERTIA

It is the inability of a body to change its state of rest or of uniform motion or its direction by itself.

• Mass is a measure of inertia in translatory motion
• Heavier the mass, larger the inertia & vice–versa.

Types of inertia

There are three types of inertia. (i) Inertia of rest (ii) Inertia of motion and (iii)Inertia of direction.

Inertia of rest:

It is the inability of a body to change its state of rest by itself .

Ex:When a bus is at rest and starts suddenly moving forward the passengers inside it will fall back.

Inertia of motion: It is the inability of a body to change its state of uniform motion by itself.

Ex: Passengers in a moving bus fall forward, when brakes are applied suddenly.

Inertia of direction: It is the inability of a body to change its direction of motion by itself.

Ex:When a bus takes a turn, passengers in it experience an outward force.

• A person sitting in a moving train, throws a coin vertically upwards, then

i. it falls behind him, if the train is accelerating

ii. it falls in front of him, if the train is retarding

iii. it falls into the hand of the person, if the train is moving with uniform

iv. It falls into the hand of the person if the train is at rest

2. NEWTON’S FIRST LAW

• Every body continues to be in its state of rest (or) uniform motion in a straight line unless it is  acted upon by  a net external force to change its state

• It defines inertia, force and mechanical

• If the net external force on an object is zero , then acceleration of object is

3. LINEAR MOMENTUM

Linear momentum is the product of the mass of a body and its velocity. $\overrightarrow{p}=m\overrightarrow{v}$

• Linear momentum is a It has the same direction as the direction of velocity of the body. SI unit: kg m s^-1, CGS unit: g cm s^-1

• Dimensional formula : MLT^-1

Change in momentum of a body in different cases

• Consider a body of mass m moving with velocity ${\overrightarrow{v}}_i$ and momentum ${\overrightarrow{P}}_i$. Due to a collision (or) due to the action of a force on it suppose its velocity changes to $\overrightarrow{v_f}$ Change in and momentum changes to $\overrightarrow{P_f}$ in a small time interval Δt.

Change in momentum of body = $\Delta \overrightarrow{P}={\overrightarrow{P}}_f–{\overrightarrow{P}}_i$

Where P_i = initial momentum  

             P_f  = final momentum

$\Delta \overrightarrow{P}=m\overrightarrow{v_f}–m\overrightarrow{v_i}$

$\left|\mathrm{\Delta }\overrightarrow{\mathrm{P}}\right|=\left|{\overrightarrow{\mathrm{P}}}_{\mathrm{f}}–{\overrightarrow{\mathrm{P}}}_{\mathrm{i}}\right|=\sqrt{{\mathrm{P}}_{\mathrm{f}}^2+{\mathrm{P}}_{\mathrm{i}}^2–2{\mathrm{P}}_{\mathrm{f}}{\mathrm{P}}_{\mathrm{i}}\mathrm{cos\theta }}$ where θ = angle between ${\overrightarrow{P}}_f\text{ and }{\overrightarrow{P}}_i$

Consider a body of mass ‘m’ moving

with velocity ‘ $\overrightarrow{v}$ ’along a straight line

• Case (i) : If it hits a wall and comes to rest, Change in momentum of the body

$\mathrm{\Delta }\overrightarrow{\mathrm{P}}={\overrightarrow{\mathrm{P}}}_{\mathrm{f}}–{\overrightarrow{\mathrm{P}}}_{\mathrm{i}}=0–\left(\mathrm{m}\overrightarrow{\mathrm{v}}\right)\hat{\mathrm{i}}$

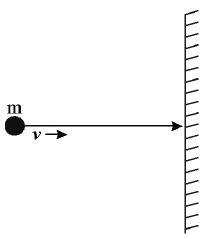
$=–\mathrm{m}\overrightarrow{\mathrm{v}}\hat{\mathrm{i}}; \left|\mathrm{\Delta }\overrightarrow{\mathrm{P}}\right|=\mathrm{mv}$, along the normal and away from the wall.  

• Case(ii) : If the body rebounds with same speed ‘ v ’ then θ = 180⁰

$\mathrm{\Delta }\overrightarrow{\mathrm{P}}={\overrightarrow{\mathrm{P}}}_{\mathrm{f}}–{\overrightarrow{\mathrm{P}}}_{\mathrm{i}}=[–(\mathrm{m}\overrightarrow{\mathrm{v}}\left)\hat{\mathrm{i}}\right]–\left[\right(\mathrm{m}\overrightarrow{\mathrm{v}}\left)\hat{\mathrm{i}}\right]=–\left(2\mathrm{m}\overrightarrow{\mathrm{v}}\right)\hat{\mathrm{i}} \therefore \left|\mathrm{\Delta }\overrightarrow{\mathrm{P}}\right|=2\mathrm{mv}$, 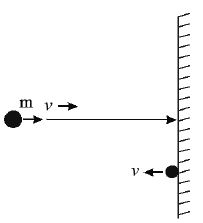along the normal and away from the wall.

• Case (iii) : If the body hits a rigid wall normally with speed v₁ and rebounds with speed v₂ then θ = 180⁰,

$\Delta \overrightarrow{P}={\overrightarrow{P}}_f–{\overrightarrow{P}}_i=\left[–\left(n{\overrightarrow{v}}_2\right)\hat{i}\right]–\left[\left(n{\overrightarrow{v}}_1\right)\hat{i}\right]$,

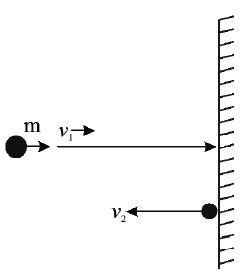
$\left|\mathrm{\Delta }\overrightarrow{\mathrm{P}}\right|=\mathrm{m}\left({\mathrm{v}}_2+{\mathrm{v}}_1\right)$, along the normal and away from the wall.

• Case (iv) : A body of mass ‘m’ moving with speed ‘ v ’ hits a rigid wall at an angle of incidence θ and rebounds with same speed ‘ v ’

$\Delta \overrightarrow{P}$ is along the normal, away from the wall

$\mathrm{\Delta }{\overrightarrow{\mathrm{P}}}_{\mathrm{x}}=–\mathrm{mvcos\theta } i–\mathrm{mvcos\theta } i$

$\mathrm{\Delta }{\overrightarrow{\mathrm{P}}}_{\mathrm{y}}=\mathrm{mvsin\theta } \mathrm{j}–\mathrm{mvsin\theta } \mathrm{j}$

$\mathrm{\Delta }\overrightarrow{\mathrm{P}}=\mathrm{\Delta }{\overrightarrow{\mathrm{P}}}_{\mathrm{x}}+\mathrm{\Delta }{\overrightarrow{\mathrm{P}}}_{\mathrm{y}}=2\mathrm{mvcos\theta }(–\mathrm{i})$

$\left|\Delta \overrightarrow{P}\right|=2mv \cos \theta$

                  

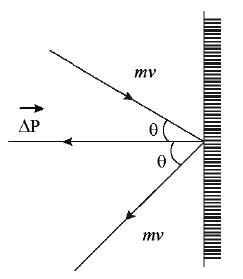
• Case(v) : In the above case if θ is the angle made with wall then away from the $\left|\Delta \overrightarrow{P}\right|=2mv \sin \theta$, along the normal and away from the wall

• Case(vi) : Projectile motion :

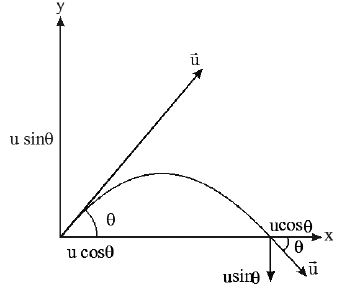
a) In case of projectile motion the change in momentum of a body between highest point and point of projection is

${\overrightarrow{\mathrm{P}}}_{\mathrm{i}}=\left(mu\cos \theta \right)\hat{i}+\left(mu\sin \theta \right)\hat{j}$

$\overrightarrow{{\mathrm{P}}_{\mathrm{f}}}=\left(mu\cos \theta \right)\hat{i}+0, \overrightarrow{\Delta P}=–\left(mu\sin \theta \right)\hat{j}$

The change in momentum of the projectile between the striking point and point of projection is

$\overrightarrow{{\mathrm{P}}_{\mathrm{i}}}=(mu \cos \theta )\hat{i}+(mu \sin \theta )\hat{j}$

$\overrightarrow{{\mathrm{P}}_{\mathrm{f}}}=(mu \cos \theta )\hat{i}–(mu \sin \theta )\hat{j}$

$\overrightarrow{\Delta P}=–(2\mathrm{mu} \sin \theta )\hat{j}$

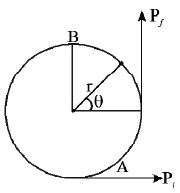
• A particle of mass ‘m’ is moving uniformly with a speed ‘ v ’ along a circular path of radius ‘r’. As it moves from a point A to another point B, such that the arc AB subtends an angle θ at the centre, then the magnitude of change in momentum is 2 m v sin(θ/2) and is directed towards the centre of the circle.

4. NEWTON’S SECOND LAW OF MOTION

• The rate of change of momentum of a body is directly proportional to the resultant (or) net external force acting on the body and takes place along the direction of

• ${\overrightarrow{\mathrm{F}}}_{\mathrm{net}}=\frac{\mathrm{d}\overrightarrow{\mathrm{p}}}{\mathrm{dt}}\text{ (or) }{\overrightarrow{\mathrm{F}}}_{\mathrm{net}}=\frac{\mathrm{d}\left(\mathrm{m}\overline{\mathrm{v}}\right)}{\mathrm{dt}}$

• In a system if only velocity changes and mass remain constant, ${\overrightarrow{\mathrm{F}}}_{\mathrm{net}}=\mathrm{m}\frac{\mathrm{d}\overrightarrow{\mathrm{v}}}{\mathrm{dt}}=\mathrm{m}\overrightarrow{\mathrm{a}}$

• In a system, if only mass changes and velocity remains constant ${\overrightarrow{F}}_{net}=\overrightarrow{v}\frac{dm}{dt}$

• Force is a vector and the acceleration produced in the body is in the direction of net force,

• SI unit : newton (N). CGS unit : dyne.

• One newton = 10⁵ dyne

• F = MLT ^-2

Gravitational units of force:

Kilogram weight (kg wt) and gram weight (g wt); 1 kg.wt = 9.8 N, 1 gm.wt= 980 dyne.

• A metallic plate of mass ‘M’ is kept held in mid air by firing ‘n’ bullets in ‘t’ seconds each of mass ‘m’ with a velocity ‘v’ from below.

• If the bullet falls dead after hitting the plate then $\frac{\mathrm{mnv}}{\mathrm{t}}=\mathrm{Mg}$

• If the bullet rebounds after hitting the plate with same velocity then  $\frac{2mnv}{t}=Mg$

Applications of variable mass

• When a machine gun fires ‘n’ bullets each of mass ‘m’ with a velocity v in a time interval ‘t’ then force needed to hold the gun steadily is $F=\frac{nmv}{t}$

• When a jet of liquid coming out of a pipe strikes a wall normally and falls dead , then force exerted by the jet of l iqui d on  the  wall  is  F = Adv²

A = Area of cross section of the pipe 

v = Velocity of jet d = density of the liquid

• If the liquid bounces back with the same velocity then the force exerted by the liquid on the wall is F = 2Adv²

• If the liquid bounces back with velocity v ‘ then the force exerted on the wall is F = Adv(v + v‘)

• When a jet of liquid strikes a wall by making an angle ‘θ’ with the wall with a velocity ‘ v ’ and rebounds with same velocity then force exerted by the water jet on wall is   dm F  2 Adv² sin θ

• If gravel is dropped on a conveyor belt at the rate of $\frac{dm}{dt}$, extra force required to keep the belt moving with constant velocity ‘u‘ is  $F=u\left(\frac{dm}{dt}\right)$

5. IMPULSE
• It is the product of impulsive force and time of act ion that produces a finite change in momentum of body.
• J = Ft = m(v-u) = change in momentum. SI unit: Ns (or) Kg – ms^-1; DF: MLT^-1
• It is a vector directed along the force
• change in momentum and Impulse are always in the same direction.

For constant force, J=Ft,
• Impulsive force is a variable, then

$\overrightarrow{\mathrm{F}}=\frac{\mathrm{d}\overrightarrow{\mathrm{p}}}{\mathrm{dt}}, \mathrm{J}={\int }_{{\mathrm{t}}_1}^{{\mathrm{t}}_2} \mathrm{F} \mathrm{dt}$

• The area bounded by the force-time graph measures Impulse.

Application of Impulse
a) shock absorbers are used in vehicles to reduce the magnitude of impulsive force.
b) A cricketer lowers his hands, while catching the ball to reduce the impulsive force.
6. EQUILIBRIUM
The necessary and sufficient conditions for the translational equilibrium of the rigid body.

$\sum \mathrm{F}=0; \sum {\mathrm{F}}_{\mathrm{x}}=0, \sum {\mathrm{F}}_{\mathrm{y}}=0,$

$\sum {\mathrm{F}}_{\mathrm{z}}=0$  For rotational equilibrium

$\sum \mathrm{\tau }=0: \sum {\mathrm{\tau }}_{\mathrm{x}}=0, \sum {\mathrm{\tau }}_{\mathrm{y}}=0, \sum {\mathrm{\tau }}_{\mathrm{z}}=0$

• As for a body, $\overrightarrow{\mathrm{F}}=0, \mathrm{m}\overrightarrow{\mathrm{a}}=0 (\propto \overrightarrow{\mathrm{F}}=\mathrm{n}\overrightarrow{\mathrm{a}}) \frac{\mathrm{d}\overrightarrow{\mathrm{v}}}{\mathrm{dt}}=0$ (as m is finite and $\overrightarrow{\mathrm{a}}=\frac{\mathrm{d}\overrightarrow{\mathrm{v}}}{\mathrm{dt}}$) $\overrightarrow{v}$ = constant or zero

• If a body is in translatory equilibrium it will be either at rest or in uniform motion. If it is at rest, the equilibrium is called static, otherwise dynamic.
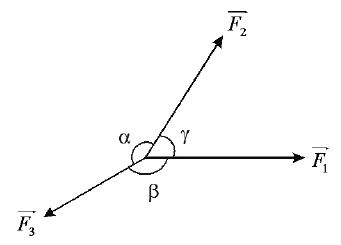
• If ‘ n ’coplanar forces of equal magnitudes acting simultaneously on a particle at a point, with the angle between any two adjacent forces is ‘θ’ and keep it in equilibrium, then $\theta =\frac{360}{n}$

Lami’s Theorem

• If an object O is in equilibrium under three concurrent forces ${\overrightarrow{F}}_1,\overrightarrow{F_2}\text{ and }\overrightarrow{ F_3}$ as shown in figure. Then, $\frac{{\mathrm{F}}_1}{\mathrm{sin\alpha }}=\frac{{\mathrm{F}}_2}{\mathrm{sin\beta }}=\frac{{\mathrm{F}}_3}{\mathrm{sin\gamma }}$

• If the bob of simple pendulum is held at rest by applying a horizontal force ‘F’ as shown in fig

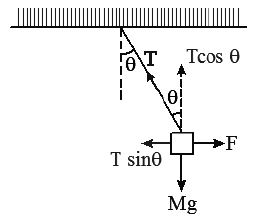
If body is in equilibrium

$T\sin \theta =F, T\cos \theta =mg$

$\mathrm{F}=\mathrm{mg} \mathrm{tan\theta }, \sqrt{{\mathrm{F}}^2+(\mathrm{mg}{)}^2}=\mathrm{T}$

$\frac{x}{F}=\frac{l}{T}=\frac{\sqrt{l^2–x^2}}{mg}$

7. NEWTON’S THIRD LAW
For every action there is always an equal and opposite reaction
• Action and reaction do not act on the same body and they act on different bodies at same instant of time
• Action and reaction, known as pair of forces, are equal in magnitude and opposite in directions acting on
different bodies in interaction. So they never cancel each other
• Newton’s third law is not applicable to pseudo forces.
• Newton’s third law defines nature of force and gives the law of conservation of linear momentum.

Examples
• When we walk on a road we push the road backwards and road applies equal (in magnitude) and opposite force
on us, so that we can move forward.
• When we swim on water we push water backward and water applies equal (in magnitude) and opposite force on
us, so that we can move forward.
• A bird is in a wire cage hanging from a spring balance. When the bird starts flying in the cage, the reading of the
balance decreases.
• If the bird is in a closed cage (or) air tight cage and it hovers in the cage the reading of the spring balance does
not change.
• In the closed cage if the bird accelerates upward the reading of the balance is bird $R=W_{\text{bird }}+ma$
Limitations of newton’s third law:-
• Newton’s third law is not strictly applicable for the interaction between two bodies separated by large distances,
of the order of astronomical units.
• It does not apply strictly when the objects move with velocity nearer to that of light
• It does not apply where the gravitational field is strong.

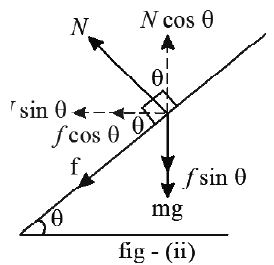
Normal reaction/force
Normal force acts perpendicular to the surfaces in contact when one body tries to press on the surface of the second body. In this way second body tries to push away the first body.

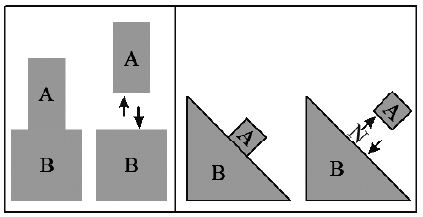
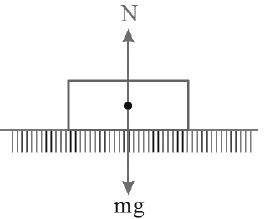
• When the body lies on a horizontal surface N = mg

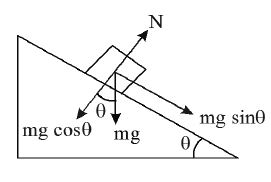
• When the body lies on an inclined surface
N = mg cos θ

8. FREE BODY DIAGRAM NET FORCE
When several bodies are connected by strings, springs, surfaces of contact, then all the forces acting on a body are
considered and sketched on the body under consideration by just isolating it . Then the diagram so formed is called Free Body Diagram (FBD).
Some examples:
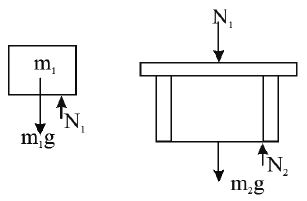
i) A block is placed on a table and the table is kept on earth. Assuming no other body in the universe exerts any
force on the system, make the FBD of block and table.

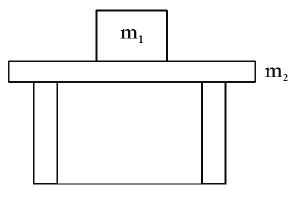
FBD of block,     N₁ = m₁g
FBD of table

$N_2=N_1+m_{2}g=m_{1}g+m_{2}g=\left(m_1+m_2\right)g$

ii) A block of mass M is suspended from the ceiling by means of a uniform string of mass m. Find the tension in the string at points A,B and C. B is the mid point of string. Also find the tensions A,B and C if the mass of string is
negligible or it is massless.

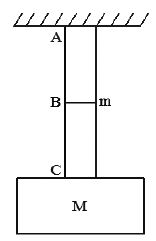
Tension at any point will be weight of the part below it.

So, ${\mathrm{T}}_{\mathrm{A}}=(\mathrm{M}+\mathrm{m})\mathrm{g},{\mathrm{T}}_{\mathrm{B}}=\left(\frac{\mathrm{m}}{2}+\mathrm{M}\right)\mathrm{g}, {\mathrm{T}}_{\mathrm{C}}=\mathrm{Mg}$

Now if the string is massless: m=0 then $T_A=T_B=T_C=Mg$. So in a massless string, tension is the same at every point.

(iii) Find the tension in the massless string connected to the block accelerating upward.

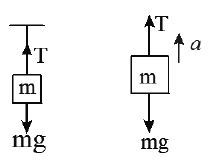
Net force :

F_net = T – mg Now apply net F_net = ma

$\Rightarrow$ T – mg = ma $\Rightarrow$ T = mg + ma = m(g + a)

Note: If ‘a’ is downward, then replace a with -a; we get T = m(g – a)

In free fall a=g then T=0.

9. FRAMES OF REFERENCE
A system of coordinate axes which defines the position of a particle or an event in two or three dimensional space is called a frame of reference.
There are two types of frames of reference
a) inertial or non-accelerated frames of reference
b) non-inertial or accelerated frames of reference
Inertial frames of reference
a) Frames of reference in which Newton’s Laws of motion are applicable are called inertial frame.
b) Inertial frames of reference are either at rest or move with uniform velocity with respect to a fixed imaginary axis.
c) In inertial frame, acceleration of a body is caused by real forces.
d) Equation of motion of mass ‘m’ moving with acceleration ‘a’ relative to an observer in an inertial frame is $\sum {\overrightarrow{F}}_{\text{real }}=ma$
Examples:
1) A lift at rest,
2) Lift moving up(or)down with constant velocity,
3) Car moving with constant velocity on a straight road.
Real Force
Force acting on an object due to its interaction with another object is called a real force.
Ex: Normal force, Tension, weight, spring force, muscular force etc.
a) All fundamental forces of nature are real.
b) Real forces form action, reaction pair.
Non-Inertial frames
a) Frames of reference in which Newton Laws are not applicable are called non-inertial frames.
b) Accelerated frames move with either uniform acceleration or non uniform acceleration.
c) All the accelerated and rotating frames are non-inertial frames of reference.
d) Examples:
1) Accelerating car on a road.
2) Merry go round.
3) Artificial satellite around the earth.

Pseudo force
a) In non-inertial frame Newton’s second law is not applicable. In order to make Newton’s second law applicable in non-inertial frame a pseudo force is introduced.
b) If $\overrightarrow{a}$ is the acceleration of a non-inertial frame, the pseudo force acting on an object of mass m, as measured by an observer in the given non-inertial frame is ${\overrightarrow{F}}_{P\text{seudo }}=–m\overrightarrow{a}$
i.e. Pseudo force acts on an object opposite to the direction of acceleration of the non-inertial frame.
c) Pseudo forces exist for observers only in non-inertial frames, such forces have no existence relative to an inertial frame.
d) Equation of motion relative to non-inertial frame is $\sum \left({\overrightarrow{F}}_{\text{real }}+{\overrightarrow{F}}_{\text{Pseudo }}\right)=m\overrightarrow{a^{‘}}$
Where a’ is the acceleration of body as measured in non-inertial frame.
e) Earth is an inertial frame for an observer on the earth but it is an accelerated frame for an observer at centre of earth (or) in a satellite.
Examples : (i) Centrifugal force and deflection of pendulum relative to accelerating car.(ii) Gain or loss of weight experienced in an accelerating elevator.

10. APPARENT WEIGHT OF A BODY IN A MOVING ELEVATOR
Weight of a body on a surface comes due to the reaction of a supporting surface, i.e., Apparent weight of a body in a lift.
W_app = Reaction of supporting surface. Consider a person standing on a spring balance , or in a lift. The following situations are possible:
Case(i) : If lift is at rest or moving with constant velocity then the person will be in translatory equilibrium. So, R = mg

$\therefore W_{app}=mg \left[\text{ as }{W}_{app}=R\right]$

or $W_{app}=W_{0 }\left[\text{ as }{W}_0=mg=\text{ true weight }\right]$

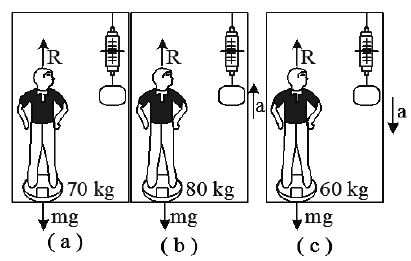
i.e., apparent weight (reading of balance) will be equal to true weight.
Case(ii) : If lift is accelerated up or retarding down with acceleration a from Newton’s II law we have
R – mg = ma or R = m (g + a)

or  ${\mathrm{W}}_{\mathrm{app}}=\mathrm{m}(\mathrm{g}+\mathrm{a})=\mathrm{mg}\left[1+\frac{\mathrm{a}}{\mathrm{g}}\right]={\mathrm{W}}_0\left[1+\frac{\mathrm{a}}{\mathrm{g}}\right]\text{ or }{\mathrm{W}}_{\mathrm{app}}>{\mathrm{W}}_0$
i.e., apparent weight (reading of balance) will be more than true weight.
Case (iii) : If lift is accelerated down: or retarding up with acceleration ‘a’ mg – R = ma i.e., R = m(g – a)

or  $W_{app}=m(g–a)\left[\text{ as }{W}_{app}=R\right]=mg\left[1–\frac{a}{g}\right]$

$\text{ i.e., }{\mathrm{W}}_{\mathrm{app}}={\mathrm{W}}_0\left[1–\frac{\mathrm{a}}{\mathrm{g}}\right] {\mathrm{W}}_{\mathrm{app}}<{\mathrm{W}}_0$

i.e., apparent weight (reading of balance) will be lesser than true weight.

Note: If , $a>g,W_{app}$ will be negative; negative weight will mean that the body is pressed against the roof of the lift instead of floor (as lift falls more faster than the body) and so the reaction will be downwards, the direction of apparent weight will be upwards.
Case (iv) : If lift is in freely falling, Then a=g ,

So mg – R = mg    i.e., R = 0.  So, $W_{app}=0$

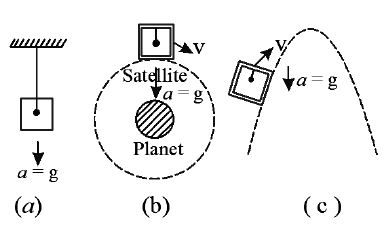
(a) Freely falling lift
(b) Satellite motion
(c) Projectile motion
i.e., apparent weight of a freely falling body is zero.
• This is why the apparent weight of a body is zero, or body is weightless if it is in a (i) lift whose cable has broken, (ii) orbiting satellite.

11. CONNECTING BODIES
• If masses are connected by strings then acceleration of system and tension in the strings on smooth horizontal surface are

a)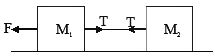

Free body diagram for M₂

$\mathrm{T}\leftarrow \boxed{{\mathrm{M}}_2} \mathrm{T}={\mathrm{M}}_{2}a\dots ..\left(1\right)$

Free body diagram for M₁

$\mathrm{F}\leftarrow \boxed{{\mathrm{M}}_1}\to \mathrm{T} \mathrm{F}–\mathrm{T}={\mathrm{M}}_{1}a\dots \left(2\right)$

from (1) and (2)

$\mathrm{a}=\frac{\mathrm{F}}{\left({\mathrm{M}}_1+{\mathrm{M}}_2\right)}\text{ and }\mathrm{T}=\frac{{\mathrm{M}}_2\mathrm{F}}{\left({\mathrm{M}}_1+{\mathrm{M}}_2\right)}$

b)

$\mathrm{a}=\frac{\mathrm{F}}{{\mathrm{M}}_1+{\mathrm{M}}_2+{\mathrm{M}}_3};{\mathrm{T}}_1=\frac{\left({\mathrm{M}}_2+{\mathrm{M}}_3\right)\mathrm{F}}{\left({\mathrm{M}}_1+{\mathrm{M}}_2+{\mathrm{M}}_3\right)}$

${\mathrm{T}}_2=\frac{{\mathrm{M}}_3\mathrm{F}}{\left({\mathrm{M}}_1+{\mathrm{M}}_2+{\mathrm{M}}_3\right)}$

• If masses are connected by a string and suspended from a support then tension in the string when force F is applied downwards as shown in the figure

From (1) and (2), $T_2=F+\left(M_1+M_2\right)g$

Contact Forces
When two objects are in contact with each other, the molecules at the interface interact with each other. This interaction results in a net force called contact force. The contact force can be resolved into two components.
(a) Normal force (N): Component of the contact force along the normal to the interface. Normal force is independent of nature of the surfaces in contact.
(b) Friction (f): Component of the contact force along the tangent at the interface. Friction depends on the roughness of the surfaces in contact. This component can be minimised by polishing the surfaces.
• The tension and contact forces are self adjustable forces. Their magnitude and direction change when other forces involved in a physical arrangement change.
• Masses are in contact on a smooth horizontal surface:

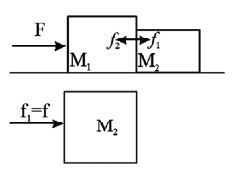
contact force ${\mathrm{f}}_1={\mathrm{f}}_2=\mathrm{f}={\mathrm{M}}_2\mathrm{a}$

free body diagram for M₁

$\mathrm{F}–\mathrm{f}={\mathrm{M}}_1\mathrm{a} \dots \dots \dots \left(1\right)$

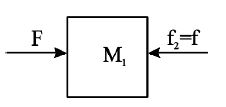
free body diagram for M₂

$\mathrm{f}={\mathrm{M}}_2\mathrm{a}\dots \dots \dots \left(2\right)$

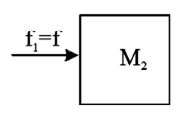
From (1) and (2)

$\mathrm{a}=\frac{\mathrm{F}}{\left({\mathrm{M}}_1+{\mathrm{M}}_2\right)}$, contact force, $\mathrm{f}=\frac{{\mathrm{M}}_2\mathrm{F}}{{\mathrm{M}}_1+{\mathrm{M}}_2}$

• Contact forces are as shown in the figure

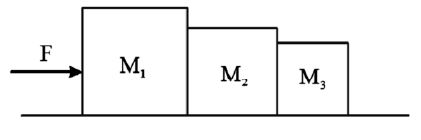
a) Acceleration of system,  $\mathrm{a}=\frac{\mathrm{F}}{\left({\mathrm{M}}_1+{\mathrm{M}}_2+{\mathrm{M}}_3\right)}$

b) Contact force between  ${\mathrm{M}}_1\text{ and }{\mathrm{M}}_2$

$\mathrm{f}=\left({\mathrm{M}}_2+{\mathrm{M}}_3\right)\mathrm{a}$

c) Contact force between ${\mathrm{M}}_2\text{ and }{\mathrm{M}}_3, {\mathrm{f}}^1={\mathrm{M}}_3\mathrm{a}$

Atwood’s Machine

• Masses M₁ and M₂ (M₁ > M₂ )are tied to a string , which passes over a frictionless light pulley The string is light and inextensible.

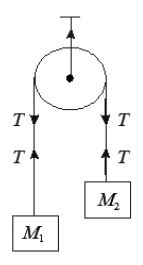
Acceleration of the system, $a=\frac{\left(M_1–M_2\right)g}{M_1+M_2}$

Tension in the string, $T=\left(\frac{2M_1{M}_2}{M_1+M_2}\right)g$

Thrust on the pulley,  $2T=\left(\frac{4M_1{M}_2}{M_1+M_2}\right)g$

• If the pulley begins to move with acceleration $\overrightarrow{a}$ then

i) If the pulley accelerates upward , then $a_{net}=\left(\frac{M_1–M_2}{M_1+M_2}\right)(g+a)$ and $T_{net}=\left(\frac{2M_1{M}_2}{M_1+M_2}\right)(g+a)$

ii) If the pulley accelerates downward, then $a_{net}=\left(\frac{M_1–M_2}{M_1+M_2}\right)(g–a)\text{ and }{T}_{net}=\left(\frac{2M_1{M}_2}{M_1+M_2}\right)(g–a)$

• Two blocks are connected by a string passing over a pulley fixed at the edge of a horizontal table then the acceleration of system and tension in the string $\left({\mathrm{M}}_2>{\mathrm{M}}_1\right)$

$M_{2}g–T=M_{2}a\text{ and }T=M_{1}a$

$\Rightarrow \mathrm{a}=\frac{{\mathrm{M}}_2\mathrm{g}}{\left({\mathrm{M}}_1+{\mathrm{M}}_2\right)}$

$T=M_{1}a=\frac{M_1{M}_{2}g}{\left(M_1+M_2\right)}$

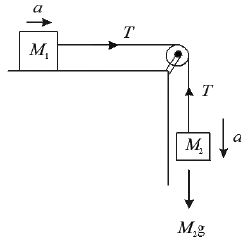
• Acceleration and Tension in the string when bodies are connected as shown in the figure if
M₁ > M₃.

$M_{1}g–T_1=M_{1}a; T_1–T_2=M_{2}a$

$T_2–M_{3}g=M_{3}a$

$\Rightarrow a=\frac{\left(M_1–M_3\right)g}{\left(M_1+M_2+M_3\right)}$

$T_2=\frac{M_{3}g\left(2M_1+M_2\right)}{M_1+M_2+M_3}; T_1=\frac{M_{1}g\left(2M_3+M_2\right)}{M_1+M_2+M_3}$

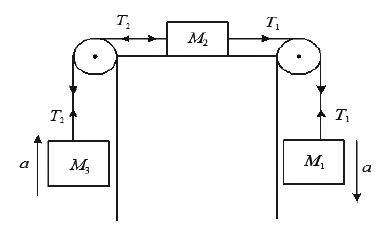
Ø Masses are attached to a string passing through the pulley attached to the edge of an inclined plane, acceleration of system and tension in the string if M₂ moves down

$a=\left(\frac{M_2–M_1\sin \theta }{M_1+M_2}\right)g$

$T=\left[\frac{M_1{M}_2(1+\sin \theta )}{\left(M_1+M_2\right)}\right]g$

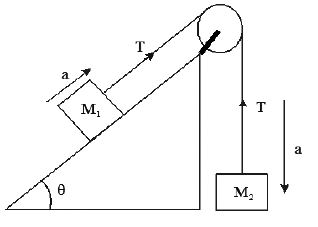
Thrust on the pulley : Resultant Tension =

$T_g=\sqrt{T^2+T^2+2T^2\cos (90–\theta )}$

$T_g=\sqrt{2T^2(1+\sin \theta )}=T\sqrt{2(1+\sin \theta )}$

• If position of masses is interchanged, then the tension in the string and acceleration remains unchanged.

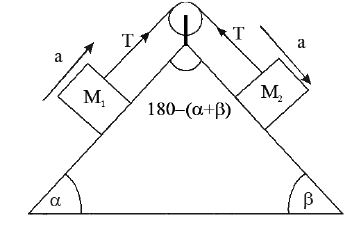
• If M₂ slides down then M₁ moves up on double smooth inclined plane then the acceleration of system and tension in the string are given by, acceleration , a = $\left(\frac{M_2\sin \beta –M_1\sin \alpha }{M_1+M_2}\right)g$

Tension, $\mathrm{T}=\frac{M_1{M}_{2}g}{\left(M_1+M_2\right)}(\sin \alpha +\sin \beta )$

Resultant Tension $T_R=\sqrt{T^2+T^2+2T^2\cos [180–(\alpha +\beta \left)\right]}$

$=\sqrt{2T^2[1–\cos (\alpha +\beta \left)\right]}$

Note:- If M₂ sinβ = M₁ sinα $\Rightarrow$a = 0

$\Rightarrow$ System does not accelerate
b) For the tension in the string between A and B.
FBD of Body A

$m_{A}g\sin 60–T_1=m_{A}a$

$T_1=m_{A}g\sin 60–m_{A}a=m_A(g\sin 60–a)$

$T_1=\left(1\right)\left(10\times \frac{\sqrt{3}}{2}–4.1\right)=4.56N$

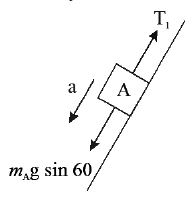
For the tension in the string between B and C
FBD of body C

$T_2–m_{C}g\sin 30°=m_{c}a; T_2=m_C\left(g\sin 30°+a\right)$

$T_2=2\left(10\left(\frac{1}{2}\right)+4.1\right)=18.2N$

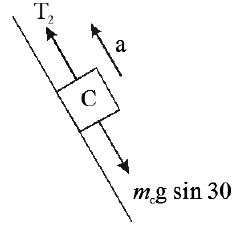
• A force F is applied on the massless pulley as shown in the figure and string is connected to the block on smooth horizontal surface. Then

$\mathrm{F}=2 \mathrm{T}\text{ and }T=m{a}_{\text{block }}$

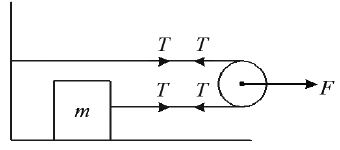
• If the block moves a distance ‘x’ the pulley moves x/2 (Total length of the string remains constant)

Therefore acceleration of the pulley = $\frac{a_{\text{block }}}{2}$

$=\frac{T}{2m}=\frac{F/2}{2m}=\frac{F}{4m}$.

12. CONSTRAINED MOTION
(a) Constraint : Restriction to the free motion of body in any direction is called constraint.
(b) Constrained Body : A body, whose displacement in space is restricted by other bodies, either connected to or in contact with it, is called a constrained body.
(c) Kinematic Constraints : These are equations that relate the motion of two or more particles.
(d) Types of Constraints :
i) General constraints 
ii) Pulley constraints
iii) Wedge constraints
iv) Mixed constraints

General Constraints
i) A body placed on floor : The floor acting as a constraint restricts the kinematical quantities in the downward direction such that

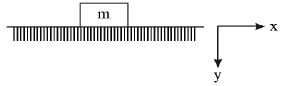
y = 0 ; $v_y=0\text{ and }{a}_y=0$ for the body placed on the floor.

ii) Two bodies connected with a string or rod.

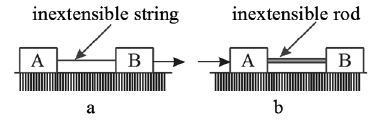
The string / rod is inextensible.

∴ Displacements of A and B are equal in horizontal direction $\Rightarrow s_A=s_B$

Differentiating w.r.t time, $\frac{d{s}_A}{dt}=\frac{d{s}_B}{dt}\Rightarrow v_A=v_B$

Again differentiating

$\frac{d{v}_A}{dt}=\frac{d{v}_B}{dt}\Rightarrow a_A=a_B$

iii) Two bodies in contact with each other
• Displacement of A and B are equal in horizontal direction.

$\Rightarrow s_A=s_B$

By differentiating, we will get

$v_A=v_B\text{ and }{a}_A=a_B$ in horizontal direction

Pulley Constraints
• For example, the motion of block A is downwards along the inclined plane in fig. will cause a corresponding motion of block B up the other inclined move, the string AB length is inextensible, i.e., length of AB is constant.

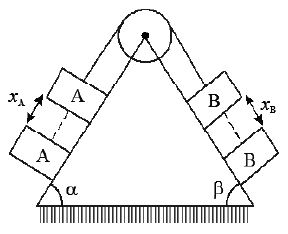
∴ The displacements of $A\left(x_A\right)\text{ and }B\left(x_B\right)$ are equal $\therefore x_A=x_B$

Differentiating w.r.t. time, $\Rightarrow v_A=v_B$

Once again differentiating w.r.t. time, $\Rightarrow a_A=a_B$

i.e., if one body (A) moves down the inclined plane with certain acceleration, then the other body will move up inclined plane with an equal acceleration (magnitude).
Alternate Method : First specify the location of the blocks using position co-ordinates ${\mathrm{S}}_{\mathrm{A}}\text{ and }{\mathrm{S}}_{\mathrm{B}}$.

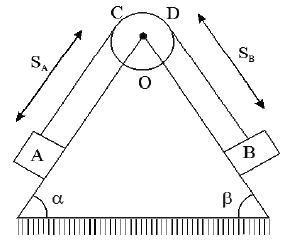
From the fig. the position co-ordinates are related by the equation $s_A+l_{CD}+s_B=L$

where $l_{CD}=$the length of the string over arc

CD = constant L = total length of the string = constant Differentiating w.r.t. time, we get

$\frac{d{s}_A}{dt}+\frac{d{s}_B}{dt}=0\Rightarrow v_B=–v_A$

The negative sign indicates that when block A has a velocity downward, i.e., in the direction of positive A, s it causes a corresponding upward velocity of block B, i.e., B moves in the negative B s direction.
Again differentiating w.r.t. time,

$\frac{d{v}_B}{dt}=–\frac{d{v}_A}{dt}\Rightarrow a_B=–a_A$

Similarly

1)

$x_A=x_B\Rightarrow v_A=v_B\Rightarrow a_A=a_B$

2)

$x_A=x_B\Rightarrow v_A=v_B\Rightarrow a_A=a_B$

Mixed constraints
Ring sliding on a smooth rod :
• Consider a ring of mass m connected through a string of length L with a block of mass M. If the ring is moving up with acceleration $a_m\text{ and }{a}_M$ is the acceleration of block. As the length of the string is constant,

$L=\sqrt{d^2+y^2}+x$

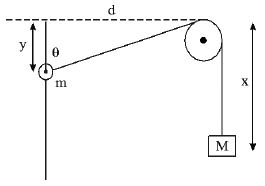
Since, L is constant, differentiating with respect to time t, we get

$\frac{dL}{dt}=\frac{1}{2}\frac{2y}{{\left(d^2+y^2\right)}^{\frac{1}{2}}}\left(\frac{dy}{dt}\right)+\frac{dx}{dt}=0$

Since $\frac{dy}{dt}=v_m\text{ and }\frac{dx}{dt}=v_M\text{ and }$

$\cos \theta =\frac{y}{\sqrt{d^2+y^2}} \text{ so }{v}_M=–v_m\cos \theta$

By differentiating, relation between ${\mathrm{a}}_{\mathrm{m}}\text{ and }{\mathrm{a}}_{\mathrm{M}}$ can be obtained, however, while doing so remember that cosθ is not constant, but it is variable.
Two blocks connected with pulley : If the blocks are connected as shown in fig, then the length of the string is

$L=2\sqrt{d^2+y^2}+x$

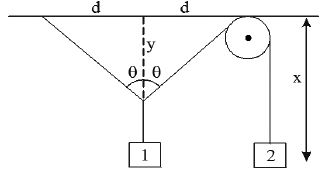
Since, L is constant, differentiating with respect to time t, we get

$\frac{dL}{dt}=\frac{2\times 2y}{2{\left(d^2+y^2\right)}^{\frac{1}{2}}}\left(\frac{dy}{dt}\right)+\frac{dx}{dt}=0$

$\Rightarrow 2v_1\cos \theta +v_2=0;v_2=–2v_1\cos \theta$

Note :If inclination is given as 1 in x, $\sin \theta =\frac{1}{x}$

$\tan \theta =\frac{1}{\sqrt{x^2–1}}$

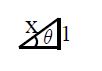
$\Rightarrow$ Acceleration $a=g\tan \theta =\frac{g}{\sqrt{x^2–1}}$

13. LAW OF CONSERVATION OF MOMENTUM
When the resultant external force acting on a system is zero, the total momentum (vector sum) of the system remains constant. This is called “law of conservation of linear momentum”.
• Newton’s third law of motion leads to the law of conservation of linear momentum.
• Walking, running, swimming, jet propulsion, motion of rockets, rowing of a boat, recoil of a gun etc., can be explained by Newton’s third law of motion.
• Explosions, disintegration of nuclei, recoil of gun, collisions etc., can be explained on the basis of the law of conservation of linear momentum.

Applications
• When a shot is fired from a gun, while the shot moves forwards, the gun moves backwards. This motion of gun is called recoil of the gun. When a gun of mass ‘M’ fires a bullet of mass ‘m’ with a muzzle velocity ‘v’, the gun recoils with a velocity ‘V’ given by V = mv/M.
• When a bullet of mass ‘m’ moving with a velocity ‘v’ gets embedded into a block of mass M at rest and free to move on a smooth horizontal surface, then their common velocity` V = mv/ (M + m).
• A boy of mass ‘m’ walks a distance ‘s’ on a boat of mass ‘M’ that is floating on water and initially at rest. If the boat is free to move, it moves back a distance d = ms / (M + m).

Explosion of Bomb
• A shell of mass ‘M’at rest explodes into two fragments and one of masses ‘m’ moves out with a velocity ‘ v ’ the other piece of mass (M– m) moves in opposite direction with a velocity of V = mv / (M – m).
• Suppose a shell of mass m at rest explodes into three pieces of masses $m_1,m_2\text{ and }{m}_3$, moving with velocities

$\overrightarrow{v_1},\overrightarrow{v_2}\text{ and }\overrightarrow{v_3}$ respectively.

$m_1{\overrightarrow{v}}_1={\overrightarrow{p}}_1; m_2{\overrightarrow{v}}_2={\overrightarrow{p}}_2; m_3{\overrightarrow{v}}_3={\overrightarrow{p}}_3$

${\overrightarrow{p}}_1+{\overrightarrow{p}}_2+{\overrightarrow{p}}_3=m_1\overrightarrow{v_1}+m_2\overrightarrow{v_2}+m_3\overrightarrow{v_3}=0$

(as shell is at rest initially)   $\therefore {\overrightarrow{p}}_3=–\left({\overrightarrow{p}}_1+{\overrightarrow{p}}_2\right)$

So the third piece moves with the same magnitude of the resultant momentum of the other two pieces but in opposite direction.

$P_3=\sqrt{P_1^2+P_2^2+2P_1{P}_2\cos \theta }$

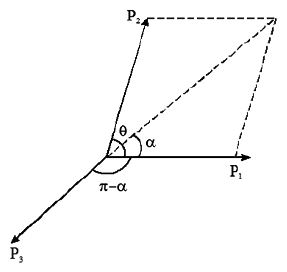
θ = angle between ${\overrightarrow{P}}_1,{\overrightarrow{P}}_2$

$(\pi –\alpha )$ = angle between ${\overrightarrow{P}}_3,{\overrightarrow{P}}_1$

$\tan \alpha =\frac{P_2\sin \theta }{P_1+P_2\cos \theta }$

Explosion of a shell travelling in a parabolic path at its highest point: (into two fragments)
• Consider a shell of mass M as a projectile with velocity u and angle of projection θ. Suppose the shell breaks into two fragments at maximum height and their initial velocities are $\overrightarrow{v_1}\text{ and }\overrightarrow{v_2}$

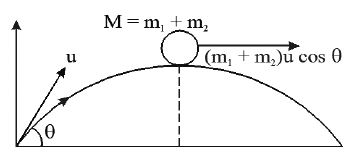
Total momentum of the two parts is constant just before and just after the explosion.

$\left[m_1+m_2\right]u\cos \theta \overrightarrow{i}=m_1{\overrightarrow{v}}_1+m_2{\overrightarrow{v}}_2$

Case : (i) If the fragments travel in opposite direction after explosion then

$\left(m_1+m_2\right)u\cos \theta \overrightarrow{i}=m_1{v}_1\overrightarrow{i}–m_2{v}_2\overrightarrow{i}$

Case : (ii) If one fragment retraces its path and falls at the point of projection

$\left(m_1+m_2\right)u\cos \theta \overrightarrow{i}=–m_{1}u\cos \theta \overrightarrow{i}+m_2{\overrightarrow{v}}_2$

Case:(iii) If one fragment falls freely after explosion

$\left(m_1+m_2\right)u\cos \theta \overrightarrow{i}=m_{1}0+m_2{\overrightarrow{v}}_2$

$\left(m_1+m_2\right)u\cos \theta \overrightarrow{i}=m_2{\overrightarrow{v}}_2$

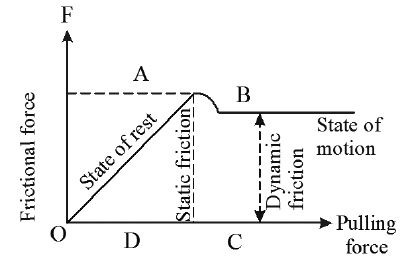
14. FRICTION
If we slide or try to slide a body over another surface, the motion of the body is resisted by bonding between the body and the surface.This resistance is called friction.
• The force of friction is parallel to the contact surfaces and opposite to the direction of intended or relative motion.
• There are three types of frictional forces
i. Static friction
ii. Dynamic friction
iii. Rolling friction
• If a body is at rest and no pulling force is acting on it,force of friction on it is zero.
• If a force is applied to move the body and it does not move,the friction developed is called static friction, which is equal in magnitude and opposite in direction to the applied force (moves, the is self adjusting force).
• If a force is applied to move the body and it moves,the friction developed is called dynamic or kinetic friction.
• When a body rolls or rotates on the surface of another body friction developed is called as rolling friction.
• It is due to the deformation at the point of contact and depends on area of contact.

Note-i: If you are walking due east the feet slides relatively due west so the frictional force is due east.
Note-ii: Engine is connected to rear wheels of a car. When the car is accelerated, direction of frictional force on the rear wheels will be in the direction of motion and on the front wheels in the opposite direction of motion
Note-iii: In cycling ,the force exerted by rear wheel on the ground makes the force of friction to act on it in the forward direction. Front wheel moving by itself experience force of friction in backward direction.
Note-iv: When pedaling is stopped, the frictional force is in backward direction for both the wheels.
Laws of Friction:
• Friction is directly proportional to the normal reaction acting on the body.
• The law of static friction may thus be written as

$f_s\le {\mu }_{s}N$. Where the dimensionless constant ${\mu }_s$ is called the coefficient of static friction and N is the magnitude of the normal force.

${\left(f_s\right)}_{max}=f_l={\mu }_{s}N; f_l$ = Limiting friction

• Coefficient of static friction (${\mu }_s$) depends on the nature of the two surfaces in contact and is independent of the area of contact.
• Static friction is independent of the area of contact between the two surfaces
• Coefficient of kinetic friction $\left({\mu }_k\right)=\frac{f_k}{N}$.
It is independent of velocity of the body.
• Coefficient of rolling friction $\left({\mu }_R\right)=\frac{f_R}{N}$
• Rolling friction depends on the area of the surfaces in contact.
Note : ${\mathrm{\mu }}_{\mathrm{S}}>{\mathrm{\mu }}_{\mathrm{K}}>{\mathrm{\mu }}_{\mathrm{R}}$
• Friction depends on the nature of the two surfaces in contact i.e., nature of materials, surface finish, temperature of the two surfaces etc.

Angle of Friction

• Angle made by the resultant of f and N with the normal reaction N is called angle of friction.
• Friction is parallel component of contact force to the surfaces.
• Normal force is perpendicular component of contact force to the surfaces.

$R=\sqrt{f^2+N^2}$

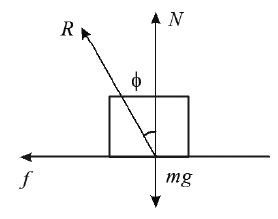
When the block is static  $\tan \varphi =\frac{f}{N}; \varphi \le {\varphi }_s$

When the block is in impending state, $\tan {\varphi }_s=\frac{{\mu }_{s}N}{N}={\mu }_s$

Where ${\varnothing }_s \to$ maximum angle of friction.

When block is sliding, $\tan {\varphi }_k=\frac{{\mu }_{k}N}{N}={\mu }_k$

Since ${\mu }_s>{\mu }_k$, it follows that ${\varphi }_s>{\varphi }_k$.

$F_R=\sqrt{f_l^2+N^2}=\sqrt{{\left({\mu }_{s}N\right)}^2+N^2}=N\sqrt{{\mu }_s^2+1}$

$F_R=mg\sqrt{{\tan }^2\varphi +1} \left(\therefore {\mu }_s=\tan \varphi \right)$

$F_R=mg\sec \varphi$

15. MOTION ON A HORIZONTAL ROUGH SURFACE
Consider a block of mass m place on a horizontal surface with normal reaction N.
Case (i) : If applied force F = 0, the force of friction is zero.

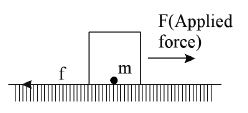
Case (ii): If applied force $F<{\left(f_s\right)}_{\max }$, the block does not move and the force of friction is $\boxed{f_s=F}$

Case (iii): If applied force F = ${\left(f_s\right)}_{max}$ , block just ready to slide and frictional force $\boxed{{\left(f_s\right)}_{\max }=f_l={\mu }_{s}N}$

$F={\mu }_{s}mg (\because N=mg); \text{ (at time }\mathrm{t}=0\text{)}$

Case(iv): If the above applied force continues to act ( t $\ne$ 0) the body gets motion, static friction converts as kinetic friction and body possesses acceleration

$a=\frac{F_{ext}–f_k}{m}=\frac{f_l–f_k}{m}=\left({\mu }_s–{\mu }_k\right)g$

Case (v): If the applied force is greater than limiting friction the body starts moving and gets acceleration

$a=\frac{F_{\text{ext }}^1–f_k}{m}\text{ Here }{F}_{ext}^1>F_{\text{ext }}$

• If the block slides with an acceleration ‘ a ’under the influence of applied force ‘F’,

$F_R=F–f_k; ma=F–f_k$

$\therefore a=\frac{F–f_k}{m}=\frac{F–{\mu }_{k}mg}{m}\left(f_k={\mu }_{K}N={\mu }_{K}mg\right)$

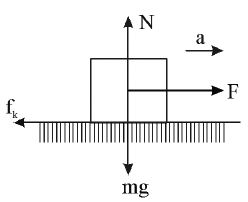
Bodies in contact with vertical surfaces:

• A block of mass m is pressed against a wall without falling, by applying minimum horizontal force F. Then

$\mathrm{F}=\frac{\mathrm{mg}}{{\mu }_s}$

$f_s=mg; {\mu }_{s}N=mg$

${\mu }_{s}F=mg (\because N=F)\Rightarrow F=\frac{mg}{{\mu }_s}$

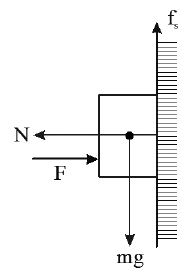
• A block is pressed between two hands without falling, by applying minimum horizontal force ‘F’ by each hand. Then $\mathrm{F}=\frac{\mathrm{mg}}{2{\mu }_s}$

$\mathrm{W}=2{\mathrm{f}}_{\mathrm{s},}; mg=2{\mu }_{s}F\Rightarrow F=\frac{mg}{2{\mu }_s}$

Sliding block on a horizontal rough surface coming to rest :

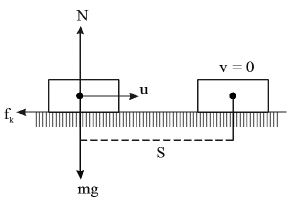
a) The acceleration of the block is $\boxed{a=–{\mu }_{k}g}$

b) Distance travelled by the block before coming to rest is $\boxed{S=\frac{u^2}{2{\mu }_{k}g}}$

c) Time taken by the block to come to rest is  $t=\frac{u}{{\mu }_{k}g}$

• An insect is crawling in a hemispherical bowl of radius ‘r’. Maximum height up to which it can crawl is

$\mathrm{h}=\mathrm{r}(1–\cos \theta )=\mathrm{r}\left(1–\frac{1}{\sqrt{{\mu }_{\mathrm{s}}^2+1}}\right)$

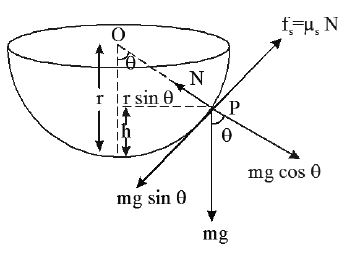
Maximum angular displacement up to which it can crawl is ‘ θ ’. Then ${\mu }_s=\tan \theta$

• A block is placed on rear horizontal surface of a truck moving along the horizontal with an acceleration ‘a’.
Then

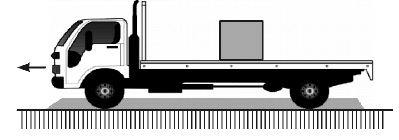
1) The maximum acceleration of the truck for which block does not slide on the floor of the truck is $a=\mu g$

2) If s a < ${\mu }_s$g block does not slide and frictional force on the block is f = ma.

3) If s a < ${\mu }_s$g block slips or slides on the floor the acceleration of the block relative to the truck is $\mathrm{a}‘=\mathrm{a}–{\mu }_{\mathrm{k}}\mathrm{g}$

4) If l is the distance of the block from rear side of the truck, time taken by the block to cover a distance l.

$\mathrm{t}=\sqrt{\frac{2\ell }{\mathrm{a}–{\mu }_{\mathrm{k}}\mathrm{g}}}$

4) Acceleration of the block relative to ground is $\mathrm{a}“={\mu }_{\mathrm{k}}\mathrm{g}$

Body placed in contact with the front surface of accelerated truck:
• When a block of mass ‘m’ is placed in contact with the front face of the vehicle moving with acceleration a then a pseudo force ‘${\mathrm{F}}_{\mathrm{pf}}$ ‘ acts on the block in a direction opposite to the direction of motion of the vehicle

Under equilibrium, ${\mathrm{f}}_1=\mathrm{mg}; \mathrm{N}=\mathrm{ma}$

${\mu }_{S}N=mg\Rightarrow {\mu }_S.ma=mg\Rightarrow a_{\min }=\frac{g}{{\mu }_s}$

Sliding of a chain on a horizontal table
• Consider a uniform chain of mass “m” and length “L” lying on a horizontal table of coefficient of friction “ ${\mu }_s$ ”.
When 1/nth of its length is hanging from the edge of the table, the chain is found to be about to slide from the table. Weight of the hanging part of the chain = $\frac{mg}{n}$

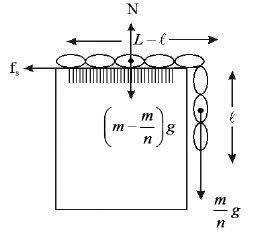
Weight of the chain lying on the table

$=mg–\frac{mg}{n}=mg\left(1–\frac{1}{n}\right)$

When the chain is about to slide from edge of the table,
The weight of the hanging part of the chain = frictional force between the chain and the table surface.

$\frac{mg}{n}={\mu }_{s}mg\left(1–\frac{1}{n}\right)$

$\Rightarrow \frac{mg}{n}={\mu }_{s}mg\left(\frac{n–1}{n}\right) \therefore {\mu }_s=\frac{1}{(n–1)}$

If l is the length of the hanging part, then n = $\frac{L}{l}$ Substituting this in the above expression we get,

${\mu }_s=\frac{l}{L–l}\left(\text{ or }\right)n=\frac{L}{l}=\frac{{\mu }_s+1}{{\mu }_s}$

∴ The maximum fractional length of chain hanging from the edge of the table in equilibrium is

$\frac{\ell }{L}=\frac{{\mu }_s}{{\mu }_s+1}$

• Fractional length of chain on the table

$\frac{L–\ell }{L}=\frac{1}{{\mu }_s+1}$

Connected Bodies
• A block of mass m₁ placed on a rough horizontal surface, is connected to block of mass m₂ by a string which passes over a smooth pulley. The coefficient of friction between 1 m and the table is $\mu$.

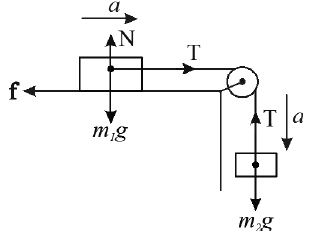
For body of mass m₂

$m_{2}g–T=m_{2}a$ ……..(1)

For body of mass m₁

$T–f_k=m_{1}a\Rightarrow T–{\mu }_{k}N=m_{1}a$

Solving Eqs (i) and (ii), we get

$a=\left(\frac{m_2–{\mu }_k{m}_1}{m_1+m_2}\right)g; T=\frac{m_1{m}_{2}g}{m_1+m_2}(1+\mu )$

16. MOTION OF A BODY ON AN INCLINED PLANE
CASE (I)
Body sliding down on a smooth inclined plane :

Let us consider a body of mass ‘m’ kept on the plane as shown in fig.
• Normal reaction N = mg cosθ
• Acceleration of sliding block a = g sinθ
• If l is the length of the inclined plane and h is the height. The time taken to slide down starting from rest from the top is $t=\sqrt{\frac{2l}{g\sin \theta }}=\frac{1}{\sin \theta }\sqrt{\frac{2h}{g}}$

• Sliding block takes more time to reach the bottom than to fall freely in air from the top of the inclined plane to the ground.
• Velocity of the block at the bottom of the inclined plane is same as the speed attained if block falls freely from the top of the inclined plane.

$V=\sqrt{2gl\sin \theta }=\sqrt{2gh}$

Case(II) :
Body projected up on a smooth inclined plane

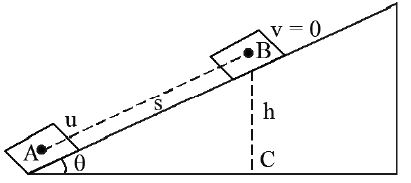
• If a block is projected up the plane with a velocity u, the acceleration of the block is a = -g sinθ
• Distance travelled by the block up the plane before its velocity becomes zero is $S=\frac{u^2}{2g\sin \theta }$
• Time of ascent $t=\frac{u}{g\sin \theta }$

Case (III)
Motion of a body down the rough inclined plane:
• Let a body of mass m be sliding down a rough inclined plane of angle of inclination θ and coefficient of kinetic friction ${\mu }_k$.

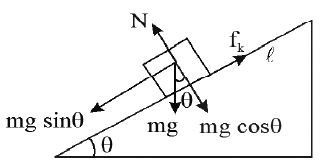
Angle of Repose (α) :
Angle of repose is the minimum angle of the rough inclined plane for which body placed on it may just start sliding down. It is numerically equal to the angle of friction.
• Let θ be the angle of inclination of a rough inclined plane, α be the angle of repose, m be the mass of the body and $\mu$ be the coefficient of friction.

At limiting equilibrium (about to slide) $mg\sin \alpha ={\mu }_{s}mg\cos \alpha \Rightarrow \tan \alpha ={\mu }_s\Rightarrow \alpha ={\tan }^{–1}\left({\mu }_s\right)$

1. When ${\theta }_1<\alpha$ ; the block remains at rest on the inclined plane. Frictional force mg sinθ₁ (self adjusting) acceleration a=0
2. When${\theta }_2=\alpha ;$ the block remains at rest on inclined plane or impending state of motion is achieved.
$mg\sin {\theta }_2={\mu }_{s}mg\cos {\theta }_2$ (at time t=0)
Here ${\theta }_2>{\theta }_1\text{ and }{f}_s=f_l$ acceleration a = 0
3. When ${\theta }_2>\alpha$; and the same inclination is continued the block moves downwards with accleration a.
$mg\sin {\theta }_2>{\mu }_{k}mg\cos {\theta }_2$ acceleration

$a=\frac{mg\sin {\theta }_2–{\mu }_{k}mg\cos {\theta }_2}{m}$

$a=\frac{{\mu }_{s}mg\cos {\theta }_2–{\mu }_{k}mg\cos {\theta }_2}{m}=g\cos {\theta }_2\left({\mu }_s–{\mu }_k\right)$

4. When $\theta >\alpha$, the body slides $f_k={\mu }_{k}mg\cos \theta$
The resultant force acting on the body down the plane is ${\mathrm{F}}_R=\mathrm{mgsin}\theta –{\mathrm{f}}_K$
$F_R=mg\left(\sin \theta –{\mu }_k\cos \theta \right)$
The acceleration of the body $a=g\left(\sin \theta –{\mu }_k\cos \theta \right)$

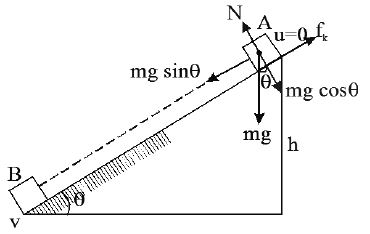
• Velocity of the body at the bottom of the plane $V=\sqrt{2g\left(\sin \theta –{\mu }_k\cos \theta \right)l}$

• If ‘t’ is the time taken to travel the distance ‘l’ with initial velocity u = 0 , at the top of the plane,

$t=\sqrt{\frac{2l}{g\left(\sin \theta –{\mu }_k\cos \theta \right)}}$

• The time taken by a body to slide down on a rough inclined plane is ‘n’ times the time taken by it to slide down on a smooth inclined plane of same inclination and length then coefficient of friction is….

$n=\frac{t_{\text{rough }}}{t_{\text{smooth }}}=\frac{\sqrt{\frac{2l}{g\left(\sin \theta –{\mu }_k\cos \theta \right)}}}{\sqrt{\frac{2l}{g\sin \theta }}}$

$n^2=\frac{\sin \theta }{\sin \theta –{\mu }_k\cos \theta }$

$\Rightarrow n^2\sin \theta –n^2{\mu }_k\cos \theta =\sin \theta$

$\Rightarrow {\mu }_k=Tan\theta \left[1–\frac{1}{n^2}\right]$

Body projected up a rough inclined plane:
If a body is projected with an initial velocity ‘u’ to slide up the plane, the kinetic frictional force acts down the plane and the body suffers retardation due to a resultant force

$F_R=\left(mg\sin \theta +f_{\mathrm{k}}\right)$

• acceleration a = $–\mathrm{g}\left(\sin \theta +{\mu }_{\mathrm{k}}\cos \theta \right)$

• Time taken to stop after travelling a distance l along the plane, $\mathrm{t}=\sqrt{\frac{2l}{ \mathrm{g}\left(\sin \theta +{\mu }_{\mathrm{k}}\cos \theta \right)}}$

• Force required to drag with an acceleration ‘a’ is $\mathrm{F}=\left({\mu }_{\mathrm{k}}\mathrm{mgcos}\theta +\mathrm{mgsin}\theta +\mathrm{m}a\right)$

• Two blocks of mass m and M are placed on a rough inclined plane as shown, when $(\theta >\alpha )$

i) Minimum value of M for which m slides upwards is $\mathrm{M}=\mathrm{m}\left(\sin \theta +{\mu }_{\mathrm{s}}\cos \theta \right)$

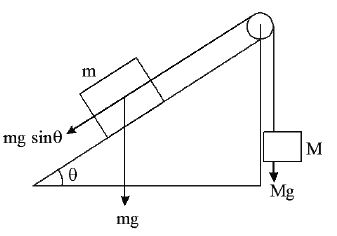
ii) Maximum value of M for which m slides downwards: $\mathrm{M}=\mathrm{m}\left(\sin \theta –{\mu }_{\mathrm{s}}\cos \theta \right)$

• A body is released from rest from the top of an inclined plane of length ‘L’ and angle of inclination ‘θ ’. The top of plane of length $\frac{L}{n}\left(n>1\right)$ is smooth and the remaining part is rough. If the body comes to rest on reaching the bottom of the plane then find the value of coefficient of friction of rough

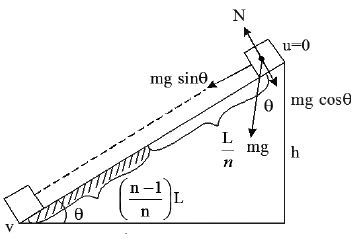
For smooth part :

Using ${\mathrm{v}}^2–{\mathrm{u}}^2=2\mathrm{as}; {\mathrm{V}}^2=2{\mathrm{a}}_1\frac{\mathrm{L}}{\mathrm{n}}$,

$a_1=g\sin \theta , a_2=g(\sin \theta –\mu \cos \theta )$

For rough part   $0–V^2=2a_2\left(\frac{n–1}{n}\right)L$

$2a_1\frac{L}{n}=–2a_2\left(\frac{n–1}{n}\right)L$

$g\sin \theta =–g[\sin \theta –\mu \cos \theta ](n–1)$

$\mu =Tan\theta \left[\frac{n}{n–1}\right]$

• A body is pushed down with velocity ‘u’ from the top of an inclined plane of length ‘L’ and angle of inclination ‘θ ’. The top of plane of length $\frac{L}{n}\left(n>1\right)$ is rough and the remaining part is smooth. If the body reaches the bottom of the plane with a velocity equal to the initial velocity ‘u’, then the value of coefficient of friction of rough plane is $\boxed{{\mu }_K=n\left(\tan \theta \right)}$

17. PUSHING & PULLING OF A LAWN ROLLER

i) A Roller on Horizontal Surface Pushed by an Inclined Force

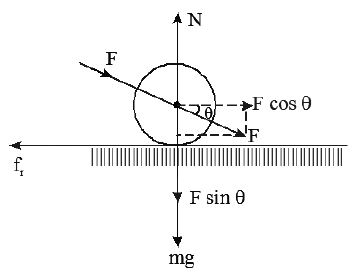
• When a lawn roller is pushed by a force ‘F’, which makes an angle θ with the horizontal, then
• Normal reaction N = mg + F sinθ.
• Frictional force $f_r={\mu }_{r}N={\mu }_r(mg+F\sin \theta )$
∴ The net horizontal pushing force is given by

${\mathrm{F}}_1=\mathrm{F}\left(\cos \theta –{\mu }_{\mathrm{r}}\sin \theta \right)–{\mu }_{\mathrm{r}}\mathrm{mg}$

ii) A Lawn Roller on a Horizontal Surface Pulled by an Inclined Force

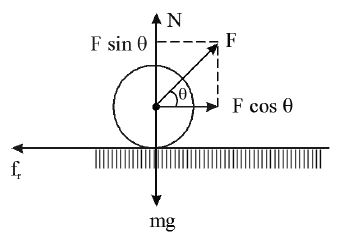
• Let a lawn roller be pulled on a horizontal road by a force ‘F’, which makes an angle θ with the horizontal.
• Normal reaction N =mg – Fsinθ
• Frictional force ${\mathrm{f}}_{\mathrm{r}}={\mu }_{\mathrm{r}}\mathrm{N}={\mu }_{\mathrm{r}}(\mathrm{mg}–\mathrm{Fsin}\theta )$
• The net horizontal pulling force is ${\mathrm{F}}_2=\mathrm{F}\left(\cos \theta +{\mu }_r\sin \theta \right)–{\mu }_r\mathrm{mg}$ Pulling is easier than Pushing.

Applying an Inclined Pulling Force
Let an inclined force F be applied on the body so as to pull it on the horizontal surface as shown in the figure.

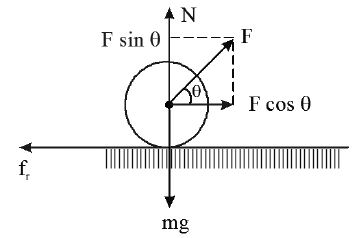
The body is in contact with the surface, and just ready to move

$\mathrm{N}+\mathrm{Fsin}\theta =\mathrm{mg}\Rightarrow \mathrm{N}=\mathrm{mg}–\mathrm{Fsin}\theta$

frictional force ${\mathrm{f}}_r=F\cos \theta$

$\mathrm{Fcos}\theta ={\mu }_r \mathrm{N}, \mathrm{Fcos}\theta ={\mu }_r(\mathrm{mg}–\mathrm{Fsin}\theta )$

$F=\frac{{\mu }_{r}mg}{\left(\cos \theta +{\mu }_r\sin \theta \right)}$

$\Rightarrow F=\frac{mg\sin \varphi }{\cos (\theta –\varphi )} \left(\because Tan\varphi ={\mu }_r\right)$

For F to be minimum $\cos \left(\theta –\varphi \right)$ should be

maximum $\Rightarrow \cos (\theta –\varphi )=1\Rightarrow \theta –\varphi =0, \theta =\varphi$

$\varphi =$angle of friction

$\therefore F_{\min }=mg\sin \theta =mg\sin \varphi$ From the figure, $\sin \varphi =\frac{{\mu }_r}{\sqrt{{\mu }_r^2+1}}, F_{\min }=\frac{{\mu }_{r}mg}{\sqrt{{\mu }_r^2+1}}$

Minimum horizontal pulling force, when θ = 0

$\cos (0–\varphi )=\cos \varphi$

$F=\frac{mg\sin \varphi }{\cos \varphi }=mg\tan \varphi$

Applying an Inclined Pushing Force

Let an inclined force F is applied on the body so as to push it on the horizontal surface as shown in the figure.

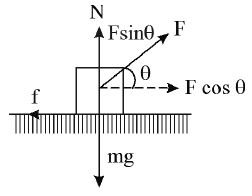
The body is in contact with the surface, and just ready to move, N = mg+Fsinθ

frictional force ${\mathrm{f}}_l=\mathrm{Fcos}\theta$

$F\cos \theta ={\mu }_{s}N\Rightarrow F\cos \theta ={\mu }_s(mg+F\sin \theta )$

$F=\frac{{\mu }_{s}mg}{\left(\cos \theta –{\mu }_s\sin \theta \right)}$

$F=\frac{mg\sin \varphi }{\cos (\theta +\varphi )} \left(\because Tan\varphi ={\mu }_s\right)$

For F to be minimum θ = 0

$F=\frac{mg\sin \varphi }{\cos (\theta +\varphi )} \left(\because Tan\varphi ={\mu }_s\right)$    $\text{ (since }\left.{\mu }_s=\tan \varphi \right)$

Block on Block

• Case I: Bottom block is pulled and there is no friction between bottom block and the horizontal surface.

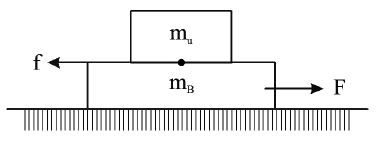
• When the bottom block is pulled upper block is accelerated by the force of friction acting upon it.

• The maximum acceleration of the system of two blocks to move together without slipping is $a_{\max }={\mu }_{s}g$

where ${\mu }_s$ is the coefficient of static friction between the two blocks. The maximum applied force for which both the blocks move together is ${\mathrm{F}}_{\max }={\mu }_{\mathrm{s}}\mathrm{g}\left({\mathrm{m}}_{\mathrm{u}}+{\mathrm{m}}_{\mathrm{B}}\right)$

• If $a<{\mu }_{s}g$ blocks move together and applied force is $F=\left({\mathrm{m}}_B+{\mathrm{m}}_u\right)a$. In this case frictional force between the two block $f=m_{u}a$.

• If $a>{\mu }_{s}g$ blocks slip relative to each other and have different accelerations. The acceleration of the upper block is $a_u={\mu }_{k}g$ and that for the bottom block is $a_B=\frac{F–{\mu }_k{m}_{u}g}{m_B}$.

• Case – II: Upper block pulled and there is no friction between bottom block and the horizontal surface.

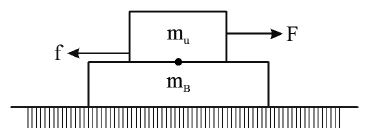
• When the upper block is pulled, bottom block is accelerated by the force of friction acting on it.

• The maximum acceleration of the system of two blocks to move together without slipping is $a_{\max }={\mu }_s\frac{m_u}{m_B}g$ where , ${\mu }_s$ = coefficient of static friction between the two blocks The maximum force for which both blocks move together is ${\mathrm{F}}_{\max }={\mu }_{\mathrm{s}}\frac{{\mathrm{m}}_{\mathrm{u}}}{{\mathrm{m}}_{\mathrm{B}}}\mathrm{g}\left({\mathrm{m}}_{\mathrm{u}}+{\mathrm{m}}_{\mathrm{B}}\right)$

• If $a<a_{max}$, blocks move together and frictional force between the two blocks is $f=m_{B}a$ The applied force on the upper block is $F=\left(m_B+m_u\right)a$

• If $a>a_{max}$  blocks slide relative to each other and hence they have different accelerations. The acceleration of the bottom block is $a_B={\mu }_K\frac{m_u}{m_B}g$ and the acceleration of the upper block is $a_u=\frac{F–{\mu }_k{m}_{u}g}{m_u}$

• A number of blocks of identical masses m each are placed one above the other. Force required to pull out ${\mathrm{N}}^{\mathrm{th}}$ block from the top is

$\mathrm{F}=(2\mathrm{N}–1) \mu \mathrm{mg}$

18. UNIFORM CIRCULAR MOTION
Uniform circular motion
• When a particle moves in a circular path with constant speed then it is said to be in uniform circular motion. In this case the acceleration of the particle is $\mathrm{a}=\mathrm{v}\left(\mathrm{\omega }\right)=\frac{{\mathrm{v}}^2}{\mathrm{r}}={\mathrm{r\omega }}^2$, Where v, r & ω are linear velocity, radius and angular velocity of the particle.
In uniform circular motion
(a) magnitude of linear velocity does not change
(b) direction of linear velocity changes
(c) Linear velocity changes
(d) Angular velocity is constant
(e) Linear momentum changes
(f) Angular momentum w.r.t to centre does not change
Centripetal force (${\mathbf{F}}_{\mathbf{C}}$):
• It is the force required to keep the body in uniform circular motion. This force changes the direction of linear velocity but not its magnitude ${\mathrm{F}}_{\mathrm{C}}=\frac{{\mathrm{mv}}^2}{\mathrm{r}}={\mathrm{mr\omega }}^2=\mathrm{mv\omega } (\mathrm{v}=\mathrm{r\omega })$

• Direction of centripetal force is always perpendicular to the direction of linear velocity. The work done by centripetal force is always zero, as it is perpendicular to velocity and hence instantaneous displacement

Ex1: When an electron moves around the nucleus in a circular orbit, the electrostatic force between the electron and nucleus is the centripetal force.
Ex2: If an electron of mass m and charge e moves around the nucleus of atomic number Z in a circular orbit of radius r , centripetal force on it is $\frac{{\mathrm{mv}}^2}{\mathrm{r}}=\frac{1}{4{\mathrm{\pi \epsilon }}_0}\frac{{\mathrm{Ze}}^2}{{\mathrm{r}}^2}$.

Ex3: When planet of mass m moves around the sun in a circular orbit of radius r , centripetal force on it is $\frac{m{v}^2}{r}=\frac{GMm}{r^2}$

Ex4: When a stone is whirled round in horizontal circle by attaching it at the end of string, tension in the string provides the centripetal force.

$\frac{m{v}^2}{r}=T$

Centrifugal force
• The Pseudo force which acts radially outward on the body moving along a circle is called centrifugal force.
Even though centripetal and centrifugal forces are equal in magnitude and opposite in direction, they do not form action – reaction pair because they act on the same body in two different frames.

Circular turning on roads
• The necessary centripetal force while taking a circular turn is being provided to a vehicle by following three ways
1) by friction only
2) by banking of roads only
3) by both friction and banking of roads
Friction only
In this case the necessary centripetal force is provided by static friction

$v\le \sqrt{{\mu }_{s}gr}; v_{\max }=\sqrt{{\mu }_{s}gr}$

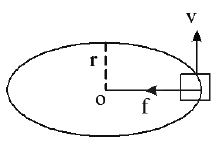
• For a given radius of curvature and coefficient of friction, the safe maximum velocity of the vehicle is given by

$v_{\max }=\sqrt{{\mu }_{s}rg}$

• Banking of roads only:

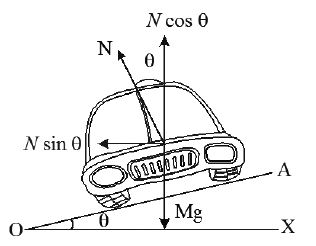
• Let θ be the angle through which the outer edge is raised relative to the inner edge. This angle is also called “angle of banking”. The normal reaction N exerted by the road on the vehicle is directed normal to the surface as shown in the figure.
N cosθ balances the weight of the vehicle. N cosθ = mg
N sinθ is directed towards the centre of the circular path. Which provides the centripetal force.

$N\sin \theta =\frac{m{v}^2}{r}$

From the above equations, we get

$\tan \theta =\frac{v^2}{rg}\text{ (or) }v=\sqrt{rg \tan \theta }$

Motion of a vehicle on a rough banked road

• If friction is present between the road is in rotational equilibrium, thencomponents of friction and normal reaction provide the centripetal force.

Case-I: If $N\sin \theta >\frac{m{v}^2}{r}$, the vehicle possesses the tendency to slip down the plane. The minimum speed for avoiding slipping down the plane can be obtained by taking friction up the plane.

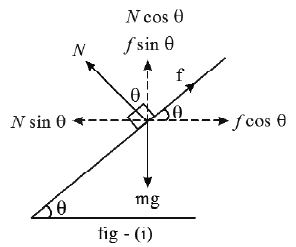
To find minimum speed we can use fig (i), $N\sin \theta –f\cos \theta =\frac{m{v}_{\min }^2}{r}\dots .\left(1\right)$

$N\cos \theta +f\sin \theta =mg\dots .\left(2\right) \left(f=\mu N\right)$

From (1) and (2) we get

$v_{\min }=\sqrt{\frac{rg(\sin \theta –\mu \cos \theta )}{(\cos \theta +\mu \sin \theta )}}=\sqrt{\frac{rg(\tan \theta –\mu )}{(1+\mu \tan \theta )}}$

Case-II: If $N\sin \theta <\frac{m{v}^2}{r}$, the vehicle possesses the tendency to skid up the plane. The safe maximum speed for avoiding skidding can be obtained by taking friction acting down the plane.

To find maximum safe speed, we have to consider figure (ii).

$N\sin \theta +f\cos \theta =\frac{m{v}_{\max }^2}{r}\dots .\left(1\right)$

$N\cos \theta –f\sin \theta =mg\dots \dots \dots .\left(2\right)$

From (1) and (2) we get

$v_{\max }=\sqrt{\frac{rg(\sin \theta +\mu \cos \theta )}{(\cos \theta –\mu \sin \theta )}}=\sqrt{\frac{rg(\tan \theta +\mu )}{(1–\mu \tan \theta )}}$

• A cyclist is taking a turn of radius r with speed v then he should bend through an angle  with the vertical such that $\tan \theta =\frac{v^2}{rg}$

b) In the second case force of friction f will act downwards

$N\sin \theta +f\cos \theta =\frac{m{v}^2}{r};N\cos \theta –f\sin \theta =mg$

Substituting $\theta ={\tan }^{–1}\left(\frac{1}{2}\right)$, v = 15m/s, m=200kg and r = 20m, in the above equations, we get $f=500\sqrt{5} \mathrm{N}$

Conical pendulum
A bob of mass M is given a horizontal push a little through angular displacement θ and arranged such that the bob describes a horizontal circle of radius ‘ r’ with uniform angular velocity ω in such a way that the string always makes an angle θ with the vertical and T is the tension in the string.
Suppose the body is in rotational equilibrium,then

$T\cos \theta =Mg$……..(1)

$T\sin \theta =Mr{\omega }^2$……(2)

$\omega =\sqrt{\frac{g\tan \theta }{r}}$

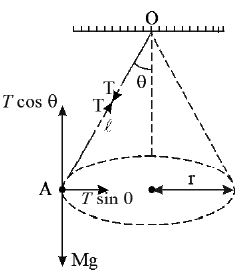
but $r=l\sin \theta \text{ and }\omega =\frac{2\pi }{T_0}$ ($T_0$ is the time period of pendulum)

Time period of the pendulum is $T_0=2\pi \sqrt{\frac{l\cos \theta }{g}}$

• For the coin not to fly off on the turn table, the condition is

$\Rightarrow \frac{m{v}^2}{r}\le {\mu }_{s}mg$

• Motion of a Cyclist in a Death Well:
For equilibrium of cyclist in a death well, as shown in the figure, the normal reaction N provides the centripetal force needed and the force of friction balances his weight mg.

Thus, $N=\frac{m{v}^2}{r}$

and $f=\mu N=mg$

$\Rightarrow V_{\max }=\sqrt{\frac{rg}{\mu }}$

SOLVED EXAMPLES

1. A force produces an acceleration 16 ms^-2 in a mass 0.5 kg and an acceleration 4 ms^-2 in an unknown mass when applied separately. If both the masses are tied together, what will be the acceleration under same force?
Sol. Force F=ma=0.5⨯16=8N when both masses are joined and same force acts, acceleration is given by

$a^1=\frac{F}{m+m^1}=\frac{8}{0.5+(8/4)}=3.2{ \mathrm{ms}}^{–2}$

2. When the forces $F_1,F_2,F_3$ are acting on a particle of mass m such that $F_2\text{ and }{F}_3$ are mutually perpendicular, then the particle remain stationary. If the force $F_1$ is now removed, then find the acceleration of the particle .
Sol. If mass ‘m’ is stationary under three forces,

$\begin{array}{l}{\overrightarrow{F}}_1+{\overrightarrow{F}}_2+{\overrightarrow{F}}_3=0\\ {\overrightarrow{F}}_1=–\left({\overrightarrow{F}}_2+{\overrightarrow{F}}_3\right)\\ \sqrt{F_2^2+F_3^2}=F_1\end{array}$

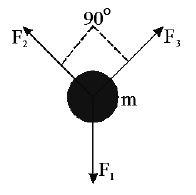
Obviously if $F_1$ is removed then the mass will have acceleration, $a=\frac{\sqrt{F_2^2+F_3^2}}{m} \left(\text{ or }\right) a=\frac{F_1}{m}$

3. A very flexible chain of length L and mass M is vertically suspended with its lower end just touching the table. If it is released so that each link strikes the table and comes to rest. What force the chain will exert on the table at the moment ‘y’ part of length falls on the table ?

Sol. Since chain is uniform , the mass of ‘y’ part of the chain will be $\left(\frac{\mathrm{M}}{\mathrm{L}}\mathrm{y}\right)$. When this part reaches the table, its total force exerted must be equal to the weight of y part resting on table + Force due to the momentum imparted

$\mathrm{F}=\frac{M}{L}yg+\frac{\left(\frac{M}{L}dy\right)\sqrt{2gy}}{dt}$

$=\frac{Mg}{L}y+\frac{M}{L}v.\sqrt{2gy} \left(\because \frac{dy}{dt}=v\right)=\frac{Mg}{L}y+\frac{M}{L}\sqrt{2gy}.\sqrt{2gy}=3\frac{My}{L}g$

4. A particle is at rest at x=a. A force $\overrightarrow{\mathrm{F}}=–\frac{\mathrm{b}}{{\mathrm{x}}^2}\overrightarrow{\mathrm{i}}$ begins to act on the particle. The particle startsits motion, towards the origin, along X–axis. Find the velocity of the particle, when it reaches a distance x from the origin.

Sol. $F=–\frac{b}{x^2}\Rightarrow \frac{d}{dt}\left(p\right)=–\frac{b}{x^2}$

$\frac{d}{dt}\left(mv\right)=–\frac{b}{x^2}\Rightarrow m\frac{dv}{dx}\frac{dx}{dt}=–\frac{b}{x^2}$

$mvdv=–\frac{b}{x^2}dx\Rightarrow vdv=–\frac{b}{m{x}^2}dx$

${\int }_0^{\mathrm{v}}\mathrm{vdv}={\int }_{\mathrm{a}}^{\mathrm{x}}–\frac{\mathrm{b}}{{\mathrm{mx}}^2}\mathrm{dx}\Rightarrow \frac{{\mathrm{v}}^2}{2}=\frac{\mathrm{b}}{\mathrm{m}}{\left[\frac{1}{\mathrm{x}}\right]}_{\mathrm{a}}^{\mathrm{x}}$

$\frac{v^2}{2}=\frac{b}{m}\left[\frac{1}{x}–\frac{1}{a}\right] \therefore v=\sqrt{\frac{2b}{m}\left(\frac{a–x}{xa}\right)}$

5. A gardener is watering plants at the rate 0.1litre/sec using a pipe of cross- sectional area 1 cm2. What additional force he has to exert if he desires to increase the rate of watering two times?

Sol. $\mathrm{F}=\mathrm{Ad}{v}^2=\frac{(Av{)}^{2}d}{A}$. If rate of watering of plant (Av ) is doubled, it means that the amount of water poured/sec is doubled which is possible only if velocity is doubled. Hence, force is to be made 4 times.

∴ Additional force = 3 times initial force = $3Ad{v}^2=3\frac{(Av{)}^2}{A}d=\frac{3\times 0.1\times 0.1\times {10}^3}{{10}^{–4}}=3\times {10}^{5}N$

6. A ball falling with velocity ${\overrightarrow{v}}_i=(–0.65\hat{i}–0.35\hat{j}){\mathrm{ms}}^{–1}$ is subjected to a net impulse $\overrightarrow{I}=(0.6\hat{i}+0.18\hat{j})\mathrm{Ns}$. If the ball has a mass of 0.275kg, calculate its velocity immediately following the impulse

Sol : $m{\overrightarrow{v}}_f–m{\overrightarrow{v}}_i=\overrightarrow{I}; {\overrightarrow{v}}_f={\overrightarrow{v}}_i+\frac{\overrightarrow{I}}{m}$

${\overrightarrow{v}}_f=–0.65\hat{i}–0.35\hat{j}+\frac{0.6\hat{i}+0.18\hat{j}}{0.275}$

${\overrightarrow{v}}_f=–0.65\hat{i}–0.35\hat{j}+2.18\hat{i}+0.655\hat{j}$

${\overrightarrow{v}}_f=(1.53\hat{i}+0.305\hat{j})m{s}^{–1}$

7. A bullet is fired from a gun. The force on a bullet is, $F=600–2\times {10}^{5}t$ t newton. The force reduces to zero just when the bullet leaves barrel. Find the impulse imparted to the bullet.

Sol. $\mathrm{F}=600–2\times {10}^5\mathrm{t}$, F becomes zero as soon as the bullet leaves the barrel.

$0=600–2\times {10}^5\mathrm{t}\Rightarrow 600=2\times {10}^{5}t$

$\mathrm{t}=3\times {10}^{–3} \mathrm{s}\Rightarrow \text{ Impulse }={\int }_0^{t}Fdt$

$={\int }_0^t\left(600–2\times {10}^{5}t\right)\mathrm{dt}={\left[600t–2\times {10}^5\frac{t^2}{2}\right]}_0^{3\times {10}^{–3}}$

$=600\times 3\times {10}^{–3}–{10}^5\times 9\times {10}^{–6}=0.9\mathrm{Ns}$

8. A mass M is suspended by a weightless string. The horizontal force required to hold the mass at 600 with the vertical is

Sol.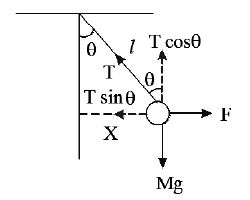

F = T sinθ – – – – – (1)

Mg = T cosθ – – – – – (2)

Dividing Eq.(1) and Eq.(2)

$\frac{F}{Mg}=\frac{T\sin \theta }{T\cos \theta }; F=Mg\tan \theta$

$F=Mg\tan 60°; F=\sqrt{3}Mg$

9. A mass of 1kg attached to one end of a string is first lifted up with an acceleration 4.9m/s² and then lowered with same acceleration. What is the ratio of tension in string in two cases.

Sol. When mass is lifted up with acceleration 4.9m/s²
${\mathrm{T}}_1=m(g+a)$ =1 (9.8 + 4.9)=14.7N
When mass is lowered with same acceleration
${\mathrm{T}}_2=m(g–a)$ =1(9.8 – 4.9)=4.9 N

$\therefore \frac{T_1}{T_2}=\frac{14.7}{4.9}=3:1$

10. Figure shows three blocks of mass ‘m’ each hanging on a string passing over a pulley. Calculate the tension in the string connecting A to B and B to C?
Sol. Net pulling force = 2 mg – mg = mg
Total mass = m+ m + m = 3m

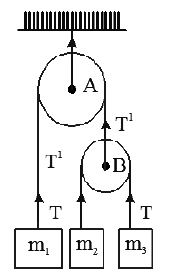
Acceleration, $a=\frac{mg}{3m}=\frac{g}{3}$

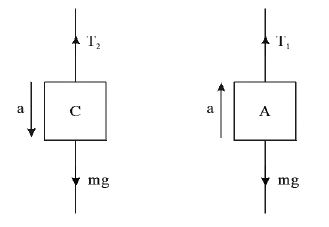
Considering block A,

$T_1–mg=ma; T_1=mg+ma$

$T_1=mg+m\left(\frac{g}{3}\right)\Rightarrow T_1=\frac{4}{3}mg$

Considering block C,

$mg–T_2=ma\Rightarrow T_2=mg–ma$

$\Rightarrow T_2=mg–\frac{mg}{3}=\frac{2}{3}mg$.

11. By what acceleration the boy must go up so that 100 kg block remains stationary on the wedge. The wedge is fixed and is smooth.(g = 10m/s²)

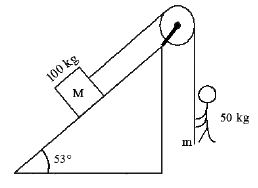
Sol. For the block to remain stationary,

T = Mg sinθ = 100 ⨯ 10 ⨯ sin 53

$=100\times 10\times \frac{4}{5}=800 \mathrm{N}$

For man ; T – mg = ma

$\mathrm{T}=\mathrm{m}(\mathrm{g}+a)\Rightarrow 800=50(10+a) a=6 \mathrm{m}/{\mathrm{s}}^2$

12. In the adjacent fig, masses of A, B and C are 1kg, 3kg and 2kg respectively. Find a) the acceleration of the system b) tension in the string (g = 10m/s²)

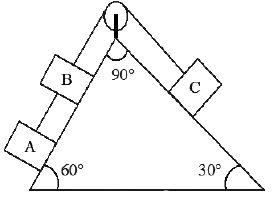
Sol. a) In this case net pulling force

$=m_{A}g\sin 60°+m_{B}g\sin 60°–m_{C}g\sin 30°$

$=\left(1\right)\left(10\right)\frac{\sqrt{3}}{2}+\left(3\right)\left(10\right)\left(\frac{\sqrt{3}}{2}\right)–\left(2\right)\left(10\right)\left(\frac{1}{2}\right)=24.64 \mathrm{N}$

Total mass = 1 + 3 + 2 = 6kg

∴ Acceleration of the system $a=\frac{24.64}{6}=4.1 \mathrm{m}/{\mathrm{s}}^2$

13. A rod of length ‘ l ’is inclined at an angle ‘θ’with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v₁, what is the velocity of end B at the instant when rod makes ‘θ’ angle with the horizontal.

Sol. Let at any instant, end B and A are at a distance x and y respectively from the point ‘O’.

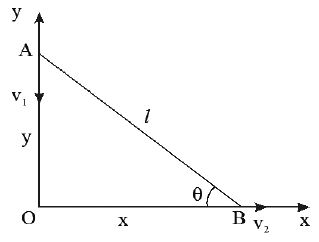
Thus we have, $x^2+y^2=l^2\dots \dots \dots \dots \left(1\right)$

Here l is the length of the rod, which is constant. Differentiating eq (1) with respect to time, we get

$\frac{d}{dt}\left(x^2+y^2\right)=\frac{d}{dt}\left(l^2\right); 2x\frac{dx}{dt}+2y\frac{dy}{dt}=0$

If $\frac{dx}{dt}=v_2\text{ and }\frac{dy}{dt}=–v_1$

$x\left(v_2\right)+y\left(–v_1\right)=0$

$\Rightarrow v_2=\frac{y}{x}{v}_1=v_1\tan \theta$

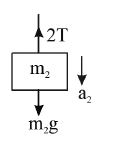
14. In the fig, find the acceleration of ${\mathrm{m}}_1\text{ and }{\mathrm{m}}_2$

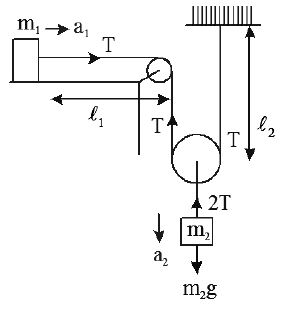
Sol. ${\ell }_1+2{\ell }_2=cons\tan t$ 

$a_1=2a_2; T=m_1{a}_1$

$m_{2}g–2T=m_2{a}_2; m_{2}g=2m_1{a}_1+m_2{a}_2$

$m_{2}g=2m_1\left(2a_2\right)+m_2{a}_2$

$a_2=\frac{m_{2}g}{4m_1+m_2}, a_1=\frac{2m_{2}g}{4m_1+m_2}$

15. For what value of ‘a’ the block falls freely?

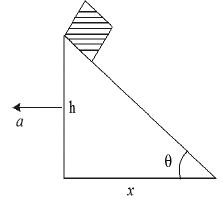
Sol. In the time the wedge moves a distance ‘x’ towards left with an acceleration a the block falls from a height ‘h’ with acceleration ‘g’

$x=\frac{1}{2}a{t}^2, h=\frac{1}{2}g{t}^2\Rightarrow \frac{x}{h}=\frac{a}{g}, \Rightarrow \cot \theta =\frac{a}{g}$

$\Rightarrow a=g\cot \theta$

16. For what value of ‘a’ block slides up the plane with an acceleration ‘g’ relative to the inclined plane.

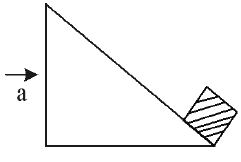
Sol.

$F_{net}=ma\cos \theta –mg\sin \theta$

$ma‘=ma\cos \theta –mg\sin \theta$

If $a‘=g, mg=ma \cos \theta –mg \sin \theta$

$a\cos \theta =g+g\sin \theta \Rightarrow a=g\left(\frac{1+\sin \theta }{\cos \theta }\right)$

$\Rightarrow a=g(\sec \theta +\tan \theta )$

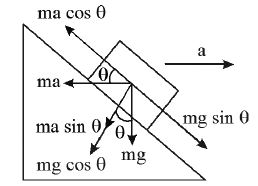
17. A block is placed on an inclined plane moving towards right with an acceleration $a_0$ = g. The length of the inclined plane is $l_0$ . All the surfaces are smooth. Find the time taken by the block to reach from bottom to top.

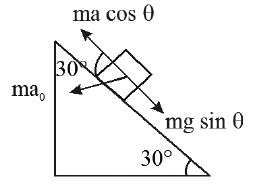
Sol. $ma=m{a}_0\cos 30°–mg\sin 30°$

$a=\frac{m{a}_0\cos 30°–mg\sin 30°}{m}$

$a=\frac{m{a}_0\frac{\sqrt{3}}{2}–mg\frac{1}{2}}{m}=g\left(\frac{\sqrt{3}–1}{2}\right)$

from $s=ut+\frac{1}{2}a{t}^2; {\ell }_0=\frac{1}{2}a{t}^2$

${\ell }_0=\frac{1}{2}g\left(\frac{\sqrt{3}–1}{2}\right)t^2\Rightarrow t=\sqrt{\frac{4{\ell }_0}{g(\sqrt{3}–1)}}\sec$

18. A pendulum of mass m hangs from a support fixed to a trolley. The direction of the string when the trolley rolls up a plane of inclination α with acceleration $a_0$ is

Sol.  

$T\sin \theta =m{a}_0+mg\sin \alpha$……..(1)

$T\cos \theta =mg\cos \alpha$……..(2)

$\frac{\overline{)1}}{\overline{)2}}\Rightarrow \tan \theta =\frac{a_0+g\sin \alpha }{g\cos \alpha }$

$\theta ={\tan }^{–1}\left[\frac{a_0+g\sin \alpha }{g\cos \alpha }\right]$

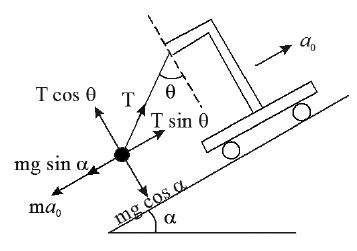
19. A block slides down from top of a smooth inclined plane of elevation θ fixed in an elevator going up with an acceleration $a_0$. The base of incline has length L. Find the time taken by the block to reach the bottom.

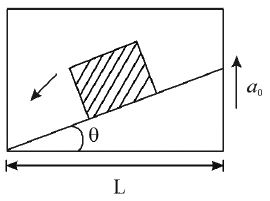
Sol. Let us solve the problem in the elevator frame. The free body diagram is shown. The forces are

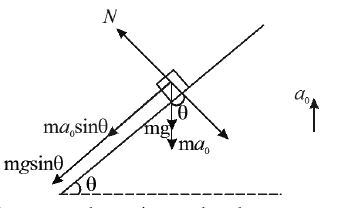
(i) N normal reaction to the plane,
(ii) mg acting vertically downwards,
(iii) $m{a}_0$ ( pseudo force). acting vertically down
If a is acceleration of the body with respect to inclined plane, taking components of forces parallel to the inclined plane.

$mg\sin \theta +m{a}_0\sin \theta =ma \therefore a=\left(g+a_0\right)\sin \theta$

This is the acceleration with respect to the elevator

The distance travelled is $\frac{L}{\cos \theta }$. If ‘t’ is the time for reaching the bottom of inclined plane

$\frac{L}{\cos \theta }=0+\frac{1}{2}\left(g+a_0\right)\sin \theta .t^2$

$t={\left[\frac{2L}{\left(g+a_0\right)\sin \theta \cos \theta }\right]}^{\frac{1}{2}}={\left[\frac{4L}{\left(g+a_0\right)\sin 2\theta }\right]}^{\frac{1}{2}}$

20. A bomb moving with velocity(40i+50j-25k)m/s explodes into two pieces of mass ratio 1:4. After explosion the smaller piece moves away with velocity (200i+70j+15k)m/s.The velocity of larger piece after explosion is

Sol. From Law of conservation of linear momentum

$\mathrm{MU}={\mathrm{m}}_1{\mathrm{v}}_1+{\mathrm{m}}_2{\mathrm{v}}_2; \mathrm{M}=5\mathrm{x}, {\mathrm{m}}_1=\mathrm{x}, {\mathrm{m}}_2=4\mathrm{x}$

$\begin{array}{l}U=40\hat{i}+50\hat{j}–25\hat{k}m{s}^{–1}\\ v_1=200\hat{i}+70\hat{j}+15\hat{k}m{s}^{–1}\end{array}$

here $v_2$ is the velocity of the larger piece

$5x(40\hat{i}+50\hat{j}–25\hat{k})=$$x(200\hat{i}+70\hat{j}+15\hat{k})+4x\left(v_2\right)$

On simplification, we get  $v_2=45\hat{j}–35\hat{k}$

21. All surfaces are smooth. Find the horizontal displacements of the block and the wedge when the block slides down from top to bottom.

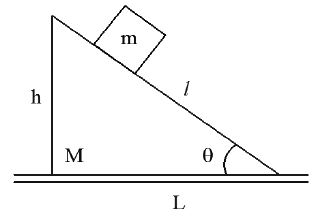
Sol. When the block slides down on the smooth wedge, the wedge moves backwards. In the horizontal direction there is no external force ; ${\overrightarrow{F}}_x=0$

$\therefore {\overrightarrow{P}}_x=\text{ constant }$

${\overrightarrow{P}}_f={\overrightarrow{P}}_i$ (along x-axis) ; $m\overrightarrow{u}+M\overrightarrow{V}=\overrightarrow{0}$

x₁ = forward distance moved by the block along X-axis.
x₂ = backward distance moved by the wedge along X-axis.

$m\overrightarrow{u}=–M\overrightarrow{V}$;

$m\frac{x_1}{t}=M\frac{x_2}{t}$

$m{x}_1=M{x}_2, x_1=\frac{ML}{M+m}=\frac{M\ell \cos \theta }{M+m}$

$x_2=\frac{mL}{M+m}=\frac{m\ell \cos \theta }{M+m}$

22. A bomb of 1 kg is thrown vertically up with speed 100 m/s. After 5 seconds, it explodes into two parts. One part of mass 400gm goes down with speed 25m/s. What will happen to the other part just after explosion

Sol. After 5 sec, velocity of the bomb,

v = u + at

$\overrightarrow{v}=\mathrm{u}\hat{j}–\mathrm{gt}\hat{j}=(100–10\times 5)\hat{j}=50\hat{j} \mathrm{m}/\mathrm{s}$

$m=1 \mathrm{kg}, m_1=0.4 \mathrm{kg}, m_2=0.6 \mathrm{kg}, v_1=25{ \mathrm{ms}}^{–1}$

According to law of conservation of momentum $m\overline{v}=m_1{\overline{v}}_1+m_2{\overline{v}}_2$

$1\times 50\hat{j}=–0.4\times 25\hat{j}+0.6{\overrightarrow{v}}_2$

$\Rightarrow v_2=100\hat{j}$

$\therefore v_2=100m{s}^{–1}$, vertically upwards

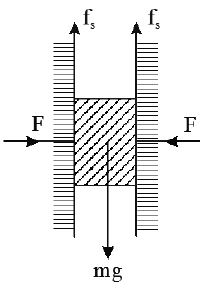
23. A man of mass 40 kg is at rest between the walls as shown in the figure. If ‘ $\mu$ ’ between the man and the walls is 0.8, find the normal reactions exerted by the walls on the man.
Sol. Since man is at rest,

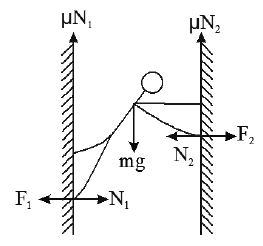
$N_1–N_2=0$    (horizontal equilibrium)

$\therefore N_1=N_2=N, F_1=F_2=\mathrm{F}\left(\text{ say }\right)$

$\therefore 2\mu N=mg$   (vertical equilibrium)

$=2\times 0.8\times N=400 \therefore N=250N$

24. A block of mass 4 kg is placed on a rough horizontal plane. A time dependent horizontal force F = kt acts on the block (k = 2 N/s). Find the frictional force between the block and the plane at t = 2 seconds and t = 5 seconds
(μ = 0.2)

Sol. Given F = kt
When t = 2sec ; F = 2(2) = 4N ….. case (i)

$f_{ms}={\mu }_{s}mg=0.2\times 4\times 10=8 \mathrm{N}$

Here $\mathrm{F}<{\mathrm{f}}_{\mathrm{ms}}$   ∴  friction = applied force = 4N

When t = 5 sec ; F = 2(5) = 10N……case(ii)

F > f

∴ frictional force < 8N

25. When a car of mass 1000 kg is moving with a velocity of 20ms^-1 on a rough horizontal road, its engine is switched off. How far does the car move before it comes to rest if the coefficient of kinetic friction between the road and tyres of the car is 0.75 ?

Sol. Here $\mathrm{v}=20{ \mathrm{ms}}^{–1}, {\mu }_k=0.75, \mathrm{g}=10{ \mathrm{ms}}^{–2}$

Stopping distance $S=\frac{v^2}{2{\mu }_{k}g}=26.67 \mathrm{m}$

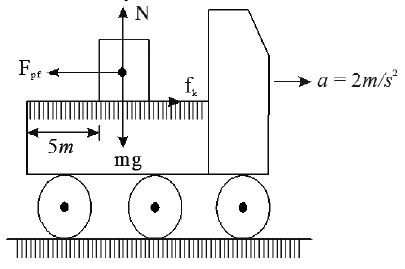
26. The rear side of a truck is open. A box of 40 kg mass is placed 5m away from the open end as shown in figure.

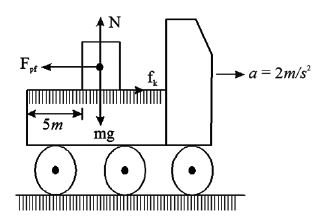
The coefficient of friction between the box and the surface is 0.15. On a straight road, the truck starts from rest and accelerating with 2m/s². At what distance from the starting point does the box fall off the truck? (Ignore the size of the box).

Sol. Because of the acceleration of the truck the pseudo force on the box = m⨯a = 40⨯2 = 80N.
This force acts opposite to the acceleration of the truck. The frictional force on the truck which acts in the forward direction $f_k=\mu N=0.15\times 40 \mathrm{g}=58.8 \mathrm{N}$ Since pseudo force is greater than frictional force, the block will accelerate in backward direction relative to truck with a magnitude

$a=\frac{80–58.8}{40}=0.53 \mathrm{m}/{\mathrm{s}}^2$

The time taken by box to cover the distance 5m is given by

$s=0+\frac{1}{2}a{t}^2\Rightarrow t=\sqrt{\frac{2s}{a}}=4.34\sec$

The distance travelled by truck in this time is, a’ = 2ms^-2

$s‘=\frac{1}{2}a‘t^2=\frac{1}{2}\times 2\times (4.34{)}^2=18.87 \mathrm{m}$

27. A block of mass ‘m’ is placed on a rough surface with a vertical cross section of $y=\frac{x^3}{6}$. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is
Sol.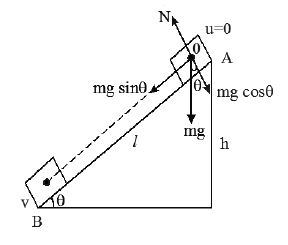  

$Tan\theta =\frac{dy}{dx}=\frac{d}{dx}\left(\frac{x^3}{6}\right)\Rightarrow Tan\theta =\frac{x^2}{2}$

At limiting equilibrium, we get $\mu =Tan\theta \Rightarrow 0.5=\frac{x^2}{2}; x^2=1\Rightarrow x=\pm 1$

Now putting the values of ‘ x ’in $y=\frac{x^3}{6}$, we get

When $x=1\Rightarrow y=\frac{1}{6}; x=–1\Rightarrow y=–\frac{1}{6}$

So the maximum height above the ground at which the block can be placed without slipping is $y=\frac{1}{6}m$

28. A block of mass 4kg is placed on another block of mass 5kg, and the block B rests on a smooth horizontal table, for sliding the block A on B, a horizontal force 12N is required to be applied on it. How much maximum horizontal force can be applied on ‘B’ so that both A and B move together? Also find out the acceleration produced by this force.

Sol. Here $M_1=4 \mathrm{kg}\text{ and }{M}_2=5 \mathrm{kg}$

Limiting friction between the blocks is ${\mathrm{f}}_{\lim }$ Acceleration of system is

$a=\frac{F}{M_1+M_2}=\frac{F}{4+5}=\frac{F}{9} \mathrm{m}/{\mathrm{s}}^2$

Because of this acceleration the block A experiences a pseudo force of magnitude

$F_{pseudo}=M_{1}a=4\times \frac{F}{9}$

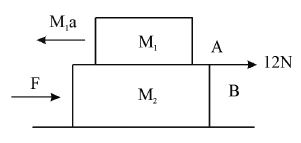
As block A move together with B, $F_{pseudo}\le f_{\lim }$ For maximum value of applied force

${\mathrm{F}}_{\mathrm{pseudo}}={\mathrm{f}}_{\lim }; \frac{4\mathrm{F}}{9}=12\Rightarrow \mathrm{F}=27\mathrm{N}$

The acceleration of blocks = $\frac{27}{9}=3 \mathrm{m}/{\mathrm{s}}^2$

29. A car is driven round a curved path of radius 18m without the danger of skidding. The coefficient of friction between the tyres of the car and the surface of the curved path is 0.2. What is the maximum speed in kmph of the car for safe driving? $\left(\mathrm{g}=10{ \mathrm{ms}}^{–2}\right)$

Sol. Maximum speed $v=\sqrt{{\mu }_{s}gr}$

$v=\sqrt{0.2\times 10\times 18}=\sqrt{36}=6{ \mathrm{ms}}^{–1}$

30. A turn of radius 20m is banked for the vehicle of mass 200kg going at a speed of 10m/s. Find the direction and magnitude of frictional force acting on a vehicle if it moves with a speed a) 5 m/s b) 15 m/s Assume that friction is sufficient to prevent slipping $\left(\mathrm{g}=10 \mathrm{m}/{\mathrm{s}}^2\right)$

Sol. v = 10m/s

$\tan \theta =\frac{v^2}{rg}=\frac{(10{)}^2}{\left(20\right)\left(10\right)}=\frac{1}{2}\Rightarrow \theta ={\tan }^{–1}\left(\frac{1}{2}\right)$

Now, as speed is decreased, force of friction f acts upwards. Using the equations

$N\sin \theta –f\cos \theta =\frac{m{v}^2}{r}$

$N\cos \theta +f\sin \theta =mg$

Substituting $\theta ={\tan }^{–1}\left(\frac{1}{2}\right), \mathrm{v}=5 \mathrm{m}/\mathrm{s}$, m=200kg and r = 20m, in the above equations, we get $\mathrm{f}=300\sqrt{5} \mathrm{N}$