Probability

1. Probability-Definitions and Terms [Include problems on Dices, Cards, Balls, Leap year, etc]

1. INTRODUCTION

There are two approaches to probability viz. (i) Classical approach and (ii) Axiomatic approach. In both the approaches we use the term ‘experiment’, which means an operation which can produce some well-defined outcome(s). There are two types of experiments:

(1) Deterministic experiment: Those experiments which when repeated under identical conditions produce the same result or outcome are known as deterministic experiments. When experiments in science or engineering are repeated under identical conditions, we get almost the same result every time.

(2) Random experiment: If an experiment, when repeated under identical conditions, do not produce the same outcome every time but the outcome in a trial is one of the several possible outcomes then such an experiment is known as a probabilistic experiment or a random experiment. In a random experiment, all the outcomes are known in advance but the exact outcome is unpredictable.

For example, in tossing of a coin, it is known that either a head or a tail will occur but one is not sure if a head or a tail will be obtained. So it is a random experiment.

2. DEFINITIONS OF VARIOUS TERMS.

1. Sample space

The set of all possible outcomes of a trial (random experiment) is called its sample space. It is generally denoted by S and each outcome of the trial is said to be a sample point.

2. Event

An event is a subset of a sample space.

(i) Simple event: An event containing only a single sample point is called an elementary or simple event.

(ii) Compound events: Events obtained by combining together two or more elementary events are known as the compound events or decomposable events.

(iii) Equally likely events: Events are equally likely if there is no reason for an event to occur in preference to any other event.

(iv) Mutually exclusive or disjoint events: Events are said to be mutually exclusive or disjoint or incompatible if the occurrence of any one of them prevents the occurrence of all the others.

(v) Mutually non-exclusive events: The events which are not mutually exclusive are known as compatible events or mutually non exclusive events.

(vi) Independent events: Events are said to be independent if the happening (or non-happening) of one event is not affected by the happening (or non-happening) of others.

(vii) Dependent events: Two or more events are said to be dependent if the happening of one event affects (partially or totally) other event.

3. Exhaustive number of cases

The total number of possible outcomes of a random experiment in a trial is known as the exhaustive number of cases.

4. Favourable number of cases

The number of cases favourable to an event in a trial is the total number of elementary events such that the occurrence of any one of them ensures the happening of the event.

5. Mutually exclusive and exhaustive system of events

Let S be the sample space associated with a random experiment. Let A₁, A₂, …..A_n be subsets of S such that

(i) ${\mathrm{A}}_{\mathrm{i}}\cap {\mathrm{A}}_{\mathrm{j}}=\mathrm{\varphi }$ for i ≠ j and (ii) ${\mathrm{A}}_1\cup {\mathrm{A}}_2\cup \dots .\cup {\mathrm{A}}_{\mathrm{n}}=\mathrm{S}$

Then the collection of events $A_1,A_2,\dots \dots A_n$ is said to form a mutually exclusive and exhaustive system of events.

If ${\mathrm{E}}_1,{\mathrm{E}}_2,\dots \dots ,{\mathrm{E}}_{\mathrm{n}}$ are elementary events associated with a random experiment, then

(i) ${\mathrm{E}}_{\mathrm{i}}\cap {\mathrm{E}}_{\mathrm{j}}=\mathrm{\varphi }$  for i ≠ j  and (ii) ${\mathrm{E}}_1\cup {\mathrm{E}}_2\cup \dots \cup {\mathrm{E}}_{\mathrm{n}}=\mathrm{S}$

So, the collection of elementary events associated with a random experiment always form a system of mutually exclusive and exhaustive system of events.

In this system, $\mathrm{P}\left({\mathrm{A}}_1\cup {\mathrm{A}}_2\dots \dots \cup {\mathrm{A}}_{\mathrm{n}}\right)$

$=\mathrm{P}\left({\mathrm{A}}_1\right)+\mathrm{P}\left({\mathrm{A}}_2\right)+\dots ..+\mathrm{P}\left({\mathrm{A}}_{\mathrm{n}}\right)=1$.

Illustration-1

In the experiment of throwing a fair die, consider the following events A = {1, 3, 5}, B = {2, 4, 6}, C = {1, 2, 3}.  Are these events equally likely ?

Solution

n(A)= n(B) = n(C)=3,  Hence A, B and C are equally likely.

Illustration-2

In the experiment of throwing a fair die, consider the following events A = {1, 3, 5}, B = {2, 4}, C = {6}. Are these events mutually exclusive ?

Solution

A ⋂ B = B ⋂ C = C ⋂ A = $\varphi$.  Hence A, B and C are mutually exclusive.

Illustration-3

In the experiment of throwing a fair die, consider the following events A = {2, 4, 6}, B = {3, 6}, C = {1, 5, 6}. Are these events exhaustive ?

Solution

A ⋃ B ⋃ C = S= {1, 2, 3, 4, 5, 6}.  Hence A, B and C are exhaustive.

Illustration-4

Give two examples of  mutually exclusive events.

Solution

i) The events {1, 2} and {3, 5} are disjoint in the sample space S = {1, 2, 3, 4, 5, 6}. So, they are mutually exclusive.

ii) When two dice are thrown, the probability of getting the sum 10 and 11 are mutually exclusive.

Illustration-5

Give two examples of  exhaustive events. Solution

i) The events {1, 2, 3, 4,5}, {2, 4, 6} are exhaustive in the sample space S= {1, 2, 3, 4, 5, 6}

ii) The events {HH, HT}, {TH, TT} are exhaustive in the sample space S = {HH, HT, TH, TT}

Illustration-6

Give examples of two events which are neither mutually exclusive nor exhaustive.

Solution

i) Let A be the event of getting an even prime number and let B be the event of getting even number when throwing a fair die is rolled once

i.e., A = {2}, B = {2, 4, 6} A and B are neither mutually exclusive nor exhaustive

ii) Let A be the event of getting exactly one head when two coins are tossed once and B be the event of getting atleast one head when  two coins are tossed once.

Then A = {HT, TH}, B = {HT, TH, HH} A and B are neither mutually exclusive nor exhaustive.

3. CLASSICAL DEFINITION OF PROBABILITY

If a random experiment results in n mutually exclusive, equally likely and exhaustive outcomes, out of which m are favorable to the occurrence of an event A, then the probability of occurrence of A is given by $\mathrm{P}\left(\mathrm{A}\right)=\frac{\mathrm{m}}{\mathrm{n}}=\frac{\text{ Number of outcomes favourable to }\mathrm{A}}{\text{ Number of total outcomes }}$

It is obvious that 0 ≤ m ≤ n. If an event A is certain to happen, then m = n, thus P(A) = 1.

If A is impossible to happen, then m = 0 and so P(A) = 0. Hence we conclude that 0 ≤ P(A) ≤ 1.

Further, if $\overline{A}$ denotes negative of A i.e. event that A doesn’t happen, then for above cases m, n; we shall have

$P\left(\overline{A}\right)=\frac{n–m}{n}=1–\frac{m}{n}=1–P\left(A\right)$

$\therefore P\left(A\right)+P\left(\overline{A}\right)=1$.

Notations: For two events A and B,

(i) A‘ or  or A^C stands for the non-occurrence or negation of A.

(ii) A ⋃ B stands for the occurrence of at least one of A and B.

(iii) A ⋂ B stands for the simultaneous occurrence of A and B.

(iv) A‘ ⋂ B‘ stands for the non-occurrence of both A and B.

(v) A $\subseteq$ B stands for “the occurrence of A implies occurrence of B”.

Some important remarks about Coins, Dice , Playing cards and Envelopes.

(1) Coins: A coin has a head side and a tail side. If an experiment consists of more than a coin, then coins are considered to be distinct if not otherwise stated.

Number of exhaustive cases of tossing n coins simultaneously (or of tossing a coin n times) = 2ⁿ.

(2) Dice: A die (cubical) has six faces marked 1, 2, 3, 4, 5, 6. We may have tetrahedral (having four faces 1, 2, 3, 4) or pentagonal (having five faces 1, 2, 3, 4, 5) die. As in the case of coins, if we have more than one die, then all dice are considered to be distinct if not otherwise stated.

Number of exhaustive cases of throwing n dice simultaneously

(or throwing one dice n times) = 6ⁿ.

(3) Playing cards: A pack of playing cards usually has 52 cards. There are 4 suits (Spade, Heart, Diamond and Club) each having 13 cards. There are two colours red (Heart and Diamond) and black (Spade and Club) each having 26 cards.

In thirteen cards of each suit, there are 3 face cards or coart cards namely king, queen and jack. So there are in all 12 face cards (4 kings, 4 queens and 4 jacks). Also there are 16 honour cards, 4 of each suit namely ace, king, queen and jack.

(4) Probability regarding n letters and their envelopes: If n letters corresponding to n envelopes are placed in the envelopes at random, then

(i) Probability that all letters are in right envelopes = $\frac{1}{\mathrm{n}!}$.

(ii) Probability that all letters are not in right envelopes $=1–\frac{1}{\mathrm{n}!}$.

(iii) Probability that no letter is in right envelopes = $\frac{1}{2!}–\frac{1}{3!}+\frac{1}{4!}–\dots +(–1{)}^{\mathrm{n}}\frac{1}{\mathrm{n}!}$.

(iv) Probability that exactly r letters are in right envelopes = $\frac{1}{\mathrm{r}!}\left[\frac{1}{2!}–\frac{1}{3!}+\frac{1}{4!}–\dots ..+(–1{)}^{\mathrm{n}–\mathrm{r}}\frac{1}{(\mathrm{n}–\mathrm{r})!}\right]$.

Illustration-7

A page is opened at random from a book containing 600 pages. What is the probability that the number on the page is a perfect square.

Solution

Since we are selecting one page from 600 pages

S = {1, 2, …….., 600},  n(S) = 600;

Let A be the event of selecting page whose number is a perfect square.

Since 24 is the largest number such that

24² = 576 < 600, we have,

A = {1², 2², ……, 24²}

So, n(A) = 24

P(A) = $\frac{24}{600}$  =  $\frac{3}{75}$

Illustration-8

Find the probability that a leap year will have 53 Sundays.

Solution

A leap year contains 366 days. which can be split into

366 = 7 52 + 2

So, a leap year contains 52 complete weeks leaving two more days.

The last two consecutive days may be any one of the following 7 possibilities.

365^th day              366^th day

1) Sunday           Monday

2) Monday         Tuesday

3) Tuesday         Wednesday

4) Wednesday    Thursday

5) Thursday        Friday

6) Friday            Saturday

7) Saturday         Sunday

Let A be the event that the leap year will have 53 sundays.

Here A = {(sat, sun) ; (sun, mon)}

So, A has exactly two favourable outcomes

P(A) = $\frac{\mathrm{n}\left(\mathrm{A}\right)}{\mathrm{n}\left(\mathrm{S}\right)}=\frac{2}{7}$

Illustration-9

If 4 fair coins are tossed once then find the probability of getting 2 heads and 2 tails.

Solution

Since 4 coins are tossed,

we have, number of elementary events = 2⁴ = 16

Here n(S) = 2⁴ = 16;

Let A be the event of getting 2 heads and 2 tails  out of  4tosses getting two heads always implies getting 2tails

Two heads out of 4 can be selected in $C_2^4$ ways

So n(A) = ⁴C₂ = 6

P(A) = $\frac{\mathrm{n}\left(\mathrm{A}\right)}{\mathrm{n}\left(\mathrm{S}\right)}=\frac{6}{16}=\frac{3}{8}$

Illustration-10

Find the probability of throwing a total score 8 with 2 dice.

Solution

Since, two dice are rolled,

Sample space S = {(x₁, x₂) / 1  x₁, x₂ ≤ 6}

Here, n(S) = 6 ⨯ 6 = 36 ;

Let A be the event of getting a total score 8

A = {(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)}

Here n(A) = 5

P(A) = $\frac{\mathrm{n}\left(\mathrm{A}\right)}{\mathrm{n}\left(\mathrm{S}\right)}=\frac{5}{36}$

Illustration-11

Two dice are rolled. What is the probability that none of the dice shows the number 2 ?

Solution

Total out comes n(S) = 6²

Let A be the event that none of the dice shows the number 2 when 2 dice are rolled.

Now n(A) = 5² (excluding 2 on each face)

$\therefore \mathrm{P}\left(\mathrm{A}\right)=\frac{\mathrm{n}\left(\mathrm{A}\right)}{\mathrm{n}\left(\mathrm{S}\right)}=\frac{5^2}{6^2}={\left(\frac{5}{6}\right)}^2$

Illustration-12

A single die is rolled twice in succession. What is the probability that the number on the second toss is greater than that on the first rolling ?

Solution

If a single die is rolled twice, the total out comes  n(S) = 36

Let A be the event that the number on the second toss is greater than that on the first rolling.

A  = {(1,2), (1,3), (1,4), (1,5), (1,6), (2,3), (2,4), (2,5), (2,6), (3,4), (3,5), (3,6), (4,5), (4,6), (5,6)}

n(A) = 15

$\mathrm{P}\left(\mathrm{A}\right)=\frac{\mathrm{n}\left(\mathrm{A}\right)}{\mathrm{n}\left(\mathrm{S}\right)}=\frac{15}{36}=\frac{5}{12}$

Illustration-13

From a set of 17 cards 1, 2, 3, ……16, 17, one is drawn at random. Find the probability that number on the drawn card would be divisible by 3 or 7.

Solution

Numbers which are divisible by three are 3, 6, 9, 12, 15.  Similarly numbers which are divisible by 7 are 7, 14.

$\Rightarrow$ Probability of the number written on the card to be divisible by 3 or 7 is

= $\frac{7}{17}$.

Illustration-14

Seven accidents occur in a week. What is the probability that they happen on the same day.

Solution

Total no. of cases=Total no. of ways in which 7 accidents can happen in a week (or be distributed)= 7⁷

Favourable no. of cases out of these = number of those in which all 7 happen on one day (any day of the week) = 7

$\therefore$ Required. probability = $\frac{7}{7^7}=\frac{1}{7^6}$

2. Problems based on combination and permutation

1. PROBLEMS BASED ON COMBINATION OR SELECTION

To solve such kind of problems, we use $\mathrm{C}_{\mathrm{r}}^{\mathrm{n}}=\frac{\mathrm{n}!}{\mathrm{r}!(\mathrm{n}–\mathrm{r})!}$.

2. PROBLEMS BASED ON PERMUTATION OR ARRANGEMENT

To solve such kind of problems, we use $\mathrm{P}_{\mathrm{r}}^{\mathrm{n}}=\frac{\mathrm{n}!}{(\mathrm{n}–\mathrm{r})!}$.

3. IMPORTANT FORMULAE USEFUL IN SOLVING THE PROBELMS

1. When ‘n’ fair coins are tossed the probability of getting exactly ‘r’  (≤n) heads (tails) = $\frac{\mathrm{c}_{\mathrm{r}}^{\mathrm{n}}}{2^{\mathrm{n}}}$

2. When ‘n’ fair coins are tossed the probability of getting atleast one head (tail) = $1–\frac{1}{2^{\mathrm{n}}}$

3. A coin is tossed (m + n) times (m>n), then the probability of getting at least ‘m’ consecutive heads is $\frac{\mathrm{n}+2}{2^{\mathrm{m}+1}}$

4. A coin is tossed (m + n) times (m>n), then the probability of getting exactly ‘m’ consecutive heads is $\frac{\mathrm{n}+2}{2^{\mathrm{m}+2}}$

5. The probability of getting a sum of ‘S’ points when ‘n’ symmetrical dice are rolled is

$\mathrm{P}(\mathrm{X}=\mathrm{S})=\sum _{\mathrm{k}=0}^{\frac{\mathrm{s}–\mathrm{n}}{6}}\frac{(–1{)}^{\mathrm{k}}.\mathrm{c}_{\mathrm{k}}^{\mathrm{n}}.\mathrm{c}_{\mathrm{n}–1}^{(\mathrm{s}–6\mathrm{k}–1)}}{6^{\mathrm{n}}}$ where k=0,1,2… $\left[\frac{\mathrm{s}–\mathrm{n}}{6}\right]$.

6. If ‘p’ and ‘q’ are the probability of success, failure of a game in which $A_1, A_2, A_3,\dots .A_n$ play then

i ) probability of $A_1 ‘s$ winning is $\frac{p}{1–q^n}$

ii) probability of  $A_2 ‘s$ winning is $\frac{qp}{1–q^n}$

iii) probability of $A_k ‘s\left(1\le k\le n\right)$ winning is $\frac{q^{k–1}.p}{1–q^n}$

7. Out of n pairs of shoes if shoes are selected at random, the probability that there is no pair is $\frac{\mathrm{C}_{\mathrm{K}}^{\mathrm{n}}.2^{\mathrm{K}}}{\mathrm{C}_{\mathrm{K}}^{2\mathrm{n}}}$.

8. The probability that two subsets of A having n elements at random will have r elements in common is $\frac{\mathrm{C}_{\mathrm{r}}^{\mathrm{n}}.3^{\mathrm{n}–\mathrm{r}}}{4^{\mathrm{n}}}$ (or) $\mathrm{C}_{\mathrm{r}}^{\mathrm{n}}.{\left(\frac{3}{4}\right)}^{\mathrm{r}}.\frac{1}{3^{\mathrm{r}}}$

Illustration-15

If two cards are drawn from pack of 52 cards at random, then find the probability of getting both club cards.

Solution

Since 2 cards are drawn at random, n(S) = ⁵²C₂

Let A be the event of selecting both club cards.

In a pack there are 13 club cards.

n(A) = ¹³C₂

P(A) = $\frac{C_2^{13}}{C_2^{52}}=\frac{13\times 12}{52\times 51}==\frac{1}{17}$

Illustration-16

A and B are among 20 persons who sit at random along a round table. Find the probability that there are exactly six persons between A and B.

Solution

In circular permutations, there is no first place. At the same time, which thing we use first and in which place we fill first has no importance.

So, arrange A in any one of the 20 places. Now there are 19 places at which B can be arranged. But since 6 persons are to be seated between A and B, B has only two favourable positions to sit in both directions, One to right and the other to the left of A,  as shown in the following diagram.

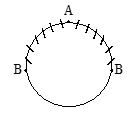
The required probability =  $\frac{2}{19}$;

Illustration-17

A class has 15 boys and 5 girls. Suppose three students are selected at random from the class. Find the probability that they are all boys.

Solution

Let A be the event of selecting three boys. Total number of children = 15 + 5 = 20.

Now $\mathrm{n}\left(\mathrm{S}\right)={20}_{{\mathrm{C}}_3},\mathrm{n}\left(\mathrm{A}\right)={15}_{{\mathrm{C}}_3}$

required probability = $\mathrm{C}_3^{15}/\mathrm{C}_3^{20}$

Illustration-18

A box contains 20 screws of which 5 are defective. Two screws are drawn at random. Find the probability of the event that

i) neither of the 2 screws is defective.

ii) atleast one of them is defective.

Solution

i) The given a box contains 20 screws of which 5 are defective and15 are non defective.

Since 2 screws are drawn at random from the box,

n(s) = ²⁰C₂

Let A be the event that neither of the 2 screws is defective.

Then n(A) = ¹⁵C₂

ii) If A represents the event of getting no defective screw, then represents the event of getting atleast one defective.

$\therefore \mathrm{P}\left(\overline{\mathrm{A}}\right)=1–\mathrm{P}\left(\mathrm{A}\right)=1–\frac{21}{38}=\frac{17}{38}$

Illustration-19

Out of 30 consecutive integers, two integers are drawn at random. Find the probability that their sum is (i) an odd number (ii) an even number

Solution

i) Let A be the event that the sum of the two numbers is odd when two integers are drawn at random from 30 consecutive integers and S be the sample space.

Now n(s) = ³⁰C₂. There are 15 odd integers and 15 even integers from 1 to 30.

The sum of the two integers is odd if one of integer drawn is odd and other even.    

ii) Since the sum may be either odd or even if A denotes the event that the sum is odd then denotes the event that sum is even. The probability that the sum of the two integers is even = $P\left(\overline{A}\right)$

= $1–P\left(A\right)$

= $1–\frac{15}{29}=\frac{14}{29}$

Illustration-20

If 4 people are chosen at random, then find the probability that no two of them were born on the same day of the week.

Solution

Since a person can be born on any day of a week, he can born in 7 ways.

By product rule,

The total number of ways that 4 people can born

= 7 ⨯ 7 ⨯ 7 ⨯ 7 = 7⁴

∴ n(S) = 7⁴

Let A be the event that no two of the 4 people chosen were born on the same day of the week.

Here n(A) = number of ways to arrange the 7 days of the week taken 4 at a time  when repetitions are not allowed = ⁷P₄

∴   P(A) = $\frac{\mathrm{P}_4^7}{7^4}$

Illustration-21

From a pack of 52 cards two cards are drawn at random. Find  the probability of the following events:

(a) Both cards are of spade.

(b) One card is of spade and one card is of diamond.

Solution

The total number of ways in which 2 cards can be drawn = ⁵²C₂

= $\frac{52\times 51}{1\times 2}$ = 26 ⨯ 51 = 1326.

∴ Number of elements in the space S are n(S) = 1326

(a) Let the event, that both cards are of spade, be denoted by E₁, then n(E₁) = Number of elements in E₁ = Number of ways in which 2 cards can be selected out of 13 cards of spade = ¹³C₂ = $\frac{13\times 12}{1\times 2}$= 78.

∴ Probability of E₁ = P(E₁) = $\frac{\mathrm{n}\left({\mathrm{E}}_1\right)}{\mathrm{n}\left(\mathrm{S}\right)}=\frac{78}{1326}=\frac{1}{17}$.

(b) Let E₂ be the event that one card is of spade and one is of diamond then n(E₂) = number of elements in E₂ =number of ways in which one card of spade can  be selected out of 13 spade cards and one card of diamond can be selected out of 13 diamond cards.

= ¹³C₁⨯¹³C₁ = 13⨯13 =169

∴ P(E₂) = $\frac{\mathrm{n}\left({\mathrm{E}}_2\right)}{\mathrm{n}\left(\mathrm{S}\right)}=\frac{169}{1326}=\frac{13}{102}$.

Illustration-22

A has 3 shares in a lottery containing 3 prizes and 6 blanks; B has one share in a lottery containing one prize and 2 blanks. Compare their chances of success.

Solution

Total number of tickets in the first lottery = 3 + 6 =9

A may select any three tickets out of these 9 tickets.  Therefore, the number of elements in the sample space S is given by =n(S) =⁹C₃ = $\frac{9\times 8\times 7}{3\times 2\times 1}$ =84

Let E₁ be the event of winning the prize in the first lottery by A .So, $\overline{{\mathrm{E}}_1}$ is he event of not winning the prize of A, Then number of elements in $\overline{{\mathrm{E}}_1}$ is given by

n($\overline{{\mathrm{E}}_1}$) = number of ways of selecting 3 tickets out of six blank tickets

= ⁶C₃ = $\frac{6\times 5\times 4}{1\times 2\times 3}$ = 20

∴ The probability of not winning the prize by A is ($\overline{{\mathrm{E}}_1}$) = $\frac{\mathrm{n}\left({\overline{\mathrm{E}}}_1\right)}{\mathrm{n}\left(\mathrm{S}\right)}=\frac{20}{84}=\frac{5}{21}$

Since P(E₁) +P($\overline{{\mathrm{E}}_1}$) =1    

∴ P(E₁) = 1-P($\overline{{\mathrm{E}}_1}$)

Or P(E₁) = $1–\frac{5}{21}=\frac{16}{21}$.

Now for B

n(S) = number of ways of selecting 1 ticket out of 3 tickets.

Or n(S) = ³C₁ = 3.

Let E₂ be the event of winning the prize by B.

∴ n(E₂) = number of ways of selecting one ticket out of 1 prize ticket = ¹C₁ = 1

∴ The probability of winning the prize by B.

P(E₂) = $\frac{\mathrm{n}\left({\mathrm{E}}_2\right)}{\mathrm{n}\left(\mathrm{S}\right)}=\frac{1}{3}$

∴ The ratio of the probabilities of winning the prizes by A and B

= $\frac{\mathrm{P}\left({\mathrm{E}}_1\right)}{\mathrm{P}\left({\mathrm{E}}_2\right)}=\frac{16/21}{1/3}=\frac{16}{7}$. 

3. Odds in favour and odds against an event

As a result of an experiment if “a” of the outcomes are favourable to an event E and “b” of the outcomes are against it, then we say that odds are a to b in favour of E or odds are b to a against E.

Thus odds in favour of an event E $=\frac{\text{ Number of favourable cases }}{\text{ Num ber of unfavourable cases }}=\frac{\mathrm{a}}{\mathrm{b}}=\frac{\mathrm{a}/(\mathrm{a}+\mathrm{b})}{\mathrm{b}/(\mathrm{a}+\mathrm{b})}=\frac{\mathrm{P}\left(\mathrm{E}\right)}{\mathrm{P}\left(\overline{\mathrm{E}}\right)}$.

Similarly, odds against an event E $=\frac{\text{ Num ber of unfavourable cases }}{\text{ Number of favourable cases }}=\frac{\mathrm{b}}{\mathrm{a}}=\frac{\mathrm{P}\left(\overline{\mathrm{E}}\right)}{\mathrm{P}\left(\mathrm{E}\right)}$.

Important Tips

If odds in favour of an event are a: b, then the probability of the occurrence of that event is $\frac{\mathrm{a}}{\mathrm{a}+\mathrm{b}}$

and the probability of non-occurrence of that event is $\frac{\mathrm{b}}{\mathrm{a}+\mathrm{b}}$.

If odds against an event are a: b, then the probability of the occurrence of that event is $\frac{\mathrm{b}}{\mathrm{a}+\mathrm{b}}$ and the probability of non-occurrence of that event is $\frac{\mathrm{a}}{\mathrm{a}+\mathrm{b}}$.

Illustration-23

A card is drawn from a pack of 52 cards. A gambler bets that it is a spade or an ace. What are the odds against his winning this bet

(A) 17: 52                      (B) 52: 17                       (C) 9: 4                            (D) 4: 9

Solution

(C)

Probability of the card being a spade or an ace $=\frac{16}{52}=\frac{4}{13}$.

Hence odds in favour is 4 : 9

So the odds against his winning is 9 : 4.

Illustration-24

The odds against a certain event is 5: 2 and the odds in favour of another event is  6: 5. If both the events are independent, then the probability that at least one of the events will happen is

(A) $\frac{50}{77}$          (B) $\frac{52}{77}$          (C) $\frac{25}{88}$          (D) $\frac{63}{88}$

Solution

(B)

Let A and B be two given events. The odds against A are 5 : 2, therefore $P\left(A\right)=\frac{2}{7}$.

The odds in favour of B are 6 : 5,

therefore $P\left(B\right)=\frac{6}{11}$

The required probability $=1–P\left(\overline{A}\right) P\left(\overline{B}\right)$

= $1–\left(1–\frac{2}{7}\right)\left(1–\frac{6}{11}\right)=\frac{52}{77}$.

Illustration-25

If odds against solving a question by three students are 2: 1,  and  respectively, then probability that the question is solved only by one student is

(A) $\frac{31}{56}$          (B) $\frac{24}{56}$          (C) $\frac{25}{56}$          (D) None of these

Solution

(C)

The probability of solving the question by these three students are $\frac{1}{3},\frac{2}{7}$ and $\frac{3}{8}$ respectively.

$P\left(A\right)=\frac{1}{3}; P\left(B\right)=\frac{2}{7}; P\left(C\right)=\frac{3}{8}$

Then probability of question solved by only one student

$=\mathrm{P}(\mathrm{A} \overline{\mathrm{B}} \overline{\mathrm{C}} \mathrm{or} \overline{\mathrm{A}} \mathrm{B} \overline{\mathrm{C}} \mathrm{or} \overline{\mathrm{A}} \overline{\mathrm{B}} \mathrm{C})$

$=P\left(A\right)P\left(\overline{B}\right)P\left(\overline{C}\right)+P\left(\overline{A}\right)P\left(B\right)P\left(\overline{C}\right)+P\left(\overline{A}\right)P\left(\overline{B}\right)P\left(C\right)$

$=\frac{1}{3}·\frac{5}{7}·\frac{5}{8}+\frac{2}{3}·\frac{2}{7}·\frac{5}{8}+\frac{2}{3}·\frac{5}{7}·\frac{3}{8}=\frac{25+20+30}{168}=\frac{25}{56}$.

4. Axiomatic approach to probability and Addition theorems on probability

1. AXIOMATIC APPROACH TO PROBABILITY

Axiomatic approach is another way of describing probability of an event. In this approach some axioms or rules are depicted to assign probabilities.

Let S be the sample space of a random experiment. The probability P is a real valued function whose domain is the power set of S and range is the interval [0,1] satisfying the following axioms

(i) For any event E, P (E) ≥ 0

(ii) P (S) = 1

(iii) If E and F are mutually exclusive events, then P(E ∪ F) = P(E) + P(F).

It follows from (iii) that P(φ) = 0.

Let S be a sample space containing outcomes ω₁, ω₂,…,ω_n , i.e., S = {ω₁, ω₂, …, ω_n}

It follows from the axiomatic definition of probability that

(i) 0 ≤ P (ω_i) ≤ 1 for each ω_i ∈ S

(ii) P (ω₁) + P (ω₂) +…..+ P(ω_n) = 1

(iii) For any event A, P(A) = $\Sigma$P(ω_i), ω ∈ A.

2. ADDITION THEOREM ON PROBABILITY

Notations:

(i) $P(A+B)\text{ or }P(A\cup B)$ = Probability of happening of A or B

= Probability of happening of the events A or B or both

= Probability of occurrence of at least one event A or B

(ii) P(AB) or P(A⋂B) =  Probability of happening of events A and B together.

1. When events are not mutually exclusive

If A and B are two events which are not mutually exclusive, then

$\mathrm{P}(\mathrm{A}\cup \mathrm{B})=\mathrm{P}\left(\mathrm{A}\right)+\mathrm{P}\left(\mathrm{B}\right)–\mathrm{P}(\mathrm{A}\cap \mathrm{B})\text{ or }\mathrm{P}(\mathrm{A}+\mathrm{B})=\mathrm{P}\left(\mathrm{A}\right)+\mathrm{P}\left(\mathrm{B}\right)–\mathrm{P}\left(\mathrm{AB}\right)$.

For any three events A, B, C

$P(A\cup B\cup C)=P\left(A\right)+P\left(B\right)+P\left(C\right)–P(A\cap B)–P(B\cap C)–P(C\cap A)+P(A\cap B\cap C)$

or $P(A+B+C)=P\left(A\right)+P\left(B\right)+P\left(C\right)–P\left(AB\right)–P\left(BC\right)–P\left(CA\right)+P\left(ABC\right)$.

2. When events are mutually exclusive

If A and B are mutually exclusive events, then

$n(A\cap B)=0\Rightarrow P(A\cap B)=0$

$\therefore P(A\cup B)=P\left(A\right)+P\left(B\right)$.

For any three events A, B, C which are mutually exclusive,

$P(A\cap B)=P(B\cap C)=P(C\cap A)=P(A\cap B\cap C)=0$

$\therefore P(A\cup B\cup C)=P\left(A\right)+P\left(B\right)+P\left(C\right)$.

The probability of happening of any one of several mutually exclusive events is equal to the sum of their probabilities, i.e. if $A_1,A_2\dots \dots A_n$ are mutually exclusive events, then

$P\left(A_1+A_2+\dots +A_n\right)=P\left(A_1\right)+P\left(A_2\right)+\dots ..+P\left(A_n\right)$ i.e. $P\left(\sum A_i\right)=\sum P\left(A_i\right)$.

3. When events are independent

If A and B are independent events, then $P(A\cap B)=P\left(A\right).P\left(B\right)$

$\therefore P(A\cup B)=P\left(A\right)+P\left(B\right)–P\left(A\right).P\left(B\right)$.

4. Some other theorems

(i) Let A and B be two events associated with a random experiment, then

(a) $P(\overline{A}\cap B)=P\left(B\right)–P(A\cap B)$     (b) $P(A\cap \overline{B})=P\left(A\right)–P(A\cap B)$

If B $\subseteq$ A, then

(a) $P(A\cap \overline{B})=P\left(A\right)–P\left(B\right)$                               (b) $P\left(B\right)\le P\left(A\right)$

Similarly if A $\subset$ B, then

(a) $(\overline{A}\cap B)=P\left(B\right)–P\left(A\right)$                                 (b) $P\left(A\right)\le P\left(B\right)$.

Note:  Probability of occurrence of neither A nor B is $P(\overline{A}\cap \overline{B})=P\left(\overline{A\cup B}\right)=1–P(A\cup B)$.

(ii) Generalization of the addition theorem: If $A_1,A_2,\dots ,A_n$ are n events associated with a random experiment, then

$\mathrm{P}\left(\underset{\mathrm{i}=1}{\overset{\mathrm{n}}{\cup }}{\mathrm{A}}_{\mathrm{i}}\right)$ = $\sum _{\mathrm{i}=1}^{\mathrm{n}}\mathrm{P}\left({\mathrm{A}}_{\mathrm{i}}\right)–\sum _{\begin{array}{c}\mathrm{i}, \mathrm{j}=1\\ \mathrm{i}\ne \mathrm{j}\end{array}}^{\mathrm{n}}\mathrm{P}\left({\mathrm{A}}_{\mathrm{i}}\cap {\mathrm{A}}_{\mathrm{j}}\right)+$$\sum _{\begin{array}{c}\mathrm{i},\mathrm{j},\mathrm{k}=1\\ \mathrm{i}\ne \mathrm{j}\ne \mathrm{k}\end{array}}^{\mathrm{n}}\mathrm{P}\left({\mathrm{A}}_{\mathrm{i}}\cap {\mathrm{A}}_{\mathrm{j}}\cap {\mathrm{A}}_{\mathrm{k}}\right)+$…+$(–1{)}^{\mathrm{n}–1}\mathrm{P}\left({\mathrm{A}}_1\cap {\mathrm{A}}_2\cap \dots ..\cap {\mathrm{A}}_{\mathrm{n}}\right)$.

If all the events ${\mathrm{A}}_{\mathrm{i}}(\mathrm{i}=1,2\dots ,\mathrm{n})$ are mutually exclusive, then $P\left(\underset{i=1}{\overset{n}{\cup }}{A}_i\right)=\sum _{i=1}^{n}P\left(A_i\right)$

i.e. $\mathrm{P}\left({\mathrm{A}}_1\cup {\mathrm{A}}_2\cup \dots .\cup {\mathrm{A}}_{\mathrm{n}}\right)=\mathrm{P}\left({\mathrm{A}}_1\right)+\mathrm{P}\left({\mathrm{A}}_2\right)+\dots .+\mathrm{P}\left({\mathrm{A}}_{\mathrm{n}}\right)$.

(iii) Booley’s inequality: If $A_1,A_2,\dots ,A_n$ are n events associated with a random experiment, then

(a) $P\left(\underset{i=1}{\overset{n}{\cap }}{A}_i\right)\ge \sum _{i=1}^{n}P\left(A_i\right)–(n–1)$                       (b) $P\left(\underset{i=1}{\overset{n}{\cup }}{A}_i\right)\le \sum _{i=1}^{n}P\left(A_i\right)$

These results can be easily established by using the Principle of Mathematical Induction.

Important Tips

Let A, B, and C  are three arbitrary events. Then

Verbal description of event	Equivalent Set Theoretic Notation
(i) Only A occurs	(i) $A\cap \overline{B}\cap \overline{C}$
(ii) Both A and B, but not C occur	(ii) $A\cap B\cap \overline{C}$
(iii) All the three events occur	(iii) $A\cap B\cap C$
(iv) At least one occurs	(iv) $A\cup B\cup C$
(v) At least two occur	(v) $(A\cap B)\cup (B\cap C)\cup (A\cap C)$
(vi) One and no more occurs	(vi) $(A\cap \overline{B}\cap \overline{C})\cup (\overline{A}\cap B\cap \overline{C})\cup (\overline{A}\cap \overline{B}\cap C)$
(vii) Exactly two of A, B and C occur	(vii) $(A\cap B\cap \overline{C})\cup (\overline{A}\cap B\cap C)\cup (A\cap \overline{B}\cap C)$
(viii) None occurs	(viii) $\overline{A}\cap \overline{B}\cap \overline{C}=\overline{A\cup B\cup C}$
(ix) Not more than two occur	(ix) $(A\cap B)\cup (B\cap C)\cup (A\cap C)–(A\cap B\cap C)$
(x) Exactly one of A and B occurs	(x) $(A\cap \overline{B})\cup (\overline{A}\cap B)$

Illustration-26

Let a sample space be S = {ω₁, ω₂,…, ω₆}.Which of the following assignments of probabilities to each outcome are valid?

Condition	ω1	ω2	ω3	ω4	ω5	ω6
(a)	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$
(b)	1	0	0	0	0	0
(c)	$\frac{1}{8}$	$\frac{2}{3}$	$\frac{1}{3}$	$\frac{1}{3}$	$–\frac{1}{4}$	$–\frac{1}{3}$
(d)	$\frac{1}{12}$	$\frac{1}{12}$	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{3}{2}$
(e)	0.1	0.2	0.3	0.4	0.5	0.6

Solution

Condition (i): Each of the number p(ω_i) is positive and less than one.

Condition (ii): Sum of probabilities

$=\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}=1$

Therefore, the assignment is valid

Condition (i): Each of the number p(ω_i) is either 0 or 1.

Condition (ii) Sum of the probabilities = 1 + 0 + 0 + 0 + 0 + 0 = 1

Therefore, the assignment is valid

Condition (i) Two of the probabilities p(ω₅) and p(ω₆) are negative, the assignment is not valid

(d) Since p(ω₆) = $\frac{3}{2}>1$, the assignment is not valid

(e) Since, sum of probabilities = 0.1 + 0.2 + 0.3 + 0.4 + 0.5 + 0.6 = 2.1, the assignment is not valid.

Illustration-27

If  E₁, E₂ are two events with $E_1\cap E_2=E$, then show that $P\left({\overline{E}}_1\cap {\overline{E}}_2\right)=P\left({\overline{E}}_1\right)–P\left(E_2\right)$

Solution

L.H.S. = $\mathrm{P}\left({\overline{\mathrm{E}}}_1\cap {\overline{\mathrm{E}}}_2\right)$

= $1–P\left(E_1\cup E_2\right)$

= $1–\left[P\left(E_1\right)+P\left(E_2\right)\right] \because E_1\cap E_2=\varphi$

= $\left[1–P\left(E_1\right)\right]–P\left(E_2\right)=P\left({\overline{E}}_1\right)–P\left(E_2\right)$

Illustration-28

If P(A) = x, P(B) = y and $P\left(A\cap B\right)=z$ . Find $P\left(A^c\cap B^c\right)$.

Solution

Given that P(A) = x, P(B) = y,

$\therefore P(\overline{A}\cap \overline{B})=1–P(A\cup B)$

$=1–\left[P\right(A)+P(B)–P(A\cap B\left)\right]$

= 1 – [x + y – z] = 1 – x – y + z.

Illustration-29

Two events A and B have the probabilities 0.25 and 0.5 respectively. The probability that both A and B occur simultaneously is 0.14. Find the probability that neither A nor B occurs.

Solution

Given, P(A) = 0.25; P(B) = 0.5; P(AB) = 0.14

P(neither A nor B occurs)

= P($\overline{A}\cap \overline{B}$)

= 1 – P(A ⋃ B)     (By Demorgan law)

= 1 – {P(A) + P(B) – P(A ⋂ B)}

= 1 – {0.25 + 0.5 – 0.14}

= 1 – {0.75 – 0.14} = 1 – 0.61 = 0.39

Illustration-30

P(A) = 0.5 ; P(B) = 0.3 and A, B are mutually exclusive Then what is the probability that neither A nor B occurs.

Solution

Given P(A) = 0.5;  P(B) = 0.3 and A⋂B = $\varphi$

P(neither A nor B occurs)

$=P(\overline{A}\cap \overline{B})$

= 1 – P(A⋃ B)      (∵ By Demorgan law)

= 1 – [P(A) + P(B)]                [ A⋂B = $\varphi$]

= 1 – [0.5 + 0.3] = 0.2

Illustration-31

For any two events A and B show that $P(A\cap B)–P\left(A\right)P\left(B\right)=P\left(A^c\right)P\left(B\right)–P\left(A^C\cap B\right)$ = $=P\left(A\right)P\left(B^c\right)–P\left(A\cap B^c\right)$

Solution

Consider,  P(A^c)P(B)–P(A^cB)

= [1–P(A)]P(B)–[P(B) – P(A⋂B)]

= P(B) – P(A)P(B) – P(B)+P(A⋂B)

= P(A⋂B)–P(A)P(B)

Consider,  P(A)P(B^c)–P(A⋂B^c)

= P(A) [1–P(B)] – [P(A) – P(A⋂B)]

= P(A⋂B) – P(A) P(B)

= P(A^c)P(B)–P(A^c⋂B)

= P(A)P(B^c)–P(A⋂B^c)

Illustration-32

A and B are seeking admission into IIT. If the probability for A to be selected is 0.5 and that of both to be selected is 0.3. Is it possible that, the probability of B to be selected is 0.9 ?

Solution

Given P(A) = 0.5; P(A⋂B) = 0.3

We know for any event A, 0 ≤ P(A) ≤ 1

So, 0 ≤ P(A⋃B) ≤ 1

Now,  by addition theorem,

P(A⋃B) = P(A) + P(B)  – P(A⋂B)

P(B) = P(A⋃B) – P(A) +  P(A⋂B)

= P(A⋃B) – 0.5 + 0.3 ≤ 1 – 0.2 = 0.8

P(B) ≤ 0.8

So, P(B) can not be equal to 0.9

Illustration-33

In an experiment of drawing a card at random from a pack, the event of getting a spade is denoted by A and getting a pictured card (King, Queen or Jack) is denoted by B. Find the probabilities of A, B,  A⋂B and A⋃B

Solution

$\mathrm{n}\left(\mathrm{S}\right)=\mathrm{C}_1^{52}=52,$

$\mathrm{n}\left(\mathrm{A}\right)=\mathrm{C}_1^{13}=13, \mathrm{n}\left(\mathrm{B}\right)=\mathrm{C}_1^{12}=12$

$\mathrm{P}\left(\mathrm{A}\right)=\frac{13}{52}=\frac{1}{4}, \mathrm{P}\left(\mathrm{B}\right)=\frac{12}{52}=\frac{3}{13}$

A⋂B = Event of getting a spade picture card i.e., spade king or spade queen or spade jack.

$\therefore n(A\cap B)=C_1^3=3$

$\therefore P(A\cap B)=3/52$

A⋃B =  Event of getting a spade card or a  picture card

P(A⋃B) = P(A) + P(B) – P (A⋂B)

$=\frac{13}{52}+\frac{12}{52}–\frac{3}{52}=\frac{22}{52}=\frac{11}{26}$

Illustration-34

If two cards are drawn from a pack of 52 cards then find the probability of getting both red or both kings.

Solution

Since 2 cards are drawn from pack of cards, n(S) = ⁵²C₂

Let A be the event of getting two red cards, n(A) = ²⁶C₂

Let B be the event of getting two king cards, n(B) = ⁴C₂

Here A, B  are not mutually exclusive

A⋂B is the event of getting two red king cards. There are only two red king cards (king of hearts and king of diamonds) and they can be selected in ²C₂ ways.

∴ n(A⋂B) = 1;

By addition theorem,

P(AB) = P(A)+P(B)–P(A⋂B)

$=\frac{\mathrm{C}_2^{26}}{\mathrm{C}_2^{52}}+\frac{\mathrm{C}_2^4}{\mathrm{C}_2^{52}}–\frac{1}{\mathrm{C}_2^{52}}$

$=\frac{325+6–1}{52C_2}=\frac{330}{26\times 51}=\frac{55}{221}$

Illustration-35

In a swimming competition, only 3 students A, B and C are taking part. The probability of A‘s winning or the probability of B‘s winning is three times the probability of C‘s winning. Find the probability of the event either B or C to win.

Solution

Suppose that A, B and C denote the events that the 3 students A, B and C win the competition respectively. By data, P(A) = P(B) = 3P(C)

Here A, B and C are mutually exclusive and exhaustive

(∵ one and only one of  A, B and C  can win the competition)

∴ P(A) + P(B) + P(C) = 1

$\Rightarrow$ 3P(C) + 3P(C) + P(C) = 1

$\Rightarrow$ P(C) = 1/7  and  P(A)  = P(B) = 3/7

P(B⋃C) = P(B) + P(C)        [∵ B⋂C = $\varphi$]

$=\frac{3}{7}+\frac{1}{7}=\frac{4}{7}$

Illustration-36

Let A, B, C  be three events. If the probability of occurring one event out of A and B is 1 – a, out of B and C is 1 – 2a, out of C and A is 1 – a and that of occurring three events simultaneously is a2,  then prove that the probability that at least one out of A, B, C will  occur is greater than or equal to 0.5.

Solution

Probability that exactly one event out of A and B occur is p(A) + p(B) – 2p(A⋂B) and probability that exactly one event out of B and C occur is p(B) + p(C) – 2p(B⋂C) and so on.

Now,  p(A⋃B⋃C) = p(A) + p(B) + p(C) – p(A⋂B) – p(A⋂C) – p(B⋂C) + p(A⋂B⋂C)

= $\frac{1}{2}$[p(A)+ p(B) – 2p(A⋂B) + p(B) + p(C)-2p(B⋂C)+p(C)+p(A)-2p(A⋂C)] +p(A⋂B⋂C)

= $\frac{1–\mathrm{a}+1–2\mathrm{a}+1–\mathrm{a}}{2}+{\mathrm{a}}^2=\mathrm{a}2–2\mathrm{a}+\frac{3}{2}$

Let   ${\mathrm{a}}^2–2\mathrm{a}+\frac{3}{2}=\mathrm{y}\Rightarrow {\mathrm{a}}^2–2\mathrm{a}+\frac{3}{2}–\mathrm{y}=0$

Since a is real, so $4–4\left(\frac{3}{2}–\mathrm{y}\right)\ge 0\Rightarrow \mathrm{y}\ge 1/2$.

5. Conditional probability and Independent and Dependent Events

1. CONDITIONAL PROBABILITY

Let A and B be two events associated with a random experiment. Then, the probability of occurrence of A under the condition that B has already occurred and P(B) ≠ 0, is called the conditional probability and it is denoted by P(A/B).

Thus, P(A/B) = Probability of occurrence of A, given that B has already happened.

$=\frac{\mathrm{P}(\mathrm{A}\cap \mathrm{B})}{\mathrm{P}\left(\mathrm{B}\right)}=\frac{\mathrm{n}(\mathrm{A}\cap \mathrm{B})}{\mathrm{n}\left(\mathrm{B}\right)}$.

Similarly, P(B/A) = Probability of occurrence of B, given that A has already happened.

$=\frac{\mathrm{P}(\mathrm{A}\cap \mathrm{B})}{\mathrm{P}\left(\mathrm{A}\right)}=\frac{\mathrm{n}(\mathrm{A}\cap \mathrm{B})}{\mathrm{n}\left(\mathrm{A}\right)}$.

Note:  Sometimes, P(A/B) is also used to denote the probability of occurrence of A when B occurs. Similarly, P(B/A) is used to denote the probability of occurrence of B when A occurs.

1. Multiplication theorems on probability

(i) If A and B are two events associated with a random experiment, then, if P(A) ≠ 0 or $P(A\cap B)=P\left(B\right)$, if P(B) ≠ 0.

(ii) Extension of multiplication theorem: If $A_1,A_2,\dots ,A_n$ are n events related to a random experiment, then

$P\left(A_1\cap A_2\cap A_3\cap \dots .\cap A_n\right)$ $=P\left(A_1\right)P\left(A_2/A_1\right)P\left(A_3/A_1\cap A_2\right)$$P\left(A_n/A_1\cap A_2\cap \dots \cap A_{n–1}\right)$, where $P\left(A_i/A_1\cap A_2\cap \dots \cap A_{i–1}\right)$ represents the conditional probability of the event $A_i$, given that the events $A_1,A_2,\dots \dots ,A_{i–1}$ have already happened.

(iii) Multiplication theorems for independent events: If A and B are independent events associated with a random experiment, then $P(A\cap B)=P\left(A\right).P\left(B\right)$ i.e., the probability of simultaneous occurrence of two independent events is equal to the product of their probabilities.

By multiplication theorem, we have $P(A\cap B)=P\left(A\right).P(B/A)$.

Since A and B are independent events, therefore $P(B/A)=P\left(B\right)$. Hence, $P(A\cap B)=P\left(A\right).P\left(B\right)$.

(iv) Extension of multiplication theorem for independent events: If $A_1,A_2,\dots ,A_n$ are independent events associated with a random experiment, then

$P\left(A_1\cap A_2\cap A_3\cap \dots \cap A_n\right)=P\left(A_1\right)P\left(A_2\right)\dots P\left(A_n\right)$.

By multiplication theorem, we have

$P\left(A_1\cap A_2\cap A_3\cap \dots \cap A_n\right)$$=P\left(A_1\right)P\left(A_2/A_1\right)P\left(A_3/A_1\cap A_2\right)\dots$$P\left(A_n/A_1\cap A_2\cap \dots \cap A_{n–1}\right)$

Since $A_1,A_2,\dots ,A_{n–1},A_n$ are independent events, therefore

$P\left(A_2/A_1\right)=P\left(A_2\right),P\left(A_3/A_1\cap A_2\right)$$=P\left(A_3\right),\dots ,P\left(A_n/A_1\cap A_2\cap \dots \cap A_{n–1}\right)=P\left(A_n\right)$

Hence, $P\left(A_1\cap A_2\cap \dots \cap A_n\right)=P\left(A_1\right)P\left(A_2\right)\dots P\left(A_n\right)$.      

2. Probability of at least one of the n independent events:

If $p_1,p_2,p_3,\dots \dots \dots ,p_n$ be the probabilities of happening of n independent events $A_1,A_2,A_3,\dots \dots \dots ,A_n$ respectively, then

(i) Probability of happening none of them $=P\left({\overline{A}}_1\cap {\overline{A}}_2\cap {\overline{A}}_3\dots \dots \cap {\overline{A}}_n\right)$ = $P\left({\overline{A}}_1\right).P\left({\overline{A}}_2\right).P\left({\overline{A}}_3\right)\dots .P\left({\overline{A}}_n\right)=\left(1–p_1\right)\left(1–p_2\right)\left(1–p_3\right)\dots .\left(1–p_n\right)$.

(ii) Probability of happening at least one of them

$=P\left(A_1\cup A_2\cup A_3\dots \cup A_n\right)=1–P\left({\overline{A}}_1\right)P\left({\overline{A}}_2\right)P\left({\overline{A}}_3\right)\dots .P\left({\overline{A}}_n\right)$$=1–\left(1–p_1\right)\left(1–p_2\right)\left(1–p_3\right)\dots \left(1–p_n\right)$.

(iii) Probability of happening of first event and not happening of the remaining $=P\left(A_1\right)P\left({\overline{A}}_2\right)P\left({\overline{A}}_3\right)\dots .P\left({\overline{A}}_n\right)$ $=p_1\left(1–p_2\right)\left(1–p_3\right)\dots \dots .\left(1–p_n\right)$

Illustration-37

i) If A, B, C are any three events in an experiment and $A\subseteq B$, P(C) > 0 then show that  P(A/C) ≤ P(B/C)

ii) If A, B are mutually exclusive and P(B) ≠ 1 then show that P(A/B^c) = $\frac{P\left(A\right)}{1–P\left(B\right)}$

iii) If A, B are mutually exclusive and P(A⋃B) ≠ 0 then P(A/A⋃B) = $\frac{P\left(A\right)}{P\left(A\right)+P\left(B\right)}$

Solution

i) Since A$\subseteq$B

We have A⋂C$\subseteq$B⋂C for any event C

But we know, if A, $\subseteq$ B are any two events of a random experiment such that AB then P(A) ≤ P(B) Therefore P(A⋂C) ≤ P(B⋂C)

$\Rightarrow \frac{P(A\cap C)}{P\left(C\right)}\le \frac{P(B\cap C)}{P\left(C\right)}$   [∵ P(C) > 0]

$\Rightarrow$ P(A/C) ≤ P(B/C)

ii) Since A and B are exclusive

$A\cap B=\varphi$

Therefore $A\subseteq B^C\Rightarrow A\cap B^C=A$;

Now $P\left(A/B^C\right)=\frac{P\left(A\cap B^C\right)}{P\left(B^C\right)}=\frac{P\left(A\right)}{1–P\left(B\right)}$

iii) Since A and B are exclusive ,

$A\cap B=\varphi \text{ and }P(A\cap B)=0$

$P(A/A\cup B)=\frac{P[A\cap (A\cup B\left)\right]}{P(A\cup B)}=\frac{P\left(A\right)}{P(A\cup B)} [\because A\subseteq A\cup B]$

$=\frac{\mathrm{P}\left(\mathrm{A}\right)}{\mathrm{P}\left(\mathrm{A}\right)+\mathrm{P}\left(\mathrm{B}\right)–\mathrm{P}(\mathrm{A}\cap \mathrm{B})}=\frac{\mathrm{P}\left(\mathrm{A}\right)}{\mathrm{P}\left(\mathrm{A}\right)+\mathrm{P}\left(\mathrm{B}\right)}=(\because \mathrm{P}(\mathrm{A}\cap \mathrm{B})=0)$

Illustration-38

Suppose  A  and  B  are  independent  events  with  P(A) = 0.6, P(B) = 0.7 then compute

i) $P(A\cap B)$          ii) $P(A\cup B)$          iii) P(B/A)          iv) $P\left(A^c\cap B^c\right)$

Solution

Given  P(A) = 0.6, P(B) = 0.7

i) Since A and B are independent

$P(A\cap B)=P\left(A\right).P\left(B\right)=(0.6)(0.7)=0.42$

ii) $P(A\cup B)=P\left(A\right)+P\left(B\right)–P(A\cap B)$

$=P\left(A\right)+P\left(B\right)–P\left(A\right)P\left(B\right)=0.6+0.7–0.6\times 0.7$

= 0.6 + 0.7 – 0.6 ×  0.7

= 1.3 – 0.42 = 0.88

iii) $P(B/A)=P\left(B\right)=0.7$        (∵ A and B are independent)

iv) $P\left(A^c\cap B^c\right)=1–P(A\cup B)$ = 1 – 0.88 = 0.12

Illustration-39

A pair of dice are rolled. What is the probability that neither die shows a 2 given that they sum to 7.

Solution

Let A be the event that the sum is 7 and B be the event that neither die shows a 2 when a pair of dice are rolled and S be the sample space.

A = {(1,6), (2,5), (3,4), (4,3), (5,2) (6,1)}

$A\cap B=\left\{\right(1,6),(3,4),(4,3),(6,1\left)\right\}$

$P(B/A)=\frac{n(A\cap B)}{n\left(A\right)}=\frac{4}{6}=\frac{2}{3}$

Illustration-40

An urn contains 12 red balls and 12 green balls. Suppose two balls are drawn one after another without replacement. Find the probability that the second ball drawn is green, given that the first ball drawn is red.

Solution

Let A be the event of drawing the first ball red and  B be the event of drawing the second ball green. Then $P\left(A\right)=\frac{12}{24}$  But, after one red ball is drawn out,

11 red balls and 12 green balls remain in the urn.

Required probability = $P(B/A)=\frac{12}{23}$

Illustration-41

Suppose there are 12 boys and 4 girls in a class. If we choose three children one after another is succession at random, find the probability that all the three are boys.

Solution

Let A be the event of choosing a Boy in 1^st Trial.

Let B be the event of choosing a Boy in 2^nd Trial.

Let C be the event of choosing a Boy in 3^rd Trial.

By multiplication theorem for three events

Required probability = $P(A\cap B\cap C)$

= $P\left(A\right).P(B/A).P(C/A\cap B)$

= $\frac{12}{16}·\frac{11}{15}·\frac{10}{14}=\frac{11}{28}$

Illustration-42

A bag contains 10 balls; 5 of which are red and the remaining blue. Two balls are drawn at random from the bag one after the other with replacement. Let A be the event that the first ball drawn is red and B be the event that the second ball is red. Find whether these events are independent.

Solution

$P\left(A\right)=\frac{5}{10}=\frac{1}{2},P\left(B\right)=\frac{5}{10}=\frac{1}{2}\text{ and }$

$P(A\cap B)=\frac{5\times 5}{10\times 10}=\frac{1}{4}=P\left(A\right)P\left(B\right).$

∴ A and B are independent.

Illustration-43

Find the probability of drawing 2 red balls in succession from a bag containing 4 red balls and 5 black balls when the ball that is drawn first is

i) not replaced          ii) replaced

Solution

Let A and B be the events of drawing a red ball in the first and second draws respectively.

i) Draws are done without replacement.

$P(A\cap B)=P\left(A\right)P(B/A)=\frac{4}{9}\times \frac{3}{8}=\frac{1}{6}$

ii) Draws are done with replacement. Then the events A and B are independent.

$P(A\cap B)=P\left(A\right)P\left(B\right)=\frac{4}{9}\times \frac{4}{9}=\frac{16}{81}$

Illustration-44

The probability that A hits a target is 1/4 and the probability that B hits the target is 1/3. If each of them fired once, what is the probability that the target will be hit atleast once?

Solution

Let A be the event that A hits target

$\Rightarrow$ P(A) = 1/4

Let B be the event that B hits target

$\Rightarrow$ P(B) = 1/3

Here A, B are independent events

∴ The probability that the target will be hit atleast once = $P(A\cup B)=P\left(A\right)+P\left(B\right)–P(A\cap B)$

$=P\left(A\right)+P\left(B\right)–P\left(A\right).P\left(B\right)$

$=\frac{1}{4}+\frac{1}{3}–\frac{1}{4}·\frac{1}{3}=\frac{1}{2}$

Illustration-45

An urn contains ‘w’ white balls and ‘b’ black balls. Two players Q and R alternatively draw a ball with replacement from the urn. The player who draws a white ball first wins the game. If Q begins the game, find the probability of his winning the game.

Solution

Let p be the probability of drawing a white ball from bag by any person in one trail.

Here $p=\frac{w}{w+b}$

Let q = 1 – p = $1–\frac{w}{w+b}=\frac{b}{w+b}$ ;

Since Q starts the game, Q wins the game if he draws a white ball in 1^st time or Q and R both fail and Q draws a white ball in second time in the third trial  and so on.

P(Q wins in 1^st time) = p

P(Q wins in 2^nd time) in the third trial = q q p = q² p

P(Q wins in 3^rd time)  in 5th trial = (q q)² p = q4p and so on

Since all the above cases are mutually exclusive,

P(Q wins)  = p + q²p + q⁴p + ….. $\infty$

$=\frac{\mathrm{p}}{1–{\mathrm{q}}^2}=\frac{\frac{\mathrm{w}}{\mathrm{w}+\mathrm{b}}}{1–\frac{{\mathrm{b}}^2}{(\mathrm{w}+\mathrm{b}{)}^2}}$

$=\frac{w(w+b)}{(w+b{)}^2–b^2}=\frac{w(w+b)}{w^2+2wb}=\frac{w+b}{w+2b}$

2. INDEPENDENT AND DEPENDENT EVENTS

Two events A and B are said to be independent if occurrence or non-occurrence of one does not affect the occurrence or non-occurrence of the other,

i.e. P(B/A) = P(B), P(A) ≠ 0 similarly P(A/B) = P(A), P(B) ≠ 0

$\Rightarrow \mathrm{P}(\mathrm{B}/\mathrm{A})=\frac{\mathrm{P}(\mathrm{A}\cap \mathrm{B})}{\mathrm{P}\left(\mathrm{A}\right)}=\mathrm{P}\left(\mathrm{B}\right)\Rightarrow \mathrm{P}(\mathrm{A}\cap \mathrm{B})=\mathrm{P}\left(\mathrm{A}\right).\mathrm{P}\left(\mathrm{B}\right)$

If the events are not independent, they are said to be dependent.

Remarks:

· If P(A) = 0 $\Rightarrow$ for event ‘B’, 0 ≤ P(A⋂B) ≤ P(A).

$\Rightarrow$ P(A⋂B) = 0, thus P(A⋂B) = P(A).P(B) = 0.

Hence an impossible event would be independent of any other event. 

· Distinction between independent and mutually exclusive events must be carefully made. Independence is a property of probability whereas the mutual exclusion is a set-theoretic concept. If A and B are two mutually exclusive and possible events of sample space ‘S’  then P(A) > 0, P(B) > 0 and P(A⋂B) = 0 ≠ P(A).P(B) so that A and B can’t be independent. Infact P(A/B) = 0 similarly P(B/A) = 0. Consequently, mutually exclusive events are strongly dependent.

· Two events A and B are independent if and only if A and B’ are independent or A’ and B are independent or A’ and B’ are independent.

We have P(A⋂B) = P(A).P(B)

Now P(A⋂B’) = P(A) – P(A⋂B) = P(A) – P(A).P(B) = P(A) (1-P(B)) = P(A).P(B’)

Thus A and B’ are independent.

Similarly P(A’⋂B) = P(B) – P(A⋂B) = P(B).P(A’)

Finally P(A’ ⋂ B’)  = 1 – P(A⋃B) = 1 – P(A) – P(B) + P(A⋂B)

= 1 – P(A) – P(B) + P(A).P(B) = (1-P(A)) – P(B) (1-P(A))

= (1-P(A)) (1-P(B)) = P(A’).P(B’)

Thus A’ and B’ are also independent.

Mutual Independence and Pairwise Independence:

Three events A, B, C are said to be mutually independent if,

P(A⋂B) = P(A).P(B), P(A⋂C) = P(A).P(C), P(B ⋂ C) = P(B).P(C) and P(A⋂B⋂C) = P(A).P(B).P(C)

These events would be said to be pairwise independent if,

P(A⋂B) = P(A).P(B), P(B⋂C) = P(B).P(C) and P(A⋂C) = P(A).P(C).

Thus mutually independent events are pairwise independent but the converse may not be true.

Illustration-46

An event A₁ can happen with probability p₁ and event A₂ can happen with probability p₂.

What is the probability that

(i) exactly one of them happens

(ii) at least one of them happens(Given A₁ and A₂ are independent events).

Solution

(i) The probability that A₁ happens is p₁ 

∴  The probability that A₁ fails is 1 – p₁

Also the probability that A₂ happens is p₂

Now, the chance that A₁ happens and A₂ fails is p₁(1 – p₂) and the chance that A₁ fails and A₂ happens is p₂(1-p₁)

∴ The probability that one and only one of them happens is

p₁(1 – p₂) + p₂(1 – p₁) = p₁ + p₂ – 2p₁p₂

(ii) The probability that both of them fail = (1 – p₁) (1 – p₂).

∴ probability that atleast one happens=1 -(1 – p₁) (1 – p₂) = p₁+p₂ – p₁ p₂

Illustration-47

A lot contains 50 defective and 50 non-defective bulbs. Two bulbs are drawn at random, one at a time with replacement. The events A, B, C are defined as under;

A = {the first bulb is defective}

B = {the second bulb is non defective}

C = {the two bulbs are both defective or both are non-defective}.

Categorise the events A, B, C to be pairwise independent or mutually independent.

Solution

Let D_i (N_i) denote the occurrence of a defective (non-defective) bulb at the i^th draw (i = 1, 2). Now sample-space ‘S’ is;

S = {D₁ D₂, D₁ N₂, N₁ D₂, N₁ N₂}

$\Rightarrow$ P(D_i) = $\frac{50}{100}=\frac{1}{2}=P\left({ \mathrm{N}}_i\right)$ (i = 1, 2)

A = {D₁ D₂, D₁ N₂},  B = {D₁ N₂, N₁ N₂}, C = {D₁ D₂, N₁ N₂}

$\Rightarrow$ A⋂B = {D₁ N₂} $\Rightarrow$ A⋂C = {D₁ D₂}

$\Rightarrow$ B⋂C = {N₁ N₂} and A ⋂ B ⋂ C = $\varphi$

P(A) = P(D₁ D₂) + P(D₁N₂) = $\frac{1}{2}·\frac{1}{2}+\frac{1}{2}·\frac{1}{2}=1/2$

P(B) = P(D₁ N₂) + P(N₁ N₂) = $\frac{1}{2}·\frac{1}{2}+\frac{1}{2}·\frac{1}{2}=1/2$

P(C) = P(D₁ D₂) + P(N₁N₂) = $\frac{1}{2}·\frac{1}{2}+\frac{1}{2}·\frac{1}{2}=1/2$

P(A⋂B) = P(D₁ N₂) = $\frac{1}{2}.\frac{1}{2}=\frac{1}{4}$ = P(A).P(B)

P(B⋂C) = P(N₁ N₂) == P(B).P(C)

P(A⋂C) = P(D­₁ D₂) = = P(A).P(C)

And P(A ⋂ B ⋂ C) = 0 ≠ P(A).P(B).P(C)

$\Rightarrow$ Events are not mutually independent but are pairwise independent.

6. Total probability and Baye’s rule

1. THE LAW OF TOTAL PROBABILITY

Let S be the sample space and let $E_1,E_2,\dots .E_n$ be n mutually exclusive and exhaustive events associated with a random experiment. If A is any event which occurs with E₁ or E₂ or …. or E_n, then $P\left(A\right)=P\left(E_1\right)P\left(A/E_1\right)+P\left(E_2\right)P\left(A/E_2\right)+\dots +P\left(E_n\right)P\left(A/E_n\right)$. 

2. BAYE’S RULE

Let S be a sample space and $E_1,E_2,\dots .E_n$ be n mutually exclusive events such that $\underset{i=1}{\overset{n}{\cup }}{E}_i=S$ and $\mathrm{P}\left({\mathrm{E}}_{\mathrm{i}}\right)>0$ for i = 1, 2, ……, n. We can think of (E_i’s as the causes that lead to the outcome of an experiment. The probabilities P(E_i), i = 1, 2, ….., n are called  prior probabilities. Suppose the experiment results in an outcome of event A, where P(A) > 0. We have to find the probability that the observed event A was due to cause E_i, that is, we seek the conditional probability . These probabilities are called posterior probabilities, given by Baye’s rule as

$\mathrm{P}\left({\mathrm{E}}_{\mathrm{i}}/\mathrm{A}\right)=\frac{\mathrm{P}\left({\mathrm{E}}_{\mathrm{i}}\right).\mathrm{P}\left(\mathrm{A}/{\mathrm{E}}_{\mathrm{i}}\right)}{{\displaystyle \sum _{\mathrm{k}=1}^{\mathrm{n}}}\mathrm{P}\left({\mathrm{E}}_{\mathrm{k}}\right)\mathrm{P}\left(\mathrm{A}/{\mathrm{E}}_{\mathrm{k}}\right)}$.

Illustration-48

Bag B₁ contains 4 white and 2 black balls. Bag B₂ contains 3 white and 4 black balls. A bag is drawn at random and a ball is chosen at random from it. What is the probability that the ball drawn is white ?

Solution

Let A₁ and A₂ be the events of selecting bag B₁ and B₂ respectively.  Since their probabilites of selection are not given, assume them to be equally likely.

$\therefore P\left(A_1\right)=\frac{1}{2}\text{ and }P\left(A_2\right)=\frac{1}{2}$

Let E be the event of drawing a white ball

$P\left(E/A_1\right)=4/6\text{ and }P\left(E/A_2\right)=3/7$

By total probability theorem

$P\left(E\right)=P\left(A_1\right)P\left(E/A_1\right)+P\left(A_2\right)P\left(E/A_2\right)$

$=\frac{1}{2}\times \frac{4}{6}+\frac{1}{2}\times \frac{3}{7}=\frac{23}{42}$

Illustration-49

Bag A contains 4 white and 7 black balls. Bag B contains 5 white and 6 black balls. A die is rolled. If 2 or 5 turns up then choose bag A otherwise choose bag B. If one ball is drawn at random from the selected bag, then find the probability that it is black.

Solution

Let E be the event of selecting black ball from the selected bag.

Let A₁ be the event of throwing 2 or 5 on the die and A₂ be the event of not getting them.

P(A₁) = 2/6 and P(A₂) = 4/6

P( E / A₁) = $\frac{7}{11}$;   P(E /A₂) = 6 / 11

by total probability theorem,

P(E) = P(A₁) P(E/A₁) + P(A₂) P(E/A₂)

$=\frac{2}{6}\times \frac{7}{11}+\frac{4}{6}\times \frac{6}{11}=\frac{38}{66}=\frac{19}{33}$

Illustration-50

Bag A contains 4 white and 3 black balls. Bag B contains 3 white and 2 black balls. One ball is transferred from bag A to bag B. Now one ball is drawn from bag B. Find the probability that it is white.

Solution

Let A₁ and A₂ be the events of transferring white ball and black ball from 1^st bag to second bag respectively

Here P(A₁) = 4/7 and P(A₂) = 3/7

We can easily observe that A₁ and A₂ are mutually exclusive and exhaustive.

Let E be the event of selecting white ball from 2^nd bag.

P(E/A₁) = P(drawing a white ball from 2nd bag if white ball is transferred from 1^st bag to 2^nd bag)

= $\frac{4}{6}=\frac{2}{3}$

Similarly, P (E/A₂) = $\frac{3}{6}=\frac{1}{2}$

By total probability theorem,

$P\left(E\right)=P\left(A_1\right)P\left(E/A_1\right)+P\left(A_2\right)P\left(E/A_2\right)$

$=\frac{4}{7}\times \frac{2}{3}+\frac{3}{7}\times \frac{1}{2}=\frac{8}{21}+\frac{3}{14}=\frac{25}{42}$

Illustration-51

Three boxes numbered I, II, III contain the balls as follows.

	White	Black	Red
I	1	2	3
II	2	1	1
III	4	5	3

One box is randomly selected and a ball is drawn from it. If the ball is red, then find the probability that it is from box II.

Solution

Let A_i be the event of selecting i^th bag for i = 1, 2, 3, are mutually exclusive and exhaustive events. Since their probabilities of selection are not given, assume them to be equally likely.

P(A₁) = P(A₂) = P(A₃) = $\frac{1}{3}$

Let E be the event of getting a red ball.

Now, P(E/A₁) = $\frac{3}{6}$;  P(E/A₂) = $\frac{1}{4}$; P(E/A₃) = $\frac{3}{12}$

By Baye’s theorem,

P(A₂/E) = $\frac{P\left(A_2\right)P\left(E/A_2\right)}{{\displaystyle \sum _{i=1}^3}P\left(A_i\right)P\left(E/A_i\right)}$         …. (1)

$=\frac{\frac{1}{3}\frac{1}{4}}{\frac{1}{3}\frac{3}{6}+\frac{1}{3}\frac{1}{4}+\frac{1}{3}\frac{3}{12}}=\frac{\frac{1}{4}}{\frac{1}{2}+\frac{1}{4}+\frac{1}{4}}=\frac{1}{4}$

Illustration-52

A survey shows that in a certain village 2 out of every 100 men and 1 out of every 100 women have stomach ulcers. A person selected at random from the village is found to have stomach ulcer. Find the probability that the person is a male, given that the probability of selecting a male from the village is 0.55.

Solution

Let A₁ and A₂ be the events that the selected person is a male and female respectively. Now A₁ and A₂ are mutually exclusive and exhaustive events.

P(A₁) = 0.55, P(A₂) = 0.45

Let E be the event that the selected person have stomach ulcer.

P(E/A₁) = $\frac{2}{100}$; P(E/A₂) = $\frac{1}{100}$

By Baye’s theorem,

$\mathrm{P}\left(\raisebox{1ex}{$\mathrm{E}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{A}}_1$}\right.\right)=\frac{\mathrm{P}\left({\mathrm{A}}_1\right)\mathrm{P}\left(\raisebox{1ex}{$\mathrm{E}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{A}}_1$}\right.\right)}{\mathrm{P}\left({\mathrm{A}}_1\right)\mathrm{P}\left(\raisebox{1ex}{$\mathrm{E}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{A}}_1$}\right.\right)+\mathrm{P}\left({\mathrm{A}}_2\right)\mathrm{P}\left(\raisebox{1ex}{$\mathrm{E}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{A}}_2$}\right.\right)}$

$=\frac{0.55\times \frac{2}{100}}{0.55\times \frac{2}{100}+0.45\times \frac{1}{100}}=\frac{110}{155}=\frac{22}{31}$

Illustration-53

A bag contains 5 balls the colours of which are known. Two balls are drawn and found them to be red. Find the probability that all the balls in the bag are red.

Solution

It is very clear that the bag contains atleast 2 red balls

Let A₁, A₂, A₃ and A₄ be the events that there are 2, 3, 4 and 5 red balls in the bag respectively. The events are mutually exclusive and exhaustive. Since their probabilities of selection are not given, assume them to be equally. There fore

P(A₁) = P(A₂) = P(A₃) = (A₄) = $\frac{1}{4}$

Let E be the event that the two balls which are drawn are red.

$\mathrm{P}\left(\mathrm{E}/{\mathrm{A}}_1\right)=\frac{\mathrm{C}_2^2}{\mathrm{C}_2^5},\mathrm{P}\left(\mathrm{E}/{\mathrm{A}}_2\right)=\frac{\mathrm{C}_2^3}{\mathrm{C}_2^5}$,

$P\left(E/A_3\right)=\frac{C_2^4}{C_2^5}, P\left(E/A_4\right)=\frac{C_2^5}{C_2^5}$

By Baye’s theorem,

$\mathrm{P}\left({\mathrm{A}}_4/\mathrm{E}\right)=\frac{\mathrm{P}\left({\mathrm{A}}_4\right)\mathrm{P}\left(\mathrm{E}/{\mathrm{A}}_4\right)}{{\displaystyle \sum _{\mathrm{i}=1}^4}\mathrm{P}\left({\mathrm{A}}_{\mathrm{i}}\right)\mathrm{P}\left(\mathrm{E}/{\mathrm{A}}_{\mathrm{i}}\right)}=\frac{1}{\frac{1}{10}+\frac{3}{10}+\frac{6}{10}+\frac{10}{10}}=\frac{1}{2}$

Illustration-54

A man is known to speak the truth 3 out of 4 times. He throws a die and reports that it is a six. Find the probability that it is actually six.

Solution

Let A₁ be the event that six occurs on the die and A₂ be the event that a digit other than six occurs.

Let E be the event that the man makes a statement that six is obtained

P(E/A₁) = Probability that the man speaks truth =3/4

P(E/A₂) = Probability that the man does not speak truth  = 1/4

By Baye’s theorem,

$P\left(A_1/E\right)=\frac{P\left(A_1\right)P\left(A_1/E\right)}{P\left(A_1\right)P\left(A_1/E\right)+P\left(A_2\right)P\left(A_2/E\right)}$

$=\frac{\frac{3}{4}\times \frac{1}{6}}{\frac{3}{4}\times \frac{1}{6}+\frac{1}{4}\times \frac{5}{6}}=\frac{3}{8}$

Illustration-55

A letter is known to have come from either ‘MAHARASTRA’ or ‘MADRAS’ on the post mark only consecutive letters ‘RA’ can be read clearly. What is the chance that the letter came from ‘MAHARASTRA’.

Solution

Let A₁ and A₂ be the events that the letter will come from  ‘MAHARASTRA’ and ‘MADRAS’ respectively.

Let E be the event that the two consecutive letters ‘RA’ can be read clearly.

Here A₁ and A₂ are exclusive and exhaustive

P(A₁) = P(A₂) = $\frac{1}{2}$

MAHARASTRA contains 9 possible consecutive  letters MA, AH, HA, AR, RA, AS, ST, TR and RA. Among these 9 possibilities two are favour to E  

$\therefore$ P(E/A₁) = $\frac{2}{9}$

The word MADRAS contains 5 consecutive letters MA, AD, DR, RA, AS. Among these 5 possibilities exactly one is favourable to B.

$\therefore$ P(E/A₂) = $\frac{1}{5}$

By Baye’s theorem,

P(A1/E) = $\frac{P\left(A_1\right)P\left(E/A_1\right)}{P\left(A_1\right)P\left(E/A_1\right)+P\left(A_2\right)P\left(E/A_2\right)}$

$=\frac{P\left(E/A_1\right)}{P\left(E/A_1\right)+P\left(E/A_2\right)} \left(\because P\left(A_1\right)=P\left(A_2\right)\right)$

$=\frac{\frac{2}{9}}{\frac{2}{9}+\frac{1}{5}}=\frac{10}{19}$

7. Random Variables, Its Probability Distributions, Binomial distribution and Geometric Probability

1. RANDOM VARIABLES

Let S be a sample space. A random variable X is a function from the set S to R, the set of real numbers.

For example, the sample space for a throw of a pair of dice is S = $\begin{array}{cccc}\{11,& 12,& \cdots ,& 16\\ 21,& 22,& \cdots ,& 26\\ ⋮& ⋮& \ddots & ⋮\\ 61,& 62,& \cdots ,& 66\}\end{array}$

Let X be the sum of numbers on the dice. Then X(12)=3, X(43)=7, etc. Also, {X = 7} is the event {61, 52, 43, 34, 25, 16}. In general, if X is a random variable defined on the sample space S and r is a real number, then  {X = r} is an event. If the random variable X takes n distinct values $x_1,x_2,\dots ,x_n$, then $\left\{X=x_1\right\}, \left\{X=x_2\right\},\dots ,\left\{X=x_n\right\}$ are mutually exclusive and exhaustive events.

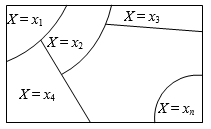
Now, since $\left(X=x_i\right)$ is an event, we can talk of $P\left(X=x_i\right)\text{ . If }P\left(X=x_i\right)=P_i(1\le i\le n)$, then the system of numbers.

$\left(\begin{array}{llll}{x}_1& x_2& \cdots & x_n\\ p_1& p_2& \cdots & p_n\end{array}\right)$

is said to be the probability distribution of the random variable X. The expectation (mean) of the random variable X is defined as $E\left(X\right)=\sum _{i=1}^n{p}_i{x}_i$

and the variance of X is defined as $var\left(X\right)=\sum _{i=1}^n{p}_i{\left(x_i–E\left(X\right)\right)}^2=\sum _{i=1}^n{p}_i{x}_i^2–\left(E\right(X){)}^2$.

Note:

1. If the mean of the random variable x is, then the mean of the random variable $ax\pm b$, where a and b are constants is $a\overline{x}\pm b$.

2. If the variance of the random variable x is ${\sigma }^2$, then the variance of the random variable $ax\pm b$, when a and b are constants is $a^2\times {\sigma }^2$.

3. The positive square root of variance ${\sigma }^2$ is called the standard deviation $\sigma$.

Illustration-56

Find the mean and variance of the random variable X which follows the following distribution

X = x	1	2	3	4
P(X = x)	0.1	0.2	0.3	0.1

Solution

Mean of X = $\mu =\sum x_{i}P\left(X=x_i\right)$

= 1(0.1) +  2(0.2) + 3(0.3) + 4(0.4)

= 3

variance of $X={\sigma }^2=\sum x_i^{2}P\left(x=x_i\right)–{\mu }^2$

= (1)²(0.1) + 2²(0.2)+3²(0.3)+4²(0.4)–(3)²

= 0.1 + 0.8 + 2.7 + 6.4 – 9

= 10 – 9

= 1

Illustration-57

Find the mean and variance of the random variable X whose distribution is

X = xr	1	2	3	…….n
P(X = xr)	1/n	1/n	1/n	……1/n

Solution

Mean = $\mu =\sum x_{i}P\left(X=x_i\right)$

$=1\left(\frac{1}{n}\right)+2\left(\frac{1}{n}\right)+3\left(\frac{1}{n}\right)+\dots +n\left(\frac{1}{n}\right)$

$=\frac{1}{n}(1+2+3+\dots +n)$

$=\frac{1}{n}.\frac{n(n+1)}{2}=\frac{n+1}{2}$

variance of $X={\sigma }^2=\sum x_i^{2}P\left(x=x_i\right)–{\mu }^2$

$=1^2\left(\frac{1}{n}\right)+2^2\left(\frac{1}{n}\right)+\dots ..+n^2\left(\frac{1}{n}\right)–{\left(\frac{n+1}{2}\right)}^2$

$=\frac{1}{n}\left(1^2+2^2+\dots +n^2\right)–{\left(\frac{n+1}{2}\right)}^2$

$=\frac{1}{\cancel{n}}\left(\frac{\cancel{n}(n+1)(2n+1)}{6}\right)–{\left(\frac{n+1}{2}\right)}^2$

$=\frac{(n+1)(2n+1)}{6}–\frac{(n+1{)}^2}{4}=\frac{n^2–1}{12}$

Illustration-58

Find the constant c, so that $F\left(x\right)=c{\left(\frac{2}{3}\right)}^x,x=1,2,3,\dots ..$ is the probability distribution for a discrete random variable X.

Solution

Sum of probabilities = 1

$\Rightarrow c{\left(\frac{2}{3}\right)}^1+c{\left(\frac{2}{3}\right)}^2+c{\left(\frac{2}{3}\right)}^3+\dots ..=1$

$\Rightarrow c{\left(\frac{2}{3}\right)}^1+c{\left(\frac{2}{3}\right)}^2+\dots ..=1$

$\Rightarrow c\left(\frac{\frac{2}{3}}{1–\frac{2}{3}}\right)=1$ (using sum of infinite G.P. formula = a/1–r  where a= 2/3 and r = 2/3)$\Rightarrow c\left(2\right)=1 \Rightarrow c=1/2$.

2. BINOMIAL PROBABILITY DISTRIBUTION

A random variable X which takes values 0, 1, 2, …, n is said to follow binomial distribution if its probability distribution function is given by $P(X=r)=C_r^n{p}^r{q}^{n–r},r=0,1,2,\dots \dots ,n$

where p, q > 0 such that p + q = 1.

The notation X ~ B(n, p) is generally used to denote that the random variable X follows binomial distribution with parameters n and p.

We have

$P(X=0)+P(X=1)+\dots +P(X=n)$ = $C_0^n{p}^0{q}^{n–0}+C_1^n{p}^1{q}^{n–1}+\dots +C_n^n{p}^n{q}^{n–n}=(q+p{)}^n=1^n=1$

Now probability of

(a) Occurrence of the event exactly r times

$P(X=r)=C_r^n{q}^{n–r}{p}^r$.

(b) Occurrence of the event at least r times

$\mathrm{P}(\mathrm{X}\ge \mathrm{r})=\mathrm{C}_{\mathrm{r}}^{\mathrm{n}}{\mathrm{q}}^{\mathrm{n}–\mathrm{r}}{\mathrm{p}}^{\mathrm{r}}+\dots +{\mathrm{p}}^{\mathrm{n}}=\sum _{\mathrm{X}=\mathrm{r}}^{\mathrm{n}}\mathrm{C}_{\mathrm{X}}^{\mathrm{n}}{\mathrm{p}}^{\mathrm{X}}{\mathrm{q}}^{\mathrm{n}–\mathrm{X}}$.

(c) Occurrence of the event at the most r times

$P(0\le X\le r)=q^n+C_1^n{q}^{n–1}p+\dots +C_r^n{q}^{n–r}{p}^r=\sum _{X=0}^r{p}^X{q}^{n–x}$.

(iv) If the probability of happening of an event in one trial be p, then the probability of successive happening of that event in r trials is $p^r$.

Note:  If n trials constitute an experiment and the experiment is repeated N times, then the frequencies of 0, 1, 2, …, n successes are given by $N.P(X=0), N.P(X=1), N.P(X=2),\dots ,N.P(X=n)$.

I. Mean and variance of the binomial distribution:

The binomial probability distribution is

X	0	1	2	n
P(X)	$C_0^n{q}^n{p}^0$	$C_1^n{q}^{n–1}p$	$C_2^n{q}^{n–2}{p}^2$	……$C_n^n{q}^0{p}^n$

The mean of this distribution is $\sum _{i=1}^n{X}_i{p}_i=\sum _{X=1}^{n}X.C_X^n{q}^{n–X}{p}^X=np$,

the variance of the Binomial distribution is ${\sigma }^2=npq$ and the standard deviation is $\sigma =\sqrt{\left(npq\right)}$.

II. Use of multinomial expansion

If a die has m faces marked with the numbers 1, 2, 3, ….m and if such n dice are thrown, then the probability that the sum of the numbers exhibited on the upper faces equal to p is given by the coefficient of $x^p$ in the expansion of $\frac{{\left(x+x^2+x^3+\dots .+x^m\right)}^n}{m^n}$.

The mode of B.D. depends on the value of np + p.

CASE-1: If np + p=k, where k is an integer, then there will be two modes namely k & k-1. In this case the distribution is said to be a Bi-modal binomial distribution.

CASE-2: If np + p = k+f, where k is an integer and f is a proper fraction then there will be only one mode namely k. i.e., the integral part of np+p will be the mode. In this case the distribution is said to be uni-modal binomial distribution.

If we consider n independent Bernoullian trials as one experiment and if we repeat such an experiment N times, then the expected frequency or the theoretical frequency of x successes is given by

$f(X=x)=N\times p(X=x)$

$=N\times c_x^n{p}^x{q}^{n–x}, x=0,1,2,3,\dots .n$

and this is called as Binomial frequency distribution.

Illustration-59

If $X~B(20,1/2)$. Find mean and variance.

Solution

$X~B(20,1/2)$

$\Rightarrow$ n = 20, p = 1/2, q = 1/2

mean = np = 10

variance = npq = 20(1/2)(1/2) = 5

Illustration-60

If 8 coins one tossed simultaneously and the number of heads turned up is denoted by the variable X, then find mean and variance of X.

Solution

Let X be the number of heads on the turned up coins.

then p = q = 1/2 and X follows Binomial distribution

So, mean of X = np = 8 × 1/2 = 4

variance of X = n p q = 8 × 1/2 × 1/2 = 2

Illustration-61

Find the least number of times a fair coin must be tossed so that the probability of getting atleast one head is atleast 0.8.

Solution

Tossing a coin is a Bernoulli trial.

Let  X be the number of heads on the turned up coins.

p=probability of getting head if one coin is tossed is 1/2

q = 1– p = 1– 1/2 = 1/2 and X follows binomial distribution with probability function given by

P(X = x) =  (when the experiment is repeated n times)

P(getting atleast one head)

= $P\left(X\ge 1\right)$

= 1– P(X = 0)

$=1–C_0^n{\left(\frac{1}{2}\right)}^{n–0}{\left(\frac{1}{2}\right)}^0=1–\frac{1}{2^n}$,

Now $P(\mathrm{X}\ge 1)\ge 0.8$

$\iff 1–\frac{1}{2^n}\ge 0.8$

$\iff \frac{1}{2^n}\le 0.2=\frac{1}{5}$

$\iff 2^n\ge 5$

$\iff$ n = 3, 4, 5, ………

So, the least number of coins to be tossed such that $P(X\ge 1)\ge 0.8$ is 3

Illustration-62

Five coins are tossed 320 times. Find the frequencies of the distribution of number of heads and tabulate the result.

Solution

Tossing a coin is Bernoulli trial. That is it can be repeated any number of times under similar conditions.

In one attempt, the trial is repeated 5 times i.e., n = 5;

But in the problem, given that the number of such attempts = 320 = m (say)

Let X be the number of heads on the tossed 5 coins.

Here X ~ B (n,p) where n = 5; p = 1/2

The frequency of r successes in 320 attempts

$=m^n{C}_r{q}^{n–r}{p}^r$

$={320}^5{C}_r{\left(\frac{1}{2}\right)}^{5–r}{\left(\frac{1}{2}\right)}^r$

$=320\times \frac{C_r^5}{2^5}=10{.}^5{\mathrm{C}}_r$

So, the frequency distribution is

Number of  heads	Frequency C
0	$10\times C_0^5=10$
1	$10\times C_1^5=50$
2	$10\times C_2^5=100$
3	$10\times C_3^5=100$
4	$10\times C_4^5=50$
5	$10\times C_5^5=10$

Total frequency =   320

3. POISSIONS DISTRIBUTION

In some problems n is so large or n may not be finite and p is so small then we feel inconvenience to compute P(X = x) using binomial distribution.

Let X denote the random variable and n is so large and p is so small that np = $\lambda$, a constant then Binomial distribution  tends to Poission distribution whose probability function is given by

P(X = x ) = $\frac{e^{–\lambda }{\lambda }^x}{x!}$, x = 0,1,2,3,……

Definition of Poisson variate

Let > 0 be a real number. A random variable X with range {0, 1, 2, …….n, …..} is said to have poisson distribution with parameter if

P(X = x) = $\frac{e^{–\lambda }{\lambda }^x}{x!}$ for  x= 0, 1, 2, ……

Note:- If X is a poission random variable with parameter $\lambda$, then mean of X is $\lambda$ and Variance of X is also $\lambda$ so that standard deviation (S.D) is $\lambda$

Applications of Poisson distribution:

The poisson random variable has very good applications in various areas. Some of the common applications where poisson distribution is used are

i) Number of accidents on a national highway in one day.

ii) Number of deaths of a policy holder in one year.

iii) Number of misprints on a page.

iv) Number of calls received at the reception of an organisation.

v) Number of vehicles arriving at a petrol pump in a specified time.

vi) Number of earthquakes occuring in one year in a particular seismic zone.

The characteristics of P.D.

1. The mean of random poisson variate X is $\lambda$. i.e., $\overline{x}=\lambda =np$.

2. The variance of r.p.v. X is $\lambda$. i.e., ${\sigma }^2=\lambda$ .

3. The S.D. of r.p.v. X is $\sqrt{\lambda }$. i.e., $\sqrt{\lambda }$ .

4. In poisson distribution mean and variance are equal. i.e., $\overline{x}={\sigma }^2=\lambda$ .

5. The mode of poisson distribution depends on the value of $\lambda$.

CASE-I: If $\lambda =K$, where K is an integer, then there will be two modes namely K and K-1 i.e. $\lambda \& \lambda –1$,  themselves. In this case the distribution is said to be Bi-modal poisson distribution.

CASE-II: If $\lambda =K+f$ where K is an integer and f is a proper fraction, then there will be only one mode namely K i.e., the integral part of  will be the mode. In this case the distribution is said to be Uni-modal poisson distribution.

6. The expected frequency or the theoretical frequency of X successes in P.D. is given by

$f(X=x)=N\times P(X=x)$

$=\frac{N\times e^{–\lambda }{\lambda }^x}{\angle x}; x=0,1,2,3,\dots \dots$

and this is called as poisson frequency distribution.

Illustration-63

If X is a poisson variate such that P(X=0)=P(X=1)= K, then show that K = 1/e

Solution

Since P(X = 0) = P(X=1) = K

$\Rightarrow \frac{e^{–\lambda }{\lambda }^0}{\lfloor 0}=\frac{e^{–\lambda }{\lambda }^1}{\lfloor 1}=K \Rightarrow \lambda =1$ and $K=\frac{e^{–\lambda }{\lambda }^1}{\underline{\overline{)1}}}=e^{–1}$

$\therefore$ K = 1/e

Illustration-64

Number of accidents on a national highway each day is a poisson variable with an average of three accidents per a day. Find the probability that no accidents will occur on a given day.

Solution

This is a problem of poisson distribution

X = number of accidents per day

Range of X = {0, 1, 2, ….}

Given average number of accidents per day = $\lambda =3$

Probability that there is no accident on a given day

= P(X = 0) = $e^{–\lambda }$ = $e^{–3}$ = 0.0498

Illustration-65

A factory produces lazor blades and 1 in 500 blades is estimated to be defective. The blades are supplied in packets of 10. In a consignment of 10,000 packets, using poisson distribution, find approximately the number of packets which contain no defective blades.

Solution

Let X be the number of defective blades in a lot of 10 blades.

The probability that a blade to be defective = 1/500;

The average number of defective blades in a lot of 10  = $10\times \frac{1}{500}=\frac{1}{50}=0.02$

Poission parameter = $\lambda$ = 0.02

P (no of defective blades is a lot of 10)

$=\frac{e^{–\lambda }{\lambda }^0}{\underline{\overline{)0}}}=e^{–0.02}=1–\frac{0.02}{\underline{\overline{)1}}}+\frac{0.0004}{\underline{\overline{)2}}}–\frac{0.000008}{\underline{\overline{)3}}}+\dots \dots ..$ = 1– 0.02 + 0.0002 = 0.9802

Therefore the number of packets in a consignment of 10000 packets which contain no defective blade  = 10000 × 0.9802 = 9802

GEOMETRICAL PROBABILITY

Classical definition of probability fails if the total outcomes and number of favourable cases are infinite. Then we use geometrical methods for their computation and hence the name geometric probability.

The probability that a point drawn randomly into a region will fall in the region A is given by the geometrical probability formula.

$P\left(A\right)=\frac{\text{ measure of }A}{\text{ measure of }\Omega }=\frac{mes\left(A\right)}{mes\left(\Omega \right)}$

In case of one dimension if a point is taken at random on a given line AB, the chance that it falls on a particular segment PQ of the line = $\frac{\text{ favourable length }}{\text{ total length }}=\frac{PQ}{AB}$ or we may say that total number of cases is represented by AB and the number of favourable cases by PQ.

In case of two dimensions  if a point is taken  at random in an area S which includes an area then the chance that the point lies on $\sigma$ is $\raisebox{1ex}{$\sigma $}\!\left/ \!\raisebox{-1ex}{$S$}\right.$ = $\frac{\text{ favourable area }}{\text{ total area }}$.

Similarly in case of three dimensions,  geometric probability = $\frac{\text{ favourable volume }}{\text{ total volume }}$.

Illustration-66

A point is selected at random inside a circle of radius ‘a’ then find the probability that it is nearer to the centre than the circumference.

Solution

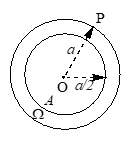
Let O be the centre and P be any interior point. The distance OP varies from O to A.  All points which lie on or inside a concentric circle with radius a/2 will be closer to the centre, than the circumference.

Total area = Area of the bigger circle with radius a = ${\mathrm{\pi a}}^2$.

Favourable area n(A) = $\pi (a/2{)}^2=\frac{1}{4}\pi a^2$

Probability of A = P(A) = $\frac{\text{ measure of }A}{\text{ measures of }\Omega }=\frac{\pi {\left(\frac{a}{2}\right)}^2}{\pi (a{)}^2}=\frac{1}{4}$

Note:

In the above problem, the probability that a point selected is nearer to circumference than centre is $P\left(\overline{A}\right)=1–P\left(A\right)=1–\frac{1}{4}=\frac{3}{4}$.

Illustration-67

A point is randomly chosen inside an equilateral triangle. Find the probability that it lies inside its incircle.

Solution

Let ‘a’ be the side of an equilateral triangle.

A point may be selected inside it.

$\therefore \Omega$ consists of all points inside triangle

Measure of $\Omega =\frac{\sqrt{3}}{4}{a}^2$ = area of the equilateral triangle  …(1)

The inradius $r=\frac{a}{2\sqrt{3}}$

$\therefore$ measure of A = Area of incircle =$\mathrm{\pi }{\left(\frac{\mathrm{a}}{2\sqrt{3}}\right)}^2$ … (2)

$\therefore$ Probability of A = P(A) = $\frac{\text{ measure of }A}{\text{ measure of }\Omega }=\frac{\pi {\left(\frac{a}{2\sqrt{3}}\right)}^2}{\frac{\sqrt{3}}{4}{a}^2}=\frac{\pi }{3\sqrt{3}}$

Illustration-68

A point is randomly chosen inside the circumcircle of an equilateral triangle. Find the probability that it lies inside the inscribed circle of that triangle.

Solution

Let ‘a’ be the side of an equilateral triangle.

Radius of circumcircle = $\frac{a}{\sqrt{3}}$

Radius of incircle = $\frac{a}{2\sqrt{3}}$

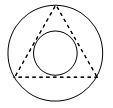
Let  denotes the set of points inside the circumcircle.

A is the set of points which lie inside the inscribed circle.

Measure of $\Omega$ = $\pi {\left(\frac{a}{\sqrt{3}}\right)}^2$  = area of the circumcircle  …. (1)

Measure of A = $\mathrm{\pi }{\left(\frac{\mathrm{a}}{2\sqrt{3}}\right)}^2$  = area of the incircle  …. (2)

$\therefore$ Probability of A = P(A) = $\frac{\text{ measure of }A}{\text{ measure of }\Omega }=\frac{\pi {\left(\frac{a}{2\sqrt{3}}\right)}^2}{\pi {\left(\frac{a}{\sqrt{3}}\right)}^2}=\frac{1}{4}$