Mathematical Reasonning

1. STATEMENTS OR PROPOSITIONS

The following types of sentences are normally used in our every day communication.
(1) Assertive sentence                           (2) Imperative sentence
(3) Exclamatory sentence                    (4) Interrogative sentence

In this chapter, we shall be discussing about a specific type of sentences which will called as statement or propositions.

Assertive Sentence
A sentence that makes an assertion is called an ‘assertive sentence or a declarative sentence’.

Imperative Sentence
A sentence that expresses a request or a command is called an imperative sentence.

Exclamatory Sentence
A sentence that expresses some strong feeling is called an exclamatory sentence.

Interrogative Sentence
A sentence that asks some question is called an interrogative sentence.

DEFINITIONS
Propositions

A statement or a proposition is an assertive (or declarative) sentence which is either true or false but not both a true statement is called valid statement. If a statement is false, then it is called invalid statement.

Open statement
A declarative sentence containing variable (s) is an open statement if it becomes a statement when the variable (s) is (are) replaced by some definite value (s).

Truth Set
The set of all those values of the variable (s) in an open statement for which it becomes a true statement is called the truth set of the open statement.

Truth Value
The truth or falsity of a statement is called its truth value.
If a statement is true, then we say that its truth value is ‘True’ or ‘T’. On the other hand the truth value of a false statement is ‘False’ or ‘F’.

Logical variables
In the study of logic, statements are represented by lower case letters such as p, q, r, s.. These letters are called logical variables.
For example, the statement ‘The sun is a star’ may be represented or denoted by p and we write p : The sun is a star
Similarly, we may denote the statement 14 – 5 =– 2.

Quantifiers
The symbol $\forall$(stands for ‘for all’) and $\exists$(stands for “there exists”) are known as quantifiers.
In other word, quantifiers are symbols used to denote a group of words or a phrase.
The symbols ∀ and ∃ are known as existential quantifiers. An open sentence used with quantifiers always becomes a statement.

Quantified statements
The statements containing quantifiers are known as quantified statements.

$x^2>0.\forall x\in R$ is a quantified statement. Its truth value is T.

Illustration -1

1. Which of the following sentences are statements ? State the truth values of the statements :

(i) The quadratic equation x² – 3x + 2 = 0 has two equal roots.
(ii) Every quadratic equation has two distinct roots.
(iii) He is a popular person.
(iv) Have you finished your work ?
(v) (x – 2) (x – 3) = x² – 5x + 6, for all x ∈ R.
(vi) $\sqrt{2}$ is a complex number.
(vii) sin 2θ = 2 sinθ cosθ or all θ ∈ R.
(viii) Is this red colour ?
(ix) 6 has three prime factors.
(x) Please mind your own business.  
Solution
(i)  Statement, F           (ii) Statement, F          (iii) No. Statement          (iv) Not a Statement

(v) Statement, T           (vi) Statement, T          (vii) Statement, T           (viii) Not a statement

(ix) Statement, F          (x) Not a statement

Illustration -2

Write the truth values of the following statements

(i) ax² + bx + c = 0 may have non-real roots.
(ii) The capital of India is New Delhi.
(iii) Two individuals may be relative.
(iv) –$\sqrt{11}$ is a rational number.
(v) The number of ways in which 4 persons can be seated in four chairs out 6 is P (6, 4)

Solution

(i) T          (ii) T          (iii) T          (iv) F          (v) T

2. TYPES OF STATEMENTS AND TRUTH TABLES

1. TYPES OF STATEMENTS

In Mathematical logic, we generally come across two types of statements or proposition, namely, simple statements and compound statements as defined below.

i. Simple statements

Any statement or proposition whose truth value does not explicity depend on another statement is said to be a simple statement.
In other words, a statement is said to be simple if it cannot be broken down into simpler statements, that is, if it is not composed of simpler statements.

ii. Compound statements

If a statement is combination of two or more simple statements, then it is said to be a compound statement or a compound proposition.

Note:

True statements : (i)  2012 is a leap year, (ii) The sum of all interior angles of a triangle is 180°.

False statements : (i) All prime numbers are odd integers. (ii) Two plus two is five.

Not a statement : (i)  Mathematics is difficult. (ii) Tomorrow is Sunday.

Illustration -3

Find the component statements of the following and check whether they are true or not.

(i) A square is a quadrilateral and its four sides equal.
(ii) All prime numbers are either even or odd.
(iii) A person who has taken Mathematics or Computer Science can go for MCA.
(iv) Chandigarh is the capital of Haryana and UP.
(v) $\sqrt{2}$ is a rational number or an irrational number.

Solution

(i) The component statements are
p: A square is a quadrilateral.
q: A square has all its sides equal.
We know that both these statements are true. Here the connecting word is ‘and’.

(ii) The component statements are
p: All prime numbers are odd number.
q: All prime numbers are even number.
Both these statements are false and the connecting word is ‘or’.

(iii) The component statements are
p: A person who has taken Mathematics can go for MCA.
q: A person who has taken computer science can go for MCA.
Both these statements are true. Here the connecting word is ‘or’.

(iv) The component statements are
p: Chandigarh is the capital of Haryana.
q: Chandigarh is the capital of UP.
The first statement is true but the second is false. Here the connecting word is ‘and’.

(v) The component statements are
p: $\sqrt{2}$ is a rational number.
q: $\sqrt{2}$ is an irrational number.
The first statement is false and second is true. Here the connecting word is ‘or’.

2. TRUTH TABLES

Definition
A table that shows the relationship between the truth value of a compound statement S (p, q, r,..) and the truth values of its sub-statement  p, q, r, …..etc, is called the truth table of statement S.

Construction of truth table
In order to construct the truth table for a compound statement, we first prepare a table consisting of rows and columns. At the top of the initial columns, we write the variables denoting the sub-statements or constituent statements and then we write their truth values, in the last column. We write the truth value of the compound statement on the basis of the truth values of the constituent statements written in the initial columns. If a compound statement is made up of two simple statement, then the number of rows in the truth table will be 2² and if it is made up of three simple statements, then the number of rows will be 2³. In general, if the compound statement is made up of n sub-statements, then its truth table will contain 2ⁿ rows.

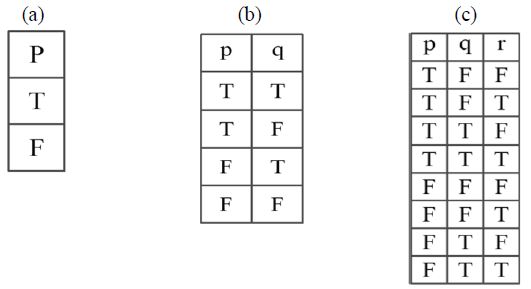
Illustration -4

(a) Truth table for a single statement p, number of rows=2¹=2
(b) For two statements p and q, number of rows=2²=4
(c) For the three statements p, q, r,
Number of Rows =2³=8

Solution

3. BASIC LOGICAL CONNECTIVES OR LOGICAL OPERATORS

DEFINITION

The phrases or words which connect simple statements are called logical connectives or sentential connectives or simply connectives or logical operators.
In the following table, we list some possible connectives, their symbols and the nature of the compound statement formed by them.

Connective	Symbol	Nature of the compound statement formed by using the connective
and	$\wedge$	Conjunction
or	$\vee$	disjunction
If….then	$\Rightarrow$ or $\to$	Implication or conditional
If and only if (iff)	$\iff$ or $\leftrightarrow$	Equivalence or bi-conditional
not	~ or ┓	Negation

Conjunction

Any two simple statements can be connected by the word “and” to form a compound statement called the conjunction of the original statements.
Symbolically if p and q are two simple statements, then $p\wedge q$ denotes the conjunction of p and q and is read as “p and q”.
Truth table for p $\wedge$ q:

p	q	p $\wedge$ q
T	T	T
T	F	F
F	T	F
F	F	F

Illustration -5

Write the component statements of the following compound statements and check whether the compound statement is true or false.
(i) A line is straight and extends indefinitely in both directions.
(ii) 0 is less than every positive integer and every negative integer.
Solution
(i) The component statements are
p: A line is straight.
q: A line extends indefinitely in both directions.
Both these statements are true, therefore, the compound statement is true.

(ii) The component statements are
p: 0 is less than every positive integer.
q: 0 is less than every negative integer.
The second statement is false. Therefore, the compound statement is false.

Disjunction or alternation

Any two statements can be connected by the word “or” to form a compound statement called the disjunction of the original statements.
Symbolically, if p and q are two simple statements, then $p\vee q$ denotes the disjunction of p and q and is read as “ p or q”.
Truth table for p $\vee$ q :

p	q	p $\vee$ q
T	T	T
T	F	T
F	T	T
F	F	F

Illustration -6

For each of the following statements, determine whether an inclusive “Or” or exclusive “Or” is used. Give reasons for your answer.
(i) To enter a country, you need a passport or a voter registration card.
(ii) The school is closed if it is a holiday or a Sunday.
(iii) Two lines intersect at a point or are parallel.
(iv) Students can take French or Sanskrit as their third language.

Solution
(i) Here “Or” is inclusive since a person can have both a passport and a voter registration card to enter a country.
(ii) Here also “Or” is inclusive since school is closed on holiday as well as on Sunday.
(iii) Here “Or” is exclusive because it is not possible for two lines to intersect and parallel together.
(iv) Here also “Or” is exclusive because a student cannot take both French and Sanskrit.

Negation

The denial of a statement p is called its negation, written as ~ p.
Negation of any statement p is formed by writing “ It is not the case that ….. “ or “ It is false that…….” before p or, if possible by inserting in p the word “not”.
Negation is called a connective although it does not combine two or more statements. In fact, it only modifies a statement.

Illustration -7

Write the negation of the following statement: p: The square root of every positive number is positive.

Solution

The negation of the given statement can be written as:
The square root of every positive number is not positive.                                    (or)
It is false that the square root of every positive number is positive.                   (or)
It is not the case that the square root of every positive number is positive.      (or)
There exists a positive number whose square root is not positive.

Illustration -8

With respect to the complex number z = 5 − 7i, two statements are given as:
p: The real part of z is 5.
q: The imaginary part of z is not 7.
With respect to the given statements, ∼p and ∼q can be written as
(A) ∼p: The real part of z is 5. ∼q: The imaginary part of z is −7.
(B) ∼p: The real part of z is 5. ∼q: The imaginary part of z is not −7.
(C) ∼p: The real part of z is not 5. ∼q: The imaginary part of z is 7.
(D) ∼p: The real part of z is not 5. ∼q: The imaginary part of z is not 7.

Solution

For the complex number z = 5 − 7i, the two given statements are:
p: The real part of z is 5.
q: The imaginary part of z is not 7.
The denial of a statement is called the negation of the statement.
Thus, for the given statements, ∼p and ∼q can be written as:
∼p: The real part of z is not 5.
∼q: The imaginary part of z is 7.

Implication or conditional statements

Any two statements connected by the connective phrase “if.. then” give rise to a compound statement which is known as an implication or a conditional statement.

If p and q are two statements forming the implication  ‘if p then q‘, then we denote this implication by

$“p\Rightarrow q“\text{ or ” }p\to q“$.

In the implication $“p\Rightarrow q“$, p is the antecedent and q is the consequent.

Truth table for a conditional a statement

p	q	$p\Rightarrow q$
T	T	T
T	F	F
F	T	T
F	F	T

Contrapositive and Converse of a Statement

• The contrapositive of the statement p $\Rightarrow$ q is the statement ~q $\Rightarrow$ ~p.

• The converse of a statement p $\Rightarrow$ q is the statement q $\Rightarrow$ p.

Illustration -9

Write the converse and the contrapositive of the following statement: “If an object is made up of only line segments, then it is a polygon.”

Solution

The converse of the given statement can be written as follows:
“If an object is a polygon, then it is made up of only line segments.”
The contra positive of the given statement can be written as follows:
“If an object is not a polygon, then it is not made up of only line segments.”
The equivalent forms of the statement “p if and only if q” (denoted by p $\iff$ q) are as follows:

• q if and only if p
• p if and only if q
• p is a necessary and sufficient condition for q and vice-versa

Illustration -10

Write the converse of the following statements.
(i) If a number n is even, then n² is even.
(ii) If you do all the exercises in the book, you get an A grade in the class.
(iii) If two integers a and b are such that a > b, then a – b is always a positive integer.    

Solution

The converse of these statements are
(i)   If a number n² is even, then n is even.
(ii) If you get an A grade in the class, then you have done all the exercises of the book.
(iii) If two integers a and b are such that a – b is always a positive integer, then a > b.

Illustration -11

Given below are two pairs of statements. Combine these two statements using “if and only if”.

(i) p: If a rectangle is a square, then all its four sides are equal.
q: If all the four sides of a rectangle are equal, then the rectangle is a square.

(ii) p: If the sum of digits of a number is divisible by 3, then the number is divisible by 3.
q: If a number is divisible by 3, then the sum of its digits is divisible by 3.

Solution

(i) A rectangle is a square if and only if all its four sides are equal.
(ii) A number is divisible by 3 if and only if the sum of its digits is divisible by 3. 

Biconditional statement
A statement is a biconditional statement if it is the conjunction of two conditional statements (implications) one converse to the other.

Thus, if p and q are two statements, then the compound statement $p\Rightarrow q$  and $q\Rightarrow p$ is called a biconditional statements or an equivalence and is denoted by $p\iff q$.

Thus, $p\iff q:(p\Rightarrow q)\wedge (q\Rightarrow p)$

Truth table for a biconditional statement : Since $p\iff q$ is the conjunction of  $p\Rightarrow q$ and $q\Rightarrow p$. So, we have the following truth table for $p\iff q$.

p	q	$p\Rightarrow q$	q$\Rightarrow$p	$p\iff q=(p\Rightarrow q)\wedge (q\Rightarrow p)$
T	T	T	T	T
T	F	F	T	F
F	T	T	F	F
F	F	T	T	T

4. LOGICAL EQUIVALENCE

Two compound $S_1(p,q,r,\dots )$ and $S_2(p,q,r\dots )$ are said to be logically equivalent, or simply equivalent if they have the same truth values for all logically possibilities.

If statements $S_1(p,q,r\dots )$ and $S_2(p,q,r\dots )$ are  logically equivalent, then we write

$S_1(p,q,r,\dots )\equiv S_2(p,q,r\dots )$

It follows from the above definition that two statements $S_1$ and $S_2$ are logically equivalent if they have identical truth tables i.e., the entries in the last column of the truth tables are same.

Illustration -12

Given that water freezes below zero degree celsius.

Consider the following statements :

p : Water froze this morning,

q : This morning temperature was below 0°C.

Which of the following is correct?

A. p and q are logically equivalent

B. p is the inverse of q

C. p is the converse of p

D. p is the contra positive of q

Solution

[A] p and q are logically equivalent

Illustration -13

$\mathrm{p}\wedge (\mathrm{q}\wedge \mathrm{r})$ is logically equivalent to

A. ${\mathrm{p}}_{\vee }(\mathrm{q}\wedge \mathrm{r})$

B. $(p\wedge q)\wedge r$

C. $(\mathrm{p}\vee \mathrm{q})\vee \mathrm{r}$

D. $\mathrm{p}\to (\mathrm{q}\wedge \mathrm{r})$

Solution

$\mathrm{p}\wedge (\mathrm{q}\wedge \mathrm{r})\equiv (\mathrm{p}\wedge \mathrm{q})\wedge \mathrm{r}$

5. NEGATION OF COMPOUND STATEMENTS

We have learnt about negation of a simple statement. Writing the negation of compound statements having conjunction, disjunctions, implication, equivalence, etc, is not very simple. So, let us discuss the negation of compound statement.

Negation of conjuntion

If p and q are two statements, then $~(p\wedge q)\equiv (~p\vee ~q)$

Negation of disjuntion

If p and q are two statements, then $~(p\vee q)\equiv (~p\wedge ~q)$

Negation of implication

If p and q are two statements, then $~(p\Rightarrow q)=(p\wedge ~q)$

Negation of biconditional statement or equivalence

If p and q are two statements, then

$~(p\iff q)=(p\wedge ~q)\vee (q\wedge ~p)$

Illustration -14

The negation of p$\leftrightarrow$q is

A. $(~p\vee q)\wedge (~q\vee p)$

B. $(~p\vee q)\vee (~q\vee p)$

C. $(~p\wedge q)\wedge (~q\wedge p)$

D. $(~\mathrm{p}\wedge \mathrm{q})\vee (~\mathrm{q}\wedge \mathrm{p})$

Solution

$~(\mathrm{p}\iff \mathrm{q})=\left[\right(~\mathrm{p}\vee \mathrm{q})\wedge (~\mathrm{q}\vee \mathrm{P}\left)\right]$

Illustration -15

Negation of the statement $(\mathrm{p}\wedge \mathrm{r})\to (\mathrm{r}\vee \mathrm{q})$ is

A. $(\mathrm{p}\wedge \mathrm{r})\wedge (~\mathrm{r}\wedge ~\mathrm{q})$

B. $~(\mathrm{p}\wedge \mathrm{r})\to ~(\mathrm{r}\vee \mathrm{q})$

C. $~(\mathrm{p}\vee \mathrm{r})\to ~(\mathrm{r}\wedge \mathrm{q})$

D. $(\mathrm{p}\wedge \mathrm{r})\vee (\mathrm{r}\vee \mathrm{q})$

Solution

$~\left[\right(\mathrm{p}\wedge \mathrm{q})\to (\mathrm{r}\vee \mathrm{q}\left)\right]\equiv (\mathrm{p}\wedge \mathrm{r})\wedge (\mathrm{r}\vee \mathrm{q})$

$=(p\wedge r)\wedge (~r\wedge ~q)$

6. TAUTOLOGIES AND CONTRADICTIONS

Let p,q,r,…. be statements, then any statement involving p,q,r,….and the logical connectives $\wedge ,\vee ,~,\Rightarrow ,\iff$ is called a statement pattern or a Well Formed Formula (WFF).

For example

(i) $p\vee q$

(ii) $p\Rightarrow q$

(iii) $\left(\right(p\wedge q)\vee r)\Rightarrow (s\wedge ~s)$

(iv) $(p\Rightarrow q)\iff (~q\Rightarrow ~p)$ etc.

are statement patterns.

A statement is also a statement pattern.

Thus, we can define statement pattern as follows.

Statement pattern
A compound statement with the repetitive use of the logical connectives is called a statement pattern or a well- formed formula.

Tautology
A statement pattern is called a tautology, if it is always true, whatever may be the truth values of constitute statements.
A tautology is called a theorem or a logically valid statement pattern. A tautology, contains only T in the last column of its truth table.

Contradiction
A statement pattern is called a contradiction, if it is always false, whatever may the truth values of its constitute statements.
In the last column of the truth table of contradiction there is always F.
The negation of a tautology is a contradiction and vice versa.

Illustration -16

Show that $(\mathrm{p}\to \mathrm{Q})\mathrm{V}(\mathrm{Q}\to \mathrm{p})$ is a tautology.

Solution
I construct the truth table for $(\mathrm{p}\to \mathrm{Q})\mathrm{V}(\mathrm{Q}\to \mathrm{p})$  and show that the formula is always true.

P	Q	$P\to Q$	$Q\to P$	$(P\to Q)\vee (Q\to P)$
T	T	T	T	T
T	F	F	T	T
F	T	T	F	T
F	F	T	T	T

7. ALGEBRA OF STATEMENTS

In the previous section, we have seen that statements satisfy many standard results. In this section, we shall state those results as laws of algebra of statements.
The following are some laws of algebra of statements.

1. Idempotent laws

For any statement p, we have

(a)  $p\vee p\equiv p$            (b) $p\wedge p\equiv p$

2. Commutative laws :

For any two statements p and q, we have

(a) $p\vee q\equiv q\vee p$       (b) $p\wedge p\equiv q\wedge p$

3. Association laws

For any three statements p, q, r,  we have

(a) $(p\vee q)\vee r\equiv p\vee (q\vee r)$   (b) $(p\wedge q)\wedge r\equiv p\wedge (q\wedge r)$

4. Distributive laws

For any three statements p, q, r we have

(a) $p\wedge (p\vee q)\equiv (p\wedge q)\vee (q\wedge r)$

(b) $p\vee (p\wedge q)\equiv (p\vee q)\wedge (q\vee r)$

5. Demorgan’s laws

If p and q are two statements, then

(a) $~(p\wedge q)\equiv ~p\vee ~q$

(b) $~(p\vee q)\equiv ~p\wedge ~q$

6. Identity laws

If t and c denote a tautology and a contradiction respectively, then for any statement p, we have

(a) $p\wedge t\equiv p$

(b) $p\vee c\equiv p$

(c) $p\vee t\equiv t$

(d) $p\wedge c\equiv c$

7. Complement laws

For any statements p, we have

(a) $p\vee ~p=t$

(b) $p\wedge ~p=c$

(c) $~t=c$

(d) $~c=t$

where t and c denote a tautology and a contradiction respectively.

8. Law of contrapositive

For any two statements p and q, we have

$p\Rightarrow q\equiv ~q\Rightarrow ~p$

9. Involution laws

For any statement p, we have $~\left(~p\right)\equiv p$

Illustration -17

If p, q are two statements, then

A. $~(\mathrm{p}\wedge \mathrm{q})=~\mathrm{p}\wedge ~\mathrm{q}$

B. $~(p\vee q)=~p\vee ~q$

C. $~(p\to q)=p\wedge q$

D. $~(\mathrm{p}\to \mathrm{q})=\mathrm{p}\wedge ~\mathrm{q}$

Solution

By De Morgan laws (a), (b) not true

We know that  $\mathrm{p}\Rightarrow \mathrm{q}=~\mathrm{p}\vee \mathrm{q}$

$~(\mathrm{p}\Rightarrow \mathrm{q})=\mathrm{p}\wedge ~\mathrm{q}$

8. DUALITY

Two compound statements $S_1$ and $S_2$ are said to be duals of each other if one can be obtained from the other by replacing $\wedge$ by $\vee$ and $\vee$ by $\wedge$.

The connective and are also called duals of each other

If a compound statements contains the special variable

t (tautology) or c (contradiction),  then to obtain its dual we replace t by c and c by t in addition to replacing $\wedge$ by $\vee$ and $\vee$ by $\wedge$.

Let S(p,q) be a compound statement containing two sub- statements and S*(p, q) be its dual. Then,

(i) $~S(p,q)\equiv S^{*}(~p,~q)$

(ii) $~S^{*}(p,q)\equiv S(~p,~q)$

The above result can be extended to the compound statements having finite number of sub- statements. Thus, if $S\left(p_1,p_2,,......,p_n\right)$ is a compound statement containing n sub-statement $p_1,p_2,......,p_n$ and $S*\left(p_1,p_2,,......,p_n\right)$ is its dual. Then,

(i) $~S\left(p_1,p_2,\dots ,p_n\right)\equiv S^{*}\left(~p_1,~p_2,\dots ,~p_n\right)$

(ii) $~S^{*}\left(p_1,p_2,\dots ,p_n\right)\equiv S\left(~p_1,~p_2,\dots ,~p_n\right)$

Illustration -18

The dual of the statement $\mathrm{p}\wedge ~\mathrm{p}=\mathrm{c}$ is

A. $\mathrm{p}\vee ~\mathrm{p}=\mathrm{c}$

B. $\mathrm{p}\wedge ~\mathrm{p}=\mathrm{t}$

C. $\mathrm{p}\vee ~\mathrm{p}=\mathrm{t}$

D. none of these

Solution

$P\vee ~P\equiv T$

9. MISCELLANEOUS CONCEPTS AND PROBLEMS

Applications of Logic in switching circuits (Application of truth tables to switching networks)

Let p, q, ….denote electrical switches and let p and p¹ denote switches with the property that if one is ‘on’, the other is ‘off’ and vice versa. Two switches say p and q, can be connected by wire in a series or parallel combination as follows. :

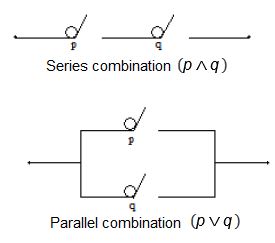
Parallel network $(p\vee q)$

p	q	$p\vee q$
T	T	T
T	F	T
F	T	T
F	F	F

A switching network is an arrangement of wires and switches that can be constructed by repeated use of series and parallel combinations.

A switch allows only two possibilities (i) it is either open, F, in which case there is no flow of  current (ii) it is closed, T, in which there is flow of current. Therefore every switch has only two  truth values T or F.

Series network $(p\wedge q)$

p	q	($p\wedge q$)
T	T	T
T	F	F
F	T	F
F	F	F

Nature of Switches p and p¹

p	p1
T	F
F	T

Series network, parallel network, nature of switches are identical with the tables of conjunction, disjunction and negation.

Illustration -19

The following circuit when expressed in the symbolic form of logic is

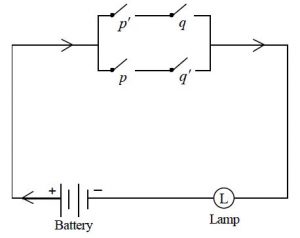
A. $(~p\wedge q)\vee (p\wedge ~q)$

B. $(~p\vee q)\vee \left(p_V~q\right)$

C. $(~p\wedge p)\wedge (~q\wedge p)$

D. $(~\mathrm{p}\wedge ~\mathrm{q})\wedge (\mathrm{q}\wedge \mathrm{p})$

Solution

$(~\mathrm{p}\wedge \mathrm{q})\vee (\mathrm{p}\wedge ~\mathrm{q})$