Conic Sections

CIRCLE

1. EQUATION OF CIRCLE IN VARIOUS FORMS

A point moving in a plane such that its distance from a fixed point is always constant describes a circle. The fixed point is called centre and the constant distance is called radius.

We present below the equation of circle in various forms : 

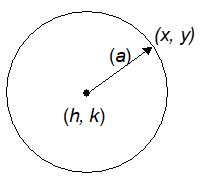
1. CIRCLE WITH CENTRE AT THE POINT (h, k) AND RADIUS a

The equation of the circle is  (x – h)² + (y – k)² = a².

Particular Case :

The equation of a circle with centre at the origin and radius a is x² + y² = a².

2. GENERAL EQUATION OF A CIRCLE

General equation of second degree in x and y is

ax² + 2hxy + by² + 2gx + 2fy + c  = 0     …(i)

The equation of a circle with centre ($\mathrm{\alpha },\mathrm{\beta }$) and radius r is

(x – $\alpha$)² + (y – $\beta$)² = r²

x² + y² – 2$\alpha$x – 2$\beta$y + ($\alpha$² + $\beta$² – r²) = 0     …(ii)

Comparing (i) and (ii),

$\frac{1}{\mathrm{a}}=\frac{1}{\mathrm{b}}=\frac{0}{\mathrm{h}}=\frac{\mathrm{g}}{–\mathrm{\alpha }}=\frac{\mathrm{f}}{–\mathrm{\beta }}=\frac{\mathrm{c}}{\left({\mathrm{\alpha }}^2+{\mathrm{\beta }}^2–{\mathrm{r}}^2\right)}$

$\Rightarrow$ a = b i.e., coefficient of x² = coefficient of y².

h = 0 i.e., coefficient of xy = 0

The general equation of a circle is

x² + y² + 2gx + 2fy + c  = 0       …(i)

where g, f and c are constants.

To find  the centre and radius.

Equation (i) can be written as

$(\mathrm{x}+\mathrm{g}{)}^2+(\mathrm{y}+\mathrm{f}{)}^2={\left[\sqrt{\left({\mathrm{g}}^2+{\mathrm{f}}^2–\mathrm{c}\right)}\right]}^2$

Comparing with the equation of the circle given in (1.1), h =  – g, k = – f and a = $\sqrt{\left({\mathrm{g}}^2+{\mathrm{f}}^2–\mathrm{c}\right)}$

$\therefore$ Coordinates of the centre are (-g, -f) and radius = $\sqrt{\left(g^2+f^2–c\right)}$

Important remarks

(i) If g² + f ² – c > 0, equation (i) represents real circle with centre (-g, -f).

(ii) If g² + f ² – c = 0, the equation (i) represents a circle whose centre is (-g, -f) and radius is zero i.e., the circle coincides with the centre and so it represents a point (-g, -f). It is, therefore, called a point circle.

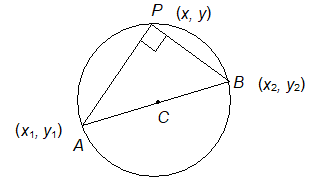
3. DIAMETER FORM i.e., CIRCLE WITH THE LINE JOINING THE POINTS A(x₁, y₁) AND B(x₂, y₂) AS DIAMETER

Let P(x, y) be any point on the circle with AB as diameter then $\angle$APB = $\mathrm{\pi }$/2 (angle in semicircle). i.e.,

AP is $\perp$ to BP.

$\therefore \left(\frac{\mathrm{y}–{\mathrm{y}}_1}{\mathrm{x}–{\mathrm{x}}_1}\right)\left(\frac{\mathrm{y}–{\mathrm{y}}_2}{\mathrm{x}–{\mathrm{x}}_2}\right)=–1$  i.e., (x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0, is the required equation.

4. PARAMETRIC EQUATION OF A CIRCLE

(i) The parametric equations of a circle

x² + y² = a² are x = a cos$\theta$ and y = a sin$\theta$.

(ii) The parametric equations of circle (x – h)² + (y – k)² = a² are x = h + a cos$\theta$, and y = k + a sin$\theta$, where $\theta$ is a parameter.

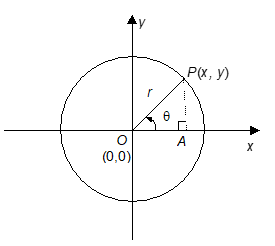
Illustration-1:

If the equations of the two diameters of a circle are x + y = 6 and x + 2y = 4 and the radius of the circle is 10, find the equation of the circle.

Solution:

Here radius of the circle = 10. Equations of two diameters say AB and ML of the circle are respectively

x + y = 6             …(i)

and   x + 2y = 4            …(ii)

solving (i) and (ii), we get  x = 8 and y = -2.

Hence centre of the circle is (8, -2).

Now the equation of the required circle is

(x – 8)² + (y + 2)² = 10²  or  x² + y² – 16x + 4y – 32 = 0.

Illustration-2:

The abscissae of two points A and B are the roots of the equation x² + 2ax  b² = 0 and the ordinates are the roots of the equation x² + 2px – q² = 0. Find the equation and the radius of the circle with AB as diameter.

Solution:

Given equations are

x² + 2ax – b² = 0        ….(i)

and       x² + 2px – q² = 0         ….(ii)

Let the roots of equation (i) be $\alpha$ and $\beta$ and those of equation (ii) be $\gamma$ and $\delta$, then

$\left.\begin{array}{r}\mathrm{\alpha }+\mathrm{\beta }=–2\mathrm{a}\\ \mathrm{\alpha \beta }=–{\mathrm{b}}^2\end{array}\right\}$ and $\begin{array}{c}\mathrm{\gamma }+\mathrm{\delta }=–2\mathrm{p}\\ \mathrm{\gamma \delta }=–{\mathrm{q}}^2\end{array}$

Let A $\equiv$ ($\mathrm{\alpha }, \mathrm{\gamma }$) and B $\equiv$ ($\mathrm{\beta }, \mathrm{\delta }$)

Now equation of the circle whose diameter is AB will be

$(\mathrm{x}–\mathrm{\alpha })(\mathrm{x}–\mathrm{\beta })+(\mathrm{y}–\mathrm{\gamma })(\mathrm{y}–\mathrm{\delta })=0$

or   ${\mathrm{x}}^2+{\mathrm{y}}^2–(\mathrm{\alpha }+\mathrm{\beta })\mathrm{x}–(\mathrm{\gamma }+\mathrm{\delta })\mathrm{y}+\mathrm{\alpha \beta }+\mathrm{\gamma \delta }=0$ 

or   x² + y² + 2ax + 2py – (b² + q²) = 0              …(iii)

Centre of circle (iii) is (-a, -p)

and radius = $\sqrt{(–a{)}^2+(–p{)}^2+b^2+q^2}=\sqrt{a^2+b^2+p^2+q^2}$.

Illustration-3:

Express a point lying in the circle x² + y² + 10x + 2y + 1 = 0 in parametric form.

Solution:

The centre (h, k) is (-5, -1) and radius a is $\sqrt{25+1–1}=5$.

So, the parametric form is

x = h + a cos$\theta$ = -5 + 5cos$\theta$

y = k + a sin$\theta$ = -1 + 5sin$\theta$

$\therefore$ Any point in this circle can be taken as (-5 + 5cos$\theta$, -1 + 5sin$\theta$)

5. GENERAL EQUATION OF SECOND DEGREE IN x, y AND CIRCLE

The general equation of second degree ax² + 2hxy + by² + 2gx + 2fy + c  = 0, will represent a circle if

(a) coeff. of x² = coeff. of y² i.e., a = b  and (b)  coeff. of xy = 0. i.e., h = 0.

To find the centre and radius of the circle given in general form, first make the coefficients of x² and y² equal to unity by dividing the equation by their coefficient if it is not equal to unity. Then find the values of g, f and c by comparing with x² + y² + 2gx + 2fy + c  = 0.

Illustration-4:

For what value(s) of $\mathit{\lambda }$, the equation (10 – $\mathit{\lambda }$²)x² + ($\mathit{\lambda }$² – 8)y² + (3 – $\mathit{\lambda }$)yx – 10x + 4y + 3 = 0 represent a real circle.

Solution:

We must have

coeff. of x² = coeff. of y²

$\Rightarrow$ 10 – $\lambda$² = $\lambda$² – 8   $\Rightarrow$  $\lambda$² = 9    $\Rightarrow$  $\lambda$ = ± 3

and coeff. of xy = 0

$\Rightarrow$ 3 – $\lambda$ = 0         $\Rightarrow \lambda =3$

So,  the common value is $\lambda$ = 3.

2. CIRCLE AND A LINE

We consider 3 cases:

Case I:

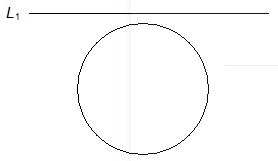
Line L₁ does not intersect the circle

Case II:

Line L₁ touches the circle

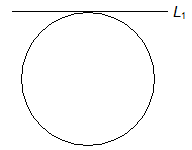
Case III:23

Line L₁ intersects the circle in two points.

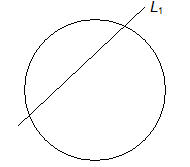
Now we proceed to derive the conditions of the three cases.

For the ease of calculations we take the circle as,

x² + y² = a²             …(i)

and the equation of the line as

y = mx + c          …(ii)

substituting the value of y in equation (i),

x² + (mx + c)² = a²

$\Rightarrow$   x²(1 + m²) + 2mcx + (c² – a²) = 0      …(iii)

Equation (iii) represents a quadratic equation in x. The discriminant of the equation is

$∆$ = 4m²c² – 4(1 + m²) (c² – a²)

Case I:

There is no real point of intersection.

i.e.,  $∆$ < 0

$\Rightarrow$ 4m²c² – 4(1 + m²) (c² – a²) < 0

$\Rightarrow$ m²c² – (1 + m²) (c² – a²) < 0

$\Rightarrow$ m²c² – c² – m²c² + a² + a²m² < 0

$\Rightarrow$  a² (1 + m²) < c²

$\Rightarrow {\mathrm{a}}^2<\frac{{\mathrm{c}}^2}{\left(1+{\mathrm{m}}^2\right)}\Rightarrow \mathrm{a}<\left|\frac{\mathrm{c}}{\sqrt{1+{\mathrm{m}}^2}}\right|$

Case II:

There are two coincident points of intersection.

i.e.,  $∆$ = 0

4m²c² – 4(1 + m²) (c² – a²) = 0

$\Rightarrow$  a²(1 + m²) = c²

$\Rightarrow \mathrm{a}=\left|\frac{\mathrm{c}}{\sqrt{1+{\mathrm{m}}^2}}\right|$

$\Rightarrow \mathrm{c}=\pm \mathrm{a}\sqrt{1+{\mathrm{m}}^2}$

This is the required condition of tangency.

$\therefore$  the equation of the tangents are

$\mathrm{y}=\mathrm{mx}+\mathrm{a}\sqrt{1+{\mathrm{m}}^2}$

and $\mathrm{y}=\mathrm{mx}–\mathrm{a}\sqrt{1+{\mathrm{m}}^2}$

Case III:

There are two different real points of intersection.

i.e.,  $∆$ > 0

$\Rightarrow$ 4m²c² – 4(1 + m²) (c² – a²) > 0.

$\therefore$  a² (1 + m²) > c²

or   $\mathrm{a}>\left|\frac{\mathrm{c}}{\sqrt{1+{\mathrm{m}}^2}}\right|$

Let S = x² + y² + 2gx + 2fy + c  = 0 and L = lx + my + n  = 0.

Let r be the radius of the circle and p be the length of the perpendicular drawn from the centre (-g, -f) on the line L.

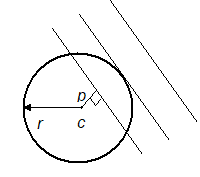
Then.

(i) line intersect the circle in two distinct points if p < r.

(ii) line touch the circle if p = r.

(iii) line neither intersects nor touches the circle i.e., passes outside the circle if p > r.

Illustration-5:

Show that the line 3x – 4y – c = 0 will meet the circle having centre at (2, 4) and the radius 5 in real and distinct points if –35 < c < 15.

Solution:

Given line is 3x – 4y – c = 0        …(i)

(x – 2)² + (y – 4)² = 5²

or   x² + y² – 4x – 8y – 5 = 0           …(ii)

From (i), $\mathrm{y}=\frac{1}{4}$ (3x – c). Putting the value of y in (ii), we get

${\mathrm{x}}^2+\frac{1}{16}(3\mathrm{x}–\mathrm{c}{)}^2–4\mathrm{x}–8.\frac{1}{4}(3\mathrm{x}–\mathrm{c})–5=0$

or   16x² + 9x² – 6cx + c² – 64x – 96x + 32c – 80 = 0

or   25x² – 2(80 + 3c) x + c² + 32c – 80 = 0         …(iii)

Line (i) will meet the circle (ii) in real and distinct points if discriminant of equation (iii) > 0 i.e.,

if  4(80 + 3c)² – 100 (c² + 32c – 80) > 0  or      (80 + 3c)² – 25(c² + 32c – 80) > 0

or   6400 + 9c² + 480c – 25c² – 800c +  2000 > 0

or   -16c² – 320c +  8400 > 0 or  16c² + 320c – 8400 < 0

or   c² + 20c – 525 <  0

sign scheme for c² + 20c – 525 :

When c² + 20c – 525 = 0,

$c=\frac{–20\pm \sqrt{400+2100}}{2}=\frac{–20\pm 50}{2}=–35, 15$

Therefore, sign scheme for c² + 20c – 525 is as follows

$\therefore$   c² + 20c – 525 < 0 $\iff$ -35 < c < 15. 

3. THE EQUATION T = 0

1. Circle x² + y² = r²

Take a point P(x₁, y₁) on the circle x² + y² = r²       …(i)

$\therefore$  P(x₁, y₁) should satisfy the equation of the circle

$\therefore {\mathrm{x}}_1^2+{\mathrm{y}}_1^2={\mathrm{r}}^2$      …(ii)

Let the slope of the tangent be m,

$\therefore$    Equation of the line through (x₁, y₁) and slope m is,

(y – y₁) = m(x – x₁)

$\Rightarrow$  y = mx + (y₁ – mx₁)         …(iii)

The line represented by (iii) is a tangent to the circle,

$\therefore {\mathrm{y}}_1–{\mathrm{mx}}_1=\pm \mathrm{r}\sqrt{1+{\mathrm{m}}^2}$

$\Rightarrow {\left({\mathrm{y}}_1–{\mathrm{mx}}_1\right)}^2={\mathrm{r}}^2\left(1+{\mathrm{m}}^2\right)$       …(iv)

substituting the value of r² from (ii) in (iv) we have,

${\left({\mathrm{y}}_1–{\mathrm{mx}}_1\right)}^2=\left(1+{\mathrm{m}}^2\right)\left({\mathrm{x}}_1^2+{\mathrm{y}}_1^2\right)$

$\begin{array}{ll}\Rightarrow & {\mathrm{y}}_1^2+{\mathrm{m}}^2{\mathrm{x}}_1^2–2{\mathrm{mx}}_1{\mathrm{y}}_1={\mathrm{x}}_1^2+{\mathrm{y}}_1^2+{\mathrm{m}}^2{\mathrm{x}}_1^2+{\mathrm{m}}^2{\mathrm{y}}_1^2\\ \Rightarrow & {\mathrm{x}}_1^2+2{\mathrm{mx}}_1{\mathrm{y}}_1+{\mathrm{m}}^2{\mathrm{y}}_1^2=0\\ \Rightarrow & {\left({\mathrm{x}}_1+{\mathrm{my}}_1\right)}^2=0\\ \Rightarrow & \left({\mathrm{x}}_1+{\mathrm{my}}_1\right)=0\end{array}$

substituting the value of m from (iii),

${\mathrm{x}}_1+\frac{\left(\mathrm{y}–{\mathrm{y}}_1\right)}{\left(\mathrm{x}–{\mathrm{x}}_1\right)}{\mathrm{y}}_1=0$

$\Rightarrow$ (y – y₁) y₁ + (x – x₁) x₁ = 0

$\begin{array}{ll}\Rightarrow & {\mathrm{xx}}_1+{\mathrm{yy}}_1–{\mathrm{x}}_1^2–{\mathrm{y}}_1^2=0\\ \Rightarrow & {\mathrm{x}}_1{\mathrm{x}}_1+{\mathrm{yy}}_1={\mathrm{r}}^2..............\left(\mathrm{v}\right)\end{array}$

The equation (v) gives the required equation of the tangent to the circle.  

2. Circle x² + y² + 2gx + 2 fy + c = 0

Consider a point P(x₁, y₁) on the circle, where the tangent touches the circle

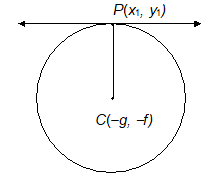
scope of CP = $\frac{\left({\mathrm{y}}_1+\mathrm{f}\right)}{\left({\mathrm{x}}_1+\mathrm{g}\right)}$.

Tangent being perpendicular to the radius, slope of the tangent = $\frac{–\left({\mathrm{x}}_1+\mathrm{g}\right)}{\left({\mathrm{y}}_1+\mathrm{f}\right)}$.

Equation of the tangent at P is,

$\left(\mathrm{y}–{\mathrm{y}}_1\right)=\frac{–\left({\mathrm{x}}_1+\mathrm{g}\right)}{\left({\mathrm{y}}_1+\mathrm{f}\right)}\left(\mathrm{x}–{\mathrm{x}}_1\right)\Rightarrow$ (y – y₁) (y₁ + f) + (x₁+ g) (x – x₁) = 0

$\Rightarrow {\mathrm{yy}}_1–{\mathrm{y}}_1^2+\mathrm{yf}–{\mathrm{y}}_1\mathrm{f}+{\mathrm{xx}}_1+\mathrm{xg}–{\mathrm{x}}_1^2–{\mathrm{x}}_1\mathrm{g}=0$

$\Rightarrow {\mathrm{xx}}_1+{\mathrm{yy}}_1+\mathrm{xg}+\mathrm{fy}={\mathrm{x}}_1^2+{\mathrm{y}}_1^2+{\mathrm{x}}_1\mathrm{g}+{\mathrm{y}}_1\mathrm{f}$

Adding (gx₁ + y₁f + c) to both sides, we have

xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c  = ${\mathrm{x}}_1^2+{\mathrm{y}}_1^2+2{\mathrm{x}}_1\mathrm{g}+2{\mathrm{fy}}_1+\mathrm{c}$       …(i)

$\because$ the point P(x₁, y₁) lies on the circle,

$\therefore {\mathrm{x}}_1^2+{\mathrm{y}}_1^2+2{\mathrm{gx}}_1+2{\mathrm{fy}}_1+\mathrm{c}=0$

$\therefore$ Equation (i) reduces to,  ${\mathrm{xx}}_1+{\mathrm{yy}}_1+\mathrm{g}\left(\mathrm{x}+{\mathrm{x}}_1\right)+\mathrm{f}\left(\mathrm{y}+{\mathrm{y}}_1\right)+\mathrm{c}=0$.

$\therefore$ We conclude that in order to write the equation of the tangent to the circle             x² + y² + 2gx + 2fy + c = 0,

we put,

xx₁ in place of x²

yy₁ in place of y²

$\frac{(x+x_1)}{\mathbf{2}}$ in place of x

$\frac{(y+y_1)}{\mathbf{2}}$ in place of y

3. EQUATIONS OF TANGENTS TO THE CIRCLE AT THE POINT P(x₁, y₁) ON IT

Let P(x₁, y₁­) be a point lying on the circle. Then equations of tangents in different forms of circles are given below:

Equation of the circle               Equation of the tangent at P(x₁, y₁)

1. x² + y² = r²                                                  T = xx₁ +  yy₁ – r² = 0

2. (x – h)² + (y – k)² = r²                   T = (x – h) (x₁ – h) + (y – k) (y₁ – k) – r² =0

3. x² + y² + 2gx + 2fy + c = 0          T $\equiv$ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c =0

Note that T = 0 always represents a line whether P(x₁, y₁) lies on the circle or not, but T = 0 represents the equation of the tangent at P(x₁, y₁) only when P lies on the circle.

Illustration-6:

Consider the circle S $\equiv$ x² + y² – 4 = 0 and P(1, 1). Then T = x + y – 4 = 0 does not represent the equation of the tangent since S(P) = 1² + 1² – 4 = -2 < 0, i.e., P lies inside the circle, not on the circle.

Illustration-7:

Find the equation of the tangent to circle ${\mathbf{x}}^{\mathbf{2}}\mathbf{+}{\mathbf{y}}^{\mathbf{2}}\mathbf{–}\mathbf{26}\mathbf{x}\mathbf{+}\mathbf{12}\mathbf{y}\mathbf{+}\mathbf{105}\mathbf{=}\mathbf{0}$ at point (7, 2).

Solution:

Comparing the above equation of the circle with the general equation of the circle ${\mathrm{x}}^2+{\mathrm{y}}^2+2\mathrm{gx}+2\mathrm{fy}+\mathrm{c}=0$

We have $2\mathrm{g}=–26, 2\mathrm{f}=12, \mathrm{c}=105$

Also ${\mathrm{x}}_1=7, {\mathrm{y}}_1=2$

$\therefore$ Equation of tangent is $7\mathrm{x}+2\mathrm{y}–\frac{26}{2}(\mathrm{x}+7)+\frac{12}{2}(\mathrm{y}+2)+105=0$

or  $7\mathrm{x}+2\mathrm{y}–13(\mathrm{x}+7)+6(\mathrm{y}+2)+105=0$

or  $7\mathrm{x}+2\mathrm{y}–13\mathrm{x}–91+6\mathrm{y}+12+105=0$   or  $–6\mathrm{x}+8\mathrm{y}+26=0$

or  $3\mathrm{x}–4\mathrm{y}–13=0$

4. TANGENTS DRAWN FROM A POINT OUTSIDE THE CIRCLE

Let S = x² + y² + 2gx + 2fy + c = 0 and P(x₁, y₁) lies outside the circle

i.e., S₁ = x₁² + y₁² + 2gx₁ + 2fy₁ + c > 0.

Then two tangents can be drawn to the circle from the point P.

Let S $\equiv$ x² + y² + 2gx + 2fy + c = 0 be the circle,

T = xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c

and  S₁ = x₁² + y₁² + 2gx₁ + 2fy₁ + c.

Then combined equation of the tangents from P i.e., PA and PB is given by SS₁ = T ². Before using this formula, check the condition S₁ > 0.

Illustration-8:

Find the equation of the pair of tangents drawn to the circle x² + y² – 2x + 4y = 0 from the point (0, 1).

Solution:

Given circle is S $\equiv$ x² + y² – 2x + 4y = 0          …(i)

Let P $\equiv$ (0, 1)

For point P, S₁ = 0² + 1² – 2.0 + 4.1 = 5 > 0

Point P lies outside the circle and T  $\equiv$ x.0 + y.1 – (x + 0) + 2(y + 1)

i.e.,      T = -x + 3y + 2

Now equation of the pair of tangents from P(0, 1) to circle (i) is

SS₁ = T ²

or   5(x² + y² – 2x + 4y) = (-x + 3y + 2)²

or   5x² + 5y² – 10x + 20y = x² + 9y² + 4 – 6xy – 4x + 12y

or   4x² – 4y² – 6x + 8y + 6xy – 4 = 0

or   2x² – 2y² + 3xy – 3x + 4y – 2 = 0      …(ii)

From (ii), 2x² + 3(y – 1)x – (2y² – 4y + 2) = 0

$\therefore \mathrm{x}=\frac{3(\mathrm{y}–1)\pm \sqrt{9(\mathrm{y}–1{)}^2+8\left(2{\mathrm{y}}^2–4\mathrm{y}+2\right)}}{4}$

or   4x – 3y + 3 = ± $\sqrt{25{\mathrm{y}}^2–50\mathrm{y}+25}=\pm 5(\mathrm{y}–1)$

$\therefore$ Separate equations of tangents are

4x – 8y + 8 = 0   i.e., x – 2y + 2 = 0

and  4x + 2y –  2 = 0   or   2x + y – 1 = 0.

5. LENGTH OF TANGENT FROM A POINT OUTSIDE THE CIRCLE

$\therefore$ If the equation of the circle is

S $\equiv$ x² + y² + 2gx + 2fy + c = 0 and

S₁ $\equiv$ x₁² + y₁² + 2gx₁ + 2fy₁ + c

$\therefore$ The length of the tangent drawn from an external point P(x₁, y₁) to the circle is $\sqrt{{\mathbf{s}}_{\mathbf{1}}}$

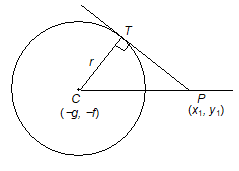
Method : First reduce the equation of the circle to the standard form with the coefficients of x² and y² equal to unity, and right hand side equal to zero, then substitute the coordinate of the given point in the equation of the circle. The square root of the L.H.S. thus obtained is the length of the tangent from the given point.

Illustration-9:

Find the area of the quadrilateral formed by a pair of tangents from the point (4, 5) to the circle x² + y² – 4x – 2y – 11 = 0 and a pair of its radii.

Solution:

Given circle is S $\equiv$ x² + y² – 4x – 2y – 11 = 0     …(i)

Let C be its centre and a be its radius; then C $\equiv$ (2, 1) and a = 4.

Let P $\equiv$ (4, 5)

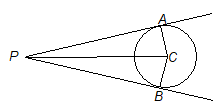
Now length of tangent PA or PB from P to circle = $\sqrt{4^2+5^2–4.4–2.5–11}=2$

and radius CA = 4

$\therefore$ area of $\mathrm{\Delta PAC}=\frac{1}{2}\mathrm{PA}.\mathrm{AC}=\frac{1}{2}2.4=4$

$\therefore$ area of quadrilateral PACB

= 2 area of $∆$PAC = 8 square units.

CONIC SECTION

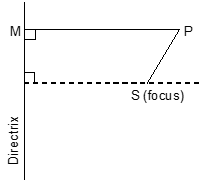
A conic section or a conic is the locus of a point which moves in a plane such that the ratio of its distance from a fixed point to its perpendicular distance from a fixed straight line is always a constant quantity. The fixed point is called the focus of the conic and the fixed line is called the directrix of the conic. Also this constant ratio is called the eccentricity of the conic and is denoted by e.

If e = 1, the conic is called parabola.

If e < 1, the conic is called ellipse.

If e > 1, the conic is called hyperbola.

If e = 0, the conic is called circle.

If e $\to$ $\infty$, the conic is called a pair of straight lines.

In the figure

$\frac{\mathrm{SP}}{\mathrm{PM}}$= constant = e

or SP = e (PM)

If the focus is ($\mathrm{\alpha }, \mathrm{\beta }$) and the directrix is ax + by + c = 0, then the equation of the conic section whose eccentricity e given as

$\sqrt{(\mathrm{x}–\mathrm{\alpha }{)}^2+(\mathrm{y}–\mathrm{\beta }{)}^2}=\mathrm{e}.\frac{|\mathrm{ax}+\mathrm{by}+\mathrm{c}|}{\sqrt{\left({\mathrm{a}}^2+{\mathrm{b}}^2\right)}}$

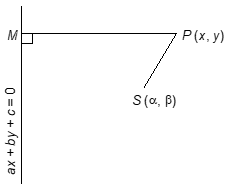
or   $(\mathrm{x}–\mathrm{\alpha }{)}^2+(\mathrm{y}–\mathrm{\beta }{)}^2={\mathrm{e}}^2.\frac{(\mathrm{ax}+\mathrm{by}+\mathrm{c}{)}^2}{\left({\mathrm{a}}^2+{\mathrm{b}}^2\right)}$

Axis: The straight line passing through the focus and perpendicular to the directrix is called the axis of the conic section.

Vertex: The points of intersection of the conic section and the axis is (are) called vertex (vertices) of the conic section.

Focal chord: Any chord passing through the focus is called focal chord of the conic section.

Double ordinate: A straight line drawn perpendicular to the axis and terminated at both ends of the curve is a double ordinate of the conic section.

Latus rectum: The double ordinate passing through the focus is called the latus rectum of the conic section.

Centre: The point which bisects every chord of the conic passing through it, is called the centre of the conic section.

The general equation of second degree in x, y is

ax² + by² + 2hxy + 2gx + 2fy + c = 0     …(i)

it will represent a conic if

$∆$ = abc + 2fgh – af² – bg² – ch² $\ne$ 0

further (i) will represent

an ellipse if  h² < ab

a parabola if h² = ab

a hyperbola if h² > ab

PARABOLA

A parabola is the locus of a point which moves in a plane such that its distance from a fixed point is equal to its perpendicular distance from a fixed line. The fixed point is called focus and the fixed line is called the directrix. The line through focus perpendicular to directrix is called the axis. Mid-point of point of intersection of axis and directrix and focus is called the vertex.

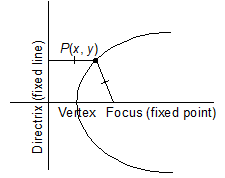
Illustration-10: Find the equation of the parabola whose focus is (1, 1) and the directrix is x + y + 1 = 0.

Solution:

Let P(x, y) be any point on the parabola.

Then the distance of (x, y) from the focus (1, 1).

= distance of P(x, y) from the directrix (x + y + 1 = 0)

$\therefore \sqrt{(\mathrm{x}–1{)}^2+(\mathrm{y}–1{)}^2}=\frac{|\mathrm{x}+\mathrm{y}+1|}{\sqrt{(1{)}^2+(1{)}^2}}$       …(i)

Squaring (i), we get $(\mathrm{x}–1{)}^2+(\mathrm{y}–1{)}^2={\left(\frac{\mathrm{x}+\mathrm{y}+1}{\sqrt{2}}\right)}^2$

or $2\left[{\mathrm{x}}^2+1–2\mathrm{x}+{\mathrm{y}}^2+1–2\mathrm{y}\right]={\mathrm{x}}^2+{\mathrm{y}}^2+2\mathrm{xy}+2\mathrm{y}+2\mathrm{x}+1$

or ${\mathrm{x}}^2–2\mathrm{xy}+{\mathrm{y}}^2–6\mathrm{x}–6\mathrm{y}+3=0$

This is the required equation of the parabola.

7. STANDARD EQUATION OF A PARABOLA

If we take axis of the parabola as x-axis with vertex as origin, focus as S(a, 0), then clearly directrix will be x + a = 0.

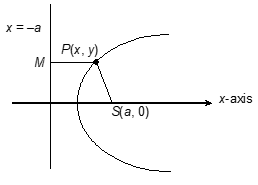
Now if P(x, y) is a general point on the parabola, then by definition PS = PM.

$\Rightarrow$  (x – a)² + y² = (x + a)²

$\Rightarrow$ y² = 4ax

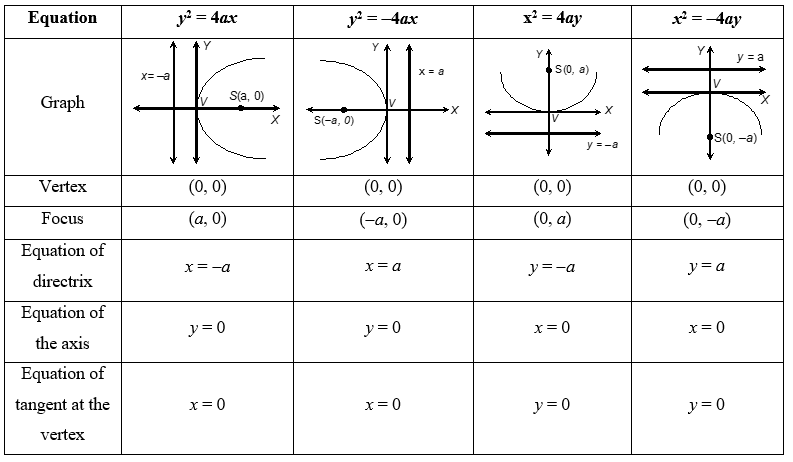
There are other three forms also. All the four forms are listed as follows:

If the vertex is not the origin and the axis and directrix are parallel to the coordinate axes, then the equation of parabola with vertex at (h, k) can be obtained by using translation of axes as follows:

Form	Vertex	Focus	Equation of directrix	Equation of axis	Tangent at the vertex
(y – k)2 = 4a(x – h)	(h, k)	(h + a, k)	x = h – a	y = k	x = h
(y – k)2 = -4a(x – h)	(h, k)	(h – a, k)	x = h + a	y = k	x = h
(x – h)2 = 4a(y – k)	(h, k)	(h, k + a)	y = k – a	x = h	y = k
(x – h)2 = -4a(y – k)	(h, k)	(h, k – a)	y = k + a	x = h	y = k

Note: in all the above cases a > 0.

Illustration-11: Find the vertex, focus, equations of directrix, axis and tangent at the vertex of the parabola x² + 4x + 6y – 8 = 0.

Solution:

The equation of the parabola can be rewritten as

(x + 2)² = – 6y + 8 + 4

(x + 2)² = – 6 [y – 2]

So, vertex is (-2, 2) and a = 3/2

focus is $\left(–2,\frac{1}{2}\right)$

Equation of directrix is $y=\frac{7}{2}$

Equation of axis is x = – 2

Equation of tangent at the vertex is y = 2.

8. PARAMETRIC FORM OF A PARABOLA

Let y² = 4ax be a parabola, then for any real t, x = at², y = 2at satisfy the equation of parabola, so point (at², 2at) lie on the parabola. Here x = at², y = 2at is known as parametric form of the parabola. In short, we denote the point P(at², 2at) as P(t).

9. IMPORTANT CONCEPTS IN PARABOLA

1. Focal distance

Distance of any point P on the parabola from its focus is known as focal distance of the point P. The focal distance of any point on the parabola is equal to sum of one fourth of length of latus rectum and its distance from the tangent at the vertex. In simple words, focal distance of  P(x, y), a point on the parabola y² = 4ax, is equal to |x + a| as

$\mathrm{PS}=\sqrt{(\mathrm{x}–\mathrm{a}{)}^2+(\mathrm{y}–0{)}^2}=\sqrt{(\mathrm{x}–\mathrm{a}{)}^2+4\mathrm{ax}}=\sqrt{(\mathrm{x}+\mathrm{a}{)}^2}=|\mathrm{x}+\mathrm{a}|$

2. Double ordinate

Any chord of the parabola y² = 4ax, which is parallel to its directrix or in other words perpendicular to axis of parabola is known as double ordinate.

3. Latus rectum

A focal chord of the parabola, which is parallel to its directrix is known as latus rectum. In parabola y² = 4ax, end point of latus rectum are (a, 2a) and (a, -2a) and length of latus rectum is 4a. Two parabola are said to be equal if the length of their latus rectums are equal.

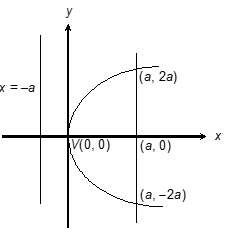
To obtain end points of a latus rectum, putting x = a in

y² = 4ax

y² = 4a²

$\Rightarrow$ y = $\pm$ 2a

Illustration-12:

Prove that a circle with focal distance of a point on parabola y² = 4ax as diameter will always touch the tangent at the vertex.

Solution:

Let (at², 2at) be a point on the parabola y² = 4ax. The equation of circle with focal distance of the point as diameter will be

x² + y² – (at² + a) x – 2aty + a²t² = 0.

When this circle cuts the tangent at the vertex i.e., x = 0, we get

y² – 2aty +  a²t² = 0

D = 4a²t² – 4a²t² = 0, so circle cuts the line at two coinciding  points. Hence it touch the tangent at the vertex.

ELLIPSE

10. DEFINITION AND EQUATION

An ellipse is the locus of a point, which moves such that the ratio of its distances from a fixed point to a fixed line is constant and value of the constant is less than unity. Here, fixed point is called as focus, fixed line as directrix and constant as eccentricity.

Generally, the equation of the an ellipse, whose focus is the point (h, k) and directrix lx + my + n = 0 and whose eccentricity is e, is

$(\mathrm{x}–\mathrm{h}{)}^2+(\mathrm{y}–\mathrm{k}{)}^2={\mathrm{e}}^2.\frac{(l\mathrm{x}+\mathrm{my}+\mathrm{n}{)}^2}{\left(l^2+{\mathrm{m}}^2\right)}$(e < 1)

Illustration-13:

Find the equation of an ellipse whose focus is (–1, 1), eccentricity is 1/2 and the directrix is  x – y + 3 = 0.

Solution:

Let P(x, y) be any point on the ellipse whose focus is S(-1, 1) and the directrix is x – y + 3 = 0.

Draw PM perpendicular from P (x, y) on the directrix x – y + 3 = 0.

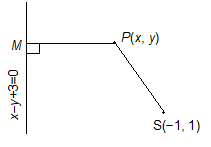
Then by definition  SP = ePM

$\Rightarrow$   (SP)² = e² (PM)²

$\Rightarrow (\mathrm{x}+1{)}^2+(\mathrm{y}–1{)}^2=\frac{1}{4}{\left\{\frac{\mathrm{x}–\mathrm{y}+3}{\sqrt{2}}\right\}}^2$

$\Rightarrow 8\left({\mathrm{x}}^2+{\mathrm{y}}^2+2\mathrm{x}–2\mathrm{y}+2\right)={\mathrm{x}}^2+{\mathrm{y}}^2+9–2\mathrm{xy}+6\mathrm{x}–6\mathrm{y}$

$\Rightarrow 7{\mathrm{x}}^2+7{\mathrm{y}}^2+2\mathrm{xy}+10\mathrm{x}–10\mathrm{y}+7=0$, which is the required equation of the ellipse.

11. STANDARD EQUATION

If we take focus as ($\pm$ae, 0) and directrix as $\mathrm{x}=\pm \frac{\mathrm{a}}{\mathrm{e}}$, we get equation of ellipse as ,

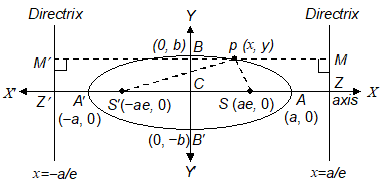
$\frac{{\mathrm{x}}^2}{{\mathrm{a}}^2}+\frac{{\mathrm{y}}^2}{{\mathrm{b}}^2}=1$, where b² = a² (1 – e²)

Results

(i) Equation of the directrix corresponding to focus (-ae, 0) is $\mathrm{x}=\frac{–\mathrm{a}}{\mathrm{e}}$

(ii) If a > b, 2a is the length of major axis and 2b is the length of minor axis.

Centre

Point of intersection of major axis and minor axis is the centre of the ellipse. In the above case centre $\equiv$ (0, 0).

Focal chord

Any chord of the ellipse passing through the focus is called focal chord.

Latus rectum

A focal chord, which is perpendicular to the major axis of the ellipse is known as latus-rectum. In the ellipse $\frac{{\mathrm{x}}^2}{{\mathrm{a}}^2}+\frac{{\mathrm{y}}^2}{{\mathrm{b}}^2}=1$ (a > b),

(i) End points of the latus rectum are $\left(\pm \mathrm{ae}, \pm \frac{{\mathrm{b}}^2}{\mathrm{a}}\right)$.

(ii)     Length of the latus rectum is $\frac{2{\mathrm{b}}^2}{\mathrm{a}}$.

Illustration-14:

Find the equation of the ellipse referred to its centre as origin and whose minor axis is equal to the distance between the foci and whose latus rectum is 10.

Solution:

Let the equation of the ellipse is

$\frac{{\mathrm{x}}^2}{{\mathrm{a}}^2}+\frac{{\mathrm{y}}^2}{{\mathrm{b}}^2}=1$ (let a > b)

Then the foci are S (ae, 0) and S’ (-ae, 0), length of minor axis BB’ = 2b and length of latus rectum = $\frac{2{\mathrm{b}}^2}{\mathrm{a}}$.

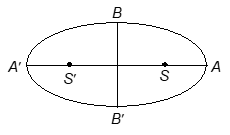
$\therefore$ According to the question

BB’ = SS’

$\Rightarrow$ 2b = 2ae

$\Rightarrow$  b = ae    …(i)

and $\frac{2{\mathrm{b}}^2}{\mathrm{a}}=10$

$\Rightarrow$ b² = 5a  …(ii)

also we have  b² = a² (1 – e²)        …(iii)

Putting the value of b from equation (i) in (iii), we have

a²e² = a² (1 – e²) – e² = 1 – e²  $\Rightarrow$  2e² = 1

$\therefore \mathrm{e}=\frac{1}{\sqrt{2}}$

from equation of (i) we have $\mathrm{b}=\frac{\mathrm{a}}{\sqrt{2}}$

$\therefore {\mathrm{b}}^2=\frac{{\mathrm{a}}^2}{2}\Rightarrow 5\mathrm{a}=\frac{{\mathrm{a}}^2}{2}$ { from equation (ii)} 

$\Rightarrow$    a = 10

From equation (ii), b² = 5 $\times$ 10 = 50

Putting the values of a and b in $\frac{{\mathrm{x}}^2}{{\mathrm{a}}^2}+\frac{{\mathrm{y}}^2}{{\mathrm{b}}^2}=1$, the equation of required ellipse is

$\frac{{\mathrm{x}}^2}{100}+\frac{{\mathrm{y}}^2}{50}=1$

or   x² + 2y² = 100

Focal distance of a point

Let P be a point on the ellipse, where S and S are the foci, then PS and PS are known as focal distance of the point P.

$\mathrm{PS}=\mathrm{ePM}=\mathrm{e}\left(\frac{\mathrm{a}}{\mathrm{e}}–\mathrm{x}\right)=\mathrm{a}–\mathrm{ex}$ and  ${\mathrm{PS}}^{‘}={\text{ ePM }}^{‘}$

Remark:

(i) In any ellipse sum of the focal distances of any point is constant and is equal to length of major axis.

(ii) For the ellipse $\frac{(\mathrm{x}–\mathrm{\alpha }{)}^2}{{\mathrm{a}}^2}+\frac{(\mathrm{y}–\mathrm{\beta }{)}^2}{{\mathrm{b}}^2}=1$ (a > b) ,

Eccentricity = $\mathrm{e}=\sqrt{1–\frac{{\mathrm{b}}^2}{{\mathrm{a}}^2}}$

Equation of major axis $\equiv$ y = $\mathrm{\beta }$

Equation of minor axis $\equiv$ x = $\alpha$

Centre $\equiv$ ($\alpha , \beta$)

Vertices $\equiv$ ($\alpha \pm a, \beta$)

Foci $\equiv$ ($\alpha \pm$ ae, $\beta$)

Directrices $\equiv$$x=\alpha \pm \frac{a}{e}$

Ends of minor axis $\equiv \left(\alpha , \beta \pm b\right)$

Length of latus rectum = $\frac{2b^2}{a}$

Parametric coordinates $\equiv$ (acos$\theta$ + $\alpha$, bsin$\theta$ + $\beta$)  (where 0 $\le \theta$ < 2$\mathrm{\pi }$).

Illustration-15:

Show that the following equation represents an ellipse. Also find its centre and eccentricity: 4(x – 2y + 1)² + 9(2x + y + 2)² = 25.

Solution:

On simplification the equation becomes

$4\left({\mathrm{x}}^2+4{\mathrm{y}}^2+1–4\mathrm{xy}+2\mathrm{x}–4\mathrm{y}\right)+9\left(4{\mathrm{x}}^2+{\mathrm{y}}^2+4+4\mathrm{xy}+8\mathrm{x}+4\mathrm{y}\right)=25$

or, $40{\mathrm{x}}^2+20\mathrm{xy}+25{\mathrm{y}}^2+80\mathrm{x}+20\mathrm{y}+15=0$

or, $8{\mathrm{x}}^2+4\mathrm{xy}+5{\mathrm{y}}^2+16\mathrm{x}+4\mathrm{y}+3=0$.

Comparing with the general equation of the second degree

${\mathrm{h}}^2–\mathrm{ab}=2^2–8.5=4–40<0$

$∆$ = 8.5.3 + 2.2.8.2 – 8.2² – 5.8² – 3.2²

= 120 + 64 − 32 − 320 − 12 ≠ 0, h ≠ 0

∴ the curve is an ellipse.

For the equation 4(x − 2y + 1)² + 9(2x + y + 2)² = 25, we find that x − 2y + 1 = 0 and 2x + y + 2 = 0 are mutually perpendicular lines.

∴   substituting   $\frac{\mathrm{x}–2\mathrm{y}+1}{\sqrt{1^2+(–2{)}^2}}=\mathrm{X}$  …(i)

and  $\frac{2\mathrm{x}+\mathrm{y}+2}{\sqrt{2^2+1^2}}=\mathrm{Y}$     …(ii)

the equation changes to $4(\sqrt{5}\mathrm{X}{)}^2+9(\sqrt{5}\mathrm{Y}{)}^2=25$

or,   4X² + 9Y² = 5   or  $\frac{{\mathrm{X}}^2}{5/4}+\frac{{\mathrm{Y}}^2}{5/9}=1$

which is in the standard form of equation of an ellipse.

$\therefore {\mathrm{a}}^2=\frac{5}{4}\text{ and }{\mathrm{b}}^2=\frac{5}{9};$

but  b² = a² (1 − e²)

$\therefore \frac{5}{9}=\frac{5}{4}\left(1–{\mathrm{e}}^2\right)$   or  ; $\frac{4}{9}=1–{\mathrm{e}}^2; \therefore {\mathrm{e}}^2=1–\frac{4}{9}=\frac{5}{9}; \therefore \mathrm{e}=\frac{\sqrt{5}}{3}$

Now, centre = (0, 0)_{X, Y} ;

when X = 0, Y = 0 we have from (i), (ii)

x − 2y + 1 = 0  and 2x + y + 2 = 0

Solving these, 5x + 5 = 0

∴    x = −1; so y = 0

∴    centre = (−1, 0).

12. PARAMETRIC EQUATION OF ELLIPSE

If ellipse be $\frac{{\mathrm{x}}^2}{{\mathrm{a}}^2}+\frac{{\mathrm{y}}^2}{{\mathrm{b}}^2}=1$ (a > b), then auxiliary circle will be x² + y² = a² and point Q will be (acosθ, asinθ), hence point P will be (acosθ, bsinθ).

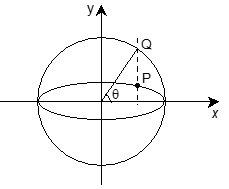
Here x = acosθ, y = bsinθ is called as parametric equation of the ellipse $\frac{{\mathrm{x}}^2}{{\mathrm{a}}^2}+\frac{{\mathrm{y}}^2}{{\mathrm{b}}^2}=1$

13. ANOTHER FORM OF ELLIPSE (when b > a)

In this case major and minor axis of the ellipse along y-axis and x-axis respectively.

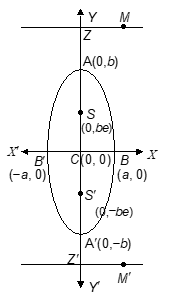
Then AA’ = 2b (length of major axis) and BB’ = 2a (length of minor axis)

The foci S and S’ are (0, be) and (0, −be) respectively.

The directrices are MZ and M’Z’ are $\mathrm{y}=\frac{\mathrm{b}}{\mathrm{e}}$ and $\mathrm{y}=\frac{–\mathrm{b}}{\mathrm{e}}$ respectively.

${\mathrm{e}}^2=1–\frac{{\mathrm{a}}^2}{{\mathrm{b}}^2}$

Length of latus rectum = $\frac{2{\mathrm{a}}^2}{\mathrm{b}}$

HYPERBOLA

14. DEFINITION AND EQUATION

A hyperbola is the locus of a point, which moves such that ratio of its distance from a fixed point to a fixed line is constant and value of the constant is greater than unity. Here, fixed point is known as focus, fixed line as directrix and constant as eccentricity.

Generally, the equation of the hyperbola, whose focus is the point (h, k), directrix is lx + my + n = 0 and eccentricity e, is $(\mathrm{x}–\mathrm{h}{)}^2+(\mathrm{y}–\mathrm{k}{)}^2={\mathrm{e}}^2.\frac{(l\mathrm{x}+\mathrm{my}+\mathrm{n}{)}^2}{\left(l^2+{\mathrm{m}}^2\right)}$ (e > 1)

Illustration-16:

Find the equation of the hyperbola one of whose focus is (2, 2), eccentricity 2 and the equation of directrix x + y = 9.

Solution:

Let P(x, y) be any point on the hyperbola. Let PM be perpendicular from P on the directrix.

Then $\frac{\mathrm{SP}}{\mathrm{PM}}=\mathrm{e}$

$\Rightarrow (\mathrm{x}–2{)}^2+(\mathrm{y}–2{)}^2=2^2{\left[\frac{\mathrm{x}+\mathrm{y}–9}{\sqrt{2}}\right]}^2$ $\Rightarrow$  x² + y² − 4x − 4y + 8 = 2(x + y − 9)²

$\Rightarrow$  x² + y² + 4xy − 32x − 32y + 154 = 0

Definition:

A hyperbola is the locus of a point, which moves such that the difference in its distances from two fixed points is constant and value of the constant is less than the distance between these two fixed points.

15. STANDARD EQUATION

If we take focus as ($\pm$ae , 0) and directrix as $\mathrm{x}=\pm \frac{\mathrm{a}}{\mathrm{e}}$, we get equation of hyperbola as

$\frac{{\mathrm{x}}^2}{{\mathrm{a}}^2}+\frac{{\mathrm{y}}^2}{{\mathrm{b}}^2}=1$

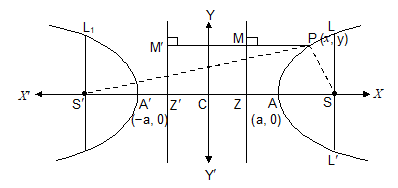
where b² = a² (e² − 1)

Results

(i) Equation of the directrix corresponding to focus (−ae, 0) is $\mathrm{x}=\frac{–\mathrm{a}}{\mathrm{e}}$

(ii) 2a is the length of transverse axis and 2b is the length of conjugate axis.

Focal chord

Any chord of the hyperbola passing through the focus is called focal chord.

Illustration-17:

Obtain the equation of a hyperbola with coordinate axes as principal axes given that the distances of one of its vertices from the foci are 9 and 1 units.

Solution:

Let equation of hyperbola is

$\frac{{\mathrm{x}}^2}{{\mathrm{a}}^2}+\frac{{\mathrm{y}}^2}{{\mathrm{b}}^2}=1$  …(i)

If vertices are A(a, 0) and A’ (−a, 0) and foci are S (ae, 0) and S’ (−ae, 0)

given  l (S’A) = 9 and l (SA) = 1

$\Rightarrow$  a + ae = 9 and ae − a  = 1

or  a(1 + e) = 9 and or a (e − 1) = 1

$\therefore \frac{\mathrm{a}(1+\mathrm{e})}{\mathrm{a}(\mathrm{e}–1)}=\frac{9}{1}$

$\Rightarrow$    1 + e = 9e − 9  $\Rightarrow \mathrm{e}=\frac{5}{4}$

∵    a (1 + e) = 9

$\therefore \mathrm{a}\left(1+\frac{5}{4}\right)=9$

$\Rightarrow$ a = 4

b² = a² (e² − 1)

$=16\left(\frac{25}{16}–1\right)$

∴   b² = 9

from (i), equation of hyperbola is $\frac{{\mathrm{x}}^2}{16}–\frac{{\mathrm{y}}^2}{9}=1$.

Latus rectum

A focal chord, which is perpendicular to the transverse axis of the hyperbola is known as latus-rectum. In a hyperbola $\frac{{\mathrm{x}}^2}{{\mathrm{a}}^2}–\frac{{\mathrm{y}}^2}{{\mathrm{b}}^2}=1$ (a > b),

(i) End points of the latus rectum are $\left(\pm \mathrm{ae}, \pm \frac{{\mathrm{b}}^2}{\mathrm{a}}\right)$

(ii) Length of the latus rectum is $\frac{2{\mathrm{b}}^2}{\mathrm{a}}$

Focal distance of a point

Let P be a point on the hyperbola, where S and S’ are the foci, then PS and PS’ are known as focal distance of the point P.

Remark:

In any hyperbola difference in the focal distances of any point is constant and is equal to length of transverse axis.

Illustration-18:

Find the equation to the hyperbolas of given transverse axes whose vertex bisects the distance between the centre and the focus.

Solution:

Let vertex be (a, 0) and focus (ae, 0) then $\frac{\mathrm{ae}+0}{2}=\mathrm{a}\Rightarrow \mathrm{e}=2$

Again b² = a² (e² − 1) = 3a²

The equation of hyperbola is $\frac{{\mathrm{x}}^2}{{\mathrm{a}}^2}–\frac{{\mathrm{y}}^2}{3{\mathrm{a}}^2}=1$.

16. PARAMETRIC EQUATION OF HYPERBOLA

If hyperbola be $\frac{{\mathrm{x}}^2}{{\mathrm{a}}^2}–\frac{{\mathrm{y}}^2}{{\mathrm{b}}^2}=1$,

Then parametric coordinates of point P will be (asecθ, btanθ), here ‘θ’ is the eccentric angle of point P.

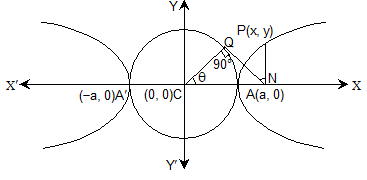
Here x = asecθ, y = btanθ is called parametric equation of the hyperbola $\frac{{\mathrm{x}}^2}{{\mathrm{a}}^2}–\frac{{\mathrm{y}}^2}{{\mathrm{b}}^2}=1$.

Illustration-19:

If two points P and Q on the hyperbola $\frac{{\mathbf{x}}^{\mathbf{2}}}{{\mathbf{a}}^{\mathbf{2}}}\mathbf{–}\frac{{\mathbf{y}}^{\mathbf{2}}}{{\mathbf{b}}^{\mathbf{2}}}\mathbf{=}\mathbf{1}$, whose centre C be such that CP is perpendicular to CQ, a < b, then prove that $\frac{\mathbf{1}}{{\mathbf{CP}}^{\mathbf{2}}}\mathbf{+}\frac{\mathbf{1}}{{\mathbf{CQ}}^{\mathbf{2}}}\mathbf{=}\frac{\mathbf{1}}{{\mathbf{a}}^{\mathbf{2}}}\mathbf{–}\frac{\mathbf{1}}{{\mathbf{b}}^{\mathbf{2}}}$.

Solution:

Let CP = r₁ be inclined to transverse axis at an angle θ so that P is (r₁cosθ, r₁sinθ) and P lies on the hyperbola.

$\Rightarrow {\mathrm{r}}_1^2\left(\frac{{\cos }^2\mathrm{\theta }}{{\mathrm{a}}^2}–\frac{{\sin }^2\mathrm{\theta }}{{\mathrm{b}}^2}\right)=1$

Replacing θ by 90° + θ, then ${\mathrm{r}}_2^2\left(\frac{{\sin }^2\mathrm{\theta }}{{\mathrm{a}}^2}–\frac{{\sin }^2\mathrm{\theta }}{{\mathrm{b}}^2}\right)=1$

$\Rightarrow \frac{1}{{\mathrm{r}}_1^2}+\frac{1}{{\mathrm{r}}_2^2}=\frac{{\cos }^2\mathrm{\theta }}{{\mathrm{a}}^2}–\frac{{\sin }^2\mathrm{\theta }}{{\mathrm{b}}^2}+\frac{{\sin }^2\mathrm{\theta }}{{\mathrm{a}}^2}–\frac{{\cos }^2\mathrm{\theta }}{{\mathrm{b}}^2}$  $\Rightarrow \frac{1}{{\mathrm{r}}_1^2}+\frac{1}{{\mathrm{r}}_2^2}=\frac{1}{{\mathrm{a}}^2}–\frac{1}{{\mathrm{b}}^2}$

$\Rightarrow \frac{1}{{\mathrm{CP}}^2}+\frac{1}{{\mathrm{CQ}}^2}=\frac{1}{{\mathrm{a}}^2}–\frac{1}{{\mathrm{b}}^2}$