A straight line is a curve, every point on the line segment joining any two points on it lies on it. Any first degree equation in x, y which is of the form ax + by + c = 0 always represents a straight line (where a, b, c are constants and at least one of a and b is non-zero).
1. Slope
(i) If a line makes angle θ with positive direction of x-axis in anticlockwise direction, then slope of line m = tan θ(where 0 ≤ θ < π).
If θ is 90°, m does not exist, but the line is parallel to the y-axis. If θ = 0, then m = 0 & the line is parallel to the x-axis

(ii) Slope of a line passing through two points (x1, y1) and (x2, y2) is
2. Intercept of a Straight Line on The Axis
If a line cuts the x-axis and y-axis at A and B respectively then OA and OB (with proper sign) are called the intercepts of the line on x-axis and y-axis respectively (where O is the origin)
(i) If length of intercept is given (say 3) it means that intercept is either 3 or – 3.
(ii) If intercept of a line is k units then length of intercept will be |k|.
Illustration -1
A line l1 passes through points (5, −3) and (4, −6). Another line, l 2, passes through points (8, 1) and (2, 3). Are lines l1 and l2 perpendicular, parallel or neither of the two?
Solution
We will first find the slopes of the two lines.
We know that if a line passes through points (x1, y1) and (x2, y2), then the slope of that line is given by .
Thus,
Slope of line l1 is given by
Slope of line l2 is given by
Here, we can observe that m1 m2 = −1. Hence, lines l1 and l2 are perpendicular to each other.
Illustration -2
1. Find the slopes of the straight lines passing through the following pairs of points.
(i) (-3,8), (10,5) (ii) (3,4), (7,-6)
Solution
1. (i) The slope of the straight line passing through the pb (–3, 8), (10, 5)
(ii) The slope of the straight line passing through the points (3, 4), (7, –6)
Illustration -3
The line passing through points (0, 2) and (8, 4) is parallel to the line passing through points and (2, p). Find the value of p.
Solution
We know that two lines are parallel if and only if their slopes are equal. The slope of a line passing through points (x1, y1) and (x2, y2) is given by .
Therefore,
Slope of the line passing through points (0, 2) and (8, 4) is given by
Slope of the line passing through points and (2, p) is given by
Since the two lines are parallel,
m1 = m2
⇒ 10 = – 20p + 32
⇒ 5 = – 10p + 16
⇒ 10p = 16 – 5 = 11
⇒
Thus, the value of p is .
Illustration -4
The given graph shows the temperature of water, which was kept on fire for some time, at different intervals of time.
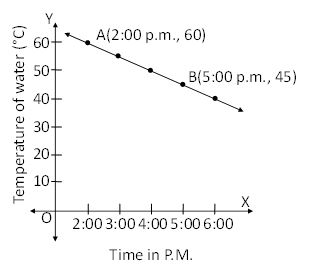
What will be the temperature of water at 8 p.m. if it was kept in the same conditions from 2 p.m. to 9 p.m.?
Solution
Since line AB passes through points A (2:00 p.m., 60°C) and B (5:00 p.m., 45°C), its slope is.
.
Let y be the temperature of water at 8:00 p.m. Accordingly, on the basis of the given graph, line AB must pass through point C (8:00 p.m., y).
∴ Slope of AB = Slope of BC
⇒ – 15 = y – 45 ⇒ y = – 15 + 45
⇒ y = 30
Thus, the temperature of water will be 30°C at 8:00 p.m.
3. Equation of a straight line in various forms
1. Slope- Intercept form
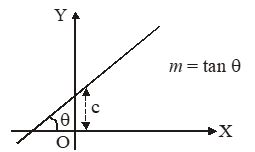
y = mx + c
where m = slope of line
c = intercept of line on y-axis
2. Slope-point form
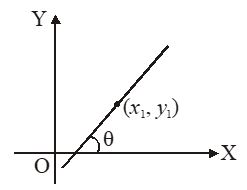
If a line passes through a point (x1, y1) whose slope is m (m = tanθ) then equation of line is
y – y1 = m (x – x1)
3. Two point form
Equation of a line passing through two points (x1, y1) and (x2, y2) is
4. Intercept form
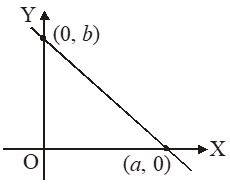
where a = intercept of line on x-axis
b = intercept of line on y-axis
5. Normal form
x cos α + y sin α = p
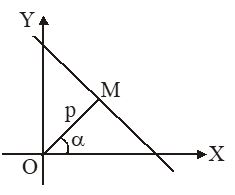
where p = length of perpendicular from origin to the line
α = angle which the perpendicular to the line from origin makes with x-axis.
6. Parametric form
Let a line passes through a point A(x1, y1) and makes angle θ with positive direction of x-axis. Let P(x, y) be any point on the line at a distance r from the point A(x1, y1) then parametric form of the line is used to find out the co-ordinate of point P(x, y).

Let AP = r
Hence from figure, x – x1 = r cos θ
y – y1 = r sin θ
∴
The above equation is called as parametric equation of the given line.
Note:
Co-ordinate of any point P on the line will be of the form (x1 + r cos θ, y1 + r sin θ) where | r | is the distance of point P from the fixed point (x1, y1).
Reduction of The General Equation of Line to Different Standard Forms
1. Slope-Intercept form
To reduce the equation Ax + By + C = 0 to the form y = mx + c
Given equation is Ax + By + C = 0 ⇒ y =
which is of the form y = mx + c
where
Hence slope of line = –
y-intercept of line = –
2. Intercept form
To reduce the equation Ax + By + C = 0 to the form
This reduction is possible only when C ≠ 0
Since the given equation is
Ax + By = – C
which is of the form
& intercept on x-axis = –
intercept on y-axis = –
Note:
To find intercept of a line on x-axis, put y = 0 and value of x gives the intercept on x-axis. Similarly intercept on y-axis can be obtained by putting x = 0 and solving for y.
3. Normal form
To reduce the equation Ax + By + C = 0 to the form x cos α + y sin α = p.
Given equation is Ax + By + C = 0 or Ax + By = – C
Case-I: when – C > 0, then normal form is
where
Case-II: when – C < 0, then write the equation as – Ax – By = C
where
Note:
In normal form, x cos α + y sin α = p, p is taken as positive.
Illustration -5
Find the equation of the straight line which makes an angles of 15° with the positive direction of x-axis and which cuts an intercept of length 4 on the negative direction of y-axis.
Solution
Here m = slope of the line = tan 15° = tan (45° – 30°)
=
=
and c = intercept on y-axis = – 4
Therefore, equation of the required line will be
Illustration -6
Find the equation of the straight line which passes through the point (3, 2) and whose gradient is . Find the co-ordinates of the points on the line that are 5 units away from the point (3, 2).
Solution
Let P (3, 2) and let the required line make an angle θ with the positive direction of x-axis. Given tan θ =
Now equation of the required line will be
or 3 (x – 3) = 4 (y – 2) or 3x – 4y – 1 = 0 … (i)
Now the co-ordinates of the points which are at a distance of 5 units from P are
(3 ± 5 cos θ, 2 ± 5 sin θ) or (3 ± 4), (2 ± 3) or (7, 5) and (– 1, – 1)
Illustration -7
Reduce the line 2x – 3y + 5 = 0, in slope intercept, intercept and normal form.
Solution
Slope Intercept Form
Intercept Form
Normal Form
Illustration -8
Find the value(s) of p for which the equation (p2 + 2p − 3)y + (p2 + 4p + 1)x + 5 = 0 is parallel to the y-axis.
Solution
We know that if a line is parallel to the y-axis, then the coefficient of y in its equation will be zero. Therefore,
p2 + 2p − 3 = 0
⇒ p2 + 3p − p − 3 = 0
⇒ p(p + 3) −1(p + 3) = 0
⇒ (p + 3)(p − 1) = 0
⇒ p = −3 or p = 1
Thus, the required values of p for which the given equation is parallel to the y-axis are −3 and 1.
Illustration -9
Find the equation of the line that passes through the points and (−5, 2).
Solution
Using the two-point form of the equation of line, we know that the equation of the line passing through the points (x1, y1) and (x2, y2) is given by .
Thus, the required equation of the line passing through the points and (−5, 2) is given by
⇒ – 16(2y – 1) = 3 (3x – 1)
⇒ – 32y + 16 = 9x – 3
⇒ 9x + 32y – 19 = 0
Illustration -10
Find the equation of the line that passes through the point (8, 5) and makes an inclination of 210° with the x-axis.
Solution
It is given that the line makes an inclination of 210° with the x-axis. Therefore, the slope of the line is given by
m = tan 210° = tan (180° + 30°) = tan 30°=
Using point-slope form of equation of line, we know that the equation of the line with slope m that passes through the point (x1, y1) is given by
(y − y1) = m(x − x1).
Thus, the required equation of the line is given by
Illustration -11
Find the equation of the line that passes through the intersection of lines 2x + y + 6 = 0 and x − y + 9 = 0 and is perpendicular to the line that passes through points (−6, 3) and (4, 5).
Solution
It is given that the required line passes through the intersection of lines 2x + y + 6 = 0 and x−y + 9 = 0.
The points of intersection of lines 2x + y + 6 = 0 and x − y + 9 = 0 can be found by adding the two equations.
Hence,
3x + 15 = 0
⇒ x = −5
∴ y = 4
Thus, the required equation passes through the point (−5, 4).
It is also given that the required line is perpendicular to the line that passes through points (−6, 3) and (4, 5). We know that the slope of a line that passes through points (x1, y1) and (x2, y2) is given by .
Thus, the slope of the line that passes through points (−6, 3) and (4, 5) is given by .
We also know that if two lines are perpendicular to each other, then their slopes are negative reciprocals of each other.
Thus, the slope of the required line is −5.
Thus, we are required to find the equation of the line that passes through the point (−5, 4) having slope −5.
Using point-slope form, the equation of the required line is given by
y − 4 = (−5)(x + 5)
⇒ y − 4 = −5x – 25 ⇒ 5x + y + 21 = 0
Illustration -12
Write the equation of the line through the points (1, –1) and (3, 5).
Solution
Here x1 = 1, y1 = -1, x2 = 3 and y2 = 5. Using two-point form (2) above for the equation of the line, we have
or -3x + y + 4 = 0, which is the required equation.
Illustration -13
The equation of a line is given by 12x + 8y − 9 = 0. Find the angle made by this line with the positive direction of the x-axis.
Solution
The equation of the line is given by
12x + 8y − 9 = 0
⇒ 8y = 9 − 12x
On comparing this equation with the general form y = mx + c, we obtain the slope of the line as
Thus, the angle made by the line with the positive direction of the x-axis is .
Illustration -14
Find the equation of the line that makes x-intercept as 5 and is perpendicular to the line 16x + 4y = 5.
Solution
It is given that the line is perpendicular to the line 16x + 4y = 5.
The slope of this line can be calculated as
4y = −16x + 5
Thus, the slope of this line is −4. Therefore, the slope of the required line is .
Also, it is given that the line makes the x-intercept as 5.
By using the slope-intercept form, we get the required equation of the line as
⇒ 4y = x – 5
⇒ x – 4y – 5 = 0
Illustration -15
Write the equation of the lines for which tan θ = , where θ is the inclination of the line and
(i) y-intercept is
(ii) x-intercept is 4.
Solution
(i) Here, slope of the line is m = tan θ = and y – intercept c = –.
Therefore, by slope-intercept form (3) above, the equation of the line is (or) 2y – x + 3 = 0
which is the required equation.
(ii) Here, we have m = tan θ = and d = 4.
Therefore, by slope-intercept form (4) above, the equation of the line is
which the required equation is.
Illustration -16
The equation of a line is given by 11x − 8y + 12 = 0. Find the x– and y-intercepts made by this line.
Solution
The equation of the given line is
11x − 8y + 12 = 0
Thus, the given line makes the x-intercept as and y-intercept as .
Illustration -17
The sum of x and y-intercepts made by a line is 25 and their product is 144. Find the equation of the line.
Solution
We know that the equation of the line that makes x and y-intercepts as a and b is given by .
It is given that
a + b = 25 and a × b = 144
a × b = 144 gives .
Therefore, on using a + b = 25, we obtain
⇒ a2 – 25a + 144 = 0
⇒ a2 – 9a – 16a + 144 = 0
⇒ a(a – 9) –16(a – 9) = 0
⇒ (a – 9)(a – 16) = 0
⇒ a = 9 or a = 16
This gives b = 16 or b = 9.
Therefore, the required equation of the line is .
Illustration -18
Find the equation of the line, which makes intercepts –3 and 2 on the x- and y-axes respectively.
Solution
Here a = –3 and b = 2. By intercept form (5) above, equation of the line is
or 2x – 3y +6 = 0
Illustration -19
Find the equation of the line whose perpendicular distance from the origin is 10 units and the angle which the normal makes with the positive direction of x-axis is 240°.
Solution
We know that the normal form of the equation is given by
x cos ω + y sin ω = p
Here, we are given that
p = 10 and ω = 240°
Thus, the required equation of the line is given by
x cos 240° + y sin 240° = 10
⇒ x cos (180° + 60°) + y sin (180° + 60°) = 10
⇒ −x cos 60° − y sin 60° = 10
Illustration -20
Find the equation of the line AB in normal form where the coordinates of points A and B are A(16, 4), and B(10, 10).
Solution
Using the two-point form, the equation of line AB is given by
⇒ y – 4 = – x + 16
⇒ x + y – 20 = 0
On dividing this equation by , we obtain
This is the required equation of line AB in the normal form.
Illustration -21
The equation of a line is given as −x + y + 7 = 0. Find the normal distance of the line from the origin and the angle which the normal makes with the positive direction of x-axis.
Solution
The given equation of the line is −x + y + 7 = 0.
On dividing this equation by , we obtain
⇒ x cos 45° − y sin 45°=
⇒ x cos (360° − 45°) + y sin (360° − 45°) =
⇒ x cos 315° + y sin 315°=
On comparing this equation with the standard normal form i.e., x cos ω + y sin ω = p, we obtain
ω = 315°, p =
Thus, the normal distance of the line from the origin is and the angle which the normal makes with the positive direction of the x-axis is 315°.
Illustration -22
The Fahrenheit temperature F and absolute temperature K satisfy a linear equation. Given that K = 273 when F = 32 and that K = 373 when F = 212. Express K in terms of F and find the value of F, when K = 0.
Solution
Assuming F along x-axis and K along y-axis, we have two points (32, 273) and (212, 373) in XY-plane. By two-point form, the point (F, K) satisfies the equation
or (F – 32) + 273 _________________ (1)
which is the required relation.
When K = 0, Equation (1) gives
or or F= 459.4
Alternate method
We know that simplest form of the equation of a line is y = mx + c.
Again assuming F along x-axis and K along y-axis, we can take equation in the form
K = mF + c ________________ (1)
Equation (1) is satisfied by (32, 273) and (212, 373).
Therefore 273 = 32m + c ________________ (2)
and 373 = 212m + c ________________ (3)
Solving (2) and (3), we get
Putting the values of m and c in (1), we get _______ (4)
which is the required relation. When K = 0, (4) gives F = – 459.4.
5. Angle Between Two Straight Lines when their Equations are given
If θ is the acute angle between two lines, then
where m1 and m2 are the slopes of the two lines and are finite.
Note:
(i) Any line parallel to the line ax + by + c = 0 is of the form ax + by + k = 0
(ii) If two lines are perpendicular to each other then m1m2 = – 1
(iii) Any line perpendicular to ax + by + c is of the form bx – ay + k = 0
(iv) If one of the two lines are perpendicular to x-axis, then the slope of that line is infinite.
Let m1 = then
where tan α = m2
Illustration -23
Find the equations of the straight lines passing through the point (2, 3) and inclined at radians to the line 2x + 3y = 5.
Solution
Let the line 2x + 3y = 5 makes angle θ with positive x-axis. Then tan θ =
Slope of the required lines are
and = – 5
∴ the equations of the required lines are y – 3 = (x – 2) i.e., x – 5y + 13 = 0
y – 3 = – 5(x – 2) i.e., 5x + y – 13 = 0
Illustration -24
Find the equation to the sides of an isosceles right-angled triangle, the equation of whose hypotenuse is x – 2y = 3 and the opposite vertex is the point (2, 2).
Solution
Clearly other two sides of the triangle will be making an angle of 45o with the given line. That means we have to find the equation of line passing through the point (3, 2) and making an angle of 45o with the given line. Slope of the given line x – 2y = 3 is m1 = 1/2.
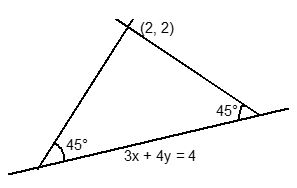
.
Hence the required equations of the two lines are 3x – y – 7 = 0 and x + 3y – 9 = 0.
Illustration -25
Find the equation of the straight line that passes through the point (3, 4) and perpendicular to the line 3x + 2y + 5 = 0
Solution
The equation of a line perpendicular to 3x + 2y + 5 = 0 is 2x – 3y + = 0 ………..(i)
This passes through the point (3, 4)
∴ 3 × 2 – 3 × 4 + λ = 0 ⇒ λ = 6
Putting λ = 6 in (i), we get 2x – 3y + 6 = 0, which is the required equation.
Aliter
The slope of the given line is –3/2. Since the required line is perpendicular to the given line. So, the slope of the required line is 2/3. As it passes through (3, 4). So, its equation is y – 4 = (x – 3) or 2x – 3y + 6 = 0
Illustration -26
The coordinates of a quadrilateral ABCD are A(−4, −3), B(0, 5), C(10, 5), and D(4, −3). Find the measures of angles A, B, C, and D.
Solution
The coordinates of the vertices of the quadrilateral ABCD are given as A(−4, −3), B(0, 5), C(10, 5) and D(4, −3).
We know that the angle between two lines with slopes m1 and m2 is given by
Slope of line AB =
Slope of line BC =
Slope of line CD =
Slope of line DA =
Tan ∠A = ⇒ ∠A = tan−1(2)
Tan ∠B = ⇒ ∠B = tan−1(2)
Tan ∠C =
Tan ∠D =
Illustration -27
The angle made by two line segments is tan−1. If the slope of one line segment is , then find the slope of the other line segment.
Solution
We know that the angle between two lines with slopes m1 and m2 is given by
Let the required slope of the other line be m.
According to the given information,
⇒ 2 + m = 7 – 14m or 2 + m = 14m – 7
⇒ 15m = 5 or 13m = 9
⇒
Thus, the required slope of the line is or .
Illustration -28
If the angle between two lines is and slope of one of the lines is , find the slope of the other line.
Solution
We know that the acute angle θ between two lines with slopes m1 and m2 is given by
_________ (1)
Let .
Now, putting these values in (1), we get
which gives
Therefore m = 3 or m =
Hence, slope of the other line is 3 or .
Figure 10.12 explains the reason of two answers.
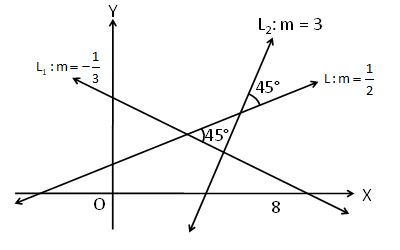
Illustration -29
Line through the points (–2, 6) and (4, 8) is perpendicular to the line through the points (8, 12) and (x, 24). Find the value of x.
Solution
Slope of the line through the points (– 2, 6) and (4, 8) is
Slope of the line through the points (8, 12) and (x, 24) is
Since two lines are perpendicular, m1 m2 = -1, which gives or x = 4
1. Equation of a Line Passing Through a Given Point and Equally Inclined to a Given Line
Let the straight lines passes through point (x1, y1) and makes equal angles with the given line y = m1x + c.
Let the angle is θ.
Let slope of the required line is m.
then tan θ = ± … (i)
Equation (i) gives two values of m, hence we will get two lines.
Let the values of m are mA and mB
then
&
Hence equations of lines are
y – y1 = mA (x – x1)
& y – y1 = mB (x – x1)
Illustration -30
Find the equation to the sides of an isosceles right-angled triangle, the equation of whose hypotenuse is 3x + 4y = 4 and the opposite vertex is the point (2, 2).
Solution The problem can be restated as:
Find the equations to the straight lines passing through the given point (2, 2) and making equal angles of 45° with the given straight line 3x + 4y – 4 = 0. Slope of the line 3x + 4y – 4 = 0 is m1 = – .
⇒ tan 45° = ± i.e., 1 = ±
mA = and mB = – 7
hence the required equations of the two lines are
y – 2 = mA (x – 2) and y – 2 = mB (x – 2)
⇒ 7y – x – 12 = 0 and 7x + y = 16
6. Area of parallelogram
The area of the parallelogram = , where p1 & p2 are distances between two pairs of opposite sides & θ is the angle between any two adjacent sides. Note that area of the parallelogram bounded by the lines y = m1x + c1, y = m1x + c2 and y = m2x + d1, y = m2x + d2 is given by .
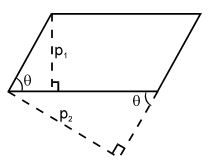
Illustration -31
Find the area of the parallelogram whose sides are x + 2y + 3 = 0, 3x + 4y – 5 = 0, 2x + 4y + 5 = 0 and 3x + 4y – 10 = 0
Solution
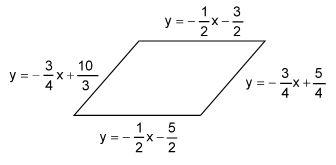
Here, c1 = – , c2 = , d1 = , d2 = – , m1 = – , m2 = –
∴ Area = sq. units Ans.
7. Area of a Triangle
Let (x1, y1), (x2 ,y2) and (x3, y3) respectively be the coordinates of the vertices A, B, C of a triangle ABC. Then the area of triangle ABC, is
= Modulus of
Illustration -32
The area of the triangle with vertices at (p–4, p+5), (p+3, p–2) and (p, p) is
(A) 3p + p2 (B) |p| + 5 (C) |p – 3| (D) none of these
Solution
(D). The area of triangle is
(R1 → R1 – R3, R2 → R2 –R3)
= ,
which remains constant for all values of p.
8. STANDARD POINTS OF A TRIANGLE
1. Centroid
The point of intersection of the medians of a triangle is called its centroid. It divides the medians in the raito 2 : 1. If and are the vertices of a triangle, then the coordinates of its centroid are
2. Incentre
The point of intersection of the internal bisectors of the angles of a triangle is called its in-centre. If are the vertices of a triangle ABC such that BC = a, CA = b and AB = c, then the coordinates of its incentre are
.
If the equations of the sides of the triangle are given, then we find the bisectors of internal angles and then their point of intersection to determine the in-centre.
3. Circum-Centre
The point of intersection of the perpendicular bisectors of the sides of a triangle is called its circum-centre. It is equidistant from the vertices of a triangle.
If O is the circumcentre of a triangle ABC, then OA = OB = OC and OA is called the circum-radius.
To find the circum-centre of ΔABC, we use the relation OA = OB = OC. This gives two simultaneous linear equations and their solution provides the coordinate of circumcentre..
4. Ortho-Centre
The point of intersection of the altitudes of a triangle is called its orthocenter. To determine the orthocenter, first we find equations of lines passing through vertices and perpendicular to the opposite sides. Solving any two of these three equations we get the coordinates of orthocenter.
The circumcentre O, centroid G and orthocenter O‘ of a triangle ABC are collinear such that G divides O‘ O in the ratio 2 : 1 i.e., O‘G : OG = 2 : 1.
Illustration -33
If the lines ax + y + 1 = 0, x + by + 1 = 0 and x + y + c = 0 (a, b and c being distinct and different from
1) are concurrent, then prove that .
Solution
Since the given lines are concurrent
Operating C2 → C2 – C2 and C3 → C3 – C1, we get
⇒ a(b – 1) (c – 1) – (b – 1) (1 – a) – (c – 1) (1 – a) = 0
⇒
⇒
⇒ .
9. Concurrency of Three Lines
The condition for 3 lines a1x + b1y + c1 = 0, a2x + b2y + c2 = 0, a3x + b3y + c3 = 0 to be concurrent is
(i)
Alternatively: If three constants A, B & C (not all zero) can be found such that
A(a1x + b1y + c1) + B(a2x + b2y + c2) + C(a3x + b3y + c3) 0, then the three straight lines are concurrent.
(ii) There exists 3 constants l, m, n (not all zero at the same time) such that lL1 + mL2 + nL3 = 0, where l + m + n = 0, where L1 = 0, L2 = 0 and L3 = 0 are the three given straight lines.
(iii) The three lines are concurrent if any one of the lines passes through the point of intersection of the other two lines.
Illustration -34
Prove that the straight lines 4x + 7y = 9, 5x – 8y + 15 = 0 and 9x – y + 6 = 0 are concurrent.
Solution
Given lines are
4x + 7y – 9 = 0 ……..(1)
5x – 8y + 15 = 0 ……..(2)
and 9x – y + 6 = 0 ……..(3)
= 4(–48 + 15) – 7 (30 – 135) – 9 (– 5 + 72) = –132 + 735 – 603 = 0
Hence lines (1), (2) and (3) are concurrent. Proved
10. Distance of a Point From a Line
1. Length of Perpendicular From a Point to a Line
Let length of perpendicular from a point P(x1, y1) to a line ax + by + c = 0 is p then
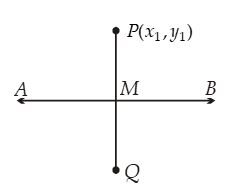
2. Foot of Normal or Perpendicular
The foot of perpendicular or normal from a point P(x1, y1) to a line ax + by + c = 0 is
3. Image of a Point w.r.t. a Line
The image of a point P(x1, y1) w.r.t. a line ax + by + c = 0 is
4. Distance Between two Parallel Lines
Distance between two parallel lines ax + by + c1 = 0 and ax + by + c2 = 0 is .
Illustration -35
Three lines x + 2y + 3 = 0, x + 2y – 7 = 0 and 2x – y – 4 = 0 form 3 sides of two squares. Find the equation of remaining sides of these squares.
Solution
Distance between the two parallel lines is . The equations of sides A and C are of the form 2x – y + k = 0.
Since distance between sides A and B = distance between sides B and C hence
⇒ k = 6, – 14
Hence the fourth sides of the two squares are
(i) 2x – y + 6 = 0, (ii) 2x – y – 14 = 0
Illustration -36
Find the foot of the perpendicular, drawn from the point (2, 3) to the line 3x – 4y + 5 = 0. Also, find the image of (2, 3) in the given line.
Solution
Let AB 3x – 4y + 5 = 0
P (2, 3) and PM AB
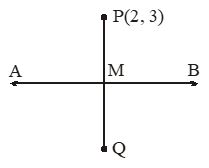
Foot of normal from P (2, 3) to 3x – 4y + 5 = 0 is given by
Image of P (2, 3) on 3x – 4y + 5 = 0 is given by
Illustration -11
The distance between two parallel lines is given as . If the equation of one of the parallel lines is 2x + 3y − 17 = 0, then find the equation of the other line.
Solution
We know that the distance between two parallel lines Ax + By + C1 = 0 and Ax + By + C2 = 0 is given by .
It is given that the required line is parallel to line 2 x + 3y − 17 = 0. Hence, the equation of the required line is 2x + 3y + C = 0.
Therefore, using the given information, we obtain
⇒ 12 = |– 17 – C|
⇒ – 17 – C = 12 or – 17 – C = – 12
⇒ C = –29 or C = –5
Thus, the required equation of the line is 2x + 3y − 29 = 0 or 2x + 3y − 5 = 0.
Illustration -38
The distance of line 4x − 3y + 7 = 0 from a point P that is lying on the x-axis is 3 units. Find the coordinates of point P.
Solution
We know that the perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is given by .
Let the required point P lying on the x-axis be (x’, 0).
Therefore, on using the given information, we obtain
|4x’ + 7| = 3 × 5 = 15
⇒ 4x’ + 7 = – 15 or 4x’ + 7 = 15
⇒ 4x’ = – 22 or 4x’ = 8
⇒ or x’ = 2
Thus, the required point P can be or (2, 0).
Illustration -39
Find the distance between the lines y = 7x + 11 and y = 7x − 5.
Solution
We know that the distance between the parallel lines y = mx + c1 and y = mx + c2 is given by .
Thus, the distance between the given parallel lines is given by
.
Thus, the required distance between the given parallel lines is .
Illustration -40
Find the image of (5, 7) about line x –y + 6 = 0
Solution
Slope of line PP’ = –1
Hence equation of PP’
y – 7 = – 1 (x – 5) ⇒ x + y – 12 = 0
Point of intersect of x + y – 12 = 0 with x – y + 6 = 0 is (3, 9).
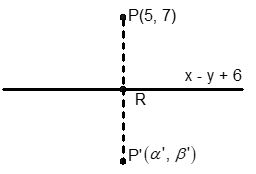
Hence
12. Position of Points Relative to a Line
Let the given line be ax + by + c = 0 and A(x1, y1), B(x2, y2) be two points. If quantities ax1 + by1 + c and ax2 + by2 + c have the same signs, then both the points P and Q lie on the same side of the line ax + by + c = 0. If the quantities ax1 + by1 + c and ax2 + by2 + c have opposite signs, then they lie on the opposite side of the line.
Illustration -41
Find the range of θ in the interval (0, π) such that the point (3, 5) and (sinθ, cosθ) lie on the same side of the line x + y – 1 = 0.
Solution
3 + 5 – 1 = 7 > 0
Illustration -42
Show that (1, 4) and (0, –3) lie on the opposite sides of the line x + 3y + 7 = 0.
Solution
At (1, 4), the value of x + 3y + 7 = 1 + 3(4) + 7 = 20 > 0.
At (0, – 3), the value of x + 3y + 7 = 0 + 3(–3) + 7 = –2 < 0
∴ The points (1, 4) and (0, – 3) are on the opposite sides of the given line
Illustration -43
Find the range of α such that the point (α2, 2α) and (2, 6) lies on the same side of the line x + y –1 = 0.
Solution:
For (2, 6) x + y – 1 = 2 + 6 –1 is + ve. Hence α2 + 2α –1 > 0
⇒ (α + 1)2 – 2 > 0
13. Equations of Bisectors of the angles between the lines
1. Bisectors of The Angles Between Two Given Lines
Locus of a point, which moves such that its distance from two intersecting lines remains same, is called as angle bisector.
Let the two intersecting lines are
a1x + b1y + c1 = 0 … (i)
a2x + b2y + c2 = 0 … (ii)
Then equation of angle bisector of the angles between the lines (i) & (ii) will be
…… (iii)
Above equation gives two angle bisectors.
Note
(i) Angle bisectors of two lines are always mutually perpendicular.
(ii) If the two given lines are not perpendicular i.e., a1a2 + b1b2 ≠ 0 then one of the bisector will be bisector of acute angle and other will be that of obtuse angle.
2. The Bisectors of The Acute and Obtuse Angle
Take one of the lines and let its slope is m1 and take one of the bisectors and let its slope be m2. Then find
(i) If tanθ < 1 then the bisectors taken is the bisector of acute angle and the other will be the bisector of the obtuse angle.
(ii) If tanθ > 1 then the bisectors taken is the bisector of obtuse angle and the other will be the bisector of the acute angle.
3. Equation of The Bisector of The Angle Containing Origin
First make the constants c1 and c2 in both the equations positive then equation gives the equation of bisector of the angle containing origin.
Note
(i) If a1a2 + b1b2 < 0 then the origin lies in acute angle.
(ii) If a1a2 + b1b2 > 0 then the origin lies in obtuse angle.
Hence we can find the equation of bisector of acute angle and obtuse angle directly.
4. Equation of the Bisector of the Angle Which Contains a Given Point
Let the given point is (x1, y1)
(i) If a1x1 + b1y1 + c1 and a2x1 + b2y1 + c2 are of same sign then equation of bisector of angle containing point (x1, y1) is
(ii) If a1x1 + b1y1 + c1 and a2x1 + b2y1 + c2 are of opposite sign then equation of angle containing point (x1, y1) is
Illustration -44
For the straight lines 4x + 3y – 6 = 0 and 5x + 12y + 9 = 0, find the equation of the
(i) Bisector of the obtuse angle between them
(ii) Bisector of the acute angle between them
(iii) Bisector of the angle which contains (0, 0)
(iv) Bisector of the angle which contains (1, 2)
Solution
Equations of bisectors of the angles between the given lines are
⇒ 9x – 7y – 41 = 0 and 7x + 9y – 3 = 0
If θ is the acute angle between the line 4x + 3y – 6 = 0 and the bisector 9x – 7y – 41 = 0, then
Hence
(i) The bisector of the obtuse angle is 9x – 7y – 41 = 0
(ii) The bisector of the acute angle is 7x + 9y – 3 = 0
(iii) The bisector of the angle containing the origin
⇒ 7x + 9y – 3 = 0
(iv) For the point (1, 2), 4x + 3y – 6 = 4 × 1 + 3 × 2 – 6 > 0
5x + 12y + 9 = 12 × 2 + 9 > 0
Hence equation of the bisector of the angle containing the point (1, 2) is
⇒ 9x – 7y – 41 = 0
Alternative:
Making C1 and C2 positive in the given equations, we get – 4x – 3y + 6 = 0 and 5x + 12y + 9 = 0 Since a1a2 + b1b2 = – 20 – 36 = – 56 < 0,
So the origin will lie in the acute angle. Hence bisector of the acute angle is given by
i.e., 9x – 7y – 41 = 0
Similarly bisector of obtuse angle is 7x + 9y – 3 = 0
5. The ratio in which a given line divides the line segment joining two points:
Let the given line ax + by + c = 0 divide the line segment joining A(x1, y1) & B(x2, y2) in the ratio m : n, then .
If A & B are on the same side of the given line then m/n is negative but if A & B are on opposite sides of the given line, then m/n is positive
Illustration -45
Find the ratio in which the line joining the points A (1, 2) and B(– 3, 4) is divided by the line x + y – 5 = 0.
Solution
Let the line x + y = 5 divides AB in the ratio k : 1 at P
∴ coordinate of P are
Since P lies on x + y – 5 = 0
∴ Required ratio is 1 : 2 externally
Aliter Let the ratio is m : n
∴ ratio is 1 : 2 externally
14. Family of Straight lines
If L1 = 0 and L2 = 0 are two given lines then family of lines through the point of intersection of the two given lines is L1 + λL2 = 0.
One Parameter Family of Straight Line
If a linear expression L1 contains an unknown coefficient, then the line L1 = 0 can not be a fixed line. Rather it represents a family of straight lines known as one parameter family of straight lines, e.g. family of lines parallel to the x-axis i.e., y = C and family of straight lines passing through the origin i.e., y = mx.
Each member of the family passes throu43gh a fixed point. We have two methods to find the fixed point.
Method I
If a family of straight lines can be written as L1 + λL2 = 0, where L1, L2 are two fixed lines and λ is a parameter then each member of it will pass through a fixed point given by point of intersection of L1 = 0 and L2 = 0.
Method II
Let the family of straight lines be of the form ax + by + c = 0 where a, b, c are variable parameters satisfying the condition al + bm + cn = 0, where l, m, n are given and n ≠ 0.
Rewriting the condition as , and comparing with the given family of straight lines, we find that each member of it passes through the fixed point .
Note: If L1 = 0 and L2 = 0 are parallel lines, they will meet at infinity.
Illustration -46
Find the equation of the straight line passing through the point (2, 0) and through the point of intersection of the lines x + 2y = 3 and 2x – 3y = 4.
Solution
Equation of any straight line passing through the intersection of the lines
x + 2y = 3 and 2x – 3y – 4 = 0 is
λ(x + 2y – 3) + (2x – 3y – 4) = 4 … (i)
Since it passes through the point (2, 0)
∴ λ(2 + 0 – 3) + (4 – 0 – 4) = 0
i.e., λ = 0
Now substituting this value of λ in (i) we get
2x – 3y – 4 = 0 as the equation of the required line
Illustration -47
If the algebraic sum of perpendiculars from n given points on a variable straight line is zero then prove that the variable straight line passes through a fixed point.
Solution
Let n given points be (xi, yi) where i = 1, 2, … n and the variable straight line is ax + by + c = 0. Given that
Hence the variable straight line always passes through the fixed point .
Illustration 48
Prove that each member of the family of straight lines (3 sinθ + 4 cosθ) x + (2 sinθ – 7 cosθ) y + (sinθ + 2 cosθ) = 0 (θ is a parameter) passes through a fixed point.
Solution
The given family of straight lines can be rewritten as
(3x + 2y + 1) sinθ + (4x – 7y + 2) cosθ = 0
or (4x – 7y + 2) + tanθ (3x + 2y + 1) = 0
which is of the form L1 + λL2 = 0
Hence each member of it will pass through a fixed point which is the intersection of 4x – 7y + 2 = 0
and 3x + 2y + 1 = 0 i.e., .
Illustration -49
Find the equation of the straight line which passes through the point (2, –3) and the point of intersection of the lines x + y + 4 = 0 and 3x – y – 8 = 0.
Solution
Any line through the intersection of the lines x + y + 4 = 0 and 3x – y – 8 =0 has the equation (x + y + 4) + λ (3x – y – 8) = 0 ………(i)
This will pass through (2, –3) if
(2 – 3 + 4) + λ (6 + 3 – 8) = 0 or 3 + λ = 0
⇒ λ = – 3.
Putting the value of λ in (i), the required line is (x + y + 4) + (–3) (3x – y – 8) = 0
or – 8x + 4y + 28 = 0 or 2x – y – 7 = 0
Illustration -50
Obtain the equations of the lines passing through the intersection of lines 4x – 3y – 1 = 0 and 2x – 5y + 3 = 0 and equally inclined to the axes.
Solution
The equation of any line through the intersection of the given lines is
(4x – 3y – 1) + λ (2x – 5y + 3) = 0
or x (2λ + 4) – y (5λ + 3) + 3λ – 1 = 0 …….(i)
Let m be the slope of this line. Then m =
As the line is equally inclined with the axes, therefore
m = tan 45º of m = tan 135º ⇒ m = ±1, , putting the values of λ in (i), we get 2x + 2y – 4 = 0 and 14x – 14y = 0
i.e. x + y – 2 = 0 and x = y as the equations of the required lines.
Illustration 51
Find the equation of the straight line which belongs to both of the following family of lines 5x + 3y – 2 + λ1 (3x – y – 4) = 0 and x – y + 1 + λ2 (2x – y – 2) = 0
Solution
Lines of first family are concurrent at (1, -1) and that of second at (3, 4)
∴ Required line passes through both of these points
∴ Equation is 5x – 2y – 7 = 0
Illustration -52
If a, b and c are three consecutive odd integers then prove that the variable line ax + by + c = 0 always passes through (1, –2).
Solution
Since a, b and c are three consecutive odd integers, these must be in form of 2n + 1, 2n +3 and 2n + 5 respectively where n∈I. The given line can be written as (2n + 1)x + (2n +3)y + (2n + 5) = 0
⇒ n/2 (x + y + 1) + (x + 3y + 5) = 0.
Now we can say this will represent a family of line passing through the point of intersection x + y + 1 = 0 and x + 3y + 5 = 0, which is (1, -2)
Illustration -53
The base BC of ΔABC is bisected at (p, q) and equation of sides AB and AC are px + qy = 1 and qx + py = 1.
Then show that the equation of median through A is ( px + qy –1) – .
Solution
Any line through A is given by (px + qy – 1) + λ(qx + py – 1) = 0.
If this line represent the median through A then this will be passing through (p, q).
Hence λ = .
Thus the required line is (px + qy –1) –
15. Pair of Straight Lines
A rational integral algebraic equation in two variables x and y is said to be a homogeneous equation of second degree, if the sum of indices of x and y in each term is 2.
Thus the equation ax2 + 2hxy + by2 = 0 represents pair of straight line passing through origin.
Proof: We can write ax2 + 2hxy + by2 = 0
as …(i)
which is a quadratic equation in
Thus
Thus the equations are of the form y = and y = representing straight lines passing through origin.
1. The value of m1 and m2 are real and distinct if h2 > ab
2. The value of m1 and m2 are real and coincident if h2 = ab
3. The value of m1 and m2 are imaginary if h2 < ab
Angle between pair of lines given by ax2 + 2hxy + by2 = 0. Let ‘θ’ be the angle between the lines, then from equation
…(a)
…(b)
We know,
Note:
(i) If the lines are parallel (coincident) i.e. θ = 0°, then h2 = ab
(ii) If the lines are perpendicular i.e. θ = 90°, then a + b = 0.
1. Bisector of Angles Between the Lines
Let y – m1x = 0 and y – m2x = 0 be the lines represented by ax2 + 2hxy + by2 = 0, then .
Since bisector of the angles between two lines are the locus of a point which is equidistant from the two given lines. Then,
Let P (h, k) be a point on a bisector of the angle between the given lines. Then, PM = PN.
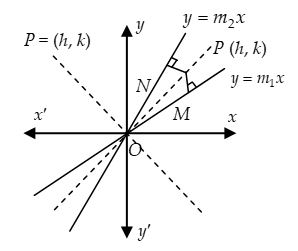
The joint equation of the two bisector is
⇒ (m1 + m2) (x2 – y2) = 2xy (1 – m1m2)
⇒ or hx2 – hy2 = (a – b)xy
Note:
Co-efficient of x2 + coefficient of y2 = 0. Thus the bisectors of the angle between the lines are perpendicular to each other.
2. General Equation of Second Degree
An equation of the form ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 where a,b, c, f, g, h are constants is said to be general equation of second degree in x and y.
Condition for General Equation to Represent pair of Straight Lines
The necessary and sufficient condition for ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 to represent pair of straight lines is that
Δ = abc + 2fgh – af2 – bg2 – ch2 =
Point of Intersection of Pair of Straight Lines Given by General Equation
The point of intersection of the lines represented by the equation
U: ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 …(i)
is given by
…(ii)
…(iii)
where the roots of gives x co-ordinates of the point of intersection and the roots of gives y co-ordinates of the point of intersection of the lines.
3. Angle Between Lines
Let y = m1x + c1 and y = m2x + c2 be the lines represented by general equation of second degree. Then ax2 + 2hxy + by2 + 2gx + 2fy + c = (y – m1x – c1) (y – m2x – c2) = 0.
Comparing co-efficient, we get
⇒ m1 + m2 = and m1m2 =
Let θ be the angle between the lines.
Thus
Note:
(i) The lines are parallel if h2 = ab
(ii) The lines are perpendicular if a + b = 0
4. Equation of Bisector of Angles Between the Lines
Let P(x1, y1) be the point of intersection of the lines and (x, y) be the moving point of the shifting of origin
Then equation of bisector is given by
5. Homogenization of General Equation
Let the curve be ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 …(i)
and the line be lx + my + n = 0 … (ii)
Then the lines joining origin to the point of intersection of curve and line is obtained by homogenizing the equation of curve.
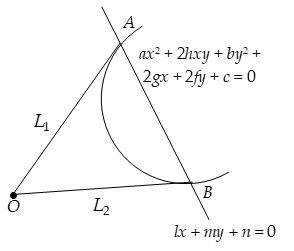
As lx + my + n = 0 …(iii)
Equation (i) can be written as
ax2 + 2hxy + by2 + 2gx . 1 + 2 fy . 1 + c . 12 = 0
Thus
ax2 + 2hxy + by2 + 2gx
represents the lines from origin to point of intersection of curve and the given lines.
Illustration -54
Prove that the equations to the straight lines passing through the origin and making an angle with the straight line y + x = 0 are given by x2 + 2xy sec 2α + y2 = 0.
Solution
Let y = mx be the equation of the straight line passing through the origin and making angle α with y + x = 0. Now, slope of line y + x = 0 is – 1.
[squaring]
or m2 (1 – tan2 α) + 2m (1 + tan2 α) + (1 – tan2 α) = 0
This is a quadratic equation in m, therefore there will be two values of x and hence two straight lines which make an angle α with y + x = 0. Let the two values of m be m1 and m2, then
Now the join equation of the straight line passing through the origin and making an angle α with y + x = 0 is
(y – m1x) (y – m2x) = 0
or y2 – xy(m1 + m2) + m1m2x2 = 0 or y2 + 2xy sec 2α + x2 = 0
Illustration -55
Discuss the nature of the lines represented by the equation
(i) 2x2 – 5xy + 2y2 + 4x – 5y + 2 = 0
(ii) 2x2 + 2xy + y2 + 6x + 2y + 5 = 0
(iii) x2 + 2xy + y2 + 12 = 0
Solution
It is easy to see that in each case Δ = 0.
In (i) h2 – ab > 0, hence (i) represents a pair of interesting lines.
In (ii) h2 – ab < 0, thus (ii) represents a pair of imaginary lines.
In (iii) h2 – ab = 0 and f2 – bc < 0. Thus a pair of imaginary lines.
Illustration -56
Show that the equation 6x2 – 5xy + y2 = 0 represents a pair of distinct straight lines, each passing through the origin. Find the separate equations of these lines.
Solution
The given equation is a homogeneous equation of second degree. So, it represents a pair of straight lines passing through the origin. Comparing the given equation with ax2 + 2hxy + by2 = 0, we obtain a = 6, b = 1 and 2h = – 5.
⇒ h2 > ab
Hence, the given equation represents a pair of distinct lines passing through the origin.
Now, 6x2 – 5xy + y2 = 0
⇒ y – 3x = 0 or y – 2x = 0
So the given equation represents the straight lines y – 3x = 0 and y – 2x = 0
Illustration -57
Find the equations to the pair of lines through the origin which are perpendicular to the lines represented by 2x2 – 7xy + 2y2 = 0.
Solution
We have 2x2 – 7xy + 2y2 = 0.
⇒ 2x2 – 6xy – xy + 3y2 = 0
⇒ 2x(x – 3y) – y (x – 3y) = 0
⇒ (x – 3y) (2x – y) = 0
⇒ x – 3y = 0 or 2x – y = 0
Thus the given equation represents the lines x – 3y = 0 and 2x – y = 0. The equations of the lines passing through the origin and perpendicular to the given lines are y – 0 = –3 (x – 0) and y – 0 = – (x – 0) [ ∵ (Slope of x – 3 y = 0) is 1/3 and (Slope of 2x – y = 0) is 2]
⇒ y + 3x = 0 and 2y + x = 0
Illustration -58
Find the angle between the pair of straight lines 4x2 + 24xy + 11y2 = 0
Solution
Given equation is 4x2 + 24xy + 11y2 = 0
Here a = coeff. of x2 = 4, b = coeff. of y2 = 11
and 2h = coeff. of xy = 24 ∴ h = 12
Now tanθ =
Where θ is the acute angle between the lines.
∴ acute angle between the lines is and obtuse angle between them is π –
Illustration -59
Find the equation of the bisectors of the angle between the lines represented by 3x2 – 5xy + y2 = 0
Solution
Given equation is 3x2 – 5xy + y2 = 0 …….(1)
comparing it with the equation ax2 + 2hxy + by2 = 0 …….(2)
we have a = 3, 2h = –5; and b = 4
Now the equation of the bisectors of the angle between the pair of lines (1) is
or ;
or ; or 5x2 – 2xy – 5y2 = 0
Illustration -60
Prove that the equation 2x2 + 5xy + 3y2 + 6x + 7y + 4 = 0 represents a pair of straight lines. Find the co-ordinates of their point of intersection and also the angle between them.
Solution
Given equation is 2x2 + 5xy + 2y2 + 6x + 7y + 4 = 0
Writing the equation (1) as a quadratic equation in x we have
2x2 + (5y + 6) x + 3y2 + 7y + 4 = 0
or 4x + 4y + 4 = 0 and 4x + 6y + 8 = 0
or x + y + 1 = 0 and 2x + 3y + 4 = 0
Hence equation (1) represents a pair of straight lines whose equation are x + y + 1 = 0 …..(1) and 2x + 3y + 4 = 0 ………(2)
Solving these two equations, the required point of intersection is (1, – 2)
Illustration -61
Prove that the angle between the lines joining the origin to the points of intersection of the straight line y = 3x + 2 with the curve x2 + 2xy + 3y2 + 4x + 8y – 11 = 0 is .
Solution
Equation of the given curve is x2 + 2xy + 3y2 + 4x + 8y – 11 = 0
and equation of the given straight line is y – 3x = 2
Making equation (1) homogeneous equation of the second degree in x any y with the help of (1), we have
x2 + 2xy + 3y2 + = 0
or x2 + 2xy + 3y2 + (4xy + 8y2 – 12x2 – 24xy) – (y2 – 6xy + 9x2) = 0
or 4x2 + 8xy + 12y2 + 2(8y2 – 12x2 – 20xy) – 11 (y2 – 6xy + 9x2) = 0
or –119x2 + 34xy + 17y2 = 0 or 119x2 – 34xy – 17y2 = 0
or 7x2 – 2xy – y2 = 0
This is the equation of the lines joining the origin to the points of intersection of (1) and (2).
Comparing equation (3) with the equation ax2 + 2hxy + by2 = 0
we have a = 7, b = –1 and 2h = –2 i.e. h = –1
If θ be the acute angle between pair of lines (3), then
Illustration -62
If the lines joining origin to the points of intersection of the curve 2x2 + 3y2 + m = 0 and the line y = 2x + 3 are perpendicular, then find the value of m.
Solution
Homogenise the given curve with line, we get the required line
Since, the lines are perpendicular
⇒ Coefficient of x2 + coefficient of y2 = 0
⇒ m = -9
Illustration -63
Find the value of unknowns for which the given equation represents two coincident lines x2 + 9y2 + pxy + qx + ry + 1 = 0.
Solution
Let the line is ax + by + c = 0
Equation of pair of lines
(ax + by + c)2 = 0
a2x2 + 2abxy + b2y2 + 2acx + 2bcy + c2 = 0
Comparing this with given equation
a2 = 1
a = 1
b2 = 9
b = 3
c2 = 1 c = 1
∴ p = 2ab = 6
q = 2ac = 2
r = 2bc = 6
16. miscellaneous Concepts and problems
1. Reflection on the surface
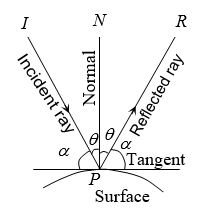
Here, IP = Incident Ray
PN = Normal to the surface
PR = Reflected Ray
Then,
Angle of incidence = Angle of reflection
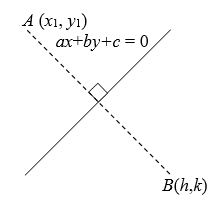
2. Image of a point in different cases
(1) The image of a point with respect to the line mirror The image of with respect to the line mirror ax+by+c=0 be B (h, k) is given by,
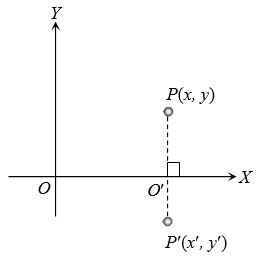
(2) The image of a point with respect to x-axis : Let P(x, y) be any point and P'(x’, y’) its image after reflection in the x-axis, then x’ = x, y’ = – y, (∵ O’ is the mid-point of P and P’)
(3) The image of a point with respect to y-axis : Let P(x,y) be any point and P'(x’, y’) its image after reflection in the y-axis, then x’ = -x, y’ = y,
(∵ O’ is the mid- point of P and P’)
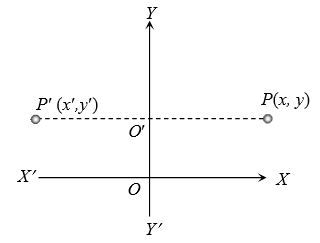
(4) The image of a point with respect to the origin : Let P(x, y) be any point and P'(x’, y’) be its image after reflection through the origin, then x’=-x, y’=-y
(∵ O is the mid- point of P, P’).
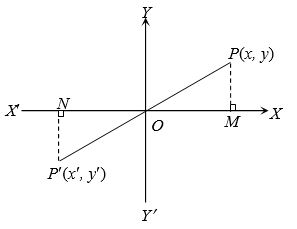
(5) The image of a point with respect to the line y = x : Let P(x,y) be any point and P'(x’, y’) be its image after reflection in the line y=x, then x’=y, y’=x
(∵ O’ is the mid point of P and P’).
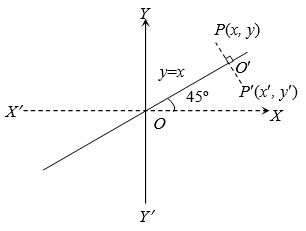
(6) The image of a point with respect to the line y = x tanθ : Let P(x,y) be any point and P'(x’,y’) be its image after reflection in the line y = x tanθ, then
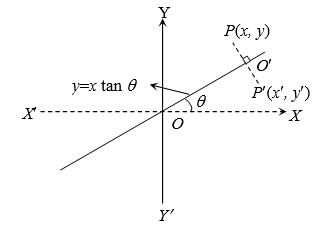
x’ = xcos2θ+ysin2θ
y’ = xsin2θ-ysin2θ, (∵ O’ is the mid- point of P and P’)