LINEAR INEQUATIONS
The mathematical expressions (a>b) or (a<b) are used to compare the two real numbers a and b i.e. it implies that ‘a is greater than b’ or ‘a is smaller than b’ respectively.
1. GENERAL RULES
(i) implies that a is greater than or equals to b.
(ii) If a > b ⇒ a+c > b+c
(iii) If a > b ⇒ a-c > b-c
(iv) If
(v) If a > b ⇒ ka > kb or , where .
(vi) If a > b ⇒ ka < kb or , where
Illustration-1:
Solve x < 7 for the following cases
(a) x ∈ I (b) x ∈ N (c) x ∈ R
Solution: (a) x ∈ I
In this case x = {…..-2, -1, 0, 1, 2, 3,…..6}
![]()
The infinite solutions are represented by dots
(b) x < 7, x ∈ N
In this case x = {1,2,3,4,5,6}
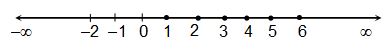
The finite solutions are represented by dots.
(c) x < 7, x ∈ R

The infinite solutions are represented by a dark line as shown. A circle over 7 indicates that point 7 is not included in the solution .
Illustration2-:
Solve .
Solution:
Rule-3
or Rule-2
or Rule-6
![]()
2. SOLUTION OF SYSTEM OF LINEAR INEQUATIONS IN ONE VARIABLE
System of linear inequations consists of more than one linear inequations. To solve a system, we first solve each linear inequation separately and then look for the common values of the variable satisfying each of the linear inequations.
Illustration-3:
Solve the following system of inequations:
Solution:
2x-3 > x+1
⇒ x > 4 …(i)
Also,
…(ii)
The common solution of equations (i) and (ii) is x > 4 as required x is such that it is greater than or equal to –1 as well as greater than 4 ⇒ x > 4
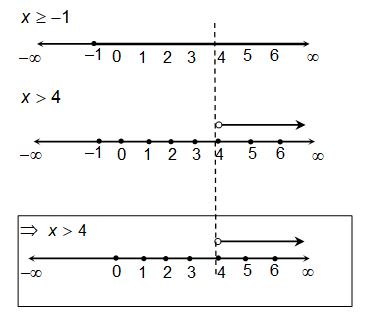
Illustration-4:
Solve: .
Solution:
Consider
Separately,
Similarly,
Common values of x are such that
Graphically,
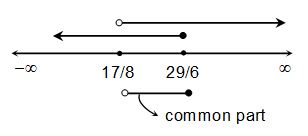
Alternate:
Multiplying the inequation by 12,
3. GRAPHICAL SOLUTION OF LINEAR INEQUATIONS IN TWO VARIABLES
Any linear inequation in two variable is of the form or . The graphical solution of the inequations will be discussed assuming x, y to be real numbers.
Illustration-5:
Solve graphically.
Solution:
First consider .
This is equation of a straight line which divides the coordinate plane in two half planes. Since inequation doesn’t involve the sign of equality, so we will draw this line dotted or broken.
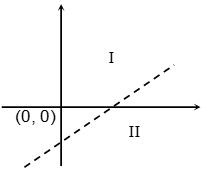
Now, consider any point which doesn’t lie on this line, i.e. doesn’t satisfy the equation for Illustration- take (0, 0) and check whether this point satisfies the inequation
or not.
⇒ false statement.
Since (0, 0) is a point lying in the plane I and it doesn’t satisfy the inequation, hence half plane II will be the required solution. This region is called solution region and it is shaded as shown:
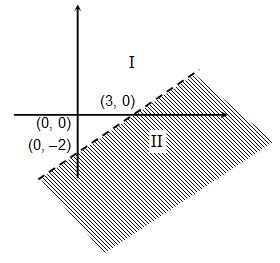
Illustration-6:
Solve graphically.
Solution:
Draw a continuous line corresponding to y = 2
Putting y = 0 in the inequation
False statement
Which implies that I is the solution region.
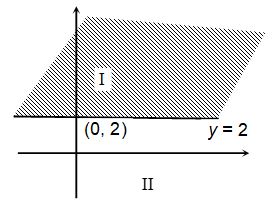
4. SOLUTIONS OF SYSTEM OF LINEAR INEQUATIONS IN TWO VARIABLES
Illustration-7:
Solve the following system of linear inequations graphically
Solution:
Obtain the graphical solution for each of the inequations on the same set of axis and shade them. Thus obtained double shaded region is the required solution region.
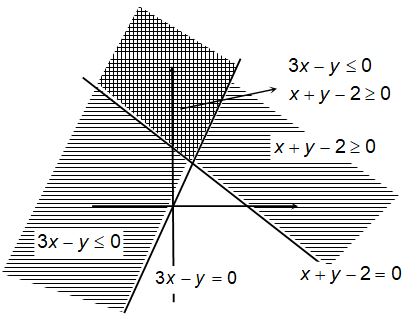
Illustration-8:
Find the linear inequations for which the shaded area in the given figure is the solution set.
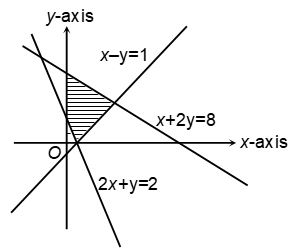
Solution:
The shaded area is bounded by the lines
Line (i) : The shaded area and the origin lies on the same side of .
∴ The corresponding inequation is because 0+2(0) = 0<8
Line (ii) : The shaded area and the origin lies on the same side of .
∴ The corresponding inequation is because 0 – 0 = 0 < 1
Line (iii) : The shaded area and the origin lies on the opposite sides of 2x+y = 2.
∴ The corresponding inequation is , because 2(0) + 0 = 0 < 2
Line (iv) : The shaded area lies on the right of x = 0.
∴ The corresponding inequation is
The required system of inequations is








