Relations and Functions

1. CARTESIAN PRODUCT OF SETS

Ordered pair

Let A and B are any two non-empty sets. If and then (a, b) is called and ordered pair. a is called the first component (first coordinate) and b is called the second component (second coordinate) of the ordered pair (a, b).

Cartesian product of sets

The Cartesian product (also known as the cross product) of two sets A and B, denoted by A´B (in the same order) is the set of all ordered pairs (x, y) such that x∈A and y∈B. What we mean by ordered pair is that the pair(a, b) is not the same the pair as (b, a) unless a = b. It implies that A⨯B ≠ B⨯A in general. Also if A contains m elements and B contains n elements then A⨯B contains m⨯n elements. Similarly we can define A⨯A = {(x, y); x∈A and y∈A}. We can also define cartesian product of more than two sets.

e.g.  A₁⨯ A₂⨯A₃ ⨯ . . . .⨯ A_n = {(a₁, a₂, . . . , a_n): a₁ ∈ A₁, a₂ ∈ A₂, . . . , a_n ∈ A_n}

Illustration -1

If A ={a, b, c} and B = {b, c, d} then evaluate

(i). A⋃B ,  A⋂B , A-B and B-A

(ii). A⨯B and B⨯A

Solution

(i) A⋃B = {x: x∈A or x∈B} = {a, b, c, d}

     A⋂B = {x: x∈A and x∈B} = {b, c}

     A-B = {x: x∈A and x∉B} = {a}

     B-A = {x: x∈B and x∉B} = {d}

(ii) A⨯B = {(x, y): x∈A and y∈B} = {(a, b), (a, c), (a, d), (b, b), (b, c), (b, d), (c, b), (c, c), (c, d)}

B⨯A = {(x, y):  x∈B and y∈A}

= {(b, a), (b, b), (b, c),(c, a), (c, b), (c, c),(d, a), (d, b), (d, c)}

Note that A⨯B ≠ B⨯A.

Properties of cartesian product

Theorem 1 : For any three sets A, B, C

(i)  A × (B ⋃ C) =(A × B) ⋃ (A × C)

(ii) A × (B ⋂ C) =(A × B) ⋂ (A × C)

Theorem 2 : For any three sets A, B, C

A × (B – C) = (A × B) – (A × C)

Theorem 3 :  If A and B are any two non-empty sets, then

A × B = B × A $\iff$ A = B

Theorem 4 :  If A ⊆ B, then A × A ⊆ (A × B) ⋂ (B × A)

Theorem 5 :  If A ⊆ B, then A × C ⊆ B × C for any set C.

Theorem 6 :  If A ⊆ B and C ⊆ D, then A × C ⊆ B × D

Theorem 7 :  For any sets A, B, C, D

(A × B) ⋂ (C × D) = (A ⋂ C) × (B ⋂ D)

Theorem 8 :  For any three sets A, B, C

(i)  A × (B‘ ⋃ C‘)’ = (A × B) ⋂ (A × C)

(ii) A × (B‘ ⋂ C‘)’ = (A × B) ⋃ (A × C)

Number of elements in the cartesian product of two finite sets

Illustration -2

If A = {1,2}, B = {a, b} then find A × B & B × A .

Solution

$\begin{array}{l}A\times B=\left\{\right(1,a),(1,b),(2,a),(2,b\left)\right\}\\ B\times A=\left\{\right(a,1),(b,1),(a,2),(b,2\left)\right\}\end{array}$

2. RELATION

Let A and B be two non-empty sets, then every subset of A × B defines a relation from A to B and every relation from A to B is a subset of A × B.

Let $R\subseteq A\times B$ and (a, b) ∈ R. Then we say that a is related to b by the relation R and write it as aRb. If (a,b)∈R, we write it as aRb.

Example : Let A {1, 2, 3, 4, 5}, B = {1, 3}

We set a relation from A to B as: a R b iff $\mathrm{a}\le \mathrm{b}; \mathrm{a}\in \mathrm{A}, \mathrm{b}\in \mathrm{B}$. Then

R ={(1, 1), (1, 3), (2, 3), (3, 3)}$\subset$A⨯B

Representation of relation

Roster Form

In this method of describing a relation, all the ordered pairs which satisfying the formula given in the relation are listed. Let’s understand this method by an example.

If A = {5, 2, 1} write the following relations of A × A in the Roster form.

a) B is the relation “is greater than”

b) C is the relation “is less than”

Given A = {5, 2, 1}

A × A = {(5, 5), (5, 2), (5, 1), (2, 2), (2, 5), (2, 1),   (1,1), (1, 5), (1, 2)}

a) B  is the relation is greater than.

∴ B = {(5, 2), (5, 1), (2, 1)}

b) C is the relation is less than

∴ C = {(1, 2), (1, 5), (2, 5)}

Set-Builder Form

In this method, the property connecting the first coordinate and the second co-ordinate of every ordered pair of the relation is stated. Let’s understand this method by an example.

If A = {6, 3, 1} write the following relations of A × A in the set-builder form.

a) B is the relation “is greater than”

b) C is the relation “is less than”

Given A = {6, 3, 1}

A × A = {(6, 6), (6, 3), (6, 1), (3, 3), (3, 6), (3, 1), (1, 1), (1, 6), (1, 3)}

a) B = {(6, 3), (3, 1), (6, 1)

= {(x, y) / (x, y) ∈ A × A, x > y}

b) C = {(1, 3), (3, 6), (1, 6)} = {(x, y)/(x, y) ∈ A × A, y > x}

Representation of Arrow Diagram and Tree Diagram

Arrow Diagram

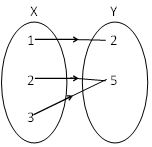
Let the relation from X to Y be described as {(1, 2) (2, 5), (3, 5)}; then it can be represented in the form of arrow diagram as follows:

Tree diagram

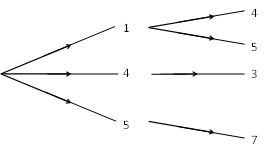
If the relation between two sets is described as {(1, 4) (1, 5), (4, 3) (5, 7)} It can be represented in the form of tree diagram as shown in below.

Graphical Representation of A × B

Let’s see this method of describing a relation by an example.

Let A = {1, 2, 3, 4} B = {2, 3, 4} be two sets.

Now, let’s represent A × B in a graph.

i) Draw two lines, one horizontal and other vertical, which are perpendicular to each other, denote 1, 2, 3…. on the horizontal and vertical lines.

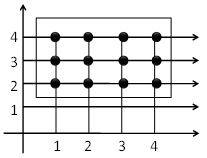
ii) Now, A × B = {(1, 2) (1, 3) (1, 4) (2, 2) (2, 3) (2, 4) (3, 2) (3, 3) (3, 4) (4, 2),(4, 3) (4, 4)}

iii) The intersecting point of the vertical line from point 1 and horizontal line from point 2 is denoted as (1, 2).

iv) Similarly, the intersecting point of the vertical line from point 1 and the horizontal line from point 3 is denoted as (1, 3).

v) The set of points so obtained is called the graph of A × B.

Number of relations

Let A and B be two non-empty finite sets consisting of m and n elements respectively. Then A × B consists of mn ordered pairs. So, total number of subset of A × B is 2^mn. Since each subset of A × B defines relation from A to B, so total number of relations from A to B is 2^mn. Among these 2^mn relations the void relation f and the universal relation A × B are trivial relations from A to B.

Domain and range of a relation

Let R be a relation from a set A to a set B. Then the set of all first components or coordinates of the ordered pairs belonging to R is called the domain of R, while the set of all second components or coordinates of the ordered pairs in R is called the range of R.

Thus, Dom (R) = {a : (a, b) ∈ R} and Range (R) = {b : (a, b) ∈ R}.

Inverse relation

Let A, B be two sets and let R be a relation from a set A to a set B. Then  the inverse of R, denoted by R^–1, is a relation from B to A and is defined by $R^{–1}=\left\{\right(b,a):(a,b)\in R\}$

Clearly (a, b) ∈ R $\iff$ (b, a) ∈ R^–1. Also, Dom (R) = Range  and Range (R) = Dom

Example :  Let A = {a, b, c}, B = {1, 2, 3} and R = {(a, 1), (a, 3), (b, 3), (c, 3)}.

Then,  (i)  R^–1 = {(1, a), (3, a), (3, b), (3, c)}

(ii)  Dom (R) = {a, b, c} = Range $\left(R^{–1}\right)$

(iii)  Range (R) = {1, 3} = Dom $\left(R^{–1}\right)$

Illustration -3

Relation between the sets P and Q. Write this relation (i) in set-builder form, (ii) in roster form. What is its domain and range?

Solution

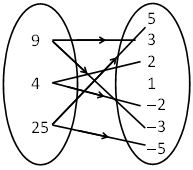
It is obvious that the relation R is “x is the square of y”.

(i) In set-builder form, R = {(x, y): x is the square of y, x ∈ P, y ∈ Q}

(ii) In roster form, R = {(9, 3), (9, –3), (4, 2), (4, –2), (25, 5), (25, –5)}

The domain of this relation is {4, 9, 25}.

The range of this relation is {– 2, 2, –3, 3, –5, 5}.

Note that the element 1 is not related to any element in set P.

The set Q is the codomain of this relation.

Note

The total number of relations that can be defined from a set A to a set B is the number of possible subsets of A × B. If n(A ) =  p and n(B) = q, then n (A × B) = pq and the total number of relations is 2pq.

Illustration -4

Let A = {1, 2} and B = {3, 4}. Find the number of relations from A to B.

Solution

We have, A × B = {(1, 3), (1, 4), (2, 3), (2, 4)}.

Since n (A × B) = 4, the number of subsets of A×B is 24. Therefore, the number of relations from A into B will be 2⁴.

Remark

A relation R from A to A is also stated as a relation on A.

Illustration -5

If R = {(2, 3), (2, 4), (3, 4), (4, 3), (3, 2), (4, 2)} Is a relation in A = {2, 3, 4}. Find R^–1.

Solution

^–1 = {(3, 2), (4, 2), (4, 3), (3, 4), (2, 3), (2, 4)}

Observe that R = R^–1.

3. TYPES OF RELATIONS

1. Void relation

The relation having no ordered pairs is called a void relation and is denoted by $\varphi$

2. Universal relation

Let A be a set then

A×A is called universal relation on A

Note: The void and the universal relations on a set A are respectively the smallest and the largest relations on A.

Example : If A = {1, 2} then universal relation in A is A×A{(1,1),(1,2), (2,1), (2,2)} 

3. Identity Relation

Let A be a set. Then the relation I_A = {(a, a) : a ∈ A} on A is called the identity relation on A.

In other words, a relation I_A on A is called the identity relation if every element of A is related to   itself only. Every identity relation will be reflexive, symmetric and transitive.

Example : On the set = {1, 2, 3}, R = {(1, 1), (2, 2), (3, 3)} is the identity relation on A.

It is interesting to note that every identity relation is reflexive but every reflexive relation need not be an identity relation.

4. Reflexive relation

A relation R on a set A is said to be reflexive if every element of A is related to itself. Thus, R is reflexive $\iff$ (a, a) ∈ R for all a ∈ A.

Example : Let A = {1, 2, 3} and R = {(1, 1); (1, 3)}

Then R is not reflexive since 3∈A but (3, 3) ∉ R

A reflexive relation on A  is not necessarily the identity relation on A.

The universal relation on a non-void set A is reflexive.

5. Symmetric relation

A relation R on a set A is said to be a symmetric relation iff (a, b) ∈ R $\Rightarrow$ (b, a) ∈ R for all a, b ∈ A

i.e.,       aRb $\Rightarrow$ bRa for all a, b ∈ A.

it should be noted that R  is symmetric iff R^–1 = R.

The identity and the universal relations on a non-void set are symmetric relations.

A reflexive relation on a set A  is not necessarily symmetric.

Example : Let A = {1, 2, 3}, then R = {(1, 1), (1, 3), (3, 1)} is symmetric.

6. Anti-symmetric relation

Let A be any set. A relation R on set A is said to be an anti-symmetric relation iff (a, b) ∈ R and (b, a) ∈ R $\Rightarrow$ a = b for all a, b ∈ A.

Thus, if a ≠ b then a may be related to b or b may be related to a, but never both.

Example: Let N be the set of natural numbers. A relation R ⊆ N ⨯ N is defined by x R y iff x divides y (i.e. x/y)

Then x R y, y R x $\Rightarrow$ x divides y, y divides x $\Rightarrow$ x = y

7. Transitive relation

Let A be any set. A relation R on set A is said to be a transitive relation iff (a, b) ∈ R and (b, c) ∈ R $\Rightarrow$ (a, c) ∈ R for all a, b, c ∈ A i.e.,  aRb and bRc $\Rightarrow$ aRc for all a, b, c Î A. Transitivity fails only when there exists a, b, c such that a R b, b R c but a R c.

Example : Consider the set A = {1, 2, 3} and the relations

$R_1$ = {(1, 2),(1,3)}; $R_2$ = {(1, 2)}; $R_3$ = {(1, 1)};

$R_4$= {(1, 2), (2, 1), (1, 1)}

Then $R_1, R_2, R_3$  are transitive while $R_4$ is not transitive since in $R_4,(2,1)\in R_4;(1,2)\in R_4$ but $\left(2,2\right)\notin R_4$ .

The identity and the universal relations on a non-void sets are transitive.

Note:

It is interesting to note that every identity relation is reflexive but every reflexive relation need not be an identity relation. Also identity relation is reflexive, symmetric and transitive.

8. Equivalence relation

A relation R on a set A is said to be an equivalence relation on A iff

(i) It is reflexive i.e. (a, a) ∈ R for all a ∈ A

(ii) It is symmetric i.e. (a, b) ∈ R $\Rightarrow$ (b, a) ∈ R, for all a, b ∈ A

(iii) It is transitive i.e. (a, b) ∈ R and (b, c) ∈ R $\Rightarrow$ (a, c) ∈ R for all a, b, c ∈ A.

Equivalence classes of an equivalence relation

Let R be equivalence relation in $A\left(\ne \varphi \right)$. Let a ∈ A. Then the equivalence class of a, denoted by [a] or $\left\{\overline{a}\right\}$  is defined as the set of all those points of A which are related to a under the relation R. Thus [a] = {x ∈ A : x R a}.

It is easy to see that

(1) $\mathrm{b}\in \left[\mathrm{a}\right]\Rightarrow \mathrm{a}\in \left[\mathrm{b}\right]$

(2) $\mathrm{b}\in \left[\mathrm{a}\right]\Rightarrow \left[\mathrm{a}\right]=\left[\mathrm{b}\right]$

(3) Two equivalence classes are either disjoint or identical.

Congruence modulo (m) :

Let m be an arbitrary but fixed integer. Two integers a and b are said to be congruence modulo m  if  is divisible by m  and we write $a\equiv b$ (mod m).

Thus $a\equiv b$ (mod m) $\iff a–b$ is divisible by m. For example, $18\equiv 3$ (mod 5) because 18 – 3 = 15 which is divisible by 5. Similarly, $3\equiv 13$ (mod 2) because 3 – 13 = –10 which is divisible by 2. But 25 ≠ 2 (mod 4) because 4 is not a divisor of 25 – 3 = 22.

The relation “Congruence modulo m” is an equivalence relation.

Composition of relations

Let R and S be two relations from sets A to B and B to C respectively. Then we can define a relation SoR from A to C such that (a, c) ∈ SoR $\iff \exists$ b ∈ B such that (a, b) Î R and (b, c) ∈ S.

This relation is called the composition of R and S.

Example, if A = {1, 2, 3}, B = {a, b, c, d}, C={p, q, r, s} be three sets such that R = {(1, a), (2, b), (1, c), (2, d)} is a relation from A to B and S = {(a, s), (b, r), (c, r)} is a relation from B to C. Then SoR is a relation from A to C given by SoR = {(1, s) (2, r) (1, r)} In this case RoS does not exist.

In general RoS ≠ SoR. Also (SoR)^–1 = R^–1oS^–1.

Illustration -6

A relation P in set Z of integers is given as P = {(a, b): (a + b) is a multiple of 5}. What kind of relation is P?

Solution

P is not reflexive as it is not necessary that a + a = 2a is a multiple of 5 for all a ∈ Z.

If (a, b) ∈ P, then a + b is a multiple of 5. Hence, b + a is also a multiple of 5.

$\Rightarrow$ (b, a) ∈ P

Thus, P is a symmetric relation.

Similarly, if (a, b) ∈ P and (b, c) ∈ P, then (a + b) and (b + c) are multiples of 5.

However, it is not necessary that (a + c) is also a multiple of 5.

Hence, (a, b) ∈ P and (b, c) ∈ P  (a, c) ∉ P

Thus, P is not transitive.

Thus, P is a symmetric relation.

Illustration -7

Let T be the set of ages of all people of a locality with R, a relation in T, given by R = {(T₁, T₂) : T₁ ≥ T₂}. What kind of relation is R?

(A) Reflexive and symmetric
(B) Reflexive and transitive
(C) Symmetric and Transitive
(D) Equivalence relation

Solution

[B]

R is reflexive as the age of each member of the locality will be the same as the age of a particular person himself.

For (T₁, T₂) ∈ R ⇒ T₁ ≥ T₂ though it is not necessary that T₂ ≤ T₁.
Hence, the relation is not symmetric.
For (T₁, T₂) ∈ R and (T₂, T₃) ∈ R
$\Rightarrow$ T₁ ≥ T₂ and T₂ ≥ T₃
$\Rightarrow$ T₁ ≥ T₃
$\Rightarrow$ (T₁, T₃) ∈ R

Therefore, the relation is transitive.

Thus, relation R is reflexive and transitive..

Illustration -8
Consider a set A = {−2, −1, 3, 4}. Which of the following relations on A represents a trivial relation?
(A) R = {(a, b): ab is an even number, a, b ∈ A}
(B) R = {(a, b): ab is an odd number, a, b ∈ A}
(C) R = {(a, b): a + b ≥ − 3, a, b ∈ A}
(D) R = {(a, b): a − b ≥ − 6, a, b ∈ A}

Solution
[D]
A relation is called a trivial relation if it is an empty relation or a universal relation.
We have A = {− 2, − 1, 3, 4}.
If (a, b) ∈ R, then the minimum value of a − b will be −2 − 4 = −6.
In this case, a = − 2, b = 4
For all other ordered pairs (− 2, −1), (− 2, − 3), (− 2, − 2) etc. we will always have a + b ≥ − 6.
Hence, R = {(a, b): a − b ≥ − 6, a, b ∈ A} is a universal relation. Hence, it is a trivial relation.

Illustration -9
Relation R in the set H of human beings of a particular locality, defined as R = {(x, y): x is brother of y}, is a/an
(A) reflexive relation
(B) transitive relation
(C) symmetric relation
(D) equivalence relation
Solution
[B]
The given relation is R = {(x, y): x is brother of y}
The relation R is not reflexive as a human being x cannot be a brother of himself or herself.
If (x, y) ∈ R, then x is the brother of y.
It is not necessary that y is the brother of x because if y is a girl, then y cannot be the brother of x.
Therefore, (y, x) may or may not belong to R.
Therefore, R is not symmetric.
(x, y), (y, z) ∈ R
$\Rightarrow$ x is the brother of y and y is the brother of z
$\Rightarrow$ x is the brother of z
$\Rightarrow$ (x, z) ∈ R Thus, the given relation R is a transitive relation.

Illustration -10
Let P be the set of all triangles in a plane. A relation R in P is defined as
R = {(P₁, P₂): P₁ is similar to P₂} The relation R in the set P is a/an
(A) reflexive relation
(B) transitive relation
(C) symmetric relation
(D) equivalence relation
Solution
[B]
It is known that a relation R in a set X is said to be an equivalence relation, if R is reflexive, symmetric, and transitive.
The given relation is R = {(P₁, P₂): P₁ is similar to P₂}
The relation R is reflexive as every triangle is similar to itself.
If (P₁, P₂) ∈ R, then P₁ is similar to P₂.
$\Rightarrow$ P₂ is similar to P₁
$\Rightarrow$ (P₂, P₁) ∈ R
Therefore, R is symmetric.
(P₁, P₂), (P₂, P₃) ∈ R
$\Rightarrow$ P₁ is similar to P₂ and P₂ is similar to P_{3
$\Rightarrow$} P₁ is similar to P₃ $\Rightarrow$ (P₁, P₃) ∈ R
Therefore, R is transitive. Thus, the given relation R is an equivalence relation.

Illustration -11
N is the set of natural numbers. The relation R is defined on N⨯N as follows:
(a, b) R (c, d) $\iff$ a + d = b + c
Prove that R is equivalence relation.
Solution
(i) (a, b) R (a, b) $\iff$ a + b = b + a
∴ R is reflexive.
(ii) (a, b) R (c, d) $\Rightarrow$ a + d = b + c
                                $\Rightarrow$ c + b = d + a
                                $\Rightarrow$ (c, d) R (a, b)
                                ∴ R is symmetric.
Now (iii) (a, b) R (c, d) and (c, d) R (e, f) Þ a + d = b + c & c + f = d + e
$\Rightarrow$ a + d + c + f = b + c + d + e
$\Rightarrow$ a + f = b + e
$\Rightarrow$ (a, b) R (e, f)
∴ R is transitive. Thus R is an equivalence relation on N⨯N.

Illustration -12
A relation R on the set of complex numbers is defined by ${\mathrm{z}}_1{\mathrm{Rz}}_2\iff \frac{{\mathrm{z}}_1–{\mathrm{z}}_2}{{\mathrm{z}}_1+{\mathrm{z}}_2}$  is real, show that R is an equivalence relation.
Solution
(i) ${\mathrm{z}}_1{\mathrm{Rz}}_2\Rightarrow \frac{{\mathrm{z}}_1–{\mathrm{z}}_2}{{\mathrm{z}}_1+{\mathrm{z}}_2}$    is real
∴ R is reflexive
∴ $\forall z_1\in C\Rightarrow 0$ is real.
(ii) ${\mathrm{z}}_1{\mathrm{Rz}}_2\Rightarrow \frac{{\mathrm{Z}}_1–{\mathrm{Z}}_2}{{\mathrm{Z}}_1+{\mathrm{z}}_2}$  is real $\Rightarrow –\left(\frac{z_2–z_1}{z_1+z_2}\right)$ is real
$\Rightarrow \left(\frac{{\mathrm{z}}_2–{\mathrm{z}}_1}{{\mathrm{z}}_1+{\mathrm{z}}_2}\right)$  is real $\Rightarrow z_2 R z_1\forall z_1, z_2\in C$
∴ R is symmetric.

(iii) Let z₁ = a₁ + ib₁, z₂ = a₂ + ib₂ and z₃ = a₃ + ib₃
where a_1­, b₁, a₂, b₂, a₃, b₃ ∈ R
now ${\mathrm{z}}_1{\mathrm{Rz}}_2\Rightarrow \frac{{\mathrm{Z}}_1–{\mathrm{z}}_2}{{\mathrm{Z}}_1+{\mathrm{z}}_2}$ is real
$\Rightarrow \frac{\left({\mathrm{a}}_1+{\mathrm{ib}}_1\right)–\left({\mathrm{a}}_2+{\mathrm{ib}}_2\right)}{\left({\mathrm{a}}_1+{\mathrm{ib}}_1\right)+\left({\mathrm{a}}_2+{\mathrm{ib}}_2\right)}\text{ is real }\Rightarrow \frac{\left({\mathrm{a}}_1–{\mathrm{a}}_2\right)+\mathrm{i}\left({\mathrm{b}}_1–{\mathrm{b}}_2\right)}{\left({\mathrm{a}}_1+{\mathrm{a}}_2\right)+\mathrm{i}\left({\mathrm{b}}_1+{\mathrm{b}}_2\right)}\text{ is real }$

$\Rightarrow \frac{\left({\mathrm{a}}_1–{\mathrm{a}}_2\right)+\mathrm{i}\left({\mathrm{b}}_1–{\mathrm{b}}_2\right)}{\left({\mathrm{a}}_1+{\mathrm{a}}_2\right)+\mathrm{i}\left({\mathrm{b}}_1+{\mathrm{b}}_2\right)}\times \frac{\left({\mathrm{a}}_1+{\mathrm{a}}_2\right)–\mathrm{i}\left({\mathrm{b}}_1+{\mathrm{b}}_2\right)}{\left({\mathrm{a}}_1+{\mathrm{a}}_2\right)–\mathrm{i}\left({\mathrm{b}}_1+{\mathrm{b}}_2\right)}\text{ is real }$

$\Rightarrow \frac{\left({\mathrm{a}}_1–{\mathrm{a}}_2\right)\left({\mathrm{a}}_1+{\mathrm{a}}_2\right)+\left({\mathrm{b}}_1–{\mathrm{b}}_2\right)\left({\mathrm{b}}_1+{\mathrm{b}}_2\right)+\mathrm{i}\left[\left({\mathrm{b}}_1–{\mathrm{b}}_2\right)\left({\mathrm{a}}_1+{\mathrm{a}}_2\right)–\left({\mathrm{b}}_1+{\mathrm{b}}_2\right)\left({\mathrm{a}}_1–{\mathrm{a}}_2\right)\right]}{{\left({\mathrm{a}}_1+{\mathrm{a}}_2\right)}^2+{\left({\mathrm{b}}_1+{\mathrm{b}}_2\right)}^2}$is real

$\Rightarrow \left(a_1+a_2\right)\left(b_1–b_2\right)–\left(a_1–a_2\right)\left(b_1+b_2\right)=0$(for purely real, imaginary part = 0

$\Rightarrow 2{\mathrm{a}}_2{ \mathrm{b}}_1–2{ \mathrm{b}}_2{\mathrm{a}}_1=0$

$\Rightarrow \frac{{\mathrm{a}}_1}{{\mathrm{a}}_2}=\frac{{\mathrm{b}}_1}{{\mathrm{b}}_2}\Rightarrow \frac{{\mathrm{a}}_1}{{\mathrm{b}}_1}=\frac{{\mathrm{a}}_2}{{\mathrm{b}}_2}$

similarly, z₂ R z₃ $\Rightarrow \frac{{\mathrm{a}}_2}{{\mathrm{b}}_2}=\frac{{\mathrm{a}}_3}{{\mathrm{b}}_3}$

z₁ R z₂ and z₂ R z₃ $\Rightarrow \frac{{\mathrm{a}}_1}{{\mathrm{b}}_1}=\frac{{\mathrm{a}}_2}{{\mathrm{b}}_2}$

and $\frac{{\mathrm{a}}_2}{{\mathrm{b}}_2}=\frac{{\mathrm{a}}_3}{{\mathrm{b}}_3}\Rightarrow \frac{{\mathrm{a}}_1}{{\mathrm{b}}_1}=\frac{{\mathrm{a}}_3}{{\mathrm{b}}_3}\Rightarrow {\mathrm{z}}_1{\mathrm{Rz}}_3$

∴ R is transitive

Hence R is equivalence relation.

Illustration -13
Find all congruent solutions of 8x $\equiv$ 6 (mod 14)
Solution
given 8x $\equiv$ 6 (mod 14)

$\mathrm{\lambda }=\frac{8\mathrm{x}–6}{14}\text{ where }\mathrm{\lambda }\in {\mathrm{I}}_{+}$

$\therefore 8\mathrm{x}=14\lambda +6\Rightarrow \mathrm{x}=\frac{14\lambda +6}{8}$

$\Rightarrow \mathrm{x}=\frac{7\mathrm{\lambda }+3}{4}=\frac{4\mathrm{\lambda }+3(\mathrm{\lambda }+1)}{4}$

$\mathrm{x}=\mathrm{\lambda }+\frac{3}{4}(\mathrm{\lambda }+1)\text{ where }\mathrm{\lambda }\in {\mathrm{I}}_{+}$

and here greatest common divisor of 8 and 14 is 2 so, there are two required solutions for $\lambda$ = 3 and $\lambda$ = 7, x = 6, 13

4. DEFINITION OF A FUNCTIONS

Definition 1
A function f is a relation from a non-empty set A to a non-empty set B such that domain of f  is A and no two distinct ordered pairs in f have the same first element.

Definition 2
Let A and B be two non-empty sets, then a rule of which associates each element of A with a unique element of B is called a mapping or a function from A to B we write $\mathbf{f}\mathbf{:}\mathbf{A}\mathbf{\to }\mathbf{B}$(read as f is a function from A to B).
For a function from A to B:
(i) A and B should be non-empty.
(ii) Each element of A should have image in B.
(iii) No element of A should have more than one images in B.

Illustration -13

Examine each of the following relations given below and state in each case, giving reasons whether it is a function or not?
(i) R = {(1, 2), (2, 2), (3, 1), (4, 2)}
(ii) R = {(2, 2), (1, 2), (1, 4), (4, 4)
(iii) R = {(1, 2), (2, 3), (4, 5), (5, 6), (6, 7)}
Solution
(i) Since first element of each ordered pair is different, therefore this relation is a function.
(ii) Since the same first element 1 corresponds to two different images 2 and 4, hence this relation is not a function.
(iii) Since first element of each ordered pair is different, therefore this relation is a function.

5.  DOMAIN, CO-DOMAIN AND RANGE OF A FUNCTION

The set A is called as the domain of the map f and the set B is called as the co-domain. The set of the images of all the elements of A under the map f is called the range of f and is denoted by $\mathrm{f}\left(\mathrm{A}\right)$.

Thus, range of f i.e. $\mathrm{f}\left(\mathrm{A}\right)=\left\{\mathrm{f}\right(\mathrm{x}):\mathrm{x}\in \mathrm{A}\}$.

Clearly $\mathrm{f}\left(\mathrm{A}\right)\subseteq \mathrm{B}$

6. IMPORTANT FUNCTIONS AND THEIR GRAPHS

Polynomial functions: f(x) = a₀ + a₁x + a₂x² + ………+ a_nxⁿ , where a₀, a₁, a₂, ……, a_n ∈ R is said to be a polynomial function of degree n.

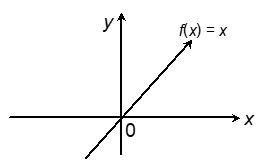
Identity function: An identity function in x is defined as f : R $\to$ R, f(x) = x.

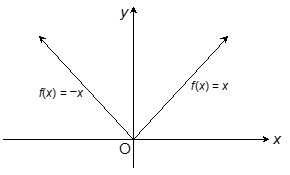
Absolute value function: An absolute value function in x is defined as f : R $\to$ R, f(x) = |x|.

y = f(x) = | x | = $\left\{\begin{array}{cl}–x,& x\le 0\\ x,& x>0\end{array}\right.$

Domain : R ;    Range : [0, $\infty$) ;

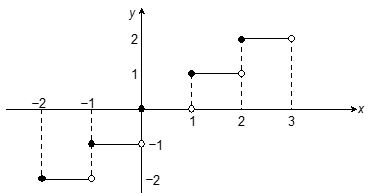
Greatest integer function (step function): The function f(x) = [x] is called the greatest integer function and is defined as follows:

[x] is the greatest integer less than or equal to x.

Then [x] = x if x is an integer

= integer just less than x if x is not an integer.

y = f(x) = [ x ]        Domain : R ;           Range : I

 

Signum function: The function is defined as

y = f(x) = sgn (x)

sgn (x) = $\left\{\begin{array}{cc}\frac{\left|x\right|}{x},& x\ne 0\\ 0,& x=0\end{array}\right.$

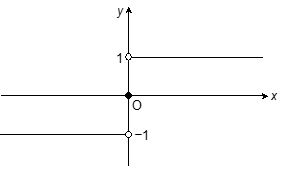
or   sgn(x) = $\left\{\begin{array}{ll}–1,& x<0\\ 0,& x=0\\ 1,& x>0\end{array}\right.$

Domain: R;             Range $\to$ {-1, 0, 1}

Rational algebraic function: A function of the form $f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)}$, where p(x) and q(x) are polynomials and q(x) ≠ 0, is called a rational function.

The domain of a rational function $\frac{p\left(x\right)}{q\left(x\right)}$ is the set of all real numbers except points where q(x) = 0.

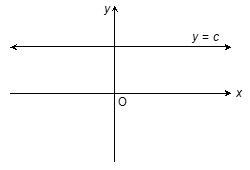
Constant function: The function defined as  f : R $\to$ {c} where f(x) = c

7. ALGEBRAIC OPERATIONS ON FUNCTIONS

Let us consider two functions.

f : D₁ $\to$ R and g : D₂ $\to$ R. We describe functions f + g, f – g, f.g and f/g as follows:

• f + g : D $\to$ R is a function defined by

(f + g) x = f(x) + g(x),  where D = D₁ ⋂ D₂

• f – g : D ® R is a function defined by

(f – g) x = f(x) – g(x),   where D = D₁ ⋂ D₂

• f . g : D $\to$ R is a function defined by

(f . g) x = f(x) . g(x),   where D = D₁ ⋂ D₂

• f / g : D $\to$ R is a function defined by

(f / g) x =$\frac{f\left(x\right)}{g\left(x\right)}$,   where D = D₁ ⋂ {x ∈ D₂ : g(x) ≠ 0}

• $\left(\mathrm{\alpha f}\right)\left(\mathrm{x}\right)=\mathrm{\alpha f}\left(\mathrm{x}\right), \mathrm{x}\in {\mathrm{D}}_1$ and $\alpha$ is any real number.

Illustration-14

If $f:R\to R$ is defined by  $f\left(x\right)=x^3+1\text{ and }g:R\to R$  is defined by $g\left(x\right)=x+1$, then find $\mathrm{f}+\mathrm{g}, \mathrm{f}–\mathrm{g}, \mathrm{f}.\mathrm{g}, \frac{\mathrm{f}}{\mathrm{g}}\text{ and }\mathrm{\alpha f}(\mathrm{\alpha }\in \mathrm{R})$.

Solution:

$\mathrm{f}+\mathrm{g}:\mathrm{R}\to \mathrm{R}$ is defined by $(\mathrm{f}+\mathrm{g})\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{x}\right)+\mathrm{g}\left(\mathrm{x}\right)={\mathrm{x}}^3+1+\mathrm{x}+1={\mathrm{x}}^3+\mathrm{x}+2$

$\mathrm{f}–\mathrm{g}:\mathrm{R}\to \mathrm{R}$ is defined by $(\mathrm{f}–\mathrm{g})\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{x}\right)–\mathrm{g}\left(\mathrm{x}\right)={\mathrm{x}}^3+1–\mathrm{x}–1={\mathrm{x}}^3–\mathrm{x}$

$\mathrm{f}.\mathrm{g}:\mathrm{R}\to \mathrm{R}$ is defined by $\left(\mathrm{fg}\right)\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{x}\right)\mathrm{g}\left(\mathrm{x}\right)=\left({\mathrm{x}}^3+1\right)(\mathrm{x}+1)={\mathrm{x}}^4+{\mathrm{x}}^3+\mathrm{x}+1$

$\frac{\mathrm{f}}{\mathrm{g}}:\mathrm{R}–\{–1\}\to \mathrm{R}$ is defined by $\left(\frac{\mathrm{f}}{\mathrm{g}}\right)\left(\mathrm{x}\right)=\frac{\mathrm{f}\left(\mathrm{x}\right)}{\mathrm{g}\left(\mathrm{x}\right)}=\frac{{\mathrm{x}}^3+1}{\mathrm{x}+1}=\frac{(\mathrm{x}+1)\left({\mathrm{x}}^2–\mathrm{x}+1\right)}{\mathrm{x}+1}={\mathrm{x}}^2–\mathrm{x}+1$

$\mathrm{\alpha f}:\mathrm{R}\to \mathrm{R}$is defined by $\left(\mathrm{\alpha f}\right)\left(\mathrm{x}\right)=\mathrm{\alpha f}\left(\mathrm{x}\right)=\mathrm{\alpha }\left({\mathrm{x}}^3+1\right)={\mathrm{\alpha x}}^3+\mathrm{\alpha }$

Illustration-15 Let $\mathrm{f}\left(\mathrm{x}\right)=\sqrt{\mathrm{x}}\text{ and }\mathrm{g}\left(\mathrm{x}\right)=\mathrm{x}$  be two functions defined over the set of non-negative real numbers. Find  $(\mathrm{f}+\mathrm{g})\left(\mathrm{x}\right)(\mathrm{f}\to \mathrm{g})\left(\mathrm{x}\right)\left(\mathrm{fg}\right)\left(\mathrm{x}\right)\text{ and }\left(\frac{\mathrm{f}}{\mathrm{g}}\right)\left(\mathrm{x}\right)$.

Solution:

Given  $(\mathrm{f}+\mathrm{g})\left(\mathrm{x}\right)=\sqrt{\mathrm{x}}+\mathrm{x}, (\mathrm{f}–\mathrm{g})\left(\mathrm{x}\right)=\sqrt{\mathrm{x}}–\mathrm{x}$,

$\left(\text{ fg }\right)\mathrm{x}=\sqrt{\mathrm{x}}\left(\mathrm{x}\right)={\mathrm{x}}^{3/2}$ and  $\left(\frac{\mathrm{f}}{\mathrm{g}}\right)\left(\mathrm{x}\right)=\frac{\sqrt{\mathrm{x}}}{\mathrm{x}}={\mathrm{x}}^{–1/2}, \mathrm{x}\ne 0$