Sets

1 Sets, representation and Types of Sets

SET 

A set is a well-defined collection of distinct objects. Well-defined collection means that there exists a rule with the help of which it is possible to tell whether a given object belongs or does not belong to given collection. Generally, sets are denoted by capital letters A, B, C, X, Y, Z etc.

REPRESENTATION OF A SET

Roster method or Listing method

In this method a set is described by listing elements, separated by commas, within braces {}. The set of vowels of English alphabet may be described as {a, e, i, o, u}.

Example: Let B be the set of natural numbers between 3 and 9. Then,  B = {4, 5, 6, 7, 8}

Set-builder method or Rule method

In this method, a set is described by a characterizing property P(x) of its elements x. In such a case the set is described by {x : P(x) holds} or {x | P(x) holds}, which is read as ‘the set of all x such that P(x) holds’. The symbol ‘|’ or ‘:’ is read as ‘such that’.

The set A= (0,1,4,9,16,..) can be written as $A=\left(x^2\right|x\in z)$

Example: Let A be a set of even numbers less than 10. It can be represented by set builder form as: A = {x : x is an even number and x < 10}  

Illustration -1

Write the solution set of the equation x² + x – 2 = 0 in roster form.

Solution

The given equation can be written as (x – 1)  (x + 2) = 0, i. e.,   x = 1, – 2 Therefore, the solution set of the given equation can be written in roster form as {1, – 2}.

Illustration -2

Write the set A = {1, 4, 9, 16, 25, . . .}in set-builder form.  

Solution

We may write the set A as A = {x : x is the square of a natural number} Alternatively, we can write A = {x : x = n², where n ∈ N}

TYPES OF SETS

1. Empty set/null set/void set

The set which contains no element at all is called the null set. This set is sometimes also called the ‘empty set’ or the ‘void set’. It is denoted by the symbol $\varphi$ or {}.

Example: Let A be a set of VI class students in class VIII.

A = { }

2. Singleton set

A set consisting of a single element is called a singleton set. The set {5} is a singleton set.

Example: A = {1, 2, 3, 4, 5, 6}, {x/x is a factor of 24} 

3. Finite set

A set is called a finite set if it is either void set or its elements can be listed (counted, labelled) by natural number 1, 2, 3, … and the process of listing terminates at a certain natural number n (say).

Example

i) Set of peoples in a village.

ii) A set containing students of your class.

iii) A = {x/x ∈ N, x < 500000}

Cardinal number of a finite set

The number n in the above definition is called the cardinal number or order of a finite set A and is denoted by n(A) or O(A).

Example:

Let B = {x / x is a letter in the word ‘Mathematics’}, then B = {M, A, T, H, E, M, A, T, I, C, S}. Hence, n(B) = 8. 

4. Infinite sets

A set whose elements cannot be listed by the natural numbers 1, 2, 3, …., n, for any natural number n is called an infinite set.

Example:

i) The multiples of 3 are 3, 6, 9, 12……… i.e., A = {x/x is a multiple of 3} is an infinite set.

ii) A set of Natural numbers.

iii) {x∈z : x < 0} 

5. Equivalent sets

Two finite sets A and B are equivalent if their cardinal numbers are same i.e. n(A) = n(B). Example : ; A={1,3,5,7}; B= {10,12,14,16} are equivalent sets, . [∴ 0=(A)=0(B)=4].

6. Equal sets

 Two sets A and B are said to be equal if f every element of A is an element of B and also every element of B is an element of A. Symbolically, A = B if x ∈ A $\iff$ x ∈ B.

Example : If A = { 2,3,5,6,}  and B= {6,5,3,2}. Then A=B  because each element of A is an element of B and vice-versa.

Illustration -3

Which of the following sets are empty, singleton, pair and which of them are equal.

A = {x : x² = 9 and 2x = 3}

B = {x : x² – 5x + 6 = 0, 2x = 6}

C = {x : x² – 4x + 3 = 0}

D = {x : x² = 25}

E = {x : 2x = 6 or x = 1}

Solution

The multiples of 7 are 7, 14, 21, 28, 35… Hence, the number of elements in set A = {7, 14, 21, 28, 35…} is not definite. Hence, it is an infinite set.

The two given points are (1, 1) and (0,0) and we know that there is one and only one line passing through two fixed points. Hence, there will be only one line that passes through the given points. Thus, the set contains only one element. Hence, it is a finite set.

Illustration -4

State which of the following sets are finite or infinite:

(i) {x : x ∈ N and (x – 1) (x – 2) = 0}

(ii) {x : x ∈ N and x² = 4}

(iii) {x : x ∈ N and 2x – 1 = 0}

(iv) {x : x ∈ N and x is prime}

(v) {x : x ∈ N and x is odd}

Solution

The multiples of 7 are 7, 14, 21, 28, 35… Hence, the number of elements in set A = {7, 14, 21, 28, 35…} is not definite. Hence, it is an infinite set.

The two given points are (1, 1) and (0,0) and we know that there is one and only one line passing through two fixed points. Hence, there will be only one line that passes through the given points. Thus, the set contains only one element. Hence, it is a finite set.

Illustration -5

State whether each of the following sets is finite or infinite: Set of multiples of 7 Set of lines passing through the point (1, 1) as well as the origin

Solution

The multiples of 7 are 7, 14, 21, 28, 35… Hence, the number of elements in set A = {7, 14, 21, 28, 35…} is not definite. Hence, it is an infinite set.

The two given points are (1, 1) and (0,0) and we know that there is one and only one line passing through two fixed points. Hence, there will be only one line that passes through the given points. Thus, the set contains only one element. Hence, it is a finite set.

Illustration -6

State which of the following sets are finite or infinite:

(i) {x : x ∈ N and (x – 1) (x – 2) = 0}

(ii) {x : x ∈ N and x² = 4}

(iii) {x : x ∈ N and 2x – 1 = 0}

(iv) {x : x ∈ N and x is prime}

(v) {x : x ∈ N and x is odd}

Solution

The multiples of 7 are 7, 14, 21, 28, 35… Hence, the number of elements in set A = {7, 14, 21, 28, 35…} is not definite. Hence, it is an infinite set.

The two given points are (1, 1) and (0,0) and we know that there is one and only one line passing through two fixed points. Hence, there will be only one line that passes through the given points. Thus, the set contains only one element. Hence, it is a finite set.

SUBSET AND SUPER SET

subset

Let A and B be two sets. If every element of A is an element of B, then A is called a subset of B. If A is subset of B, we write A $\subseteq$ B, which is read as “A is a subset of B” or “A is contained in B”. Thus, . $A\subseteq B\Rightarrow a\in A\Rightarrow g\in B$.

superset

If , A $\subseteq$ B  then ,B is called superset of A and we write B ⊇ A

Proper subset

If A is a subset of B and A ≠ B then A is a proper subset of B. We write this as A ⊂ B.

The null set $\varphi$ is subset of every set and every set is subset of itself, i.e., $\varphi \subset A\text{ and }A\subseteq A$ for every set A.

They are called improper subsets of A. Thus every non-empty set has two improper subsets. It should be noted that $\varphi$ has only one subset $\varphi$ which is improper.

All other subsets of A are called its proper subsets. Thus, if A ⊂ B, A ≠ B, A ≠ $\varphi$, then A  is said to be proper subset of B.

Example : Let A={1,2}. Then A has $\varphi$ ; {1}, {2}, {3} as its subsets out of which $\varphi$ and {1, 2} are improper and {1} and {2} are proper subsets.

Comparable Set

In two sets one is a subset of the other ,then the sets are called comparable sets.

Properties of subsets

i) Every set is its own subset.

ii) Empty set is a subset of each set.

Let A = {    } = $\varphi$  f [i.e., empty set] and B = {1, 2, 3, 4}

It is clear that set A has no element and we can say that there is no element $\varphi$ in  which is not in B.

Hence, each element of $\varphi$ is an element of B.

⇒$\varphi$ ⊆ B

Therefore, empty set is a subset of each set.

iii) For any two sets A and B, A = B ⇔ A ⊆ B and B ⊆ A.

Let A and B be two unequal sets, i.e., do not contain exactly same elements, like an element a that belongs to one set but not to the other.

But if a∈ A, then a ∈ B since A ⊆ B and if a ∈ B, then a  ∈ A since B$\subset$A.

Hence, ‘a’ belongs to both A and B.

That is, there cannot be any element in one set that does not belong to the other set. So, and B  contain exactly the same elements i.e., A = B.

Therefore, for any two sets, A = B ⇔ A ⊆ B and B ⊆ A.

iv) If A ⊆ B and B ⊆ C, then A ⊆ C.

Let’s observe the figure

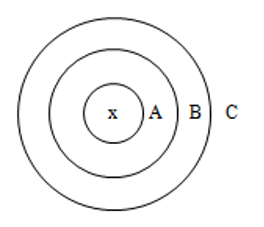
From the figure, it is clear that x is the part of A (x ∈ A) and x is the part of B (x ∈ B)

[∵ A ⊂ B] x is the part of C (x ∈ c) [∵ B ⊂ C]

∴ x ∈ A  ⇒ x ∈ c

i.e., A ⊂ C.

Illustration -7

List all the subsets and all the proper subsets of the set {-1, 0, 1}.

Solution

Let A = {-1, 0, 1}.

Subset of A having no element is: $\varphi$

Subsets of A having one elements are: {-1}, {0}, {1}.

Subsets of A having two elements are: {-1, 0}, {0, 1}, {-1, 1}.

Subsets of A having three elements: {-1, 0, 1}.

Thus, all the subsets of A are: $\varphi$, {-1}, {0}, {1}, {-1, 0}, {0, 1}, {-1, 1}, {-1, 0, 1}

Proper subsets of A are: $\varphi$, {-1}, {0}, {1}, {-1, 0}, {0, 1}, {-1, 1}.  

Illustration -8

Let A = {1, 2, 3, 4}, B = {1, 2, 3} and C = {2, 4}. Find all sets X such that:

(i) X ⊆ B and X ⊆ C

(ii) X ⊆ A and X ⊆ B

Solution

Given, A = {1, 2, 3, 4}, B = {1, 2, 3} and C = {2, 4}.

(i) Subsets of B are: $\varphi$, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}.

Subsets of C are: $\varphi$, {2}, {4}, {2, 4}

Since X is a subset of both B and C, therefore, X = $\varphi$,{2}.

(ii) A = {1, 2, 3, 4} B = {1, 2, 3}

Here 1, 2, 3 are elements of both A and B and 4 is the only element of A which is not in B.

Since, X $\subseteq$ A and X ⊄ B, therefore, 4 must belong to X.

Hence X = {4}, {1, 4}, {2, 4}, {3, 4}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4}, {1, 2, 3, 4}.

Illustration -9

Consider the sets $\varphi$, A = {1, 3 },   B = {1, 5, 9},   C = {1, 3, 5, 7, 9}. Insert the symbol ⊂ or ⊄ between each of the following pair of sets:

(i) $\varphi$ . . . B      (ii) A . . . B      (iii) A . . . C    (iv) B . . . C

Solution

(i) $\varphi$ ⊂ B as $\varphi$ is a subset of every set.

(ii) A ⊄ B as 3 ∈ A and 3 ∉ B

(iii) A ⊂ C as 1, 3 ∈ A also belongs to C

(iv) B  ⊂ C as each element of B is also an element of C.

Illustration -10

Let A = { a, e, i, o, u} and B = { a, b, c, d}. Is A a subset of B?  Is B a subset of A?

Solution

No, as some of the element of set A are not present in set B, A is not a subset of B.

No, similarly, few element of set B are not present in set A, B is not a subset of A.

Illustration -11

Let A, B and C be three sets. If A ∈ B and B ⊂ C, is it true that A ⊂ C ? If not, give an example.

Solution

No. Let A = {1}, B = {{1}, 2} and C = {{1}, 2, 3}. Here A ∈ B as A = {1} and B ⊂ C. But A ⊄ C as 1 ∈ A and 1 $\notin$ C.

Note that an element of a set can never be a subset of itself.

Illustration -12

Let B be a subset of A and let P(A : B) = (X ∈ P(A) : X $\supseteq$ B}. Show that P(A : $\varphi$) = P(A).

Solution

Given, P(A : B) = set of all those subsets of A which are supersets of B.

∴ P(A = $\varphi$) = set of all those subsets of A which are supersets of $\varphi$.

= set of all subsets of A   [∵ every subset of A is a superset of f] = P(A)

Intervals as Subsets of R

A subset of the real line is called an interval. Intervals are important in solving inequalities or in finding domains etc. If there are two numbers a, b ∈R such that a < b, following type of intervals can be defined

Finite Intervals

Open Interval:     (a, b) = {x|a < x < b}

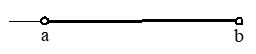
Close Interval:    [a, b] = {x|a $\le$ x $\le$ b}

Open-close Interval:   (a, b] = {x|a < x $\le$ b}

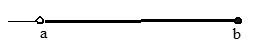
Close-open Interval:      [a, b) = {x|a $\le$ x < b}

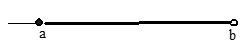
Infinite Intervals

$(a,\infty )=\{x\mid x>a\}$

$[a,\infty )=\{x\mid x\ge a\}$

$(–\infty ,b)=\{x\mid x<b\}$

$(–\infty ,b]=\{x\mid x\le b\}$

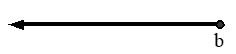
$\left(–\infty ,\infty \right)=R$ (set of all real number)

POWER SET

If S is any set, then the family of all the subsets of S is called the power set of S.

The power set of S is denoted by P(S). Symbolically, P(S) = {T : T  $\subseteq$ S}. Obviously $\varphi$ and S are both elements of P(S).

Example :  Let S = {a, b, c}, then P(S) = {$\varphi$, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}. Power set of a given set is always non-empty

UNIVERSAL SET

A set that contains all sets in a given context is called the universal set.

It should be noted that universal set is not unique. It may differ in problem to problem.

Example: Let A = {1, 2, 3}; B = {3, 4, 6, 9} and C = {0, 1}.

We can take m = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} as the universal set of sets A,B and C.

VENN DIAGRAMS

The diagrams drawn to represent sets are called Venn diagrams or Euler -Venn diagrams. Here we represent the universal set U by points within rectangle and the subset A of the set U represented by the interior of a circle. If a set A is a subset of a set B then the circle representing A is drawn inside the circle representing B. If A and B are no equal but they have some common elements, then to represent A and B by two intersecting circles

Illustration -13

A class has 175 students. The following table shows the number of students studying one or more of the following subjects in this case

Subjects	No. of students
Mathematics	100
Physics	70
Chemistry	46
Mathematics and Physics	30
Mathematics and Chemistry	28
Physics and Chemistry	23
Mathematics, Physics and Chemistry	18

How many students are enrolled in Mathematics alone, Physics alone and Chemistry alone? Are there students who have not offered any one of these subjects?

Solution

Let P, C, M denote the sets of students studying Physics, Chemistry and Mathematics respectively. Let a, b, c, d, e, f, g denote the number of elements (students) contained in the bounded region as shown in the diagram then

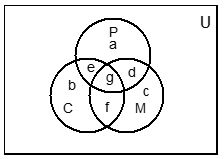
a + d + e + g  = 70
c + d + f + g = 100
b + e + f + g = 46
d + g = 30
e + g = 23
f + g = 28
g = 18

after solving we get g = 18, f = 10, e = 5, d = 12, a = 35, b = 13 and c = 60

∴ a + b + c + d + e + f + g = 153

So, the number of students who have not offered any of these three subjects

= 175 –153 = 22

Number of students studying Mathematics only, c = 60

Number of students studying Physics only, a = 35

Number of students studying Chemistry only, b = 13.

2 OPERATIONS ON sets and their algebraic properties 

1. UNION OF SETS

Let A and B be two sets. The union of A and B is the set of all elements which are in set A or in B. We denote the union of A and B by $A\cup B$, which is usually read as “A union B”. Symbolically, $A\cup B=\left\{x:x\in A or x\in B\right\}$

Illustration -14

Let X = {Ram, Geeta, Akbar} be the set of students of Class XI, who are in school hockey team.

Let Y = {Geeta, David, Ashok} be the set of students from Class XI who are in the school football team.

Find X $\cup$ Y and interpret the set.

Solution

We have, X $\cup$ Y = {Ram, Geeta, Akbar, David, Ashok}. This is the set of students from Class XI who are in the hockey team or the football team or both.

2. INTERSECTION OF SETS

Let A and B be two sets. The intersection of A and B is the set of all those elements that belong to both A and B.

The intersection of A and B is denoted by A $\cap$ B (read as “A intersection B”).

Thus, A $\cap$ B = {x : x ∈ A and x ∈ B}.

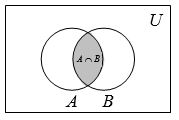
Illustration -15

Let A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and B = {2, 3, 5, 7}. Find A $\cap$ B and hence show that A $\cap$ B = B.  

Solution

We have A ⋂ B = {2, 3, 5, 7} = B. We note that B ⊂ A and that A ⋂ B = B.’

3. DISJOINT SETS

Two sets A and B are said to be disjoint, if A ⋂ B = $\varphi$. If A ⋂ B ≠$\varphi$, then A and B are said to be non-intersecting or non-overlapping sets.

Example : Sets {1, 2}; {3, 4} are disjoint sets.

4. DIFFERENCE OF SETS

Let A and B be two sets. The difference of A and B written as A – B, is the set of all those elements of A which do not belong to B.

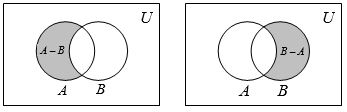
Thus, A – B = {x : x ∈ A and x $\notin$ B}

Similarly, the difference is the set of all those elements of B that do not belong to A i.e., $B–A=\{x\in B:x\notin A\}$.

Example : Consider the sets  and , then A – B = {1, 2}; B – A = {4, 5}.

Symmetric difference of two sets

Let A and B be two sets. The symmetric difference of sets A and B is the set $(A–B)\cup (B–A)$and is denoted by $A∆B$. Thus, $A\Delta B=(A–B)\cup (B–A)=\{x:x\notin A\cap B\}$ .

Properties on symmetric difference

A, B, C are any three sets

i) $\mathrm{A\Delta \varphi }=\mathrm{A}$

ii) $\mathrm{A\Delta A}=\mathrm{\varphi }$

iii) $\mathrm{A\Delta B}=\mathrm{A\Delta C}\Rightarrow \mathrm{B}=\mathrm{C}$

iv) $\mathrm{A\Delta B}=\mathrm{B\Delta A}$

v) $\left(\mathrm{A\Delta B}\right)\mathrm{\Delta C}=\mathrm{A\Delta }\left(\mathrm{B\Delta C}\right)$

vi) $\mathrm{A}\cap \left(\mathrm{B\Delta C}\right)=(\mathrm{A}\cap \mathrm{B})\mathrm{\Delta }(\mathrm{A}\cap \mathrm{C})$

Illustration -16

If A = {1, 2, 3, 4}, B = {2, 4, 6}

Let’s find

i) A – B                       ii) B – A          iii) (A – B) ⋃ (B – A)

Solution

i) A – B = {1, 2, 3, 4} – {2, 4, 6} = {1, 3}

ii) B – A = {2, 4, 6} – {1, 2, 3, 4} = {6}

iii)    (A – B) ⋃ (B – A) = {1, 3} ⋃ {6} = {1, 3, 6}

Thus, set (A – B) ⋃ (B – A) contains the elements that belong to one of the sets A and B, but not to both. This set is denoted by AΔB.

∴ AΔB = {1, 3, 6}’

5. COMPLIMENT OF A SET

Let U be the universal set and A a subset of U. Then the complement of A is the set of all elements of U which are not the elements of A. Symbolically, we write A’ to denote the complement of A with respect to U. Thus, A’ = {x : x ∈ U and x ∉ A }. Obviously A’ = U – A

Example

If μ = {1, 2, 3, 4, 5, 6} and A = {1, 2, 3}, then A’ consists of all the elements that are in μ and not in A.

A’ = {4, 5, 6}

In the set-builder form:

If A = {x/x ∈ μ and x ∉ A’}; then

A’= {x/x ∈ μ and x ∉ A}

Venn Diagram Representation Of Complement Set

The elements of all that are not in A constitute a new set called the complement of A and denoted by A° or Ac and read as “A complement”

Properties Of Complement Sets

If A be a set, A’ be its complement and S be the universal set, then

(i) A ⋂ A’ = f               (ii) A ⋃ A’ = S              (iii) $\varphi$’ = S                     (iv) S’ = $\varphi$

These laws are called complement laws.

Proof

Let x ∈ A ⋂ A’ $\Rightarrow$ x ∈ A and x ∈ A’

                          $\Rightarrow$ x ∈ A and x ∉ A’     [No such x exists]

Hence A ⋂ A’ contains no element ∴ A ⋂ A’ = $\varphi$

(ii) Let x $\varphi$ A ∈ A’ $\iff$ x ∈ A or x ∈ A’

$\iff$ x ∈ A or x ∉ A’     [This is true for all x ∈ S]

$\iff$ x ∈ S

Hence A ⋃ A’ = S        [This is true for all x ∈ S]

(iii) Let x = $\varphi$’         $\iff$ x ∉ $\varphi$

$\iff$ x ∈ S

Hence $\varphi$ = S

(iv) Let x ∈ S’ $\Rightarrow$ x ∉ S     [No such x is possible]

Hence S’ contains no element of S

∴  S’ = $\varphi$

Illustration -17

Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and A = {1, 3, 5, 7, 9}. Find A’.

Solution

We note that 2, 4, 6, 8, 10 are the only elements of U which do not belong to A. Hence A¢ = {2, 4, 6, 8,10}.

Illustration -18

Let U be universal set of all the students of Class XI of a coeducational school and A be the set of all girls in Class XI. Find A’.

Solution

Since A is the set of all girls, A’ is clearly the set of all boys in the class..

Illustration -19

Let U = {1, 2, 3, 4, 5, 6}, A = {2, 3} and B = {3, 4, 5}.

Find A’, B’, A’ ⋂ B’, A ⋂ B and hence show that (A ⋃ B)’ = A’ ⋂ B’.

Solution

Clearly A’ = {1, 4, 5, 6}, B’ = {1, 2, 6}. Hence A’ ⋂ B’ = {1, 6}

Also, A ⋃ B = {2, 3, 4, 5}, so that (A ⋃ B)’ = {1, 6}

(A ⋃ B)’ = {1, 6} = A’ ⋂ B’

3 Laws of algebra of sets 

1. IDEMPOTENT LAWS

Union of sets follows Idempotent Law

Let A = {x, y, z}

Can we find out A ⋃ A?

A ⋃ A = {x, y, z} ⋃ {x, y, z} = {x, y, z} = A

$\Rightarrow$ A ⋃ A = A

Therefore, union of sets follows the Idempotent law.  

2. IDENTITY LAWS

Union of sets follows Law of Identity

Let A = {a, b, c}

$\varphi$ = {  } null set.

Now, let’s find A ⋃ B and   A:

A ⋃ $\varphi$   = {a, b, c} ⋃ {  } = {a, b, c}

$\varphi$ ⋃ A = {   } ⋃ {a, b, c} = {a, b, c}

We observe that (A ⋃ $\varphi$) and ($\varphi$ ⋃ A) have the same elements.

Therefore, union of sets follows law of identity.

Note

i) We see that union of any set A and empty set is the set A.

ii) $\varphi$ is the identity set for the operation of the union.

3. COMMUTATIVE LAWS

Union of sets is Commutative

Let A = {a, b, c}, B = {p, q, r}

A ⋃ B = {a, b, c} ⋃ {p, q, r}

$\Rightarrow$ A ⋃ B = {a, b, c, p, q, r}

B ⋃ A = {p, q, r} ⋃ {a, b, c}

$\Rightarrow$ B ⋃ A = {p, q, r, a, b, c}

It is clear that A ⋃ B and B ⋃ A have the same elements.

They are equal sets: A ⋃ B = B ⋃ A.

Therefore, the union of sets is commutative.

4. ASSOCIATIVE LAWS

Union of sets is Associative

Let A = {a, b, c, d}, B = {p, q, r, s} and C = {w, x, y, z} then

A ⋃ B = {a, b, c, d} ⋃ {p, q, r, s}

            = {a, b, c, d, p, q, r, s}

B ⋃ C = {p, q, r, s} ⋃ {w, x, y, z}

            = {p, q, r, s, w, x, y, z}

A ⋃ (B ⋃ C) = {a, b, c, d} ⋃ {p, q, r, s, w, x, y, z}

                       = {a, b, c, d, p, q, r, s, w, x, y, z}

(A ⋃ B)C = {a, b, c, d, p, q, r, s} ⋃ {w, x, y, z}

                  = {a, b, c, d, p, q, r, s, w, x, y, z}

We observe that A ⋃ (B ⋃ C) and (A ⋃ B) ⋃ C have the same elements.

They are equal sets: A ⋃ (B ⋃ C) = (A ⋃ B) ⋃ C.

Therefore, the union of sets is Associative. 

5. DISTRIBUTIVE LAWS

If A, B and C are any three sets, then

(i) A ⋃ (B Ç C) = (A ⋃ B) Ç (A ⋃ C)

(ii) A ⋂ (B ⋃ C) = (A ⋂ B) ⋃ (A ⋂ C)

i.e., union and intersection are distributive over intersection and union respectively.

(iii) $A\times (B\cap C)=(A\times B)\cap (A\times C)$

(iv) $A\times (B\cup C)=(A\times B)\cup (A\times C)$

(v)  $A\times (B–C)=(A\times B)–(A\times C)$

6. DE MORGAN’S LAWS

If A, B and C are any three sets, then

(i)         (A È B)¢ = A¢ Ç B¢

(ii)        (A Ç B)¢ = A¢ È B¢

(iii)       A – (B Ç C) = (A – B) È (A – C)

(iv)       A – (B È C) = (A – B) Ç (A – C)

If A and B are any two sets, then

(i) A – B = A ⋂ B‘

(ii) B – A = B ⋂ A‘

(iii) A – B = A $\iff$ A ⋂ B = $\varphi$

(iv) (A – B) ⋃ B = A ⋃ B

(v) (A – B) ⋂ B = $\varphi$

(vi) A $\subseteq$ B $\iff$ B‘ $\subseteq$ A”

(vii) (A – B) ⋃ (B – A) = (A ⋃ B) – (A ⋂ B)

If A, B and C are any three sets, then

(i) A ⋂ (B – C) = (A ⋂ B) – (A ⋂ C)

(ii) A ⋂ (B Δ C) = (A ⋂ B) D (A ⋂ C)

Illustration -20

For the given sets A = {–10, 0, 1, 9, 2, 4, 5} and B = {–1, –2, 5, 6, 2, 3, 4}. Verify that Set Union is commutative.

Solution

A = {–10, 0, 1, 9, 2, 4, 5}

B = {–1, –2, 5, 6, 2, 3, 4}

A ⋃ B = {–10, –2, –1, 0, 1, 2, 3, 4, 5, 6, 9}

B ⋃ A = {–10, –2, –1, 0, 1, 2, 3, 4, 5, 6, 9}

Here A ⋃ B = B ⋃ A

Illustration -21

For A = {–3, –1, 0, 4, 6, 8, 10}, B = {–1, –2, 3, 4, 5, 6} and C = {–1, 2, 3, 4, 5, 7} Show that A ⋃ (B ⋂ C) = (A ⋃ B) ⋂ (A ⋃ C)

Solution

Given          A = {–3, –1, 0, 4, 6, 8, 10}

                     B = {–1, –2, 3, 4, 5, 6}

                     C = {–1, 2, 3, 4, 5, 7}

First we find A ⋃ (B ⋂ C)

(B ⋂ C) = {–1, 3, 4, 5}

A ⋃ (B ⋂ C) = {–3, –1, 0, 3, 4, 5, 6, 8, 10} ^{_____________} (1)

Now, we find (A ⋃ B) ⋂ (A ⋃ C)

A ⋃ B = {–3, –2, –1, 0, 3, 4, 5, 6, 8, 10}

A ⋃ C = {–3, –1, 0, 2, 3, 4, 5, 6, 7, 8, 10}

(A ⋃ B) ⋂ (A ⋃ C) = {–3, –1, 0, 3, 4, 5, 6, 8, 10} ^{_____________} (2)

From (1) and (2),

A ⋃ (B ⋂ C) = (A ⋃ B) ⋂ (A ⋃ C)

4. SOME IMPORTANT RESULTS ON NUMBER OF ELEMENTS IN SETS

Let A, B and C be finite sets and U be the finite universal set, then

(i) n (A ⋃ B) = n (A) + n (B) – n (A ⋂ B)

(ii) If A and B are disjoint, then n (A ⋃ B) = n (A)   + n (B)

(iii) n (A –B) = n (A) – n (A Ç B) i.e. n (A) = n (A – B) + n (A ⋂ B)

(iv) n (A ⋃ B ⋃ C) = n (A) + n (B) + n (C) – n (A ⋂ B) – n (B ⋂ C) – n (A ⋂ C) + n (A ⋂ B ⋂ C)

(v) n (set of elements which are in exactly two of the sets A, B, C) = n (A ⋂ B)+n (B ⋂ C) + n (C ⋂ A) –3n(A ⋂ B ⋂ C)

(vi) n(set of elements which are in atleast two of the sets A, B, C) = n (A ⋂ B) + n (A ⋂ C) + n (B ⋂ C) –2n(A ⋂ B ⋂ C)

(vii) n (set of elements which are in exactly one of the sets A, B, C) = n (A) + n (B) + n (C) – 2n (A ⋂ B) – 2n (B ⋂ C) – 2n (A ⋂ C) + 3n (A ⋂ B ⋂ C)

Illustration -22

If A and B be two sets containing 3 and 6 element respectively, what can be the minimum number of elements in A ⋃ B? Find also, the maximum number of elements in A ⋃ B.

Solution

We have, n (A ⋃ B) = n(A) + n(B)    – n(A ⋂ B)

This shows that n (A ⋃ B) is minimum or maximum according as

n (A ⋂ B) is maximum or minimum respectively.

Case 1: When n (A ⋂ B) is minimum, ie. n (A ⋂ B) = 0. This is possible only when A ⋂ B = $\varphi$.

In this case,

n(A ⋃ B) = n (A)  + n (B) – 0 = n(A) + n (B) = 3 +6 = 9

n (A ⋃ B)_max = 9

Case 2: When n (A ⋂ B) is maximum

This is possible only when A $\subseteq$ B.

In this case n (A ⋂ B) = 3

∴ n (A ⋃ B) = n(A)  + n(B) – n (A ⋂ B) = (3 + 6-3) = 6

n (A ⋃ B)_min = 6.’

Illustration -23

In a group of 1000 people, there are 750 who can speak Hindi and 400 who can speak Bengali. How many can speak Hindi only? How many can speak Bengali? How many can speak both Hindi and Bengali?

Solution

Total number of people = 1000

n(H) = 750

n (B) = 400

n(H ⋃ B) = n (H) + n (B) – n (H ⋂ B)

n(H ⋂ B) = 750 + 400 – 1000

= 150 speaking Hindi and Bengali both.

People speaking only Hindi = n (H) – n (H ⋂ B) = 750 – 150 = 600

People speaking only Bengali = n (B) – n (H ⋂ B) = 400 – 150 = 250.’

Illustration -24

A survey shows that 63% of the Americans like cheese whereas 76% like apples. If x% of the Americans like both cheese and apples, find the value of x.

Solution

Let A denote the set of Americans who like cheese and let B denote those who like apples. Let the population of America be 100. Then,

n(A)= 63, n(B) = 76

Now, n(A ⋃ B) = n(A) + n(B) – n(A ⋂ B)

$\Rightarrow$ n(A ⋃ B) = 63+76-n(A ⋂ B)

$\Rightarrow$ n (A ⋂ B) = 139 – n(A ⋃ B)

But n(A ∪ B) ≤ 100 ⇒ n (A  ∩ B ) ≥ 39      …(i)

Now, A ∩ B ⊆ A and A ∩ B ⊆ B

⇒(A ∩ B) ≤ n (A) and n (A ∩ B) ≤ n (B)

⇒ (A ∩ B) ≤ 63     …(ii)

From (i) and (ii), we have 39 ≤ n (A ∩ B ) ≤ 63 ⇒ 39 ≤ x ≤ 63.’

Illustration -25

Out of 120 members of a class, 50 play Cricket, 60 play Football, 48 play Hockey, 18 play Cricket and Hockey, 20 play Cricket and Football, 24 play Hockey and Football and 10 play all the three games. Answer the following questions.

(i) How many of them play only Cricket?

(ii) How many of them play none?

(A) i = 22, ii = 14          (B) i = 22, ii = 44          (C) i = 32, ii = 24          (D) i = 32, ii = 42

Solution

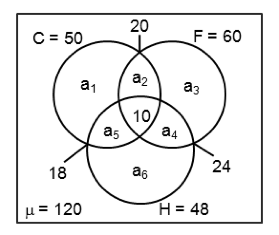
First let us draw then Venn diagram to note the information given in the problem.

i) Let $a_1$ = the members who play cricket only.

$a_2$ = the members who play cricket and football but not hockey.

$a_3$ = the members who play only football.

$a_4$ = the members who play football and hockey but not cricket.

$a_5$ = the members who play cricket and   hockey but not football.

a6 = the members who play only hockey.

$a_2$ = 20 – 10 = 10

$a_5$ = 18 – 10 = 8

$a_1$ = 50 – (a2 + a5 + 10)

$\Rightarrow$ 50 – (10 + 8 + 10) = 50 – 28 = 22

∴ 22 play only Cricket.

n(C ∪ F ∪ H) = n(C) + n(F) + n(H) – n(C ∩ F) – n(F ∩ H) – n(H ∩ C) +  n(C ∩ F ∩ H)

N(C) = 50, n(F) = 60, n(H) = 48, n(C ∩ F) = 20, n(F ∩ H) = 24, n(H ∩ C) = 18, n(C ∩ F ∩ H) = 10

n(C ∪F ∪ H)= 50 + 60 + 48 – 20 – 24 – 18 + 10

= 158 – 62 + 10= 168 – 62 = 106

Out of 120 students who play atleast one of the games is 106.

Therefore, 120 – 106 = 14 students do not play any game.