Redox Reactions

REDOX REACTIONS

Oxidation Number:

It is the charge which an atom appears to have when it is in combination. If all the polar covalent bonds of molecule are assumed to be 100% ionic then the charge appeared on corresponding atoms is known as their oxidation states. It may be a whole number or fractional, it depends on nature of compound in which it is present. There are some operational rules to determine oxidation number.

Calculation of Oxidation State / Oxidation Number   

There are several chemical reactions in which oxidation – reduction takes place.

Oxidation is

i) the gain of oxygen

ii) the loss of hydrogen

iii) the loss of electrons

iv) the increase of O.N.

Reduction is

i) the loss of oxygen

ii) the gain of hydrogen

iii)  the gain of electron

iv) the decrease in O.N.

To describe these changes, the concept of oxidation state becomes necessary. For ionic species, the charge on each ion is said to be the oxidation state for that atom. For example in NaCl, Na exists as Na+ and Cl exists as Cl-. Therefore the oxidation state of Na in NaCl is +1 and that of Cl- is – 1. But in covalent molecules, the charge on an atom would be so small that sometimes it becomes impossible to calculate the exact charge on each atom of a molecule. Therefore, the Oxidation State (O.S.) or Oxidation Number (O.N.) is defined as the charge, an atom would have in a molecule if all the bonds associated with this atom in the molecule are considered to be completely ionic. For example in H₂O there are two O–H bonds. If we assume both the O–H bonds to be completely ionic, then each H would possess a charge of +1, while O possess a charge of –2. This is because oxygen is more electronegative than hydrogen. On the other hand, in H₂O₂ there are two O–H bonds and one O–O bond. Considering each O–H bond to be ionic both the oxygen atoms acquire a charge of -1 and both the H, +1. This is because O–O bond can not be assumed to be ionic as both the atoms have the same electronegativity.

To calculate the oxidation state of an element in a molecule you need not always know the structure of the molecule. There are certain set of rules used to assign oxidation states in polyatomic molecules:     

Rules For Assigning Oxidation Number:

(i) Oxidation number of free elements or atoms is zero .

(ii) Oxidation number of allotropes is zero .

(iii) Oxidation number of atoms in homo-nuclear molecules is zero .

(iv) Oxidation number of mono-atomic ions is equal to the algebric charge on them .

(v) Oxidation number of F in compounds is – 1 .

(vi) Oxidation number of H in its compounds is + 1, except in metal hydrides where it is – 1.

(vii) Oxidation number of O is – 2 in its compounds, but in F₂O it is + 2 and in peroxides it is – 1 and – 0.5 in $K{O}_2$ .

(viii) Oxidation number of alkali metals in their compounds + 1 .

(ix) Oxidation number of alkaline earth metals in their compounds is + 2 .

(x) Oxidation number of an ion is equal to its charge .

(xi) Oxidation number of a molecule as a whole is zero .

(xii) The sum of oxidation number of all the atoms in a molecule should be zero and in an ion equal to its charge.

Illustration: Calculate the oxidation state of the underlined atoms in the given species.

(a) $\underline{N}{O}_2^{+}$                        (b) ${\underline{\mathrm{N}}\mathrm{O}}_3^{-}$

(c) ${\mathrm{K}\underline{\mathrm{Mn}}\mathrm{O}}_4$                    (d) ${\underline{\mathrm{Cr}}}_2{\mathrm{O}}_7^{2-}$

(e) ${\underline{\mathrm{Fe}}}_2{\mathrm{O}}_3$                      (f) ${\underline{\mathrm{Fe}}}_3{\mathrm{O}}_4$

Solution:

(a) Let the oxidation state of N in NO₂⁺ be x.

x + [2(-2)] = +1

x = + 5

Thus, oxidation state of N in ${\mathrm{NO}}_2^{+}$ is +5.

(b) Let x be the oxidation state of N in ${\mathrm{NO}}_3^{-}$.

x + [3(-2)] = -1

x = + 5

Thus, oxidation state of N in ${\mathrm{NO}}_3^{-}$ is + 5.

(c) Let the oxidation state of KMnO₄ be x.

[1(+1)] + x + [4(-2)] = 0

x = +7

Thus, oxidation state of Mn in KMnO₄ is + 7.

(d) Let the oxidation state of Cr in ${\mathrm{Cr}}_2{\mathrm{O}}_7^{2-}$ be x.

2x + [7(-2)] = -2

x = + 6

Thus, oxidation state of Cr in ${\mathrm{Cr}}_2{\mathrm{O}}_7^{2-}$ is +6.

(e) Let x be the oxidation state of Fe in Fe₂O₃.

2x + [3(-2)] = 0

x = + 3

Thus, oxidation state of Fe in Fe₂O₃ is +3.

(f) Let the oxidation state of Fe in Fe₃O₄ be x.

3x + [4(-2)] = 0

x = + 8/3

Thus, oxidation state of Fe in Fe₃O₄ is +8/3.

This is the average oxidation state of Fe in Fe₃O₄. Actually, Fe₃O₄ is made up of equimolar quantity of FeO and Fe₂O₃.

2. Most common oxidation states

Group	Outer shell configuration	Common oxid. States except zero in free state
I A	ns1	+ 1
II A	ns2	+ 2
III A	ns2 np1	+ 3, + 1
IV A	ns2 np2	+ 4, + 3, + 2, + 1, – 1, – 2, – 3, – 4
V A	ns2 np3	+ 5, + 3, + 1, – 1, – 3
VI A	ns2 np4	+ 6, + 4, + 2, – 2
VII A	ns2 np5	+ 7, + 5, + 3, + 1, – 1

Redox Reactions :

A reaction in which oxidation & reduction occur simultaneously .

Oxidising Agents :

They oxidise others, themselves are reduced & gain electrons. eg. O₂, O₃, HNO₃, MnO₂, H₂O₂, halogens, KMnO₄, K₂Cr₂O₇, KIO₃, FeCl₃, NaOCl.

Reducing Agents:

They reduce others, themselves get oxidised & lose electrons. eg C, CO, H₂S, SO₂, SnCl₂, Sodium thio Sulphate, Al, Na, CaH₂, NaBH₄, LiAlH₄ .

Both Oxidising & Reducing Agents:

SO₂ , H₂O₂ , O₃ , NO₂ ,  etc .

Balancing of Redox Reactions

Redox reactions involve oxidation and reduction both. Oxidation means loss of electrons and reduction means gain of electrons. Thus redox reactions involve electron transfer and the number of electrons lost are same as the number of electrons gained during the reaction. This aspect of redox reaction can serve as the basis of a pattern for balancing redox reactions.

There are 2 common and useful methods to balance redox reactions. These are

(A) Oxidation number method

(B) Ion-electron method.

(a) Oxidation Number Method

For balancing a redox reaction by oxidation number method, follow the order of steps as listed below (of course, all steps may not be required for balancing some reactions).

(i) For each redox reaction, deduce the oxidation state of the elements that are undergoing oxidation and reduction.

(ii) Separate the reactants and products into two half-reactions involving the elements that change their oxidation state. Write the skeletal equations for each half-reaction.

(iii) For each half-reaction, first balance the number of atoms of the element undergoing change in oxidation state.

(iv) Now find the total change in oxidation number by determining the change per atom and multiplying it by the total number of atoms that undergoes change. Also, decide whether electrons are lost or gained. An increase in oxidation state is loss of electrons and a decrease in oxidation state is gain of electrons.

(v) Add the electrons lost or gained to the half equation. Lost electrons are placed on the product side and gained electrons are kept on the reactant side.

(vi) Now add both the half reactions after multiplying by suitable integers to make the number of electrons lost and gained same.

(vii)  Transfer the coefficients of each reactant and product to the main skeleton equation.

(viii) If the coefficients developed are not correct, then change them by inspection.
Such coefficient changes are required when an element from a compound goes in
2 different compounds, one with the same oxidation state & the other with different oxidation state.

(ix) Count the charges on both sides of the equation and balance the charges in the equation by adding requisite H+ or OH- to the required side. If the reaction occurs in acidic solution, use H+ and if it occurs in basic solution, use OH-. If the reaction occurs in neutral solution, use H+ or OH- on any of the side as needed i.e. in a neutral solution, if negative charges are needed for balancing, use OH- and if positive charges are needed, use H+.

(x) Balance the hydrogens and oxygens by adding the appropriate number of $H_{2}O$ molecules on the required side.

Illustration: Balance the following oxidation–reduction equation,

${\mathrm{KMnO}}_4+\mathrm{KCl}+{\mathrm{H}}_2{\mathrm{SO}}_4⟶{\mathrm{MnSO}}_4+{\mathrm{K}}_2{\mathrm{SO}}_4+{\mathrm{H}}_2\mathrm{O}+{\mathrm{Cl}}_2$

Solution:

(i) Identify the oxidation & reduction half equations in ionic form.

Reduction half: ${\mathrm{Mn}}^{7+}⟶{\mathrm{Mn}}^{2+}$

Oxidation half: ${\mathrm{Cl}}^{-}⟶{\mathrm{Cl}}_2$

(ii) Balance the atoms that undergo change in oxidation state.

Reduction half: ${\mathrm{Mn}}^{7+}⟶{\mathrm{Mn}}^{2+}$

Oxidation half: $2{\mathrm{Cl}}^{-}⟶{\mathrm{Cl}}_2$

(iii) Add the electrons lost or gained to each half equation.

Reduction half: $5{\mathrm{e}}^{-}+{\mathrm{Mn}}^{7+}⟶{\mathrm{Mn}}^{2+}$     ……………….. a

Oxidation half: $2{\mathrm{Cl}}^{-}⟶{\mathrm{Cl}}_2+2{\mathrm{e}}^{-}$      ………………..  b

(iv) Multiply equation  with 2 and equation  with 5 and then add the two half reactions.

$$\begin{gathered} \left[{\mathrm{Se}}^{-}+{\mathrm{Mn}}^{7+}⟶{\mathrm{Mn}}^{2+}\right]\times 2 \\ \left[2\mathrm{Cl}\stackrel{-}{⟶}{\mathrm{Cl}}_2+2{\mathrm{e}}^{-}\right]\times 5 \\ ––––––––––– \\ 2{\mathrm{Mn}}^{7+}+10{\mathrm{Cl}}^{-}⟶5{\mathrm{Cl}}_2+2{\mathrm{Mn}}^{2+} \end{gathered}$$

(v) Transfer the coefficients to the main equation.

$2{\mathrm{KMnO}}_{\underset{\_}{4}}+10\mathrm{KCl}+{\mathrm{H}}_2{\mathrm{SO}}_4⟶2{\mathrm{MnSO}}_4+{\mathrm{K}}_2{\mathrm{SO}}_4+{\mathrm{H}}_2\mathrm{O}+5{\mathrm{Cl}}_2$

(vi) Balance H & O atoms

$2{\mathrm{KMnO}}_4+10\mathrm{KCl}+8{\mathrm{H}}_2{\mathrm{SO}}_4⟶5{\mathrm{Cl}}_2+2{\mathrm{MnSO}}_4+8{\mathrm{H}}_2\mathrm{O}+{\mathrm{K}}_2{\mathrm{SO}}_4$

(vii) Finally balance by inspection method.

$2{\mathrm{KMnO}}_4+10\mathrm{KCl}+8{\mathrm{H}}_2{\mathrm{SO}}_4⟶2{\mathrm{MnSO}}_4+6{\mathrm{K}}_2{\mathrm{SO}}_4+8{\mathrm{H}}_2\mathrm{O}+5{\mathrm{Cl}}_2$

(B) IN-ELECTRON METHOD

This method of balancing redox reaction involves following steps.

(i) For each redox reaction, deduce the oxidation state of the elements that are undergoing oxidation and reduction.

(ii) Separate the reactants and products into two half-reactions involving the elements that changes its oxidation state. Write the skeleton equations for each half-reaction.

(iii) Balance each half-reaction separately involving given steps.

1. First balance the atoms of the element undergoing oxidation or reduction.
2. Then balance atoms of the elements other than hydrogen and oxygen.
3. For balancing oxygen atoms in acidic or neutral medium, add suitable number of H₂O molecules to the side deficient in O while in alkaline medium, add equal number of H₂O molecules as the excess of O on the side having excess of O atoms and add double the number of OH^– ions on the opposite side of the equation.
4. In order to balance the hydrogen atoms in acidic or neutral medium, add required number of H⁺ to the side deficient in H while in alkaline medium, add equal number of OH^– ions as the excess number of H atoms on the side having excess H and add equal number of H₂O molecules on the opposite side of the equation.

(iv) Multiply each half-reaction by suitable integer to make the number of electrons lost and gained same and add both the half-equations to get a completely balanced reaction.

Illustration: Balance the redox equation, HNO₃ + H₂S  → NO + S by ion electron method (acidic medium).

Solution:

(i) Identify the oxidation & reduction halves.

Reduction half: HNO₃ → NO

Oxidation half:  H₂S → S

(ii) Atoms of the element undergoing oxidation and reduction are already balanced.

(iii) Balancing O atoms,

Reduction half: HNO₃ → NO + 2H₂O

Oxidation half:  H₂S → S

(iv) Balancing H atoms,

Reduction half: 3H⁺ + HNO₃ → NO + 2H₂O

Oxidation half:  H₂S → S + 2H⁺

(v) Balancing charge,

Reduction half: 3e^– + 3H⁺ + HNO₃  → NO + 2H₂O ……………….. A

Oxidation half:  H₂S  $\to$ S + 2H⁺ + 2e^–    ……………….. B

(vi) Multiplying equation A by 2 and equation B by 3 and then adding them.

3e^– + 3H⁺ + HNO₃ → NO + 2H₂O ] $\times$2 ………………..A

H₂S → S + 2H⁺ + 2e^– ] $\times$ 3   ………………..B

———————————————————–

2HNO₃ + 3H₂S  → 3S + 2NO + 4H₂O

Illustration: Balance the following redox equation,

FeC₂O₄  +  KMnO₄  +  H₂SO₄  → Fe₂(SO₄)₃ + CO₂  +  MnSO₄ + K₂SO₄

using ion–electron method (acidic medium).                                             

Solution:

(i) Identify the oxidation & reduction halves.

Oxidation half:  KMnO₄ →  MnSO₄

Reduction half: FeC₂O₄  → Fe₂(SO₄)₃ + CO₂

(ii) In both the half-reactions, all the atoms (other then O and H) are not appearing on both sides of the reaction. So, in the oxidation half, H₂SO₄ is to be added on the reactant side while in reduction half, H₂SO₄ and K₂SO₄ are to be added on reactant and product side respectively.

(iii) Balancing of the atoms of the element undergoing oxidation & reduction.

Reduction half: H₂SO₄ + 2KMnO₄ → 2MnSO₄ + K₂SO₄

Oxidation half:  H₂SO₄ + 2FeC₂O₄  → Fe₂(SO₄)₃ + 4CO₂

(iv) Balancing of the atoms of elements other than O and H.

Reduction half: 3H₂SO₄ + 2KMnO₄  → 2MnSO₄ + K₂SO₄

Oxidation half:  3H₂SO₄ + 2FeC₂O₄  → Fe₂(SO₄)₃ + 4CO₂

(v) Balancing O atoms,

Reduction half: 3H₂SO₄ + 2KMnO₄  → 2MnSO₄ + K₂SO₄ + 8H₂O

Oxidation half:  3H₂SO₄ + 2FeC₂O₄ → Fe₂(SO₄)₃ + 4CO₂

(vi) Balancing H atoms,

Reduction half: 10H⁺ + 3H₂SO₄ + 2KMnO₄  → 2MnSO₄ + K₂SO₄ + 8H₂O

Oxidation half:  3H₂SO₄ + 2FeC₂O₄  → Fe₂(SO₄)₃ + 4CO₂ + 6H⁺

(vii) Balancing charge,

Reduction half: 10e^– + 10H⁺ + 3H₂SO₄ + 2KMnO₄ → 2MnSO₄ + K₂SO₄ + 8H₂O  …….. A

Oxidation half:  3H₂SO₄ + 2FeC₂O₄  → Fe₂(SO₄)₃ + 4CO₂ + 6H⁺ + 6e^– ………….. B

(viii) Multiply equation A by 5 and equation B by 3 and then adding them.

10e^– + 10H⁺ + 3H₂SO₄ + 2KMnO₄ → 2MnSO₄ + K₂SO₄ + 8H₂O] $\times$ 3

3H₂SO₄ + 2FeC₂O₄  → Fe₂(SO₄)₃ + 4CO₂ + 6H⁺ + 6e^– ] $\times$ 5

——————————————————————————————————

10FeC₂O₄ + 6KMnO₄ + 24H₂SO₄ → 5Fe₂(SO₄)₃ + 6MnSO₄ + 3K₂SO₄ + 20CO₂ + 24H₂O

Illustration: Balance the following redox equation,

$\mathit{A}\mathit{s}{\mathit{O}}_{\mathbf{3}}^{\mathbf{3}\mathbf{-}}\mathbf{+}\mathit{M}\mathit{n}{\mathit{O}}_{\mathbf{4}}\mathbf{⟶}\mathit{A}\mathit{s}{\mathit{O}}_{\mathbf{4}}^{\mathbf{3}\mathbf{-}}\mathbf{+}\mathit{M}\mathit{n}{\mathit{O}}_{\mathbf{2}}$

using ion–electron method (alkaline medium).                                          

Solution:

(i) Identify the oxidation & reduction halves.

Reduction half: ${\mathrm{MnO}}_4^{-}⟶{\mathrm{MnO}}_2$

Oxidation half: ${\mathrm{ASO}}_3^{3-}⟶{\mathrm{AsO}}_4^{3-}$

(ii) Atoms of the element undergoing oxidation and reduction are already balanced.

(iii) Balancing O atoms,

Reduction half: $2{\mathrm{H}}_2\mathrm{O}+{\mathrm{MnO}}_4^{-}⟶{\mathrm{MnO}}_2+4{\mathrm{OH}}^{-}$

Oxidation half: $2{\mathrm{OH}}^{-}+{\mathrm{AsO}}_3^{3-}⟶{\mathrm{AsO}}_4^{3-}+{\mathrm{H}}_2\mathrm{O}$

(iv) Balancing H atoms,

H atoms are already balanced in both the half-reactions.

(v) Balancing charge,

Reduction half: $3{\mathrm{e}}^{-}+2{\mathrm{H}}_2\mathrm{O}+{\mathrm{MnO}}_4^{-}⟶{\mathrm{MnO}}_2+4{\mathrm{OH}}^{-}$………….. B

Oxidation half: $2{\mathrm{OH}}^{-}+{\mathrm{AsO}}_3^{3-}⟶{\mathrm{AsO}}_4^{3-}+{\mathrm{H}}_2\mathrm{O}+2{\mathrm{e}}^{-}$………….. A

(vi) Multiply equation A by 3 and equation B by 2 and then add A and B .

$\left[3{\mathrm{e}}^{-}+2{\mathrm{H}}_2\mathrm{O}+{\mathrm{MnO}}_4^{-}⟶{\mathrm{MnO}}_2+4{\mathrm{OH}}^{-}\right]\times 2$

$\left[2{\mathrm{OH}}^{-}+{\mathrm{AsO}}_3^{3-}⟶{\mathrm{AsO}}_4^{3-}+{\mathrm{H}}_2\mathrm{O}+2{\mathrm{e}}^{-}\right]\times 3$

—————————————————-

${\mathrm{AsO}}_3^{3-}+2{{\mathrm{MnO}}^{–}}_4+{\mathrm{H}}_2\mathrm{O}⟶3{\mathrm{AsO}}_4^{3-}+2{\mathrm{MnO}}_2+2{\mathrm{OH}}^{-}$

Mostly, the medium in which a redox reaction is to be balanced is given in the problem but if the problem does not state the medium explicitly, then the medium is decided by looking at the reactants or products. If an acid or base is one of the reactants or products, then the medium is the same. If ammonia is present, the solution would be basic, for example ammonium ion is present, it would be acidic. If metals which forms insoluble hydroxides are shown in their ionic form, the solution is acidic.

Although, the oxidation number method and ion-electron method both lead to the correct form of the balanced redox reaction but ion-electron method is considered superior to oxidation number method due to following advantages:

(i) In ion-electron method, all reactants and products are completely balanced
(i.e. coefficient is developed for each one of them) whether they participate in the redox change or not, while in oxidation number method, the balancing coefficient is developed only for the species involved in redox change.

(ii) The balancing coefficients developed in ion-electron method are always correct and needs no amendment while such coefficients are to be changed sometimes in oxidation number method.

COMMON OXIDATION AND REDUCTION PARTS

OXIDATION PARTS

REDUCTION PARTS

$\begin{array}{l}{\mathrm{Fe}}^{2+}⟶{\mathrm{Fe}}^{3+}\\ \mathrm{Zn}⟶{\mathrm{Zn}}^{2+}\\ X^{-}⟶X_2\\ {\mathrm{S}}^{2-}⟶\mathrm{S}\\ {\mathrm{H}}_2{\mathrm{O}}_{\overrightarrow{2}}⟶{\mathrm{O}}_2\\ {\mathrm{SO}}_3^{2-}⟶{\mathrm{SO}}_4^{2-}\\ {\mathrm{C}}_2{{\mathrm{O}}_4}^{2-}⟶{\mathrm{CO}}_2\\ {\mathrm{S}}_2{{\mathrm{O}}_3}^{2-}⟶{\mathrm{S}}_4{{\mathrm{O}}_6}^2\\ I_2⟶I{O}_3^{-}\end{array}$

$$\begin{gathered} {\mathrm{Fe}}^{3+}-\to {\mathrm{Fe}}^{2+} \\ \begin{array}{l}{X}_2⟶X^{-}\\ {\mathrm{Cr}}_2{\mathrm{O}}_7^2 ⟶{\mathrm{Cr}}^{3+}\\ {\mathrm{NO}}_3^{-}⟶\mathrm{NO}\\ \begin{array}{l}{\mathrm{MnO}}_4^{-}\to {\mathrm{Mn}}^{2+}\left(\text{ neutral med. }\right)\\ {{\mathrm{MnO}}^{–}}_4\to {\mathrm{MnO}}_2\text{ (Basic med.) }\\ \begin{array}{l}{\mathrm{SO}}_4^{2-}⟶{\mathrm{SO}}_2\\ {\mathrm{MnO}}_2⟶{\mathrm{Mn}}^{2+}\end{array}\end{array}\end{array} \end{gathered}$$

Disproportionation Reactions

In same atom is getting oxidised as well as reduced. Such type of redox reactions are called Disproportionation reaction. Examples are

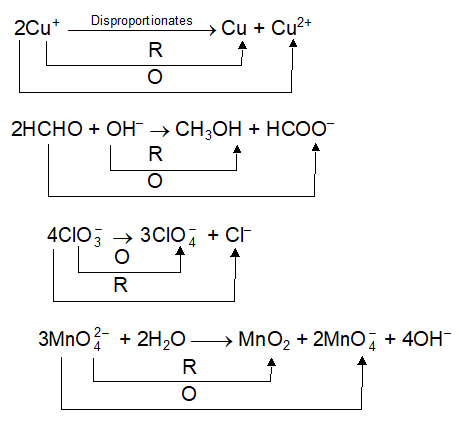
Metathesis Reactions:

In these two compounds react to form two new compounds and no change  in oxidation number occur .

(i) $\mathrm{Pb}{\left({\mathrm{NO}}_3\right)}_2+{\mathrm{K}}_2{\mathrm{CrO}}_4⟶{\mathrm{PbCrO}}_4+2{\mathrm{KNO}}_3$  (ii) $\mathrm{HCl}+\mathrm{NaOH}⟶\mathrm{NaCl}+{\mathrm{H}}_2\mathrm{O}$

Chemical Equivalence

Equivalent Weight

The equivalent weight of a substance is the number of parts by weight of the substance that combine with or displace directly of indirectly 1.008 parts by weight of hydrogen or 8 parts by weight of oxygen or 35.5 parts by weight of chlorine.

Otherwise,

Equivalents mass = $\frac{\text{ Atomic or molecular mass }}{{}^{‘}n\text{ factor }}$

Also,

Number of equivalents = $\frac{\text{ mass }}{\text{ equivalent mass }}=\frac{\text{ mass }}{\text{ molecular mass / }n\text{ factor }}$

So,

Number of equivalents = (n factor) x (no. of moles)

Normality (N)

It is defined as the number of equivalents of a solute present in one litre of solution. Equivalent is also the term used for amount of substance like mole with the difference that one equivalent of a substance in different reactions may be different as well as the one equivalent of each substance is also different.

Normality (N) = $\frac{\text{ number of equivalents of solute }}{\text{ Volume of solution (in litres) }}$

Let the weight of solute be w g, equivalent mass of solute be E g/eqv., molecular mass be M_w g/mole and the volume of solution be V litre.

Number of equivalents of solute =$\frac{\text{ weight of solute }}{\text{ Equivalent mass of solute }}=\frac{\mathrm{W}}{\mathrm{E}}$

$\therefore \mathrm{N}=\frac{w}{E}\times \frac{1}{V\left(\text{ inlitres }\right)}=\frac{w}{M_w/n}\times \frac{1}{v\left(\text{ in litre }\right)}=\mathrm{n}\times \text{ Molarity }$

Hence ,

Normality of solution = n factor $\times$ molarity of solution

Law of Chemical Equivalence

According to the law of equivalence, whenever two substances react, the equivalents of one will be equal to the equivalents of other and the equivalents of any product will also be equal to that of the equivalents of the reactant.

 or a reaction nA + mB → pC + qD     (It is not necessary to balance the equation)

Equivalents of A = Equivalents of B = Equivalents of C = Equivalents of D

n-factor calculation 

(A) ACIDS

Acids are the species which furnish H⁺ ions when dissolved in a solvent. For acids, n-factor is defined as the number of H⁺ ions replaced by 1 mole of acid in a reaction. Note that the n-factor for acid is not equal to its basicity; i.e. the number of moles of replaceable H⁺ atoms present in one mole of acid.

For example, n-factor of HCl = 1,

n-factor of HNO₃ = 1,

n-factor of H₂SO₄ = 1 or 2, depending upon extent of reaction it undergoes.

H₂SO₄ + NaOH  → NaHSO₄  +  H₂O.

Although one mole of H₂SO₄ has 2 replaceable H atoms but in this reaction H₂SO₄ has given only one H⁺ ion, so its n-factor would be 1.

H₂SO₄ + 2NaOH  → Na₂SO₄ + 2H₂O

The n-factor of H₂SO₄ in this reaction would be 2.

Similarly,

n-factor of H₂SO₃ = 1 or 2

n-factor of H₂CO₃ = 1 or 2

n-factor of H₃PO₄ = 1 or 2 or 3

n-factor of H₃PO₃ = 1 or 2  because one of the H is not replaceable in H₃PO₃.

The H atoms which are linked to oxygen are replaceable while the H atom linked directly to central atom (P) is nonreplaceable.

n-factor of H₃BO₃ = 1

In H₃BO₃, although all three H are linked to oxygen, yet all 3 H are not replaceable. Here, boron atom is electron deficient, so it acts as a Lewis acid. When H₃BO₃ is added to water, then oxygen atom of H₂O through its lone pair attack the boron atom, as follows

The net reaction is H₃BO₃ + 2H₂O → [B(OH)₄]^–  + H₃O⁺.

Thus, one mole of H₃BO₃ in solution gives only one mole of H⁺, so its n-factor is 1.

(B) BASES

Bases are the species, which furnish OH^– ions when dissolved in a solvent. For bases, n-factor is defined as the number of OH^– ions replaced by 1 mole of base in a reaction. Note that n-factor is not equal to its acidity i.e. the number of moles of replaceable OH^– ions present in 1 mole of base.

For example,

n-factor of NaOH = 1

n-factor of Zn(OH)₂ = 1 or 2

n factor of Ca(OH)₂ = 1 or 2

n factor of Al(OH)₃  = 1 or 2 or 3

n factor of NH₄(OH) = 1.

(C) SALTS WHICH REACT SUCH THAT NO ATOM UNDERGOES CHANGE IN OXIDATION STATE

The n-factor for such salts is defined as the total moles of cationic /anionic charge replaced in 1 mole of the salt. For the reaction,

${\mathrm{Na}}_3{\mathrm{PO}}_4+{\mathrm{BaCl}}_2⟶\mathrm{NaCl}+{\mathrm{Ba}}_3{\left({\mathrm{PO}}_4\right)}_2$

To get one mole of Ba₃(PO₄)₂, two moles of Na₃PO₄ are required, which means six moles of Na⁺ are completely replaced by 3 moles of Ba²⁺ ions. So, six moles of cationic charge is replaced by 2 moles of Na₃PO₄, thus each mole of Na₃PO₄ replaces 3 moles of cationic charge. Hence, n-factor of Na₃PO₄ in this reaction is 3.

(D) SALTS WHICH REACT IN A MANNER THAT ONLY ONE ATOM UNDERGOES CHANGE IN OXIDATION STATE AND GOES IN ONLY ONE PRODUCT

The n-factor of such salts is defined as the number of moles of electrons exchanged
(lost or gained) by one mole of the salt.

Let us have a salt A_aB_b in which oxidation state of A is +x. It changes to a compound,
which has atom D in it. The oxidation state of A in A_cD be +y.

${\mathrm{A}}_{\mathrm{a}}^{+x}{\mathrm{B}}_{\mathrm{b}}⟶{\mathrm{A}}_{\mathrm{c}}^{+y}\mathrm{D}$

The n-factor of A_aB_b is calculated as n = | ax – ay |

To calculate n-factor of a salt of such type, we take one mole of the reactant and find the number of mole of the element whose oxidation state is changing. This is multiplied with the oxidation state of the element in the reactant, which gives us the total oxidation state of the element in the reactant. Now, we calculate the total oxidation state of the same element in the product for the same number of mole of atoms of that element in the reactant. Remember that the total oxidation state of the same element in the product is not calculated for the number of mole of atoms of that element in the product.

For example, let us calculate the n-factor KMnO₄ for the given chemical change.

${\mathrm{KMnO}}_4\stackrel{{\mathrm{H}}^{+}}{⟶}{\mathrm{Mn}}^{+2}$

In this reaction, oxidation state of Mn changes from +7 to +2. Thus, KMnO₄ is acting as oxidising agent, since it is reduced.

$\therefore$n-factor of KMnO₄ = $\mid 1\times (+7)-1\times (+2)\mid =5$

Similarly,

$\begin{array}{l}\text{ (a) }{\mathrm{KMnO}}_4\stackrel{{\mathrm{H}}_2\mathrm{O}}{⟶}{\mathrm{Mn}}^{+4}\\ \text{ n-factor of }{\mathrm{KMnO}}_4=|1\times (+7)-1\times (+4\left)\right|=3\end{array}$

$\begin{array}{l}\text{ (b) }{\mathrm{KMnO}}_4\stackrel{O{H}^{–}}{\to }{\mathrm{Mn}}^{+6}\\ \text{ n-factor of }{\mathrm{KMnO}}_4=|1\times (+7)-1\times (+6\left)\right|=1\end{array}$

It can be seen that in all the above chemical changes, KMnO₄ is acting as oxidising agent, yet its n-factor is not same in all reactions. Thus, the n-factor of a compound is not fixed,
it depends on the type and the extent of reaction it undergoes.

(E) SALTS THAT REACT IN A MANNER THAT ONLY ONE ATOM UNDERGO CHANGE IN OXIDATION STATE BUT GOES IN TWO PRODUCTS WITH THE SAME OXIDATION STATE.

Let us have a salt A_aB_b in which oxidation state of A is –x. It undergoes a reaction such that element A changes it oxidation state and goes in more than one (two) products with the same oxidation state (but different oxidation state than in the reactant). In such case, the n-factor is calculated in the same manner as in case 4.

Let the chemical change be ${\mathrm{A}}_{\mathrm{a}}^{+x}{\mathrm{B}}_{\mathrm{b}}⟶{\mathrm{A}}_{\mathrm{c}}^{+\mathrm{y}}\mathrm{D}+{\mathrm{A}}_{\mathrm{e}}^{+\mathrm{y}}\mathrm{F}$

In such cases, the number of products in which element A is present is of no significance since the oxidation state of A in both the products is same. The point of importance is not the number of products containing that element which undergoes change in oxidation state but the oxidation state of the element is of importance. The n-factor of A_aB_b is calculated in the same way as in case 4.

$\therefore$n-factor of A_aB_b = |ax – ay|

For example, let us calculate the n-factor of K₂Cr₂O₇ for the given chemical change.

${\mathrm{Cr}}_2{\mathrm{O}}_7^{2-}⟶{\mathrm{Cr}}^{3+}+{\mathrm{Cr}}^{3+}$

In this reaction, oxidation state of Cr changes from +6 to +3 in both products.

$\therefore$n-factor of K₂Cr₂O₇ = $|2\times (+6)-2\times (+3\left)\right|=6$

(F) SALTS WHICH REACT IN A MANNER THAT ONLY ONE ATOM UNDERGOES CHANGE IN OXIDATION STATE BUT GOES IN TWO PRODUCTS WITH DIFFERENT OXIDATION STATE (DIFFERENT THAN IN THE REACTANT) AS A RESULT OF EITHER OXIDATION OR REDUCTION.

Let the chemical change be ${\mathrm{A}}_{\mathrm{a}}^{+x}{\mathrm{B}}_{\mathrm{b}}⟶{\mathrm{A}}_{\mathrm{c}}^{+\mathrm{y}}\mathrm{D}+{\mathrm{A}}_{\mathrm{e}}^{+\mathrm{z}}\mathrm{F}$

In such cases, n-factor calculation is not possible until we know that how much of A has changed its oxidation state to +y and how much of A has changed its oxidation state. to +z. This is because the number of moles of electrons lost or gained by one mole of A_aB_b would depend on the fact that how much of A underwent change to oxidation state +y and how much of A underwent change to oxidation state +z.

This is possible only by knowing the balanced chemical reaction.  If we know the balanced chemical reaction, then the n-factor calculation is of no use because problem can be solved using mole concept. But nevertheless, n-factor calculation in such cases can be done as follows.

Let us take a chemical change, $2{\mathrm{Mn}}^{+7}\to {\mathrm{Mn}}^{+4}+{\mathrm{Mn}}^{+2}$ out of the two moles of Mn⁺⁷, one mole Mn⁺⁷ changes to Mn⁺⁴ by gaining 3 mole of electrons and the other mole of Mn⁺⁷ changes to Mn⁺² by gaining 5 mole of electrons, so in all 8 mole of electrons are gained by 2 mole of Mn⁺⁷.
So each mole of Mn⁺⁷ has gained 8/2 = 4 mole of electrons. Thus, 4 would be the n-factor of Mn⁺⁷ in this reaction.

If the reaction would have been $3{\mathrm{Mn}}^{+7}⟶2{\mathrm{Mn}}^{+2}+{\mathrm{Mn}}^{+4}$

Out of 3 moles of $M{n}^{+7}$ two moles of ${\mathrm{Mn}}^{+7}$ changes to ${\mathrm{Mn}}^{+2}$ by gaining 10 mole of electrons and one mole of ${\mathrm{Mn}}^{+7}$ changes to ${\mathrm{Mn}}^{+4}$ by gained 3 mole of electrons. Thus each mole of ${\mathrm{Mn}}^{+7}$ have gained 13/3 mole of electrons. Therefore, the n-factor of in this reaction would be 13/3.

Note that n–factor can be a fraction because it is not the number of electrons exchanged but it is the number of moles of electrons exchanged which can be a fraction.

Now, if the reaction would have been $3{\mathrm{Mn}}^{+7}⟶{\mathrm{Mn}}^{+2}+2{\mathrm{Mn}}^{+4}$. Thus, each mole of  Thus, each mole of $M{n}^{+7}$have gained 11/3 mole of electron. Therefore, n-factor of $M{n}^{+7}$ in this reaction would be 11/3.

(G) Salts which react in a fashion that only one atom undergoes change in oxidation state but goes in two products with different oxidation state (in one product with same oxidation state and in other with different oxidation state than in the reactant)

Let the reaction be ${\mathrm{A}}_{\mathrm{a}}^{+x}{\mathrm{B}}_{\mathrm{b}}⟶{\mathrm{A}}_e^{+x}\mathrm{F}+{\mathrm{A}}_{\mathrm{c}}^{+\mathrm{y}}\mathrm{D}$

For such reactions also, the n-factor calculation is not possible without the knowledge of balanced chemical reaction because n-factor of A_aB_b would depend on the fact that how much of A underwent change to oxidation state +y and how much of A remained in the same oxidation state +x.

For example, if we have a chemical change as

$2{\mathrm{Mn}}^{+7}⟶{\mathrm{Mn}}^{+7}+{\mathrm{Mn}}^{+2}$(the compounds containing Mn in +7 state in reactant and product are different.

In this reaction, 5 moles of electrons are gained by 2 moles of  so each mole of Mn⁺⁷ takes up 5/2 mole of electrons. Therefore, n-factor of Mn⁺⁷ in this reaction would be 5/2.

(H) SALTS THAT REACT IN A MANNER THAT TWO TYPE OF ATOMS IN THE SALT UNDERGO CHANGE IN OXIDATION STATE (BOTH THE ATOMS ARE EITHER GETTING OXIDISED OR REDUCED).

Let the change be represented as ${\mathrm{A}}_{\mathrm{a}}^{+x}{\mathrm{B}}_{\mathrm{b}}⟶{\mathrm{A}}_{\mathrm{c}}^{+y}\mathrm{D}+{\mathrm{E}}_{\mathrm{f}}{\mathrm{B}}^{+\mathrm{z}}$

In this reaction, both A and B are changing their oxidation states and both of them are either getting oxidised or reduced. In such cases, the n-factor of the compound would be the sum of individual n-factors of A and B.

n-factor of A = |ax – ay|

n-factor of B = |- ax – bz| because the total oxidation state of ‘b’ B’s in the reactant is -ax (as the total oxidation state of ‘a’ A’s in the reactant is +ax) and the total oxidation state of
y B’s in the product is bz.

$\therefore$ n-factor of A_aB_b = |ax – ay| + |-ax – bz|

In general, the n-factor of the salt will be the total number of mole of electrons lost or gained by one mole of the salt.

For example, we have a reaction, ${\mathrm{Cu}}_2^{+1}{\mathrm{S}}^{-2}⟶{\mathrm{Cu}}^{2+}+{\stackrel{+4}{\mathrm{SO}}}_2$

in which Cu⁺ and S^2– both are getting oxidised to Cu²⁺ and S⁺⁴ respectively.

$\therefore$ n-factor of ${\mathrm{Cu}}_2\mathrm{S}=|2\times (+1)-2\times (+\underset{\_}{2}\left)\right|+|1\times (-2)-1\times (+4\left)\right|=8$                               

(I) SALTS THAT REACT IN A MANNER THAT TWO ATOMS IN THE SALT UNDERGOES CHANGE IN OXIDATION STATE (ONE ATOM IS GETTING OXIDISED AND THE OTHER IS GETTING REDUCED).

If we have a salt which react in a fashion that atoms of one of the element are getting oxidised and the atoms of another element are getting reduced and no other element on the reactant side is getting oxidised or reduced, than the n-factor of such a salt can be calculated either by taking the total number of moles of electrons lost or total number of mole of electrons gained by one mole of the salt.

For example, decomposition reaction of KClO₃ is represented as ${\mathrm{K}\stackrel{+5}{\mathrm{Cl}} \stackrel{–2}{\mathrm{O}}}_3⟶\mathrm{K}\stackrel{–1}{\mathrm{Cl}}+{\stackrel{0}{\mathrm{O}}}_2$

In this reaction, O^2– is getting oxidised to O₂ and Cl⁺⁵ is getting reduced to Cl^–1. In each case, 6 mole of electrons are exchanged whether we consider oxidation or reduction.

n-factor of KClO₃ considering oxidation = |3(-2)-3(0)| = 6

or n-factor of KClO₃ considering reduction =$|1\times (+5)-1\times (-1\left)\right|=6$

(J) SALTS OR COMPOUNDS WHICH UNDERGOES DISPROPORTIONATION REACTION.

Disproportionation reactions are the reactions in which oxidising and reducing agents are same or the same element from the same compound is getting oxidised as well as reduced.

n-factor of a disproportionation reaction can only be calculated using a balanced chemical reaction. We will categorize disproportionation reactions into two types.

(a) Disproportionation reactions in which moles of compound getting oxidised and reduced are same i.e. moles of oxidising agent and reducing agent are same. The n-factor for such compounds is calculated by either the number of mole of electrons lost or gained by one mole of the compound because in such a case, n-factor of the compound acting as oxidizing agent or as reducing agent would be same.

For example, 2H₂O₂ → 2H₂O + O₂

Out of the 2 mole of H₂O₂ used in reaction, one mole of H₂O₂ gets oxidised to O₂ (oxidation state of O changes from -1 to 0) while the other mole of H₂O₂ gets reduced to H₂O (oxidation state of O changes from -1 to -2). When 1 mole of H₂O₂ gets oxidised to O₂, the half-reaction would ${\mathrm{O}}_2^{2-}⟶{\mathrm{O}}_2^0+2{\mathrm{e}}^{-}$be and when 1 mole of H₂O₂ gets reduced to H₂O, the half-reaction would be ${\mathrm{O}}_2^{2-}+2{\mathrm{e}}^{-}⟶2{\mathrm{O}}^{2-}$

Thus, it is evident that one mole of H₂O₂ (which is either getting oxidised or reduced) will lose or gain 2 mole of electrons. Therefore, n-factor of H₂O₂ as oxidizing as well as reducing agent in this reaction is 2. Thus,

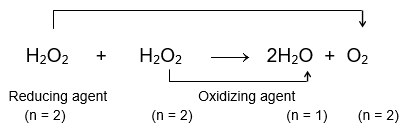
or when the reaction is written as $2{\mathrm{H}}_2{\mathrm{O}}_2⟶2{\mathrm{H}}_2\mathrm{O}+{\mathrm{O}}_2$

where, H₂O₂ is not distinguished as how much of it functions as oxidizing agent and how much as reducing agent, then n-factor calculation can be done in the following manner. Find the number of electrons exchanged (lost or gained) using the balanced equation and divide it by the number of moles of H₂O₂ involved in the reaction. Thus, the n-factor of H₂O₂ when the reaction is written without segregating oxidising and reducing agent is $\frac{2}{2}$ = 1.

$\underset{\left(n=1\right)}{2{\mathrm{H}}_2{\mathrm{O}}_2}⟶\underset{\left(\mathrm{n}=1\right)}{2{\mathrm{H}}_2\mathrm{O}}+\underset{\left(n=2\right)}{{\mathrm{O}}_2}$                                                                                                                              

(b) Disproportionation reactions in which moles of compound getting oxidised and reduced are not same i.e. moles of oxidising agent and reducing agent are not same.

For example, $6{\mathrm{Br}}_2+12{\mathrm{OH}}^{-}⟶10{\mathrm{Br}}^{-}+2{\mathrm{BrO}}_3^{-}+6{\mathrm{H}}_2\mathrm{O}$

In this reaction, the mole of electrons lost by the oxidation of some of the moles of Br₂ are
same as the number of mole of electrons gained by the reduction of rest of the moles of Br₂. Of the 6 moles of Br₂ used, one mole is getting oxidized, losing 10 electrons (as reducing agent) and 5 moles of Br₂ are getting reduced and accepts 10 moles of electron (as oxidizing agent).

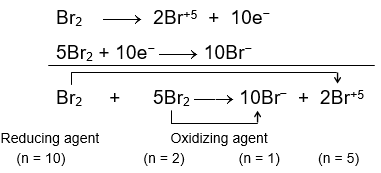
Thus, n-factor of Br₂ acting as oxidizing agent is 2 and that Br₂ acting as reducing agent has n-factor 10.

Or when the reaction is written as $6{\mathrm{Br}}_2⟶10{\mathrm{Br}}^{-}+2{\mathrm{Br}}^{+5}$

where, Br₂ is not distinguished as how much of it functions as oxidizing agent and how much as reducing agent, then for calculating n-factor of compound in such reactions, first find the total number of mole of electrons exchanged (lost or gained) using the balanced equation and divide it with the number of mole of Br₂ involved in the reaction to get the number of mole of electrons exchanged by one mole of Br₂.

In the overall reaction, the number of mole of electrons exchanged (lost or gained) is
10 and the moles of Br₂ used in the reaction are 6. Thus, each mole of Br₂ has exchanged 10/6 or 5/3 mole of electrons. Therefore, the n-factor of Br₂ when the reaction is written without segregating oxidising and reducing agent is 5/3.

$\underset{\left(n=5/3\right)}{6{\mathrm{Br}}_2}⟶\underset{\left(n=1\right)}{10{\mathrm{Br}}^{-}}+\underset{\left(n=5\right)}{2{\mathrm{Br}}^{+5}}$

VOLUMETRIC ANALYSIS

Now, we have developed enough platforms to understand the law of equivalents and volumetric analysis.

The volumetric analysis is an analytical method of estimating the concentration of a substance in a solution by adding exactly same number of equivalents of another substance present in a solution of known concentration.

This is the basic principle of titration. Volumetric analysis is also known as titrimetric analysis.

The substance whose solution is employed to estimate the concentration of unknown solution is called titrant and the substance whose concentration is to be estimated is called titrate.

The volumetric analysis is divided into following types:

(A) Simple titrations

(B) Back titrations

(C) Double titrations

Simple titration

The aim of simple titration is to find the concentration of an unknown solution with the help of the known concentration of another solution.

Let us take a solution of a substance ‘A’ of unknown concentration (say N₁). We are provided with solution of another substance ‘B’ whose concentration is known (N₂). We take a certain known volume (V₁ litre) of ‘A’ in a flask and start adding ‘B’ from burette to ‘A’ slowly till all the ‘A’ is consumed by ‘B’. This can be known with the aid of suitable indicator, which shows colour change after the complete consumption of ‘A’.  Let the volume of B consumed is V₂ litre.

According to the law of equivalents, the number of equivalents of ‘A’ would be equal to the
number of equivalents of ‘B’.

$\therefore$ N₁V₁ = N₂V₂, where N₁ is the concentration of ‘A’.

Thus using this equation, the value of N₁ can be calculated.

For example, in a redox titration, an oxidant is estimated by adding reductant or vice-versa.
For example, Fe²⁺ ions can be estimated by titration against acidified KMnO₄ solution when Fe²⁺ ions are oxidised to Fe³⁺ ions and KMnO₄ is reduced to Mn²⁺ in the presence of acidic medium. KMnO₄ functions as self-indicator as its purple colour is discharged at the equivalence point.

$$\begin{gathered} \begin{array}{r}{\mathrm{MnO}}_4^{-}+8{\mathrm{H}}^{+}+5{\mathrm{e}}^{-}⟶{\mathrm{Mn}}^{2+}+4{\mathrm{H}}_2\mathrm{O}\\ \left[{\mathrm{Fe}}^{2+}⟶{\mathrm{Fe}}^{3+}+{\mathrm{e}}^{-}\right]\times 5\end{array} \\ –––––––––––––––––– \\ \underset{\left(n=5\right)}{{\mathrm{MnO}}_4^{-}}+8{\mathrm{H}}^{+}+\underset{\left(n=1\right)}{5{\mathrm{Fe}}^{2+}}⟶{\mathrm{Mn}}^{2+}+5{\mathrm{Fe}}^{3+}+4{\mathrm{H}}_2\mathrm{O} \end{gathered}$$

In addition to acidified KMnO₄, acidified KCr₂O₇ can also be employed. Other redox titrations are iodimetry, iodometry etc.

(i) IODIMETRY

This titration involves free iodine. Such direct estimation of iodine is called iodimetry.  This involves the titration of iodine solution with known sodium thiosulphate solution, whose normality is N. Let the volume of sodium thiosulphate used be V litre.

$\underset{\left(\mathrm{n}=2\right)}{{\mathrm{I}}_2}+\underset{\left(n=1\right)}{2{\mathrm{Na}}_2{\mathrm{S}}_2{\mathrm{O}}_3}⟶2\mathrm{Nal}+{\mathrm{Na}}_2{\mathrm{S}}_4{\mathrm{O}}_6$

(n=2)        (n=1)

Equivalents of I₂ = Equivalents of Na₂S₂O₃ used = N$\times$V

Moles of $I_2=\frac{N\times V}{2}$

Mass of free I₂ in the solution = $\left[\frac{\mathrm{N}\times \mathrm{V}}{2}\times 254\right]\mathrm{g}$

(ii) IODOMETRY

This is an indirect method of estimation of iodine. An oxidising agent is made to react with excess of solid KI. The oxidising agent oxidises I^– to I₂. This liberated iodine is then made to react with Na₂S₂O₃ solution of normality N. Let the volume of thiosulphate solution required be V litre.

Oxidising Agent $$\begin{gathered} Oxidi\sin g Agent \left(\mathrm{A}\right)+\mathrm{KI}⟶\underset{+}{{\mathrm{I}}_2}\stackrel{2{\mathrm{Na}}_2{\mathrm{S}}_2{\mathrm{O}}_3}{\to }2\mathrm{Nal}+{\mathrm{Na}}_2{\mathrm{S}}_4{\mathrm{O}}_6 \\ reduced form of \\ oxidizing agent \end{gathered}$$

Equivalents of ‘A’ = Equivalents of I₂ = Equivalents of Na₂S₂O₃ used = N $\times$ V

Equivalents of I₂ liberated from KI = N $\times$ V

Equivalents of ‘A’ = N $\times$ V

Let the n-factor of ‘A’ in its reaction with KI be x, then

Mass of ‘A’ consumed = $\frac{\mathrm{N}\times \mathrm{V}}{x}\times {\mathrm{M}}_{\mathrm{A}}$  (where M_A is the molar mass of A)

For  iodimetric and iodometric titrations, starch solution is used as indicator. Starch solution give blue or violet colour with free iodine. At the end point the blue or violet colour disappears when iodine is completely changed to iodide.

Back titration

 Let us assume that we have an impure solid substance ‘C’, weighing ‘w’ g and we are required to calculate the percentage purity of ‘C’ in the sample. We are also provided with two solutions ‘A’ and ‘B’, where the concentration of ‘B’ is known (N₁) and that of ‘A’ is unknown. For the back titration to work, following conditions are to be satisfied (a) Compounds ‘A’, ‘B’ and ‘C’ should be such that ‘A’ and ‘B’ react with each other. (b) ‘A’ and pure ‘C’ also react with each other but the impurity present in ‘C’ does not react with ‘A’. (c) Also the product of ‘A’ and ‘C’ should not react with ‘B’.

Now we take out certain volume of ‘A’ in a flask (the equivalents of ‘A’ taken should be ³ equivalents of pure ‘C’ in the sample) and perform a simple titration using ‘B’. Let us assume that the volume of ‘B’ used be V₁ litre.

Equivalents of ‘B’ reacted with ‘A’ = N₁V₁

$\therefore$ Equivalents of ‘A’ initially = N₁V₁

In another flask, we again take same volume of ‘A’ but now ‘C’ is added to this flask. Pure part of ‘C’ reacts with ‘A’ and excess of ‘A’ is back titrated with ‘B’. Let the volume of ‘B’ consumed is V₂ litre.

Equivalents of ‘B’ reacted with excess of ‘A’ = N₁V₂

$\therefore$ Equivalents of ‘A’ in excess = N₁V₂

Equivalents of ‘A’ reacted with pure ‘C’ = (N₁V₁ – N₁V₂)

Equivalents of pure ‘C’ = (N₁V₁ – N₁V₂)

Let the n-factor of ‘C’ in its reaction with ‘A’ be x, then the moles of pure ‘C’ = $=\frac{\left({\mathrm{N}}_1{\mathrm{V}}_1-{\mathrm{N}}_1{\mathrm{V}}_2\right)}{x}$

$\therefore$Mass of pure ‘C’ = $\frac{\left({\mathrm{N}}_1{\mathrm{V}}_1-{\mathrm{N}}_1{\mathrm{V}}_2\right)}{x}$ $\times$ Molar mass of ‘C’.

$\therefore$Percentage purity of ‘C’ = $\frac{\left({\mathrm{N}}_1{\mathrm{V}}_1-{\mathrm{N}}_1{\mathrm{V}}_2\right)}{x}\times \frac{\text{ Molar mass of ‘ }{\mathrm{C}}^{\mathrm{\prime }}}{\mathrm{w}}\times 100$

Double titration

The purpose of double titration is to determine the percentage composition of an alkali mixture or an acid mixture. In the present case, we will find the percentage composition of an alkali mixture. Let us consider a solid mixture of NaOH, Na₂CO₃ and some inert impurities, weighing ‘w’ g. We are required to find the % composition of this alkali mixture. We are also given an acid reagent (HCl) of known concentration M₁ that can react with the alkali sample.

We first dissolve this mixture in water to make an alkaline solution and then we add two indicators, (Indicators are substances that indicate colour change of solution when a reaction gets completed), namely phenolphthalein and methyl orange to the solution. Now, we titrate this alkaline solution with standard HCl.

NaOH is a strong base while Na₂CO₃ is a weak base. So it is obvious that NaOH reacts first with HCl completely and Na₂CO₃ reacts only after complete NaOH is neutralized.

NaOH + HCl → NaCl + H₂O                       …..(i)

Once NaOH has reacted completely, then Na₂CO₃ starts reacting with HCl in two steps, shown as

Na₂CO₃ + HCl → NaHCO₃ + NaCl            …..(ii)

NaHCO₃ + HCl → NaCl + CO₂ + H₂O      …..(iii)

It is clear that when we add HCl to the alkaline solution, alkali is neutralized and the pH of the solution decreases. Initially the pH decrease would be rapid as strong base (NaOH) is neutralized completely. When Na₂CO₃ is converted to NaHCO₃ completely, the solution is still weakly basic due to the presence of NaHCO₃ (which is weaker as compared to Na₂CO₃). At this point, phenolphthalein changes colour since it requires this weakly basic solution to show its colour change. When HCl is further added, the pH again decreases and when all the NaHCO₃ reacts to form NaCl, CO₂ and H₂O the solution becomes weakly acidic due to the presence of the weak acid (H₂CO₃). At this point, methyl orange changes colour as it requires this weakly acidic solution to show its colour change.

Thus in general, phenolphthalein shows colour change when the solution contains weakly basic NaHCO₃ along with other neutral substances while methyl orange shows colour change when solution contains weakly acidic H₂CO₃ along with other neutral substances.

Let the volume of HCl used up for the first and the second reaction be V₁ litre (this is the volume of HCl used from the beginning of the titration up to the point when phenolphthalein shows colour change) and the volume of HCl required for the third reaction be V₂ litre (this is the volume of HCl used from the point where phenolphthalein had changed colour upto the point when methyl orange shows colour change). Then,

Moles of HCl consumed by NaHCO₃ = Moles of NaHCO₃ reacted = M₁V₂

Moles of NaHCO₃ formed from Na₂CO₃ = M₁V₂

Moles of Na₂CO₃ in the mixture = M₁V₂

Mass of Na₂CO₃ in the mixture = M₁V₂$\times$106

% of Na₂CO₃ in the mixture = $\frac{{\mathrm{M}}_1{\mathrm{V}}_2\times 106}{\mathrm{w}}\times 100$

Moles of HCl used in the reaction (i) and (ii) = M₁V₁

Moles of HCl used in reaction (ii) = M₁V₂

Moles of HCl used in reaction (i) = (M₁V₁ – M₁V₂)

$\therefore$ Moles of NaOH = (M₁V₁ – M₁V₂)

Mass of NaOH = (M₁V₁ – M₁V₂) $\times$ 40

% of NaOH in the mixture = $\frac{\left({\mathrm{M}}_1{\mathrm{V}}_1-{\mathrm{M}}_1{\mathrm{V}}_2\right)\times 40}{\mathrm{W}}\times 100$

Illustration: A solution contains a mixture of Na₂CO₃ and NaOH. Using phenolphthalein as indicator, 25 ml of mixture required 21 ml of 1.1 N HCl for the end point. With methyl orange as indicator, 25 ml of solution required 25 ml of the same HCl for the end point. Calculate grams per litre of each substance in the mixture.                                    

Solution: Since, the volume of HCl required in titration using methyl orange is greater than the volume of HCl required using phenolphthalein, this means that the titration is carried out separately two times using phenolphthalein and methyl orange indicators, respectively.

NaOH  +   HCl  →   NaCl  +  H₂O               ……(i)

Na₂CO₃ + HCl → NaHCO₃ + NaCl              ……(ii)

NaHCO₃ + HCl → NaCl  +  CO₂   +  H₂O   ……(iii)

Thus, the volume of HCl used in third reaction = (25 – 21) = 4.0 ml

$\therefore$ Moles of HCl used in third reaction = $4.0\times {10}^{-3}\times 1.1$

Moles of NaHCO₃ reacted = 4.4 $\times$ 10^–3

Moles of NaHCO₃ produced = 4.4 $\times$ 10^–3

$\therefore$ Moles of Na₂CO₃ present in 25 ml = 4.4 $\times$ 10^–3

$\therefore$ Mass of Na₂CO₃ present in 1 litre = $4.4\times {10}^{-3}\times 106\times 40=18.656\mathrm{g}$

Moles of HCl reacted in second reaction = 4.4 $\times$ 10^–3

Moles of HCl used in first two reactions = $21\times {10}^{-3}\times 1.1=23.1\times {10}^{-3}$

$\therefore$ Moles of HCl used in first reaction = $(23.1-4.4)\times {10}^{-3}=18.7\times {10}^{-3}$

Moles of NaOH present in 25 ml = 18.7 $\times$ 10^–3

$\therefore$ Mass of NaOH present in 1 litre = $18.7\times {10}^{-3}\times 40\times 40=29.92\mathrm{g}.$