Thermodynamics

THE THREE LAWS OF THERMODYNAMICS

First Law:

“We never get something out of nothing.”

OR

“To get something we must have to loose something else.”

Second Law:

“You never get as much as you spend.”

OR

“You always get somewhat less than that you spend.”

Third Law:

“Perfection is unattainable.”

OR

“Nothing/Nobody is perfect in the world.”

Energetics

Energetics is the study of energy, its forms and conversion of one form into other forms.  Thermodynamics (Greek, thermos = heat, dynamics = motion or flow). Though literal meaning of thermodynamics is flow of heat, but in general it refers to all aspects of energy and its transfer and transformations in various physical and chemical processes. Basically it is a quantitative relationship of heat and other forms of energy in various physico-chemical transformations.

The concern of chemical energetics includes:

• If two substances A and B are mixed (or put together, in contact with each other) whether they will react?
• If they react, whether energy will be absorbed or released?
• If they don’t react, what will be effect of variation of temperature, pressure and concentration on the fate of reaction?
• If a reaction starts, upto which extent will they convert into products?

The thermodynamics is based on some generalizations called laws of thermodynamics, which are derived from experiments. There is no formal proof of these laws, but nothing contrary to these laws has been known so far and neither it is suppose to happen ever.

Thermodynamics:  Scopes Versus Limitations

Scope/Application	Limitation
Valid, rather governs all macroscopic systems.	Not valid at molecular or atomic levels.
Predicts a reaction under given conditions will proceed or not	Does not tell anything about the rate of the reaction. e.g., H2 and O2, as per thermodynamics react to yield H2O, but in fact the reaction is extremely slow in the absence of catalyst.

An outline of the laws of thermodynamics:

Temperatures of two bodies and transfer of heat energy between them is linked with zeroth law of thermodynamics. The first law relates work and heat which are produced during chemical processes wherein the energy stored in the chemicals is converted into either work or energy or both. The second law holds the quantitative relationship between convertibility of heat into work. The third one deals with the variation of entropy with temperature.

Thermodynamic scale of temperature:

In order to discriminate the degree of hotness or coldness of an object with respect to a reference, it was necessary to have some scale.  Two such references very familiar with us, are the ice point (0^oC-the temperature at which water converts into ice under normal conditions) and steam point (100^oC – the temperature at which water starts to boil and converts into steam). There could be several such objects whose temperature will lie somewhere between these two reference temperatures. This temperature could be worked out by dividing the interval of these two reference points into hundred parts – this is called the centigrade (centi = 100, grade = gradation, division) or celcius scale.  While in fahrenheit scale, the points are taken as 32 F and 212F with 180 divisions in between them.

The International Committee on Weights and Measures has, since 1954 adopted the Kelvin scale, which is based on absolute zero and the triple point of water.

The absolute zero is the temperature at which the limiting value of PV_m (the product of P and V_m at pressures approaching zero) is zero.

The triple point of a substance is the set of conditions of temperature and pressure at which all of its phases i.e. solid, liquid and vapour coexist in equilibrium. For water it is observed at 4.58 torr and 0.01^oC at which ice, liquid water and water vapour coexist.

One Kelvin is the 1/273.15^th of the triple point of water (273.15 K). The scale has its zero point at (as) the lowest possible temperature hence called the absolute zero, whereas the zero point of celcius scale or so else is the arbitrary selection of the inventor of the scales. As a matter of chance, the size of the degree on the absolute scale is exactly same as that of the celcius or centigrade scale.

The temperature on the absolute scale is denoted by T, which is related with celcius scale temperature, t as T = 273.15 + t      . . . .   (1)

However, for all practical purposes, the absolute zero can be taken as – 273^oC.

The Zeroth Law of Thermodynamics

The law was formulated after the enunciation of first law of thermodynamics, but because of its prime importance, it was named zeroth law.

When two objects of different temperature are brought in thermal contact, the transfer of heat from the hotter object to the cooler continues until the temperature of the two bodies becomes equal i.e. they achieve the state of thermal equilibrium. No further heat transfer now takes place. The same thing happens with thermometer also when it is brought in contact with an object whose temperature is to be recorded. At thermal equilibrium the reading of thermometer becomes constant and the indication mark of thermometer is the temperature of the object.

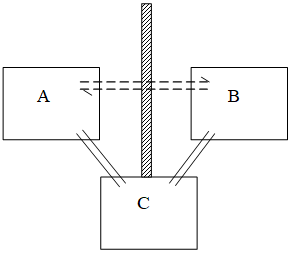
The zeroth law can be stated as “two objects at different temperatures in thermal contact with each other tend to move toward the same common temperature” or “two objects in thermal equilibrium with third one are in equilibrium with each other”.

The second statement of the law can be stated as “If a body A is in thermal equilibrium with a body C and body B is also in thermal equilibrium with C, then bodies A and B are in thermal equilibrium with each other”.

The principal of thermometer is based upon the zeroth law.  The measurement of temperature exploits any of the property of a fluid or any other substance which changes throughout in proportion to the temperature e.g., in mercury thermometer, the height of mercury column; change in volume and pressure of air (or a gas) in air (gas) thermometer; change in emf in thermocouple thermometer etc.

Thermodynamic Terms

System

A thermodynamic system stands for any specified portion of matter or the universe under experimental investigation, separated from the universe by real or imaginary boundaries. e.g. hot milk in closed bottle, the earth and universe.  The boundary may be rigid that does not let the matter pass through it) or non-rigid (the matter can pass through). If the boundary is thermal conductor it is called diathermic wall and if non-conductor the term adiabatic wall is used.

Types of Systems

Open system: If a system can exchange matter and energy with the surroundings, it is said to be open.  e.g. a cup of coffee – heat and vapours are given off to the surroundings; an opened bottle of cold drink takes heat from surroundings and gives out the vapours; a glass full of ordinary water – does not exchange heat from surroundings but it can if there is any variation in temperature with surroundings, but of course it exchanges the vapours with the surroundings.

Closed system: The system that can exchange energy with the surroundings but not the matter are called closed systems. The energy can be in the form of heat, work or radiations.  e.g.. tiffin carriers – although the food remains hot for a longer period but the exchange of heat do takes place which makes it to be colder, however, there is no exchange of food, unless the lid is opened; radioisotope kept in a closed chamber.

Isolated system:  If a system cannot interact with the surroundings in the terms of matter and energy, it is called an isolated system. It is achieved by sealing and insulating the boundaries.  e.g. an ideal thermos flask – though there is no perfectly insulator, hence perfectly isolated system is not easier to be achieved, but for practical purposes we regard them isolated, if a system is thermally insulated with sealed boundaries.

On the basis of composition, systems may also be classified into homogeneous and heterogeneous, the former having one phase, completely uniform throughout and the latter having more than one phases i.e. non-uniform.

Thermodynamic Properties

Intensive properties:  The properties which do not depend upon the quantity of the matter present in the system are called intensive properties.  e.g., pressure, temperature, density, viscosity, mp, bp, specific heat, surface tension, refractive index.

Extensive Properties:  The properties which depend on the quantity of the matter present in the system are called extensive properties. e.g. volume, mass, energy.

Macroscopic Property:  The properties associated with a macroscopic system (i.e. having a large number of particles) are called macroscopic properties.  e.g. P, V, T, d, η, surface tension, refractive index, colour etc.

State of a System:  When the total mass, temperature, volume, number of moles and composition have definite values, the system is in a definite state. When there is any change in any of these properties, the system is called to have change of state.

Surroundings: While studying a thermodynamic system, all the rest part of universe other than the system is called surroundings which can interact (exchange matter and energy) with the system.

i.e. universe = system + surroundings

Generally by surroundings we mean, the air around the system, water bath etc., where the experiment is being carried out.

State variables or state functions: The macroscopic property which determine the state of a system are called state variables or state functions or thermodynamic parameters. So, when a system changes from one state (called initial state) to another state (the final state), there is a change in one or more of its macroscopic properties. The change in state functions depends only upon the initial and final states and not on the path followed. Common thermodynamic state variables are pressure, volume, temperature, number of moles, internal energy, enthalpy, entropy, free energy.

Of these variables P, V, T mass and composition are the most important variables.  But it is not necessary to specify all the state variables to define a system, as some of these are interdependent.  If only few of these are defined, the rest can easily be calculated or accessed.  For example, for a single gas, composition is not the variable (it will be always 100%).  For one mole of an ideal gas, if only P and V are known, the third variable, T can be calculated from PV = RT.

Generally, the two variables which are specified are temperature and pressure, called independent variables. The third variable of a system generally volume is called the dependent variable, as its value depend upon P and T.

Thermodynamic equilibrium: If the macroscopic properties of a system do not alter with time, it is said to be in thermodynamic equilibrium. The term thermodynamic equilibrium implies the existence of three kinds of equilibria.

i) Thermal equilibrium

ii) Mechanical equilibrium

iii) Chemical equilibrium

Thermal equilibrium: If there is no flow of heat from one part of a system to the another, it is said to be in thermal equilibrium. It is the condition when the temperature is same throughout the system.

Mechanical equilibrium: It is the state of a system when no mechanical work is done by the one part of the system on another part. This is possible only when pressure is same throughout the system.

Chemical equilibrium: A system is called to be in chemical equilibrium, if the composition of the various phases in the system does not change with time.

Thermodynamic processes: Change of thermodynamic state of a system is called the process.

TYPES OF PROCESSES:

Isothermal process (dT = 0): If the temperature of a system remains unchanged during a process, it is called isothermal process. It is achieved by placing the system in the thermostat or constant temperature bath, and making the boundaries of the system thermal conductor. If heat is evolved/absorbed during the process it is exchanged with the thermostat making no change in the temperature of the system.

Adiabatic process (dQ = 0): If the process is carried out in such a way that no heat enters or leaves the system, it is called adiabatic. The condition is obtained by keeping the system in an isolated container.

Note: The temperature of the system varies in adiabatic process.

Isobaric process (dP = 0): If a process is carried out under constant pressure, it is called as isobaric.

Isochoric process (dV = 0): It is the process in which initial and final volumes of a system are the same.

Cyclic process (dE = 0 and dH = 0): If a number of changes are made in a system in such a way that it returns to its initial state, it is called a cyclic process.

Reversible process: This process is carried out infinitesimally slowly so that the opposing force is infinitesimally smaller than the driving force. Hence, if the opposing force is increased infinitesimally it will reverse the process.

A reversible process is considered to be infinite series of infinitesimally small stages, which are in equilibrium with each other at every stage. In practice, a reversible process cannot be realized as it would required infinite time for its completion. Henceforth, a reversible process is only imaginary and theoretical process, though very useful in the understanding and explanations of the some thermodynamic results.

Irreversible process: If a system goes from initial thermodynamic state into final state in a single step and finite time and cannot be reversed, the process is called to be irreversible.

All most of the natural and laboratory processes are irreversible.

Reversible	Irreversible
An ideal process (imaginary) Takes infinite time to complete Driving force infinitesimally greater than the opposing force In equilibrium all stages Work obtained is maximum	A real process Takes finite time Driving force much greater than the opposing force   Equilibrium only in initial and final stages Work is not maximum

Nature of work and heat: When a system changes from one state into another, there is some change in energy, which may appear in the form of work, heat or other forms of energy.

Work is a mode of energy transfer between system and surroundings. Quantitatively, it is the displacement (dx) of an object under the influence of a force (F), i.e.

W = F.dx              . . . . (2)

The work can be of either of the following types:

a) Gravitational work = mgh          . . . ..(3)

m = mass of the body, g=gravitational acceleration, h = height (to be moved)

b) Electrical work = qV             . . . . (4)

q = charge, V = potential gradient

c) Mechanical work = P_ext.$△$V             . . . . (5)

P_ext = external pressure

$△$V = increase or decrease in volume (=V₂-V1)

Energy manifests itself in the form of work, heat, electrical or chemical energy. All forms of energy can be expressed with the help of two factors:

i) Intensity factor ii) Capacity factor

The product of these two factors gives the energy.

For example heat energy is measured by the product of temperature (intensity factor) and heat capacity (capacity factor) of the concerned system.  If a substance of mass, m (kg) having specific heat, s(kJ kg^–1) is heated through temperature (t^oC), the heat energy involved with the substance will be m.s.t (kJ)

The SI unit of energy, work and heat is joule (J).

The cgs unit of energy is erg.

1 joule = 10⁷ ergs

James Joule showed that the mechanical work and heat energy are related (directly proportional to with each other as

W = JH             . . . . (6)

W= work, H = Heat, J = Joule mechanical equivalent of heat (4.184)

Heat is very often expressed in calorie also.

1 calorie = 4.184 joules

Calorie: Quantity of heat required to raise the temperature of 1 gram of water by 1^oC.

1 joule = 0.2390 cal,  1 litre-atm = 101.3 J

Sign convention for q & W

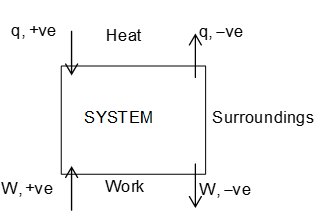
The key idea for the convention lies in fact whether energy content of the system increases or decreases.  If it increases the sign taken would be positive, else negative

hence, if

Heat is absorbed by the system, q is positive.

Heat is evolved from the system, q is negative.

Work is done on the system, W is positive.

Work is done on the system, W is negative.

The First Law of Thermodynamics (Law of Conservation of Energy)

It was given by Rober Mayer and Helmholtz.  The law can be stated in many ways, like

1. Energy can neither be created nor destroyed, it can only be transformed into another form.

2. The total energy of the universe is constant.

3. If a quantity of energy disappears, an exactly equivalent quantity of some another form must appear.

4. The total energy of an isolated system remains constant.

The law, well in accordance with cumulative experience of ages, infers that to construct a perpetual motion machine (a machine which can produce energy, without expenditure of any other form of energy) is impossible.

Pressure–Volume Work

In order to have an idea of the work done on the system or by the system, consider a cylinder having one mole of an ideal gas with a frictionless piston with a total volume of gas V₁ at the pressure P.

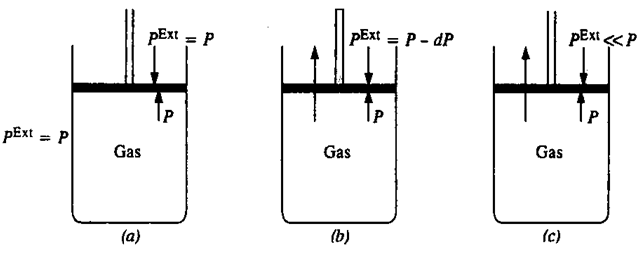
If an external pressure, P_ext is applied (P_ext is slightly greater than p), the piston moves downwards until the pressure of gas inside the cylinder becomes equal to P_ext. If the distance moved by the piston is d and area of cross section of the piston is A.

Then, volume change = $=\mathrm{A}\times \mathrm{d}=\mathrm{\Delta V}={\mathrm{V}}_2-{\mathrm{V}}_1$

and, pressure = $\frac{\text{ force }}{\text{ area }},P=\frac{F}{\mathrm{A}}$

Force on the piston, F = P_ext. A

If W is the work done on the system

W = F.d

= P_ext.A.d

$=\mathrm{Pext}(-\mathrm{\Delta V})\text{ (since }{V}_1>{\mathrm{V}}_2{\mathrm{V}}_2-{\mathrm{V}}_1=-\mathrm{ve}$

$\begin{array}{l}=-{\mathrm{P}}_{\mathrm{ext}}\mathrm{\Delta V}\\ =-{\mathrm{P}}_{\text{ext. }}\left({\mathrm{V}}_2-{\mathrm{V}}_1\right) ..........\left(7\right)\end{array}$

The negative sign of this expression is necessary to give the conventional sign for W which will be positive in case of compression as the work is done on the system. Since V₂-V₁ is negative, which multiplied by the other negative sign of the above equation will become positive.

Illustration 1:

A gas expands against a constant pressure of one atmosphere from initial volume of 1.5 to 2.5 L. Calculate the work done.

Solution.

$W=-P_{\text{ext }}\cdot \mathrm{\Delta }V$

$\begin{array}{l}=-1.0\left(\mathrm{atm}\right)\times 1.0\left(\mathrm{L}\right)\\ =-1.0(\mathrm{L}-\mathrm{atm})\times 101.328(\mathrm{J}/\mathrm{L}-\mathrm{atm})\\ =-101.328\mathrm{J}\end{array}$

Illustration 2:

One mole of an ideal gas is subjected to the changes as shown in the graph, A through B to C.

a) Calculate the pressures at the three stages of system A, B and C.

b) Name the process I, II and III and the overall change A through C to A.

Solution.   

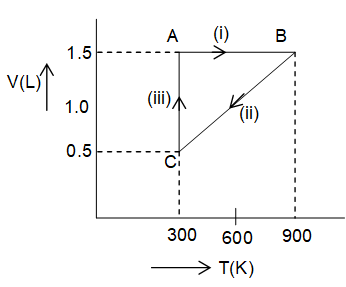
Pressure A: At point A, V_A=1.5 L, T_A=300K, n = 1 mole, R = 0.0821 L-atm/K-mole

${\mathrm{P}}_{\mathrm{A}}{\mathrm{V}}_{\mathrm{A}}={\mathrm{nRT}}_{\mathrm{A}}$

$P_A=\frac{1\left(\mathrm{mole}\right)\times 0.0821\left(\mathrm{L}-{\mathrm{atmK}}^{-1}{\mathrm{mole}}^{-1}\times 300\mathrm{K}\right.}{1.5\mathrm{L}}=16.42\mathrm{atm}$

At point B:  The change from state A to B is brought about by isochoric process; pressure law holds good for the change i.e.,

$\frac{P_A}{T_A}=\frac{P_B}{T_B}, else \frac{P}{T}=\text{ constant }$

Since temperature increases 3 fold, the pressure must increase by three times to make the P/T ratio constant.

Hence,  $P_B=\frac{P_A{T}_B}{T_A}=\frac{16.462\left(\mathrm{atm}\right)\times 300\left(\mathrm{K}\right)}{300\left(\mathrm{K}\right)}=39.26\left(\mathrm{atm}\right)$

At point C: Since the temperature is reducing to one third i.e. from 900 to 300K and volume is also reducing to one third, the pressure shall be equal to that of point B. Else, we can consider the process-III taking place at constant temperature (300 K), which will hold the Boyle’s law i.e.,

$\begin{array}{l}{P}_A{V}_A=P_C{V}_C\\ P_C=\frac{16.42\left(\mathrm{atm}\right)\times 1.5\left(\mathrm{L}\right)}{0.5\left(\mathrm{L}\right)}=39.26\left(\mathrm{atm}\right)\end{array}$

Note that at point A the state variable P, V and T were 16.42 atm, 1.5 L and 300 K respectively which changed to 39.26 atm  1.5 L and 900 K  at point B in process-I (V_constant followed by 39.26 atm, 0.5 L and 300 K at point C and finally to 16.42 atm, 1.5 L and 300 K(T_constant). Hence, after the three successive processes the system returns into its initial state-the cyclic process.

Process I: Volume is constant i.e. 1.5 L while temperature increases from 300K to 500K hence the process is isochoric.

Process III: The temperature is constant i.e. 300K, hence it is an isothermic process.

Process II: Volume and temperature both are decreasing by the same proportion (i.e., 1/3) in this process, hence the pressure must be constant (Charles’ law).

Overall process: Since the system returns into its initial state, it is a cyclic process.

Illustration 3:

The figure shows a P–V curve.  Find out :

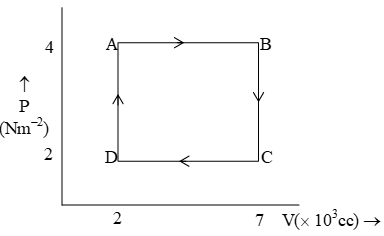
(i) Work done in the processes A→B, B→C, C→D, D→A

(ii) work done in the complete cycle

Solution.

i) The process: A→B is the expansion (volume increases as from 2 to 7($\times$10³ cc), the work is done by the gas]

${\mathrm{W}}_{\mathrm{A}\to B}=-\left(\mathrm{PdV}\right)$

$\begin{array}{l}=-\left(4{\mathrm{Nm}}^{-2}\right)\times \left(5\times {10}^3\times {10}^{-3}{\mathrm{m}}^3\right)\\ {}^{ \left(1{\mathrm{m}}^3={10}^3\mathrm{L}\right)}\\ =-20\mathrm{J} (1\mathrm{Nm}=1\text{ Joule })\end{array}$

The process C→D is isochoric.

$W_{\mathrm{B}\to \mathrm{C}}=–P.dv = 0 dv=0$

Process C→D is compression (volume increases from $7\text{ to }2\left(\times {10}^3\mathrm{cc}\right)$.

The work is done on the gas (by surroundings)

${\mathrm{W}}_{\mathrm{C}\to \mathrm{D}}=\mathrm{P}.\mathrm{dV}=2\left({\mathrm{Nm}}^{-2}\right)\times \left(5\times {10}^3\times {10}^{-3}{\mathrm{m}}^3\right)=10$

The process D→A is again isochoric involving $△$V = 0, and hence W = 0.

ii) Work done is the whole cycle $\mathrm{A}\to \mathrm{B}\to \mathrm{C}\to \mathrm{D}\to \mathrm{A}$

W_total = W_A→B + W_B→C + W_C→D + W_D→A = -20 J + 0 + 10 J + 0 = -10 J

Hence, the work is done by the gas.

Illustration 4:

Calculate the work done in vaporization of 9.0 g water, at 100⁰ C at atmospheric pressure, assuming the behaviour of water vapour to be ideal.

Solution.

When water vapourizes into vapours, the volume occupied increases much greater than the initial volume. Hence, regarding the final volume i.e. the volume of the vapours as $△$V.

9.0 g water = 0.5 mole of water (vapour)

If 0.5 mole of water vapors are at NTP, their volume would be 22.4$\times$0.5 L, but since they are at 100^oC (373K, the actual volume will however differ and in fact be given by

$\mathrm{V}=\frac{\mathrm{nRT}}{\mathrm{P}}=\frac{0.5\left(\mathrm{mol}\right)\times 0.0821\left(\mathrm{L}-{\mathrm{atmK}}^{-1}{\mathrm{mol}}^{-1}\right)\times 373\left(\mathrm{K}\right)}{1\left(\mathrm{atm}\right)}$= 15.31165 L

Alternatively, applying Charle’s law

Volume of 9.0 g water vapours at NTP = 0.5$\times$22.4 = 11.2 L

$\frac{V_1}{T_1}=\frac{V_2}{T_2}$

$\frac{11.2\left(\mathrm{L}\right)}{\mathrm{L}273\left(\mathrm{K}\right)}=\frac{{\mathrm{V}}_2}{373\left(\mathrm{K}\right)}$

$\begin{array}{l}{\mathrm{V}}_2=15.302564\mathrm{L}\\ \mathrm{W}=-\mathrm{P}\times \mathrm{\Delta V}=-1\left(\mathrm{atm}\right)\times 15.3\left(\mathrm{L}\right)=-15.3(\mathrm{L}-\mathrm{atm})\times 101.3=-1549.89\mathrm{J}(1\mathrm{L}-\mathrm{atm}=101.3\mathrm{J})\end{array}$

The equivalence of mechanical work and heat energy as established by Joule is the consequence of first law of thermodynamics. As far now, we know from Einstein’s energy equation E = mc² that mass can be destructed into equivalent amount of energy.

E = energy produced upon the destruction of mass m, c = velocity of light. Henceforth, the modified law states the total mass and energy of an isolated system remains unchanged.

INTERNAL ENERGY (E OR U)

Every substance is associated with a definite amount of energy at a given temperature and pressure. The value of internal energy is different for different substances. Its exact value is not known as it includes some indeterminant factors as translational, vibrational, rotational and electronic movements of the molecules (kinetic energy components) as well as nature of molecules, their arrangements, arrangement and number of electrons, energy possessed by molecules etc. (the potential energy component).

Since value of internal energy depends upon the state variables, it is a state function. The change in E i.e. $△$E (E_final­ – E_initial) is independent of the path.

Note that heat q and work W are path dependent and hence called path functions.

In fact the values of q and W adjust themselves during a transformation (or a process) so that the amount  (q-W) is equal to $△$E.

Internal Energy and First Law of Thermodynamics

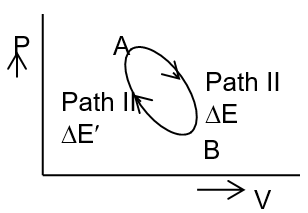
Let a system undergoes a change from its initial state A to the final state B. The internal energy, as P and V change, changes from E_A to E_B.

The change in internal energy when path-I is followed,

$\mathrm{\Delta E}={\mathrm{E}}_{\mathrm{B}}-{\mathrm{E}}_{\mathrm{A}}$                        . . . .  (8)

This change is brought about by

i) Either absorption of heat by the system or evolution by it.

ii) Doing work on the system or letting the system to do work.

If in path-I, the system is supplied q heat, the overall energy of the system will be E_A+q.  If W work is also done on the system, the final internal energy becomes E_B.

$\begin{array}{l}\mathrm{Thus} {\mathrm{E}}_{\mathrm{B}}={\mathrm{E}}_{\mathrm{A}}+\mathrm{q}+\mathrm{W}\\ {\mathrm{E}}_{\mathrm{B}}-{\mathrm{E}}_{\mathrm{A}}=\mathrm{q}+\mathrm{W}\\ \mathrm{\Delta E}=\mathrm{q}+\mathrm{W} ......\left(9\right)\end{array}$

It is mathematical formulation of first law of thermodynamics.

In the case q is the heat absorbed and W is the work done by the system,

$\begin{array}{l}\mathrm{\Delta E}=\mathrm{q}+(-\mathrm{W}\\ \mathrm{\Delta E}=\mathrm{q}-\mathrm{W} \mathrm{or} \mathrm{q}=\mathrm{\Delta E}+\mathrm{W} ..............\left(10\right)\end{array}$

Hence, the first law of thermodynamics may also be stated as the net energy change of a closed system is equal to the heat absorbed and work done on the system.

$△$E doesn’t depend on the path and can be realized in the light of first law and the figure.  Let the change of internal energy during path I be $△$E and the same change of state by the path-II involving internal energy change be $△E‘$.

If $△$E >, by coupling the two processes, i.e. repeating the process successively we will get $\left(△E–△E‘\right)$  surplus energy. By the process we can constitute a perpetual motion machine.  But this is contrary to first law. The same will be the case if $\mathrm{\Delta E}<{\mathrm{\Delta E}}^{\mathrm{\prime }}$ with opposite sign which by converting the direction of change be made positive again to give the continuous source of energy.

Hence, $\mathrm{\Delta E}={\mathrm{\Delta E}}^{\mathrm{\prime }}$

Some Conclusions from the First Law

1. When a system undergoes a change $△$E = 0 i.e. the initial and final thermodynamic states are the same, the first law reduces to,

$\begin{array}{l}\mathrm{\Delta E}=\mathrm{q}+\mathrm{W}\\ \mathrm{q}=-\mathrm{W} .............\left(11\right)\end{array}$

i.e. heat absorbed by the system = work done by the system (on the surroundings)

$or -q=w$

heat evolved by the system = work done on the system (by the surroundings)

2. When no work is done i.e. W = 0, the first law becomes

$△$E = q              . . . .  (12)

i.e. increase in internal energy of the system = heat absorbed by the system or

decrease in internal energy of the system = heat lost by the system

3. When there is no exchange of heat between system and surroundings i.e. q = 0.

First law gives, $△$E = W           . . . .  (13)

i.e. change in internal energy = work done

For gaseous systems the mechanical work is generally obtained by change in pressure and volume during a reaction, called pressure volume work.  If at constant P, the volume changes from V₁ to V₂, the work done by the system will be given by

$-W=-P\left(V_2-V_1\right)=-P\mathrm{\Delta }V$                  . . . .  (14)

The equation is applicable for expansion as well as compression of gases.  While expansion, $\left({\mathrm{V}}_2-{\mathrm{V}}_1\right)>0,-\mathrm{P\Delta V}$ is negative which implies that system does the work on surroundings (W is negative).

In compression, $\left({\mathrm{V}}_2-{\mathrm{V}}_1\right)<0,-\mathrm{P\Delta V}$ is positive i.e., work is done on the system by the surroundings.

Hence the first law becomes

$\mathrm{\Delta E}=q-\mathrm{P\Delta V}$            . . . .  (15)

However if a process is carried out at constant volume, i.e. $△$V = 0.

Then $\mathrm{\Delta E}=q_v$            . . . . (16)

(v subscript denotes the condition of volume, V being constant)

The above equation infers that we can determine $△$E for a process by measuring the heat change at constant volume. To achieve constant volume condition the container should be closed and rigid, which is possible with bomb calorimeter.

Enthalpy or Heat Content (H)

The heat content of a system at constant pressure is called enthalpy, H.

From the first law of thermodynamics,

q = E + PV

For a process, carried out at constant volume, the heat change is equal to the internal energy change i.e. q =$△$E.

But in chemical sciences most of the reactions are carried out at constant pressure i.e. in an open vessel (at 1 atm). To measure the heat changes of such reactions, a new term has been assigned, called enthalpy, H.

From equation no ____ q = E + PV

At constant temperature q = H

Hence, H = E + PV

Now since magnitude of H depends on the three state functions P, V and E, hence, it is also a state function. The change in enthalpy, $△$H can be given by

$\mathrm{\Delta H}=\mathrm{\Delta E}+\mathrm{\Delta }\left(\mathrm{PV}\right)=\mathrm{\Delta E}+\mathrm{P\Delta V}+\mathrm{V\Delta P}$      . . . . (17)

Since the change is carried out at constant pressure $△$P will be zero,

$\mathrm{\Delta H}=\mathrm{\Delta E}+\mathrm{P\Delta V}$           . . . .  (18)

From equation (xvi) and (xviii)

$\mathrm{\Delta H}={\mathrm{q}}_{\mathrm{p}}$                   . . . .  (19)

(P subscript denotes the condition of pressure, P being constant)

Obviously we can determine the $△$H for a reaction by measuring the heat change at constant pressure. It can be very easily measured using coffee-cup calorimeter. Besides, we can measure the enthalpy change of a process in a constant pressure calorimeter.

Equation (xvi) and (xix) infer that $△$E and $△$H differ only by P$△$V.  Since change in volume for solids and liquids is usually not very significant, $\mathrm{\Delta E}\approx \mathrm{\Delta H}$.  But for gases, it is not insignificant and hence we cannot ignore P$△$V.  We can correlate them, using the gas equation PV = nRT.

Let the volume of reactants and products be V_A and V_B of their respective amounts n_A and n_B at a constant temperature and pressure.

From the gas equation,

Before the reaction, $P{V}_A=n_{A}RT$          . . . .  (20)

After the reaction,  $P{V}_B=n_{B}RT$            . . . .  (21)

Thus, $P{V}_B-P{V}_A=n_{B}RT-n_{A}RT$     (subtraction)

$\mathrm{P}\left({\mathrm{V}}_{\mathrm{B}}-{\mathrm{V}}_{\mathrm{A}}\right)=\left({\mathrm{n}}_{\mathrm{B}}-{\mathrm{n}}_{\mathrm{A}}\right)\mathrm{RT}$

$\mathrm{P\Delta V}=\mathrm{\Delta nRT}$            . . . .  (22)

$△$n = no. of moles of products – no. of moles of reactants

From equations (18) and (22)  

$\mathrm{\Delta }H=\mathrm{\Delta }E+\mathrm{\Delta }nRT$            . . . .  (23)

Illustration 5: Calculate the difference between $△$H and $△$E for the reaction at 527⁰ C in K. Cals ${\mathrm{N}}_2\left(\mathrm{g}\right)+3{\mathrm{H}}_2\left(\mathrm{g}\right) \to 2{\mathrm{NH}}_3\left(\mathrm{g}\right)$

Solution. ${\mathrm{N}}_2\left(\mathrm{g}\right)+3{\mathrm{H}}_2\left(\mathrm{g}\right) \to 2{\mathrm{NH}}_3\left(\mathrm{g}\right)$

$\mathrm{\Delta }n=\{2-(1+3\left)\right\}=-2$

$\begin{array}{l}\mathrm{\Delta H}=\mathrm{\Delta E}+\mathrm{\Delta n}\left(\mathrm{RT}\right); \mathrm{T}=527+273=800\mathrm{K}\\ (\mathrm{\Delta H}-\mathrm{\Delta E})=\mathrm{\Delta n}\left(\mathrm{RT}\right)=(-2)\times \left(2\times {10}^{-3}\right)\times 800\mathrm{kcals}\\ =-2\times 2\times {10}^{-3}\times {10}^2\times 8\\ =-32\times {10}^{-1}=-3.2\mathrm{k}\text{ cals. }\end{array}$

Illustration 6: What is $△$E for the reaction in kJ?

${\mathrm{C}}_{\left(s\right)}+{\mathrm{O}}_2\left(\mathrm{g}\right)⟶{\mathrm{CO}}_2\left(\mathrm{g}\right)\text{ at }{327}^0\mathrm{C}\text{ if }\mathrm{\Delta H} \text{ is }-393.5\mathrm{kJ}$

Solution. ${\mathrm{C}}_{\left(\mathrm{s}\right)}+{\mathrm{O}}_2⟶{\mathrm{CO}}_2\left(\mathrm{g}\right)$

$\mathrm{\Delta n}=(1-1)=0[\because \mathrm{C}=\text{ solid }]$

T = 327⁰C + 273 = 600 K

$\begin{array}{l}R=8.3\times {10}^{-3}\mathrm{kJ}\\ \mathrm{\Delta H}=\mathrm{\Delta E}+\mathrm{\Delta nRT}=\mathrm{\Delta E}+0\times \mathrm{R}\times \mathrm{T}=\mathrm{\Delta E}\\ \mathrm{\Delta E}=\mathrm{\Delta E}=-393.5\mathrm{kJ}\end{array}$

Heat Capacity (C)

“Quantity of heat required to raise the temperature of a system by one degree (celcius or Kelvin) is called the heat capacity of the system. If very small amount of heat dq given to a system changes (rises) the temperature of the system by dT, then

Heat capacity  $\mathrm{C}=\frac{\mathrm{dq}}{\mathrm{dT}}$         . . . .  (24)

If the mass of the system taken is one gram, the heat capacity is called the specific heat of the system. However, if the mass of the system is one mole, it is regarded as molar heat capacity. Generally C stands for molar heat capacity or simply molar heat. The molar heat capacity of a gaseous system is determined in two ways:

(i) at constant volume, C_V        (ii) at constant pressure, C_P

In the former case, no external work is to be done ($\mathrm{\Delta V}=0\to \mathrm{P\Delta V}=0$) is zero, hence from the first law, $\mathrm{q}=\mathrm{\Delta E}$

So, the heat capacity at constant volume, ${\mathrm{C}}_{\mathrm{v}}={\left[\frac{\mathrm{\partial }\mathrm{q}}{\mathrm{\partial }\mathrm{T}}\right]}_{\mathrm{V}}$

${\mathrm{C}}_{\mathrm{V}}={\left[\frac{\mathrm{\partial }\mathrm{E}}{\mathrm{\partial }\mathrm{T}}\right]}_{\mathrm{V}}$           . . . . (25)

The curly d, called ‘dever’ stands for partial differentiation, i.e., keeping the volume constant.

At constant pressure, $q=\mathrm{\Delta }E-w=\mathrm{\Delta }E+P\mathrm{\Delta }V$.

Hence, ${\mathrm{C}}_{\mathrm{P}}={\left[\frac{\mathrm{\partial }\mathrm{q}}{\mathrm{\partial }\mathrm{T}}\right]}_{\mathrm{p}}={\left[\frac{\mathrm{\partial }\mathrm{E}+\mathrm{P}\mathrm{\partial }\mathrm{V}}{\mathrm{\partial }\mathrm{T}}\right]}_{\mathrm{P}}$

${\mathrm{C}}_{\mathrm{P}}={\left[\frac{\mathrm{\partial }\mathrm{H}}{\mathrm{\partial }\mathrm{T}}\right]}_{\mathrm{P}}$            . . . . (26)

Illustration 7:

To raise the temperature of a substance by 5^oC at constant volume, 72.5J of heat is required. What will be quantity of heat to raise the temperature of the substance from 20^oC to 27^oC.

Solution.

$\begin{array}{l}{\mathrm{C}}_{\mathrm{V}}=\frac{\mathrm{q}}{\mathrm{T}}=\frac{72.5\mathrm{J}}{5^{\circ }\mathrm{C}}=14.5\mathrm{J}{/}^{\circ }\mathrm{C}\\ \mathrm{q}={\mathrm{C}}_{\mathrm{v}}\mathrm{\Delta T}=14.5\mathrm{J}{/}^{\circ }\mathrm{C}\times \left({27}^{\circ }\mathrm{C}-{20}^{\circ }\mathrm{C}\right)=101.5\mathrm{J}\end{array}$

Relation between C_p and C_v in Gaseous State

If a gas is heated at constant volume, no extra work is to be done as there is no change in the volume ($W=P\cdot \mathrm{\Delta }V=0\text{ as }\mathrm{\Delta }V=0$). So if the temperature is raised by 1^oC (from T to T+1), the increase in its internal energy is equal to the heat capacity at constant volume, C_V.  However, when heated at constant pressure (i.e. volume change involved, $\mathrm{\Delta V}\ne 0$), the internal energy increases, which is accompanied, by an increase in volume i.e. expansion which needs some work to be done. Obviously, besides increasing the temperature, the heat is used to raise the temperature as well hence called heat capacity at constant pressure used in doing some work. Definitely the latter will be greater than the former i.e. C_P > C_V.  We can see, the difference between the two is equal to the work done by one mole of gas in expansion when its temperature is raised by 1^oC at constant P.

Since work done by a gas in expansion at constant P is numerically, W = P$△$V

For one mole of gas, PV = RT              . . . .  (27)

When temperature is increased by 1^oC the volume becomes V+$△$V, then

P(V+$△$V) = R(T+1)              . . . .  (28)

From equation (27) and (28)

P$△$V = R               …… (29)

Work done by one mole of an ideal gas in expansion at constant pressure when heated through 1^oC is equal to R. 

Hence  C_P – C_V = R        . . . .  (30)

Expansion of an Ideal Gas

In expansion the volume increases. Expansion can be carried out reversibly or irreversibly isothermally or adiabatically. Applying the first law of thermodynamics, the changes in the properties like $\text{ q, }W,\mathrm{\Delta }E\text{ and }\mathrm{\Delta }H$ can be calculated.

1. Isothermal Expansion: In an isothermal system the temperature of the system is to be constant, which can only be achieved if the heat generated or consumed can be exchanged to compensate the temperature with its surroundings.

Calculation of $△$E: For an ideal gas the internal energy depends upon the temperature and since in isothermal process, the temperature does not change, the internal energy will remain the same i.e. $△$E = 0.

Calculation of $△$H: From the equation

H = E + PV

$\mathrm{\Delta H}=\mathrm{\Delta }(\mathrm{E}+\mathrm{PV})=\mathrm{\Delta E}+\mathrm{P\Delta V}$

$\mathrm{\Delta H}=\mathrm{\Delta E}+\mathrm{\Delta nRT}$        . . . .  (31)

Since $△$T as well as $∆$E for an isothermal process are zero, $△$H is zero, i.e. H =0 for an isothermal process are zero, $△$H is zero, i.e. $△$H = 0.

Calculation of q & W: From the first law of thermodynamics E = q+W

For an isothermal process $△$E = 0.  Hence, q = -W or W = -q

That means the work is done at the expense of heat of the system. Since it is an isothermal process, the temperature does not change, the energy is compensated by absorption from its surroundings. The magnitude of q (or W) depends on the manner in which the expansion is carried out reversibly or irreversibly.

Work Done in The Reversible Isothermal Exapansion

Consider an ideal gas enclosed in cylinder fitted with a frictionless and weightless piston. The cylinder is not insulated so that it is in thermal equilibrium with the surroundings-this makes the temperature of gas constant all along the process, by exchanging the heat energy with the surroundings. In condition I, the P_ext. (external pressure) is equal to the P_gas(the pressure of the gas); let it be equal to P i.e.

P_ext = P_gas = P.

In condition II, if P_ext is decreased infinitesimally (by an amount dP), the gas will expand by an infinitesimal volume (dV). After expansion the external pressure falls from P_ext to P_ext – dP (or P – dP) and the volume of gas increases from V to V+dV. As a result of expansion the pressure within the cylinder P_gas falls to P_gas-dP (or P – dP) i.e. becomes equal to the external pressure. The piston now comes to the rest.

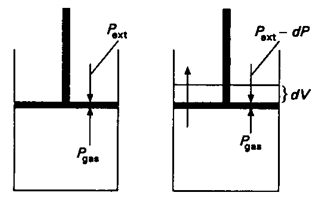
It should be noted that, the system undergoes infinitesimal cooling as a result of expansion of gas; the energy for the work done comes from the internal energy of the gas, which decreases the temperature of the gas. The cylinder being in thermal equilibrium with the surroundings absorbs an infinitesimal amount of heat from the surroundings to regain its internal energy to make the temperature constant. If the external pressure is lowered again by the same infinitesimal amount dP, the gas will undergo the second infinitesimal expansion dV until the P_ext becomes equal to P_gas.

Since work is done by the gas (system) its sign will be designated as negative.

$\mathrm{dW}=-\left(P_{\text{ext }}-\mathrm{dP}\right)\mathrm{dV}=-{\mathrm{P}}_{\text{ex }}\mathrm{dV}+\mathrm{dPdV}$

Since dP and dP are themselves infinitesimally small amounts, their product will be smaller enough to be ignored, hence,

$\mathrm{dW}=-{\mathrm{P}}_{\mathrm{ext}}\mathrm{dV}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\text{ or }\mathrm{dW}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}=-\mathrm{PdV}\hspace{0.25em} \hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\left(\text{ as }{\mathrm{P}}_{\mathrm{ext}}=\mathrm{P}\right)$   . . . .  (32)

However, if the expansion is carried out from volume V₁ to V₂ reversibly, it may be considered as the sum of a series of terms PdV in which the pressure keeps on decreasing gradually. The work done by the gas, is in this case given by

$W=-{\int }_{v_1}^{v_2} P_{d}V$             . . . . (33)

where V₁ = initial volume, V₂=final volume (after expansion)

The above integral equation can be evaluated by substituting the P term, using the relation,

$P=\frac{RT}{V}$          (for one mole of an ideal gas)

Thus,  $W=-{\int }_{v_1}^{v_2} RT\frac{dV}{V}$

Since R and T are constant in the process, above equation be rewritten as $W=-RT{\int }_{v_1}^{v_2} \frac{dV}{V}$

$\int \frac{dx}{x}={\log }_{0}x\text{ and }{\int }_{x_1}^{x_2} \frac{dx}{x}={\log }_0\left(x_2-x_1\right)={\log }_a\frac{x_2}{x_1}$

$W=-RT\ln \frac{V_2}{V_1}\left(\ln ={\log }_e\right)$   . . . . (34)

Rearranging above equation

$W=-2.303RT\log \frac{V_2}{V_1} \text{ (In or }\left.{\log }_e=2.303{\log }_{10} \text{ or }2.303\text{ log }\right)$

$=2.303RT\log \frac{V_1}{V_2}\left(-\log \frac{M}{N}=\log \frac{N}{N}\right)$

For n moles $W=-2.303nRT\log \frac{V_2}{V_1}$          . . . . (35)

Since at constant temperature $P_1{V}_1=P_2{V}_2$ (Boyle’s law)

$\frac{P_1}{P_2}=\frac{V_2}{V_1}$

Putting these values of $\frac{{\mathrm{V}}_2}{{\mathrm{V}}_1}$ in equation (35)

$W=-2.303nRT\log \frac{P_1}{P_2}$                . . . . (36)

From equation (35) and (36) we see that V₂ > V₁ and P₁ > P₂ hence, the quantity $\frac{{\mathrm{V}}_2}{{\mathrm{V}}_1}\text{ and }\log \frac{{\mathrm{P}}_1}{{\mathrm{P}}_2}$ will be positive making the work negative as per convention.

Work done in reversible isothermal compression

For a gas undergoing reversible isothermal compression from volume V₁ to V₂, the pressure this time will be higher i.e. P₂ > P₁.  Considering an infinitesimal change in pressure P + dP leading into an infinitesimal decrease in volume dV, the work done by the surroundings on the gas.

$\mathrm{dW}=\mathrm{P}(\mathrm{P}+\mathrm{dP})\mathrm{dV}=-\mathrm{PdV}$

Alternatively, work obtained on the gas = PdV       . . . . (37)

Considering a series of such infinitesimal compressions leading into change of volume from V₁ to V₂, the work done by the surroundings on the gas will be designated as negative (as work is obtained)

$W^{\mathrm{\prime }}=-{\int }_{v_1}^{v_2} PdV$

substituting the P term and integrating within the limits V₁ to V₂.

$W^{\mathrm{\prime }}=-RT\ln \frac{V_2}{V_1}$          . . . .  (38)

or  $W^{\mathrm{\prime }}=-RT\ln \frac{P_2}{P_1}$       . . . .  (39)

Considering equations 38 & 39 we can see that V₂ < V₁ and P₁ < P₂

Hence, the value of $\ln \frac{V_2}{V_1}\text{ and }\ln \frac{P_1}{P_2}$ shall be – ve, giving the sign of W +ve well in accordance with the convention.

Work Done in Isothermal Irreversible Expansion

When the external force (the opposing force), the P_ext, is much smaller than the P_gas.

Case I: When P_ext < P (intermediate expansion)

$W=-{\int }_{v_1}^{v_2} P_{ext}\cdot dV=-P_{ext}\left(V_2-V_1\right)$              . . . . (40)

Comparing equation (32) with (40) reveals that P_ext is less than P_gas hence the work done in the irreversible isothermal expansion is less than that of work done in reversible isothermal expansion.

Case II: When P_ext = 0, i.e. the gas expands into vacuum, (free expansion)

$W=-P_{\text{ext }}\left(V_2-{\overline{V}}_1\right)=0$        (Since P_ext = 0)

Maximum work:  It can be calculated that the work done by a system depends upon the external pressure. The higher the P_ext, the more is the work done by the gas. Provided that P_ext  > P_gas. Hence the work done is maximum when the two opposing pressures differ only infinitesimally-the condition of thermodynamic reversibility.

2. Adiabatic expansion: In an adiabatic process, the heat cannot be exchanged between system (the gas) and the surroundings i.e. q=0.

From the first law of thermodynamics $△$E = W

Since, in expansion, work is done by the system, by the convention its sign is negative.  Accordingly $△$E will be negative implying that there is a decrease in internal energy of the system and consequently accompanied by the fall in the temperature of the gas. Hence in adiabatic expansion work is done at the expense of internal energy of the system. Obviously in case of compression, work will be positive (work and hence, energy shall be obtained on the system) hence $△$E shall also be positive i.e. increase of internal energy which means increase in temperature. (in compression work is done by the surroundings and stored in the system in the form of internal energy reflected in the increase of temperature).

Calculation of $△$E: Molar heat capacity of a system at constant volume of an ideal gas is ${\mathrm{C}}_{\mathrm{V}}={\left[\frac{\mathrm{\partial }\mathrm{E}}{\mathrm{\partial }\mathrm{T}}\right]}_{\mathrm{V}}$

Hence, dE = C_V.dT     (for infinitesimal change)

And  $\mathrm{\Delta E}={\mathrm{C}}_{\mathrm{v}}\mathrm{\Delta T}$      (for finite change)           . . . .  (41)

Calculation of $△$H

From equation $\mathrm{\Delta H}=\mathrm{\Delta E}+\mathrm{\Delta }\left(\mathrm{PV}\right)=\mathrm{\Delta E}+\mathrm{R\Delta T}$   (for one mole of gas)

Substituting value of $△$E from equation (41)

$\mathrm{\Delta H}={\mathrm{C}}_{\mathrm{V}}\mathrm{\Delta T}+\mathrm{R\Delta T}=\left({\mathrm{C}}_{\mathrm{V}}+\mathrm{R}\right)\mathrm{\Delta T}={\mathrm{C}}_{\mathrm{P}}\Delta T$            . . . .  (42)

(C_P – C_V = R)

Work done during reversible expansion of ideal gas under ADIABATIC conditions:

$W=C_v\left(T_2-T_1\right)\text{ or }W=\frac{\mathrm{nR}}{\gamma -1}\left(T_2-T_1\right)$

Relationship between P, T, V for adiabatic expansion of ideal gas: 

In the following relations, $\gamma =\frac{C_p}{V_v}$(subscript 1 represents initial state, subscript 2 represents final state)

a) Relationship between P and V   $P_1{V}_1^{\gamma }=P_2{V}_2^{\gamma }$   or  ${\text{ PV}}^{\gamma }$ = constant

b) Relationship between T and V  $\frac{{\mathrm{T}}_1}{{\mathrm{T}}_2}={\left(\frac{{\mathrm{V}}_2}{{\mathrm{V}}_1}\right)}^{\gamma -1}\text{ or }{\mathrm{TV}}^{\gamma -1}=\mathrm{constant}$

c) Relationship between T and P  $\frac{T_1}{T_2}={\left(\frac{P_2}{P_1}\right)}^{\frac{1-\gamma }{\gamma }} \text{ or TP }\frac{1-\gamma }{\gamma }=\text{ constant }$.

Workdone in free-expansion of gas: When a gas expands into vacuum, the P_ext. i.e., the opposing force is zero.  Therefore, the work done in free expansion is zero.

Thermochemsitry

Study of energy changes associated with the chemical transformations, is themrochemistry. Almost of the chemical reactions are accompanied by energy changes which generally appear in the form of heat.  This change is principally brought about by breaking of old bonds and formation of new ones. The energy changes are governed by first law of thermodynamics along with two other laws of thermochemistry, which are as follows:

Laws of Thermochemistry

Lavoisier–Laplace law: The heat required to break a bond is equal to the heat evolved during its formation. Alternatively, the heat of decomposition is equal to the heat of formation.

Mathematically, $\mathrm{\Delta }{H}_{\text{decamposition }}=-\mathrm{\Delta }{H}_{\text{formation }}$

In fact it is a transformation of the first law of thermodynamics; else we can say combining the two changes a perpetual motion nucleic can be generated.

2. Hess’s law of the constant heat summation: The total enthalpy change of a process (transformation) is same, whether it takes place in one or more steps.

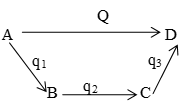
Let a system changes from state A to state D. If it takes place in a single step the enthalpy change is $△$H and if in more steps (A→B→C→D), the enthalpy changes are ${\mathrm{\Delta H}}_1,{\mathrm{\Delta H}}_2,{\mathrm{\Delta H}}_3$ respectively. Then it follows $\mathrm{\Delta H}={\mathrm{\Delta H}}_1+{\mathrm{\Delta H}}_2+{\mathrm{\Delta H}}_3$

or  Q = q₁ + q₂ + q₃

We can say that the enthalpy change of a process (reaction) depends upon the initial state (reactants) and the final state (products) and is independent of the intermediate steps (reaction intermediates). Again this law can be related to the first law :

Let the summation of enthalpies all the steps from $\mathrm{A}\to \mathrm{B}\to \mathrm{C}\to \mathrm{D}$ be $△$H¹; while that of A→B (directly) be $△$H, then if $△$H and  are not equal, suppose ${\mathrm{\Delta H}}^{\mathrm{\prime }}$ is greater than $△$H.  We can get a surplus of energy by converting D directly into a and then $\mathrm{A}\to \mathrm{B}\to \mathrm{C}\to \mathrm{D}$.  It can more easily be understood by considering the quantities $△$H and ${\mathrm{\Delta H}}^{\mathrm{\prime }}$ numerically e.g.

Example:

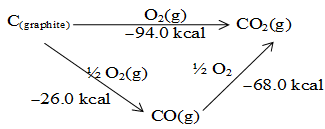
Path I: When C (graphite is directly converted into CO₂ (g) the heat liberated is 94.0 kcal

$\mathrm{C}\left(\mathrm{s}\right)+{\mathrm{O}}_2\left(\mathrm{g}\right)⟶{\mathrm{CO}}_2\left(\mathrm{g}\right)\mathrm{\Delta H}=-94.0\mathrm{kcal}$

Path II: C(graphite) is first converted into CO(g) (partial combustion) with liberation of 26 kcal (heat energy) followed by conversion into CO₂(g), the heat liberated this time is 68 kcal making an overall change for C_(graphite) into CO₂ (g) to be 94 kcal

$\begin{array}{l}{\mathrm{C}}_{\text{(graphite) }} + 1/2{\mathrm{O}}_2\left(\mathrm{g}\right)⟶\mathrm{CO}\left(\mathrm{g}\right),\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\mathrm{\Delta H}=-26.0\mathrm{kcal}\\ \mathrm{CO}\left(\mathrm{g}\right) + 1/2{\mathrm{O}}_2\left(\mathrm{g}\right)⟶{\mathrm{CO}}_2\left(\mathrm{g}\right),\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\mathrm{\Delta H}=-68\mathrm{kcal}\end{array}$

Adding  ${\mathrm{C}}_{\text{(graphite) }}+{\mathrm{O}}_2\left(\mathrm{g}\right)⟶{\mathrm{CO}}_2\left(\mathrm{g}\right),\mathrm{\Delta H}=-94.0\mathrm{kcal}$

Change of Internal Energy in Chemical Reactions

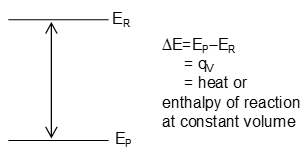
Let a reaction takes place at constant temperature and volume

Since $\mathrm{\Delta V}=0.\mathrm{W}=0$, from the 1^st law of thermodynamics, $△$E = q – W = q_v.

If E_R is the internal energy of reactants and $\propto$E_p is that of products then

$\mathrm{\Delta E}={\mathrm{E}}_{\mathrm{P}}-{\mathrm{E}}_{\mathrm{R}}$

It may be represented systematically as

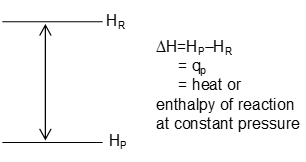
Change of Enthalpy in Chemical Reaction

If a reaction takes place at constant temperature and constant pressure, let the heat exchanged be q_p then from first law (at constant pressure).

$\mathrm{\Delta E}=\mathrm{q}-\mathrm{W}$

Putting $W=P\mathrm{\Delta }V\text{ and }\mathrm{\Delta }H=\mathrm{\Delta }E+W$

$\mathrm{\Delta H}=q_p$

If H_R is the heat content of reactants and H_P that of products then, $\mathrm{\Delta H}=\mathrm{HP}-\mathrm{HR}={\mathrm{q}}_{\mathrm{P}}$

Exothermic and Endothermic Reactions

The reactions which proceed with the evolution of heat are called exothermic reactions. It is the case when bond energy of the reactants is less than that of the products. Bond energy in fact, is the energy that is liberated from a compound when its formation takes place-greater the evolution of energy (greater the bond energy) greater its stability due to lesser energy content. As in the universe, the systems having less energy content are more stable and in fact all the systems tend to achieve the lesser energy state and thereby become more stable.

${\mathrm{H}}_{\mathrm{R}}>{\mathrm{H}}_{\mathrm{P}}\text{ so that }\mathrm{\Delta H}\text{ -ve (at constant }\mathrm{Pand} E_R>E_P\text{ so that }\mathrm{\Delta }E=-ve\text{ (at constant }V )$

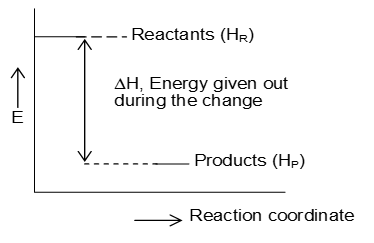
On the other hand, the reactions taking place with the absorption of heat are called endothermic reactions.

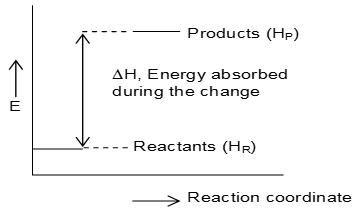
It is the case of reactions where the bond energy of the reactants is greater than that of the products.

$\text{i.e. }\left.{\mathrm{H}}_{\mathrm{P}}>{\mathrm{H}}_{\mathrm{R}}\text{ hence }\mathrm{\Delta H}=+\mathrm{ve}\text{ (at constant }\mathrm{P}\right)\mathrm{and} {\mathrm{E}}_{\mathrm{P}}>{\mathrm{E}}_{\mathrm{R}}\text{ hence }\mathrm{\Delta E}=\text{ +ve }\left(\text{ at constant }\mathrm{E}\right)$.

Sign conventions   

$\begin{array}{l}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} \mathrm{\Delta Q}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\mathrm{\Delta E}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\mathrm{\Delta H}\\ \text{Exothermic }\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} (-)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}(-)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}(-)\\ \text{Endothermic }\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} (+)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}(+)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}(+)\end{array}$

Relation between enthalpy of a reaction at constant volume and constant pressure

From equation $\mathrm{\Delta }H=\mathrm{\Delta }E+P\mathrm{\Delta }V$

Since,$q_V=\mathrm{\Delta }E\text{ and }{q}_p=\mathrm{\Delta }H$, the above relation may be rewritten as

${\mathrm{q}}_{\mathrm{p}}={\mathrm{q}}_{\mathrm{v}}+\mathrm{P\Delta V}$       . . . . (43)

For n moles of an ideal gas PV = nRT

If n₁ and n₂ be the numbers of gaseous reactants and gaseous products respectively, the difference in the number of gaseous moles will be ${\mathrm{\Delta n}}_{\mathrm{g}}={\mathrm{n}}_2-{\mathrm{n}}_1$

The corresponding increase in the number of volume,$△$V will be given by

$\mathrm{P\Delta V}={\mathrm{\Delta n}}_{\mathrm{g}}\mathrm{RT}$        . . . . (44)

Caution 1: For calculating $△$n of a reaction, only gaseous reactants and products are considered neglecting the liquid and solid phases as their volumes are negligible in compared to gases.

Heat of a Reaction or Enthalpy of a Reaction

The amount of heat evolved or absorbed when the reaction represented by a reaction reaches to the completion.  It is in fact, the difference between the enthalpies of products and reactants.

Mathematically  $\mathrm{\Delta H}=\sum {\mathrm{H}}_{\mathrm{P}}-\sum {\mathrm{H}}_{\mathrm{R}}$

For example, ${\mathrm{H}}_2\left(\mathrm{g}\right)+{\mathrm{Cl}}_2\left(\mathrm{g}\right)⟶2\mathrm{HCl}\left(\mathrm{g}\right)\mathrm{\Delta H}=-44.0\mathrm{kcal}$

The above reaction indicates that when 1 mole each of H₂(g) and Cl₂(g) completely react to form 2 moles of HCl(g), the amount of heat evolved is 44 kcal. We can say the enthalpy of the system (H₂ & Cl₂ mixture) decreases or the system loses this much amount of heat.

Factors which affect the Heat of a Reaction

1. Physical state of reactants and products: If the physical state of a reactant is to be changed (to say, form a solid into liquid), some energy is to be provided which shall alter the value of the heat of reaction. So, the chemical changes taking place must be mentioned their physical state while writing the thermochemical equations.

$\begin{array}{l}{\mathrm{H}}_2\left(\mathrm{g}\right)+\frac{1}{2}{\mathrm{O}}_2\left(\mathrm{g}\right)⟶{\mathrm{H}}_2\mathrm{O}\left(\mathrm{g}\right),\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\mathrm{\Delta H}=-57.8\mathrm{kcal}\\ {\mathrm{H}}_2\left(\mathrm{g}\right)+\frac{1}{2}{\mathrm{O}}_2\left(\mathrm{g}\right)⟶{\mathrm{H}}_2\mathrm{O}\left(\ell \right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\mathrm{\Delta H}=-68.32\mathrm{kcal}\end{array}$

The two thermochemical equations involving conversion of H₂ and O₂ gases into steam and water respectively, mentioned herewith, can be observed with a difference in their heats of the reactions. The reason?  If H₂O(g) has to convert into H₂O$\left(\mathcal{l}\right)$, it should lose some energy. What will be the quantity of heat during the conversion? The difference between the two values, of course! We conclude that the physical state of reactant or product shall affect the heat of a reaction.

2. Allotropic forms of an element: If we try to peep into the structural details, in fact, the bonding patterns of atoms in allotropes we shall come across with a difference. This difference will lead into a different amount of heat to break the bounds than that of the another allotrope. For example in graphite and diamond, the sp² and sp³ hybridized carbon atoms are arranged in hexagonal planar and tetrahedral 3-dimensional networks respectively, hence their C-C bonds will require different amount of energy to be broken with. As we know the enthalpy of a reaction depends upon the differences in energy of bonds in products and reactants, the $△$H shall be influenced when allotropes are to be considered.

$\begin{array}{l}{\mathrm{C}}_{\text{diamond }}+{\mathrm{O}}_2\left(\mathrm{g}\right)⟶{\mathrm{CO}}_2\left(\mathrm{g}\right),\mathrm{\Delta H}=-94.3\mathrm{kcal}\\ {\mathrm{C}}_{\text{(amorphous) }}+{\mathrm{O}}_2\left(\mathrm{g}\right)⟶{\mathrm{CO}}_2\left(\mathrm{g}\right),\mathrm{\Delta H}=-97.6\mathrm{kcal}\end{array}$

In the above two equations the value of heat liberated is greater for the (combustion) reaction of amorphous carbon than the diamond (its crystalline allotrope). Why?  The bonds between atoms of amorphous carbon are not as stronger as they are in diamond, hence the latter would need more energy, which we shall observe in the form of decreased value of heat or enthalpy of reaction.

What is the difference between the two values? It is 3.3 kcal, which is equal to the amount of heat required to convert 1 mole (12 g) of diamond into 1 mole of (12g) of amorphous carbon.  It is termed as heat or enthalpy of transition.  $\text{ i.e. }{C}_{\left(\text{diamond }\right)}⟶C_{\left(\text{amorphous }\right)},$ $△$H = 3.3 kcal.

3. Enthalpy of solution: If a reaction takes place in absence of a solvent, the solvent solute interactions shall be absent which in another case (when the reaction takes place in the presence of solvent) shall on account of being stronger or weaker than that existing between the atoms/molecules of the reactants and product will differ the enthalpy of the reaction.

$\begin{array}{l}{\mathrm{H}}_2\mathrm{S}\left(\mathrm{g}\right)+{\mathrm{I}}_2\left(\mathrm{g}\right)⟶2\mathrm{H}+\mathrm{S}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} \mathrm{\Delta H}=17.2\mathrm{kcal}\\ {\mathrm{H}}_2\mathrm{S}\left(\mathrm{g}\right)+{\mathrm{I}}_2\left(\text{ solution }\right)⟶2\mathrm{Hl}\left(\text{ solution }\right)+\mathrm{S}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} \mathrm{\Delta H}=-21.93\mathrm{kcal}\end{array}$

The difference in the two reactions indicating evolution of more energy when the reaction is carried out in presence of a solvent is more, signifies that there is a greater interaction of HI with the solvent molecules than that of I₂.

4. Temperature: Since the heat capacity which is the amount of energy that it can held within its molecules/atoms of a substance changes with temperature the heat content associated with them also changes. This change is not in the same ratio in the reactants and products, hence reflected in the variation of $△$H values if measured at different temperatures. However, more often the reactions are carried out at 25^oC or 298K (the standard temperature for thermochemistry; please note that in gaseous state or while calculating volume etc. by applying gas laws (by standard temperature as in STP we mean zero degree centigrade i.e. 273 K), and if they have been performed at any other temperature the temperature is to be mentioned along with the thermochemical equation.

Standard Enthalpy Changes

As discussed earlier, the enthalpy of a reaction depends upon the various variables of the experimental conditions regarded as the standard conditions.

Pressure = 1 atm or 1 bar or 101.325 kPa

Temperature = 25^oC or 298 K

And all the reactants and products should be in their standard state at this (25^oC) temperature.  e.g., H₂O in liquid state i.e. water, N₂ in gaseous and carbon in solid state.

Hence, the enthalpy change of a reaction when all the reactants and products are in their standard state at 1 atm is called standard enthalpy change.  It is generally selected at temperature 25^oC and denoted by $△$H^o (scribing a superscript O to the $△$H) e.g.

${\mathrm{CH}}_4\left(\mathrm{g}\right)+2{\mathrm{O}}_2\left(\mathrm{g}\right)⟶{\mathrm{CO}}_2\left(\mathrm{g}\right)+2{\mathrm{H}}_2\mathrm{O}\left(\ell \right),{\mathrm{\Delta H}}^{\circ }=-890.4\mathrm{kJ}{\mathrm{mol}}^{-1}$

CH₄, O₂ and CO₂ are gases at RT (room temperature) and H₂O is liquid when the reaction proceed at 1atm, the temperature is 298 K which increases due to exothermic reaction (heat is liberated). This heat if absorbed by the surroundings so that the products formed after the completion of reaction are at 298K, the heat released (in fact absorbed by the surroundings) will be called as the standard heat of reaction or combustion. It is immaterial here that the reaction does not proceeds at a constant temperature of 298 K. Because the state function (P, V & T) of the reactants and products are not path dependent for a given change. The difference in enthalpy will not depend upon the path chosen (i.e. the temperature of reaction) provided that the initial and final states for the change are the same.

Similarly for a endothermic reaction which starts at 298K and proceeds with an absorption of heat, may have intermediate temperature and finally the products at 298 K; for such a reaction, the heat is supplied by the surroundings which can be observed with an decreases in its temperature.  Knowing its heat capacity and applying the relation q = ms$∆$t, the energy absorbed can be calculated.

Measurement of $∆$E and $∆$H: Calorimetry (Determination of heat of reaction)

The experimental technique used for the determination of energy changes associated with a physical or chemical process is called calorimetry and the setup used for the purpose is called calorimeter.

Whenever there is a change in the heat content of a system, it either absorbs or evolves heat which is reflected in the form of decrease or increases in the temperature of its surroundings respectively. The principle applied in the calculation of $∆$H or $∆$E is

Heat given out by a system = Heat absorbed by the surroundings

or

Heat absorbed out by a system  = Heat given by the surroundings $=\mathrm{ms}\left({\mathrm{T}}_2-{\mathrm{T}}_1\right)$

where m is the mass of the system (generally the liquid of calorimeter)

s = heat capacity of the system

and T₁ and T₂ the initial and final temperature of the system

For the chemical systems it is customary to express the $△$H in the terms of per mole and the mass in calorimeter whose temperature increases may be expressed (in a given case) including that of participants of the reaction. Hence, redefining the terms

$q=\frac{M}{m}Z\mathrm{\Delta }t$

where, q = heat exchanged by a system

m = mass (in grams) of the substance

M = molar mass of the substance

Z = thermal capacity of the calorimeter system

$\mathrm{\Delta t}={\mathrm{T}}_2-{\mathrm{T}}_1$ = difference in the initial and final temperatures

Different types of calorimeters are in use, but the most common are:

(i) Water calorimeter and   (ii) Bomb calorimeter.

Water calorimeter: It is the lab calorimeter consisting of a large vessel wherein a calorimeter containing a known amount of water is held on corks. In between the calorimeter and vessel an insulating material (like glass wool) is packed. From the holes of calorimeter emerge out the thermometer, stirrer and the boiling tube having the reactants.  The heat evolved or absorbed by the reaction will be exchanged by the water. The variation in the temperature gives the heat of the reaction.

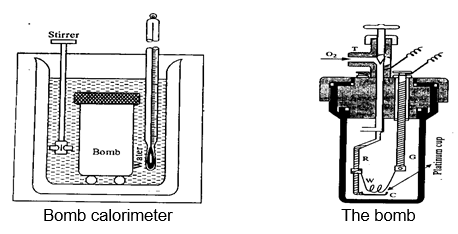
Bomb calorimeter:  The most commonly used calorimeter to find the heat of reaction of organic substances, consists of an inner sealed combustion vessel called ‘bomb’ and hence is named as bomb calorimeter. This bomb is immersed in a large volume of water, contained within another vessel and is provided with a thermometer and a stirrer. The bomb contains a known amount of the substance under the pressure (20-25 atm) of pure oxygen along with electrical ignition set up.  When current is passed through set up, the combustion is initiated. The heat generated is transferred to the water around the bomb. Since the volume of water is too much, the variation in temperature shall be very slight and hence a highly sensitive thermometer is required. Since the reaction proceeds within closed bomb, the heat calculated shall be q_v.

What about the heat of water calorimeter? Pressure is constant in that case, hence that one shall be q_P.

As we know ${\mathrm{q}}_{\mathrm{v}}=\mathrm{\Delta E}\text{ and }\mathrm{qp}=\mathrm{\Delta H}$

Hence, the heat calculated in the water calorimeter is $∆$H and that in bomb calorimeter is $∆$E.

Thermochemical equations: Earlier we have learnt balancing of a chemical equation, which has equal number of atoms in the reactant and products. But if we consider energy changes involved with the participants of a chemical reaction, energy in the overall reaction either evolves or is absorbed. Hence a balanced chemical equation along with the designation of $∆$H value for the reaction is called a thermochemical equation.

e.g., ${\mathrm{C}}_6{\mathrm{H}}_5\mathrm{COOH}\left(\mathrm{s}\right)+\frac{15}{2}{\mathrm{O}}_2\left(\mathrm{g}\right)⟶7{\mathrm{CO}}_2\left(\mathrm{g}\right)+3{\mathrm{H}}_2\mathrm{O}\left(\ell \right),{\mathrm{\Delta H}}^{\circ }=-3201.9 kj mo{l}^{-1}$

The above thermochemical equation infers that the combustion of one mole of solid benzoic acid at constant temperature (298 K) and pressure (1 atm) evolves 7 moles of gaseous CO₂, 3 moles of liquid H₂O (water) and 3201.9 kJ heat. The negative sign of $∆$H indicates exothermic nature of the reaction.

A thermochemical equation should contain

a) The balance chemical equation

b) The condition of temperature and pressure (if reaction does not proceed in standard conditions)

e.g. if a reactions proceeds at 350 K and 2 atm, it must be mentioned along with the value of $∆$H

c) The physical states must be mentioned.

e.g. H₂O – if not mentioned, its physical state could mean anything out of ice, water or steam.

d) Allotropic modification (if any) an amorphous form of carbon, coke, coal, graphite or diamond etc.

e) The value of $∆$H along with its sign has to be mentioned in proper units (although positive sign is omitted in practice). g. If the value of $∆$H for a reaction $2\mathrm{A}+3\mathrm{B}⟶\frac{3}{2}\mathrm{C}$ has been mentioned as 101.5kJ. It means the value refers when the stoichiometric ratio as mentioned in the reaction, are reached; and if it is mentioned as $101.5\mathrm{kJ}{\mathrm{mol}}^{-1}$, it refers to the one mole of the participant (either of reactants for products) irrespective of the stoichiometric ratio expressed in the chemical equation of such a reaction.

f) For reactions proceeding at standard conditions (mentioned earlier) the sign $∆$H^o is used, but the sign $∆$ is often subscribed (e.g. $\mathrm{\Delta }{\mathrm{fH}}^0$) with some general abbreviations, which signifies, the nature of a reaction or the process taking place. (although in some texts it is H which is subscribed e.g. ${\mathrm{\Delta H}}^{\circ }\mathrm{f}$)

For a reaction, ${\mathrm{C}}_2{\mathrm{H}}_5\mathrm{OH}\left(\ell \right)+3{\mathrm{O}}_2\left(\mathrm{g}\right)⟶2{\mathrm{CO}}_2\left(\mathrm{g}\right)+3{\mathrm{H}}_2{\mathrm{O\Delta H}}^{\circ }=-1367\mathrm{kJ}{\mathrm{mol}}^{-1}$

We can correlate the relation between the value of $∆$H and each of the participant (reactant/product) of the reaction called unit of factors.

1367 kJ energy is given per mole of reaction = 1367 kJ energy is given per mole of C₂H₅OH$\left(\mathcal{l}\right)$ reacted.

= 1367 kJ energy is given per 3 moles of O₂(g) reacted

= 1367 kJ energy is given per 2 moles of CO₂(g) produced

= 1367 kJ energy is given per 3 moles of H₂O$\left(\mathcal{l}\right)$produced

$\frac{+1367\mathrm{kJ}}{\text{ mole of reaction }}=\frac{+1367\mathrm{kJ}}{\text{ mole of }{\mathrm{C}}_2{\mathrm{H}}_5\left(\ell \right)}=\frac{+1367\mathrm{kJ}}{3\text{ moles of }{\mathrm{O}}_2\left(\mathrm{g}\right)}=\frac{+1367\mathrm{kJ}}{2\text{ moles of }{\mathrm{CO}}_2\left(\mathrm{g}\right)}=\frac{+1367\mathrm{kJ}}{3\mathrm{moles}\text{ of }{\mathrm{H}}_2\mathrm{O}}$

Please note that

1. While writing a thermochemical equation, we stress on the participant concerned (e.g. in heat of combustion on the reactants but not O₂; in heat of formation on the one mole of the particular product formed) and not on the rest, hence we don’t mind if their stoichiometric ratio is not an integer.

2. ${\mathrm{\Delta }}_r{H}^{\circ }$refers to the value of heat associated with the numbers of participants of the reaction as specified the unit of ${\mathrm{\Delta }}_r{H}^{\circ }$ is (and will remain) kJ mole^–1 (or kcal mole^–1) even if the stoichiometric ratio of the reaction is changed.

Some abbreviations used in thermochemical equations

2. Phase abbreviations

s    solid

$\mathcal{l}$  liquid

g    gas

cd  condensed phase (solid and/or liquid)

$f\mathcal{l}$  fluid phase (liquid and/or gas)

cr   crystalline

am  amorphous

1. Transformation abbreviations (physical or chemical changes generally used as subscript with $∆$ e.g. ${\mathrm{\Delta }}_r{H}^{\circ }$ = change of enthalpy of the reaction)

r         reaction

fus     fusion

vap    vaporization

subl   sublimation

f         formation

c         combustion

h         neutralization

sol       solution

trans   transition (of an allotrope into another)

3. When a chemical reaction is reversed, the value of $∆$H is also reversed from the +ve value to -ve and vice versa.

4. The value of $∆$_rH usually shows, small change with an increase in temperature usually excluding those associated with phase transformations.

Enthalpy Changes of Phase Transformations

The changes associated with interconversion of solid, liquid and gaseous states are termed phase transformation. These are always associated with some energy changes. But it is important to note that, surprisingly, the temperature does not change during these transformations e.g. ice (temperature 0^oC) needs energy (heat) to melt into the water whose temperature is 0^oC.

Where does this energy go then? Well, this energy is used up to the overcome the intermolecular forces of attraction between the molecules/ions/atoms of the substance. As in the case of ice and water, energy is required to break the crystal of ice along with some of the hydrogen bonds which become more prominent at the lower temperature. This quantity of energy which is required to bring about a phase change is called the heat of transition or more appropriately the latent heat of transition.

Enthalpy of fusion (${\mathrm{\Delta }}_{\text{fus }}{\mathrm{H}}^{\mathrm{O}}$)

The enthalpy change associated with the melting of 1 mole of a substance at constant temperature and pressure is called enthalpy of fusion or molar enthalpy of fusion.

e.g.  ${\mathrm{H}}_2\mathrm{O}⟶{\mathrm{H}}_2\mathrm{O}\left(\mathrm{s}\right){\mathrm{\Delta }}_{\text{fus }}{H}^{\circ }=6.00\mathrm{kJ}{\mathrm{mole}}^{-1}$

However if water freezes into ice the some amount of energy is to be liberated, i.e.,

${\mathrm{\Delta }}_{\text{freez}}{\mathrm{H}}^{\circ }=-{\mathrm{\Delta }}_{\text{fus}}{\mathrm{H}}^{\circ }$

Melting of a solid is an endothermic process, hence all the enthalpies of fusion are positive.

${\mathrm{\Delta }}_{\text{fus}}{\mathrm{H}}^{\circ }={{\mathrm{H}}^{\circ }}_{\text{iquid}}-{{\mathrm{H}}^{\circ }}_{\text{solid}}$

Enthalpy (Heat) of Vaporization (${\mathrm{\Delta }}_{\text{vap }}{H}^{\circ }$)

The enthalpy change associated with the vaporization of one mole of a liquid at constant pressure and temperature is called (molar) enthalpy of vaporization. The constant temperature referred herein the boiling temperature (T_b) of the liquid.

e.g.  ${\mathrm{H}}_2\mathrm{O}\left(\ell \right)⟶{\mathrm{H}}_2\mathrm{O}\left(\mathrm{g}\right){\mathrm{\Delta }}_{\mathrm{vap}}{\mathrm{H}}^{\circ }=40.79{\mathrm{kJmol}}^{-1}$

Same as in fusion, here also if the reaction is reversed, the sign of $∆$H will get reversed i.e. if steam changes into water, heat will be evolved.

${\mathrm{\Delta }}_{\text{liq}}{H}^{\circ }=-{\mathrm{\Delta }}_{\text{vap}}{H}^{\circ }$

Vaporisation is also endothermic hence $∆$_vapH^o values are positive.

${\mathrm{\Delta }}_{\mathrm{vap}}{\mathrm{H}}^{\circ }={{\mathrm{H}}^{\circ }}_{\text{vapour}}-{{\mathrm{H}}^{\circ }}_{\text{liquid}}$

Enthalpy of sublimation (${\mathrm{\Delta }}_{\text{sub }}{H}^{\circ }$)

The enthalpy change involving conversion of one mole of a solid directly into vapours is known as (molar) enthalpy of sublimation.

e.g. $$\begin{gathered} {\mathrm{CO}}_2\left(\mathrm{s}\right)⟶{\mathrm{CO}}_2\left(\mathrm{g}\right) {\mathrm{\Delta }}_{\text{sub }}{\mathrm{H}}^{\circ }=25.2{\mathrm{kJmol}}^{-1} \\ dry ice \end{gathered}$$

Considering the phase changes in H₂O

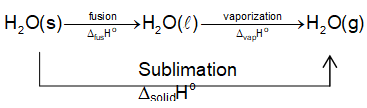
Since, enthalpy is a state property; its value does not depend upon the path followed.

The enthalpy of sublimation can be expressed as ${\mathrm{\Delta }}_{\text{sub}}{H}^{\circ }={\mathrm{\Delta }}_{\text{fus}}{H}^{\circ }+{\mathrm{\Delta }}_{\text{vap}}{H}^{\circ }$

It is so because the total energy required to convert a solid into gas depends upon the nature of the type of interactions present between the constituent particles.

Substance	Melting point Tf(K)	${\mathrm{\Delta }}_{\text{fus}}{\mathrm{H}}^{\circ }\left({\mathrm{kJmo}}^{-1}\right)$	Boiling point Tb(K)	${\mathrm{\Delta }}_{\text{vap}}{\mathrm{H}}^{\circ }$ (kJ mol–1)
N2 CO HCl CH3COCH3 NH3 CCl4 H2O C6H6 NaCl	63.15 68.0 159.0 177.8 195.40 250.16 273.15 278.65 1081.0	0.72 6.836 1.992 5.72 5.65 2.50 6.01 9.83 28.8	77.35 82.0 188.0 329.4 293.73 349.69 373.15 353.25 1665.0	5.59 6.04 16.15 29.1 23.35 30.0 40.79 30.8 170.0

Enthalpy of Phase transition or transformation: Transition is the conversion of one form into another form/phase. The heat change involved is called the enthalpy of phase transition or transformation.

Transformation	Process	Symbol
Transition	Phase $\alpha$ → Phase $\beta$	$∆$tr H
Fusion	Solid (s) → Liquid$\left(\mathcal{l}\right)$	$∆$fusH
Vaporization	Liquid $\left(\mathcal{l}\right)$→ vapour (v)	$∆$vapH
Sublimation	Solid (s) → vapour (v)	$∆$subH
Solution	Solute → solution	$∆$solH
Atomization	Species (s, $\mathcal{l}$, g)→ atoms (g)	$∆$at H
Ionization	M(g) → ${{\mathrm{M}}^{+}}_{\left(\mathrm{g}\right)}+{{\mathrm{e}}^{-}}_{\left(\mathrm{g}\right)}$	$∆$ionH

Illustration 8:   Calculate $∆$H for $C_{\text{(graphite })}⟶{\mathrm{C}}_{\text{(diamand })}$ from the equation

$\begin{array}{l}{\mathrm{C}}_{\left(\text{graphite }\right)}+{\mathrm{O}}_2\left(\mathrm{g}\right)⟶{\mathrm{CO}}_2\left(\mathrm{g}\right); \mathrm{\Delta H}=-393.5\mathrm{kJ}\\ {\mathrm{C}}_{\left(\text{diamond }\right)}+{\mathrm{O}}_2\left(\mathrm{g}\right)⟶{\mathrm{CO}}_2\left(\mathrm{g}\right); \mathrm{\Delta H}=-395.4\mathrm{kJ}\end{array}$

Solution.

$\begin{array}{l}{\mathrm{C}}_{\text{(graphite) }}+{\mathrm{O}}_2\left(\mathrm{g}\right)⟶{\mathrm{CO}}_2\left(\mathrm{g}\right); \mathrm{\Delta H}=-393.5\mathrm{kJ}\\ {\mathrm{C}}_{\text{(diamond })}+{\mathrm{O}}_2\left(\mathrm{g}\right)⟶{\mathrm{CO}}_2\left(\mathrm{g}\right); \mathrm{\Delta H}=-395.4\mathrm{kJ}\end{array}$

on subtraction ${\mathrm{C}}_{\left(\text{graphite }\right)}-{\mathrm{C}}_{\left(\text{diamond }\right)}=-393.5-(-395.4)$

$∆$H = + 1.9 kJ

Standard enthalpy of formation$\left({\mathrm{\Delta }}_f{\mathrm{H}}^{\circ }\right)$: The enthalpy change (the quantity of heat absorbed or released) associated with formation of one mole of a substance from its constituents (atoms) in their standard state. Please note that if the constituents atoms are not in their standard state these H^o will not be the enthalpy of formation.

e.g. ${\mathrm{A}}_2+\frac{2}{3}{\mathrm{B}}_3⟶{\mathrm{A}}_2{\mathrm{B}}_3\mathrm{\Delta H}={\mathrm{\Delta }}_{\mathrm{f}}{\mathrm{H}}^{\circ }\left(\text{ of }{\mathrm{A}}_2{\mathrm{B}}_3\right)$

One mole of A₂B₃ is formed by one mole of A₂ and 2/3 mole of B₃.  We need to balance the stoichiometric ratios of reactants in such a way that one mole of the product is formed.  The value of  may be positive or negative depending upon the substance.

Reaction	Compound	${\mathrm{\Delta }}_f{H}^{\circ }\left(kJ mo{l}^{-1}\right)$
2 C(s) + H2 (g) →	C2H2(g)	+226.8
10C (s) + 4H2(g) →	C10H8(s)	+60.2
N2(g)+2H2(g) →	N2H4($\mathcal{l}$)	+50.6
6C (s) + 3H2(g) →	C6H6($\mathcal{l}$)	+49.0
½ N2(g)+ (3/2) H2(g) →	NH3$\left(g\right)$	– 46.0
C(s) + 2H2(g) →	CH4 (g)	– 74.8
2C(s) + 3H2(g) →	C2H6(g)	– 89.2
½ H2(g) + ½ F2 (g) →	HF (g)	– 271.1
H2(g) + ½ O2(g) →	H2O ($\mathcal{l}$)	– 285.5
S(s) + O2(g) →	SO2 (g)	– 297.5
C(s) + O2(g) →	CO2(g)	– 393.5
Na(s) + ½ Cl2(g) →	NaCl(s)	– 411.0
Ca(s) + ½ O2(g) →	CaO (s)	– 635.5
Si(s) + O2 (g) →	SiO2	– 910.0

Note: 1. Enthalpies of all elements in their standard state have arbitrarily been assumed as zero e.g., that of C(s), Na(s), O₂(g) H₂(g) etc.

2. The compounds having positive enthalpies of formation are called endothermic compounds and are less stable than their reactants, while those with negative values are exothermic compounds which are more stable than their reactants.

Intrinsic energy: “The additional amount of energy that one mole of a compound possesses than that of its constituent elements, is called intrinsic energy.”

Mathematically, Intrinsic energy = – Heat (enthalpy of formation).

“Heat evolved or decrease in enthalpy when one mole of the substance (compound or element) is completely oxidized”. Enthalpy of combustion is always negative.

e.g. $\mathrm{C}\left(\mathrm{s}\right)+{\mathrm{O}}_2\left(\mathrm{g}\right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}⟶{\mathrm{CO}}_2(\mathrm{g}{)}_2\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\mathrm{\Delta }}_c{\mathrm{H}}^{\circ }=-94.3{\mathrm{Kcalmol}}^{-1}$

${\mathrm{CH}}_4\left(\mathrm{g}\right)+2{\mathrm{O}}_2\left(\mathrm{g}\right)⟶\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\mathrm{CO}}_2\left(\mathrm{g}\right)+2{\mathrm{H}}_2\mathrm{O}\left(\ell \right), {\mathrm{\Delta }}_c{\mathrm{H}}^{\circ }=-890.3{\mathrm{kJmol}}^{-1}$

Illustration 9: $∆$H for the reaction.

${\mathrm{H}}_2\left(\mathrm{g}\right)+{\mathrm{Cl}}_2\left(\mathrm{g}\right)⟶2\mathrm{HCl}\left(\mathrm{g}\right)$is – 184.6 kJ. What is heat of formation of HCl.

Solution. Heat of formation is $∆$H for 1 mole

$\therefore \mathrm{\Delta }H=-\frac{184.6}{2}=-92.3\mathrm{kJ}$

Standard Enthalpy of Combustion (${\mathbf{\Delta cH}}^{\circ }$)

Enthalpy change accompanying the complete combustion of one mole of the substance at 25^oC and 1 atm pressure is called as the enthalpy of combustion.

The combustion reactions are exothermic in nature and hence extremely important in our daily life, industry and space missions (particularly rocket propulsion).

Illustration 10: The heat evolved when 10 grams of CH₄ is burnt in excess O₂ is 558.6 kJ. Calculate heat of combustion of CH₄.

Solution. Head of combustion of CH₄ is heat evolved when 16g of CH₄ is burnt in excess oxygen.

for 10gms – 558.6 kJ

$16\mathrm{gm}-\frac{558.6}{10}\times 16=893.76\mathrm{kJ}$

Calorific Value of Fuels and Foods

“Amount of heat energy produced upon complete combustion of one gram of a substance (fuel or food)”. In industry we come across mostly with the processes which are feasible only at high temperature. To achieve this high temperature, we need some source of energy which generally comes from exothermic reaction as heat energy. This heat energy is in fact the energy contained within the bonds of the molecules. The enthalpy of these molecules is greater than that of their oxidation (combustion) products; hence, the enthalpy change accompanying oxidation is –ve. Such substances are called fuels e.g. coal, petroleum, natural gas etc. Cooking gas contains mainly butane along with some other alkanes. e.g. propane.

Ex: During complete combustion of one mole of butane = 2658 kJ heat is liberated.

${\mathrm{C}}_4{\mathrm{H}}_{10}\left(\mathrm{g}\right)+\frac{13}{2}{\mathrm{O}}_2\left(\mathrm{g}\right)⟶4{\mathrm{CO}}_2\left(\mathrm{g}\right)+5{\mathrm{H}}_2\mathrm{O}\left(\ell \right),{\mathrm{\Delta }}_c{\mathrm{H}}^{\circ }=-2658.0{\mathrm{kJmol}}^{-1}$

Combustion of glucose (if carried out in bomb calorimeter) gives 2802 kJ mol^–1 of heat.

${\mathrm{C}}_6{\mathrm{H}}_{12}{\mathrm{O}}_6\left(\mathrm{s}\right)+6{\mathrm{O}}_2\left(\mathrm{g}\right)⟶6{\mathrm{CO}}_2\left(\mathrm{g}\right)+6{\mathrm{H}}_2\mathrm{O}\left(\ell \right), {\mathrm{\Delta H}}^{\circ }=-2002{\mathrm{kJmol}}^{-1}$

Energy is required for all machines to do work. Human body is also a complex machine. In order to perform various functions (works) in our body, this energy is provided by the food, which can be regarded as the fuel for human machines. An adult human requires 2500-3000 kcal of energy per day. In our body this energy is stored in the form of ATP, which are therefore, called as the energy currency of cell. The conversion of food into ATP is basically a combustion or oxidation which in living systems proceeds via a series of complex biochemical reactions involving specific enzymes for each step a detailed study of which shall came across to you in biological sciences under physiology.

Fuel	Calorific value (kJg–1)		Food	Calorific value (kJ g–1)
Wood	17		Milk	3.1
Charcoal	33		Egg	6.7
Kerosene	48		Rice	16.7
Methane	55		Sugar	17.3
LPG	55		Butter	30.4
Hydrogen	150		Ghee	37.6

Enthalpy of Solution:  The enthalpy change associated with dissolution of one mole of a solute in excess of solvent is called the heat of solution.

e.g. $\mathrm{KCl}\left(\mathrm{s}\right)+\mathrm{aq}\to \mathrm{KCl}\left(\text{aq}\right) {\mathrm{\Delta }}_{\mathrm{sol}}{\mathrm{H}}^{\circ }=4.4\mathrm{Kcal}$

$\begin{array}{l}\mathrm{KOH}\left(\mathrm{s}\right)+\mathrm{sq}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\to \hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\mathrm{KOH}\text{(aq)}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} \mathrm{\Delta }{\mathrm{fH}}^{\circ }=-13.3\mathrm{Kcal}\\ {\mathrm{H}}_2{\mathrm{SO}}_4\left(\mathrm{I}\right)+\mathrm{aq}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\to \hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\mathrm{H}}_2{\mathrm{SO}}_4\left(\mathrm{aq}\right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} \mathrm{\Delta }{\mathrm{fH}}^{\circ }=-20.2\mathrm{kcal}\end{array}$

Generally dissolution is distribution of a solute in a solvent. Energy is required for this interaction e.g. dissolution of KCl or sugar in water, hence $∆$_solH^o is positive, which is reflected by the cooling down of the solution. As the energy required is supplied by the energy contained within the molecules of solvent, whose internal energy decreases eventually henceforth the temperature also.

But in few cases, besides disintegration there is solvate formation (e.g. with water, hydrate).  During salvation (hydration) heat is evolved due to strong interaction (e.g. ion-dipole interaction) between the solute and solvent. The net enthalpy change in such cases depends upon the values of salvation energy and dissociation energy. There are few cases where the two values are equal to each other. Hence No heat is evolved. As in case of NaCl, there is very little enthalpy change, hence no appreciable heating or cooling effect is observed.

Enthalpy of Neutralization

When one gram equivalent of an acid is neutralized by 1 gram equivalent of a base in dilute solution, the enthalpy change connected is called as he enthalpy of neutralization.

$\begin{array}{l}\mathrm{HCl}\left(\mathrm{aq}\right)+\mathrm{NaOH}\left(\mathrm{aq}\right)\to \mathrm{NaCl}\left(\mathrm{aq}\right)+{\mathrm{H}}_2\mathrm{O}\left(\ell \right) \mathrm{\Delta }{\mathrm{nH}}^{\circ }=-13.75\mathrm{kcal}\\ {\mathrm{HNO}}_3\left(\mathrm{aq}\right)+\mathrm{NaOH}\left(\mathrm{aq}\right)\to {\mathrm{NaNO}}_3\left(\mathrm{aq}\right)+{\mathrm{H}}_2\mathrm{O}\left(\ell \right) \mathrm{\Delta }{\mathrm{nH}}^{\circ }=-13.7\mathrm{kcal}\end{array}$

Acid	Alkali	${\mathrm{\Delta }}_{\mathrm{n}}{\mathrm{H}}^{\circ }\left(\mathrm{kJ}{\mathrm{mol}}^{-1}\right)$
HCl	NaOH	–57.32
HNO3	NaOH	–57.28
HCl	KOH	–57.45
HCl	LiOH	–57.38
HCOOH	NaOH	–56.06
CH3COOH	NaOH	–55.23
H2S	NaOH	–15.90
HCN	NaOH	–12.13
CH3COOH	NH4OH	–2.84

It can be observed from the table that the neutralization energy of a strong acid against a strong base is always near to –57 kJ (or 13.7 kcal) and is independent of type of acid or base involved. But if either or both them is/are weak the ${\mathrm{\Delta }}_{\mathrm{n}}{\mathrm{H}}^{\circ }$ is some what less than the above mentioned value. Why So? The theory of ionization provides the solution. Since strong electrolytes (acids and bases) ionize completely. One gram equivalent of an acid gives one gram equivalent H⁺ similarly OH^–. These each one gram equivalent of H⁺ and OH^– combine to form one mole of water. The value of enthalpy change (decrease) for the reaction is 57 kJ.

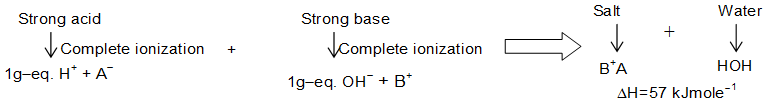
Although hydrogen has the highest calorific value out of the listed fuels in the table but it is not used for domestic or industrial purposes due to some technical problems like problem in storage of highly inflammable hydrogen. (Refer hydrogen economy phase II)

 Illustration 11:

Heat of neutralization of ${\mathrm{HCl}}_{\left(\mathrm{aq}\right)}+{\mathrm{NaOH}}_{\left(\mathrm{aq}\right)}⟶{\mathrm{NaCl}}_{\left(\mathrm{aq}\right)}+{\mathrm{H}}_2{\mathrm{O}}_{\left(1\right)}; \mathrm{\Delta H}=-57.3\mathrm{kJ}$

Heat of neutralization of ${\mathrm{HCl}}_{\left(aq\right)}+{\mathrm{NH}}_4{\mathrm{OH}}_{\text{(ag) }}⟶{\mathrm{NH}}_4{\mathrm{Cl}}_{\left(\text{aq}\right)}+{\mathrm{H}}_2{\mathrm{O}}_{\text{l }}; \mathrm{\Delta H}=-51.46\mathrm{kJ}$

Calculate heat of ionization of NH₄OH_(aq)

Solution.

Heat of ionization of NH₄OH

= [Heat of neutralization of (NH₄OH + HCl)- Heat of neutralization of (NaOH + HCl)

= 51.46 kJ – (57.3 kJ) = 57.3 – 51.46 = + 5.84 kJ

Illustration 12:

Calculate the ionization enthalpy of NH₄OH from $∆$H of neutralization of (HCl + NaOH) (–57.4 kJ).  HCl + NH₄Oh (–51.46 kJ).

Solution.

 $\mathrm{\Delta H}\text{ of }\left(\mathrm{HCl}+{\mathrm{NH}}_4\mathrm{OH}\right)-\mathrm{\Delta H}\text{ of }(\mathrm{HCl}+\mathrm{NaOH})$$$

$\begin{array}{r}=\mathrm{\Delta }H\text{ of ionization of }{\mathrm{NH}}_4\mathrm{OH}\\ \mathrm{\Delta H}=\left\{\right(-51.46)-(-57.40\left)\right\}\mathrm{kJ}\\ \mathrm{\Delta }H=\left\{\right(-51.46)-(-57.49\left)\right\}\mathrm{kJ}\\ \mathrm{\Delta H}=\{57.40-51.46\}=5.94\mathrm{kJ}\end{array}$

Standard Enthalpies of Bond Formation

Bond	$∆$Hoo(kJmol–1)	Bond	$∆$Hoo(kJmol–1)
H–H	435.1	O = _	493.7
H – F	564.8	N = N	418.4
H – Cl	430.9	C = C	615.0
O – H	464.4	C = O	351.4
N – H	389.1	C = N	615.0
C – H	416.2	N $\equiv$ N	945.6
Cl – Cl	242.7	C $\equiv$ C	811.7
C – C	347.3	C $\equiv$ N	878.6

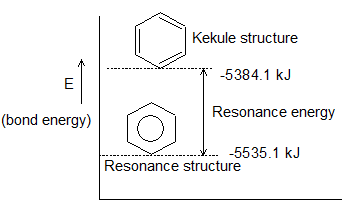
Resonance Energy: There are compounds for which experimental value of sum of the bond energies is different (usually less than) from the calculated value. This difference, brought about by some dynamic structures which contribute to its stability, is called the resonance energy. e.g. considering benzene to be a cyclohexatriene (three single and three double bonds, the bond energy of benzene molecule shall be

${\mathrm{\Delta H}}^{\circ }=3\left({\mathrm{\Delta }}_{\mathrm{C}-\mathrm{c}}{\mathrm{H}}^{\circ }\right)+3\left({\mathrm{\Delta }}_{\mathrm{C}-\mathrm{C}}{\mathrm{H}}^{\circ }\right)+6\left({\mathrm{\Delta }}_{\mathrm{C}-\mathrm{H}}{\mathrm{H}}^{\circ }\right)=3\left(347.3\right)+3(615.0)+6\left(416.2\right)=5384.1{\mathrm{kJmol}}^{-1}.$

However, the experimental vmol^–1.alue is known to be 5535.1 kJmol^–1. Since, the experimental value is greater, it means, the dissociation of benzene molecule will in fact require (5535.1–5384.1 = 151 kJ) more than the calculated value. We infer that the actual structure of benzene is more stable than the Kekule’s structure by 151 kJ mol^–1.

Applications of Hess’s Law

Using Hess’s law and thermochemical calculations, we can calculate so many enthalpies as discussed further.

1. Calculation of Enthalpies of Reactions: For some reactions it is almost impossible to calculate the enthalpy change. Hence the experimental value is accessed by, for example, partial combustion of carbon into carbon monoxide, applying Hess’s law as discussed hereunder:

$\mathrm{C}\left(\mathrm{s}\right)+\frac{1}{2}{\mathrm{O}}_2\left(\mathrm{g}\right)⟶\mathrm{CO}\left(\mathrm{g}\right){\mathrm{\Delta }}_{\mathrm{f}}{\mathrm{H}}^{\circ }=?$

The enthalpy of combustion of carbon is 393.5 kJ mol^–1 i.e.

$\mathrm{C}\left(\mathrm{s}\right)+{\mathrm{O}}_2\left(\mathrm{g}\right)⟶{\mathrm{CO}}_2\left(\mathrm{g}\right){\mathrm{\Delta H}}^{\circ }=-393.5{\mathrm{kJmol}}^{-1}$.

We have experimental value of combustion of carbon monoxide (282.0 kJ mol^–1).

$\mathrm{CO}\left(\mathrm{g}\right)+\frac{1}{2}{\mathrm{O}}_2\left(\mathrm{g}\right)⟶{\mathrm{CO}}_2\left(\mathrm{g}\right),{\mathrm{\Delta H}}^{\circ }=-282.0\mathrm{kJ}$.

Let there be a reaction, as represented by eq. Applying Hess’s law

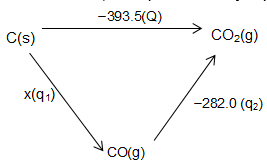
Q = q₁ + q₂

–393.5 = x+(–282.0)

x = –111.5 kJ

Illustration 13:

Why it is not possible to experimentally determine the enthalpy of the reaction? $\mathrm{C}\left(\mathrm{s}\right)+\frac{1}{2}{\mathrm{O}}_2\left(\mathrm{g}\right)⟶\mathrm{CO}\left(\mathrm{g}\right)?$

Solution.

As CO is produced in two conditions, one the combustion of carbon in limited oxygen supply and the other at the temperature above 1100^oC (as in metallurgy). The problem arises in first case that there is always some formation of CO₂ along with CO, and in the other case, at such a high temperature, the calculation of variation of enthalpy is really an inefficient task.

2. Calculation of enthalpy changes of slow reactions: For experimental conditions, time period is a prominent aspect to consider. If a reaction competes in couple of days or so, the exact value of enthalpy change even in a bomb calorimeter or other devices will not bear fruits as, the walls of laboratory instruments are not perfectly insulator, this can of course, be not a problem while dealing with the reactions which complete within a couple of hours, but the dissipation of heat from such an instrument will always give a value different than the actual value.  Hess’s law provides the alternative.

Transformation of Rhombic Sulphur into Monoclinic

Since we have the data of enthalpies of combustion of monoclinic and rhombic sulphur.

(i)$\begin{array}{l}{\mathrm{S}}_{\text{rhombic }}+{\mathrm{O}}_2\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}⟶\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\mathrm{SO}}_2\left(\mathrm{g}\right); \hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\mathrm{\Delta }}_{\mathrm{C}}{\mathrm{H}}^{\circ }=-297.5{\mathrm{kJmol}}^{-1}\end{array}$

(ii) ${\mathrm{S}}_{\text{monodinic }}+{\mathrm{O}}_2\left(\mathrm{g}\right)⟶{\mathrm{SO}}_2\left(\mathrm{g}\right);{\mathrm{\Delta }}_{\mathrm{C}}{\mathrm{H}}^0=-300.0{\mathrm{kJmol}}^{-1}$

Applying Hess’s law

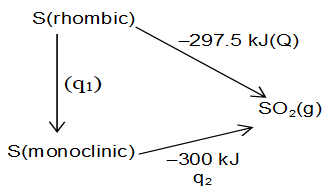
Q = q₁ + q₂

(–297.5) = q₁ + (–300.0)      $\left[{\mathrm{S}}_{\text{rhombic }}⟶{\mathrm{S}}_{\text{monoclinic }}\right]$

q₁ =  2.5 kJ

Alternatively

Subtracting eq. (ii) from (i)

${\mathrm{S}}_{\left(\text{rhombic }\right)}⟶{\mathrm{S}}_{\left(\text{monoclinic }\right)}{\mathrm{\Delta H}}^{\circ }=2.5\mathrm{kJ}{\mathrm{mol}}^{-1}.$

The small difference between the values of $∆$H^o for two different pairs of strong acidic and bases is due to their differences in values of dissociation energies.

But if an acid or a base is weak, the dissociation/ionization is not complete. 1 gm equivalent weak acid produces less than 1 gram equivalent H⁺ and so is the case with a weak base. The result is that the product formed is H₂O but less than 1 mole, hence is the enthalpy change.

From above discussion, it is clear that, heat of neutralization of a strong acid and a strong base is only the heat of formation of water from H⁺ and OH^– of acids and bases respectively. In fact the decrease in enthalpy of weak acids acids/bases is due to expenditure of energy in dissociation of the H⁺ and OH^– from the total amount to be observed as enthalpy of neutralization. Average value of enthalpy change for the combination of H⁺ and OH^– is taken as –57.32 kJmol^–3.

The enthalpy of neutralization of HCl and NH₄OH at 25^oC is $-51.34{\mathrm{kJmol}}^{-1}$, hence the standard enthalpy of dissociation of NH₄OH can be deduced to (–51.34) – (–51.32) = +5.98 kJmol^–1.

Bond energy:  Average amount of energy required to dissociate (i.e. break) one mole (i.e. Avogadro number) of bonds of that type in a compound. During the formation of bonds, enthalpy content tends to decrease to a minimum value. This decrease in enthalpy which makes the bond system more stable, is called as the bond energy.

Bond energy (enthalpy of bond formation) is an additive property.

Illustration 14:

From the data given below calculate the heat of reaction for hydrogenation of acetylene at constant volume at 298^oK.

Heat of formation of water, $\mathrm{\Delta f}{H}^{\circ }=-68.3 \mathrm{kcal}{\mathrm{mol}}^{-1}$

Heat of combustion of acetylene, $\mathrm{\Delta }{\mathrm{cH}}^{\circ }=-310.6\mathrm{kcal}{\mathrm{mol}}^{-1}$

Heat of combustion of ethylene,${\mathrm{\Delta }}_{\mathrm{C}}{\mathrm{H}}_{\left({\mathrm{CH}}_2={\mathrm{CH}}_2\right)}^{\circ }=-33.2\mathrm{kcal}{\mathrm{mol}}^{-1}$

Solution.

Writing the desired thermochemical equation

Although hydrogenation of acetylene can be carried out upto ethane CH₃-CH₃, but in between ethylene (CH₂=CH₂) is also formed. Since the further data about CH₃-CH₃ has not been mentioned, its desired that the equation to be used should involve CH₂=CH₂.

(i) ${\mathrm{C}}_2{\mathrm{H}}_2\left(\mathrm{g}\right)+{\mathrm{H}}_2\left(\mathrm{g}\right)\to {\mathrm{C}}_2{\mathrm{H}}_4\left(\mathrm{g}\right)\mathrm{\Delta }{\mathrm{H}}^{\circ }=?$

Writing other concerned equations Heat of formation of water:

ii) ……… ${\mathrm{H}}_2\left(\mathrm{g}\right)+\frac{1}{2}{\mathrm{O}}_2\left(\mathrm{g}\right)\to {\mathrm{H}}_2\mathrm{O}\left(\ell \right){\mathrm{\Delta H}}^{\circ }=-68.3\mathrm{kcal}{\mathrm{mol}}^{-1}$

Heat of combustion of acetylene

iii) …………. ${\mathrm{C}}_2{\mathrm{H}}_2\left(\mathrm{g}\right)+(5/2){\mathrm{O}}_2\left(\mathrm{g}\right)\to 2{\mathrm{CO}}_2\left(\mathrm{g}\right)+H_{2}O\left(\mathcal{l}\right){\mathrm{\Delta H}}^{\circ }=-310.6\mathrm{kcal}{\mathrm{mol}}^{-1}$

Heat of combustion of ethylene

iv) …………………${\mathrm{C}}_2{\mathrm{H}}_4\left(\mathrm{g}\right)+3{\mathrm{O}}_2\left(\mathrm{g}\right)\to 2{\mathrm{CO}}_2\left(\mathrm{g}\right)+2{\mathrm{H}}_2\left(\ell \right), {\mathrm{\Delta H}}^{\circ }=-337.2\mathrm{kcal}{\mathrm{mol}}^{-1}$

Rearranging the equation to get the desired one:  Since C₂H₂(g) is to be produced (i.e. on the RHS of the thermo equation), the equation (iv) should be reversed, the sign of $∆$H will became positive.

(iva) …………. $2{\mathrm{CO}}_2\left(\mathrm{g}\right)+2{\mathrm{H}}_2\mathrm{O}\left(\mathrm{I}\right)\to {\mathrm{C}}_2{\mathrm{H}}_4\left(\mathrm{g}\right)+3{\mathrm{O}}_2\text{ (g) }{\mathrm{\Delta H}}^{\circ }=+337.2\mathrm{k}\text{ cal }{\mathrm{mol}}^{-1}$

The reactant has to be acetylene, in equation (iii) It is on he reactant side, no change required. One H₂O from the LHS in equation (iva) has to be cancelled which can be achieved by adding equation (ii).

$\begin{array}{l}{\mathrm{H}}_2\left(\mathrm{g}\right)+1/2{\mathrm{O}}_2\left(\mathrm{g}\right)\hspace{0.25em}\to \hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\mathrm{H}}_2\mathrm{O}\left(\ell \right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} {\mathrm{\Delta H}}^{\circ }=-68.3\mathrm{kcal}\end{array}$

${\mathrm{C}}_2{\mathrm{H}}_2\left(\mathrm{g}\right)+(5/3){\mathrm{O}}_2\left(\mathrm{g}\right)⟶2{\mathrm{CO}}_2\left(\mathrm{g}\right)+{\mathrm{H}}_2\mathrm{O}\left(\ell \right){\mathrm{\Delta H}}^{\circ }=-310.6\mathrm{kca}$

$\begin{array}{l}2{\mathrm{CO}}_2\left(\mathrm{g}\right)+2{\mathrm{H}}_2\mathrm{O}\left(\ell \right)\hspace{0.25em}⟶\hspace{0.25em}{\mathrm{C}}_2{\mathrm{H}}_4\left(\mathrm{g}\right)+3{\mathrm{O}}_2\left(\mathrm{g}\right)\hspace{0.25em} \hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\mathrm{\Delta H}}^{\circ }=337.2\mathrm{kcal}\end{array}$

—————————————————————————–

$\text{ Adding }{\mathrm{C}}_2{\mathrm{H}}_2\left(\mathrm{g}\right)+{\mathrm{H}}_2\left(\mathrm{g}\right)\begin{array}{l}\text{→ }\hspace{0.25em}{\mathrm{C}}_2{\mathrm{H}}_4\left(\mathrm{g}\right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} {\mathrm{\Delta H}}^{\circ }=-41.7\mathrm{kcal}\end{array}$

Hence the standard heat of hydrogenation is –41.7 kcal (at constant pressure of 1 atm and 298 k). Relation it with the standard enthalpy at constant volume,

Thermochemical Calculations

Like algebraic equations, thermochemical equations can also be treated upon by the simple mathematical operations like addition, subtraction, multiplication and division. However, few cautions are to be exercised while performing calculations.

1. Balanced thermochemical equations are written fro each transformation.

$\mathrm{C}\left(\mathrm{s}\right)+2{\mathrm{H}}_2\left(\mathrm{g}\right)\to {\mathrm{CH}}_4\text{ (g). }{\mathrm{\Delta H}}^{\circ }=-74.8\mathrm{kJ}{\mathrm{mol}}^{-1}$

2. Rearrangement of these equations to give the final equation (required) is achieved by

a) while reversing an equation, the value of enthalpy be reversed.

b) Enthalpy change of reaction is equal to the difference between the sum of enthalpies of products and that of reactants.

3. The physical states of the participants of the deduced (from calculations) equation must be as per the standard equation.

How to deduce the desired enthalpy from the given data?

• The first thing required is the balanced thermochemical equation for the reaction, we are interested in transformation. Then all the available data should be in the form of thermochemical equations along with (if not already specified) the value of $∆$H with proper sign.
• It must be borne in the mind that some information like the sign of enthalpy of composition, which is always negative, should be assigned proper sign, even if the sing is not mentioned in the problem.
• Some of the thermochemical equations can be framed on the basis of the definition e.g. combustion of methane means ${\mathrm{CH}}_4\left(\mathrm{g}\right)+3{\mathrm{O}}_2\to {\mathrm{CO}}_2+2{\mathrm{H}}_2\mathrm{O}$Similarly formation of acetic acid means $2\mathrm{C}\left(\mathrm{s}\right)+2{\mathrm{H}}_2\left(\mathrm{g}\right)+{\mathrm{O}}_2\left(\mathrm{g}\right)\to {\mathrm{CH}}_3\mathrm{COOH}\left(\ell \right)$
• The standard state of thermochemical equations should be taken care of.
• If the value of enthalpy change has been mentioned in terms of $∆$E^o (or q_o) it should be converted into $∆$H^o (or C_vp) using the relation $\mathrm{\Delta H}=\mathrm{\Delta E}+\mathrm{\Delta nRT}$
• Rearrangement of the given equation should then be performed so as to give the desired balanced equation with proper sign of $∆H$
• When a thermochemical equation is multiplied by some number (as in case of equation (ii) & (iii) in previous example, the value of $∆H$ must also be multiplied by the same number.
• If we revert the reaction, the sign of $∆$H must be reversed or we can say while subtracting an equation the $∆$H must also be treated like an algebraic quantity.

Determination of resource energy

Determination of enthalpies of transformation    (already discussed in the chapter)

Determination of bond energies

Determination of lattice energy    (discussed in Phase – I, Structure & Bonding)

Illustration 15:

Which one do you think will thermodynamically be more stable–rhombic or monoclinic sulphur?

Solution.

As we know, lower the energy content, greater the stability. Hence, S(rhombus) with less energy is more stable than the S(monoclinic), as energy is required (endothermic transformation) to convert rhombic sulphur into monoclinic.

3. Calculation of enthalpy of formation

When direct measurement of enthalpy of formation of a compound is not possible for some or the other reasons, Hess’s law is applied to calculate the value. e.g. the enthalpy of formation of benzene as represented by the equation (as per definition) will be given by

$6\mathrm{C}\left(\mathrm{s}\right)+3{\mathrm{H}}_2\left(\mathrm{g}\right)⟶{\mathrm{C}}_6{\mathrm{H}}_6\left(\ell \right),\mathrm{\Delta H}=?$

Since the equation proceeds in the presence of electric arc at an extremely high temperature, the change in enthalpy is extremely difficult to determine instead, Hess’s law is used along with implementation of thermochemical equation.

We have          

(i) ${\mathrm{C}}_6{\mathrm{H}}_6\left(\ell \right)+\frac{15}{2}{\mathrm{O}}_2\left(\mathrm{g}\right)⟶6{\mathrm{CO}}_2\left(\mathrm{g}\right)+3{\mathrm{H}}_2\mathrm{O}\left(\ell \right){\mathrm{\Delta H}}^{\circ }=-3267.7\mathrm{kJ}$

(ii) $\mathrm{C}\left(\mathrm{s}\right)+{\mathrm{O}}_2\left(\mathrm{g}\right)⟶{\mathrm{CO}}_2\left(\mathrm{g}\right) {\mathrm{\Delta H}}^{\circ }=-393.5\mathrm{kJ}$

(iii) ${\mathrm{H}}_2\left(\mathrm{g}\right)+\frac{1}{2}{\mathrm{O}}_2\left(\mathrm{g}\right)⟶{\mathrm{H}}_2\mathrm{O}\left(\ell \right) {\mathrm{\Delta H}}^{\circ }=285.9\mathrm{kJ}$

Rearranging the equations, i.e.

Multiplying equation (ii) by 6 and equation (iii) by (3)

$\begin{array}{l}6\mathrm{C}\left(\mathrm{s}\right)+6{\mathrm{O}}_2\left(\mathrm{g}\right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}⟶\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}6{\mathrm{CO}}_2\left(\mathrm{g}\right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} {\mathrm{\Delta H}}^{\circ }=-2361.0\mathrm{kJ}\\ 3{\mathrm{H}}_2\left(\mathrm{g}\right)+\frac{3}{2}{\mathrm{O}}_2\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}⟶\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}3{\mathrm{H}}_2\mathrm{O}\left(\ell \right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} {\mathrm{\Delta H}}^{\circ }=-857.7\mathrm{kJ}\end{array}$

—————————————————————

Adding  $6\mathrm{C}\left(\mathrm{x}\right)+3{\mathrm{H}}_2\left(\mathrm{g}\right)+\frac{15}{2}{\mathrm{O}}_2\left(\mathrm{g}\right)⟶6{\mathrm{CO}}_2\left(\mathrm{g}\right)+3{\mathrm{H}}_2\mathrm{O}\left(\ell \right) {\mathrm{\Delta H}}^{\circ }=-3218.7\mathrm{kJ}$  ………  (iv)

Subtracting equation (1) from equation (iv)

$\begin{array}{l}6\mathrm{C}\left(\mathrm{s}\right)+3{\mathrm{H}}_2\left(\mathrm{g}\right)+\frac{15}{2}{\mathrm{O}}_2\left(\mathrm{g}\right)⟶6{\mathrm{CO}}_2\left(\mathrm{g}\right)+3{\mathrm{H}}_2\mathrm{O}\left(\ell \right){\mathrm{\Delta H}}^{\circ }=-3218.7\mathrm{kJ}\\ 6{\mathrm{CO}}_2\left(\mathrm{g}\right)+3{\mathrm{H}}_2\mathrm{O}\left(\ell \right) ⟶ {\mathrm{C}}_6{\mathrm{H}}_6\left(\ell \right)+\frac{15}{2}{\mathrm{O}}_2\left(\mathrm{g}\right), {\mathrm{\Delta H}}^{\circ }=49.0\mathrm{kJ}\end{array}$

---

$6\mathrm{C}\left(\mathrm{s}\right)+3{\mathrm{H}}_2\left(\mathrm{g}\right)⟶{\mathrm{C}}_6{\mathrm{H}}_6\left(\ell \right) {\mathrm{\Delta H}}^{\circ }=49.0\mathrm{kJ}$

Illustration 16:

The enthalpy change at 25^oC for the reaction of graphite and hydrogen gas to form ethene and ethane are 52.26 kJmol^–1 and –84.68 kJmol^–1 respectively. Calculate enthalpy change for the hydrogenation of ethene to give ethane.

Sol:

The thermochemical equations for the given data are

Formation of ethene: $2\mathrm{C}\text{ (graphite) }+2{\mathrm{H}}_2\left(\mathrm{g}\right)\to {\mathrm{C}}_2{\mathrm{H}}_4\left(\mathrm{g}\right){\mathrm{\Delta fH}}^0=52.26\mathrm{kJ}{\mathrm{mol}}^{-1}$         ……(i)

formation of ethane: $2\mathrm{C}\left(\text{ graphite }\right)+3{\mathrm{H}}_2\left(\mathrm{g}\right)\to {\mathrm{C}}_2{\mathrm{H}}_8\left(\mathrm{g}\right) \mathrm{\Delta }{\mathrm{fH}}^{\circ }=-84.68{\mathrm{kJmol}}^{-1}$        ……(ii)

The desired thermochemical equation for the calculation of enthalpy change

${\mathrm{C}}_2{\mathrm{H}}_4\left(\mathrm{g}\right)+{\mathrm{H}}_2\left(\mathrm{g}\right)\to {\mathrm{C}}_2{\mathrm{H}}_6\text{ (g) }$                                    ……(iii)

$2\mathrm{C}\left(\text{ graphite }\right)+3{\mathrm{H}}_2\left(\mathrm{g}\right)\left[2\mathrm{C}\left(\text{ graphite }\right)+2{\mathrm{H}}_2\left(\mathrm{g}\right)\right]⟶\left[{\mathrm{C}}_2{\mathrm{H}}_6\left(\mathrm{g}\right)-{\mathrm{C}}_2{\mathrm{H}}_4\left(\mathrm{g}\right)\right]\mathrm{\Delta H}=\mathrm{\Delta H}\text{ (ii) }-\mathrm{\Delta H}\text{ (i) }$

Equation (iii) can be obtained by reverting eq (i) and adding it to equation (ii)

Alternatively by subtracting equation (i) from equation (ii).

$\begin{array}{l}{\mathrm{C}}_2{\mathrm{H}}_4\left(\mathrm{g}\right)⟶2\mathrm{C}\left(\text{ graphite }\right)+2{\mathrm{H}}_2\left(\mathrm{g}\right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} \mathrm{\Delta H}=-52.26\mathrm{kJ}{\mathrm{mol}}^{-1}\\ 2\mathrm{C}\left(\text{ graphite }\right)+3{\mathrm{H}}_2\left(\mathrm{g}\right)⟶{\mathrm{C}}_2{\mathrm{H}}_8\left(\mathrm{g}\right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} \mathrm{\Delta H}=-84.68\mathrm{kJ}{\mathrm{mol}}^{-1}\end{array}$

---

$\begin{array}{r}\text{ Adding }{\mathrm{C}}_2{\mathrm{H}}_4\left(\mathrm{g}\right)+{\mathrm{H}}_2\left(\mathrm{g}\right)⟶{\mathrm{C}}_2{\mathrm{H}}_6\left(\mathrm{g}\right) \mathrm{\Delta H}=-136.94{\mathrm{kJmol}}^{-1}\\ {\mathrm{H}}_2\left(\mathrm{g}\right)⟶{\mathrm{C}}_2{\mathrm{H}}_6\left(\mathrm{g}\right)-{\mathrm{C}}_2{\mathrm{H}}_4\left(\mathrm{g}\right) \mathrm{\Delta H}=(-84.68)-\left(52.26\right)\mathrm{kJ}{\mathrm{mol}}^{-1}\\ {\mathrm{C}}_2{\mathrm{H}}_4\left(\mathrm{g}\right)+{\mathrm{H}}_2\left(\mathrm{g}\right)⟶{\mathrm{C}}_2{\mathrm{H}}_6\left(\mathrm{g}\right) \mathrm{\Delta H}=-136.94\mathrm{kJ}{\mathrm{mol}}^{-1}\end{array}$

$∆$H (enthalpy of hydrogenation of ethene) = $-136.94\mathrm{kJ}{\mathrm{mol}}^{-1}$

Hence, enthalpy of formation of benzene is 49.0 kJ mol^–1.

Limitations of the First Law of Thermodynamics

The essence of the first law is that the total energy of the system and surroundings is constant during all the physical and chemical processes. No transformation till date has been observed violating the law. But there are the limitations of the law:

1. Although the first law correlates the heat absorbed and the work done by a system but it does not tell anything about the direction of flow of heat. For instance, as per first law, heat can be extracted from ice by cooling it to a lower temperature and then it (heat) can be used to warm the water. But from our experience we know that such transfer of heat from a lower temperature to a higher is not possible without expenditure of some (spare) energy i.e. without doing some external work. Rather conversely, it is found that heat flows from a higher to a lower temperature spontaneously i.e. of its own accord, without any external aid.

2. The First law does not tell anything about the fate of a reaction whether a given process take place i.e. if it is feasible and if so, whether it will reach upto completion.

3. Why the natural spontaneous processes are irreversible – is not referred to in the first law of thermodynamics.

4. Though one form of energy can be converted into an equivalent amount of another form, but upto which extent e.g. conversion of heat energy into work is not governed by the first law.

The aforesaid facts lead us to need of some another law which may rectify the limitation of the first law. The result came as the second law of thermodynamics. Although almost of the forms of energy can completely be converted into another but heat is a typical form which cannot be completely converted into work. Before studying the 2^nd law, it will be convenient to discuss the terms like spontaneity, entropy and free energy.

Spontaneous Processes

Whether the two given reactants will react under the given set of conditions can be predicted by applying thermodynamics which is of great significance. A reaction that proceeds under a given set of conditions is called to be spontaneous and if does not, it will be non-spontaneous. All natural processes are spontaneous and irreversible. Few examples are discussed as follows:

1. Water flows downhill spontaneously. We cannot reverse the direction of flow without some external aid.  All liquids have tendency to flow from a higher level to the lower until their levels become equal. Why it is so? Because, the liquid at high altitude will have a greater value of h, for the calculation of energy contained within it (as potential energy), and hence will tend to achieve such a position (height), where it may have minimum energy content with it.

2. If a metal bar is hot at one end and cold at the other, heat flows spontaneously from the hot end to the cold until the temperature of rod becomes uniform throughout (thermal equilibrium). The reason can be accounted to the high internal energy of the atoms at hot end. Since, atoms or else tend to achieve minimum energy, they shall pass on this energy to the nearby atoms through their vibrations (thermal vibration). This transfer of energy will continue until all the atoms achieve a uniform temperature. (an inference of energy indeed). Temperature of rod shall decrease further if the surroundings have lower energy content than the metal, and will continue until the temperature of its surroundings and itself confronts uniformity. A metal bar having uniform temperature has not been observed ever to become hot at one end and cold at another end spontaneously.

3. A gas expands from a region of higher pressure to a lower or in vacuum. During expansion some work is done at the cost of its energy, hence a decrease in energy is achieved inferred by decrease in temperature.

4. Electricity flows spontaneously from a point of higher potential to a point of lower potential. The direction of flow of the electricity can only be reversed only when an external field with higher magnitude in opposite direction is applied.

5. Diffusion of a solute from a concentrated solution to dilute or less concentrated solution proceeds spontaneously if they are brought in contact, until the concentration becomes uniform throughout (physical equilibrium).

The process of osmosis is pretty fine example of spontaneity, where the solvent molecules travel through the semi-permeable membrane in order to pass into the solution where the concentration of water molecules (note that concentration of the solution is just opposite to the concentration of solvent molecule) is lower. Why do only solvent and not the solute molecules/ions pass through the membrane? The reason is the size of pore of the membrane. As the membranes are selectively permeable for the smaller size particles. Can the direction of flow of water molecules from the solution of lower concentration to a higher one be achieved? The answer is yes, and being industrially exploited in the purification of water, called reverse osmosis (abbreviated as RO system by the water purifiers) wherein the external pressure over the impure water (a relatively concentrated solution) bound by a semipermeable membrane, compels to move water molecules against the usual direction of flow.

What do you think, if water can flow form a lower altitude to a higher on its own? No! But it of course can, if there is some source of energy e.g., a motor pump or the solar energy which drives the water as vapours from sea into clouds.

6. If a piece of zinc metal is placed in the solution of copper sulphate, the former dissolves in (in fact, passes on into) the solution spontaneously, with the precipitation (expelling out) of the latter.

$\mathrm{Zn}\left(\mathrm{s}\right)+{\mathrm{CuSO}}_4\left(\mathrm{aq}\right)⟶{\mathrm{ZnSO}}_4\left(\mathrm{aq}\right)+\mathrm{Cu}\left(\mathrm{s}\right)$

The above reaction is exothermic (some heat is evolved) but the reaction cannot be reversed by the effect of heat. However, the flow of electric current between the copper and zinc rods immersed in aqueous sulphate solution of course can. What will be the relation between electrical energy required to reverse the reaction and the heat energy evolved in the direct reaction? The electrical energy will be somewhat greater than the heat energy.

A process which has an urge or a natural tendency to occur (proceed) either of its own or after proper initiation under the given set of conditions, is called as the spontaneous process. A spontaneous reaction does not means that it completes instantaneously rather it is practically feasible without any external source of energy. The spontaneous reactions may be extremely fast or very slow like an acid-base neutralization and conversion of lime and atmospheric CO₂ into CaCO₃. From experience, we know that all the natural processes are spontaneous and irreversible i.e., they proceed in one direction only. The spontaneous reaction may in some cases require initiation to take place.

a) Spontaneous processes wherein no initiation is required

1. Melting of ice into water ${\mathrm{H}}_2\mathrm{O}⟶{\mathrm{H}}_2\mathrm{O}\left(\ell \right)$

2. Evaporation of water from water bodies (ponds, lakes, rivers, sea etc) ${\mathrm{H}}_2\mathrm{O}\left(\ell \right)\stackrel{\text{ evporation }}{⟶}{\mathrm{H}}_2\mathrm{O}\left(\mathrm{g}\right)$

3. Dissolution of sugar/salt in water

$\begin{array}{l}\mathrm{Sugar}\left(\mathrm{s}\right)+\mathrm{aq}⟶\mathrm{sugar}\left(\mathrm{aq}\right)\\ \mathrm{Salt}\left(\mathrm{s}\right)+\mathrm{aq}⟶\mathrm{salt}\left(\mathrm{aq}\right)\end{array}$

4. Reaction between H₂ and I₂ to form HI ${\mathrm{H}}_2\left(\mathrm{g}\right)+{\mathrm{I}}_2\left(\mathrm{g}\right)⟶2\mathrm{H}\left(\mathrm{g}\right)$

5. Reaction of sodium metal with water  $2\mathrm{Na}\left(\mathrm{s}\right)+2{\mathrm{H}}_2\mathrm{O}\left(\ell \right)⟶2\mathrm{NaOH}\left(\mathrm{aq}\right)+{\mathrm{H}}_2\left(\mathrm{g}\right)$

b) Spontaneous processes where initiation is required

1. Lighting up of candle or lamp

$\text{ Hydrocarbons }+{\mathrm{O}}_2\left(\mathrm{g}\right)\stackrel{\text{ ignition }}{⟶}{\mathrm{CO}}_2\left(\mathrm{g}\right)+{\mathrm{H}}_2\mathrm{O}\left(\ell \right)+\text{ heat }+\text{ light }$

2. Combustion of fuels (coal, petroleum, fuel gases etc).

$\begin{array}{l}\mathrm{C}\left(\mathrm{s}\right)+{\mathrm{O}}_2\left(\mathrm{g}\right)\stackrel{\text{ ignition }}{⟶}{\mathrm{CO}}_2\left(\mathrm{g}\right)\\ \mathrm{CO}+{\mathrm{H}}_2\left(\mathrm{g}\right)+{\mathrm{O}}_2\left(\mathrm{g}\right)\stackrel{\text{ spark }}{⟶}{\mathrm{CO}}_2\left(\mathrm{g}\right)+{\mathrm{H}}_2\mathrm{O}\left(\ell \right)\end{array}$

3. Reaction between H₂ and O₂ to form water

${\mathrm{H}}_2\left(\mathrm{g}\right)+\frac{1}{2}{\mathrm{O}}_2\left(\mathrm{g}\right)\frac{\text{ electric }}{\text{ spark }}{\mathrm{H}}_2\mathrm{O}\left(\ell \right)$

Non–spontaneous processes

A process which does not have a natural urge to take place i.e. neither can take place itself nor by proper initiation is known as non-spontaneous process. It is not so that non-spontaneous processes do not take place at all. They do take place but in such processes, some source of energy is always required continuously for the process to take place accordingly. Some spontaneous processes, which are irreversible, there opposite process may be a non-spontaneous process, but may require different source of energy than that released in the main reaction. e.g. reaction of H₂ and O₂ to form water. ${\mathrm{H}}_2\left(\mathrm{g}\right)+1/2{\mathrm{O}}_2\left(\mathrm{g}\right)\to {\mathrm{H}}_2\mathrm{O}\left(\ell \right)$ is a spontaneous process (with ${\mathrm{\Delta H}}^{\circ }=-285.9\mathrm{kJ}{\mathrm{mol}}^{-1}$) but the opposite reaction can never be observed by the effect of heat. But it has been found to take place by the effect of electric current i.e. electrolysis of water.

${\mathrm{H}}_2\mathrm{O}\left(\ell \right)\stackrel{\text{ electric current }}{⟶}{\mathrm{H}}_2\left(\mathrm{g}\right)+\frac{1}{2}{\mathrm{O}}_2\left(\mathrm{g}\right)$

The reaction, however, stops if the current supply is cutoff.

The other examples of non-spontaneous processes are

1. Hydrolysis of NaCl

2. Diffusion of a gas from a lower pressure to the higher

3. Reverse osmosis

4. Flow of heat from a cold body to the hot

5. Dissolution of gold in water

Driving Force for a Spontaneous Process:

After bringing out differences between a spontaneous and non-spontaneous process, a very crucial question, ‘why some reactions are spontaneous’ arises in our mind. There must be some forces which drive the reaction to proceed.

The force which is responsible for the spontaneity of a process is called the driving force.

Tendency to acquire minimum energy: As we know lesser the energy, greater is the stability.  Hence, every system tends, to acquire minimum energy, which can be reconsidered in following examples.

• Downhill flow of water
• Flow of heat to a colder region/part
• Projecting the arrow of a stretched bow or stone from a catapult
• Metallic sodium or atomic hydrogen

Most of the spontaneous processes have been observed to be exothermic

e.g.

$\begin{array}{l}\mathrm{C}\left(\mathrm{s}\right)+{\mathrm{O}}_2\left(\mathrm{g}\right)⟶{\mathrm{CO}}_2\left(\mathrm{g}\right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\mathrm{\Delta H}}^{\circ }=-395{\mathrm{kJmol}}^{-1}\\ {\mathrm{HNO}}_3\left(\mathrm{aq}\right)+\mathrm{NaOH}\left(\mathrm{aq}\right)⟶{\mathrm{NaNO}}_3+{\mathrm{H}}_2\mathrm{O}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\mathrm{\Delta }{H}^{\circ }=-57.33\mathrm{kJ}{\mathrm{mol}}^{-1}\\ \mathrm{KOH}\left(\mathrm{s}\right)+\mathrm{aq}⟶\mathrm{KOH}\left(\mathrm{aq}\right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\mathrm{\Delta H}}^{\circ }=-55.60{\mathrm{kJmol}}^{-1}\\ \frac{1}{2}{\mathrm{N}}_2\left(\mathrm{g}\right)+\frac{3}{2}{\mathrm{H}}_2\left(\mathrm{g}\right)⟶{\mathrm{NH}}_3\left(\mathrm{g}\right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\mathrm{\Delta H}}^{\circ }=-92.4{\mathrm{kJmol}}^{-1}\end{array}$

Which infers that they are accompanied by the decrease in energy i.e. the value of $∆$H is negative.  We conclude that negative value of $∆$H is the criterion of spontaneity.

Limitations of the Criterion of Minimum Energy

a) Spontaneous endothermic process: A number of spontaneous reactions are known for which enthalpy change is positive (increase in enthalpy content) i.e. $∆$H = +ve.

Examples:

1. Melting of the, ${\mathrm{H}}_2\mathrm{O}\left(\mathrm{s}\right)⟶{\mathrm{H}}_2\mathrm{O}\left(\ell \right),\mathrm{\Delta }{H}^{\circ }=6.0{\mathrm{kJmol}}^{-1}$

2. Evaporation of water, ${\mathrm{H}}_2\mathrm{O}\left(\ell \right)⟶{\mathrm{H}}_2\mathrm{O}\left(\mathrm{g}\right){\mathrm{\Delta H}}^{\circ }=44.0{\mathrm{kJmol}}^{-1}$

3. Dissolution of NH₄Cl in water

${\mathrm{NH}}_4\mathrm{ClOH}+\mathrm{aq}⟶{\mathrm{NH}}_4\mathrm{Cl}(\mathrm{aq}{)}_2{\mathrm{\Delta H}}^{\circ }=15.1\mathrm{kJ}{\mathrm{mo}}^{-1}$

4. Decomposition of dinitrogen pentoxide at RT.

${\mathrm{N}}_2{\mathrm{O}}_5\left(\mathrm{g}\right)⟶2{\mathrm{NO}}_2\left(\mathrm{g}\right)+\frac{1}{2}{\mathrm{O}}_2\left(\mathrm{g}\right),{\mathrm{\Delta H}}^{\circ }=219\mathrm{kJ}{\mathrm{mol}}^{-1}$

5. Decomposition of CaCO₃ at higher temperature

$\mathrm{Ca}{\mathrm{CO}}_3\left(\mathrm{s}\right)⟶\mathrm{CaO}\left(\mathrm{s}\right)+{\mathrm{CO}}_2(\mathrm{g}{)}_2,{\mathrm{\Delta H}}^{\circ }=178.3{\mathrm{kJmol}}^{-1}.$

In the process 1 and 2 the energy required to bring about the change is provided by the surroundings. After absorption of energy the molecules (H₂O) achieve a higher state of energy and hence change from solid into liquid or from liquid into vapour. In 3, the water molecules provide the energy required for the dissolution, the energy is consumed in overcoming the attraction forces of NH₄⁺ and Cl^–, hence the temperature of the system (solution) falls, it becomes cooler than the initial temperature. Although process 4 is highly endothermic but manages to proceed even at root temperature. However reaction 5 does not take place at RT but if temperature is raised, it becomes spontaneous.

b) Occurrence of reversible reactions: If a reaction is spontaneous with a negative value of $∆$H, the reverse reaction should be non-spontaneous due to a positive value but in fact, many of the reactions ha been found to be reversible in nature.

Examples:

$\begin{array}{l}1. {\mathrm{H}}_2\left(\mathrm{g}\right)+{\mathrm{I}}_2\left(\mathrm{g}\right)⟶2\mathrm{Hl}\left(\mathrm{g}\right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\mathrm{\Delta H}}^{\circ }=-\mathrm{ve}\\ 2\mathrm{Hl}\left(\mathrm{g}\right)⟶{\mathrm{H}}_2\left(\mathrm{g}\right)+{\mathrm{I}}_2\left(\mathrm{g}\right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\mathrm{\Delta H}=+\mathrm{ve}\\ {\mathrm{H}}_2\left(\mathrm{g}\right)+{\mathrm{I}}_2\left(\mathrm{g}\right)\text{ →}2\mathrm{Hl}\left(\mathrm{g}\right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\end{array}$

$\begin{array}{l}2. 2{\mathrm{N}}_2\left(\mathrm{g}\right)+3{\mathrm{H}}_2\left(\mathrm{g}\right)⟶2{\mathrm{NH}}_3\left(\mathrm{g}\right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\mathrm{\Delta H}=-\mathrm{ve}\\ 2{\mathrm{NH}}_3\left(\mathrm{g}\right)⟶{\mathrm{N}}_2\left(\mathrm{g}\right)+3{\mathrm{H}}_2\left(\mathrm{g}\right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} \mathrm{\Delta H}=+\mathrm{ve}\\ {\mathrm{N}}_2\left(\mathrm{g}\right)+3{\mathrm{H}}_2\left(\mathrm{g}\right)\text{ → }2{\mathrm{NH}}_3\left(\mathrm{g}\right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\end{array}$

c) Reactions with $∆$H = 0: A number of reactions are known which takes place neither by evolution nor absorption of energy and hence are spontaneous. It is however not as per the consideration of the minimum energy concept.

Example: ${\mathrm{CH}}_3\mathrm{COOH}+{\mathrm{C}}_2{\mathrm{H}}_5\mathrm{OH}⟶{\mathrm{CH}}_3{\mathrm{COOC}}_2{\mathrm{H}}_5+\raisebox{1ex}{${\displaystyle 1}$}\!\left/ \!\raisebox{-1ex}{$2$}\right. {\mathrm{H}}_2$

d) Exothermic reactions fail to achieve completion: Exothermic reaction rarely proceeds to the completion in spite of negative value of $∆$H although the minimum energy concept favours it. In fact all spontaneous reactions proceed in a direction until an equilibrium is attained.

As we observed, some of the spontaneous reactions are exothermic while the other are endothermic hence there must be some other factors also, besides the minimum energy concept, for the condition of spontaneity of a process.

 2. Tendency to acquire maximum randomness

Nature tends to move from an organized stated to a disorganized one (from an ordered state to the randomness). The disordered or disorganized state of a system has higher probability than the ordered or organized one. And the state of a higher probability is very much akin to take place. We can see the processes through the vision of probability or randomness.

The probability curve of the toss of a coin to get a ‘head’ or a ‘tail’ is expressed herein the diagram. The maximum probability that the coin can get head corresponds to just in between the two extremes. If 100 coins are dropped from some height, it will be most probable that of 50 of them will get head and the other 50, the tail  the disordered arrangement which may not always be a 50-50 ratio, being sometime 49-51, 52-48 or so, but the probability that all the 100 coins will get head or all 100 will get tail is just impossible.

Consider the mixing of two inert gases say, He and Ne. The two gases are kept in two bulbs, which are joined together by a tube having a valve. Initially, valve is kept closed. The system is by now in somewhat ordered state-as in one bulb there is He and in another there is Ne.  When valve is opened the intermixing of the two gases due to diffusion takes place. As they are inert, there shall be no chemical reaction and the heat change of the mixing shall be negligible. As the gases have tendency to occupy maximum volume, He from the first and Ne from the second bulb move to the opposite direction and finally a mixture of gases in each more bulb shall have almost 50% of each of the gas a more disordered sate is achieved. Whether the gaseous mixture is perfectly disordered? No! As it can further be disordered if comes in contact with some other system or gases.e.g. if the wall of the bulb is punctured the gas mixture will start to flow from the bulb to the outside. Why? Because by doing so maximum randomness can be achieved.

As these mixed gases can not be separated on their own (the reverse reaction does not proceeds on its own) the diffusion is a spontaneous process. A process takes place spontaneously in a direction if the randomness of the system increases.

Examples:

Melting of ice : ${\mathrm{H}}_2\mathrm{O}\left(\mathrm{s}\right)⟶{\mathrm{H}}_2\mathrm{O}\left(\ell \right){\mathrm{\Delta H}}^{\circ }=6.06{\mathrm{kJmol}}^{-1}$

In melting process solid ice has an ordered arrangement of H₂O molecules. It has an inherent tendency to go into an disordered (more random) state, which is brought about by melting the crystal. Hence, inspite of being endothermic process, as heat is required, the melting of ice is spontaneous process.

Evaporation of liquids (water): ${\mathrm{H}}_2\mathrm{O}\left(\ell \right)⟶{\mathrm{H}}_2\mathrm{O}\left(\mathrm{g}\right){\mathrm{\Delta H}}^{\circ }=44\mathrm{kJ}{\mathrm{mol}}^{-1}$

Once again the randomness of the process is increasing since a relatively more orderly arranged water molecule change into comparatively much less arranged vapours. Hence it is also a spontaneous process.

Dissolution of NH₄Cl: In NH₄Cl (s) NH₄⁺ and Cl^– are bound to each other by electrostatic forces which gives a some what ordered arrangement. When dissolved in water, these attraction forces are superceded by dielectric forces of water, the free NH₄⁺ and Cl^– ions can now move more randomly throughout the solution. We see dissolution is accompanied with an increase in randomness, hence is spontaneous.

Decomposition of N₂O₅:  In decomposition of N₂O₅, one molecule produces two and half a molecules overall. This will definitely bring an increase in randomness as these 2 ½ molecules shall be moving faster and hence more randomly than a single one.

Limitations of the Criterion for Maximum Randomness:

The randomness factor like the energy factor also has its limitations, like

a) Liquefaction of a gas: When a gas liquefied into a liquid its volume decreases due to increased interparticle interactions. Since they are unable to move so freely, their randomness decreases but so many of such processes are spontaneous e.g. rain fall in nature.

b) Solidification of a liquid: In solidification the liquid molecules undergo into a smaller volume i.e., more closely packed arrangement (the solid form). As solids have the more ordered arrangement, the change is accompanied by the decrease in disorderness.  g. solidification of wax and fats.

c) Crystallization: Saturated solution when are kept for purification, show deposition of crystal from the solution. In the process, the previously randomly moving ion/molecules get almost fixed to a definite lattice points involving a decrease in the randomness.

Hence, it is clear that like energy factor, randomness alone cannot be the sole criterion of spontaneity. These two tendencies of a system i.e. to achieve minimum energy and maximum randomness together decide whether a reaction shall take place or not. The resultant of the two tendencies is called as the driving force.

The energy and randomness are independent of each other. They may have their effect on a reaction in the same direction or opposite to each other.

For a process to take place, the following factors should be considered:

Case I: If randomness factor is absent (there is no change in randomness), enthalpy or energy factor decides the spontaneity.

Case II: If enthalpy or energy factor is absent, the randomness factor decides the spontaneity.

Case III: If both factors are present, magnitude of these tendencies decides the spontaneity.

ENTROPY: It is thermodynamic state function which is the measure of randomness or disorderness of molecules of the system. Entropy always changes in a characteristic fashion whenever a process is brought about.

Earlier, what we were using as randomness factor is in fact, entropy. Since a disordered state can be achieved in more than one ways – It is easily attainable and hence there is a greater probability that such a process shall take place. Suppose, a box with 10 identical coins can have all the heads or all the tails is possible only in one way while that of that 5 will go head (or tail) and the rest reverse of it a perfectly disordered state in 2¹⁰ (1024) ways.

Entropy is represented by S, it is difficult to define the actual entropy of a system, but the change of entropy during a change can be of course. Let the entropy of a system in its initial state and final state be S_initial and S_final, then the entropy change of the process will be

$\mathrm{\Delta }S=S_{\text{final}}-{\text{S}}_{\text{initial}}$

For a chemical reaction,

The entropy change $\mathrm{\Delta }S=S_{\text{products }}-S_{\text{reactants}}$

Mathematical Definition of Entropy

For an isothermal reversible process, the summation of all q/T terms is zero. (q = heat exchanged, T=absolute temperature)

$\sum \frac{\mathrm{q}}{\mathrm{T}}=0$   …… (45)

If the heat changes are infinitesimally small $\sum \frac{\mathrm{dq}}{\mathrm{T}}=0$

Let a system changes by path I from state A to state B and then from B to A by path II, it follows that

$\sum \frac{\mathrm{dq}}{\mathrm{T}}={\int }_{\mathrm{A}}^{\mathrm{B}} \frac{\mathrm{dq}}{\mathrm{T}}+{\int }_{\mathrm{B}}^{\mathrm{A}} \frac{\mathrm{dq}}{\mathrm{T}}=0$

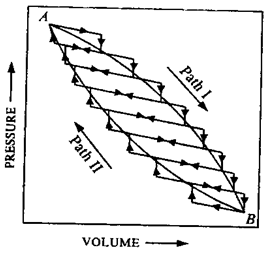
where ${\int }_A^B \frac{dc}{T}$ is the summation of all the $\frac{dq}{T}$ terms by path-I from state A to B and similarly ${\int }_{\mathrm{B}}^{\mathrm{A}} \frac{\mathrm{dq}}{\mathrm{T}}$ is the summation of all the  terms by the path-II from the state B to A.

From equation (72) 

${\int }_A^B \frac{dq}{T}=-{\int }_B^A \frac{dq}{T}$  $or {\int }_A^B \frac{dq}{T}={\int }_A^B \frac{dq}{T}$

or, the value of ${\int }_{\text{initial }}^{\text{final }} \frac{\mathrm{dq}}{\mathrm{T}}$ for the given conditions of P, V and T will be the same for two given states independent of the path followed.

We can say, $\mathrm{\Delta S}={\mathrm{S}}_{\text{final }}-{\mathrm{S}}_{\text{intitial }}={\int }_{\text{initial }}^{\text{final }} \frac{\mathrm{dq}}{\mathrm{T}}$      . . . .  (46)

For each infinitesimal small change $\mathrm{ds}=\frac{\mathrm{dq}}{\mathrm{T}}$       . . . . (47)

At constant temperature, for finite change, $\mathrm{ds}\to \mathrm{\Delta S}\text{ and }\mathrm{dq}\to \mathrm{q}$

$\mathrm{\Delta S}=\frac{\mathrm{q}}{\mathrm{T}}$    . . . . (48)

Change in entropy ($∆$S) is independent of path and manner i.e. whether path I or II; whether reversibly or irreversibly.

However, we mathematically represent it only when the change is brought about reversibly.  The reason? We deduce this equation on the basis of Carnot cycle which is a reversible process.

Henceforth,  $\mathrm{\Delta S}=\frac{{\mathrm{q}}_{\mathrm{rev}}}{\mathrm{T}}$

Factors Affecting Entropy

1. The value of entropy of a system depends on the mass of the system (extensive property).

2. A liquid has more entropy than a solid for the same substance.

3. A gas has higher entropy than a liquid, as the gas molecules/atoms have greater freedom to move to and fro.

4. Increase of temperature increases the entropy of a substance, as the raising of temperature increases the kinetic energy and hence more freedom to move.

So, more the heat absorbed by a system, more the disorder. If a system absorbs some amount of heat at lower temperature, more disorderness is brought than when the same amount of heat is added at higher temperature.

Units of entropy:  Since entropy is the heat term divided by temperature. Hence, the unit will be joule per kelvin or calorie per degree kelvin (1 JK^–1 = 1 e.u).

Since it is an extensive property i.e. it depends on the amount of substance, unit of entropy is expressed as $joule {\mathrm{deg}}^{-1}{\mathrm{mol}}^{-1}\left({\mathrm{JK}}^{-1}{\mathrm{mol}}^{-1}\right)\text{ or calorie }{\mathrm{deg}}^{-1}{\mathrm{mole}}^{-1}\left({\mathrm{calK}}^{-1}{\mathrm{mol}}^{-1}\right)$.

Spontaneity and entropy change: In an isolated system, there is no exchange of entropy and matter e.g. mixing of gases, which is accompanied by randomness i.e. increase in entropy. Hence, for a spontaneous process in isolated system, the entropy change is positive, i.e. $∆$S > 0. However if the system is not isolated, the entropy changes of both the system and surroundings should be taken into consideration. (system+surroundings = isolated systems)

$$\begin{gathered} \mathrm{\Delta }{S}_{\text{total }}=\mathrm{\Delta }{S}_{\text{system }}+\mathrm{\Delta }S\text{ surroundings } \\ {\mathrm{\Delta S}}_{\text{total }}=\text{ total entropy change for a process } \\ {\mathrm{\Delta S}}_{\text{system }}=\text{ entropy change of the system } \\ {\mathrm{\Delta S}}_{\text{surroundinas }}=\text{ entropy change of the surroundings } \\ \left({\mathrm{\Delta S}}_{\text{total }}\text{ may also be termed as }{\mathrm{\Delta S}}_{\text{universe }}\right) \end{gathered}$$

For reversible process,

${\mathrm{\Delta S}}_{\text{total }}\text{ i.e. }{\mathrm{\Delta S}}_{\text{system }}+{\mathrm{\Delta S}}_{\text{surroundinas }}=0$         . . . . (49)

For irreversible process:

${\mathrm{\Delta S}}_{\text{total }}\mathrm{i}.\mathrm{e}, {\mathrm{\Delta S}}_{\text{system }}+{\mathrm{\Delta S}}_{\text{surroundings }}=0$         . . . . (50)

Combining the two equations,

$\mathrm{\Delta }{\text{ S }}_{\text{system }}+{\mathrm{\Delta S}}_{\text{surroundings }}\ge 0$                   . . . . (51)

Since all processes in nature occur spontaneously i.e. irreversibly it infers that the entropy of universe (system+surroundings) is increasing continuously. In fact, the entropy of a system during a spontaneous process, goes on increasing until the system attains the equilibrium state i.e. the entropy attains the maximum value, after which no more increase in entropy of the system is possible.

Let us consider entropy changes of conversion of water into ice at different temperatures:

Temperature oC (K)	$$\begin{gathered} \mathrm{\Delta }{\mathbf{S}}_{\text{system }} \\ {\mathbf{JK}}^{\mathbf{-}\mathbf{1}}{\mathbf{mol}}^{\mathbf{-}\mathbf{1}} \end{gathered}$$	$$\begin{gathered} \mathrm{\Delta }{\mathbf{S}}_{\text{surroundings }} \\ {\mathbf{JK}}^{\mathbf{-}\mathbf{1}}{\mathbf{mol}}^{\mathbf{-}\mathbf{1}} \end{gathered}$$	$$\begin{gathered} \mathrm{\Delta }{\mathbf{S}}_{\text{total }} \\ {\mathbf{JK}}^{\mathbf{-}\mathbf{1}}{\mathbf{mol}}^{\mathbf{-}\mathbf{1}} \end{gathered}$$	Spontaneity
–1 (272)	–21.05	21.93	0.08	Spontaneous
0(273)	–21.99	21.99	0.00	In equilibrium
1 (274)	–22.13	22.05	–0.08	Non-spontaneous

ENTROPY CHANGES IN VARIOUS PROCESSES

1. Reversible isothermal process: Let a system absorb a heat from the surroundings at temperature T

$\mathrm{\Delta }{S}_{\text{system }}=\frac{q}{T}$     And    $\mathrm{\Delta }{S}_{\text{surroundings }}=-\frac{\mathrm{q}}{\mathrm{T}}$

Total entropy change ${\mathrm{\Delta S}}_{\text{total }}={\mathrm{\Delta S}}_{\text{system }}+{\mathrm{\Delta S}}_{\text{surroundings }}=\frac{\mathrm{q}}{\mathrm{T}}-\frac{\mathrm{q}}{\mathrm{T}}=0$

2. Reversible adiabatic process: In reversible adiabatic process, there is no exchange of heat between system and surroundings i.e., q = 0

Hence, ${\mathrm{\Delta S}}_{\text{system }}=0\text{ and }{\mathrm{\Delta S}}_{\text{surroudnigs }}=0$

$\mathrm{\Delta }{\text{ S}}_{\text{total}}=\mathrm{\Delta }{S}_{\text{system }}+\mathrm{\Delta }{\text{ S}}_{\text{surroundings}}=0$

3. Irreversible process: Let a system at higher temperature T₁ evolves q amount of heat irreversibly to its surroundings at lower temperature T₂.

$\mathrm{\Delta }{S}_{\text{system }}=-\frac{q}{T_1}$

$\mathrm{\Delta }{\text{ S}}_{\text{surroundings}}=\frac{\mathrm{q}}{{\mathrm{T}}_2}$

$\mathrm{\Delta }{S}_{\text{total }}=\frac{-q_1}{T_1}+\frac{q}{T_2}=q\left[\frac{T_1-T_2}{T_1{T}_2}\right]$

Since T₁ > T₂, T₁ – T₂ will be positive

Hence, $∆$S_total > 0

i.e.  the process will involve an increase in the entropy

PHYSICAL SIGNIFICANE OF ENTROPY

1.Disorder or randomness: As we learnt earlier that processes like flow of heat from hot to cold, expansion of gas into vacuum, diffusion of solute, melting of solid, evaporation of liquid etc all are accompanied by an increase in the disorder of the system where a definite ordered (less random) state is transformed into a disordered (more random) state. There spontaneous processes are accompanied by an increase in entropy as well as in the disorder. Hence entropy is regarded as the measure of randomness or disorderness.

2. Probability: Spontaneous processes lead to an increase in disorder and at the same time an increase in entropy. Spontaneous means in fact, proceeding from a less probable state to a more probable one. Therefore, there is a close relation between entropy and thermodynamic probability as both of them increase simultaneously.

$S=k \ln \omega$               . . . . (52)

Where, k → Boltzmann constant i.e. gas constant per molecule $\left(\text{ i.e. }\frac{\text{ gas constant(R)}}{\text{ Avogadro number( }{\mathrm{N}}_{\mathrm{A}}\text{ )}}\right)$

$\omega \to$ Thermodynamic probability

The equation is called Boltzmann entropy equation.

At absolute zero (0 K), a solid is regarded to be in most ordered state i.e. W = 1.

Hence S = 0

i.e. entropy of crystalline solids at absolute zero is zero it self.

3. Entropy: unavailable energy: Since heat energy cannot completely be converted into other forms of energy it seems there is some disappearance of energy during transformations. This energy goes into the forms of entropy. We can say

$\text{ Entropy }=\frac{\text{ unavailable energy }}{\text{ temperature in kelvin (K) }}$

Characteristics of entropy

1. It is an extensive property (value of entropy depends upon the number of moles of the substance of a system)

2. The absolute value of entropy is difficult to determine but the change in entropy for a process can easily be,

3. Entropy is a state function as its value depends on the state variables P, V, T and n.

4. Entropy change does not depend on the path followed but on the initial and final states.

5. The entropy change for a cyclic process is zero.

6. The entropy change in equilibrium state is also zero.

7. For natural irreversible process the entropy change is positive i.e. entropy of universe increases.

8. For reversible processes the entropy of universe does not change i.e. $\mathrm{\Delta }{\text{S}}_{\text{total}}\text{ or }\mathrm{\Delta }{\text{ S}}_{\text{universe}}=0$  or  $\mathrm{\Delta }{S}_{\text{system }}=-\mathrm{\Delta }{\text{S}}_{\text{surroundings}}$

9. For adiabatic reversible process $\mathrm{\Delta }{S}_{\text{system }}=\mathrm{\Delta }{S}_{\text{surroundings }}=\mathrm{\Delta }{S}_{\text{total }}=0$

Entropy changes of a system: 

$\mathrm{\Delta }S=n{C}_V \ln \frac{T_2}{T_1}+nR \mathrm{Rn}\frac{V_2}{V_1}$          . . . . (53)

$\mathrm{\Delta }S=n{C}_P\ln \frac{T_2}{T_1}+nR\ln \frac{P_1}{P_2}$

Isothermal expansion: The temperatures T₁ and T₂ are equal hence,

$\mathrm{\Delta }S=nR\ln \frac{V_2}{V_1}=nR\ln \frac{P_1}{P_2}$    . . . . (54)

Isobaric expansion:  P₁ = P₂

$\mathrm{\Delta S}={\mathrm{nC}}_{\mathrm{P}}\ln \frac{{\mathrm{T}}_2}{{\mathrm{T}}_1}$              . . . . (55)

Isochoric process: V₁ = V₂

$\mathrm{\Delta }S=n{C}_{\vee }\ln \frac{T_2}{T_1}=n{C}_v\ln \frac{P_2}{P_1}$    . . . . (56)

Entropy changes during phase transformation: The conversion of one of a substance into another is called phase transformation. For a given substance this transformation takes place at a certain temperature and is accompanied by some entropy change. During the phase transformations heat energy may either increase or decrease accordingly will be the change in entropy. Thus entropy change for a phase transformation be given by $\mathrm{\Delta }{S}_{\text{trans }}=\frac{q_{\text{rev }}}{T}$     . . . . (57)

q_rev = heat exchanged (molar enthalpy of transformation of the substance)

T = temperature of transition

Entropy of fusion: Change in entropy when one mole of a solid substance changes into liquid form at the melting temperature. The heat absorbed at the melting or a fusion temperature will be the enthalpy (or latent heat) of fusion.

${\mathrm{\Delta }}_{\text{fus }}S=S_{\text{liquid }}-S_{\text{solid }}=\frac{{\mathrm{\Delta }}_{\text{fus }}H}{T_f}$     . . . . (58)

$∆$_fusH  = latent heat of fusion    

T_f = temperature of fusion

e.g. for melting of ice, $\mathrm{\Delta }\text{ fusion(ice) }S=S_{\text{water }}-S_{\text{ice }}=\frac{{\mathrm{\Delta }}_{fus}H}{T_f}=\frac{6000\left({\left.Jmo\right|}^{-1}\right)}{273\left(K\right)}=21.98{\mathrm{JK}}^{-1}{\mathrm{mol}}^{-1}$

Entropy of vaporization: The entropy change associated with conversion of one mole of a liquid into vaporous (gas) at its boiling point, is called the entropy of vaporization.

${\mathrm{\Delta }}_{\text{vap }}S=S_{\text{vapour }}-S_{\text{liquid }}=\frac{{\mathrm{\Delta }}_{\text{vap }}H}{T_{\text{b }}}$. . . . (59)

${\mathrm{\Delta }}_{\text{vap }}H$= latent heat of vaporization

T_b = boiling point of the substance

e.g. For boiling of water

${\mathrm{\Delta }}_{\text{vap }\left(\text{ water }\right)}S=S_{\text{steam }}-S_{\text{watr }}=\frac{{\mathrm{\Delta }}_{\text{vap }}H}{T_b}=\frac{40626\left(J{\mathrm{mol}}^{-1}\right)}{373\left(\mathrm{K}\right)}=108.9{\mathrm{JK}}^{-1}{\mathrm{mol}}^{-1}$

Entropy of sublimation: The entropy of sublimation is the entropy change that accompanies the sublimation (conversion of solid into vapours directly) of one mole of a substance.

${\mathrm{\Delta }}_{\text{sub }}S=S_{\text{vapour }}-S_{\text{solid }}=\frac{{\mathrm{\Delta }}_{\text{sub }}H}{T_s}$

$$\begin{gathered} {\mathrm{\Delta }}_{\text{sub }}\mathrm{H}=\text{ latent heat of sublimation } \\ {\mathrm{T}}_{\mathrm{s}}=\text{ temperature of sublimation } \end{gathered}$$

Entropy of transition:  The change in entropy when 1 mole of a substance undergoes the transition of one form (allotrope) into another is called the entropy of transition of the substance.

${\mathrm{\Delta }}_{\text{trans }}S=S_{2\text{ nd allotrope }}-S_{1\text{ st allotope }}=\frac{{\mathrm{\Delta }}_{\text{trans }}H}{T_{\text{tr }}}$. . . . (60)

${\mathrm{\Delta }}_{\text{trans }}H=\text{ enthalpy of transition }$

$T_{\mathrm{tr}}=\text{ transition temperature }$

e.g. Transition of rhombic sulphur into monoclinic

${\mathrm{\Delta }}_{\text{trans }}S=S_{\text{monoclinic }}-S_{\text{rhombic }}=\frac{{\mathrm{\Delta }}_{\text{trans }}H}{T_{\text{tr }}}=\frac{322.17\left({\mathrm{Jmol}}^{-1}\right)}{368.6\left(\mathrm{K}\right)}=0.874{\mathrm{JK}}^{-1}{\mathrm{mol}}^{-1}$            

Entropy of mixing of ideal gases: Entropy change involved with the mixing of a mixture of gases is the entropy of mixture minus the sum of the entropies of the separate gases each at a same pressure.

${\mathrm{\Delta }}_{\text{mix }}S=-R\sum x_i\ln x_i$     . . . . (61)

where  is the mole fraction of i^th (e.g. 3^rd or 4^th) component of the mixture. Since x_i is a fraction, the value of ln x shall be negative, which give a positive value of entropy of mixing i.e., entropy of mixing is always positive.

The Second Law of Thermodynamics

Whether a given process can occur spontaneously and if yes upto which extent – is the scope of second law of thermodynamics. Convertibility of one firm of energy (e.g. heat) into other forms (e.g. work) is also calculated applying the second law. Like first law, the second law is also a postulate and cannot be derived from any prior concept. The law can be stated is as many as possible forms comprising of the same meaning:

1. Clausius Statement: It is impossible for a system to undergo a cyclic process, whose sole effects are the flow of heat into the system from a cold reservoir and the flow of an equal amount heat out of the system into a hot reservoir.

$q^{\mathrm{\prime }}=q+W$

Some other transformations of the Clausius’s statement are:

“It is impossible to convert heat into work without compensation”.

“All forms of energy can be converted into heat energy, but heat cannot completely be converted into other forms of energy by any process”.

Some other statements are

2. Thomson’s statement: The heat of the coldest body among those participating in a cyclic process cannot serve as a source of work. Rudolph Clausius and William Thomson (later on, Lord Kelvin) in 1850 corrected Carnot’s work with conform to the first law of thermodynamics.

3. Kelvin Plank’s statement: (Originally given by William Thomson and later rephrased by Plank) “It is impossible for a system to undergo a cyclic process whose sole effects are the flow of heat into the system from a heat reservoir and the performance of an equivalent amount of work done by the system on the surroundings.

It means besides doing some work (after absorbing heat from the heat reservoir) some other (extra) work has also to be done i.e., the efficiency of conversion of heat into work cannot be 100% i.e. W < q.

4. Ludwig Boltzmann statement: “Nature tends to pass from a less probable to more probable state”

5. All spontaneous or naturally occurring processes are thermodynamically irreversible. Without the help of an external agency, such process cannot be reversed.

6. The entropy of universe increases in a spontaneous process and remains unchanged in an equilibrium process.

Thus the entropy of universe is increasing.

First Law and Second Law of Thermodynamics: At a Glance

FIRST LAW	SECOND LAW
1. Energy of the universe is constant	Entropy of the universe is constantly increasing and tends to be maximum
2. It deals with the conservation of energy	It tells the direction of flow of the energy
3. Mathematical expression: dq = dE + pdV	Mathematical expression: dS =  dq / T (for reversible process) and $\mathrm{dS}>\mathrm{dq}/\mathrm{T}$(for reversible process) $\Rightarrow \mathrm{dS}\ge \mathrm{dq}/\mathrm{T}$

Combining the two laws (for a reversible process)

TdS = dE + PdV               . . . . (62)

Work Function and Free Energy:

The total entropy change for a process serves as a criterion of spontaneity or feasibility of the process, but to decide feasibility of a process, we shall consider the enthalpy change of the system as well as of surroundings. As it becomes less convenient to speak about both the terms at the same time for a given process, some new terms are the work function A, and free energy function, G. These are defined as,

A = E – TS                        . . . . (63)

G = H – TS                      . . . . (64)

As E, H & S are the state functions, obviously A and G shall also be the state functions.

If the functions A, E & S of a system at a given temperature be A₁, E₁ and S₁ which after an appreciable change become A₂, E₂ and S₂ so that,

A₁ = E₁ – TS₁                                     . . . . (63a)

And,  A₂ = E₂ – TS₂                         . . . . (63b)

Subtracting equation (63a) from equation (63b)

$A_2-A_1=\left(E_2-E_1\right)-T\left(S_2-S_1\right) or \mathrm{\Delta A}=\mathrm{\Delta E}-\mathrm{T\Delta S}$                                           . . . . (65)

If the change is brought reversibly and isothermally and if the heat absorbed is given

From equation $\mathrm{\Delta S}=\frac{{\mathrm{q}}_{\mathrm{rev}}}{\mathrm{T}}$

Hence $∆$;     $A=\mathrm{\Delta }E-{\text{ q}}_{\text{rev}}$                 . . . . (66)

But from the first law,   $\mathrm{\Delta E}=\mathrm{q}+\mathrm{W} \text{ or }\mathrm{Wrev}=\mathrm{\Delta E}-\mathrm{qrev}$

For the system under consideration, W will be negative as the work is being done by the system.

$-{\mathrm{W}}_{\mathrm{req}}=\mathrm{\Delta E}=-q_{\mathrm{rev}}$                  . . . . (67)

Comparing eq (66) and equation (67)

$\mathrm{\Delta }A=-W_{\text{rev }}$           . . . . (68)

i.e. the decrease in work function ($∆$A) gives the maximum work that can be done by a system during a given change. That is why the function A is called the work function or Helmholtz fee energy or function. Treating equation (64) in the same way,

If G₁, H₁ and S₁ are the thermodynamic functions for the system in initial state which change after a process into G₂, H₂ and S₂ at the same temperature

Then, ${\mathrm{G}}_1={\mathrm{H}}_1-{\mathrm{TS}}_1$              . . . . (64 a)

${\mathrm{G}}_2={\mathrm{H}}_2-{\mathrm{TS}}_2$      . . . . (64 b)

Subtracting equation (64a) from equation (64 b)

${\mathrm{G}}_2-{\mathrm{G}}_1=\left({\mathrm{H}}_2-{\mathrm{H}}_1\right)-\mathrm{T}\left({\mathrm{S}}_2-{\mathrm{S}}_1\right) \mathrm{or} \mathrm{\Delta G}=\mathrm{\Delta H}-\mathrm{T\Delta S}$    . . . . (69)

From equation        $\mathrm{\Delta H}=\mathrm{\Delta E}+\mathrm{P\Delta V}$

It follows    $\mathrm{\Delta G}=\mathrm{\Delta E}+\mathrm{P\Delta V}-\mathrm{T\Delta S}$                  . . . . (70)

Hence,    $\mathrm{\Delta }G=\mathrm{\Delta }A+P\mathrm{\Delta }V$                    . . . . (71)

or  $\mathrm{\Delta }G=-W+P\mathrm{\Delta }V$

or  $\mathrm{\Delta }G=P\mathrm{\Delta }V-W$                                   . . . . (72)

$-\mathrm{\Delta }G=W-P\mathrm{\Delta }V$

The quantity P$∆$V is the work done by the gas on expansion against a constant pressure P and W is the total work that can be done by the system. The net available work then can be given by W-P$∆$V which in turn is $–∆$G,

Net work, $W-P\mathrm{\Delta }V=-\mathrm{\Delta }G$                      . . . . (73)

The quantity G, called Gibbs function or Gibbs free energy or free energy was introduced by Willard Gibbs, an American theoretical physicist. $–∆G$ is the decrease in free energy which converts into net work-electrical or chemical.

Since E, H and S all are extensive properties; the terms A and G shall also be extensive in nature.

Gibbs Free Energy and Spontaneity

For a spontaneous process, there shall be a decrease in the free energy of the system which, in fact performs some work. Hence if the sign of $∆$G is negative for a process, the process shall be spontaneous. This negative value of $∆$G is achieved by a positive value of T$∆$S (i.e. high temperature and increase in entropy), and/or a negative value of $∆$H.

(i) If $∆$G is negative the process is spontaneous

(ii) If $∆$G is positive, the process does not proceed in the forward direction, it of course, may proceed backward.

(iii) If $∆$G is zero, the system is in equilibrium condition of the given the process (as indicated possibly) does not occur.

Conditions for Spontaneity

From the relation $\mathrm{\Delta }G=\mathrm{\Delta }H-T\mathrm{\Delta }S$

$∆$H	T$∆$S	Condition	$∆$G	Spontaneity
– ve (favourable	+ve (favourable)	Any	–ve	Spontaneous
– ve ((favourable)	– ve (unfavourable)	$\left|\mathrm{\Delta H}\right|>\left|\mathrm{T\Delta S}\right|$	–ve	Spontaneous
+ve (unfavourable)	+ve (favourable)	$\left|T\mathrm{\Delta }S\right|>\left|\mathrm{\Delta }H\right|$	–ve	Spontaneous
+ve (unfavourable)	– ve (unfavourable)	Any	+ve	Non-spontaneous

Effect of Temperature on Spontaneity

In the equation, $\mathrm{\Delta G}=\mathrm{\Delta H}-\mathrm{T\Delta }S$

Apart from $∆$H and $∆$S, the value of T also plays an important role. Consider for example, the case when the two factors i.e. $∆$H and $∆$S are opposing each other i.e., one is favouring and the other is disfavouring.

Case I: $∆$H = (unfavourable) for the reaction to have a negative value of $∆$G, $∆$S must be positive.  Morever if the temperature is much less that $\left|\mathrm{T\Delta S}\right|<\left|\mathrm{\Delta H}\right|$, the reaction shall not proceed until the condition $\left|\mathrm{T\Delta S}\right|>\left|\mathrm{\Delta H}\right|$ is achieved and this can be made to happen only by increasing the temperature as for the given reaction the value of $∆$S shall not change.

That is why most of the endothermic reactions, which do not take place at ambient temperature are brought about by increasing the temperature.

Case–II: $\mathrm{\Delta }H=-ve$ (favourable) and $\mathrm{T\Delta S}=+\mathrm{ve}$ (favourable) when all factors are in the favour, what can prevent from anything to occur! $∆$G shall be –ve, hence spontaneous.

Case–III: $\mathrm{\Delta H}=-\mathrm{ve}$ (favourable) and $\mathrm{T\Delta S}=-\mathrm{ve}$ (unfavourable)

The reaction under these conditions can proceed when $\left|\mathrm{\Delta H}\right|>\left|\mathrm{T\Delta S}\right|$ i.e. to make the $∆$G negative, the T$∆$S should be decreased.  As for a given reaction/change the value of $∆$S shall remain constant, the decisive role (for the fate of reaction) is played by decreasing the temperature.

For some reactions to proceed, decrease in temperature (i.e. cooling) should be carried out.

We conclude that a reaction which is non-spontaneous at low temperature may become spontaneous at high temperature and vice-versa.

SUMMARY OF SPONTANEITY AND EFFECT OF $∆$H, $△$S and T

$∆$H	$∆$S	T	$∆$G	Spontaneity
–ve	+ve	All	–ve	Spontaneous
–ve	–ve	Low	–ve	Spontaneous
		High	+ve	Non-spontaneous
+ve	+ve	Low	+ve	Non-spontaneous
		High	–ve	Spontaneous
+ve	–ve	All	+ve	Non-spontaneous

Coupled Reactions:  Till now, we learnt that all the processes with a positive value of $∆$G are non-spontaneous.  But such reactions can be made to occur if they are coupled (made to happen along with some other reactions) with the one having a larger, negative value of $∆$G.  Such reactions are sometimes called tendem reactions.

e.g.

$\begin{array}{l}2{\mathrm{Fe}}_2{\mathrm{O}}_3\left(\mathrm{s}\right)⟶4\mathrm{Fe}\left(\mathrm{s}\right)+3{\mathrm{O}}_2+3{\mathrm{O}}_2\left(\mathrm{g}\right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} {\mathrm{\Delta G}}^{\circ }=1487{\mathrm{kJmol}}^{-1}\\ 6\mathrm{CO}\left(\mathrm{g}\right)+3{\mathrm{O}}_2\left(\mathrm{g}\right)⟶6{\mathrm{CO}}_2\left(\mathrm{g}\right)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} {\mathrm{\Delta G}}^{\circ }=-1543.2{\mathrm{kJmol}}^{-1}\end{array}$

—————————————————————————

Adding $2{\mathrm{Fe}}_2{\mathrm{O}}_3\left(\mathrm{s}\right)+6\mathrm{CO}\left(\mathrm{g}\right)+3{\mathrm{O}}_2\left(\mathrm{g}\right)⟶4\mathrm{Fe}\left(\mathrm{s}\right)+6{\mathrm{CO}}_2\left(\mathrm{g}\right){\mathrm{\Delta G}}^{\circ }=-52.2{\mathrm{kJmol}}^{-1}$

The first reaction cannot happen on its own due to highly negative value of $∆$G^o, unless any such reaction, like the second one, is taking place alongwith the former. To make a change (process) to happen, the free energy has to be negative.

For coupling of the two reactions, at least one of the participants must be common between the two reactions. As then only the equilibrium position of one reaction is influenced by the other. Let M be common in the reaction 1 and 2, and being the product of the first reaction while reactant for the second,

Reaction 1: $\mathrm{A}+\mathrm{B} \text{→ }\mathrm{C}+\mathrm{M}$                Reaction 2: $\mathrm{M}+\mathrm{R} \text{→ }\mathrm{S}+\mathrm{T}$

If reaction-1 has $∆$G^o >> 0 (i.e., highly positive) and K_c <<1 (i.e. very small), at ordinary conditions of temperature and concentration, very little A and B will react to produce C and M.  If reaction-2 has $∆$G^o << 0 (i.e., highly negative) and K_c >> 1 (i.e., very large), reaction-2 will proceed substantially and during the process use up M and R, which there by shall have to be provided by the commencement of reaction-1. We can say the equilibrium of the reaction-1 shall be shifted to the right. It must be noted here that the reaction-1 does not proceed because of some energy barriers. Unless and until the sufficient energy (to come across the energy barriers) is provided by any source, the reaction shall not proceed. That is why the value of $∆$G^o of the reaction-2 shall have to be sufficiently large (though negative i.e. $∆$G^o <<0).

Biological Coupling

Coupling reaction in biological world is of crucial importance. The hydrolysis of ATP (adenosine triphosphate) into ADP (adenosine diphosphate) and inorganic phosphate (P_i) has a very large negative value of $∆$G^o and hence thermodynamically favoured. This hydrolysis, in all living organisms, is coupled with many thermodynamically unfavoured reactions (processes) like synthesis of macromolecules, from small molecules, transport of chemical species from the regions of low chemical potential to high (active transport) and muscle contraction to do mechanical work etc. As hydrolysis of ATP in ADP & P₂ is thermodynamically favoured the reverse reaction i.e. synthesis of ATP from ADP & P_i is unfavoured which in turn is coupled with highly favoured another biological reaction – oxidation of glucose into CO₂ and H₂O. The synthesis of glucose is made favourable by high energy photons from sunlight in the chlorophyll through a series of reactions collectively called as photosynthesis. Thus, ultimately, our all life processes are powered by the sun.  That is the reason of calling the sun as a primary source of energy for us. You might be aware with the fact that the energy of the sun comes in fact, from the nuclear fusion reactions that are running in it since its origin or so. The Einstein’s relation E = mc² gives the interrelation between the two forms – energy and matter.

The Standard Free Energy Change ($∆$G^o) and the Equilibrium Constant (K)

Like enthalpy and internal energy, absolute value of (Gibbs) free energy cannot be determined but for a process, the change in the value can of course be. When this change is determined for 298K and 1-atm while the reactants and products are in their standard states, it is called as the standard free energy change $∆$G^o. Relating with standard enthalpy and standard entropy change

$\mathrm{\Delta }{G}^{\circ }=\mathrm{\Delta }{H}^{\circ }-T\mathrm{\Delta }{S}^{\circ }$          . . . . (74)

It can be calculated from the standard free energies of formation of products and reactants, i.e., ${\mathrm{\Delta G}}^{\circ }=\sum {\mathrm{G}}_{{\mathrm{f}}_{\text{(product })}}^{\circ }-\sum {{\mathrm{G}}_i^{\circ }}_{\text{(reactants)}}$

Standard Free Energy of Formation

Free energy change associated with the formation of one mole of a compound from its elements in their standard states at 298 K and 1 atm. The free energy of an element in its standard state is taken as zero.

$∆$G^o of some compounds (in kJ mol^–1)

Compound	${\mathrm{\Delta }}_f{\mathrm{G}}^{\circ }\left({\mathrm{kJmol}}^{-1}\right)$	Compound	$\mathrm{\Delta }\left({\mathrm{G}}^{\circ }\left(kJmo{I}^{-1}\right)\right.$)
NO2	51.84	NH3	–16.6
NO	86.69	HCl	–95.27
N2O	104.00	CO	–137.30
O3	163.40	H2O	–228.6
C2H6	229.0	CO2	–394.4
C4H10 (n-butane)	310.0	NaCl	–384.4
C4H10 (isobutene)	310.0	SiO2	–805.0
CH4	– 50.79	CaCO3	–112.5
C6H6	– 124.5	Al2O3	–1582.4

 Relation between $∆$G^o and K (Equilibrium Constant)

Let, the value of standard free energy change and equilibrium constant for the reaction

$\mathrm{A}+\mathrm{B}\rightleftharpoons \mathrm{C}+\mathrm{D}$

be $∆$G^o and K respectively. The free energy change for the reaction at a temperature T is given by

$\mathrm{\Delta }G=\mathrm{\Delta }{G}^{\circ }+RT\ln Q$         . . . . (75)

where R is the gas constant and Q is the reaction quotient given by

$Q=\frac{\left[C\right]\left[D\right]}{\left[A\right]\left[B\right]}$        . . . . (76)

Since at equilibrium state, $∆$G = 0 and Q = K

$0=\mathrm{\Delta }{G}^{\circ }+RT \ln K\mathrm{\Delta }{G}^{\circ }=-RT \ln K$. . . . (77)

From equation (77) $∆$G^o and K can be interrelated and hence be calculated if either of the two is known.

Gibbs Free Energy and Work: $∆$G is in fact, the non expansion work or the useful work that can be harnessed from a process. The greater the free energy change, greater the work obtained from a process. This work may be mechanical, electrical or else.

Free Energy Change and Electrical Work

The electrical work done by a cell is given by $\mathrm{\Delta }G=-nFE$

where, n = number of moles of e^– involved in the transformation

F = Faraday constant (= 96500 coulomb)

E = Electromotive force (emf) of the cell

If the reactant and products of the cell are in their standard states,

$\mathrm{\Delta }{G}^{\circ }=-nF{E}^{\circ }$where $E^{\circ }$ = standard emf of the cell

THE THIRD LAW OF THERMODYNAMICS

The increase in temperature of the substance at constant pressure increases its disorder.  Conversely, if the temperature of the substance decreases, its disorder also decreases.  Eventually, as the temperature approaches zero Kelvin, the disorder also approaches zero and the substance tends to become perfectly ordered. Based upon the above facts Nernst formulated third law of thermodynamics in 1906. The law states that, At absolute zero, the entropy of a perfectly crystalline substance is zero.

If S₀ be the entropy of the substance at 0 kelvin and S_T be its entropy at T Kelvin, then $\mathrm{\Delta }S=\left(S_T-S_0\right)={\int }_0^{\mathrm{\top }} \frac{C_p}{T}dT$

According to third law, S₀ i.e., entropy at 0 kelvin = 0.

$\therefore S_{\mathrm{T}}={\int }_0^{\mathrm{\top }} \frac{{\mathrm{C}}_{\mathrm{p}}}{\mathrm{T}}\mathrm{dT}$

The value of the integral in the above equation can be determined from the graph obtained by plotting various values of C_p/T against temperature (T). The area of the curve between 0 (K) and T (K) gives the value of integral and thus value of S_T, i.e., entropy at temperature T can be calculated.

Debye T³ law or Debye equation:  At a temperature near absolute zero (like, 0 < T < 15K) the difference between C_P and C_V is negligible, i.e. C_P $\approx$ C_V, and which in turn varies with third power of temperature T.

${\mathrm{C}}_{\mathrm{P}}\approx {\mathrm{C}}_{\mathrm{V}}\approx {\mathrm{aT}}^3$

Where a = an empirical constant for the substance.  Hence absolute value of entropy, S^o is calculated using C_V values.

Absolute Entropies of some typical substances ${\mathrm{S}}_{288}^{\circ }\left({\mathrm{JK}}^{-1}{\mathrm{mol}}^{-1}\right)$

Substance	So	Substance	So
Cs[Diamond]	2.43	NaCl(s)	72.38
C(c) [graphite]	5.69	Hg($\mathcal{l}$)	77.40
Cuprous Iodide (s)	6.65	Br2 (g)	245.34
H2O(s) [ice]	45.0	CH4(s)	186.14
H2O([water]	70.29	C2H6(g)	229.49
H2O(g) [steam]	188.74	C2H4(g)	185.35
CO(g)	197.90	C2H2 (g)	201.10
CO2(g)	213.80	C6H6 ($\mathcal{l}$)	172.79
S (rhombic)	31.88	${\mathrm{C}}_6{\mathrm{H}}_{12}{\mathrm{O}}_6\left(\mathrm{s}\right)$[D-glucose]	212.0
S(monoclinic)	32.55)	C12H22O11 (s) [Sucrose]	360.2

Calculation of Entropy Changes in Chemical Reactions

Like enthalpy changes we define the entropy (changes) of a reaction as the difference in standard entropy of products from that of the reactants.

$\mathrm{\Delta }{S}_{288}^0\left(\text{ reaction }\right)=\sum u_i{S}_{zs8}^0\left(\text{ products }\right)-\sum u_i{S}_{298}^0\left(\text{ reactants }\right)$   . . . . (78)

where $\upsilon$_i signifies the stoichiometric ratio

For the general reaction aA + bB → cC + dD

$\mathrm{\Delta }{S}_{298}^0=\left[\mathrm{C}{S}_{298}^{\circ }\left(\mathrm{C}\right)+\mathrm{d}{S}_{298}^{\circ }\left(\mathrm{D}\right)\right]-\left[\mathrm{a}{S}_{298}^0\left(\mathrm{A}\right)+{\mathrm{bS}}_{298}^{\circ }\left(\mathrm{B}\right)\right]$

 Illustration 18: Consider the entropy change for the reaction $2{\mathrm{H}}_2\left(\mathrm{g}\right)+{\mathrm{O}}_2\left(\mathrm{g}\right)\to 2{\mathrm{H}}_2\mathrm{O}\left(\ell \right)$ (and predict the spontaneity. (Use data given earlier in tables)

Solution. $\mathrm{\Delta }{S}_{298}^0=\left[2\times S_{z98}^0\left({\mathrm{H}}_2\mathrm{O}\right)\right]-\left[2\times S_{288}^0\left({\mathrm{H}}_2\right)+S_{298}^0\left({\mathrm{O}}_2\right)\right]$

$=(2\times 70)-(2\times 131+205)=-327{\mathrm{JK}}^{-1}{\mathrm{mol}}^{-1}$

There is a large loss of entropy while formation of water from H₂ and O₂ as we may expect, the three moles of (H₂ & O₂) -a highly disordered gaseous system accompanied in 3$\times$22.4 L volume after the reaction transform into much more ordered fashion (though not perfectly, as the motion of water molecules continues in zig-zag fashion through the volume of the liquid) contained within 18 mL (taking density of water 1g mL^–1 at 298K).  But from the stability (or reactivity) view point, water is far more stable than either of H₂ and O₂ at 298K. We also know from our experience that the above reaction is spontaneous – just try to lit a math stick into the hydrogen – oxygen mixture and see what happens! But the second law of thermodynamics states that all spontaneous processes increase entropy. This is just contrary to the negative value of our problem. And we cannot just say that it’s an exception to the second law, no! There has not been any to any of the laws of thermodynamics so far.

The reason is no doubt, the process is spontaneous due to increasing entropy of a universe for a process to proceed the overall entropy of the universe, and not only that of system, should be taken into account. ${\mathrm{\Delta }}_f{\mathrm{H}}^{\circ }$for water is -285.8 kJ mol^–1, hence the enthalpy change for the reaction (as expressed in the equation) is –571.6 kJ (i.e., – 285 $\times$2)

From $-\mathrm{\Delta }{H}^{\circ }\text{ (system) }=\mathrm{\Delta }{H}^{\circ }\text{ (surroundings) }$

and $\mathrm{\Delta }S\left(\text{ surroundings }\right)=\frac{\mathrm{\Delta }{H}^{\circ }\left(\text{ surroundings }\right)}{T}=-\frac{\mathrm{\Delta }{H}^{\circ }\left(\text{ system }\right)}{T}=\frac{+571.6\times {10}^3\left(\mathrm{J}{\mathrm{mol}}^{-1}\right)}{298\left(\mathrm{K}\right)}=1920{\mathrm{JK}}^{-1}{\mathrm{mol}}^{-1}$

Considering the total entropy change

$\mathrm{\Delta }{S}_{\text{(universe) }}=\mathrm{\Delta }{S}_{\text{system }}+\mathrm{\Delta }{S}_{\text{(surroundings) }}=-327+1920=+1593\left({\mathrm{JK}}^{-1}{\mathrm{mol}}^{-1}\right)$

Hence, there is an overall increase in the total entropy of the universe, well in accordance with the second law of thermodynamics. 

Sources of Energy

Energy is required to perform a process.  Running of a vehicle, cooking of food, glowing of a light, rotating of a fan, walking, breathing, wherever something is happening, energy is required. Moreover in the modern age of materialization, rather industrialization the energy requirement due to luxurious or even modern life style is increasing tremendously.  For the progress (development) of a country, the energy requirements are very high and must be met with. K although petroleum and coke are the prominent sources of energy, the foremost form we come across in our day-today life is the electrical energy which usually comes from coal, hydrostatic energy and nuclear energy. Inspite of introduction of new (non-conventional) sources like nuclear, hydroelectric and wind sources, in India almost 90% of total energy supply is provided by the fossil fuels.

Since, the reserves of the fossil fuels are limited as they are not growing day by day rather depleting, we can imagine a day when all the stores of fossil fuels will go dry. Moreover, the excessive use of fossil fuel has led to the rise in the concentration of gases like CO₂, NO₂, SO₂ which have been nuisance in the form of air pollution and eventually leading to global warming and acid rains. Hence, it has been realized that some alternative sources of energy must be looked for.  In 1950, Indian scientists had suggested the use of solar energy for cooking and water heating with the devices that were technologically sound but the then scenario of cheaper petroleum products did not let welcome the non-conventional source of energy. After 1970, the increasing oil demand and price along with environmental concerns led to the revival of non-conventional sources. In order to increase the participation of more and more persons, their efforts and outcomes in this area, the Government of India has an exclusive department for the cause under the name of Ministry of Non-conventional Energy Sources (MNES). Eventually an increasing realization that in order to meet with the growing energy needs in the long run, we must have to switch over to the alternative (non-conventional and renewable) sources.

However, the important sources of energy available with us these days are:

A. Renewable sources: Those sources of energy which can be renewed in nature by its own, hence are available for mankind for its use time and again, are the renewable sources e.g. biomass, hydroelectric energy wind energy, solar energy etc. Although we can use solar energy again and again as the energy from solar instruments or thorough biological systems (especially plants) is introduced in the living world. The source of biomass and other forms of energy e.g. hydroelectric, tidal energy which can be used again and again are due to the sun. But in long run, as we know, the source of sun’s energy the hydrogen shall be depleted after billions of years.  What next? Thus in broader perspective we say the energy from sun or the solar energy is not the renewable source.

B. Non–renewable sources: The sources of energy which cannot be replenished once they are used up are called as the non-renewable sources of energy e.g. fossil fuels and nuclear fuels.

1. Fossil fuels: Fossil fuels are those which are formed after a long time in the due course of fossilization of organic matter or more accurately decomposition at high temperature and pressure. Almost of our chemical fuels are fossil fuels like coal, petroleum products and natural gas. The main uses of fossil fuels are transport, household fuel, industrial heating and production of electricity.

a) Coal: A solid, crude from of carbon along with some higher hydrocarbons and S, O, N containing compounds. There are various forms of coals which have already been discussed in Phase – II Group – IV Chemistry.

b) Petroleum: A liquid, mixture of hundreds of hydrocarbons and other S, N, O containing compounds.  Fractional distillation leads to many important fuels like, kerosene, diesel, petrol and LPG (liquefied petroleum gas, mixture of gaseous hydrocarbons mainly butane and isobutene)

c) Natural gas: Gaseous hydrocarbons found with petroleum substances in oil wells. Mixture of methane with ethane, propane and butane.

2. Traditional Biomass (Wood & Dung): They are cheap and easily available sources of energy in rural and town areas. In recent decades gober gas has been introduced as a source of energy wherein organic waste like animal dung, vegetable waste etc are made to decay under absence of air (in closed chambers methane is produced along with some other gases, which burns with a blue flame upon combustion.

These two sources are the conventional sources. The fossil fuels are non-renewable as once they are spent, their reserves cannot be regained and the rate of rejuvenation is very slow.  The biomass is renewable sources of energy provided that the mentioned continues to maintain the ratio between deforestation (cutting down) and reforestation or forestation (plantation).

3. Hydroelectricity (Hydro energy): The mechanical energy contained within the flowing water is used to run turbines to generate electricity the hydroelectric power. Few of the important hydroelectric power stations in India are at Nangal and Shivasamudram.  In the time to come, for a country like India hydroelectricity can play a crucial role in the energy scenario.

If we observe carefully, the energy in flowing water comes from the sun! How?  Almost of the flowing water including that of rainwater, comes from glaciers or ice caps of the mountains. Wherefrom does ice and rain water get there? The vapours from the sea and other water bodies are lifted by the energy of the sun. These vapours then while travelling through the very cold regions like mountains condense there to replenish the source of hydroelectricity or hydro-energy.

4. Tidal energy: The tidal waves of the ocean move against the seashore and after a little while (during ebb) the large amounts of water of the wave return back to the sea. During this ebb phase the water can be used in the same way as that of flowing water, to produce energy (electricity). Where does the energy in these tides come from? The gravitational pull of the sun and moon are behind the reason.

5. Geothermal energy: The core of the earth consists of very hot liquid. The evidences are the natural geysers and hot springs etc at various places of the world where hot gases and steams rush out of earth. The geothermal energy can be utilized by either directly using these natural geysers or sending a jet of water into the core region, wherefrom the coming out steam can be used for energy production.

6. Nuclear energy: The fission of heavier nuclei like uranium and plutonium yields a vast amount of energy. Hence, it emerges as prominent source of electrical power worldwide.  The heat energy produced in the controlled fission of nuclear fuel is used to run the steam turbines which in turn generate electricity. These are four nuclear power plants operating (generating electricity) in India at :

a) Kalapakkam (Tamilnadu)

b) Kota (Rajasthan)

c) Narora (Uttar Pradesh)  

d)Tarapur (Maharashtra)

7. Wind energy: The kinetic energy of wind currents are used by wind mills – which directly generate electricity. The problem with wind energy is of the storage of electricity, as it is not always that wind is blowing whenever we are going to use the electricity.

 Conservation of Energy

From the first law of thermodynamics we know that the energy is conserved, whichever form it may transform into. Hence the overall energy is always conserved. Then, why energy crisis and what is the need of energy conservation?  Since the sources of energy available with us, that can be utilized for our life and various processes, are limited and are being used at such a high rate that they are not refreshed/replenished e.g. combustion of fossil fuels (coke and petroleum) is almost one way process as either they are not converted back into the fuel or the conversion is extremely slow. Carbon, for example burns into CO₂ with the liberation of energy. Nature in turn tends to convert back the CO₂ into carbon compounds through photosynthesis in the presence of sunlight.  If the two rates i.e. conversion of fuel into combustion products by the humanity and the formation of fuel differ by a great extent, very shortly, there will be no available fuel for us to utilize.  By the measures of conservation energy, we try to decrease the difference between the two rates by slowing down the use of such fuels. This can only be achieved by the introduction of some alternative sources of energy.

Although efforts for maximum utilization of non-conventional sources of energy are on the rise, with sincere efforts of the energy scientist, energy saving measures to avoid the wastage of energy must be exercised by everybody. A few practical suggestions to conserve energy in our day to day life are hereunder.

1. Use the most efficient fuels available.

2. Prefer the use of renewable fuel.

3. Use high efficiency devices/instruments for fuel combustion to ensure complete and most efficient energy output, as the incomplete combustion produces less energy (heat) and poisonous CO.

4. Use CFLs instead of bulbs.

5. Use pressure cookers for cooking in order to save energy.

6. Use flat bottom vessels/utensils for heating purposes instead of round bottom.

7. Get regularly serviced electrical instruments and combustion engine based devices like bikes, cars etc.

8. Avoid loose connections as due to sparking (electric arc) they result in wastage of energy and material as well.

9. Switch off the fans, lights, pumps etc when not need.

10. Switch off the engine of vehicle while stopping for a longer.

11. Use of casseroles for keeping the eatables hot instead of reheating them.

12. Use solar water heaters instead of geysers.

13. Use gober gas instead of using dung cakes.

14. Use bicycles for traveling shorter distances.

15. Keep the electronic gadgets like cell phones and PCs in the energy saving mode and leaving the latter ones in stand by when leaving for more than five minutes.

FORMULAE CONCEPTS AT A GLANCE

1. $W=F\cdot dx$

2. $\text{ Mechanical work }={\mathrm{P}}_{\text{ext }}\mathrm{\Delta V}$

$$\begin{gathered} {\mathrm{P}}_{\text{ext }}=\text{ external pressure } \\ \mathrm{\Delta V}=\text{ increase or decrease in volume }\left(={\mathrm{V}}_2-{\mathrm{V}}_1\right) \end{gathered}$$

3. $\mathrm{W}=\mathrm{JH}$

W= work, H = Heat, J = Joule mechanical equivalent of heat (4.184)

4. 1 calorie = 4.184 joules 1 joule = 0.2390 cal,  1 litre-atm = 101.3 J

5. $\mathrm{\Delta E}=\mathrm{q}+\mathrm{W}\mathrm{\Delta H}=\mathrm{\Delta E}+\mathrm{P\Delta V}\mathrm{P\Delta V}=\mathrm{\Delta nRT}$

6. $C=\frac{dq}{dT}$

7. $C_V={\left[\frac{\mathrm{\partial }\mathrm{E}}{\partial \top }\right]}_{\mathrm{V}};{\mathrm{C}}_{\mathrm{P}}={\left[\frac{\mathrm{\partial }\mathrm{H}}{\mathrm{\partial }T}\right]}_{\mathrm{P}}$

8. ${\mathrm{C}}_{\mathrm{P}}-{\mathrm{C}}_{\mathrm{V}}=\mathrm{R}$

9. $W=-{\int }_{V_1}^{V_2} PdV$

10. $\mathrm{W}=-2.303\mathrm{RTlog}\frac{{\mathrm{V}}_2}{{\mathrm{V}}_1};\mathrm{W}=-2.303\mathrm{nRTlog}\frac{{\mathrm{P}}_1}{{\mathrm{P}}_2}$

11. $\frac{T_1}{T_2}={\left(\frac{V_2}{V_1}\right)}^{\gamma -1}{P}_1{V}^{\gamma }=P_2{V}_2^{\gamma }{\left(\frac{T_1}{T_2}\right)}^{\gamma }={\left(\frac{P_1}{P_2}\right)}^{\gamma -1}$

12. $W=\frac{\mathrm{nR}}{(\gamma -1)}\left({\mathrm{T}}_2-{\mathrm{T}}_1\right)$

13. ${\mathrm{T}}_{\mathrm{i}}=\frac{2\mathrm{a}}{\mathrm{RT}}$

14. $\mathrm{\Delta }{H}_{\text{decomposition }}=-\mathrm{\Delta }{H}_{\text{formation }}$

15. $\mathrm{Q}={\mathrm{q}}_1+{\mathrm{q}}_2+{\mathrm{q}}_3$

16. $\mathrm{\Delta }S=S_{\text{final }}-S_{\text{initial }}={\int }_{\text{initial }}^{\text{final }} \frac{dq}{T}$

17. For reversible process, ${\mathrm{\Delta S}}_{\text{total }}\text{ i.e. }{\mathrm{\Delta S}}_{\text{system }}+\mathrm{\Delta }{\text{ S}}_{\text{surroundings}}=0$

For irreversible process: $\mathrm{\Delta }{S}_{\text{total}} i.e., \mathrm{\Delta }{S}_{\text{system }}+\mathrm{\Delta }{S}_{\text{surroundings }}>0$

Combining the two equations : ${\mathrm{\Delta S}}_{\text{system }}+{\mathrm{\Delta S}}_{\text{surroundings}}\ge 0$

18. $\mathrm{\Delta }{S}_{\text{trans }}=\frac{{\mathrm{q}}_{\mathrm{rev}}}{\mathrm{T}}$ q_rev = heat exchanged (molar enthalpy of transformation of the substance) ; T = temperature of transition

19. $\mathrm{\Delta A}=\mathrm{\Delta E}-\mathrm{T\Delta S}\mathrm{\Delta A}=-{\mathrm{W}}_{\mathrm{rev}}$

20. $\mathrm{\Delta G}=\mathrm{\Delta H}-\mathrm{T\Delta S}-\mathrm{\Delta G}=\mathrm{W}-\mathrm{P\Delta V}$

21. ${\mathrm{\Delta G}}^{\circ }=-\mathrm{RTlnK}\mathrm{\Delta G}=-\mathrm{nFE}$

22. $\underset{\mathrm{T}\to 0}{lim} {\left[\frac{\mathrm{\partial }\left(\mathrm{\Delta G}\right)}{\mathrm{\partial }T}\right]}_P=\underset{\mathrm{T}\to 0}{lim} {\left[\frac{\mathrm{\partial }\left(\mathrm{\Delta H}\right)}{\partial \top }\right]}_P=0;{\mathrm{S}}_T-{\mathrm{S}}_0={\mathrm{S}}_T={\int }_0^T \frac{{\mathrm{C}}_{\mathrm{P}}\mathrm{dT}}{\mathrm{T}}={\int }_0^{\mathrm{T}} {\mathrm{C}}_{\mathrm{P}}\mathrm{d} \mathrm{lnT}$

23. $\eta =\frac{\left(T_2-T_1\right)}{T_2};\eta =\frac{q_2-q_1}{q_2}$

24. $\frac{\mathrm{dP}}{\mathrm{dT}}=\frac{{\mathrm{\Delta }}_{\mathrm{vap}}\mathrm{H}}{\mathrm{T}\left({\mathrm{V}}_g-{\mathrm{V}}_{\ell }\right)}\ln \frac{{\mathrm{P}}_2}{{\mathrm{P}}_1}=\frac{{\mathrm{\Delta }}_{\mathrm{vap}}\mathrm{H}}{\mathrm{R}}\left[\frac{{\mathrm{T}}_2-{\mathrm{T}}_1}{{\mathrm{T}}_1{\mathrm{T}}_2}\right]$

SOLVED PROBLEMS -1

Prob 1:

Calculate the volume occupied by 1 mole of an ideal gas at 25^oC and 1 atm.

Sol:

PV = nRT

$\begin{array}{l}\left(1.01325\times {10}^5{\mathrm{Nm}}^{-2}\right)\left(\mathrm{V}/{\mathrm{m}}^3\right)=\left(1\mathrm{mol}\right)\left(8.314{\mathrm{JK}}^{-1}{\mathrm{mol}}^{-1}\right)\left(298.15\mathrm{K}\right)\\ \mathrm{V}=0.02447{\mathrm{m}}^3=24.47{\mathrm{dm}}^3.\end{array}$

Prob 2:

Calculate the energy required to lift a volley ball weighting 250 g upto 8 m of height.

Sol:

While lifting the volley ball upto the height, the work against the acceleration due to gravity is done on the ball, it can be given by

Energy = work = force $\times$ displacement

$\begin{array}{l}=0.25\left(\mathrm{kg}\right)\times 9.8{\mathrm{ms}}^{-2}\times 8\left(\mathrm{m}\right)\\ =19.6\left({\mathrm{kgm}}^2{\mathrm{s}}^{-2}\right)\\ =19.6\mathrm{J}\end{array}$

Prob 3:

Calculate the work done when 8.5 g of NH₃ gas expands from 5L to 10L against a constant pressure of 1 bar.

Sol: 

Since in expansion, work is done by the gas, the energy of the system decreases, the sign of work is given by the negative sign

Work = $-P_{\text{ext }}\mathrm{\Delta }V=-P_{\text{ext }}\left(V_2-V_1\right)$

$\begin{array}{l}=-\left(1\times {10}^5{\mathrm{Nm}}^{-2}\right)\left[(10-5){\mathrm{dm}}^3\times {10}^{-3}{\mathrm{m}}^3{\mathrm{dm}}^{-3}\right]\\ =-5\times {10}^2\mathrm{J}\end{array}$

This is amount of work done for 1 mole of gas.

For 8.5 g of  ${\mathrm{NH}}_3=\frac{8.5\left(\mathrm{g}\right)}{17\left(\mathrm{a}{\mathrm{mol}}^{-1}\right)}=0.5$ of gas, the work done shall be half of it, i.e. $-2.5\times {10}^2\text{ Joule or }-250\mathrm{J}$

Prob 4:

If 1.12 g of N₂ expands reversibly to a final volume 5 times greater than its initial volume at 25^oC. What will be the work done?

Sol:

Again it’s an expansion, hence work has to be done by the gas. The work done will be negative.  Let the initial volume be V,

Work (W) = $-\mathrm{nRTln}\frac{{\mathrm{V}}_2}{{\mathrm{V}}_1}=-2.303\left(\frac{1.12\mathrm{g}}{28{\mathrm{gmol}}^{-1}}\right)\left(8.314{\mathrm{JK}}^{-1}{\mathrm{mol}}^{-1}\right)\left(298.15\mathrm{K}\right)\cdot \frac{5\mathrm{V}{\mathrm{dm}}^3}{\mathrm{V}{\mathrm{dm}}^3}$$=-\left(228.35{\mathrm{Nm}}^2{\mathrm{s}}^{-2}\right)\log \left(5\right)=-159.62\mathrm{J}$

Prob 5:

The temperature of 1 mole of a substance is raised by heating it with 750J of energy. While expansion it performs 200 J of work. Find the change in internal energy concerned.

Sol:

While increasing the temperature, energy content increases, q = +750 J

During expansion, the energy content of the system decreases, W = – 200 J

From the first law of thermodynamics

$\mathrm{\Delta }E=q+W=(+750J)+(-200J)=+550\mathrm{J}$

Prob 6:

The complete combustion of ethane gives 1558.8 kJ mol^–1 energy at 25^oC.  Calculate the enthalpy change of combustion at 100^oC.

${\mathrm{C}}_{\mathrm{P}}\left({\mathrm{JK}}^{-1}{\mathrm{mol}}^{-1}\right):{\mathrm{C}}_2{\mathrm{H}}_6\left(\mathrm{g}\right)52.6; {\mathrm{O}}_2\left(\mathrm{g}\right)29.4;{\mathrm{CO}}_2\left(\mathrm{g}\right)\text{ 37.1; }{\mathrm{H}}_2\mathrm{O}75.3$

Sol:

Enthalpy of a reaction/substance varies with temperature. The variation is given by the Kirchoff’s equation.

$\mathrm{d}\left(\mathrm{\Delta H}\right)=\mathrm{\Delta CpdT}\text{ or }{\mathrm{\Delta H}}_2-{\mathrm{\Delta H}}_1={\mathrm{\Delta C}}_{\mathrm{P}}\mathrm{\Delta T}$

where d($∆$H) is the variation in the values of $∆$H on the variation in the temperature dT

$∆$C_P is the change in heat capacities of the products and reactants for a give reaction.

Writing the thermochemical equation for the given data.

$\begin{array}{l}{\mathrm{C}}_2{\mathrm{H}}_8\left(\mathrm{g}\right)+3\frac{1}{2}{\mathrm{O}}_2\left(\mathrm{g}\right)⟶2{\mathrm{CO}}_2\left(\mathrm{g}\right)+3{\mathrm{H}}_2\mathrm{O}\left(\ell \right){\mathrm{\Delta H}}_{298}^0=-1558.8{\mathrm{kJmol}}^{-1}.\\ {\mathrm{\Delta C}}_{\mathrm{P}}=\sum {\mathrm{v}}_{\mathrm{i}}{\mathrm{C}}_{\mathrm{P}}\left(\text{ products }\right)-\sum {\mathrm{v}}_{\mathrm{i}}{\mathrm{C}}_{\mathrm{P}}\left(\text{ reactants }\right)\end{array}$

where $\sum$ is the summation term ${\upsilon }_i$ stands for stoichiometric ratio

${\mathrm{\Delta C}}_{\mathrm{P}}=\left[2{\mathrm{C}}_{\mathrm{P}}\left({\mathrm{CO}}_2\right)+3{\mathrm{C}}_{\mathrm{P}}\left({\mathrm{H}}_2\mathrm{O}\right)\right]-\left[{\mathrm{C}}_{\mathrm{P}}\left({\mathrm{C}}_2{\mathrm{H}}_8\right)+3\frac{1}{2}{\mathrm{C}}_{\mathrm{P}}\left({\mathrm{O}}_2\right)\right]$

$\begin{array}{l}=\left[\right(2\times 37.1)+3(75.3\left)\right]-\left[\left(52.6\right)+3\frac{1}{2}\left(29.4\right)\right]\\ =144.6{\mathrm{JK}}^{-1}{\mathrm{mol}}^{-1}\end{array}$

$$\begin{gathered} {\mathrm{\Delta H}}_{373}^0={\mathrm{\Delta H}}_{298}^0+{\mathrm{\Delta C}}_{\mathrm{P}}\mathrm{\Delta T} \\ =-\left(1558.8\times {10}^3{\mathrm{Jmol}}^{-1}\right)+\left(144.6{\mathrm{JK}}^{-1}{\mathrm{mol}}^{-1}\right)\left(75\mathrm{K}\right) \\ =-1547.9{\mathrm{kJmol}}^{-1} \end{gathered}$$

Prob 7:

Calculate the standard enthalpy change for the isomerization reaction${\mathrm{CH}}_3{\mathrm{OCH}}_3\left(\mathrm{g}\right)⟶{\mathrm{C}}_2{\mathrm{H}}_5\mathrm{OH}\left(\mathrm{g}\right)$

Using the bond enthalpy data:

$\mathrm{\Delta }{H}_{(C-H)},415\mathrm{kJ}{\mathrm{mol}}^{-1};\mathrm{\Delta }{H}_{(C-0)};350{\mathrm{kJmol}}^{-1};{\mathrm{\Delta H}}_{(\mathrm{C}-\mathrm{C}),}344\mathrm{kJ}{\mathrm{mol}}^{-1};{\mathrm{\Delta H}}_{(\mathrm{O}-\mathrm{H})},465\mathrm{kJ}{\mathrm{mol}}^{-1}$

Sol: 

The structures of CH₃OCH₃ and C₂H₅OH

Dissociation of CH₃OCH₃ : For the thermochemical change consider that first of all, all the bonds in CH₃OCH₃ break which later on recombine to form CH₃CH₂OH.

CH₃OCH₃ consists of 6C-H bonds and 2C-O bonds, to beak them the energy required will be

$\begin{array}{l}{\mathrm{\Delta H}}_1=6{\mathrm{\Delta H}}_{(\mathrm{C}-\mathrm{H})}+2{\mathrm{\Delta H}}_{\mathrm{c}-0)}\\ =6\times 415{\mathrm{kJmol}}^{-1}+2\times 350{\mathrm{kJmol}}^{-1}\\ =3190{\mathrm{kJmol}}^{-1}.\end{array}$

Formation of C₂H₅OH: During formation of C₂H₅OH 5 C-H bonds, 1 C-C bond, 1 C-O bond and 1 O-H bond are to be formed. During the process energy shall evolve as the system achieves more stable state.

$$\begin{gathered} {\mathrm{\Delta H}}_2={\mathrm{\Delta H}}_{(\mathrm{C}-\mathrm{H})}+{\mathrm{\Delta H}}_{(\mathrm{C}-\mathrm{C})}+{\mathrm{\Delta H}}_{(\mathrm{C}-0)}+{\mathrm{\Delta H}}_{(\mathrm{C}-\mathrm{H})} \\ =5\times 415\left(1{\mathrm{Jmol}}^{-1}+344{\mathrm{kJmol}}^{-1}+350+350{\mathrm{kJmol}}^{-1}+465{\mathrm{kJmol}}^{-1}\right. \\ =3234{\mathrm{kJmol}}^{-1} \end{gathered}$$

Hence, this is amount of energy released from the system. The sign of the $∆$H should be negative i.e.  ${\mathrm{\Delta H}}_2=-3234$

The overall enthalpy change for both the process can be given by

$\mathrm{\Delta H}\text{ (reaction/isomerization) }={\mathrm{\Delta H}}_1+{\mathrm{\Delta H}}_2=\left(3190\right)+(-3234){\mathrm{kJmol}}^{-1}=-44{\mathrm{kJmol}}^{-1}$

Prob 8:

How much energy is required to convert 100g of ice at 0^oC into steam at 100^oC?

Sol:

The process for convenience is split into three parts:

1: Fusion:  Conversion of 100 g ice into 100g water at $0^{\circ }\mathrm{C},{\mathrm{\Delta H}}_1={\mathrm{\Delta }}_{\text{fus }}\mathrm{H}\text{ for }100\mathrm{g}$

2. Heating: Heating of 100g water from 0^oC upto ${100}^{\circ }\mathrm{C}={\mathrm{\Delta H}}_2={\mathrm{C}}_{\mathrm{P}}\mathrm{\Delta T}\text{ for }100\mathrm{g}$

3. Vaporization: Evaporation of 100g water into steam at${100}^{\circ }\mathrm{C}, {\mathrm{\Delta H}}_3={\mathrm{\Delta }}_{\mathrm{vap}}\mathrm{H}\text{ for }100\mathrm{g}$

Since the value in our thermochemical equation correspond to one mole of water, for 100g i.e.  $\frac{100\mathrm{g}}{18{\mathrm{gmol}}^{-1}}=5.56\text{ mole ;}{\mathrm{\Delta H}}_{\text{total }}=5.56\left[{\mathrm{\Delta H}}_1+{\mathrm{\Delta H}}_2+{\mathrm{\Delta H}}_3\right]$

$=5.56\left[\left(6.01\times {10}^3{\mathrm{Jmol}}^{-1}\right)+\left(75.1{\mathrm{JK}}^{-1}{\mathrm{mol}}^{-1}\right)(373-273\mathrm{K})+\left(40.7\times {10}^3{\mathrm{Jmol}}^{-1}\right)\right]=301.46\mathrm{kJ}{\mathrm{mol}}^{-1}$

Prob 9:

Calculate the entropy change for the freezing of 1 mole of super cooled water at – 10^oC.  Given, heat capacities of ice and water at 0^oC are 2.2 and 4.10 JK ^–1 and enthalpy of fusion is 332 Jg^–1.

Sol:

Since entropy is a state function, the value of entropy change does not depend upon the path followed.  Moreover the process

${\mathrm{H}}_2\mathrm{O}\left(\ell \right),-{10}^{\circ }\mathrm{C}⟶{\mathrm{H}}_2\mathrm{O}\left(\mathrm{s}\right)-{10}^{\circ }\mathrm{C}$

cannot be a reversible process. Hence, it will be easier to split it into (small) series of reversible changes and then adding them for the value of $∆$S.

Water, $-{10}^{\circ }\mathrm{C}\stackrel{∆\mathrm{s}}{\to }\text{ water, }{0}^{\circ }\mathrm{C}\stackrel{∆{\mathrm{s}}_2}{\to }\text{ ice, }{0}^{\circ }\mathrm{C}\stackrel{∆{\mathrm{s}}_3}{\to }\text{ ice }-{10}^{\circ }\mathrm{C}$

$\mathrm{\Delta S}={\mathrm{\Delta S}}_1+{\mathrm{\Delta S}}_2+{\mathrm{\Delta S}}_3$$=C_P\ln \frac{T_2}{T_1}+\frac{{\mathrm{\Delta }}_{\text{fus }}{H}^{\circ }}{T_f}+C_P\ln \frac{T_2}{T_1}$

$=4.10\ln \frac{273}{263}+\frac{-332}{273}+2.2\ln \frac{263}{273}\left({\mathrm{JK}}^{-1}{\mathrm{g}}^{-1}\right)$

$\begin{array}{l}=\left(0.156\right)+(-1.216)+\left(0.082\right){\mathrm{JK}}^{-1}{\mathrm{g}}^{-1}=-1.142{\mathrm{JK}}^{-1}{\mathrm{g}}^{-1}\end{array}$

Since it is customary to express the thermochemical values in moles

$\mathrm{\Delta S}=\left(-1.142{\mathrm{JK}}^{-1}{\mathrm{g}}^{-1}\right)\left(18{\mathrm{gmol}}^{-1}\right)=-20.556{\mathrm{JK}}^{-1}{\mathrm{mol}}^{-1}$

The negative value of entropy reveals that a more disordered liquid phase is transforming into a comparatively more ordered solid phase.

Prob 10:

An electrochemical cell has standard electrode potential (E^o) of 1.055 volt at 25^oC. Calculate the free energy change. If the SEP changes to 1.015 volt at 0^oC, calculate the entropy change ($∆$S^o) and standard enthalpy change ($∆$H^o) for the reaction at 25^oC.

The electrochemical reaction within the cell is $\mathrm{Zn}\left(\mathrm{s}\right)+2\mathrm{AgCl}\left(\mathrm{s}\right)⟶{\mathrm{ZnCl}}_2\left(\mathrm{aq}\right)+2\mathrm{Ag}\left(\mathrm{s}\right)$

Sol:

From the equation ${\mathrm{\Delta G}}^{\circ }=-{\mathrm{nFE}}^{\circ }=-2\times 96485\left(\text{ coloumb }\right)\times \left(1.055\mathrm{volt}\right)=-203.58\mathrm{kJm}{\mathrm{ol}}^{-1}$

$\mathrm{\Delta }{S}^{\circ }$can be evaluated from $\mathrm{\Delta }{S}^{\circ }=\mathrm{nF}\left(\frac{{\mathrm{dE}}^{\circ }}{\mathrm{dT}}\right)$

$\begin{array}{l}=2\times \left(96485\mathrm{col}\right)\times \left(\frac{1.055-1.015}{298.15-272.15}\right)\\ =308.75{\mathrm{JK}}^{-1}{\mathrm{mol}}^{-1}\end{array}$

And hence $\mathrm{\Delta }{H}^{\circ }=\mathrm{\Delta }{G}^{\circ }+T\mathrm{\Delta }{S}^{\circ }=\left(-203.58\times {10}^3{\mathrm{Jmol}}^{-1}\right)+\left(298.15\mathrm{K}\right)\left(308.75{\mathrm{JK}}^{-1}{\mathrm{mol}}^{-1}\right)=-111.53\mathrm{kJ}{\mathrm{mol}}^{-1}$

(C) $\mathrm{\Delta H}=894\text{ cal and }\mathrm{\Delta E}=1490\text{ cal }$          

(D) $\mathrm{\Delta H}=\mathrm{\Delta E}=894\mathrm{cal}$

SOLVED PROBLEMS -2

Prob 1:

One mole of a non-ideal gas undergoes a change of state (2.0 atm, 3.0 L, 95 K) → (4.0 atm, 5.0L, 245 K) with a change in internal energy $∆$U = 30.3L atm.  The change in enthalpy of the process in L-atm is

(A) 40.0          (B) 42.3

(C) 44.0         (D) not defined because it is not constan

Sol.

(C) $\mathrm{\Delta H}=\mathrm{\Delta U}+\left({\mathrm{P}}_2{\mathrm{V}}_2-{\mathrm{P}}_1{\mathrm{V}}_1\right)=30+(4\times 5-2\times 3)=44\mathrm{L}-\mathrm{atm}$

Prob 2:

What is the heat change (cal) when 40g of He gas at 27⁰C undergoes isothermal and reversible compression from initial pressure of 1 atm to 10 atm (R = 2 cal K^–1 mol^–1)?

(A) 13.818 k cal             (B) – 13.818 k cal

(C) 55.272 k cal             (D) – 55.272 k cal

Sol.

(B) $q=w_{rev}=-\left(2.303nRT\log \frac{P_1}{P_2}\right)=2.303\times \frac{40}{4}\times 2\times 300\log \frac{1}{10}=-13.82\mathrm{kcal}$

Prob 3:

Standard enthalpy of combustion of CH₄ is – 890 kJ mol^–1 and standard enthalpy of vaporization of water is 40.5 kJ mol^–1. Calculate the enthalpy change for the reaction

(A) – 890 kJ mol^–1          (B) – 809 kJ mol^–1

(C) 890 kJ mol^–1                   (D) – 971 kJ mol^–1

Sol.

(B) ${\mathrm{CH}}_4\left(\mathrm{g}\right)+2{\mathrm{O}}_2\left(\mathrm{g}\right)\to 2{\mathrm{CO}}_2\left(\mathrm{g}\right)+2{\mathrm{H}}_2\mathrm{O}\left(\mathrm{I}\right),\mathrm{\Delta H}=-890\mathrm{kJ}$     . . . . (i)

$2{\mathrm{H}}_2\mathrm{O}\left(\mathrm{I}\right)\to 2{\mathrm{H}}_0\mathrm{O}\left(\mathrm{a}\right)\cdot \mathrm{\Delta H}=2\times 40.5=81\mathrm{kJ}$    . . . . (II)

Adding (i) + (ii)

 ${\mathrm{CH}}_4\left(\mathrm{g}\right)+2{\mathrm{O}}_2\left(\mathrm{g}\right)\to 2{\mathrm{CO}}_2\left(\mathrm{g}\right)+2{\mathrm{H}}_2\mathrm{O}\left(\mathrm{g}\right),\mathrm{\Delta H}=-890+81=-809\mathrm{kJ}$

Prob 4:

 If temperature of 5 moles of a gas is decreased by 2K at constant pressure, then

(A) work done by the gas = 5R                   (B) work done by the gas = 10 R

(C) work done over the gas = 10 R            (D) work done = 0

Sol.

(C) For 5 moles of gas at T,   PV₁ = 5RT

For 5 moles of gas at $T_{–2}$                 PV₂ = 5R (T-2)

Hence, PV₂ – PV₁ = P(V₂ – V₁) = P$∆$V = 5R [T-2-T] = – 10R   or    – P$∆$V = 10R ($∆$V is negative, W is + ve)

Prob 5:

Enthalpy of combustion of carbon, hydrogen and C₃H₈ are x₁, x₂ and x₃ per mol^–1 respectively.  Estimate the enthalpy of formation of C₃H₈

(A) $x_3-x_1-x_2$                (B) $3x_1+4x_2-x_3$

(C) $3x_1-3x_3-x_3$           (D) $x_1-x_2-x_3$

Sol.

(B) ${\mathrm{C}}_3{\mathrm{H}}_8\left(\mathrm{g}\right)+5{\mathrm{O}}_2\to 3{\mathrm{CO}}_2\left(\mathrm{g}\right)+4{\mathrm{H}}_2\mathrm{O}\left(\mathrm{I}\right), \mathrm{\Delta H}={\mathrm{x}}_3$

${\mathrm{\Delta H}}_{\mathrm{r}}={\mathrm{x}}_3=3{\mathrm{\Delta H}}_{\mathrm{f}}\left({\mathrm{CO}}_2\right)+4{\mathrm{\Delta H}}_{\mathrm{f}}\left({\mathrm{H}}_2\mathrm{O}\right)-{\mathrm{\Delta H}}_{\mathrm{f}}\left({\mathrm{C}}_3{\mathrm{H}}_8\right)-5{\mathrm{\Delta H}}_{\mathrm{f}}\left({\mathrm{O}}_2\right)=3{\mathrm{x}}_1+4{\mathrm{x}}_2-{\mathrm{\Delta H}}_{\mathrm{f}}\left({\mathrm{C}}_3{\mathrm{H}}_8\right)-5\times 0$

or    ${\mathrm{\Delta H}}_{\mathrm{f}}\left({\mathrm{C}}_3{\mathrm{H}}_8\right)=3{\mathrm{x}}_1+4{\mathrm{x}}_2-{\mathrm{x}}_3$

Prob 6:

The enthalpy of atomization of CH₄ and C₂H₆ are 360 and 620k cal mol^–1 respectively.  The C–C bond energy is expected to be

(A) 210 k cal mol^–1            (B) 130 k cal mol^–1

(C) 180 k cal mol^–1            (D) 80 k cal mol^–1

Sol.

(D) ${\mathrm{CH}}_4\left(\mathrm{g}\right)\to \mathrm{C}\left(\mathrm{g}\right)+4\mathrm{H}\left(\mathrm{g}\right),\mathrm{\Delta H}=360\mathrm{cal}$

Hence, $\mathrm{C}-\mathrm{H}\text{ bond energy }=\frac{360}{4}=90\mathrm{k}{\text{ calmol }}^{-1}$

Hence, ${\mathrm{H}}_{\mathrm{C}-\mathrm{c}}+6{\mathrm{H}}_{\mathrm{C}-\mathrm{H}}=620$  or  ${\mathrm{H}}_{\mathrm{C}-\mathrm{c}}=620-6{\mathrm{H}}_{\mathrm{C}-\mathrm{H}}=620-6\times 90=80\mathrm{kcal}$

Prob 7:

Enthalpy of combustion of CH₄, C₂H₆ and C₃H₈ are – 210.8, 368.4 and – 526.2 k cal mol^–1 respectively. Enthalpy of combustion of hexane can be predicted as

(A) – 840 k cal mol^–1               (B)  – 684 k cal mol^–1

(C)- 1000 k cal mol^–1              (D none of these

Sol.

(C) ${\mathrm{\Delta H}}_{\mathrm{c}}\left({\mathrm{C}}_2{\mathrm{H}}_8\right)-{\mathrm{\Delta H}}_{\mathrm{C}}\left({\mathrm{CH}}_4\right)=-368.2-(-210.8)=-157.4$

${\mathrm{\Delta H}}_{\mathrm{C}}\left({\mathrm{C}}_3{\mathrm{H}}_8\right)-{\mathrm{\Delta H}}_{\mathrm{C}}\left({\mathrm{C}}_2{\mathrm{H}}_8\right)=-526-(-268.4)=-157.8$

Thus, average $\mathrm{\Delta Hc}\left(-{\mathrm{CH}}_2\right)=-\frac{(-157.4)+(-157.8)}{2}=-157.6\mathrm{k}{\mathrm{calmol}}^{-1}$

Then , ${\mathrm{\Delta H}}_{\mathrm{c}}\left({\mathrm{C}}_6{\mathrm{H}}_{14}\right)={\mathrm{\Delta H}}_{\mathrm{C}}\left({\mathrm{C}}_3{\mathrm{H}}_8\right)+3{\mathrm{\Delta H}}_{\mathrm{C}}\left(-{\mathrm{CH}}_2-\right)=(-526.2)+3(-157.6)=-999\mathrm{k}\text{ cal }$

Prob 8:

The enthalpy of neutralization of NH₄OH and CH₃COOH is – 10.5 k cal mol^–1 and enthalpy of neutralization of CH₃COOH with strong base is –12.5k cal mol^–1. The enthalpy of ionization of NH₄OH will be

(A) 4.0 k cal mol^–1          (B) 3.0 k cal mol^-1

(C) 2.0 k cal mol^–1          (D) 3.2 k cal mol^–1

Sol.

(C) H_N for strong acid with strong base = – 13.7k cal equiv^–1

$\begin{array}{l}{\mathrm{\Delta H}}_{\text{ion }}\left({\mathrm{CH}}_3\mathrm{COOH}\right)=-12.5-(-13.7)=+1.2{\mathrm{kcalmol}}^{-1}\\ {\mathrm{\Delta H}}_{\text{ion }}\left({\mathrm{NH}}_4\mathrm{OH}\right)=-10.5-(-13.7)-{\mathrm{\Delta H}}_{\text{ion }}\left({\mathrm{CH}}_3\mathrm{COOH}\right)=13.7-10.5-1.2=2\mathrm{k}\text{ cal }{\mathrm{mol}}^{-1}\end{array}$

Prob 9:

A gas absorbs 200 J heat and undergoes simultaneous expansion against a constant external pressure of 10⁵ Pa.  The volume changes from 4L to L.  The change in internal energy is

(A) 300 J              (B) 100 J

(C) – 300 J        (D) – 100 J

Sol.

(B) $\mathrm{\Delta E}=\mathrm{q}+\mathrm{W}=\mathrm{q}-\mathrm{P\Delta V}$

$\begin{array}{l}=200\mathrm{J}-{10}^5\mathrm{Pa}\times (5-4)\times {10}^{-3}{\mathrm{m}}^3\\ =200\mathrm{J}-100{\mathrm{Pam}}^3\\ =200\mathrm{J}-100\mathrm{J}=100\mathrm{J}\end{array}$

Prob 10:

Given that $S_{{\mathrm{H}}_2}^0=131{\mathrm{JK}}^{-1}{\mathrm{mol}}^{-1},{\mathrm{S}}_{{\mathrm{Cl}}_2}^0=223{\mathrm{JK}}^{-1}\text{ and }{\mathrm{S}}_{\mathrm{HCl}}^0=187{\mathrm{JK}}^{-1}{\mathrm{mol}}^{-1}$ The standard entropy change in the formation of one mole of HCl(g) from H₂(g) and Cl₂(g) will be

(A) 20 JK^–1               (B) 10 JK^–1

(C) 187 JK^–1              (D) 374 JK^–

Sol.

(B) $\frac{1}{2}\mathrm{H}\left(\mathrm{g}\right)+\frac{1}{2}{\mathrm{Cl}}_2\left(\mathrm{g}\right)\to \mathrm{HCl}\left(\mathrm{g}\right)$         ${\mathrm{\Delta S}}^0=\mathrm{\Sigma }{S}^0\left(\text{ reactants }\right)$

$=S_{\mathrm{HCI}}^0-\left(\frac{1}{2}{S}_{{\mathrm{H}}_2}^0+\frac{1}{2}{S}_{{\mathrm{Cl}}_2}^0\right)=187-\frac{1}{2}(131+223)=10{\mathrm{JK}}^{-1}$