INTRODUCTION
In this chapter, we shall take up the physical classification of matter. Matter can be classified into three categories depending upon its physical state, namely: solid, liquid and gaseous states.
The matter in solid state possesses a definite volume, a definite shape and a definite mass. Some common examples are: table, chair, common salt, silver, etc. The matter in liquid state possesses a definite volume, a definite mass, but no definite shape. In fact, it acquires the shape of the container. Some examples are: milk, water, alcohol, etc.
The matter in gaseous state neither has definite volume nor definite shape but it has definite mass. It acquires the shape and volume of the container. Some common examples are: air, oxygen, and hydrogen, sulphur dioxide, etc.
Almost all the substances exist in three states under appropriate conditions of temperature and pressure. A substance is said to be solid if its melting point is above the room temperature at the atmospheric pressure. A substance may be called a liquid if its boiling point is more but melting point is less than the room temperature at the atmospheric pressure and likewise, it is a gas if its boiling point is below the room temperature at the atmospheric pressure.
Fourth state called plasma state refers to the super-heated gaseous state consisting of mixture of electrons and positively charge ions with unusual properties. It is found at extremely high temperatures such as interiors of sun or stars or in intense electrical fields as in discharge tube. Astronomers reveal that 99% of all matter in the universe is present in this plasma state.
Fifth state refers to super cooled solid in which atoms lose their separate identity. In fact, get condensed and behave like a single super atom. The study of this phenomenon was based upon Bose-Einstein Condensation (BEC) concept developed in 1924.
DYNAMIC PARTICLE MODEL
The intensive investigation by the scientists over the years, led to the development of a mental model regarding the constitution of matter. This model is known as dynamic particle model.
Some of its assumptions are:
All matter is made of tiny particles. However, the state of aggregation of particles is different in the three states of matter.
The particles are separated by empty spaces called voids.
The particles exert attractive forces on one another. However, the magnitudes of these interparticle forces differ in three states of matter.
The particles are not stationary, but they have tendency to acquire motion.
The basic difference between the three states of matter can be explained on the basis of particle model as follows:
i) In solid state, the particles are closely packed and the voids between them are very small.
ii) The average distance between the particles is of the order of
iii) Due to small voids the particle motion is limited to vibratory motion only and the magnitude of interparticle forces is quite large.
iv) The definite shape and volumes of solids are attributed to the definite geometric pattern involved in the close packing of particles.
v) In gaseous state the particles are very loosely packed.
vi) The voids between the particles are quite large so much so that the actual volume of the particles is negligible as compared to the total volume of gas.
vii) The attractive forces between the particles are negligibly small. The particle motion is very rapid and they move in all the directions in straight lines.
viii) Because of the random motion and weak inter-particle forces, the particle does not have any bonding surface. As a result they do not have definite shape or definite volume.
ix) The liquid state is intermediate of solids and gases. The particles are relatively loosely packed as compared with solids.
x) The average distance between the particles is of the order of
xi) The attractive forces are relatively weaker than those in solids but stronger than those in In liquids, particles can move about, however, they cannot separate from one another due to stronger attractive forces. That is why liquids have definite volume but no definite shape.
BULK PROPERTIES OF MATTER
Most of the observable properties of chemical species in different physical states represent bulk properties of matter. These bulk properties depict the collective behaviour of large number of particles taken together. For example, boiling of liquid is the bulk of liquid which boils. The individual molecules of liquid do not boil. Similarly, water (which is a collection of large number of molecules) has wetting properties, but individual molecules do not wet. Also when gas expands, the individual molecules do not expand but the bulk molecules occupy more space. Some of the bulk properties of matter are boiling point, vapours pressure, density, surface tension, viscosity, etc.
Bulk properties of matter depend upon its physical state and they change with the change of physical state. The change of physical state and bulk properties of matter further depend upon the energy of constituent particles and also on electrostatic interactions between the constituent particles. These particles may be atoms, ions or molecules.
The physical state of existence of a substance at given conditions is a balance between the thermal energy of molecules and intermolecular interactions. It is because both these factors affect the molecular motion which further determines the physical state. Let us learn about the nature and types of intermolecular forces.
INTERMOLECULAR FORCES
i) The attractive and repulsive forces operating between the particles (atoms and molecules) of the substance are called interparticle forces.
ii) If the particles are atoms these may be termed as interatomic forces, on the other hand, if these are molecules, they are called intermolecular forces.
iii) These force are collectively called van der Waal’s forces in the honour of Dutch scientist Johannes van der Waal (1837-1923).
iv) van der Waal’s forces are further classified as
(a) Dispersion forces or London forces
(b) Dipole-Dipole forces and
(c) Dipole-induced dipole forces.
v) It is worth noting that the electrostatic forces between the ions of opposite charges (interionic forces) and those between ions and polar molecules (ion-dipole forces) do not fall in category of van der Waal forces.
vi) There is yet another category of intermolecular force called Hydrogen-bonds which exist among the molecules in which H-atom is covalently bonded to elements like F, O and N.
vii) It may also be kept in mind that the melting and boiling points of the substances depend on the magnitude of intermolecular forces. Larger the magnitude of these forces higher is the melting point or boiling point of the substance.
1. DISPERSION FORCES OR LONDON FORCES
(i) These are the interparticle forces among the monatomic or non-polar molecules such as N2, He, H2, CO2, etc.
(ii) Non-polar molecules are electrically symmetrical and have no dipole moment because their electronic charge cloud is symmetrically distributed. However, an instantaneous dipole may develop in such atoms and molecules, as described below.
(iii) Suppose we have two atoms of neon ‘A’ and ‘B’ in the close vicinity of each other.
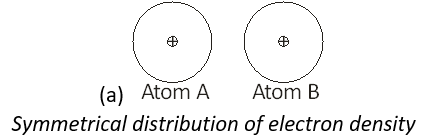
Rapid movement of electrons in A may cause momentary accumulation of electron density on one side thus causing the charge distribution to become unsymmetrical. In other words, the charge cloud is more concentrated on one side than the other. This will result in the development of temporary instantaneous dipole on the atom ‘A’ for a very short time.
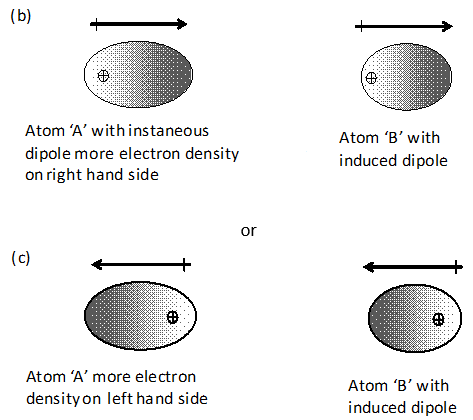
This instantaneous or transient dipole distorts the electron density of the atom ‘B’, which is close to it. In other words, a dipole is induced in the atom ‘B’ also. The temporary dipoles of atom ‘A’ and ‘B’ attract each other. Similar temporary dipoles are induced in non-polar molecules also.
(iv) Magnitude of such a force of attraction was first calculated by the German physicist Fritz London. For this reason force of attraction between two temporary dipoles is known as London force. Another name for this force is dispersion force. These forces are always attractive and interaction energy is inversely proportional to the sixth power of the distance between two interacting particles (i.e., where r is the distance between two particles). These forces are important only at short distances (~ 500 pm) and their magnitude depends on the ability of the particles to undergo polarization. Dispersion forces are present among all the particles.
2. DIPOLE-DIPOLE FORCES
(i) Dipole-dipole forces operate between the molecules possessing permanent dipole. Ends of the dipole possess “partial charges” and these charges are shown by Greek letter delta ().
(ii) Partial charges are always less than the unit charge () because of electron sharing effect. The polar molecules interact with neighbouring molecules.
(iii) This interaction is weak as compared to ion-ion interaction because only partial charges are involved.
(iv) The interaction energy decreases with the increase of distance between the dipoles. It is also proportional to where ‘r’ is the distance between polar molecules.
(v) Besides dipole-dipole interaction, polar molecules can interact by London forces also.
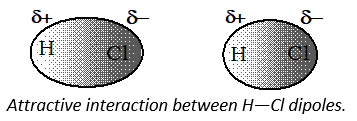
(vi) The cumulative effect of both the interactions is the total increase of intermolecular forces in polar molecules. The figure shows electron cloud distribution and attractiveinteractions between H—Cl dipoles.
3. DIPOLE-INDUCED DIPOLE FORCES
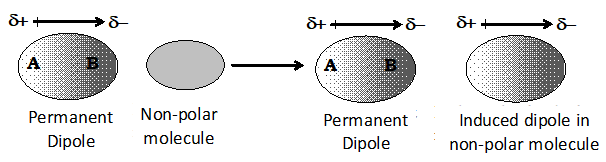
(i) This type of attractive forces operate between polar molecules having > 0 and the non-polar molecules having = 0.
(ii) Permanent dipole of the polar molecule induces dipole on the electrically neutral molecule by deforming its electron cloud.
(iii) The interaction energy is proportional to where r is the distance between two molecules. Induced dipole moment depends upon the dipole moment of the permanent dipole and the polarizability of the electrically neutral molecule.
(iv) Molecules of larger size can be easily polarized. Higher polarizability increases the strength of attractive interactions.
(v) There is a cumulative effect of dispersion forces and dipole-induced dipole interactions
4. HYDROGEN BONDS
i) This is a special type of dipole-dipole interaction operating between the molecules in which hydrogen atom is covalently bonded to a highly electronegative atom such as fluorine (F), oxygen (O) or nitrogen (N).
ii) The bond pair of electrons forming covalent bond is displaced towards electronegative atom.
iii) When solitary electron of H atom lies away, it behaves almost as a bare proton and exerts a strong electrostatic force of attraction on the electronegative atom of the other molecule in its vicinity. This interaction is represented by a dotted line and is called hydrogen bond.
….H — F…..H — F……H — F…..
iv) Energy of hydrogen bond varies between . This is very significant amount of energy, therefore hydrogen bonds are powerful force in determining the structure and properties of many compounds.
v) Strength of hydrogen bond is determined by the columbic interaction between the lone-pair electrons of the electronegative atom and the hydrogen atom.
vi) Formation of hydrogen bond is depicted as follows:
Note:
(i) Intermolecular forces which we have discussed so far, are all attractive forces.
(ii) Molecules also exert repulsive forces on one another. When two molecules are brought into close contact with each other, the repulsion between the electrons and between the nuclei in the molecules comes into play.
(iii) Magnitude of the repulsive forces rises very rapidly as the distance separating the molecules decreases. This is why liquids and solids are very hard to compress. In these states molecules are already in close contact, therefore they resist further compression.
THERMAL ENERGY
Thermal energy which is also called heat energy, is largely responsible for the movement of particles in matter. It is directly proportional to the temperature of the substance.
It is the measure of kinetic energy of the particles of the matter which in turn is responsible for particle movement. Higher the temperature of substance is higher will be the thermal energy of its molecules and consequently more vigorous and rapid will be the molecular movement. The particle movement is also called thermal motion.
INTERMOLECULAR FORCES Vs. THERMAL INTERACTIONS
We have learnt that intermolecular forces tend to keep the molecules close together but thermal energy of the molecules tends to keep them apart and randomize them. The three states of matter are assumed to be the resulting balance between intermolecular forces and thermal energy.
In solids, the molecular interactions are very strong but the molecular motion is restricted to oscillatory or vibratory movement about their mean position. The molecules possess low thermal energy and, therefore, cannot break free from mutual attraction. When we heat the solid, thermal energy gradually increases which weakness the intermolecular forces and causes them to move apart. When the average distance between the molecules increases beyond cm, the solid melts into liquid.
In liquid state, a fine balance exists between attractive forces and thermal energy, so that molecules can break away from one another and at the same time get attracted while approaching the other molecules. Further increase in temperature results in further increase in the thermal energy and ultimately a state reaches when the molecules fall apart and behave almost as independent entities. This state is referred to as gaseous state.
In gaseous state, the molecular interactions are very weak. The molecules do not cling together like those in liquids or solids unless the thermal energy of the gas is reduced by lowering the temperature of the gas. Decrease of thermal energy causes molecules to come close and they gradually develop intermolecular attraction till the gas condenses into liquid first and finally into solid state. It may be noted that gases do not liquefy by compression only through compression also causes molecules to come close. For condensation of gas into liquid we need to decrease the thermal energy also. Predominance of thermal energy and molecular interaction of a substance in three states is shown in figure.
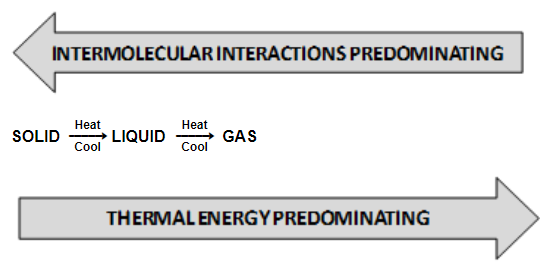
Illustration -1
Match the following
State of matter Void distance
1) Solid i) 10–7 to 10–5m
2) Liquid ii) 10–5 cm
3) Gas iii) 10–8 cm
Choose the option:
(A) 1→ i, 2 → ii, 3 → iii (B) 1 → iii, 2 → ii, 3 → I
(C) 1 → ii, 2 → i, 3 → iii (D) 1 → iii, 2 → i, 3 → ii
Solution: D, 1 → iii, 2 → i, 3 → ii
Illustration -2
Assertion (A): The melting and boiling points are more, if the inter molecular forces are more.
Reason (R): Greater are the intermolecular forces, greater is the force required to break the bonds.
(A) Both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
(B) Both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.
(C) Assertion is correct and Reason is incorrect.
(D) Assertion is incorrect and Reason is correct.
Solution: A
Both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
Illustration -3
Dispersion forces are also called London forces, because
(A) The forces were first identified in London.
(B) The forces were first identified by German Physicist Fritz London.
(C) The magnitude of the forces was first calculated by Fritz London.
(D) All the above.
Solution : C
The magnitude of the forces was first calculated by Fritz London.
Illustration -4
The interaction energy between two molecules interacting with dipole induced dipole forces is E. If the distance between them is doubled, then the energy becomes
(A) E (B) (C) 8E (D)
Solution : D
Introduction:
In general chemistry (Atomic structure, chemical bonding, etc.) we deal with the properties concerned with a single particle of matter, such as
Atomic size, Ionisation enthalpy, Electron gain enthalpy, Molecular structure and shape.
Majority of the observable/measurable features of chemical substances we come across in everyday interaction are bulk properties.
The properties linked with a group of a very large number of representative particles of matter are called bulk properties. The following examples illustrate the bulk properties:
An individual molecule of water (a liquid at room temperature) does not boil but the collection of its molecules (bulk) boils.
A single molecule of water is never an ice, the liquid or the steam, but the bulk of water can exist as ice (a solid), can exist as liquid we drink, or can exist as steam (water vapour).
Single molecules of water do not wet the surface but the bulk has wetting properties.
Ice, liquid water and steam differ very much in their physical properties, but in all the three states of water, chemical composition remains the same.
Matter on earth exists in 3 different states, solid, liquid and gas. Although the huge majority of the substances on earth are solids, of the earth’s surface is covered by a single liquid (); and throughout our life on the earth we remain immersed in the ocean of air (the earth’s atmosphere) which is composed of , Ar and other gases.
Temperature and pressure decide whether a substance is a solid, a liquid or a gas under normal conditions.
Why Three States of Matter?
By examining the “microscopic structure” of matter i.e. the arrangement of the atoms, molecules, or ions of which a substance is composed, we conclude that the 3 states of matter are the end result of a balance between two opposing tendencies: thermal energy which acts to keep atoms, molecules or ions apart, and the interparticle interaction energy which acts to bring them together.
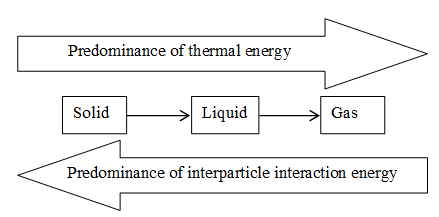
For convenience, in the following discussions we shall use the word molecule to describe all species including atoms or ions, that are the basic units of structure of substances.
Molecules tend to separate because they are in constant motion called thermal motion. Thermal energy, responsible for this motion, is simply the internal kinetic energy of a substance (i.e., the energy arising from motion of its molecules). When we say that the thermal energy of a substance increases, we mean that there is increased motion of its molecules. Thermal energy is directly proportional to the temperature of the substance and hence is the measure of average kinetic energy of the molecules of the substance. Most forms of energy tend to change into thermal energy. In fact, any other type of energy can be converted completely into thermal energy.
The tendency to separate is counteracted by intermolecular interactions which become stronger as molecules come closer to each other. If two molecules at a relatively high temperature approach each other, their thermal motion is great enough to overcome the attractive force between them, so the molecules remain apart. If the temperature is lower, the thermal motion of the two molecules is not great enough to overcome their mutual attraction, and they “stick” together.
Features of the states of Matter:
The most significant aspect of a gas; is that its molecules move freely and in a completely random arrangement in space. A substance exists in the gas phase when the temperature is high enough for thermal motion to overcome the intermolecular attractions. Other characteristics of a gas are:
i) A gas has mostly empty space, because its molecules are widely separated.
ii) A gas has no definite shape or volume, because its molecules are in constant free and random motion. It assumes the shape and volume of its container.
iii) A gas is expansiblee. even a small amount expends to fill a large container.
iv) A gas is compressiblee. even a large amount can be squeezed into a small container.
When thermal motion is not great enough to overcome the intermolecular attractions, molecules stick together in a condensed phase. One such phase is the liquid state.
Thermal motion in the liquid state is still substantial, but the intermolecular attractions prevent a completely random arrangement of the molecules. Other attributes of a liquid are:
A liquid does not have a definite shape. Usually, it takes its shape from the portion of the container it occupies.
A liquid does have a definite volume.
If the temperature of a liquid is lowered a point is reached at which thermal motion becomes relatively unimportant. The molecules arrange themselves in a way that maximizes the intermolecular attractions. The partial randomness of the liquid phase is replaced by a more ordered arrangement. This condensed phase is called the solid state, the molecules generally are closer together than in the liquid state. Thus, the solid phase of a substance is generally denser than the liquid phase. Other traits of the solid are:
They are rigid and have definite shape.
They maintain their volume independent of the size or shape of the container in which they are placed.
They are nearly incompressible.
They diffuse very-very slowly as compared to gases or even liquids.
The Gaseous State::
This is the simplest state of matter due to the fact that intermolecular interactions are negligible. Only 11 elements exist in the gaseous state under normal conditions of temperature and pressure.
The gaseous state is characterized by the following physical properties:
The volume and the shape of gases are not fixed. Gases assume volume and shape of the container.
Gases mix evenly and completely in all proportions without any mechanical aid.
Gases have much lower density than the solids and liquids.
Gases exert pressure equally in all directions.
Gases are highly compressible.
Temperature, pressure, volume, amount, viscosity, specific heat are some of the many measurable properties of gases. The most important properties of gases are however, the temperature, pressure, volume and amount as these four interdependent variables describe the state of any gas.
Temperature:
It is that property of the substance that decides the direction of flow of heat energy when the substance comes in contact with another substance through a thermally conducting wall.
Temperature scales:
The fixed points on the Celsius or centigrade scale, devised by Anders Celsius are exactly 00C and 1000C for the freezing and boiling points, respectively, of pure water at 1 atm pressure. This range is divided into 100 equal parts, each division corresponds to C.
The lowest temperature theoretically possible is logically called the absolute zero of temperature. A scale of temperature based on this choice of zero is known as the absolute scale or the Kelvin scale, as this scale was first suggested by Lord Kelvin.
Since the absolute zero of temperature is , the relation between the Kelvin scale and the Celsius scale is
….. (1)
where T is the Kelvin temperature and t is the Celsius temperature.
Note that the temperatures on the Kelvin scale are indicated simply by writing the letter K. By convention, the degree sign () is not used while expressing temperatures on the Kelvin scale. The Kelvin scale is also called the thermodynamic scale of temperature, is used in all scientific work.
The fixed points on the Fahrenheit scale, named after G.D. Fahrenheit, are exactly 00F for the freezing point of a saturated NaCl – water solution and for the normal boiling point of pure water.
Illustration1: Derive an Equation relating the Fahrenheit and Celsius temperature scales, if the freezing point of a saturated NaCl – water solution is .
Solution: Data given is
Find the relative size of the respective degrees by comparing the number of degrees for the same interval:
Derived relation between the two scales should be
where K corrects for the difference between the zero points of the scales. This constant can be evaluated by substituting the freezing – point (or boiling – point) temperature:
The desired relation is thus …… (2)
Pressure:
It is defined as the force exerted normally by a gas on a given unit of area of surface with which the gas is in contact.
…… (3)
In a closed container, pressure is exerted by the gas on the walls of the container.
Evangelista Torricelli (1608 – 1647), a student of Galileo, first measured the pressure exerted by the atmosphere. He used the height of a column of mercury in the simple device called the barometer to measure atmospheric pressure.
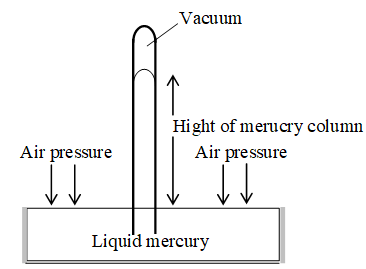
A decrease in atmospheric pressure causes a drop in the height of the column cuticle on increase in atmospheric pressure increases its height.
Thus, air pressure can be measured by measurement of the height of the column of mercury, as discussed below.
Let, Height of mercury column = h cm
Area of cross section of Hg = A
Density of mercury at room temperature = d g
Force (F) exerted by the mercury column
= (Mass of Mg column) (Acceleration due to gravity)
= (Volume of Hg column) (density of Hg) (Acceleration due to gravity)
= (Area of Hg column) (Height of Hg column) (density of Hg column).
(Acceleration due to gravity) = (A ) (h cm) (d g) (g )
F = A.h.d.g.
Substituting this result in Equation (3), we get
… (4)
Thus, the height of a column of liquid supported by atmospheric pressure depends in part on the density of the liquid. At sea level, the atmosphere can support a column of mercury 76cm (0.76 m) high. Commonly used unit for expressing pressure include:
The SI unit of a Pascal (Pa), which is equal to a Newton meter .
The most commonly used unit of an atmosphere (atom), which is the pressure exerted by the atmosphere of the sea level. Also called standard (or normal pressure), it is defined as the pressure exerted by exactly 76cm column of mercury at . Thus
A torr; which is equal to the pressure exerted by a one mm column of mercury. It is used in the field of high vacuum. Thus,
1 torr = 1mm Hg = 133.3224 Pa
760 torr = 1atm
A pound–per–square–inch, which is equal to
A bar, unit of pressure in the c.g.s. system.
For convenience, mercury is used in most liquid level barometer.
To measure the pressure of a gas in a closed vessel, we use a device called manometer which works on the same principle as a barometer. It is a simple device with a horizontal arm and a U tube carrying mercury (or any other suitable liquid). The vessel containing the gas is connected to the horizontal arm of the manometer.
In a manometer, the pressure of a gas is related to the difference between the height of two columns of mercury. Since the atmospheric pressure is known, the gas pressure can be determined by measurement of h, the difference in levels of mercury in the two arms of the tube. If h = 0, then the gas pressure is equal to atmospheric pressure. Thus, the gas pressure is the pressure of the atmosphere plus/minus the pressure exerted by the height (h) of the mercury, i.e.
Illustration 2: Calculate the height of a column of water equivalent to one atmosphere, if there are 760 torr in an atmosphere.
Solution: According to Equation (4), the heights of various liquid columns that are equivalent to the same pressure are inversely proportional to the densities of the liquids, thus or,
Volume, V:
The volume of a gas is the volume of the container holding the gas. Volume has the unit of (length)3, thus, in SI system, it has units of cubic meter (). Smaller volumes are expressed in cubic centimeter () or cubic decimeter (). Litre (L), a non SI unit is also used for measurement of volume.
Amount of substance, n:
In SI system, unit of amount of a substance is mole (mol). The amount of the gas (number of moles of gas) can easily be calculated by dividing its mass (m) by its molar mass (M, mass of one mole of gas) :
…..(6)
First weigh the empty container and then get the mass of the gas by weighing the filled container.
The Ideal Gas and Gas Laws:
Regardless of their chemical composition, all gases have some properties in common. To some degree, all gases follow certain simple laws of behavior. These laws are relationships between measurable properties of gases. Interdependence of these variables leads to the formulation of gas laws.
An ideal gas or perfect gas can be imagined as a gas whose behavior can be explained completely by these ‘ideal’ laws. The behavior of any real gas only approximates that of an ideal gas. The closeness of the approximation depends on:
the chemical composition of a real gas and, the conditions under which the gas is studied .
At sufficiently low pressures (at atmospheric pressure or lower) and sufficiently high temperatures (at temperatures somewhat higher than that at which a gas condenses), all real gases have been found to obey (within good approximation) all the ‘ideal’ gas laws.
Boyle’s Law:
Proposed by Robert Boyle (1662), it states that the volume (V) occupied by a fixed amount (i.e., number of moles, n) of an ideal gas is inversely proportional to the pressure (P) applied on it, provided the temperature (T) is kept constant.
In mathematical terms, for a fixed amount of gas under isothermal (constant temperature) conditions:
…..(7)
or …..(8)
i.e., …..(9)
or, PV = constant (k). …..(10)
where P is pressure, V is volume and k is a proportionality constant whose value depends upon
the amount (n) of the gas,
the temperature (T) of the gas and,
the units in which P and V are expressed.
In comparing the properties of a given amount of an ideal gas at a given temperature under two conditions, which we may call the initial and final states, we may write the following Equation, that is more suitable for calculations:
or, …..(11)
or, …..(12)
where represent one set of pressure and volume conditions, and represent another set of conditions for the same amount of gas at the same temperature. A given subscript 1 or 2, refers to a given state of the gas; 1 usually refers to an initial state and 2 to a final state.
Knowing any three variables, the fourth can be computed. Any unit for pressure and volume can be used provided it is same for .
There are ways of graphical representation of Boyle’s law.
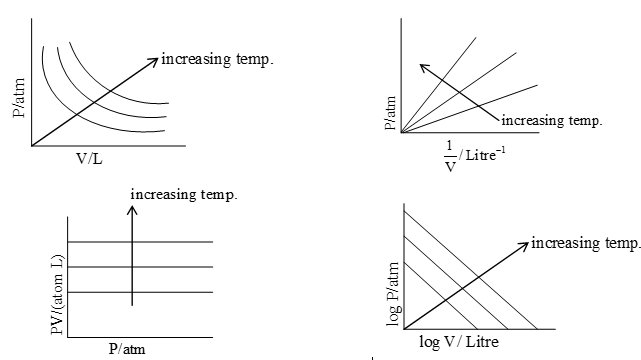
Figure (a) is the graph of gas pressure (P) versus gas volume (V) at different temperatures. The value of constant (k) for each P–V curve (a rectangular hyperbola) is different because for a given amount of gas, it varies only with temperature. Each curve corresponding to a different constant temperature is known as an isotherm (constant temperature plot).
Figure (b) represents the graph between P and 1/V. It is a straight line with positive slope and zero intercept.
Figure (c) represents the plot of PV against P. It is a straight line parallel to the X-axis.
Figure (d) is a plot of log P versus log V. It is a straight line with negative slope.
Illustration 3: A cylinder whose volume is 2.0 L is filled with helium (He) at a pressure of 5.0 atm. If helium is used to fill a balloon to a pressure of 1.0 atm at the same temperature, find the volume of the expanded balloon.
Solution: Boyle’s law is applicable as the amount and temperature of gas are unaltered.
We can find the unknown, , by using Equation (11). Substitution gives
Illustration 4: A sample of gas at room temperature is placed in an evacuated bulb of volume 0.4L and is found to exert a pressure of 25 kPa. This bulb is connected to another evacuated bulb whose volume is 0.6L. If the gas is allowed to fill both bulbs, find the new pressure of the gas at room temperature.
Solution: Given information at constant n and T:
Boyle’s law gives
Illustration 5: When a given amount of a gas is compressed at a given temperature, the same numbers of molecules occupy a smaller space i.e., gas becomes denser at high pressure. Find a relationship between density and pressure of a gas using Boyle’s law.
Solution: By definition, density (d) is related to the mass (m) and the volume (v) by the relation:
Boyle’s law gives
PV = k or
Putting this value of V in the density Equation, we obtain
where . This shows that at a constant temperature, density is directly proportional to the pressure of a gas
Charles’ and Gay–Lussac’s law:
Two French physicists, J.A. Charles and J.L. Gay-Lussac studied the relationship between the volume and the temperature of gases. They found that for a fixed amount of a gas at constant pressure, volume increases on heating and decreases on cooling. Charles found that gases expand by the same fractional amount of their original volume for equal increases in temperature. Gay Lussac worked out that for every change in temperature, all gases change by of their volume at .
These observations, based on the Celsius temperature scale, can be expressed as:
…..(13)
where Vt is the volume of the gas at a temperature of , V0 is the volume of the gas at , and t, the temperature of the gas on the Celsius scale, is also the number of degrees away from . Positive sign will be used for heating while negative sign will be for cooling. Charles law may thus be stated as the volume of a fixed amount of an ideal gas at constant pressure increases or decreases by of its volume at for each rise or fall in temperature.
If we plot Equation (13), we obtain a straight line.
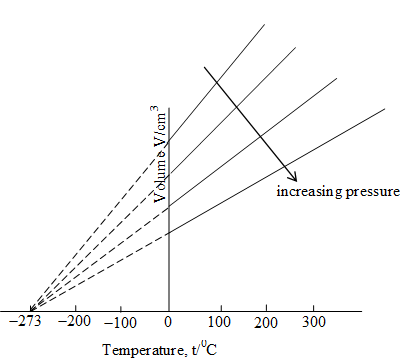
Fig: The relationship between gas volume and Celsius temperature
Each line of the volume versus temperature graph is called isobar. These plots obtained at different pressure when extrapolated to zero volume intersect the temperature axis at (more accurately at ).
This implies that the volume of an ideal gas at any given pressure will be zero at and below this its volume would become negative. Thus, is called the absolute zero and is the lowest possible temperature because negative values of volumes are not possible physically.
The volume of a real gas has never been reduced to zero because every real gas condenses first to a liquid and then to a solid well before , the absolute zero, is reached. Practically, zero gas volume and 0K can never be achieved.
A simpler relationship between temperature and gas volume can be formulated by replacing the Celsius temperature scale by the Kelvin temperature scale or absolute temperature scale, in which the interval of temperature (the degree) is the same Celsius degree but the zero point is below the Celsius zero point.
Equation(13) can be written considering only the heating of gas,
Writing in the Equation (14) we get
Writing a general Equation gives
Thus, for a fixed amount of ideal gas under isobaric (constant pressure) conditions:
Thus, …..(16)
where V is the volume, T is the absolute temperature and is the proportionality constant. The value of constant depends upon
the amount of the gas,
pressure of the gas, and
the units in which volume V is expressed.
Equation (16) is a simple direct proportionality and a more convenient expression of the Charles’ and Gay-Lussac’s law or simply Charles’ Law, which states that at constant pressure, the volume of a fixed amount of an ideal gas varies directly with its absolute temperature.
Equation (15) expresses the same relationship in a form more suitable for calculations. Here represent one set of volume and absolute temperature conditions for a given amount of gas and another set for the same amount of gas at the same pressure. The following figure shows this relationship graphically:
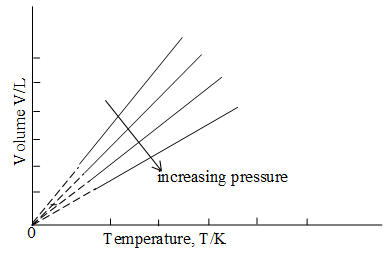
Illustration 6: Equation (16) can be stated as . Plot this relationship graphically.
Solution: Since this Equation can be correlated with the linear Equation y = mx + c, the plot between logV and logT is a straight line with positive slope and a non-zero intercept on the y-axis.
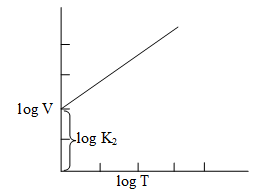
Illustration 7: Find the decrease in volume, when the temperature of 640mL of air decreases fro at constant pressure.
Solution: Since the pressure and amount of air remain constant, Charles’ law is applicable.
First convert the Celsius temperatures to the Kelvin scale:
Equation (15) gives
Thus
The decrease in volume of air is
Gay Lussac’s law:
French physicist, Joseph Louis Gay – Lussac investigated the relationship between pressure and absolute temperature for a fixed amount of gas at constant volume. He found that volume remaining constant, pressure of a fixed amount of an ideal gas varies directly with its absolute temperature. This is known as Gay Lussac’s law.
Mathematically
The value of constant depends upon
the amount of gas, the volume of gas, and the units in which pressure is expressed.
Pressure versus absolute temperature graph for an ideal gas is shown in the following figure. Each line of this graph is called an isochore (constant – volume).
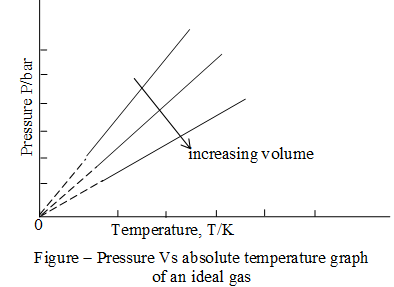
Illustration 8: A steel tank contains carbon dioxide and at pressure of 12.0 atm. Find the internal gas pressure if the tank and its contents are heated to .
Solution: At constant volume and amount of gas, Gay – Lussac’s law gives:
Combined Gas law:
The Boyle’s and Charles’ laws can be combined into a single relationship between the three variables P, V and T. Suppose we have a fixed amount of a gas with volume , pressure and absolute temperature , and that these are changed to . Imagine that the change is carried out in 2 steps:
Step (1): If the temperature is kept at while the pressure is charged to Boyle’s law applies. If the volume of the gas after this step is takes as . (i means intermediate), then
Step (2): Now the pressure is kept constant at while the temperature is changed from T1 to . This changes the volume from .
Applying Charles’ law:
Substituting the value of found from Boyle’s law into the above expression gives the desired single relationship:
…..(19)
Equation (19) called the combined gas law, connects two sets of pressure, volume and temperature conditions for any given amount of an ideal gas. Knowing any five variables, the sixth can be calculated. Equation (19) can also be read as: The quantity PV/T is a constant for a given amount of an ideal gas. Thus
…..(20)
The value of constant, depends upon
the amount of gas, the units in which P and V are expressed.
Since many gas calculations are concerned with determining a new volume given an old volume, the combined gas law is often written as (for a fixed amount).
…..(21)
This expression indicates that the volume of a given amount of gas varies directly with the absolute temperature and inversely with their pressure. Notice that, while must be in Kelvins, any convenient pressure unit may be used for and any convenient volume unit may be used for .
Illustration 9: An automobile tyre is inflated to a total pressure of 190 kPa with air at 20. After 5 hours of driving, the volume of the tyre has increased by 5.0% and the total pressure is 210 kPa. Assuming ideal gas behavior, calculate the temperature of the air inside the tyre.
Solution: List all the data in suitable units:
Combined gas law gives .
Thus
Canceling the V gives .
Illustration 10: A balloon containing helium (He) gas at a temperature of 295K and a pressure of 1.0 atm has a volume of 91L. When the balloon reaches an altitude of 20 km, the pressure is 0.083atm and the temperature is 225 K. Find the volume of the balloon at that altitude.
Solution: List the given data
Substitution into Equation (24) gives
Density of an Ideal Gas:
As the volume of a given mass of gas increases, the mass per unit volume (i.e., the density) decreases proportionately. Therefore, the density (d) of an ideal gas varies inversely with its volume:
using the combined gas law, Equation (24), gives
Standard conditions (S.T.P.):
As both the volume and density of any ideal gas are affected by changes of temperature and pressure, it is convenient to define, a standard set of conditions, for an ideal gas for purposes of comparison. These conditions are referred to as standard temperature and pressure (S.T.P.) conditions. These days standard temperature and pressure means temperature and 1 bar ( pascal) pressure. These values approximate freezing temperature of pure water and atmospheric pressure of sea level. At STP molar volume (i.e., volume of one mole) of an ideal gas or a combination of ideal gases is .
The previous standard is still often used. In this definition S.T.P. denotes the same temperature of , but a slightly higher pressure of 1 atm (101325 pascal). One mole of any ideal gas or a combination of ideal gases occupies 22.413996 L of volume at this S.T.P. conditions.
Standard ambient temperature and pressure (SATP), conditions are also used in some scientific works. SATP conditions mean 298.15K () and 1 bar (exactly Pa). At SATP, the molar volume of an ideal gas is .
Illustration 11: A sample of nitric oxide (NO) gas occupies a volume of 3.2L at a temperature of 298K and a pressure of 0.5 bar. What is the volume of the sample at STP?
Solution: STP means 273K and 1 bar. Listing the given data:
Applying the combined gas law, Equation (21) gives
Avogadro’s law:
In 1811, Italian scientist Amedeo Avogadro proposed a remarkable relationship to explain gas behaviour. He said that at a given pressure and temperature, the number of molecules of the ideal gas in any sample depends only on the volume of the sample, not on the nature of the gas. This relationship, now called Avogadro’s law, can be stated as:
Equal volumes of all ideal gases (or vapors) under identical pressure and temperature conditions contain equal numbers of molecules.
This implies that at constant T and P, the volume V of an ideal gas is directly proportional to the number of molecules of the gas or more appropriately to its amount in moles, n. Mathematically we have
…..(22)
or, in a form more suitable for calculations:
…..(23)
Number of moles (n) of a gas can be calculated by Equation (6).
Illustration 12: A balloon whose volume is 5.0 L contains 7.0g of nitrogen (2) gas. What mass of hydrogen () gas must be added to the balloon to expand its volume to 10L at the same temperature and pressure.
Solution: Listing the data gives
Avogadro’s law gives
mol, the total amount of gas required for the volume to be 10L.
Therefore,
Mass of hydrogen gas to be added:
The Ideal gas Equation:
It provides a complete description of the state of an ideal gas and is thus one of the most useful relationships in chemistry. It combines in one relationship the three gas laws: the laws of Boyle, Charles, and Avogadro.
Boyle’s law: V [n, T constant]
Charles law: V T [n, P constant]
Avogadro’s law: V n [T, P constant].
Thus,
or PV nT
or PV = nRT …..(24)
which is called the ideal gas Equation. R is the conventional symbol for the proportionality constant, which is called the universal gas constant, because it is same for all the ideal gases. It is also called the molar gas constant because
….. (25)
Using ideal gas Equation, the numerical value of the universal gas constant can be determined. This value depends on the units of measurement chosen for P and V. While T is always expressed in Kelvins and n is always expressed in moles, there is a choice of units for P and V.
Under a pressure of 1 bar (exactly Pascal) and at temperature 273.15 K, the volume of 1 mol of an ideal gas is . Substituting these values in the Equation (24) we get
Nm = J.
If p is expressed in dynes cm-2, V in cubic centimeters, we get
At STP conditions used earlier ( and 1 atm pressure), value of R is 0.0821L atm [1 litre = 1000 mL, 1 atm = 760 mm Hg].
Since, the ideal gas Equation describes the state of any ideal gas, it is also called Equation of state. There are four unknowns in the ideal gas Equation. When the value of any three are specified, the value of the fourth is fixed.
Illustration 13: Find the volume of one mole of an ideal gas at STP.
Solution: Listing the data gives
Ideal gas Equation gives
Thus,
V = 22.71 L
One can use the ideal gas Equation to solve a large number of problems, if the problems specify (or imply) the values of any three of the four variables in the Equation.
Illustration 14: A rabbit is placed in a gas chamber that is filled with and contains some KOH to absorb The volume of the bulb, after we allow for the rabbit and the KOH, is 1.02L. The pressure of the is 0.953 atm, and the temperature of the gas is . After 2 hours, the pressure in the bulb drips to 0.774 atm. Find the mass of consumed by the rabbit.
Solution: Assuming that the consumption of is the only reason for the drop in pressure, the pressure of consumed is 0.953 atm – 0.774 atm = 0.179 atm. Listing the other data gives: V = 1.02 L ; T = (37 + 273)K
Ideal gas Equation gives
consumed.
Molar mass and Density of an ideal gas:
Amount in moles of a sample of a gas is related to the mass of the gas and the molar mass of the gas as:
where ‘m’ is the mass in grams and M is the molar mass in grams per mole.
Substituting this expression for n into the ideal gas Equation gives:
…..(26)
If we investigate a real gas under ideal conditions, we can find the molecular weight of the gas as it is numerically equal to the molar mass, by making the approximate measurements and using Equation (26).
Illustration 15: A sample of an unknown liquid having mass 1.35g is introduced into an evacuated bulb of volume 502. After all of the liquid is vaporized, the gas pressure is 0.477 atm at 333K. Assuming ideal gas behavior, find the molecular mass of the liquid.
Solution: Listing the given data in suitable units gives
R = 0.0821 L atm/K.mol = 0.502L
Using Equation (25), we get
The molecular mass of the unknown liquid is 154, since it is numerically equal to the molar mass.
The density d of a gas is expressed as the mass in grams per litre of the gas:
where m is the mass in grams and V is the volume in litres. Equation (25) can be rewritten as:
…..(27)
which expresses the relationship between the molar mass and the density of an ideal gas at a given temperature and pressure.
Illustration 16: The density of an unknown gas at STP is 9.91g/L. Find the molar mass of the gas.
Solution: Listing the data gives
d = 9.91g/L ; P = 1 bar ; T = 273K ; R = 0.083 bar L/Kmol
Equation (27) gives
Another way: AT STP, one mole of an ideal gas has mass equal to its molar mass and occupies a volume of 22.71L.
Therefore,
Illustration 17: The thermal decomposition of potassium chlorate once was a standard laboratory method to produce oxygen gas:
A quantity of is heated. If oxygen gas produced is collected in a balloon at 1.0 atm and 300k, find the mass of reacted, provided the volume of the balloon is found to be 0.79L.
Solution: Listing the data gives
P = 1.0 atm V = 0.79L
T = 300 K R = 0.0821 L atm/K mol
Ideal gas Equation gives
Mass of reacted according to the chemical Equation:
mass of
Dalton’s Law of partial pressure:
Formulated by John Dalton in 1801, it states that the total pressure exerted by a mixture of non-reacting ideal gases is equal to the sum of the partial pressures of the individual gases, provided that all the measurements are done at the same temperature and volume.
Thus, the total pressure, pt, of a mixture of ‘S’ non reacting ideal gases is given by
….. (28)
where is the partial pressure of component ‘i’ in the mixture.
The pressure exerted by the individual gas in a mixture of gases is called the partial pressure of the gas. It is defined as the pressure exerted by the gas if it present alone in the same container at the same temperature. It can be calculated by the ideal gas Equation.
…..(29)
where is the number of moles of the component i in the mixture, V, the volume of the container and T its absolute temperature.
Dalton’s law has a broad range of applications. It is useful in the study of systems where substances in the gas phase are in contact with condensed phases of other volatile substances. Once such system which is frequently encountered deals with the collection of the gases over a liquid.
If a gas is collected over a volatile liquid, such as water, a correction is to be made for the amount of water vapour present with the gas. A gas collected over water is saturated with water vapor, which occupies the total gas volume and exerts a partial pressure. The partial pressure of the water vapor is a constant for each temperature and is independent of the nature or pressure or even volume of the confined gas. This definite value of the vapor pressure of water, called the aqueous tension, may be found tabulated as a function of temperature in reference books.
According to Dalton’s law, to calculate the partial pressure of the gas collected by displacement of water, the vapor pressure of water (at the temperature of the experiment) must be subtracted from the total pressure (of the gas plus water vapour) i.e.
When a gas is collected over mercury, it is not essential to make a correction for the vapour pressure of mercury, which is negligible at ordinary temperatures.
Illustration 18: A 2.5L flask contains 0.25 mol each of sulphur dioxide () and nitrogen () gas at . Find the partial pressure exerted by each gas and also the total pressure.
Solution: Equation (27) gives
Similarly , as it has the same number of moles.
Applying Dalton’s law gives
It can also be calculated by the ideal gas Equation.
Alternatively, the partial pressure of component i in the mixture can be calculated from the total pressure, and the molar composition of the mixture.
…..(28)
where , the mole fraction for component i, is defined as
…..(29)
Illustration 19: A neon-dioxygen mixture contains 167.5g neon and 70.6g dioxygen. If pressure of the mixture of gases in the cylinder is 25 bar. What is the partial pressure of neon and dioxygen in the mixture.
Solution: Calculate the number of moles:
Now calculate the mole tractions using Equation (29)
Alternately
Since the sum of the mole fractions is always one
Finally, calculate the partial pressure using Equation (28)
Alternatively
Illustration 20: The hydrogen gas can be collected over water. The volume of the gases ( vapor) is found to be 0.35L. If the total pressure of gases is found to be 1.041 atm and the aqueous tension of water at 299K is 0.0332 atm, find the mass of hydrogen () gas collected.
Solution: Find the by using Dalton’s law:
Applying ideal gas Equation gives
or
Graham’s law of Diffusion and Effusion:
If we introduce a gas into a container that already holds another gas, for example, by opening a stopcock it eventually spreads through out the container.
The process by which a gas spreads throughout a space, occupying the whole available volume, irrespective of other gases present in the space is called diffusion.
If a small hole (an orifice of molecular size) is made in the wall of the container holding a gas, and if the hole leads to a vacuum, the gas in the container will leak out through the hole. This phenomenon in which gas molecules leak out under pressure gradient one by one through an orifice of molecular size is called effusion.
The process of effusion is always followed by the process of diffusion. The basic difference between diffusion and effusion is the fact that in the former case molecules spread out in bulk while in the latter case molecules leak out one by one. Also, the former occurs without pressure gradient but the latter happens only under a pressure gradient.
Diffusion, the process by which molecules (or other particles) mix because of their random thermal motion, occurs not only in gases but also in liquids, solutions, and even solids.
Thomas Graham observed that lighter gases diffuse/effuse out faster than the denser gases. In, 1831, he proposed the law of diffusion and effusion, which states that under identical conditions of temperature and pressure, the rate of diffusion or effusion of an ideal gas is inversely proportional to the square root of its density.
Mathematically
where r is the rate of diffusion (or effusion), d is the density of the gas under consideration and is the proportionality constant.
The relative rates of diffusion (or effusion) of two different gases, A and B, under the same conditions of temperature and pressure, can be expressed as:
…..(30)
where are the rates of diffusion (or effusion) of gas A and gas B, are the densities of these gases.
According to Equation (26), the density of an ideal gas at constant temperature and pressure is directly proportional to its molar mass. Thus, the relative rates of diffusion (or effusion) of two different gases, A and B, under identical conditions of temperature and pressure, can be expressed as:
…..(31)
where are the molar masses of the gases A and B respectively
Depending upon the type of the apparatus used, the rate of diffusion (or effusion) can be calculated as follows:
Case I: …..(32,a)
Case II: …..(32,b)
Case III: …..(32,c)
If two different gases, A and B, diffuse (or effuse) for the same time period, t, then
Thus, …..(33)
If, however, the same volume, V, of two different gases is diffused (or effused), then
Thus, …..(34)
The average distance traveled by a molecule between successive collisions is called the mean free path. The mean free path of a gas is inversely proportional to its, density.
Illustration 21: Compare the diffusion rates of helium and molecular oxygen at the same temperature and pressure.
Solution: Using Graham’s law of diffusion we write
Thus, helium diffuses 2.8 times faster than oxygen.
Illustration 22: A sample of is placed in an effusion apparatus. After 15 min, the pressure in the evacuated portion of the apparatus has risen to 0.21 atm. The 2 is removed from the apparatus and the experiment is repeated with a quantity of at the same temperature. When is the pressure of in the evacuated portion of the apparatus after 15 min?
Solution: The rate of increase in pressure depends on the rate of effusion. The rate of effusion depends on the molar masses of the gases.
Using Graham’s law of effusion, we write
The effuses 2.4 times faster than the . If the pressure of after 15 min is 0.21 atm, then the pressure of after the same period will be
Applications of Graham’s Law:
1. One of the most important practical consequences of Graham’s law is that mixtures of gases can be separated into their pure components by taking advantage of the different rates of diffusion (or effusion) of the components.
Thus, Graham’s law finds an important application in the separation of isotopes.
Based on mathematical expression of Graham’s law, we define a quantity called the separation factor (s) such that
The value of s indicates how well gases 1 and 2 can be separated from each other in a one-stage effusion (or diffusion) process; the larger the separation factor, the more efficient the separation process.
Relatively pure is needed to make an atomic bomb. The natural abundances of the two uranium isotopes are 0.72 percent and 99.28 percent, respectively. Since isotopes of the same element have virtually the same chemical behavior, the problem of separating from the more abundant isotope was formidable indeed. The separation method finally chosen was gaseous effusion.
Uranium can be converted into uranium hexafluoride, , which is easily vaporized above room temperature. The advantage of this compound is that fluorine consists of a single stable isotope, so the separation involves only two species: . Note that differs from by less than 1 percent by mass! The separation factor for these two substances is given by
This is a very small separation factor. But after a second effusion process, the overall separation factor becomes , a slight improvement.
In the particular case of uranium hexafluoride, then, the separation factor for an n-stage process is 1.0043. If n is a large number, say 2000, then it is indeed possible to obtain uranium with about 99 percent enrichment of the isotope. This is essentially what happens.
2. Molecular mass of an unknown gas can be determined by comparing its rate of diffusion (or effusion) with that of a known gas.
3. Diffusion phenomenon is also applied to detect explosive marsh gas () in coal mines [Ansil’s alarm].
The following example shows that measuring effusion rates can help us identity gases.
Illustration 23: A flammable gas made up only of carbon and hydrogen is generated by certain anaerobic bacterium cultures in marshlands and areas where sewage drains. A pure sample of this gas was found to effuse through a certain porous barrier in 1.50 min. Under identical conditions of temperature and pressure, it takes an equal volume of bromine gas (the molar mass of Br2 is 159.8) 4.73 min to effuse through the same barrier. Calculate the molar mass of the unknown gas, and suggest what this gas might be.
Solution: In practice, the rate of effusion of a gas is inversely proportional to the time it takes for the gas to effuse through a barrier – the longer the time, the slower the effusion rate. Using graham’s law, we can write
where are the times for effusion for gases 1 and 2, respectively.
where M is the molar mass of the unknown gas. Solving for M, we obtain
Since the molar mass of carbon is 12.01g and that of hydrogen is 1.008g, the gas is methane ().
Kinetic Molecular Theory (KMT) of Gases:
Simply the kinetic theory of gases was developed mainly by Clausius, Ludwig Eduard Boltzmann and James Clerk Maxwell. The theory, which is strictly meant for an ideal gas, provides an explanation of observed features (such as Boyle’s law, Charles’ law and Avogadro’s law) of an ideal gas.
It also helps us understand why real gases do not behave like ideal gases. The important assumptions of KMT that can account for these observations are as follows:
1) An ideal gas consists of a large number of particles (molecules or atoms) that are so small and so apart (on the average), that the actual volume of the molecules is negligible compared to the volume of gas.
2) There is no interaction between the particles i.e. they exert neither attractive nor repulsive force on one another except when they collide.
3) The gas particles are not at rest but are in constant straight line motion in random directions with great speeds.
4) During their random motion, the particles of an ideal gas frequently collide with one another as well as with the walls of their container.
5) Collisions of the gas particles (either with other particles or with the walls of a container) are elastic – that is, although energy may be transferred from one molecule to another as a result of a collision, the total energy of all the molecules in a system remains the same at constant temperature (T).
6) Though the kinetic energy of one particular gas particle may vary enormously depending on the nature of the collisions it undergoes, the average kinetic energy of the gas particles, is proportional to the temperature of the gas in kelvins.
Derivation of the Kinetic Gas Equation:
By making some helpful simplifying approximations about the random motion of gas molecules, we can derive kinetic gas Equation from the ideal model.
Consider an ideal gas in a cubical container. The cube therefore contains a large number of molecules moving randomly. Let us assume that:
the length of each side of the cube = l cm
the number of gas molecules in the cube = N
the mass of each gas molecule = m gms
the root mean square (RMS) speed of the gas molecule = C
the volume of the gas (volume of the cube) = V =
The root mean square is a rather unusual way of expressing an average value. The average of such quantities as 1, 2, 3, 4 and 6 would most commonly be taken as the sum of the quantities divided by five i.e. 16/5 or 3.2. This is correctly described as the arithmetic mean of the quantities.
To get the root mean square of the quantities, take the root of the mean of the squares of the quantities:
The root mean square speed of gas molecules, C, is therefore obtained from the expression (the speeds of the gas molecules are not all equal):
Where N is the total number of gas molecules concerned and are their individual speeds.
Deduction of Gas Laws from Kinetic Gas Equation:
Let us see how the kinetic molecular model explains the different gas laws:
i) Boyle’s law: The kinetic molecular model assumes that pressure exerted by a gas results from the impact of its molecules on the walls of the container. The more the frequency of collisions, the higher would be the pressure. The frequency (rate), or the number of molecular collisions with the walls per second, is proportional to the number density (that is, number of molecules per unit volume, N/V) of the gas. Decreasing the volume of a given amount of gas increases its number density and hence its collision frequency (rate). For this reason, the pressure of a gas is inversely proportional to the volume it occupies. We have already derived that
Kinetic energy, the energy of motion, is . We can rewrite kinetic gas equation to relate it to kinetic energy by introducing the factor :
…..(44)
Since m is the mass of a molecule of ideal gas and is the average of the squares of the velocities (speeds) of all the molecules, the term is the average kinetic energy per molecule of gas. The total kinetic energy of all the molecules, , is the number of molecules N multiplied by the average kinetic energy per molecule, so Equation (44) gives us a simple relationship between PV and the total kinetic energy.
…..(45)
At a given temperature, the total kinetic energy of a sample of an ideal gas is a constant equation (45) is therefore equivalent to Boyle’s law, which states that PV is a constant for a sample of gas at a given temperature.
ii) Charles’ law: Temperature is a measure of the average kinetic energy of the gas particles. The higher the temperature at constant n and P, the faster the gas particles move and the more room they need to move around in order to avoid increasing their collisions with the walls of the container. Thus, volume increases as temperature increases.
According to the kinetic molecular theory, the average kinetic energy of the molecules is proportional to the temperature of the gas in kelvins, that is .
where ‘k’ is a proportionality constant. On substituting this result in the Equation (45) we get .
At constant Pressure (P), we have V = constant. T or V T (P, n are constants). This is Charles’ Law.
iii) Avogadro’s Law: The more particles there are in a gas sample, the more volume the particles need at constant T and P to avoid increasing their collisions with the walls of the container. Thus, volume increases as amount increases.
Another way of stating Avogadro’s law is that at the same pressure and temperature, equal volumes of gases, whether they are the same, or different gases, contain equal numbers of molecules.
Consider equal volumes of two different gases 1 and 2 at the same temperature and pressure. Applying the kinetic gas equation we have
Equating the two, we get
…..(46)
Since temperature (T) is the same for the two gases, their average kinetic energy per molecule will be the same, that is
…..(47)
Dividing Equation (46) by Equation (47), we get
This is Avogadro’ law.
iv) Dalton’s law of partial pressures: It is assumed that there are no attractive (or repulsive) forces between the molecules of a gas. If non-interacting gases are present together, then their molecules do not attract or repel one another. Each molecule behaves independently of all the others in the container. Then, the pressure exerted by one type of molecules is unaffected by the presence of another gas. The pressure of each component in the gaseous mixture depends only upon its amount, or number of molecules present in the container. Consequently, the total pressure of the mixture is given by the sum of individual gas pressures. Consider a gas ‘1’ in a container of volume V. Applying the kinetic gas equation, pressure of the gas ‘1’ is given as
If the gas ‘1’ is replaced by another gas ‘2’ in the same container, then
Suppose that the two gases are non-interacting and are taken together in the same container. If P is the total pressure of the mixture, then
This is Dalton’s law of partial pressures.
v) Graham’s law of diffusion: Average kinetic energy of any gas is same at the same temperature. Therefore of the two gases the one with the lower molar mass will have higher speed, hence it will diffuse/effuse faster. According to kinetic gas equation, we have
Representing the mass of gas by ‘w’, we get
Since the density of a gas, d, is equal to mass/volume, we can write
…..(48)
At constant pressure (i.e. at a given pressure)
since rate of diffusion (or effusion) of a gas is directly proportional to the speed of its molecules, we can say rate of diffusion (or effusion)
This is Graham’s Law of diffusion (or effusion).
vi) Kinetic energy and temperature: We can show that the average kinetic energy of a sample of an ideal gas is a property only of temperature. Therefore, it can be used to define temperature.
For mathematical convenience, we can define a temperature scale in which the average kinetic energy of a sample of ideal gas is directly proportional to the temperature. This temperature scale is the absolute or Kelvin scale.
According to kinetic gas Equation, we have
where mN represents mass of the gas. Since for 1 mole of gas, mN = M, the molar mass, we can write
….. (49)
Since kinetic energy, the energy of motion, is , we can rewrite Equation (52) to relate it to kinetic energy by introducing the factor :
…..(50)
where is the average translational kinetic energy per mole of an ideal gas.
Writing the ideal gas Equation for 1 mole of an ideal gas we have PV = RT
Substituting this result into Equation (50) gives
…..(51)
It readily follows from Equation (51) that average translational kinetic energy of a sample of an ideal gas is directly proportional to the absolute temperature of gas and is independent of the pressure, volume, molar mass and chemical nature of gas. This is referred to as Maxwell’s generalization. This implies that any two gases at the same temperature will have the same average kinetic energy per mole.
The value of Ek depends on the units of gas constant ‘R’.
Dividing both sides of Equation (51) by the Avogadro’s constant , we get the average translational kinetic energy per molecule of an ideal gas:
…..(52)
where ‘k’ is equal to and is known as Boltzmann constant – that is, the gas constant per molecule.
Boltzmann constant has the value:
Average translational kinetic energy of ‘n’ moles of an ideal gas is given as:
…..(53)
Distribution of Molecular Speeds (or Velocities):
The kinetic theory of gases allows us to investigate molecular motion in more detail. Suppose we have a large number of gas molecules, say 1 mole, in a container.
The motion of these molecules is totally random and unpredictable. As they constantly undergo collisions among themselves and with the walls of the container, there is exchange of energy, thereby changing their speed and hence kinetic energy.
Therefore at any particular moment, different molecules in the gas have different speeds and hence different kinetic energies.
Even if initial speed of all the gas molecules was same, the molecular collisions will disrupt this uniformity. Consequently the particles must have different speeds, which go on changing constantly.
As long as we hold the temperature constant, however, the average kinetic energy and the root mean square speed will remain unchanged as time passes. The characteristic that is of interest to us here is the spread, or distribution, of molecular speeds–that is, at a given instant, how many molecules are moving at a particular speed?
An Equation to solve this problem was formulated by Maxwell in 1860. The Equation, which incorporates the assumptions of the kinetic molecular theory, is based on a statistical analysis of the behavior of the molecules.
The following figure shows typical Maxwell-Boltzmann speed distribution curves for an ideal gas at two different temperatures.
At a given temperature, the distribution curve tells us even though the speed of individual molecules is constantly changing at a given temperature (due to large number of molecular collisions), the fraction of the molecules with a particular speed (i.e. the ratio of the number of molecules with a certain speed (velocity) to the total number of molecules) always remains constant. This distribution of speeds is known as Maxwell-Boltzmann Distribution as they were the first to formulate it.
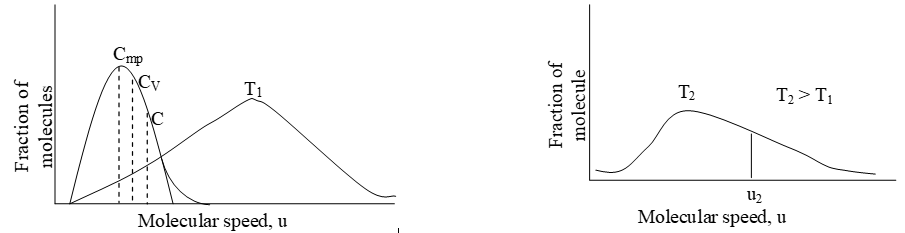
Each point on the curve represents the fraction of molecules moving with a particular speed (velocity). The following important conclusions can be drawn from the distribution curves.
- A very small fraction of molecules has very low (close to zero) or very high speed (velocity)
- As the molecular speed increases, the fraction of the molecules possessing a particular speed also increases, upto a maximum value and then decreases.
- The peak of each curve gives the most probable speed (), that is, the speed of the largest number of molecules.
- Besides the most probable speed we also define the average and the root mean square speed. The average speed of gas molecules () is higher than the most probable speed () of the molecules. The RMS speed () of the molecules is higher than the most probable speed as well as the average speed of the molecules.
- Note that the curve flattens out at the higher temperature i.e. as the temperature increases, the curve shifts to the right side, the height of the curve decreases. This suggests that with increase in temperature, the fraction of molecules with lower speed (velocity) decreases and the fraction of molecules with higher speed increases.
- The shaded areas represent the number of molecules traveling at a speed equal to or greater than a certain speed u1. The higher the temperature, the greater the number of molecules moving at high speed.
- Note that at the higher temperature the most probable speed is greater than that at the lower temperature.
If there are N molecules in a given sample of gas, then the number of molecules having a particular energy is given by the following Equation, called the Maxwell Boltzmann equation:
where
N = total number of molecules
= Number of molecules with a particular energy Ei
T = Kelvin temperature
K = Boltzmann constant
Types of Molecular Speeds (Velocities):
Three types of speeds (velocities) are used:
i) Root mean square speed (velocity): It is the square root of the mean of squares of speeds (velocities) of the gas molecules. It is represented by C or .
Thus, RMS of gas molecules is the square root of the ratio of the sum of the squares of speeds (velocities) of all the molecules to the total number of molecules.
a) Calcculation of RMS speed (velocity) when pressure and volume are given:
According to the kinetic gas Equation:
Since for 1 mole of gas, mN = M, the molar mass,
We can write …..(54)
If the units of pressure are expressed in dynes and volume in , the units of ‘C’ will be . If the units of pressure are in Newton and volume in , the units of ‘C’ will be .
b) Calculation of RMS speed (Velocity) when density is given:
According to Equation (54) we have
Since,
where d is the density of gas, we can rewrite Equation (54) as
…..(55)
If the units of pressure are dynes and the units of density are in gm , the units of ‘C’ will be . If the units of pressure are in Newton and the units of density are , the units of C will be .
c) Calculation of RMS speed (velocity) when the temperature is given:
According to Equation (54) we have
From the ideal gas Equation we have PV = nRT
For 1 mole of an ideal gas PV = RT
Combining the above two Equations, we obtain, …..(56)
Equation (56) shows that the root mean square speed of a gas increases with the square root of its temperature (in kelvins). Because M appears in the denominator it follows that the heavier the gas, the more slowly its molecules move.
In the expression, if the value of R used is , the units of ‘C’ will be cm/s. If we use 8.314 J/K.mol for R and convert the molar mass to kg/mol, then C will be calculated in meters per second. This procedure is used in the forthcoming example:
Illustration 24: Calculate the root mean square speeds of helium atoms and nitrogen molecules in m/s at C.
Solution: We need Equation (56) for this calculation. For He the molar mass is 4.0g/mol, or kg/mol:
Using the conversion factor,
We get
Similarly for
Because of its smaller mass, a helium atom, on the average, moves about 2.6 times faster than a nitrogen molecule at the same temperature (1360/515 = 2.64)
ii) Average speed (velocity): It is the ratio of the sum of the different speeds of gas molecules present in a given sample of gas to the total number of molecules. If are the individual speeds of different molecules then average speed is
Alternatively, if is the speed of n1 molecules, is the speed of n2 molecules, is the speed of n3 molecules, and so on, then average speed is
where
The average speed, which falls on the right of in the speed distribution curve, is also calculated as follows:
…..(57)
It is related to root mean square speed as follows:
…..(58)
iii) Most probable speed: It is the speed possessed by maximum fraction of molecules of a gas at a particular temperature. The maximum of Maxwell’s speed distribution curve gives the most probable speed of a gas molecule at a given temperature
It is represented by and is calculated as follows:
…..(59)
It is related to root-mean-square speed as follows:
…..(60)
iv) Ratio of different molecular speeds : It can be calculated with the help of Equations (56) (58) and (59):
Deviation from Ideal gas laws (shown by the real gases):
The concept of ideal gases is only theoretical or hypothetical. Because there is no any gas which follows the ideal gas equation (PV = nRT) or other gas laws under all conditions of temperatures and pressures. Hence all the gases are therefore real gases.
Real gas follows ideal gas equation only when the temperature is high or the pressure is low.
The deviation from ideal behaviour by the real gases in studied in terms of compressibility factor (Z)
Where .
For ideal gas PV = Z nRT
Where Z = 1
Hence PV = nRT
On the other hand for real gases, PV nRT, because Z 1. hence the two cases are as follows:
i) when , then the gas is said to show negative deviation. Such gases are more compressible than expected from ideal behaviour.
The positive and negative deviations shown by some gases have been shown in the graph. Greater is the departure in the value of Z from unity, greater is the deviation from the ideal behaviour. The extent of deviation from ideal behaviour depends upon the nature of the gas under consideration.

Causes of deviation from ideal behaviour:
Real gases follow ideal behaviour only when the temperature is high or the pressure is low. When there is marked increase in the pressure and marked decrement in temperature, then real gases deviate from ideal behaviour. The reason for deviation from ideal behaviour is due to some faulty assumptions in the postulates of kinetic Molecular theory of gases:
The two faulty assumptions are
i) Forces of attraction or repulsion between the gas molecules are negligible.
ii) Volume occupied by the gas molecules is negligible in comparison to the total volume of the gas.
Under the conditions of high pressure and low temperature, the above two assumptions do not hold true, hence modified assumptions of the two above are as follows :
i) Force of attraction or repulsion between the gas molecules may not be negligible.
ii) The volume occupied by the gas may be so small that the volume occupied by the gaseous molecules may not be negligible.
Modified form of ideal gas equation: (Equation of state for Real gases)
van der Waal modified the ideal gas equation by considering the following:
i) Volume of the gas molecules.
ii) Attractive forces between gas molecules.
At high pressures, molecular interactions i.e. intermolecular attraction forces start operating, and the molecules strike the walls of the container with less impact. This is because the molecules are dragged back by other molecules (attractive forces).
Therefore the pressure exerted by the gas is lower than the pressure exerted by the ideal gas.
i.e.
Observed Correction term Pressure
a = van der Waal’s constant
V = Volume of the gas (container)
Again at high pressures, the volume occupied by the gas molecules become significant, and now the molecules of the gas are restricted to the volume V-nb, where n = moles of the gas and b = van der Waal’s constant.
After inserting the necessary corrections, the new equation is
In the correction term of volume,`b’ is called excluded volume or co-volume. If the molecules are having a volume , then the volume of the molecules become four times the original volume, i.e..
(excluded volume or co-volume)
Significance of `a’: The van der Waal’s constant a’ denotes the magnitude of intermolecular attractive forces.
Unit of a: is pressure term. i.e.
unit of a is
Significance of b: Here b is called the excluded volume or covolume. b is the measure of the effective size of the gas molecules.
Unit of b: In the volume correction term (V-nb), nb is volume of the molecules.
Boyle temperature / Boyle point:
In any gas the extent of deviation depends upon the temperature. In the adjoining graph, of , the deviation at different temperatures have been plotted.
It is found that as the temperature increases, the minimum of the curve shifts upwards. A stage is reached at which the value of Z remains close to unity at a particular temperature for an appreciable pressure range. This temperature is called Boyle temperature or Boyle point.
In the above case the value of Z remains close to unity, at 323K for an appreciable pressure range. Therefore 323K is the Boyle temperature of gas.
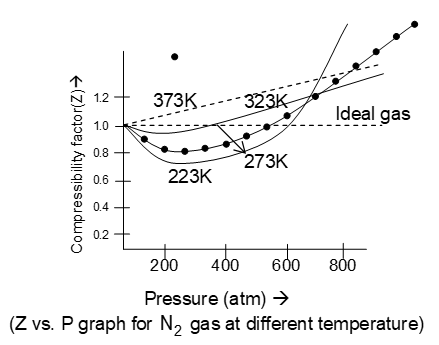
Illustration 25: The van der Waals constant `b’ for oxygen gas is 0.0316 . Find the diameter of the oxygen molecule.
Solution:
Volume occupied by one molecules =
Considering molecule to be spherical having radius `r’ , we get,
Diameter of molecule
Difference between ideal and real gas:
The differences between the two have been grouped below :
|
Real gas |
Ideal Gas |
|
1.This gas follows the gas laws under low pressure and high temperature 2. All the known gases are real gases 3. The intermolecular attraction can’t be neglected at high pressure or low temperature 4. Volume of the molecules is not negligible in comparison to the total volume of gas. 5. These gases obey the equation |
1. This gas follows gas laws under all conditions of temperature and pressures 2. The concept of ideal gas is hypothetical or conceptual only 3. The intermolecular attraction forces are Negligible 4. Volume of the gas molecules is negligible in comparison to the total volume of the gas. 5. These gases follow the equation PV = nRT |
Critical temperature for liquefaction of gases:
Out of the three states of matter (solid, liquid and gases), the constituent particles in case of gaseous state of matter are separated by large distances. Therefore in order to liquefy a gas, it is required to bring the constituent particles close to each other.
The constituent particles of a gas can be brought together either by reducing the temperature, or by increasing the pressure. But the reduction of temperature is more effective than increment of pressure. Or it can be said that by application of both the factors, the constituent particles can be brought together, keeping the dominating effect of temperature reduction in mind.
When the constituent particles (molecules/atoms) of a gas are brought sufficiently near, then they join together and get liquefied, at a particular temperature.
In the graph, the isotherms of have been plotted at various temperatures. Thus at , liquid appears for the first time. This phenomenon takes place at 73.9 atm pressure.
Therefore is called the critical temperature of the gas. The pressure applied on a gas at the to liquefy a gas is called critical pressure . The gas at and changes to liquid. Thus the volume of 1 mole of gas at critical temperature is called critical volume . Thus for ,
For if the temperature is maintained at a higher value than , then whatever be the applied pressure, it does not liquefy .
In general, it can be said that, higher the critical temperature of a gas, more ease is offered by it for liquefaction.
Interparticle interactions or forces:
In addition to the strong attractive forces, the electrostatic forces that hold the two oppositely charged ions in ionic compounds, and the forces that hold atoms (of a molecule) together in covalent compounds, there are a number of weaker attractive forces between interacting particles (atoms, molecules) that are not bonded to each other.
All these weak interactions are electrostatic, i.e. the attraction between opposite charges. Weak interactions are substantially weaker than chemical bonds. For instance, bromine () is a liquid at room temperature because of less attractions between molecules and less heat of vaporization. The heat of vaporization, the heat energy required to overcome these attractions, is 31kJ/mol, but the bond dissociation energy of the Br–Br bond is 193 kJ/mol.
The magnitude of these weak interactions is very sensitive to distance while the energy of the interaction between a cation and an anion is simply a function of 1/r, where r is the distance between their centers, the energy of some weak interactions varies as . Thus, these weak interactions are consequential only when the interacting species are very close.
Weak interactions varying considerably in magnitude are :
i) Ion – Dipole interactions,
ii) Dipole – Dipole interactions,
iii) Dipole – Induced dipole interactions,
iv) London forces or dispersion forces
All the weak intermolecular interactions are collectively known as van der Waals forces in honour of Dutch scientist, who explained the deviation of real gases from ideal gas bahaviour through these forces.
Attractive forces between an ion and a dipole (Ion–Dipole interactions) are not van der Waals forces.
A special kind of dipole–dipole interaction is the hydrogen bond. It is relatively a strong type of interparticle interaction but weaker than a chemical bond. It is treated as a separate category because, only highly electronegative elements, F, O, and N can participate in hydrogen bond formation.
i) Ion – Dipole Interactions:
When an ion (e.g. ) and a polar molecule
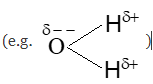
with a permanent dipole are near each other, there will be an attraction between the charge on the ion and the opposite charge on one of the ends of the dipole, called Ion–Dipole interaction. These attractions/interactions are relatively stronger and hence less sensitive to distance than the other weak interactions. The energy is a function of where r is the distance between the center of the ionic charge and the center of the dipole. These interactions are very important in solutions of ionic solutes in polar solvents.
ii) Dipole-Dipole Interactions:
These intermolecular interactions operate between the polar molecules, which have permanent dipoles. Polar molecules can attract each other if the dipoles of the molecules are oriented correctly. Dipole – dipole attractions account for the relatively high melting points and boiling points of many polar compounds.
In condensed phases (as in solids), polar molecules tend to orient themselves favorably, hence the interaction energy is a function of . In the gas phase or in the liquid phase at relatively high temperatures, the orientation of polar molecules is random. Thus, the interaction energy is a function of and is considerably less important.
iii) Induced Dipole Interactions:
These interactions are of two types:
a) Ion – Induced dipole interaction,
b) Dipole – Induced dipole interaction.
When an ion or a molecule with a permanent dipole approaches an atom or a molecule that has no dipole, a dipole can be induced through deformation of the electron cloud. An interaction can now take place between the ion and the induced dipole or between the permanent dipole and the induced dipole.
These interactions tend to be quite weak and quite sensitive to distance. The interaction energy of the ion – induced dipole interaction is a function ofwhile that of the dipole – induced dipole interaction is a function of .
These interactions are quite important in solutions of ionic or polar substances in nonpolar solvents and in some gas mixtures.
Magnitude of the induced dipole moment depends upon:
the amount of permanent dipole moment, and the polarizability of the atom or molecule lacking permanent dipole. Atoms or molecules of larger size have higher polarizability.
iv) London forces or Dispersion forces:
These attraction/interaction forces exist between atoms or molecules of completely non polar substances. The existence of such forces can be deduced from the fact that nonpolar substances such as are liquid or solid at room temperature. This must be due to some relatively strong intermolecular interactions holding the molecules of these substances together.
These intermolecular interactions, called London or Dispersion forces, are believed to arise from momentarily unequal distributions of electron density in atoms or nonpolar molecules.
According to quantum mechanical model, on a time average the electrons are distributed symmetrically about an atom or nonpolar molecule but at any instant, there may be an excess of electron density in one region of the atom or molecule and a corresponding deficiency of electron density elsewhere in the atom or molecule. This uneven distribution of electron density creates an “instantaneous or transient electric dipole” in the atom or molecule.
Suppose there is another atom or a nonpolar molecule nearby. A dipole is induced in this neighbouring atom or molecule by the instantaneous dipole of the first atom or molecule. An attractive force results. This force of attraction, first proposed by the German physicist Fritz London, is used to account for the attraction between nonpolar species.
The energy of the interaction between an instantaneous dipole and an induced dipole is a function of . As a result these forces become important only at short distances (~ 500 pm). But these interactions can still be relatively substantial, especially in large molecules,
For example, the heat of vaporization of , a fairly large nonpolar molecule, is . Except some small polar molecules, London forces (also called dispersion forces) are the most weak interactions.
The extent to which a dipole can be induced in a given nonpolar molecule depends on two factors:
i. the force that induces the dipole i.e., the magnitude of the instantaneous dipole, and
ii. the ease with which the electron distribution in the neighbouring molecule can be distorted.
The responsiveness of the electron distribution of a molecule to a distorting influence is called the polarizability.
Several factors such as volume of molecule and no. of electrons in the molecule influence polarizability.
An increase in the volume of a molecule or an increase in the number of electrons in the molecule results in an increase in the polarizability of the molecule.
The physical properties of the halogens illustrate the increase in London forces in the large members of a family of elements. At room temperature, is a gas, is a liquid, and is a solid. The molecule is the smallest of the three and is the largest. The intermolecular interactions between the molecules in the liquid or solid are weaker than the interactions between the molecules in the liquid or solid.
v) The Hydrogen bond:
It is a special case of dipole – dipole interaction. When a hydrogen atom is covalently bonded to an atom of a highly electronegative element, such as fluorine, oxygen and nitrogen, the bond become highly polar. As a result, there is a partial positive charge () on the H atom and a partial negative charge () on the atom of high electronegativity.
Such polar bonds lead to dipole – dipole interactions, particularly in condensed phases. For many reasons, the dipole – dipole attractions/interaction are unusually large for a polar bond containing a hydrogen atom. One of the most important factors is the small size of the hydrogen atom, because the dipole – dipole attraction is very large if the atom with the partial positive charge is very close to the atom with the partial negative charge.
The closeness of the approach is however, restricted by the repulsion between the electrons of the atoms. Since a H atom in a polar bond has no inner – shell electrons, a highly electronegative atom with a partial negative charge can get closer to a hydrogen atom than to any other possible atom.
In addition, the highly electronegative atom has one or more non bonding (valence shell) electron pairs. One of these electron pairs may be directed towards the positively charged hydrogen atom of another polar molecule, thereby resulting into a strong localized –ve charge that further strengthens the dipole – dipole interaction involving hydrogen atom.
The unusually strong coulombic attraction occurring between a hydrogen atom covalently bonded to an atom of an element of great electronegativity and the lone pair of electrons on such an atom is called a hydrogen bond.
A hydrogen bond is substantially weaker than a chemical bond but it is substantially stronger than the weak interactions described earlier.
Energy of interaction of hydrogen bond varies between 10 to 100 kJ/mole, quite a significant amount of energy. Thus, this interaction leads to strong cohesive forces between molecules of many compounds like proteins and nucleic acids.
Although hydrogen bonding is regarded as being limited to F, O and N, but species such as Cl may also participate in hydrogen bonding.
Hydrogen bonding has significant effect on the physical properties of compounds. The unusually high boiling point, melting point of and also the open structure of ice which makes it less dense than liquid water are all because of intermolecular H bonding.
Intermolecular interactions are, in general, the forces of attraction and repulsion between interacting particles which may be atoms or molecules or both. So far we have discussed attractive intermolecular forces. When two particles (atoms / molecules) are brought into close contact with each other, the repulsion between the electron clouds and that between the nuclei of the two particles comes into existence. Magnitude of the inter particle repulsion rises very rapidly as the distance between the particles decreases. This explains why liquids and particularly solids are hard to compress.
Liquid State: Properties of liquids in terms of intermolecular attractions:
I) Vapour pressure: If an evacuated container is partially filled with a liquid, a portion of the liquid evaporates to fill the remaining volume with vapour. Initially the liquid evaporates and the pressure exerted by the vapours on the walls of the container increases. After some time at given temperature it becomes constant and there is an equilibrium state between the liquid phase and vapour phase. The vapour pressure at this stage is known as equilibrium vapour pressure (or) saturated vapour pressure.
II) Surface tension: We observe small drops of mercury on the surface forming spherical beads instead of spreading. When a capillary touches the surface of a liquid the liquid rises or falls in it. These phenomena are due to the characteristic property of liquids known as surface tension.
III) Viscosity: Strong intermolecular forces between the molecules of successive layers of liquid holding them together show resistance to the flow and create friction between the layers of fluid. The layers slip past one another when the liquid flow of liquid.
When a liquid flows over a surface the layer of molecules in the immediate contact of that layer from the fixed surface is stationary. The velocity of the upper layer increases as the distance of that layer from the fixed layer increases. In this way there is a regular gradation of velocity for layers in passing from one layer to the next and it is called “Laminar flow”.
More the viscosity, the more slowly the liquid flows. Hydrogen bonding and van der Waals forces cause high viscosity.
FORMULAE AND CONCEPTS AT A GLANCE
- Boyle’s law states that at constant temperature for a given mass of gas.
- Charle’s law: (at constant pressure for a given mass of gas)
- Pressure – Temperature law (Gay Lussac law): P T (at constant volume)
- Ideal gas equation: PV = nRT
- Dalton’s law of partial pressure :
where PT = total presure of gases;
PA, PB, PC = Partial pressure of gases A, B and C respectively
6. Grahm’s law of diffusion :
7. Kinetic gas equation :
where . P = Pressure of the gas
V = Volume of the gas
m = mass of a molecule
n = number of molecular present in given mass of gas
Vrms = Root mean square speed.
8. Root mena square speed:
(d = density)
Average speed =
Most probable speed =
9. Average speed : most probable speed : root mean square speed = 1.128 : 1 : 1.224
10. van der Waal’s equation :
11. Compressibility factor :
(i) for an ideal gas, z = 1 and is independent of P and T.
(ii) for real gases, z 1 and depneds on P and T.
(a) if z < 1; gas is more compressible
(b) if z > 1; gase is less compressible
12. Boyle’s temperature : ; where = Boyle’s temperature
13. Critical temperature :
SOLVED PROBLEMS
Prob 1. 10 g of a gas at NTP occupies 5 litres. The temperature at which the volume becomes double for the same mass of gas at the same pressure is
(A) 273 K (B) C
(C) C (D) 546oC
Sol: (C) According to Charle’s law
Prob 2. A 2.24 L cylinder of oxygen at N.T.P. is found to develop a leakage. When the leakage was plugged the pressure dropped to 570 mm of Hg. The number of moles of gas that escaped will be
(A) 0.025 (B) 0.050
(C) 0.075 (D) 0.09
Sol: (A) The number of moles of the gas leaked out,
Prob 3. Under what conditions will a pure sample of an ideal gas not only exhibit a pressure of 1 atm but also a concentration of 1 mol / litre
(A) at STP (B) when V = 22.4 L
(C) when T = 12 K (D) impossible under any condition
Sol: (C) According to gas equation,
Prob 4. A box of 1 L capacity is divided into two equal compartments by a thin partition which are filled with respectively. The pressure in compartment filled with H2 is recorded as P atm. The total pressure when partition is removed will be
(A) P (B) 2P
(C) (D)
Sol:
(m = Mass of gas, M = Molecular mass)
Partial pressure of
Partial pressure of
Prob 5. A closed vessel contains equal number of molecules at a total pressure of 740 mm. If oxygen is completely removed the pressure will
(A) Drop to (B) Drop to
(C) Remain unchanged (D) cannot be predicted
Sol: (A)
Since,
is the pressure of 2 moles.
Hence,
Prob 6. A football bladder contains equimolar proportions of . The composition by mass of the mixture effusing out of punctured football is in the ratio ()
(A) 1: 4 (B)
(C) (D) 4: 1
Sol: (A)
Prob 7. A temperature of –C shall be equal to
(A) 233 K (B) –40 K
(C) –32 K (D) Both A and B
Sol: (A).
Prob 8. The rate of diffusion of a gas is proportional to
(A) (B)
(C) (D)
Sol: (A)
Rate of diffusion, ;
Prob 9. 4.4 g of a gas at STP occupies a volume of 22.4 litre, the gas can be
(A) (B)
(C) (D)
Sol: (D) 22.4 litre of a gas will have mass = 44 g
i.e., molecular mass of the gas = 44
Hence gas is .
Prob 10. V vs T curves at constant pressure for an ideal gas are shown below:
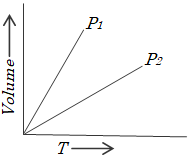
Which is correct?
(A) (B)
(C) (D) All of the above
Sol: (B) At a constant temperature, the product of PV is constant.
For a given temperature T as is more hence shall be greater than 1.








