Structure of Atom

STRUCTURE OF ATOM

Introduction:

“The rich diversity of chemical behavior of different elements can be traced to the differences in the internal structure of atoms of these elements”.

Maharshi Kanad [600 BC] the Indian Philosopher proposed that matter is made up of small particles called Parmanu and anu.

Later on Democritus [400 BC], a Greek Philisopher also proposed that the matter is made up of extremely small particles, i.e., atoms are fundamental building blocks of the matter.

The word ‘atom’ has been derived from the Greek word ‘a–tomio’ means ‘which cannot be cut’ or ‘non–divisible’.

These earlier ideas were mere speculations and there was no way to test them experimentally.

John Dalton (1808–1809) could give a scientific basis to the old ideas or hypothesis by proposing his famous atomic theory called as Dalton’s atomic theory, regarded the atom as the ultimate particle of matter and considered to be indivisible and indestructible.

Infact, the atom as the whole is electrically neutral as number of protons in it is equal to number of electrons.

The researches show that atom can be divided into about 200 sub atomic particles.

The electron, proton and neutron are the main fundamental particles of an atom.

Discovery of electron – study of Cathode rays:

William Crookes discovered that the gases start conducting electricity under reduced pressure. William Crookes, Julius Plucker and J.J. Thomson observed that, when a high voltage (~ 10,000  volts) is applied between the electrodes fitted in discharge tube, through a gas at a very low pressure (~ 10^-3 Torr) , some invisible radiations are emitted from the cathode.  At this stage the glass wall of the discharge tube opposite to the cathode, start glowing with a faint greenish light.

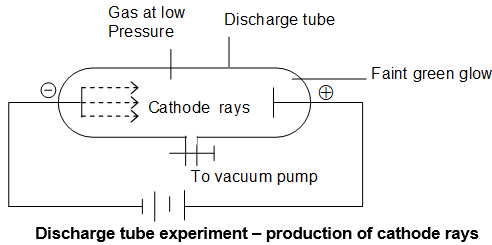
It is now known that this greenish glow on the walls must be due to the bombardment of glass wall by the cathode rays.  It may be noted that when the gas pressure in the tube is 1 atm, no electric current flows through the tube. This is because the gases are poor conductor of electricity.

Origin of Cathode rays:

The cathode rays are first produced from the material of the cathode and then from the gas inside the discharge tube due to bombardment of the gas molecules  by the high speed electrons emitted first from the cathode.

Properties of Cathode rays (W. Crooks, J. Plucker & J.J. Thomson):

i. They produce a sharp shadow of the solid object placed in their path. This show that cathode rays travel in straight lines.

ii. If a light paddle wheel (e.g., that of mica mounted on an axle is placed in their path, the wheel begins to rotate.  This shows that cathode rays are made up of material particles.

iii. When an electric field is applied on the cathode rays, they are deflected towards the positive plate of the electric field.  This shows that cathode rays carry negative charge.  The negatively charged material particles constituting the cathode rays are called electrons.

iv. When cathode rays strike a metal foil, the latter becomes hot. This indicates that cathode rays produce heating effect.

v. They cause ionization of the gas through which they pass.

vi. They produce X-rays when they strike against the surface of hard metals like tungsten, molybdenum etc.

vii. They produce green fluorescence on the glass walls of the discharge tube as well as on certain other substances such as zinc sulphide.  e.g., Television picture tube.

viii. They affect the photographic plates.

ix. They possess penetrating effect (i.e., they can easily pass through thin foils of metals). They are stopped only by the metal foils of greater thickness.

x. The nature of the cathode rays does not depend upon the nature of the gas, taken in the discharge tube and the nature of cathode material.

xi. For each negatively charged particles of cathode rays, the ratio of charge (e) to mass (m) is constant i.e., e/m = 1.76 $\times$ 10⁸ c/g = 1.76 $\times$ 10¹¹ c/kg. Thus the mass of cathode ray particle is 1837 times smaller than that of the H – atom.

Discovery of proton – study of Anode rays:

Goldstein was able to show the presence of positive rays in 1886.

For this purpose Goldstein performed discharge tube experiment in which he took perforated cathode and a gas at low pressure was kept inside a discharge tube.

He observed that, on applying high voltage between electrodes, some new type of luminous rays were coming from the side of anode and passing through the hole in the cathode and  produced green fluorescence on the opposite glass wall coated with zinc sulphide.

These rays were called anode rays or canal rays or positive rays (by J. J. Thomson because they were found to carry positive charge).

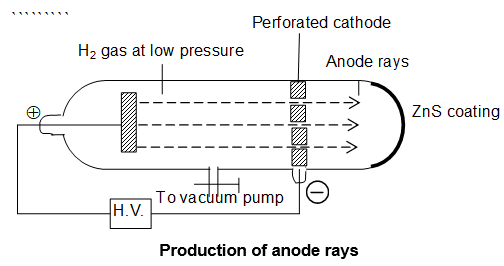
Origin of anode or positive rays:

In the discharge tube the atoms of gas lose negatively charged electrons.  These atoms, thus, acquire a positive charge.  The positively charged particle produced from hydrogen gas was called the proton.

$H\stackrel{–e }{\to }\underset{\left(Proton\right)}{H^{+}}$

Properties of Anode rays:  

i) They travel in straight lines. However, their speed is much less than that of the cathode rays.

ii) They are made up of material particles.

iii) They are positively charged, as indicated by the direction of deflection of these rays in the electric and magnetic fields.  That is why they are called ‘positive rays.’

iv) The nature of anode rays depends on the gas taken in the discharge tube.

v) For different gases taken in discharge tube the charge to mass ratio (e/m) of the positive particles constituting the positive rays is different.

vi) When hydrogen gas is taken in the discharge tube, discharge to mass ratio (e/m) obtained for anode rays is found to be maximum. i.e., e/m = 9.58 $\times$ 10⁴ c/g.

Fundamental particles:

1) Electron:  Electron is a universal constituent of matter.

i) Discovery: It was discovered by J. Thomson in 1886, through the study of cathode rays (Julius Plucker) and the name electron was proposed by Stoney.

ii) Charge: It was determined by Millikan by oil drop experiment as -1.602×10^-19 coulombs or 4.803 $\times$ 10^-10s.u.

iii) Mass: It was found by J.J.Thomson as 9.11×10^-28 g. (nearly equal to 1/1837^th of mass of hydrogen atom).

iv) Specific charge: e/m ratio is called specific charge and was determined by Thomson as 1.76$\times$10⁸ coulombs/gm.

v) Mass of electron moving with speed v, $m=\frac{m_{rest}}{{\sqrt{1–\left({\displaystyle \frac{v}{c}}\right)}}^2}$ , where c = velocity of light (3$\times$10⁸ m/s)

vi) Mass in amu: It is 0.0005486 amu.

vii)  Mass of one mole of electrons:  It is 0.55 mg.

viii) Charge on one mole of electron is approx. 96500 coulombs or 1 faraday.

ix) Density: 2.17$\times$10¹⁷ g/cc.

x) Radius: It is of the order of 10^-15

xi) Symbol: $e^0_{–1}$.

xii)  Location: Outside the nucleus.

Proton:

i) Discovery: It was discovered by Goldstein through perforated cathode rays experiment which showed the presence of anode or canal rays.

ii) Charge: It carries unit positive charge i.e. 1.602 $\times$ 10^-19 coulombs or 4.803$\times$10^-10

iii) Mass: It was found to be 1.672$\times$10^-24 g or 1.672 $\times$ 10^-27 kg.  This mass is 1837 times heavier than an electron.

iv) Specific charge (e/m): It is 9.58 $\times$ 10⁴ coulomb/gm (The value of e/m was maximum four hydrogen gas when taken inside the discharge tube.

v) Mass of 1 mole of proton is nearly 1.007 mg.

vi) Charge on 1 mole of proton is $\approx$ 96500 coulombs or 1 faraday

vii) The volume of a proton is approximately 1.5$\times$10^-38 cm³.

viii) Symbol: $\mathrm{P}_0^{+1}\text{ or }1{\mathrm{H}}^1$

ix) Location: lies inside the nucleus.

Neutron:

i) Discovery: It was discovered by Chadwick in 1932 by bombarding Be atom with high speed $\alpha$-particles.

${}_4{\mathrm{Be}}^9{+}_2{\mathrm{He}}^4{⟶}_6{\mathrm{C}}^{12}{+}_0{\mathrm{n}}^1$

ii) Charge: Charge less or neutral particle.

iii) Mass: Its mass is 1.675$\times$10^-24 g or 1.675$\times$10^-27 kg.

iv) Density: Its density is 1.5$\times$10¹⁴ g/cm³ and is heavier than proton by 0.18%.

v) Specific charge: It is zero.

vi) Mass of 1 mole of neutron is nearly 1.0087 g.

vii) Disintegration: Isolated neutron is unstable and disintegrates into electron, proton and neutrino.

viii) Among all the elementary particles neutron is the heaviest and least stable.

ix) Symbol: $\mathrm{n}_1^0$

x) Location: Lies inside the nucleus.

Properties of Electron, Proton and Neutron

Properties	Electron	Proton	Neutron
Discovery	J.J.Thomson	Goldstein	Chadwick
Charge	-1.6022$\times$10-19 C	1.6022$\times$10-19 C	Zero
Mass	9.109$\times$10-31 kg	1.672$\times$10-27 kg	1.675$\times$10-27 kg
Mass relative to the electron	1	1836	1839
Spin	$\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$	$\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$	$\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$
Charge relative to proton	-1	+1	0
Location	Outside the nucleus	In the nucleus	In the nucleus

Classical Models of Atom:

Thomson’s Atomic Model (1898 – 1904):

According to Thomson, an atom is a sphere of positive charge having a number of embedded electrons in it and sufficient enough to neutralize the positive charge.  The stability of the atom was explained as a result of the balance between the repulsive forces between the electrons and their attraction towards the centre of the positive sphere.  This model is compared with a water melon in which seeds are embedded or pudding in which raisins are embedded.  Therefore, this model, sometime called watermelon model or raisin or plum pudding model.

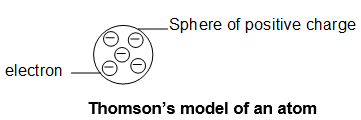
Limitation:  Though this model was able to explain overall neutrality of the atom.  But this model could not satisfactorily explain the results of scattering experiment of Rutherford and was thus rejected.

Rutherford’s Nuclear Model of Atom – Discovery of Nucleus:

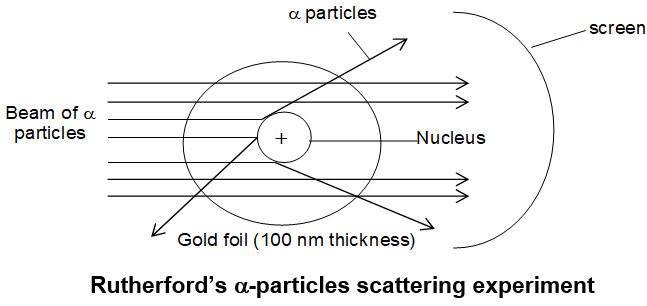
$\alpha$-particle-scattering experiment:  Rutherford, (in 1909-1911) tested the distribution of charges proposed by Thomson in his model.  He performed some $\alpha$-particle scattering experiments in which he bombarded thin foils of metals like gold, silver, copper or platinum with a beams of fast moving $\alpha$-particles (i.e. emitting from Ra or Po).

Observations

The results of Rutherford’s experiment were however, quite unexpected.  He made the following observations:

i) Most of the $\alpha$-particles passed through the gold foil undeflected.

ii) A small fraction of the $\alpha$-particles was deflected by small angles.

iii) Very few $\alpha$-particles (1 in 20,000) were deflected by nearly 180^o i.e. bounced back.

Conclusions: On the basis of these observations, Rutherford drew the following conclusions regarding the structure of an atom:

i) Most of the space in the atom is empty as most of the $\alpha$-particles passed through the foil.

ii) A few positively charged alpha particles were deflected through small angle. These could be deflected only by some positive body present within the atom, concentrated in a very small volume.  This very small portion of the atom was called nucleus by Rutherford.

Rutherford’s Atomic Model:  On the basis of $\alpha$ – particle experiment, Rutherford, put forward his nuclear model in 1912.

Main postulates of Rutherford Model are

i) An atom consists of two parts i.e. nucleus and extra nuclear part.

ii) All the mass and entire positive charge of an atom is concentrated in the centre of atom called nucleus.

iii) The positive charge of a nucleus is due to proton, but mass of the nucleus is due to both protons and neutrons.

iv) The total number of protons and neutrons in the nucleus determines the nuclear mass.

v) Most of the space outside the nucleus is empty.

vi) Electrons are distributed in extra nuclear part of atom and revolve around the nucleus at very high speed like planets revolving around the sun, hence electrons are called planetary electrons.

vii) Electrons actually revolve around the nucleus in circular planetary orbits in which the required centripetal force is derived from the electrostatic force of attraction (working) between nucleus and electron.

viii) The dimension of nucleus is of the order of 10^-13 cm and the dimension of atom is of the order of 10^-8 cm.

r = R₀A^1/3, where  R₀ (constant) = 1.4 $\times$ 10^-13cm = 1.4$\times$10^-15 m

where r = radius of the nucleus, A = mass of the nucleus

Thus, Rutherford’s atomic model is comparable with solar system.  So, it is also called as planetary model.

Drawbacks of Rutherford’s Model:

i) It does not obey the Maxwell’s law of electrodynamics – a small charged particle moving under the influence of an attractive force continuously loses energy in the form of electromagnetic radiations.

Thus, the electron (a charged body) moving around the nucleus must emit radiations and gradually lose energy.  Due to this loss of energy its motion would slow down and therefore, it would not be able to withstand the attraction of the nucleus.

Consequently, the orbit would because smaller and smaller following the spiral path and ultimately the electron would fall into the nucleus.  Practically it does not happen.

Therefore, this model fails to explain the stability of atom(s).

ii) It could not suggest for the discontinuous nature of spectrum.

iii) It could not explain the emission of various spectral lines during emission spectrum of hydrogen i.e. it fails to explain the atomic spectrum or line spectrum of hydrogen.

Atomic Number or Proton Number (Z):  The number of protons present in an atom is called the atomic number which is, denoted by Z. Hence, atomic number of an element = total number of protons present in an atom.

$Z=\text{ no. of }{p}^{+}=e^{-}$

In 1913 Moseley postulated that the frequency of X-ray produced when a strong beam of electrons fall on the nucleus of atom is related to the atomic number of atom of an element.

Mathematically, $\sqrt{\mathfrak{u}}=a(Z-b)$

where, = frequency of X-ray, Z=nuclear charge (atomic number), a & b = constants

For a neutral atom: No. of proton (p⁺) = No. of electrons (e^– ) = Atomic No. (Z).

For a negative ion (X^n-)

No. of electrons (e^–) > No. of protons (p⁺)

$\therefore$No. of electrons = Atomic number (Z) + Negative charge

For a positive ion (Xⁿ⁺)

No. of electrons < No. of protons

$\therefore$No. of electrons = atomic number (Z) – positive charge.

Mass Number (A): Proposed after the discovery of neutron.  The sum of the number of protons and neutrons (i.e. collectively known as nucleons) present in the nucleus of an element is called mass number and is denoted by A. It is nearly equal to the atomic mass of that element.

Hence, for an atom mass number = number of protons + number of neutrons.

A = p + n      or     A = Z + n     or     n = A – Z

Difference between Mass Number and Atomic Mass:  Mass number is always a whole number whereas atomic mass is usually not a whole number because mass number is the sum of two integers so it can never be fractional, else we can say number of protons and neutrons can never be fractional.

While atomic number is the average of atomic weights of all the isotopes of an element present in the nature.  So it can be an integer or fractional value.

Representation of Atomic no (Z) and Mass number (A) of an element:

The atomic number (z) and mass number (A)  of an element are usually represented as follows.

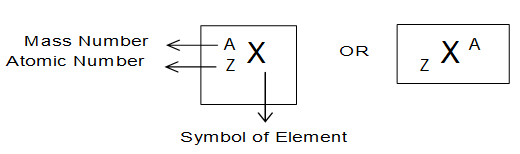
Illustration 1: 

i) Calculate the total number of electrons present in one mole of methane.

Solution: 1 molecule of CH₄ contains electrons = 6 + 4 = 10

$\therefore$ 6.022$\times$10²³ molecules (i.e. 1mol) of CH₄ will contain electrons = 6.022$\times$10²⁴

Illustration 2:  An element with mass number  81 contains 31.7% more neutrons as compared to protons.  Assign the atomic symbol..

Solution: A = p + n = 81

Let,  no. of protons = x and no. of neutron =$x+\frac{31.7x}{100}=1.317x(\because p+n=x+1.317x=81)$

$$\begin{gathered} x(1+1.317)=81 \\ \therefore x=\frac{81}{2.317}=34.96=35 \end{gathered}$$

Therefore, atomic number = 35, Mass number = 81, so Symbol ${=}_{35}{\mathrm{Br}}^{81}$.

Isotopes, Isobars, Isotones and Isoelectronics:

Isotopes: Atoms of the same element having same atomic number but different mass numbers (different no. of neutrons) are called isotopes. e.g.,

	${}_1{\mathrm{H}}^1{,}_1{\mathrm{H}}^2{,}_1{\mathrm{H}}^3$	${}_6{\mathrm{C}}^{12}{,}_6{\mathrm{C}}^{13}{,}_6{\mathrm{C}}^{14}$	${}_8{\mathrm{O}}^{16}{,}_8{\mathrm{O}}^{17}{,}_8{\mathrm{O}}^{18}$	${}_{17}{\mathrm{Cl}}^{35}{,}_{17}{\mathrm{Cl}}^{37}$
Protons	1     1     1	6       6        6	8       8       8	17,       17
Electrons	1     1     1	6       6        6	8       8       8	17,       17
Neutrons	0     1     2	6       7        8	8       9      10	18         20

Isobars: atoms of different elements having same mass number but different atomic numbers are (different number of protons and neutrons) called isobars.

e.g.,${}_{18}{\mathrm{Ar}}^{40}{,}_{19}{\mathrm{K}}^{40}{,}_{20}{\mathrm{Ca}}^{40}$

Isotones: Atoms of different elements which contain the same number of neutrons are called isotones

$eg: i) { }_6{C}^{14}{,}_7{N}^{15}{,}_8{O}^{16}\left(n=8\right)$

$eg ii{)}_{ 14}{\mathrm{Si}}^{30}{,}_{15}{\mathrm{P}}^{31}{,}_{18}{\mathrm{S}}^{32}\left(\mathrm{n}=16\right)$

Isoelectronics: The species (atoms or ions) containing the same number of electrons are called isoelectronic.

e.g: i)${\mathrm{O}}^{2-},{\mathrm{F}}^{-},\mathrm{Ne},{\mathrm{Na}}^{+},{\mathrm{Mg}}^{2+},{\mathrm{Al}}^{3+}$ are isoelectronic because all contain 10 electrons.

ii) CO &  $C{N}^{–}$are isoelectronic (14 electrons)

Note: The ionic radii of isoelectronic decreases with increase in nuclear charge.

Illustration 3:   Nitrogen atoms has atomic number 7 and Oxygen has atomic number 8.  Calculate the total no. of electrons in a nitrate ion.

Solution: Formula of nitrate ion = NO₃^–

$\therefore$No. of electrons in NO₃^–  =  No of electrons in ‘N’ + no of electrons in 3 ‘O’ + 1 (-ve charge) = 7 + 3$\times$8 + 1 = 32.

Nature of Light (Electromagnetic Radiation):  Electromagnetic radiations are energy radiations which do not need any medium for propagation e.g visible, ultra violet, infrared, x-rays, $\gamma$-rays, radio waves, radiant energy etc.  These are generated by oscillations of a charged body in a magnetic field or a magnet in an electrical field.  Two theories were proposed to explain the nature and the propagation of light (an electromagnetic radiation) these are :

i. Corpuscular theory: This theory was proposed by Newton. According to this theory light is propagated in the form of invisible small particles. i.e. light has particle nature.  The particle nature of light explained some of the experimental facts such as reflection and refraction of light but it failed to explain the phenomenon of interference and diffraction.  After the advent of wave theory of light, corpuscular theory, therefore, was discarded and ignored.

ii. Wave theory of light (electromagnetic wave theory): This theory was put forward by James Clark Maxwell in 1864 to explain and understand the nature of electromagnetic radiation.

The main points of this theory are:

i) The light is a form of electromagnetic radiations.

ii) The light radiations consist of electric and magnetic fields oscillating perpendicular to each other and also to the direction of propagation of the radiation.

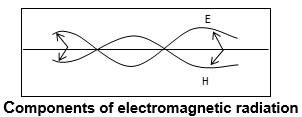
iii) The vertical component of wave, ‘E’ indicates the change in the strength of the electric field and the horizontal component of the wave ‘H’ indicates the change in the strength of the magnetic field.

iv) These radiation do not require any medium for propagation.

v) The radiations posses wave character and travel with the velocity of light i.e. 3$\times$10⁸ m/sec because of the above characteristics, the radiation are called electromagnetic radiations or waves.

Some important characteristics of a wave:

A wave is always characterized by the following six characteristic.

i. Wavelength ($\lambda$):

The distance between two nearest crests or nearest troughs is called the wavelength.  It is represented by $\lambda$ (lambda) and is expressed in Å or pm (picometer) or nm (nanometer) or cm or m.

$\begin{array}{l}1\mathrm{nm}={10}^{-9}\mathrm{m}={10}^{-7}\mathrm{cm}\\ 1\text{Å}={10}^{-10}\mathrm{m}={10}^{-8}\mathrm{cm}\\ 1\mathrm{pm}={10}^{-12}\mathrm{m}={10}^{-10}\mathrm{cm}\end{array}$

Frequency ($\mathfrak{u}$): Frequency of a wave is defined as the number of waves passing through a  point in one second.  It is represented by  (nu) and is expressed in simply sec^-1 or s^-1 or Hertz or cycle/sec. (1 cycle/sec = 1 Hz).  A cycle is said to be completed when a wave consisting of crest and trough passes through a point.

$\therefore \mathfrak{u}=\mathrm{c}/\lambda \text{ or }\mathrm{u}=\mathrm{c}\overline{\mathfrak{u}}$

A wave of higher frequency has a shorter wavelength while a wave of lower frequency has longer wavelength.  Different electromagnetic radiation have different wavelength and frequency.

iii. Amplitude(a):  The height of the crest or the depth of the trough of a wave is called amplitude.  It is represent by ‘a’ and in expressed is unit of length.  It determines the intensity or brightness of the radiation.

Velocity (c): The distance covered by the wave in one second is called velocity. It is represented by c and is expressed in cm/sec or m/sec. (c = $\mathfrak{u}\lambda$). All electromagnetic waves travel with the same velocity i.e. 3$\times$10⁸ m/sec.  The speed of light in air is slightly less than its speed in vacuum, but the difference is so small that it can be ignored in most cases.

Relation ship between velocity, wavelength and frequency of a wave $\mathrm{c}=\mathfrak{u}\lambda$

 Wave number ($\overline{\mathfrak{u}}$):

This is the reciprocal of wavelength i.e. the number of wavelengths per centimitre  or per mitre.  It is represented by the symbol $\overline{\mathfrak{u}}$ (nu bar). $\overline{\mathfrak{u}}=\frac{1}{\lambda }=\frac{\mathfrak{u}}{c}$ It is expressed in cm^–1 or m^–1.

Relationship between velocity, wavelength and frequency of a wave. $\mathrm{c}=\mathfrak{u}\lambda$

Time period (T): Time taken by the wave for one complete cycle or vibration is called time period.  It is represented by ‘T’ and expressed in second per cycle. $T=\frac{1}{v}$( where = frequency)

Illustration 4:   The Vividh Bharathi station of All India Radio, Delhi broadcasts on a frequency of 1368 KHz (kilohertz).  Calculate the wavelength of the electromagnetic radiation emitted by the transmitter.  Which part of the electromagnetic spectrum does it belong to?  

Solution: Speed of electromagnetic radiation c = 3$\times$10⁸ m/s

$$\begin{gathered} \mathrm{frequency}, \mathfrak{u}=1368\mathrm{kHz} \\ \therefore \text{ wavelength, }\mathrm{\lambda }=\frac{\mathrm{c}}{\mathfrak{u}}=\frac{3\times {10}^8{\mathrm{ms}}^{-1}}{1368\times 1000{\mathrm{s}}^{-1}}=219.3\mathrm{m} \end{gathered}$$

This is a characteristic radio wavelength.

Limitation of Electromagnetic Wave theory:  The electromagnetic wave theory of radiation believed in the continuous generation of energy.  This theory was successful in explaining the phenomenon of propagation of light such as diffraction (i.e. the bending of waves around an obstacle) and interference (i.e. the combining of two waves of approximately same frequency to give a resultant wave, whose disturbance at each point in space is the algebraic or vector sum of the disturbances produced by each interfering wave at the point), but it could not explain the following:

i. The black body radiation, and

ii. The photo electric effect.

iii. The variation of heat capacity of solids as a function of temperature.

iv. The line spectra of atoms with special reference to hydrogen.

Modern approach to the structure of the atom:

Planck’s Quantum Theory:

To explain the phenomena of ‘Black body radiation’ and ‘Photoelectric effect’, Max Planck in 1901, put forward a new revolutionary theory known as Planck’s quantum theory of radiation.  This theory was further extended by Einstein in 1905.

The main points of Planck’s quantum theory are:

i) The radiant energy is not emitted or absorbed continuously but discontinuously in the form of small discrete packets of energy called quanta. Each such packet of energy is called a ‘quantum’.

ii) In case of light, the quantum of energy is called a photon.

iii) Each quantum is associated with a definite amount of energy.   The energy of each quantum is directly proportional to the frequency of the light radiation ($\mathfrak{u}$)

i.e. Energy associated with quantum, $E\propto \mathfrak{u}$

or, E = h$\mathfrak{u}$        ……… (1)

Where, h = Planck’s constant = 6.626$\times$10^-34 Js (SI unit) =  6.626$\times$10^-27 erg sec(CGS unit) = 6.626$\times$10^-13 kJ s mol^–1

iv) The total amount of energy emitted or absorbed by a body will be some whole number multiple of a quantum $E=nh\mathfrak{u}$. where, n = integer ( 1, 2, 3 …)

v) Thus a body can emit or absorb energy equal to $\mathrm{h}\mathfrak{u}, 2\mathrm{h}\mathfrak{u}, 3\mathrm{h}\mathfrak{u}$ or any other integral multiple of.

Photoelectric effect:

The phenomenon of ejection of electrons from the surface of a metal when light of suitable frequency strikes on it is called photoelectric effect.  The emitted electrons are called photoelectrons.

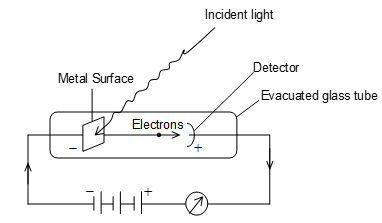
Law of Photoelectric effect:

i) Rate of emission of photoelectrons from a metal surface is directly proportional to the intensity of incident light (r $\propto$ I).

ii) The maximum kinetic energy of photoelectrons is directly proportional to the frequency of incident light radiation (E_k $\propto$). But independent of the intensity of light (used).

iii) There is no time lag between incidence of light and emission of photo electrons.

Iv) For emission of photo electrons the frequency of incident light must be equal to or greater than the threshold frequency $\left(\mathfrak{u}\ge {\mathfrak{u}}_0\right)$.

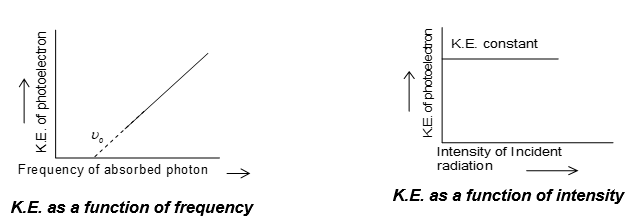
Explanation of photoelectric effect:

Photoelectric effect was explained by Einstein (1905) by using Planck’s quantum theory.  When light of suitable frequency falls on a metal surface, the light photon gives its energy to the electron of metal atom and the electron is ejected from metal surface by absorbing this energy.  The minimum energy of a photon required to eject an electron from a metal is called work function ($\varphi$) of the metal.  The remaining part of the energy ($h\mathfrak{u}–\varphi$) of photon is used to increase the kinetic energy of the ejected electron. If  is the threshold frequency and, the frequency of incident light then

Work function, $\varphi =h{\mathfrak{u}}_0$.

$\therefore$ According to Einstein, E = h$\mathfrak{u}$

$\therefore$ Kinetic energy of photo electron $E_k=E-\varphi =h\mathfrak{u}-h{\mathfrak{u}}_0$  (Einstein’s photoelectric equation)

Table: The values of work function for a few metals

Metal	Li	Na	K	Cs	Mg	Cu	Ag
$\varphi$o(eV)	2.42	2.3	2.25	1.9	3.7	4.8	4.3

Note: The minimum potential at which the plate photo electric current becomes zero is called stopping potential.  If V_o is the stopping potential then ${\mathrm{eV}}_{\circ }=\mathrm{h}\left(\mathfrak{u}-{\mathfrak{u}}_0\right)$.

Explanation of black body radiation:

Planck’s theory successfully explains the emission of radiation from a hot body (i.e., black body radiations).  When solids are heated.  They emit radiation over a wide range of wavelengths.

e.g., When iron rod is heated in a furnace, it first turns to dull red and then becomes more and more red as the temperature increases.  As this is heated further, the radiation emitted becomes white, then blue.  In terms of frequency, it means that the radiation emitted goes from a lower frequency to higher frequency region of the electromagnetic spectrum.

The ideal body, which emits and absorbs all frequencies is called a black body and the radiation emitted by such a body is called black body radiation.  A hollow sphere coated inside with platinum black and having a small hole in its wall acts as a near black body.

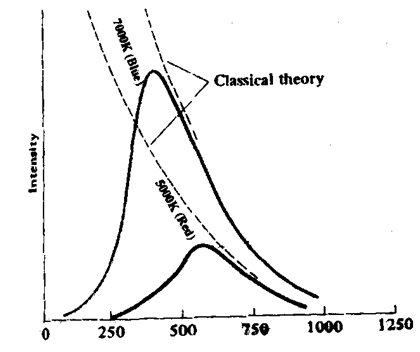
The exact frequency distribution of the emitted radiation i.e., intensity of the radiation versus frequency gives a curves.  Such curves obtained at different temperatures of the black body are shown in the figure.

         Wavelength in nm

Radiations emitted by a black body at different temperature

The study of the curves shows that the nature of the radiation depends on the temperature of the black body.  If the energy emitted is continuous the curve should be as shown by the dotted liens, but it is not so.

The following conclusions are drawn from the study of the shape of the curves.

i) At a given temperature, the intensity of the radiant energy increases with the wave length, reaches a maximum and then decreases.

ii) As the temperature increases, the peak of the curve shifts to lower wavelength.

The above experimental results could be explained satisfactorily on the basis of the wave theory of light.

Intensity of light: It is defined as number of photon falling per unit area per second and depends upon the number of photons.  It is also defined as amount of energy falling per unit area per second and depends upon the wavelength of photon.

Dual Nature of light:  Light is said to have a dual character because it behaves as a wave as well a particle.  Some properties of light such as interference and diffraction show the wave nature of light radiation, while the phenomena of black body radiation and photoelectric effect show the characteristic particle nature of light.

Illustration 5:   Calculate the energy of one mole of photons of radiation whose frequency is 6$\times$10¹⁴ Hz. (h = 6.626$\times$10^-34 Js)

Solution: Energy of one photon,

$E=h\mathfrak{u}=6.626\times {10}^{-34}Js\times 6\times {10}^{14}{s}^{-1}=39.756\times {10}^{-20}\mathrm{J}=3.9756\times {10}^{-19}\mathrm{J}$

Now, energy of one mole of photons = $\mathrm{E}\times {\mathrm{N}}_{\mathrm{A}}$

$=3.9756\times {10}^{-19}\mathrm{J}\times 6.022\times {10}^{23}{\mathrm{mol}}^{-1}$

$=23.94\times {10}^4\mathrm{J}{\mathrm{mol}}^{-1}=239.4\mathrm{kJ}{\mathrm{mol}}^{-1}$

Illustration 6:   The work function for cesium atom 1.9 eV.  Calculate

i) threshold wavelength               ii) threshold frequency of radiation.

If cesium element is radiated with a wavelength of 500 nm, calculate the kinetic energy and the velocity of the ejected electron.

Solution:  Work function, $h{v}_o=1.9\mathrm{eV}=1.9\times 1.602\times {10}^{-19}\mathrm{J}=3.04\times {10}^{-19}\mathrm{J}$

$\therefore \text{ Threshold frequency, }{v}_0=\frac{3.04\times {10}^{-19}\mathrm{J}}{6.626\times {10}^{-34}\mathrm{Js}}=4.59\times {10}^{14}{\mathrm{s}}^{-1}\left(\because \varphi =\mathrm{h}{v}_0\right)$

$\text{ Threshold wavelength, }{\lambda }_0=\frac{c}{v_0}=\frac{3.0\times {10}^8{\mathrm{ms}}^{-1}}{4.59\times {10}^{14}{s}^{-1}}=6.54\times {10}^{-7}\mathrm{m}$

$\text{ Now, energy of radiant light, }E=\frac{hc}{\lambda }=\frac{6.626\times {10}^{-34}\times 3.0\times {10}^8}{500\times {10}^{-9}}=3.98\times {10}^{-19}\mathrm{J}$

$\therefore \text{ K.E. of ejected electron }=E-h{v}_0=3.98\times {10}^{-19}\mathrm{J}-3.04\times {10}^{-19}\mathrm{J}=9.4\times {10}^{-20}\mathrm{J}$

$$\begin{gathered} \text{ or }\frac{1}{2}m{v}^2=9.4\times {10}^{-20}\mathrm{J} \text{ or }{\mathrm{v}}^2=\frac{2\times 9.4\times {10}^{-20}\mathrm{J}}{9.1\times {10}^{-31}\mathrm{kg}}=20.66\times {10}^{10} \\ \therefore \mathrm{v}=4.54\times {10}^5{\mathrm{ms}}^{-1} \end{gathered}$$

The electromagnetic spectrum:

The arrangement of all the electromagnetic radiations in the increasing order of their wave lengths or decreasing order of their frequencies is called electromagnetic spectrum.  A complete electromagnetic spectrum can be represented as:

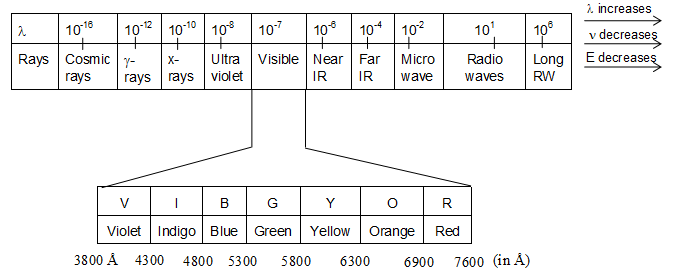
Wavelengths of different radiations increase in the following order:

Cosmic rays < $\gamma$-rays < X-rays < ultraviolet rays < visible < infrared < micro waves < radio waves

Remember that visible light is just a small portion of electromagnetic spectrum.

Emission, Absorption, Line and Band spectra:

i) Emission spectrum:

It is obtained by passing radiations from atoms through prism.  It has few bright lines against a dark background.  Emission spectra are mainly of two types.

a) Continuous spectra: It is obtained by passing sun light through a prism. The light is resolved/dispersed into continuous spectra of 7 colours.  It contains radiation of all frequency.

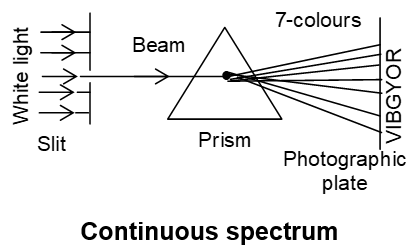
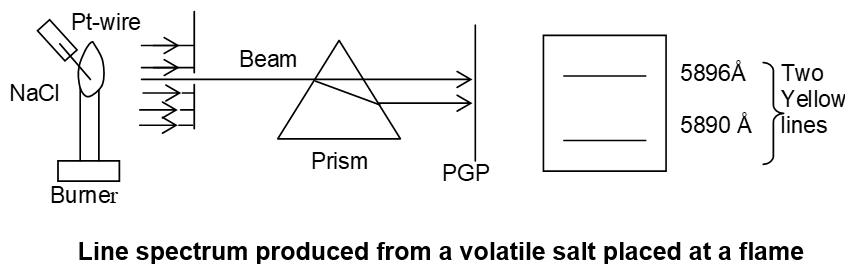
b) Line spectra: It is an atomic spectrum of an element, which consists of a number of bright lines separated by dark bands.

ii) Absorption spectra: It is obtained by passing white light through solutions or vapours of chemical substance and then analyzed by spectroscope. It has few dark lines in the continuous spectrum.

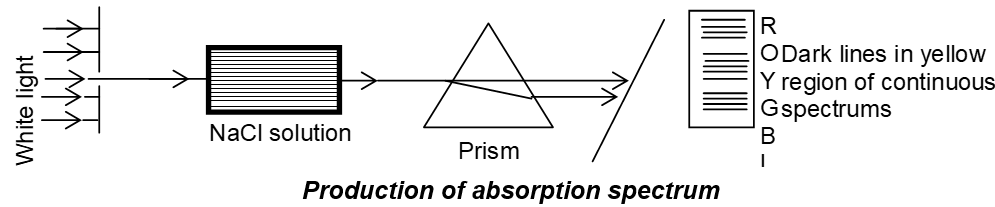
iii) Band Spectra: Bright bands are obtained in dark back ground.  All substances in molecular gaseous state produce Band spectra.

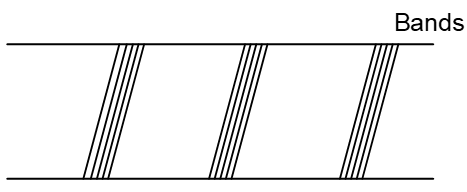
Spectroscopy: The study of emission or absorption spectra is referred to as spectroscopy.

Characteristics of Hydrogen spectrum:

Off all the atomic spectra the hydrogen spectrum is the simplest.  When an electric discharge is passed through gaseous hydrogen, the hydrogen molecules dissociate and the energetically excited hydrogen atoms produced emit electromagnetic radiation of discrete frequencies.  The hydrogen spectrum consists of several series of lines named after their discovers.

$\overline{\mathfrak{u}}=\frac{1}{\lambda }=R_H\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right){\mathrm{cm}}^{-1}$

where R_H is a Rydberg’s constant, its value for ‘H’ is 1,09,677 and n₁ & n₂ = integer  (1, 2, 3 )

For a particular series n₁ remains constant, while n₂ = n₁ + 1…….

i)	For Lyman series (UV region)	n1 = 1	n2 = 2,3,4, …
ii)	For Balmer series (visible)	n1  = 2	n2 = 3,4,5…..
iii)	For Paschen Series (near IR)	n1 = 3	n2 = 4,5,6 . . .
iv)	For Brackett series (IR)	n1 = 4	n2 = 5,6,7 . . .
v)	Pfund series (far IR)	n1 = 5	n2 = 6, 7, 8 . . .

Note: The first line in the Blamer series is called H_{$\mathrm{\alpha }$} line and its wavelength is found to be 6563 Å.

 

$\begin{array}{r}\text{ Similarly }{2}^{\text{nd }}\text{ line }\to H_{\beta },\lambda =4,861\text{Å}\\ 3^{\text{rd }}\text{ line }\to \mathrm{H}\gamma ,\lambda =4340\text{Å}\\ 4^{\text{th }}\text{ line }\to {\mathrm{H}}_{\delta },\lambda =4101\text{Å}\end{array}$

 

A line with n₂ = $\infty$ in Rydberg formula is called limiting line of shortest $\mathrm{\lambda }$ and high E.

Rydberg’s formula for H-like species:

$\overline{\mathfrak{u}}=R\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)z^2$where, Z = At. No. of H like species.

The maximum no. of spectral lines when an electron jumps from the n^th level to the ground level = $\frac{n(n-1)}{2}$

e.g. If an electron jumps from 3^rd level to the ground level, the no. of  possible spectral lines, 3 (3-1)/2 = 3 i.e. (3 → 2), (3 → 1) and (2→1)

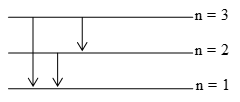
Illustration 7: What is the maximum number of emission lines when the excited electrons of a sample of H-atoms in n = 6 drop to the ground energy level?

Solution:  n₂ = 6, n = 1

No. of lines emitted during transition from 6^th orbit to 1^st orbit  =  $\sum \mathrm{\Delta }n=\sum (6-1)=\sum 5=15$

$\text{ i.e., }\left\{\sum \mathrm{\Delta }n=(6-1)+(5-1)+(4-1)+(3-1)+(2-1)\right\}$

Illustration 8:   Calculate the frequency of the spectral line emitted when the electron in n = 3 in H atom de-excites to ground state (R = 109737 cm^-1)

Solution:  We know that $\frac{1}{\lambda }=\mathrm{R}\left(\frac{1}{{\mathrm{n}}_1^2}-\frac{1}{{\mathrm{n}}_2^2}\right)$

$v=\frac{c}{\lambda }=\mathrm{RxC}\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right]=109737\times 3.0\times {10}^{10}\left[\frac{1}{1^2}-\frac{1}{3^2}\right]s^{-1}=2.92\times {10}^{15}{\mathrm{s}}^{-1}$

Bohr’s Model of Atom:

Neils Bohr, a Danish physicist in 1913, on the basis of Planck’s quantum theory proposed a new model of atom to overcome the drawbacks of Rutherford’s model of atom and to explain the line spectrum of hydrogen.

Postulates of Bohr’s Model:

i) An atom consists of a dense nucleus located at the centre with electrons revolving around it in circular orbits without emitting energy.

ii) Of the infinite no. of possible circular orbits around the nucleus, an electron can revolve only in those orbits whose angular momentum (mvr) is an integral multiple of a factor h/2$\mathrm{\pi }$e. angular momentum, mvr = $\mathrm{mvr}=\frac{\mathrm{nh}}{2\pi }$

where, m = mass of electron,  v = velocity of electron,  r = radius of the orbit,

n = orbit number in which the electron is present (1, 2, 3 ……)

This is called the condition of quantization of angular momentum.

iii) An electron ordinarily continues to move in a particular orbit called stationary orbit or energy level, without losing energy.  This state is called ground state.

iv) If energy is supplied to an electron, it may excite (jump) instantaneously from a lower energy level (say n₁) to a higher energy level (say n₂) by absorbing one or more photon of energy. This new state is called excited state.

The quantum or photon of energy absorbed in a jump is equal to the difference in energies of the two concerned levels and same amount of energy is emitted during de-excitation.  Thus, energy absorbed or released in an electron jump ($△$E) is given by the expressions.

$\mathrm{\Delta }E=E_2-E_1=hv=\frac{hc}{\lambda }\text{ where, }{E}_1\mathrm{\&}{E}_2$  = energies of 1^st and 2^nd Bohr’s orbits, $\mathfrak{u} =$Frequency of radiation absorbed. C = Speed of light (3.0$\times$10⁸ m/s) and $\mathfrak{u}$ = Wavelength of light absorbed.

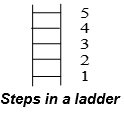
Note: The quantization concept may seem to be mysterious but it is very easy to understand.  The discrete energy levels in Bohr model may be compared with steps of a ladder. Imagine a ladder having steps labeled as 1, 2, 3, 4…….. from the bottom.

Your position on the ladder can only be on a step and never in between.  These steps in a ladder are similar to energy levels or orbits in an atom.

Success of Bohr’s Model:

i) Radius (r) of n^th Bohr’s Orbit:

Hydrogen atom contains a single proton in its nucleus with + ve.  An electron with – ve revolves found the nucleus in a circular orbit of radius ‘r’.  As per coulomb’s law, electrostatic force of attraction between the nucleus and the electron in given by the following expression.

Attractive force (F) $=\frac{-{\mathrm{e}}^2}{{\mathrm{r}}^2}$           ………. (i)

Because of revolution of electron around the nucleus a centrifugal force can be given as follows F =  $\frac{-m{v}^2}{r}$                        ………. (ii)

Where m is mass of electron, v is the velocity of electron and r is the radius of the electron.

From (i) and (ii) $\frac{{\mathrm{e}}^2}{\mathrm{r}}={\mathrm{mv}}^2$                 ………. (iii)

As per Bohr’s quantum condition

$\therefore v=\frac{nh}{2\pi mr}\left(\text{ or }\right)v^2=\frac{n^2{h}^2}{4{\pi }^2{m}^2{r}^2}$            ………. (iv)

Substitute the value of v² in equation (iii)

$\frac{e^2}{r}=\frac{m{n}^2{h}^2}{4{\pi }^2{m}^2{r}^2}\text{ (or) }r=\frac{n^2{h}^2}{4{\pi }^{2}m{e}^2}$

where n = principle quantum number, h = Planck’s constant = $6.6256\times {10}^{-27}$erg. sec

m = mass of electron = $9.1\times {10}^{-28}\mathrm{g}$ ,  e = charge on electron = $4.8\times {10}^{-10}$ e.s.u. and $\pi =3.14$

$\therefore$ Radius of nth orbit $\left(r_n\right)=\frac{n^2{h}^2}{4{\pi }^{2}m{e}^2}=0.529\times {10}^{-8}{\mathrm{n}}^2\mathrm{cm}$

If n = 1,  then $r_1=0.529\times {10}^{-8}\mathrm{cm}=0.529\stackrel{\circ }{\mathrm{A}}$ (radius of Bohr first orbit).  Similarly $r_2=2.116 \stackrel{\circ }{\mathrm{A}}$ and so on.

ii) Energy of electron in n^th Bohr orbit:

The total energy of electron revolving in a n orbit is obtained by summing up its kinetic energy and potential energy.

Kinetic energy due to motion of an electron (K.E) = 1/2 mv².      ………. (i)

where m is the mass of electron and v is its velocity.

Potential energy due to position $(P.E)=\frac{-e^2}{r}$         ………. (ii)

From equation (i) and (ii)  total energy of electron = KE + P.E

$=\frac{1}{2}m{v}^2-\frac{e^2}{r}=\frac{e^2}{2r}-\frac{e^2}{r}.\left(\because m{v}^2=\frac{e^2}{r}\right)$

$=\frac{-{\mathrm{e}}^2}{2\mathrm{r}}$      ………. (iii)

Substituting the value of ${}^{‘}{r}^{\mathrm{\prime }}=\frac{n^2{h}^2}{4{\pi }^{2}m{e}^2}$, in equation (iii)

The energy of electron in n^th orbit

 

$$\begin{gathered} {\mathrm{E}}_{\mathrm{n}}=\frac{-2{\pi }^2{\mathrm{me}}^4}{{\mathrm{n}}^2{\mathrm{h}}^2}{\mathrm{Z}}^2=\frac{-21.8\times {10}^{-12}}{{\mathrm{n}}^2}\text{ erg/atom }=\frac{-2.1\times {10}^{-18}}{{\mathrm{n}}^2}\mathrm{J}/\text{ atom } \\ \left(\because 1\mathrm{ev}=1.6022\times {10}^{-19}\mathrm{J}\right)=-\frac{1312}{{\mathrm{n}}^2}{\mathrm{kJmol}}^{-1} \end{gathered}$$

Order of Energy of various levels : K < L < M < N ………… and so on

Energy of H-like species (He⁺, Li²⁺ etc.):

 

$E_n=-\frac{2{\pi }^{2}m{e}^4}{n^2{h}^2}{Z}^2=-\frac{1312}{n^2}{Z}^{2}kJmo{l}^{-1}=-\frac{13.6}{n^2}{Z}^{2}eV=\frac{-2.18\times {10}^{-18}}{n^2}{Z}^{2}J/\text{ atom }$

 

$\begin{array}{l}{\mathrm{E}}_{\mathrm{k}}=\frac{-2{\pi }^2{\mathrm{n}}^2{\mathrm{me}}^4}{{\mathrm{n}}^2{\mathrm{h}}^2}{\mathrm{Z}}^2=\frac{-13.6}{{\mathrm{n}}^2}{\mathrm{Z}}^2\\ {\mathrm{E}}_{\mathrm{P}}=\frac{-{\mathrm{e}}^2}{\mathrm{r}}=\frac{27.2}{{\mathrm{m}}^2}{\mathrm{Z}}^2\mathrm{eV}\end{array}$

 $\text{ Total }{E}_n=E_k+E_p=\frac{-13.6}{n^2}{Z}^{2}eV$

Significance of negative electronic energy:

The energy of the electron in a hydrogen atom has negative sign for all possible orbits.

This negative sign means that the energy of the electron in the atom is lower than the energy of a free electron at rest.

A free electron at rest is an electron that is infinitely far away from the nucleus and is assigned the energy value of zero.

Mathematically, this corresponds to setting n equal to infinity in the equation so that E_{$\mathrm{\alpha }$}= 0.

As the electron gets closer to the nucleus (as n decreases), E_n becomes larger in absolute value and more and more negative.

The most negative energy value is given by n = 1 which corresponds to most stable orbit (i.e. ground state)

iii. Calculation of velocity (speed) of electron in an orbit:

Velocity of electron in n^th Bohr orbit $v_n=\frac{nh}{2\pi mr}=\frac{2\pi Z{e}^2}{nh}\mathrm{cm}/\sec$

${\mathrm{v}}_{\mathrm{n}}=\frac{2.182\times {10}^8}{\mathrm{n}}{\mathrm{Zcms}}^{-1}$

The velocity of e^–  in 1^st orbit of H is $\frac{1}{137}$ of the velocity of light.

iv) In explaining the spectrum of H-atom:

Spectrum of H-atom consists of a number of lines grouped into five series namely, Lyman, Balmer, Paschen, Brackett and Pfund series as shown below:

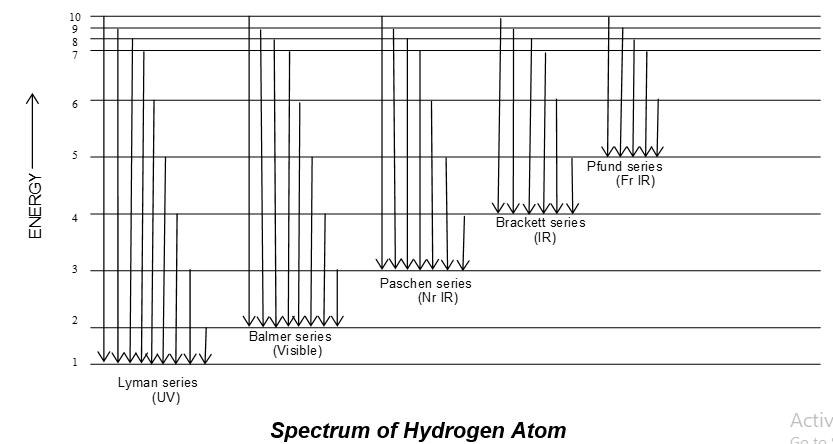
In any spectral series of hydrogen spectrum the intensity of line decreases as n₂ increases.

The frequency or wavelength or wave number of any spectral line in any of the series of
H-atom can be calculated by using Bohr theory by the following expression.

$\overline{\mathfrak{u}}=\frac{1}{\lambda }=R_H{Z}^2\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)$

v) In explaining of the stability of the atom:

An electron cannot lose energy as long as it stays in a particular orbit.

Therefore, the question of losing energy continuously and falling into the nucleus does not arise.

vi) Bohr was awarded Noble Prize in Physics in 1992 for his valuable work on spectra of hydrogen.

Limitations of Bohr’s Model:

Bohr’s model is true only for one electron systems.  e.g. H, He⁺, Li²⁺, Be³⁺ and so on.  And it fails for atoms or ions having more than one electron.

Thus, Bohr’s model suffers from following limitations

i) It explains only the spectrum of elements having only one electron.

ii) It does not explain splitting of spectral lines in magnetic field (Zeeman effect) and electric field (Stark effect)

iii) It does not explain quantization of angular momentum.

iv) It goes against the Heisenberg’s uncertainty principle.

Zeeman Effect and Stark Effect: Splitting of spectral lines under magnetic field is called Zeeman effect whereas splitting under electrical field is called Stark effect.

Sommerfeld Model: Bohr’s theory could not explain the fine structure of the spectrum i.e. the Zeeman and Stark effects. The theory was therefore, extended by Sommerfeld by introducing the idea of elliptical orbits in place of circular orbits.

The Main points of this model are:

i) The nucleus in an atom is situated at one of the foci of the ellipse and the electron revolves round this nucleus in elliptical orbits.

ii) Angular momentum of the electron moving in an elliptical orbit is quantized (i.e. nh/2$\mathrm{\pi }$).

$\text{ The ratio }\frac{\mathrm{n}}{\mathrm{k}}=\frac{\text{ length of major axis }}{\text{ length of minor axis }}$

The relation suggests for the possible no. of subshell.

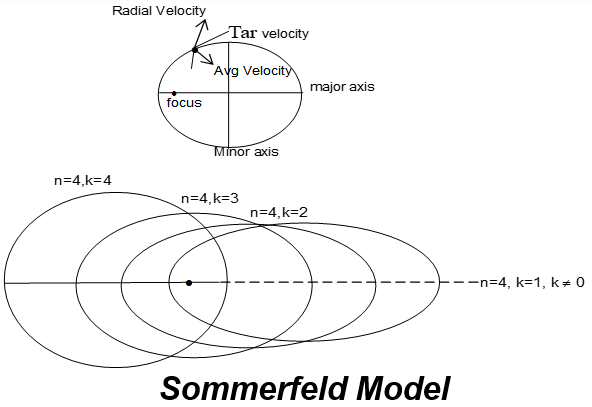
For n = 4, possible values of k are 1,2,3,4 respectively i.e. 4^th orbit has four sub orbits, three are elliptical and fourth one is circular.

Thus, Sommerfeld introduced the concept of sub-energy shells.  Smaller the value of k for any n_f the greater is the centricity of the elliptical orbit and more deeply it penetrate into the core of atom.

Limitations of Bohr – Sommerfeld Model:

i) It could not explain the spectrum of poly electronic systems so satisfactorily as they could do for one electron atoms.

ii) It does not explain distribution of electrons in extra nuclear part of atom for poly electronic atoms.

iii) It also does not explain de Broglie concept.  No doubt, Bohr and Sommerfeld proposed that angular momentum in closed orbits are quantized but they could not derive it mathematically.

Illustration 9:  Calculate the energy associated with the first orbit of He⁺.  What is the radius of the orbit?

Solution:  From equation ${\mathrm{E}}_{\mathrm{n}}=-\frac{13.6}{{\mathrm{n}}^2}{\mathrm{xZ}}^2\mathrm{eV}/\text{ atom }=-\frac{13.6\mathrm{x}4}{1^2}\mathrm{eV}$

Radius of the orbit, $r_n=\frac{0.529\times n^2}{Z}{A}^0(\because n=1)$

 

$\therefore r_1=\frac{0.529\times 1^2}{2}=0.2645{\mathrm{A}}^{\circ }$

Dual Nature of Matter:

In 1924, de Broglie, a French chemist proposed that all microscopic objects (material particles) such as electron, proton, atom, molecule, like photon have dual nature.  i.e., wave nature as well as particle nature.

This proposal gave birth to a new theory known as wave mechanical theory of matter.  According to this theory the electrons, protons and even atoms, when in motion, possess wave characters.

Therefore, the wave associated with a particle is called a matter wave or de Broglie wave.

de Broglie equation:

de Broglie derived an expression for calculating the wave-length of the wave associated with the electron.

According to Planck’s theory $E=hv=\frac{hc}{\lambda }$   ………. (i) (wave character)

where h = Planck’s constant = 6.626 $\times$ 10^-34 Js , c = velocity of light = 3.0 $\times$ 10⁸ m/s.

According to Einstein E = mc²      ……….. (ii) (particle character)

Where, m = mass of photon, c = the velocity of light

From equation (i) and (ii) we get $\mathrm{hu}={\mathrm{mc}}^2$

 

$\frac{\mathrm{hc}}{\lambda }={\mathrm{mc}}^2\left(\because \mathrm{v}=\frac{\mathrm{c}}{\lambda }\right)\mathrm{or}, \lambda =\frac{\mathrm{h}}{\mathrm{mc}}=\frac{\mathrm{h}}{\mathrm{p}}\propto \frac{1}{\mathrm{p}}$     ……… (iii)

Thus, for any material particles like, electron it may be written as (c = v)

$\lambda =\frac{\mathrm{h}}{\mathrm{mv}}=\frac{\mathrm{h}}{\mathrm{p}}=\frac{\mathrm{h}}{\sqrt{2}\mathrm{mE}}$     (de Broglie equation for particles)

where,

h = Planck’s constant = (6.626 $\times$ 10^-34Js)

m = mass of the electron (particle)

v = speed of electron (particle)

mv = momentum of the particle

$\mathrm{\lambda }$ = de Broglie wavelength = particle wavelength = material wavelength

Significance of de Broglie equation:

It is applicable to all material objects but it has more significance only in case of microscopic particles. e.g. the wavelength of macroscopic bodies such as cricket ball or bullet calculated by using de Broglie equation are too small in magnitude and are generally ignored.

e.g.  Let us consider a ball of mass 0.1 kg, moving with a speed of 60 ms^-1.

$\therefore \lambda =\frac{\mathrm{h}}{\mathrm{mv}}=\frac{6.62\times {10}^{-34}{\mathrm{kgm}}^2{\mathrm{s}}^{-1}}{0.1\mathrm{kg}\times 60{\mathrm{ms}}^{-1}}\approx {10}^{-34}\mathrm{m}$ (too small, so it is ignored)

Similarly mass of bullet = 2 gram; velocity = 2$\times$10⁵ cm/sec

$\therefore \lambda =\frac{\mathrm{h}}{\mathrm{mv}}=\frac{6.62\times {10}^{-34}{\mathrm{kgm}}^2{\mathrm{s}}^{-1}}{2\times {10}^{-3}\mathrm{kg}\times 2\times {10}^3{\mathrm{ms}}^{-1}}=7.656\times {10}^{-34}\mathrm{m}$ (too small so it is ignored)

On the other hand, let us consider the case of an electron moving with the same velocity of 60 m/sec in an orbit, would have a wave length

This wavelength associated with the electron can be easily measured experimentally.  Hence its wave nature is of significance.

de Broglie relationship has no significance in every day life, since we come across macroscopic objects in our everyday life.  This is the region why we don’t observe any wave nature associated with the motion of running car, or cricket ball etc.

Experimental verification of the dual character of matter:

i) Davisson and Germer’s experiment: It confirms the wave nature of electron(s).

ii) Scintillation method, Photo electric effect, Compton effect and black body radiation confirm the particle nature of the electron. (The decrease in energy or increase in wavelength of X-rays after scattering from the surface of carbon or lighter elements is known as Compton effect).

de Broglie concept and Bohr’s theory:

According to Bohr’s model as electron is a particle and revolves round the nucleus in circular orbit, in which the angular momentum of the electron is an integral multiple of h/2$\mathrm{\pi }$

$\text{ i.e. }\mathrm{mvr}=\frac{\mathrm{nh}}{2\pi }$

But according to de Broglie concept the electron behaves both as particle and as a wave.  The revolution of an electron in a circular path involves two cases.

Case-I:

The wave train of electrons may be continuously in phase or out of phase.  If the two ends of the wave meet of to give a regular series of crests and troughs, the wave motion is said to be in phase.

If the circumference of electron orbit (2$\mathrm{\pi }$r) is an integral multiple of wavelength then electron waves are said to be in phase because two ends of the electron wave meet to give a regular series of crests and troughs.

In this case constructive interference of the electron wave occurs and the electron is considered to behave as a standing or stationary wave or non-energy radiating wave i.e., electron doesn’t lose energy as long as it revolves in such an orbit.

Case-II:

If the two ends of the wave do not meet to give a regular series of crests and troughs, it is said to be out of phase.

For wave motion to be continuously in phase, the circumference of circular orbit must be integral multiple of $\mathrm{\lambda }$.

If the circumference of the electron orbit is not a integral multiple of the wavelength then the electron waves are said to be out of phase.

A destructive interference of waves occurs causing radiation of energy.  In this case Bohr’s orbit is bigger or smaller than n$\mathrm{\lambda }$ i.e. orbit cannot exist.

Therefore to get a electron wave in phase, the circumference of the Bohr’s orbit (2$\mathrm{\pi }$r) must be equal to the integral multiple of wavelength of an electron-wave i.e

$n\lambda =2\pi r$

or,  $\lambda =\frac{2\pi }{\mathrm{n}}$     where, n = integer.        [1, 2, 3…….]

From de Broglie concept, $\lambda =\frac{\mathrm{h}}{\mathrm{mV}}$

$\therefore \frac{2\pi }{n}=\frac{h}{mv}\text{ or }mvr=\frac{nh}{2\pi }$

$\therefore$ This proves that Bohr’s theory and de Broglie concept are in perfect agreement with each other.

Illustration 10: Find out:

a) velocity of electron in first Bohr orbit of hydrogen atom (r = a_o)

b) de Broglie wavelength of the electron in Bohr orbit of H-atom

Solutions: $\text{ a) }\mathrm{mvr}=\frac{\mathrm{nh}}{2\pi }$

$v=\frac{\mathrm{nh}}{2\pi \mathrm{mr}}=\frac{1\times 6.626\times {10}^{-34}}{2\times 3.14\times 9.1\times {10}^{-31}\times 0.529\times {10}^{-10}}=2.19\times {10}^6\mathrm{m}/\mathrm{s}$

$\text{ b) }\lambda =\frac{\mathrm{h}}{\mathrm{mu}}=\frac{6.626\times {10}^{-34}}{9.1\times {10}^{-31}\times 2.19\times {10}^8}=3.32\times {10}^{-10}=3.32\dot{\mathrm{A}}$

Heisenberg’s Uncertainty Principle: It states that it is not possible to determine precisely both the position and the momentum or velocity of moving microscopic particle simultaneously.

Mathematically, $△\mathrm{x}\cdot \mathrm{\Delta }p\ge \frac{h}{4\pi }\text{ or }\mathrm{\Delta }x\cdot m\mathrm{\Delta }v\ge \frac{h}{4\pi }$

Where, $△$x, $△$p and $△$v are uncertainties with respect to position, momentum and velocity respectively and  h = Planck’s constant. (6.626 $\times$10^-34 Js or kg m²s^-1)

This inability is not due to lack of proper instruments but due to the limitations imposed by nature on such measurements.

Thus Heisenberg’s uncertainty principle is one of the basic principles of wave mechanics.

Physical concept of uncertainty principle:

To determine the position of an object we must be able to ‘see’ the object.  This can be done with help of light of suitable wavelength.

When a beam of light falls on an object, the photon of this incident light strikes the electron and the reflected light photon is seen in microscope.

Case-I: If the object is large, its position and velocity will not change by the impact of striking photons.  Thus it will be possible to determine both the position and velocity of the object  simultaneously.

Case-II: If the target object is a microscopic body i.e. electron, the position as well as the momentum (or velocity) of the electron are disturbed.

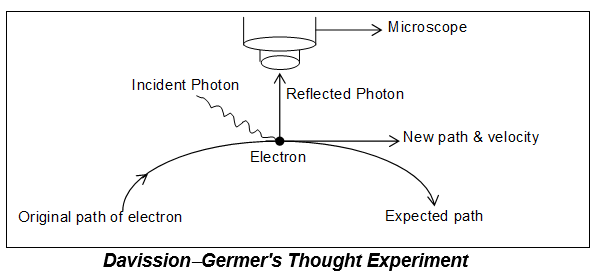
According to principle of optics, the accuracy in measurement depends upon the wavelength of light. The uncertainty in position = $\pm \mathrm{\lambda }$

Hence, shorter the $\mathrm{\lambda }$, greater the accuracy, higher the frequency, higher the energy

Hence, this high energy photon on striking the electron changes its speed as well as direction (i.e. position)

In other words,  shorter $\mathrm{\lambda }\Rightarrow$ higher momentum (p), greater uncertainty in v

                             larger $\mathrm{\lambda }\Rightarrow$ lower momentum (p), greater uncertainty in $△$x

Thus, uncertainty principle is valid for all conjugate pair of physical quantities, for example position and momentum, energy and time and so on.

Significance of Heisenberg’s uncertainty principle:

Like de Broglie equation, it has more significance for microscopic particles (i.e electrons).

Reason: The energy of photon is not sufficient to charge the position and velocity of larger bodies when it collides with them.  e.g. the light from a torch falling on a running cat in a dark room neither changes the speed of the cat nor its position (i.e. direction).

This principle is more significant for the microscopic particles because the product of the $△$x and $△$v is quite measurable i.e.

i) For an electron $\mathrm{\Delta }x\cdot \mathrm{\Delta }p=\frac{h}{4\pi m}=\frac{6.626\times {10}^{-34}{\mathrm{kgm}}^2{\mathrm{s}}^{-1}}{4\times 3.14\times 9.1\times {10}^{-31}\mathrm{kg}}\approx {10}^{-4}{\mathrm{m}}^2{\mathrm{s}}^{-1}$(measurable)

Here, if uncertainty  in $△$x  is 10^-4 m then uncertainty in $△$v is 1.0 ms^-1 (measurable – more significantly)

ii) For a particle of 10^-6 kg;

$\mathrm{\Delta }x.\mathrm{\Delta }p=\frac{h}{4\pi m}=\frac{6.626\times {10}^{-34}{\mathrm{kgm}}^2{\mathrm{s}}^{-1}}{4\times 3.14\times 9.1\times {10}^{-31}\mathrm{kg}}\approx {10}^{-28}{\mathrm{m}}^2{\mathrm{s}}^{-1}$ (no significance $\because$ not measurable)

Therefore, for a particle of mass greater than 1 mg (or 10^-6 kg) the product of $△$x and $△$p will be still smaller, hence, these values are ignored (Not measurable).

Since, in everyday life, we come across large objects only, the position and velocity of which can be measured accurately.  Hence, Heisenberg’s uncertainty principle has no significance in every day life.

In other words, uncertainty principle has the fundamental limitation of nature. 

Illustration 11: A photon is accelerated to a velocity of 3$\times$10⁷ ms^-1.  If the velocity can be measured with a precision of $\pm$ 0.5%, calculate the uncertainty in position of photon (h = 6.6×10^-34 JS, mass of photon = 1.66×10^-27 kg)

Solution: $\mathrm{\Delta v}=\frac{3\times {10}^7\times 0.5}{100}=3\times 0.5\times {10}^5=1.5\times {10}^7{\mathrm{ms}}^{-1}$

According to Heisenberg’s principle$\mathrm{\Delta }x=\frac{h}{4\pi m\mathrm{\Delta }v}=\frac{6.6\times {10}^{-34}{\mathrm{kgm}}^2{s}^{-1}}{4\times 3.14\times 1.66\times {10}^{-27}\mathrm{kg}\times 1.5\times {10}^5{\mathrm{ms}}^{-1}}=2.11\times {10}^{-13}\mathrm{m}$

 

Illustration 12: A Golf ball has a mass of 40 gm and a speed of 45 m/s.  If the speed can be measured within accuracy of 2%, calculate the certainty in position.

Solution: Uncertainty in speed $\mathrm{\Delta v}=45\times \frac{2}{100}=0.9{\mathrm{ms}}^{-1}$

From uncertainty principle,  $\mathrm{\Delta }x=\frac{h}{4\pi \times m\times \mathrm{\Delta }V}=\frac{6.626\times {10}^{-34}{\mathrm{kgm}}^2{\mathrm{s}}^{-1}}{4\times 3.14\times 40\times {10}^{-3}\mathrm{kg}\times 0.9{\mathrm{ms}}^{-1}}=1.46\times {10}^{-33}\mathrm{m}$

Schrödinger Wave equation:  (Wave mechanical model):

It is based on the de Broglie and Heisenberg’s uncertainty Principle and put forward by Erwin Schrödinger, in 1926 to describe the behaviour of electron in three dimensional space around the nucleus in terms of equation known as Schrödinger wave equation, which is considered as the heart of quantum mechanics i.e.

$\frac{{\mathrm{\partial }}^2\psi }{\mathrm{\partial }{\mathrm{x}}^2}+\frac{{\mathrm{\partial }}^2\psi }{\mathrm{\partial }{\mathrm{y}}^2}+\frac{{\mathrm{\partial }}^2\psi }{\mathrm{\partial }{z}^2}+\frac{8{\pi }^2\mathrm{m}}{{\mathrm{h}}^2}(\mathrm{E}-\mathrm{V})\psi =0 or {\mathrm{\nabla }}^2\psi +\frac{8{\pi }^2\mathrm{m}}{{\mathrm{h}}^2}(\mathrm{E}-\mathrm{V})\psi =0$

${\mathrm{\nabla }}^2=\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\mathrm{x}}^2}+\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\mathrm{y}}^2}+\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\mathrm{z}}^2}$

where, m = mass of the electron,  E = total energy of the electron (KE+PE), V = potential energy of the electron, h = Planck’s constant, $\psi$ = wave function or amplitude of the wave, x, y, z = three dimensional coordinates and $\mathrm{\nabla }$ (read as ’del squared’) = Laplacian operator

This equation applies to stationary states or waves as it does not have time dependence part of the wave function.

Putting $ħ=\frac{h}{2\pi }$  in above equation

$\left[-\frac{{ħ}^2}{2\mathrm{m}}{\mathrm{\nabla }}^2+\mathrm{V}\right]\psi =\mathrm{E}\psi$

$\widehat{\mathrm{H}}=-\frac{{ħ}^2}{2\mathrm{m}}{\mathrm{\nabla }}^2+\mathrm{V} \widehat{\mathrm{H}}\left(\text{ read as’ech hat’ }\right)=$Hamiltonian operator

$\widehat{\mathrm{H}}\psi =\mathrm{E}\psi$

Schrödinger shared 1933 Physics Nobel Prize with Dirac for discovery of new productive forms of atomic theory.

Meaning and Significance of $\psi$ (wave function): 

Max Born called it ‘probability amplitude function’ – for his this interpretation Born received 1954 Physics Nobel. In the physical sense, $\psi$(psi) gives the amplitude of the wave associated with the electron. The wave function may have positive or negative values depending upon the values of coordinates. $\psi$ has no physical significance.

Significance of ${\psi }^2$:

${\psi }^2$ is a probability factor. It gives the intensity of electrons and thus gives probability of electron in a particular region.  For ${\psi }^2$ = 0, the probability of finding the electrons is zero.  If${\psi }^2$ is maximum, probability of finding the electrons is one.  Schrödinger wave equation is a differential equation of second order and solutions of it provide several values of $\psi$ including imaginary values which are not valid only those values of $\psi$ are valid which satisfy the following conditions:

i) The wave function must be finite and continuous.

ii) $\psi$ must be single valued at any point.

iii) The solution must be normalized and should satisfy the relation ${\int }_0^{\mathrm{\infty }} \psi \mathrm{dr}=0$ .

iv) The probability of finding the electron overall the space from + $\infty$ to –$\infty$ must be equal to one.

v) $\frac{\mathrm{\partial }\psi }{\mathrm{\partial }x},\frac{\mathrm{\partial }\psi }{\mathrm{\partial }y},\frac{\mathrm{\partial }\psi }{\mathrm{\partial }z}$must be continuous functions of x, y, z respectively.

Eigen functions:

When Schrödinger’s equation is solved for a hydrogen atom several solutions are obtained which are known as wave function or Eigen functions.

Quantum Numbers:

The solution of Schrödinger wave equation gives a set of numbers called quantum numbers.  In other words, four identification numbers are required to locate a particular electron in an atom.  These identification numbers are called quantum numbers.

i) Principal quantum No. (n):

It was given by Bohr.  It is used to specify the size, position and energy of electron in an orbit or shell.  It is denoted by n where, n = 1, 2, 3…… $\infty$.

Values of n	1	2	3	4	5	6	7	8
Shell	K	L	M	N	O	P	Q	R

Position of electron from the nucleus in the n^th orbit =  (r $\propto$ n)

r₁ < r₂ < r₃ ……..

$r_n=a_0\times \frac{n^2}{7}=0.529\frac{n^2}{7}{A}^0$

Higher the value of n, greater is the energy E₁ < E₂ < E₃      (E$\propto$n)

$E_n=-\frac{13.6}{n^2}\times Z^2\mathrm{eV}/\text{ atom }$

Maximum number of electrons in shell = 2n²

angular momentum mvr = nh/2$\mathrm{\pi }$.

Thus ‘n’ specifies the orbit number of the electron.

Shell symbol	K	L	M	N
Shell No(n)	1	2	3	4
No of orbitals(n2)	1	4	9	16
No of electrons (2n2)	2	8	18	32

ii) Azimuthal or Angular quantum number(l):

It was given by Sommerfeld.  It is also called as subsidiary quantum number or secondary quantum no.  It is denoted by l .  Possible values of l are 0  to  n-1.  It is used to describe a subshell.

Value of l	0	1	2	3	4
Subshell	s	p	d	f	g

Here s, p, d, f and g are spectral terms and signify sharp, principal, diffuse, fundamental, degenerated spectral lines. ‘l’ also specifies the shape of orbitals occupied by an electron i.e s is spherical in shape, p is dumb-bell shaped while that of d is double-dumb bell.

Order of energy of subshell : s < p < d < f < g

A sub shell is only possible if, l < n

Any subshell is represented by ‘nl’

If n = 1, l = 0 $\Rightarrow$ 1s subshell and if n = 2, l = 1 $\Rightarrow$ 2p subshell

Total No. of subshells in a shell = n

Orbital angular momentum (L) is quantized and is given a $L=\sqrt{l(l+1)}\frac{h}{2\pi }$

Maximum electrons present in a subshell = 2(2l+1) 

iii. Magnetic quantum number (m):

It was proposed by Lande in 1921.  It determines the preferred orientations of orbitals in space. It is denoted by m or m_l  Possible values of m are from -l, through + l (including zero).

For l = 0, m = 0, $\Rightarrow$ s-subshell
for  l = 1, m = – 1, 0, + 1 $\Rightarrow$ three orientations $\Rightarrow$ p_x, p_y, p_z
for  l = 2, m = -2, -1, 0, +1, +2 $\Rightarrow$ five orientations

Value of m	$\pm$2	$\pm$1	0
Orbital	dxy  or	dyz or dzx

For l = 3, m = -3, -2, -1, 0, +1, +2, +3 $\Rightarrow$ 7 orientations

Total values of m = (2l+1)

In the absence of magnetic field, the p-orbitals are degenerate.  The sub-sub shell (orbitals) having same energy level are known as degenerate orbitals.

iv. Spin quantum number(s):

Wave mechanical treatment requires no more than three quantum numbers n, l & m.  The existence of multiple structure led to the introduction of a spin quantum number.  It was given by Goudsmit and Uhlenbeck and is denoted by ‘s’ or m_s.  It represents the direction of spin of electron around its own axis.

For clockwise spin, $\mathrm{s}=+\frac{1}{2}(\uparrow )$ and for anticlockwise spin, $s=-\frac{1}{2}(\downarrow )$

Spin angular momentum is given by ${\mu }_s=\frac{h}{2\pi }\sqrt{s(s+1)}=\frac{h}{2\pi }\sqrt{\frac{1}{2}\left(\frac{1}{2}+1\right)}=\frac{\sqrt{3h}}{4\pi }$.

Each orbital can accommodate two electrons.

Electrons having same spins are called spin parallel while  those having opposite spin are called spins paired.

Total spin of an atom or an ion $=\mathrm{nx}\frac{1}{2}$; where n is the number of unpaired electrons.

Spin multiplicity of atom (S) = 2s+1 i.e.

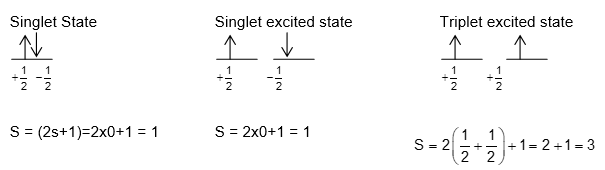
Note:

(i) For system with single electron energy of an electron in an orbital depends on the principal quantum number.

(ii) For multi-electron systems, energy depends on both principal and azimuthal quantum numbers.

Illustration 13: Calculate the value of Bohr magneton. For hydrogen like atom with a 3d electron, what is the value of the orbital angular momentum in terms of it?

Solution: We have

${\mu }_{\mathrm{B}}\left(\mathrm{BM}\right)=\frac{\mathrm{eh}}{\mu \pi \mathrm{m}}=\frac{1.6\times {10}^{-19}\mathrm{x}6.626\times {10}^{-34}}{4\times 3.14\times 9.1\times {10}^{-31}}=\frac{10.60\times {10}^{-53}}{342.88\times {10}^{-25}}=9.266\times {10}^{-24}{\mathrm{JT}}^{-1}(T=\text{ tesla })$

Further, orbital angular momentum, $L=\sqrt{I(1+1)}\frac{h}{2\pi }$

For  3d electron, l = 2, $I=2,L=\sqrt{2(2+1)}\frac{h}{2\pi }=\sqrt{6}\frac{h}{2\pi }$

Illustration 14: Write down the quantum numbers n, l and m for the following orbitals.

i) 3p_x    ii) 3d_xy   iii) 3dx^2­­­­– y²   iv) 3d_xz    v) 4dz²    vi) 2p_z

Solution: 

$$\begin{gathered} \text{ i) }n=3,I=1,m=-1\text{ or }+1 \\ \text{ ii) }n=3,I=2,m=-2\text{ or }+2 \\ \text{ iii) }n=3,I=2,m=-2\text{ or }+2 \\ \text{ iv) }n=4,1=2,m=-1\text{ or }+1 \\ \text{ v) }n=4,I=2,m=0 \\ \text{ vi) }n=2,1=1,m=0 \end{gathered}$$

Shells:

There are main energy levels occupied by the electron.  Shells are represented by the principal quantum no (n).  e.g. n=1 represent K-shell, n-2 represent L-shell & so on.

Subshells:

These are sub energy levels occupied by the electron.  Subshells are represented by the ‘l’.  These are denoted by s, p, d, f notations.

Orbitals:

Orbitals are the 3dimensional regions of space around nucleus where probability of finding the electron is maximum (90 to 95%).  Probability does not become zero, even at infinity and is given by ${\psi }^2$. Electron orbitals in atom are called atomic orbitals while those in molecules are called molecular orbitals.  Orbitals have definite energy and momentum and they are quantized  i.e ${\mathrm{i}}_{\mathrm{m}}{\mathrm{E}}_{\mathrm{n}}=-\frac{{\mathrm{E}}_1}{{\mathrm{n}}^2}$.

Thus Bohr concept of well defined orbitals is ruled out.

Shape of Orbitals:

The electron cloud represents the shape of orbital.  Electron cloud is not uniform but it is dense where the probability for finding the electron is maximum (90%).  The problems associated with the representations of the variations of $\left|{\psi }^2\right|$  in space have circumvented by the following two approaches.

i. Charge Cloud Diagrams:

In this approach, the charge cloud is represented as a collection of dots such that the density of dots in any region represents the electron probability density in that region.  These sources give idea about the shape of the orbital s.

ii. Boundary Surface diagrams:

In this approach, the shape of an orbital is defined as a surface of constant probability density that encloses some large fraction (90%) of the probability of finding the electron.

s-orbitals:

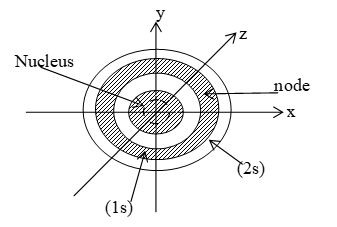
s-orbitals do not have directional dependence i.e. s-orbitals do not vary with angles. All the s-orbitals are called spherically symmetrical.  Size increases with increases in the value of n.  Radial nodes or spherical nodes (the plane at which electron density is zero) = n-1.

for 1s, nodal plane = 1-1 = 0

for 2s, nodal plane = 2-1 = 1

for 3s, nodal plane = 3-1 = 2

Therefore, number of nodal planes increases with increasing value of n electron.  The 2s-orbital differs in detail from 1s-orbital.  The electron in 2s-orbital is likely to be found in two regions, one near the nucleus and other in spherical shell about the nucleus.

p-orbitals: 

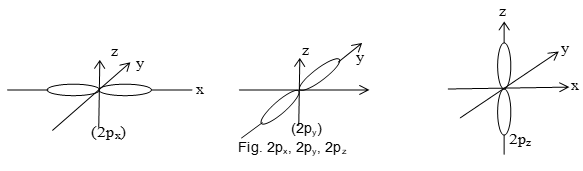
All p-orbitals with l $\ne$0 have angular dependence.  Angular dependence orbitals like p and d are not spherically symmetrical. Each p-orbital consist of two lobes and is dumbbell shaped. (lobe are separated by a plane of zero probability). p-orbital has three possible orientations of electron cloud along x, y, z axis named as p_x, p_y, p_z orbitals are perpendicular to each other.

All the three p-orbitals of a subshell have the same size and shape but differ from each other in orientation.

The subscripts x, y and z indicates axis along which orbitals are oriented and possess maximum electron density.

Total nodes = (n – l – 1).

d-orbitals:

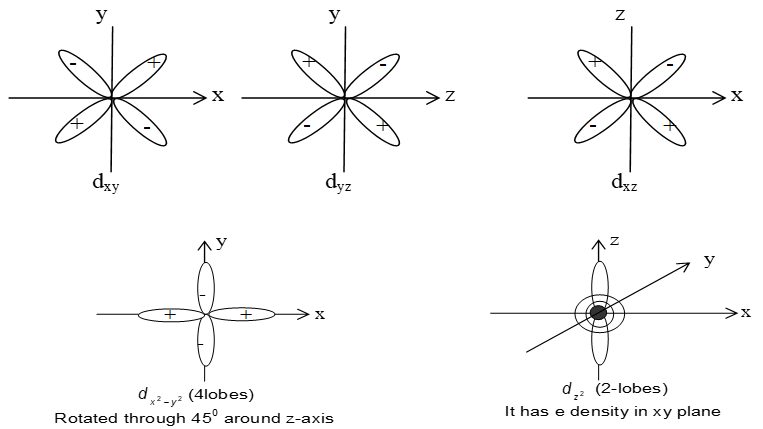
d-orbitals have five different orientation.  Each d-orbital possess same energy but differ in their orientation in space.  Each orbitals consists of four lobes and is double dumb-bel shaped except dz² which consists of only two lobes along z-axis and a dough nut in the xy-plane i.e dz² contain a ring of negative charge surrounding nucleus in xy-plane.  The d-orbitals for which n is greater than 3 (4d, 5d, …) have similar shapes.  d-orbitals have two nodal planes. Orbitals of sub-shell having same energy are called degenerated orbitals.

f-orbitals:

f-orbitals have seven orientations, which are designated as $f_{x\left(x^2-y^2\right)},f_{y\left(x^2-y^2\right)},f_{z\left(x^2-y^2\right)},f_{x{z}^2},f_{y{z}^2},f_{y{x}^2}, f_{xyz}$. 

The shapes of these orbitals are complicated.  They in fact are triple dumbbell.

Spherical or Radial nodes and nodal planes:

Spherical nodes:

The spherical surface where the probability of finding the electron is zero called radical node or spherical node or simply node.  Number of spherical nodes in an orbital = n – l – 1.  e.g. for 1s, no. of spherical nodes = 1 – 0 – 1 = 0 and for 2s, no of spherical nodes = 2 – 0 – 1 – 1 & so on…

Nodal Planes:

The plane in which the probability of finding an electron is zero is called a nodal plane.  No. of nodal planes for an orbital = l = number of angular nodes or number of spherical nodes.  e.g. for s orbital l = 0,$\therefore$ No. of nodal plane = 0, for p orbital  l = 1

Note:

(i)  Total no. of nodes = n-1

(ii)  The region of maximum electron density is called antinodes.

Radial probability distribution curves for 1s, 2s, 3s, 2p, 3p, orbitals:

Electron radial probability distribution function $\left(\mathrm{D}\right)=4\pi r^2\mathrm{dr}{\psi }^2$.

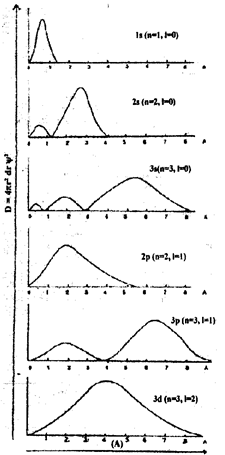
The radial probability distribution curves as obtained for is, 2s, 3s, 2p, 3p orbitals are shown in figure.

i) From the figures the probability of finding an electron in each case at the nucleus is zero indicating that the electron is never found at the nucleus.

ii) The distance, at which the maximum probability of finding an electron increases with increase in the value of the principle quantum number. e.g., for 1s orbital the maximum probability is at 0.53 Ǻ; for 2s orbital it is at about 2.6 Ǻ and for 3s orbital it is still farther away. Thus the size of the orbital increases in the order 1s< 2s <3s.

iii) The total number of peaks appearing in the radial distribution curves drawn for 8 orbitals is equal to the principle quantum number, n. The maximum probability of finding a 1s electron is only at a radial distance of 0.53 Ǻ spherically symmetrical around the nucleus. 2s orbital has two peaks a lower maximum at 0.53 Ǻ and a higher maximum at 2.6 Ǻ of radial distance. That means a 2s electron is found at 0.53 Ǻ though the probability is low and to the maximum extent at 2.6 Ǻ. 

At a radial distance of about 1.1 Ǻ the curve touches the line of zero probability.  This signifies that within the spherical orbital of a 2s electron, there is a spherical shell in which the probability of finding the electron is zero. This is called a “radial node”. The surface at which the probability of finding an electron is zero is called a radial node. Radial nodes are given by nodes are given by (n – 1-1). For example, for 3s, they are (3 -0 – 1) = 2, for 3p (3 – 1 – 1 ) = 1 for 3d(3 – 2 -1) = 0.

Electronic configuration of elements:

It is simple distribution of electrons into various shells subshells and orbitals.  The electronic configuration of any orbital can be simply represented by following notation nl^x, where

n = principal quantum number l = azimuthal quantum number  x = no. of electrons.

Rules for filling of orbitals in an atom:

I) Aufbau principle:

Aufbau is a German term meaning “building up”.  It states that “the subshell with minimum energy is filled up first and when this obtain maximum quota of electrons then the next subshell of higher energy starts filling. i.e. electrons are added to orbitals in increasing order of energies as (n+l).

II) Pauli’s Exclusion Principle:

Put forward by Pauli in 1925.  It imposes some restrictions on the assignment of the values to quantum number of electrons in the same orbital of an atom and hence it is called exclusion principle.

It states that “no two electrons in an atom can have same values for all the four quantum numbers”, or an orbital can have maximum two electrons and these must have opposite spins.
Maximum no. of electrons in a:

Shell	Subshell	Orbital
2n2	s    p    d     f 2    6   10  14	2

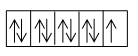
Nitrogen. _­7N : 1s², 2s²p³

7N	1s2	2s2	2px1	2py1	2pz1
n	1	2	2	2	2
l	0	0	1	1	1
m	0	0	+1	-1	0
S	$\pm$ ½	$\pm$ ½	$\pm$ ½	$\pm$ ½	$\pm$½

III) (n+l) Rule:

(i) Subshell with lower value of (n+l) possesses lower energy level.  e.g. Which subshell has

Sub shell	3d	4s
n+l	3+2 = 5	4+0 = 4 (low – occupied first)

$\therefore$ 4s has lower energy and occupies electron first.

ii) If (n+l) for two orbitals is same, the one with lower value of n possesses lower energy level and filled up first.

e.g.	Subshell	4p	3d
	n+l	4+1=5	3+2 = 5 (filled up 1st)

IV) Hund’s Rule of Maximum Multiplicity:

It states that pairing of electrons in various orbitals like p, d and f of same subshell cannot occur until each orbital of a given subshell is singly occupied.

e.g. ₆C $\Rightarrow$ 2, 4 or  1s², 2s² 2p²

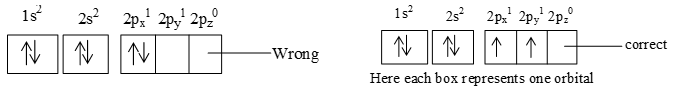
e.g. II) ₇N $\Rightarrow$ 2, 5 or 1s², 2s² 2p³

Electronic configuration of elements with Atomic No. 1 to 10 & from 21 to 30:

At. No.	Element	Configuration		At. No.	Element	Configuration
1	1H	1s1		21	21Sc	[Ar]3d1,4s2
2	2He	1s2		22	22Ti	[Ar]3d2, 4s2
3	3Li	[He]2s1		23	23V	[Ar] 3d2, 3s2
4	4Be	[He]2s2		24	24Cr	[Ar] 3d5 4s1
5	5B	[He]2s2p1		25	25Mn	[Ar] 3d54s2
6	6C	[He]2s2 2p2		26	26Fe	[Ar] 3d6 4s2
7	7N	[He]2s22p3		27	27Co	[Ar] 3d74s2
8	8O	[He]2s22p4		28	28Ni	[Ar] 3d8 4s2
9	9F	[He]2s23p5		29	29Cu	[Ar] 3d104s1
10	10Ne	[He]2s22p6		30	30Ag	[Ar] 3d10 4s2

 Exception to Aufbau Principle:

It has some exceptions but a simple reason behind this is that, half filled and full filled subshells have got extra stability.

₂₅Cr   $\Rightarrow$1s²2s²2p⁶3s²3p⁶3d⁴4s²   (Wrong)

          $\Rightarrow$ 1s²2s²2p⁶3s²3p⁶3d⁵4s¹  (Correct)

₂₉Cu $\Rightarrow$ 1s²2s²2p⁶3s²3p⁶3d⁹4s²  (Wrong)

         $\Rightarrow$1s²2s²2p⁶3s²3p⁶3d¹⁰4s¹ (Correct)

Similarly the following elements have slightly different configurations than expected.

Nb   $\Rightarrow$ [Kr] 4d4.5s1 Mo  $\Rightarrow$ [Kr] 4d5.5s1 Ru  $\Rightarrow$ [Kr] 4d7.5s1 Rh  $\Rightarrow$ [Kr] 4d8.5s1

Pd    $\Rightarrow$  [Kr] 4d10.5s0 Ag    $\Rightarrow$  [Kr] 4d10.5s1 Pt     $\Rightarrow$  [Xe] 4f14.5d9, 6s1 Au    $\Rightarrow$  [Xe] 4f14.5d10,6s1

 Exceptional configuration and stability of atoms:

Chromium and copper show exceptional configuration to gain the extra stability.  The half filled and completely filled degenerate orbitals in an atom give it greater stability because of more symmetrical distribution of electrons and higher exchange energy.

i) Symmetrical distribution: For example the expected electronic configuration of chromium is ₂₄Cr – [Ar] 3d⁴ 4s²

ii) Exchange energies: The electrons with parallel spins present in degenerate orbitals tend to exchange their position. The energy released during such exchange is called exchange energy.  Such exchanges can be maximum only when the degenerate orbitals are exactly half filled or completely filled.  Greater is the exchange energy greater is the stability of atom.

Magnetic properties of atoms:

All the atoms which consist of at least one orbital singly occupied, behave as paramagnetic while all those having doubly occupied orbitals are diamagnetic in nature.

$\text{ magnetic moment }\left(\mu \right)=\sqrt{n(n+2)}$B.M.

where n = no. of unpaired electrons, BM = Bohr magneton

The calculated magnetic moments for some metal ion are given in the table as

Metal Ions	n	$\mu$cal (BM)	$\mu$ex (BM)
Sc3+	0	0	0
Ti3+	1	1.73	1.7  – 1.8
Cu2+	1	1.73	1.9 – 2.1
Cr2+	4	4.9	4.8 – 4.9

Illustration 15:.  Predict the magnetic moment of Cu²⁺ ion.

Solution: E.C. of Cu²⁺ = [Ar] 3d⁹

Hence, Cu²⁺ has one unpaired e^–

$\therefore \mu =\sqrt{n(n+2)}=\sqrt{1(1+2)}=1.73BM$

FORMULAE AND CONCEPTS AT A GLANCE

1. $\begin{array}{l}\text{(i) }c=v\lambda \hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\text{ (ii) }u=1/\lambda \hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\text{ (iii) }\overline{v}=v/c\end{array}$

2. $E=hv\text{ also }E=\frac{hc}{\lambda }$, h = Planck’s constant = $6.6\times {10}^{-34}\mathrm{Js}$

3. ${\mathrm{E}}_n=\frac{-2{\pi }^2{\mathrm{me}}^4{\mathrm{Z}}^2}{{\mathrm{n}}^2{\mathrm{h}}^2}{\mathrm{E}}_n=\frac{-13.6}{{\mathrm{n}}^2}{\mathrm{Z}}^2 \mathrm{eV}{\text{ atom }}^{-1}$

4. Frequency, $v=R{Z}^2\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right]$

    Wave number $\overline{v}=R^{\mathrm{\prime }}{Z}^2\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right]=109678{\mathrm{cm}}^{-1}$

5. Radius of nth orbit, $r_n=\frac{{\mathrm{n}}^2{\mathrm{h}}^2}{4{\pi }^2\mathrm{m}{\mathrm{KZe}}^2}=\frac{{\mathrm{n}}^2}{\mathrm{Z}}\times 0.529\mathrm{A}$

6. Velocity in nth orbit, $v_n=\frac{2\pi {\mathrm{KZe}}^2}{\mathrm{nh}}=2.188\times {10}^6\times \frac{\mathrm{Z}}{\mathrm{n}}{\mathrm{ms}}^{-1}$

7. de-Broglie’s equation, $\lambda =\frac{n}{mv}=\frac{n}{p}$

8. Heisenberg’s Uncertainty Principle $\mathrm{\Delta }x\cdot \mathrm{\Delta }p\ge \frac{h}{4\pi } \text{ or }\mathrm{\Delta }E\times \mathrm{\Delta }t\ge \frac{h}{4\pi }$

9. Magnetic moment (spin only), $\mu =\sqrt{n+(n+2)}$ Bohr magnetons

10. $\frac{{\mathrm{\partial }}^2\psi }{{\mathrm{dx}}^2}+\frac{{\mathrm{\partial }}^2\psi }{\mathrm{\partial }{\mathrm{y}}^2}+\frac{{\mathrm{\partial }}^2\psi }{\mathrm{\partial }{\mathrm{z}}^2}+\frac{8{\pi }^2\mathrm{m}}{{\mathrm{h}}^2}(\mathrm{E}-\mathrm{V})\psi =0$

11. Electrons, protons and neutrons are called subatomic particles.

12. Protons and neutrons are present in the nucleus and electrons revolve around it.

13. J.J.Thomson’s atomic model placed the electron inside the nucleus. This could not explain the atomic spectra.

14. Rutherford proposed ‘planetary model’ for atoms basic on his a-ray scattering experiments.

15. According to Rutherford’s model, electrons are subjected to two types of forces viz., the force of attraction between electrons and the nucleus and the centrifugal force. These two forces are equal and opposite.

16. Max Planck proposed quantum theory of radiation.

17. Energy, E is given by $E=hv$ .

18. Bohr proposed his atomic model based on the Planck’s quantum theory.

19. According to Bohr model, electrons are revolving in specified paths called “stationary orbits or stationary shell”. The energy of these shells is constant.

20. The stationary states are designated by K, L, M, N, O, ……..

21. When an electron jumps from a higher orbit (higher energy) to lower orbit (lower energy), energy is liberated.

22. The angular momentum of electron is equal to integral multiples of h/2p.

23. Bohr calculated the radii and energies of various orbits of hydrogen atom.

24. Bohr’s model is applicable for species containing one electron only (ex. H, He⁺, Li²⁺ etc)

25. Sommerfeld proposed the elliptical orbits.

26. Stationary state is indicated by principal quantum number ‘n’ and sub-stationary states by azimuthal quantum number l.

27. The principal quantum number n can take values 1, 2, 3, 4, …..

28. Principal quantum number gives the size and energy of stationary orbits.

29. Azimuthal quantum number (l) gives the shape of sub-shell or orbital.

30. Magnetic quantum number is proposed by Lande’ and designated as m.

31. Spin quantum number (s), can take only + 1/2 or -1/2 values.

32. The region in space where there is finite probability of finding electron is called ‘atomic orbital’.

33. s orbital is spherically symmetric, p orbital dumb-bell shaped and d orbital has double dumb-bell shape.

34. Aufbau principle states that electron occupies the orbital having the least energy.

35. Orbitals having same energy are called ‘denerate’ orbitals.

36. Hund’s rule state that pairing of electrons takes place when all the available degenerate orbitals are occupied by one electron each.

37. Pauli exclusion principle states that no two electrons will have all the four quantum numbers same.