Work Power Energy

Work

4.1. PHYSICAL UNDERSTANDING
In our day – to – day life, the transfer of energy plays a major role. To understand this, let’s imagine for a moment that no energy transfer takes place in the world.
Observe the following examples.
1. If there is no energy transfer from the Sun to the Earth, then life will not exist.
2. If there is no sound energy transfer, then people cannot hear.
3. If there is no energy transfer in automobiles, then there will be no transportation.
4. If there is no transfer of energy from our food our food to our body, then we will do not survive similarly the list goes on.
From the above examples, it is clear that transfer of energy from one point to another, or form one body to another, we require someone or something. If there is no energy transfer, probably nothing will work in the universe. Overall,
we say that, to transfer the energy from one body to another, we required mediators like wave, force, etc. In mechanical situations, energy transferred by a force form one body to another is what we call work done by that force.
But, in Physics, work is said to be done only when a body moves a body moves under the influence of a ‘force’. If there is no motion produced in the body even when a force acts on it, the work done is said to be zero. Let us now define it.
Work is said to be done by a force on a body, when the force displaces the body through a certain distance in the direction or against the direction of the force.

4.2. MEASUREMENT OF WORK
The amount of work done by a body depends upon.
(i) the magnitude of the force (F) and        (ii) the displacement of the body (S).
So, by knowing the force and displacement, we can measure the work done.
The amount of work done is equal to the product of the fore and the displacement of the body from the point of application of the force, in the direction of force.

$\boxed{\mathrm{Work} = \mathrm{Force} \mathrm{displacement} \mathrm{of} \mathrm{the} \mathrm{body}}$

Nature of the quantity: Even though force and displacement are vectors, work is a scalar quantity. Work is independent of time.

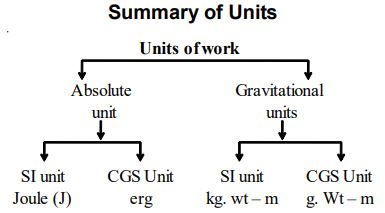
4.3. UNITS WORK
The work has following units:
Absolute units: SI unit: joule (J)
                                 CGS unit: erg
Joule: The work done is said to be 1 joule, if 1N of the force displaces the body through 1m in the direction of the force.
Erg: The work done is said to be 1 erg, if 1dyne of the fore displaces the body through 1cm in the direction of the force.
Other than these units, work also has units called ‘gravitational units’.
Gravitational units: SI unit: kg.wt-m
                                           GS unit: g.wt-cm
Relation between joule and erg:
We know that, 1J = 1newton × m
But, 1 newton = 105 dyne and 1 metre

$\text{ But, }1\text{ newton }={10}^5\text{ dyne and }1\text{ metre }={10}^2\mathrm{m}$

$\begin{array}{l}\Rightarrow 1\mathrm{J}={10}^5\text{ dyne }\times {10}^2\mathrm{cm}\\ \Rightarrow 1\mathrm{J}={10}^7\text{ dyne }-\mathrm{cm}\\ \Rightarrow 1\mathrm{J}={10}^7\text{ erg }(\because 1\text{ erg }=1\text{ dyne }-\mathrm{cm})\end{array}$

1 kg. wt – m = 9.8 N – m = 9.8J
1 g. wt – cm = 980 dyne – cm or 980 erg

4.4. DIFFERENT EXPRESSIONS TO CALCULATE THE MAGNITUDE OF WORK
The magnitude of work done mainly depends on the magnitude of force and displacement. The different possibilities are as follows:
1. Both force and displacement are in same direction.
2. Both the directions of displacement and force are opposite to each other.
3. The direction of fore makes an angle with direction of displacement.
4. Work done against gravity.
Work done when Force and displacement in same direction
Work done when fore and displacement are in the same direction Consider a body at point ‘A’. It reaches the point ‘B’ when a force ‘F’ is applied, such that the displacement of the body in the direction of force is ‘S’.

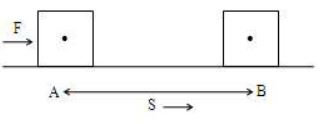
Thus

$$\begin{gathered} \boxed{Work done \left(W\right) = Force\left(F\right)displacement\left(S\right) in same direction \\ W = F S} \end{gathered}$$

Note:
i) The above formula should be applied only if the direction of force and displacement are the same.
ii) The work done by a body is zero, if fore is acting and displacement is zero.
iii) As direction of displacement and direction of force are the same, work done is said to be positive.
Example
When a lawn roller pushed by a person to level the pitch of a cricket ground, the force does the work, since the roller displaces in the direction of the force applied by the person.
Work done when the force and displacement are in opposite direction

Consider a moving car. Try to stop the car by applying some force ‘F’. We observe that the car comes to rest after travelling some distance ‘S’ opposite to the direction of force. In this case, the fore ‘F’ is applied opposite to the direction of the motion or displacement of the car. Therefore, the displacement is taken as ‘–S’.

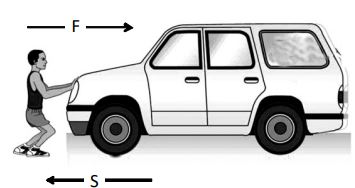
Thus

 $$\begin{gathered} \boxed{Work done \left(W\right) = Force acting Displacement in opposite direction. \\ W = F (–S) = –FS} \end{gathered}$$

Note:
As direction of displacement and direction of fore are opposite to each other, work done is said to be negative.
Work done by a force that makes an angle with the direction of displacement
We have seen that whenever work is done, a body displaces in the same direction or in opposite direction of the force applied.
But, in some cases, the body moves in a direction that makes an angle with the direction of the applied force of the body which is horizontal to the surface of the ground as shown in the figure.

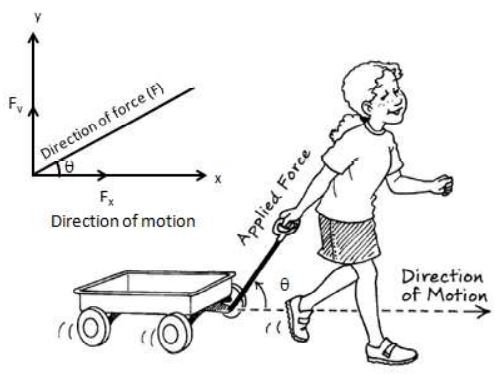
The toy car moves along the horizontal ground surface ‘OX’, but, the fore is along the string ‘OA’. Thus, the direction of force makes an angle ‘ $\theta$ ’ with the direction of the motion.
In such cases, we cannot use the formula, W = F × S to calculate the work done, as the displacement ‘S’, is not exactly in the direction of the force applied. Therefore, we need to know the magnitude of force in the direction of motion of the body. Let us try to find the magnitude of force (F) that acts horizontally.
As force is a vector quantity and makes some angle with the horizontal, it can be resolved into two components (parts) as shown in the figure:
i) One component along the direction in which the body moves, called horizontal component of force ($F_H$).
ii) And the other component acting perpendicular to the horizontal i.e., vertically upwards called vertical component ($F_V$).
The vertical component tries to lift the body, but does not actually lift it. Therefore the vertical component does no work as there is no displacement vertically upwards.
The work is done only by the horizontal component of force ($F_H$), as the body moves in horizontal direction. $F_H$ can be expressed in terms of F and $\theta$as follows:
From the figure,

$\begin{array}{l}\mathrm{Cos}\theta =\frac{\text{ Adjacent side }}{\text{ Hypotenuse }}=\frac{\mathrm{OX}}{\mathrm{OA}}=\frac{{\mathrm{F}}_{\mathrm{H}}}{\mathrm{F}}\\ \therefore \mathrm{Cos}\theta =\frac{{\mathrm{F}}_{\mathrm{H}}}{\mathrm{F}}\Rightarrow {\mathrm{F}}_{\mathrm{H}}=\mathrm{FCos}\theta \end{array}$

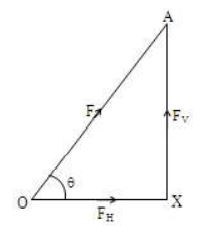
Here, work done is measured as product of magnitude of component of force, along the direction of displacement and magnitude of displacement.
Thus,

$$\begin{gathered} \boxed{Work \left(W\right) = Magnitude of component of force displacement of the body \\ \therefore W = F Cos\theta S = FS Cos\theta } \end{gathered}$$

$\mathbf{\text{Note}}\text{: }\mathrm{Cos}{0}^{\circ }=1,\mathrm{Cos}{30}^{\circ }=\frac{\sqrt{3}}{2},\mathrm{Cos}{45}^{\circ }=\frac{1}{\sqrt{2}},\mathrm{Cos}{60}^{\circ }=\frac{1}{2}\text{ and }\mathrm{Cos}{90}^{\circ }=0$

Work done against gravity
Consider a book or an object lifted from a table, we do work against the force of gravity.
Whenever work is done against gravity, the force required to lift the body is equal to its weight. Therefore, the amount of work done is equal to the product of weight of the body and the body and the vertical distance through which the body is lifted.

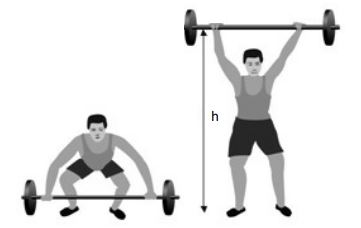
Suppose a body of mass ‘m’ is lifted vertically upwards through a distance ‘h’, then the force required to lift the body will be equal to the weight of the body, m × g, where ‘g’ is acceleration due to gravity.

Thus

$$\begin{gathered} \boxed{Work done by the person in lifting a body \left(W\right) = weight of the body vertical distance \\ W = mgh} \end{gathered}$$

Note:
When work is done against gravity ‘acceleration due to gravity’ is taken as ‘–g’. The magnitude of work is always positive.
Example: When a suitcase is lifted from the ground to some height, work is done against gravity.
4.5. SOME EXAMPLES OF ZERO WORK
1. Consider a person standing in front of a wall, trying to push it. He is unable to move it. Here, displacement of the wall is zero. Hence, no work is done by him.
2. A coolie standing with a heavy load on his head does no work, although he feels tired, as his displacement is zero.
3. Work done by the Sun to move the Earth:
In the case of the Earth revolving round the Sun, the direction of the force and the direction of displacement is as shown in the figure.

Observe that the angle $\theta ={90}^0$

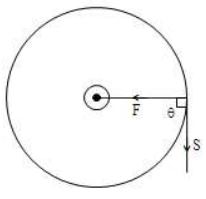
We know, when force makes an angle with displacement, work done is
W = FS Cos $\theta$

$\begin{array}{l}\text{ We get, }W=F\times S\times \mathrm{Cos}{90}^{\circ }\\ \text{ As }\mathrm{Cos}{90}^{\circ }=0\\ W=F\times S\times 0\\ \Rightarrow W=0\end{array}$ 

Therefore, work done by the Sun to move the Earth is zero.
4. Work done by a porter in carrying a load
In the case of a porter carrying a load and moving, the direction of fore (weight of the load) and displacement are as shown in figure:

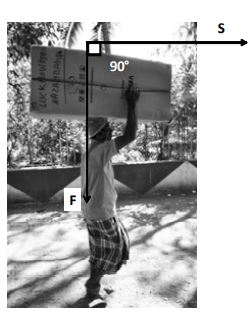
Observe that $\theta$= 90°
We know that when force makes an angle with displacement, work done is $\mathrm{W}=\mathrm{FSCos}\theta =\mathrm{FSCos}{90}^{\circ }$

$$\begin{gathered} \mathrm{Substituting} \mathrm{Cos}{90}^{\circ }=0 \\ \mathrm{Weget}, W=F\times S\times 0 \\ \Rightarrow W=0 \end{gathered}$$

Therefore, work done by a porter in carrying the load, by moving horizontally, is zero.
From the above examples, we can conclude that.
The work is said to be zero
i) If the force alone acts and there is no displacement.
ii) If both force and displacement are perpendicular to each other

ENERGY

4.6. INTRODUCTION TO ENERGY
Have you ever heard the caption of “Boost” advertisement, the caption being ‘Boost is
the secret of energy”? This word ‘energy’ is very often used in our day-to-day life. For
instance, if a man does laborious work or if a child works energetically, we say that he
is full of energy. Much the similar way, in physics, too anything that has the ability to
do work is said to possess energy.

Definition: Energy can be defined as the capacity to do work.
Let us take an example, for our better understanding. A stone cutter raises his hammer
vertically above the stone and then hits it to break into small pieces. In doing so, he
does some work in raising the hammer. If the hammer is allowed to fall on the stone, it
can do work in breaking the stone.
Thus, the work done in raising the hammer has been stored up in it, giving it the ability
of doing work. Now, when the hammer is resting on the stone, it can no longer do any
work. Thus, we can say that the raised hammer has the energy or ability to do work. The amount of energy possessed by a body is equal to the amount of work it can do when its energy is released.

4.7. MEASURING FORMULA AND UNITS
As energy is the capacity to do work, its measuring formula is same as that of the work done.
Energy of a body (E) = Work done (W) of the same body.
Units: SI unit: joule
             CGS unit :erg
[Energy is the capacity to do work. Hence, its units are same as that of work.]

4.8. FORMS OF ENERGY
There are many forms of energy such as:
Heat energy, electrical energy, chemical energy, light energy, magnetic energy, nuclear energy, sound energy, mechanical energy, etc. All these energies are interchangeable.
Mechanical Energy: The energy possessed by a body due to its state of rest or of motion is called “Mechanical energy”
Example: A falling stone has mechanical energy.
The mechanical energy is found in two forms: Kinetic energy and Potential energy

4.9. KINETIC ENERGY
Have you ever thrown a stone against a glass window? What happens if you do so?
As the stone hits the glass, it breaks into pieces. Why does glass break inot pieces? When you throw the stone, it sets into motion, acquiring some velocity. As a result, some energy is stored by the moving body (stone). This energy results in breaking of the window, when stone strikes it. Here, the body possesses energy as a result of its motion. This energy is called Kinetic energy.
Kinetic energy can be defined as energy possessed by an object by virtue of its motion.
Examples of Kinetic energy:
i) Energy possessed by a moving bicycle.   ii) Energy possessed by running water of a river.

Mathematical Expression for K.E.
Consider a boy of mass ‘m’ at rest. When a force is applied, it sets into motion and acquires a velocity after travelling a distance of ‘S’.

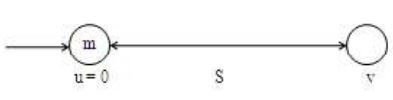
Force = ma, where ‘a’ is the acceleration of the body.
In this case, kinetic energy is measured by the amount of work done by the force to acquire the velocity.
$\Rightarrow$K.E. = Force × Displacement = ma × S —– (1)

$\text{ We know, }{v}^2-u^2=2aS\Rightarrow a=\frac{v^2-u^2}{2S}$

substituting the above value in (1), we get

$\begin{array}{l}\text{ Kinetic energy }=\mathrm{m}\times \frac{{\mathrm{v}}^2-0^2}{2\mathrm{S}}\times \mathrm{S}\\ \mathrm{K}.\mathrm{E}=\frac{{\mathrm{mv}}^2}{2}\text{ (or) }\frac{1}{2}{\mathrm{mv}}^2\\ \text{ Kinetic Energy }=\frac{1}{2}\times \mathrm{mass}\times (\text{ velocity }{)}^2\end{array}$

Thus, the kinetic energy of the body is equal to half of hte product of its mass and square of the velocity of the body.
We see that kinetic energy of a body is directly proportional to the square of the velocity and mass of the body.
i) K.E. $\propto$ mass of the body ‘m’
$\Rightarrow$ Larger the mass of the body, greater its K.E.
ii) Also K.E. $\propto$ $v^2$
$\Rightarrow$ If velocity of a body is doubled, then its K.E. also gets increased by four times.
Relation between momentum and kinetic energy
Consider a body of mass ‘m’ moving with velocity ‘v’
We know, Momentum = mass × velocity 

$\Rightarrow p=m\times v –––\left(1\right)$

$$\begin{gathered} \text{ Kinetic energy }=\frac{1}{2}\times \text{ mass }\times {\text{ velocity }}^2 \\ \Rightarrow \mathrm{K}.\mathrm{E}=\frac{1}{2}\times \mathrm{m}\times {\mathrm{v}}^2 –––––\left(2\right) \end{gathered}$$

On multiplying and dividing the R.H.S of eq(2)by ‘m’ in , we get $\mathrm{K}.\mathrm{E}=\frac{{\mathrm{m}}^2\times {\mathrm{v}}^2}{2\mathrm{m}}=\frac{(\mathrm{mv}{)}^2}{2\mathrm{m}}$

But, from equation (1), p = mv 

$\therefore \mathrm{K}.\mathrm{E}=\frac{{\mathrm{p}}^2}{2\mathrm{m}}$

Work – Energy Theorem
Let a body of mass ‘m’ move with a velocity u m/s. Let a force (F) act on it in the direction of motion. This increases the velocity of the body to ‘v’m/s.

Let the displacement of the body be ‘S’ m
Selection of the formula: ${\mathrm{v}}^2-{\mathrm{u}}^2=2\mathrm{aS}\Rightarrow \mathrm{a}=\frac{{\mathrm{v}}^2-{\mathrm{u}}^2}{2\mathrm{S}}$

Let us now calculate the force acting one the body.
Force = mass × acceleration $=m\left(\frac{v^2-u^2}{2S}\right)$

We know work done, W = Force × displacement $=\mathrm{m}\left(\frac{{\mathrm{v}}^2-{\mathrm{u}}^2}{2\mathrm{S}}\right)\times \mathrm{S}=\mathrm{m}\left(\frac{\mathrm{v}-{\mathrm{u}}^2}{2\mathrm{S}}\right)=\frac{{\mathrm{mv}}^2}{2}-\frac{{\mathrm{mu}}^2}{2}$

Thus, we conclude that ‘work done on a moving body is equal to the change in its kinetic energy’. This is known as work energy theorem.
4.10. POTENTIAL ENERGY
Consider the following to understand potential energy:
Place a small black of wooden piece before a compressed spring. Release the spring and see what happens. Obviously, the block will be pushed to a certain distance.

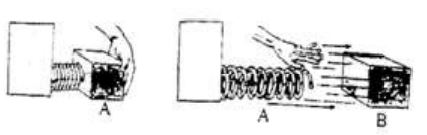
Repeat the same exercise in case of spring with its natural length (i.e., non compressed spring). we observe that, there will be no change in the position of the block.

From the above, we understand that spring in compressed state has stored some energy and has capacity to deliver work.
Potential energy can now be defined as “energy possessed by body, due to the virtue of its position”.
Examples:
1. Energy possessed by a body lying at certain height, above the ground.
2. Energy possessed by a stretched bow or by a stretched string.

Mathematical Expression for potential energy
Consider a body of mass ‘m’ lifted to a height ‘h’, against gravity from a point A to a point B.
Force required to lift the body, ‘F’ = weight of the body

$\Rightarrow \mathrm{F}=\mathrm{m}\times \mathrm{g}$   ——-(1)

At distance moved by the body ‘S’ = h
Work done (W) = F × S = mg × h [ using (1)]

$\Rightarrow \mathrm{W}=\mathrm{mgh}$   ——–(2)

This work done is stored in the form of energy, called “Potential energy”

$\Rightarrow \mathrm{W}=\mathrm{P}.\mathrm{E}.=\mathrm{mgh}$

Therefore, Potential energy = mgh
Note:
i) The potential energy of a body lying on the surface of earth is taken as zero.
ii) The potential energy of the body decreases as it falls towards the surface of the earth.
iii) The potential energy of the body increases as the height of the body form the surface of the earth increases.
The other forms of energy are light energy, heat energy, chemical energy, magnetic energy, nuclear

4.11. LAW OF CONSERVATION OF ENERGY
The energy can neither be created, nor can it be destroyed. It may be transformed from one form to another form, but the total energy of the system remains constant.
Furthermore, we may say that sum total of energy in this universe is a constant quantity. It cannot be created, nor can it be destroyed, no matter it can change its form, provided the universe is considered as single system.
Mathematical Explanation
Case 1: Consider a stone of mass ‘m’ held at a height ‘h’ from the ground level, such that ‘g’ is the acceleration due to gravity, as illustrated by the position A.
At position A:

$$\begin{gathered} \mathrm{PE}=\mathrm{mgh},\mathrm{KE}=\frac{1}{2}{\mathrm{mv}}^2=\frac{1}{2}\mathrm{m}(0{)}^2=0 \\ \therefore \text{ Total energy }=\mathrm{PE}+\mathrm{KE}=\mathrm{mgh}+0=\mathrm{mgh} \dots ...\left(i\right) \end{gathered}$$

Case 2: Consider the stone at point B, during its free fall, such that it falls through a
height ‘x’ and has a velocity v.

$\text{ Applying, }{\mathrm{v}}^2-{\mathrm{u}}^2=2\mathrm{aS},\text{ we get }{\mathrm{v}}^2=2\mathrm{gx}$

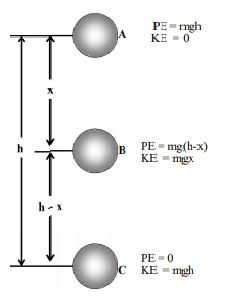
At position B:

$\begin{array}{l}\mathrm{KE}=\frac{1}{2}{\mathrm{mv}}^2=\frac{1}{2}\mathrm{m}\times 2\mathrm{gx}=\mathrm{mgx}\\ \mathrm{PE}=\mathrm{mg}(\mathrm{h}-\mathrm{x})=\mathrm{mgh}-\mathrm{mgx}\end{array}$

$\therefore$Total energy at B = PE + KE = mgh – mgx + mgx = mgh ….. (ii)

Case 3: Consider-the stone at point C, during its free fall, such that it reaches the surface of earth. Let v be its velocity.
Applying ${\mathrm{v}}^2-{\mathrm{u}}^2=2\mathrm{aS}$

$\Rightarrow {\mathrm{v}}^2-(0{)}^2=2\mathrm{gh}\Rightarrow {\mathrm{v}}^2=2\mathrm{gh}$

At position C:

$\begin{array}{l}\mathrm{KE}=\frac{1}{2}{\mathrm{mv}}^{\mathrm{\prime }}=\frac{1}{2}\mathrm{m}\times 2\mathrm{gh}=\mathrm{mgh}\\ \mathrm{PE}=\mathrm{mg}\left(0\right)=0\end{array}$

$\therefore$Total energy at B = PE + KE = mgh + 0 = mgh ……… (iii)

From the above discussion it can be concluded:
1. Sum total of energy in the system of the stone and the Earth is a constant quantity at all points.
2. The potential energy changes to kinetic energy.
3. Conversely, if the stone is projected upwards, the kinetic energy will change to potential energy.
Dissipation of Energy
When a body falls from a height and strikes the ground, it may come to rest or rebound. If it comes to rest, the whole of its energy is converted into heat and sound energy. These energies are diffused into the surrounding space. They cannot be further utilized for doing any useful work. Thus, the energy is transformed from a useful form to a useless
form.
However, when on striking the ground, the body begins to rebound, the height to which it rebounds decreases every time and ultimately, it comes to rest.
A part of its energy changes into heat and sound energies in every rebound and ultimately the body comes to rest and rebounds no more. The heat and sound energies thus formed, are diffused into the surrounding space. The phenomenon of transformation of the energy, from the useful form to the useless form, is known as dissipation of energy.
Examples of inter-conversion of energy
1. When hands are rubbed, the mechanical energy due to friction changes into heat energy.
2. When two stones are struck, the mechanical energy changes into heat and light energy.
3. When a knife is rubbed against grinding stone, the mechanical energy changes to the heat, light and sound energy.
4. When the brakes are applied, the mechanical energy changes into heat energy at the point where the brakes rub against the moving wheel.
5. When a watch is wound, the mechanical energy changes into potential energy of the spring. When the spring unwinds the potential energy changes into kinetic energy. this drives the hands of the clock.
6. When an arrow is stretched in a bow, the mechanical energy changes into potential energy. On releasing the string, the potential energy changes into kinetic energy of the arrow.
7. The water stored in dams has potential energy. When this water is released, it changes kinetic energy of the flowing water. The kinetic energy of the flowing water turns blades of the turbine and changes into mechanical energy. The mechanical energy of the turbine drives the dynamo and changes into electrical energy.
8. When a torch is switched on, the chemical energy changes into electrical energy. The electrical energy on flowing through the filament of the bulb changes into heat and light energy.
9. The electrical energy in an electromagnet changes into magnetic energy.
10. The electrical energy flowing through an electric motor or fan changes into mechanical energy. It partly changes into heat energy.
11. The sound energy in a microphone changes into electrical energy.
12. The electrical energy changes into sound energy, while flowing through the speaker,
13. In an electric heater, electric oven, electric geyser, etc., the electrical energy changes into heat energy.

14. In the steam engine the heat energy of the steam changes into mechanical energy.
15. In an electric generator, the mechanical energy changes into electrical energy.
16. In photovoltaic cell, the light energy changes into electrical energy.
17. In television, the electrical energy changes into sound and light energy.
18. When fuels are burnt, the chemical energy of the fuels changes into heat energy.
19. When match head strikes against the side of a match box, due to friction, the chemical energy changes into heat and light energy.
20. When a cracker is exploded, the chemical energy changes into heat, light and sound energy
21. During the photosynthesis, the light energy changes into chemical energy.
22. During charging of a battery, the electrical energy changes into chemical energy.
23. During respiration, the chemical energy of the food changes into heat energy. It is the heat energy which keeps our bodies warm. It is the heat energy which changes into mechanical energy when we do locomotion.
24. During nuclear fission or fusion, it is the nuclear energy, which ultimately changes into heat and light energy.
25. During the pumping up of water in an overhead tank by an electric motor pump, the electrical energy changes into kinetic energy of the water. The kinetic energy of the water, changes into potential energy.

POWER

4.12. INTRODUCTION TO POWER
The quantity of work has to be done with a force causing a displacement. Work has nothing
to do with the amount of time in which this force acts to cause the displacement. Sometimes,
the work is done very quickly and at other times the work is done rather slowly. For example, a rock climber takes an abnormally long time to elevate his body up a few meters along the side of a cliff. On the other hand, a trail hiker (who selects the easier path up the mountain) might elevate his body a few meters in a short time. The two people might do the same amount of work, yet the hiker does the work in considerably less time than the rock climber. The quantity which has to do with the rate at which a certain amount of work is done is known as the power. The hiker has a greater power rating, than the rock climber.
Power is defined as is the rate at which work is done.
4.13. MEASUREMENT OF POWER
The amount of power of a body depends upon.
i) The magnitude of the work and
ii) The time taken by the body.
So by knowing the work and time, we can measure the power. The amount of power is the ratio of work and time.

$\boxed{\text{ Power }=\frac{\text{ Work }}{\text{ Time }}}$

4.14. UNITS OF POWER
i) CGS unit: $erg s^{–1}$ .
ii) SI unit: $J{s}^{–1}$ or watt (W)
$\therefore$ The SI unit of power is watt and is defined as follows:
Watt: If 1 joule of work is done in 1 second, then the power is said to be 1 watt.

$1\text{ watt }=\frac{1\text{ joule }}{1\text{ sec ond }}$

iii) Bigger units of power: The bigger units of power are kW and MW.
1 kilo watt (kW) = 1000 W
1 Mega watt (MW) = ${10}^6$ W
iv) Practical unit of power: The widely used practical unit of power is Horse – power(hp)
1 hp = 746 = 0.746 kW

Horse power
The idea of horsepower persists as a legacy term in many languages, particularly in the automotive industry, for listing the maximum rate of power application of internal – combustion engines.
Horsepower is defined as work done over time. The exact definition of one horsepower is 33,000 1b.ft./minute. Put another way, if you were to lift 33,000 pounds one foot over a period of one minute, you would have been working at the rate of one horsepower.

Electrical unit of energy
The electrical unit of energy is Kilowatt – hour (kWH). The electric bill which we get monthly is always in terms of units.
Example: If our electricity bill shows 50 units, it means the electrical appliances of our house had consumed 50 kWs.
$\Rightarrow$ 1 unit = 1k WH
Thus, kWH is the amount of electric energy used by 1000 W electrical appliances, when they operate for 1 hour.
$\therefore$ 1kWH = 1000 WH
Relation between kWH and Joule:
1 k WH = 1000 WH –––––– (1)($\therefore$ 1kW = 1000W)
As we know that, 1W = 1$J{s}^{–1}$ and
1hr = (60 × 60)s = 3600
Substitute the above values in (1), we have
1k WH = 1000 WH = 1000 × 1$J{s}^{–1}$ × 3600 s = 3.6 × ${10}^6$J

1k WH = 3.6 × ${10}^6$J

4.15. DIFFERENT EXPRESSIONS TO CALCULATE THE MAGNITUDE OF POWER
1. Power to move a body
Consider a force ‘F’ acting on a body that is displaced in the direction of force by a distance ‘S’.

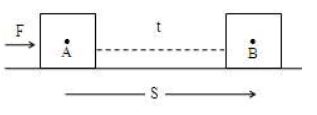
Then the power is given by the following expression:

$\begin{array}{l}\text{ Power }\left(\mathrm{P}\right)=\frac{\text{ Workdone }\left(\mathrm{W}\right)}{\text{ Time }\left(\mathrm{t}\right)}=\frac{\text{ Force }\left(\mathrm{F}\right)\times \text{ displacement }\left(\mathrm{S}\right)}{\text{ Time }\left(\mathrm{t}\right)}\\ \Rightarrow \mathrm{P}=\frac{\mathrm{FS}}{\mathrm{t}}\\ \text{ Formula: Power }=\frac{\mathrm{FS}}{\mathrm{t}}\end{array}$

2. Power to stop a moving body
Consider a force ‘F’ acting on a body against the direction of the motion of the body. The body is stopped in time ‘t’ after travelling through a distance ‘S’.

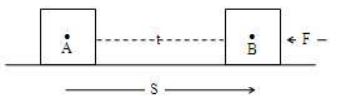
Then, the power used to stop the body can be obtained by the following expression.

$\begin{array}{l}\mathrm{Power}\left(P\right)=\frac{\text{ Workdone }\left(\mathrm{W}\right)}{\text{ Time }\left(\mathrm{t}\right)}=\frac{\text{ Force }\left(\mathrm{F}\right)\times \text{ displacement }\left(\mathrm{S}\right)}{\mathrm{Time}\left(\mathrm{t}\right)}\\ \Rightarrow \mathrm{P}=\frac{-\mathrm{FS}}{\mathrm{t}}\\ \text{ Formula: Power }=\frac{-\mathrm{FS}}{\mathrm{t}}\end{array}$

Note: –ve sign indicates the power is used against the direction of motion of the body.

3. Power to pull a body
Consider a force ‘F’ acting in the direction that makes an angle ‘ $\theta$’ with the direction of the motion.

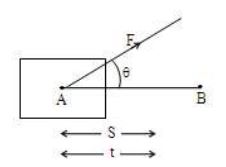
If ‘S’ is the distance travelled by the body in time(t), then power used by the body can be calculated by the following expression:

$\text{ Power }\left(P\right)=\frac{\text{ Workdone }\left(\mathrm{W}\right)}{\text{ Time }\left(\mathrm{t}\right)}$

$\text{ Formula: Power }=\frac{\text{ FS }\mathrm{Cos}\theta }{t}$

4. Power to lift a body against gravity
Consider a mass ‘m’ lifted from the surface to a height ‘h’ against gravity. If ‘t’ is the time taken to lift the body, then the power can be calculated by the following expression:

$$\begin{gathered} \text{ Power }\left(\mathrm{P}\right)=\frac{\text{ Workdone }\left(\mathrm{W}\right)}{\text{ Time }\left(\mathrm{t}\right)} \\ =\frac{{\displaystyle \text{ Force used against gravity }\left(\mathrm{W}\right)\times Dis \tan e through which it is lifted h}}{{\displaystyle \text{ Time }\left(\mathrm{t}\right)}} \end{gathered}$$

$\mathbf{\text{Formula:}}\text{ Power}=\frac{\mathrm{mgh}}{\mathrm{t}}$

5. Power of a body moving with velocity
Consider a body moving with a speed or velocity of ‘v’ m/s. If ‘F’ is the force applied to stop the body, then the power of the body is given by the following expression:

$$\begin{gathered} \mathrm{Power}\left(P\right)=\frac{\text{ Workdone }\left(\mathrm{W}\right)}{\mathrm{Time}\left(\mathrm{t}\right)}=\frac{\text{ Force }\left(\mathrm{F}\right)\times \text{ displaement }\left(\mathrm{S}\right)}{\mathrm{Time}\left(\mathrm{t}\right)} \\ \Rightarrow P=\frac{\mathrm{FS}}{\mathrm{t}} \\ \Rightarrow \mathrm{P}=\mathrm{F}\times \frac{\mathrm{S}}{\mathrm{t}} \left(\because \mathrm{v}=\frac{\mathrm{S}}{\mathrm{t}}\right) \\ \mathit{F}\mathit{o}\mathit{r}\mathit{m}\mathit{u}\mathit{l}\mathit{a}\mathbf{:}\mathrm{Power} =\mathrm{Fv} \end{gathered}$$